渗透测试是一种针对信息系统实施的授权模拟攻击,旨在寻找威胁其安全的脆弱点,以便对其安全性进行评估。传统渗透测试过程过于依赖渗透测试人员的经验和操作,成本较高,而自动化渗透测试技术的出现在一定程度上缓解了传统渗透测试的不足。
强化学习(reinforcement learning, RL)是机器学习的一个分支,其灵感来源于心理学中的行为主义理论[1],涵盖了概率论、统计学、逼近论、凸分析、计算复杂性理论、运筹学等多领域的知识,是与人类学习最相似的一种学习形式[2]。Kröse[3]设计的Q-learning算法是诸多强化学习算法中的一种,能够在处理MDP问题时找到最优的动作选择策略,其Q值更新不受动作选择策略的影响,与通过值函数间接求解最优策略相比,策略梯度方法可以直接对收益函数求导来获得最优的梯度方向。Srinivasan等[4]提出了actor-critic算法,通过引入优势函数,进一步提高了训练的稳定性。Kang等[5]在actor-critic算法的基础上引入了多线程,提出了A3CC算法,多个线程可以同时学习最优策略,从而加快了训练的收敛速度。
近年来,强化学习算法被广泛应用于自动化渗透测试领域,主要用于探索自动化渗透测试的攻击路径。相关研究[6-9]设计了一种使用强化学习的自动化渗透测试方法,对网络进行渗透测试,可在一定程度上节省人力资源。Schwartz等[10]提出了一种基于部分可观测马尔可夫决策过程(partially observable Markov decision process, POMDP)的自动化渗透测试框架,主要解决渗透测试过程中网络拓扑变化引发的问题。Mnih等[11]对Q-learning算法进行改进,提出了Deep Q-Network算法。Zhou等[12]借鉴POMDP理论框架,将渗透测试过程视为一个动态决策问题提出了一种改进的DQN算法,名为NDSPI-DQN,用于解决大规模场景中的稀疏奖励问题,提高了收敛速度。Nguyen等[13]提出了一种双代理架构方法,适用于多主机场景。
基于 POMDP 的自动化渗透测试方法虽然能够有效地反映渗透过程中的不确定性,更符合渗透测试这一过程,但具有求解复杂度高、收敛速度慢、对计算硬件的要求高、不适用于大规模网络等缺点。考虑到基于 MDP 的深度强化学习方法是对 POMDP 的一种折中方法,能够兼顾渗透测试的成功率和求解效率,因此,本文尝试将基于MDP过程的A3C深度强化学习方法引入到自动化渗透测试场景中来,并对A3C算法进行改进,提出一种改进的强化学习算法NoisyNet-A3C(noisy networks integrated with asynchronous advantage actor-critic)。在NoisyNet-A3C算法模型中,智能体基于训练后的概率值选择最优的攻击路径,根据Nmap端口扫描信息确定漏洞和载荷,实时更新网络信息,不需要提前获取网络拓扑,从而使效率更高,渗透测试更为便捷。本文主要贡献如下:
(1)提出了改进的强化学习NoisyNet-A3C算法,通过建立多个智能体与环境交互,并最终更新到全局环境上,使用多线程执行多个智能体,减弱了训练智能体之间相关性过强的影响,进一步加快了训练过程中模型收敛速度。同时,通过引入NoisyNet机制,增加了模型探索能力,提高了训练收敛速度。
(2)设计并实现了一个自动化渗透测试框架,该框架包括扫描组件、模型训练与测试组件、漏洞探测与利用组件、数据库组件、Metasploit组件、NoisyNet-A3C算法对应该框架的模型训练与测试组件。
1 NoisyNet-A3C算法
MDP和POMDP模型是一种通用框架,为渗透测试中的不确定性建模提供了形式化分析框架。MDP可以看作是POMDP的简化版本,其与POMDP相比在计算上更易于求解,这种计算效率的提升使得MDP在实践中应用更广泛[14]。寻找最佳攻击路径的方法是强化学习RL,RL能够通过与环境交互生成样本来优化性能[15]。因此,将MDP与RL结合催生了一系列算法,其中就包括Q-learning算法、A3C算法以及本文提出的对A3C算法改进的NoisyNet-A3C算法。
1.1 A3C算法
A3C算法是Google DeepMind 团队提出的一种解决actor-critic算法不收敛问题的算法[5],是对actor-critic算法的进一步优化。在actor-critic算法中进行两组近似运算,第一组是对策略函数的近似:
πθ(s,a)=P(a|s,θ)≈π(a|s)。
(1)
式中:策略π是一个包含参数θ的函数;s表示某一状态;a表示某一动作。
另一组是对价值函数的近似,对于动作价值函数和状态价值可近似为
(2)
(3)
此时,策略函数被表示为一个连续的函数,对于连续函数,可以采用梯度上升法、牛顿法、拟牛顿法等优化方法寻找最优策略。最优化的目标就是使状态收获的期望最大,这个状态可以是初始状态,可以是所有状态的平均价值,也可以是所有状态的平均奖励,无论采用哪种方法作为优化目标,最终对θ求导的梯度都可以表示为
(4)
在梯度更新部分
为分值函数,无须改变,Qπ(s,a)部分应从critic得到[16]。总的来说,actor利用vt更新策略函数的参数,基于概率选择动作,并得到奖励和新的状态,critic基于actor的动作评判动作的奖励更新网络参数,actor根据critic的奖励更新策略。
A3C算法既可以处理连续和离散动作的问题,又可以单步更新,提升了学习效率。相较于actor-critic算法,A3C主要基于3点进行优化:①采用异步训练框架;②优化了网络结构;③对critic进行优化。
A3C异步训练框架如图1所示。A3C将actor-critic放到多个线程中同步训练,充分利用并行的环境。将每个线程中的运行结果反馈给主网络,同时从主网络获取最新的参数更新,这样将多个线程结合在一起,同时进一步降低数据之间的相关性,加快训练速度,利于程序收敛。
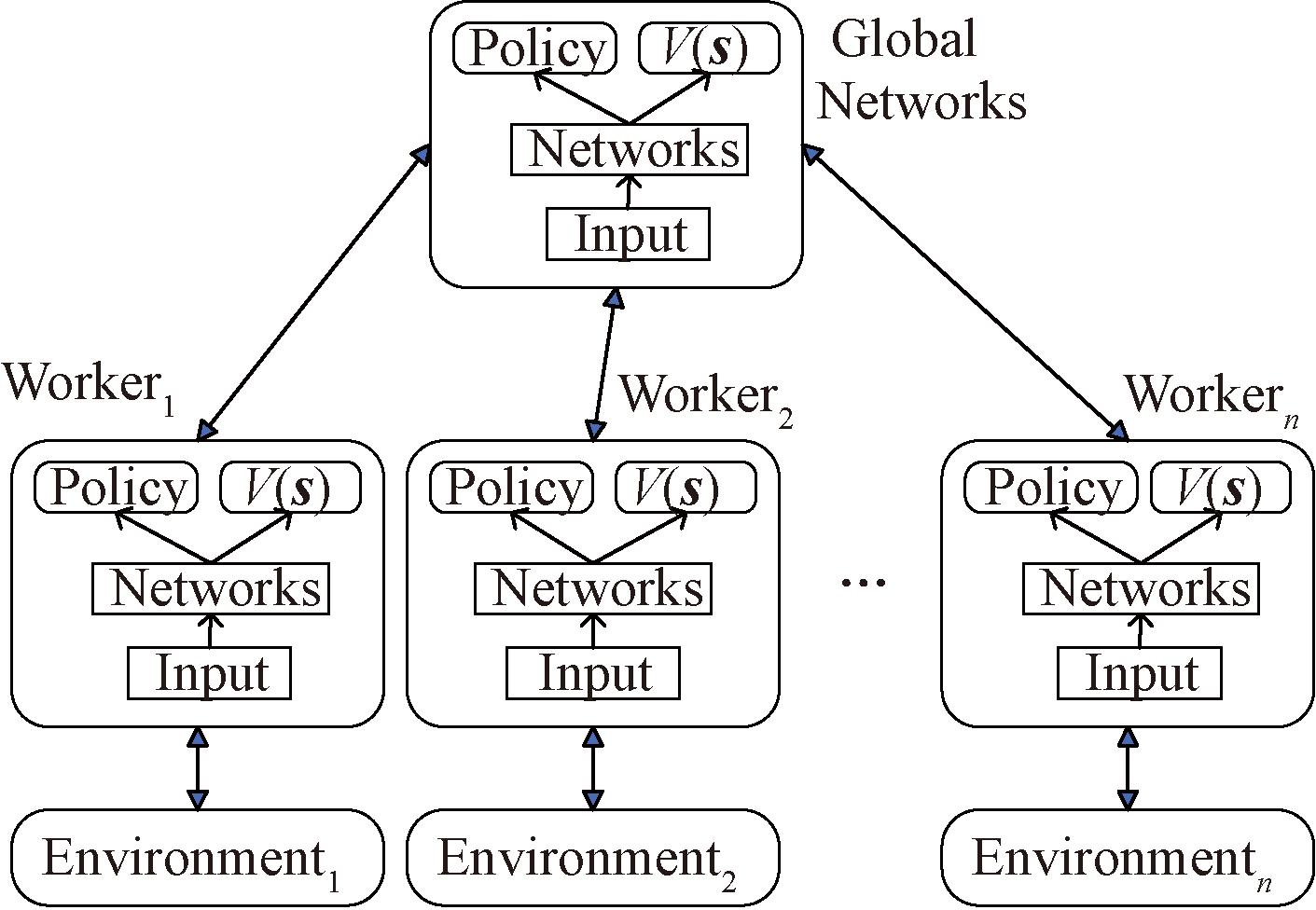
图1 A3C异步训练框架
Figure 1 A3C asynchronous training framework
对于A3C网络结构的优化,与actor-critic算法不同的是A3C算法将两个网络放在一起,如图2所示。
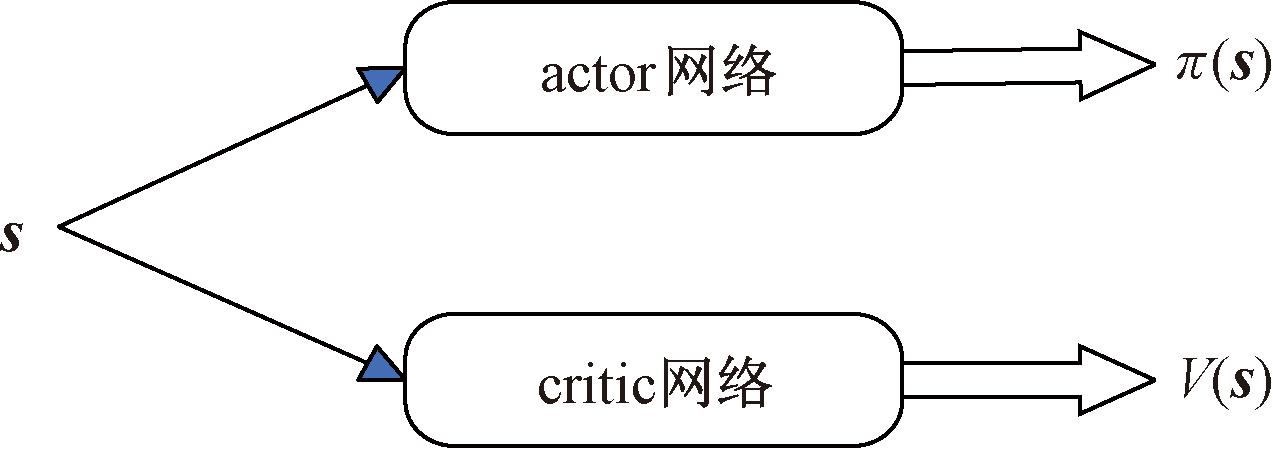
图2 A3C网络结构优化
Figure 2 A3C network architecture optimization
对于critic评估点的优化,引入优势函数A作为critic评估点,优势函数在A3C算法中的表达式为
A(st)=Rt+γRt+1+…+γn-1Rt+n-1+γnV(st+n)-V(sn)。
(5)
式中:t为时间;γ为衰减因子;R为奖励值;V(sn)通过critic网络学习得到。
对于损失函数的优化主要是加入策略π的熵项,系数为c,最终策略参数的梯度变为
(6)
最后对A3C算法进行总结,其算法流程如下。
算法1 A3C算法。
输入:公共部分的A3C神经网络结构,对应参数位θ、w,本线程的A3C神经网络结构,对应参数θ′、w′,全局共享的迭代轮数T,全局最大迭代次数Tmax,单次迭代时间序列最大长度tmax,状态特征n,动作集A,步长α、β,熵系数c,衰减因子γ;
输出:策略π和价值函数V。
① 更新时间序列t=1;
② 重置actor和critic的梯度更新量dθ←0,dw←0;
③ 从公共部分的A3C神经网络同步参数到本线程的神经网络θ′=θ,w′=w;
④ tstart=t,初始化状态st;
⑤ 基于策略π(at|st,θ)选择出动作at;
⑥ 执行动作at得到奖励rt和新状态st+1;
⑦ t←t+1,T←T+1;
⑧ 如果st是终止状态,或t-tstart=tlocal,则进入步骤⑨,否则回退到步骤⑤;
⑨ 计算最后一个时间序列位置st的Q(s,t):
⑩ for i∈(t-1,t-2,…,Q,tstart):
计算每个时刻Q(si):(si)=ri+γQ(si-1);
累计actor的本地梯度更新:
累计Critic的本地梯度更新:
更新全局网络的模型参数:
θt+1=θt-αdθt,wt+1=wt-βdwt;
如果T>Tmax,结束循环,输出公共部分的A3C神经网络参数θ、w,否则进入步骤③。
1.2 NoisyNet-A3C算法
A3C算法的探索效率较低,训练过程过于盲目,容易陷入局部最优解,在自动化渗透测试领域效果并不显著。本文引入NoisyNet改进A3C算法,使之能更好地适应自动化渗透测试这一场景。
NoisyNet是一种神经网络,其权值和偏差受到噪声参数的干扰,一般数学表示为y=fθ(x),是一个由噪声参数θ参数化的神经网络,本文将噪声参数θ表示为θ=μ+∑⊙ε,将ζ=(μ,∑)定义为一组可学习的参数向量,ε是一个具有固定统计量的零均值噪声向量,⊙表示逐元素乘法。神经网络的损失函数被重新表示为
(7)
本文对ζ进行优化,带有噪声参数的全连接层数学表示如下:
y=(μw+σw⊙εw)x+μb+σb⊙εb。
(8)
式中:μw+σw⊙εw等价于w;μb+σb⊙εb 等价于b。μw∈Rq×p、σw∈Rq×p、 μb∈Rq、σb∈Rq、εw∈Rq×p和εb∈Rq均为噪声随机变量。
在强化学习中,智能体需要在探索未知环境和利用已知信息之间进行平衡[17]。本文主要通过引入独立高斯噪声来调节这一平衡,该噪声通过增加行为策略的随机性,促使智能体探索新的动作空间,而非依赖当前的最优策略,这种方法能有效避免智能体过早陷入局部最优,同时提升训练过程的稳定性和收敛效率。噪声层每个权重都是独立的,并且具有模型自己学习的μ和σ,也就是对于任意的
和
的参数都来自高斯分布。
为了将NoisyNet引入到A3C算法中,本文对A3C进行如下修改:首先,删除了策略损失的熵加成;其次,将策略网络的全连接层用独立高斯噪声参数化为噪声网络层,本文将这种模型称为NoisyNet-A3C,具体改进如下。
A3C算法中,为了训练策略,需要为每个状态计算策略梯度的近似值,策略梯度U(θ)如下:
(9)
式中:
是对
的估计,然后将梯度相加,得到累积梯度:
A3C通过最小化估计回报与价值之间的误差来训练价值
然后更新网络参数(θπ,θV),推出如下更新公式:
(10)
(11)
在NoisyNet-A3C算法中,熵损失定义为
(12)
式中:
熵损失能够提升强化学习过程中的探索效率。当采用带有噪声层替换价值和策略中的线性层时,效果更佳,最终对A3C算法中值函数优化为
(13)
是当前策略回报的一致估计值。为了达到这个目的,本文强制∀i,εi=ε。由于A3C算法是一个强化学习算法,这意味着需要固定噪声和策略,因此,参数ζπ、ζV的每次更新都是在整个网络的噪声保持不变的情况下进行的,以便策略保持不变。最终参数更新公式修改为
(14)
(15)
(16)
NoisyNet-A3C算法通过不断与环境进行交互获得奖励值,以最大化
为目标,根据奖励不断更新参数ζπ和ζV,从而选出最优的攻击策略。
2 基于NoisyNet-A3C算法的自动化渗透测试框架
基于NoisyNet-A3C算法的自动化渗透测试框架如图3所示。该框架包括扫描组件、Metasploit组件、数据库组件、漏洞探测与利用组件、模型训练与测试组件。
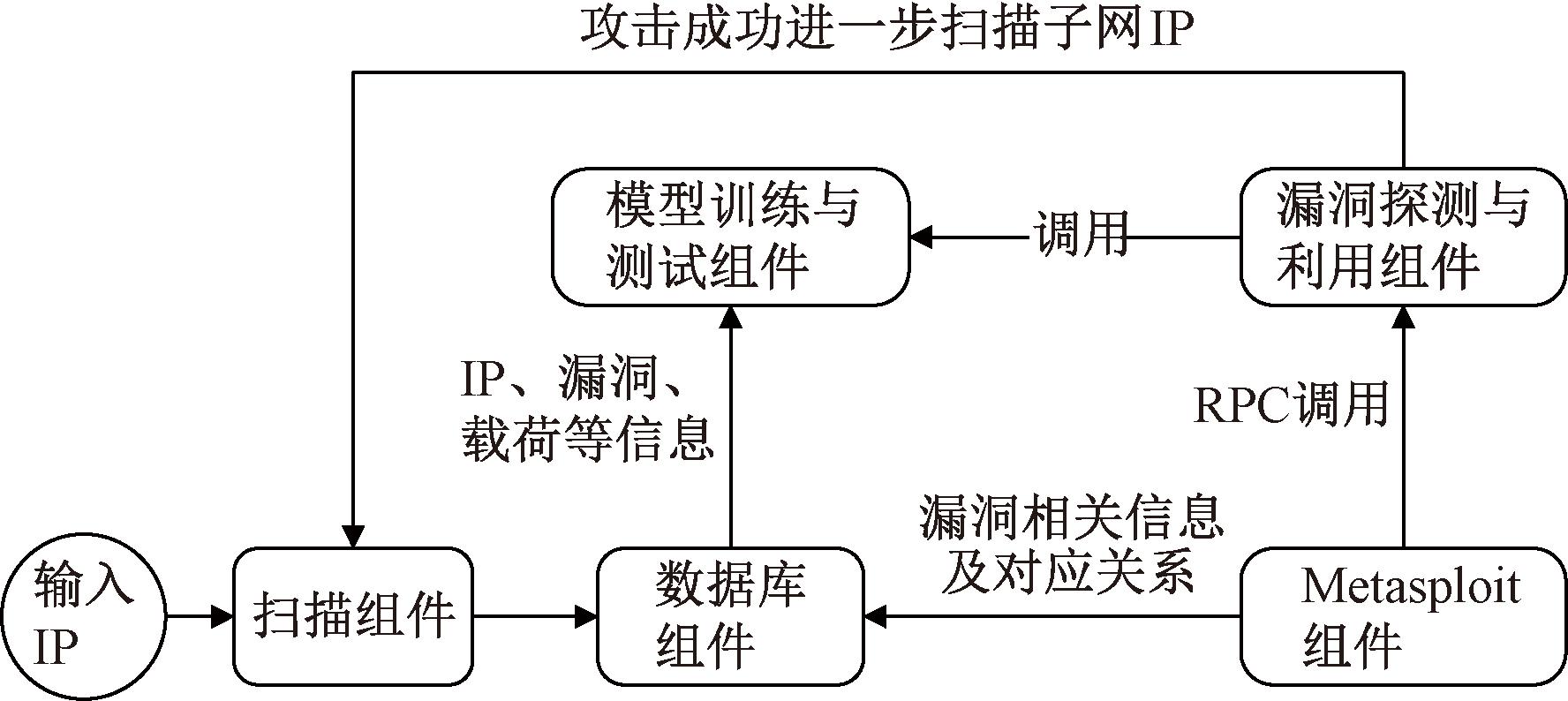
图3 基于NoisyNet-A3C算法的自动化渗透测试框架
Figure 3 Penetration testing automation framework based on NoisyNet-A3C algorithm
2.1 扫描组件
使用深度强化学习的关键在于有训练和测试数据,本文通过Nmap扫描模块对目标设备进行扫描,并对Nmap扫描结果进行解析,以获取漏洞探测与利用组件所需的IP信息。扫描模块完成扫描和解析后,获得的开放端口列表和操作系统信息如下。
port_list:[
{′portid′: ′21′, ′protocol′: ′tcp′, ′version′: 0.0, ′prod_name′: ′ftp′, ′product′: ftpd′},
...
]
os_info:{
′rhost′: ′192.168.79.129′,
′os_name′: ′windows′,
′os_version′: ′Microsoft Windows Server 2008 SP2 or Windows 10 or Xbox One...′
}
将解析后的数据存入数据库中,后续漏洞探测与利用组件根据这些信息执行攻击行为,模型训练与测试组件将这些信息作为模型输入。
2.2 Metasploit组件
Metasploit组件是一个能够查找、利用和验证漏洞的渗透测试平台,其本身附带数百个已知软件漏洞以及专业级漏洞攻击工具,被广泛用于漏洞探测与利用过程。数据库组件根据Metasploit组件获取已知的漏洞信息,漏洞探测与利用组件通过RPC调用Metasploit组件执行具体模拟攻击操作。
2.3 数据库组件
数据库设计主要分为exploits攻击模块表、targets模块表、payloads模块表和额外拓展表,主要存储exploit、target、payload在Metasploit组件中的索引以及各自对应关系信息,便于执行漏洞探测与利用操作。数据表设计以及对应关系如图4所示。
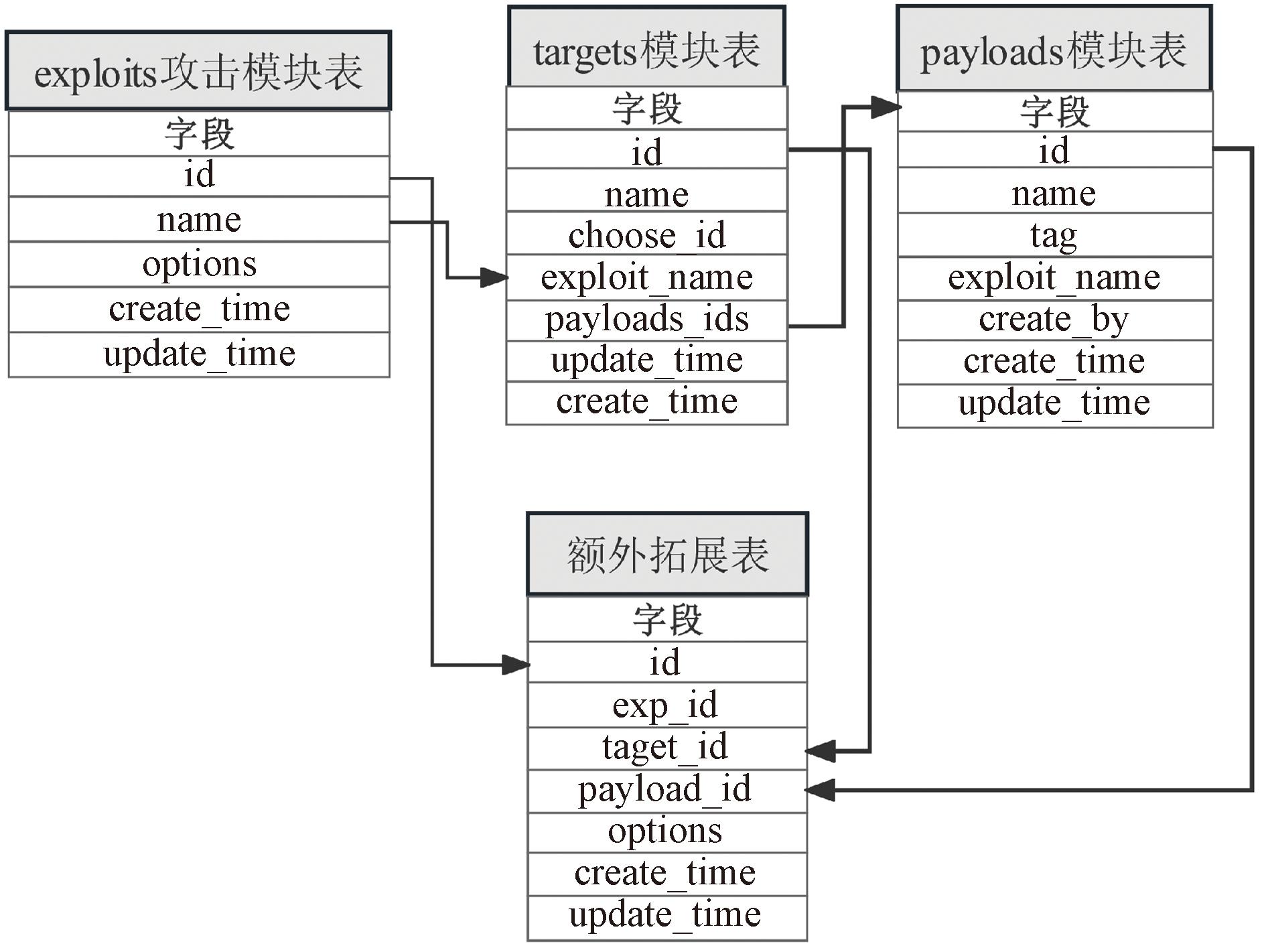
图4 漏洞相关数据表设计
Figure 4 Design of the vulnerability-related data table
2.4 漏洞探测与利用组件
漏洞探测与利用组件依据NoisyNet-A3C模型训练与测试组件选择的exploit、target、payload信息顺序执行漏洞利用程序,攻击完成后,获取模块的攻击结果,判断是否成功获取session,获取成功则为获取的session配置代理,并将目标IP重新提交给扫描组件。
2.5 模型训练与测试组件
该组件从数据库中获取数据,将数据向量化、正则化后作为模型的输入数据。按照输入数据对应的exploits信息、targets信息、payloads信息执行漏洞探测与利用组件,实时获取漏洞探测和攻击行为的奖励,并以最大化奖励值为训练目标来训练NoisyNet-A3C模型。
3 基于NoisyNet-A3C算法的自动化渗透测试框架
3.1 漏洞探测与利用组件设计
漏洞探测与利用组件是程序的主要组件之一,在程序启动后驻留在后台,等待扫描组件生成攻击表。在获取到攻击目标数据之后,该组件会对数据进行向量化和归一化处理。处理后的数据将经过NoisyNet-A3C算法的训练,根据渗透测试攻击路径攻击成功概率筛选排序,生成从优到劣的攻击方案。然后,按攻击方案对目标进行攻击,最终获得sessions。
在成功获取sessions后,将跳出该目标的攻击循环,通过这个sessions发送指定的命令,收集主机的基本信息,并利用代理模块配置攻击代理,将收集到的新的待攻击IP地址加入扫描组件的待扫描列表,等待扫描组件处理后重复NoisyNet-A3C算法训练操作。漏洞探测与利用组件设计如图5所示。
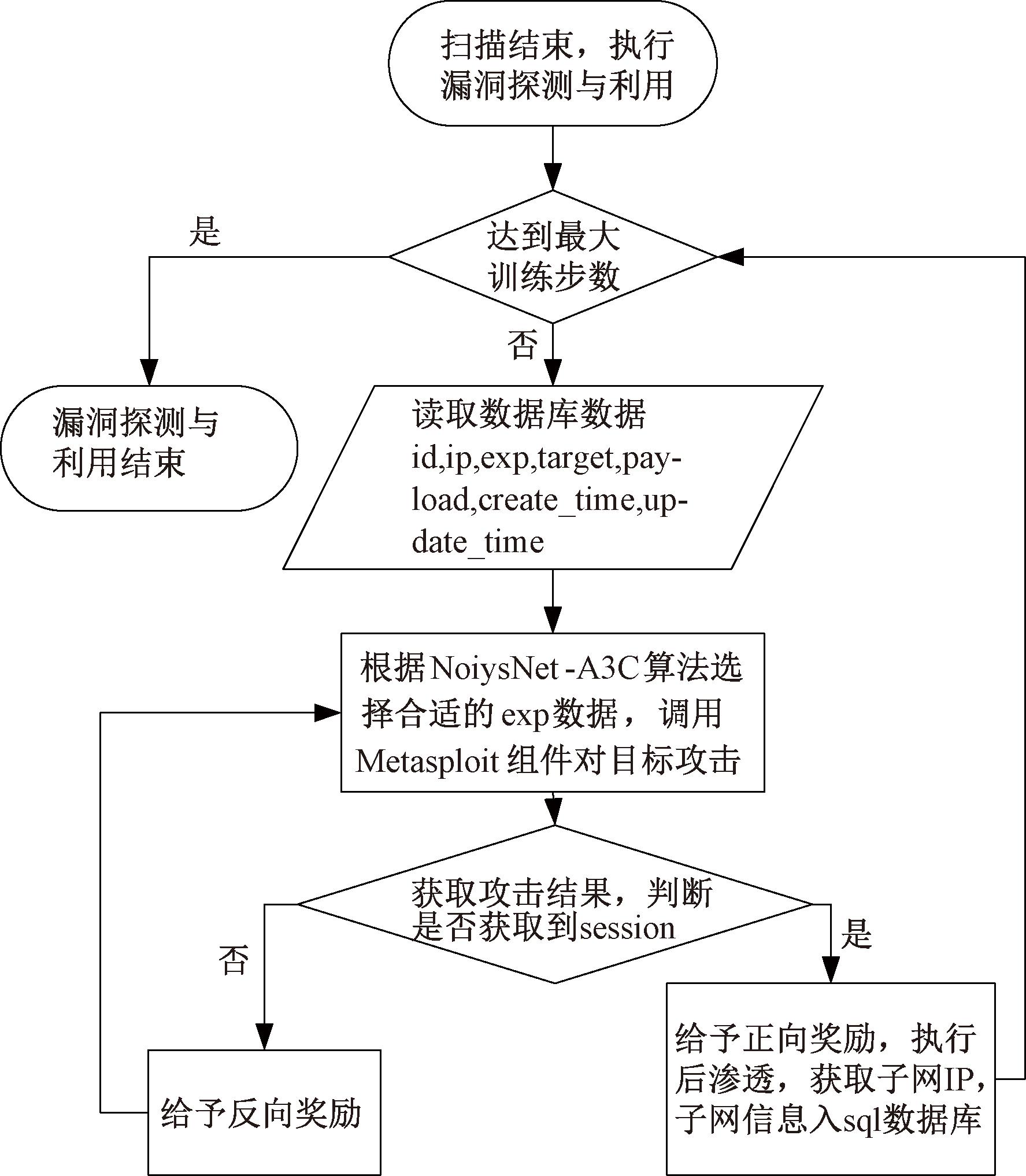
图5 漏洞探测与利用组件设计
Figure 5 Design of vulnerability detection and exploitation components
3.2 模型训练与测试组件设计
在训练模式中,首先,将“service_name”、“service_version”、“exploit_id”和“target_id”作为状态“state”,其中“service_name”和“service_version”是在扫描组件识别的设备的服务和版本;其次,确定“service_name”后,通过语句“search name:+ service_name type:exploit app:server”在Metasploit中查询并随机选择一个“exploit”模块,确定“exploit_id”;再次,根据Nmap扫描得到的主机类型,在可选的“target”列表中选择“target_id”;最后,在确定了这些状态之后,NoisyNet-A3C算法根据状态计算要执行的动作(payload)的概率,选择概率最高的payload并调用Metasploit执行漏洞利用。循环上述过程,通过不断修正神经网络参数来训练出最优的决策路径。整个模型训练流程详见图6。
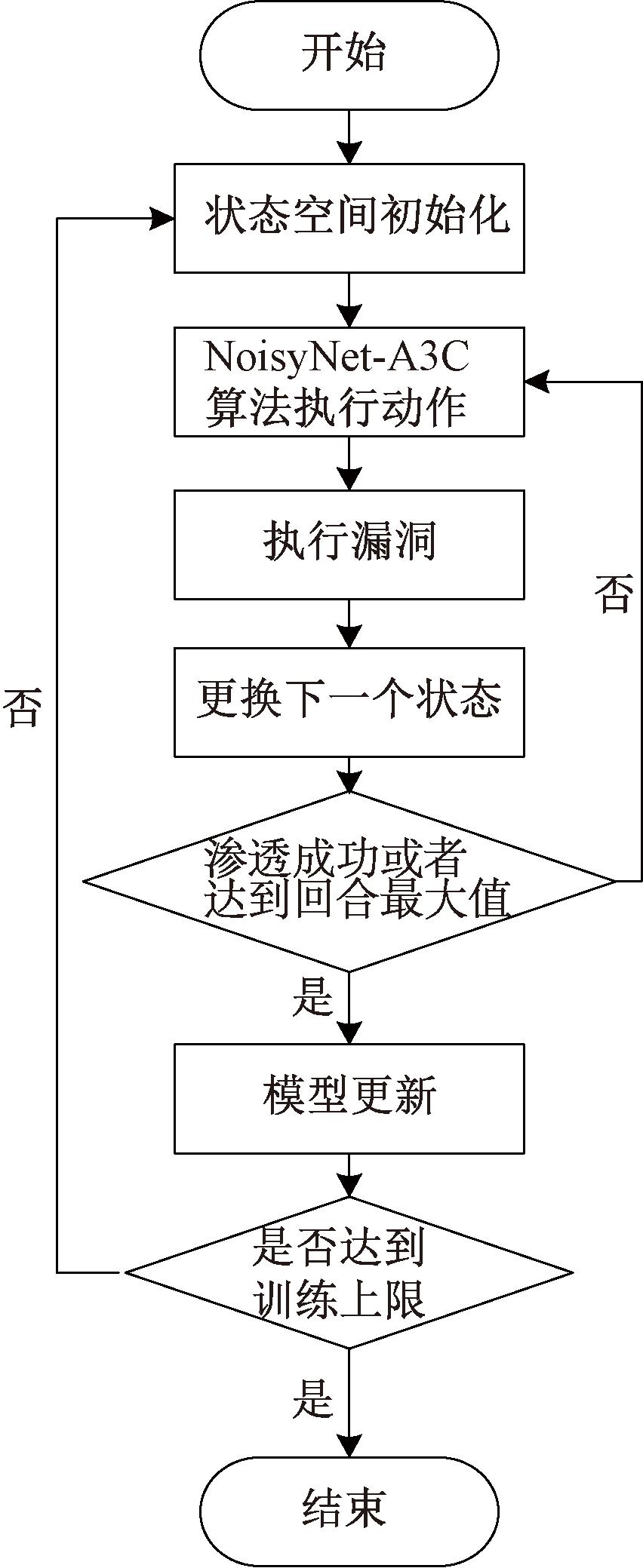
图6 NoisyNet-A3C模型训练流程图
Figure 6 Flowchart of NoisyNet-A3C model training process
在测试模式下,根据π(s)从模型中选择决策路径,提高攻击成功率。此外,测试模式还增加了后渗透阶段,计算不同状态空间下payload选择的概率,并根据概率从大到小调用Metasploit进行渗透测试,若渗透测试成功,则进行后渗透,识别出内网的存活的主机,并调用Metasploit框架中自带的代理模块“auxiliary/server/socks4a”搭建代理,对新识别到的主机进行进一步渗透测试,直到没有新的主机为止。
4 实验结果与分析
为了验证NoisyNet-A3C作为攻击路径决策算法在渗透测试框架中的效果,本文在EVE-NG网络仿真平台上设计并实现了一种网络拓扑,并测试NoisyNet-A3C、A3C、Q-learning、DQN以及2021年Zhou等[12]提出的NDSPI-DQN算法在该网络拓扑中渗透测试的性能。
4.1 实验场景
为尽可能地模拟真实内网环境,本文设计了一个由12台网络设备组成的网络拓扑环境,这些网络设备包括主机以及具有任意操作系统和应用程序的设备。图7展示了一个由12台设备(5台计算机、4台交换机和3台路由器)组成的网络拓扑,攻击者扫描网络拓扑的IP地址以识别敏感设备,并识别出设备漏洞,生成漏洞报告。
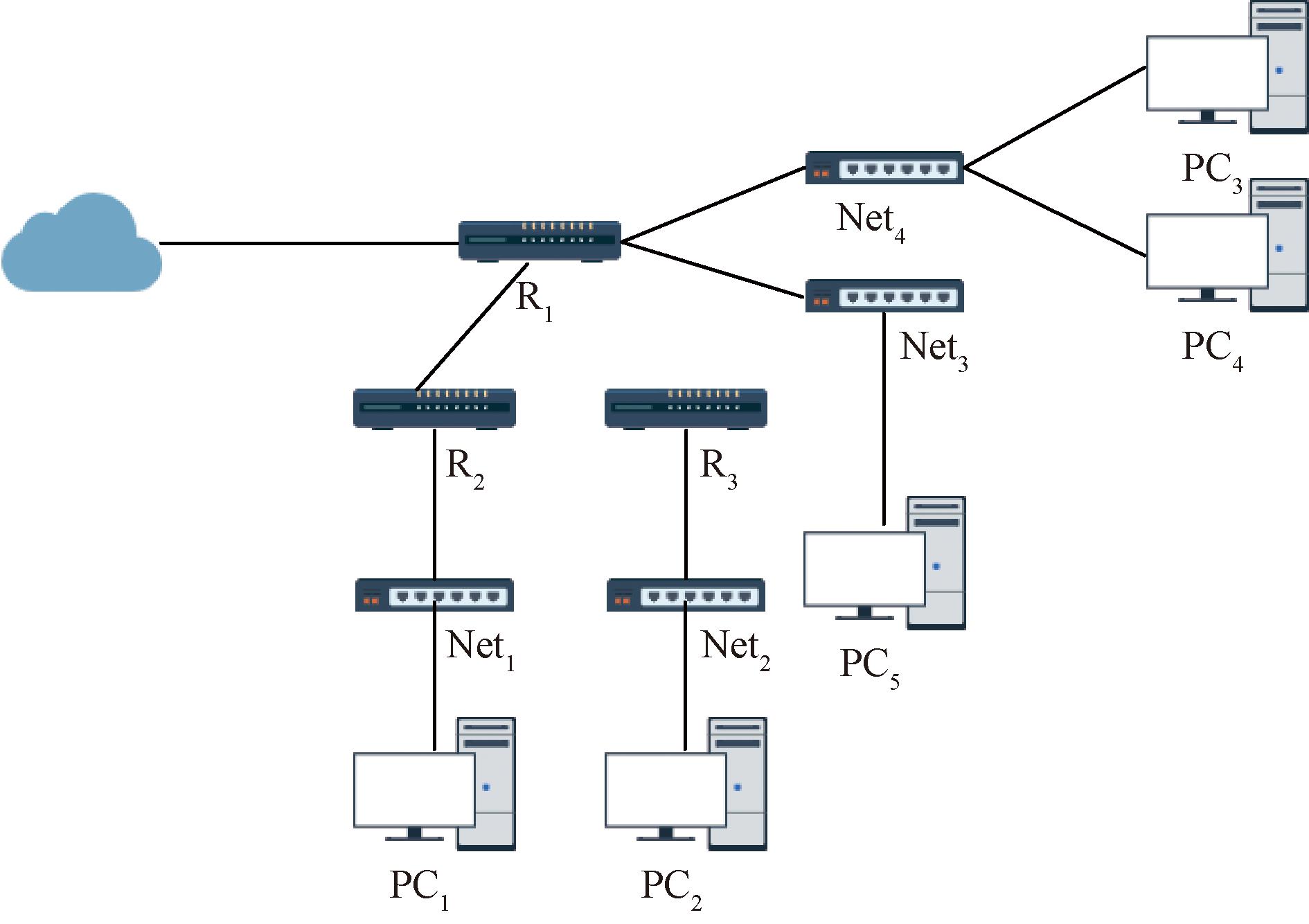
图7 网络拓扑图
Figure 7 Network topology diagram
本文旨在评估所提出的基于MDP模型的自动化渗透测试框架的有效性和收敛速度。为此,需要在网络设备中植入不同的网络漏洞,并建立网络设备、设备操作系统与漏洞及其开放端口的对应关系,如表1所示。
表1 设备漏洞对应关系
Table 1 Device vulnerability correlation
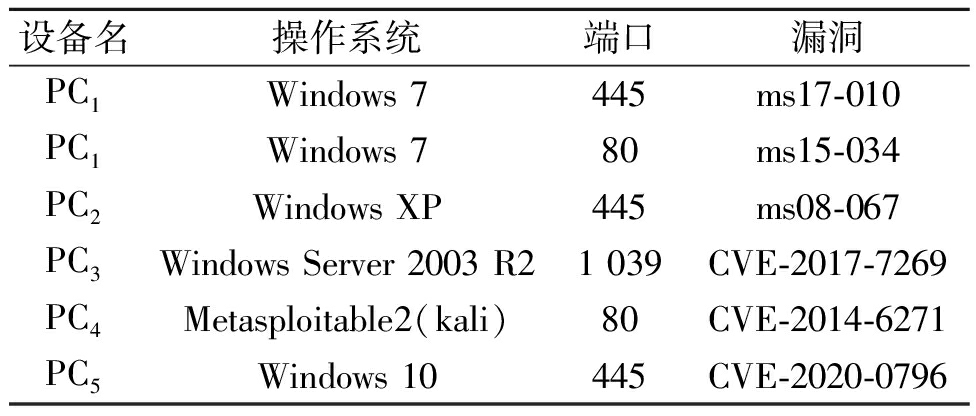
设备名操作系统端口漏洞PC1Windows 7445ms17-010PC1Windows 780ms15-034PC2Windows XP445ms08-067PC3Windows Server 2003 R21 039CVE-2017-7269PC4Metasploitable2(kali)80CVE-2014-6271PC5Windows 10445CVE-2020-0796
本文针对上述漏洞进行自动化渗透测试,测试结果显示,该漏洞在训练和测试阶段均能正常渗透。本文提出的基于NoisyNet-A3C算法的自动化渗透测试框架具有显著的有效性。接下来,本文将评估算法训练的收敛速度。
4.2 实验设置
本节主要介绍实验的硬件配置和超参数的设定。超参数包括学习率、回合步数、损失因子及学习次数。本文通过合适的超参数设定,使模型取得较好的效果。
实验采用的软件环境为Ubuntu18.04操作系统、Python3.6.9、Metasploit Framework 6.1.34、tensorflow1.8.0、Keras2.1.6 和pandas0.23.0。硬件环境为Genuine Intel(R) CPU @ 2.00 GHz,32 GB内存,Tesla K80 GPU 11 GB显存。
(1)学习率的设置。本文在评估NoisyNet-A3C算法的收敛速度的基础上,确定了相应的学习率,以期能使模型的效果得到提升。经实验证明,将学习率设置为0.005,能够使训练进程快速收敛且避免陷入局部最优解。
(2)回合(episode)步数的设置。本文所提NoisyNet-A3C算法的训练以episode为基础。具体而言,以状态state到episode结束时的返回值作为目标值,拟合到V网络,并利用V网络对policy网络进行更新。为了保证训练的有效性,本文将回合步数设置为2 000。
(3)损失因子的设置。NoisyNet-A3C算法的损失函数主要指的是熵损失。熵损失是一个非常重要的超参数,对最终性能和收敛速度有直接影响。通过实验结果显示,将熵损失设置为0.01时性能最佳,这不仅不会导致策略熵快速下降并陷入局部最优解,从而无法学习到有效数据,也不会使策略熵下降过慢,从而使有效数据被掩盖。
(4) 学习次数的设定。本文将总训练步数设为80 000。通过实验验证,80 000次训练已经足以证明算法的收敛性,并且不会过度消耗计算机资源。
(5)优化器的设定。优化器决定了神经网络的优化算法,包括SGD、Adam、RMSprop等。Adam优化器是一种常用于深度学习模型训练的优化算法,它结合了SGD和RMSprop的优势,具有自适应学习率、对稀疏梯度的鲁棒性、并行性等优点。在NoisyNet-A3C算法中,智能体通常只与环境交互一次,梯度通常是稀疏的,并且并行性具有显著提高训练效率的优势。因此,本文NoisyNet-A3C算法优化器设置为Adam。
(6)折扣因子的设置。折扣因子在强化学习中用来调整近期奖励和远期奖励的影响,其取值为(0,1]。本文将折扣因子设置为0.955。通过实验证明,当折扣因子设置为0.900时,由于折扣因子过低,算法忽略了长期目标,从而使得收敛速度减缓。而当折扣因子设置为0.990时,折扣因子过高,使得算法陷入了局部最优解,在局部最优解附近不断徘徊。经过实验,折扣因子设置为0.955时,效果最佳。不同折扣因子下平均奖励变化如图8所示。
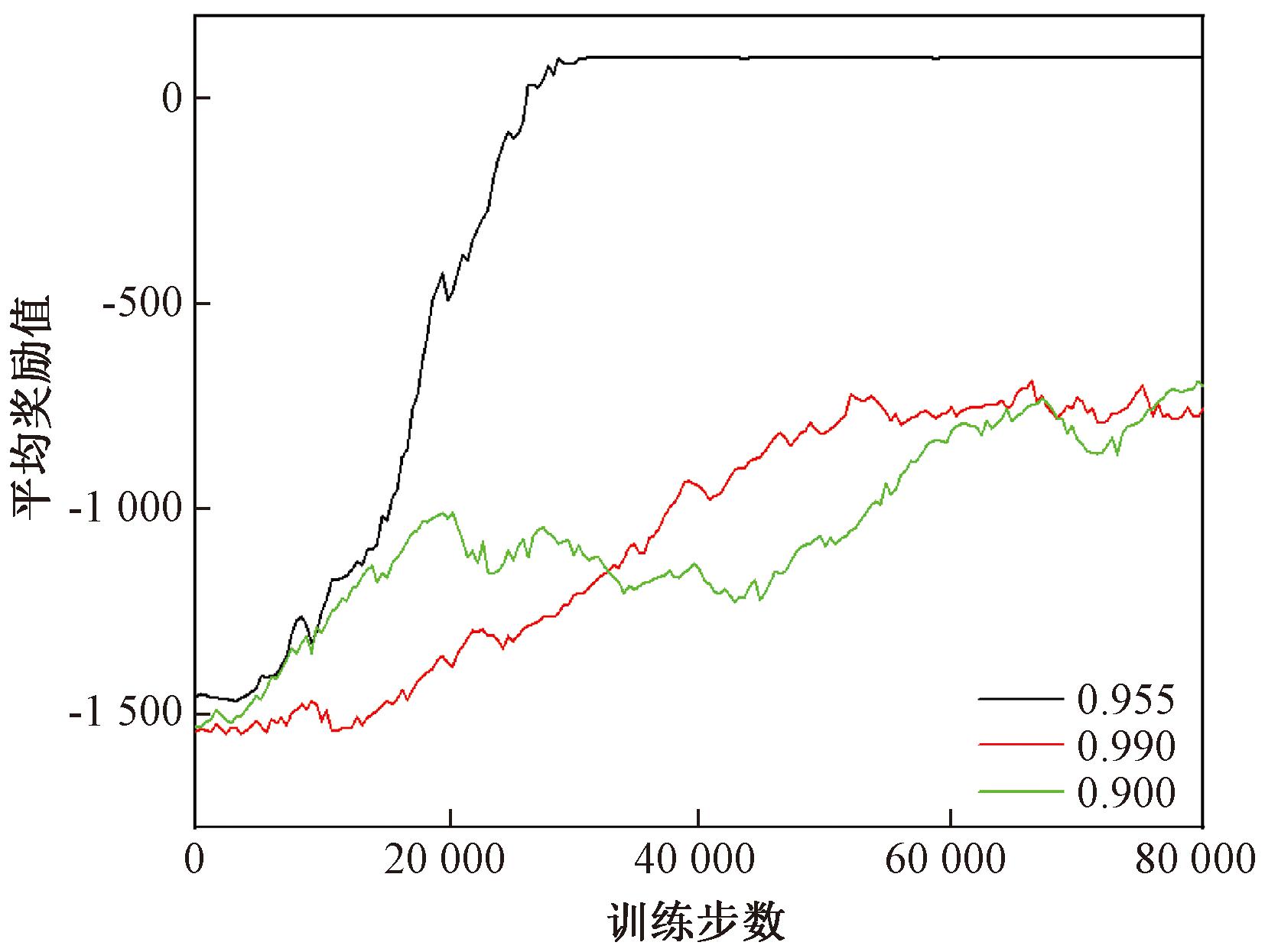
图8 不同折扣因子下平均奖励变化
Figure 8 Variation average reward with different discount factors
4.3 实验结果
强化学习的目标是通过训练优化策略,使得模型从环境中获得的奖励的期望值达到最大[18]。因此,本文选择在规定训练步数内平均奖励的变化作为评估指标。当模型在环境中获得了奖励,就会结束该回合,并给予正面的反馈,如果训练模型收敛,每回合的步数会逐渐减少。因此,本实验选择回合步数的变化作为另一个评估指标。
本文在构建的实验场景中,使用了相同的超参数对NoisyNet-A3C、A3C、Q-learning、DQN以及NDSPI-DQN算法进行了评估。平均奖励值的大小是评价算法性能的重要因素。平均奖励随训练步数的变化如图9所示。由图9可知,所有的模型在训练步数增加时,平均奖励值都有所升高。随着训练步数的增加,模型能够从环境中学习到更多的信息,从而优化其策略。NoisyNet-A3C算法在训练中表现出比A3C更好的性能,平均奖励值提前大约18 000步收敛,这是因为其引入的噪声可以帮助智能体探索环境,从而更快地学习,可以在更复杂的环境中学习和优化策略。与NDSPI-DQN算法和DQN算法相比,NoisyNet-A3C算法平均奖励值收敛提前10 000步。这主要因为NoisyNet-A3C不具有经验池的概念,更具有实时性,这意味着它可以更快地适应环境的变化,能够更及时地更新策略,从而更好地应对环境的变化。
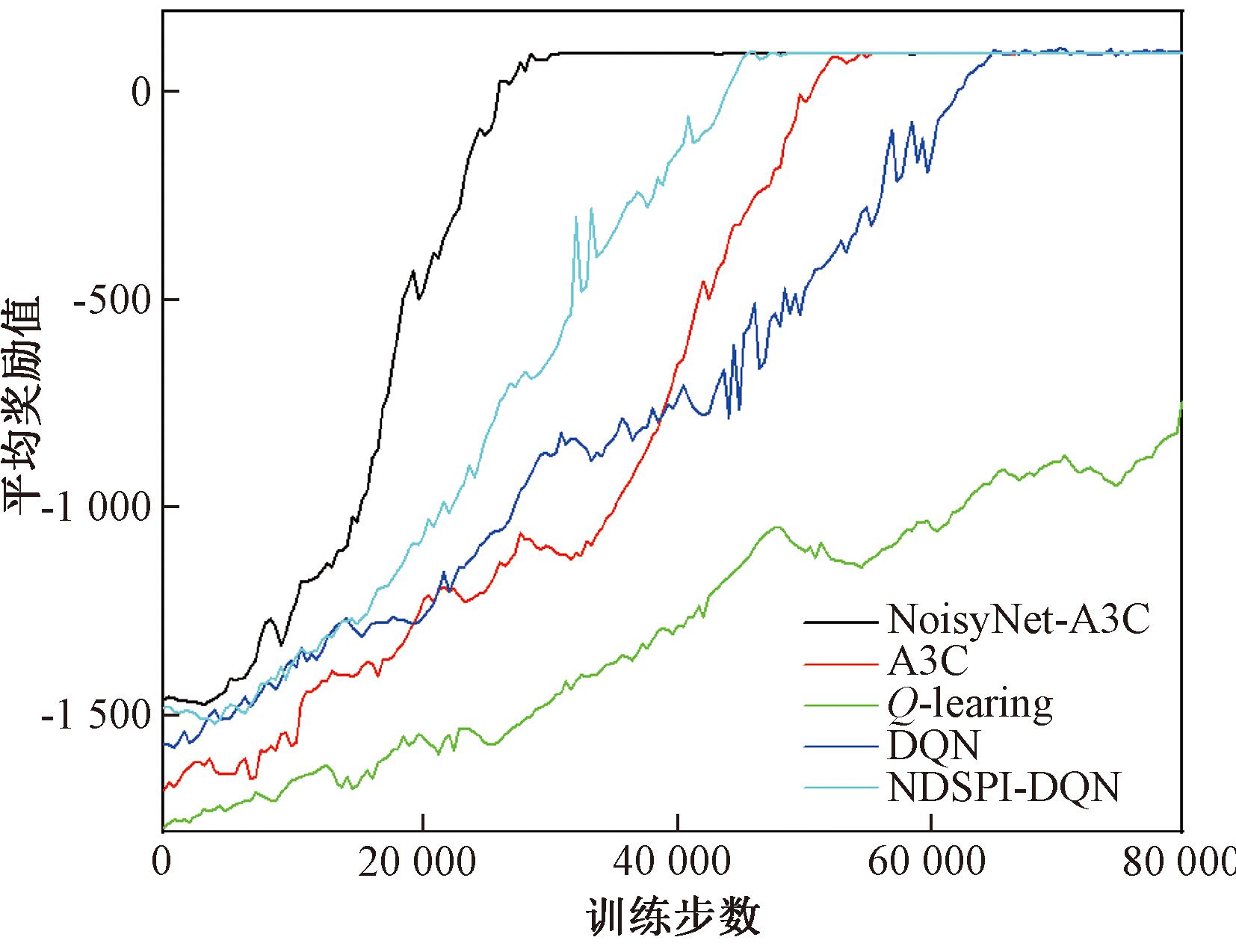
图9 平均奖励随训练步数的变化
Figure 9 Variation of average reward with training steps
实验选取的另一个评价指标是每回合训练步数的变化。当模型从环境中能有所得时,给予正反馈结束该回合,因此回合步数是逐渐减少的。每回合步数随训练步数的变化如图10所示。
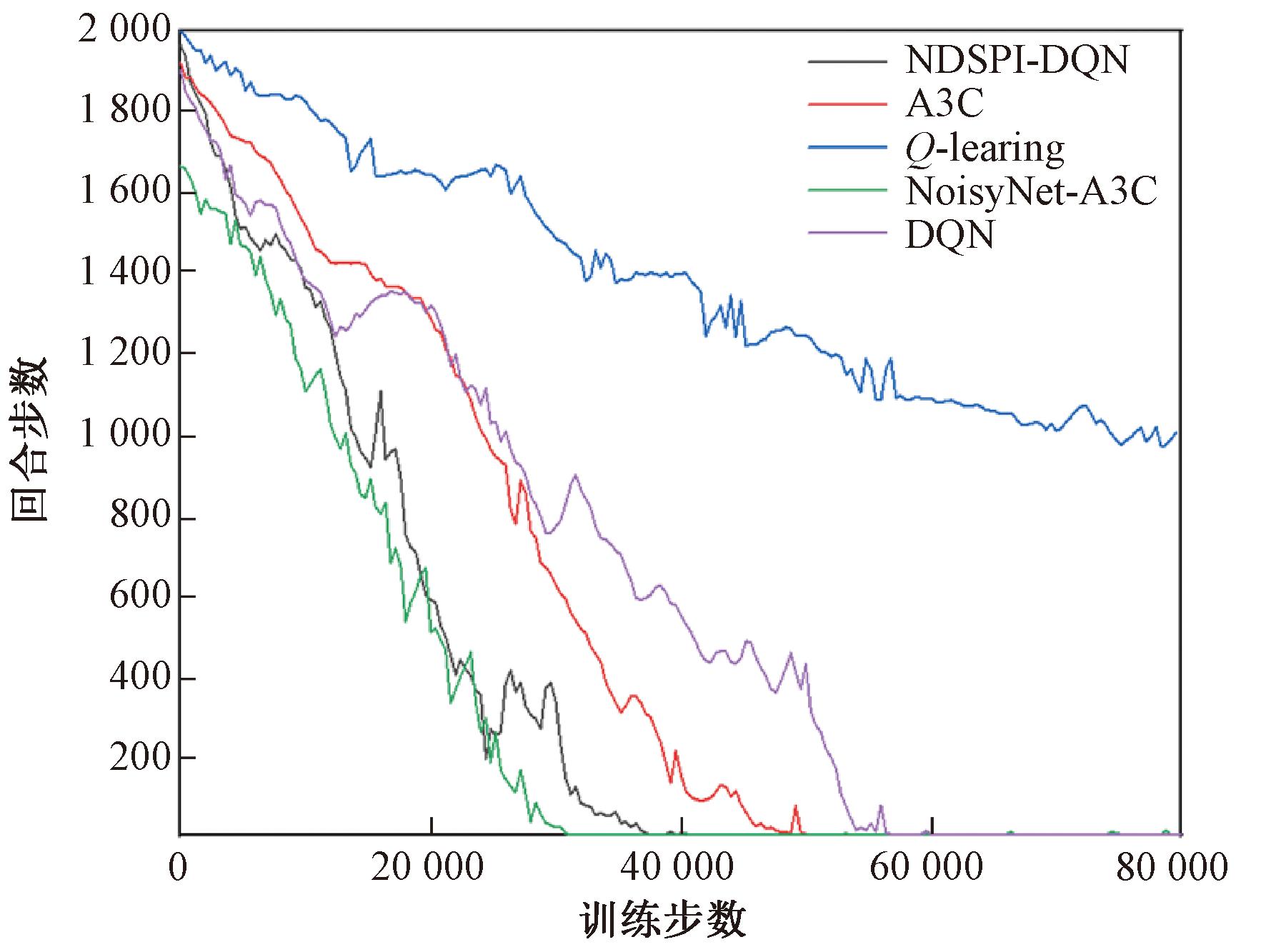
图10 每回合步数随训练步数的变化
Figure 10 Variation of number of steps per round with training steps
在本文设计的自动化渗透测试框架中,NoisyNet-A3C算法是对A3C算法的改进,因此,实验对A3C算法和NoisyNet-A3C算法进行了比较。实验结果表明,NoisyNet-A3C算法的收敛速度更快,收敛更为稳定,相对于A3C算法,其提前收敛的训练步数超过15 000步,优化效果显著。本文在实验中证明了NoisyNet-A3C、DQN和NDSPI-DQN 3种算法均具有收敛至最优状态的能力。其中,NoisyNet-A3C算法具有最快的收敛速度,与DQN算法相比,NoisyNet-A3C算法提前收敛了大约23 000步;与NDSPI-DQN算法相比,提前收敛了大约8 000步。然而,Q-learning算法在实验中的训练步数限制下未能达到最优状态,可能需要增加训练步数。由于Q-learning算法仅作为对比算法,因此本实验没有对其进行过多的训练。相较于传统的A3C算法,NoisyNet-A3C主要通过在神经网络权重上加入参数化的噪声,可以更快地适应环境的变化,并及时更新策略。相比之下,A3C可能需要更多的训练步数才能逐渐适应环境并学习到有效的策略。与Q-learning、DQN和NDSPI-DQN相比,NoisyNet-A3C没有经验池的概念,更具有实时性,结合了多线程以及基于策略和基于值的方法的优点,降低了数据之间的相关性,进一步提高了收敛速度。
5 结论
(1)本文提出了一种适用于自动化渗透测试场景的NoisyNet-A3C算法。通过对比NoisyNet-A3C、A3C、Q-learning、DQN和NDSPI-DQN 5种算法,本文提出的NoisyNet-A3C算法提前收敛的训练步数超过8 000步,收敛曲线波动更小。NoisyNet-A3C算法具有两大优势:首先,它可以提供更高精度的预测、更快的训练速度、更好的泛化能力,从而更好地抵抗过拟合,同时还可以提供更好的抗噪声能力,从而更好地处理不确定性和噪声;其次,它可以在多个环境中并行运行,提高训练速度,可以更有效地学习环境的复杂性,并且可以更快地收敛到最优策略。
(2)设计并实现了一个自动化渗透测试框架。在该框架中对NoisyNet-A3C算法的性能进行验证,此外,本框架所需的算法漏洞载荷信息来源于Metasploit,攻击信息更为充分,能覆盖更多的设备和协议。
[1] ZHOU T Y,ZANG Y C,ZHU J H, et al. NIG-AP: a new method for automated penetration testing[J]. Frontiers of Information Technology &Electronic Engineering,2019,20(9):1277-1288.
[2] 黄万伟, 郑向雨, 张超钦,等. 基于深度强化学习的智能路由技术研究[J]. 郑州大学学报(工学版),2023,44(1):44-51. HUANG W W, ZHENG X Y, ZHANG C Q, et al. Research on intelligent routing technology based on deep reinforcement learning[J]. Journal of Zhengzhou university (engineering science),2023,44(1):44-51.
[3] KRÖSE B J A. Learning from delayed rewards[J]. Robotics and Autonomous Systems, 1995, 15(4): 233-235.
[4] SRINIVASAN S, LANCTOT M, ZAMBALDI V, et al. Actor-critic policy optimization in partially observable multiagent environments[C]∥Proceedings of the 32nd International Conference on Neural Information Processing Systems.NewYork:ACM, 2018: 3426-3439.
[5] KANG Q M, ZHOU H Z, KANG Y F. An asynchronous advantage actor-critic reinforcement learning method for stock selection and portfolio management[C]∥Proceedings of the 2nd International Conference on Big Data Research. NewYork:ACM, 2018: 141-145.
[6] GHANEM M C, CHEN T M. Reinforcement learning for intelligent penetration testing[C]∥2018 Second World Conference on Smart Trends in Systems, Security and Sustainability. Piscataway:IEEE, 2018: 185-192.
[7] 周仕承, 刘京菊, 钟晓峰, 等. 基于深度强化学习的智能化渗透测试路径发现[J]. 计算机科学, 2021, 48(7): 40-46.
ZHOU S C, LIU J J, ZHONG X F, et al. Intelligent penetration testing path discovery based on deep reinforcement learning[J]. Computer Science, 2021, 48(7): 40-46.
[8] HU Z G, BEURAN R, TAN Y S. Automated penetration testing using deep reinforcement learning[C]∥2020 IEEE European Symposium on Security and Privacy Workshops. Piscataway:IEEE, 2020: 2-10.
[9] CHEN J Y, HU S L, ZHENG H B, et al. GAIL-PT: a generic intelligent penetration testing framework with generative adversarial imitation learning[EB/OL].(2022-04-05)[2023-10-11].https:∥doi.org/10.48550/arXiv.2204.01975.
[10] SCHWARTZ J, KURNIAWATI H, EL-MAHASSNI E. POMDP+information-decay: incorporating defender′s behaviour in autonomous penetration testing[J]. Proceedings of the International Conference on Automated Planning and Scheduling, 2020, 30: 235-243.
[11] MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529-533.
[12] ZHOU S C, LIU J J, HOU D D, et al. Autonomous penetration testing based on improved deep Q-network[J]. Applied Sciences, 2021, 11(19): 8823.
[13] NGUYEN H, TEERAKANOK S, INOMATA A, et al. The proposal of double agent architecture using actor-critic algorithm for penetration testing[C]∥Proceedings of the 7th International Conference on Information Systems Security and Privacy. San Francisco:Science and Technology Publications, 2021: 440-449.
[14] JIANG Z Y, ZHANG T J, KIRK R, et al. Graph backup: data efficient backup exploiting Markovian transitions[EB/OL]. (2022-05-31)[2023-10-11]. https:∥doi.org/10.48550/arXiv.2205.15824.
[15] 王丙琛, 司怀伟, 谭国真. 基于深度强化学习的自动驾驶车控制算法研究[J]. 郑州大学学报(工学版), 2020, 41(4): 41-45, 80.
WANG B C, SI H W, TAN G Z. Research on autopilot control algorithm based on deep reinforcement learning[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(4): 41-45, 80.
[16] SUTTON R S, MCALLESTER D, SINGH S, et al. Policy gradient methods for reinforcement learning with function approximation[C]∥Proceedings of the 12th International Conference on Neural Information Processing Systems. NewYork:ACM, 1999: 1057-1063.
[17] YE D H, CHEN G B, ZHANG W, et al. Towards playing full MOBA games with deep reinforcement learning[C]∥Proceedings of the 34th International Conference on Neural Information Processing Systems. NewYork:ACM, 2020: 621-632.
[18] SILVER D, HUANG A, MADDISON C J, et al. Mastering the game of go with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484-489.