传统的刚体机器人由刚性连杆和刚性关节组成,具有负载能力大、运动速度快等优点,但刚体机器人运动自由度有限,导致其灵活性和柔顺性较低,限制了其应用范围[1]。连续体机器人作为仿生机器人的研究前沿和热点,在理论上有无限的自由度,具有灵活性大、柔顺性强、安全性高等特点,能够在驱动器作用下不断改变自身形状,实现弯曲和旋转等各种运动,在手术医疗、灾难营救、勘探勘测和航空发动机(辅助)维修等领域拥有传统机器人所不能比拟的优势。
根据驱动方式的不同,可将连续体机器人分为流体驱动、肌腱/绳驱动、电磁驱动、电活性聚合物驱动和形状记忆材料驱动等多种类型。其中,绳驱动连续体机器人因其重量轻、负载能力强和具有更高的定位精度,是目前应用最为广泛的一种连续体机器人。肌腱/绳驱动连续体机器人一般采用刚柔混合结构,即在结构设计上既有用来实现无限自由运动的弹性部分,同时还具有用来增加本体刚度的刚性部分。目前国内外已经有大量文献对肌腱/绳驱动连续体机器人的结构进行了研究。Li等[2]设计了一种具有一定刚度且可弯曲的连续骨架的绳驱动连续体机器人,该机器人具有多段结构,其中每段沿中心连续骨架等间隔安装一系列带孔圆盘,通过控制电机驱动绳索可实现连续体机器人的弯曲运动,如图1(a)所示;Neppalli等[3]设计了一种以乳胶管作为中心骨架的可扩展的绳驱动连续体机器人,该设计不仅结构简单,而且易于构建,如图1(b)所示;Renda等[4]设计了一种模仿章鱼触手的软机械手,该机械手本体由锥形硅胶组成,并通过几根浸入硅胶体内的绳索驱动,其中,驱动绳索通过机械臂内的刚性塑料圆盘固定在与底座不同的距离上,如图1(c)所示;Cao等[5]提出了一种新型的肌腱驱动连续体机器人,该机器人具有2个模块和1个由螺旋弹簧构成的柔性骨架,每个模块通过4根平行排列的肌腱来实现冗余驱动,进而保证机器人的灵活运动,如图1(d)所示;Pang等[6]提出了一种轻量级的七自由度绳驱动机械手,该机械手具有新型绳索张紧机构,可实现机械臂在运动过程中的快速张紧,避免绳索松弛问题,如图1(e)所示。
图1 肌腱/绳驱动连续体机器人
Figure 1 Tendon/cable driven continuum robots
目前,在连续体机器人结构设计方面的研究工作取得了较大进展,但连续体机器人在工程实际中的成功应用还依赖于建模和控制问题的有效解决。由于连续体机器人具有高度非线性、强耦合、时变和强弹性效应等特点,给连续体机器人的建模和精准、可靠、高效的控制带来了巨大挑战。
随着对连续体机器人建模和控制研究的广泛关注和不断深入,国内外学者对相关研究进行了总结。Omisore等[7]和Zhong等[8]针对医疗领域连续体机器人的设计、驱动、运动学建模和控制进行了总结,但是只分析了连续体机器人的运动学建模方法,几乎没有涉及动力学建模。Li等[9]根据传输单元对连续体机器人进行分类,并对每种连续体机器人的优点和缺点进行评述和总结。Kolachalama等[10]从结构、材料和驱动3个方面对连续体机器人在过去二十年的演变进行了文献综述。Wang等[11]根据驱动方式不同将连续体机器人进行分类,在此基础上,将连续体机器人的控制方法分为开环控制、闭环控制和自主控制3种,并分别对每种控制方法进行了总结和讨论。Thuruthel等[12]则从基于模型和无模型的角度对连续体机器人的控制方法进行分类和阐述,为连续体机器人控制器的开发和应用提供参考。但是,上述文献均没有对肌腱/绳驱动连续体机器人的建模和控制研究状况进行系统、全面的分析。
本文对近年来肌腱/绳驱动连续体机器人在运动学和动力学建模方面的研究进行总结,并从基于模型、无模型和混合控制角度对绳驱动连续体机器人的控制方法进行总结,对其未来发展趋势进行展望。
1 运动学建模
连续体机器人是依靠其自身所具有的弹性或者柔性元件的变形而进行运动,运动学模型的建立是理解其运动机理的关键,也是建立其动力学模型和对其进行控制的基础。目前,国内外许多学者针对肌腱/绳驱动连续体机器人的运动学建模做了大量的研究工作,主要建模方法包括:有限元法、常曲率建模方法、变曲率建模方法和数据驱动方法。其中,有限元法是将连续体机器人分解为多个求解单元(正方形或者三角形),能够准确计算出连续体机器人的运动学特性,具有良好的普适性。但是连续体机器人的有限元建模通常需要依赖商业软件,建模成本较高,建模过程复杂,需要明晰连续体机器人的物理属性和几何参数。此外,有限元模型的求解速度较慢,在现场应用中的适用性有待提高,因此本文重点讨论常曲率建模方法、变曲率建模方法和数据驱动建模方法,其基本原理、优缺点以及代表性文献如表1所示。
表1 运动学建模方法比较
Table 1 Comparison of kinematic modeling methods
方法基本原理优点缺点常曲率建模[13-19]将连续体机器人等效为光滑连续曲线,并通过一组空间构型参数描述其形状简单,计算效率高,利于基于模型的控制精度相对较低 变曲率建模[2,20-23]将连续体机器人上任一点的位姿向量表示为沿机器人弧长的函数精度高计算复杂,不利于基于模型的控制数据驱动建模[24-26]基于真实物理系统输入输出数据建立映射关系适用于任何类型的连续体机器人数据采集和训练困难
1.1 常曲率建模
常曲率建模方法是应用较为广泛的一种连续体机器人运动学建模方法。该方法假设连续体机器人骨架变形后的形状是由连续的弧线组成的,每一段连续弧线上的曲率不变,并且中心骨架的长度L保持不变。如图2所示,在常曲率假设下,连续体机器人的形状可以用一组有限的圆弧参数如连续体机器人的弯曲角度θ和弯曲平面的旋转角度φ表示。另外,基于常曲率假设可知θ=L/κ,其中κ为弯曲曲率,可通过曲率半径1/κ、弧长L和旋转角度φ来描述连续体机器人的变形,简化运动学模型,有助于对连续体机器人进行实时控制。
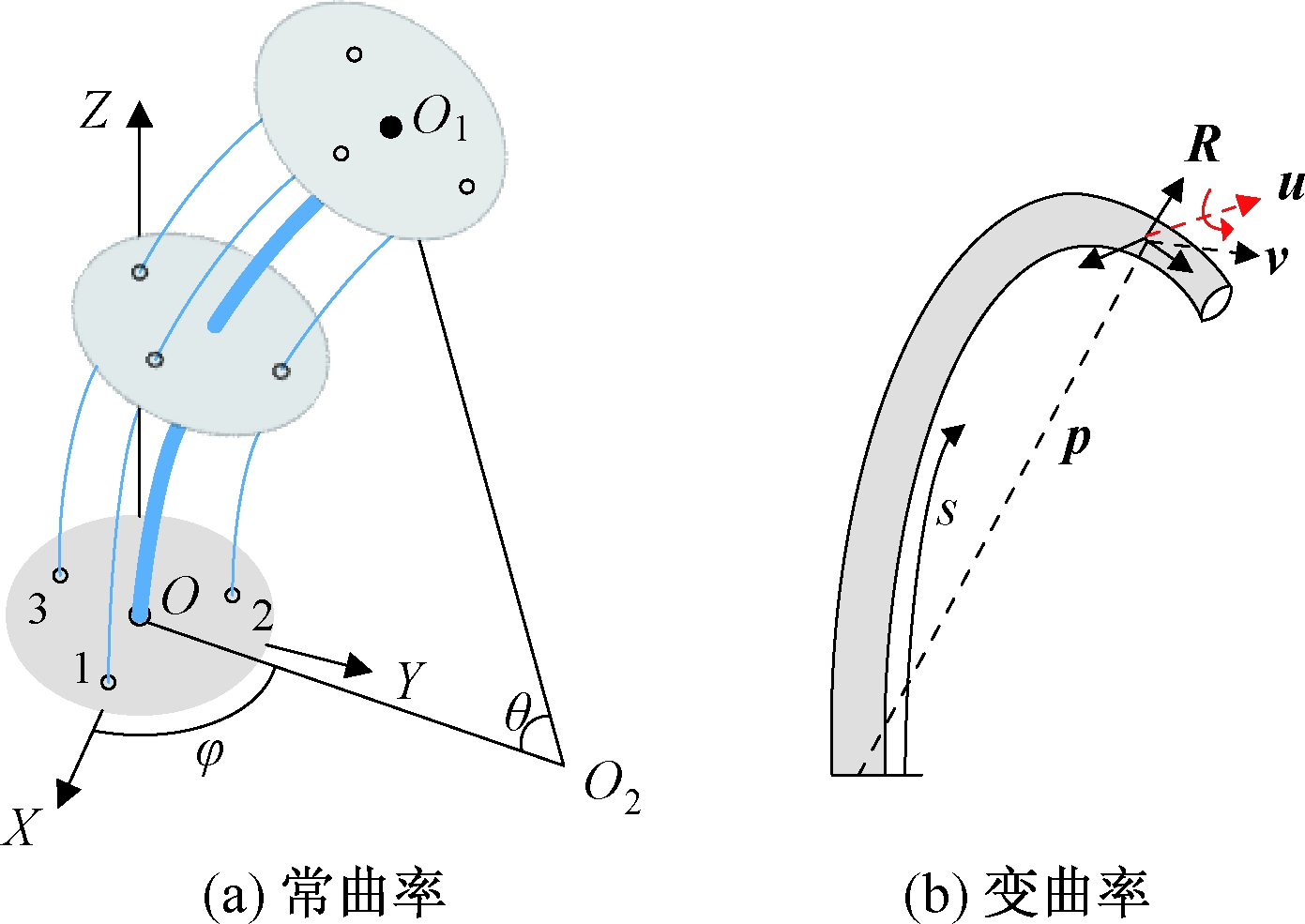
图2 连续体机器人运动学建模原理图
Figure 2 Kinematic modeling schematic diagram of
continuum robots
肌腱/绳驱动连续体机器人属于间接驱动机器人,因此其运动学模型不仅包括构型空间与任务空间之间的映射关系,还包括构型空间与关节空间之间的映射关系,如图3所示。其中,构型空间与任务空间的映射关系可以通过多种方法建立,包括几何分析法、D-H参数法、F-S框架法、指数坐标法和积分表达法等。Webster等[13]总结并比较了上述方法,指出这些方法虽然在形式和坐标选择上不同,但是在常曲率假设下,所建立的连续体机器人的映射关系是相同的。
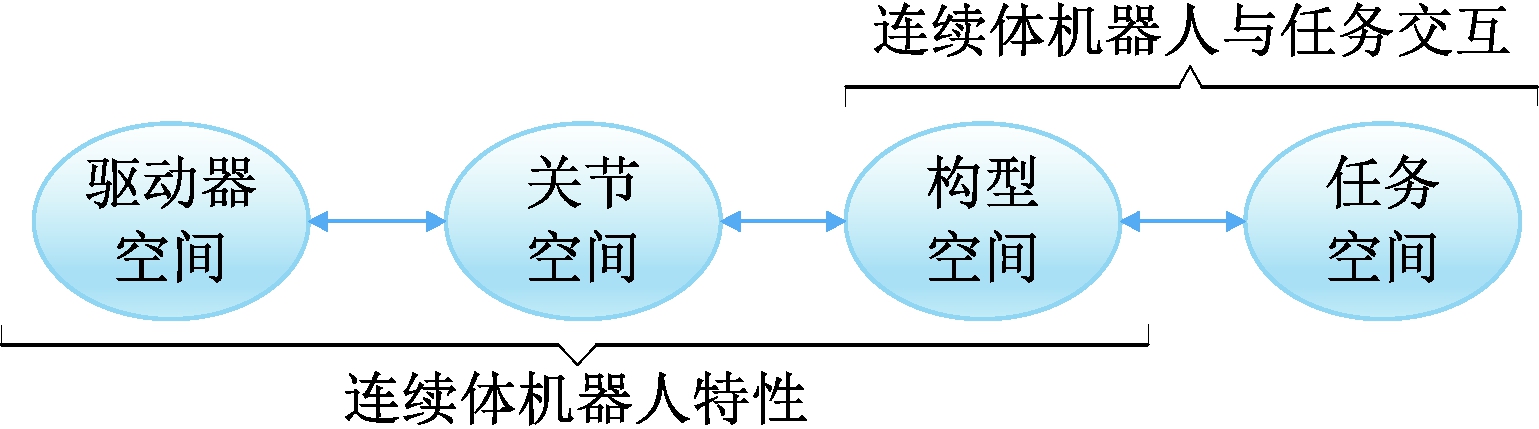
图3 连续体机器人空间映射关系
Figure 3 Spatial mapping of continuum robots
考虑到从关节空间到构型空间的映射是各机器人所特有的映射,不同驱动结构的机器人的映射关系是不同的,Jones等[14]在常曲率假设条件下提出修正的D-H参数表,通过机器人构型坐标将任务空间坐标与执行器输入(如肌腱长度)关联起来,建立了单段连续体机器人的运动学模型,同时,针对多段连续体机器人运动学,只需将单段情况下的变换矩阵相乘即可。Bajo等[15]进一步分析了常曲率假设下连续体机器人的约束条件,建立了沿中心骨架任意弧长接触位置的约束运动学,可实现对碰撞位置的检测和定位。Goldman等[16]在此基础上建立了连续体机器人的运动学模型,为刚度矩阵的求取和柔顺运动控制器的设计奠定了基础。但是上述方法均假设连续体机器人弯曲过程可以近似为光滑连续曲线,建模过程存在一定误差。
为了进一步提高连续体机器人运动学建模精度,有学者在常曲率假设的基础上提出了分段常曲率的建模方法。分段常曲率建模方法是将柔性连续体沿中心轴向分成n小段,每一小段应用常曲率假设得到上下截面坐标系之间的齐次变换矩阵,进而通过链式法则计算得到连续体机器人的整体运动学模型。Qi等[17]在分段常曲率假设的基础上,建立了关节空间、构型空间和任务空间之间的映射关系,分析了多段驱动耦合效应,提高了建模精度。Zhong等[18]在分段常曲率假设下,建立了由超弹性镍钛合金材料制成的连续体机械臂的正向运动学的齐次变换矩阵,并提出了基于位移补偿法的有效封闭解来求解连续体机械臂的逆运动学,基于逆运动学对其圆轨迹规划进行了分析和讨论,有效提高了建模的精度。在此基础上,Barrientos等[19]基于分段常曲率线性化方法,提出一种从驱动空间到构型空间的运动学求解新方法,与常规的分段常曲率方法相比,该方法计算效率更高,更有利于连续体机器人的实时控制。
常曲率模型能够显式表达连续体机器人的运动学特性,易于求取解析解,便于进行基于模型的控制。该方法在忽略重力以及负载影响的条件下是有效的,但是由于常曲率模型没有考虑轴向变形,因此当连续体机器人具有复杂的外部载荷作用时,变形后连续体机器人形状不再近似为光滑连续弧线,此时常曲率假设失效。
1.2 变曲率建模
变曲率建模方法突破了常曲率假设的限制,允许沿机器人长度的曲率变化和形状改变,更加符合实际物理系统。如图2所示,基于附着在柔性杆上的齐次参考坐标系描述变曲率模型,该坐标系包含位置向量p(s)∈R3和旋转矩阵R(s)∈SO(3),其中,R3表示实数域上的三维向量空间;SO(3)表示包含R(s)的三维旋转群。将柔性杆上任一点的位姿表示为沿机器人弧长s的函数,通过旋转矩阵和位置向量对弧长s求导得到运动学方程
(1)
(2)
式中:u(s)∈R3表示曲率向量;v(s)∈R3表示线速度向量。当u(s)和v(s)已知时,可以通过求解式(1)、式(2)得到连续体机器人的骨架形状。但是一般情况下无法得到式(1)、式(2)的封闭解,需要通过数值积分的方法进行求解,导致该方法计算效率较低,不利于进行连续体机器人的实时控制。
目前,使用最为广泛的变曲率建模方法为Cosserat杆方法,该方法同时考虑拉伸变形和横向挠度,将连续体机器人简化为由一系列的点及其对应方向组成的空间曲线,在平面连续体机器人和多段连续体机器人方面得到了广泛的应用。Li等[2]基于Cosserat杆理论建立了连续体机器人单节段的几何精确模型,用于描述由于肌腱载荷引起的骨架各部分非线性变形,并与常曲率方法进行比较,实验结果表明该方法预测精度较高。针对多段连续体机器人,Renda等[20]通过离散Cosserat杆方法建立其运动学模型,该模型不仅考虑了平面外外力作用下的剪切和扭转变形,而且兼顾了连续Cosserat杆方法的几何和力学特性,实验结果表明,离散Cosserat杆方法具有比连续Cosserat杆方法更好的性能。Lilge等[21]根据几何精确的Cosserat杆理论,探索了在载荷作用下连续体机器人的运动学方程。在此基础上,Black等[22]针对平行连续体机器人,基于Cosserat杆建立了在负载条件下的正运动学和逆运动学模型,包括一般形式的近端和远端边界条件。进一步地,Zhao等[23]将连续体机器人近似为细长杆,并将Cosserat杆理论应用到求解其运动学模型中,通过求解Cosserat杆理论方程,得到连续体机械臂末端刚度的数值表达式,进而可实现对该连续体机械臂的刚度变化控制。
1.3 数据驱动建模
由于连续体机器人运动机理复杂,在运动过程中存在显著的非线性和不确定性,增加了对其进行分析建模的难度,因此有学者提出采用数据驱动的方法来建立连续体机器人的运动学模型。该方法无须系统参数以及连续体力学方面的知识,而是借助来自真实物理系统的训练数据,通过训练数据得到描述执行器输入和系统输出之间的关系。Giorelli等[24]使用神经网络建立了三维空间运动非常曲率连续体机器人的逆运动学模型,并通过实验验证了该方法的可行性。Thuruthel等[25]在上述工作的基础上,提出在反馈控制过程中通过机器学习方法获得连续体机器人的逆运动学模型,提高了参数的辨识精度。为了避免学习算法受模型参数扰动的影响,Wang等[26]提出一种端到端无模型学习的方法,利用循环神经网络建立关节空间到构型空间的运动学模型。
基于运动学模型可以进行连续体机器人的控制系统设计。但是运动学模型忽略了机器人的动态行为,对于运动速度较快、精度要求比较高的场合,基于运动学模型的控制效果往往不能满足需求,因此需要在运动学模型的基础上进一步建立连续体机器人的动力学模型。
2 动力学建模
连续体机器人的动力学建模方法主要包括拉格朗日方法、虚功原理、基于Cosserat杆理论的方法和数据驱动方法。表2总结了各方法的基本原理、优缺点以及代表性文献。
表2 动力学建模方法比较
Table 2 Comparison of dynamic modeling methods
方法基本原理优点缺点拉格朗日方法[27-28]基于能量平衡原理建模模型为常微分方程形式,易于求解,利于实时控制只考虑弯曲变形,忽略扭转、延伸和剪切变形,模型精度相对较低虚功原理[29-31]最小化系统外力和力矩的虚功结构简单,物理意义明确,计算效率高力学分析时,忽略软材料的黏性和法向应变,精度相对较低Cosserat杆理论[32-35]基于给定本构关系,建立内力、力矩与应力之间的联系确定动态模型考虑弯曲、扭转、延伸和剪切变形,模型精度较高模型为偏微分方程形式,计算效率低,不利于实时控制数据驱动[36-38]基于真实物理系统输入输出数据建立动态模型适用于任何类型的连续体机器人数据采集和训练困难
2.1 拉格朗日方法
拉格朗日方法是从能量分析的角度来建立连续体机器人的动力学模型。首先,分别求出系统总的动能和势能,然后计算拉格朗日函数,将拉格朗日函数代入拉格朗日方程后,通过转化可得到连续体机器人的动力学普遍方程。Falkenhahn等[27]基于常曲率假设建立了连续体机器人的运动学模型,并在集中质量假设条件下,利用拉格朗日方法推导得到其动力学方程。Yang等[28]在考虑连续体机器人伸长、收缩、弯曲和扭转变形的情况下,结合欧拉伯努利梁理论和拉格朗日方程,建立了多段连续体机器人的微分代数方程形式的动力学模型,该方法能够对相邻段的系数矩阵进行解耦,适合模块化建模,有效提高了建模速度。
2.2 虚功原理
虚功原理是通过最小化施加在系统上的外力和力矩的虚功,使用变分微积分来计算系统的动力学方程。与拉格朗日方法不同,虚功原理方法可以直接将非保守效应纳入运动方程,而不需要可微的能量损失函数。一般情况下,在分析系统所受的外力和力矩时,只考虑弯曲应变,忽略软材料的黏性和法向应变,此时通过该种方法建立的模型计算效率高,但是精度相对较低。Rone等[29]在虚功原理框架下,通过计算系统惯性力、驱动力、摩擦力、重力和弹力效应推导得到连续体机器人的动力学模型,该模型适用于任何类型的外力和力矩,包括耗散效应和外部负载存在的情况。Liu等[30]基于虚功原理,利用驱动绳索的动态集中长度模拟驱动过程,建立了连续体机器人的动态模型,推导了绳索张力与拉格朗日乘子之间的关系,给出了绳索摩擦力的分布规律。为了提高建模精度,Wang等[31]在考虑连续体机器人软材料黏性和正向应变的情况下,结合Cosserat杆理论和虚功原理建立了机器人的动力学模型,并通过二维和三维实验验证了模型的正确性,但是该模型的计算复杂度有所增加。
2.3 基于Cosserat杆理论的方法
基于Cosserat杆理论的连续体机器人动态建模方法是一种数值求解方法,该方法将连续体机器人分解成无穷小段,在每一小段上进行应力分析,推导得到动力学方程,在给定弹性和黏弹性材料的本构关系的情况下,将内力和力矩建模为与应变相关的函数,并将该函数与动力学方程组合得到描述连续体机器人动态行为的偏微分方程形式的动力学模型。Gravagne等[32]利用精确几何杆理论推导出平面连续机械臂大挠度运动学与动力学方程,并对其振动进行控制。Rucker等[33]在考虑外部载荷条件下,进一步通过耦合Cosserat杆和Cosserat弦理论建立了具有一般肌腱路径的连续体机器人的静态和动态模型,该模型适用于由于弯曲、扭转、剪切等引起的大变形场合。为了解决Cosserat杆建模方法模型求解困难的问题,Alqumsan等[34]采用广义-α数值方法对所建立的模型进行求解,同时设计基于滑模的鲁棒控制器对其进行控制。Jalali等[35]将连续体机器人等效为柔性杆,基于Cosserat杆理论建立了双臂协同操作连续体机器人的大挠度动力学模型,增强了模型的适用性,并提出了一种求解动态模型的数值方法。
2.4 数据驱动方法
数据驱动方法不需要系统的先验知识,通过来自试验样机或其他仿真模型的输入输出实验数据建立机器人的数学模型。Parvaresh等[36]引入数据驱动中的ARX线性模型和NARX非线性模型结构基于神经网络对连续体机器人进行动态建模,并且从质量、计算成本和适用性等不同角度对这2种模型进行了比较。Thuruthel等[37]和Centurelli等[38]分别采用递归神经网络和循环神经网络建立了连续体机器人的正向动力学模型。
3 控制策略
与传统刚性机器人不同,柔性连续体机器人的运行空间由驱动器空间、关节空间、构型空间和任务空间组成。由于驱动器空间、关节空间到构型空间的映射关系,以及构型空间到任务空间的映射关系均具有高度的非线性,极大地增加了其控制难度。在驱动器空间、关节空间到构型空间的映射过程中,控制器的设计通常只需要建立控制输入(压力、拉力、电压和温度等)与机器人形变特征(角度、长度)的转移关系,无须运动学模型。而在构型空间到任务空间的映射过程中,控制器的设计通常需要考虑运动学和动力学特征。值得注意的是,控制系统输入变量的差异会导致转移关系的不同,而输入变量主要取决于驱动原理,因此控制策略不能够在不同驱动原理的连续体机器人之间直接移植,从而降低了控制策略的适用性,增加了控制系统设计的难度。
为了从控制角度提高柔性连续体机器人的性能,国内外学者进行了大量的研究。本文以现有柔性连续体机器人存在的问题为导向,从基于模型控制、无模型控制和混合控制角度对目前连续体机器人的控制策略进行分析并总结。其中,基于模型的控制策略需要进行动力学或者运动学的非线性建模,能够实现控制问题的实时求解和动态响应的有效调节,但是这类控制策略依赖于连续体机器人的模型精度,在模型不准确或不确定性较强时控制效果往往不佳。此外,在动态交互的非结构化环境中基于模型的控制精度较低,且在控制命令的生成过程中计算量较大。为解决上述问题,基于在线学习算法和雅可比矩阵的无模型控制策略受到了国内外学者的关注。无模型控制可以避开柔性连续体机器人的复杂非线性建模过程,进而避免了环境和参数变化对控制性能的影响,但是控制精度依赖于采用输入和输出数据训练得到的模型,且在连续体机器人高速运行时的动态响应性能较差。为了克服基于模型控制和无模型控制的缺点,同时兼顾两者的优点,学者们提出了一种混合控制策略。下面对3类控制策略分别进行分析。
3.1 基于模型的控制策略
基于模型的控制策略主要分为开环控制和闭环控制[12]。通常,在需要高精度的定位和跟踪任务中,闭环控制的性能优于开环控制,但是开环控制实施简单方便,尤其是对于一些重复任务场合具有良好的应用效果。
开环控制根据连续体机器人模型和期望输出(yd)产生控制输入(Uin),然后通过控制器的调节得到驱动器的输入(
),进而实现连续体机器人的运动控制。由于没有传感器进行位置或力信息的反馈,开环控制效果严重依赖于模型的精度。在开环控制策略中,常用的系统模型是有限元模型和解析模型。有限元模型能够精确求解得到连续体机器人到达指定位置或者产生定量力所需的控制量,适用于任意形状和驱动机理的连续体机器人。Ficuciello等[39]采用有限元和拉格朗日乘数相结合的方法得到了正向和逆向接触力模型,并以此为基础设计了开环控制器,分析了真实对象和模拟对象上的选定点位移之间误差产生原因。Webster等[13]利用有限元模型设计了基于常曲率模型的连续体机器人开环控制器,结果表明,在载荷较小时,控制误差较小。相比于有限元模型,解析模型的建模精度针对特定系统时具有更好的应用效果,但是增加了计算过程的复杂性。同时,研究表明,开环控制和路径规划算法相结合使连续体机器人在重复任务的场合具有良好的应用效果。王亚明[40]提出了改进快速扩展随机树的路径规划算法,同时结合蛇形仿真运动算法,在航空发动机原位检测中取得了良好的应用效果。Wang等[41]提出采用前馈神经网络改善逆向动力学模型,通过适当调整任务优先级和末端执行器扭曲的值,调节操纵器的收敛轨迹以避免陷入局部极小,提高了连续体机器人的末端定位精度。
闭环控制策略的实施需要依赖传感器提供连续体机器人的形变状态或者所处的环境信息,而传感器的使用类型和安装方案取决于连续体机器人的驱动机理和物理结构,因此闭环控制策略框图需要增加传感器检测部分,包括静态控制和动态控制,其中静态控制系统结构如图4所示。Thomas等[42]采用光纤FBG光栅传感器进行连续体机器人的形状感测,并设计闭环控制器进行轨迹跟踪。Fang等[43]在闭环控制器的基础上,引入运动学模型设计了改进PID控制器,实现了连续体机器人的实时控制和运行性能的提升。Zhang等[44]进一步提高了形态感知精度,提出了一种蠕虫状连续体机器人,采用可视化单元、活检技术和电磁传感器相结合的检测方案,设计了在非结构化环境中的闭环静态控制器,实现了机器人形态和所处位置的实时反馈。
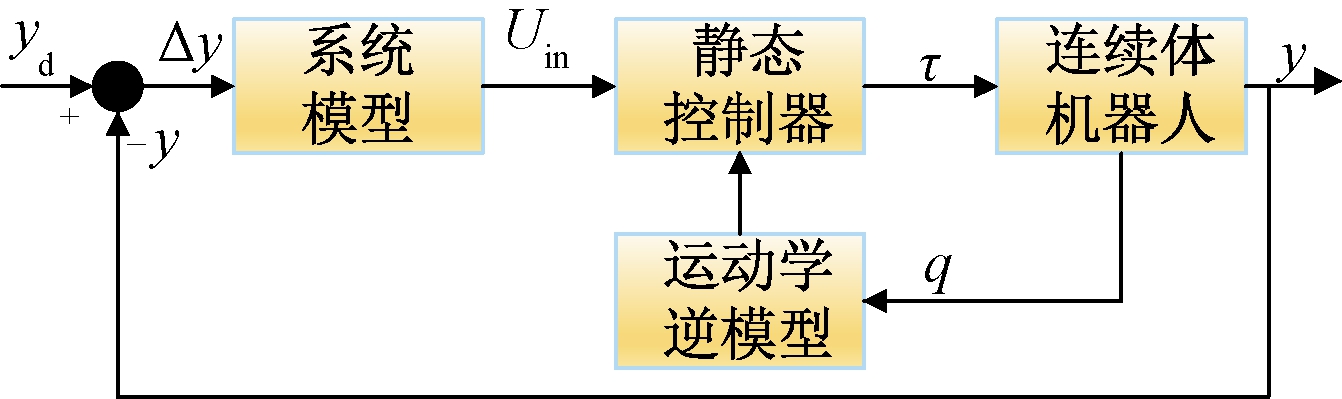
图4 基于模型的闭环静态控制框图
Figure 4 Model-based closed loop static control
block diagram
连续体机器人闭环动态控制系统结构框图如图5所示,该控制方式基于连续体机器人的动力学模型,结合非线性补偿提高系统的动态性能。Pang等[45]采用径向基神经网络建立了连续体机器人的动力学模型,并结合三轴电子罗盘传感器测量得到的位置信息,设计了连续体机器人的闭环控制器,确保了良好的多自由度弯曲性能。Santina等[46]分别设计了连续体机器人的曲率动态控制器和笛卡尔刚度控制器,保证机器人在轨迹跟踪过程中的自然柔软,并能够与非结构化环境有效交互。但是上述工作只实现了连续体机器人末端位置的控制,不能实现混合力/位控制。Liang等[47]提出了基于有限时间观测器的可变阻抗控制器进行连续体机器人的力/位混合控制,并对所提控制器的稳定性进行了研究。
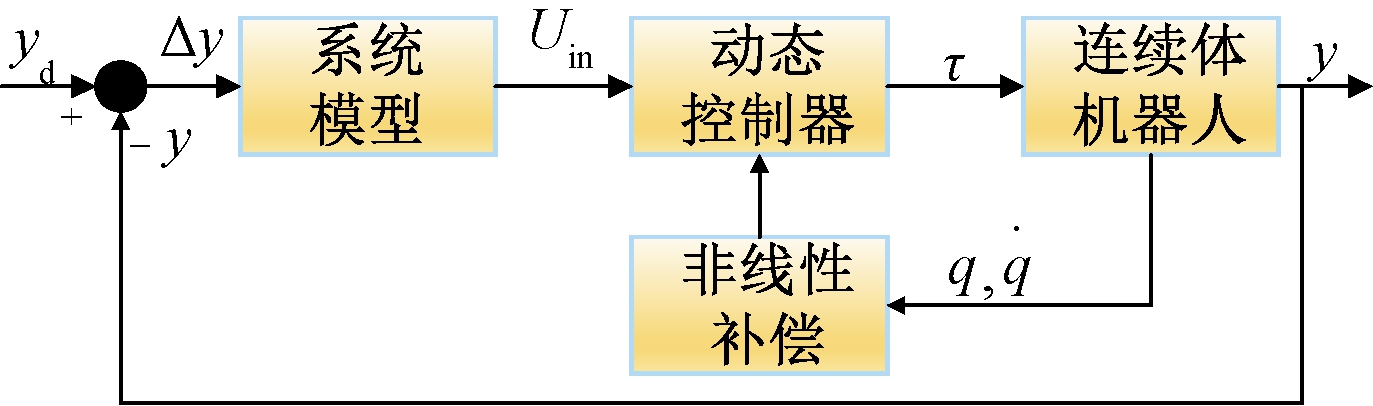
图5 基于模型的闭环动态控制框图
Figure 5 Model-based closed loop dynamic control
block diagram
基于模型的控制策略的实施效果会受到模型内部参数摄动和外部干扰的影响,因此如何提高基于模型控制的抗扰性能成为了近年来的研究热点。扩张状态观测器能够将内部参数摄动和外部干扰之和扩张为一个新的状态,在合理选取观测器增益的条件下准确地估计出该状态,通过设计反馈控制策略对扰动进行补偿,可提高系统的抗扰性能[48-49]。朱雨琪等[50]提出了一种基于线性降阶扩张状态观测器的抗扰控制策略,有效提高了连续体机器人在内部参数摄动和外部扰动影响下的运行性能。邱小璐等[51]针对空间连续体机器人系统故障下的控制问题,采用非奇异快速终端滑模控制器,并通过自适应径向基函数神经网络在线调整控制器的切换项增益,增强了控制器在模型参数扰动时的抗扰性能。
3.2 无模型控制策略
无模型控制策略同样可分为开环控制和闭环控制2类。在实施无模型开环控制策略时,除了需要利用传感器和给定轨迹生成控制量之外,往往还需要对连续体机器人姿态特征进行定性分析。Watanabe等[52]分析了绳驱动连续体机器人不同期望姿态下张力和布线的分布关系,进而推导出期望姿态的协同关系,利用该协同关系设计了控制器,取得了良好的应用效果。现有的无模型闭环控制策略主要借助运动学逆模型的在线学习或者对应雅可比矩阵的在线估计,其控制框图如图6所示。
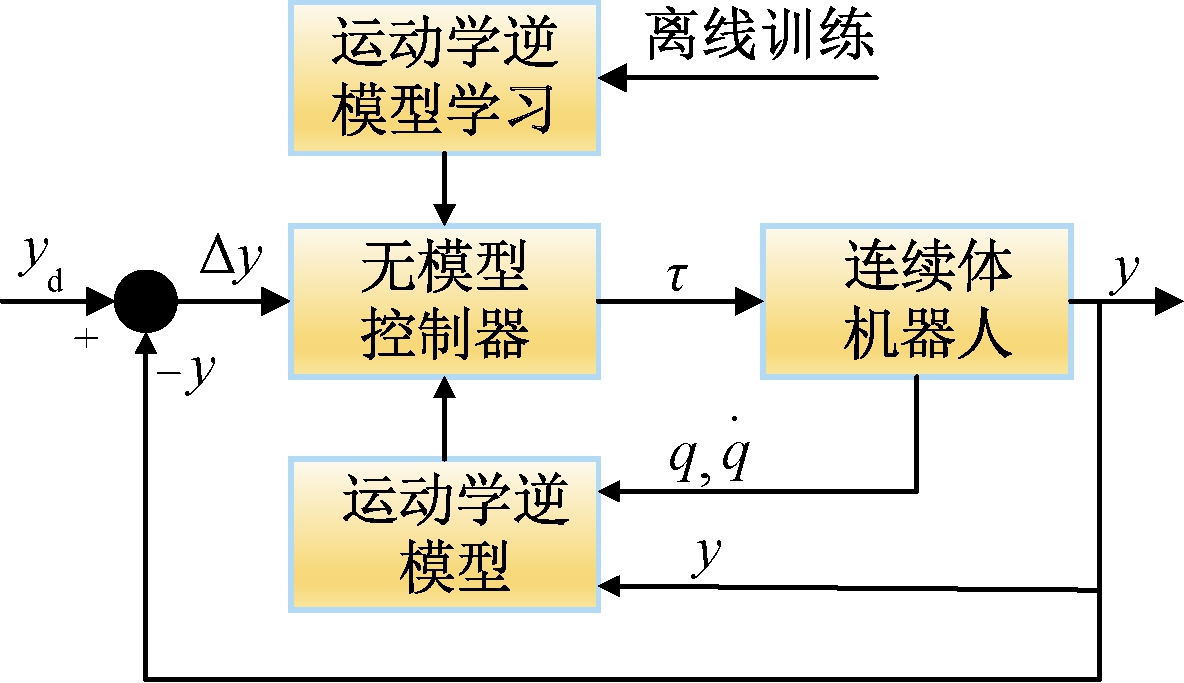
图6 无模型的闭环动态控制框图
Figure 6 Model-free closed loop dynamic control
block diagram
Yu等[53]提出了一种连续体机器人的无模型闭环控制策略,该控制策略采用2个梯度神经网络:一个用于求解逆运动学问题;另一个用于估计连续体机器人的雅可比矩阵。Tan等[54]在此基础上,提出了基于变参数递归神经网络的无模型控制方案和基于阻尼归零神经网络的闭环控制系统,实现了无模型下连续体机器人的操控。为了提高控制系统的鲁棒性,李进华等[55]提出了一种基于无模型自适应控制的连续体机器人末端位置控制方法,设计了连续体机器人末端位置和驱动输入之间的伪雅可比矩阵,利用期望轨迹和伪雅可比矩阵的估计值得到系统的输入,可实现期望轨迹的跟踪,同时所设计的伪雅可比矩阵考虑了实时的采样误差和干扰的影响,能够提升连续体机器人的轨迹跟踪精度。Kamtikar等[56]进一步引入深度学习方法,采用卷积神经网络来预测结构化环境中期望姿态所需的驱动,增强了连续体机器人控制的鲁棒性和对环境的适应性。在稳定性和鲁棒性研究方面,Gao等[57]提出了构造误差转换方案和调整函数相结合的无模型鲁棒自适应控制策略,同时分析控制策略实施时柔性连续体机器人的全局稳定性。Yip等[58]利用经验估计连续体机器人雅可比矩阵,分析了环境约束对雅可比矩阵的影响,进而设计了无模型连续体机器人控制器,仿真和实验结果表明,所提出的控制策略能够拓宽连续体机器人的运动空间,提高了与环境安全稳定交互的能力。在后续工作中,其进一步提出了一种同时实现连续体机器人末端位置和力的无模型混合控制方法,实现了连续体机器人与未知环境的安全交互。尽管无模型控制策略能够有效避免由于模型内部参数摄动和外部扰动带来的控制精度问题,但是在线学习以及雅可比矩阵的计算会增加控制系统的复杂性。
3.3 混合控制策略
混合控制策略通常将模型信息和学习算法相结合,能够兼顾基于模型控制和无模型控制的优点,降低对模型信息的依赖以及学习方法的复杂度,但是需要同时进行建模和学习算法设计,增加了控制策略的设计难度。此外,对连续体机器人的感知能力也有更高的要求。Aloi等[59]提出了一种适用于连续体机器人的力感知方法,采用最小二乘优化和扩展卡尔曼滤波器来进行负载的估算,并采用基于模型的框架设计了控制器,实验结果表明,所提方法可有效提高控制精度。Zhao等[60]提出了一种基于神经网络模型和空间曲线拟合的形状重建方法,建立了机器人的局部逆运动学模型,进而设计了基于模型的准静态控制器,提高了连续体机器人末端位置的控制精度。Tang等[61]将连续体机器人模型和学习算法相结合,提出了一种基于模型的在线学习自适应控制算法,减小了轨迹跟踪的均方根误差。相比基于模型控制和无模型控制,混合控制需要解决模型的简化、学习算法的执行效率、控制器的稳定性等诸多问题,在控制策略的工程应用方面还需要进一步探索。
4 发展趋势
由于连续体机器人本身所固有的柔顺性和安全性等特点,越来越多的学者对连续体机器人的研究产生兴趣,并已经在连续体机器人设计、驱动、建模和控制等方面取得了许多代表性的研究成果,促进了连续体机器人在诸多领域的应用。然而,尽管目前关于连续体机器人的研究有了一定的发展,连续体机器人在建模和控制方面的发展仍然面临一些重大挑战,主要包括以下几个方面。
(1)提出新的建模方法。通过对建模研究的现状分析可知,在模型复杂度、计算成本和精度之间折中是建立连续体机器人模型时需要考虑的主要因素。需要进一步研究新的建模方法,并在合理的假设下实现模型的简化,在提高计算效率的同时准确表征机器人的行为特征。
(2)提高连续体机器人的感知能力。理想的感知能力应该能够以无限自由度重构机器人的形变状态,然而目前只有FBG光纤传感器可以实现高自由度重建,在未来的研究中应结合理论算法,实现连续体机器人感知能力的提高。
(3)提出有效适用的混合学习方法的控制策略。现有研究中提出的混合控制策略还无法兼顾控制性能和算法复杂度,需要借鉴人工智能的最新研究成果,提出新的基于模型和无模型的混合学习方法,实现系统性能和执行效率的综合提升。
(4)建立高效的变刚度调控方法。连续体机器人的灵活性和柔顺性使其具有良好的环境适应能力,但是同时也存在结构刚度低的缺点。当机器人受到较大的外部载荷或需要输出较大的力时,容易产生比较大的变形,对机器人的运动精度和控制精度都会造成很大影响。因此,连续体机器人的精准变刚度调控研究是需要关注的重要研究内容。
(5)开发连续体机器人物理模拟引擎。传统的刚性机器人有一些比较成熟的仿真系统,但是这些系统一般不适用于具有无限自由度的连续体机器人。目前,模型的辨识以及控制算法的验证必须依赖于真实的机器人平台,增加了实验成本。因此,开发一种针对连续体机器人的实时物理仿真模拟引擎是非常有必要的。
(6)建立有效的可靠性分析方法。由于连续体机器人的材料性质,其本身具有高度的非线性特性,导致连续体机器人系统长时间运行后,容易出现疲劳失效的问题。因此,在使用连续体机器人,尤其是将其投入实际应用时,对其进行可靠性分析是至关重要的。
5 结束语
本文分别从建模和控制2个方面对连续体机器人的研究现状进行分析和总结。首先,总结了国内外研究中连续体机器人在运动学建模和动力学建模上主要采用的建模方法,分别对各类方法进行介绍,并从模型精度、复杂度和计算成本等方面总结了各建模方法的优缺点,以便相关研究人员根据特定需求选择相应的建模方法。其次,将连续体机器人的控制策略分为基于模型控制、无模型控制和混合控制,基于模型控制和无模型控制又分为开环控制和闭环控制2种类型。本文分别对各种类型的控制策略进行分析和总结,并对它们的优缺点进行了比较,指出混合控制策略能够继承基于模型控制和无模型控制的优点,值得进一步深入研究。最后,指出了连续体机器人研究中存在的研究挑战,并对未来发展方向进行了展望。
[1] ZHONG Y, HU L H, XU Y S. Recent advances in design and actuation of continuum robots for medical applications[J]. Actuators, 2020, 9(4): 142.
[2] LI C, RAHN C D. Design of continuous backbone, cable-driven robots[J]. Journal of Mechanical Design, 2002, 124(2): 265-271.
[3] NEPPALLI S, JONES B A. Design, construction, and analysis of a continuum robot[C]∥2007 IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway: IEEE, 2007: 1503-1507.
[4] RENDA F, GIORELLI M, CALISTI M, et al. Dynamic model of a multibending soft robot arm driven by cables[J]. IEEE Transactions on Robotics, 2014, 30(5): 1109-1122.
[5] CAO K, KANG R J, BRANSON D T III, et al. Workspace analysis of tendon-driven continuum robots based on mechanical interference identification[J]. Journal of Mechanical Design, 2017, 139(6): 062303.
[6] PANG S X, SHANG W W, ZHANG F, et al. Design and stiffness analysis of a novel 7-DOF cable-driven manipulator[J]. IEEE Robotics and Automation Letters, 2022, 7(2): 2811-2818.
[7] OMISORE O M, HAN S P, XIONG J, et al. A review on flexible robotic systems for minimally invasive surgery[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(1): 631-644.
[8] ZHONG Y, HU L H, XU Y S. Recent advances in design and actuation of continuum robots for medical applications[J]. Actuators, 2020, 9(4): 142.
[9] LI S Y, HAO G B. Current trends and prospects in compliant continuum robots: a survey[J]. Actuators, 2021, 10(7): 145.
[10] KOLACHALAMA S, LAKSHMANAN S. Continuum robots for manipulation applications: a survey[J]. Journal of Robotics, 2020, 2020: 1-19.
[11] WANG J, CHORTOS A. Control strategies for soft robot systems[J]. Advanced Intelligent Systems, 2022, 4(5): 2100165.
[12] THURUTHEL T G, ANSARI Y, FALOTICO E, et al. Control strategies for soft robotic manipulators: a survey[J]. Soft Robotics, 2018, 5(2): 149-163.
[13] WEBSTER R J, JONES B A. Design and kinematic modeling of constant curvature continuum robots: a review[J]. International Journal of Robotics Research, 2010, 29(13): 1661-1683.
[14] JONES B A, WALKER I D. Kinematics for multisection continuum robots[J]. IEEE Transactions on Robotics, 2006, 22(1): 43-55.
[15] BAJO A, SIMAAN N. Kinematics-based detection and localization of contacts along multisegment continuum robots[J]. IEEE Transactions on Robotics, 2012, 28(2): 291-302.
[16] GOLDMAN R E, BAJO A, SIMAAN N. Compliant motion control for multisegment continuum robots with actuation force sensing[J]. IEEE Transactions on Robotics, 2014, 30(4): 890-902.
[17] QI F, JU F, BAI D M, et al. Kinematic analysis and navigation method of a cable-driven continuum robot used for minimally invasive surgery[J]. The International Journal of Medical Robotics + Computer Assisted Surgery: MRCAS, 2019, 15(4): e2007.
[18] ZHONG G L, PENG B W, DOU W Q. Kinematics analysis and trajectory planning of a continuum manipulator[J]. International Journal of Mechanical Sciences, 2022, 222: 107206.
[19] BARRIENTOS J, DONG X, AXINTE D, et al. Real-time kinematics of continuum robots: modelling and validation[J]. Robotics and Computer-integrated Manufacturing, 2021, 67: 102019.
[20] RENDA F, BOYER F, DIAS J, et al. Discrete cosserat approach for multisection soft manipulator dynamics[J]. IEEE Transactions on Robotics, 2018, 34(6): 1518-1533.
[21] LILGE S, NUELLE K, BOETTCHER G, et al. Tendon actuated continuous structures in planar parallel robots: a kinematic analysis[J]. Journal of Mechanisms and Robotics, 2021, 13(1): 011025.
[22] BLACK C B, TILL J, RUCKER D C. Parallel continuum robots: modeling, analysis, and actuation-based force sensing[J]. IEEE Transactions on Robotics, 2018, 34(1): 29-47.
[23] ZHAO B, ZENG L, WU Z, et al. A continuum manipulator for continuously variable stiffness and its stiffness control formulation[J]. Mechanism and Machine Theory, 2020, 149: 103746.
[24] GIORELLI M, RENDA F, CALISTI M, et al. Neural network and Jacobian method for solving the inverse statics of a cable-driven soft arm with nonconstant curvature[J]. IEEE Transactions on Robotics, 2015, 31(4): 823-834.
[25] THURUTHEL T G, FALOTICO E, MANTI M, et al. Learning closed loop kinematic controllers for continuum manipulators in unstructured environments[J]. Soft Robotics, 2017, 4(3): 285-296.
[26] WANG Y, YIP H W, ZHENG H, et al. Design and experimental validation of a miniaturized robotic tendon-driven articulated surgical drill for enhancing distal dexterity in minimally invasive spine fusion[J]. IEEE/ASME Transactions on Mechatronics, 2021, 26(4): 1858-1866.
[27] FALKENHAHN V, MAHL T, HILDEBRANDT A, et al. Dynamic modeling of bellows-actuated continuum robots using the Euler-Lagrange formalism[J]. IEEE Transactions on Robotics, 2015, 31(6): 1483-1496.
[28] YANG J Z, PENG H J, ZHOU W Y, et al. A modular approach for dynamic modeling of multisegment continuum robots[J]. Mechanism and Machine Theory, 2021, 165: 104429.
[29] RONE W S, BEN-TZVI P. Continuum robot dynamics utilizing the principle of virtual power[J]. IEEE Transactions on Robotics, 2014, 30(1): 275-287.
[30] LIU Z Z, ZHANG X G, CAI Z Q, et al. Real-time dynamics of cable-driven continuum robots considering the cable constraint and friction effect[J]. IEEE Robotics and Automation Letters, 2021, 6(4): 6235-6242.
[31] WANG H S, WANG C, CHEN W D, et al. Three-dimensional dynamics for cable-driven soft manipulator[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(1): 18-28.
[32] GRAVAGNE I A, RAHN C D, WALKER I D. Large deflection dynamics and control for planar continuum robots[J]. IEEE/ASME Transactions on Mechatronics, 2003, 8(2): 299-307.
[33] RUCKER D C, WEBSTER III R J. Statics and dynamics of continuum robots with general tendon routing and external loading[J]. IEEE Transactions on Robotics, 2011, 27(6): 1033-1044.
[34] ALQUMSAN A A, KHOO S, NORTON M. Robust control of continuum robots using Cosserat rod theory[J]. Mechanism and Machine Theory, 2019, 131: 48-61.
[35] JALALI A, JANABI-SHARIFI F. Dynamic modeling of tendon-driven co-manipulative continuum robots[J]. IEEE Robotics and Automation Letters, 2022, 7(2): 1643-1650.
[36] PARVARESH A, MOOSAVIAN S A A. Linear vs. nonlinear modeling of continuum robotic arms using data-driven method[C]∥2019 7th International Conference on Robotics and Mechatronics (ICRoM). Piscataway: IEEE, 2020: 457-462.
[37] THURUTHEL T G, FALOTICO E, RENDA F, et al. Model-based reinforcement learning for closed-loop dynamic control of soft robotic manipulators[J]. IEEE Transactions on Robotics, 2019, 35(1): 124-134.
[38] CENTURELLI A, ARLEO L, RIZZO A, et al. Closed-loop dynamic control of a soft manipulator using deep reinforcement learning[J]. IEEE Robotics and Automation Letters, 2022, 7(2): 4741-4748.
[39] FICUCIELLO F, MIGLIOZZI A, COEVOET E, et al. FEM-based deformation control for dexterous manipulation of 3D soft objects[C]∥2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Piscataway: IEEE, 2019: 4007-4013.
[40] 王亚明. 航空发动机原位检测绳驱动机器人感知与控制技术研究[D]. 南京: 南京航空航天大学, 2020.
WANG Y M. Research on perception and control technology of aero-engine in situ inspection rope driven robot[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2020.
[41] WANG Y F, ZHU C X, DING Y, et al. Feedforward neural network assisted configuration transition control of continuum surgical manipulators[C]∥27th International Conference on Mechatronics and Machine Vision in Practice (M2VIP). Piscataway: IEEE, 2022: 617-622.
[42] THOMAS T L, SIKORSKI J, ANANTHASURESH G K, et al. Design, sensing, and control of a magnetic compliant continuum manipulator[J]. IEEE Transactions on Medical Robotics and Bionics, 2022, 4(4): 910-921.
[43] FANG Y H, HILL S, BA W M, et al. A novel method to solve the inverse kinematics for continuum robots accelerated by PID theory[C]∥12th International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER). Piscataway: IEEE, 2022: 840-844.
[44] ZHANG B Y, FAN Y W, YANG P H, et al. Worm-like soft robot for complicated tubular environments[J]. Soft Robotics, 2019, 6(3): 399-413.
[45] PANG W, WANG J B, FEI Y Q. The structure, design, and closed-loop motion control of a differential drive soft robot[J]. Soft Robotics, 2018, 5(1): 71-80.
[46] SANTINA C D, KATZSCHMANN R K, BICCHI A, et al. Model-based dynamic feedback control of a planar soft robot: trajectory tracking and interaction with the environment[J]. International Journal of Robotics Research, 2020, 39(4): 490-513.
[47] LIANG X, HE G P, SU T T, et al. Finite-time observer-based variable impedance control of cable-driven conti-nuum manipulators[J]. IEEE Transactions on Human-Machine Systems, 2022, 52(1): 26-40.
[48] 海星朔, 徐炳辉, 任羿, 等. 基于改进鸽群优化的机器人自抗扰控制方法[J]. 郑州大学学报(工学版), 2019, 40(4): 20-24, 31.
HAI X S, XU B H, REN Y, et al. Robot active distur-bance rejection control based on an enhanced pigeon-inspired optimization[J]. Journal of Zhengzhou University (Engineering Science), 2019, 40(4): 20-24, 31.
[49] 曾庆山, 周亚帅, 陶长春, 等. 电驱动机械臂的自抗扰鲁棒哈密顿跟踪控制[J]. 郑州大学学报(工学版), 2022, 43(4): 1-7, 15.
ZENG Q S, ZHOU Y S, TAO C C, et al. Active distur-bance rejection robust Hamiltonian tracking control of electrically driven manipulator[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(4): 1-7, 15.
[50] 朱雨琪, 向国菲, 马丛俊, 等. 基于建模优化的连续体机器人轨迹跟踪及扰动抑制策略研究[J]. 空间控制技术与应用, 2022, 48(2): 29-38.
ZHU Y Q, XIANG G F, MA C J, et al. Trajectory tra-cking control and disturbance-rejection strategy for conti-nuum robots with improved modeling method[J]. Aerospace Control and Application, 2022, 48(2): 29-38.
[51] 邱小璐, 蔡志勤, 刘忠振, 等. 空间连续型机器人自适应鲁棒容错控制[J]. 计算力学学报, 2021, 38(1): 46-50.
QIU X L, CAI Z Q, LIU Z Z, et al. Adaptive robust fault tolerant control of a space continuum robot[J]. Chinese Journal of Computational Mechanics, 2021, 38(1): 46-50.
[52] WATANABE Y, HIGASHIMORI M. Synergy-based analytical design of wire-driven continuum manipulators[J]. IEEE Robotics and Automation Letters, 2022, 7(4): 9310-9317.
[53] YU P, TAN N, ZHANG M, et al. Inverse-free tracking control of continuum robots with unknown models based on gradient neural networks[C]∥2022 IEEE 11th Data Driven Control and Learning Systems Conference (DDCLS). Piscataway: IEEE, 2022: 648-653.
[54] TAN N, YU P, ZHANG M, et al. Towards unified adaptive teleoperation based on damping ZNN for robot manipulators with unknown kinematics[J]. IEEE Transactions on Industrial Electronics, 2022, PP(99): 1-10.
[55] 李进华, 卜逸凡, 李晓阳, 等. 丝驱动连续体机器人的无模型自适应控制[J]. 天津大学学报(自然科学与工程技术版), 2022, 55(7): 754-763.
LI J H, BU Y F, LI X Y, et al. Model-free adaptive control for tendon-driven continuum robots[J]. Journal of Tianjin University (Science and Technology), 2022, 55(7): 754-763.
[56] KAMTIKAR S, MARRI S, WALT B, et al. Visual servoing for pose control of soft continuum arm in a structured environment[J]. IEEE Robotics and Automation Letters, 2022, 7(2): 5504-5511.
[57] GAO X F, LI X C, SUN Y, et al. Model-free tracking control of continuum manipulators with global stability and assigned accuracy[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(2): 1345-1355.
[58] YIP M C, CAMARILLO D B. Model-less feedback control of continuum manipulators in constrained environments[J]. IEEE Transactions on Robotics, 2014, 30(4): 880-889.
[59] ALOI V, DANG K T, BARTH E J, et al. Estimating forces along continuum robots[J]. IEEE Robotics and Automation Letters, 2022, 7(4): 8877-8884.
[60] ZHAO Q X, LAI J W, HUANG K C, et al. Shape estimation and control of a soft continuum robot under external payloads[J]. IEEE/ASME Transactions on Mechatronics, 2022, 27(5): 2511-2522.
[61] TANG Z Q, HEUNG H L, TONG K Y, et al. Model-based online learning and adaptive control for a “human-wearable soft robot” integrated system[J]. International Journal of Robotics Research, 2021, 40(1): 256-276.