由于能源、环境问题的日益突出,太阳能、波浪能和风力发电等新能源发电得到广泛应用[1],然而新能源发电装置受环境因素影响大,普遍存在输出电压变化大的问题[2],难以实现能量的储存。升降压转换器由于同时具有升压和降压能力,适用于新能源发电装置的储能。传统升降压转换器因寄生参数影响,在极端占空比下运行时,效率会大大降低,电压应力很大,难以工作在较宽范围的输入电压下。同时其输入电流不连续,输入电流纹波大。因此,更宽的转换比和输入电流连续成为解决问题的关键。
Banaei等[3]、Miao等[4]、Banaei等[5]、Li等[6]及李梦娇等[7]通过加入储能单元和开关器件获得更宽的转换比,但其输入电流不连续。交错型转换器[8]在低压应力下可以实现高升压或降压转换比,但控制策略复杂。Bahrami等[8]、Hsieh等[9]、Hasanpour等[10]及荣德生等[11]采用耦合电感结构,通过调节匝数比使电路获得更高升压比和降压比,但其开关管数量多,开关损耗大。Zhang等[12]和Kumar等[13]提出了单管的升降压转换器,在实现更宽转换比的同时,也能实现输入电流连续,但其开关管电压应力大。
升降压转换器通常采用传统的PI 控制,但是在某些应用场合,如输入电压变化较大时,传统的PI 控制往往无法获得满意的系统动态和静态控制性能,甚至会出现系统不稳定运行的现象。Li等[14]、Yang等[15]及周坤雨等[16]提出了预测控制、滑模控制等控制策略,这些策略能提高升降压转换器的输出动态响应的速度,但是不适用于存在较大输入扰动的情况。前馈算法通过对输入电压的采样,可以抑制输入电压扰动对输出电压的影响,能够有效改善转换器的输入暂态响应[17]。
本文提出了一种新型升降压转换器。使用耦合电感获得更宽的转换比,为提高效率,由电容和二极管组成的无源钳位电路回收漏感能量,抑制漏感造成的开关管电压尖峰,使得输入电流连续。设计了一种PI控制器结合前馈控制策略,实现转换器在整个输入电压范围内良好的输入暂态响应。这种控制策略能使转换器稳定工作在新能源发电装置储能场景。
1 转换器模态分析
所提出的升降压转换器的等效电路如图1所示,由二极管D1、D2、D3、电感L1、耦合电感、电容C1和Co、开关管S组成。为了便于转换器分析,电容C1和Co足够大,VC1和VCo在一个开关周期内可视为恒定电压;耦合电感的匝数比定义为Np∶Ns=1∶n。转换器在连续导通模式(continuous conduction mode,CCM)下工作,主要波形和能量流动分别如图2和图3所示。在一个开关周期内,转换器主要有4个工作模态,各模态的主要工作过程如下。
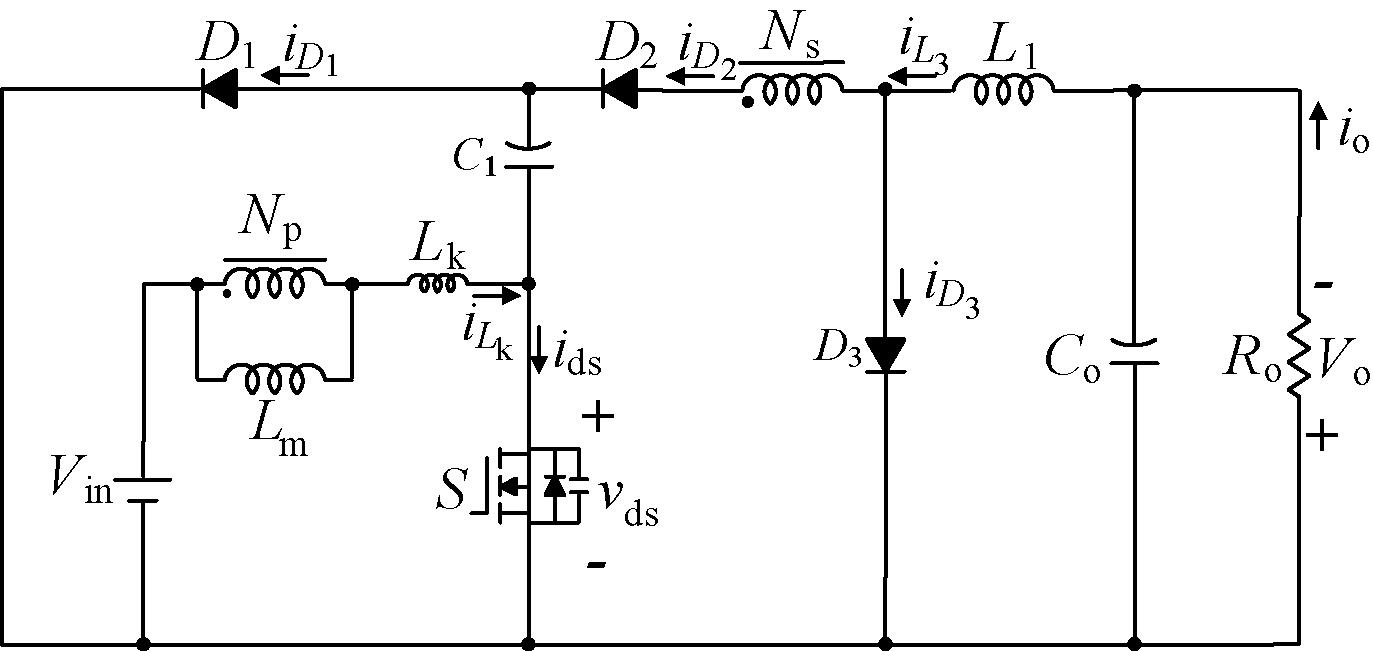
图1 所提转换器等效电路
Figure 1 Equivalent circuit of proposed converter
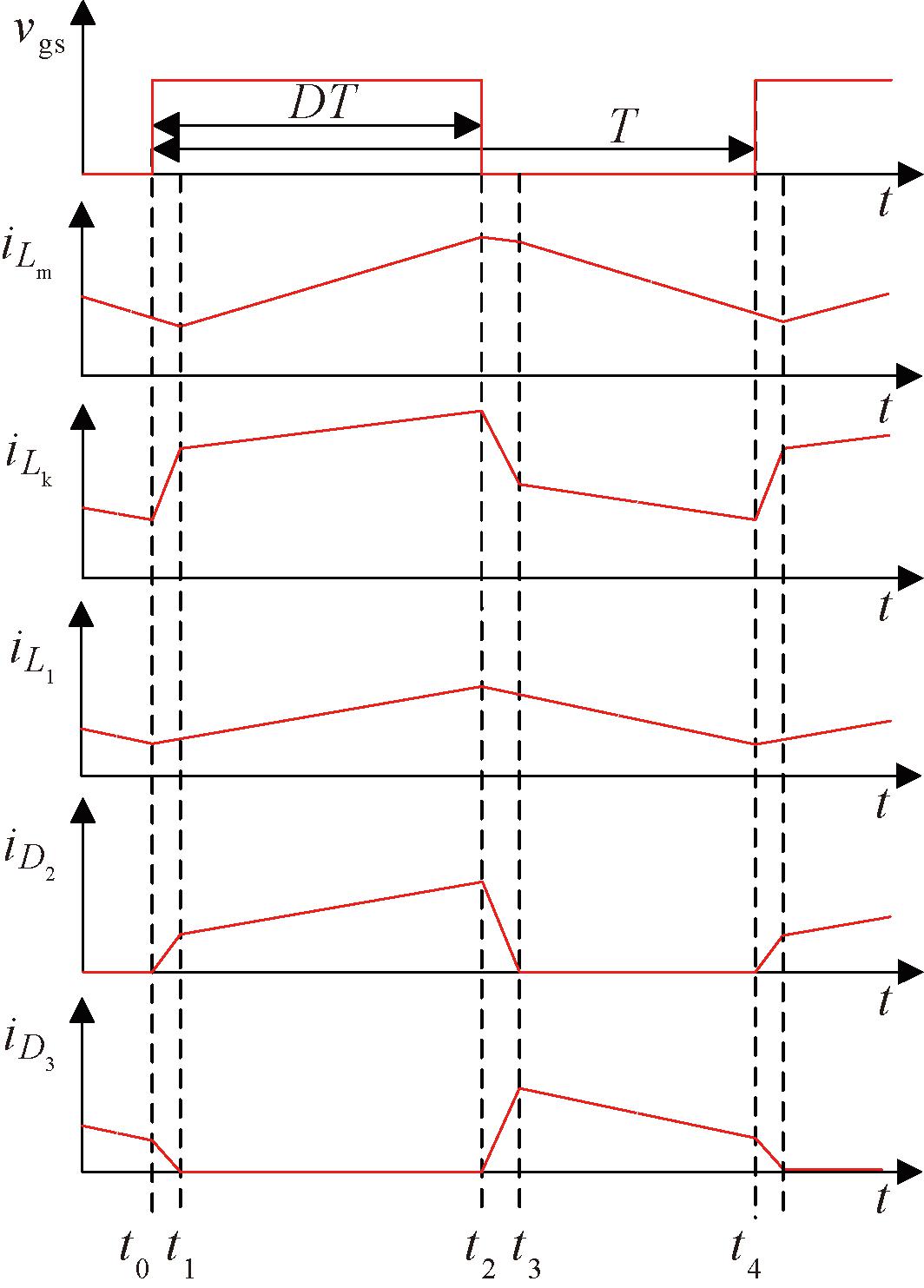
图2 所提转换器的主要波形
Figure 2 Key waveform diagram of the proposed converter
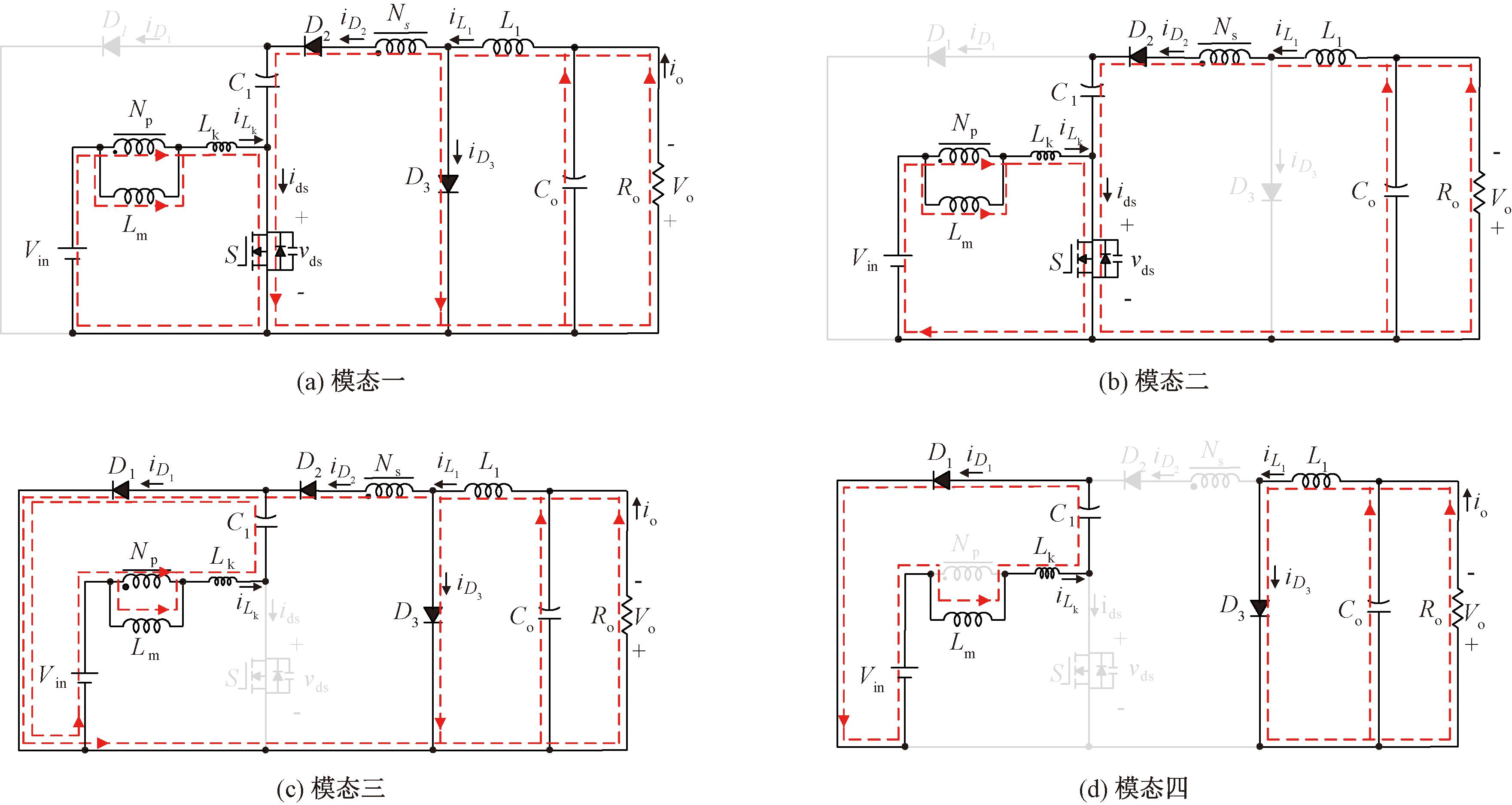
图3 转换器的4种工作模态
Figure 3 Four operation modes of the proposed converter
模态一(t0~t1,图3(a)):S、D2、D3导通,D1截止。Vin为耦合电感一次侧充电,iLk增加。电感L1通过D3为负载提供能量,C1与耦合电感二次侧为负载和L1充电,iD3减小。当iD3减小为0时,此模态结束。
模态二(t1~t2,图3(b)):S、D2导通,D1、D3截止。Vin为耦合电感一次侧充电,iLk增加,C1和耦合电感二次侧为负载和L1充电,iL1增加。当开关管S关断时,此模态结束。
模态三(t2~t3,图3(c)):S关断,D1、D2、D3导通。Vin和耦合电感一次侧为C1充电,iLm线性下降。耦合电感二次侧与L1为负载供电,iL1持续减小。当iLm等于iLk时,D2截止,此模态结束。
模态四(t3~t4,图3(d)):S关断、D2截止,D1、D3导通。Vin和耦合电感一次侧为C1充电,iLm减小。L1为负载供电,iL1下降。当开关管S导通时,此模态结束。
2 稳态分析和比较
2.1 电压转换比
为了简化分析,模态一和模态三是由于漏感Lk引起的,时间很短,只考虑模态二和模态四。
在图3(b)的0~DT期间,根据基尔霍夫电压定律(KVL),推导出的方程式为
VLm=Vin;
(1)
VL1=VC1+nVLm-VCo。
(2)
在图3(d)的DT~T期间,方程表示为
VLm=VC1-Vin;
(3)
VL1=-VCo。
(4)
根据式(1)和式(3),由Lm的伏秒平衡可得
(5)
根据式(1)、(3)、(4),由L1的伏秒平衡可得
(6)
由式(6)可得,转换器的电压转换比为
(7)
图4展示了在不同匝数比n的情况下,电压转换比M与占空比D的关系曲线,当占空比一定时,匝数比越高,电压转换比越高。
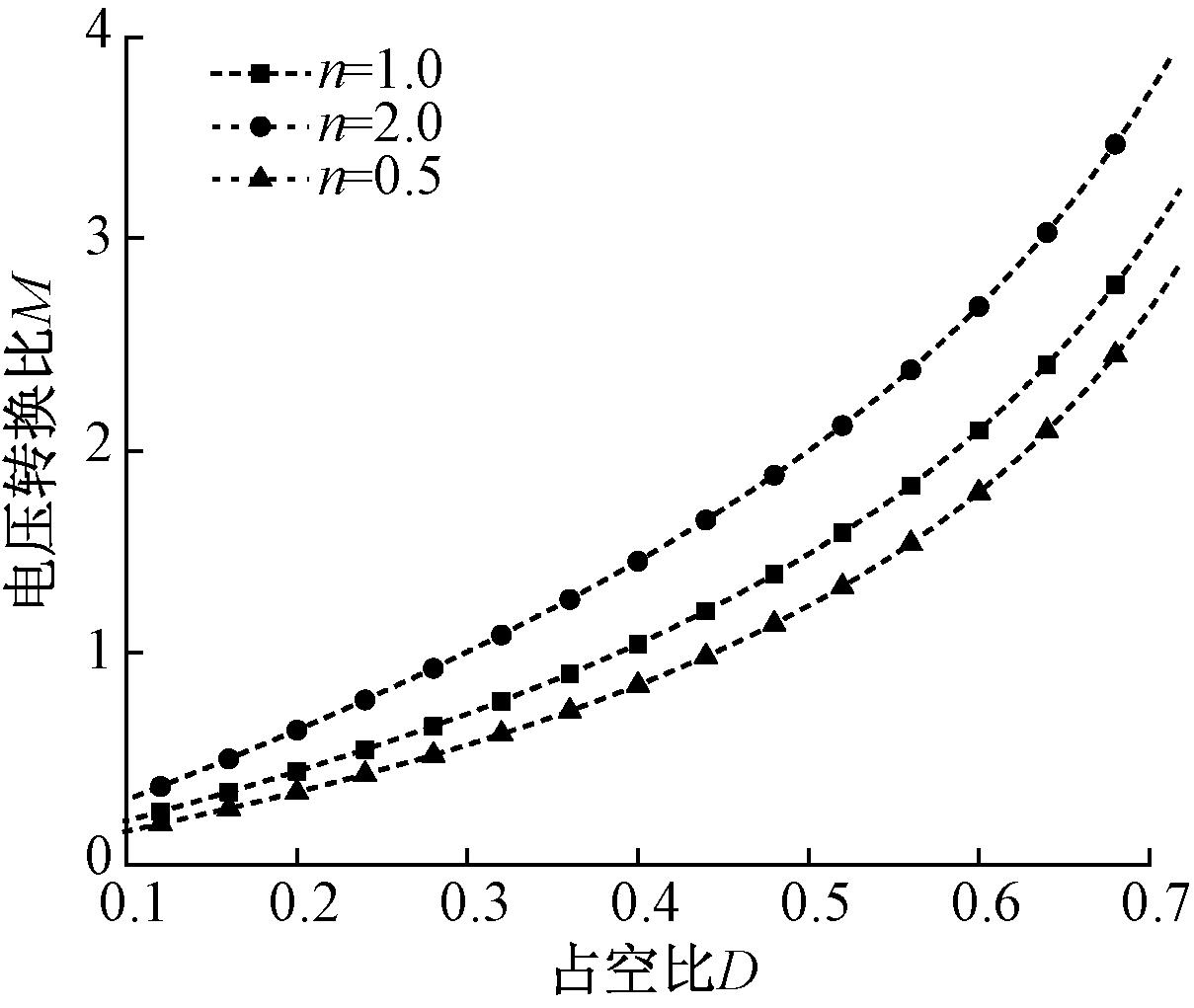
图4 不同匝数比下电压转换比与占空比之间的关系曲线
Figure 4 Curve of the relationship between conversion ratio and duty cycle under different turns ratios
2.2 电压电流应力分析
根据图3(b)和图3(d)可以推导出开关管和二极管的电压应力如下:
(8)
(9)
(10)
从图3(b)中,根据基尔霍夫电流定律(KCL),可推导出以下关系:
iCo=io-iL1;
(11)
iC1=iL1=iD2。
(12)
从图3(d)中,根据KCL,可推导出以下关系:
iC1=-iLm=-iD1;
(13)
iCo=iL1-io;
(14)
iD3=iL1。
(15)
根据式(11)和式(14),由电容Co的安秒平衡可得
![]() (io-iL1)dt+
(io-iL1)dt+![]() (io-iL1)dt=0⟹IL1=Io。
(io-iL1)dt=0⟹IL1=Io。
(16)
由图3(b)可推导出电感L1的纹波如下:
(17)
由式(16)和式(17)可得L1的电流最大值和最小值为
(18)
(19)
根据式(12)、(13)、(16),由电容C1的安秒平衡得到ILm为
(20)
根据图3(d),Lm的纹波表示为
(21)
由式(20)、(21)可得Lm的电流最大值和最小值为
(22)
(23)
根据图3(b)和3(d)以及式(16)和式(20)可以推导出开关管和二极管的电流应力如下:
ID1=ID2=DIo;
(24)
ID3=(1-D)Io;
(25)
(26)
2.3 功率器件设计
在边界导电模式(boundary conduction mode,BCM)下,输出电流为IoB,根据式(19)和(23)可以得到电感L1与Lm为
(27)
(28)
假设C1和Co的电压纹波为ΔVC1和ΔVCo,fs为开关频率,电容的计算公式为
(29)
根据式(4)、(11)、(12)、(16),电容C1、Co应该满足以下条件:
(30)
(31)
2.4 性能对比
如表1所示,本文对单开关管结构的转换器与所提出转换器进行了性能对比。与文献[6]中的转换器相比,所提转换器输入电流连续,开关管电压应力低,能够降低输入电流纹波和开关管开关损耗;与文献[13-14]中的转换器相比,所提转换器组件总量数少,开关管电压应力低,具有成本低和效率高的优点。
表1 转换器性能对比
Table 1 Converter performance comparison
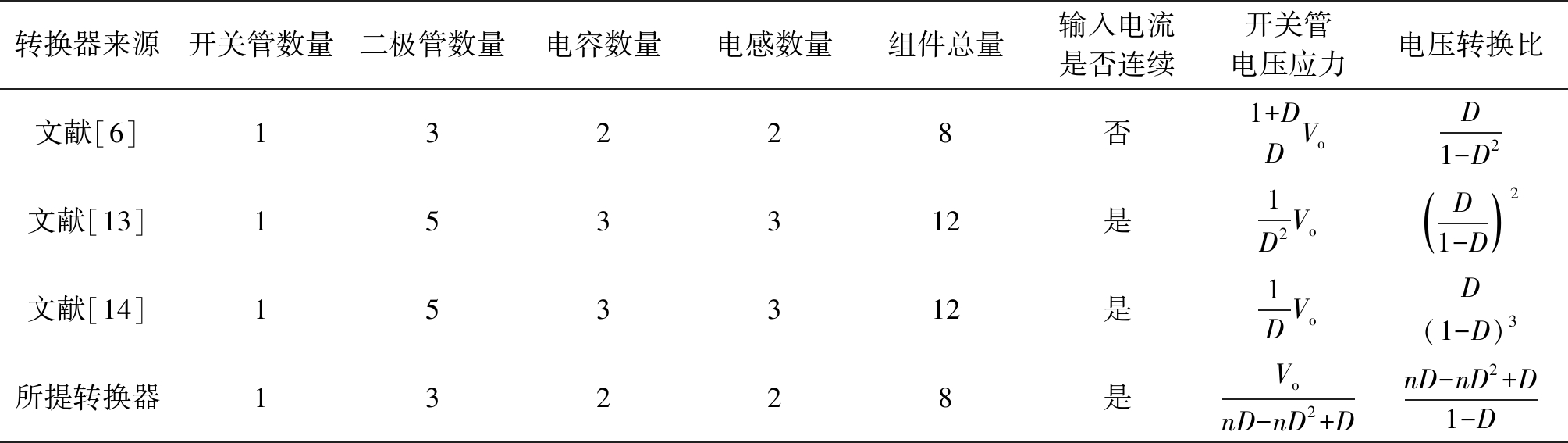
转换器来源开关管数量二极管数量电容数量电感数量组件总量输入电流是否连续开关管电压应力电压转换比文献[6]13228否1+DDVoD1-D2文献[13]153312是1D2VoD1-D()2文献[14]153312是1DVoD(1-D)3所提转换器13228是VonD-nD2+DnD-nD2+D1-D
3 转换器控制策略
3.1 小信号建模
小信号建模被用来推导后续控制的开环传递函数,本小节提供了所提出的转换器的小信号推导和分析,利用开环传递函数推导出合适的PI参数。为了简化CCM模态下该转换器的小信号模型分析,在分析过程中只考虑模态二和模态四,将状态向量定义为
(32)
(33)
并且输入向量定义为
u=[vin]。
(34)
在0~DT时间段,根据图3(b)可以得到以下状态矩阵:
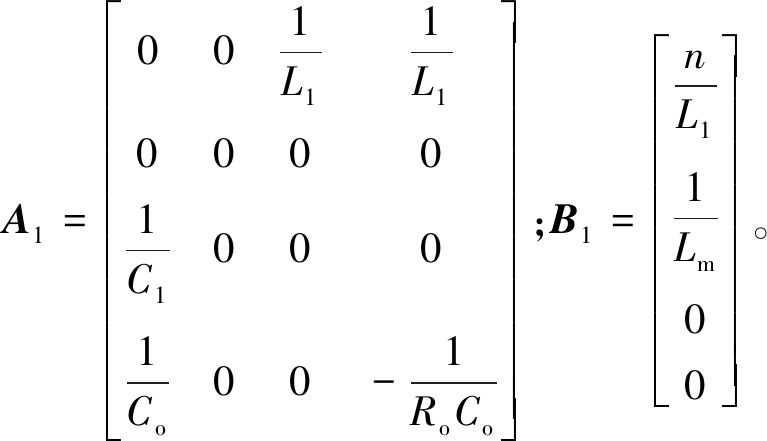
(35)
在DT~T时间段,根据图3(d)可以得到以下状态矩阵:
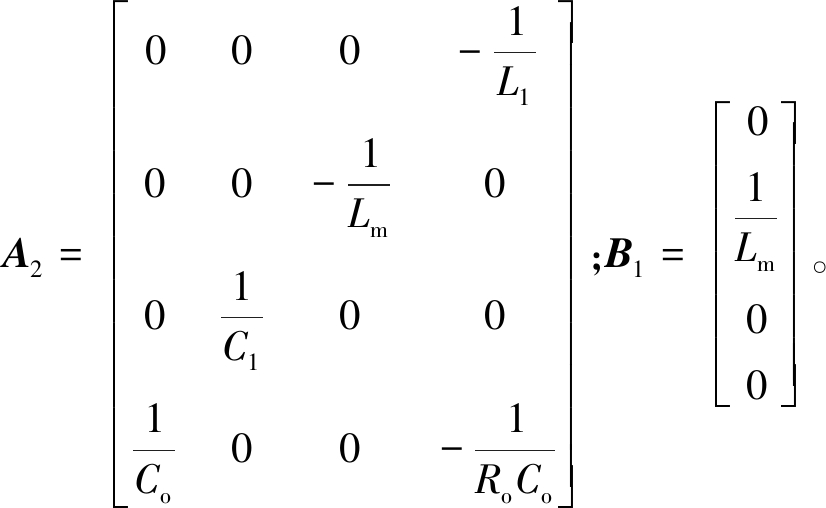
(36)
状态平均方程如下:
(37)
根据式(33)、(34)、(35)、(36)、(37)可得空间状态平均矩阵如下:
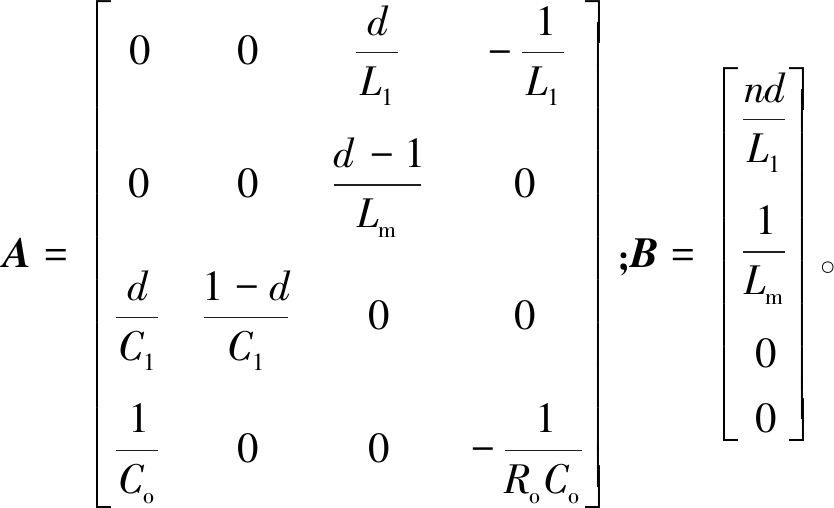
(38)
状态变量、输入变量和控制变量可以用小信号干扰变量描述为
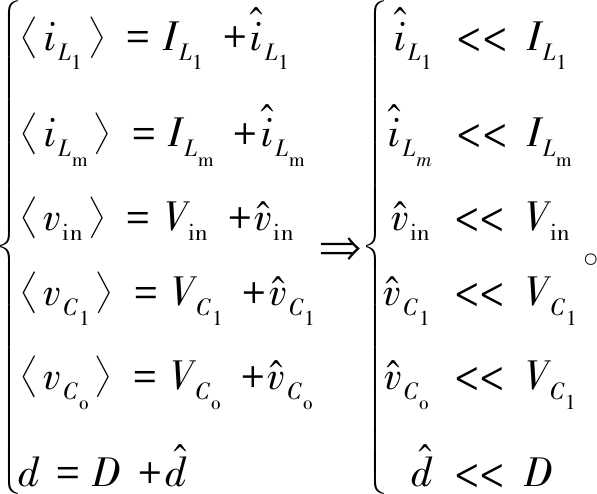
(39)
式中:IL1、ILm、Vin、VC1、VCo、D分别为iL1、iLm、vin、vC1、vCo、d的平均值。占空比到输出的传递函数如下:
(40)
式中:M0=R(1-D)2;M1=(L1(1-D)2-D2Lm);M2=R(CoL1(1-D)2+Lm(CoD2-C1));M3=C1L1Lm;M4=C1CoL1LmR;N0=R(1-D)2((1-D)2+1);N1=D2Lm(Dn-1-n);N2=-LmC1R((1-D)2n+1-D)。
3.2 PI控制器设计
为了使转换器工作能够稳定运行,在小信号模型的基础上进行PI控制器的设计,PI控制器的传递函数定义为
(41)
闭环传递函数GClose-Loop(s)表示为
GClose-Loop(s)=GVod(s)Gc(s)。
(42)
根据式(41)和式(42),采用工程近似法对Kp、Ki进行取值,Kp为0.000 78,Ki为0.001。升压模式下闭环伯德图如图5(a)所示,降压模式下的闭环伯德图如图5(b)所示。图5说明了在PI控制器的作用下,转换器在升压与降压状态下工作稳定状态均稳定。
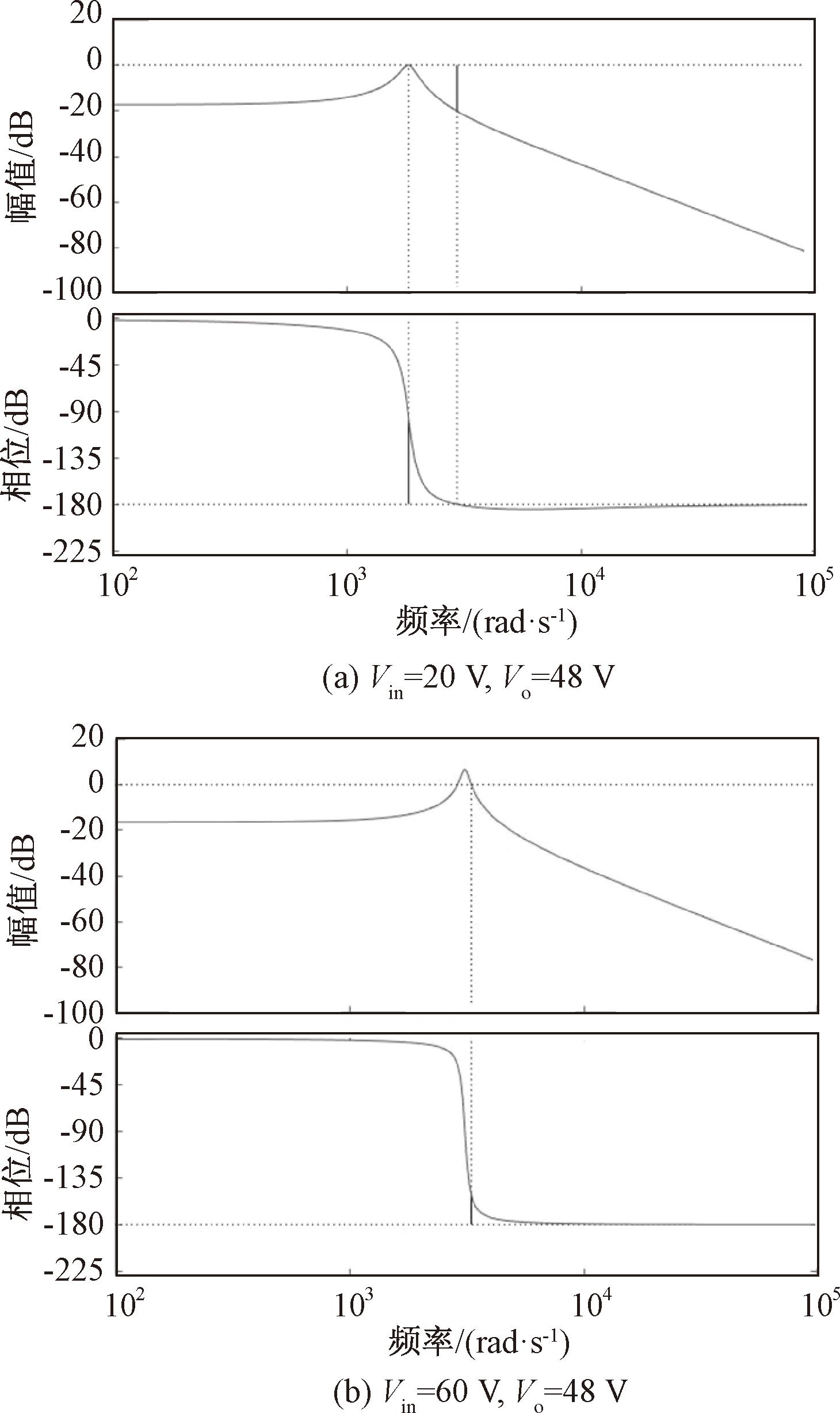
图5 加入PI控制器后的环路增益伯德图
Figure 5 Bode diagram of loop gain after adding PI controller
3.3 PI控制器结合前馈控制策略
根据输入采样电压和输出给定电压计算转换器占空比的前馈算法,通过小信号建模得出PI参数,使转换器在升压和降压模式下稳定输出电压,控制框图如图6所示。
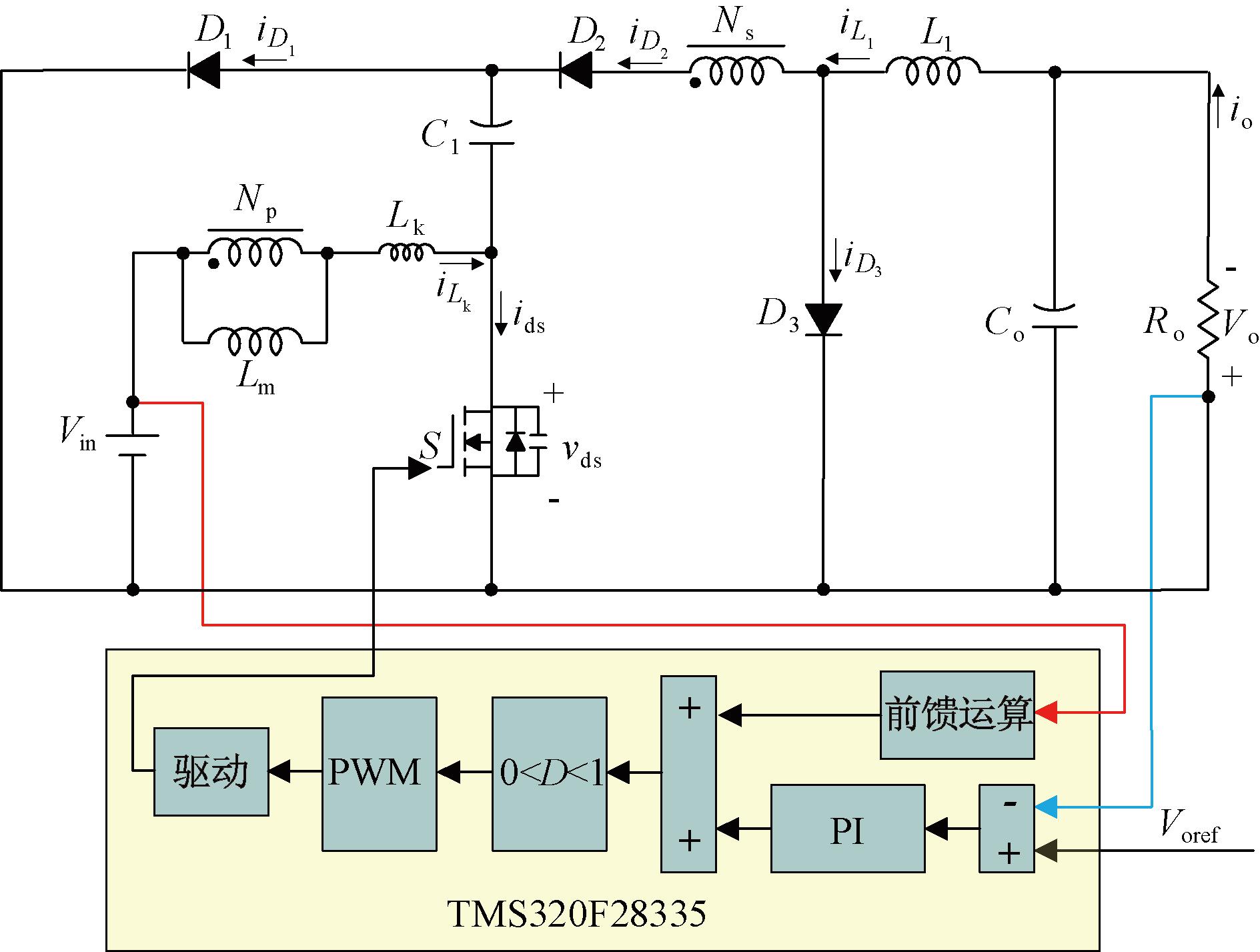
图6 闭环控制框图
Figure 6 Block diagram of the closed-loop control
4 损耗分析
转换器的效率受到寄生参数的影响。rL1、rLp、rLs、rC1及rCo分别表示电感L1、耦合电感一次侧、耦合电感二次侧、电容C1和Co的等效电阻。rds为开关管S的导通电阻,rD1、rD2和rD3分别为二极管D1、D2和D3的导通电阻,VF1、VF2和VF3分别为二极管D1、D2和D3的导通压降。
4.1 电感损耗
根据式(16)和式(20)可得L1、耦合电感一次侧和二次侧电流有效值为
(43)
(44)
(45)
根据式(43)、(44)、(45),总电感损耗为
(46)
4.2 电容损耗
根据式(13)、(14)、(16)、(20)可得电容C1和Co的电流有效值为
(47)
(48)
电容总损耗为
PC=IC1(rms)2rC1+ICo(rms)2rCo。
(49)
4.3 开关损耗
开关管损耗主要为rds引起的导通损耗以及上升时间tr和下降时间tf引起的开关损耗,根据式(26)可得开关管S的电流有效值为
(50)
开关管的导通损耗为
PS-C=Ids(rms)2rds。
(51)
开关管的开关损耗为
(52)
4.4 二极管损耗
二极管的损耗主要为导通损耗和开关损耗,根据式(24)和(25)可得二极管D1、D2和D3的电流有效值为
(53)
(54)
(55)
二极管的开关损耗可表示为
PD-S=VF1ID1+VF2ID2+VF3ID3。
(56)
二极管的导通损耗可表示为
(57)
根据式(48)、(49)、(51)、(52)、(56)、(57),转换器的总损耗为
PLoss=PL+PC+PS-C+PS-S+PD-C+PD-S。
(58)
假设Po为转换器的输出功率,则转换器效率为
(59)
5 实验验证
为了验证转换器和PI控制器结合前馈控制策略的可行性,表2给出了所提转换器的样机参数,实验样机实物如图7所示。图8展示了实验样机的实物测试图,其中直流电源型号为TH6900,直流负载型号为IT8513B+,示波器型号为WaveSurfer 4054HD,驱动芯片型号为TMS320F28335,电压探头型号为DP6150,电流探头型号为HCP8030。
表2 样机参数
Table 2 Parameters of the prototype

参数取值及型号输入电压Vin/V20~60 输出电压Vo/V48额定功率Po/W100开关频率fs/kHz50开关管SIPP110N20电感L1392.6 μH铁芯:PQ3230、材质:PC40耦合电感Lm=489.7 μH、Lk=1.8 μH、Np∶Ns=36∶36铁芯:EE4220、材质:PC40电容/μFC1=47、Co=220二极管D1:MBR20200CT、D2:MBR420、D3:MBR20300CT

图7 实验样机实物照片
Figure 7 Physical photo of experimental prototype

图8 实物测试照片
Figure 8 Physical test photo
在满载情况下,图9展示了所提转换器升压和降压2种模式下的实验波形。由图9(a)和9(d)可以看出,开关管在升压和降压情况下电压被钳位,说明漏感回收电路起作用。由图9(c)和9(f)可以看出iLk在升压和降压情况下是连续的,输入电流等于iLk,转换器输入电流连续。图9中的实验波形与图2所展示的波形图基本一致,开关管电压应力Vds在升压模式下为55 V,在降压模式下为88 V。
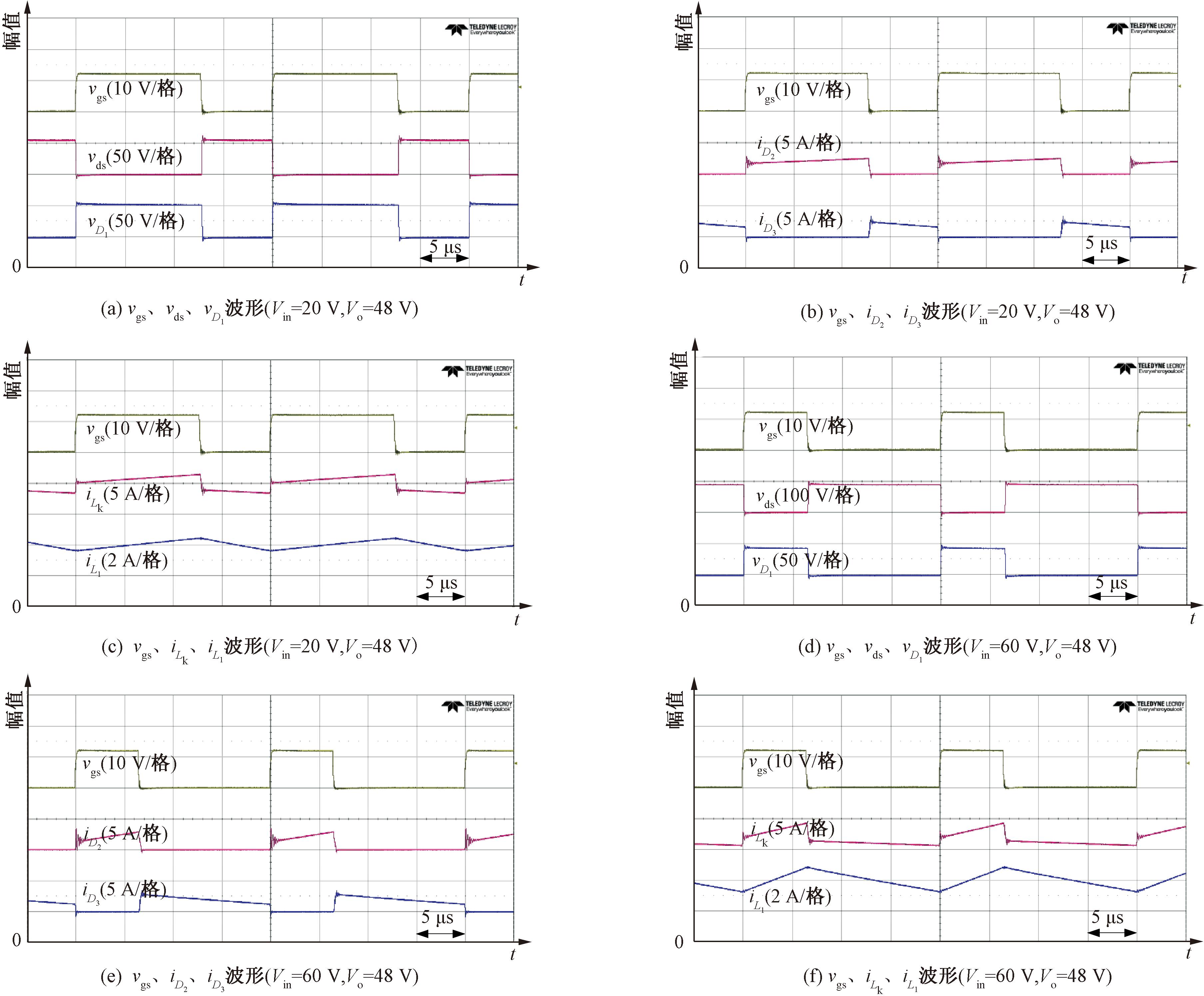
图9 满载情况下的实验波形
Figure 9 Experimental waveform under full load
图10展示了所提转换器在输入电压最大值为60 V,最小值为20 V,呈方波规律变化下加入前馈控制前后输入扰动对比测试实验波形。图10(a)展示了未加前馈的输入扰动测试波形,输出电压峰值达到72 V,超调量达50%;图10(b)展示了加入前馈控制的输入扰动测试波形,输出电压尖峰仅为50 V,超调量仅为4.2%,可见加入前馈控制提高了转换器的稳定性。图11(a)、11(b)分别展示了20 V和60 V输入电压、48 V输出电压,输出功率从半载变到满载再变回半载的扰动测试,输出电压稳定在48 V,说明所设PI参数能使所提转换器具有良好的输出暂态响应。
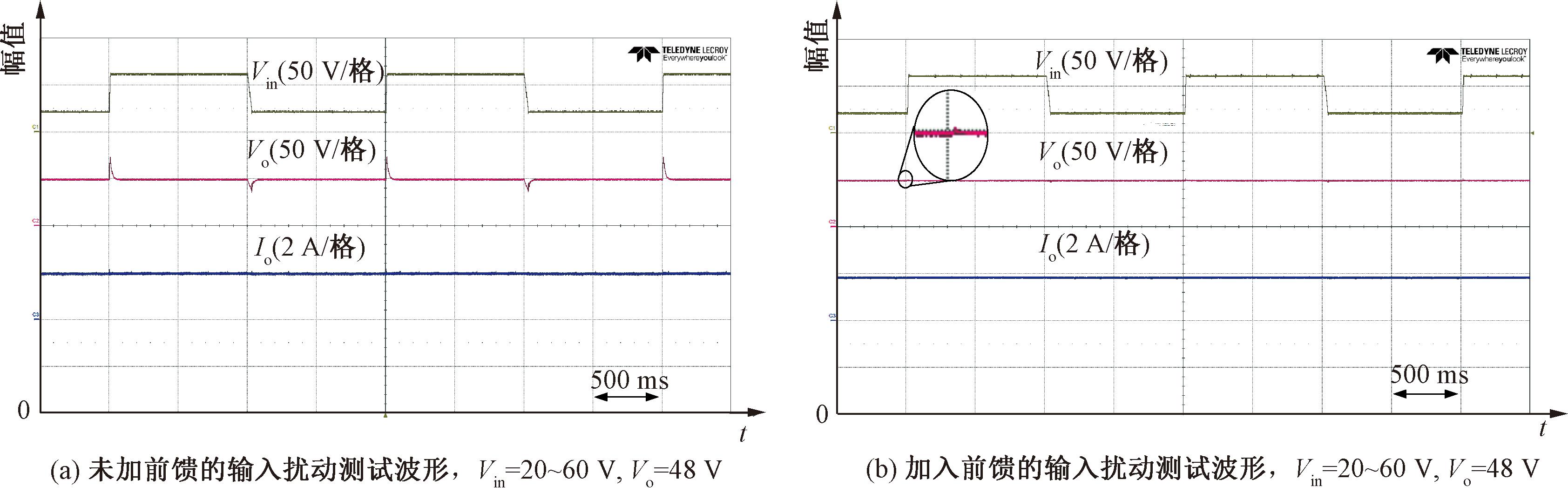
图10 加入前馈控制前后输入扰动对比测试
Figure 10 Transient experimental waveform of output power
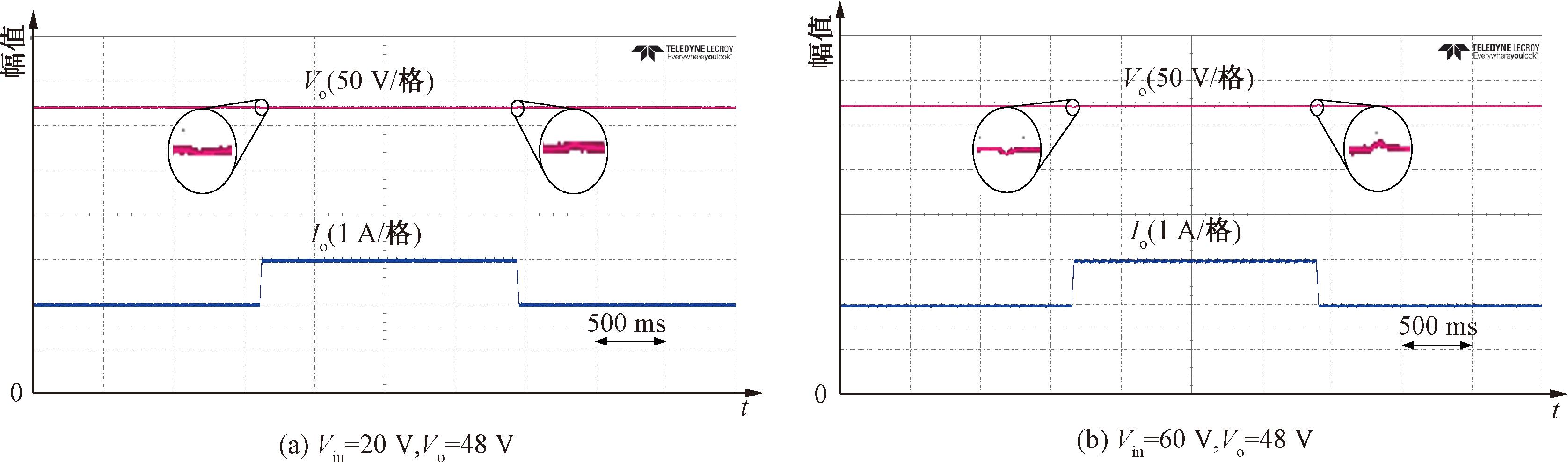
图11 输出功率的扰动测试
Figure 11 Transient experimental waveform of output power
图12为转换器升压模式和降压模式分别在不同功率下的效率曲线,满载测量效率分别为92.80%、96.03%,最大测量效率分别为97.08%、97.10%。
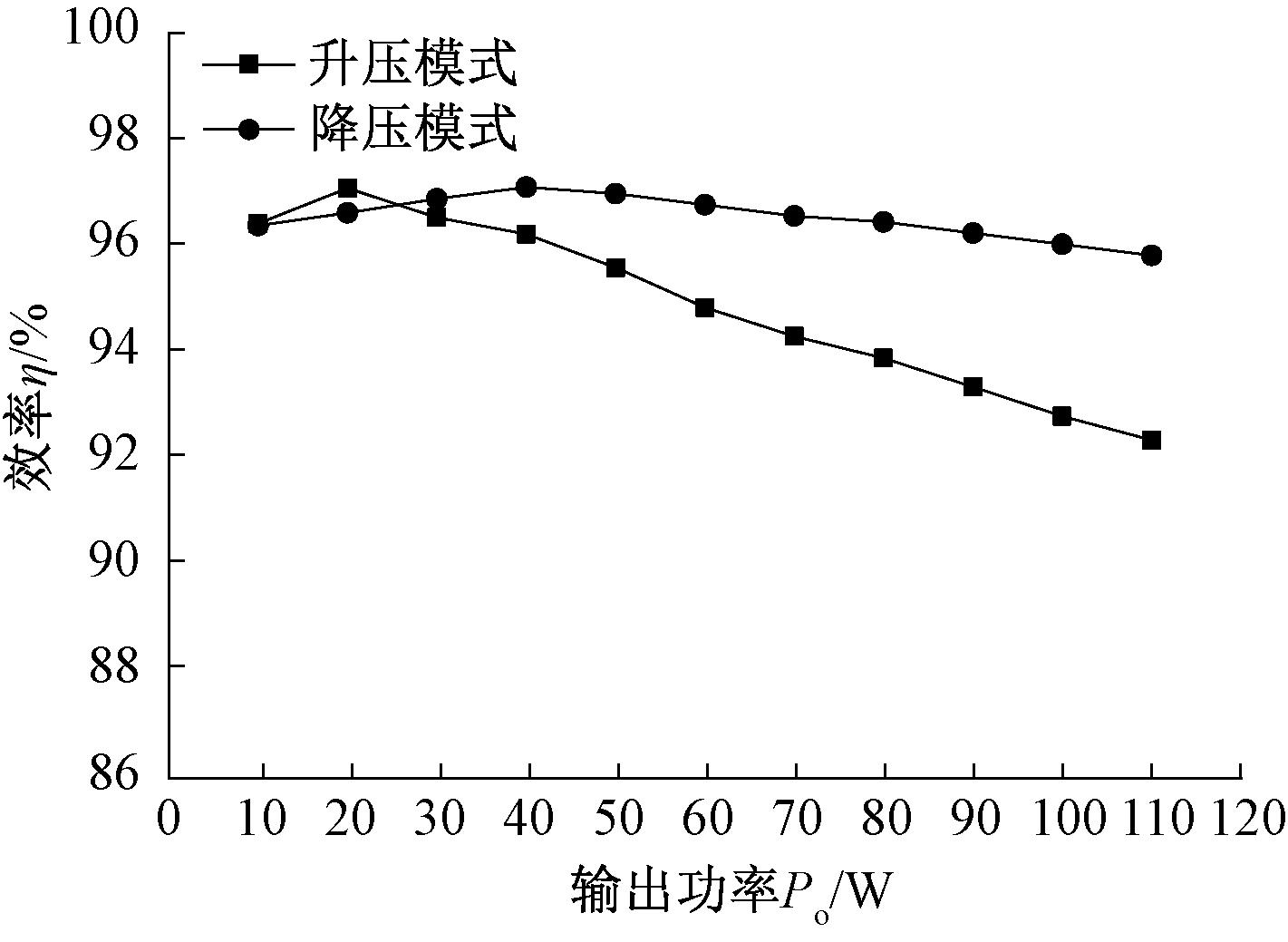
图12 升压和降压模式下实测效率曲线图
Figure 12 Measured efficiency curve of the boost and buck modes
图13展示了满载下转换器分别在20 V和60 V输入电压,48 V输出电压的计算损耗分布,升压模式总损耗为6.84 W,降压模式总损耗为3.38 W。
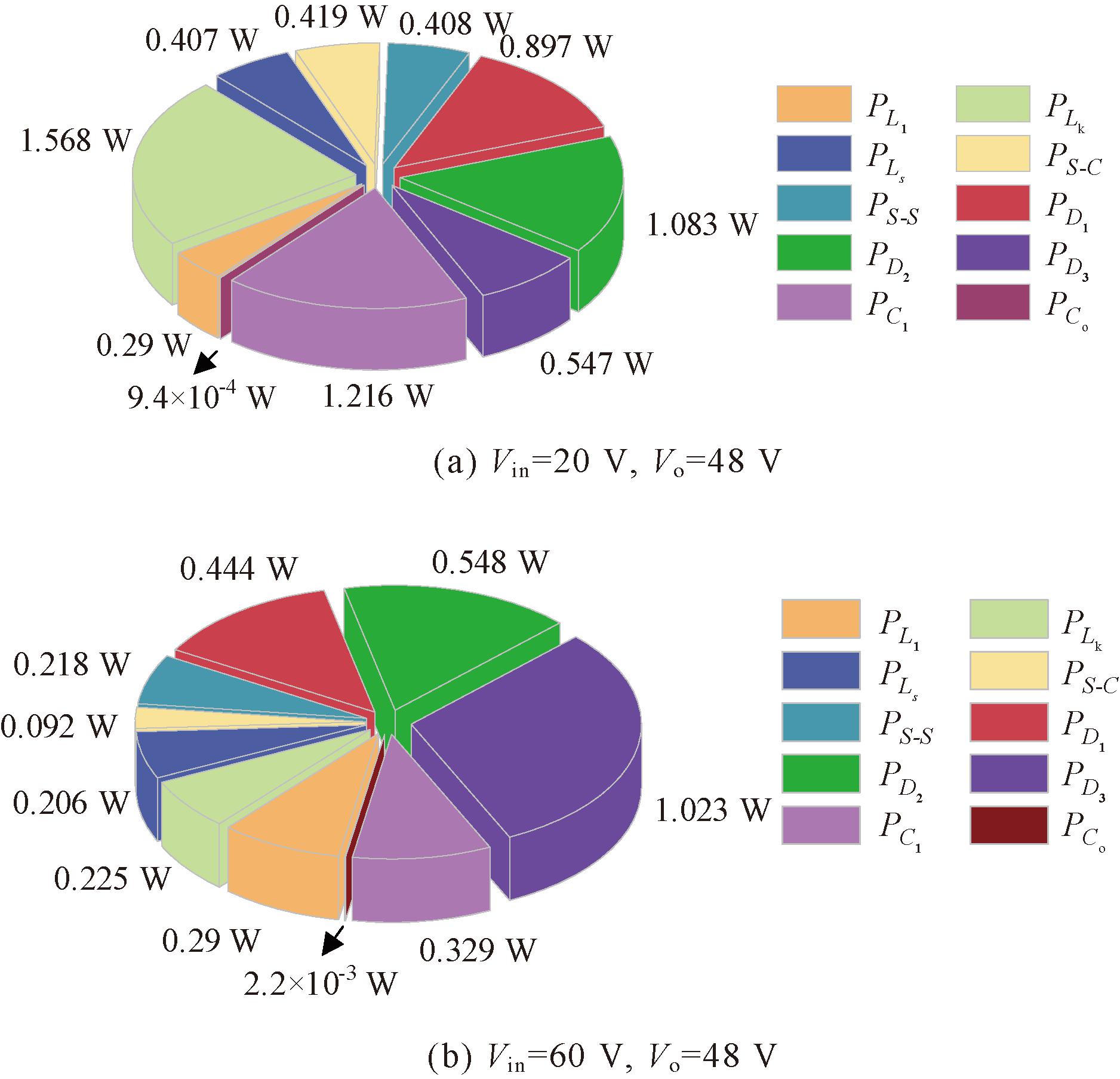
图13 满载情况下升压和降压模式计算损耗分布
Figure 13 Calculated loss distributions in boost and buck mode under full load
7 结论
针对新能源发电装置,本文提出一种基于PI 控制器结合前馈控制的新型单管耦合型升降压转换器。详细分析了转换器的工作原理,比较了相关转换器的性能,设计了转换器的控制策略。实验结果验证了转换器理论分析的可行性,所提控制策略改善了转换器对输入电压突变的响应特性。转换器升压满载测量效率为92.80%,最大效率为97.08%;降压满载测量效率为96.03%,最大效率为97.10%。
[1] 周强, 汪宁渤, 何世恩, 等. 高弃风弃光背景下中国新能源发展总结及前景探究[J]. 电力系统保护与控制, 2017, 45(10): 146-154.
ZHOU Q, WANG N B, HE S E, et al. Summary and prospect of China′s new energy development under the background of high abandoned new energy power[J]. Power System Protection and Control, 2017, 45(10): 146-154.
[2] LIU L B, WANG Z, WANG Y, et al. Optimizing wind/solar combinations at finer scales to mitigate renewable energy variability in China[J]. Renewable and Sustainable Energy Reviews, 2020, 132: 110151.
[3] BANAEI M R, BONAB H A F. A novel structure for single-switch nonisolated transformerless buck-boost DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2017, 64(1): 198-205.
[4] MIAO S, WANG F Q, MA X K. A new transformerless buck-boost converter with positive output voltage[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 2965-2975.
[5] BANAEI M R, BONAB H A F. A high efficiency nonisolated buck-boost converter based on ZETA converter[J]. IEEE Transactions on Industrial Electronics, 2020, 67(3): 1991-1998.
[6] LI J, LIU J J. A novel buck-boost converter with low electric stress on components[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 2703-2713.
[7] 李梦娇, 彭继慎, 孙瑄瑨. 具有高增益低输出电流纹波的Buck-Boost变换器[J]. 辽宁工程技术大学学报(自然科学版), 2022, 41(4): 372-378.
LI M J, PENG J S, SUN X J. Buck-boost converter with high gain and low output current ripple[J]. Journal of Liaoning Technical University (Natural Science), 2022, 41(4): 372-378.
[8] BAHRAMI H, FARHANGI S, IMAN-EINI H, et al. A new interleaved coupled-inductor nonisolated soft-switching bidirectional DC-DC converter with high voltage gain ratio[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5529-5538.
[9] HSIEH Y C, CHENG H L, CHANG E C, et al. A soft-switching interleaved buck-boost LED driver with coupled inductor[J]. IEEE Transactions on Power Electronics, 2022, 37(1): 577-587.
[10] HASANPOUR S, BAGHRAMIAN A, MOJALLALI H. Analysis and modeling of a new coupled-inductor buck-boost DC-DC converter for renewable energy applications[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 8088-8101.
[11] 荣德生, 孙瑄瑨. 高增益耦合电感组合Buck-Boost-Zeta变换器[J]. 中国电机工程学报, 2020, 40(14): 4590-4601.
RONG D S, SUN X J. High gain coupled inductance combination Buck-Boost-Zeta converter[J]. Proceedings of the CSEE, 2020, 40(14): 4590-4601.
[12] ZHANG N, ZHANG G D, SEE K W, et al. A single-switch quadratic buck-boost converter with continuous input port current and continuous output port current[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 4157-4166.
[13] KUMAR M A B, KRISHNASAMY V. A single-switch continuous input current buck-boost converter with noninverted output voltage[J]. IEEE Transactions on Power Electronics, 2023, 38(2): 2181-2190.
[14] LI X, LIU Y S, XUE Y S. Four-switch buck-boost converter based on model predictive control with smooth mode transition capability[J]. IEEE Transactions on Industrial Electronics, 2021, 68(10): 9058-9069.
[15] YANG Y, ZHONG W X, KIRATIPONGVOOT S, et al. Dynamic improvement of series-series compensated wireless power transfer systems using discrete sliding mode control[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 6351-6360.
[16] 周坤雨, 岳宁宁, 邱柯妮. 自供能系统中可配置DC-DC转换器的设计[J]. 郑州大学学报(工学版), 2021, 42(4):70-76, 97.
ZHOU K Y, YUE N N, QIU K N. A reconfigurable DC-DC converter design for energy-harvesting system[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(4):70-76, 97.
[17] SANKARANARAYANAN V, GAO Y C, ERICKSON R W, et al. Online efficiency optimization of a closed-loop controlled SiC-based bidirectional boost converter[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 4008-4021.