近些年来,中国修建了大量的系杆拱桥,但由于前期对拱桥吊杆损伤精确识别研究尚不充分,因损伤吊杆未及时更换引发的桥梁事故时有发生。因此,如何对吊杆损伤进行精准识别及精确评价是有效保证桥梁运营安全及降低桥梁养护维修费用的关键问题之一。
近年来,专家学者围绕桥梁结构损伤识别开展了一系列研究工作[1]。基于动力参数损伤识别的方法有频响函数法[2]、固有频率法[3]、应变模态法[4]等,这些方法对于系杆拱桥吊杆的整体识别效果良好,但是对于局部损伤识别效果不够显著[5];基于静力参数识别损伤方法主要通过测取静力荷载作用下的结构位移、应变等参数与原数据进行对比分析达到损伤识别的目的,其中基于影响线的损伤识别方法有挠度影响线[6]、转角影响线[7]、支座反力影响线[8]和应变影响线[9]等,这些方法避免了布置大量传感器的琐碎工作,同时数据处理也相对简单,不仅能精确识别局部损伤,而且具有可靠性强、准确性好、稳定性高等优点。
现有针对拱桥吊杆结构损伤识别研究中,基于静力参数的影响线损伤识别方法可以有效识别系杆拱桥结构的损伤位置。应变作为结构受力状态的一个局部性指标,是局部损伤识别的一个重要指标。Chen等[10]根据传统的应变影响线理论推导出一种基于长应变影响线的识别方法。Yang等[11]以应变影响线差值作为表征损伤前后的正则化指标,将其用于定位损伤位置、定量损伤程度。周宇等[12]提出基于应变影响线曲率的梁式子结构损伤识别方法。Wu等[9]针对移动车辆荷载作用下基于分布式宏观应变包络线的公路桥梁快速评估方法进行了参数化研究。上述学者在结构原理和应变影响线损伤识别方面的研究成果为开展拱桥吊杆应变影响线损伤识别研究提供了夯实的理论基础,但将应变影响线应用于拱桥吊杆损伤识别的研究还有待开展。
鉴于此,本文以下承式系杆拱桥为研究对象,首先,通过力法分析下承式系杆拱桥力学超静定结构,推导并分析吊杆损伤前后应变影响线解析表达式;其次,通过对应变影响线解析式做差分、微分处理,针对损伤吊杆建立基于吊杆的应变影响线差值、应变影响线差值曲率的损伤指标并定义损伤程度;最后,通过有限元数值模型算例证明了该方法对于下承式系杆拱桥的吊杆损伤评估效果。本文提出了一种准确识别并精准评估吊杆损伤位置及损伤程度的方法,以期为同类工程提供理论基础。
1 理论模型建立
下承式系杆拱桥中的吊杆多为柔性吊杆且主要承受轴力,而刚性吊杆需要抵抗吊杆与拱肋及系梁结点处的局部弯矩作用。因此,为简化计算,力学模型主要考虑轴力,忽略弯矩效应。以研究奇数吊杆为例,为分析跨中及1/4跨吊杆力学性能及简化计算过程,提出建立三吊杆下承式系杆拱桥模型,限于篇幅,现根据吊杆单处损伤这一情况进行分析,如图1所示。
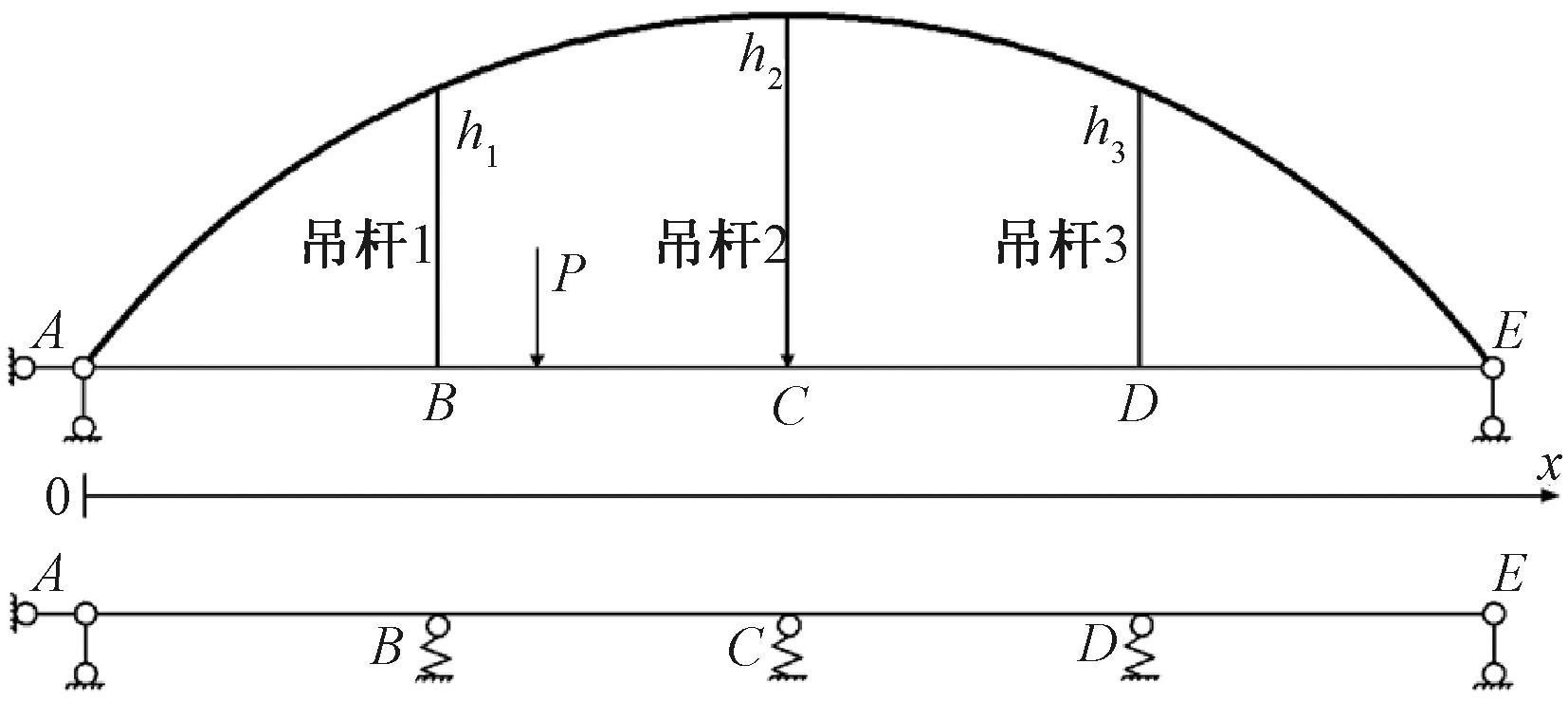
图1 下承式系杆拱桥力学及简化模型
Figure 1 Mechanics and simplified model of through tied arch bridge
为利于应变影响线解析式的分析,现假设:①下承式系杆拱桥的建筑材料均质且始终处于线弹性阶段;②假设损伤位置互不影响;③忽略吊杆的温度变形、非荷载引起的弹性变形。通过移动集中力P在纵梁上进行准静态影响线加载,假设该过程仅引起结构静态响应,本文暂不讨论因移动加载产生的动力效应。根据吊杆仅受拉的特点以及弹性地基理论,在对应吊杆下方设置仅受压弹簧以替代吊杆作用。以各吊杆的弹性系数Ki、吊杆长度hi建立新的力学模型。
2 应变影响线损伤识别方法
2.1 应变影响线分析
现假设简化模型的纵梁刚度为EI,跨径取4l,吊杆间距为l,吊杆损伤前后的弹性系数分别为K、Ks。根据吊杆受力特性及工程实际情况,吊杆材料的损伤特性主要为两端锚固约束能力降低以及本身材料锈蚀损伤两种情况。通常中承式、下承式拱桥在跨中区域的吊杆内力较大,因而在理论模型中假设损伤发生在跨中及1/4跨吊杆处且由于损伤分别产生向下位移为c的变形位移,根据位移互等定理和变形体虚功原理可以将荷载作用下任一点的弹性位移进行简化:
(1)
依据结构力学图乘法计算出结构的柔度系数和自由项,如表1所示。结合力法求解出冗余约束力Xi的具体函数解析式,将位移影响系数和广义荷载位移代入力法方程式(2):
(2)
表1 冗余约束参数表
Table 1 Table of redundancy constraint parameters

类别参数力学表达式实际解析解位移影响系数δ11∫(M12/EI)ds3l3/(4EI)δ33∫(M32/EI)ds3l3/(4EI)δ22∫(M22/EI)ds4l3/(3EI)δ12、δ21∫(M1M2/EI)ds11l3/(12EI)δ23、δ32∫(M2M3/EI)ds11l3/(12EI)δ13、δ31∫(M1M3/EI)ds7l3/(12EI)广义荷载位移Δ1P∫(M1MP/EI)ds(x3-7xl2)/(8EI),0≤x≤l;(-x3+12x2l-33xl2+4l3)/(24EI),l≤x≤4l。{Δ2P∫(M2MP/EI)ds(x3-12xl2)/(12EI),0≤x≤2l;(-x3+12x2l-36xl2+16l3)/(12EI),2l≤x≤4l。{Δ3P∫(M3MP/EI)ds(x3-15xl2)/(24EI),0≤x≤3l;(-x3+12x2l-41xl2+36l3)/(8EI),3l≤x≤4l。{
式中:δij为结构的柔度系数,表示在j处施加单位力后i处产生的位移;ΔiP为变形协调方程的自由项,表示在外力P的作用下i处产生的位移。吊杆无损伤时Δi=0;1/4跨吊杆处损伤时Δ1=-c、Δ2=Δ3=0;跨中吊杆损伤时Δ2=-c、Δ1=Δ3=0。
先求解出多余约束力Xi的具体函数解析式,再根据式(3)得出吊杆损伤前后应变影响线解析表达式εi(x)、εid(x),如表2所示。
表2 吊杆损伤前后应变影响线解析表达式
Table 2 Analytical expressions for strain impact lines before and after damage to booms

注:Φ、αi、βi、φi、ηi都是关于E、I、l、c的常数定值。
损伤前应变影响线解析式1/4跨吊杆损伤后应变影响线解析式跨中处吊杆损伤后应变影响线解析式ε1(x)=K1ΦKh1(α1x3+α2x),0≤x≤l;K1ΦKh1(β1x3+β2x2+β3x+β4), l≤x≤2l;K1ΦKh1(φ1x3+φ2x2+φ3x+φ4), 2l≤x≤3l;K1ΦKh1(η1x3+η2x2+η3x+η4), 3l≤x≤4l。ìîíïïïïïïïïïïïïïïε1d(x)=K1ΦKs(h1+c)(α1x3+α2x+α3),0≤x≤l;K1ΦKs(h1+c)(β1x3+β2x2+β3x+(α3+β4)), l≤x≤2l;K1ΦKs(h1+c)(φ1x3+φ2x2+φ3x+(α3+φ4)), 2l≤x≤3l;K1ΦKs(h1+c)(η1x3+η2x2+η3x+(α3+η4)), 3l≤x≤4l。ìîíïïïïïïïïïïïïïïε′1d(x)=K1ΦKsh1(α1x3+α2x+α′3),0≤x≤l;K1ΦKsh1(β1x3+β2x2+β3x+(α′3+β′4)), l≤x≤2l;K1ΦKsh1(φ1x3+φ2x2+φ3x+(α′3+φ′4)), 2l≤x≤3l;K1ΦKsh1(η1x3+η2x2+η3x+(α′3+η′4)), 3l≤x≤4l。ìîíïïïïïïïïïïïïïïε2(x)=K2ΦKh2(α4x3+α5x),0≤x≤l;(β6x3+β7x2+β8x+β9), l≤x≤2l;K2ΦKh2(φ6x3+φ7x2+φ8x+φ9), 2l≤x≤3l;K2ΦKh2(η6x3+η7x2+η8x+η9), 3l≤x≤4l。ìîíïïïïïïïïïïïïïïε2d(x)=K2ΦKsh2(α4x3+α5x+α6),0≤x≤l;K2ΦKsh2(β6x3+β7x2+β8x+(α6+β9)), l≤x≤2l;K2ΦKsh2(φ6x3+φ7x2+φ8x+(α6+φ9)), 2l≤x≤3l;K2ΦKsh2(η6x3+η7x2+η8x+(α6+η9)), 3l≤x≤4l。ìîíïïïïïïïïïïïïïïε′2d(x)=K2ΦKs(h2+c)(α4x3+α5x+α′6),0≤x≤l;K2ΦKs(h2+c)(β6x3+β7x2+β8x+(α′6+β′9)), l≤x≤2l;K2ΦKs(h2+c)(φ6x3+φ7x2+φ8x+(α′6+φ′9)), 2l≤x≤3l;K2ΦKs(h2+c)(η6x3+η7x2+η8x+(α′6+η′9)), 3l≤x≤4l。ìîíïïïïïïïïïïïïïïε3(x)=K3ΦKh3(α7x3+α8x),0≤x≤l;K3ΦKh3(β11x3+β12x2+β13x+β14), l≤x≤2l;K3ΦKh3(φ11x3+φ12x2+φ13x+φ14), 2l≤x≤3l;K3ΦKh3(η11x3+η12x2+η13x+η14), 3l≤x≤4l。ìîíïïïïïïïïïïïïïïε3d(x)=K3ΦKsh3(α7x3+α8x+α9),0≤x≤l;K3ΦKsh3(β11x3+β12x2+β13x+(α9+β14)), l≤x≤2l;K3ΦKsh3(φ11x3+φ12x2+φ13x+(α9+φ14)), 2l≤x≤3l;K3ΦKsh3(η11x3+η12x2+η13x+(α9+η14)), 3l≤x≤4l。ìîíïïïïïïïïïïïïïïε′3d(x)=K3ΦKsh3(α7x3+α8x+α′9),0≤x≤l;K3ΦKsh3(β11x3+β12x2+β13x+(α′9+β′14)), l≤x≤2l;K3ΦKsh3(φ11x3+φ12x2+φ13x+(α′9+φ′14)), 2l≤x≤3l;K3ΦKsh3(η11x3+η12x2+η13x+(α′9+η′14)), 3l≤x≤4l。ìîíïïïïïïïïïïïïïï
εi(x)=Xi/(Kihi)。
(3)
2.2 损伤诊断方法
分析损伤前后吊杆应变影响线解析式,针对损伤吊杆提出基于吊杆的损伤指标为应变影响线差值SILD(strain influence line difference):
{α(x),β(x),η(x),λ(x)}。
(4)
由式(4)可知,可根据其余吊杆的应变差值影响线定位损伤位置:当下承式系杆拱桥处于无损状态时,弹性系数K=Ks且c=0,则无论梁上任何位置的单位移动载荷P,应变差值影响线解析式的结果均为常数定值;当下承式系杆拱桥处于损伤状态时,应变差值影响线解析式是一个多参数函数解析式。因此,通过对损伤前后的吊杆应变影响线进行做差处理,可以精确定位损伤位置。
进行差值计算时不仅运算量大而且容易产生误差,对吊杆应变影响线进行二次微分处理,将会约去大量参数从而减少运算量且损伤识别效果更佳。这是由于结构损伤会导致截面材料特性以及整体连续性发生变化,破坏了原先曲线之间的连续性,而数学中的曲率可以放大曲线变化率的突变,因而曲率被广泛应用于影响线等曲线损伤定位中[6,9]。在工程实际中通常将曲率公式分母近似取1,近似为曲线二阶导数,得到曲率公式:
R=|y″|/(1+y′)1.5≈|y″|。
(5)
依据式(4)、(5)提出损伤指标为应变影响线差值曲率SILDC(strain influence line differential curvature):
{α(x),β(x),η(x),λ(x)}″。
(6)
根据上述损伤指标可以定义出识别吊杆的定量指标,即损伤程度DE[7]:
DE=(1-Ks/K)×100%。
(7)
当下承式系杆拱桥吊杆受损程度越大,Ks越小,即Ks/K越小,则DE就越大。
根据理论推导表明,利用应变影响线可以识别系杆拱桥吊杆的损伤位置并量化损伤程度,给出了可用于系杆拱桥吊杆结构应变影响线损伤识别的解析证明,接下来将进一步通过算例验证该方法应用于拱桥吊杆结构损伤识别的有效性。
3 算例验证
3.1 数值模型建立
某黄河下承式系杆拱桥计算跨径为95.5 m,桥面道路宽为19 m,桥面板厚为0.2 m。计算矢高为21.222 m,计算矢跨比为1.0∶4.5,拱轴线为1.347的悬链线,拱肋为哑铃形钢管混凝土断面,钢管采用Q235材料。系梁和中横梁分别为箱形截面和实腹T形截面,模型各截面尺寸见图2。该拱桥共设有24根吊杆,采用Strand1860材料。吊点中心距为7.1 m,设计截面为实腹圆形截面,直径D为0.089 m,混凝土材料的强度等级为C50。
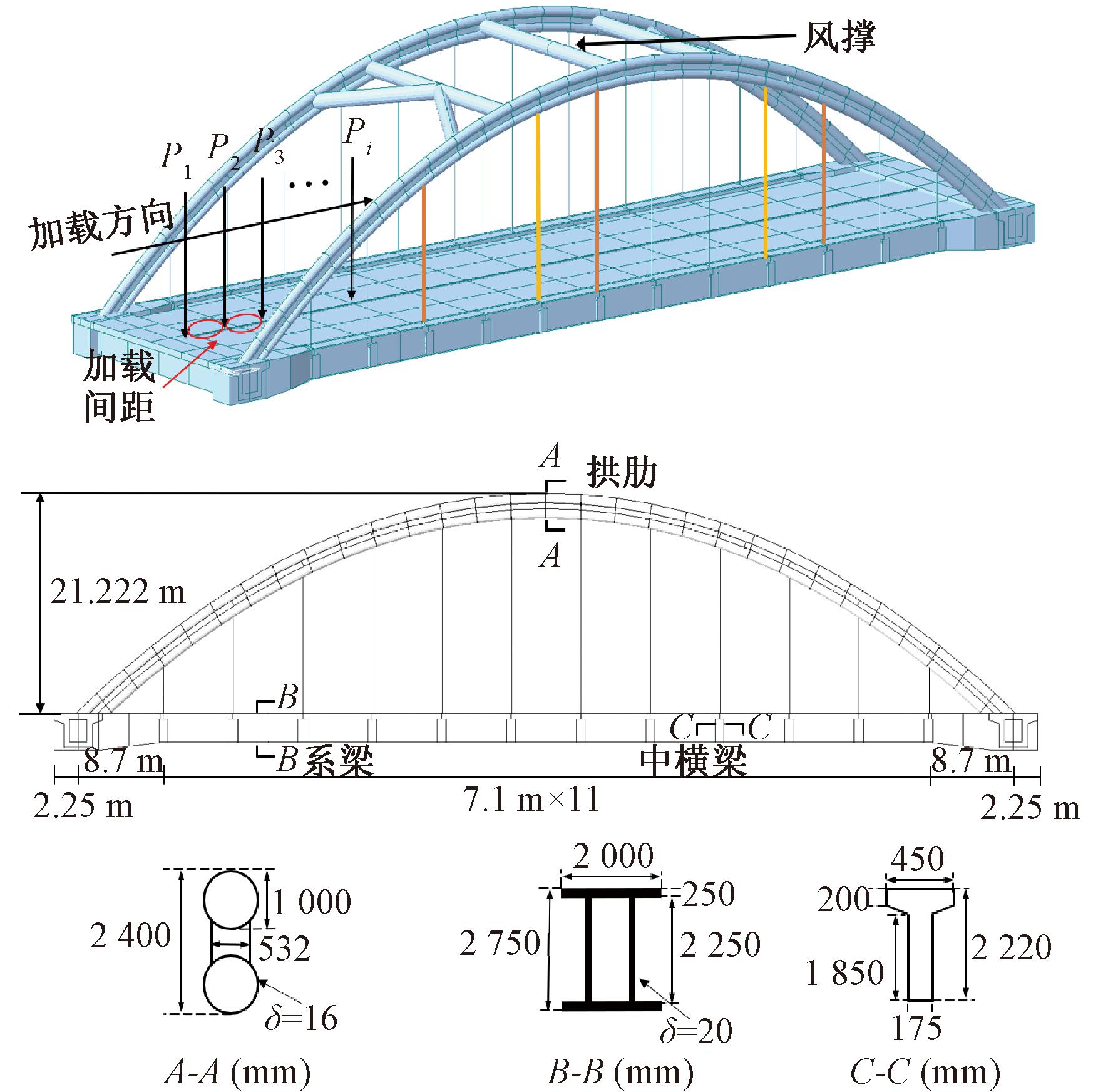
图2 下承式系杆拱桥MIDAS模型
Figure 2 Through tied arch bridge MIDAS model
采用理论推导吊杆数较多的拱桥时,公式的求解将非常困难。本文先理论推导了3根吊杆时拱桥的力学响应结果,提出应变影响线差值及差值曲率的损伤识别方法及评估指标。建立的三吊杆下承式系杆拱桥模型与力学解析式分析结果保持一致,可以有效识别吊杆损伤。为扩展该方法的适用范围,利用有限元分析法研究吊杆数目变化时SILDC对桥梁1/4跨及跨中吊杆的识别效果。限于篇幅,3~12根吊杆损伤识别效果显著性分析见表3。实际上这类桥梁的非线性特征显著,因此在本算例中不考虑结构材料及边界条件所引起的非线性特征,所施加的移动荷载集中力仅仅在于提取较为显著的应变影响线用于构建损伤评估指标。
表3 不同损伤程度下3~12根吊杆SILDC近端、远端识别效果
Table 3 The proximal and distal identification effect of 3-12 SILDC booms at different damage degrees
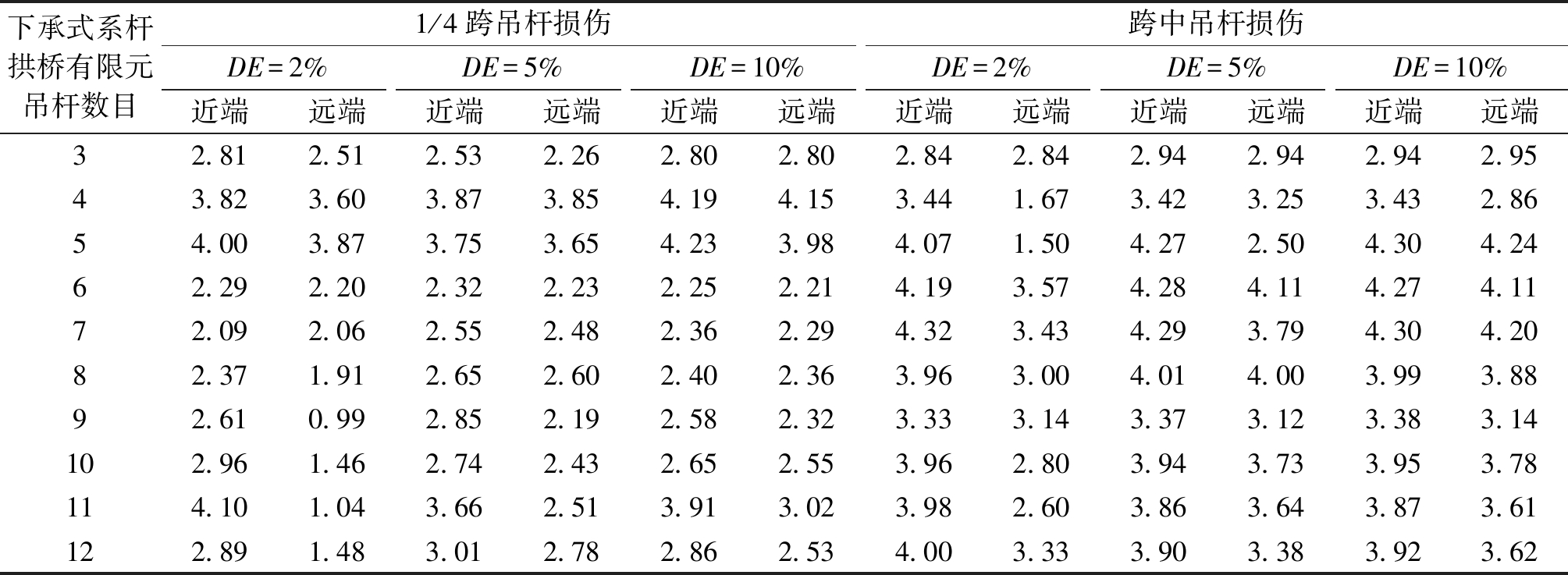
注:近端表示与损伤吊杆相邻的吊杆处;远端表示离损伤吊杆最远的同侧吊杆处。表中数据为应变影响线损伤峰值较次峰值的倍数,2倍及以上时识别效果较为显著。
下承式系杆拱桥有限元吊杆数目1/4跨吊杆损伤跨中吊杆损伤DE=2%DE=5%DE=10%DE=2%DE=5%DE=10%近端远端近端远端近端远端近端远端近端远端近端远端3 2.812.512.532.262.802.802.842.842.942.942.942.9543.823.603.873.854.194.153.441.673.423.253.432.8654.003.873.753.654.233.984.071.504.272.504.304.2462.292.202.322.232.252.214.193.574.284.114.274.1172.092.062.552.482.362.294.323.434.293.794.304.2082.371.912.652.602.402.363.963.004.014.003.993.8892.610.992.852.192.582.323.333.143.373.123.383.14102.961.462.742.432.652.553.962.803.943.733.953.78114.101.043.662.513.913.023.982.603.863.643.873.61122.891.483.012.782.862.534.003.333.903.383.923.62
由于实验车辆荷载较拱桥自重较小,本文使用100 kN的集中力模拟移动荷载,设131个加载步骤Si,均匀作用在纵梁节点上。通过改变单元弹性模量模拟损伤,用弹模下降百分比拟定损伤程度,并假设损伤单元的质量及截面尺寸无变化[6,12]。根据图3有限元分析发现,同时降低车道两侧对称吊杆单元与单侧吊杆单元的有限元分析结果相似,并不影响对结构的整体讨论。因此本文将通过改变单侧吊杆的弹性模型进行实现。由于跨中吊杆所承受内力较大以及近支座处吊杆常遭受锈蚀作用,现研究跨中及1/4跨吊杆发生损伤(损伤程度分别为2%、5%、10%)时,下承式系杆拱桥吊杆数目变化时SILDC近端、远端识别效果和各损伤工况下的结果如表3所示。
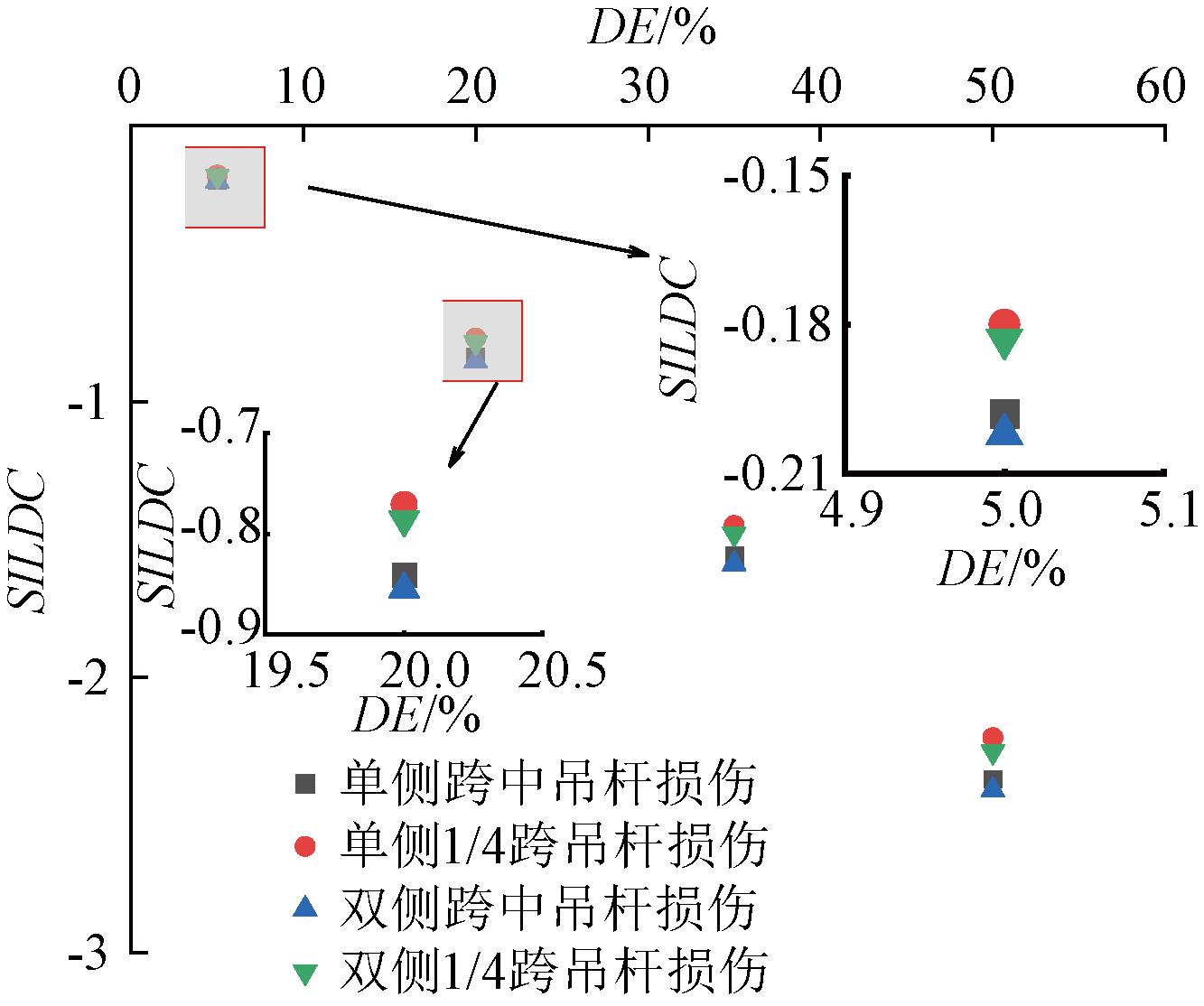
图3 模型假定吊杆损伤对识别效果的影响
Figure 3 Model assumed effect of booms damage on identification
由表3可知,在不考虑噪声因素时,在1/4跨及跨中位置的吊杆损伤识别效果与吊杆数目无显著关联,该方法可用于多吊杆模型;吊杆损伤程度不低于5%时,即使吊杆根数在3~12根内变化,仍能从损伤吊杆的远端准确识别其SILDC指标。
3.2 算例实施方案及模型工况
在实际工程中可采用移动荷载叠减的加载方案以避免实验困难[7],具体实施方法:选择多辆加载重车,通过控制加载车辆移速一致,使加载的桥梁虚拟加载节点相同,进行准静态影响线加载并提取记录应变响应数据,并根据不同荷载重量下测取的数据进行归一化处理,以减少测试数据的观测误差。而针对无损伤下的应变影响线数据,一方面通过精细化有限元模型提取;另一方面在同桥型的另一桥跨位置进行加载检测无损伤初始数据,通过BP神经网络等方式对大量数据进行训练[13-14],得到桥梁状态正常时的数据指标。
为研究移动加载步对识别精度的影响,通过单一控制变量法对拱桥模型进行分析,发现模型损伤定位的误差距离均小于实际吊杆间距,因此SILDC与SILD的损伤识别方法均可以高效定位出损伤吊杆的位置。如表4所示,随着加载步数量的增加,识别精度更加精细。因而在实际加载过程中须控制好加载间距,以免影响识别损伤效果。
表4 移动加载步对识别精度的影响
Table 4 Effect of moving loading step on recognition accuracy
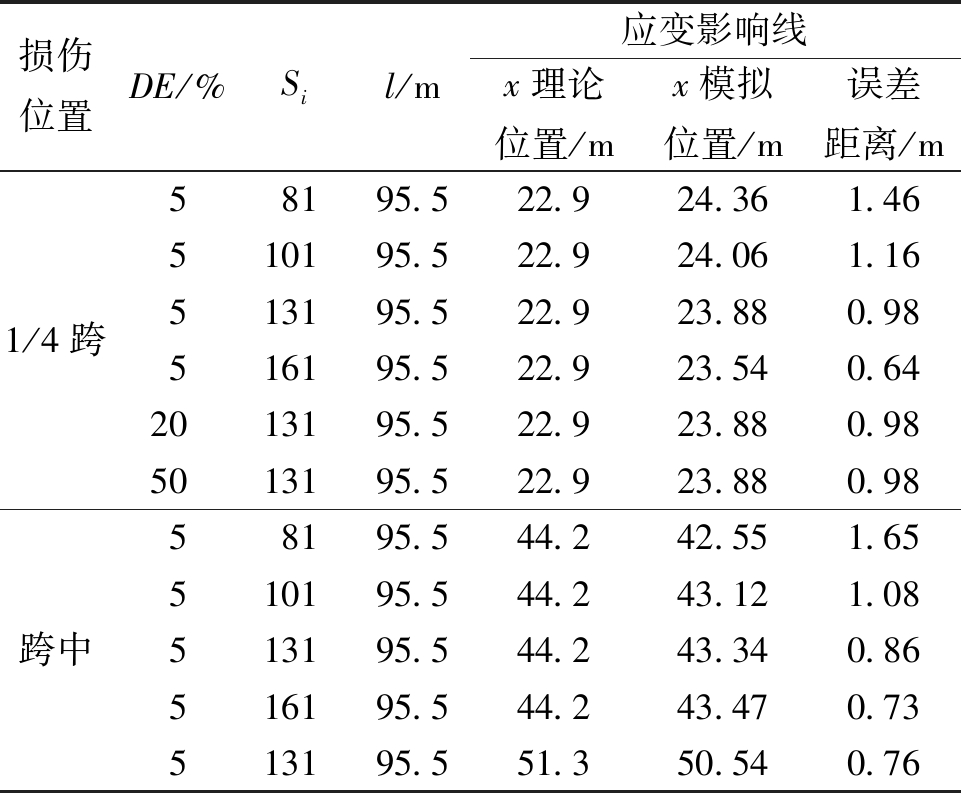
损伤位置DE/%Sil/m应变影响线x理论位置/mx模拟位置/m误差距离/m1/4跨58195.522.924.361.46510195.522.924.061.16513195.522.923.880.98516195.522.923.540.642013195.522.923.880.985013195.522.923.880.98跨中58195.544.242.551.65510195.544.243.121.08513195.544.243.340.86516195.544.243.470.73513195.551.350.540.76
在实际工程中会出现各种复杂的损伤情况。以某黄河下承式系杆拱桥有限元模型为算例,在此设立10种研究工况以探究吊杆损伤数目、位置、程度以及多构件损伤情况下该方法识别的可行性,同时引入吊杆发生4种不同损伤程度(5%、20%、35%、50%)的情况进行分析。测点与局部位置见图4,算例损伤工况如表5所示。在本算例中引入不确定系数ω(x)以考虑噪声影响,其中ω(x)为在[0.90,1.10]上服从截尾高斯分布的不确定系数[15]。噪声误差的引入方式如文献[7,12]所示。
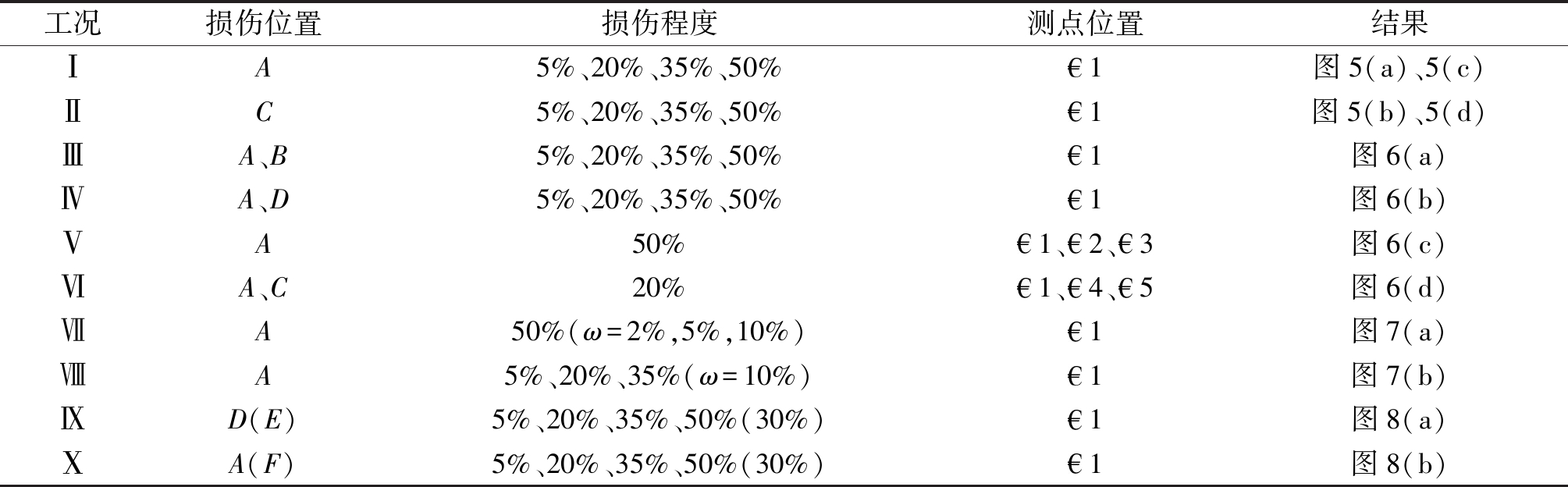
表5 算例损伤工况及测点布置
Table 5 Calculation of damage conditions and measurement point arrangement
注:A、B、C、D表示假定损伤吊杆位置,均处于桥跨的跨中及1/4跨位置附近;E、F分别表示拱桥结构系梁和风撑的损伤部位,其损伤程度均为30%;![]() 1~
1~![]() 5表示有限元模型中待测吊杆的位置。
5表示有限元模型中待测吊杆的位置。
工况损伤位置损伤程度测点位置结果ⅠA5%、20%、35%、50%1图5(a)、5(c)ⅡC5%、20%、35%、50%1图5(b)、5(d)ⅢA、B5%、20%、35%、50%1图6(a)ⅣA、D5%、20%、35%、50%1图6(b)ⅤA50%1、2、3图6(c)ⅥA、C20%1、4、5图6(d)ⅦA50%(ω=2%,5%,10%)1图7(a)ⅧA5%、20%、35%(ω=10%)1图7(b)ⅨD(E)5%、20%、35%、50%(30%)1图8(a)ⅩA(F)5%、20%、35%、50%(30%)1图8(b)
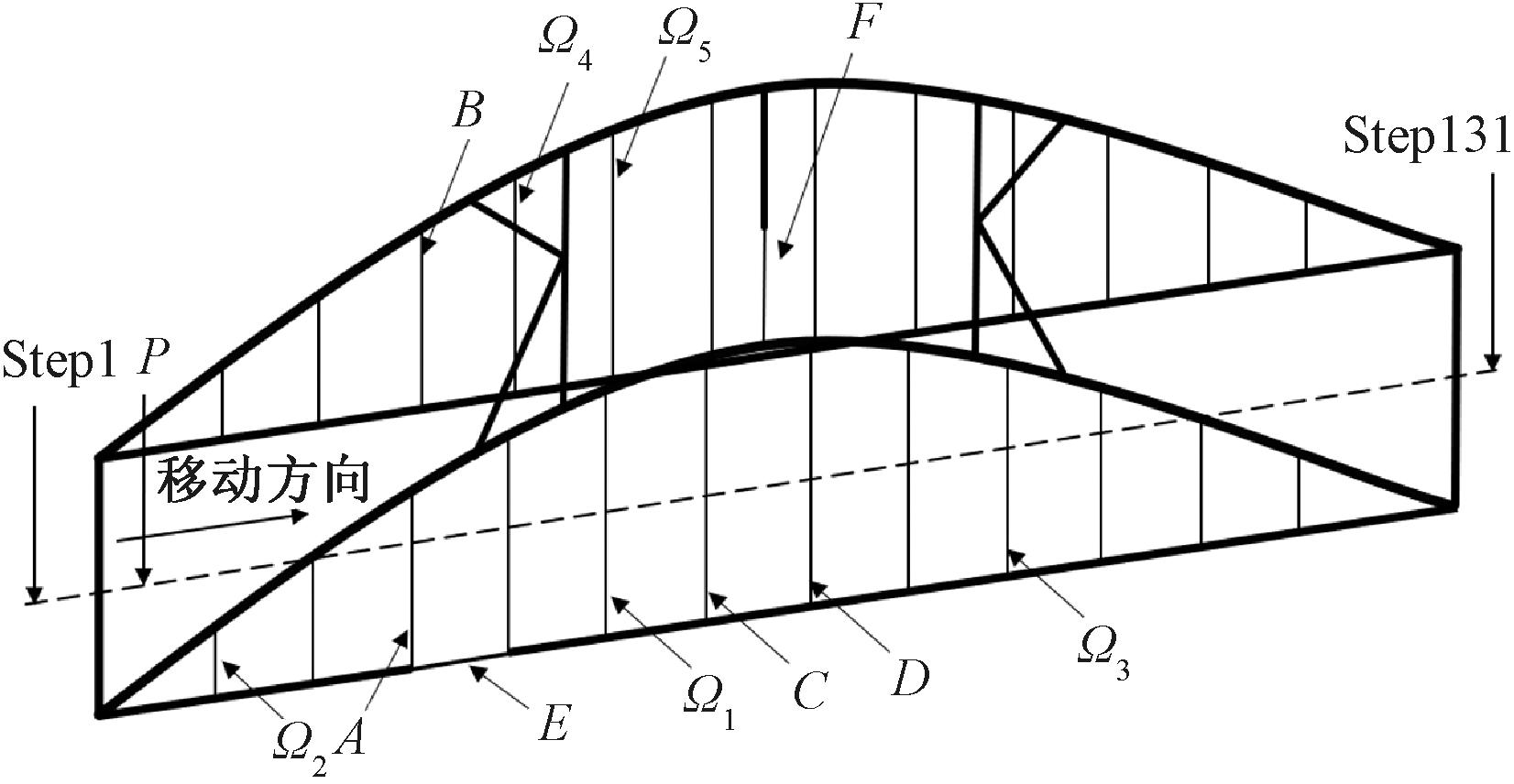
图4 算例损伤位置与测点位置
Figure 4 Example damage and measurement point location
依据SILDC作为主要损伤指标对吊杆识别情况展开分析研究,对此设立工况Ⅰ、Ⅱ验证在不同损伤位置及损伤程度下SILD、SILDC对吊杆的损伤诊断效果;同样工况Ⅲ、Ⅳ也采用类似的既定工况检验SILDC对多处吊杆损伤的诊断效果(限于研究篇幅以两处损伤为例);为探究不同测点损伤诊断结果的影响设立了工况Ⅴ、Ⅵ;为模拟实际检测过程中各种环境误差因素,设立工况Ⅶ、Ⅷ以探究噪声对吊杆损伤识别的影响。而在实际桥梁工程中,会出现多结构损伤的情况,例如,由于焊接局部疲劳损伤或材料锈蚀会引起拱肋损伤,而经受地震、侧风作用以及焊接失效等情况会致使横撑损伤等,因此通过工况Ⅸ、Ⅹ分析在拱桥其他构件发生损伤下该方法对吊杆的损伤识别效果。
3.3 损伤评估结果
首先对下承式系杆拱桥进行移动集中力加载并提取损伤前、后测点的应变影响线;其次,通过中心差分法以及滑动平均法处理应变损伤曲线。以此消除有限元算例中应变影响线数据的误差,但是会导致非损伤区域应变影响线差值曲率曲线不为0且出现次峰值的现象,如图5所示。并以加载步Si作为横坐标物理变量,以SILDC计算值作为纵坐标物理变量,绘制诊断结果如图6所示。
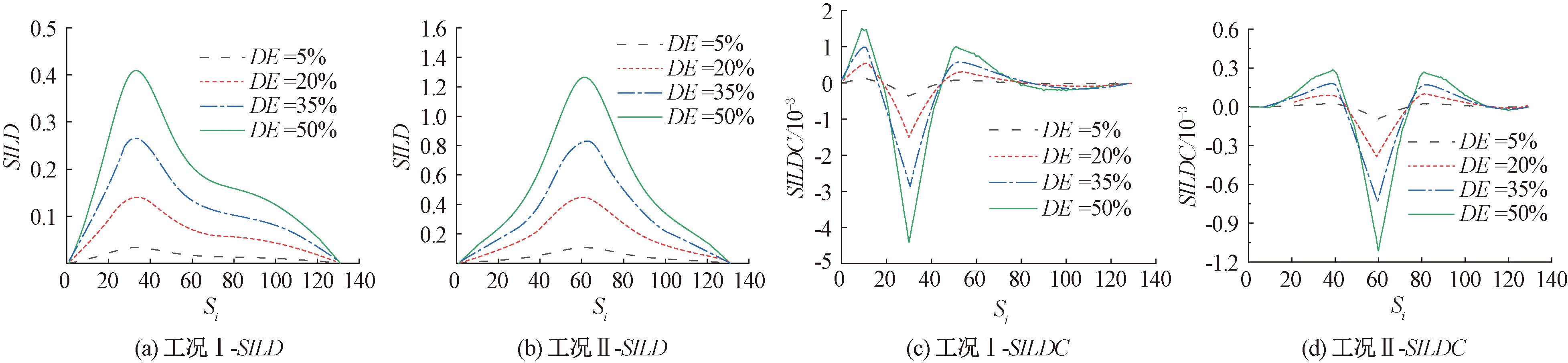
图5 单吊杆损伤应变影响线曲率图
Figure 5 Single boom damage strain influence line curvature diagram
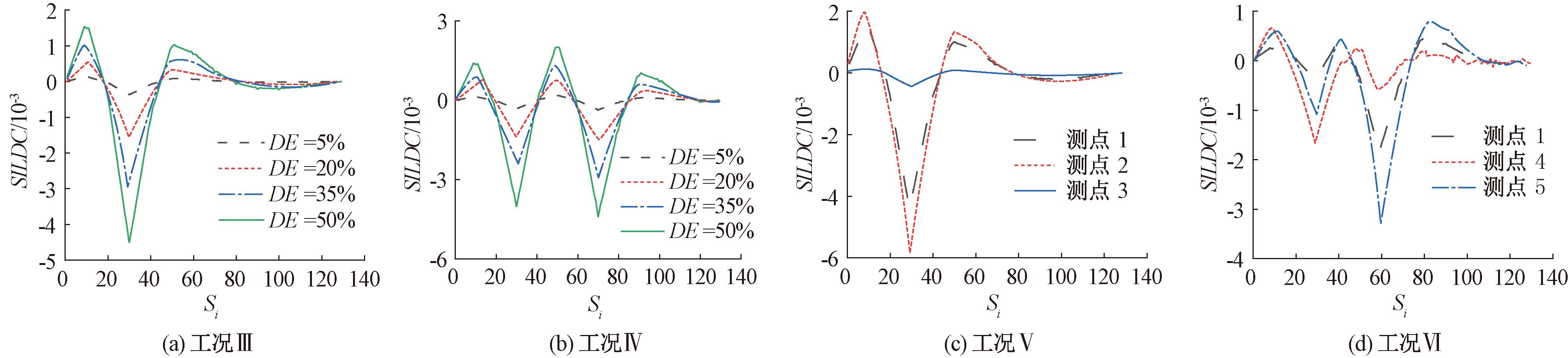
图6 多吊杆损伤及测点位置分析
Figure 6 Multi-boom damage and measurement point location analysis
如图5所示,在单一吊杆损伤时,既定损伤位置邻域出现峰值,因此在同一测量位置可以识别1/4跨及跨中附近吊杆位置的损伤情况;进一步分析发现,伴随既定损伤程度的成倍递增,对应SILDC指标值也以一定比例增加;通过对比SILD和SILDC两种指标的识别效果,发现SILDC指标在损伤处识别效果更为明显,这与第2.2节理论分析一致。
如图6(a)所示,若在桥跨同一位置不同侧发生损伤,虽可识别损伤发生的位置,但不能确定另一侧的吊杆是否损伤,因此有必要在另一侧位置进行检测识别;如图6(b)所示,发现SILDC可以较好地识别多处吊杆损伤情况,进一步发现即使吊杆在相同的损伤程度下产生的损伤指标值也不同;针对此情况,又研究不同测点位置对吊杆损伤识别的评估效果,如图6(c)、6(d)所示,由于不同测量位置所提取出的应变响应数据不同,因而在测点位置分析图中图像不够显著,但仍发现SILDC在不同检测位置均可以有效识别损伤。进一步比较发现,在同一损伤程度下,当测点越接近于损伤位置时,所得到的数据更加精准,即损伤识别的敏感性与测点到损伤处距离成反比。由于在实际检测中会出现人为测量或环境因素引起的误差,因此引入噪声及其他构件发生损伤的工况进行验证。如图7所示,由抗噪性实验验证可知,在10%测试噪声下,损伤程度诊断结果偏大,但对诊断损伤发生位置影响较小,因此该方法具有良好的抗噪性。
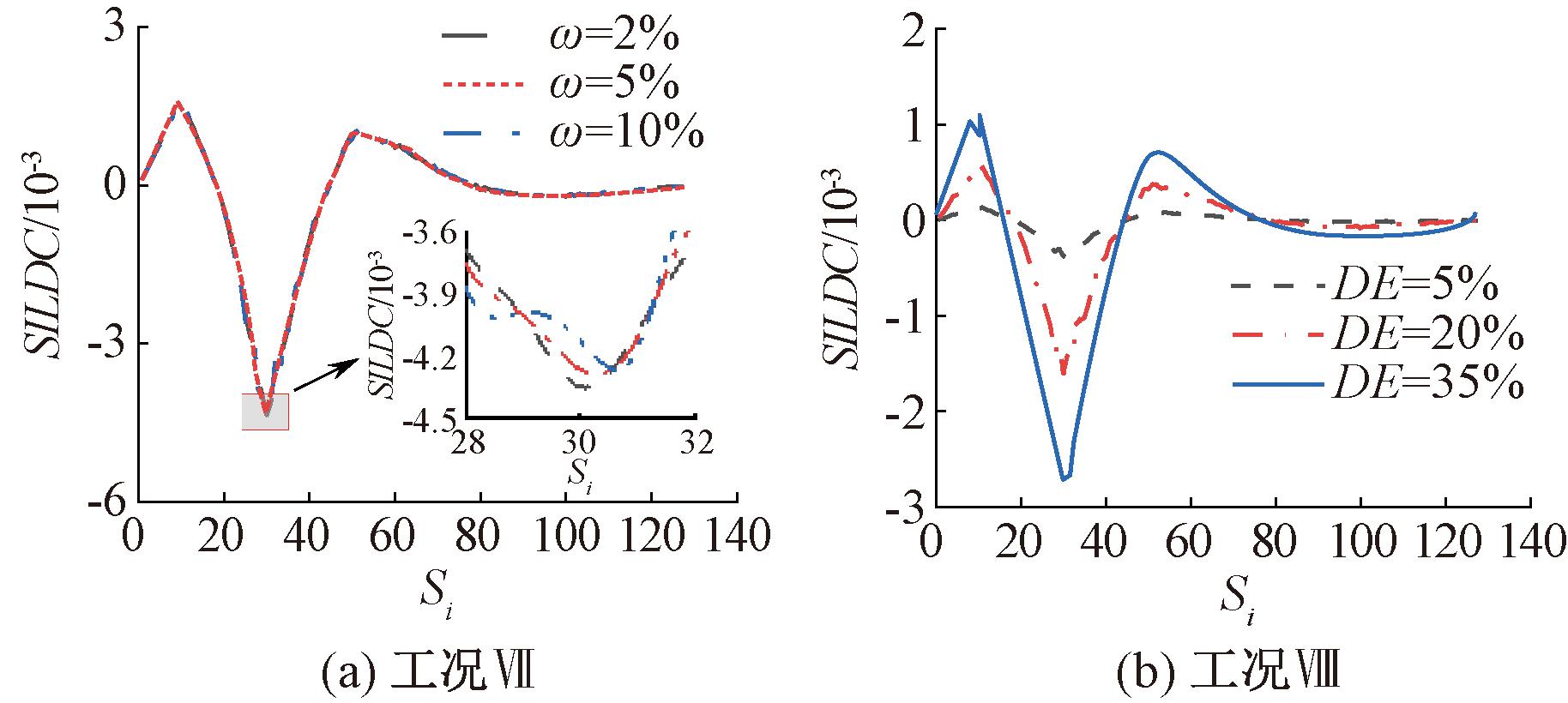
图7 噪声对SILDC损伤识别的影响
Figure 7 Effect of noise on SILDC damage identification
如图8所示,对比图5(c)、5(d),发现在拱桥其他构件发生损伤时,基于SILDC的拱桥吊杆损伤识别方法具有良好的效果。为探究其他构件对吊杆损伤的影响,考虑了拱肋、中横梁、系梁等拱桥自身构件的损伤对跨中及1/4跨吊杆损失指标的评估效果,如图9所示。由图9可知,风撑的损伤对整体影响甚微,在相同程度下,中横梁和桥面板的损伤对结构损伤影响较小,而拱肋及系梁的损伤对结构整体危害性更大。进一步对比发现,跨中吊杆损伤较边跨吊杆损伤影响更大,这也说明在工程实际中应尽可能关注系杆拱桥跨中区域吊杆的损伤情况。
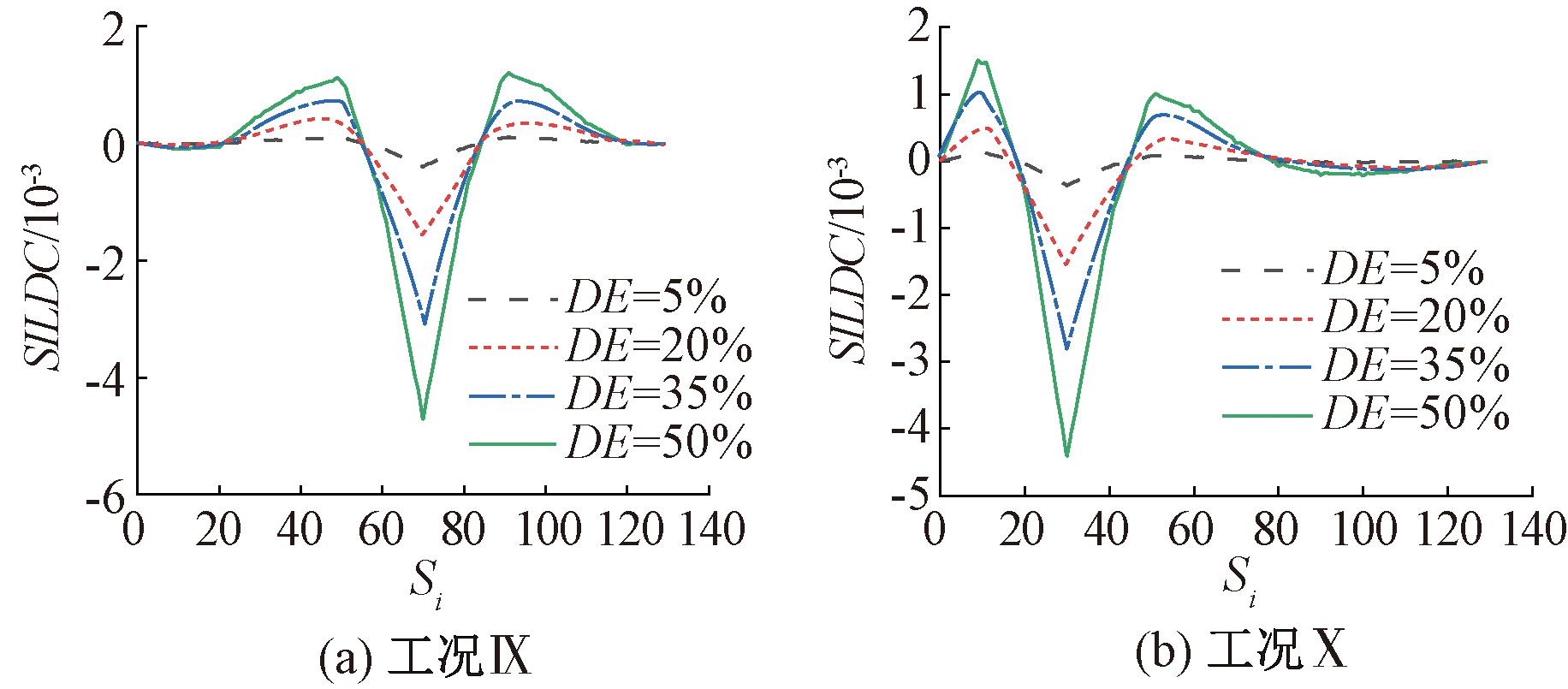
图8 系梁及拱肋对识别损伤的影响
Figure 8 Effect of tie beam and arch rib on damage identification
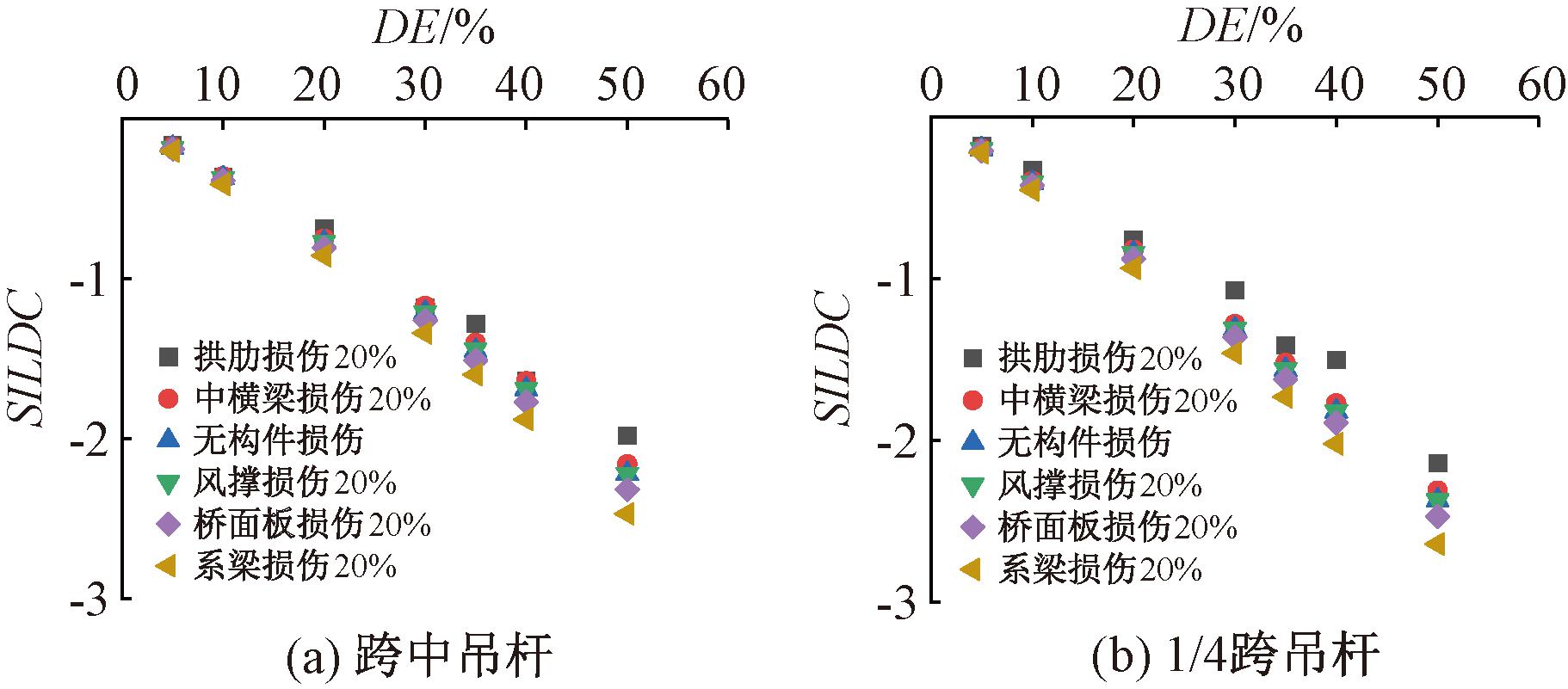
图9 拱桥构件损伤对不同位置吊杆损伤的影响
Figure 9 Effect of arch bridge component damage on booms damage at different positions
4 结论
(1)本文建立了下承式系杆拱桥吊杆应变影响线的解析表达式,提出利用应变影响线差值及应变影响线差值曲率两种损伤指标定义吊杆损伤程度,算例验证表明,该类指标可以有效识别损伤位置,且应变影响线差值曲率识别结果更精准可靠。
(2)通过理论分析提出了3根吊杆损伤识别方法,借助有限元法扩展验证了该方法在多吊杆模型中的适用性。研究发现,应变影响线差值曲率法即使在10%测试噪声下仍可以精确识别单一和多处吊杆损伤;在同一损伤程度下,测点到损伤吊杆的距离与损伤识别的敏感性成反比,即使在不同测点提取的应变响应值不同,但是仍可以有效识别损伤。
(3)研究发现在拱桥其他构件发生损伤时,应变影响线差值曲率法仍可以对吊杆损伤进行评估。在相同程度下中横梁和桥面板的损伤对结构损伤较小,而拱肋及系梁的损伤对结构整体危害性较大。
[1] ZHENG X, YANG D H, YI T H, et al. Development of bridge influence line identification methods based on direct measurement data: a comprehensive review and comparison[J]. Engineering Structures, 2019, 198: 109539.
[2] QU C X, YI T H, LI H N. Mode identification by eigensystem realization algorithm through virtual frequency response function[J]. Structural Control and Health Monitoring, 2019, 26(10): e2429.
[3] 李戎, 杨萌, 刘林霞, 等. 水下FG圆柱壳临界载荷和固有频率预测方法[J]. 郑州大学学报(工学版), 2021, 42(1):70-76.
LI R, YANG M, LIU L X, et al. Prediction method for critical buckling pressure and natural frequency of submerged functionally graded cylindrical shell[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(1):70-76.
[4] POOYA S M H, MASSUMI A. A novel damage detection method in beam-like structures based on the relation between modal kinetic energy and modal strain energy and using only damaged structure data[J]. Journal of Sound and Vibration, 2022, 530: 116943.
[5] 周宇, 狄生奎, 王立宪, 等. 基于柔度指标的系杆拱桥损伤识别与寿命预测[J]. 防灾减灾工程学报, 2018, 38(6): 1033-1043.
ZHOU Y, DI S K, WANG L X, et al. Damage detection and life prediction of tied arch bridge based on flexibility-curvature-difference-rate[J]. Journal of Disaster Prevention and Mitigation Engineering, 2018, 38(6): 1033-1043.
[6] 王立宪, 周宇, 狄生奎, 等. 考虑边界非理想的铁路桥梁挠度影响线分析与损伤识别[J]. 工程科学与技术, 2020, 52(3):123-132.
WANG L X, ZHOU Y, DI S K, et al. Influence line analysis and damage detection of railway bridge deflection with non-ideal boundaries[J]. Journal of Sichuan University (Engineering Science Edition), 2020, 52(3):123-132.
[7] 周宇, 狄生奎, 项长生, 等. 基于弹性约束支承梁转角影响线的梁结构损伤诊断[J]. 浙江大学学报(工学版), 2020, 54(5):879-888.
ZHOU Y, DI S K, XIANG C S, et al. Beam structure damage detection based on rotational-angle-influence-lines of elastic-constrained-support beam[J]. Journal of Zhejiang University (Engineering Science), 2020, 54(5):879-888.
[8] 王艺霖, 张平, 安新梅. 基于竖向支座反力的两跨连续梁桥损伤定位方法[J]. 中国公路学报, 2014, 27(4):79-84, 105.
WANG Y L, ZHANG P, AN X M. Two-span continuous bridge damage localization method based on vertical support reaction[J]. China Journal of Highway and Transport, 2014, 27(4):79-84, 105.
[9] WU B T, WU G, YANG C Q. Parametric study of a rapid bridge assessment method using distributed macro-strain influence envelope line[J]. Mechanical Systems and Signal Processing, 2019, 120: 642-663.
[10] CHEN S Z, WU G, WU B T. Simultaneous identification method of damage and vehicle parameters on bridges utilizing long-gauge strain influence line under moving vehicle loads[J]. Proceeding of the SPIE, 2017, 10168: 573-582.
[11] YANG J, HOU P, YANG C Q, et al. Study on the method of moving load identification based on strain influence line[J]. Applied Sciences, 2021, 11(2): 853.
[12] 周宇, 狄生奎, 李喜梅, 等. 基于弹性约束梁应变影响线曲率的桥梁结构损伤识别[J]. 应用基础与工程科学学报, 2021, 29(4): 901-914.
ZHOU Y, DI S K, LI X M, et al. Damage identification of bridge structural based on strain influence line curvature of elastic restrained beam[J]. Journal of Basic Science and Engineering, 2021, 29(4): 901-914.
[13] 王涛, 张丽莎, 高岩. 基于BP神经网络的改进型新奇检测技术诊断大跨度拱桥异常状态[J]. 北京理工大学学报, 2016, 36(2):157-162.
WANG T, ZHANG L S, GAO Y. Abnormality identification of large-span arch bridge based on BP neural improved novelty detection technique[J]. Transactions of Beijing Institute of Technology, 2016, 36(2):157-162.
[14] 张安琳, 张启坤, 黄道颖, 等. 基于CNN与BiGRU融合神经网络的入侵检测模型[J]. 郑州大学学报(工学版), 2022, 43(3): 37-43.
ZHANG A L, ZHANG Q K, HUANG D Y, et al. Intrusion detection model based on CNN and BiGRU fused neural network[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(3): 37-43.
[15] SEN S, ASWAL N, ZHANG Q H, et al. Structural health monitoring with non-linear sensor measurements robust to unknown non-stationary input forcing[J]. Mechanical Systems and Signal Processing, 2021, 152: 107472.