由于相量测量单元(phasor measurement unit,PMU)对数据测量的快速性与同步性,近年来被广泛应用于电力系统实时监测与控制领域[1-3]。然而,在实际测量过程中,由于测量设备故障以及外界干扰,测量数据中往往存在误差及不良数据,若直接利用这些数据对发电机的状态进行分析,可能会导致错误的分析结果和控制策略,进而严重威胁电力系统安全稳定运行[4]。状态估计能够有效滤除PMU中存在的误差与不良数据[5]。因此,为满足实际电网安全需求,对发电机进行动态状态估计意义重大[6]。
目前,国内外学者针对发电机动态状态估计进行了大量研究。秦晓辉等[7]建立发电机二阶模型,进一步提出线性卡尔曼滤波(Kalman filter, KF)的状态估计方法,但是忽略了模型的非线性特征。王大方等[8]计及系统非线性特征,提出了扩展卡尔曼滤波(extended Kalman filter, EKF)对发电机状态进行估计,但线性化过程存在较大截断误差,估计精度较低。Zhao等[9]利用无迹变换(UT)产生Sigma点集,进而提出无迹卡尔曼滤波(unscented Kalman filter, UKF),其精度比EKF高,但其受状态维数和参数取值原则约束,很难在大规模状态估计中应用。针对UKF的不足,Wang等[10]基于球面-径向法则建立了容积卡尔曼滤波(cubature Kalman filter, CKF),该方法无须选择任何参数,在估计精度和计算速度上均有所提高。Zhao等[11]和王彤等[12]分别对UKF以及CKF方法进一步改进,增强了滤波的鲁棒性。张琪等[13]基于贝叶斯理论,提出了基于粒子滤波(particle filter, PF)发电机动态状态估计方法,但以转移概率密度作为重要密度函数时未考虑最新量测信息,可能会使粒子偏离真实的后验分布。因此,Yu等[14]提出无迹粒子滤波(unscented particle filter, UPF)方法,采用无迹变换求解重要密度,相比PF,粒子分布更加接近实际后验概率,但未考虑非高斯及模型参数对估计的影响。王义等[15]考虑了非高斯及模型参数不确定性,但仍以EKF方法为框架,存在较大截断误差,无法适用于强非线性系统。
针对现有PF方法在处理模型不确定时估计精度不高的问题,本文提出一种基于H∞无迹粒子滤波(H∞ unscented particle filter, HUPF)的发电机动态估计方法。通过UT法则计算粒子的密度分布,提高了估计精度和运算效率;并有效结合H∞鲁棒控制理论和UPF,根据发电机模型参数的不确定性动态修正状态误差协方差,进一步提高了滤波精度和抗差性能。最后,以IEEE 10机39节点系统为例进行试验,结果显示,本文所提的HUPF方法可以有效降低模型不确定对状态估计的不良影响,提升模型不确定情形下发电机的状态估计精度,相比其他方法具有更强的鲁棒性。
1 动态状态估计基本原理
电力系统的动态状态估计是根据电网中的拓扑结构以及量测信息对系统状态变量实时监测;动态状态估计不仅可以实现当前时刻的系统状态的跟踪,而且可以预测下一时刻状态值,对于电力系统分析与控制至关重要[16-17]。
通常,发电机的状态空间可表示为
(1)
式中:x为状态矩阵;z为量测矩阵;u为控制矩阵;f(·)和h(·)分别表示非线性模型的状态与量测方程;w和v分别代表系统噪声矩阵和量测噪声矩阵,二者互相独立,一般假设满足均值为0、误差协方差矩阵分别为Q和R的正态分布。
具体而言,发电机的动态状态估计主要包含2个关键步骤:①状态预测,根据发电机的状态方程,由方程x=f(x,u)+w预测下一时刻的状态量;②量测更新,利用量测量由方程z=h(x,u)+v对状态预测值进行修正,并更新下一时刻的状态估计值。
为了便于动态估计计算,须将上述空间表达模型离散化,形式为
(2)
式中:F(xk,uk)=xk+f(xk,uk)Δt,其中,Δt表示采样步长,k表示采样时刻。
2 发电机动态状态估计模型
发电机动态估计模型一般包括状态方程和量测方程。由于发电机的次暂态过程十分短暂,现有PMU装置很难准确获取次暂态过程中的量测量[18],因此,将与次暂态过程相关的d、q轴绕组和定子过程忽略和简化后,可以得到发电机的四阶动态模型。其中,同步发电机的状态方程如下[19]:
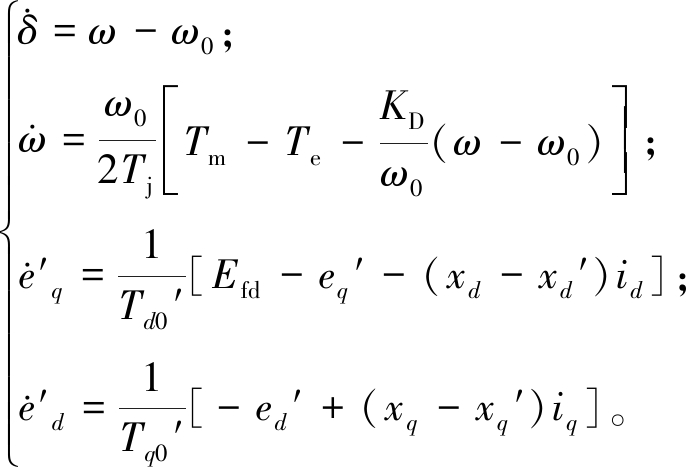
(3)
式中:δ为发电机转子绝对功角;ω和ω0分别为电角速度及其初始值;Tj为惯性时间常数;KD为阻尼系数;Tm和Te分别表示机械功率与电磁功率;e′q和e′d分别为q轴与d轴暂态电动势;Efd为发电机定子励磁电压;xd和x′d分别代表d轴同步与暂态电抗;Td0′和Tq0′分别表示q轴与d轴开路瞬态时间常数;id和iq分别表示d轴与q轴定子电流;xq和x′q分别为q轴同步电抗与暂态电抗。
在状态估计过程中,通常认为系统的相关参数已知,只有状态变量未知。为使得量测量有更高冗余度,提高估计精度,发电机动态估计的量测量设置[18]如下:
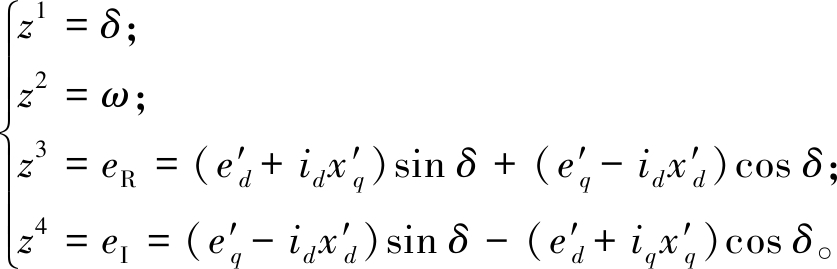
(4)
通过和式(1)对比可知,发电机的状态矩阵为x=[x1,x2,x3,x4]T=[δ,ω,e′q,e′d]T;控制矩阵为u=[u1,u2,u3,u4]T=[Tm,Efd,iR,iI]T;量测矩阵为z=[z1,z2,z3,z4]T=[δ,ω,eR,eI]T。
为了使状态传播函数和测量函数实现状态空间模型(式(1))的表达形式,需要进一步将eR、eI、id和iq表示为xk和uk的函数:
eR=(e′d+idx′q)sin δ+(e′q-idx′d)cos δ;
(5)
eI=(e′q-idx′d)sin δ-(e′d+iqx′q)cos δ;
(6)
id=iRsin δ-iIcos δ;
(7)
iq=iIsin δ+iRcos δ。
(8)
3 基于HUPF的发电机动态状态估计
3.1 约束准则
实际电力系统中,模型的不确定性主要包含两方面:一是噪声统计特性未知;二是模型参数不精确。模型不确定性严重影响状态估计器性能,导致滤波精度降低甚至发散。为抑制不确定性因素对估计精度的影响,提高状态估计方法的鲁棒性,所设计的滤波器需要满足约束准则[20]:
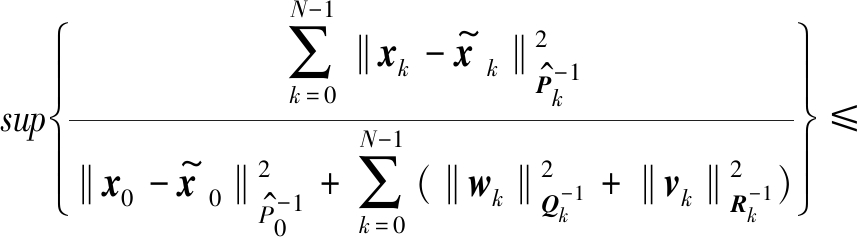
2。
(9)
式中:sup(·)为取上限值;为界定系统不确定性误差的正标量参数;‖x‖为矩阵x的二范数;x0和
分别表示t=0时的状态真实矩阵、估计矩阵;xk和
分别表示t=k时的状态真实矩阵、估计矩阵;P0和Pk分别为t=0和t=k时估计误差协方差矩阵;Qk和Rk分别为t=k时系统噪声协方差矩阵和量测噪声协方差矩阵。
3.2 HUPF方法原理及步骤
本文提出的HUPF方法以PF为框架,利用无迹变换法则求解重要密度函数,由此产生的采样粒子更加接近实际的后验状态。此外,考虑到发电机模型不确定性对估计结果的影响,基于式(5)建立不确定性约束准则,实时调整预测误差协方差矩阵,并引入重采样,增加有效粒子权重,提高了滤波精度。本文所提方法实施流程如图1所示。
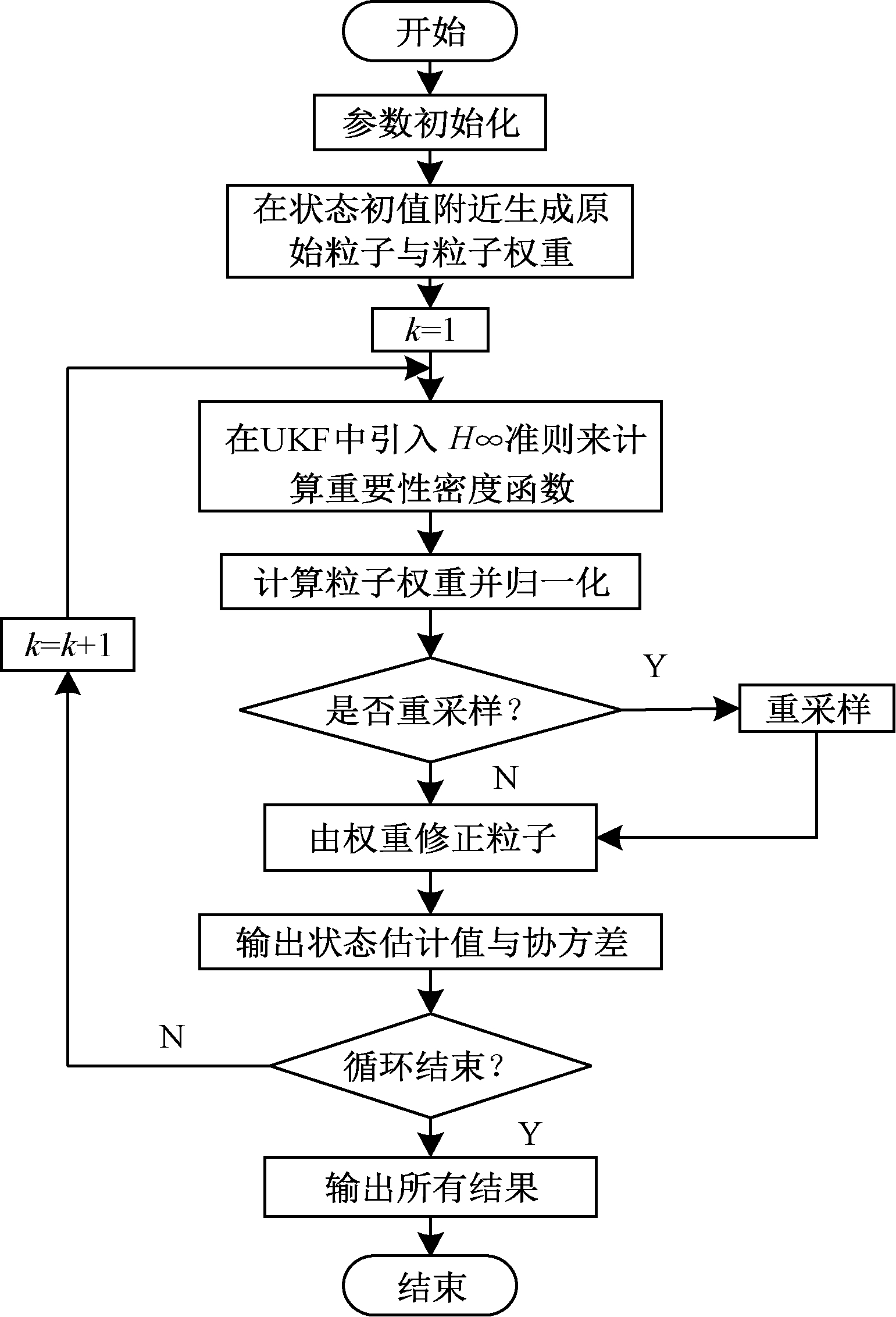
图1 HUPF程序流程图
Figure 1 Flow chart of HUPF program
运用HUPF方法对发电机动态状态估计具体步骤如下。
步骤1 初始化。k=0时,从先验概率分布p(x0)中抽取初始粒子集
粒子权重系数
=1/n,j=1,2,…,n(n为粒子数)。
步骤2 k>0时,采用对称采样方式生成Sigma点集
并构造相应权重Wi,m和Wi,c:
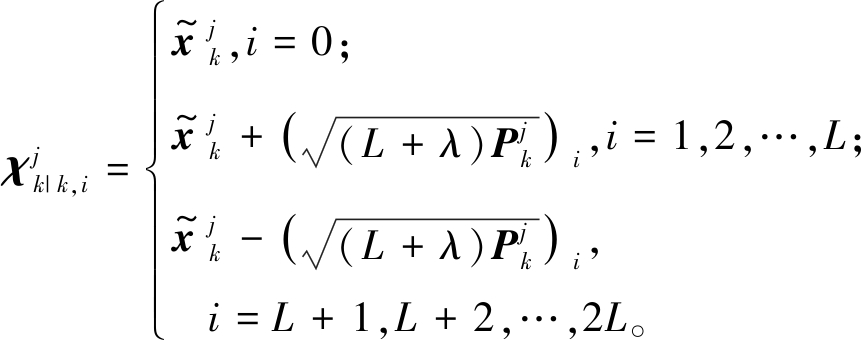
(10)
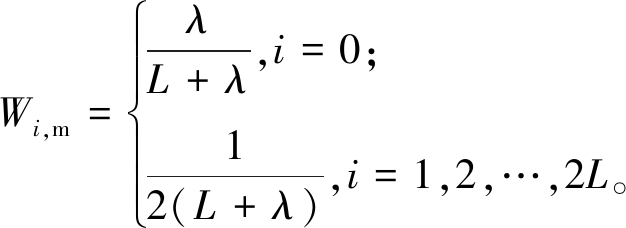
(11)
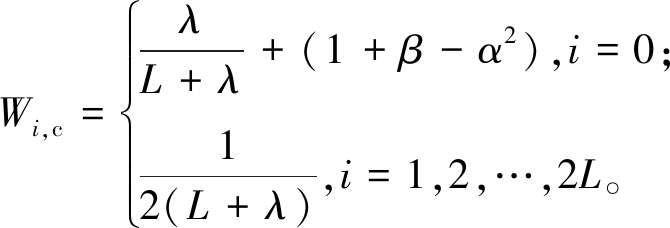
(12)
式中:
和
分别为k时刻各个粒子的估计值和协方差;λ=α2·(L+kf)-L,其中L为状态变量维数;kf为第二尺度参数,通常取为0;α表示Sigma点围绕x的波动范围,一般α∈[10-4,1];β通常包含x的先验知识,若为高斯分布,令β=2。
步骤3 对Sigma点集进行一步预测,计算粒子状态均值
和误差协方差矩阵
(13)
(14)
(15)
步骤4 更新Sigma点集,计算每个粒子的量测均值
自协方差矩阵
和互协方差矩阵
(16)
(17)
(18)
(19)
步骤5 计算k+1时刻粒子的滤波增益
和状态估计值
并依据式(5)所建立的不确定性约束准则,更新估计误差协方差矩阵
(20)
(21)
(22)
其中,
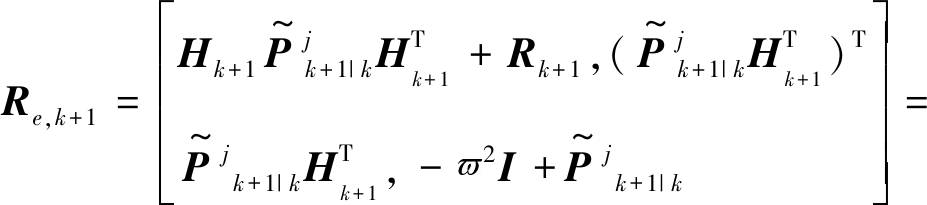
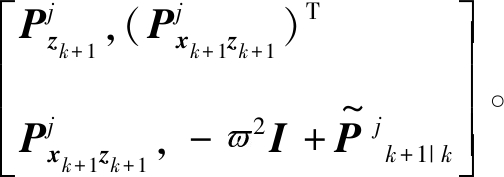
式中:
表示发电机量测方程在
处的雅克比矩阵;表示约束参数上界;I为单位矩阵。
由上述的UKF方法可以得到重要性密度函数以及采样粒子:
(23)
步骤6 计算粒子权重:
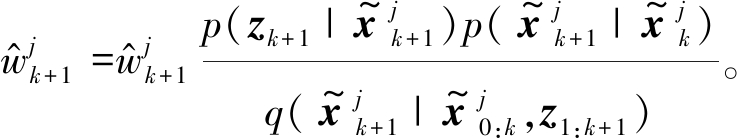
(24)
归一化: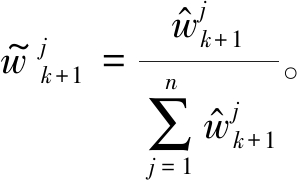
(25)
步骤7 判断是否进行重采样。令
如果a≤Nt(Nt表示设定的阈值,一般取n/3),则说明粒子退化严重,此时将需要进行重采样;否则,跳过此步骤。将粒子按照权重大小进行筛选、复制和重排列处理后,最终粒子权重
均为1/n。
步骤8 输出状态估计值与协方差,进行下一时刻的迭代计算。
步骤9 循环结束,输出状态估计结果。
4 算例分析
4.1 基本测试
为了进一步评估各种滤波方法对于发电机状态的跟踪效果,本文利用均方根误差RMSE指标对不同方法的估计结果进行量化分析,其定义式如下[18]:
(26)
式中:
为发电机第i个状态变量的均方根误差值;N为总时长;
和
分别为发电机k时刻第i个状态变量的真实矩阵和估计矩阵。
本文以IEEE 39节点系统为测试系统对各种滤波方法的效果进行验证,其拓扑见图2所示。随机选择系统中的发电机Gen2为测试对象,其中Tj为30.3,KD设为2,其他相关参数参考文献[18]。发电机的真实值是利用BPA软件模拟PMU设备采集而得。其中,系统的噪声与量测协方差矩阵分别设置为Q=10-6I4×4、R=10-8I4×4。假设系统在Bus16～Bus21线路出口处发生三相金属性短路,且故障发生时间设置在第40～45周期,经6 s后系统过渡至新稳态。
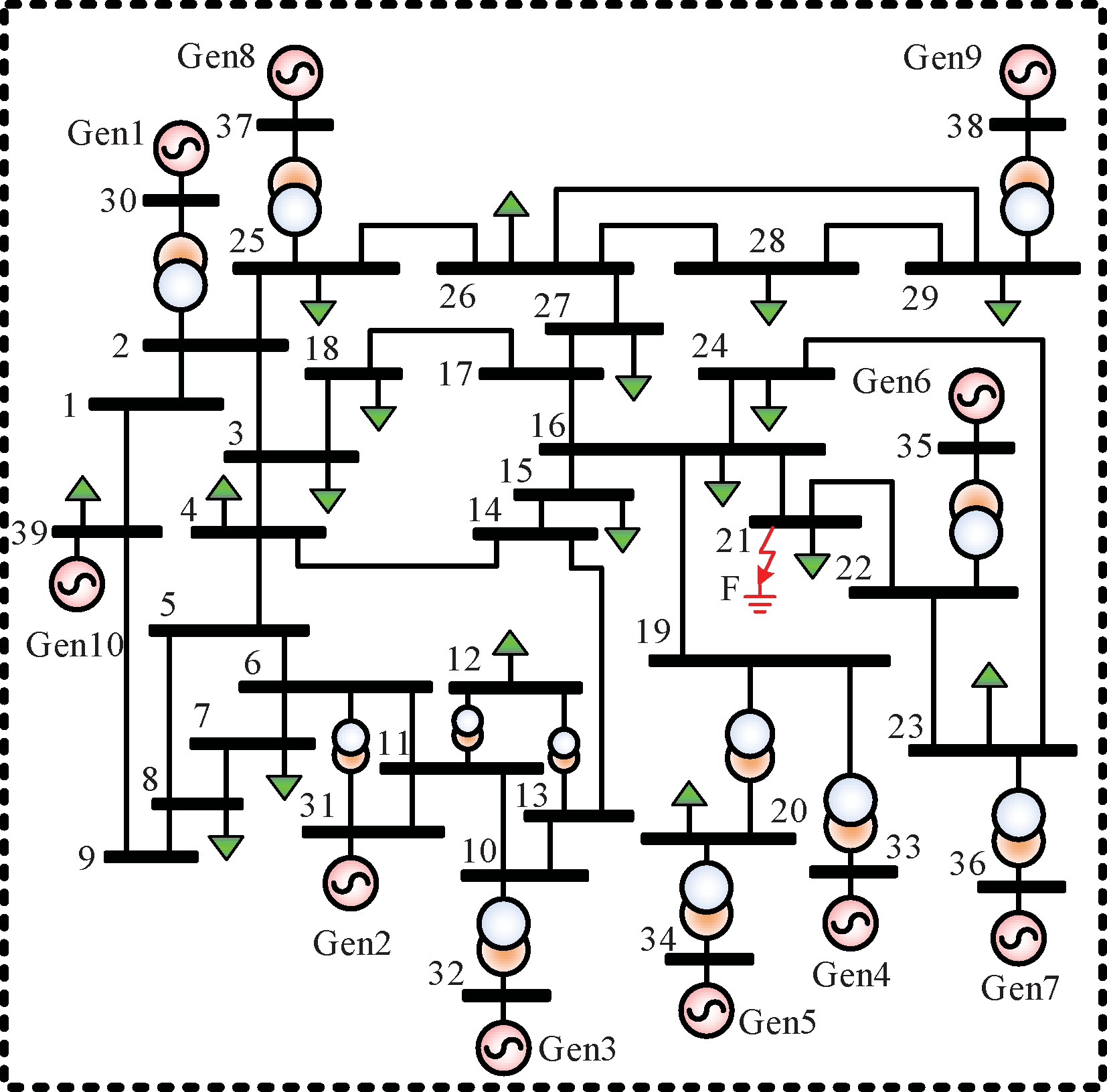
图2 IEEE 39节点系统
Figure 2 IEEE 39 bus system
为验证所提方法有效性,分别运用传统的UKF方法、文献[14]的UPF、文献[21]的AUKF以及本文所提HUPF方法对发电机Gen2状态进行估计。状态估计的初始值取上一时刻稳态值,其中,UKF及AUKF算法的波动系数α=0;先验参数β=2;尺度系数kf=3-L;初始协方差P0设为单位矩阵。UPF和HUPF方法相关参数以及协方差设置和UPF相同,本次测试中UPF和HUPF均采用系统重采样,粒子数设为100个,HUPF方法中约束参数上界=1.5。不同方法对发电机Gen 2的状态估计结果对比如图3所示。
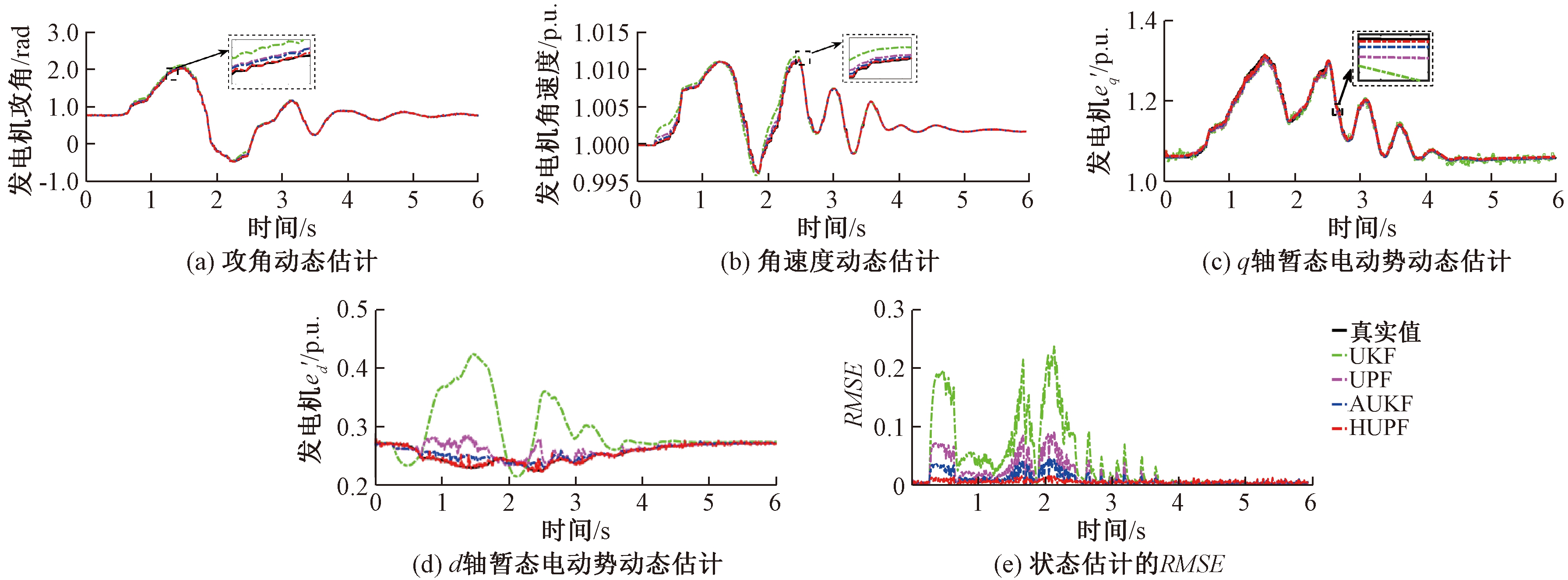
图3 发电机状态估计对比
Figure 3 Comparison of generator state estimation
由图3(a)～3(d)可知,在故障出现前,3种方法跟踪效果和滤波精度基本一致,当故障出现后,UKF和UPF方法虽然能跟踪状态变化,但精度低于AUKF和HUPF,尤其是发电机暂态电抗ed′跟踪效果严重下降;UPF方法由于利用无迹变换生成密度函数,粒子分布更接近实际后验分布,因此,相比UKF方法滤波精度有所提高。另外,AUKF方法通过噪声自适应技术,在一定程度上能够降低故障影响。相比之下,本文所提HUPF方法对UPF进一步改进,在重要性密度函数生成过程中引入不确定性约束准则,利用约束参数抑制模型不确定对发电机状态估计的影响,其跟踪速度和估计精度相比UKF和UPF方法都更好。此外,HUPF方法单步耗时小于20 ms(PMU采样周期为20 ms时),能够满足在线跟踪估计要求。
为了更加直观比较不同方法的滤波效果,本文采用式(22)定义的均方根误差进行对比分析,不同方法状态估计指标对比如表1所示。从表1中数据可以看出,本文所提的HUPF方法在均方根误差指标上优于UKF、UPF和AUKF方法,即HUPF方法的滤波精度更高,能够准确跟踪发电机状态变量。
表1 不同方法下的RMSE
Table 1 Root mean square error of different methods
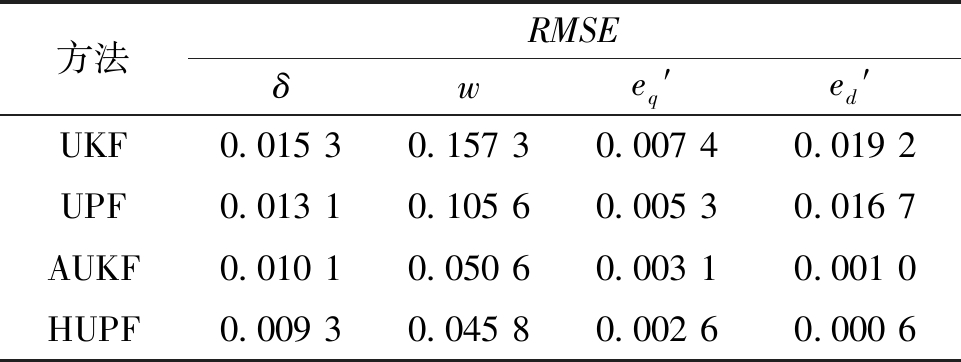
方法RMSEδweq′ed′UKF0.015 30.157 30.007 40.019 2UPF0.013 10.105 60.005 30.016 7AUKF0.010 10.050 60.003 10.001 0HUPF0.009 30.045 80.002 60.000 6
4.2 非高斯噪声测试
发电机模型中一般假设噪声为高斯白噪声,噪声协方差为常数矩阵。但是在实际电网中,由于PMU采集的量测信息在向控制中心传送数据时,通信信道容易受到噪声污染,导致出现非高斯噪声,从而影响动态状态估计性能,降低滤波精度[22]。
为了验证HUPF方法在非高斯噪声下的滤波效果,假设量测方程中5%的量测噪声协方差矩阵R=10-8I4×4,95%的量测噪声协方差矩阵R=10-6I4×4。在此种工况下,分别运用UKF、UPF和所提方法对发电机Gen 2的状态进行估计,滤波结果如图4所示。
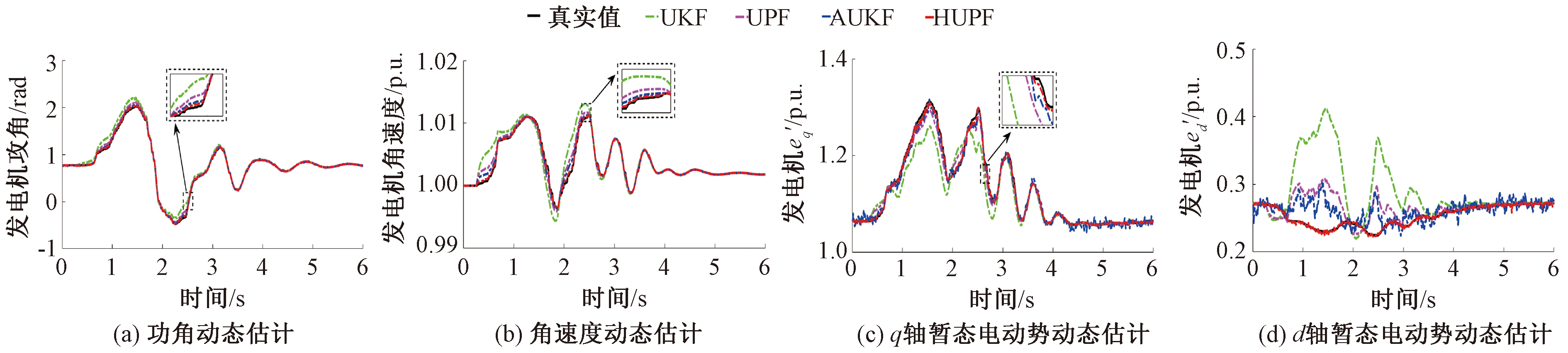
图4 非高斯噪声时状态估计对比
Figure 4 Comparison of state estimation with non-Gaussian noise
由图4(a)～4(d)对比曲线可知,当系统出现非高斯噪声时,传统的UKF和UPF方法出现较大的估计误差,已经无法对发电机的状态进行准确跟踪,估计性能严重下降;AUKF方法相比UKF方法对非高斯噪声具有一定的鲁棒性,但是仍然有较大的估计误差;对比之下,HUPF方法由于考虑了噪声不确定的影响,在出现非高斯噪声时依然能够实时准确地跟踪发电机的状态。因此,在这种情况下,HUPF方法能保持较高的估计精度,表明HUPF方法对非高斯噪声具有较强的鲁棒性。
表2给出了此种工况下UKF、UPF、AUKF和HUPF方法的RMSE对比情况。从表2中数据可知,与UKF、UPF和AUKF相比,本文所提的HUPF方法能够获得最准确的估计结果,对于非高斯噪声的鲁棒性更强。
表2 非高斯噪声时的RMSE对比
Table 2 Comparison of RMSE with non-Gaussian noise
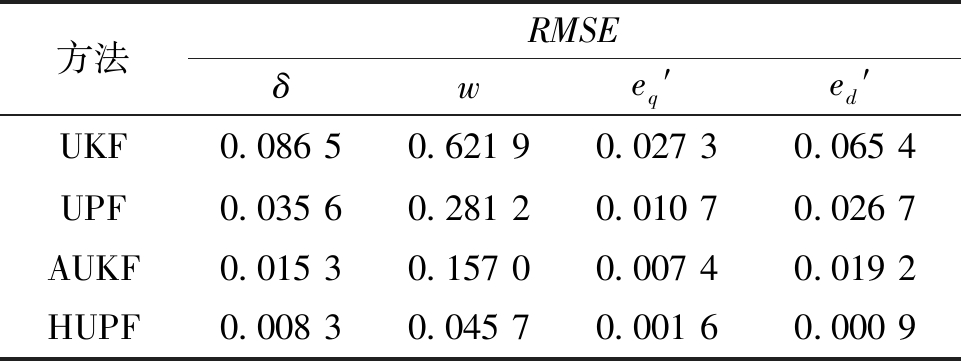
方法RMSEδweq′ed′UKF0.086 50.621 90.027 30.065 4UPF0.035 60.281 20.010 70.026 7AUKF0.015 30.157 00.007 40.019 2HUPF0.008 30.045 70.001 60.000 9
4.3 参数不确定性测试
在实际电网分析中,由于外部环境、温度等干扰,发电机内部参数容易出现波动,而这些不精确的模型参数会进一步对状态估计结果造成不良影响[18]。
为了验证本文所提方法在此种工况下的估计性能,假设发电机在受到外界干扰后,d轴和q轴暂态电抗发生不确定性扰动,偏离正常值10%。在发电机模型参数存在不确定性时,分别运用UKF、UPF、AUKF和HUPF方法对Gen2进行动态状态估计。图5和表3分别展示了发电机的暂态电抗出现不确定扰动时状态估计与均方根误差对比情况。
表3 参数不确定时的RMSE对比
Table 3 Comparison of RMSE under uncertain parameters
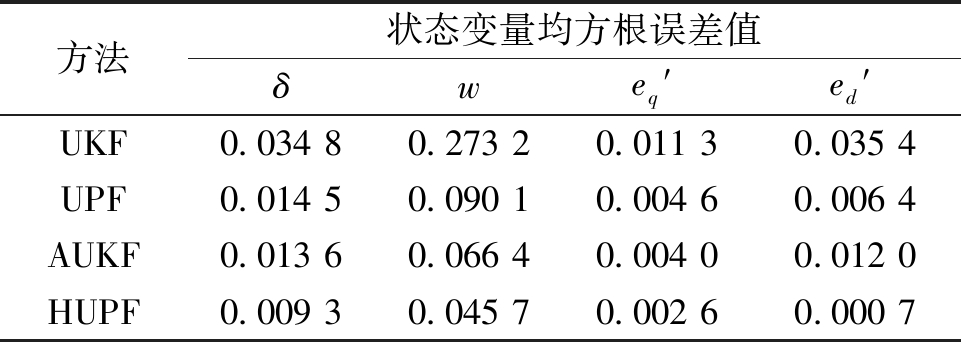
方法状态变量均方根误差值δweq′ed′UKF0.034 80.273 20.011 30.035 4UPF0.014 50.090 10.004 60.006 4AUKF0.013 60.066 40.004 00.012 0HUPF0.009 30.045 70.002 60.000 7
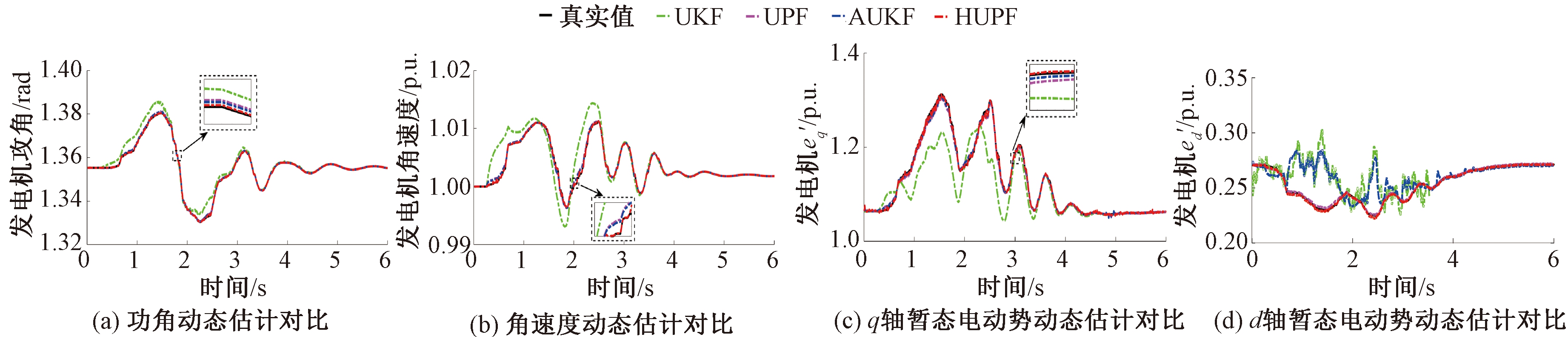
图5 参数不确定时动态估计对比
Figure 5 Dynamic estimation comparison with uncertain parameters
从测试结果中可以看出,与正常情况相比,UKF、UPF、AUKF和所提方法的估计误差结果明显增大,而HUPF方法的估计误差仍然最小。具体来说,UKF方法由于未考虑模型参数不确定的影响,估计结果存在较大偏差。UPF方法在一定程度上能减轻参数不确定的不良影响,其估计精度较UKF方法有较大提高。AUKF对于参数不确定导致的噪声协方差调整有限,因此估计精度并没有较大提高。相比之下,所提方法比UPF方法滤波性能更佳,这是因为,HUPF方法能根据参数变化,界定不确定性引起的估计偏差,动态调整式(18)中的估计误差协方差矩阵,从而更加准确地跟踪发电机状态,对发电机参数不确定表现出较强的鲁棒性。
5 结论
本文针对PMU中通信噪声以及模型参数不确定性情形下发电机状态估计精度下降的缺陷,提出了一种H∞无迹粒子滤波(HUPF)的发电机动态状态估计方法。以估计精度和抗差性能为目标,通过对IEEE 39节点系统算例的仿真与分析得出如下结论。
(1)在PF框架下利用无迹变换计算重要性密度函数,考虑了最新量测信息,使得粒子更加逼近真实的后验概率分布,能够在一定程度上提高估计精度。
(2)将不确定性约束准则引入到UPF中,实时更新粒子的状态误差协方差矩阵,能够显著增强估计方法对于噪声与模型参数不确定性的鲁棒性。
(3)仿真算例表明,相比其他DSE方法,HUPF方法在改善抗差性能的同时保持了方法的估计精度,更加适合处理非线性滤波问题,满足实际应用场景需求。
[1] 侯栋宸, 季嘉泓, 王建喜, 等. 基于伪量测自适应插值策略的发电机动态状态估计[J]. 高电压技术, 2021, 47(7): 2359-2366.
HOU D C, JI J H, WANG J X, et al. Dynamic state estimation for synchronous machines based on pseudo measurement adaptive interpolation strategy[J]. High Voltage Engineering, 2021, 47(7): 2359-2366.
[2] 巫春玲, 郑克军, 徐先峰, 等. 基于自适应插值强跟踪扩展卡尔曼滤波的电力系统动态状态估计研究[J]. 电网技术, 2023, 47(5): 2078-2088.
WU C L, ZHENG K J, XU X F, et al. Dynamic state estimation of power system based on adaptive interpolation strong tracking extended Kalman filter[J]. Power System Technology, 2023, 47(5): 2078-2088.
[3] 卢庆春, 张俊, 许沛东, 等. 考虑量测相关性的容积卡尔曼滤波动态状态估计[J]. 电测与仪表, 2022, 59(10): 161-167, 200.
LU Q C, ZHANG J, XU P D, et al. Dynamic state estimation of power system based on cubature Kalman filter considering measurement correlation[J]. Electrical Measurement &Instrumentation, 2022, 59(10): 161-167, 200.
[4] 朱茂林, 刘灏, 毕天姝, 等. 考虑输入量不良数据的发电机动态状态估计方法[J]. 电力系统自动化, 2022, 46(7): 94-103.
ZHU M L, LIU H, BI T S, et al. Dynamic state estimation method for generators considering bad data in input[J]. Automation of Electric Power Systems, 2022, 46(7): 94-103.
[5] 张晓兰, 谷永刚, 张少强, 等. 智能监测系统下的线性电网状态估计研究[J]. 电测与仪表, 2021, 58(10): 112-117.
ZHANG X L, GU Y G, ZHANG S Q, et al. Research on state estimation of linear grid based on intelligent monitoring system[J]. Electrical Measurement &Instrumentation, 2021, 58(10): 112-117.
[6] LIU Y, SINGH A K, ZHAO J B, et al. Dynamic state estimation for power system control and protection[J]. IEEE Transactions on Power Systems, 2021, 36(6): 5909-5921.
[7] 秦晓辉, 毕天姝, 杨奇逊. 基于WAMS的电力系统机电暂态过程动态状态估计[J]. 中国电机工程学报, 2008, 28(7): 19-25.
QIN X H, BI T S, YANG Q X. Dynamic state estimator based on WAMS during power system transient process[J]. Proceedings of the CSEE, 2008, 28(7): 19-25.
[8] 王大方, 李琪, 张鹏, 等. 带有相电压补偿基于EKF的无传感器感应电机转速估计[J]. 电机与控制学报, 2019, 23(1): 35-44.
WANG D F, LI Q, ZHANG P, et al. Speed estimation method based on extended Kalman filter with phase voltage compensation for sensorless ACIM drives[J]. Electric Machines and Control, 2019, 23(1): 35-44.
[9] ZHAO J B, MILI L, G
MEZ-EXPSITO A. Constrained robust unscented Kalman filter for generalized dynamic state estimation[J]. IEEE Transactions on Power Systems, 2019, 34(5): 3637-3646.
[10] WANG Y Q, YANG Z W, WANG Y, et al. Robust dynamic state estimation for power system based on adaptive cubature Kalman filter with generalized correntropy loss[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 1-11.
[11] ZHAO J B, MILI L. Robust unscented Kalman filter for power system dynamic state estimation with unknown noise statistics[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 1215-1224.
[12] 王彤, 高明阳, 黄世楼, 等. 基于自适应容积卡尔曼滤波的双馈风力发电机动态状态估计[J]. 电网技术, 2021, 45(5): 1837-1843, 14.
WANG T, GAO M Y, HUANG S L, et al. Dynamic state estimation for doubly fed induction generator wind turbine based on adaptive cubature Kalman filter[J]. Power System Technology, 2021, 45(5): 1837-1843, 14.
[13] 张琪, 张志利, 李天梅, 等. 一种摄动粒子滤波故障检测方法[J]. 电机与控制学报, 2017, 21(11): 107-113.
ZHANG Q, ZHANG Z L, LI T M, et al. A particle filter with perturbation for fault detection[J]. Electric Machines and Control, 2017, 21(11): 107-113.
[14] YU S S, GUO J H, CHAU T K, et al. An unscented particle filtering approach to decentralized dynamic state estimation for DFIG wind turbines in multi-area power systems[J]. IEEE Transactions on Power Systems, 2020, 35(4): 2670-2682.
[15] 王义, 孙永辉, 钟永洁, 等. 计及模型不确定性的发电机动态状态估计方法[J]. 电力系统自动化, 2018, 42(21):77-83.
WANG Y, SUN Y H, ZHONG Y J, et al. Dynamic state estimation method for generators considering model uncertainties[J]. Automation of Electric Power Systems, 2018, 42(21):77-83.
[16] YANG J, ZHANG W A, GUO F H. Dynamic state estimation for power networks by distributed unscented information filter[J]. IEEE Transactions on Smart Grid, 2020, 11(3): 2162-2171.
[17] NUGROHO S A, TAHA A F, QI J J. Robust dynamic state estimation of synchronous machines with asymptotic state estimation error performance guarantees[J]. IEEE Transactions on Power Systems, 2020, 35(3): 1923-1935.
[18] 王义, 孙永辉, 南东亮, 等. 考虑参数不确定性影响的发电机动态状态估计方法[J]. 电力系统自动化, 2020, 44(4): 110-118.
WANG Y, SUN Y H, NAN D L, et al. Dynamic state estimation method of generator considering the influence of parameter uncertainty[J]. Automation of Electric Power Systems, 2020, 44(4): 110-118.
[19] 李扬, 李智, 陈亮, 等. 发电机动态状态估计中的一种虚假数据注入攻击方法[J]. 电工技术学报, 2020, 35(7): 1476-1488.
LI Y, LI Z, CHEN L, et al. A false data injection attack method for generator dynamic state estimation[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1476-1488.
[20] MASOUMNEZHAD M, TEHRANI M, AKOUSHIDEH A, et al. A new adaptive fuzzy hybrid unscented Kalman/H-infinity filter for state estimating dynamical systems[J]. IET Signal Processing, 2021, 15(7): 459-466.
[21] ZHANG S Z, GUO X, ZHANG X W. An improved adaptive unscented Kalman filtering for state of charge online estimation of lithium-ion battery[J]. Journal of Energy Storage, 2020, 32: 101980.
[22] 夏添梁, 张玉敏, 杨明, 等. 联合长短期记忆神经网络和粒子滤波的配电网预测辅助鲁棒状态估计方法[J]. 高电压技术, 2022, 48(4): 1343-1355.
XIA T L, ZHANG Y M, YANG M, et al. Robust forecasting-aided state estimation method of distribution network based on long-short term memory neural network and particle filter[J]. High Voltage Engineering, 2022, 48(4): 1343-1355.