电力系统状态估计最初主要研究静态状态估计(static state estimation, SSE)。静态状态估计主要根据某一时刻断面的量测数据对电力系统进行实时状态估计。随着电力系统状态估计研究的深入发展,出现了辅助预测状态估计(forecasting-aided state estimation, FASE)。辅助预测状态估计不仅利用当前时刻量测信息,还用到前一时刻的状态预测值,同时获取电网运行状态的估计和预测值,为电网能源管理系统提供可靠信息支撑[1-2]。
近年来,研究人员围绕电网辅助预测状态估计模型的建立和估计方法设计开展了大量研究[3-5]。较早提出和应用的电力系统状态估计方法有扩展卡尔曼滤波(extended Kalman filter,EKF)。Hou等[6]提出了基于EKF的电力系统状态估计方法,针对非线性函数,该方法对相关函数进行线性化,采用泰勒级数的方法,但其估计精度较低。Qi等[7]提出无迹卡尔曼滤波(unscented Kalman filter,UKF)算法,该方法采用确定性采样以近似非线性函数的概率分布;但是,计算机的舍入误差会随着滤波计算不断累积,最终使得协方差矩阵失去正定性[8]。为解决此问题,Yu等[9]提出了平方根无迹卡尔曼滤波(square root unscented Kalman filter, SRUKF)。该方法在UKF的基础上,引入矩阵QR分解、Cholesky分解2种数学方法,利用状态协方差矩阵的平方根进行迭代计算。但值得注意的是,以上研究所采用的卡尔曼滤波只能应用在高斯分布模型中。为不受高斯分布的影响,Emami等[10]采用了粒子滤波(particle filter,PF)。PF是一种基于蒙特卡罗模拟的最优递归贝叶斯滤波方法,其滤波精度很大程度上受所选择的建议密度函数影响。对此,谢长君等[11]提出无迹粒子滤波,利用UKF获得建议密度函数。但UPF(unscented particle filter)仍然面临状态预测误差协方差矩阵不正定的问题。
在Chen等[12]和王义等[13]采用电力系统辅助预测状态估计求重要性密度函数时,由于采用了无迹粒子滤波的方法,使得UPF带有与UKF类似的状态预测误差协方差矩阵不正定的问题,降低了滤波精度,甚至中断滤波。因此,在动态导航、水下组合导航和移动机器人领域,Wei等[14]、李厚全等[15]和宋宇等[16]对UPF存在的问题进行了初步探索,并指出通过引入平方根技术能够有效提升系统状态跟踪精度。基于此,为有效提升电力系统的状态估计精度,同时考虑到电力系统状态变量多、计算复杂度高等影响,通过采用矩阵QR分解和Cholesky分解技术,求出状态预测误差协方差矩阵的平方根,以其平方根代替状态预测误差协方差矩阵进行迭代计算,建立了基于平方根UPF(square root unscented particle filter, SRUPF)的电力系统辅助预测状态估计方法。最后,在仿真系统上进行测试,结果表明,所提方法能够有效克服状态预测误差协方差矩阵的不正定问题,获得较UKF、SRUKF和UPF更高的状态估计精度,鲁棒性更强。
1 电网辅助预测状态估计模型
一般来说,电力系统辅助预测状态估计模型由系统方程和量测方程构成[17-18],如式(1)所示:
(1)
式中:下标k和k+1表示时刻;xk表示状态变量,其主要构成有节点电压相角和节点电压幅值;zk+1表示量测值,其主要构成有节点电压相角、节点电压幅值、支路无功功率、支路有功功率、节点注入无功功率、节点注入有功功率;f(·)表示系统方程,h(·)表示量测方程,两者均为非线性函数;wk表示系统噪声,vk表示观测噪声,两者均服从零均值的高斯分布,协方差矩阵分别为Q和R。
采用两参数指数平滑法构造电力系统辅助预测状态估计模型[19]。系统函数f(x)表示如下:
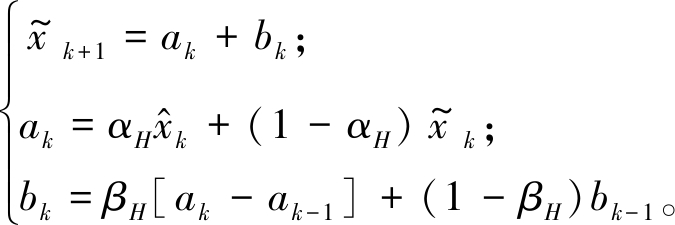
(2)
式中:ak和bk分别为两参数指数平滑法中的水平分量和倾斜分量;αH和βH为两参数指数平滑法的平滑参数。式(2)整理后可得
(1-βH)bk-1。
(3)
2 基于SRUPF的电力系统辅助预测状态估计
2.1 UPF基本原理
UPF在采样阶段利用UKF作为重要性密度函数生成预测粒子,执行预测步得到预测后Sigma点集均值
和状态预测误差协方差矩阵
(4)
(5)
(6)
执行更新步更新Sigma点的量测均值和状态预测误差协方差矩阵:
(7)
(8)
(9)
(10)
最后计算滤波增益并重采样。
以上过程在每步迭代计算时将观测量融入状态估计,为每个粒子计算均值和状态预测误差协方差矩阵建立合理的粒子分布。但是粒子的状态预测误差协方差矩阵在迭代计算过程中会出现不正定现象,导致程序运行时出现矩阵具有奇异性的警告,甚至中断运行程序。
2.2 SRUPF基本原理
SRUPF的基本思想是通过引入两种数学方法,动态更新状态预测误差协方差矩阵的平方根,从而提高UPF算法的准确性、效率和稳定性。
与UPF相比,SRUPF可以减少累积误差和计算量。这是因为在UPF中,在生成每个Sigma点时,都需对状态预测误差矩阵
进行1次开方计算,这将极大增加UPF的计算量。而且在这个大量的开方计算过程中,会增加计算误差,并在不断的迭代过程中累积。
而采用SRUPF则可以直接通过上一次迭代滤波取得的状态预测误差矩阵平方根直接生成Sigma点,省去了对状态预测误差矩阵进行开方的计算量,减少了累积误差。
SRUPF不仅可以减小累积误差和计算量,而且能增强算法稳定性。这是因为在UPF中,迭代计算中累积的截断误差、初始预测误差协方差矩阵设置不当和量测信号传输过程中引入的非高斯噪声等,这些因素会使得状态预测误差矩阵出现异常值。随着滤波过程迭代进行,最终导致预测误差协方差矩阵不能在迭代计算中开方以生成Sigma点,滤波中断。针对这些问题,平方根UPF采用Cholesky分解因子更新和矩阵QR分解的方法求取状态预测误差协方差矩阵的平方根,从而取代状态预测误差协方差矩阵来完成滤波计算,增强算法稳定性,防止滤波发散[20]。该方法通过QR分解和 Cholesky分解因子更新实现。
(1) QR分解。矩阵AT 可被分解为
AT =QR;
(11)
式中:R为一个上三角矩阵;Q为一个正交矩阵。如果P=AAT, 那么矩阵P就可进行平方根分解:
P=AAT=(QR)T(QR)=RTQTQR=RTR。
(12)
其中RT为矩阵P的Cholesky因子。
(2) Cholesky分解因子更新。P=SST可表示为S=chol(P),S为P的Cholesky因子,为下三角矩阵。因此,矩阵P±UUT的Cholesky分解因子更新可表示为cholupdate(S,U,±1)。
通过以上分解更新,状态预测误差协方差矩阵就可由状态预测误差协方差矩阵的平方根进行替代计算,并在下一次迭代计算时直接代入状态预测误差协方差矩阵平方根进行计算,无须再对状态预测误差协方差矩阵进行开方运算,从而避免矩阵不正定无法开方的问题,提高了计算效率和准确度。
在UPF计算中,为提高计算精度可增加粒子数目,这样在每次迭代计算时,每个粒子生成3个Sigma点,总Sigma点数也会随着粒子数目的增加而成倍增加,使得UPF算法的计算量较大。平方根法通过减少每个Sigma点的计算量,可以减少UPF总计算量,从而有效提高UPF滤波精度和鲁棒性。
2.3 算法流程
图1给出了本文所提SRUPF辅助预测状态估计流程。运用SRUPF方法对电网进行动态状态估计,具体步骤如下。
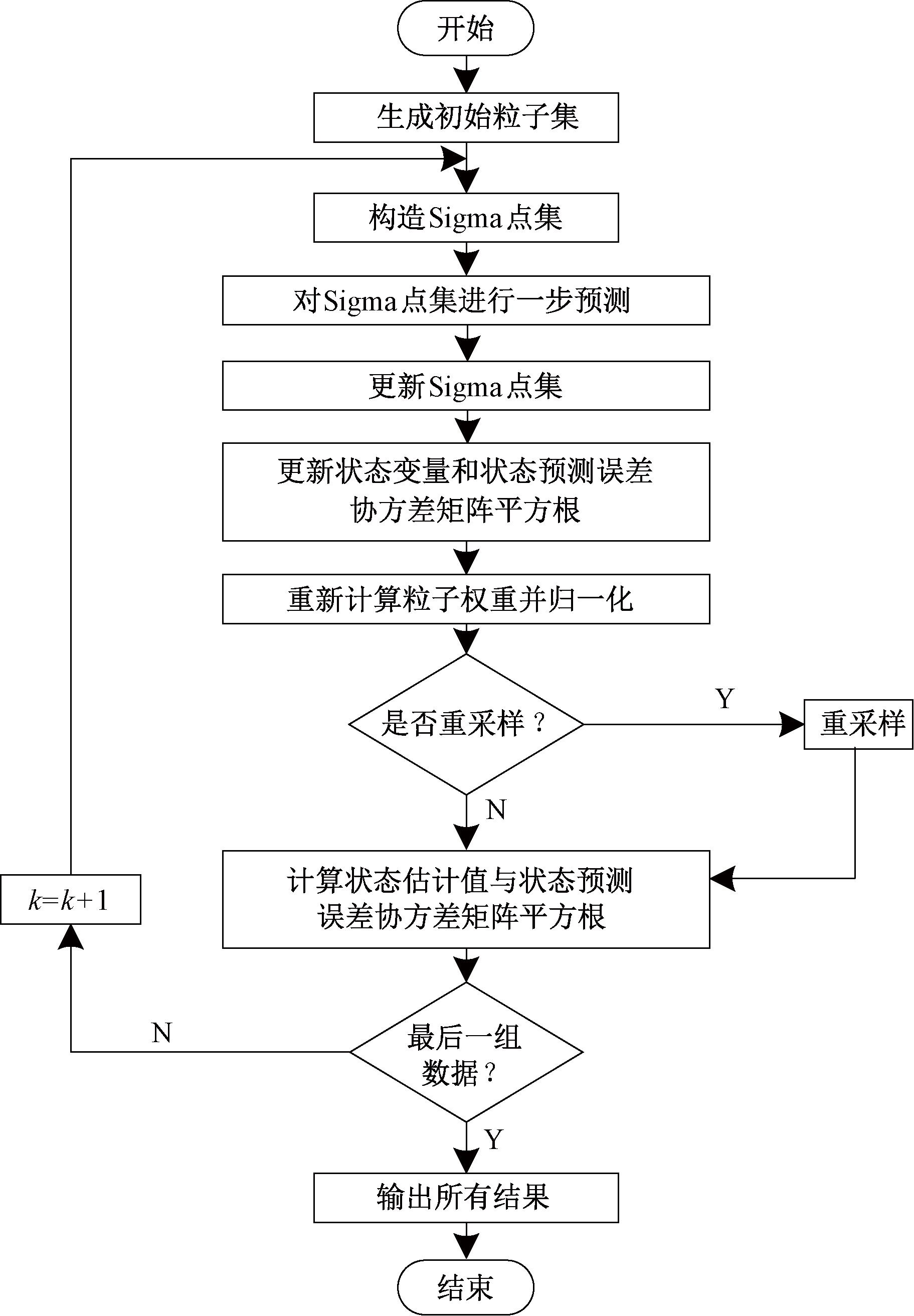
图1 SRUPF流程图
Figure 1 Flow chart of SRUPF program
步骤1 初始化。当k=0时,在初始状态变量x0附近生成初始粒子集,
其中,P(·)为概率分布函数,j=1,2,…, M。初始权值设为
表示粒子个数。
步骤2 采用Sigma点比例修正采样,构造Sigma采样点
和权值 Wi,m、Wi,c:
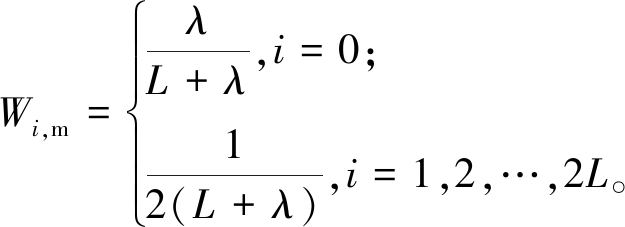
(13)
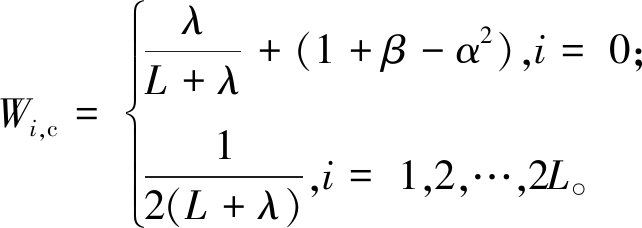
(14)
(15)
式中:α为比例修正因子,通常决定Sigma点围绕
的波动范围;β包含x分布的先验知识;L为状态变量维数;λ=α2(L+kf)-L,λ为缩放比例参数,kf为第2个尺度参数,在状态估计中通常取
表示各粒子k时刻状态量的协方差矩阵的平方根。
步骤3 由两参数指数平滑法构造的电力系统动态状态参数模型对Sigma点集进行一步预测,通过式(2)系统方程f(x)得到预测后的点集
和其均值
(16)
(17)
(18)
与式(6)直接求状态预测误差协方差矩
阵相比,式(18)先求
于是由式(6)可知
求得
后,通过式(19) 中QR分解和式(20) 中Cholesky分解因子更新来求协方差矩阵的平方根
(19)
(20)
式中:cholupdate(·)为MATLAB函数,表示该式将返回
的Cholesky因子;qr(·)表示求
的QR分解,即
其中D为正交阵。
于是
其中
为状态预测误差协方差矩阵的平方根。
步骤4 更新Sigma点集。将点集代入量测方程h(·)求得更新后的量测值
然后计算Sigma点的量测均值
与上一步类似,求量测值的自协方差矩阵的平方根矩阵
而这一步在UPF中则是求自协方差矩阵
(21)
(22)
(23)
(24)
(25)
步骤5 计算卡尔曼增益
并更新系统的状态变量
和状态预测误差协方差矩阵的平方根;
为上一步预测值更新部分计算得到量测值的自协方差矩阵平方根;
为式(10)计算得到的预测值和量测值的互协方差平方根矩阵。
(26)
(27)
(28)
(29)
步骤6 重新计算粒子权重
并归一化:
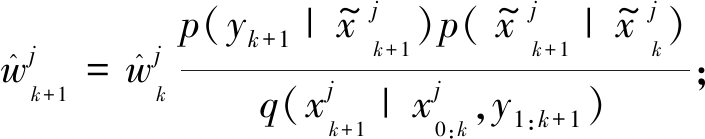
(30)
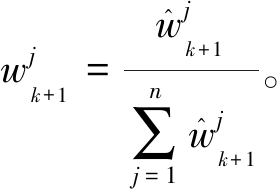
(31)
步骤7 重采样,解决粒子在采样过程中出现粒子退化的问题。根据归一化权重,对粒子集合进行复制与淘汰,并计算重采样后的均值。
步骤8 重采样完成后,若不是最后一组数据,则将状态量估计值
和已计算出的状态预测误差协方差矩阵
的平方根
代入第2步,构造Sigma点进行新一轮迭代计算。在进行下一轮计算时,式(15)中无须对求取平方根,从而解决了预测误差协方差矩阵不正定而无法开方的问题。
步骤9 迭代计算完成后,输出状态量的估计值。
3 算例分析
本文在IEEE 30节点和IEEE 57节点系统上进行仿真测试。30节点系统虽然节点数较少,但其系统设计主要考虑了非高斯噪声环境[21],更适合验证本文所提方法的稳定性。57节点系统通过样条函数插值法对日负荷曲线进行模拟能较好地保持原负荷曲线的重要特征[22],其准确度比30节点系统更高,仿真模拟真实电力系统的效果更好。
为量化评估不同滤波方法的状态估计,通过均方根误差RMSE来测量估计值与真值间的误差[23],其表达式如下:
(32)
式中:L表示状态量维数;
表示状态量估计值的第i个分量; xk,i表示状态量真值的第i个分量。均方根误差体现了滤波估计的平均估计效果,均方根误差值越小说明估计值越接近真值。
3.1 高斯噪声测试
本文在潮流计算结果上添加随机量测误差形成量测数据[24]。正常高斯噪声环境的具体设置如下:IEEE 30节点系统的系统噪声协方差矩阵Q=10-8I59×59,观测噪声协方差矩阵R=10-8I172×172; IEEE 57节点系统的系统噪声协方差矩阵Q=10-6I113×113,观测噪声协方差矩阵R=10-7I331×331;本文所测试的滤波方法采样方式均为系统重采样;粒子数100个;仿真程序总运算时间为1 440 min。
测试结果如图2和图3所示。从图2、3中可以看出,SRUPF状态估计曲线几乎与真实值重合,其估计精度远高于UKF、SRUKF和UPF。
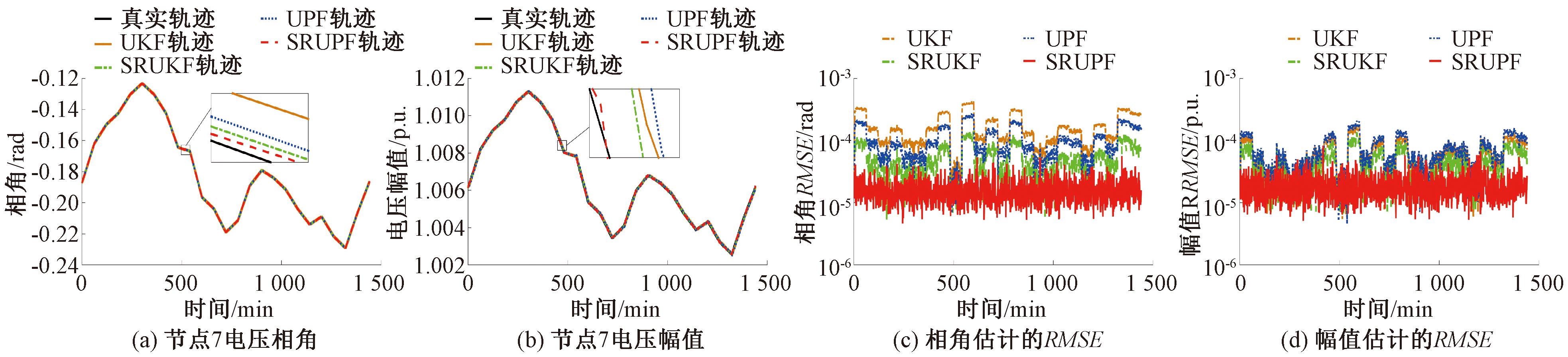
图2 高斯噪声下的IEEE 30 系统估计结果
Figure 2 Estimation results of IEEE 30 with Gaussian noises
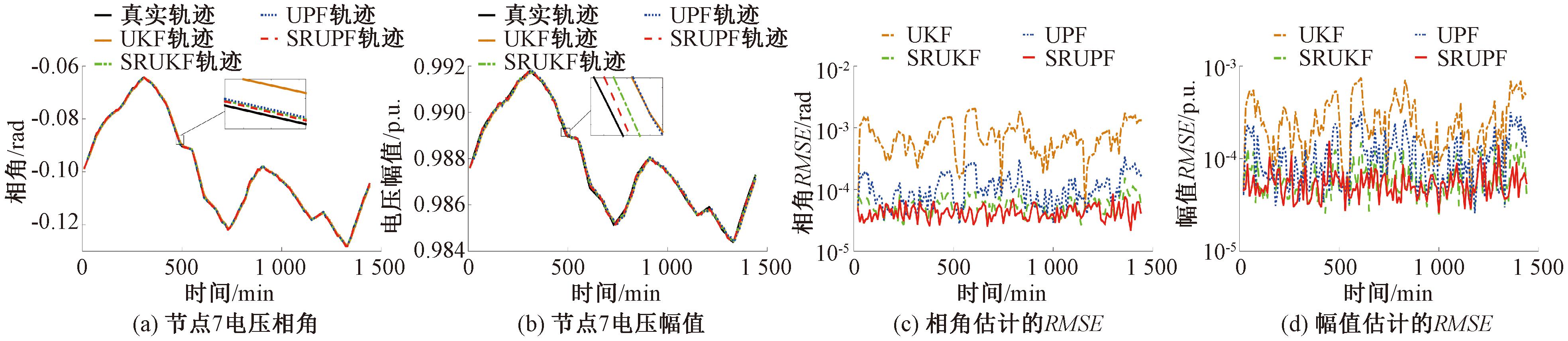
图3 高斯噪声下的IEEE 57 系统估计结果
Figure 3 Estimation results of IEEE 57 with Gaussian noises
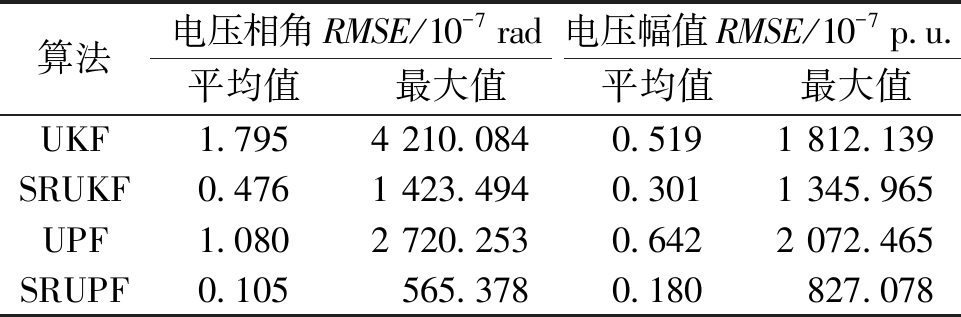
为更直观地比较UKF、SRUKF、UPF与SRUPF方法的状态估计结果与性能,表1和表2进一步给出不同方法电压相角和幅值RMSE的平均值和最大值。其中SRUPF方法的均方根误差性能指标明显优于UKF、SRUKF和UPF方法,上述结果证明了本文所提出的SRUPF方法的精确性。
表1 高斯噪声下的IEEE 30 节点系统均方根误差
Table 1 RMSE of IEEE 30 bus system with Gaussian noises
算法电压相角RMSE/10-7 rad电压幅值RMSE/10-7 p.u.平均值最大值平均值最大值UKF1.7954 210.0840.5191 812.139SRUKF0.4761 423.4940.3011 345.965UPF1.0802 720.2530.6422 072.465SRUPF0.105565.3780.180827.078
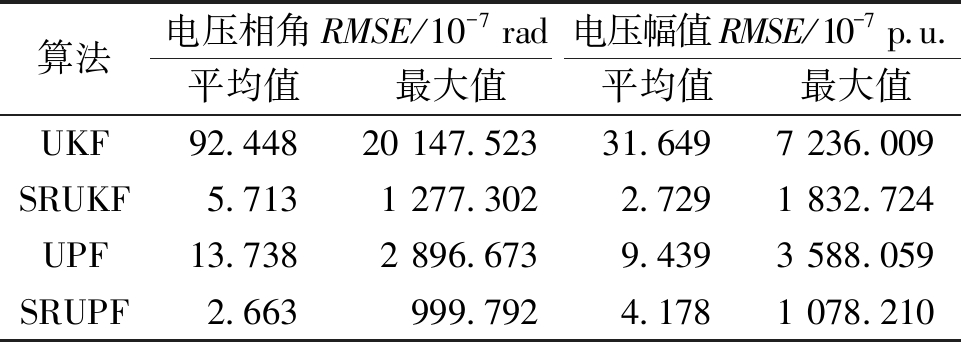
表2 高斯噪声下的IEEE 57 节点系统均方根误差
Table 2 RMSE of IEEE 57 bus system with Gaussian noises
算法电压相角RMSE/10-7 rad电压幅值RMSE/10-7 p.u.平均值最大值平均值最大值UKF92.44820 147.52331.6497 236.009SRUKF5.7131 277.3022.7291 832.724UPF13.7382 896.6739.4393 588.059SRUPF2.663999.7924.1781 078.210
3.2 预测误差协方差矩阵非正定性测试
在UPF滤波过程中,由于噪声和计算误差的影响,状态协方差矩阵会出现非正定[25]。为了验证SRUPF方法针对此工况的有效性,本文在IEEE 30和IEEE 57测试系统上进行测试。
在IEEE 30测试系统上进行的测试中,当初始预测误差协方差矩阵
时,用UPF方法的状态估计在运行过程中出现预测误差协方差矩阵不正定,运行程序中断;当初始预测误差协方差矩阵
时,用UKF方法的状态估计在运行过程中出现预测误差协方差矩阵非正定,运行程序中断。初始预测误差协方差矩阵的值设置越大,运行程序越早出现非正定。设初始协方差
系统噪声与正常工况一致,Q=10-8I59×59,粒子数为100,用SRUPF方法的状态估计误差均方根见表3。
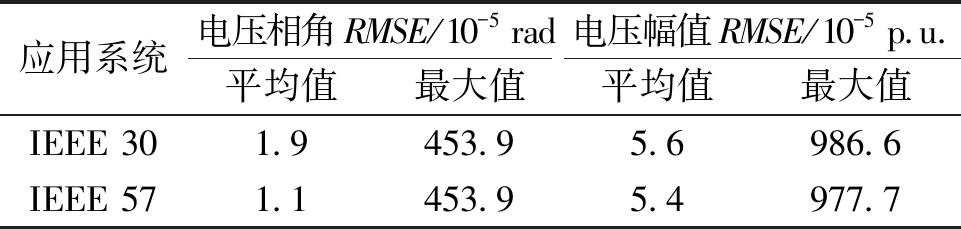
表3 SRUPF均方根误差
Table 3 RMSE of SRUPF
应用系统电压相角RMSE/10-5 rad电压幅值RMSE/10-5 p.u.平均值最大值平均值最大值IEEE 301.9453.95.6986.6IEEE 571.1453.95.4977.7
在IEEE 57测试系统上进行的仿真测试中,当初始预测误差协方差矩阵
时,用UPF方法的状态估计在运行过程中出现预测误差协方差矩阵非正定,运行程序中断;当初始预测误差协方差矩阵
时,用UKF方法的状态估计在运行过程中出现预测误差协方差矩阵非正定,运行程序中断。初始预测误差协方差矩阵的值越大,运行程序越早出现非正定。设初始协方差
系统噪声与正常工况一致,Q=10-6I113×113,粒子数为100,仿真程序总运算时间为1 440 min,用SRUPF方法的状态估计误差均方根见表3。
由表3可知,由于SRUPF采用状态预测估计协方差矩阵的平方根进行迭代计算,避免了每次迭代过程中对状态预测估计协方差矩阵的平方根的计算,保证了状态预测估计协方差矩阵的正定性,较UKF、SRUKF和UPF方法具有更强的鲁棒性,实现电网状态精确估计。
3.3 非高斯噪声测试
量测信息在传输时,通信信道中存在噪声污染,使得量测噪声的统计特性不服从高斯分布,影响状态估计精度[26]。为验证所提方法针对此种情形的估计性能,在IEEE 30系统和IEEE 57系统中,分别使用UKF、平方根UKF、UPF和SRUPF方法对系统状态进行估计跟踪。
在IEEE 30节点系统中,设定量测噪声的协方差矩阵存在不确定性,偏离真实噪声。设置量测方程中5%的量测噪声协方差矩阵R=10-10I172×172,95%的量测噪声协方差矩阵与正常工况一致,设R=10-8I172×172。系统噪声与正常工况一致,为Q=10-8I59×59;在IEEE 57系统中,设置量测方程中5%的量测噪声协方差矩阵R=10-12I331×331,95%的量测噪声协方差矩阵与正常工况一致,设为R=10-7I331×331;系统噪声与正常工况一致,为Q=10-6I113×113。粒子数为100,仿真程序总运算时间为1 440 min。测试结果如图4、5所示。表4和表5给出了电压相角和电压幅值RMSE的平均值和最大值。
表4 非高斯噪声下的IEEE 30 节点系统均方根误差
Table 4 RMSE of IEEE 30 bus system with non-Gaussian noises
算法电压相角RMSE/10-7 rad电压幅值RMSE/10-7 p.u.平均值最大值平均值最大值UKF1.8404 060.9660.5961 535.144SRUKF0.5361 230.7580.4251 024.583UPF1.1272 542.7050.7371 789.942SRUPF0.001212.1230.001186.921
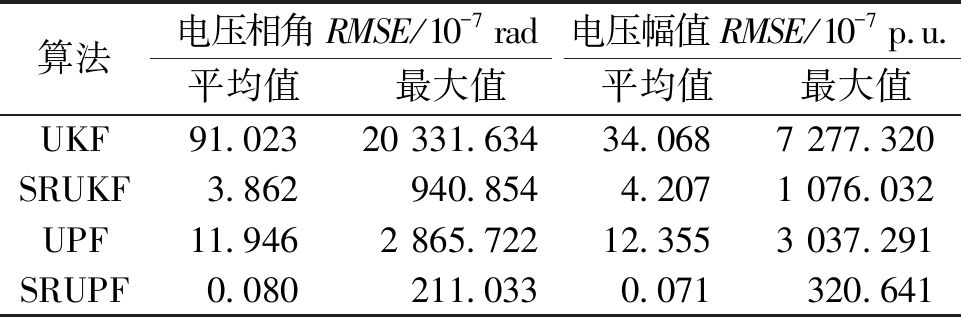
表5 非高斯噪声下的IEEE 57节点系统均方根误差
Table 5 RMSE of IEEE 57 bus system with non-Gaussian noises
算法电压相角 RMSE/10-7 rad电压幅值 RMSE/10-7 p.u.平均值最大值平均值最大值UKF91.02320 331.63434.0687 277.320SRUKF3.862940.8544.2071 076.032UPF11.9462 865.72212.3553 037.291SRUPF0.080211.0330.071320.641
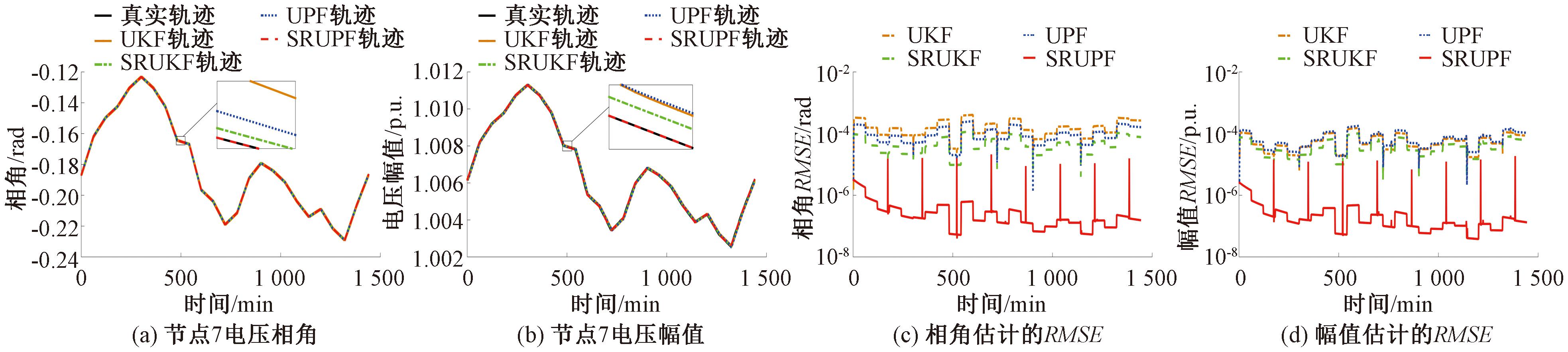
图4 非高斯噪声下的IEEE 30 系统估计结果
Figure 4 Estimation results of IEEE 30 with non-Gaussian noises
图5 非高斯噪声下的IEEE 57系统估计结果
Figure 5 Estimation results of IEEE 57 with non-Gaussian noises
由上述结果可知,IEEE 30节点系统非高斯噪声测试中,SRUPF电压相角的均方根误差平均值约为UPF的0.09%,SRUPF电压幅值的均方根误差平均值约为UPF的0.14%;IEEE 57节点系统非高斯噪声测试中,SRUPF电压相角的均方根误差平均值约为UPF的0.67%,SRUPF电压幅值的均方根误差平均值约为UPF的0.57%。综上所述,非高斯噪声测试中SRUPF的均方根误差约为UPF的均方根误差的千分之一。可见本文提出的SRUPF方法在非高斯噪声环境下依然能够实现系统状态的精确估计,较UPF和UKF具有更强的鲁棒性。
3.4 3种工况耗时情况
表6为高斯噪声工况、非高斯噪声工况和不正定测试工况耗时。由表6可知,与UPF相比,SRUPF在3种工况下用时均少于UPF,减少了计算量。但SRUPF用时多于UKF和SRUKF,这是由于SRUPF为提高滤波精度而生成粒子,从而增加了计算时长。对于SRUPF运算时长的问题,以后仍需进行更多的深入研究。
表6 高斯噪声工况、非高斯噪声工况和不正定测试工况耗时
Table 6 The times of Gaussian noises conditions, non-Gaussian noises conditions, and non positive test conditions
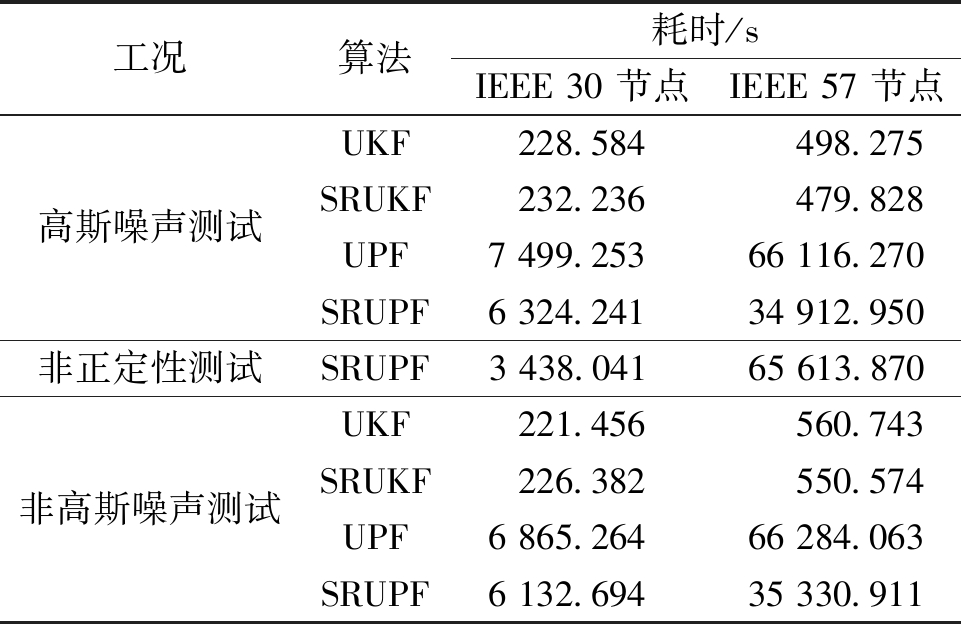
工况算法耗时/sIEEE 30 节点IEEE 57 节点高斯噪声测试UKF228.584498.275SRUKF232.236479.828UPF7 499.25366 116.270SRUPF6 324.24134 912.950非正定性测试SRUPF3 438.041 65 613.870非高斯噪声测试UKF221.456560.743SRUKF226.382550.574UPF6 865.26466 284.063SRUPF6 132.69435 330.911
4 结论
针对状态预测误差协方差矩阵非正定性引起的辅助预测状态估计精度降低甚至滤波发散问题,本文在UPF框架下,引入平方根技术,建立了一种基于SRUPF方法的电力系统动态状态估计方法。进行仿真测试,得出结论如下。
(1)在辅助预测状态估计的迭代计算过程中,SRUPF方法可以降低截断误差累积,保持状态预测误差协方差矩阵的正定性,提高估计精度。
(2)采用状态预测误差协方差矩阵的平方根S替代状态预测误差协方差矩阵P进行运算,能够避免每次迭代过程中对状态预测误差协方差矩阵平方根的计算,有效克服状态预测误差协方差矩阵的非正定性,提高了辅助预测状态估计的鲁棒性。
(3)在非高斯噪声情况下,SRUPF方法较UPF和UKF具有更好的精确性和鲁棒性。
[1] MA W T, QIU J Z, LIU X H, et al. Unscented Kalman filter with generalized correntropy loss for robust power system forecasting-aided state estimation[J]. IEEE Transactions on Industrial Informatics, 2019, 15(11): 6091-6100.
[2] 刘朋成, 项中明, 江全元, 等. 基于鲁棒容积卡尔曼滤波的同步发电机实时动态状态估计方法[J]. 电网技术, 2019, 43(8): 2860-2867.
LIU P C, XIANG Z M, JIANG Q Y, et al. Real-time dynamic state estimation method of synchronous generator based on robust volume Kalman filter[J]. Power System Technology, 2019, 43(8): 2860-2867.
[3] 艾蔓桐, 孙永辉, 王义, 等. 基于插值H_∞扩展卡尔曼滤波的发电机动态状态估计[J]. 中国电机工程学报, 2018, 38(19): 5846-5853, 5942.
AI M T, SUN Y H, WANG Y, et al. Dynamic state estimation for synchronous machines based on interpolation H_∞ extended Kalman filter[J]. Proceedings of the CSEE, 2018, 38(19): 5846-5853, 5942.
[4] 黄蔓云, 王天昊, 卫志农, 等. 基于长短期记忆网络的UKF动态谐波状态估计[J]. 电力系统保护与控制, 2022, 50(11):1-11.
HUANG M Y, WANG T H, WEI Z N, et al. Dynamic harmonic state estimation of an unscented Kalman filter based on long short-term memory neural networks[J]. Power System Protection and Control, 2022, 50(11):1-11.
[5] 侯栋宸, 季嘉泓, 王建喜, 等. 基于伪量测自适应插值策略的发电机动态状态估计[J]. 高电压技术, 2021, 47(7): 2359-2366.
HOU D C, JI J H, WANG J X, et al. Dynamic state estimation for synchronous machines based on pseudo measurement adaptive interpolation strategy[J]. High Voltage Engineering, 2021, 47(7): 2359-2366.
[6] HOU D C, SUN Y H, ZHANG L C, et al. Robust forecasting-aided state estimation considering uncertainty in distribution system[J]. CSEE Journal of Power and Energy Systems, 2022,PP(99):1-9.
[7] QI J J, SUN K, WANG J H, et al. Dynamic state estimation for multi-machine power system by unscented Kalman filter with enhanced numerical stability[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 1184-1196.
[8] ZHAO J B, MILI L, G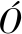
MEZ-EXP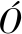SITO A. Constrained robust unscented Kalman filter for generalized dynamic state estimation[J]. IEEE Transactions on Power Systems, 2019, 34(5): 3637-3646.
[9] YU S S, FAN X Q, CHAU T K, et al. Square-root sigma-point filtering approach to state estimation for wind turbine generators in interconnected energy systems[J]. IEEE Systems Journal, 2021, 15(2): 1557-1566.
[10] EMAMI K, FERNANDO T, IU H H C, et al. Particle filter approach to dynamic state estimation of generators in power systems[J]. IEEE Transactions on Power Systems, 2015, 30(5): 2665-2675.
[11] 谢长君, 费亚龙, 曾春年, 等. 基于无迹粒子滤波的车载锂离子电池状态估计[J]. 电工技术学报, 2018, 33(17): 3958-3964.
XIE C J, FEI Y L, ZENG C N, et al. State-of-charge estimation of lithium-ion battery using unscented particle filter in vehicle[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 3958-3964.
[12] CHEN L, CHEN J, WANG H M, et al. Remaining useful life prediction of battery using a novel indicator and framework with fractional grey model and unscented particle filter[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 5850-5859.
[13] 王义, 孙永辉, 南东亮, 等. 考虑参数不确定性影响的发电机动态状态估计方法[J]. 电力系统自动化, 2020, 44(4):110-118.
WANG Y, SUN Y H, NAN D L, et al. Dynamic state estimation method for generator considering influence of parameter uncertainties[J]. Automation of Electric Power Systems, 2020, 44(4):110-118.
[14] WEI W H, GAO S S, ZHONG Y M, et al. Adaptive square-root unscented particle filtering algorithm for dynamic navigation[J]. Sensors, 2018, 18(7): 2337.
[15] 李厚全, 刘莫尘, 伍志海, 等. 球面单形平方根无迹粒子滤波在拖曳合成孔径声纳组合导航中的应用[J]. 中国惯性技术学报, 2014, 22(4): 531-535.
LI H Q, LIU M C, WU Z H, et al. Spherical simplex square-root unscented particle filter used in integrated navigation system of synthetic aperture sonar[J]. Journal of Chinese Inertial Technology, 2014, 22(4): 531-535.
[16] 宋宇, 李庆玲, 康轶非, 等. 平方根容积Rao-blackwillised粒子滤波SLAM算法[J]. 自动化学报, 2014, 40(2): 357-367.
SONG Y, LI Q L, KANG Y F, et al. SLAM with square-root cubature Rao-blackwillised particle filter[J]. Acta Automatica Sinica, 2014, 40(2): 357-367.
[17] 赵晋泉, 邓晖, 吴小辰, 等. 基于广域响应的电力系统暂态稳定控制技术评述[J]. 电力系统保护与控制, 2016, 44(5): 1-9.
ZHAO J Q, DENG H, WU X C, et al. Review on power system transient stability control technologies based on PMU/WAMS[J]. Power System Protection and Control, 2016, 44(5): 1-9.
[18] ZHAO J B, NETTO M, HUANG Z Y, et al. Roles of dynamic state estimation in power system modeling, monitoring and operation[J]. IEEE Transactions on Power Systems, 2021, 36(3): 2462-2472.
[19] 赵洪山, 田甜. 基于自适应无迹卡尔曼滤波的电力系统动态状态估计[J]. 电网技术, 2014, 38(1): 188-192.
ZHAO H S, TIAN T. Dynamic state estimation for power system based on an adaptive unscented Kalman filter[J]. Power System Technology, 2014, 38(1): 188-192.
[20] 安军, 杨振瑞, 周毅博, 等. 基于平方根容积卡尔曼滤波的发电机动态状态估计[J]. 电工技术学报, 2017, 32(12):234-240.
AN J, YANG Z R, ZHOU Y B, et al. Dynamic state estimator for synchronous-machines based on square root cubature Kalman filter[J]. Transactions of China Electrotechnical Society, 2017, 32(12):234-240.
[21] LEITE DA SILVA A M, DO COUTTO FILHO M B, DE QUEIROZ J F. State forecasting in electric power systems[J]. IEE Proceedings. Part C: Generation, Transmission and Distribution, 1983, 130(5): 237-244.
[22] 赵晖. 用样条插值法模拟典型日负荷曲线[J]. 电网技术, 1998, 22(5): 39-41, 45.
ZHAO H. Simulation of typical daily load curve with spline interpolation[J]. Power System Technology, 1998, 22(5): 39-41, 45.
[23] 葛立青, 刘青红, 王建锋, 等. 计及样本容量合理性的风电功率预测考核算法[J]. 电力系统自动化, 2017, 41(18): 118-123, 136.
GE L Q, LIU Q H, WANG J F, et al. Assessment algorithm for wind power prediction considering rationality of sample size[J]. Automation of Electric Power Systems, 2017, 41(18): 118-123, 136.
[24] 李扬, 李京, 陈亮, 等. 复杂噪声条件下基于抗差容积卡尔曼滤波的发电机动态状态估计[J]. 电工技术学报, 2019, 34(17):3651-3660.
LI Y, LI J, CHEN L, et al. Dynamic state estimation of synchronous machines based on robust cubature Kalman filter under complex measurement noise conditions[J]. Transactions of China Electrotechnical Society, 2019, 34(17):3651-3660.
[25] YU S S, GUO J H, CHAU T K, et al. An unscented particle filtering approach to decentralized dynamic state estimation for DFIG wind turbines in multi-area power systems[J]. IEEE Transactions on Power Systems, 2020, 35(4): 2670-2682.
[26] ZHAO J B. Dynamic state estimation with model uncertainties using H∞ extended Kalman filter[J]. IEEE Transactions on Power Systems, 2018, 33(1): 1099-1100.