近年来,信息技术产业飞速发展,不断变化的用户需求和日益严格的项目要求给软件开发企业带来了巨大的考验。不同于传统的瀑布式开发方法,敏捷软件开发(agile software development, ASD)以用户的需求进化为核心,将开发过程划分为若干个冲刺阶段,每个冲刺结束时交付可使用的软件版本供客户体验,然后根据客户的满意度反馈不断改进,因此受到了很多软件企业的青睐[1]。受小型敏捷公司成功案例的启发,大型软件组织开始尝试大规模敏捷软件项目开发[2]。
大规模敏捷软件项目调度问题(large scale agile software project scheduling problem, LSASPSP)是大规模ASD中的关键环节,对于提高软件项目的综合效益和减少项目成本有着至关重要的作用。用户故事是ASD从客户视角对功能的简要描述[3],LSASPSP包括3个强耦合的子问题。①故事选择,从待开发故事列表中选择用户故事进入冲刺;②故事分配,将选择进入冲刺的用户故事分配给各个团队;③任务分配,将每个团队分配到的故事分解成任务,按照任务所需技能和任务时长分配给团队中的员工。LSASPSP的目标就是在满足用户故事和团队员工之间各项约束下合理分配每个冲刺阶段的用户故事,最大化开发项目的价值。在每个冲刺阶段结束时,开发团队所交付软件的质量依赖于对用户故事任务和团队员工的有效调度。到目前为止,学者对瀑布式软件项目调度(waterfall software project scheduling problem, WSPSP)关注较多,很少研究敏捷软件项目调度。![]() 等[4]考虑了新增/删除用户故事、员工离职/加入等破坏性事件的发生,但未将用户故事划分为具体的任务。Roque等[5]关注任务分配与员工技能之间的联系,但忽略了用户需求的变更。此外,这2个模型仅在小规模实例上进行了实验验证。针对上述不足,本文建立了LSASPSP的数学模型,将故事细化成具体的小任务,并为这些任务设置相应的技能和完成时长属性。对于动态事件,考虑了每个冲刺用户需求和员工工作时长的动态变化。
等[4]考虑了新增/删除用户故事、员工离职/加入等破坏性事件的发生,但未将用户故事划分为具体的任务。Roque等[5]关注任务分配与员工技能之间的联系,但忽略了用户需求的变更。此外,这2个模型仅在小规模实例上进行了实验验证。针对上述不足,本文建立了LSASPSP的数学模型,将故事细化成具体的小任务,并为这些任务设置相应的技能和完成时长属性。对于动态事件,考虑了每个冲刺用户需求和员工工作时长的动态变化。
WSPSP已被证明是一个NP-hard问题,传统的精确算法无法在多项式时间内找到该类问题的有效解,多数学者采用元启发式算法。Xiao等[6]将WSPSP转化为基于图的搜索问题并采用蚁群算法求解;Shen等[7]提出了一种协同进化的多目标遗传算法求解多目标WSPSP。此外,强化学习算法也逐渐用于求解WSPSP,Padberg等[8]基于实际案例的调度搭建了环境转移模型,使用强化学习Sarsa算法优化调度策略,但是,该算法需要大量数据,且无法处理复杂问题。
强化学习通过不断与未知环境交互,学会在动态环境中做出最优决策。DQN(deep Q network)算法[9]利用神经网络提取轨迹的高维特征,拟合动作价值函数[10],引入经验回放池以节约存储空间。LSASPSP的环境涉及用户故事任务的完成进度、团队员工的时间利用情况等复杂因素,导致状态空间庞大,适合于用DQN算法来求解。为有效解决该问题,本文提出基于复合调度规则的优先经验回放双重深度Q网络(composite scheduling rule-based priority experience replay double deep Q network, CPDDQN)算法。该算法采用双重网络分离DQN的Q值预测和动作选择,避免Q值过估计;按优先级采样经验回放池中的轨迹进行训练,提高样本的利用效率。针对LSASPSP模型特点,设计了10个状态特征来描述调度对环境状态变化产生的影响,以及12个复合调度规则作为动作供算法选择,加速算法收敛。最后,算法以各冲刺完成故事总价值为奖励函数,指导算法优化。
1 大规模敏捷软件项目调度模型
本节描述了大规模敏捷软件项目开发调度的项目结构和开发团队的各项属性,并规定各项约束关系,建立了一个贴合实际敏捷开发的LSASPSP数学模型。
1.1 问题描述
假设一个待开发的大规模敏捷项目P,将客户的需求分解成N个用户故事usi(i=1,2,…,N),用户故事usi可以分解成tni个具体任务taskij(j=1,2,…,tni),完成这些任务需要用到S项技能。敏捷开发公司共有R个团队Teamr(r=1,2,…,R),每个团队中有Mr名员工erk(k=1,2,…,Mr)。
LSASPSP 3个强耦合子问题的分配方案分别由决策变量![]() 和
和![]() 表示,取值均为
表示,取值均为![]() 时,选择用户故事usi进入第l个冲刺;
时,选择用户故事usi进入第l个冲刺;![]() 时,将第l个冲刺选择的故事usi分配给团队
时,将第l个冲刺选择的故事usi分配给团队![]() 时,将第l个冲刺中分配给团队Teamr的故事任务taskij分配给员工erk。LSASPSP的目标就是在满足团队速度、任务和技能等约束时进行调度,最大化D个冲刺内完成用户故事的总价值。
时,将第l个冲刺中分配给团队Teamr的故事任务taskij分配给员工erk。LSASPSP的目标就是在满足团队速度、任务和技能等约束时进行调度,最大化D个冲刺内完成用户故事的总价值。
1.2 问题的数学表达
围绕3个强耦合子问题,建立LSASPSP问题的约束单目标优化模型:
(1)
(2)
(3)
(4)
(5)
(6)
式(1)为目标函数,表示最大化D个冲刺中所完成用户故事的总价值。其中,vpi表示价值点,是对用户故事usi市场收益的无单位估算值。OUTl为第l个冲刺所完成完整用户故事的集合。式(2)~(6)为约束。式(2)表示每个冲刺阶段所选择用户故事的故事点总数不超过冲刺速度svl。其中,Ul为第l个冲刺阶段开始前待开发用户故事的集合;spi表示故事点,是对用户故事usi大小和复杂度的无单位估算值。式(3)表示每个冲刺中团队Teamr分配到的故事点总数不超过团队速度![]() 冲刺速度
冲刺速度![]() 即团队速度
即团队速度![]() 之和。团队速度为各团队前两个冲刺所完成的平均故事点总数,表示为
之和。团队速度为各团队前两个冲刺所完成的平均故事点总数,表示为![]() 第一个冲刺将团队所有员工的总工作时长按1个故事点约为8 h的方式估算成初始团队速度,表示为
第一个冲刺将团队所有员工的总工作时长按1个故事点约为8 h的方式估算成初始团队速度,表示为![]() 第二个冲刺的团队速度为第一个冲刺所完成完整用户故事的点数之和,表示为
第二个冲刺的团队速度为第一个冲刺所完成完整用户故事的点数之和,表示为![]() 式(4)表示每个冲刺完成任务taskij所需要的一项技能tskij必须在所分配员工erk掌握的技能集合eskrk中。式(5)表示每个冲刺的任务task只能由一名员工来完成。式(6)表示每个冲刺过程中分配给员工erk的任务时长thij之和不超过其工作时长
式(4)表示每个冲刺完成任务taskij所需要的一项技能tskij必须在所分配员工erk掌握的技能集合eskrk中。式(5)表示每个冲刺的任务task只能由一名员工来完成。式(6)表示每个冲刺过程中分配给员工erk的任务时长thij之和不超过其工作时长![]()
2 求解LSASPSP的CPDDQN算法
算法求解框架如图1所示。首先,初始化LSASPSP环境中的用户故事任务和团队员工信息,计算初始状态特征传递给智能体。智能体依概率ε随机选取动作,依概率1-ε用当前网络选择动作。冲刺阶段结束后,环境反馈奖励和新状态特征,并判断调度是否结束。在每个冲刺阶段,将当前/新状态特征、动作、奖励以及调度是否终止的判断存放到回放池中。当有新轨迹加入时,计算其时序差分误差并更新所有轨迹的优先级。之后,轨迹按优先级采样,供给目标网络预测Q值,并采用梯度下降训练当前网络参数。当前网络定时将参数复制给目标网络,提高目标网络的预测能力。训练后的当前网络能根据每个动作对应的Q值选择Q值最大的动作,这样,智能体就能够在调度结束后获得最大的累计奖励值。
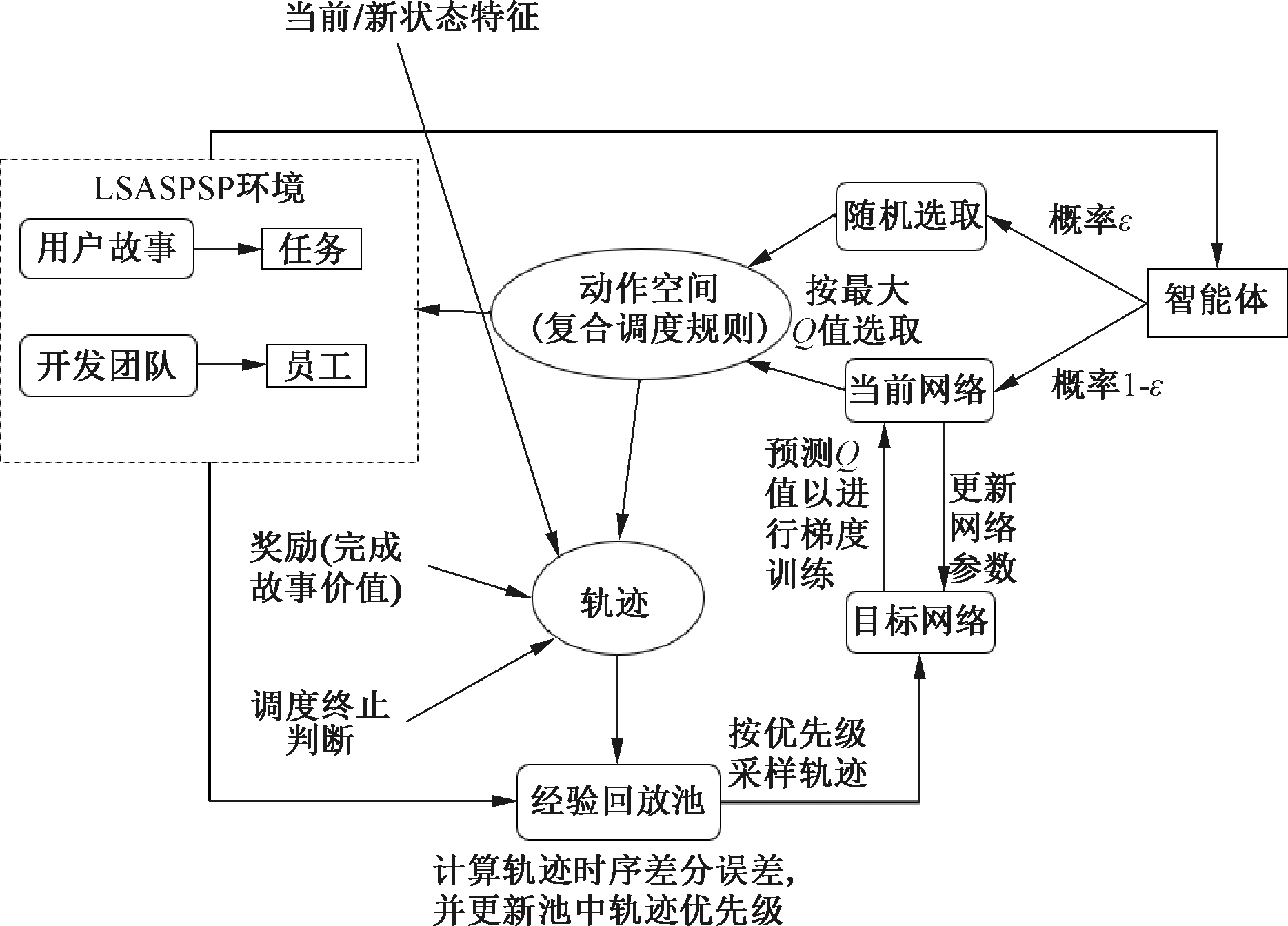
图1 LSASPSP的算法求解框架
Figure 1 Framework of CPDDQN for solving LSASPSP
2.1 马尔可夫决策过程
在使用深度强化学习求解LSASPSP前,必须先将问题转化为马尔可夫决策过程(Markov decision process, MDP)。MDP是一个四元组(S,A,R,γ),其中,S表示状态集合;A表示动作集合;R表示奖励集合;γ表示衰减因子,取值在[0,1],表示后续决策步骤对当前状态执行动作的重要程度。
2.2 状态特征设计
为保证模型的泛化能力,本文设计了10个范围在[0,1]的状态特征[11],用于描述每个冲刺阶段开始前用户故事、任务和员工的实际状态。第l个冲刺阶段结束后,调度环境的状态特征如式(7)~(16)所示。
所有团队完成完整用户故事的完成率:
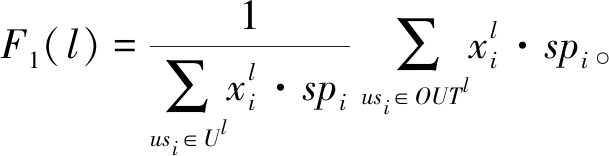
(7)
所有团队完成用户故事工作量的完成率:
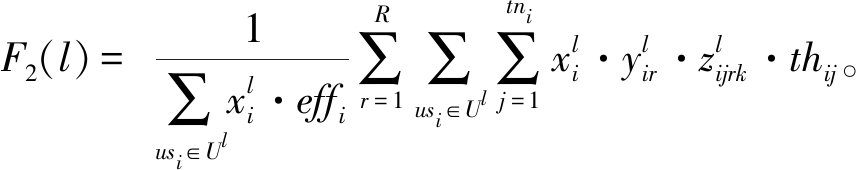
(8)
式中:effi表示完成用户故事usi花费的时间。
所有团队完成用户故事完成率的平均值:
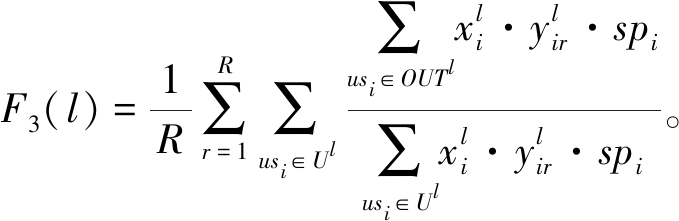
(9)
所有团队完成用户故事完成率的标准差:
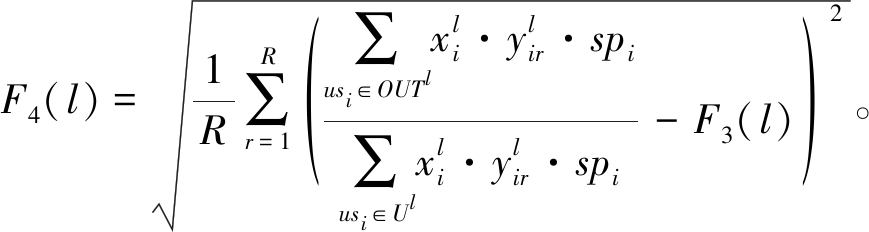
(10)
所有团队工作量完成率的平均值:
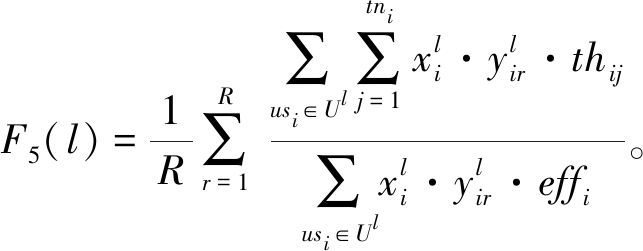
(11)
所有团队工作量完成率的标准差:
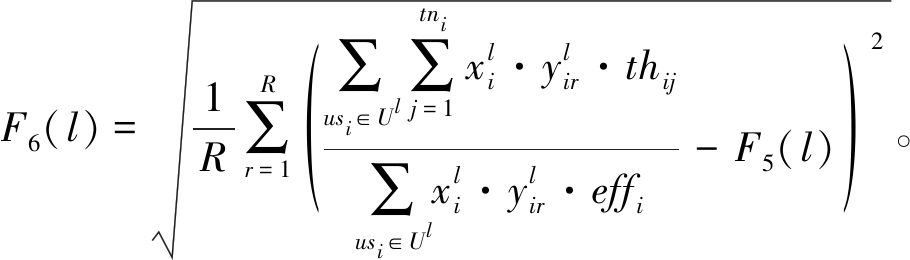
(12)
所有团队时间利用率的平均值:
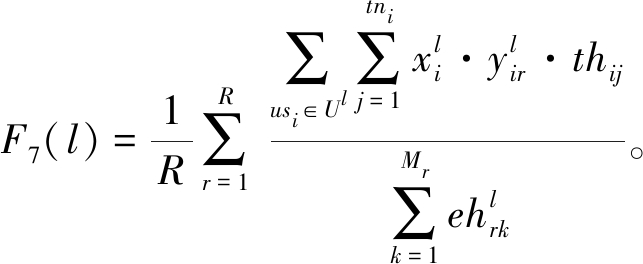
(13)
所有团队时间利用率的标准差:
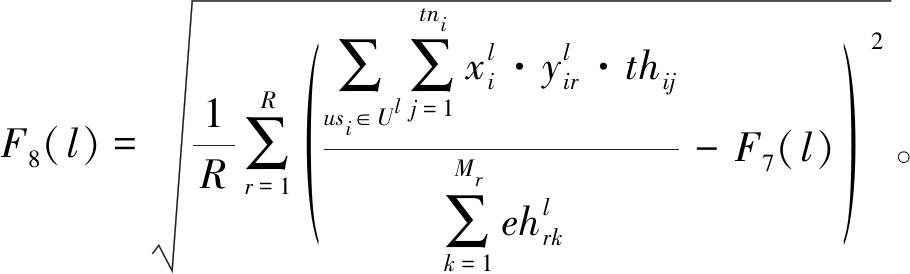
(14)
所有团队员工时间利用率的平均值:
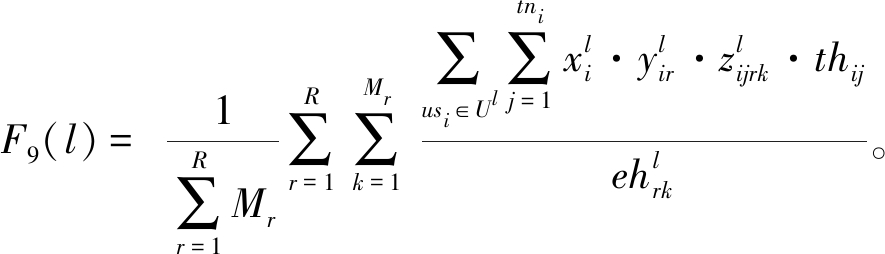
(15)
所有团队员工时间利用率的标准差:
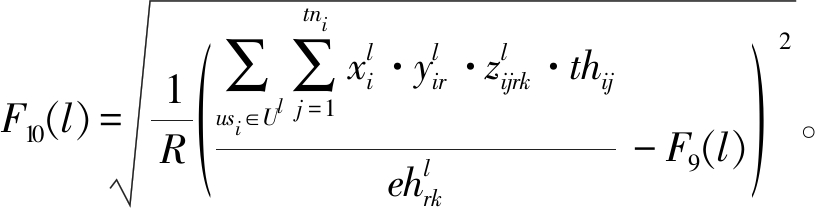
(16)
2.3 动作空间设计
动作空间是智能体在各种状态下所有能采取的动作集合,以调度规则的形式供智能体选择执行[12]。针对LSASPSP的3个强耦合子问题,本文设计了7个通用的单一调度规则,分别用于描述每个冲刺阶段的故事选择、故事分配和任务分配,如表1所示。
表1 单一调度规则
Table 1 Single scheduling rule
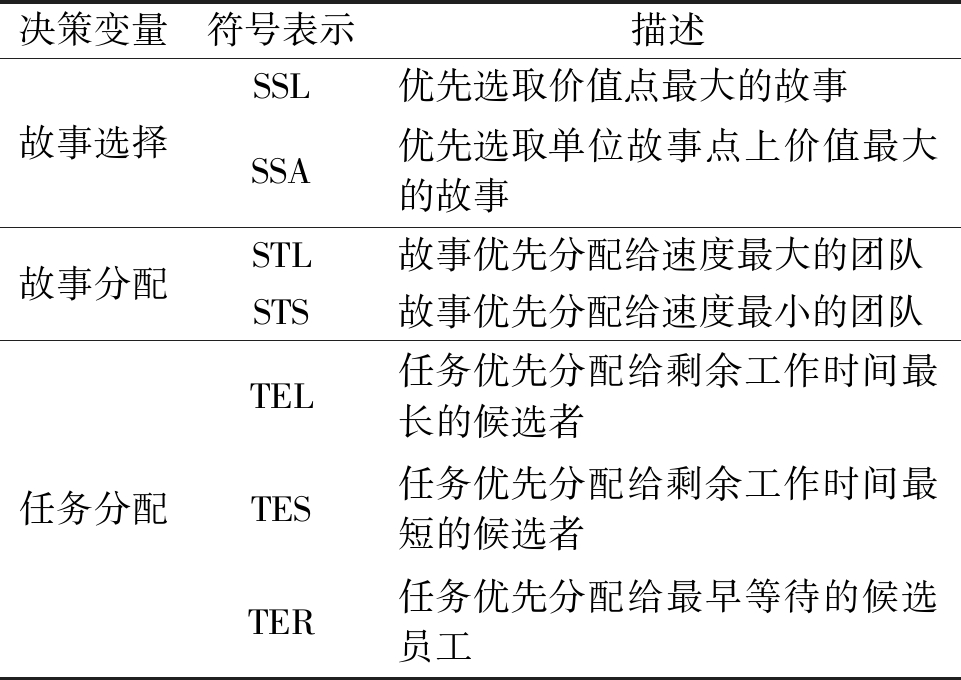
决策变量符号表示描述故事选择SSL优先选取价值点最大的故事SSA优先选取单位故事点上价值最大的故事故事分配STL故事优先分配给速度最大的团队STS故事优先分配给速度最小的团队任务分配TEL任务优先分配给剩余工作时间最长的候选者TES任务优先分配给剩余工作时间最短的候选者TER任务优先分配给最早等待的候选员工
将这3个强耦合决策变量对应的7个单一调度规则按2×2×3进行排列组合,得到了12个复合调度规则CR1~CR12,作为动作空间供智能体进行选择。
2.4 奖励函数设计
奖励函数是环境根据智能体所执行动作反馈的即时回报,用于帮助智能体进行正确的决策,一般按照问题的目标函数进行设计。本文的奖励函数为每个冲刺所完成用户故事的总价值,如式(17)所示:
(17)
2.5 双重Q网络
Q值的更新过程如式(18)所示,DQN选择动作的网络Qt+1和预测Q值的网络Qt是相同的。更新Q值时,使用max操作可以快速让Q值朝着优化目标靠拢,但是容易导致过度估计。针对该缺点,本文采用双重深度Q网络策略(double deep Q network, DDQN)[13]。当前网络观测环境在t时刻的状态st,选择Q值最大的动作at;目标网络根据t+1时刻的状态估计Q值,采用梯度下降训练当前网络的参数。每隔固定冲刺阶段,算法将当前网络的参数θ复制给目标网络的参数θ-,这样,将预测Q值和选择动作分离,提高了神经网络预测的准确性。
Qt=Qt+α(rt+1+γQt+1(s,arg max Q)-Qt)。
(18)
2.6 优先经验回放
在深度Q网络参数的训练过程中,历史轨迹的采样是均匀随机的。但是,某些相互邻近的轨迹本就相关性强,不同数据对梯度学习的贡献度也不一致,这样容易导致学习效率低和过拟合等情况发生。因此,本文引入优先经验回放策略[14],采用轨迹的时序差分(temporal difference,TD)误差作为评价轨迹重要性指标,计算轨迹间的权重改变量并训练Q网络的参数。当经验回放池中有新轨迹加入时,计算该轨迹的TD误差并更新所有轨迹的优先级。在进行网络的梯度下降训练时,会优先采样级别较高的一批轨迹。如果轨迹数量超过经验回放池的固定容量,优先级最低的轨迹会被最先剔除出去,以提高轨迹的利用效率。
2.7 算法求解流程
在算法求解过程中,首先初始化用户故事和团队员工的属性值、神经网络以及经验回放池的各项参数。智能体观测到环境状态S0,并根据ε-贪婪策略πθ(S0)选择执行动作A0。算法共有两个循环:第一个循环是智能体和调度环境交互的过程;第二个循环是采样轨迹训练当前网络参数的过程。在第一个循环中,智能体观测到环境状态特征St,按策略选择执行动作At。调度环境中已分配的用户故事和任务团队被员工完成后,环境的状态特征变为St+1。调度是否结束用done来表示,如果故事全都被完成,则done=true;反之,done=false。在第二个循环中,当调度时刻t是K的整数倍时,将轨迹tranb(b=1,2,…,V)按优先级分布![]() 采样h条轨迹。然后,根据式(19)和(20)计算所采样h条轨迹的重要性权重ωm和TD误差δm,更新轨迹的优先级pm。最后,使用目标网络预测Q(Sm-1,Am-1)值,并按式(21)对累计权重改变量Δ进行梯度训练。采样结束后,利用式(22)更新当前网络参数θ,并重置Δ=0。每隔步长K,当前网络将参数θ复制给目标网络参数θtarget。当平均累计奖励收敛稳定后,智能体使用更新后的最优策略πθ(St)选择动作At。
采样h条轨迹。然后,根据式(19)和(20)计算所采样h条轨迹的重要性权重ωm和TD误差δm,更新轨迹的优先级pm。最后,使用目标网络预测Q(Sm-1,Am-1)值,并按式(21)对累计权重改变量Δ进行梯度训练。采样结束后,利用式(22)更新当前网络参数θ,并重置Δ=0。每隔步长K,当前网络将参数θ复制给目标网络参数θtarget。当平均累计奖励收敛稳定后,智能体使用更新后的最优策略πθ(St)选择动作At。
ωm=(V·P(m))-β/max ωb;
(19)
Q(Sm-1,Am-1);
(20)
(21)
θ←θ+η·Δ。
(22)
3 仿真测试与对比分析
3.1 实验设置
本文实验基于Python编程语言和Pytorch框架在Pycharm软件上运行算法,计算机配置为AMD Ryzen 7-5800 H with Radeon Graphics @3.20 GHz,RAM 16 GB。
为了验证本文提出的算法CPDDQN,本文参考了挪威最大的大规模敏捷开发项目之一Beta的各项数据[2]以及敏捷专家对于敏捷软件开发实践的估算与计划[3],生成了6个LSASPSP算例,以用户故事和团队的数量将其命名为N_R,分别为200_3、200_5、300_3、300_5、500_3和500_5。项目的目标冲刺数D为16,每个冲刺周期为2周。新增和初始用户故事的故事点均从斐波那契数列{2,3,5,8,13}中选择。用户故事按必须故事(基础功能)、线性增加故事(具备持续收益的功能)以及兴奋点故事(具备爆发性收益的功能)划分,价值点分别在{2,3}、{5,8}、{13}中选择。而新增故事不考虑必需故事,价值点只在{5,8,13}选取。故事工作量的估算按一个故事点约为8 h进行高斯分布生成,任务的时长设置在[4 h,8 h]内。开发团队有3~5个,每个团队的员工数量在[5,9]。团队每个员工掌握的以及任务所需的技能对应于页面开发、数据库管理、美工设计、算法编程和自动化测试等软件开发岗位,用{1,2,3,4,5}表示。考虑每个冲刺客户需求的变化,根据冲刺速度和已结束的冲刺数量估算出项目的预计完成冲刺数。若预计完成冲刺数不超过D,则从新增用户故事集合中随机选取用户故事优先开发;反之,则删除单位故事点价值最低的用户故事。在新增和删除用户故事的过程中,预计完成冲刺数始终不得超过目标冲刺数D。考虑每个冲刺阶段员工面临的各种特殊情况,员工在每个冲刺阶段的总工作时长会在[60 h,80 h]动态变化。
CPDDQN算法的各项参数如下:回放池容量V为512,更新频率K为10,最小采样批次h为64,学习率η为0.002,优先级权重α为0.6,采样权重系数β为0.4,概率ε为0.01,衰减率γ为0.98。
3.2 本文算法的收敛性验证
为验证本文算法的收敛性,与DQN和DDQN算法在6个算例中进行了实验验证。算法迭代10 000次,每200次迭代将最后50个累计奖励值取平均,得到50个平均累计奖励。3种算法在算例200_5中的平均累计奖励变化曲线如图2所示。
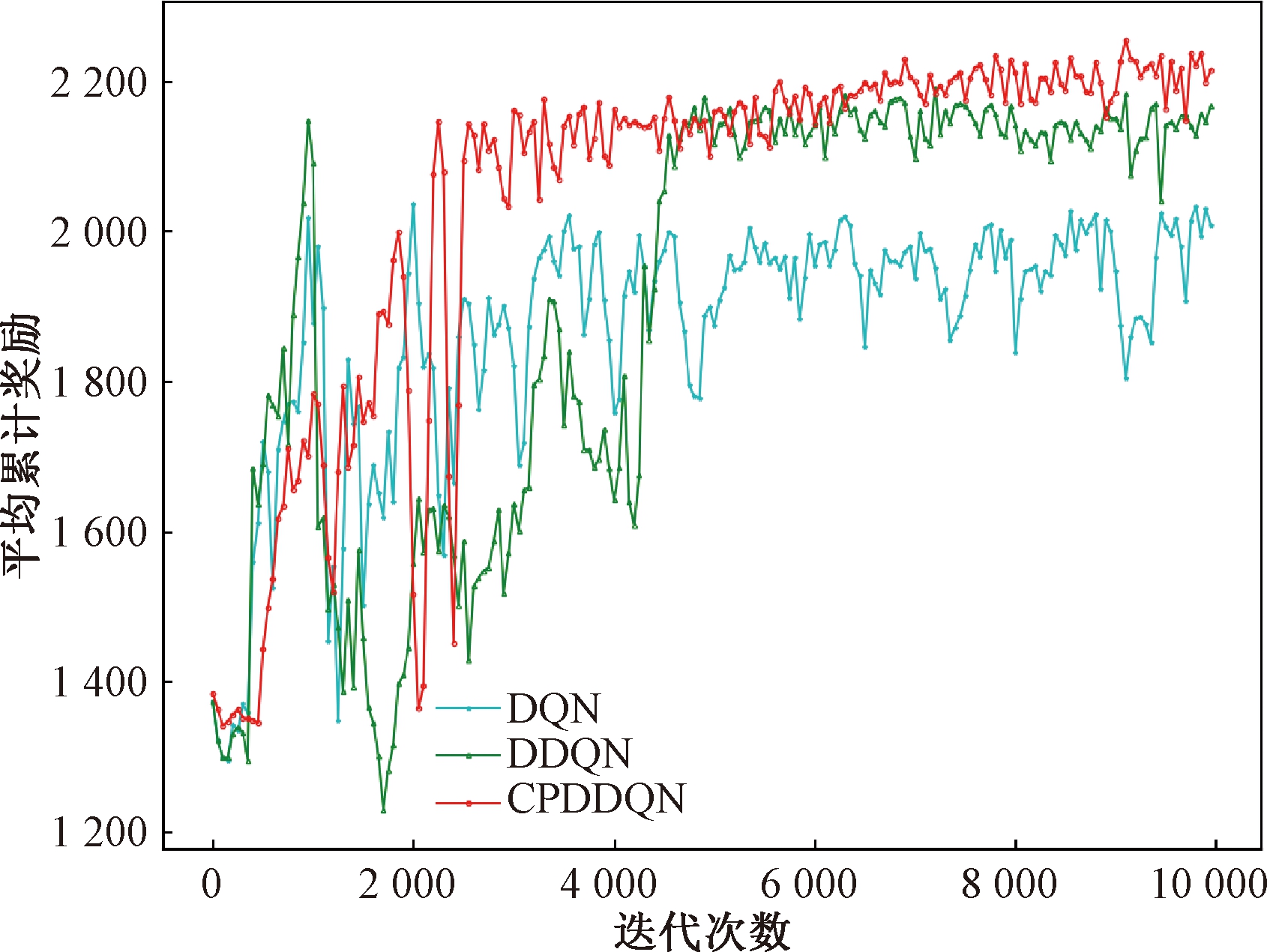
图2 3种算法的平均累计奖励变化曲线
Figure 2 Average cumulative reward of three algorithms
由图2可知,CPDDQN的平均累计奖励在迭代3 000次后收敛,而DDQN则要4 000次才趋于稳定。在收敛精度上,CPDDQN稳定后平均累计奖励上下波动最小。DQN的轨迹利用效率低,预测Q值的能力差,因此稳定性和获得的平均累计奖励值都要低于CPDDQN。算例200_5中新增故事出现的随机性较其他算例大,导致3个算法的稳定性都较差。在其他算例中,CPDDQN的收敛速度和精度也优于其他两种算法。3种算法的最大预测Q值变化如图3所示。
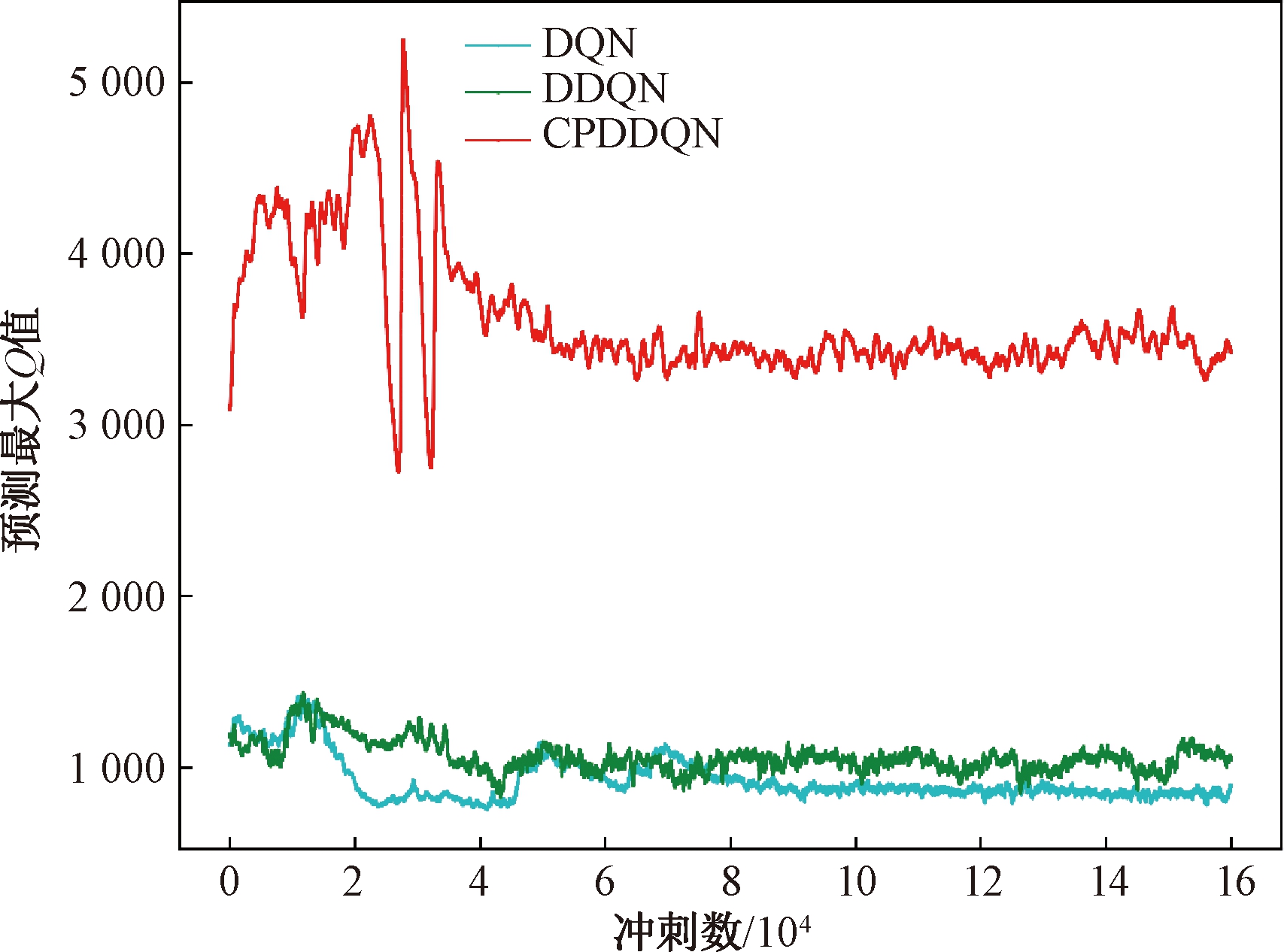
图3 3种算法的预测Q值变化
Figure 3 Predicted Q value change of three algorithms
CPDDQN只保留重要的轨迹,并按优先级采样,而DQN与DDQN均匀随机采样轨迹,因此CPDDQN的最大预测Q值远高于DQN和DDQN。
3.3 本文算法与其他算法的对比分析
为验证CPDDQN的性能,本文将DQN、DDQN和12个复合调度规则作为对比算法,在6个算例中进行实验。为保证复合调度规则不受随机性影响,每种规则运行10遍,每遍迭代1 000次,记录最后50次迭代的累计奖励值平均值,并以其最大值为运行结果。
表2为CPDDQN与对比算法的实验结果。由表2可知,CPDDQN在绝大多数算例中取得了最高的平均累计奖励。算例200_5中,5个团队很快就能完成200个初始故事,有更多价值点高的新增故事加入,故所获累计奖励要远高于其他算例。为避免陷入局部最优[15],CPDDQN根据概率随机选择动作,获得的平均累计奖励值会略低于CR7。
表2 CPDDQN算法与对比算法的实验结果
Table 2 Experimental results of CPDDQN algorithm and comparison algorithm
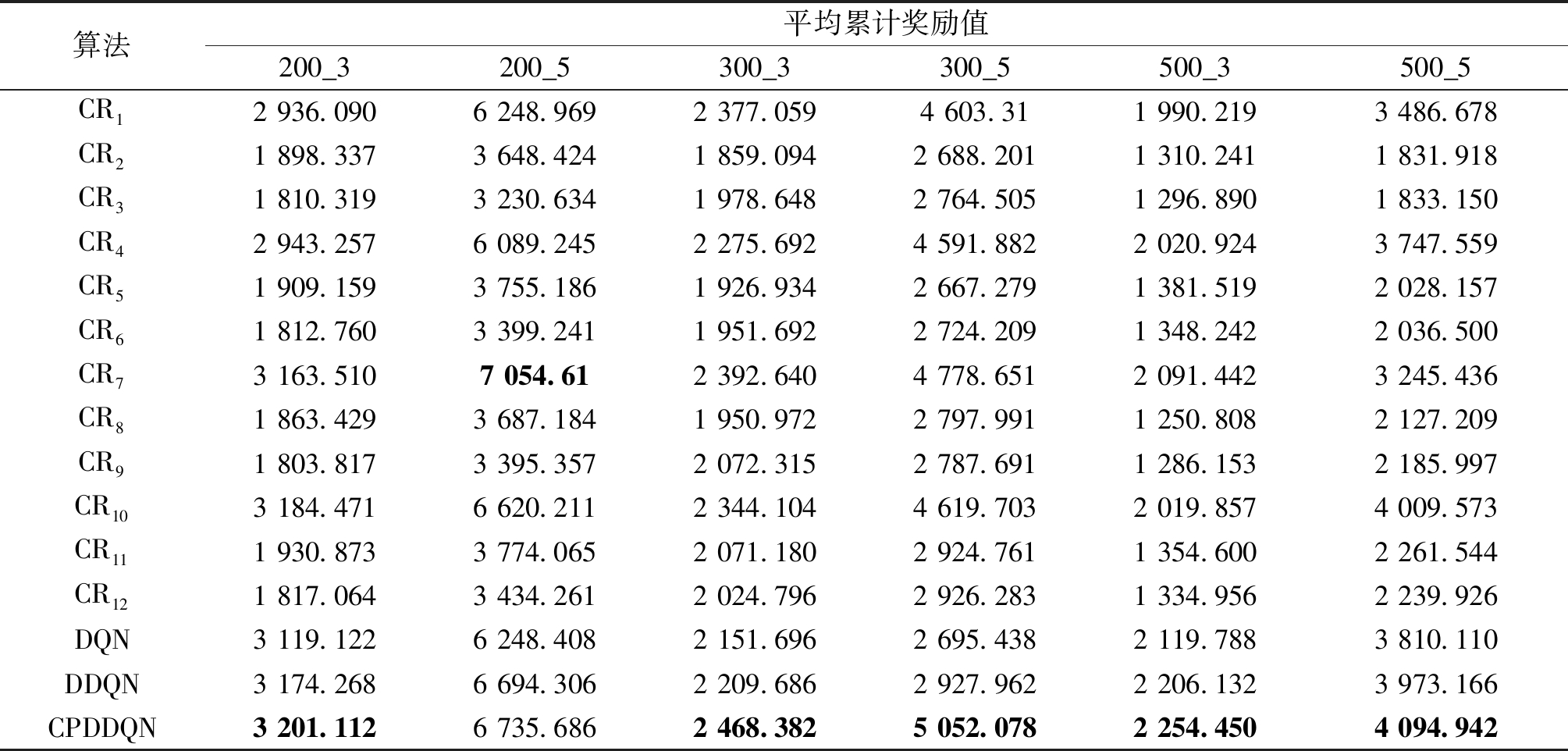
算法平均累计奖励值200_3200_5300_3300_5500_3500_5CR12 936.0906 248.9692 377.0594 603.311 990.2193 486.678CR21 898.3373 648.4241 859.0942 688.2011 310.2411 831.918CR31 810.3193 230.6341 978.6482 764.5051 296.8901 833.150CR42 943.2576 089.2452 275.6924 591.8822 020.9243 747.559CR51 909.1593 755.1861 926.9342 667.2791 381.5192 028.157CR61 812.7603 399.2411 951.6922 724.2091 348.2422 036.500CR73 163.5107 054.612 392.6404 778.6512 091.4423 245.436CR81 863.4293 687.1841 950.9722 797.9911 250.8082 127.209CR91 803.8173 395.3572 072.3152 787.6911 286.1532 185.997CR103 184.4716 620.2112 344.1044 619.7032 019.8574 009.573CR111 930.8733 774.0652 071.1802 924.7611 354.6002 261.544CR121 817.0643 434.2612 024.7962 926.2831 334.9562 239.926DQN3 119.1226 248.4082 151.6962 695.4382 119.7883 810.110DDQN3 174.2686 694.3062 209.6862 927.9622 206.1323 973.166CPDDQN3 201.1126 735.6862 468.3825 052.0782 254.4504 094.942
4 结论
本文考虑团队速度、任务时长和技能等约束,引入每个冲刺客户需求和员工工作时长的变化等动态事件,建立了以最大化团队所开发项目总价值为目标的LSASPSP约束单目标优化模型,并用CPDDQN算法求解所建模型。针对敏捷开发特点,采用10个状态特征描述调度环境信息,结合3个强耦合决策变量设计了12个复合调度规则作为智能体的候选动作。引入双重网络和优先经验回放策略,提高Q网络预测能力和轨迹利用效率。在6个LSASPSP算例上的实验结果表明,所提算法的稳定性和所获平均累计奖励值均优于其他深度强化学习算法和12种复合调度规则。
本文所建LSASPSP模型对实际大规模敏捷软件开发中的多种动态事件和不确定因素尚欠考虑,如多团队间员工的调动,员工技能提升对任务时长的影响等。在后续研究过程中,将在模型中引入更多实际因素,并探讨更多深度强化学习算法在LSASPSP中的应用,并与所提算法进行比较分析。
[1] 王映红. 企业大规模敏捷转型探索与实践[J]. 金融科技时代, 2017, 25(11): 84-85.
WANG Y H. Exploration and practice of large-scale agile transformation of enterprises[J]. Financial Technology Time, 2017, 25(11): 84-85.
[2] BIESIALSKA K, FRANCH X, MUNTÉS-MULERO V. Mining dependencies in large-scale agile software development projects: a quantitative industry study[C]∥Evaluation and Assessment in Software Engineering. New York:ACM, 2021: 20-29.
[3] COHN M. Agile estimating and planning[M].Upper Saddle River: Prentice Hall,2005.
[4] ZAPOTECAS-MART NEZ S, GARC
NEZ S, GARC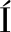 A-N
A-N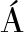 JERA A, CERVANTES H. Multi-objective optimization in the agile software project scheduling using decomposition[C]∥Proceedings of the 2020 Genetic and Evolutionary Computation Conference Companion.New York:ACM, 2020: 1495-1502.
JERA A, CERVANTES H. Multi-objective optimization in the agile software project scheduling using decomposition[C]∥Proceedings of the 2020 Genetic and Evolutionary Computation Conference Companion.New York:ACM, 2020: 1495-1502.
[5] ROQUE L, ARA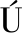 JO A A, DANTAS A, et al. Human Resource Allocation in Agile Software Projects Based on Task Similarities[C]∥International Symposium on Search Based Software Engineering. Cham: Springer, 2016: 291-297.
JO A A, DANTAS A, et al. Human Resource Allocation in Agile Software Projects Based on Task Similarities[C]∥International Symposium on Search Based Software Engineering. Cham: Springer, 2016: 291-297.
[6] XIAO J, AO X T, TANG Y. Solving software project scheduling problems with ant colony optimization[J]. Computers &Operations Research, 2013, 40(1): 33-46.
[7] SHEN X N, GUO Y N, LI A M. Cooperative coevolution with an improved resource allocation for large-scale multi-objective software project scheduling[J]. Applied Soft Computing, 2020, 88: 106059.
[8] PADBERG F, WEISS D. Optimal scheduling of software projects using reinforcement learning[C]∥2011 18th Asia-Pacific Software Engineering Conference. Piscataway: IEEE, 2012: 9-16.
[9] LIU W T, SU S, TANG T, et al. A DQN-based intelligent control method for heavy haul trains on long steep downhill section[J]. Transportation Research Part C: Emerging Technologies, 2021, 129: 103249.
[10] HUYNH T N, DO D T T, LEE J. Q-Learning-based parameter control in differential evolution for structural optimization[J]. Applied Soft Computing, 2021, 107: 107464.
[11] LUO S. Dynamic scheduling for flexible job shop with new job insertions by deep reinforcement learning[J]. Applied Soft Computing, 2020, 91: 106208.
[12] LI Y X, GU W B, YUAN M H, et al. Real-time data-driven dynamic scheduling for flexible job shop with insufficient transportation resources using hybrid deep Q network[J]. Robotics and Computer-Integrated Manufacturing, 2022, 74: 102283.
[13] Van HASSELT H, GUEZ A, SILVER D. Deep reinforcement learning with double Q-Learning[C]∥Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence. New York: ACM, 2016: 2094-2100.
[14] SCHAUL T, QUAN J, ANTONOGLOU I, et al. Prioritized experience replay[EB/OL].(2016-02-25)[2023-02-09].https:∥arxiv.org/abs/1511.05952.
[15] 王培崇, 尹欣洁, 李丽荣. 一种具有学习机制的海鸥优化算法[J]. 郑州大学学报(工学版), 2022, 43(6): 8-14.
WANG P C, YIN X J, LI L R. An improved seagull optimization algorithm with learning[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(6): 8-14.