研究者模仿自然界中生物的群体行为,或者受社会实践中某些活动的启发,提出了演化算法(evolutionary algorithm, EA)[1-3],它在求解优化问题时表现出了优越的性能。其中,差分进化算法(differential evolutionary, DE)[4-5]因其参数设置简单、搜索能力强,成为最有效的演化算法之一。DE算法同其他演化算法类似,生成随机的初始种群,通过交叉、变异、选择算子进行种群的迭代更新,在决策空间中进行搜索,直到找到最优解或者满足结束条件为止。传统的差分进化算法是从问题零知识的情况下开始搜索,在搜索过程中始终保持种群的独立性,各种交叉变异操作在种群个体之间进行,信息的交互在种群内部完成。不管是在求解的初始阶段还是在求解过程中,传统的差分进化算法没有利用已求解过的相似问题信息获得有效知识。
迁移学习[6]是机器学习中最热门的研究领域之一。迁移学习的基本思想是将已经解决的问题的结果或者方法运用到未解决的问题中,以加快新问题的求解速度或提高问题的求解精度。一般地,将已经学习过的知识领域称作源域,将待应用或待求解的新领域称作目标域。迁移学习已经在图像分类[7]、自动驾驶[8]、推荐系统[9]等领域均展现出良好的有效性。迁移学习与演化计算相结合的研究工作近期受到诸多学者的关注[10-11]。Jiang等[12]应用迁移学习机制求解动态优化问题,设计了一个集成迁移成分分析和多目标优化的算法框架,并将该算法框架与3个典型的多目标优化算法NSGA-Ⅱ、MOPSO和RM-MEDA相结合,求解动态多目标优化问题。Jiang等[13]又提出一种基于领域自适应和非参数估计的分布估计算法DANE-EDA,该算法将蒙特卡洛方法与迁移学习相结合,用以维持在动态优化中勘探与开发的平衡。张勇等[14]提出一种基于相似历史信息迁移学习的进化优化框架,该算法从历史模型库中寻找与新问题相匹配的历史问题,将历史问题对应的知识迁移到新问题中,以提高种群的搜索效率。刘璐等[15]提出Tr-NSGA Ⅱ算法,该算法将NSGA-Ⅱ算法与迁移成分分析方法相结合,对含有历史信息的种群进行搜索,以提高种群的搜索效率与算法的收敛性能。尚青霞等[16]提出一种基于降噪自动编码器的进化多任务算法,通过显式的遗传迁移方法,实现跨任务的迁移学习。Feng等[17]将基于自动编码器的显式迁移技术扩展到了多目标多任务优化,针对多目标问题的特征,提出了多目标种群排序和映射矩阵的方法,用于优选解的迁移。
现有算法中使用的迁移学习技术有迁移成分分析(transfer component analysis, TCA)[18]、测地线流式核法(geodesic flow kernel, GFK)[19]等。本文将另一种迁移学习技术——联合分布适配(joint distribution adaptation, JDA)[20]方法引入到演化计算中。JDA是一种更巧妙、更精准的求解方法,对不同问题的适配程度更好,因此本文提出一种基于联合分布适配的单向迁移差分进化算法。该算法利用已求解过的简单单目标优化问题(源问题)的种群信息,通过联合分布适配的迁移学习技术,将有效知识迁移到具有相似性的复杂单目标优化问题(目标问题)中,以提高求解目标问题的收敛速度与求解精度。
1 迁移学习基础
1.1 最大均值差异
最大均值差异是迁移学习中应用较多的一种损失函数,用来衡量2个不同但存在一定相似性的随机变量的分布距离。这里假设存在一个源域Xs=[xs1,xs2,…,xsn]满足P分布,存在一个目标域Xt=[xt1,xt2,…,xtm],假设H为再生核希尔伯特空间(reproducing kernel Hilbert space,RKHS),Φ(·):X→H表示原始特征空间映射到再生核希尔伯特空间的映射函数,当n、m→∞时,Xs和X t在再生核希尔伯特空间中的最大均值差异(maximum mean discrepancy, MMD)[15]表示如下:
(1)
实际上,MMD所求即源域与目标域映射到高维向量空间后的均值差异。目前MMD应用的实例不在少数,并且证明其具有良好的效果。但将其运用在迁移学习中并与演化计算相结合的实例仍然很少出现。
1.2 联合分布适配
联合分布适配是迁移学习中一种常用的方法,其目的是通过学习源域数据中有用的相关知识,进而对目标域的求解过程提供可靠有力的帮助。
1.2.1 边缘分布适配
为了使源域数据与目标域数据的边缘概率即P(ATXs)和P(ATXt)之间的距离尽可能小,采用最大均值差异MMD距离来度量源域与目标域的边缘概率分布差异,具体的表达式为
![]() =tr(ATXM0XTA)。
=tr(ATXM0XTA)。
(2)
式中:X为源域与目标域整合在一起的数据;M0为一个MMD矩阵,表达式为

(3)
式中: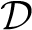 s为有标注的源域;
s为有标注的源域;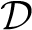 t为无标注的目标域;n和m分别为源域和目标域的样本个数。通过式(3),使得边缘分布P(ATX)在某种形式下距离尽可能地接近。
t为无标注的目标域;n和m分别为源域和目标域的样本个数。通过式(3),使得边缘分布P(ATX)在某种形式下距离尽可能地接近。
1.2.2 条件分布适配
同样地,需要对源域和目标域的条件概率分布进行适配。根据贝叶斯公式P(yt|Xt)=P(yt)P(Xt|yt)和充分统计量的定义,在样本中存在较多的未知量并且样本足够好的情况下,便可以从样本中选择一些统计量用来近似替代实际需要估计的分布,这里可用P(Xt|yt)来近似P(yt|Xt)。使用(Xs,ys)训练一个K近邻分类器,利用这个分类器,对已知的Xt进行预测,得到预测标签![]() 作为目标域标注进行计算。则此时类间的MMD距离可以表示为
作为目标域标注进行计算。则此时类间的MMD距离可以表示为
tr(ATXMcXTA)。
(4)
式中:n c、m c分别为源域和目标域中来自第c类的样本个数。Mc为
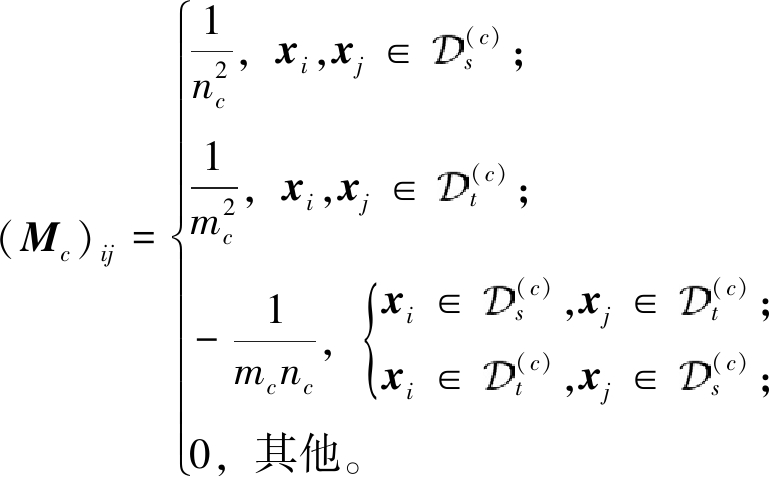
(5)
通过条件分布适配,可以使得源域与目标域之间的条件分布P(y|ATX)尽可能地减小差异。
联合分布适配要求源域和目标域之间的边缘分布适配与条件分布适配均尽可能地小,故将上述2种适配方法相结合,得到了联合分布适配的目标函数:
(6)
式中:![]() 为正则项。同时,需要一个限定条件为一个变换前后数据的方差维持不变,增加另外的一个优化目标max ATXHXTA,其中H为中心矩阵。将其与原来的优化目标合并,并使用拉格朗日法可得
为正则项。同时,需要一个限定条件为一个变换前后数据的方差维持不变,增加另外的一个优化目标max ATXHXTA,其中H为中心矩阵。将其与原来的优化目标合并,并使用拉格朗日法可得
(7)
式中:Φ为拉格朗日乘子;I=ATXHXTA。经过多次迭代过程,使得预测出的标签![]() 与真实标签之间的误差逐渐减小,且可以求出变换矩阵A,最终实现源域和目标域适配的目的。
与真实标签之间的误差逐渐减小,且可以求出变换矩阵A,最终实现源域和目标域适配的目的。
2 基于联合分布适配的单向迁移差分进化算法
当目标域数据完全无标注时,一般可以通过迁移成分分析的方法进行适配。该方法实现简单,但计算消耗时间多,且因为只对边缘概率分布进行适配,可能会存在领域间欠适配的问题,进而影响到对目标域问题的求解准确度。Long等[20]于2014年提出了联合分布适配,较好地解决了上述问题。联合分布适配方法要解决的是找到一种变换矩阵A,使得源域数据与目标域数据的边缘概率(分别为P(ATXs)和P(ATXt))和条件概率(分别为P(ys|ATXs)和P(yt|ATXt))的距离均尽可能地减小。
因此,本文提出基于联合分布适配的单向迁移差分进化算法(JDA based transfer differential evolution algorithm, JDA_TrDE),实现了两种迁移模式:第一种是对初始种群的迁移;第二种是对迭代过程中生成种群的迁移。
2.1 初始迁移的DE算法JDA_TrDE1
JDA_TrDE1算法对初始种群采用迁移技术。考虑到种群初始化的随机性,该算法在搜索之初就利用源问题优化后的种群,在初始时刻利用已学知识给目标问题一个指向性的引导,尽可能地避免种群的无效搜索。在算法中需要对源数据设置标签,本文采用的方法是将种群个体的适应值进行归一化处理后,按照大小划分成3类,分别赋予个体0、1、2 共3类标签。
JDA_TrDE1算法流程如下。
输入:种群规模NP、比例因子F和交叉概率PCR、迭代次数generation、源问题优化种群Ps;
输出:目标优化问题的最优解y和最优个体x。
Step 1 从Ps中抽取个体的基因形成源域数据Xs,个体的适应值转化为源域数据的标签ys,形成有标注的源域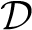 s;
s;
Step 2 在目标问题下生成随机的初始化种群Pt,从Pt中抽取个体的基因形成目标域数据Xt,转化为无标注的目标域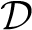 t;
t;
Step 3 将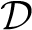 s和
s和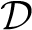 t作为JDA算法的输入,利用式(6)得到的变换矩阵A将Xt进行变换,得到新的矩阵Xt_new;
t作为JDA算法的输入,利用式(6)得到的变换矩阵A将Xt进行变换,得到新的矩阵Xt_new;
Step 4 令Xt_new作为个体的基因构建新种群,替换目标问题的初始种群;
Step 5 使用DE算法的变异、交叉、选择操作进行迭代;
Step 6 迭代次数达到设定的代数generation,算法终止;
Step 7 得到最优解y和最优个体x,结束迭代过程。
2.2 过程迁移的DE算法JDA_TrDE2
JDA_TrDE2算法在迭代过程中进行种群迁移操作。目标问题求解之初,采用DE算法进行随机搜索一定的次数,使其充分搜索可能的区域。而后加入从源问题中所学到的知识,引导种群在剩余迭代次数中尽可能快地收敛。
JDA_TrDE2算法流程如下。
输入:种群规模NP、比例因子F和交叉概率PCR、迭代次数generation_1、迭代次数generation_2、源问题优化种群Ps;
输出:单目标优化问题的最优解y和最优个体x。
Step 1 初始化种群Pt;
Step 2 使用DE算法求解最优解generation_1代;
Step 3 得到运行generation_1代的种群Pt1;
Step 4 从Ps中抽取个体的基因形成源域数据Xs个体的适应值转化为源域数据的标签ys,形成有标注的源域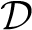 s;
s;
Step 5 从Pt1中抽取个体的基因形成目标域数据Xt,转化为无标注的目标域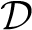 t;
t;
Step 6 将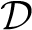 s和
s和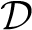 t作为JDA算法的输入,利用式(6)得到的变换矩阵A将Xt进行变换,得到新的矩阵Xt_new;
t作为JDA算法的输入,利用式(6)得到的变换矩阵A将Xt进行变换,得到新的矩阵Xt_new;
Step 7 令Xt_new作为个体的基因构建新种群,替换目标问题的Pt1,应用DE算法进行求解generation_2代;
Step 8 得到最优解y和最优个体x,结束迭代过程。
3 实验及结果分析
3.1 实验设置
本文采用文献[16]中的测试问题对所提算法的性能进行评估,每组测试问题由2个常见的单目标优化函数组成。一般地,每组测试问题中,任务1(T1)为简单函数,任务2(T2)为复杂函数。对于每组函数给出函数类型和函数间的相交程度与相似度,相似度值越高表明函数间相似程度越高(基于Pearson相关性[21]对任务间相似度进行定义),于表1中总结了实验中涉及的9组测试问题,d为维度。为了验证本文所提出的改进差分进化算法的有效性,在对比实验中增加无联合分布适配直接迁移算法,包含2种模式:一是在初始阶段直接将T1问题的最优解完全迁移到T2问题中的初始迁移TrDE1;二是generation_1代迭代过后直接将T1问题的解完全迁移到T2问题中的过程迁移TrDE2。实验具体参数设置如表2所示。
3.2 实验结果与分析
3.2.1 解的质量
本文所提算法与对比算法在测试问题实验中得到的平均目标值和标准偏差如表3所示,与文献[16]中进化多任务算法中对T2问题的求解结果进行对比,采用置信水平为95%的Wilcoxon秩和检验法对实验结果进行检测。
表3中记录每个问题求解出的平均目标值和标准偏差。在9组测试函数中,有7组测试函数是利用迁移学习的方法可以求出更优解的。在这7组求出更优解的实验中,通过本文提出的两种迁移学习方法求出最优解的测试函数一共有4组,JDA_TrDE1和JDA_TrDE2方法求出的解为这5种算法中最优的2种解;测试问题1和8,虽然使用JDA方法求出来的解不如使用直接迁移方法求出来的解更优,但都比不使用迁移学习方法直接求解的效果更优。测试问题6为文献[16]中所提迁移学习算法求解结果更优,本文提出的JDA_TrDE1和JDA_TrDE2算法为第2、第3优解,且均比不使用迁移学习方法直接求解的效果更优。通过较好的实验结果证明,使用单向迁移学习优化过后的差分进化算法是可以提高算法的优化性能的,并且实验结果显示,初始迁移的JDA_TrDE1方法比过程迁移的JDA_TrDE2方法求得的目标值更优。
采用联合分布适配方法将源问题的先验知识迁移到目标问题上,对帮助求解目标问题是有效的。将源域数据和目标域数据映射到同一高维空间中,分别进行数据间边缘分布适配与条件分布适配,减小随机变量的分布距离,使源问题数据中的有效信息更完整、更精确地帮助求解目标问题。但联合分布适配也存在一些问题,例如,在求解复杂多峰函数问题时,当源域数据与目标域数据之间的距离没有缩减到合适的范围,源域数据没有提供很好的知识帮助,就可能使目标问题陷入局部最优解,例如测试问题3和9;当源问题与目标问题之间完全相交且相似程度极高时,例如测试问题1,源问题与目标问题的最优解可能极为相似,因此进行联合分布适配以后的迁移效果略差于直接迁移。
表1 测试问题属性
Table 1 Test problem attributes
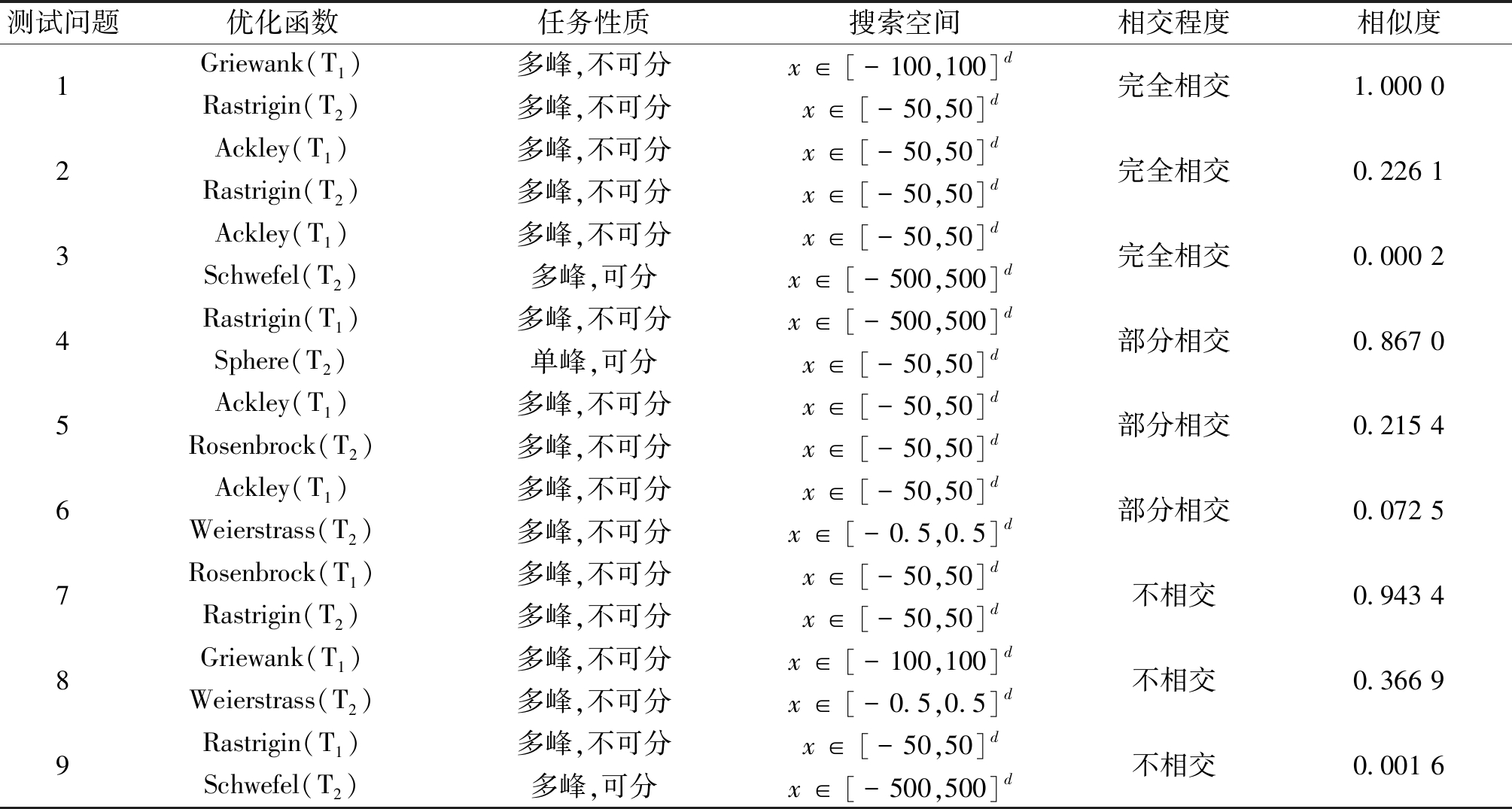
测试问题优化函数任务性质搜索空间相交程度相似度1Griewank(T1)多峰,不可分x∈[-100,100]dRastrigin(T2)多峰,不可分x∈[-50,50]d完全相交1.000 02Ackley(T1)多峰,不可分x∈[-50,50]dRastrigin(T2)多峰,不可分x∈[-50,50]d完全相交0.226 13Ackley(T1)多峰,不可分x∈[-50,50]dSchwefel(T2)多峰,可分x∈[-500,500]d完全相交0.000 24Rastrigin(T1)多峰,不可分x∈[-500,500]dSphere(T2)单峰,可分x∈[-50,50]d部分相交0.867 05Ackley(T1)多峰,不可分x∈[-50,50]dRosenbrock(T2)多峰,不可分x∈[-50,50]d部分相交0.215 46Ackley(T1)多峰,不可分x∈[-50,50]dWeierstrass(T2)多峰,不可分x∈[-0.5,0.5]d部分相交0.072 57Rosenbrock(T1)多峰,不可分x∈[-50,50]dRastrigin(T2)多峰,不可分x∈[-50,50]d不相交0.943 48Griewank(T1)多峰,不可分x∈[-100,100]dWeierstrass(T2)多峰,不可分x∈[-0.5,0.5]d不相交0.366 99Rastrigin(T1)多峰,不可分x∈[-50,50]dSchwefel(T2)多峰,可分x∈[-500,500]d不相交0.001 6
3.2.2 收敛速度
为了进一步说明使用单向迁移技术可以加快求解单目标优化问题的收敛速度,本节对原始差分进化算法(DE)、无联合分布适配技术的直接迁移差分进化算法的2种模式即初始迁移TrDE1算法和过程迁移TrDE2算法以及基于联合分布适配的迁移差分进化算法2种模式即初始迁移JDA_TrDE1算法和过程迁移JDA_TrDE2算法每次迭代结束后的最小值变化过程进行轨迹追踪分析。
图1描绘了采用5种算法求解测试问题中任务T2的每次迭代结束后的最小值变化过程。其中,横坐标为迭代次数,图1(a)、1(b)、1(d)、1(e)、1(g)的纵坐标为目标值的对数,图1(c)、(f)、(h)、(i)的纵坐标为目标值。
表2 实验具体参数设置
Table 2 Experiment-specific parameter settings
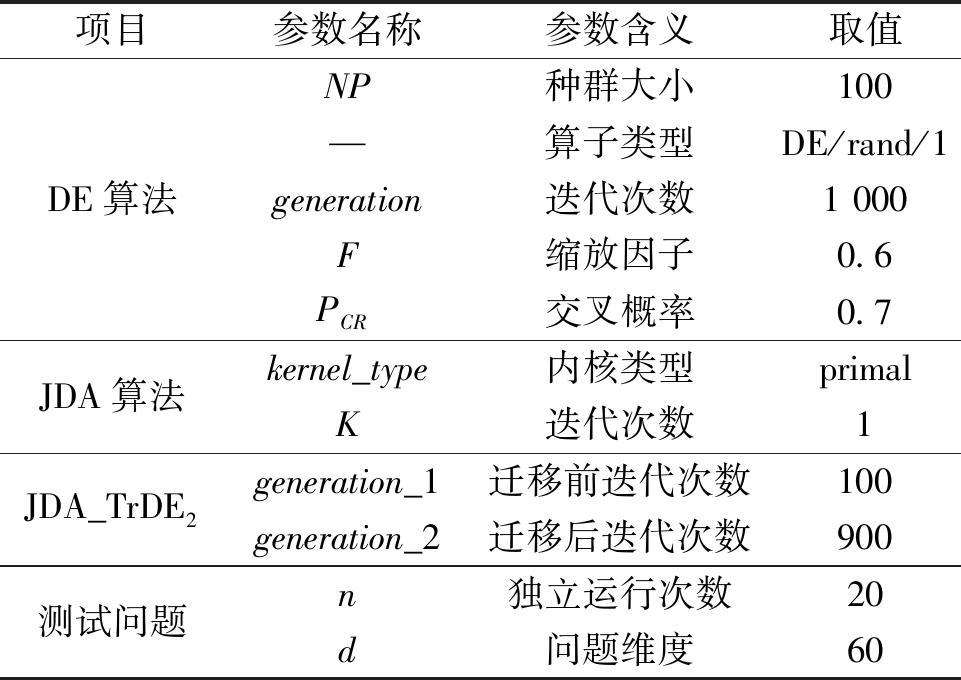
项目参数名称参数含义取值DE算法NP种群大小100—算子类型DE/rand/1generation迭代次数1 000F缩放因子0.6PCR交叉概率0.7JDA算法kernel_type内核类型primalK迭代次数1JDA_TrDE2generation_1迁移前迭代次数100generation_2迁移后迭代次数900测试问题n独立运行次数20d问题维度60
表3 不同算法在单目标问题上的平均目标值和标准偏差
Table 3 Average objective values and standard deviations of Different algorithms on the single objective problem
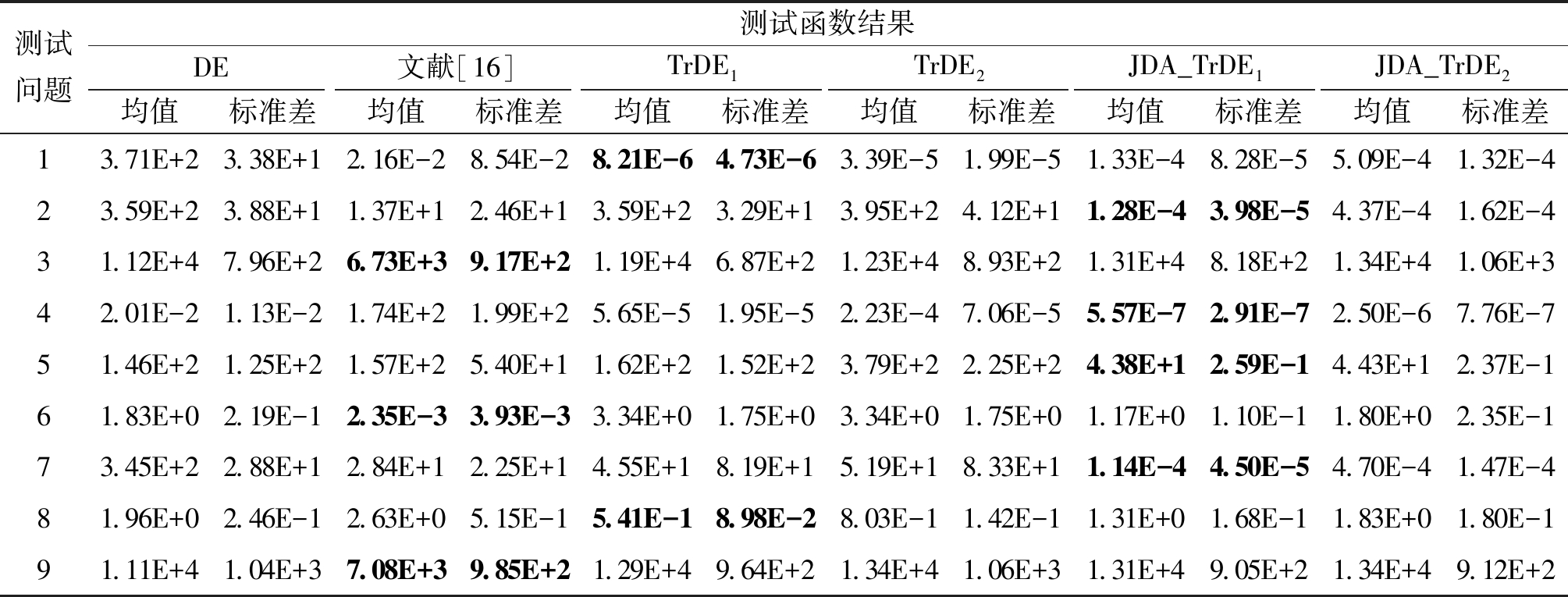
测试问题测试函数结果DE文献[16]TrDE1TrDE2JDA_TrDE1JDA_TrDE2均值标准差均值标准差均值标准差均值标准差均值标准差均值标准差13.71E+23.38E+12.16E-28.54E-28.21E-64.73E-63.39E-51.99E-51.33E-48.28E-55.09E-41.32E-423.59E+23.88E+11.37E+12.46E+13.59E+23.29E+13.95E+24.12E+11.28E-43.98E-54.37E-41.62E-431.12E+47.96E+26.73E+39.17E+21.19E+46.87E+21.23E+48.93E+21.31E+48.18E+21.34E+41.06E+342.01E-21.13E-21.74E+21.99E+25.65E-51.95E-52.23E-47.06E-55.57E-72.91E-72.50E-67.76E-751.46E+21.25E+21.57E+25.40E+11.62E+21.52E+23.79E+22.25E+24.38E+12.59E-14.43E+12.37E-161.83E+02.19E-12.35E-33.93E-33.34E+01.75E+03.34E+01.75E+01.17E+01.10E-11.80E+02.35E-173.45E+22.88E+12.84E+12.25E+14.55E+18.19E+15.19E+18.33E+11.14E-44.50E-54.70E-41.47E-481.96E+02.46E-12.63E+05.15E-15.41E-18.98E-28.03E-11.42E-11.31E+01.68E-11.83E+01.80E-191.11E+41.04E+37.08E+39.85E+21.29E+49.64E+21.34E+41.06E+31.31E+49.05E+21.34E+49.12E+2
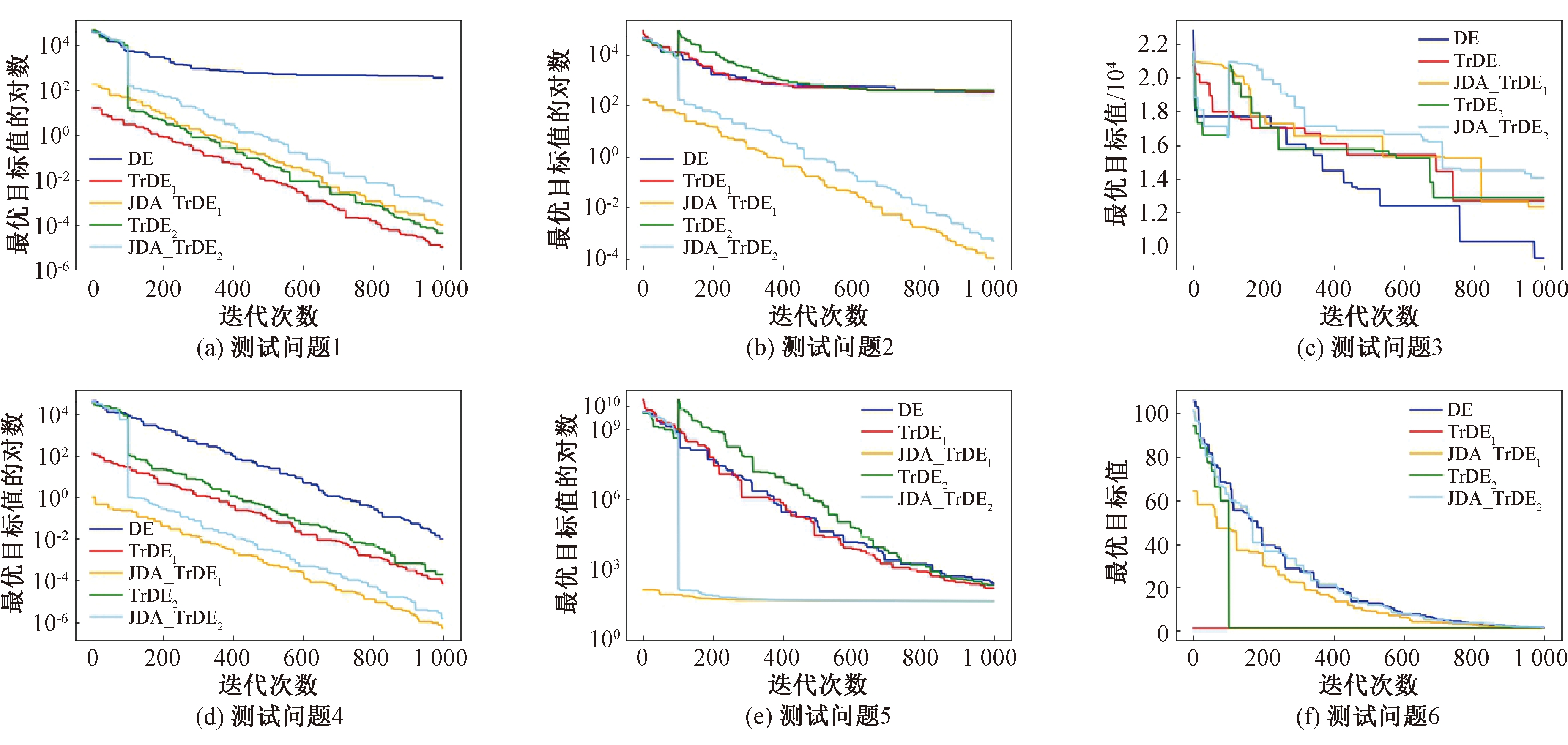
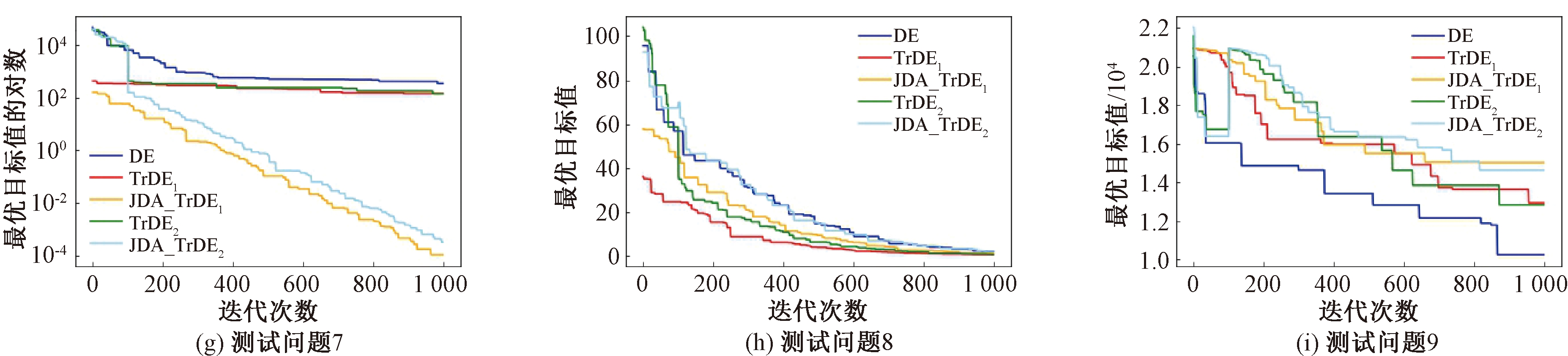
图1 优化问题迭代求解过程中的最小值变化轨迹
Figure 1 Minimax change trajectory during iterative solution of optimization problems
从图1可以看出,使用单向迁移技术后的差分进化算法在搜索过程中明显快于原始的差分进化算法。其中图1(b)、(d)、(e)和(g)中,JDA_TrDE1算法和JDA_TrDE2算法的2条曲线不仅在收敛精度上优于其他3种算法,且收敛速度也远快于其他3种算法,效果最佳。JDA_TrDE2算法在100代使用联合分布适配技术后,下一代的最小适应度值均有大幅减小,并且以后的收敛速度有明显的加快。在图1(e)中,使用联合分布适配的两种算法在400代之前就已经收敛到最优值,且最优值比其他算法迭代1 000代的收敛精度更好。在图1(a)、(f)和(h)中,收敛曲线证明单向迁移技术对求解问题最优值的有效性是存在的,同样具有较高的收敛速度和收敛精度。因此,JDA_TrDE1算法和JDA_TrDE2算法同样有较好的收敛速度和收敛精度。
3.3 对联合适配分布不同参数的对比实验
在联合分布适配算法中,有5个重要参数,即内核类型、迁移后的维度、lambda值、rbf内核带宽gamma以及迭代次数。本文对其中的内核类型kernel_type及迭代次数K,选取不同的值进行对比实验。对每种不同参数的算法独立运行10次。
表4为对联合分布适配选取不同内核的实验结果,记录每个问题求解出的平均目标值和标准偏差。对于验证的9个测试问题,其中内核为primal时有1个问题求得最优解;内核为linear时有6个问题求得最优解;内核为rbf时有2个问题求得最优解。对于内核为rbf,出现在测试问题1、2和7中求出来的解的收敛精度远小于内核为primal和内核为linear的情况,所以在作为迁移技术求解单目标问题时,不适合作为JDA算法的内核。内核为primal和内核为linear时分别求出的最优解在比较后认为精度相差不大,均可作为JDA算法在求解单目标问题时的内核。
表5为对联合分布适配选取不同迭代次数的实验结果,记录每个问题求解出的平均目标值和标准偏差。对于验证的9个测试问题,K=2时有2个问题求得最优解,K=3时有4个问题求得最优解,K=5时有3个问题求得最优解。理论上,使用实验中预测的标签作为伪目标标签并迭代运行JDA,就可以提高标签质量,直到收敛。实验结果在一定程度上也证明了这一点。不过分析9个实验的收敛精度发现,大多数问题对于迭代次数这个参数的敏感程度并不高,最优解与次优解,甚至第三优解之间的差距很小,因此在实验过程中可酌情选择JDA算法的迭代次数。
表4 联合分布适配选取不同内核的对比实验
Table 4 Comparison experiments of different kernels selected for joint distribution adaptation
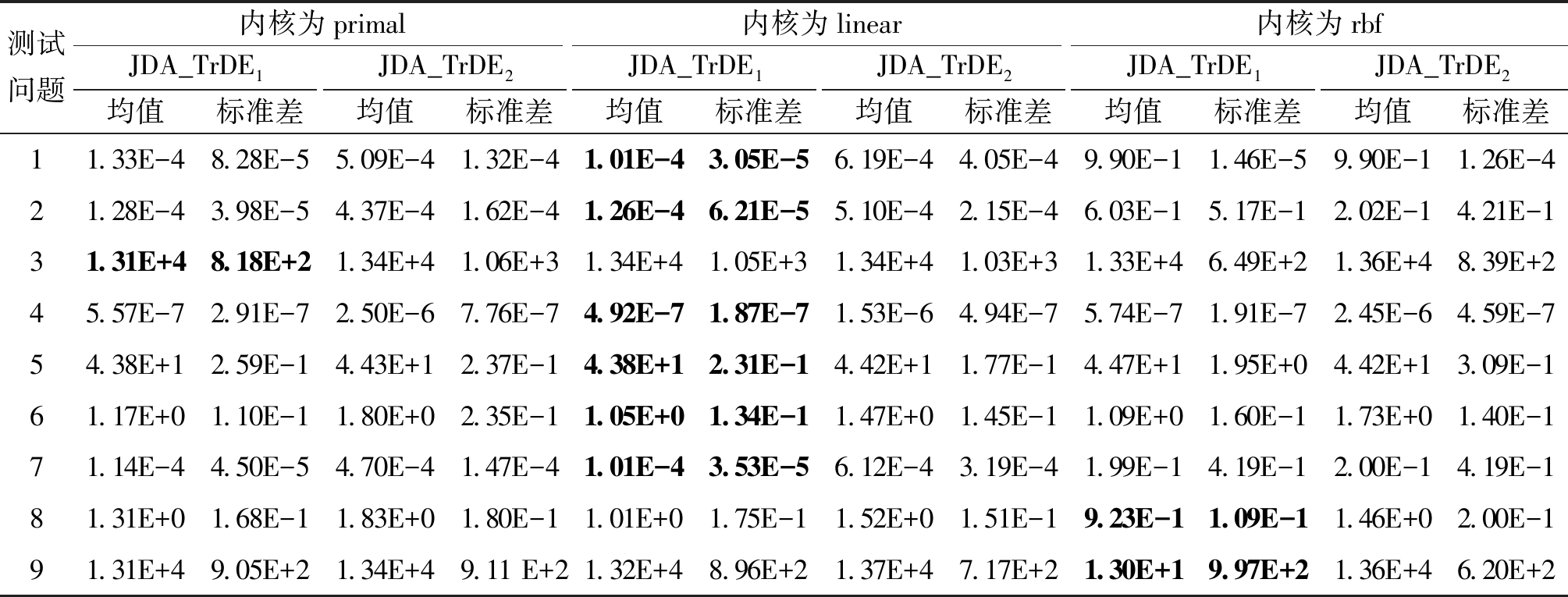
测试问题内核为primal内核为linear内核为rbfJDA_TrDE1JDA_TrDE2JDA_TrDE1JDA_TrDE2JDA_TrDE1JDA_TrDE2均值标准差均值标准差均值标准差均值标准差均值标准差均值标准差11.33E-48.28E-55.09E-41.32E-41.01E-43.05E-56.19E-44.05E-49.90E-11.46E-59.90E-11.26E-421.28E-43.98E-54.37E-41.62E-41.26E-46.21E-55.10E-42.15E-46.03E-15.17E-12.02E-14.21E-131.31E+48.18E+21.34E+41.06E+31.34E+41.05E+31.34E+41.03E+31.33E+46.49E+21.36E+48.39E+245.57E-72.91E-72.50E-67.76E-74.92E-71.87E-71.53E-64.94E-75.74E-71.91E-72.45E-64.59E-754.38E+12.59E-14.43E+12.37E-14.38E+12.31E-14.42E+11.77E-14.47E+11.95E+04.42E+13.09E-161.17E+01.10E-11.80E+02.35E-11.05E+01.34E-11.47E+01.45E-11.09E+01.60E-11.73E+01.40E-171.14E-44.50E-54.70E-41.47E-41.01E-43.53E-56.12E-43.19E-41.99E-14.19E-12.00E-14.19E-181.31E+01.68E-11.83E+01.80E-11.01E+01.75E-11.52E+01.51E-19.23E-11.09E-11.46E+02.00E-191.31E+49.05E+21.34E+49.11 E+21.32E+48.96E+21.37E+47.17E+21.30E+19.97E+21.36E+46.20E+2
表5 联合分布适配选取不同迭代次数的对比实验
Table 5 Comparison experiments of different iterations of joint distribution adaptation selection
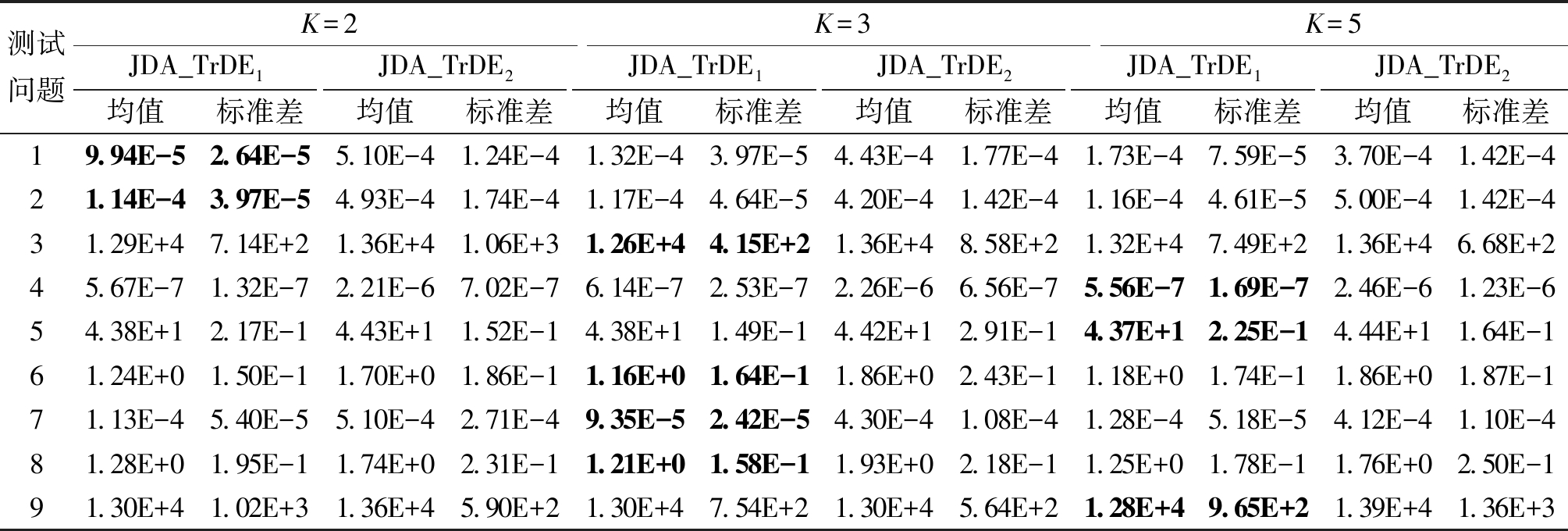
测试问题K=2K=3K=5JDA_TrDE1JDA_TrDE2JDA_TrDE1JDA_TrDE2JDA_TrDE1JDA_TrDE2均值标准差均值标准差均值标准差均值标准差均值标准差均值标准差19.94E-52.64E-55.10E-41.24E-41.32E-43.97E-54.43E-41.77E-41.73E-47.59E-53.70E-41.42E-421.14E-43.97E-54.93E-41.74E-41.17E-44.64E-54.20E-41.42E-41.16E-44.61E-55.00E-41.42E-431.29E+47.14E+21.36E+41.06E+31.26E+44.15E+21.36E+48.58E+21.32E+47.49E+21.36E+46.68E+245.67E-71.32E-72.21E-67.02E-76.14E-72.53E-72.26E-66.56E-75.56E-71.69E-72.46E-61.23E-654.38E+12.17E-14.43E+11.52E-14.38E+11.49E-14.42E+12.91E-14.37E+12.25E-14.44E+11.64E-161.24E+01.50E-11.70E+01.86E-11.16E+01.64E-11.86E+02.43E-11.18E+01.74E-11.86E+01.87E-171.13E-45.40E-55.10E-42.71E-49.35E-52.42E-54.30E-41.08E-41.28E-45.18E-54.12E-41.10E-481.28E+01.95E-11.74E+02.31E-11.21E+01.58E-11.93E+02.18E-11.25E+01.78E-11.76E+02.50E-191.30E+41.02E+31.36E+45.90E+21.30E+47.54E+21.30E+45.64E+21.28E+49.65E+21.39E+41.36E+3
4 结论
本文提出了基于联合分布适配的单向迁移差分进化算法求解单目标优化问题,实现了2种迁移模式的算法即初始迁移的JDA_TrDE1和过程迁移的JDA_TrDE2。采用9组函数进行测试,并与原始差分算法(DE)、无适配技术的直接迁移差分算法(TrDE)进行比较,实验结果表明:引入JDA后的算法不仅能更快地跳出局部最优,提高算法的求解精度,而且具有较好的收敛速度。此外实验结果还得出问题间的关系对算法性能有一定的影响,迁移模式和JDA的参数对算法性能影响不大。本文仅仅对单目标优化问题进行了测试,下一步考虑将基于JDA的迁移优化应用到约束优化问题和多目标优化问题,以全面评价所提方法的性能。另外,本文采用的测试函数具有一定的先验知识,源问题和目标问题的相交程度和相似度是已知的,如果是在任意的2个问题中迁移,需要使用JDA评测问题间的关系,并根据相似关系进行自适应迁移,这些也是后续的研究内容。
[1] DAS S, SUGANTHAN P N. Differential evolution: a survey of the state-of-the-art[J]. IEEE Transactions on Evolutionary Computation, 2011, 15(1): 4-31.
[2] 程适, 王锐, 伍国华, 等. 群体智能优化算法[J]. 郑州大学学报(工学版), 2018,39(6): 1-2.
CHENG S,WANG R,WU G H,et al. Swarm intelligence optimization algorithm[J]. Journal of Zhengzhou University (Engineering Science), 2018,39(6): 1-2.
[3] 刘倩, 冯艳红, 陈嶷瑛. 基于混沌初始化和高斯变异的飞蛾火焰优化算法[J]. 郑州大学学报(工学版), 2021, 42(3): 53-58.
LIU Q, FENG Y H, CHEN Y Y. Moth-flame optimization algorithm based on chaotic initialization and Gaussian mutation[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(3): 53-58.
[4] 汪慎文, 张佳星, 褚晓凯, 等. 两阶段搜索的多模态多目标差分进化算法[J]. 郑州大学学报(工学版), 2021, 42(1): 9-14, 110.
WANG S W, ZHANG J X, CHU X K, et al. Multimodal multi-objective differential evolution algorithm based on two-stage search[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(1): 9-14, 110.
[5] TAN Z P, LI K S, WANG Y. Differential evolution with adaptive mutation strategy based on fitness landscape analysis[J]. Information Sciences, 2021, 549: 142-163.
[6] PAN S J, YANG Q. A survey on transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10): 1345-1359.
[7] XU H P, YANG L Z, LONG X Y. Underwater sonar image classification with small samples based on parameter-based transfer learning and deep learning[C]∥2022 Global Conference on Robotics, Artificial Intelligence and Information Technology (GCRAIT). Piscataway: IEEE, 2022: 304-307.
[8] CHIBA S, SASAOKA H. Basic study for transfer learning for autonomous driving in car race of model car[C]∥2021 6th International Conference on Business and Industrial Research (ICBIR). Piscataway: IEEE, 2021: 138-141.
[9] SINGH N K, KUMAR A. Image based recommender system using transfer learning[C]∥2022 2nd International Conference on Emerging Frontiers in Electrical and Electronic Technologies (ICEFEET). Piscataway:IEEE, 2022: 1-4.
[10] TAN K C, FENG L, JIANG M. Evolutionary transfer optimization-a new frontier in evolutionary computation research[J]. IEEE Computational Intelligence Magazine, 2021, 16(1): 22-33.
[11] LIM R, GUPTA A, ONG Y S, et al. Non-linear domain adaptation in transfer evolutionary optimization[J].Cognitive Computation, 2021, 13(2): 290-307.
[12] JIANG M, HUANG Z Q, QIU L M, et al. Transfer learning-based dynamic multiobjective optimization algorithms[J]. IEEE Transactions on Evolutionary Computation, 2018, 22(4): 501-514.
[13] JIANG M, QIU L M, HUANG Z Q, et al. Dynamic multi-objective estimation of distribution algorithm based on domain adaptation and nonparametric estimation[J]. Information Sciences, 2018, 435: 203-223.
[14] 张勇, 杨康, 郝国生, 等. 基于相似历史信息迁移学习的进化优化框架[J]. 自动化学报, 2021, 47(3): 652-665.
ZHANG Y, YANG K, HAO G S, et al. Evolutionary optimization framework based on transfer learning of similar historical information[J]. Acta Automatica Sinica, 2021, 47(3): 652-665.
[15] 刘璐, 蒋艳. 基于迁移学习的NSGAⅡ算法[J]. 软件导刊, 2021, 20(3): 134-138.
LIU L, JIANG Y. NSGAⅡ algorithm based on transfer learning[J]. Software Guide, 2021, 20(3): 134-138.
[16] 尚青霞, 周磊, 冯亮. 基于降噪自动编码器的多任务优化算法[J]. 大连理工大学学报, 2019, 59(4): 417-426.
SHANG Q X, ZHOU L, FENG L. Multi-task optimization algorithm based on denoising auto-encoder[J]. Journal of Dalian University of Technology, 2019, 59(4): 417-426.
[17] FENG L, ZHOU L, ZHONG J H, et al. Evolutionary multitasking via explicit autoencoding[J]. IEEE Transactions on Cybernetics, 2019, 49(9): 3457-3470.
[18] PAN S J, TSANG I W, KWOK J T, et al. Domain adaptation via transfer component analysis[J]. IEEE Transactions on Neural Networks, 2011, 22(2): 199-210.
[19] GONG B Q, SHI Y, SHA F, et al. Geodesic flow kernel for unsupervised domain adaptation[C]∥IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2012: 2066-2073.
[20] LONG M S, WANG J M, DING G G, et al. Transfer feature learning with joint distribution adaptation[C]∥2013 IEEE International Conference on Computer Vision.Piscataway: IEEE, 2014: 2200-2207.
[21] DA B S, ONG Y S, FENG L, et al. Evolutionary multitasking for single-objective continuous optimization: benchmark problems, performance metric and baseline results[EB/OL].(2017-06-12)[2022-10-26].https:∥doi.org/10.48550/arXiv.1706.03470.