大规模优化问题广泛存在于生活中,例如空气动力学形状优化[1]、大规模空中交通流量优化[2]、以及用于大规模图像识别的深层卷积网络优化[3]等。一般来说,当决策变量维数超过100时,该问题就被称为大规模优化问题[4](large scale optimization problems,LSOP)。大规模优化问题的数学表达式如式(1)所示:
(1)
式中:Ω={x∈R|l≤x≤u}表示可行域,l和u分别表示可行域的下界和上界;x表示n维的决策向量;f(x)表示目标函数。随着决策变量维数的增加,搜索空间也会变得越来越复杂,导致很难获得问题的最优解,这也被称为“维度灾难”问题[5]。
目前用于求解大规模优化问题的方法大致可分为2类:基于分解的方法[6]和基于非分解的方法[7]。基于分解的方法是将一个高维的原始问题分解为若干个低维的子问题,然后通过对子问题的独立优化与相互合作来寻找原始问题的最优解。合作型协同演化(cooperative coevolutionary,CC)[8]是基于分解方法的常用框架。基于非分解的方法则始终将高维的原始问题视为一个整体,然后采用元启发式算法的变种算法加强算法在高维空间的搜索能力。例如竞争群体优化(competitive swarm optimizer,CSO)方法[9]、社会学习粒子群优化(social learning particle swarm optimization,SL-PSO)方法[10]以及基于分层学习的群体优化(level-based learning swarm optimizer,LLSO)方法[11]等都是基于非分解的方法。
当大规模优化问题的目标函数评价耗时或者评价成本昂贵时,称之为昂贵大规模优化问题。由于进化算法在获得最优解之前都需要消耗大量评价次数,因此,它们并不适用于求解昂贵优化问题。为了节省目标函数评价,通常引入代理模型以代替昂贵的真实目标函数评价。De Falco等[12]将代理模型嵌入到CC的框架中,提出了一种代理模型辅助的协同进化算法(surrogate-assisted CC,SACC),用于求解大规模优化问题。Fu等[13]提出了一种随机特征选择辅助的代理模型辅助进化算法(surrogate-assisted evolutionary algorithm with random feature selection,SAEA-RFS),该算法采用有放回的随机特征选择技术来构建若干个不同的子问题,然后子问题在径向基函数神经网络的辅助下进行进化优化求解。Sun等[14]提出了代理模型集成辅助的大规模昂贵进化算法(surrogate ensemble assisted large-scale expensive evolutionary algorithm with a random grouping technique,SEA-LEEA-RG),该算法采用不重复随机分组技术将大规模问题分解成若干大小不一的子问题,然后在子问题上建立全局模型和局部模型的集成模型辅助问题优化。
然而,目前求解昂贵大规模优化问题的算法仍存在以下不足:一是频繁地执行分组操作会使得某些理想的分组方案在没有得到充分优化的情况下就会被下一个随机分组方案覆盖;二是无放回的随机分组增加了相关变量划分到不同子问题的风险。为此,本文在CC框架的基础上提出惯性分组和重叠特征选择辅助的优化算法(inertial grouping and overlapping feature selection assisted optimization algorithm,IG-OFSA)。其中,惯性分组技术通过设置参数来控制优化过程中重新分组的频率,从而使得每一个分组方案都能得到较充分的优化;重叠特征选择技术通过在子问题之间增加重叠变量,使相同变量在不同子问题上进行优化,一方面能够增加相关变量被划分到同一子问题中的概率,另一方面重叠变量通过参与不同子问题的优化,在一定程度上可防止其偏离正确的搜索方向。
1 相关工作
1.1 合作型协同演化策略
Potter等[8]最早提出合作型协同演化(cooperative coevolutionary,CC)策略,他们将1个n维的问题分解成了n个1维的问题进行求解。根据分解方式的不同,基于CC框架下求解大规模优化问题的方法大致可以分为2类:基于静态分组的方法和基于动态分组的方法。
基于静态分组的方法在优化开始前将大规模问题的决策变量分解成若干个低维的子组,而这些子组在接下来的优化过程中保持不变。Van Den Bergh等[15]提出了协同粒子群优化(cooperative particle swarm optimizer,CPSO)方法,将决策变量随机分解成K个互不相交的子组后便不再执行分解操作。但当变量之间存在交互关系时,随机分解的分组精度会大大降低。Chen等[16]提出了具有变量交互学习的协同演化(CC with variable interaction learning,CCVIL)方法,CCVIL在执行分解前,需要先判断决策变量之间的交互关系。差分分组(differential grouping,DG)[17]是一种CCVIL的分组策略,DG将具有直接交互关系的变量划分到同一子组。但是DG并没有检测变量之间的间接交互,所以为了进一步提高分组精度,Omidvar等[18]提出了一种改进的差分分组(improved variant of the differential grouping,DG2)算法,DG2将所有具有直接交互和间接交互的变量都分配到同一子组。尽管CCVIL能够实现较为理想的分组,但检测变量之间的交互需要消耗大量的目标函数评价,所以,CCVIL并不适用于直接求解昂贵大规模优化问题。
基于动态分组的方法则是在整个优化过程中动态地执行分解操作,Yang等[19]提出的随机分组(random grouping,RG)策略和多级协作协同进化(multi-level cooperative co-evolution,MLCC)策略都是基于动态分组的方法,在这些策略中,子组的大小和成员在每一个协同周期都会发生改变。
1.2 差分进化算法
Storn等[20]于1997年提出了差分进化(differential evolution,DE)算法,该算法是一种基于群体差异的启发式搜索算法。DE通过依次执行种群初始化、变异、交叉和选择这4种操作,从而实现个体的进化和种群的更新。目前研究人员提出了许多DE变种,它们的主要区别在于采用了不同的变异策略。本文采用“DE/rand-to-best/1”作为变异策略,该变异操作如式(2)所示:
(2)
式中:![]() 为在第t代时,第i个目标个体
为在第t代时,第i个目标个体![]() 对应的变异向量;
对应的变异向量;![]() 为从第t代种群中随机选择的互不相同的个体,且这些个体都与当前的目标个体
为从第t代种群中随机选择的互不相同的个体,且这些个体都与当前的目标个体![]() 不同;F为一个大于0的缩放因子;
不同;F为一个大于0的缩放因子;![]() 为当前种群中适应度最小的个体。
为当前种群中适应度最小的个体。
1.3 增量克里金模型
克里金(Kriging)模型[21]在得到模型预测值的同时,还能得到该预测值的不确定度,所以克里金模型被广泛用作代理模型以辅助优化算法。在训练克里金模型的过程中,当获得新的样本点时,为了更新模型,传统的做法是从头开始训练一个新的克里金模型,但当样本量的规模很大或者问题的维度很高时,再次训练新模型花费的时间是巨大的,为了缓解计算压力,Zhan等[22]提出增量克里金辅助进化算法(incremental Kriging assisted evolution algorithm,IKAEA),IKAEA将增量学习技术引入到克里金模型的更新过程中,使得更新克里金模型的时间复杂度由O(n3)降为O(n2),并且IKAEA的预测结果与标准的克里金模型的预测结果具有一致性。
2 惯性分组和重叠特征选择辅助的昂贵大规模优化算法
2.1 算法描述
CC框架下求解大规模优化问题算法的性能取决于分组方案的合理性,所以分解操作是合作型协同演化策略的关键性操作之一。在求解决策变量不可分解的昂贵大规模优化问题时,有限的目标函数评价次数和变量之间的耦合关系对算法的搜索效率提出了更高的要求。具有变量交互学习的协同演化方法在问题的分解过程中需要消耗大量的目标函数评价,使其不适用于求解昂贵大规模优化问题。同时,变量的耦合关系会使得基于随机分组策略算法的性能大大下降。因此,为了提高求解昂贵大规模优化问题的性能和效率,本文提出了一种惯性分组和重叠特征选择辅助的优化算法。算法1给出了本文方法的步骤。算法1由3个部分组成:第一部分为初始化阶段(Step 1~Step 3),主要是使用拉丁超立方体采样采集初始样本并从初始样本中选取训练集和初始种群;第二部分为分解训练阶段(Step 4~Step 6),主要采用重叠特征选择技术将大规模优化问题分解成低维的重叠子问题,并在子问题上训练代理模型,同时采用惯性系数判断是否重新分组;第三部分为解的重构阶段(Step 7~Step 8),该阶段在所有子问题优化结束之后,将每一个子问题的期望提高(expected improvement,EI)值最大的个体合并成一个完整的解并对其进行真实的目标函数评价。在算法1中,spk表示第k个子问题。
算法1 IG-OFSA算法。
输入:问题的维度D、奇数子组的个数T、子问题的个数K、初始样本的个数NIS、训练集的初始大小Nt、种群的大小Np、最大的目标函数评价次数max_FES、在代理模型上搜索的迭代次数nIter、惯性系数I;
输出:最优解Xbest、最优解的适应值f(Xbest)。
Step 1 在解空间内用拉丁超立方体采样策略采集NIS个初始样本,计算每个样本的适应值并存入存档Arc;
Step 2 在Arc中选择适应值排名前Nt的样本作为训练集S;
Step 3 在Arc中选择适应度值排名前Np的样本作为初始种群;
Step 4 采用重叠特征选择技术将原始问题分解成K个子问题;
Step 5 若当前的协同周期是惯性系数I的整数倍,则转至Step 2,否则,转至Step 6;
Step 6 依次在每个子问题上训练/更新代理模型;
Step 7 依次在子问题上进行代理模型辅助的差分进化,并记录每一个子问题spk(k=1,2,…,K)中EI值最大的个体![]()
Step 8 将所有![]() 合并成上下文向量cv,并计算cv的适应值;
合并成上下文向量cv,并计算cv的适应值;
Step 9 将cv存入Arc和训练集S中;
Step 10 更新种群;
Step 11 如果算法不满足终止条件,则转至Step 5,否则,转至Step 12;
Step 12 输出全局最优解Xbest及其适应值f(Xbest),算法结束。
2.2 惯性分组
在求解昂贵大规模优化问题时,受资源限制,现有算法通常采用随机分组技术实现对大规模问题的分解。传统的合作型协同演化策略在每一轮协同演化周期开始前都会执行一次分解操作,这会使得某些合理的随机分组方案还没得到充分的利用就会被下一个随机分组方案取代,所以本文提出采用惯性系数I来控制分组频率,以延长每一个随机分组方案的开发周期,即只有在满足条件时才对大规模问题重新分组,使得合理的分组方案能够被充分地开发和利用,从而平衡随机分组方法的探索能力和开发能力。
2.3 重叠特征选择
如果强行将一个不可分解问题随机分解成若干个互不相交的低维子问题进行求解,算法极容易陷入局部最优,因此,本文采用了一种重叠特征选择技术来改进随机分组技术。该技术首先将高维问题的决策变量分解成T个互不相交的子组,其序号用奇数表示,再从每一个子组中随机选取至少一个决策变量构成一个与该子组对应的子组,其序号用偶数表示,即该技术将高维问题分解成了2T个子组。将这些子组按序号形成一个闭环,并从序号为2的子组开始,两两组成一个子问题。算法通过重叠特征选择技术最终将高维问题分解成T个重叠的子问题。重叠特征选择技术通过重叠变量的选取,一方面增加相关变量被划分到同一子问题中的概率,另一方面重叠变量通过参与不同子问题的优化,在一定程度上可防止其偏离正确的搜索方向。图1为重叠特征选择技术分组过程的一个简单例子。
图1中假设原始问题含有9个决策变量,首先将原始问题随机均匀地分解成3个互不相交的子组:组1、组3、组5,然后在组1中随机选取至少一个决策变量构成组2,同理分别在组3和组5中选取变量构成组4和组6。接着,由组2与组3中的变量构成子问题1,由组4与组5中的变量构成子问题2,由组6与组1中的变量构成子问题3。对于重叠变量,在合并成上下文向量cv时,采用其在不同子问题中得到的变量值的均值在cv中相应的位置进行填充。
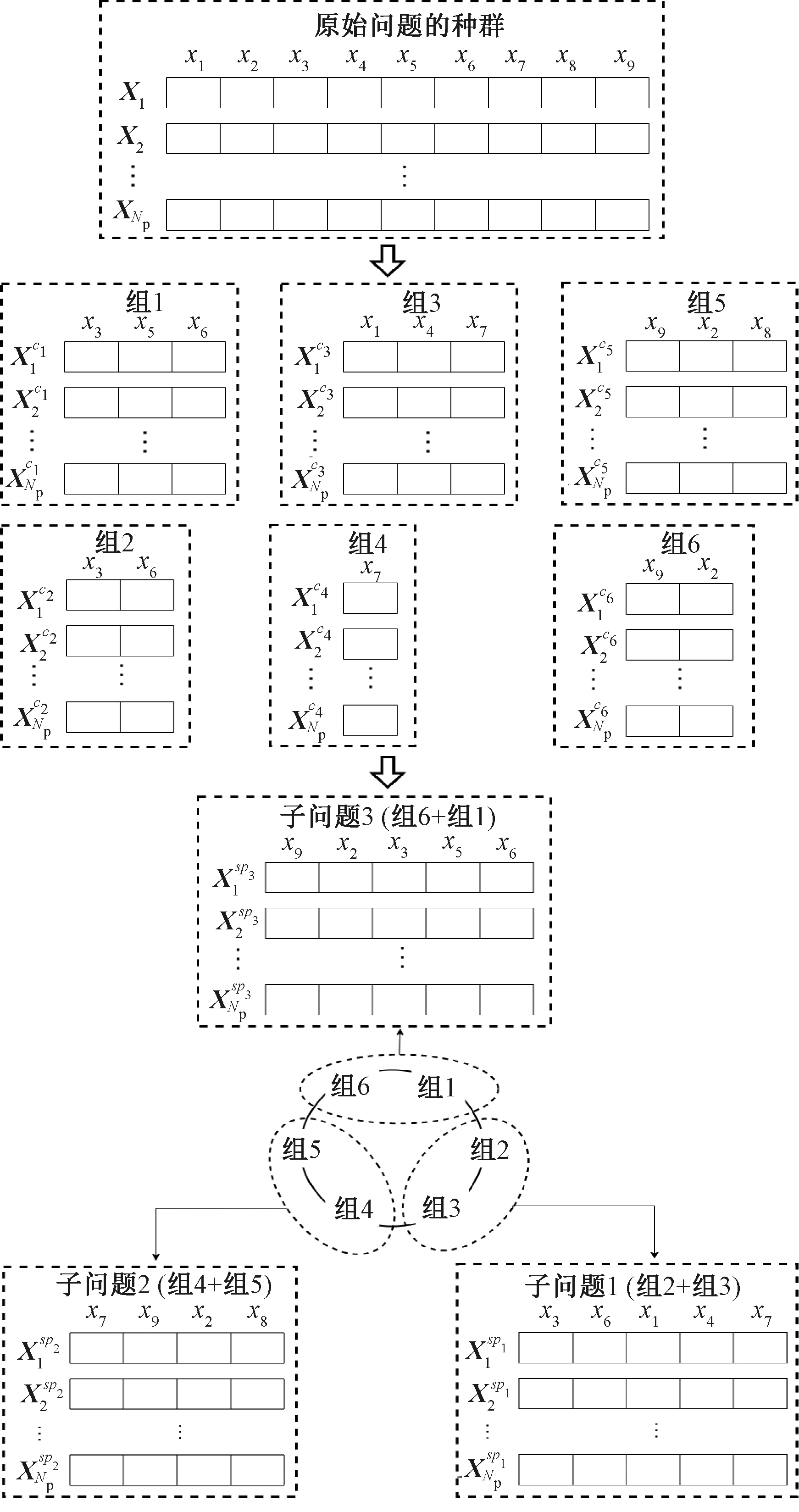
图1 重叠特征选择分组技术
Figure 1 Overlapping feature selection grouping technique
2.4 计算复杂度分析
IG-OFSA算法的运行成本主要来源于代理模型的训练和基于模型寻优2个部分。假设子问题的个数为K,训练数据集的大小为Nt,种群的规模为Np。训练增量克里金模型的时间复杂度为O(KNt2),模型寻优的时间复杂度为O(KNp)。一般情况下,Nt≫Np,因此,IG-OFSA的计算复杂度为O(KNt2)。而训练RBF代理模型的计算复杂度为O(KNt2),训练传统克里金模型的时间复杂度为O(KNt3),因此,与RBF模型辅助的或者传统克里金模型辅助的昂贵大规模优化算法相比,IG-OFSA在提高优化效果的同时,并没有增加额外的计算复杂度。
3 实验与结果分析
3.1 参数设置
本文在CEC2013标准测试函数集上进行了实验,以验证本文算法的性能。奇数子组个数设置为20,奇数子组的大小设置为sub_size=⎣D/20」,偶数子组的大小取值为[1,sub_size],初始化样本的个数和训练集的初始大小都设置为4·sub_size。本文采用增量克里金模型作为子问题的代理模型,采用差分进化算法作为优化器,缩放因子F设置为0.8,交叉概率r设置为0.95,种群的大小设置为100。最大的目标函数评价次数为11·D,这也是实验的终止条件。每一个算法在每一个基准函数上独立运行25次,并在具有Bonferroni校正的显著性水平为0.05的Wilcoxon秩和检验下检验不同算法得到的结果是否存在显著差异。
实验所用处理器为AMD Ryzen 7 4800U CPU@1.8 GHz,内存为16 GB。
3.2 参数敏感性分析
本节对本文所提算法中的2个关键参数进行了分析,一个是奇数子组的个数T,另一个是惯性系数I。奇数子组的个数T决定子问题的维度,T越小意味着子问题的维度就越高,在高维的子问题上建立代理模型存在困难,而T越大意味着子问题的个数也越多,那么训练所有子问题的代理模型的时间代价较大。从CEC2013的5类函数中各选出一个代表函数(分别为f1、f4、f9、f13及f15)来进行实验分析,T分别设置为10、20、30、40,其实验对比结果如表1所示。表中median和MAD分别为独立运行25次的结果的中位数和中值绝对偏差。由表1可以看出,当T设置为20时,算法得到的结果最好,所以本文将T设置为20。
基于协同演化策略算法的性能还与分组方案相关,为了平衡分组方案的探索能力和开发能力,本文设置一个惯性系数I来决定分组的频率。I分别设置为5、10、15、20,其在f1、f4、f9、f13及f15上的实验对比结果如表1所示。从表1可以看出,当I设置为10时,算法获得的结果最优,因此,本文将惯性系数I设置为10。
3.3 惯性分组技术的有效性
为了验证IG-OFSA算法中惯性分组技术的有效性,将IG-OFSA算法的惯性分组技术移除后产生一个变种算法OFSA。OFSA可以视为IG-OFSA中惯性系数设置为1的特殊情况,即在每一轮协同演化周期开始时都执行一次分解操作。OFSA的其他设置都与IG-OFSA的设置相同。同样,在CEC2013的5个代表函数上进行实验分析,OFSA和IG-OFSA的实验结果对比如表2所示。从表2中可以看出,IG-OFSA在3个代表函数上获得比OFSA更好的结果,说明惯性分组技术在解决大规模昂贵优化问题时能够发挥重要的作用,特别是在问题不可分的情况下。
表1 不同的T值和不同的I值的结果对比
Table 1 Comparison of results with different T values and different I values
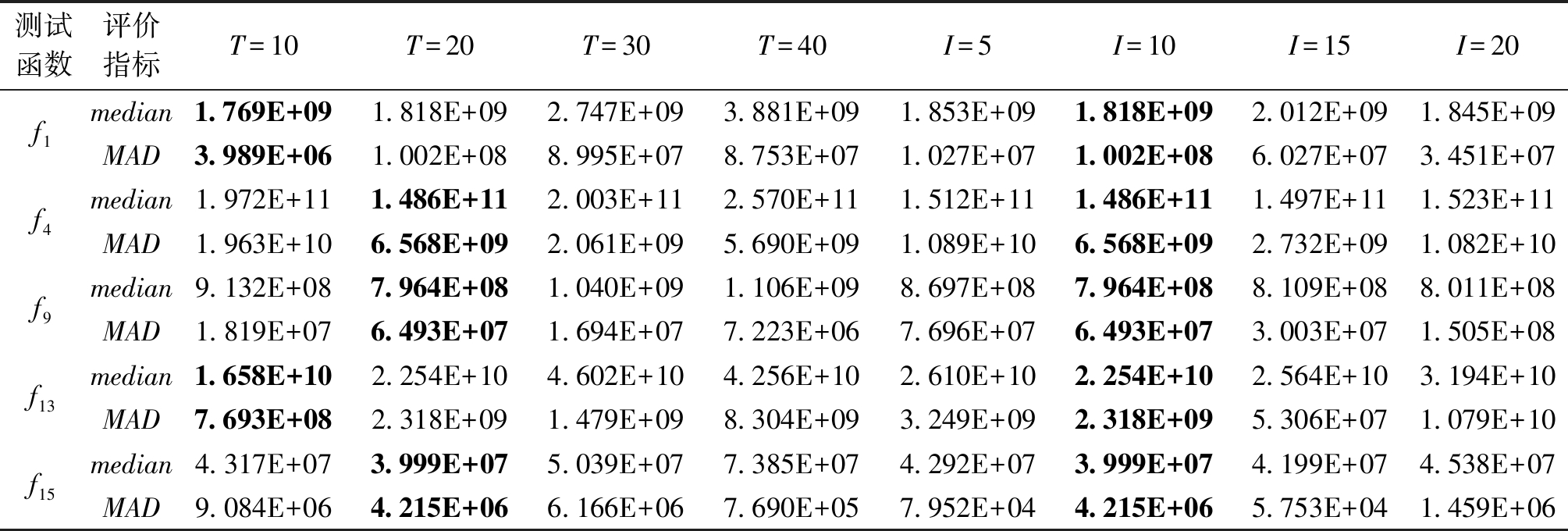
测试函数评价指标T=10T=20T=30T=40I=5I=10I=15I=20f1f4f9f13f15median1.769E+091.818E+092.747E+093.881E+091.853E+091.818E+092.012E+091.845E+09MAD3.989E+061.002E+088.995E+078.753E+071.027E+071.002E+086.027E+073.451E+07median1.972E+111.486E+112.003E+112.570E+111.512E+111.486E+111.497E+111.523E+11MAD1.963E+106.568E+092.061E+095.690E+091.089E+106.568E+092.732E+091.082E+10median9.132E+087.964E+081.040E+091.106E+098.697E+087.964E+088.109E+088.011E+08MAD1.819E+076.493E+071.694E+077.223E+067.696E+076.493E+073.003E+071.505E+08median1.658E+102.254E+104.602E+104.256E+102.610E+102.254E+102.564E+103.194E+10MAD7.693E+082.318E+091.479E+098.304E+093.249E+092.318E+095.306E+071.079E+10median4.317E+073.999E+075.039E+077.385E+074.292E+073.999E+074.199E+074.538E+07MAD9.084E+064.215E+066.166E+067.690E+057.952E+044.215E+065.753E+041.459E+06
表2 OFSA与IG-OFSA的结果对比
Table 2 Comparison of results obtained by OFSA and IG-OFSA
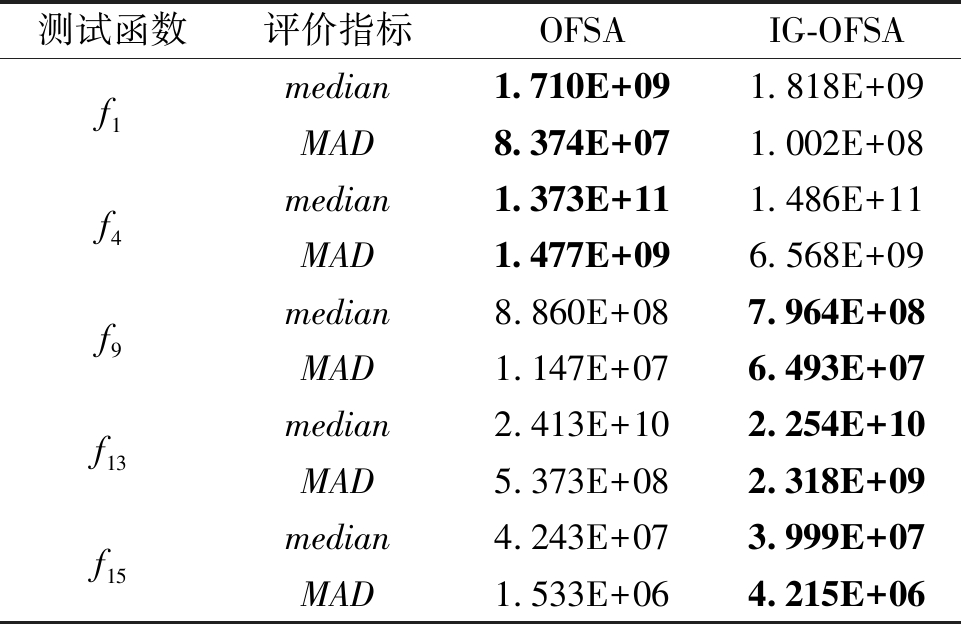
测试函数评价指标OFSAIG-OFSAf1f4f9f13f15median1.710E+091.818E+09MAD8.374E+071.002E+08median1.373E+111.486E+11MAD1.477E+096.568E+09median8.860E+087.964E+08MAD1.147E+076.493E+07median2.413E+102.254E+10MAD5.373E+082.318E+09median4.243E+073.999E+07MAD1.533E+064.215E+06
3.4 重叠特征选择技术的有效性
为了验证IG-OFSA中重叠特征选择技术的有效性,将IG-OFSA的重叠特征选择技术移除后产生一个变种算法IGA。IG-OFSA中的奇数序号子组构成IGA的全部子组,即IGA中的子组互不相交,且每一个子组独立构成一个子问题。IGA的其他设置都与IG-OFSA的设置相同。这两个算法的实验结果对比如表3所示。从表3中可以看出,IG-OFSA在5个代表函数上比IGA获得了更好的优化结果,表明重叠变量参与不同子问题的优化有助于找到更好的解。
表3 IGA与IG-OFSA的结果对比
Table 3 Comparison of results obtained by IGA and IG-OFSA
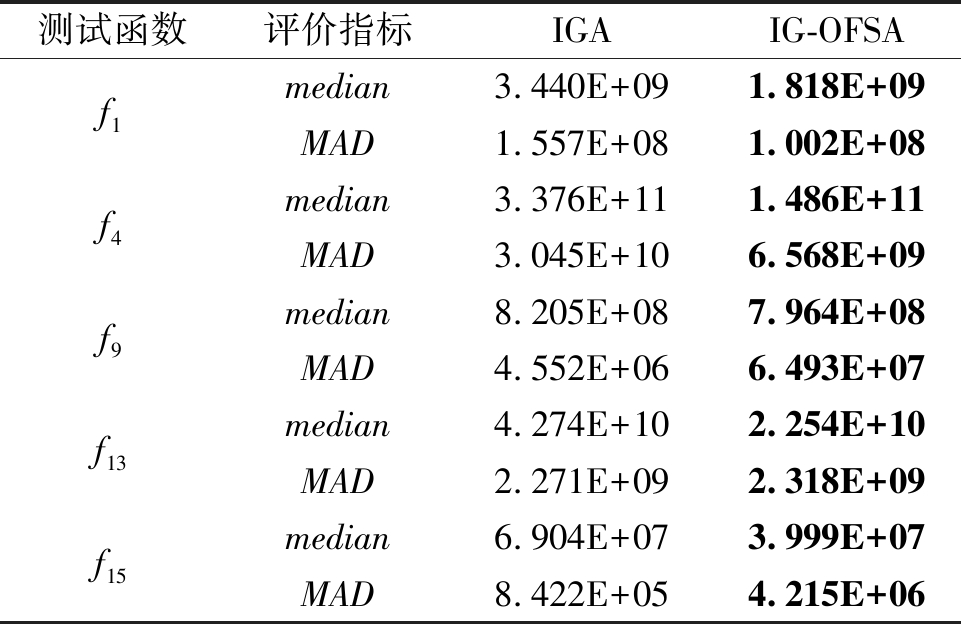
测试函数评价指标IGAIG-OFSAf1f4f9f13f15median3.440E+091.818E+09MAD1.557E+081.002E+08median3.376E+111.486E+11MAD3.045E+106.568E+09median8.205E+087.964E+08MAD4.552E+066.493E+07median4.274E+102.254E+10MAD2.271E+092.318E+09median6.904E+073.999E+07MAD8.422E+054.215E+06
3.5 2种技术的贡献程度分析
为了分析本文所提出的2种技术对提升算法性能的贡献程度,本节在CEC2013的5个代表函数上,将IGA和OFSA得到的结果与近年来求解昂贵大规模优化问题的代表算法SACC-RBFN[12]、SACC-GP[12] 、SACC-QPA[12]、SACC-SVR[12]、SAEA-RFS[13]和SEA-LEEA-RG[14]获得的结果进行了对比,实验对比结果如表4所示。从表4可以看出,IGA和OFSA在4个代表函数上相比于对比算法均获得了更好的结果,说明单一的技术改进对提升算法的性能都是有效的。同时还可以发现,OFSA在4个代表函数上能获得比IGA更好的结果,表明重叠特征选择技术对提升算法性能的贡献程度更高。
3.6 IG-OFSA与其他算法的性能对比
为了验证本文所提算法的性能,本节将其与近年来求解昂贵大规模优化问题的代表性算法(包括SACC-RBFN、SACC-GP、SACC-QPA、SACC-SVR、SAEA-RFS 和SEA-LEEA-RG)在CEC2013测试函数上进行了实验结果对比。所有算法的停止条件为满足最大目标函数评价次数11·D。所有算法在CEC2013测试函数上得到的优化结果如表5所示。使用Wilcoxon秩和检验分析所得结果是否相同,所有算法在同一测试函数上得到的最好的结果以粗体显示。
从表5中可以看出,IG-OFSA在10个CEC2013测试函数上获得的结果明显优于其他对比算法。具体地,与对比算法进行两两比较,IG-OFSA都能在多于11个测试函数上占优,尤其是在部分可分离函数、重叠函数和完全不可分离函数上更具竞争力。在函数f4、f7、f8、f9、f11、f12、f14及f15上得到的结果能够比其他对比算法低一个数量级,但是,也可以看到IG-OFSA在f1、f2及f3这3个完全可分解函数上的性能较差,这可能是在求解完全可分解函数时,重叠变量增加了子问题之间不必要的交互,反而对解的搜索产生了干扰,使得该算法在可分解函数上难以获得较好解。
表4 两种变种算法与其他算法的结果对比
Table 4 Comparison of results obtained by the two variation algorithms and other algorithms
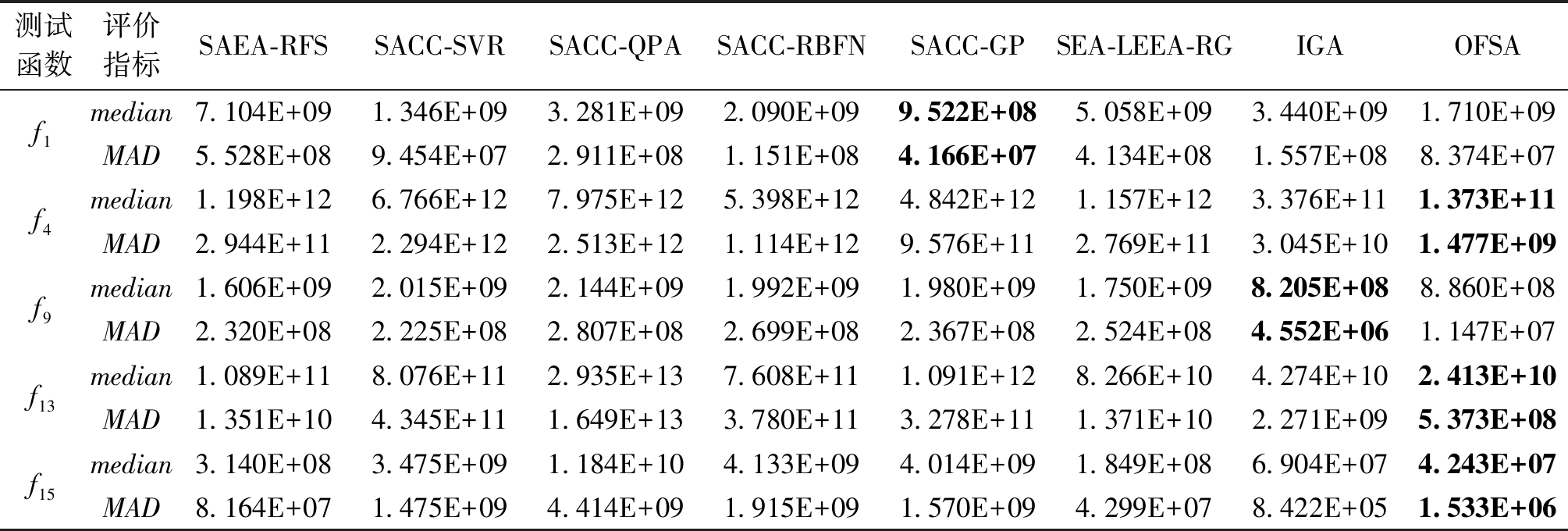
测试函数评价指标SAEA-RFSSACC-SVR SACC-QPASACC-RBFNSACC-GPSEA-LEEA-RGIGAOFSAf1f4f9f13f15median7.104E+091.346E+093.281E+092.090E+099.522E+085.058E+093.440E+091.710E+09MAD5.528E+089.454E+072.911E+081.151E+084.166E+074.134E+081.557E+088.374E+07median1.198E+126.766E+127.975E+125.398E+124.842E+121.157E+123.376E+111.373E+11MAD2.944E+112.294E+122.513E+121.114E+129.576E+112.769E+113.045E+101.477E+09median1.606E+092.015E+092.144E+091.992E+091.980E+091.750E+098.205E+088.860E+08MAD2.320E+082.225E+082.807E+082.699E+082.367E+082.524E+084.552E+061.147E+07median1.089E+118.076E+112.935E+137.608E+111.091E+128.266E+104.274E+102.413E+10MAD1.351E+104.345E+111.649E+133.780E+113.278E+111.371E+102.271E+095.373E+08median3.140E+083.475E+091.184E+104.133E+094.014E+091.849E+086.904E+074.243E+07MAD8.164E+071.475E+094.414E+091.915E+091.570E+094.299E+078.422E+051.533E+06
表5 IG-OFSA与其他算法的结果对比
Table 5 Comparison of results obtained by IG-OFSA and other algorithms
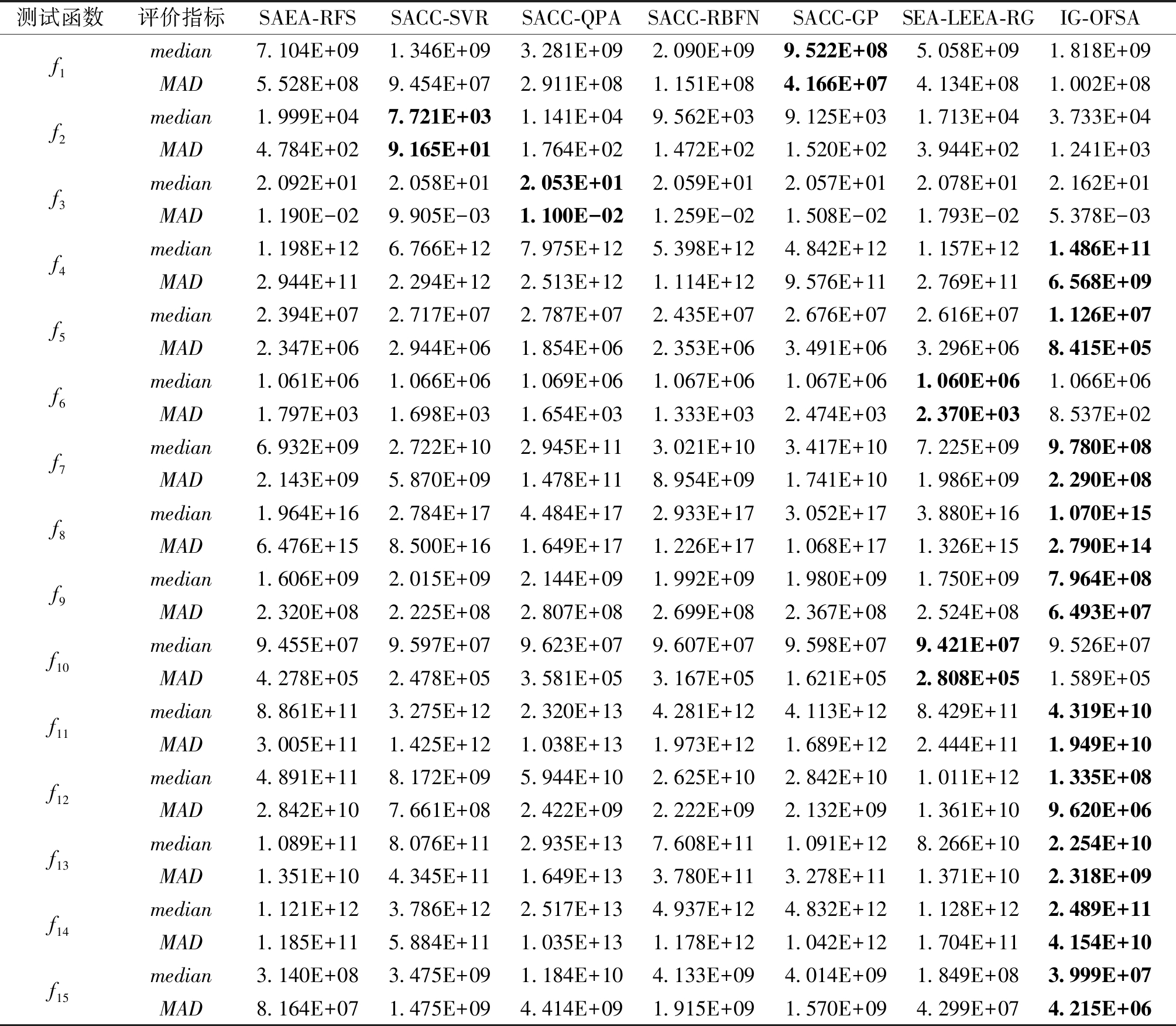
测试函数评价指标SAEA-RFSSACC-SVR SACC-QPASACC-RBFNSACC-GPSEA-LEEA-RGIG-OFSAf1f2f3f4f5f6f7f8f9f10f11f12f13f14f15median7.104E+091.346E+093.281E+092.090E+099.522E+085.058E+091.818E+09MAD5.528E+089.454E+072.911E+081.151E+084.166E+074.134E+081.002E+08median1.999E+047.721E+031.141E+049.562E+039.125E+031.713E+043.733E+04MAD4.784E+029.165E+011.764E+021.472E+021.520E+023.944E+021.241E+03median2.092E+012.058E+012.053E+012.059E+012.057E+012.078E+012.162E+01MAD1.190E-029.905E-031.100E-021.259E-021.508E-021.793E-025.378E-03median1.198E+126.766E+127.975E+125.398E+124.842E+121.157E+121.486E+11MAD2.944E+112.294E+122.513E+121.114E+129.576E+112.769E+116.568E+09median2.394E+072.717E+072.787E+072.435E+072.676E+072.616E+071.126E+07MAD2.347E+062.944E+061.854E+062.353E+063.491E+063.296E+068.415E+05median1.061E+061.066E+061.069E+061.067E+061.067E+061.060E+061.066E+06MAD1.797E+031.698E+031.654E+031.333E+032.474E+032.370E+038.537E+02median6.932E+092.722E+102.945E+113.021E+103.417E+107.225E+099.780E+08MAD2.143E+095.870E+091.478E+118.954E+091.741E+101.986E+092.290E+08median1.964E+162.784E+174.484E+172.933E+173.052E+173.880E+161.070E+15MAD6.476E+158.500E+161.649E+171.226E+171.068E+171.326E+152.790E+14median1.606E+092.015E+092.144E+091.992E+091.980E+091.750E+097.964E+08MAD2.320E+082.225E+082.807E+082.699E+082.367E+082.524E+086.493E+07median9.455E+079.597E+079.623E+079.607E+079.598E+079.421E+079.526E+07MAD4.278E+052.478E+053.581E+053.167E+051.621E+052.808E+051.589E+05median8.861E+113.275E+122.320E+134.281E+124.113E+128.429E+114.319E+10MAD3.005E+111.425E+121.038E+131.973E+121.689E+122.444E+111.949E+10median4.891E+118.172E+095.944E+102.625E+102.842E+101.011E+121.335E+08MAD2.842E+107.661E+082.422E+092.222E+092.132E+091.361E+109.620E+06median1.089E+118.076E+112.935E+137.608E+111.091E+128.266E+102.254E+10MAD1.351E+104.345E+111.649E+133.780E+113.278E+111.371E+102.318E+09median1.121E+123.786E+122.517E+134.937E+124.832E+121.128E+122.489E+11MAD1.185E+115.884E+111.035E+131.178E+121.042E+121.704E+114.154E+10median3.140E+083.475E+091.184E+104.133E+094.014E+091.849E+083.999E+07MAD8.164E+071.475E+094.414E+091.915E+091.570E+094.299E+074.215E+06
4 结论
本文提出了IG-OFSA用于求解昂贵大规模问题。该算法采用的惯性分组技术能够平衡探索分组方案多样性的能力和对具体分组方案的开发能力,而重叠特征选择技术通过重叠变量,增加了相关变量被划分到同一子问题的概率,加强了子问题之间的合作能力,从而有助于算法对全局最优解的搜索。在CEC2013标准函数上的实验结果表明:IG-OFSA在求解昂贵大规模优化问题时,尤其是在部分可分离函数、重叠函数和完全不可分离函数上能获得更好解。
对于不同类型的昂贵大规模优化问题,最优的子问题的个数T、最优的惯性系数I可能是不同的,因此,今后将考虑根据种群的状态自适应定义参数T和I,以期更好地提升搜索性能。
[1] CHAI T Y, JIN Y C, SENDHOFF B. Evolutionary co-mplex engineering optimization: opportunities and chal-lenges[J]. IEEE Computational Intelligence Magazine,2013, 8(3): 12-15.
[2] CAO Y, SUN D F. A parallel computing framework for large-scale air traffic flow optimization[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(4): 1855-1864.
[3] SIMONYAN K, ZISSERMAN A. Very deep convoluti-onal networks for large-scale image recognition[EB/OL].(2014-09-04)[2023-01-09]. https:∥doi.org/10.48550/1409.1556.
[4] 梁静, 刘睿, 瞿博阳, 等. 进化算法在大规模优化问题中的应用综述[J]. 郑州大学学报(工学版), 2018, 39(3): 15-21.
LIANG J, LIU R, QU B, et al. A survey of evolutio-nary algorithms for large scale optimization problem[J]. Journal of Zhengzhou University (Engineering Scienc-e), 2018, 39(3): 15-21.
[5] 孙迈, 孙超利. 基于随机分组集成模型的大规模昂贵问题优化算法[C]∥第32届中国过程控制会议(CPCC2021) 论文集.北京:中国自动化学会,2021.
SUN M, SUN C L, Large-scale expensive problem optimization algorithm based on stochastic grouping integration model[C]∥Collection of Papers from the 32nd China Process Control Conference (CPCC2021). Beijing: Chinese Association Automation, 2021.
[6] YANG Z Y, TANG K, YAO X. Large scale evolution-ary optimization using cooperative coevolution[J]. Info-rmation Sciences, 2008, 178(15): 2985-2999.
[7] DONG W S, CHEN T S, ![]() P, et al. Scaling up estimation of distribution algorithms for continuous op-timization[J]. IEEE Transactions on Evolutionary Com-putation, 2013, 17(6): 797-822.
P, et al. Scaling up estimation of distribution algorithms for continuous op-timization[J]. IEEE Transactions on Evolutionary Com-putation, 2013, 17(6): 797-822.
[8] POTTER M A, JONG K A. A cooperative coevolutio-nary approach to function optimization[M]∥Parallel Pr-oblem Solving from Nature-PPSN Ⅲ. Berlin: Springer Berlin Heidelberg, 1994: 249-257.
[9] CHENG R, JIN Y C. A competitive swarm optimizer for large scale optimization[J]. IEEE Transactions on Cybernetics, 2015, 45(2): 191-204.
[10] 田杰, 孙超利, 谭瑛, 等. 基于多点加点准则的代理模型辅助社会学习微粒群算法[J]. 控制与决策, 2020, 35(1): 131-138.
TIAN J, SUN C L, TAN Y, et al. Similarity-based multipoint infill criterion for surrogate-assisted social learning particle swarm optimization[J]. Control and Decision, 2020, 35(1): 131-138.
[11] YANG Q, CHEN W N, DA DENG J, et al. A level-based learning swarm optimizer for large-scale optimization[J]. IEEE Transactions on Evolutionary Computation, 2017, 22(4): 578-594.
[12] De FALCO I, DELLA CIOPPA A, TRUNFIO G A. Investigating surrogate-assisted cooperative coevolution for large-scale global optimization[J]. Information Sciences, 2019, 482: 1-26.
[13] FU G X, SUN C L, TAN Y, et al. A surrogate-assisted evolutionary algorithm with random feature selection for large-scale expensive problems[C]∥International Conference on Parallel Problem Solving from Nature. Cham: Springer, 2020: 125-139.
[14] SUN M, SUN C L, LI X B, et al. Surrogate ensemble assisted large-scale expensive optimization with random grouping[J]. Information Sciences, 2022, 615: 226-237.
[15] Van Den BERGH F, ENGELBRECHT A P. A cooperative approach to particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 225-239.
[16] CHEN W X, WEISE T, YANG Z Y, et al. Large-scale global optimization using cooperative coevolution with variable interaction learning[C]∥ International Conference on Parallel Problem Solving from Nature. Berlin: Springer, 2010: 300-309.
[17] OMIDVAR M N, LI X D, MEI Y, et al. Cooperative co-evolution with differential grouping for large scale optimization[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(3): 378-393.
[18] OMIDVAR M N, YANG M, MEI Y, et al. DG2: a faster and more accurate differential grouping for large-scale black-box optimization[J]. IEEE Transactions on Evolutionary Computation, 2017, 21(6): 929-942.
[19] YANG Z Y, TANG K, YAO X. Multilevel cooperative coevolution for large scale optimization[C]∥2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence). Piscataway:IEEE, 2008: 1663-1670.
[20] STORN R, PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359.
[21] KLEIJNEN J P C. Kriging metamodeling in simulation: a review[J]. European Journal of Operational Research, 2009, 192(3): 707-716.
[22] ZHAN D W, XING H L. A fast Kriging-assisted evol-utionary algorithm based on incremental learning[J]. IEEE Transactions on Evolutionary Computation, 2021, 25(5): 941-955.