大规模全局优化(large scale global optimization,LSGO)问题是指待求解问题的维数非常高,通常涉及上千个决策变量[1]的优化问题,这类问题通常非凸、非线性并且不可微,传统的优化算法例如动态规划、牛顿法、共轭梯度法等难以解决此类问题。实际生活中优化问题随处可见,针对各种优化问题研究者提出了各种方案[2-4],特别对于LSGO问题,由于其复杂性,一直是各个领域亟待突破的问题。所以针对LSGO算法的研究是非常必要的[5-6]。
目前合作型协同演化[7](cooperative co-evolution,CC)被广泛应用于求解LSGO问题。合作型协同演化基于分治思想[8],将大规模全局优化问题拆分成若干个子问题分别进行求解。基于CC思想,目前研究者提出了基于多模态优化[9-10]的合作型协同演化、基于贡献值[11]的合作型协同演化等算法。其中基于贡献值的合作型协同演化算法被证明在求解LSGO问题时具有良好的性能,如CCFR[12]、CCFR2[13]、CCFR3[14]。这类算法同样也是先将决策变量进行分组,分为若干个子问题分别进行优化。与原始合作型协同演化中选择所有亚种群进行优化不同,这类算法每次选择贡献值最大的分组进行优化。对于这类算法而言,决策变量分组的精确度会在很大程度上影响其性能,目前一些算法通过识别决策变量间的相互作用关系并将它们分配到相同的子问题中进行优化,如DG[15]、DG2[16]、RDG[17]、RDG2[18]、ERDG[19]。
根据决策变量的分组结果,一般可将优化问题分为3类:决策变量完全可分、决策变量完全不可分、决策变量部分可分。通常而言,决策变量分解越精准,优化效果就会越好。然而,研究中发现在解决大规模全局优化中决策变量完全可分或完全不可分的问题时,更精准的分组有时并不会使得算法在解决该类问题时有明显的性能提升,甚至有时候会导致算法性能的下降[19]。
为了更加有效地解决此类优化问题,本文提出了一种基于资源分配和动态分组的合作协同演化算法(cooperative co-evolution algorithm based on resource allocation and dynamic grouping,RG-CCFR3)。当待优化的问题为完全可分或者完全不可分时,采用动态分组,即每轮优化时对决策变量按不同的分组大小重新分组再进行优化。实验结果表明,相比CCFR3算法,该算法在处理决策变量完全可分或者完全不可分的问题时,可以达到更好的性能;与其他大规模全局优化算法相比,RG-CCFR3也有一定的优越性。
1 CCFR3算法的基本原理
CCFR3算法是一种基于贡献值的合作型协同演化算法,其中贡献值体现的是每个子问题在优化后对于原始问题优化的贡献程度,贡献值越大,说明该子问题在优化后对于原始问题优化的贡献越大,反之亦然。
CCFR3算法首先通过分组将整个问题分解为若干个子问题,然后再通过优化器算法分别求解子问题。2个部分的算法如下所示。
算法1 CCFR3算法。
输入:待优化问题的决策变量;
输出:本次优化找到的最优解。
Step 1 通过分组算法将决策变量进行分组,得到分组C={C1,C2,…,Cm}以及组数m;
Step 2 随机生成初始规模为N的初始种群P,评估所有个体并找到当前种群中的最优个体X;
Step 3 设置贡献度数组deltaFit,存放每组的贡献值;
Step 4 对每个组使用优化器算法进行优化,获得每个组的贡献值;
Step 5 每次选择贡献值最大的组进行优化,直到所有组的贡献度相等时结束本轮优化;
Step 6 若评估次数达到终止条件则程序结束,否则转到Step 4进行下一轮优化。
优化器算法描述的是对分解的子问题的优化,当优化满足停止条件时,将返回此次优化后该组的贡献值。
算法2 优化器算法。
输入:种群P、本次优化的决策变量,优化前的最优个体X;
输出:该组的贡献值。
Step 1 根据种群和本次优化的决策变量进行优化,更新全局最优解并得到优化后种群中的最优个体X1;
Step 2 比较优化前的最优个体X和优化后种群最优个体X1。根据优化前后种群中最佳个体最优值的改进情况,判断是否满足提前终止条件;
Step 3 若满足提前终止条件,程序提前终止并输出本次优化该组的贡献度;
Step 4 若评估次数达到终止条件则程序结束,否则转到Step 1。
2 RG-CCFR3算法
RG-CCFR3算法相比CCFR3算法而言,特别考虑了当分组结果为完全可分或者完全不可分的情况,增加了对这种情况的特殊处理。
当分组结果为部分可分问题时,依然采用原始CCFR3算法优化此类问题。当分组结果为完全可分或者完全不可分时,每轮优化时对决策变量按不同的分组大小重新分组再进行优化。相比于CCFR3算法,主要有以下3方面的变化。
(1)设置数组和索引以确定每轮优化时重新分组的分组大小。
(2)根据分组大小将所有决策变量进行重新分组。
(3)改进原始CCFR3算法1的Step 4和Step 5中每轮优化的逻辑。
后续部分将按顺序介绍RG-CCFR3相对CCFR3算法的改进。
2.1 分组大小设置
当分组结果为完全可分或者完全不可分的情况时,设置数组gsizeset,gsizeset={ g1 , g2 , …, gn},数组中的值均为整数,数组中的值代表的是重新分组的分组大小。同时还设置数组索引indexsize,indexsize初始值为1。每轮优化时数组索引在数组中对应位置的值表示此次优化时的分组大小。每轮优化结束后,将indexsize的值加1,指向数组中下一个值。当indexsize指向数组中最后一个值时,下一轮indexsize将重新设置为1,即指向数组gsizeset第一个值。通过对indexsize的调整便可使程序在每轮优化后更换下一轮优化时确定分组大小,从而实现动态分组。图1展示了每轮优化时分组大小随着indexsize变化的过程。
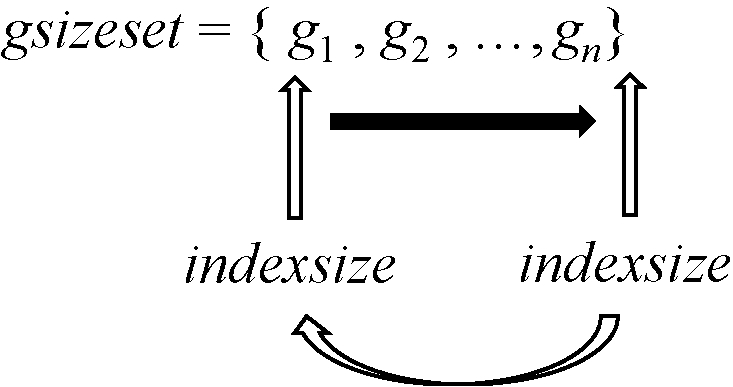
图1 分组大小的变化
Figure 1 Changes in group size
2.2 重新分组
在上一节确定了每轮优化时的分组大小,那么现在需要按确定的分组大小将决策变量进行重新分组。
重新分组时,相对于原始CCFR3而言,该算法不使用算法1中Step 1通过分组算法将决策变量分解而得到的分组C={C1,C2,…,Cm},算法将对决策变量进行重新分组。算法先将待求解问题的所有决策变量按顺序排列。然后使用MATLAB中的randperm函数得到一组决策变量的随机排列,然后按2.1节中确定的本轮优化的分组大小,依次将所有决策变量按分组大小进行重新分组,得到新的分组C′。
图2展示了对于1 000个决策变量的大规模全局优化问题,将其按分组大小为2进行重新分组的完整过程。
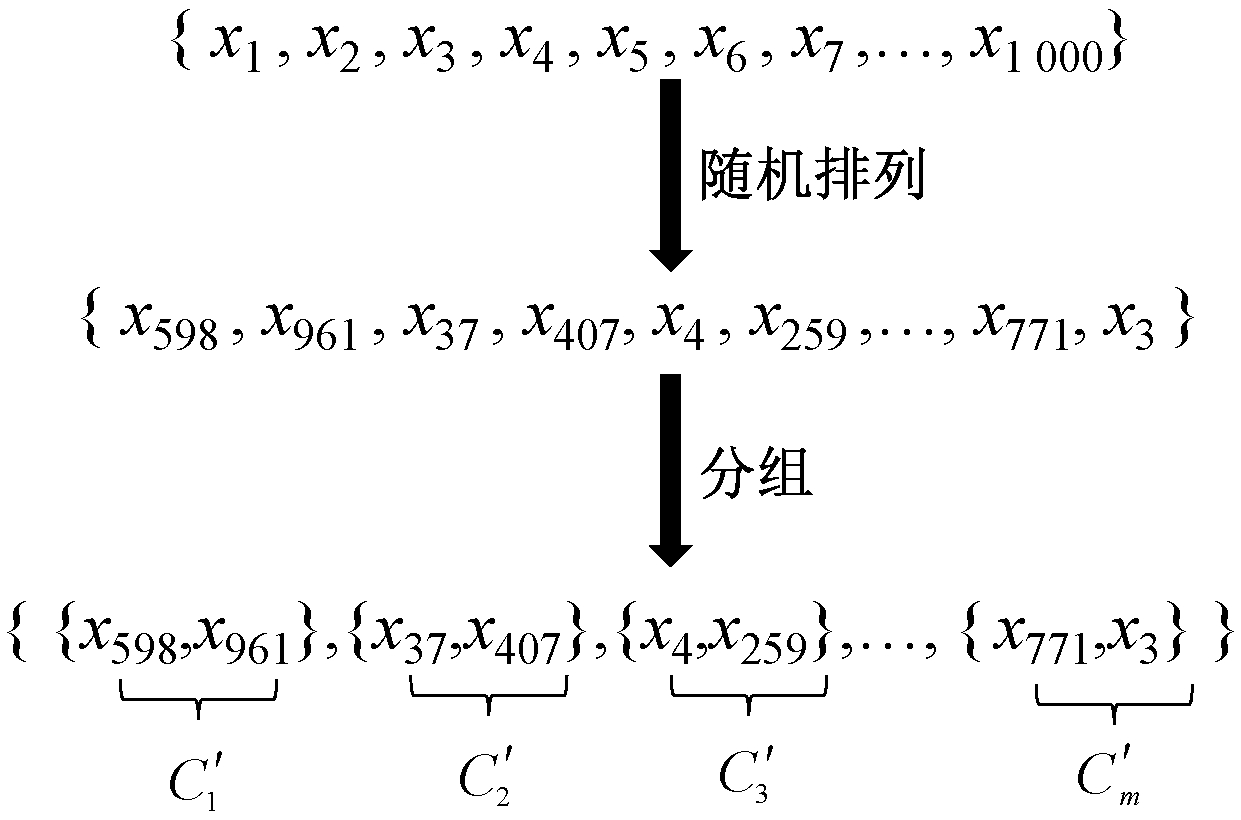
图2 重新分组的过程
Figure 2 Regrouping process
2.3 对循环次数的改进
在原始CCFR3算法1的Step 5中,除非所有组的贡献度都相等,否则会不断地对贡献值最大的组进行优化。这样不方便控制每轮优化的次数,所以为保证每轮重新分组后优化的次数一致,修改了终止条件,将每一轮的优化次数设置为![]() (⎣」为向下取整符号)。在每轮优化时,若本轮第一次优化或者所有组的贡献度都相等,则对所有组优化一遍,否则对贡献度最大的组进行优化。一轮优化结束后将索引indexsize指向数组中的下一个值并继续下一轮优化,直到程序满足终止条件结束。
(⎣」为向下取整符号)。在每轮优化时,若本轮第一次优化或者所有组的贡献度都相等,则对所有组优化一遍,否则对贡献度最大的组进行优化。一轮优化结束后将索引indexsize指向数组中的下一个值并继续下一轮优化,直到程序满足终止条件结束。
图3展示了RG-CCFR3和CCFR3每轮优化流程对比。
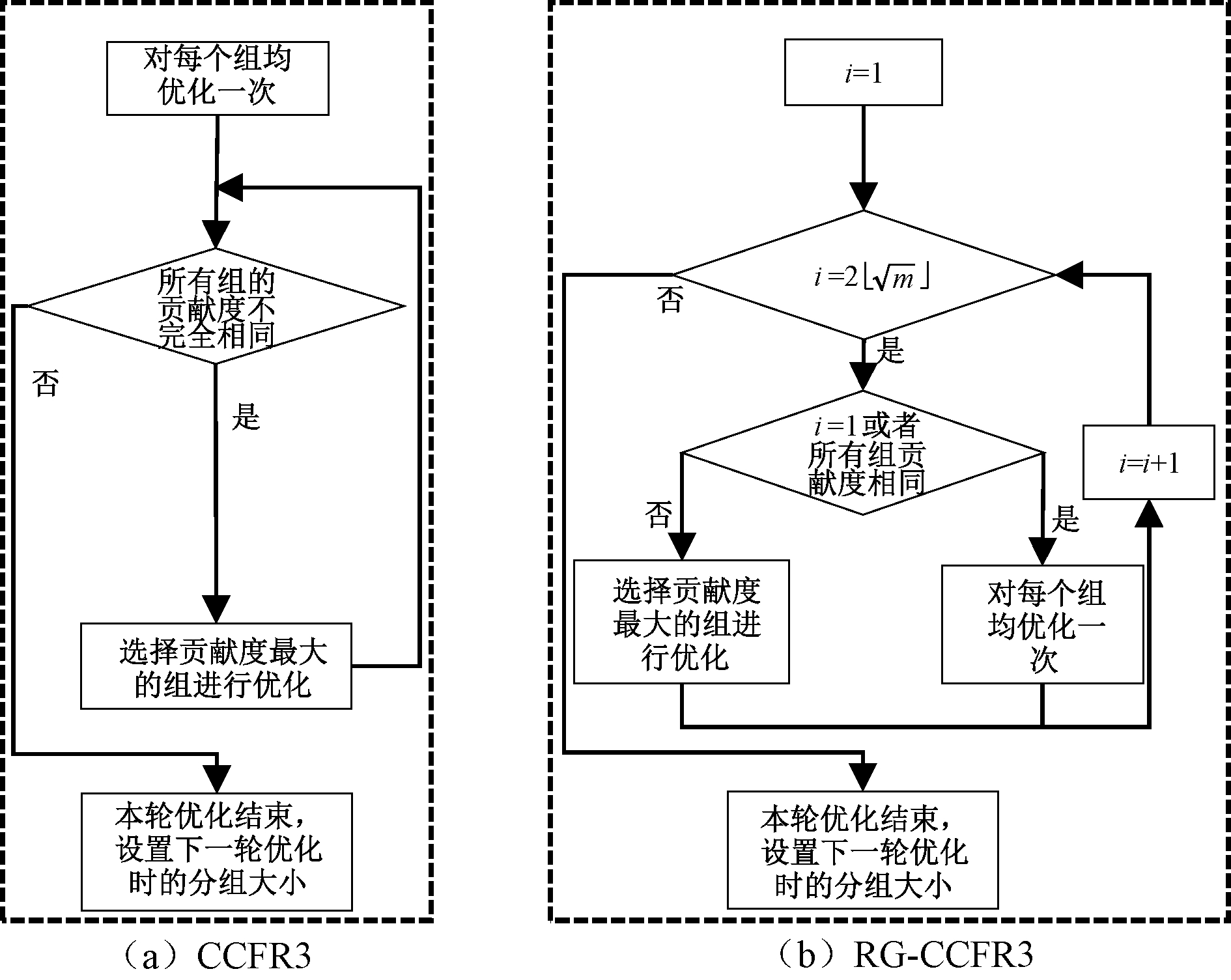
图3 CCFR3和RG-CCFR3优化流程对比
Figure 3 Comparison of CCFR3 and RG-CCFR3 optimization processes
2.4 算法描述
算法3 RG-CCFR3算法。
输入:待优化问题的决策变量;
输出:本次优化找到的最优解。
Step 1 通过分组算法将输入的所有待优化问题的决策变量进行分组,最终得到分组C={C1,C2,…,Cm}以及组数m。
Step 2 根据分组C判断当前分组结果是否为完全可分或者完全不可分问题。如果是,则设置数组gsizeset与索引indexsize,indexsize初值设为1,表示默认指向数组gsizeset中的第一个值,之后转入Step 3;否则转入算法1中的Step 2。
Step 3 随机生成初始规模为N的初始种群P,评估种群P中的所有个体并找到当前种群中的最优个体X。
Step 4 设置贡献度数组deltaFit,用于存放每组的贡献度,每一个组的初始贡献度设置为0。
Step 5 根据索引indexsize所指向数组gsizeset中的值确定当前分组大小,根据分组大小对决策变量进行重新分组,得到新分组C′并更新组数m。
Step 6 设置本轮优化次数为![]() 在本轮优化中,若此次优化为本轮第一次优化或者在deltaFit数组中所有组的贡献度都相等,则对C′中的每个组都使用优化器算法进行优化,之后更新deltaFit;否则只对deltaFit数组中贡献度最大所对应的组使用优化器算法进行优化,之后更新deltaFit。
在本轮优化中,若此次优化为本轮第一次优化或者在deltaFit数组中所有组的贡献度都相等,则对C′中的每个组都使用优化器算法进行优化,之后更新deltaFit;否则只对deltaFit数组中贡献度最大所对应的组使用优化器算法进行优化,之后更新deltaFit。
Step 7 将索引indexsize加1后的值对数组gsizeset的长度取余,再将得到的值赋值给indexsize,表示将indexsize指向下一轮优化的分组大小。
Step 8 判断当前评估次数是否达到终止条件。如果是,则输出当前的最优解并结束程序;否则转到Step 5进行下一轮优化。
3 实验条件
3.1 测试函数
本文使用CEC2013和CEC2010测试函数验证算法性能。
在CEC2013中使用ERDG对基准测试函数在决策变量为1 000维(f13,f14决策变量为905维)的情况下进行分组,用分组结果为完全可分或者完全不可分的函数来验证算法的性能,测试函数分别为f1、f2、f3、f12、f14、f15。表1展示了本文实验中所使用的CEC2013测试函数的基本信息。
在CEC2010中使用ERDG对基准测试函数在决策变量为2 000维时进行分组,用其中分组结果为完全可分或者完全不可分的函数来验证算法的性能,测试函数分别是f1、f2、f3、f19、f20。表2展示了本文实验中所使用的CEC2010测试函数的基本信息。
表1 CEC2013测试函数
Table 1 CEC2013 functions
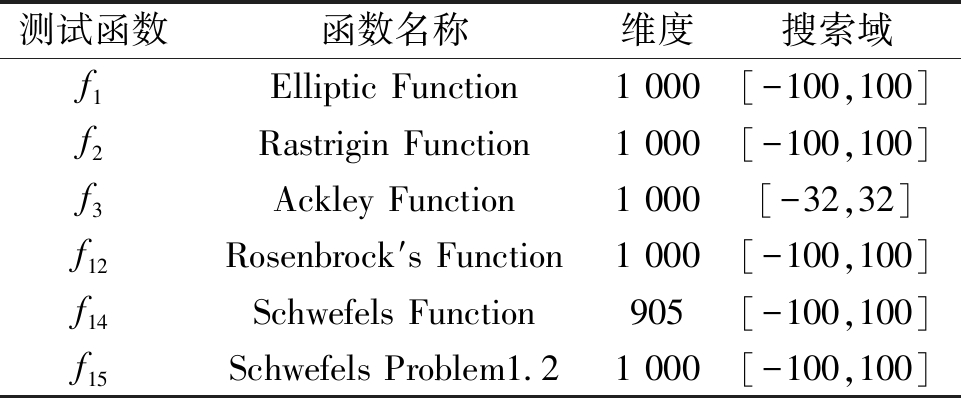
测试函数函数名称维度搜索域f1Elliptic Function1 000[-100,100]f2Rastrigin Function1 000[-100,100]f3Ackley Function1 000[-32,32]f12Rosenbrock′s Function1 000[-100,100]f14Schwefels Function905[-100,100]f15Schwefels Problem1.21 000[-100,100]
表2 CEC2010测试函数
Table 2 CEC2010 functions
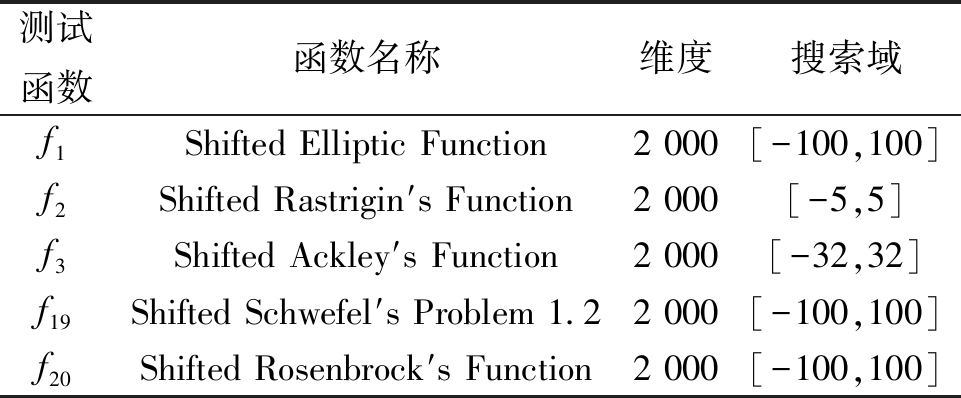
测试函数函数名称维度搜索域f1Shifted Elliptic Function2 000[-100,100]f2Shifted Rastrigin′s Function2 000[-5,5]f3Shifted Ackley′s Function2 000[-32,32]f19Shifted Schwefel′s Problem 1.22 000[-100,100]f20Shifted Rosenbrock′s Function2 000[-100,100]
本文所使用的CEC2013和CEC2010的测试函数的全局最优解均为0。
3.2 实验设置
种群规模N设置为50,每次运行最大评估次数为3×106,每个算法独立运行25次,每次运行使用不同的随机数种子对种群进行初始化,优化器选择SaNSDE[20], SaNSDE是一种基于DE[21]的进化算法。在重新分组的情况下,分组数组gsizeset={10,25,50,100}。
本文通过对比RG-CCFR3算法和CCFR3算法在测试函数独立运行25次的情况下测试函数解的最小值的平均值以及方差来评价算法的性能。由于平均值和方差并不能完全说明两者之间是否存在差异,所以本文通过对比RG-CCFR3和CCFR3算法在测试函数运行的实验数据进行显著性检验[22]来比较两者之间的差异。此外,本文还对比了各个算法在测试函数中的收敛曲线,收敛曲线可以反映算法能否高效地收敛至最优解。最后本文将RG-CCFR3算法与MMO-CC、CBCC-RDG3算法进行了比较。
3.3 实验环境
为了验证算法的性能,采用MATLAB R2021b进行编程实现该算法。实验运行环境为64位Windows10操作系统,CPU 为Intel Xeon E5,配置128 GB内存。
4 实验结果以及分析
表3展示了RG-CCFR3算法和CCFR3算法在CEC2013测试函数下独立运行25次测试函数解的平均最小值和方差。从表3可知,在6个测试函数中,对于f1、f3、f12、f15函数而言, RG-CCFR3算法的均值和方差均要比CCFR3小,说明收敛性和稳定性比较好,RG-CCFR3算法性能要优于原始CCFR3算法。特别在f1、f12这2个测试函数上,RG-CCFR3与CCFR3均值差距非常大,说明RG-CCFR3的性能要远优于CCFR3。在f2和f14测试函数上,CCFR3的性能要优于RG-CCFR3。最后对CCFR3和RG-CCFR3算法在测试函数的实验数据集上进行了显著性检验。显著性检验结果显示,有4个使用RG-CCFR3算法的函数比CCFR3显著,即f1、f3、f12、f15;有2个使用CCFR3的函数比RG-CCFR3算法显著,即f2、f14。
表3 CEC2013中每个函数独立运行25次的测试函数解的平均最小值和方差
Table 3 Average minimum value and variance of the test function solution for each function running independently 25 times in CEC2013
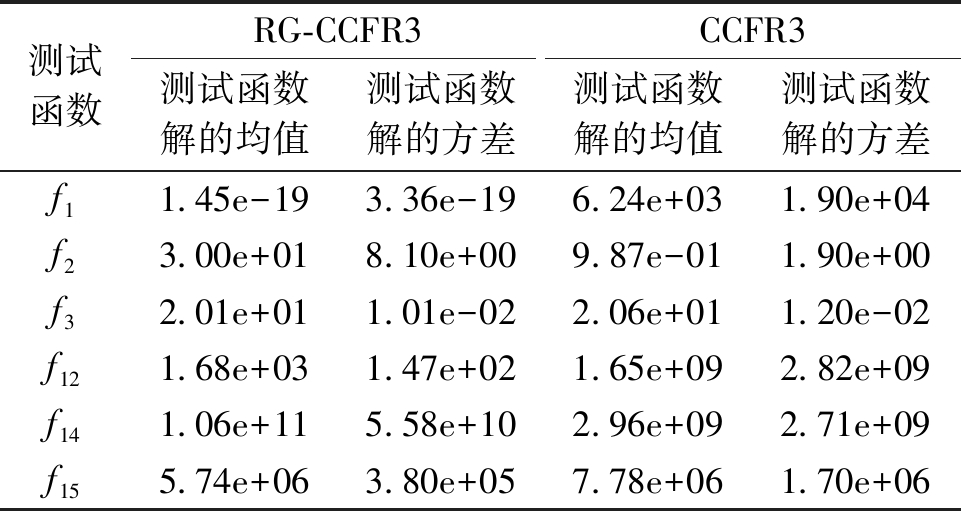
测试函数RG-CCFR3CCFR3测试函数解的均值测试函数解的方差测试函数解的均值测试函数解的方差f11.45e-193.36e-196.24e+031.90e+04f23.00e+018.10e+009.87e-011.90e+00f32.01e+011.01e-022.06e+011.20e-02f121.68e+031.47e+021.65e+092.82e+09f141.06e+115.58e+102.96e+092.71e+09f155.74e+063.80e+057.78e+061.70e+06
表4展示了RG-CCFR3算法和CCFR3算法在CEC2010测试函数决策变量为2 000的情况下独立运行25次测试函数解的平均最小值和方差。
表4 CEC2010中每个函数独立运行25次的测试函数解的平均最小值和方差
Table 4 Average minimum value and variance of the test function solution for each function running independently 25 times in CEC2010
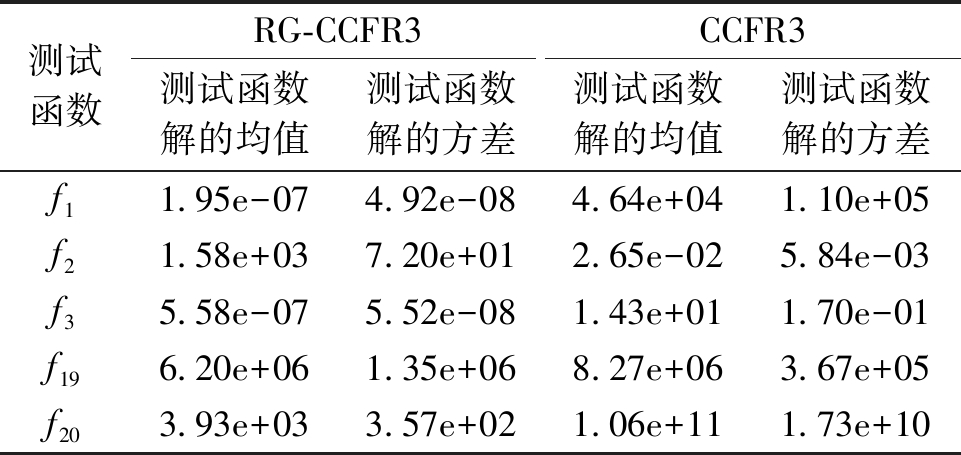
测试函数RG-CCFR3CCFR3测试函数解的均值测试函数解的方差测试函数解的均值测试函数解的方差f11.95e-074.92e-084.64e+041.10e+05f21.58e+037.20e+012.65e-025.84e-03f35.58e-075.52e-081.43e+011.70e-01f196.20e+061.35e+068.27e+063.67e+05f203.93e+033.57e+021.06e+111.73e+10
从实验结果中可以看出,对于测试函数f1、f3、f19、f20,RG-CCFR3算法性能要优于CCFR3算法,其中在f1、f3、f20函数上RG-CCFR3算法性能相比CCFR3算法有显著提升。仅在函数f2上,CCFR3的性能要优于RG-CCFR3。最后,进行了显著性检验,以比较CCFR3和RG-CCFR3算法在测试函数数据集上的表现。显著性检验结果表明在测试函数f1、f3、f19、f20上,RG-CCFR3算法要比CCFR3算法更显著。
图4展示了RG-CCFR3算法和CCFR3算法在CEC2013测试函数独立运行25次的平均最小值随着评价次数变化的情况,即平均收敛性。通过收敛性可以反映算法能否高效地收敛至最优解,它是判断算法性能好坏与否的重要指标。
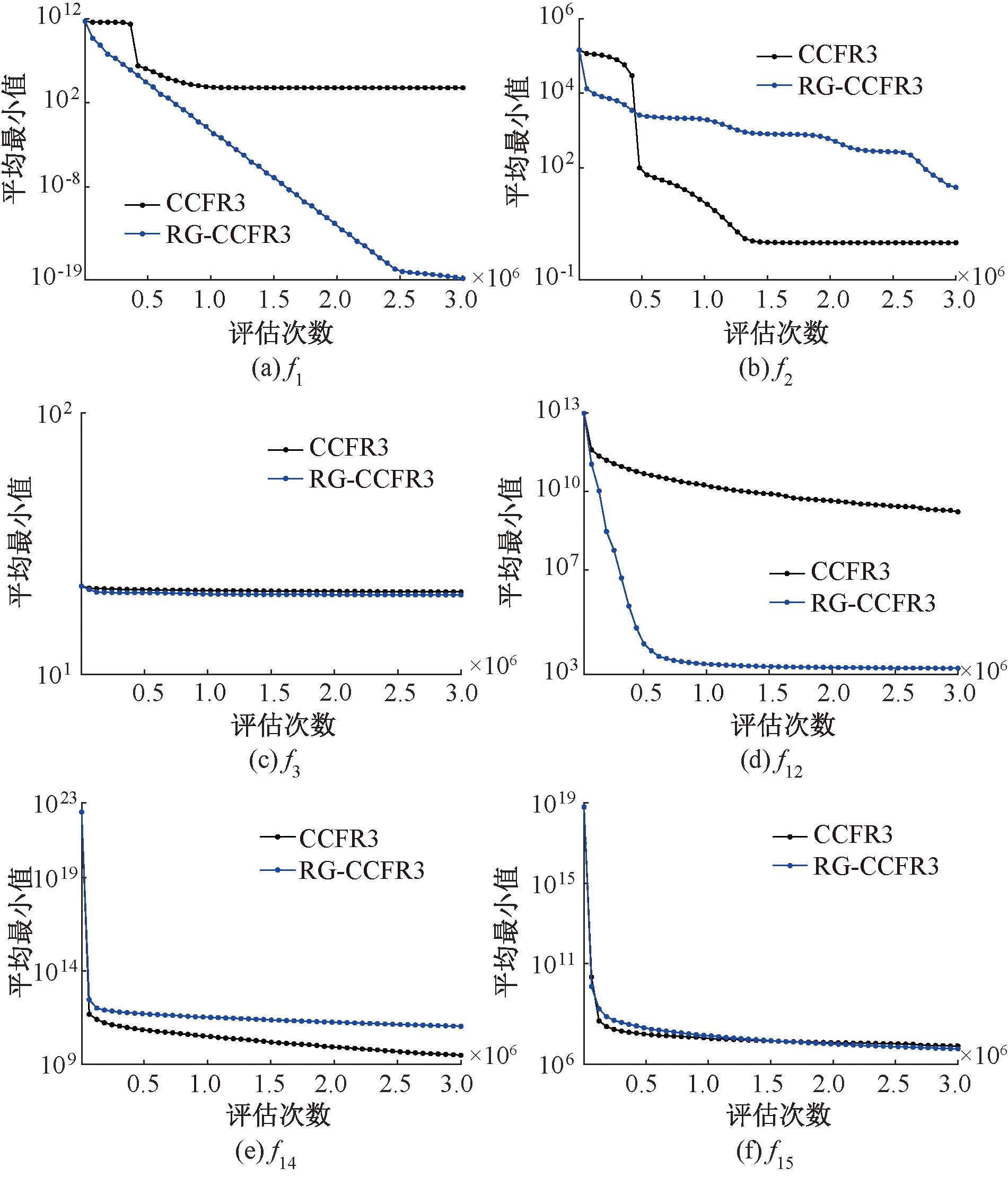
图4 CEC2013测试函数独立运行25次的平均收敛性
Figure 4 CEC2013 average convergence of 25 independent runs of each function
从图4中可以看出,对于决策变量完全可分的f1、f2、f3这3个测试函数,在函数f1和函数f3中,RG-CCFR3收敛速度整体比CCFR3快,特别在单峰函数f1上,RG-CCFR3收敛速度比CCFR3快,而且从图中很明显地可以看出CCFR3陷入了局部最优;在多峰函数f2上,CCFR3整体收敛速度比RG-CCFR3快,但是CCFR3在中后半段陷入了局部最优,而RG-CCFR3从图中看仍有下降的趋势,说明RG-CCFR3相比CCFR3而言,在处理这类问题时能有效跳出局部最优;在决策变量完全不可分测试函数f15上,前半段RG-CCFR3收敛速度比CCFR3慢,但在后半段体现出了RG-CCFR3的优势,在后半段RG-CCFR3收敛速度比CCFR3快,优化结束后的最小值也是RG-CCFR3更好;对于子部分重叠的测试函数f12、f14,其中在多峰函数f12上,RG-CCFR3收敛速度整体比CCFR3快很多,在单峰函数f14上,CCFR3收敛速度整体比RG-CCFR3快,但相对来说差距没有特别大。这表明在子部分重叠的问题上,动态分组的策略增强了全局搜索能力,但牺牲了局部搜索能力。
图5展示了RG-CCFR3和CCFR3算法在CEC2010测试函数独立运行25次的平均收敛性。从图5可以直观看到,在决策变量完全可分的f1、f2、f3这3个测试函数上,在f1和f3上RG-CCFR3收敛速度要明显比CCFR3快,并且CCFR3陷入了局部最优,而RG-CCFR3在这2个函数上的最小值始终呈现下降的趋势;对于函数f2,RG-CCFR3收敛速度不如CCFR3。在决策变量完全不可分的f19、f20这2个测试函数上,RG-CCFR3收敛速度均要比CCFR3快。在函数f19上,RG-CCFR3和CCFR3在收敛速度和最小值上比较接近;在函数f20上,RG-CCFR3收敛速度明显快于CCFR3。
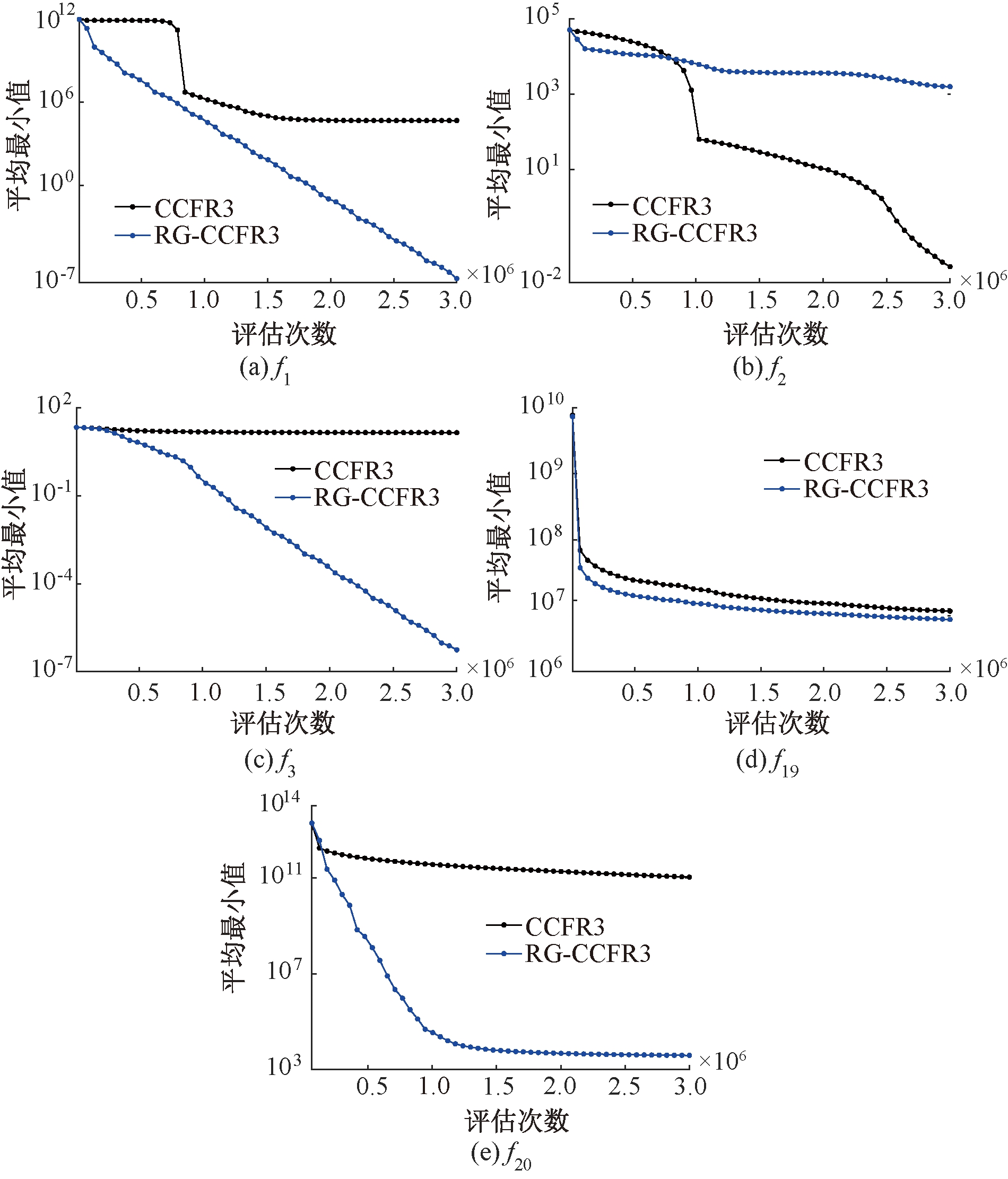
图5 CEC2010测试函数独立运行25次的平均收敛性
Figure 5 CEC2010 average convergence of 25 independent runs of each function
将RG-CCFR3与MMO-CC、CBCC-RDG3这两个解决大规模优化问题的优秀算法在CEC2013测试函数决策变量为1 000的情况下进行实验对比并进行显著性检测。MMO-CC是一种多模态优化增强的CC算法,CBCC-RDG3是CEC2019大规模全局优化竞赛的冠军算法。
表5展示了实验结果,从表5中可看出,在f2、f3函数上,RG-CCFR3算法性能是这3种算法中最好的。其中在函数f2上,RG-CCFR3算法性能要明显优于其他2个算法;在f1、f12、f15函数上,RG-CCFR3算法性能也比较接近表中对应最优算法的性能。显著性检测表明,对比MMO-CC算法,有4个使用RG-CCFR3算法的函数比MMO-CC显著,即f2、f3、f12、f15;对比CBCC-RDG3算法,有3个使用RG-CCFR3算法的函数比CBCC-RDG3显著,即f1、f2、f3。上述实验表明,对比其他大规模全局优化算法,RG-CCFR3也有一定的竞争力。
表5 RG-CCFR3与其他大规模全局优化算法的在CEC2013上的对比测试结果
Table 5 Comparison test results of RG-CCFR3 and other large-scale global optimization algorithms at CEC2013
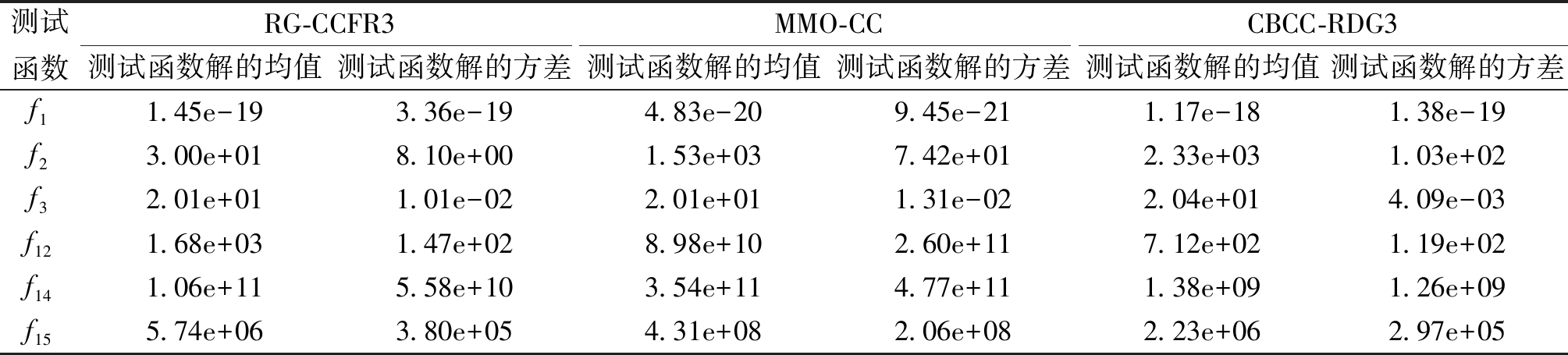
测试函数RG-CCFR3MMO-CCCBCC-RDG3测试函数解的均值测试函数解的方差测试函数解的均值测试函数解的方差测试函数解的均值测试函数解的方差f11.45e-193.36e-194.83e-209.45e-211.17e-181.38e-19f23.00e+018.10e+001.53e+037.42e+012.33e+031.03e+02f32.01e+011.01e-022.01e+011.31e-022.04e+014.09e-03f12 1.68e+031.47e+028.98e+102.60e+117.12e+021.19e+02f14 1.06e+115.58e+103.54e+114.77e+111.38e+091.26e+09f15 5.74e+063.80e+054.31e+082.06e+082.23e+062.97e+05
5 结论
为了更好地求解大规模全局优化问题中决策变量为完全可分或者完全不可分的问题,本文提出了基于资源分配和动态分组的合作协同演化算法RG-CCFR3。算法在CCFR3的基础上增加了对决策变量为完全可分或者完全不可分的问题时的处理,每轮优化时对决策变量按不同的分组大小重新分组再进行优化。本文将RG-CCFR3算法与原始CCFR3算法进行了对比实验,实验结果表明,RG-CCFR3算法在CEC2013的6个测试函数中有4个函数的性能优于CCFR3;在CEC2010的5个测试函数中有4个函数的性能优于CCFR3。这表明通过重新分组,该算法在处理决策变量完全可分或者完全不可分问题时,大多数情况下会有更好的性能。本文还将RG-CCFR3与MMO-CC、CBCC-RDG3算法进行对比,结果表明,对比这些优秀的大规模全局优化算法,RG-CCFR3也有一定的竞争力。后续的研究工作应该专注于动态分组时分组大小的确定,使得算法在处理不同完全可分或者完全不可分的大规模问题时具有更好的稳定性。
[1] BENNER P. Solving large-scale control problems[J]. IEEE Control Systems Magazine, 2004, 24(1): 44-59.
[2] LIANG J, QIAO K J, YU K J, et al. Utilizing the relationship between unconstrained and constrained Pareto fronts for constrained multiobjective optimization[J]. IEEE Transactions on Cybernetics, 2023,53(6):3873-3886.
[3] YU K J, ZHANG D Z, LIANG J, et al. A correlation-guided layered prediction approach for evolutionary dynamic multiobjective optimization[EB/OL]. (2022-07-22)[2022-11-13].https:∥ieeexplore.ieee.org/abstract/document/9837296.
[4] LIANG J, BAN X X, YU K J, et al. A survey on evolutionary constrained multiobjective optimization[J]. IEEE Transactions on Evolutionary Computation, 2022, 27(2): 201-221.
[5] 杨振宇. 基于自然计算的实值优化算法与应用研究[D]. 合肥: 中国科学技术大学, 2010.
YANG Z Y. Research on real-valued optimization algorithm based on natural computing and its application[D]. Hefei: University of Science and Technology of China, 2010.
[6] 高岳林, 杨钦文, 王晓峰, 等. 新型群体智能优化算法综述[J]. 郑州大学学报(工学版), 2022, 43(3): 21-30.
GAO Y L, YANG Q W, WANG X F, et al. Overview of new swarm intelligent optimization algorithms[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(3): 21-30.
[7] PENG X G, LIU K, JIN Y C. A dynamic optimization approach to the design of cooperative co-evolutionary algorithms[J]. Knowledge-Based Systems, 2016, 109: 174-186.
[8] YANG P, TANG K, YAO X. A parallel divide-and-conquer-based evolutionary algorithm for large-scale optimization[J]. IEEE Access, 2019, 7: 163105-163118.
[9] PENG X G, JIN Y C, WANG H D. Multimodal optimization enhanced cooperative coevolution for large-scale optimization[J]. IEEE Transactions on Cybernetics, 2019, 49(9): 3507-3520.
[10] WU Y P, PENG X G, WANG H D, et al. Cooperative coevolutionary CMA-ES with landscape-aware grouping in noisy environments[J]. IEEE Transactions on Evolutionary Computation, 2023,27(3):686-700.
[11] OMIDVAR M N, LI X D, YAO X. Smart use of computational resources based on contribution for cooperative co-evolutionary algorithms[C]∥Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation. New York: ACM, 2011: 1115-1122.
[12] YANG M, OMIDVAR M N, LI C H, et al. Efficient resource allocation in cooperative co-evolution for large-scale global optimization[J]. IEEE Transactions on Evolutionary Computation, 2017, 21(4): 493-505.
[13] YANG M, ZHOU A M, LI C H, et al. CCFR2: a more efficient cooperative co-evolutionary framework for large-scale global optimization[J]. Information Sciences, 2020, 512: 64-79.
[14] YANG M, ZHOU A M, LU X F, et al. CCFR3: a cooperative co-evolution with efficient resource allocation for large-scale global optimization[J]. Expert Systems with Applications, 2022, 203: 117397.
[15] OMIDVAR M N, LI X D, MEI Y, et al. Cooperative co-evolution with differential grouping for large scale optimization[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(3): 378-393.
[16] OMIDVAR M N, YANG M, MEI Y, et al. DG2: a faster and more accurate differential grouping for large-scale black-box optimization[J]. IEEE Transactions on Evolutionary Computation, 2017, 21(6): 929-942.
[17] SUN Y, KIRLEY M, HALGAMUGE S K. A recursive decomposition method for large scale continuous optimization[J]. IEEE Transactions on Evolutionary Computation, 2018, 22(5): 647-661.
[18] SUN Y, LI X D, ERNST A, et al. Decomposition for large-scale optimization problems with overlapping components[C]∥2019 IEEE Congress on Evolutionary Computation (CEC). Piscataway:IEEE, 2019: 326-333.
[19] YANG M, ZHOU A M, LI C H, et al. An efficient recursive differential grouping for large-scale continuous problems[J]. IEEE Transactions on Evolutionary Computation, 2021, 25(1): 159-171.
[20] YANG Z Y, TANG K, YAO X. Self-adaptive differential evolution with neighborhood search[C]∥2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence). Piscataway:IEEE, 2008: 1110-1116.
[21] YU K J, LIANG J, QU B Y, et al. Dynamic selection preference-assisted constrained multiobjective differential evolution[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(5): 2954-2965.
[22] 温忠麟, 侯杰泰, 马什赫伯特. 结构方程模型检验: 拟合指数与卡方准则[J]. 心理学报, 2004, 36(2): 186-194.
WEN Z L, HOU J T,MARSH H W. Structural equation model testing: cutoff criteria for goodness of fit indices and Chi-square test[J]. Acta Psychologica Sinica, 2004, 36(2): 186-194.