锂电池在移动储能系统中的广泛运用迫使电池管理系统性能的提升[1]。电池管理系统通过采集锂电池的参数来估计锂电池荷电状态SOC(state of charge)、温度和寿命等[2-3]。磷酸铁锂电池由于安全性高、价格便宜、能量密度高而得到了广泛应用[4]。然而,磷酸铁锂电池开路电压十分平坦,20%～80%的荷电状态变化区域都是电压平台区,且开路电压具有明显的滞回特性,荷电状态准确估计困难[5-7]。
目前,估计算法主要有安时积分法[8]、开路电压法[9]、模糊逻辑控制器法[10]、神经网络法[11]、卡尔曼滤波器[12]等。安时积分法是一种开环方法,实现简单,但受初始状态误差和电流累积误差的影响,使得SOC估计精度不高。开路电压法通过开路电压OCV(open circuit voltage)估计锂电池SOC,精度很高,但该方法不适用于电池的连续使用过程,且电池电压采样存在误差,电压采样误差足以引起SOC估计的较大误差。
基于电池模型的卡尔曼滤波器及其衍生滤波器研究最为广泛[13]。卡尔曼滤波器是一种最优自回归滤波器,不仅能消除安时积分的累积误差,还可以消除SOC初始误差,并且可以在一定程度上抑制系统噪声的影响。然而,锂电池参数随着电池温度、放电倍率、老化等因素在发生变化,采用定参数或离线方式得到的参数并不符合实际[14-15]。为此,Tran等[16]首次提出了在线辨识参数的方法,用迭代最小二乘法估计锂电池模型参数,然后用改进自适应拓展卡尔曼估计锂电池SOC,取得了不错的效果。但最小二乘法不适合辨识非线性参数。于是,提出了双重扩展卡尔曼算法估计锂电池SOC,考虑到锂电池的非线性特性,自适应无迹卡尔曼(adaptive unscented Kalman filter, AUKF)和扩展卡尔曼相结合、H∞-AUKF等算法被提出以提高SOC估计精度。
以上研究着眼于模型准确性、算法可靠性等方面,忽略了测量噪声对估计精度的影响[17]。对于磷酸铁锂电池,在电压平台区,很小的电压测量误差会引起很大的SOC估计误差[18-20]。为了精确估计电压平台区磷酸铁锂电池的SOC,提出了一种安时积分法修正的AUKF算法。首先,采用AUKF算法估计磷酸铁锂电池SOC;然后,划定电压平台区范围,在电压平台区将安时积分法的SOC估计值代入自适应算法以修正状态估计值,克服自适应算法本身的缺陷。算法有效性通过磷酸铁锂电池充放电实验得到了验证。
1 磷酸铁锂电池测试
1.1 测试平台
测试平台设置如图1所示,由磷酸铁锂电池、可编程交直流电源、控制电池温度恒定的恒温箱、控制板、用于存储电池数据的电脑等5个部分组成。
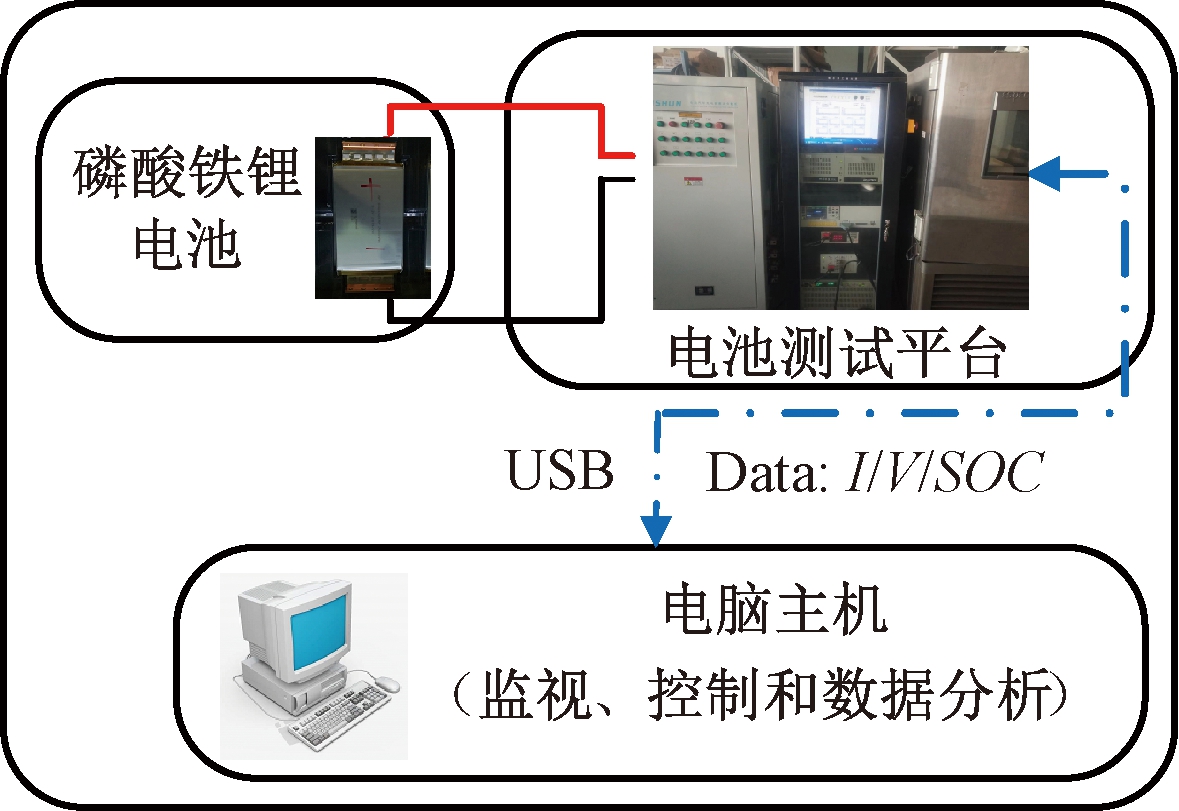
图1 电池测试平台结构
Figure 1 Platform of battery test
所有实验测试均在室温25 ℃条件下进行。实验中选用的磷酸铁锂电池型号为SDL-F8084165TP-7 000 mAh,标称电压为3.2 V;充电、放电截止电压分别为3.6、3.2 V;最大持续放电电流为350 A;最大持续充电电流为7 A;重量为235 g;工作温度为0～45 ℃。
1.2 开路电压测试
为了研究磷酸铁锂电池开路电压与荷电状态的关系,需要进行电池测试。首先是电池容量测试,容量测试采用标准测试方法。采用增量OCV测试方法测试磷酸铁锂电池SOC,如图2所示。测试结果如图3所示,由图3可知,磷酸铁锂电池充放电曲线不重合,存在电压差。
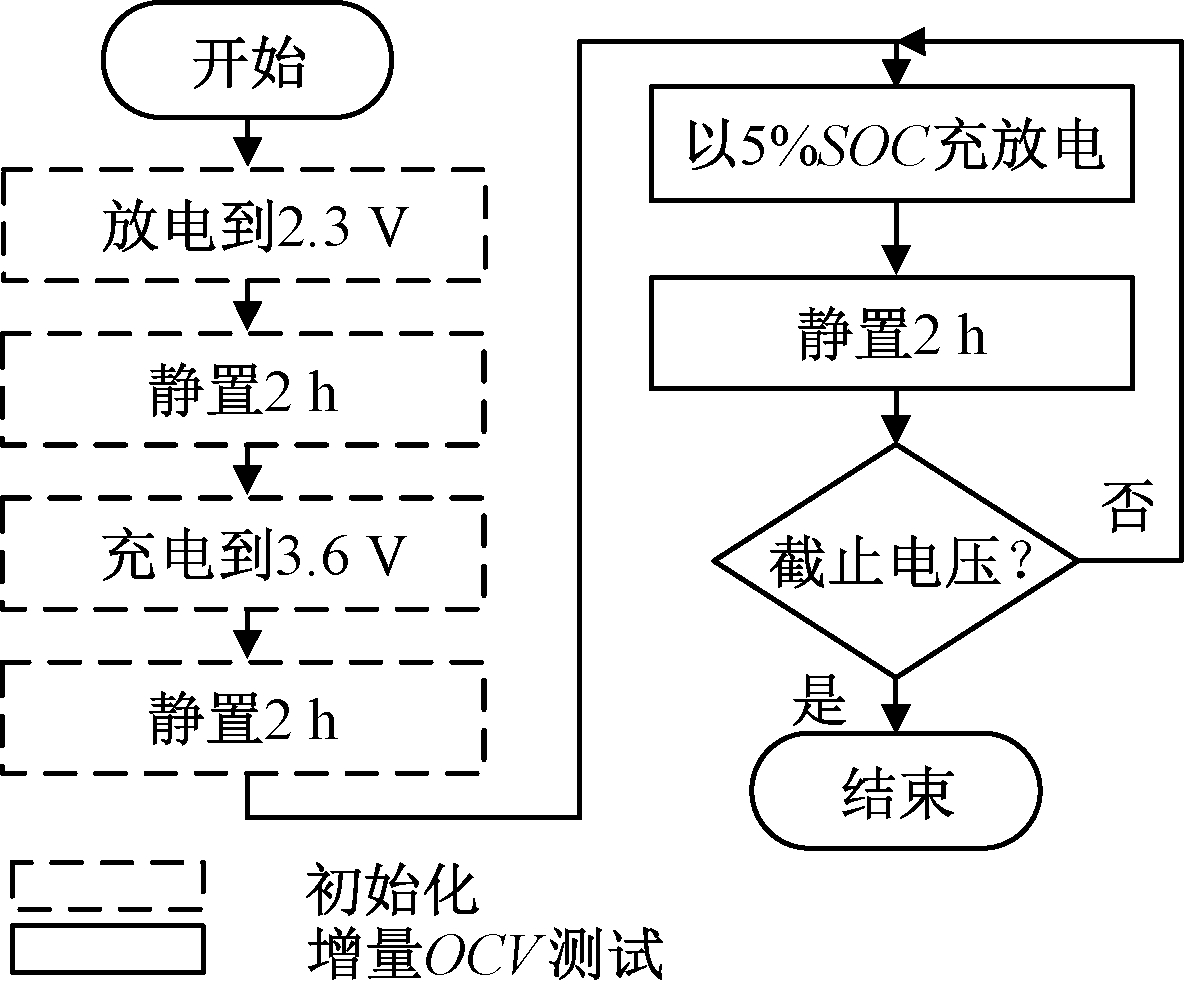
图2 增量OCV测试流程
Figure 2 Incremental OCV test process
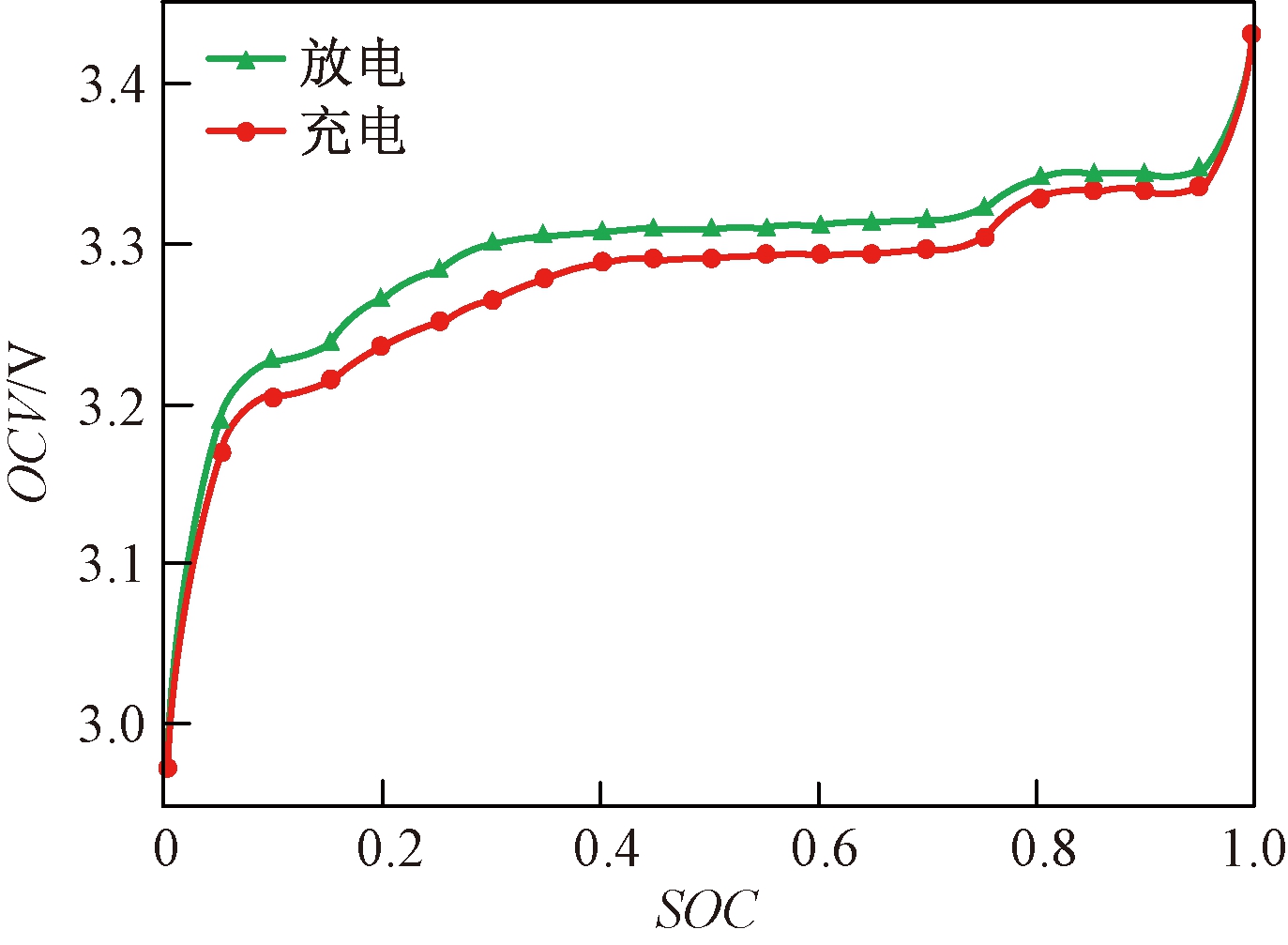
图3 磷酸铁锂电池开路电压曲线
Figure 3 OCV curve of LiFePO4 battery
2 参数化建模
2.1 磷酸铁锂电池模型
锂电池充放电时,反应极化和浓差极化的时间常数有较大差异。为了较为准确地描述磷酸铁锂电池内部反应过程,采用如图4所示的二阶RC等效电路模型。
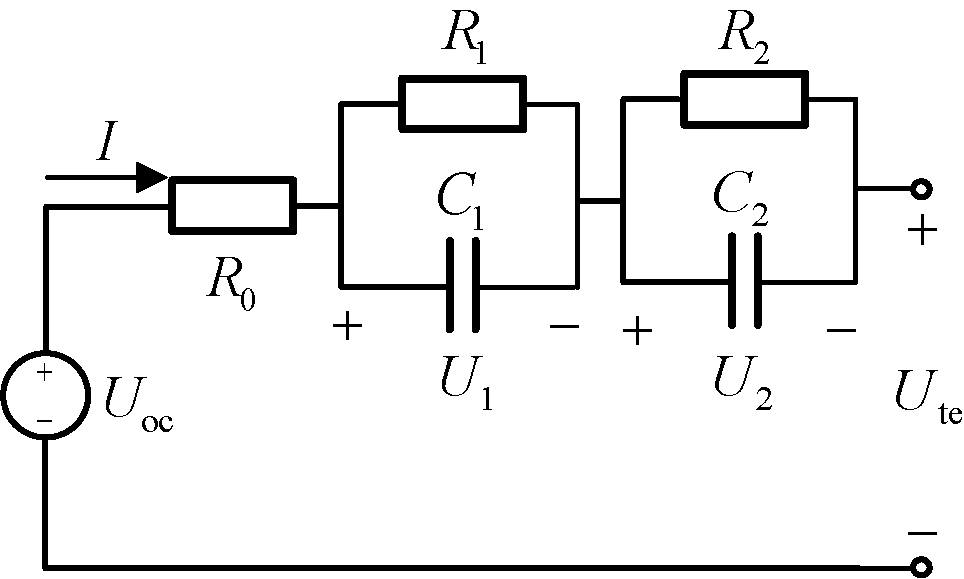
图4 二阶RC等效电路模型
Figure 4 Second order RC equivalent circuit model
图4中,R0为锂电池等效内阻;R1和R2为极化电阻;C1和C2为极化电容;以充电过程的开路电压Uoc为电池开路电压;Ute为电池端电压。Uoc与SOC的关系可表示如下:
Uoc=a0+a1SOC+a2/SOC+a3log SOC+
a4log(1-SOC)。
(1)
根据基尔霍夫定律,二阶RC等效电路输入输出关系如下:
(2)
Ute=Uoc-U1-U2-IR0。
(3)
式中:Ui为RC网络的端电压。
2.2 状态空间方程
SOC是一个相对量,是锂电池剩余容量和可用容量的比值,计算方法如下:
SOC(t)=SOC(t0)-
[ηI(τ)/Cn]dτ。
(4)
式中:SOC(t0)为初始荷电状态;I为电池电流;η为库伦效率;Cn为电池最大可用容量。
对上式进行离散化处理:
SOCk=SOCk-1-ηIk-1Δt/Cn。
(5)
式中:Δt为采样时间间隔。
集中参数等效电路的输入输出关系离散化形式如下:
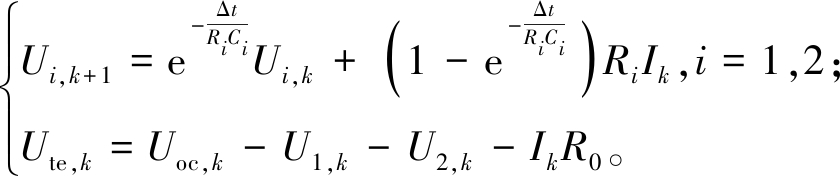
(6)
定义αi=exp(-Δt/RiCi)。一般情况下,系统状态方程可写为如下形式:
(7)
可以进一步写为
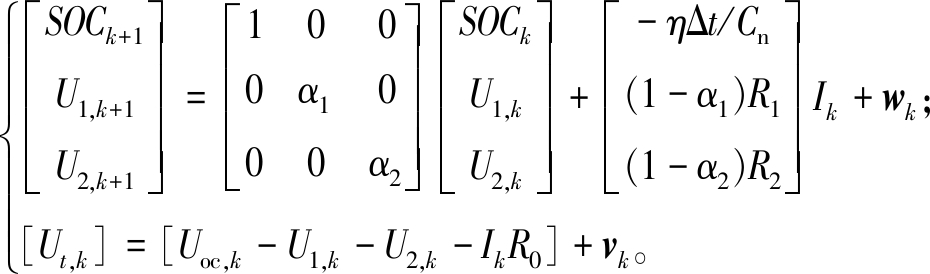
(8)
式中:xk为采样时刻为k时的状态;uk为k时刻的系统输入量;f(·)为状态转换方程;g(·)为测量方程;wk为过程噪声,满足
用来表征电流测量误差和状态方程误差;vk为测量噪声,满足
用来表征电压测量误差和输出方程误差。由对应关系可求出SOC估计算法用到的相关矩阵:
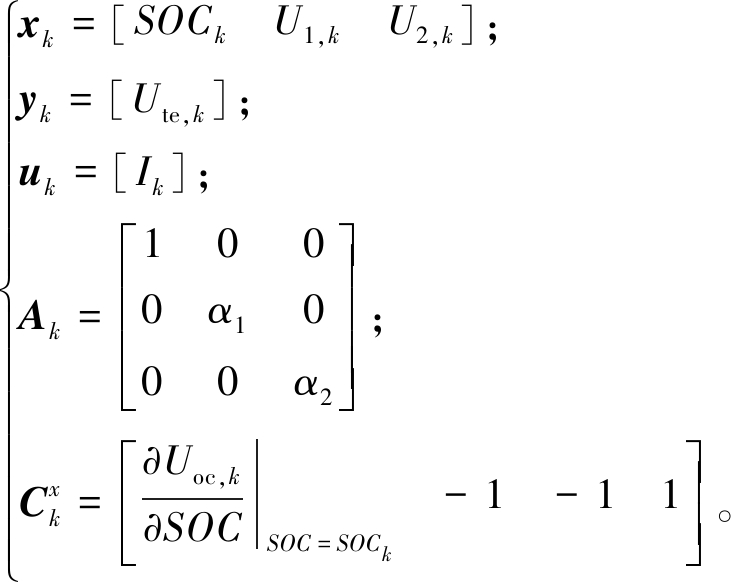
(9)
对电池输出特性进行测量,然后拟合出对应的等效电路参数,参数值列于表1。
表1 模型参数与充放电电流的关系
Table 1 Relationship between model parameters and charge-discharge current
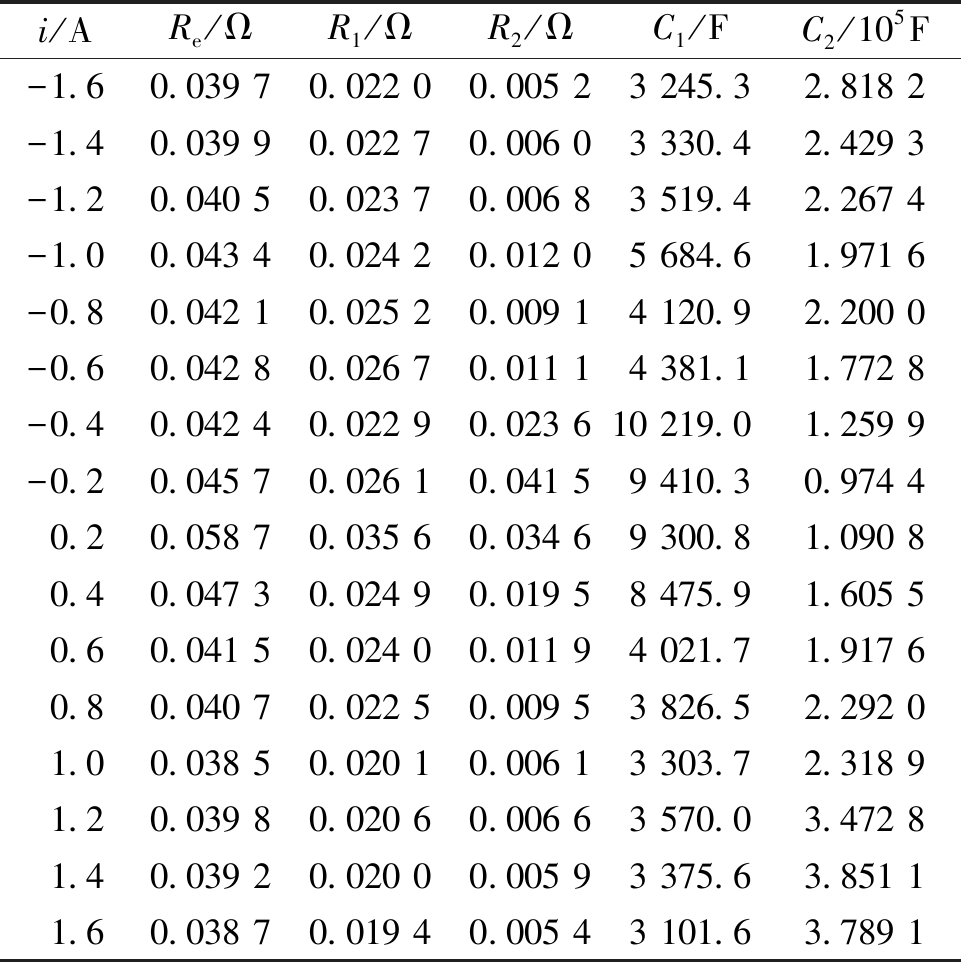
i/ARe/ΩR1/ΩR2/ΩC1/FC2/105F-1.60.039 70.022 00.005 23 245.32.818 2-1.40.039 90.022 70.006 03 330.42.429 3-1.20.040 50.023 70.006 83 519.42.267 4-1.00.043 40.024 20.012 05 684.61.971 6-0.80.042 10.025 20.009 14 120.92.200 0-0.60.042 80.026 70.011 14 381.11.772 8-0.40.042 40.022 90.023 610 219.01.259 9-0.20.045 70.026 10.041 59 410.30.974 40.20.058 70.035 60.034 69 300.81.090 80.40.047 30.024 90.019 58 475.91.605 50.60.041 50.024 00.011 94 021.71.917 60.80.040 70.022 50.009 53 826.52.292 01.00.038 50.020 10.006 13 303.72.318 91.20.039 80.020 60.006 63 570.03.472 81.40.039 20.020 00.005 93 375.63.851 11.60.038 70.019 40.005 43 101.63.789 1
2.3 状态估计算法
基于AUKF的状态估计算法流程如下。
步骤1 初始化。状态x0、后验误差协方差P0、过程噪声协方差w0、测量噪声协方差v0,窗口尺寸拟合协方差初始化。
步骤2 产生k-1步的Sigma点。
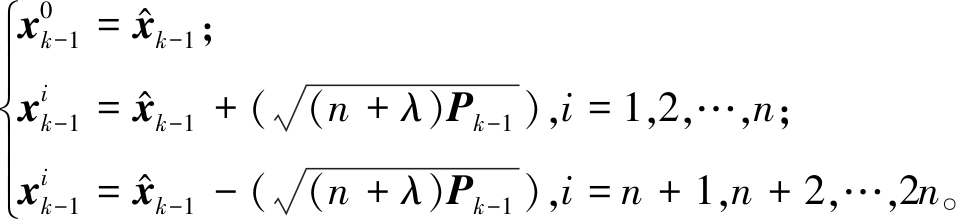
(10)
式中:
和
为k-1时间步产生的Sigma点;
为状态预测值;Pk-1为后验误差协方差;n为状态维数;λ=(n+κ)α2-n为尺度因子;α和κ的值决定Sigma点在均值点周围的扩散。
步骤3 第k步的状态和后验误差协方差预测。基于状态空间模型,可以预测每个Sigma点的状态变量。加上它们的权重,即可预测第k步的状态和后验误差协方差:
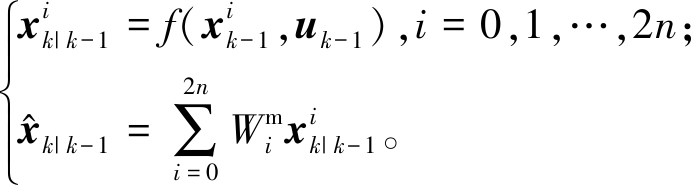
(11)
wk-1。
(12)
式中:uk-1为系统输入;Pk|k-1为先验误差协方差矩阵;Wm和Wc分别为均值和误差协方差的权重因子。
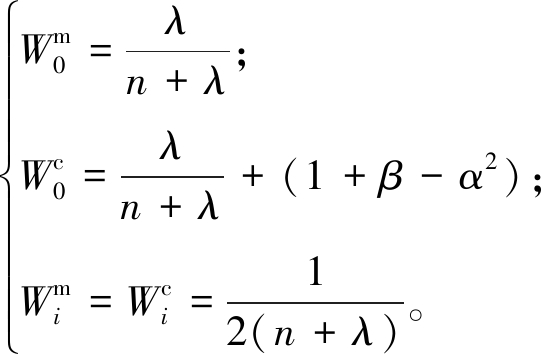
(13)
β与状态变量分布有关,当状态变量为高斯分布时,其值为2。
步骤4 预测值计算。模型输出可通过Sigma点加权求和得到:
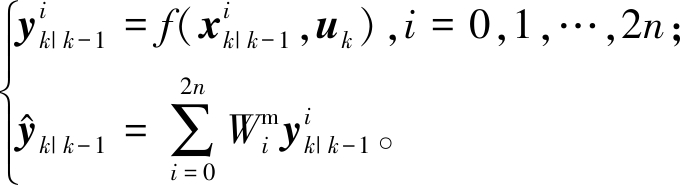
(14)
步骤5 状态更新。
(15)
(16)
(17)
式中:Pxy,k为输出量和状态量之间的交叉协方差,Pyy,k为预测输出的协方差。
步骤6 状态和后验误差协方差更新:
(18)
(19)
步骤7 噪声协方差矩阵。噪声协方差的调整是基于卡尔曼增益Gk,预测和更新的输出测量值之间的差异和窗口大小Lw。
(20)
(21)
(22)
(23)
2.4 修正算法
由式(4)可知,安时积分法计算SOC时,估计误差与初始误差和电流累积误差有关。而自适应算法的闭环设计能够有效消除安时积分法的累积误差,对于电压测量误差则没有很好的抑制作用[15]。由此可结合2种算法的优势。
(24)
式中:ΔSAh,k、ΔSAUKF,k分别为安时积分法和AUKF算法的时变增量。
修正算法最重要的一步是确定2种算法在每一个时间步内的增量可靠性。根据安时积分法和AUKF算法的SOC增量特性,安时积分法的增量比较稳定,虽然未必会比AUKF算法的估计结果可靠。因此,可以利用SOC增量特性,确定更可靠的增量值。对于某一特定的电流传感器,取其电流测量误差最大情况下的安时积分SOC估计增量作为比较的上、下限值,与AUKF算法的增量进行比较。将电流传感器的最大误差率设为λ(0<λ<1),则修正结果可表示为
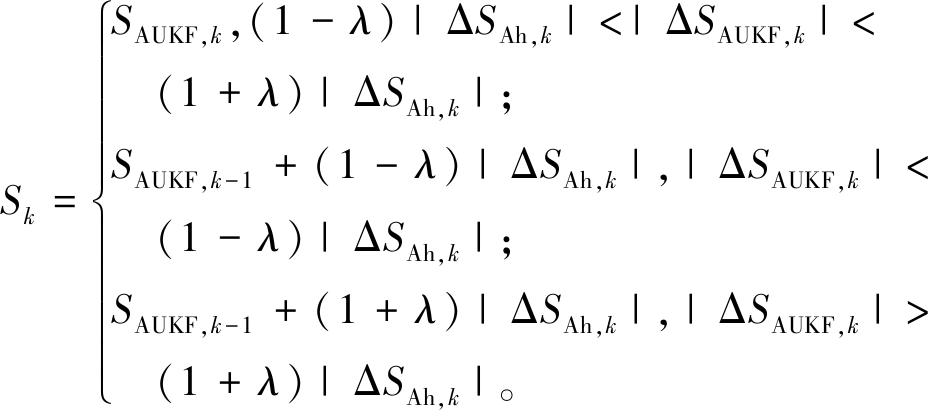
(25)
3 实验
以充电开路电压曲线作为电池的标准OCV曲线,在室温25 ℃的环境下采用恒流工况和混合脉冲功率特性测试(hybrid pulse power characteristic, HPPC)工况对磷酸铁锂电池进行测试,如图5所示。利用AUKF算法估计磷酸铁锂电池SOC,结果如图6所示。
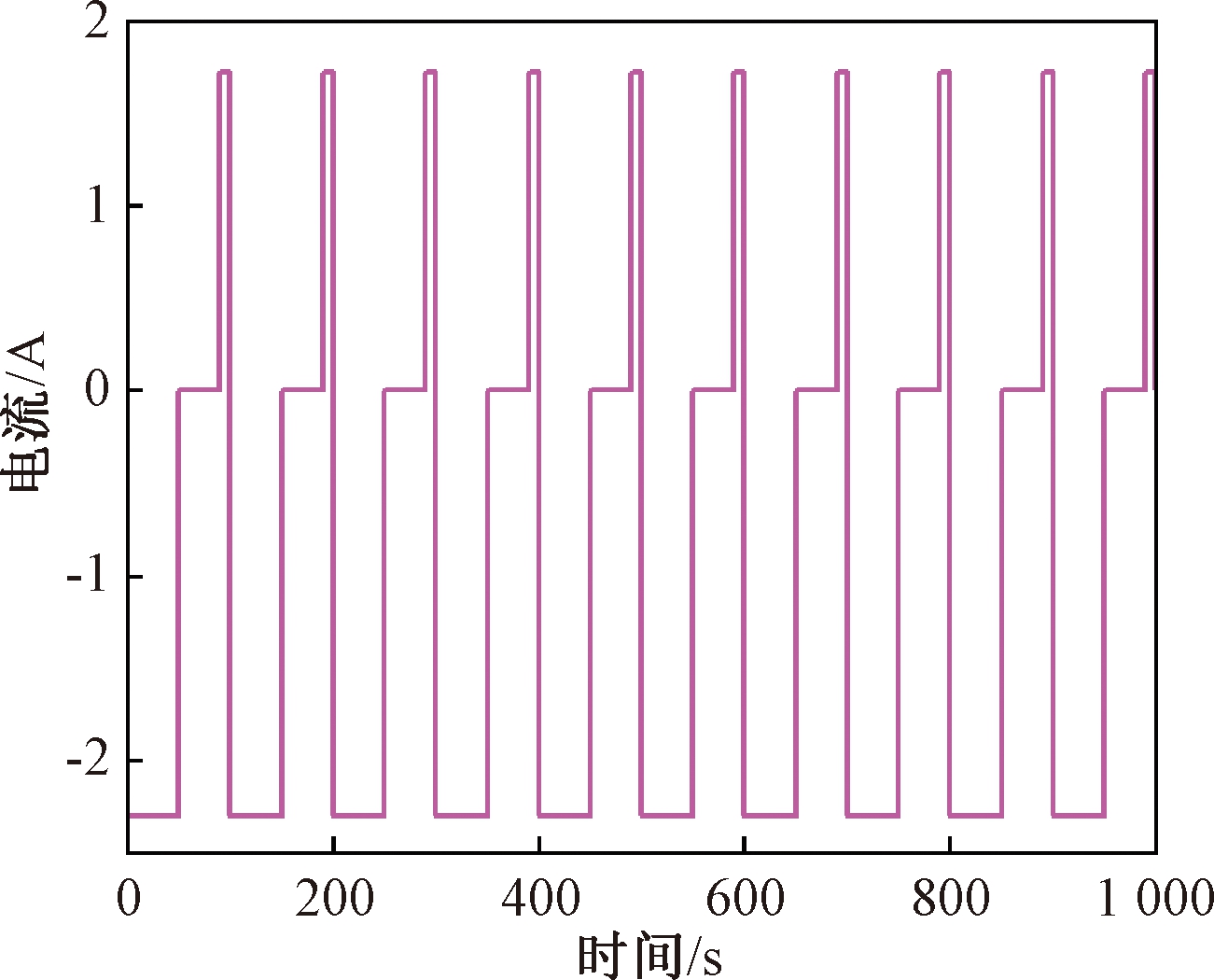
图5 HPPC工况电流波形
Figure 5 Current waveform of HPPC
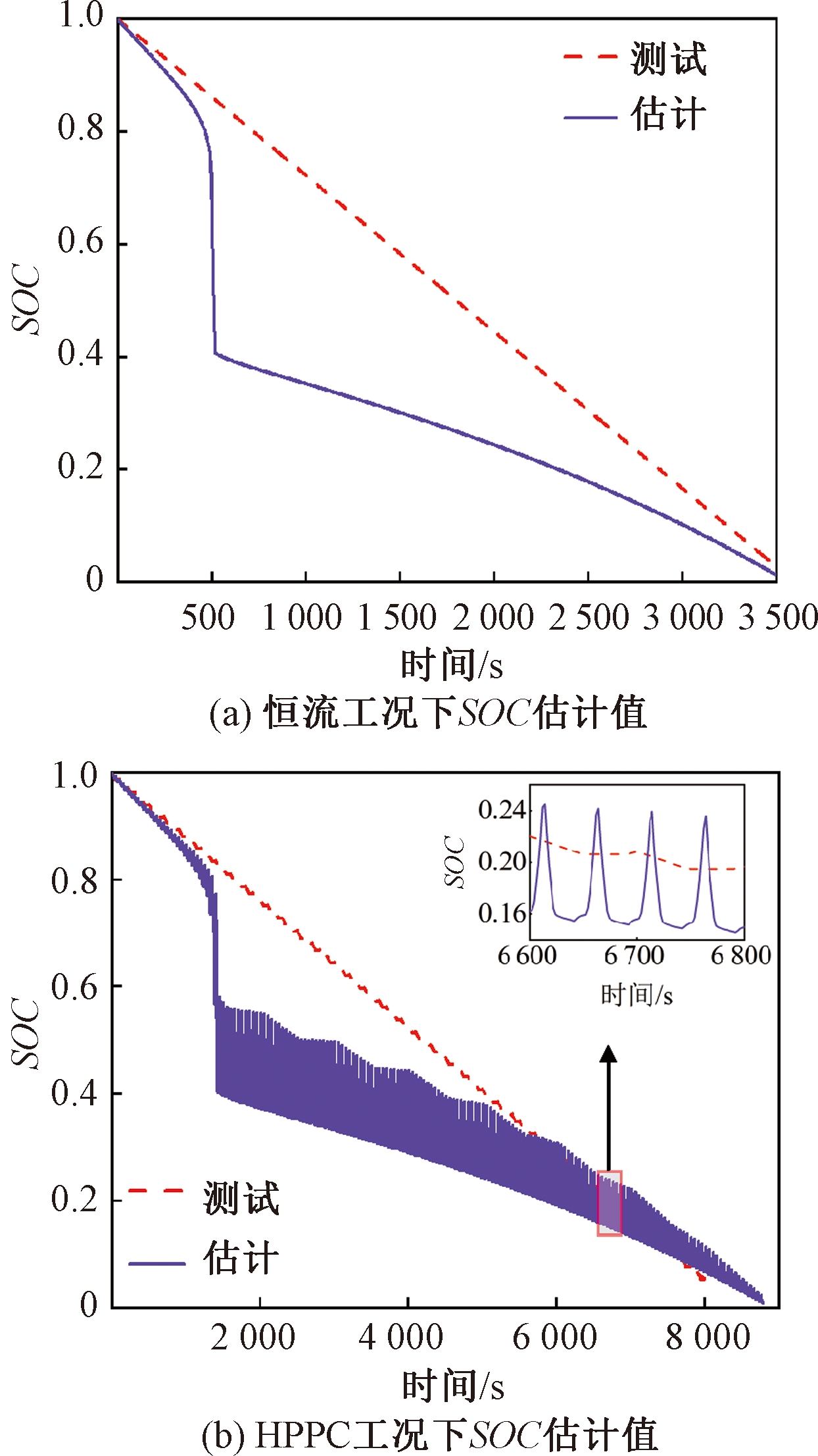
图6 不同工况下SOC估计值
Figure 6 SOC estimation in different conditions
从图6中可以看出,在放电开始和结尾阶段,算法能较为准确地估计SOC,而在中间很大范围内,SOC估计值偏离真值严重,主要原因是磷酸铁锂电池存在滞回电压。由图5、6可知,虽然电流工况不同,但SOC跃变区间是一样的,这是因为电流不影响滞回电压。变电流工况中电压变化更复杂,导致SOC估计结果波动严重。
由以上分析可知,当采用充电开路电压来计算SOC时,放电过程OCV可以理解为与开路OCV存在误差,误差即为OCV差值。而且在实际估计磷酸铁锂电池SOC的过程中,电压采样芯片也存在采样误差,常用的采样芯片采样误差为5～50 mV。因此选择特定的电压误差5、10、20和50 mV研究电压测量误差的影响,结果如图7所示。由图7可知,随着电压测量误差的增大,SOC估计结果在中间阶段误差也逐步增大。
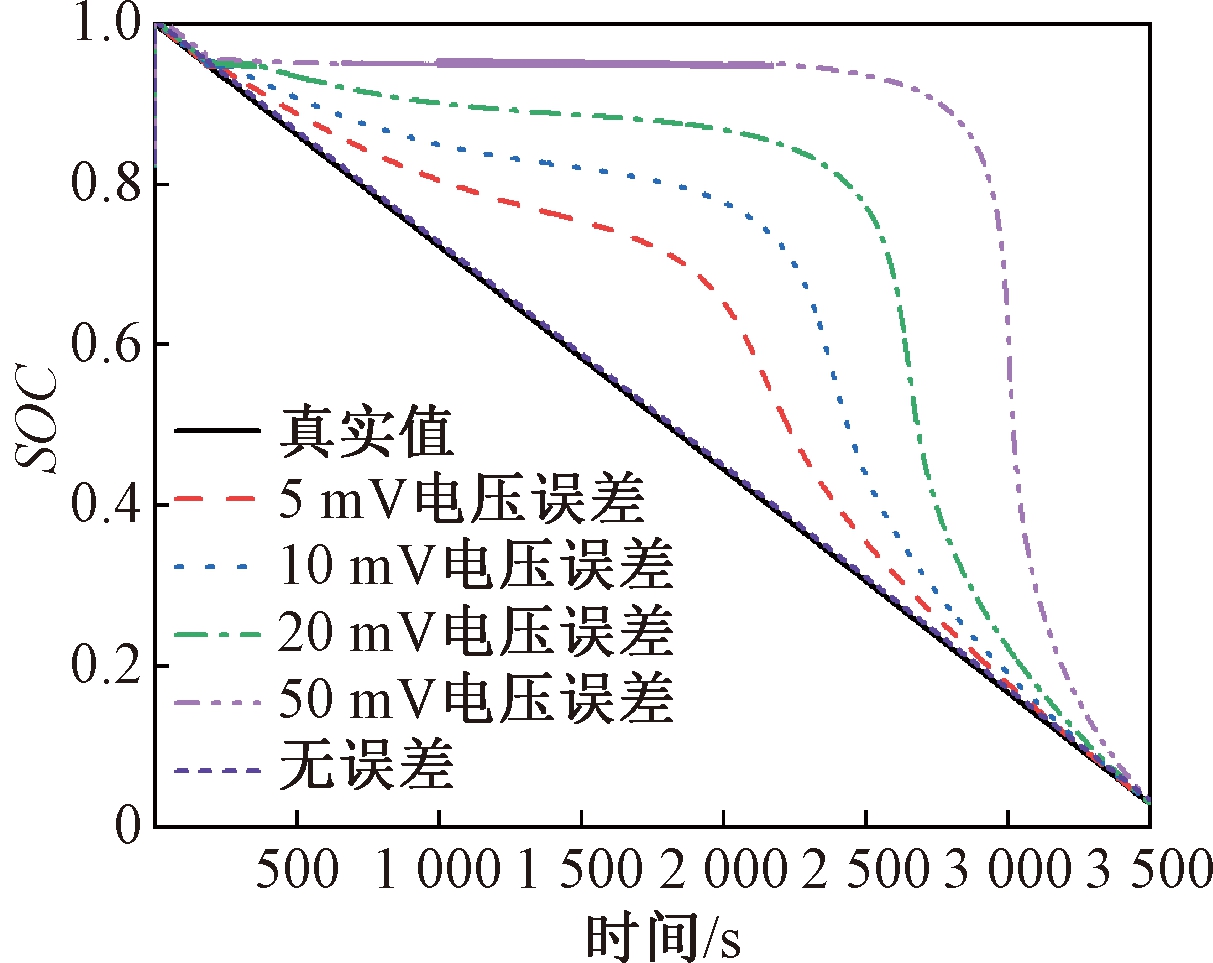
图7 不同电压测试误差下的SOC估计值
Figure 7 SOC estimation in different voltage test errors
电流测量误差也对SOC估计精度有一定影响,实验所用的电流霍尔传感器精度为1%,实验中电流倍率最大为5C(C为放电倍率),其中图8(a)为假设最大采样误差为45 mA时,电压测量误差叠加电流测量误差后的锂电池SOC估计结果;图8(b)为假设电流为幅值为40 mA、周期为1 s的正弦波叠加电压测量误差下的SOC估计结果。由图8可知,最大电流误差作用下的SOC估计值与仅有电压测量误差的SOC估计值差别不大,所以相较于电压测量误差,电流测量误差造成的SOC估计误差很小。
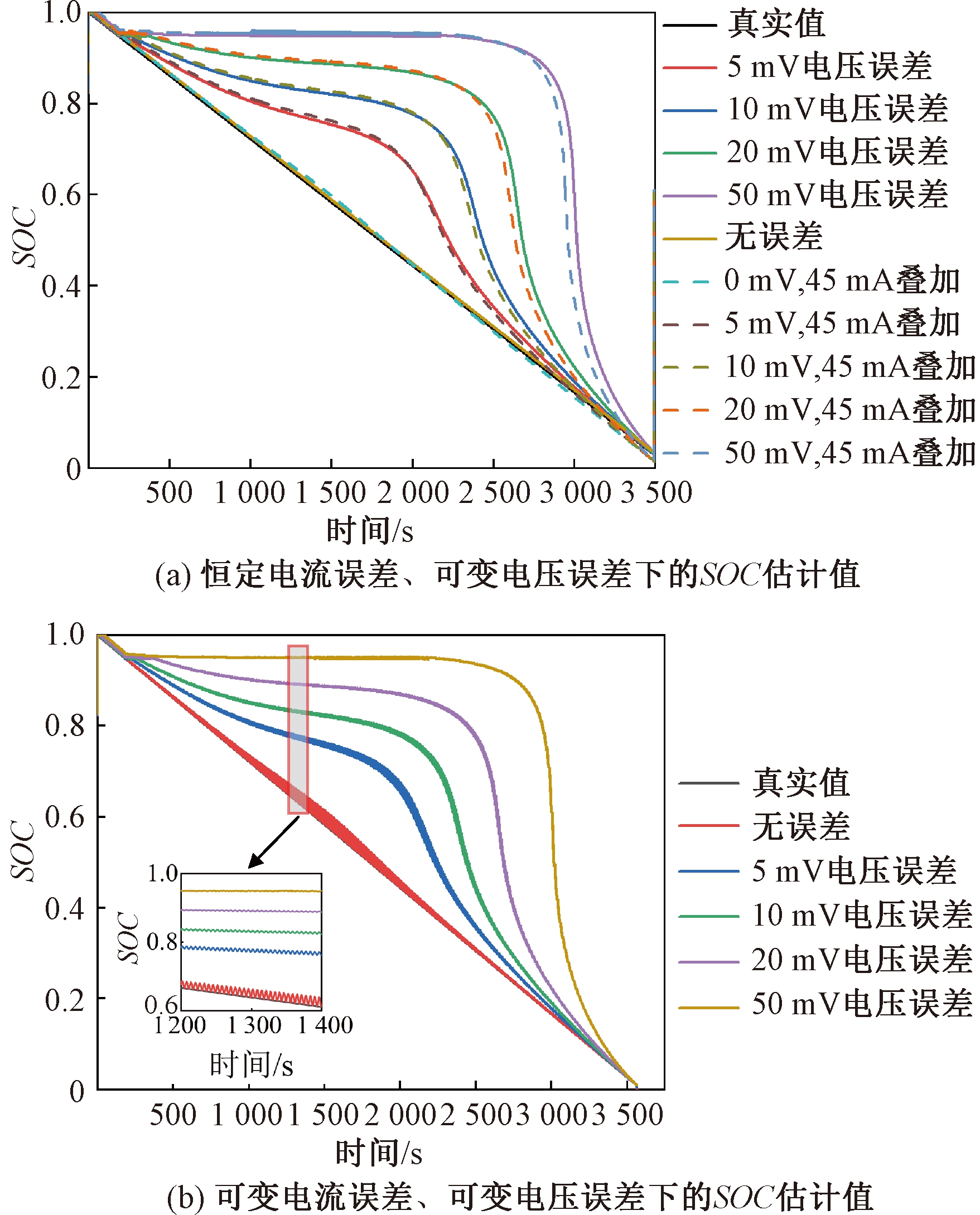
图8 电压、电流误差同时存在时的SOC估计值
Figure 8 SOC estimation when voltage and current errors exist simultaneously
采用安时积分法修正的AUKF算法估计磷酸铁锂电池SOC,估计结果如图9、10、11所示。图9(a)和图9(b)分别是恒流工况下磷酸铁锂电池充电和放电过程中的SOC估计结果。存在10 mV电压偏差时,未修正的算法和修正后的算法最大估计误差分别为0.22和0.02,估计精度提升很大。图9(c)是可变电流误差和可变电压误差共同作用下修正算法的SOC估计结果,SOC估计的最大误差为0.02,有效克服了可变电流误差和可变电压误差带来的影响。图10(a)和图10(b)分别是HPPC工况下磷酸铁锂电池充电和放电过程中的SOC估计结果,结果表明,其估计误差均保持在0.02以内。
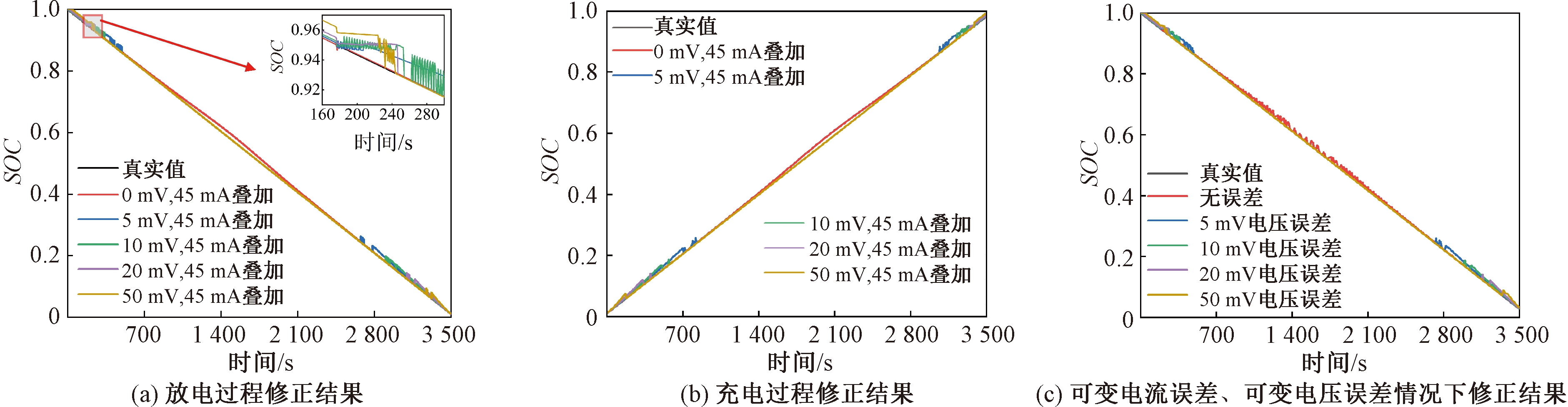
图9 恒流工况下修正后的SOC估计值
Figure 9 Corrected SOC estimation in constant current condition
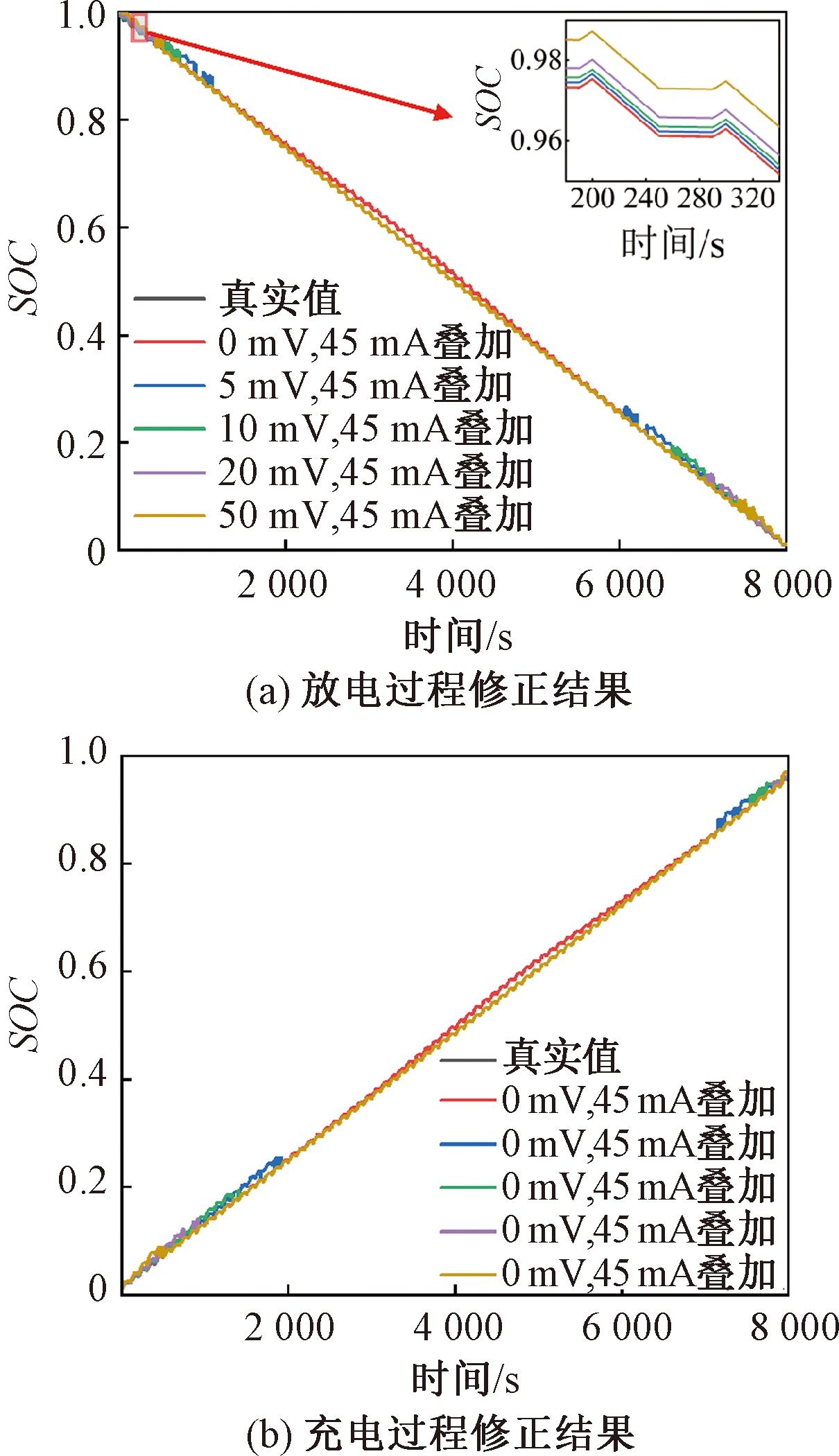
图10 HPPC工况下修正后的SOC估计值
Figure 10 Corrected SOC estimation in HPPC condition
而当锂电池初始状态在电压平台区,如图11所示,根据初始充放电电流方向求出对应的初始SOC,计算SOC估计值与真实值的差并进行相应修正,修正后的估计误差保持在0.02以内。当SOC估计误差小于均衡阈值,修正算法不起作用。
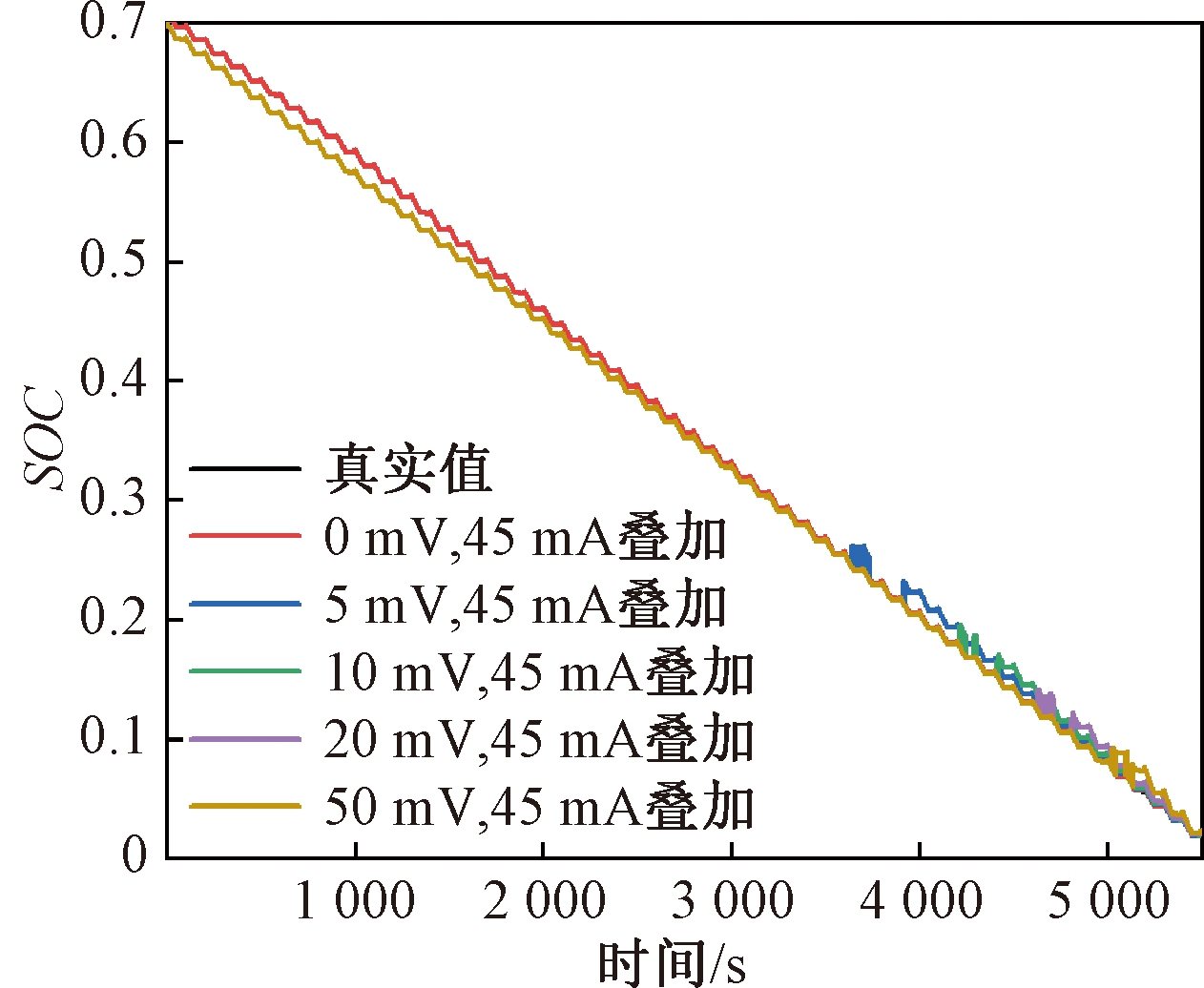
图11 电压平台区修正后的SOC估计值
Figure 11 Corrected SOC estimation in the voltage platform region
4 结论
针对磷酸铁锂电池滞回电压及电压传感器带来的电压测量误差导致的自适应算法SOC估计误差增大的问题,本文提出了基于安时积分法修正的磷酸铁锂电池SOC估计算法。
首先,研究了磷酸铁锂电池的特性;其次,设计了AUKF估计算法,还设计了安时积分法修正的逻辑;最后,进行实验。实验结果表明,磷酸铁锂电池SOC估计误差随电压测量误差的增大而增大,采用修正算法后,电压测量误差的影响减小,SOC估计结果仅在修正初始阶段有波动,SOC最大估计误差为0.02。
[1] 王少华. 电动汽车动力锂电池模型参数辨识和状态估计方法研究[D]. 长春: 吉林大学,2016.
WANG S H. Research on parameter identification and state estimation method of power lithium battery model for electric vehicle[D]. Changchun: Jilin University,2016.
[2] SHRIVASTAVA P, SOON T K, BIN IDRIS M Y I, et al. Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries[J]. Renewable and Sustainable Energy Reviews, 2019, 113: 109233.
[3] LIN X F, KIM Y, MOHAN S, et al. Modeling and estimation for advanced battery management[J]. Annual Review of Control, Robotics, and Autonomous Systems, 2019, 2: 393-426.
[4] DONG G Z, WEI J W, ZHANG C B, et al. Online state of charge estimation and open circuit voltage hysteresis modeling of LiFePO4 battery using invariant imbedding method[J]. Applied Energy, 2016, 162: 163-171.
[5] HU X S, LI S B, PENG H E. A comparative study of equivalent circuit models for Li-ion batteries[J]. Journal of Power Sources, 2012, 198: 359-367.
[6] LI W H, FAN Y, RINGBECK F, et al. Electrochemical model-based state estimation for lithium-ion batteries with adaptive unscented Kalman filter[J]. Journal of Power Sources, 2020, 476: 228534.
[7] RINGBECK F, GARBADE M, SAUER D U. Uncertainty-aware state estimation for electrochemical model-based fast charging control of lithium-ion batteries[J]. Journal of Power Sources, 2020, 470: 228221.
[8] 刘湘东, 刘承志, 杨梓杰, 等. 基于无迹卡尔曼滤波的全钒液流电池状态估计[J]. 中国电机工程学报, 2018, 38(6): 1769-1777, 16.
LIU X D, LIU C Z, YANG Z J, et al. States estimation of vanadium redox flow battery based on unscented Kalman filter[J]. Proceedings of the CSEE, 2018, 38(6): 1769-1777, 16.
[9] 续远. 基于安时积分法与开路电压法估测电池SOC[J]. 新型工业化, 2022, 12(1):123-124, 127.
XU Y. Estimation of battery SOC based on ampere-hour integration method and open circuit voltage method[J]. The Journal of New Industrialization, 2022, 12(1):123-124, 127.
[10] LIN C, TANG A H, XING J L. Evaluation of electrochemical models based battery state-of-charge estimation approaches for electric vehicles[J]. Applied Energy, 2017, 207: 394-404.
[11] MOURA S J, CHATURVEDI N A, 
M. Adaptive partial differential equation observer for battery state-of-charge/state-of-health estimation via an electrochemical model[J]. Journal of Dynamic Systems, Measurement, and Control, 2014, 136(1): 011015.
[12] STURM J, ENNIFAR H, ERHARD S V, et al. State estimation of lithium-ion cells using a physicochemical model based extended Kalman filter[J]. Applied Energy, 2018, 223: 103-123.
[13] TANIM T R, RAHN C D, WANG C Y. State of charge estimation of a lithium ion cell based on a temperature dependent and electrolyte enhanced single particle model[J]. Energy, 2015, 80: 731-739.
[14] PLETT G L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs[J]. Journal of Power Sources, 2006, 161(2): 1356-1368.
[15] WANG W H, MU J Y. State of charge estimation for lithium-ion battery in electric vehicle based on Kalman filter considering model error[J]. IEEE Access, 2019, 7: 29223-29235.
[16] TRAN N T, VILATHGAMUWA M, LI Y, et al. State of charge estimation of lithium ion batteries using an extended single particle model and sigma-point Kalman filter[C]∥2017 IEEE Southern Power Electronics Conference (SPEC). Piscataway: IEEE, 2018: 1-6.
[17] SHU X, LI G, SHEN J W, et al. An adaptive fusion estimation algorithm for state of charge of lithium-ion batteries considering wide operating temperature and degradation[J]. Journal of Power Sources, 2020, 462: 228132.
[18] LI W H, CAO D C, JÖST D, et al. Parameter sensitivity analysis of electrochemical model-based battery management systems for lithium-ion batteries[J]. Applied Energy, 2020, 269: 115104.
[19] RAMADESIGAN V, CHEN K J, BURNS N A, et al. Parameter estimation and capacity fade analysis of lithium-ion batteries using reformulated models[J]. Journal of the Electrochemical Society, 2011, 158(9): A1048.
[20] STETZEL K D, ALDRICH L L, TRIMBOLI M S, et al. Electrochemical state and internal variables estimation using a reduced-order physics-based model of a lithium-ion cell and an extended Kalman filter[J]. Journal of Power Sources, 2015, 278: 490-505.