泥浆主要包括河道疏浚泥浆和工业废弃泥浆,往往具有含水量高、渗透性低、自然沉淀分离耗时长、固结过程缓慢等特点[1-2]。中国每年的泥浆产量巨大,如果采用外运的方式处理废弃泥浆,不仅成本高昂,而且在运输过程中容易对环境造成二次污染。因此,随着经济及城市化进程的快速发展,对泥浆的无害化、减量化处理要求日益凸显。
目前,结合工程具体情况,泥浆处理技术已得到较大发展,通常利用离心、压滤和真空抽滤等设备,采用机械脱水、土工袋、化学固化、化学絮凝等固液分离方法[3-9]将泥浆中的水分快速排出,从而大大减小泥浆体积,以方便运输或二次利用。但是如果泥浆中含有较多黏粒,则其渗透性很低,泥浆中水分的排出将变得比较困难。
工程实践表明,电渗法对低渗透性软土地基的固结具有良好的适用性,这是因为电渗法可以同时排出软土中的自由水和部分结合水[10]。而泥浆体的脱水过程类似于软土的固结过程,因此,可将电渗技术引入到泥浆处理中,并参考软土的电渗固结理论研究泥浆的电渗脱水机理。Esrig[11]于1968年提出的一维电渗固结理论是建立在小变形假定之上的,但考虑到软土的固结变形较大,该假定已不再适用。王柳江等[12]在拉格朗日坐标下,以有限变形为基础,以超静孔压为变量,将Esrig电渗固结方程修正为一个高度非线性的偏微分方程,并采用有限差分法进行了求解。Fox等[13]另辟蹊径,引入分段线性化思想,不推导偏微分方程,仅利用渗流连续性条件,提出了一维大变形固结的分段线性数值模型(consolidation settlement 2,CS2)。在此基础上,周亚东等[14-15]建立了考虑饱和度变化影响的一维电渗固结模型。该模型同时考虑了孔隙比变化对电渗透系数的影响,可以进行轴对称条件下的电渗-堆载耦合固结分析。这些成果可供泥浆脱水理论分析参考。
为进一步深入探讨影响泥浆电渗脱水过程的主要因素,本文在CS2固结模型的基础上,同时考虑电渗透系数与电势梯度及孔隙比的综合关系、材料非线性本构关系和大变形效应,建立泥浆一维电渗脱水模型,并分析相关参数对泥浆一维电渗脱水过程的影响。
1 泥浆一维电渗脱水模型
假定初始泥浆均匀饱和;土颗粒和水本身不可压缩,且二者的电阻在电渗脱水过程中为常量;泥浆的脱水量与泥浆的体积压缩量数值相等;阴极排出的气体不影响电渗脱水过程。
如图1所示,以底面为基准面,向上为正。电源正负极分别放置在泥浆顶面和底面,泥浆的上、下边界可以设置为透水或不透水。在初始时刻(图1(a)),泥浆孔隙比处处相同,泥浆表面上覆荷载为q0,两端加载电压为Um,泥浆只沿竖向发生渗流和变形,泥浆初始厚度为H0,静水面高度Hw始终与泥浆表面高度一致。将泥浆自下而上均匀划分为n个单元,每个单元的初始厚度均为L0 ,此时单元j的中心点高程为
经过时间 t 后( 图1(b)),泥浆层厚度变为Ht,每个单元的厚度及位置高度随时间同步更新。
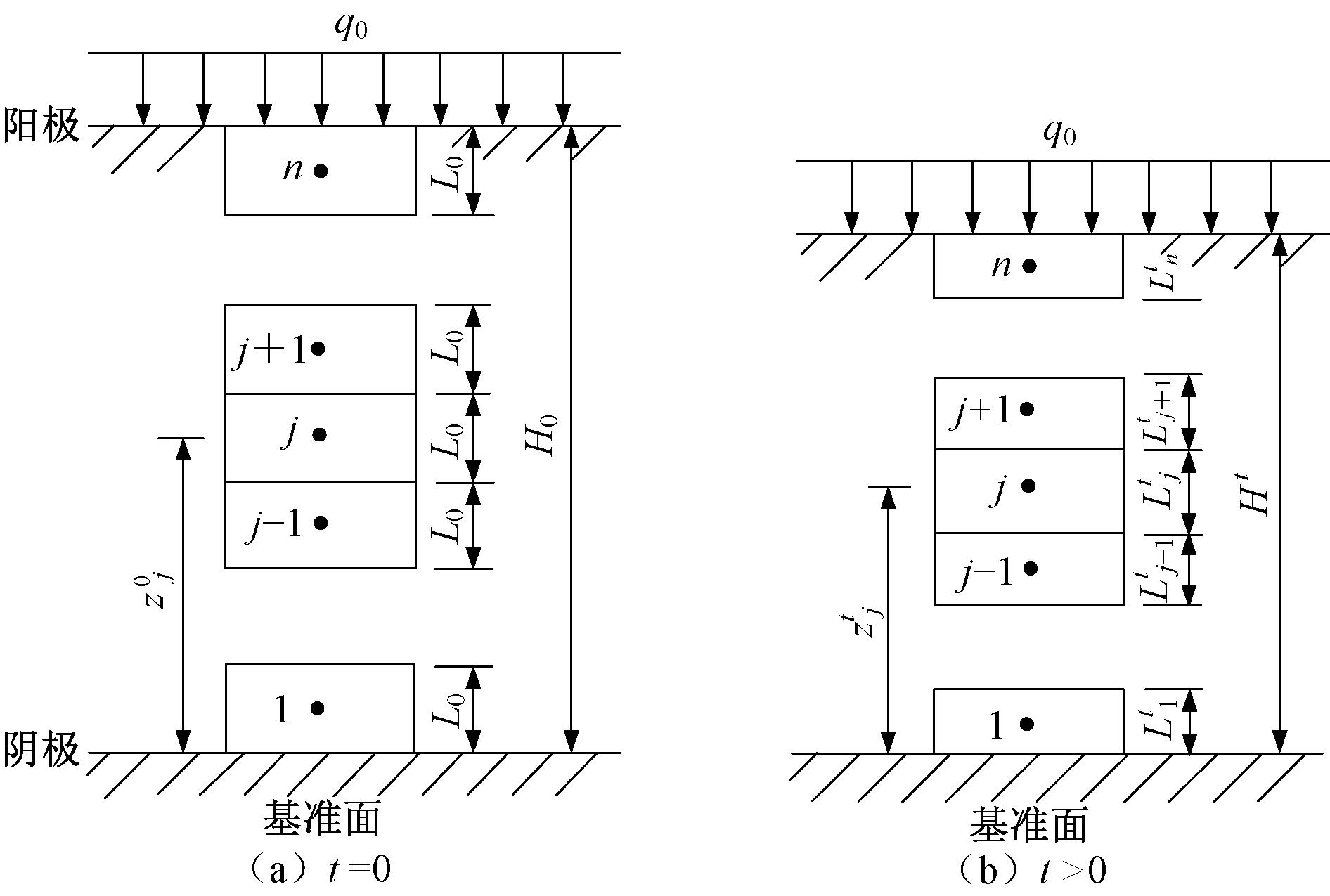
图1 模型示意图
Figure 1 Schematic diagram of the model
1.1 本构关系
为建立数值模型,采用由一维固结试验获得的孔隙比-有效应力关系曲线,由渗流试验获得的孔隙比-渗透系数关系曲线来描述其本构关系。考虑到泥浆体的脱水过程类似于正常固结土的固结过程,这里引入经典的非线性经验关系来描述其压缩过程:
e-e0=Cc(lg σ′0-lg σ′)。
(1)
式中:Cc为泥浆的压缩系数;e和e0分别为对应于有效应力σ′和某参考应力σ′0的孔隙比。
假定泥浆由于水头差引起的渗流符合达西定律,但其渗透系数会随孔隙比的变化而变化,并可用式(2)[16]表示:
(2)
假定由电势差引起的渗流符合Helmholtz-Smoluchowski理论。Mitchell[17]认为土的电渗透系数一般为2×10-9～8×10-9 m2/(s·V)。然而,周亚东等[14]、庞宽等[18]、李瑛 [19]的试验表明,电势梯度ie对电渗透系数ke有影响,并认为二者之间为线性关系。罗文培[20]的试验进一步表明,电渗透系数ke与电势梯度ie及孔隙比e都是线性相关的,因此本文将把ke表示为ie和e的线性函数,即
ke=Ae+Bie+C。
(3)
式中:A、B和C为可通过试验数据拟合获得的试验常数,其单位分别为10-5cm2/(s·V)、10-5cm3/(s·V)、10-5cm2/(s·V);ke和ie的单位分别为10-5cm2/(s·V)和V/cm。
1.2 总应力、有效应力和孔隙水压力
每个泥浆单元中心节点的总应力
为该节点以上所有泥浆层的自重与上覆荷载之和,即
(4)
(5)
式中:γj为单元j的重度,
为第j泥浆层在t时刻的孔隙比;γw为水的容重,在计算过程中取9.81 kN/m3。
在时刻t,节点j处的有效应力σ′tj可由式(1)得出。这样,节点j 处的孔隙水压力为
(6)
1.3 渗透系数和电渗透系数
在t时刻,节点j处的水力渗透系数
和电渗透系数
可根据时刻t对应的孔隙比计算。由于不同单元的水力渗透系数和电渗透系数并不相等,所以相邻单元界面处的等效渗透系数可根据相邻单元的串联原则计算[11-12],即
(7)
式中:下标x表示e或w。
1.4 电势
对于饱和泥浆,可将其电阻视为由水和土颗粒各自的电阻并联产生[15]。所以,单元j泥浆的电阻率可表示为
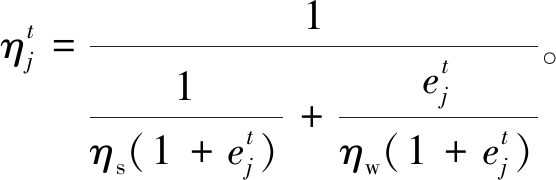
(8)
式中:ηs为泥浆土颗粒的电阻率;ηw为水的电阻率;
为泥浆单元 j 在t时刻的孔隙比。
单元j泥浆的电阻可表示为
(9)
对于整个泥浆层而言,每个单元体是相互串联的,所以在时刻t,节点j处的电势
可表示为
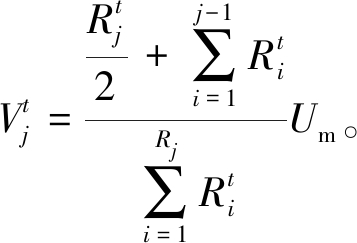
(10)
式中:为单元j中心节点处的电势;Um为施加在试样两端的电压;
为单元j在时刻t的电阻。
j单元和j-1单元中点的电势差为
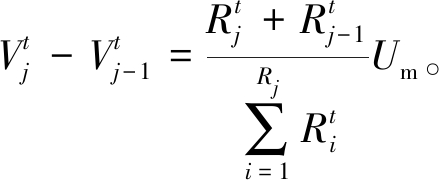
(11)
1.5 脱水量(沉降)
在时刻t,单元j和j-1之间分别由电势差和水头差引起的水的渗流速度为
(12)
(13)
时刻t电势梯度
与水力梯度
分别为
(14)
(15)
节点j的水头
为
(16)
经过时间Δt后,单元j的高度、孔隙比将分别更新为
(17)
(18)
同时,泥浆的高度Ht+Δt为
(19)
饱和泥浆的脱水量可用其表面的沉降量来表示。此时,泥浆表面的沉降量St+Δt为
St+Δt=H0-Ht+Δt。
(20)
2 模型验证
根据上述理论分析,利用Fortran编写了一个数值模拟程序。这里,分别通过将文献[12]中的解析解、室内试验结果与数值计算结果进行对比,进一步验证该数值模拟程序的正确性。
2.1 与文献[12]的对比
文献[12]针对一维电渗固结课题给出解析解。在其进行参数分析时,假定电渗固结前泥浆已经完成了自重固结沉降,初始顶面孔隙比e00=3;假定泥浆孔隙比的改变量与有效应力成正比,体积压缩系数mv=4.0 MPa-1;初始渗透系数kw0=1.0×10-9 m/s;Gs=2.75;Hw=1.0 m;完成自重固结前的泥浆初始上覆荷载为qp=10 kPa;电渗过程开始瞬间加载的上覆荷载为q0=100 kPa。设电渗透系数为定值,且按式(21)计算:
(21)
式中:电迁移系数ki=2.5×10-5 cm3/(s·A);初始导电率kσ=2.0 s/m。
这里取加载电压分别为0、2、4、8 V进行模拟,且假定电势在泥浆内随高度呈现线性分布。图2为本文解与文献[12]解析解的对比情况。这里,Tv=kw0t/(mvγwH2)为时间因子。图2表明,二者基本重合。
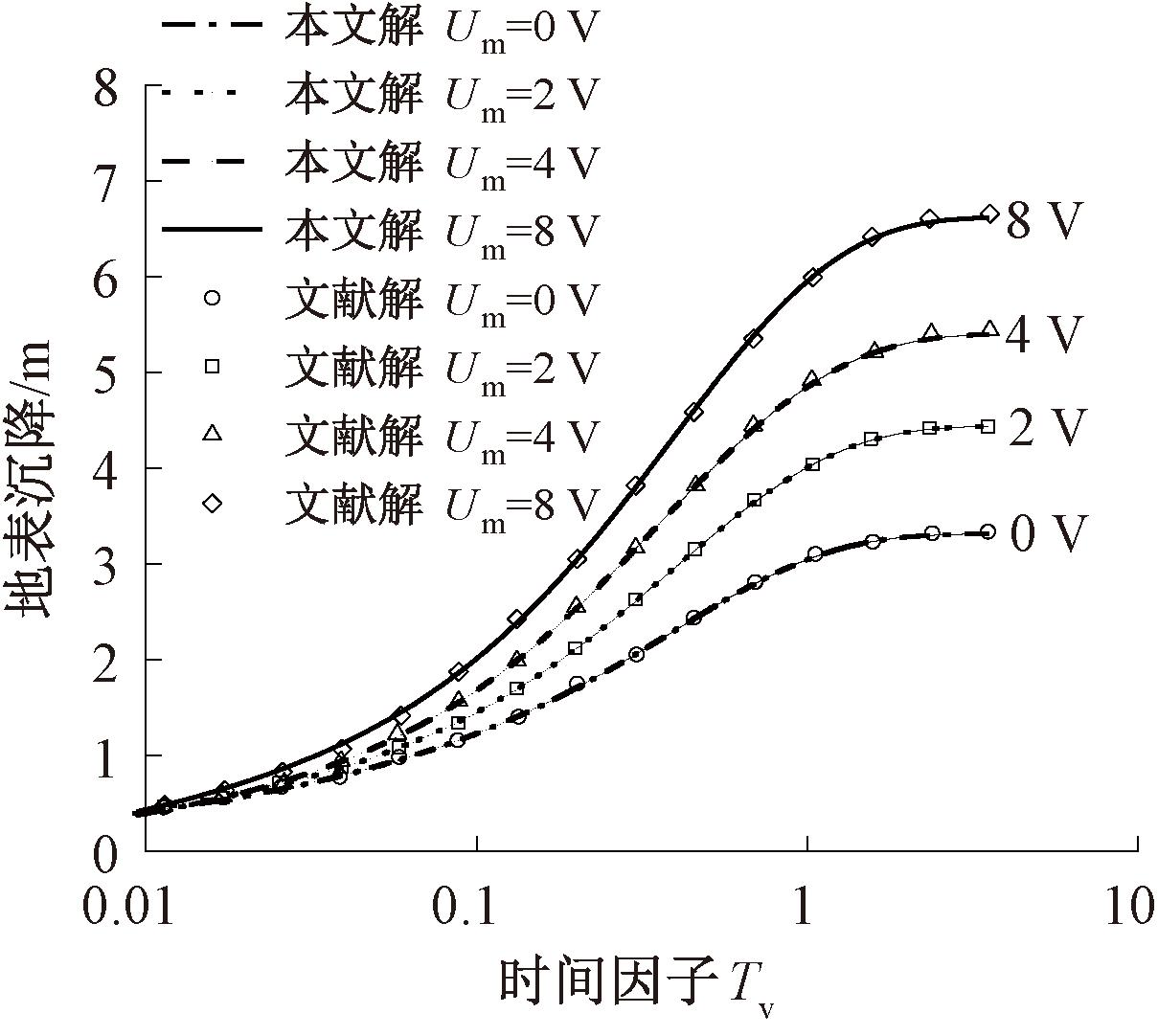
图2 本文数值解与文献[12]解析解的对比
Figure 2 Comparison between numerical solutions in this paper and analytical solutions in reference[12]
2.2 与室内模型试验结果对比
试样取自信阳市某工地。首先对其进行土粒比重、液塑限、压缩指数等基本参数测定,结果如表1所示。其中,孔隙水和土骨架的电阻率分别选用了Zhou等[21]的分析数据。
表1 泥浆的物理性质指标
Table 1 Physical properties of mud
初始孔隙比e土粒比重Gs初始重度γ0/(kN·m-3)液限wL/% 塑限wp/%塑性指数Ip压缩指数Cc初始渗透系数kw0/(m·s-1)孔隙水电阻率ηw/(Ω·m)土骨架电阻率ηs/(Ω·m)2.002.6718.940.525.614.90.4161×10-84.5608
为探究泥浆电渗脱水过程的一般规律,研制了一种泥浆电渗脱水试验装置,如图3所示。该装置主要由泥浆桶、直流电源、测量工具三部分组成,泥浆桶内径d1=15 cm,桶壁厚d2=1 cm,高度H=30 cm,桶内主要放置有透水石与电极片,桶底正中心位置开孔并安插排水管,下接放在电子秤上的集水容器,以便实时监测脱水量。同时,泥浆顶部架设百分表用于监测表面沉降。对于饱和泥浆,其表面沉降与泥浆桶横截面积的乘积应等于脱水量。所以,同时监测脱水量和泥浆表面沉降可以相互印证数据是否正确。
图3 泥浆电渗脱水试验装置
Figure 3 Test apparatus for mud electroosmotic dewatering
配置含水率为75%的4组泥浆,泥浆初始高度为20 cm,其底部设置厚度为1 cm的透水石以便脱水。电渗脱水试验方案如表2所示。分别加载不同的电压进行脱水试验,实测脱水量与时间的关系见图4。很明显,电势梯度越大,泥浆排水就越快,且排水量也越大。
表2 电渗脱水试验方案
Table 2 Electroosmotic dewatering test scheme
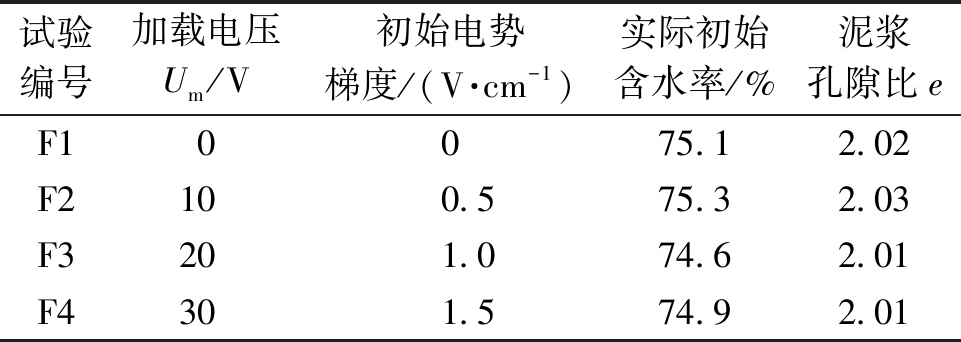
试验编号加载电压Um/V初始电势梯度/(V·cm-1)实际初始含水率/%泥浆孔隙比eF10075.12.02 F2100.575.32.03 F3201.074.62.01 F4301.574.92.01
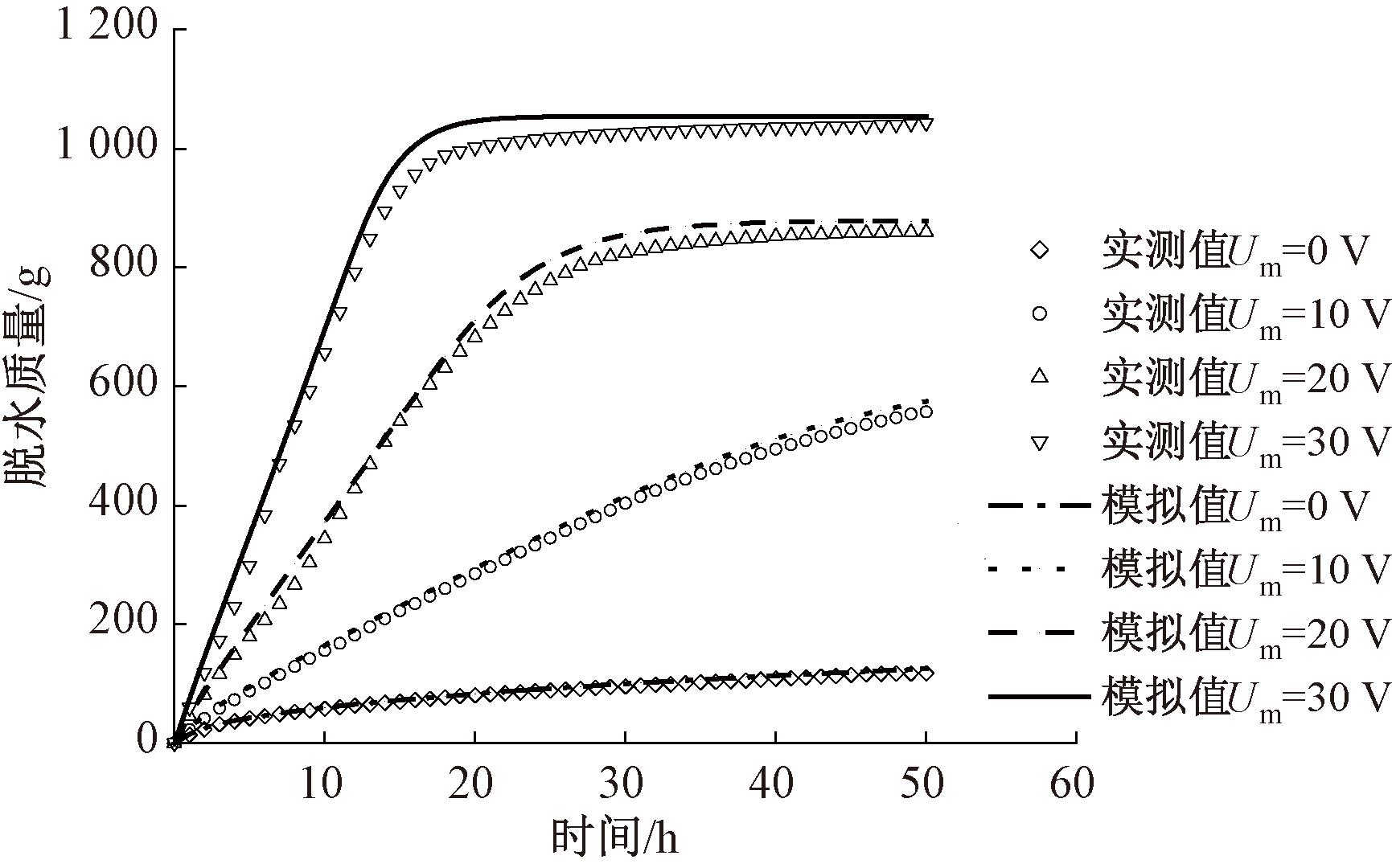
图4 累计脱水量实测值与模拟值对比
Figure 4 Comparison between measured and simulated cumulative water removal
数值模拟时,取n=20,电渗透系数与电势梯度及孔隙比的关系表达式[20]为
ke=4.583e+0.315ie-2.875。
(22)
理论计算脱水量见图4。很明显,对于自重脱水和电压为10 V的试验,理论计算结果和试验值符合很好,而对于电压为20 V和30 V的试验,在试验初期二者比较一致,但在后期,前者要略大于后者,但二者之间最大相对误差不超过5%。其原因可能有两点:一是随着试验的进行,上部泥浆的含水率在逐渐下降,可能由饱和状态转为不饱和状态,进而使得电阻增大;二是阴极产生了氢气气泡,也会堵塞孔隙。这两点原因都会减缓脱水进程,使得排水量减少。因此,对于加载电压较大即电势梯度较大时,原则上就需要考虑饱和度变化的影响。
3 参数分析
以下分析中,均取底面为阴极脱水面、顶面为阳极自由面,泥浆的物理性质指标同表1,取泥浆初始高度H0为1 m,泥浆顶面荷载q0为0 kPa。分析除加载电压外其他模型参数影响时,泥浆两端加载的电压Um取为60 V。
3.1 加载电压的影响
泥浆表面的沉降可以反映脱水量的大小。为考察加载电压对电渗脱水过程的影响,图5给出了不同加载电压Um时泥浆表面沉降随时间的变化过程。图5表明,电渗脱水导致的沉降分为近似线性脱水、减速脱水和稳定三个阶段,且随着电压的增大,脱水量加大,线性脱水阶段与减速脱水阶段所需要的时间也都不断缩短,即脱水速度也加快。
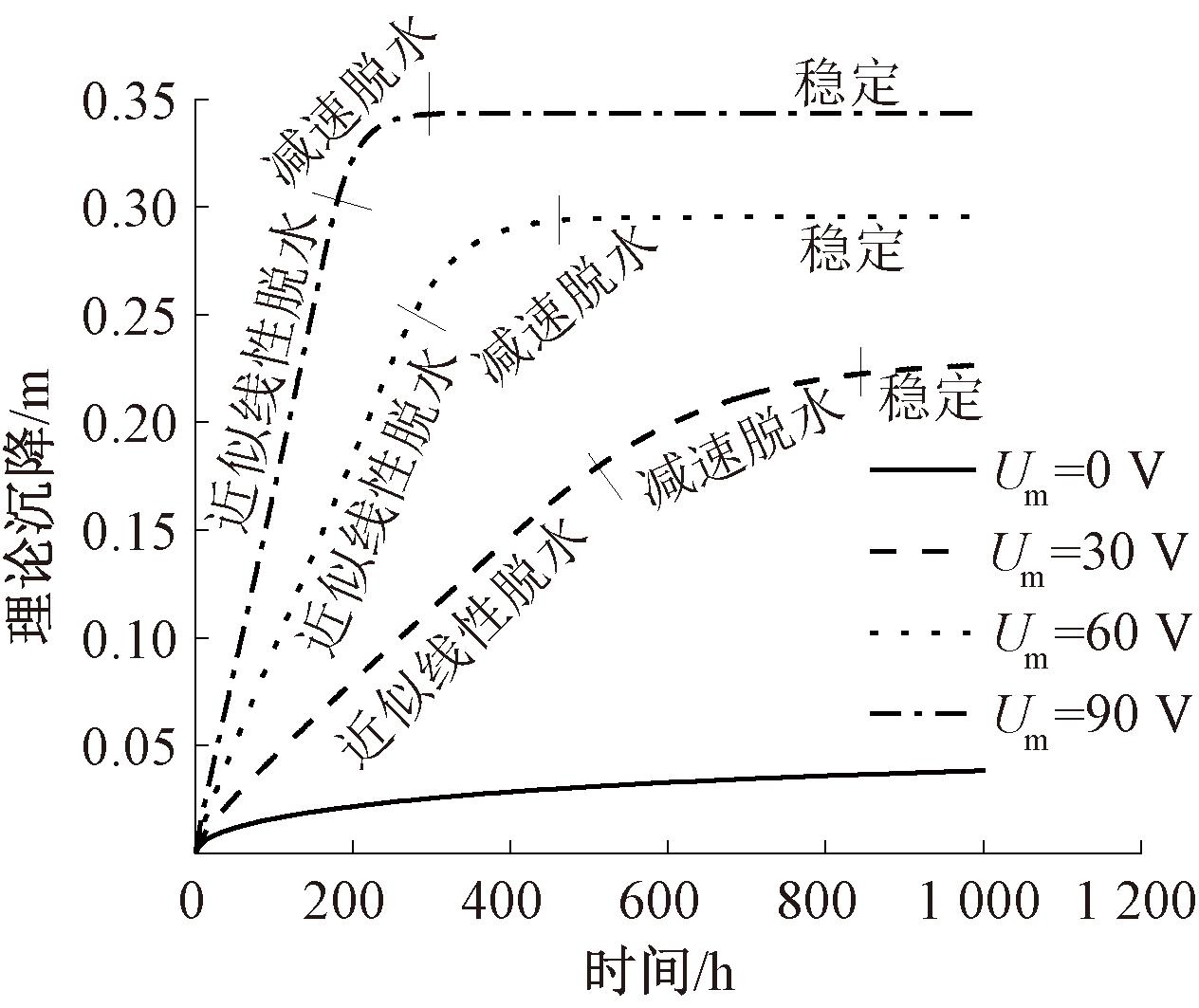
图5 电压对沉降的影响
Figure 5 Effect of voltage on settlement
图6分别给出了几个不同时刻泥浆内孔压的分布情况。图6(a)表明,脱水50 h后,加载电压大于0 V的三组泥浆,其上部的孔压均为负值,且随着加载电压的增大,负孔压区增大,孔压绝对值也增大。同时,在高度0.6 m以下泥浆内的孔压为正值,这是由于泥浆电渗脱水过程中孔隙水不断从阳极向阴极自上而下排出,上部泥浆先脱水稳定,形成负孔压,下部孔隙水压还没有完全消散。
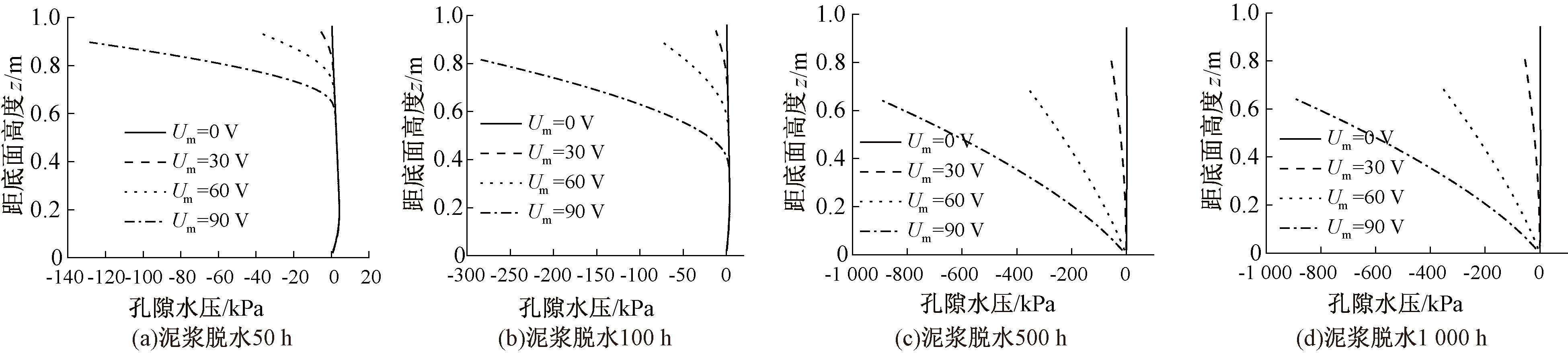
图6 加载不同电压时泥浆各高度处孔隙水压
Figure 6 Pore water pressure in mud at different voltages
从图6可以看出,随着电渗脱水的进行,泥浆高度不断降低,由于静水面高度始终与泥浆表面高度一致,试验可测得孔压的范围也不断降低。加载电压大于0 V的3组,负孔压区不断向下延伸,且孔压绝对值也持续增长,但500 h后,对应高度处的孔压变化已经不大,特别是加载电压为60 V和90 V两组泥浆中孔压基本趋于稳定。结合图5可以看出,此时这两组的沉降已达稳定状态。
3.2 压缩指数的影响
压缩指数表示泥浆压缩性的高低,图7为压缩指数对电渗脱水过程的影响。在前230 h内,几条曲线几乎重合,说明压缩指数对泥浆脱水前期的影响很小。但随着时间的推移,几条曲线之间的差异逐渐显著,说明压缩指数对脱水后期的影响较大,而且,压缩指数越大,最终沉降量就越大,达到稳定的时间就越长。
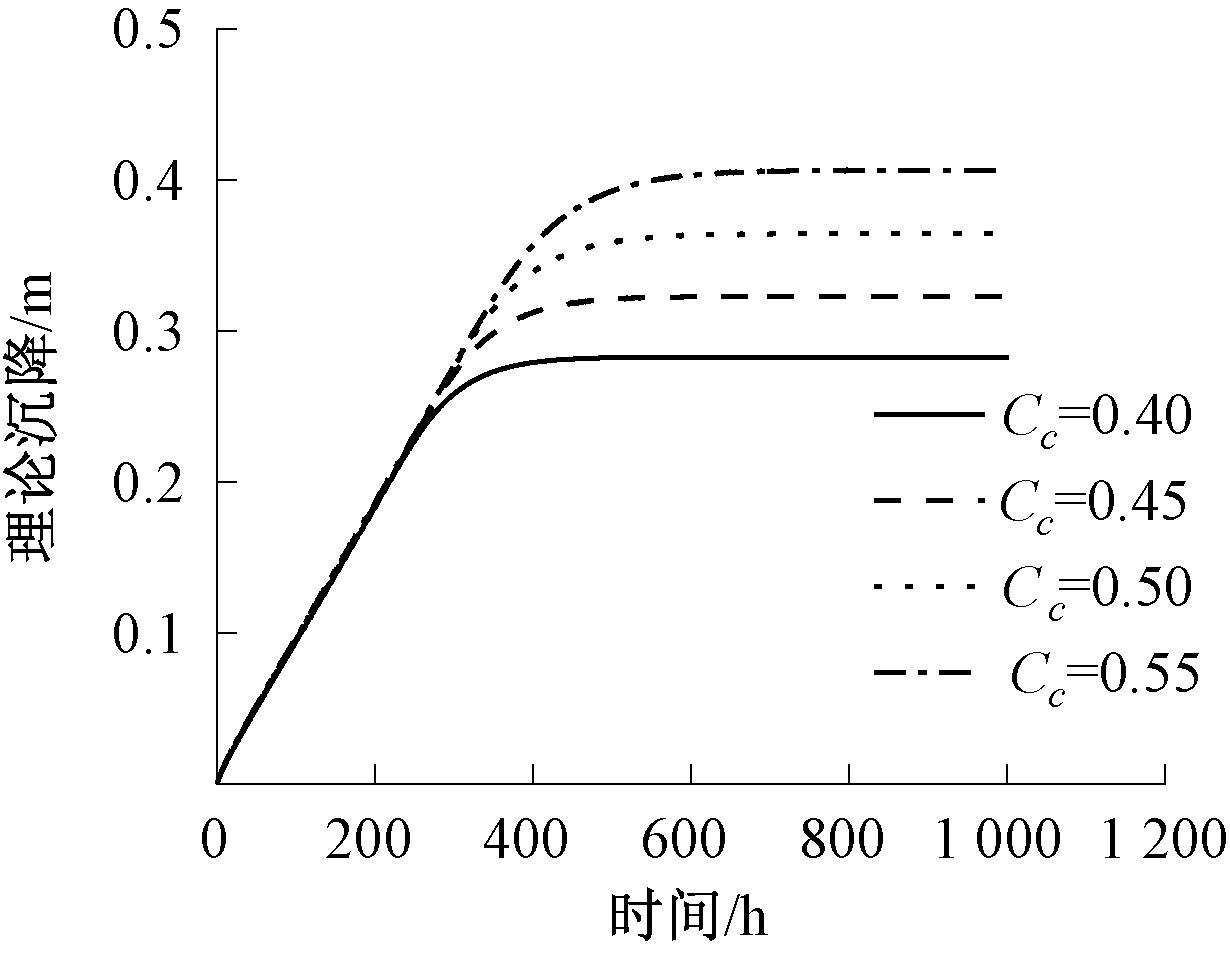
图7 压缩指数对沉降的影响
Figure 7 Effect of compression index on settlement
3.3 电渗透系数的影响
由式(22)可计算出第j层与第j-1层接触面的等效电渗透系数kes,j。图8给出了kes,5、kes,9、kes,13、kes,17等4个电渗透系数随时间变化的曲线。由图8可知,不同层间的等效电渗透系数都是在开始的一段时间内几乎没有变化,然后突然降低,最后逐渐趋于稳定。而且,越靠近底部阴极处的等效电渗透系数在开始阶段保持几乎不变的时间就越长。随着时间的增长,最上层的泥浆由于有效应力最大而孔隙率先缩小,进而导致等效电渗透系数减小。随后从上往下各层泥浆孔隙与电渗透系数都逐步减小,直至最后稳定。很明显,电渗透系数稳定值沿深度也是不均匀的。图8表明,等效电渗透系数为2.0×10-5～6.5×10-5 cm2/(s·V)。为分析电渗透系数对电渗脱水过程的影响,将电渗透系数kes设为定值,分别为2.00×10-5、4.25×10-5、6.50×10-5 cm2/(s·V)。
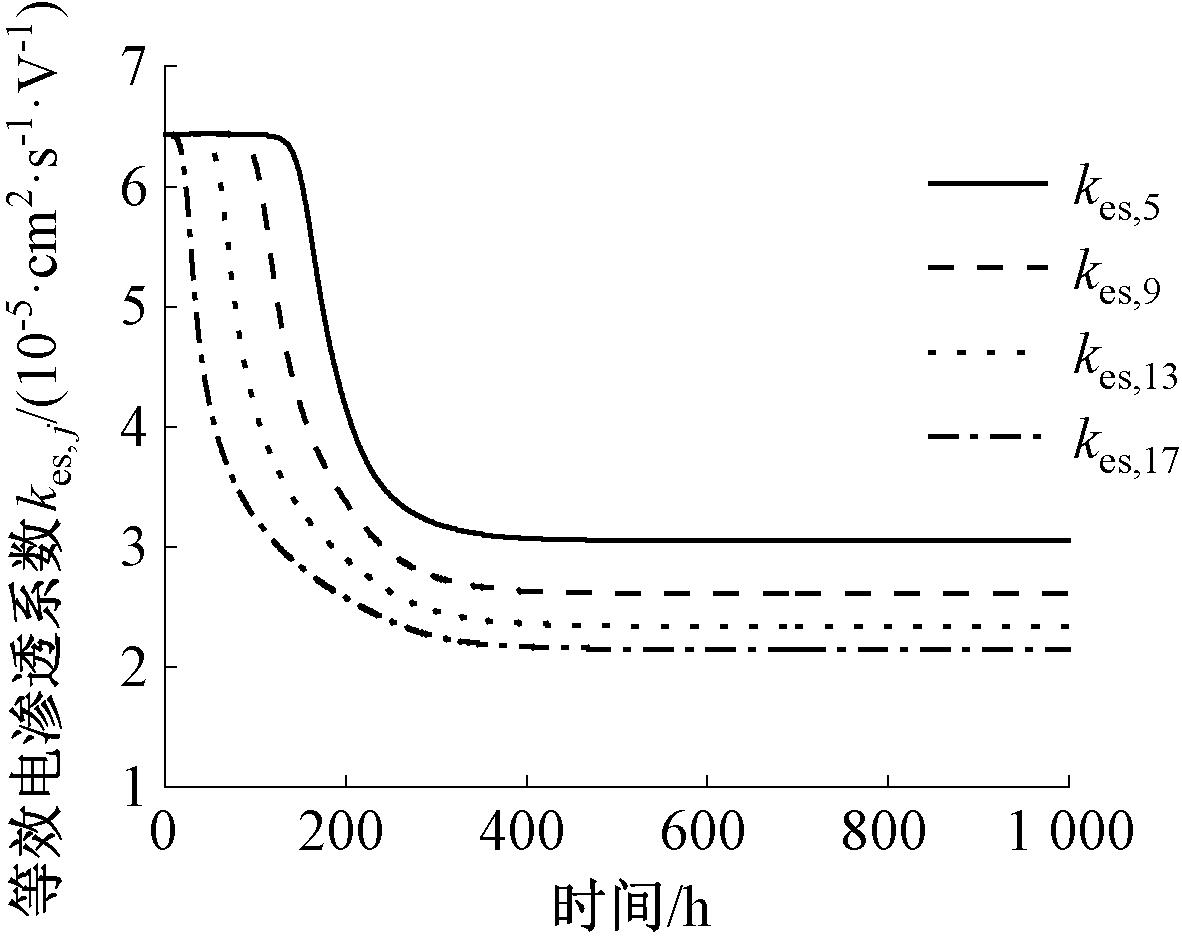
图8 等效电渗透系数与时间的关系
Figure 8 The relation between equivalent electroosmotic coefficient and time
图9分别给出了不同电渗透系数影响下的理论沉降变化曲线。由于自重脱水类似于软土的固结,所以水力渗透系数对最终沉降量并没有影响,只会影响沉降速率。与之不同的是,图9表明,电渗脱水时,电渗透系数不仅影响沉降速率,还会影响最终沉降量。电渗透系数越大,沉降量就越大,而且达到稳定的时间就越短。同时,图9也说明了电渗计算中考虑电渗透系数变化的重要性。
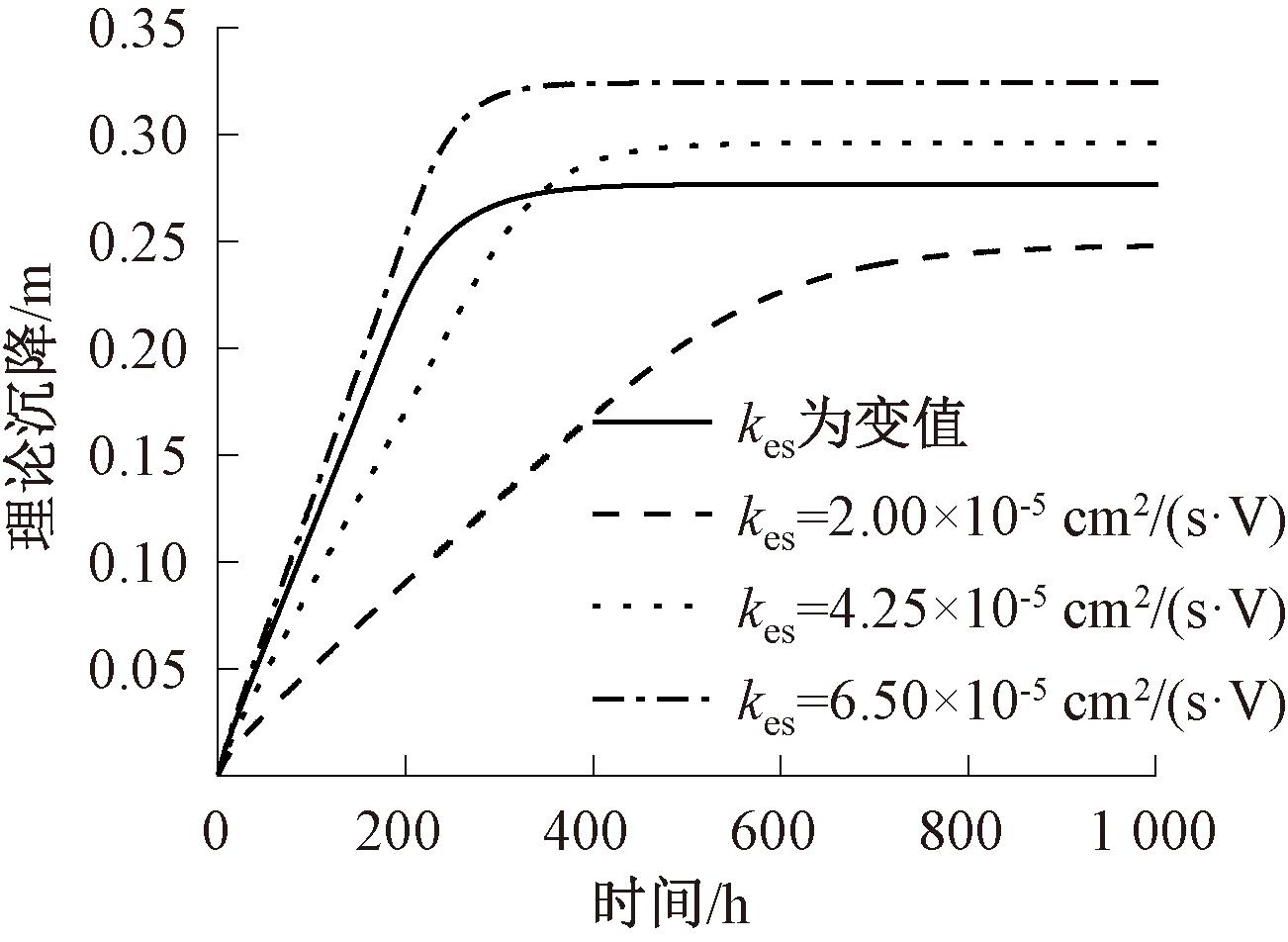
图9 电渗透系数对沉降的影响
Figure 9 Effect of electroosmotic coefficient on settlement
4 结论
本文建立了一种泥浆一维电渗脱水计算模型。与理论解析解和室内模型试验的对比表明,本文模型的计算误差不超过5%。
(1)增大加载电压可以有效提高电渗初期的脱水速率以及最终脱水量,且使得达到脱水稳定状态的时间缩短。
(2)泥浆的压缩指数越大,电渗最终脱水量就越大,达到稳定的时间也就越长。
(3)增大电渗透系数,可提高最终脱水量和缩短稳定时间。电渗分析时应同时考虑电渗透系数与孔隙比和电势梯度的关系。
[1] 詹良通, 张斌, 郭晓刚, 等. 废弃泥浆底部真空-上部堆载预压模型试验研究[J]. 岩土力学, 2020, 41(10): 3245-3254.
ZHAN L T, ZHANG B, GUO X G, et al. Physical modeling study on treatment of waste slurry with vacuum preloading at bottom combined with upper surcharge loading[J]. Rock and Soil Mechanics, 2020, 41(10): 3245-3254.
[2] 田浩, 赵会军. 废弃油基泥浆处理工艺与研究[J]. 环境工程, 2014, 32(增刊1): 310-313.
TIAN H, ZHAO H J. Waste oil-based mud treatment technology and research[J]. Environmental Engineering, 2014, 32(S1): 310-313.
[3] 严晓威, 柳忠现, 王盛, 等. 3种污泥机械脱水方式的工程应用[J]. 净水技术, 2022, 41(增刊2): 100-105.
YAN X W, LIU Z X, WANG S, et al. Engineering application of three mechanical dewatering methods of sludge[J]. Water Purification Technology, 2022, 41(S2): 100-105.
[4] 郑华,尹昭宇,林宇杰,等. 土工管袋用于湿地疏浚淤泥脱水处理效果评估[J]. 浙江水利科技,2022,50(4): 51-55.
ZHENG H, YIN Z Y, LIN Y J, et al. Evaluation of dehydration treatment effect of wetland dredged sludge with geotextile pipe bags[J]. Zhejiang Hydrotechnics, 2022, 50(4): 51-55.
[5] 王文军, 袁飞飞, 蒋建良, 等. 高含水率吹填淤泥固化土强度特性及预测模型[J]. 地下空间与工程学报, 2021, 17(2): 461-467.
WANG W J, YUAN F F, JIANG J L, et al. Strength properties and prediction models of solidified dredger filled mud with high water-content[J]. Chinese Journal of Underground Space and Engineering, 2021, 17(2): 461-467.
[6] 党星赛, 谢靖宇, 洪钊, 等. 极高含水率疏浚泥浆的絮凝机理和颗粒尺寸变化规律研究[J]. 科技通报, 2022, 38(2): 67-72.
DANG X S, XIE J Y, HONG Z, et al. Study on the flocculation mechanism and particle size change law of dredged mud with extremely high water content[J]. Bulletin of Science and Technology, 2022, 38(2): 67-72.
[7] 臧小龙. 新型泥水分离处理系统在盾构隧道施工中的应用[J]. 建筑机械, 2012(23): 122-124, 20.
ZANG X L. Application of new slurry separate disposal system for construction of shield machine tunnel[J]. Construction Machinery, 2012(23): 122-124, 20.
[8] 朱群峰, 赵士文, 杨守华, 等. 围海造地软基加固试验研究[J]. 郑州大学学报(工学版), 2012, 33(5): 16-21.
ZHU Q F, ZHAO S W, YANG S H, et al. Consolidation of soft foundation of reclamation projects[J]. Journal of Zhengzhou University (Engineering Science), 2012, 33(5): 16-21.
[9] 魏雁冰, 范明桥, 林生法, 等. 建筑废弃泥浆真空预压方法处理试验研究[J]. 郑州大学学报(工学版), 2016, 37(1): 65-69.
WEI Y B, FAN M Q, LIN S F, et al. Experimental study on construction waste slurry treatment by vacuum preloading[J]. Journal of Zhengzhou University (Engineering Science), 2016, 37(1): 65-69.
[10] 王军,张乐,刘飞禹,等. 真空预压-电渗法联合加固软黏土地基试验研究[J]. 岩石力学与工程学报,2014,33(增刊2):4181-4192.
WANG J, ZHANG L, LIU F Y, et al. Experimental study of vacuum preloading combined reinforcement with electro-osmosis in soft clay ground[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(S2): 4181-4192.
[11] ESRIG M I. Pore pressures, consolidation, and electrokinetics[J]. Journal of the Soil Mechanics and Foundations Division, 1968, 94(4): 899-921.
[12] 王柳江, 刘斯宏, 王子健, 等. 堆载-电渗联合作用下的一维非线性大变形固结理论[J]. 工程力学, 2013, 30(12): 91-98.
WANG L J, LIU S H, WANG Z J, et al. A consolidation theory for one-dimensional large deformation problems under combined action of load and electroosmosis[J]. Engineering Mechanics, 2013, 30(12): 91-98.
[13] FOX P J, BERLES J D. CS2: a piecewise-linear model for large strain consolidation[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1997, 21(7): 453-475.
[14] 周亚东, 王保田, 邓安. 分段线性电渗-堆载耦合固结模型[J]. 岩土工程学报, 2013, 35(12): 2311-2316.
ZHOU Y D, WANG B T, DENG A. Piecewise-linear model for electro-osmosis-surchargepreloadingcoupled consolidation[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(12): 2311-2316.
[15] 周亚东, 邓安, 刘中宪, 等. 考虑饱和度变化的一维电渗固结模型[J]. 岩土工程学报, 2017, 39(8): 1524-1529.
ZHOU Y D, DENG A, LIU Z X, et al. One-dimensional electroosmosis consolidation model considering variable saturation[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(8): 1524-1529.
[16] 谢康和, 郑辉, LEO C J. 软黏土一维非线性大应变固结解析理论[J]. 岩土工程学报, 2002,24(6): 680-684.
XIE K H, ZHENG H, LEO C J. An analytical theory for 1-D nonlinear large strain consolidation of soft clay[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(6): 680-684.
[17] MITCHELL J K.岩土工程土性分析原理[M].高国瑞,译.南京: 南京工学院出版社,1988: 371-382.
MITCHELL J K. Principle of geotechnical engineering and soil property analysis[M]. Translated by Gao Guorui. Nangjing: Nanjing Institute of Technology Press, 1988: 371-382.
[18] 庞宽, 刘斯宏, 吴澎, 等. 电渗法加固软土地基基本参数室内试验研究[J]. 水运工程, 2011(3): 148-153.
PANG K, LIU S H, WU P, et al. Lab experimental study on electro-osmotic parameters for soft soil consolidation[J]. Port &Waterway Engineering, 2011(3): 148-153.
[19] 李瑛. 软黏土地基电渗固结试验和理论研究[D]. 杭州: 浙江大学, 2011.
LI Y. Experimental and theoretic study on electro-osmotic consolidation of soft clay foundation[D]. Hangzhou: Zhejiang University,2011.
[20] 罗文培. 泥浆电渗脱水试验与理论研究[D]. 郑州: 郑州大学, 2022.
LUO W P. Experimental and theoretical study on electroosmotic dewatering of mud[D]. Zhengzhou: Zhengzhou University,2022.
[21] ZHOU Y D, DENG A. Modelling combined electroosmosis-vacuum-surcharge preloading consolidation considering large-scale deformation[J]. Computers and Geotechnics, 2019, 109: 46-57.