流体流动与传热现象几乎无时无处不在,其相关系统及装备的性能提升对节能降耗及碳达峰碳中和具有极端重要性,已引起学术界和工业界越来越多的关注和重视。
流体流动与传热强化的相关研究主要通过理论分析、实验方法和数值仿真方法来进行,其解决方案多依赖于设计者的经验。随着计算机技术及数值方法的快速发展,结合计算流体动力学(computational fluid dynamics,CFD)的优化设计已成为研发中不可或缺的技术手段。
与尺寸优化(size optimization)和形状优化(shape optimization)相比,拓扑优化(topology optimization)的优势在于突破了经验性固有思维对设计的影响,拥有较高的设计自由度,允许在优化过程中改变拓扑形态,可以获得富有创新想象力的新颖复杂结构,形成颠覆性设计方案,并可通过增材制造(3D打印)等方式得到实现。
拓扑优化革新了传统功能驱动的经验设计模式,实现了性能驱动的创新设计。拓扑优化起源于固体结构领域,最早于1988年由Bens e等[1]提出并成功应用。与固体结构拓扑优化一样,对承载着流体流动与传热传质的装备进行拓扑优化设计的方法被认为是一项突破性技术,越来越受到研究人员的关注。与以应力-应变为力学基本架构的固体结构拓扑优化不同,流体拓扑优化是以“流体流动为基础”的拓扑优化,在确定目标函数和约束条件下优化流体-固体界面,以最佳方式分布流体流道,寻求获得最优的性能,实现流动阻力最小、传热效率最高等目的。
e等[1]提出并成功应用。与固体结构拓扑优化一样,对承载着流体流动与传热传质的装备进行拓扑优化设计的方法被认为是一项突破性技术,越来越受到研究人员的关注。与以应力-应变为力学基本架构的固体结构拓扑优化不同,流体拓扑优化是以“流体流动为基础”的拓扑优化,在确定目标函数和约束条件下优化流体-固体界面,以最佳方式分布流体流道,寻求获得最优的性能,实现流动阻力最小、传热效率最高等目的。
2003年Borrvall等[2]开创性地提出在流体Stokes方程中添加一个阻力项对流体速度进行惩罚,使固体区域的流动阻力远大于流体区域的流动阻力,实现了流体流道的拓扑优化。之后,众多学者对流体拓扑优化及其应用进行了大量研究。但是与固体结构拓扑优化相比,流体拓扑优化目前尚未达到成熟阶段,在主流的CAD/CAE软件中很少有流体流动的拓扑优化模块,基本没有流体流动与传热的拓扑优化功能。
增材制造(3D打印)技术的快速发展,为复杂结构的制造提供了有效途径,拓扑优化与增材制造的集成可以充分发挥两者的优势和潜力。因此,为进一步拓展流体拓扑的研究,推进其在航空航天、电子芯片、核能、新能源、储能、高端装备等领域的应用,提升相关装备产品的性能和能效水平,更好实现节能降耗、碳达峰碳中和目的,本文从流体拓扑优化的理论体系、求解方法、优化方法以及工程应用等方面展开讨论,并提出相关建议。首先,对相关文献进行了较为全面的检索,总结制约流体拓扑优化工程应用的主要因素,理清流体拓扑优化研究领域的核心主题和研究热点。其次,较系统地阐述了流体拓扑优化的关键技术,并分析了现有技术的特点和应用场景。再次,对流体拓扑优化的几个工程应用场景进行了简述。最后,对流体拓扑优化的发展趋势进行了预测和总结,并提出一些有益启示。
1 文献检索及可视化分析
为了全面分析流体拓扑优化的发展情况,通过 Web of Science 以 “topology optimization and fluid flow”为主题,进行了全面检索,发现最早文献是从2003年开始发表[2],共检索出文献374篇,最终筛选出有效论文346篇。
将上述检索出的文献信息导入VOSviewer软件,利用该软件对论文中关键词进行了共现与聚类的可视化分析,获得了该研究领域的时代热点。如图1所示为关键词频次大于4的共现与聚类图,其中,关键词的节点越大,表明出现的频率越高。节点颜色代表某一阶段的研究热点,每个节点的线条表示知识流向,根据时间先后顺序从蓝色过渡到红色。
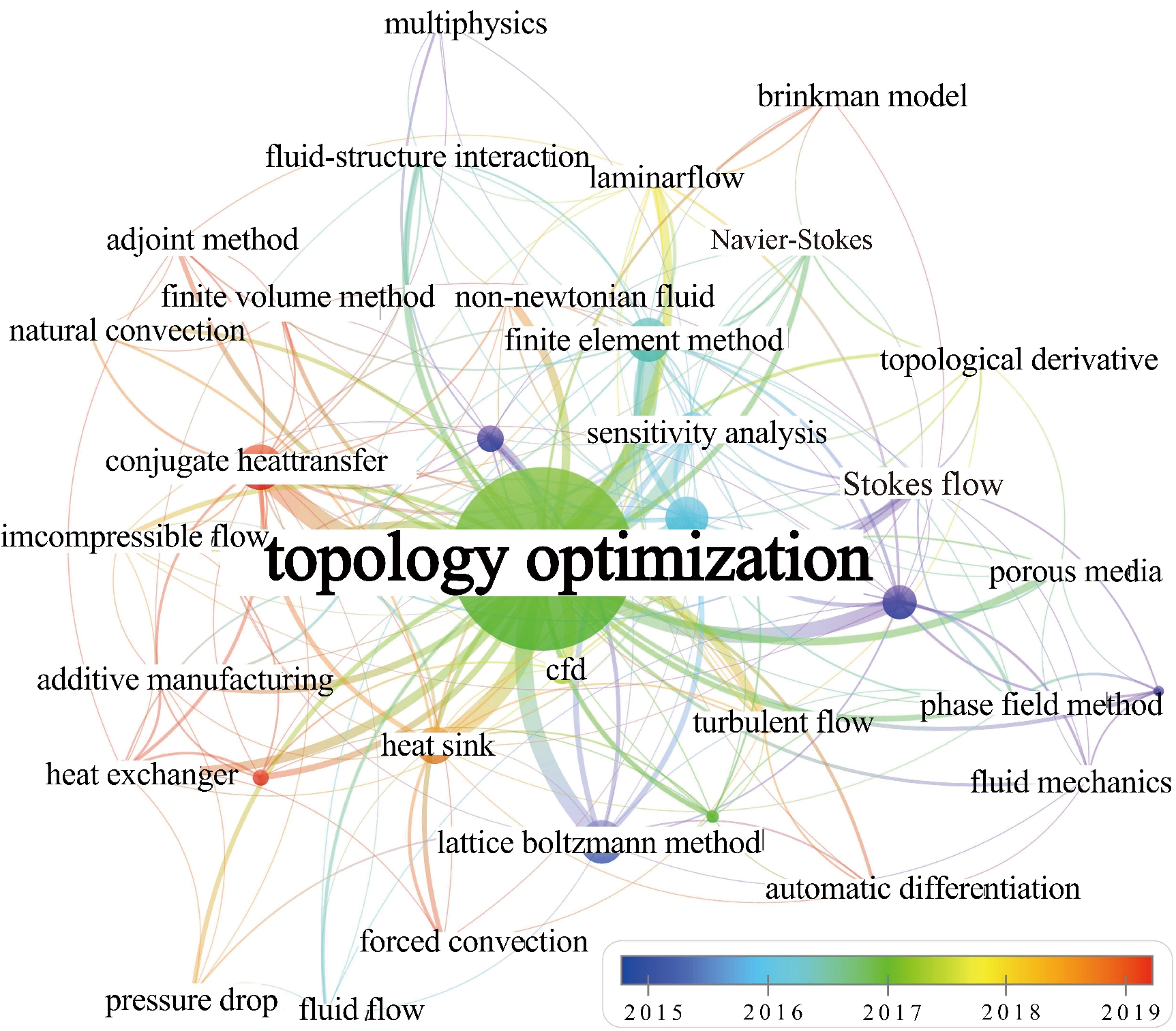
图1 关键词共现与聚类
Figure 1 Keyword co-occurrence and cluster analysis
从图1可以看出,出现频率最高的是拓扑优化(topology optimization),界定了研究领域;其次是共轭传热(conjugate heat transfer)、格子玻尔兹曼法(lattice Boltzmann method)、有限元法(finite element method)、伴随法(adjoint method)、灵敏度分析(sensitivity analysis)、湍流(turbulent flow)、层流(laminar flow)、热沉(heat sink)、换热器(heat exchanger)、增材制造(additive manufacturing)、Navier-Stokes流等,这些高频关键词体现出了目前流体拓扑优化的主要研究方向。此外,其他高频关键词主要有相场法(phase field method)、有限体积法(finite volume method)、Stokes flow、强制对流(forced convection)等。
从图1出现的高频关键词可以看出,与固体结构拓扑优化相比,流体拓扑优化涉及的领域更多,有流场、压力场,有导热、共轭传热的温度场,有流-固耦合,有流-固-热耦合等。与固体结构相比,流体流态特征更多样,有层流、湍流、Stokes flow、Navier-Stokes流;有多种湍流模型,如Spalart-Allmaras单方程模型、标准 k-ε模型、RNG k-ε模型、可实现(realizable) k-ε模型、k-ω模型等。
从图1还可以看出,换热器、湍流、多目标优化、增材制造、遗传算法、共轭传热等关键词节点偏向红色,表示这些研究方向趋向前沿,是当前流体拓扑优化研究的主要方向。
从图1中可以看到5个聚类族群。通过聚类族群的图谱展现,可以获得有关流体拓扑优化的主要热点主题,如表1所示。
表1 关键词聚类的热点主题
Table 1 Hot topics of keyword clustering
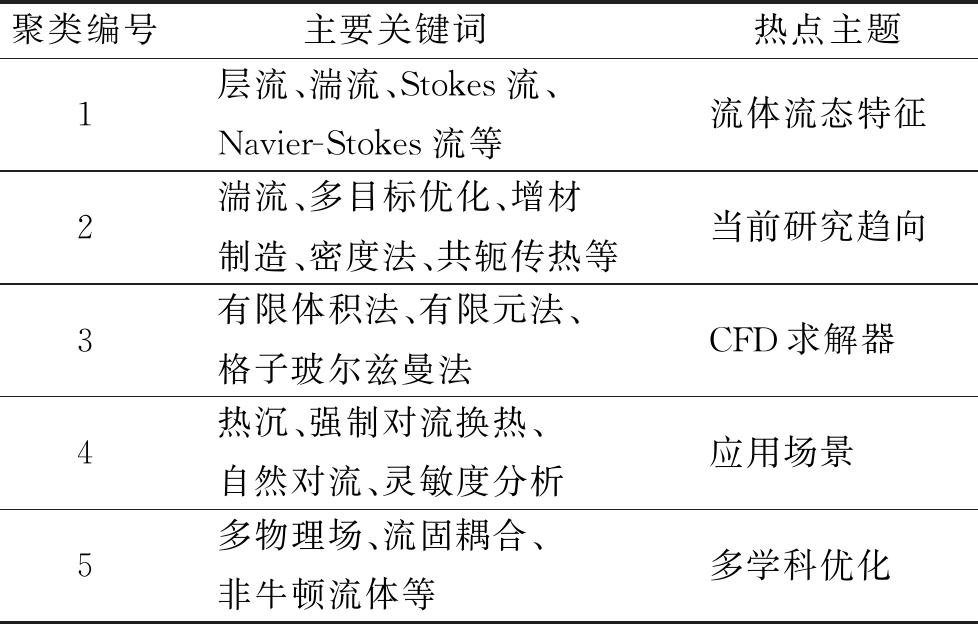
聚类编号主要关键词 热点主题1层流、湍流、Stokes流、Navier-Stokes流等流体流态特征2湍流、多目标优化、增材制造、密度法、共轭传热等当前研究趋向3有限体积法、有限元法、格子玻尔兹曼法CFD求解器4热沉、强制对流换热、自然对流、灵敏度分析应用场景5多物理场、流固耦合、非牛顿流体等多学科优化
深入查阅文献的研究内容,通过综合分析,可以发现上述5个聚类中部分研究热点重叠,经过滤整合,本文进一步将上述5个聚类统一归类为3个研究热点和关键技术:拓扑设计变量表述方法、CFD求解方法、优化求解方法。
从文献统计分析结果中可以看到,与固体结构拓扑优化相比,流体拓扑优化的研究起步较晚,文献数量比较少,在这些文献里,比较简单的稳定层流的论文比例为48%,有关共轭传热的论文比例为39%,流固耦合的论文比例为10%,而关于湍流的论文最少,只有3%。因此,与固体结构拓扑优化相比,制约流体拓扑优化研究和应用的一个主要原因是其涉及的领域更多、流态特征更多样,因而其数学模型更复杂、求解更困难、计算时间更长、计算机资源需求更大。
流体拓扑优化的基本流程如图2所示,主要包括4个环节:①拓扑设计变量表述;②确定控制方程,建立CFD模型,并进行CFD求解;③确定目标函数及约束条件,建立拓扑优化模型并进行优化求解;④后处理,输出结果。可以发现,3个研究热点和关键技术与流体拓扑优化的基本流程一致。因此,下面对拓扑设计变量表述方法、CFD求解方法、优化求解方法等3个关键环节和技术进行阐述。
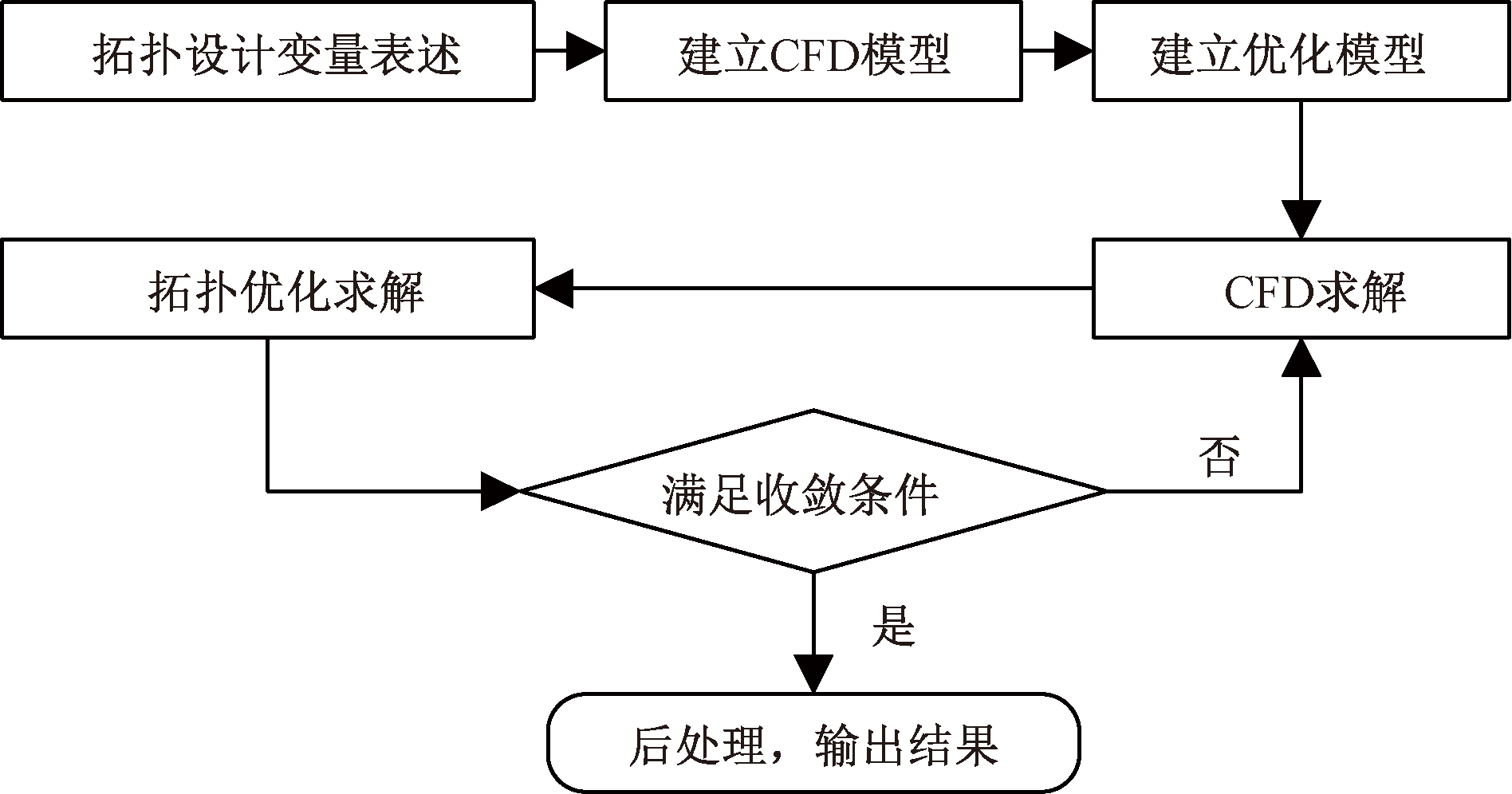
图2 流体拓扑优化基本流程
Figure 2 Workflow of fluid topology optimization
2 拓扑设计变量表述方法
由于拓扑优化类型、问题描述和物理现象各不相同,拓扑设计变量表述方法对拓扑优化的求解效率、计算精度、最终结果的影响很大。
目前最常用的拓扑设计变量表述方法主要有以下几种:变密度法(density-based)、水平集法(level set method)、双向渐进结构优化方法(BESO)、独立连续映射方法(ICM)等。
2.1 变密度法
变密度法基本思想是引入一种密度或孔隙率为0~1的可变材料,把材料密度或孔隙率作为拓扑设计变量,并通过插值函数建立拓扑设计变量与物理特性之间的关系,以寻求设计区域内最优材料分布。
图3所示为一个二维空间的拓扑优化设计域草图,该设计域为Ω,其中,固体子域为Ωs,流体子域为Ωf,且Ω = Ωs∪ Ωf。
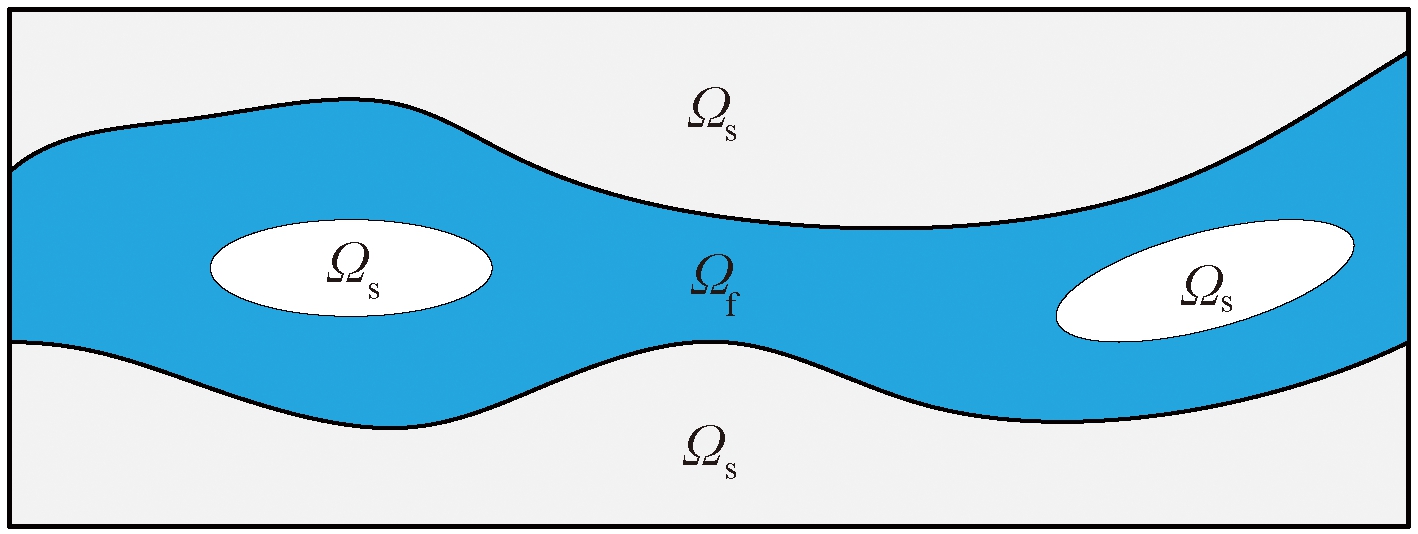
图3 流体拓扑优化设计域草图
Figure 3 Sketch of the subdomains in the design domain
在变密度法中,令γ为拓扑设计变量,表示材料密度或孔隙率,γ ∈[0,1]。当γ取0时,微元区域内没有流体,代表该微元区域为纯固体,流体不能通过;当γ取1时,微元区域内为流体材料,也就是该微元区域是流体域流体通道的一部分;当γ在0~1取值时,微元区域为多孔介质。

(1)
在设计域中,γ是通过固体或多孔介质对流体施加体力的方式来实现的。
设α为逆渗透率,令
(2)
式中:γ为拓扑设计变量;q为惩罚系数。
通过引入惩罚系数对γ在0~1的中间密度进行惩罚,使材料中间密度向0和1两个端点值逼近,从而消除中间密度。 αmax代表作用在流体上的力,其值很大,对应γ = 0; αmin代表作用在流体上的力,其值很小,对应γ = 1。
目前变密度法主要有固体各向同性惩罚模型(SIMP)、材料属性有理近似模型(RAMP)两种插值方法,建立起材料属性与拓扑设计变量的关系。
SIMP:
φ(γ)=γp·φf + (1 - γp)φs;
(3)
RAMP:
(4)
式中:φ代表材料属性,如材料密度、比热、导热系数等;φf和φs分别表示流体材料和固体材料属性;p、q均为惩罚系数。
基于变密度法的拓扑优化,为使结果不受网格影响,对设计变量进行正则化处理,采用过滤-投影法,利用亥姆霍兹方程为密度过滤器施加最小长度比例,连续细化网格。通过施加双曲正切函数的投影来消除棋盘格效应(灰度)。
变密度法是目前流体拓扑优化最流行的方法,国内外众多学者[3-9]进行了研究。Kreissl等[10]提出改进变密度法,使用离散的暂态伴随公式对非定常流进行拓扑优化。Deng等[11]基于变密度法,采用连续的瞬变伴随公式对非恒定流进行了拓扑优化。Pingen等[12]首次使用基于密度的格子玻尔兹曼公式和剪切稀化流体的Carreau-Yasuda模型,将拓扑优化应用于非牛顿流动。Matsumori等[13] 基于密度法提出了考虑Navier-Stokes方程和热传递方程耦合情况下流体和热相互作用的拓扑优化问题,通过材料拓扑来决定最佳流道布局、流道厚度等。Alexandersen等[14]基于密度法开展了自然对流问题的拓扑优化,以优化散热器和浮力驱动微型泵。Liu等[15]利用矩阵空间中的离散伴随灵敏度分析,提出一种基于格子玻尔兹曼方法的密度法。
2.2 水平集法
水平集法[5-7,9,16-21]的基本思路是引入一个水平集函数(高一维尺度函数)来隐含描述固体-流体边界,并作为控制方程的约束条件,以寻求设计区域内固体-流体边界的最优分布。
在Osher等[22]开创的水平集法上,通过演化和合并水平集函数的零轮廓来完成拓扑结构的变化。
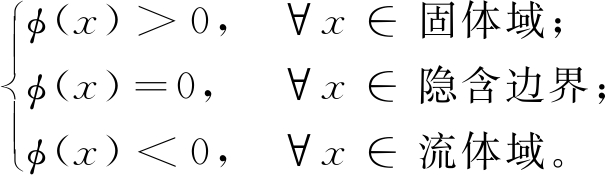
(5)
式中:φ为水平集函数;x为拓扑设计变量,表示设计域的位置。
Zhou等[16]在特定流体体积约束下,提出了一种求解定常Navier-Stokes流体拓扑优化的水平集法,并用大量的二维和三维算例说明了水平集法在解决流固形状和拓扑优化问题中的可行性和优越性。Yonekura等[23]基于水平集法研究了非定常流。Villanueva等[24]构造了一个基于有限元离散的显式水平集法,用于稳态和瞬变层流问题的二维和三维流动设计。Zhang等[25]应用基于水平集方法来最小化动脉旁路移植设计中的流动剪切应力,其中使用稳定的非牛顿修正Cross模型对血流进行建模。随后Zhang等[26]又使用具有重新网格划分的显式边界跟踪水平集法优化了非牛顿流体的微型泵。Jenkins等[27]提出建立在浸入式边界的水平集拓扑优化方法,将结构模型和流体模型耦合,对网格进行离散化处理,演示了生物主动脉心脏瓣膜的形状优化和流体中偏转梁的支撑结构优化。
2.3 双向渐进结构优化方法
双向渐进结构优化方法(BESO)是在渐进结构拓扑优化法(ESO)基础上提出的一种解决结构优化问题的数值方法[28-29]。双向渐进结构优化方法基本思想是以有限元分析结果为依据,以单元虚实为设计变量,通过单元的增加和删除,以寻求设计区域内最优的拓扑结构和形状[30]。
BESO是一种启发式算法,通过比较优化过程中产生的大量解决方案来选择最佳的解决方案[31]。近年来学者对原有的ESO/BESO算法进行了广泛的改进[32-33]。该算法目前已具有很好的稳定性与通用性,在结构拓扑优化方面得到了较好的应用。Picelli等[34]提出了一个扩展的BESO方法应用于流固耦合结构拓扑优化设计,该设计问题考虑了黏性流体流动与线弹性结构之间的相互作用。
2.4 独立连续映射方法(ICM)
独立连续映射方法(ICM)基本思想是以独立于单元具体物理参数的变量即“独立拓扑设计变量”来表征单元的“有”与“无”,通过构造过滤函数和磨光函数,把这种本质上是0和1的离散拓扑变量映射为[0,1]的连续拓扑变量,并在连续拓扑变量求解之后再把连续拓扑变量反演成离散拓扑变量,以寻求得到最优的拓扑构型。
独立连续映射方法具有很好的稳定性与通用性,求解效率高,在结构拓扑优化方面得到了较好的应用。该方法被延伸到多相材料拓扑优化、瞬态热传导问题、材料与结构一体化等方面[35-37]。Ye等[38]基于ICM方法,通过流固耦合建立了单元重量、单元质量矩阵和单元刚度矩阵的滤波函数,研究了层合板壳拓扑优化的流固耦合动力学问题。
文献信息表明,变密度法是目前流体流动与传热问题拓扑优化最流行的方法,文献量约占80%,水平集法发展较快,文献量约占15%,BESO及ICM在流体流动与传热方面的应用很少。表2对几种方法进行了归纳和总结。
表2 拓扑设计变量的表述方法
Table 2 Variable description method of topology design
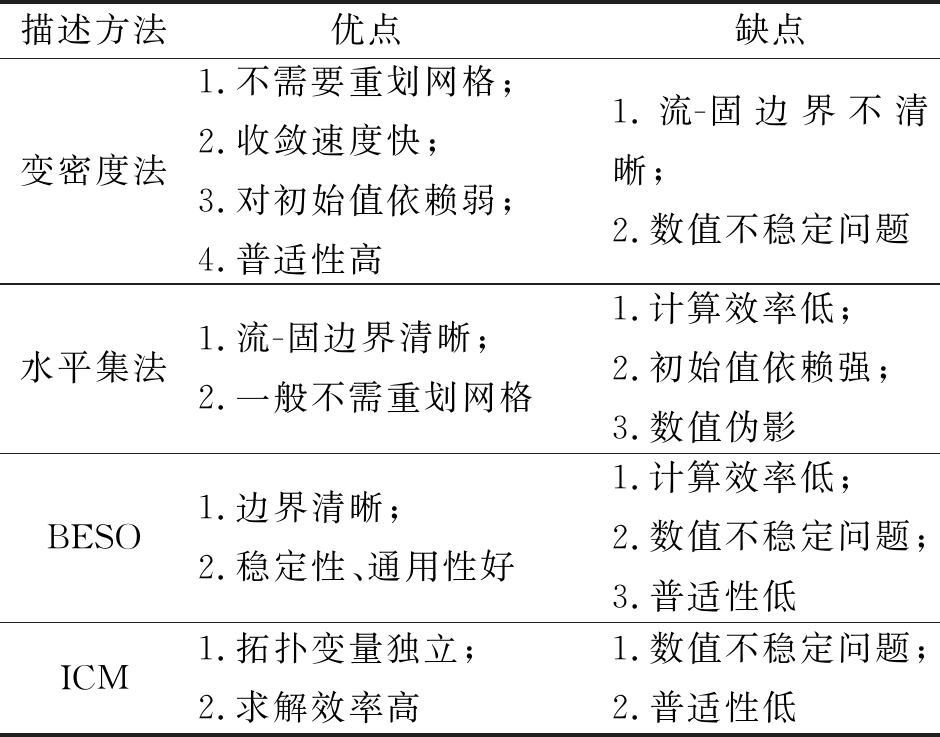
描述方法优点 缺点变密度法1.不需要重划网格;2.收敛速度快;3.对初始值依赖弱;4.普适性高1.流-固边界不清晰;2.数值不稳定问题水平集法1.流-固边界清晰;2.一般不需重划网格1.计算效率低;2.初始值依赖强;3.数值伪影BESO1.边界清晰;2.稳定性、通用性好1.计算效率低;2.数值不稳定问题;3.普适性低ICM1.拓扑变量独立;2.求解效率高1.数值不稳定问题;2.普适性低
3 CFD模型及求解方法
与固体结构承受外力载荷一样,流体流动与传热控制方程CFD模型及其求解方法决定流体拓扑优化求解难易程度、计算时间、计算资源。
3.1 流体流动与传热问题的控制方程
一般情况下,流体问题至少包含1个流体流动的控制方程,如连续方程、动量方程等,其表达式如下:
(6)
(▽u)T)]+F 。
(7)
如有能量交换,则还需添加能量方程:
(8)
式中:ρ为流体密度; p为压力; μ为流体动力黏度;μt为湍流黏度,当流动为层流时,μt=0;cp为流体比热;k为流体导热系数;u为流体速度矢量;F为作用到流体上的体积力源项;T为流体温度;Q为热源源项;t为时间;I为张量。
对于湍流问题,还需加上湍流模型。常用的湍流模型主要有Spalart-Allmaras单方程模型、标准k-ε模型、RNG k-ε模型、可实现(realizable) k-ε模型、k-ω模型、雷诺应力模型和大涡模拟。
上述连续方程、动量方程、能量方程、湍流模型等可统称为CFD模型。加上初始条件和边界条件等,可进行CFD求解。
对流体拓扑优化,方程(7)中的体积力源项F代表了固相对流体相的作用,表述为F与流体速度成正比:
F=-α(γ) u 。
(9)
当γ = 0时,α(γ)→∞(常取一个很大的值来代替无穷大),F→∞,代表作用在流体上的力很大以至于流体无法流动,该单元为固体域;当γ = 1时,α(γ)= 0,F = 0,代表作用在流体上的力很小从而可流动,该单元为流体域。
因此,流体拓扑优化,对于稳态不可压缩流体,建立的CFD模型一般为
▽·u = 0;
(10)
ρ(γ) (u · ▽) u = -▽p+(μ+μt)▽2u - α(γ)u;
(11)
ρ(γ) cp(γ) (u · ▽) T = k(γ)▽2T + Q。
(12)
对于湍流,则再加上湍流模型,如k-ε模型:
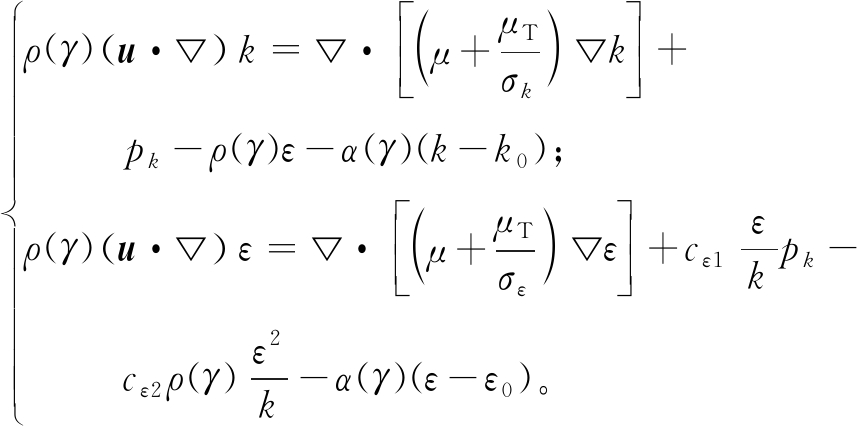
(13)
式中:ρ(γ)、cp(γ)、k(γ)分别为经SIMP或RAMP插值后的材料密度、比热、导热系数。
采用其他湍流模型时,如Spalart-Allmaras模型、k-ω模型,方法等同。
3.2 CFD求解方法
求解拓扑优化问题,一个关键的环节就是求解等式约束,即求解CFD模型的偏微分PDE方程,这需要在每次迭代中求解CFD模型以计算目标函数值。由于动量方程、湍流模型的强烈非线性,要正确而有效地模拟流动与传热是很困难的。因此,CFD求解器的计算效率和精度将极大地影响拓扑优化的性能。几十年来,研究者已经开发了有限元法(FEM)、有限体积法(FVM)、扩展有限元法(XFEM)、格子玻尔兹曼法(LBM)等多个求解器来求解控制方程。
(1)有限元法(FEM)。该方法是目前解决科学和工程问题最有效的数值方法,具有高度灵活性、准确性。
目前,基于FEM的求解器已被广泛用于二维和三维情况下的稳态层流和部分湍流。Yoon[39] 提出了一种离散伴随方法,使用SPA湍流模型和修正的壁方程应用FEM对基于密度的湍流问题进行优化并将其工作拓展到其他物理场与流体的耦合,如电场、热场。Dilgen等[40]开发了离散正向和伴随雷诺平均Navier-Stokes求解器,并采用FEM求解器进行求解。使用显式水平集法与扩展有限元法(X-FEM)相结合来解决稳态和瞬态自然对流冷却问题。
(2)有限体积法(FVM)。该方法在求解问题上显示了极好的稳健性和稳定性。FVM在稳态层流的拓扑优化中得到了很好的应用。Tawk等[41]使用基于FVM对平行流和逆流换热器进行了优化,以达到增强热力水力性能的目的。Mekki等[42]利用开源OpenFoam对换热器进行了拓扑优化。Pietropaoli等[43]应用FVM来解决换热器中的RANS方程,并采用分离涡流模拟(DES)来评估优化换热器的热性能。Kontoleontos等[44]使用FVM来解决Spalart-Allmaras湍流模型的热流体问题。
(3)扩展有限元法(XFEM)。该方法通过在不连续点附近的节点上增加丰富的自由度来改进对不连续点的描述,扩展了FEM的方法。
Coffin等[45]将XFEM和LSM结合,在拓扑优化中用于研究自然对流主导的二维和三维、稳态和瞬态单流传热问题。最近,Lin等[46]利用LSM-XFEM耦合对稳态条件下的二维散热器进行了拓扑优化,获得优化的通道拓扑结构。由于XFEM和LSM的特点,在迭代优化过程中,界面被很好地捕获,而计算负担同时增加。在基于XFEM的拓扑优化中,界面的描述可以得到改善,但在界面附近的节点上增加新的自由度会引起较高的算法复杂性,从而大大增加计算时间。
(4)格子玻尔兹曼法(LBM)。LBM是一种中尺度的方法,用于解决在宏观尺度上描述的控制方程[47-51]。LBM在传热和传质问题上显示了其稳健性和准确性,特别是在尺寸效应变得显著的微尺度情况下。它确保了局部守恒定律,在处理微观尺度上的复杂界面和尺寸效应问题时具有优势。与FEM和FVM相比,LBM与拓扑优化的整合仍处于起步阶段,在实际应用中还不够成熟。
Pingen等[52]提出了一种利用格子玻尔兹曼方法对流体流动进行建模的参数水平集法。与以往的变分水平集法不同,其采用基于梯度的数学规划方法来更新水平集函数,而不是使用传统的哈密顿-雅可比方程。Yodono等[53]提出了一种利用格子玻尔兹曼解决线性弹性体问题的拓扑优化方法,可以轻松计算基于密度法的流固耦合拓扑问题。流固耦合过程如图4所示。
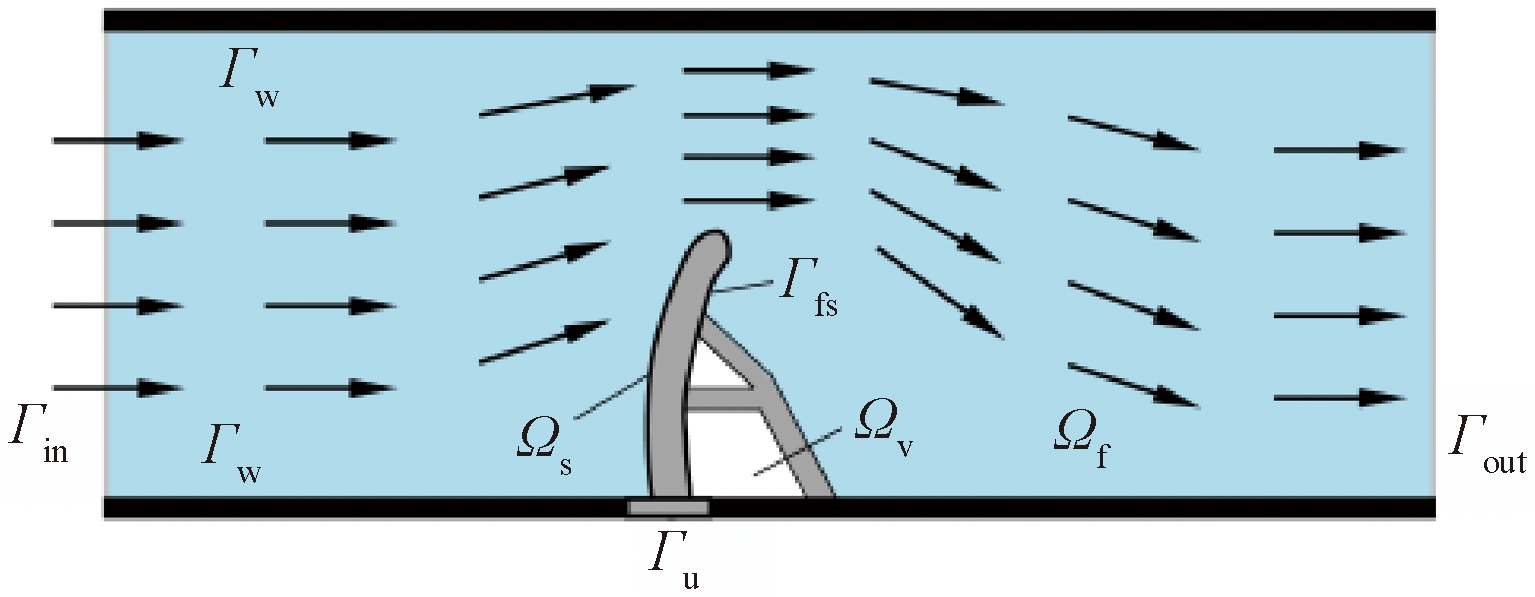
图4 流固耦合示意图
Figure 4 Schematic diagram of fluid-solid coupling
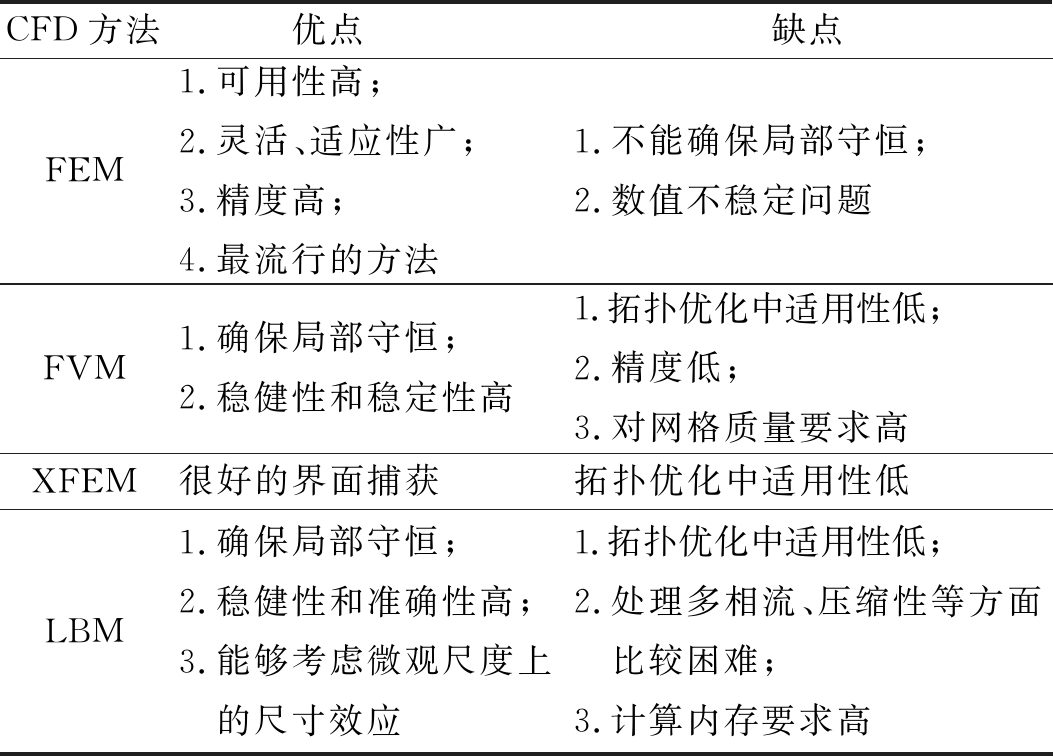
流动与传热的拓扑优化模块甚至被整合到有限元商业软件中,如COMSOL软件。文献信息表明,有限元法是目前流体拓扑优化中最常用的求解器,已发展成为一种成熟和准确的方法,文献量约占76%,格子玻尔兹曼法约占16%。尽管有限体积法多年来一直是计算流体动力学的首选求解方法,但是在拓扑优化中适用性低,约占7%左右。表3对几种CFD求解器进行了归纳和总结。
表3 CFD求解器的比较
Table 3 Comparison of CFD solvers
CFD方法优点 缺点FEM1.可用性高;2.灵活、适应性广;3.精度高;4.最流行的方法1.不能确保局部守恒;2.数值不稳定问题FVM1.确保局部守恒;2.稳健性和稳定性高1.拓扑优化中适用性低;2.精度低;3.对网格质量要求高XFEM很好的界面捕获拓扑优化中适用性低LBM1.确保局部守恒;2.稳健性和准确性高;3.能够考虑微观尺度上的尺寸效应1.拓扑优化中适用性低;2.处理多相流、压缩性等方面比较困难;3.计算内存要求高
4 拓扑优化模型及求解方法
4.1 拓扑优化模型建立
优化模型3要素:设计变量、目标函数、约束条件。一般情况下,流体拓扑优化的数学模型如下。
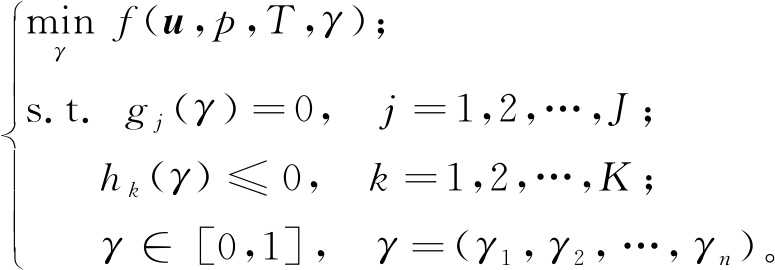
(14)
式中:γ为拓扑设计变量; f(u, p, T, γ)为目标函数,可为单目标函数或多目标函数;gj为流体流动与传热问题的控制方程;hk为状态方程或其他约束条件。
目标函数作为优化标准,对最终的拓扑结构影响极大。针对流体拓扑优化,在现有的文献中,已经有至少10多种不同的目标函数:如最小化平均温升、最小化热阻、最小化压降、最小化能量耗散、最大化换热量、最大化可回收热功率等。
目前,流体拓扑优化中,大多数研究人员处理的是单一目标函数。其中一些研究是将其他目标设定为优化约束条件来处理,还有一些研究采用加权方法来变换成单一目标函数,基本没有用多个目标函数来实现真正的多目标优化,以达到强化传热和改善水力性能的双重目标。
对于约束条件,目前常用的有水力性能、压降、最高温度、体积分数等约束。
4.2 优化求解方法
研究人员在使用CFD求解器计算出目标函数后进行优化,用以更新设计变量赋值,以便在特定约束条件下最小化或最大化目标函数。
优化求解器是拓扑优化算法的核心部分,它决定了设计域的演变,从而决定了拓扑优化的最终输出结果。因此,优化求解器的计算效率和稳定性将极大地影响拓扑优化的性能。几十年来,已经开发出基于梯度(gradient-based)、遗传算法(GA)、神经网络等多个优化求解器。
(1)基于梯度的优化算法。该方法也称为“灵敏度分析”法,是计算目标函数相对于设计变量的梯度,这些梯度代表了目标函数在每次迭代时相对于设计变量的变化,称为灵敏度。优化求解器根据这些梯度值或灵敏度来更新设计变量,以改进目标函数的值。目前已开发出以下基于梯度的优化求解器。
移动渐近线法(MMA)和全局移动渐近线法(GCMMA)是基于移动渐近线的全局收敛方法,可以广泛应用各种目标函数和约束,非常适合用于解决有多个控制变量的拓扑优化问题。
大型非线性优化求解器(SNOPT),对于解决目标和约束中具有平滑非线性函数的约束优化问题非常有效。
序列二次规划法(SQP)是一种用于大规模约束优化的算法,从二次序列规划子问题中获得搜索方向,其目标函数可以是任意形式,并可以施加任意形式的约束。当有较多的约束条件时,SNOPT是非常有效的优化求解器。
多目标序列二次规划法(MOSQP)[54]是用于边界、线性和非线性约束问题的多目标优化求解器。该算法执行顺序二次规划类型迭代,利用目标函数和约束的导数信息来构建二次模型,从中可以获得搜索方向,以构建帕累托前沿。
基于梯度的优化器是当前拓扑优化的主流优化求解器,这主要是因为它在处理涉及大量设计变量(通常等于求解器中的节点数)的问题时具有良好的效率。大量论文都采用基于梯度的优化器来解决实际问题[55-57]。
(2)遗传算法(GA)。遗传算法是一种基于染色体和基因的生物学的随机进化算法。这种进化算法在迭代几代之后获得优化的解决方案。GA避免了每次迭代时对目标函数的梯度计算。理论上,它将获得全局最优。此外,对于多目标问题来说,GA是一个很好的优化求解器。
研究人员已经在不同的领域开发和应用了GA。Sasaki等[58]提出了基于粒子方法的流体拓扑优化方法,使用瞬变运动质点半隐式(MPS)方法处理自由表面流体流动,而不需要显式的表面跟踪。
(3)神经网络算法。神经网络是一种基于机器学习的优化技术,目前贝叶斯优化算法是一种比较好的神经网络算法,该算法主要由2个部分组成:统计和采集。贝叶斯优化算法由于其较高数据效率的结构,在大数据应用中显示了较高稳健性。
Yoshimura等[59]采用贝叶斯优化算法对格子结构散热器进行了拓扑优化,采用非主导序贯遗传算法II和Kriging代用模型,最大限度地提高散热器对流传热性能,同时使材料成本最小化,以寻找具有最小CFD成本的更好设计。
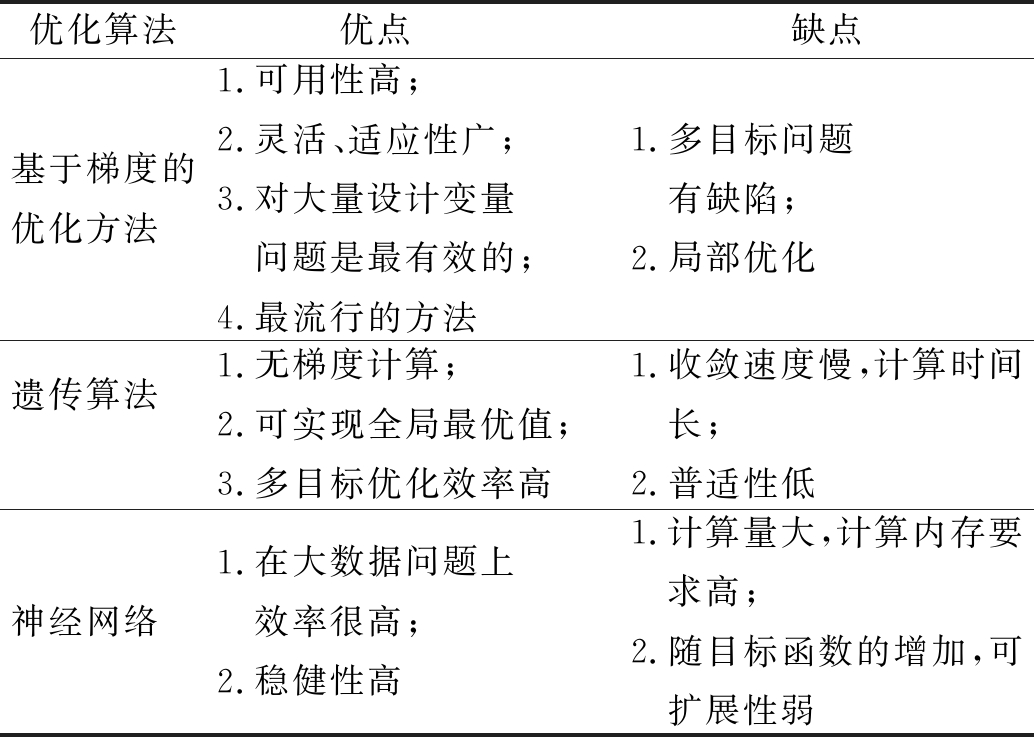
文献信息表明,基于梯度的优化算法是目前流体拓扑优化中最常用和主流的优化求解器,文献量占98%左右(其中,MMA占65%,GCMMA占23%,SNOPT占10%),遗传算法(GA)和贝叶斯优化算法所占比例很小。Sigmund[60]提出,无梯度方法对拓扑优化作用有限。因此,对于流体拓扑优化,一般应尽量避免使用无梯度方法。表4对几种优化求解器进行了归纳和总结。
表4 优化求解方法的对比
Table 4 Comparison and summary of TO methods
优化算法优点 缺点基于梯度的优化方法1.可用性高;2.灵活、适应性广;3.对大量设计变量问题是最有效的;4.最流行的方法1.多目标问题有缺陷;2.局部优化遗传算法1.无梯度计算;2.可实现全局最优值;3.多目标优化效率高1.收敛速度慢,计算时间长;2.普适性低神经网络1.在大数据问题上效率很高;2.稳健性高1.计算量大,计算内存要求高;2.随目标函数的增加,可扩展性弱
5 流体拓扑优化的应用
随着航空航天、电子芯片、核能、新能源、高端装备等领域的发展,对装备及其部件的性能要求越来越高,同时增材制造(3D打印)技术的快速发展为复杂结构的制造提供了有效途径,流体拓扑优化的推广应用将带来创新设计变革,已展现出广阔的应用前景。
5.1 在散热器方面的应用
随着高端制造业、电子芯片业及航空航天领域的发展,对各种散热技术的散热能力要求也越来越高,目前常用的散热技术主要有风冷散热、液冷散热和热管散热等。散热流道形态是决定散热器性能的重要因素。
Dede[61]对高热流密度电子冷却散热器进行了拓扑优化,采用一种多物理拓扑优化方法,获得独特的多通道流形的微通道散热器结构,该新颖结构兼具射流特性,在不增加流动阻力情况下将封装的高功率硅器件的稳态最高工作温度降低了22 K(从420 K降到398 K),增加了封装电子器件的可靠性。如图5所示为散热器速度场图。
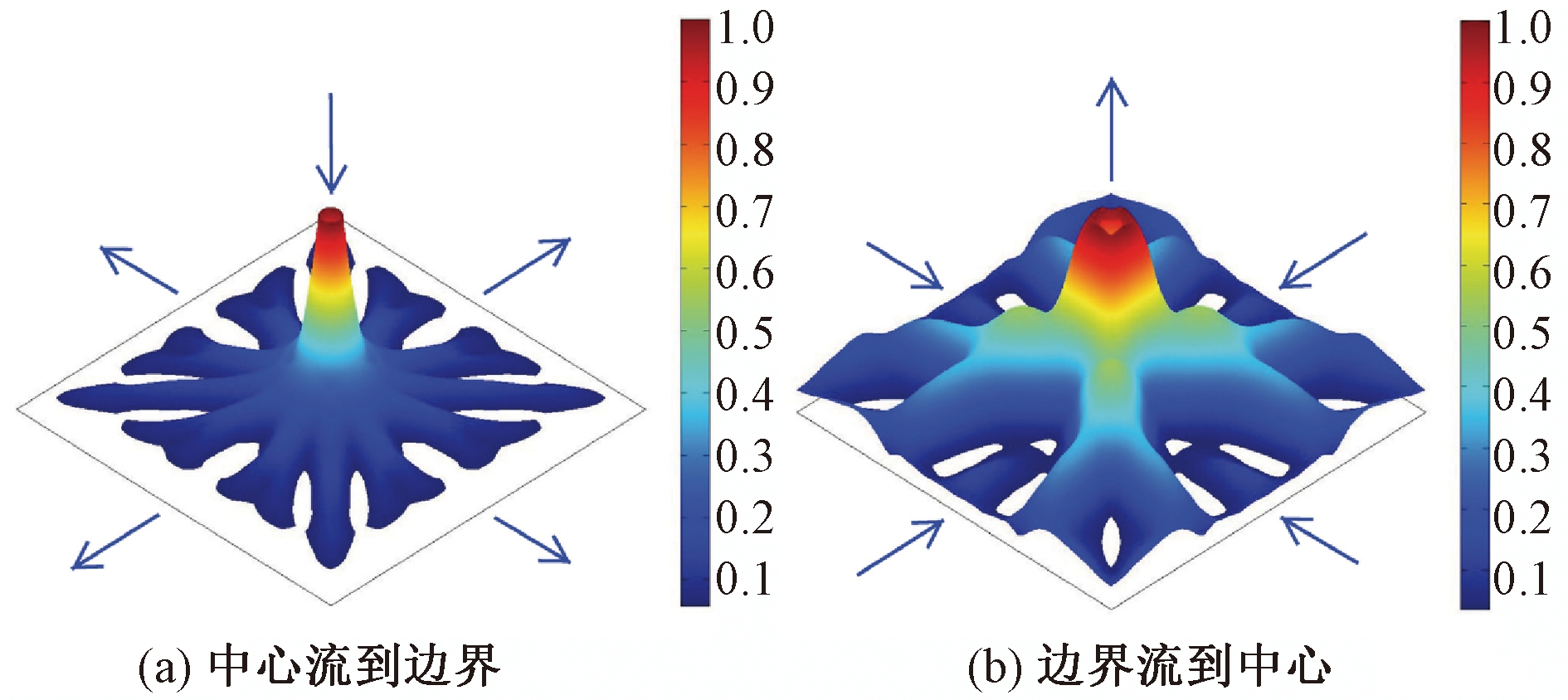
图5 拓扑优化后的冷却通道结构及速度场
Figure 5 Normalized velocity of optimized cooling channel
裴元帅等[62]利用变密度法对电子元件热沉进行拓扑优化设计,并分析了雷诺数和无量纲化产热系数对拓扑优化结果的影响,发现随着两者增加,拓扑结构的流道会随之增加,并且会变得更加细长。李含灵等[63]采用基于密度的自然对流拓扑优化方法对散热齿进行了拓扑优化设计,并采用数值模拟的方法证明了得到的新型散热齿的传热性能优于原先的散热齿。Zou等[64]以传热和水力性能为双目标,对微电子热管理中散热器进行了拓扑优化设计,针对具有不同拓扑结构的散热器设计,获得了入口雷诺数的解析公式,用于快速生成帕累托边界,并验证了设计方法的有效性和鲁棒性。其设计如图6所示。
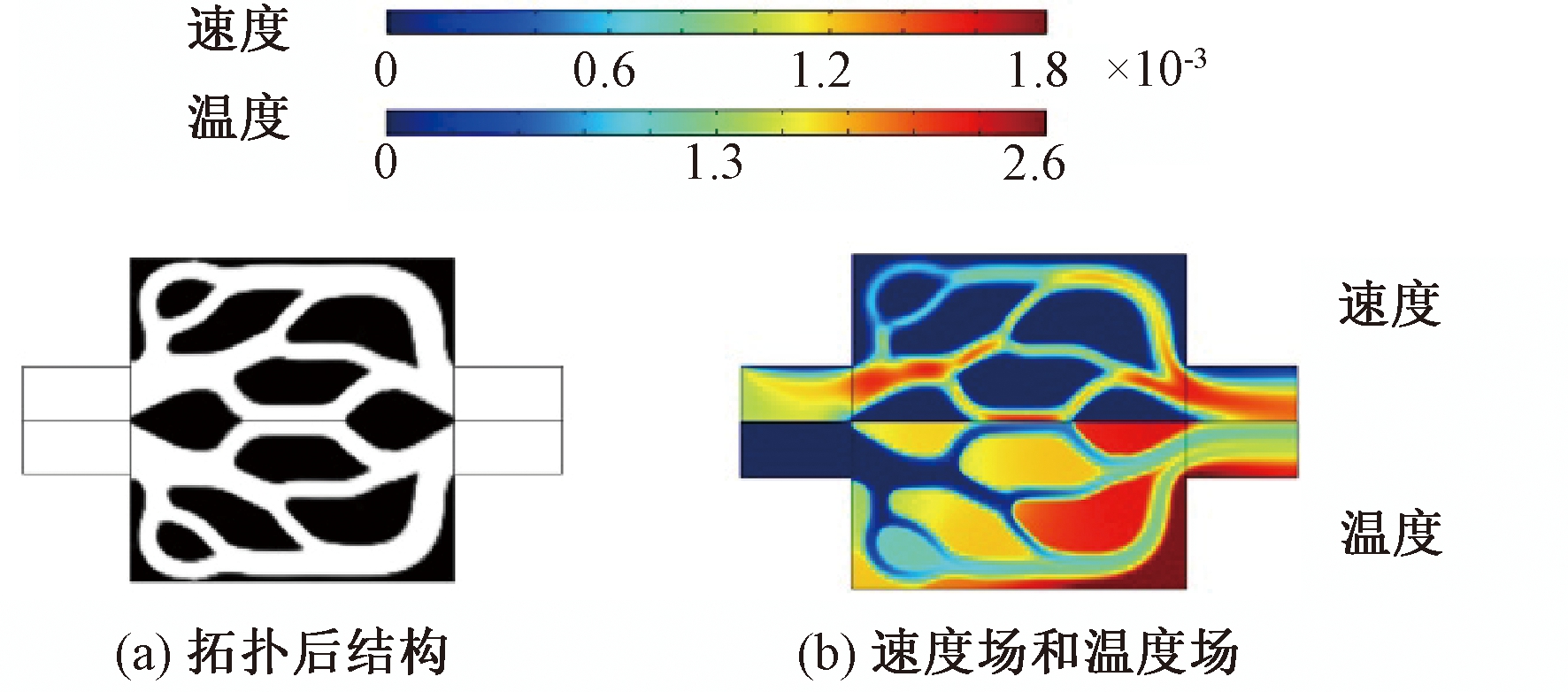
图6 电子散热器拓扑优化设计
Figure 6 Topology optimization design of electronic radiator
Yodono等[65]研究了伪三维(P3D)变密度拓扑优化在微通道散热器(MHS)设计中的应用,引入了外表面黏性耗散、自适应等效传热系数和辅助目标。结果表明,所提出的新拓扑模型可以有效地降低中间密度,提高精度,并产生清晰的结构。拓扑后的微通道散热器平均入口速度和温度均匀性分别提高305%和69%。图7所示为拓扑结构温度场。
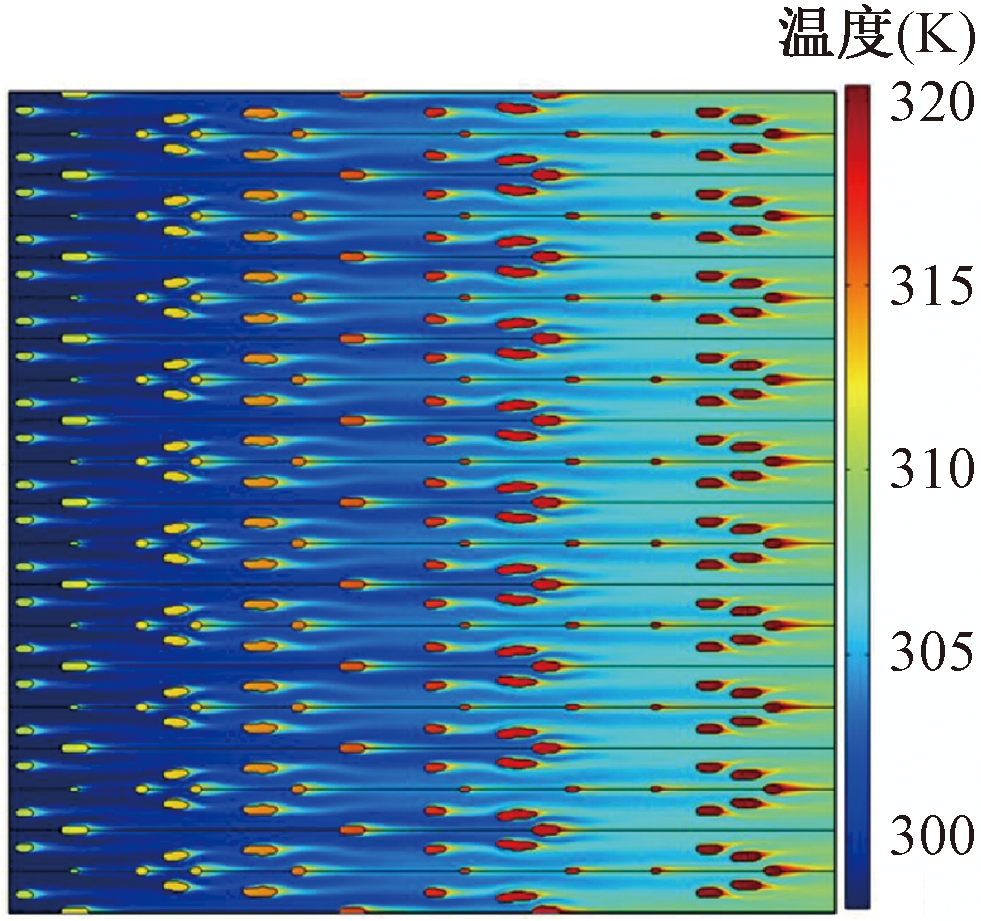
图7 微通道散热器板面温度场
Figure 7 Temperature distribution at the microchannel
5.2 在飞机汽车方面的应用
Gaymann等[66]开发了基于伴随的拓扑优化求解器,设计出具有高雷诺数流动的飞机发动机无运动部件阀门,并通过3D打印制造。拓扑优化后几何结构流动路径如图8所示。
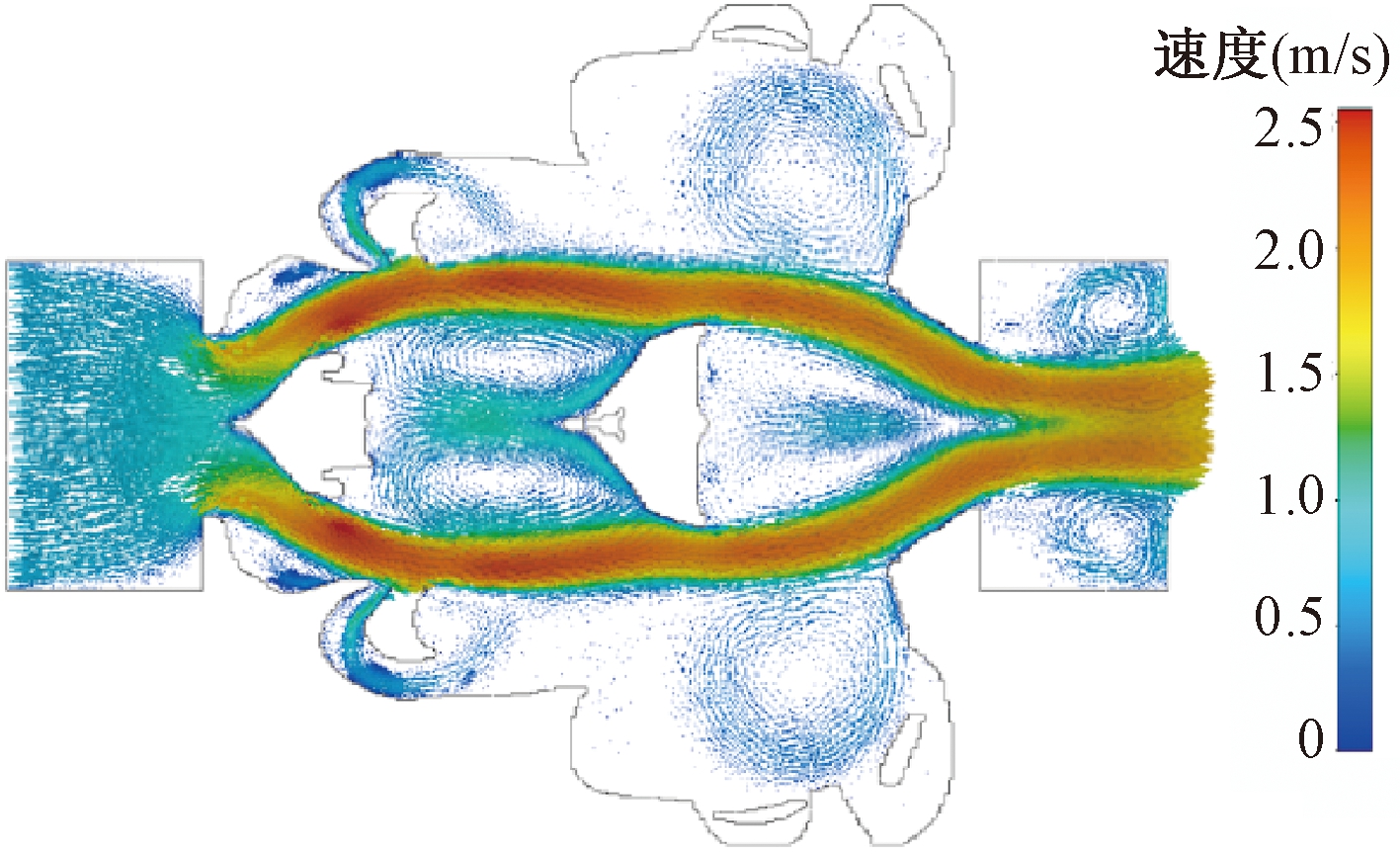
图8 拓扑优化后阀内流体速度图
Figure 8 Velocity profile of the valve optimization
Munk等[67]对具有不同耦合度的高超声速气动热弹性效应的机翼结构进行了拓扑优化,通过拓扑优化设计,机翼结构的所需质量减少了2%。此外,最大应力几乎减半。
Orbay等[68]对电动汽车永磁辅助同步磁阻电机(PMSynRM)冷却套进行了拓扑优化设计,考虑热、流体力学和电磁要求,实现了全三维共轭传热优化设计,电动机冷却套压降降低80%,散热增加11%。对于电动汽车整体而言,改进的冷却系统每消耗一次电池可多获得0.5%的续航里程。如图9为其左侧壳体和右侧冷却套边界上的温度分布。

图9 左侧壳体和右侧冷却套边界上的温度分布
Figure 9 Temperature distribution on the casing on the left and on the coolant jacket boundaries on the right
5.3 在换热器方面的应用
Hoghoj等[69]提出了以换热过程中最大换热量为目标函数,每种流体的最大压降为约束条件,对双流体换热器进行了拓扑优化研究,并基于腐蚀扩散识别技术来生成固体和流体域的界面,以确保两种流体之间的壁厚最小。结果表明,在层流流动情况下,在相同压降下,新换热器性能提高了113%。
Kobayashi等[70]提出单个设计变量解决2种流体以及2种流体之间的固体壁,防止了2种流体混合,在固定压力损失下实现了最大的传热速率。如图10所示为双流体换热器拓扑结果图。
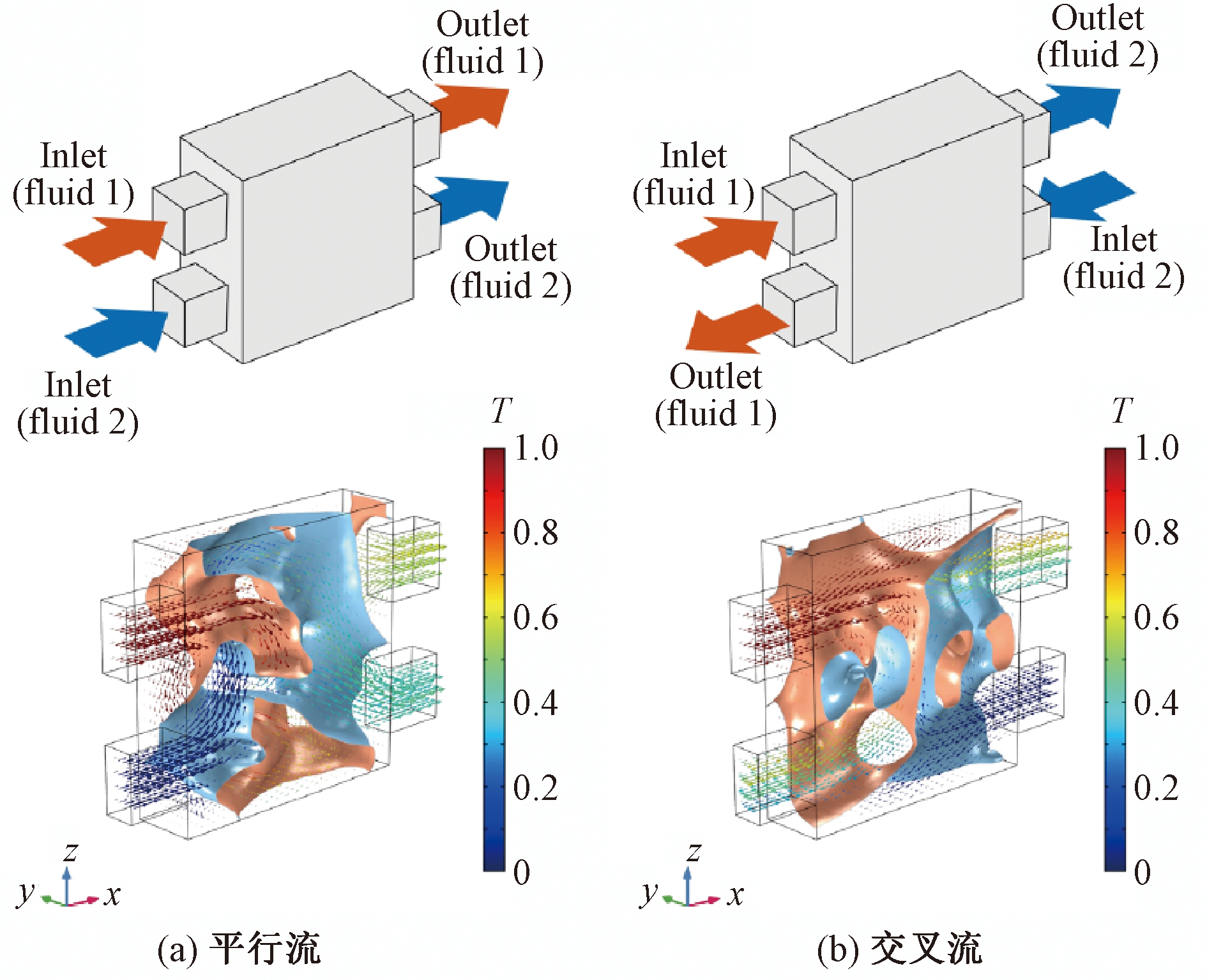
图10 双流体换热器拓扑优化
Figure 10 Topology optimization of bi-fluid heat exchanger
Liu等[71] 改进了插值方法,结合传热性能与水力性能,以动力耗散和传热率加权作为目标函数,对翅片管式换热器带状翅片结构进行了拓扑优化研究,获得了新颖呈流线型翅片小翼鳍。与传统结构相比,新颖结构传热性能增加了22.64%~28.04%;水力性能降低了33.37%~47.72%; PEC性能提高了12.7%。如图11所示。同时,在有限元框架下耦合MMA变密度法,以一种拓扑设计变量表示2种流体,实现了螺旋缠绕管换热器(双流体)的拓扑优化。换热器2D最优拓扑结果如图12所示。

图11 新颖翅片结构及速度场
Figure 11 Novel strip fins structure and velocity fields
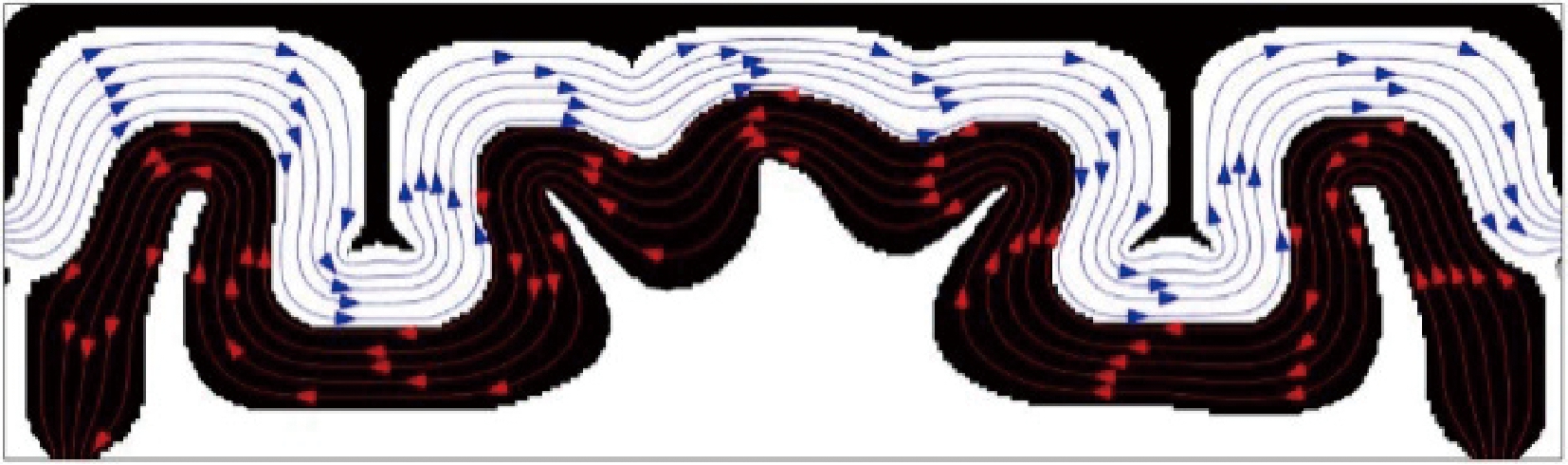
图12 换热器2D最优拓扑结果
Figure 12 2D optimal topology for heat exchanger
6 结论
增材制造(3D打印)技术的快速发展为复杂结构的制造提高了有效途径,有力促进了拓扑优化技术的发展。目前绝大多数工业CAD/CAE软件(ANSYS、COMSOL、ABAQUS、Altair、Siemens NX、nTopology等)均包含有固体结构的拓扑优化模块,并已非常成熟。但流体拓扑优化研究目前还处于起步发展阶段,现有工业CAD/CAE软件缺少成熟的流体拓扑优化模块。
在广泛查阅文献基础上,结合作者的个人经验和观点,对流体拓扑优化未来的发展趋势做以下预测。
(1) 从流态特征上,流体拓扑优化将从层流到湍流、共轭传热、流-固-热耦合、流-固-热-质耦合等方面,进一步拓展其研究深度和应用广度。
(2) 从目标函数上,流体拓扑优化将由单一目标函数向多目标函数拓展,以综合考量流动性能和传热性能的均衡。
(3) 从计算机技术上,流体拓扑优化将更加重视与人工智能的深度结合,应用机器学习、深度学习、强化学习等人工智能技术,开发更加稳健成熟的智能CFD求解器(如智能FEM法、智能LBM法等)、智能优化求解器(如遗传算法、蚁群算法等)、智能拓扑优化软件等。
[1] BENDSØE M P, KIKUCHI N. Generating optimal topologies in structural design using a homogenization method[J]. Computer Methods in Applied Mechanics and Engineering, 1988, 71(2): 197-224.
[2] BORRVALL T, PETERSSON J. Topology optimization of fluids in Stokes flow[J]. International Journal for Numerical Methods in Fluids, 2003, 41(1): 77-107.
[3] HAERTEL J H K, ENGELBRECHT K, LAZAROV B S, et al. Topology optimization of a pseudo 3D thermofluid heat sink model[J]. International Journal of Heat and Mass Transfer, 2018, 121: 1073-1088.
[4] LUNDGAARD C, ALEXANDERSEN J, ZHOU M D, et al. Revisiting density-based topology optimization for fluid-structure-interaction problems[J]. Structural and Multidisciplinary Optimization, 2018, 58(3): 969-995.
[5] SUN S C, LIEBERSBACH P, QIAN X P. Large scale 3D topology optimization of conjugate heat transfer[C]//2019 18th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm). Piscataway:IEEE, 2019: 1-6.
[6] ZENG T, WANG H,YANG M Z,et al.Topology optimization of heat sinks for instantaneous chip cooling using a transient pseudo-3D thermofluid model[J]. International Journal of Heat and Mass Transfer, 2020, 154: 119681.
[7] KUMAR P, LANGELAAR M. Topological synthesis of fluidic pressure-actuated robust compliant mechanisms[J]. Mechanism and Machine Theory, 2022, 174: 104871.
[8] ALEXANDERSEN J. A detailed introduction to density-based topology optimisation of fluid flow problems with implementation in MATLAB[EB/OL].(2022-07-19)[2022-10-11]https://doi.org/10.48550/arXiv.2207.13695
[9] KUMAR P. Towards topology optimization of pressure-driven soft robots[C]// Conference on Mechanisms and Machine Science .Cham:Springer,2022:19-30.
[10] KREISSL S, PINGEN G, MAUTE K. Optimal layout design for unsteady flows[C]//13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference. Reston: AIAA, 2010: 9400.
[11] DENG Y, LIU Z, ZHANG P, et al. Topology optimization of unsteady incompressible Navier-Stokes flows[J]. Journal of Computational Physics, 2011, 230(17): 6688-6708.
[12] PINGEN G, MAUTE K.Optimal design for non-Newtonian flows using a topology optimization approach[J]. Computers & Mathematics With Applications, 2010, 59(7): 2340-2350.
[13] MATSUMORI T, KONDOH T, KAWAMOTO A, et al. Topology optimization for fluid-thermal interaction problems under constant input power[J]. Structural and Multidisciplinary Optimization, 2013, 47(4): 571-581.
[14] ALEXANDERSEN J, AAGE N, ANDREASEN C S, et al. Topology optimisation for natural convection problems[J]. International Journal for Numerical Methods in Fluids, 2014, 76(10): 699-721.
[15] LIU G, GEIER M, LIU Z Y, et al. Discrete adjoint sensitivity analysis for fluid flow topology optimization based on the generalized lattice Boltzmann method[J]. Computers & Mathematics with Applications, 2014, 68(10): 1374-1392.
[16] ZHOU S, LI Q. A variational level set method for the topology optimization of steady-state Navier-Stokes flow[J]. Journal of Computational Physics, 2008, 227(24): 10178-10195.
[17] CHALLIS V J, GUEST J K. Level set topology optimization of fluids in Stokes flow[J]. International Journal for Numerical Methods in Engineering, 2009, 79(10): 1284-1308.
[18] DUAN XIAN BAO, QIAN FU CAI, QIN XIN QIANG. Level set method for topological optimization of the naiver-stokes fluid flow[J]. Applied Mechanics and Materials, 2012, 182/183: 1668-1672.
[19] DENG Y B, ZHANG P, LIU Y S, et al. Optimization of unsteady incompressible Navier-Stokes flows using variational level set method[J]. International Journal for Numerical Methods in Fluids, 2013, 71(12): 1475-1493.
[20] DUAN X B, DANG Y, LU J X. A variational level set method for topology optimization problems in navier-stokes flow[J]. IEEE Access, 2020, 8: 48697-48706.
[21] NEOFYTOU A, YU F M, ZHANG L, et al. Level set topology optimization for fluid-structure interactions[C]//AIAA SCITECH 2022 Forum. Reston: AIAA, 2022: 2091.
[22] OSHER S, SETHIAN J A. Fronts propagating with curvature-dependent speed: algorithms based on hamilton-jacobi formulations[J]. Journal of Computational Physics, 1988, 79(1): 12-49.
[23] YONEKURA K, KANNO Y. Topology optimization method for interior flow based on transient information of the lattice Boltzmann method with a level-set function[J]. Japan Journal of Industrial and Applied Mathematics, 2017, 34(2): 611-632.
[24] VILLANUEVA C H, MAUTE K. CutFEM topology optimization of 3D laminar incompressible flow problems[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 320: 444-473.
[25] ZHANG B, LIU X M. Topology optimization study of arterial bypass configurations using the level set method[J]. Structural and Multidisciplinary Optimization, 2015, 51(3): 773-798.
[26] ZHANG B, LIU X M, SUN J J. Topology optimization design of non-Newtonian roller-type viscous micropumps[J]. Structural and Multidisciplinary Optimization, 2016, 53(3): 409-424.
[27] JENKINS N, MAUTE K. An immersed boundary approach for shape and topology optimization of stationary fluid-structure interaction problems[J]. Structural and Multidisciplinary Optimization, 2016, 54(5): 1191-1208.
[28] QUERIN O M, STEVEN G P, XIE Y M. Evolutionary structural optimisation (ESO) using a bidirectional algorithm[J]. Engineering Computations, 1998, 15(8): 1031-1048.
[29] YANG X Y, XIE Y M, STEVEN G P, et al. Bidirectional evolutionary method for stiffness optimization[J]. AIAA Journal, 1999, 37(11): 1483-1488.
[30] 谢亿民, 黄晓东, 左志豪, 等. 渐进结构优化法(ESO)和双向渐进结构优化法(BESO)的近期发展[J]. 力学进展, 2011, 41(4): 462-471.
XIE Y M, HUANG X D, ZUO Z H, et al. Recent developments of evolutionary structural optimization (ESO) and bidirectional evolutionary structural optimization (BESO) methods[J]. Advances in Mechanics, 2011, 41(4): 462-471.
[31] ROZVANY G I N. A critical review of established methods of structural topology optimization[J]. Structural and Multidisciplinary Optimization, 2009, 37(3): 217-237.
[32] CUI N N, HUANG S P, DING X Y. An improved strategy for genetic evolutionary structural optimization[J]. Advances in Civil Engineering, 2020, 2020: 1-9.
[33] ZHUANG Z, XIE Y M, LI Q,et al. Body-fitted bi-directional evolutionary structural optimization using nonlinear diffusion regularization[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 396: 115114.
[34] PICELLI R, VICENTE W M, PAVANELLO R. Evolutionary topology optimization for structural compliance minimization considering design-dependent FSI loads[J]. Finite Elements in Analysis and Design, 2017, 135: 44-55.
[35] SUI Y, PENG X. The improvement for the ICM method of structural topology optimization [J]. Acta Mechanica Sinica, 2005, 37(2):190-198.
[36] LONG K, WANG X, GU X G. Concurrent topology optimization for minimization of total mass considering load-carrying capabilities and thermal insulation simultaneously[J]. Acta Mechanica Sinica, 2018, 34(2): 315-326.
[37] LI X, ZHAO Q, LONG K, et al. Multi-material topology optimization of transient heat conduction structure with functional gradient constraint[J]. International Communications in Heat and Mass Transfer, 2022, 131: 105845.
[38] YE H L, LI Y M, ZHANG Y M, et al. Fluid-structure interaction dynamics for laminated plate\shell topology optimization[J]. Applied Mechanics and Materials, 2013, 444/445: 55-59.
[39] YOON G H. Topology optimization for turbulent flow with Spalart-Allmaras model[J]. Computer Methods in Applied Mechanics and Engineering, 2016, 303: 288-311.
[40] DILGEN C B, DILGEN S B, FUHRMAN D R,et al. Topology optimization of turbulent flows[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 331: 363-393.
[41] TAWK R, GHANNAM B, NEMER M. Topology optimization of heat and mass transfer problems in two fluids—one solid domains[J]. Numerical Heat Transfer, Part B: Fundamentals, 2019, 76(3): 130-151.
[42] MEKKI B S, LANGER J, LYNCH S.Genetic algorithm based topology optimization of heat exchanger fins used in aerospace applications[J]. International Journal of Heat and Mass Transfer, 2021, 170: 121002.
[43] PIETROPAOLI M, GAYMANN A, MONTOMOLI F. Three-dimensional fluid topology optimization and validation of a heat exchanger with turbulent flow[EB/OL](2021-01-11)[2022-09-16].https://doi.org/10.1115/GT2020-14479.
[44] KONTOLEONTOS E A, PAPOUTSIS-KIACHAGIAS E M, ZYMARIS A S, et al. Adjoint-based constrained topology optimization for viscous flows, including heat transfer[J]. Engineering Optimization, 2013, 45(8): 941-961.
[45] COFFIN P, MAUTE K. A level-set method for steady-state and transient natural convection problems[J]. Structural and Multidisciplinary Optimization, 2016, 53(5): 1047-1067.
[46] LIN Y, ZHU W D, LI J X, et al. A stabilized parametric level-set XFEM topology optimization method for thermal-fluid problem[J]. International Journal for Numerical Methods in Engineering, 2022, 123(4): 924-952.
[47] YAJI K, YAMADA T, YOSHINO M, et al. A level set-based topology optimization using the lattice-boltzmann method[J]. Transactions of The Japan Society of Mechanical Engineers Series C, 2013, 79(802): 2152-2163.
[48] KENTARO Y, TAKAYUKI Y, MASATO Y, et al. Topology optimization in thermal-fluid flow using the lattice Boltzmann method[J]. Journal of Computational Physics, 2016, 307: 355-377.
[49] SEBASTIAN N, OLE S, BOYAN L et al. Topology optimization of unsteady flow problems using the lattice Boltzmann method[J]. Journal of Computational Physics, 2016, 307: 291-307.
[50] FLORIAN D, YANN F, CHRISTOPHE J et al. Topology optimization of thermal fluid flows with an adjoint Lattice Boltzmann Method[J]. Journal of Computational Physics, 2018, 365: 376-404.
[51] KLEMENS F, FORSTER B, DORN M,et al. Solving fluid flow domain identification problems with adjoint lattice Boltzmann methods[J]. Computers & Mathematics with Applications, 2020, 79(1): 17-33.
[52] PINGEN G, WAIDMANN M, EVGRAFOV A, et al. A parametric level-set approach for topology optimization of flow domains[J]. Structural and Multidisciplinary Optimization, 2010, 41(1): 117-131.
[53] YODONO T, YAJI K, YAMADA T, et al. Topology optimization for the elastic field using the lattice Boltzmann method[J]. Computers & Mathematics with Applications, 2022, 110: 123-134.
[54] FLIEGE J, VAZ A I F. A method for constrained multiobjective optimization based on SQP techniques[J]. SIAM Journal on Optimization, 2016, 26(4): 2091-2119.
[55] ZHOU M D, ALEXANDERSEN J, SIGMUND O, et al. Industrial application of topology optimization for combined conductive and convective heat transfer problems[J]. Structural and Multidisciplinary Optimization, 2016, 54(4): 1045-1060.
[56] SAVIERS K R, RANJAN R, MAHMOUDI R. Design and validation of topology optimized heat exchangers[C]//AIAA Scitech 2019 Forum.California. Reston: AIAA, 2019: 1465.
[57] CAO X J, WANG Y F. Optimized design of thermal insulation and fluid drag reduction for circumferentially grooved annular seal with MMA and perturbation methods[J]. Structural and Multidisciplinary Optimization, 2020, 62(2): 873-914.
[58] SASAKI Y, SATO Y, YAMADA T, et al. Topology optimization for fluid flows using the MPS method incorporating the level set method[J]. Computers & Fluids, 2019, 188: 86-101.
[59] YOSHIMURA M, SHIMOYAMA K, MISAKA T, et al. Topology optimization of fluid problems using genetic algorithm assisted by the Kriging model[J]. International Journal for Numerical Methods in Engineering, 2017, 109(4): 514-532.
[60] SIGMUND O. On the usefulness of non-gradient approaches in topology optimization[J]. Structural and Multidisciplinary Optimization, 2011, 43(5): 589-596.
[61] DEDE E M. Optimization and design of a multipass branching microchannel heat sink for electronics cooling[J]. Journal of Electronic Packaging, 2012, 134(4): 041001.
[62] 裴元帅, 王定标, 王光辉, 等. 恒定压降下电子元件热沉的拓扑优化设计[J]. 低温与超导, 2020, 48(1): 56-61.
PEI Y S, WANG D B, WANG G H, et al. Topology optimization design of electronic component heat sink under constant pressure drop[J]. Cryogenics & Superconductivity, 2020, 48(1): 56-61.
[63] 李含灵, 蓝代彦, 张显明, 等. 自然对流散热齿的拓扑优化[J]. 工程热物理学报, 2022, 43(5): 1357-1361.
LI H L, LAN D Y, ZHANG X M, et al. Topology optimization of the natural convection fin heat sink[J]. Journal of Engineering Thermophysics, 2022, 43(5): 1357-1361.
[64] ZOU A, CHUAN R, QIAN F, et al. Topology optimization for a water-cooled heat sink in micro-electronics based on Pareto frontier[J]. Applied Thermal Engineering, 2022, 207: 118128.
[65] YODONO T, YAJI K, YAMADA T. Pseudo 3D topology optimization of microchannel heat sink with an auxiliary objective[J]. International Journal of Heat and Mass Transfer, 2022, 187: 122526.
[66] GAYMANN A, MONTOMOLI F, PIETROPAOLI M. Fluid topology optimization: bio-inspired valves for aircraft engines[J]. International Journal of Heat and Fluid Flow, 2019, 79: 108455.
[67] MUNK D J, VERSTRAETE D, VIO G A. Effect of fluid-thermal-structural interactions on the topology optimization of a hypersonic transport aircraft wing[J]. Journal of Fluids and Structures, 2017, 75: 45-76.
[68] ORBAY R, TOKAT A, BECCIANI M, et al. Multiobjectively optimized PMSynRM cooling for increased vehicle efficiency[C]// 47th Annual Conference of the IEEE Industrial Electronics Society. Piscataway: IEEE, 2021: 1-6.
[69] HOGHOJ L C, NORHAVE D R, ALEXANDERSEN J, et al. Topology optimization of two fluid heat exchangers[J]. International Journal of Heat and Mass Transfer, 2020, 163: 120543.
[70] KOBAYASHI H, YAJI K, YAMASAKI S, et al. Topology design of two-fluid heat exchange[J]. Structural and Multidisciplinary Optimization, 2021, 63(2): 821-834.
[71] LIU A, WANG G, WANG D,et al. Study on the thermal and hydraulic performance of fin-and-tube heat exchanger based on topology optimization[J]. Applied Thermal Engineering, 2021, 197: 117380.