在多元化、清洁化、低碳化的新形态能源转型背景下,中国全力推进新旧能源转化,大力发展以光伏为代表的分布式清洁能源。截至2021年底,中国太阳能发电设备的装机容量为3.1亿千瓦(分布式光伏占比为35.5%),同比增长20.9%[1],分布式电源大规模接入电网带来电压越限、设备过载、功率倒送、潮流波动等问题,急需对并网分布式电源进行调控以确保电网安全稳定运行。由于分布式光伏分布的分散性以及出力的随机性[2],使用传统的集中调控模式控制分布式光伏对系统通信与计算能力要求较高,并且控制复杂。采用群调群控策略代替传统集中式调控方法是新型配电网调控的必然选择,而合理有效的集群划分方法是群调群控策略的主要基础,逐渐发展的集群调控模式为分布式光伏经济、高效地接入电网指明了方向。
德国学者最先将集群划分方法应用于电力系统,通过将多个风电站划分为一个集群,利用集群内部的协调关系应对多台风电机组大规模并网带来的电压质量问题[3]。随着中国分布式电源并网比重的增加,分布式电源调控困难问题逐渐突出,相关学者开始以物理距离为依据对分布式电源进行集群划分[4],但并未考虑节点之间的电气耦合性,集群划分效果不佳。薛峰等[5]提出将物理距离近与节点相似性强的分布式电源并入一个集群,其考虑了节点之间的电气相似性从而提高系统接纳新能源的能力。随后越来越多的学者将节点间的电气相似性作为集群划分的准则,并结合社团发现算法[6]、聚类分析算法[7-8]以及改进智能算法[9]求得集群划分最优解。魏震波等[10]利用复杂网络的社区挖掘技术划分电压控制分区,并以模块度为评价指标对电网分区质量进行评价,该算法的时间复杂度较高,不适用于节点数较多的网络。杨秀媛等[11]基于任意两节点之间电压幅值变化的灵敏度定义了电气距离,并使用模糊聚类法求得最优集群划分结果,但其在动态集群划分过程中使用的传递闭包法使计算量大幅上升,效率较低。丁明等[12]利用改进遗传算法对分布式电源进行集群划分,并用综合指标对划分结果进行评价。但遗传算法的局部搜索能力较差,进化后期搜索效率较低。为提高集群划分效率,于琳等[13]采用粒子群优化(particle swarm optimization, PSO)算法对电网节点进行集群划分,以模块度为标准评价集群划分结果,由于其惯性常数在迭代寻优时为定值,容易导致寻优过程过早收敛陷入局部最优。
为避免出现寻优时陷入局部最优的情况,本文使用惯性权重动态变化的PSO算法对分布式电源进行集群划分。首先,在模块度划分标准基础上,引入群内源荷有功匹配度与群内源荷无功匹配度2个指标,提出不仅可以反映各节点之间电气耦合性的强弱,并且可以表征群内源荷有功、无功匹配度的综合性能指标体系,构建基于综合指标体系的集群划分优化模型;其次,基于惯性权重递减策略提出惯性权重动态变化的改进二进制粒子群优化算法,以优化粒子位置与速度的更新进程,促进优化过程收敛至更佳的全局最优解;最后,采用改进二进制粒子群优化算法对IEEE33节点、某10 kV实际馈线系统的集群划分优化模型进行寻优求解。结果表明:基于综合指标所得的集群划分结果要比基于模块度指标所得的划分结果拥有更好的群内源荷有功匹配度和群内源荷无功匹配度;并且通过惯性权重动态变化的改进二进制粒子群优化算法可进一步改善集群划分效果。
1 集群划分指标
大规模分布式光伏的集群划分是集群调控的重要基础工作,通过集群划分可将无功电压灵敏度高、电气耦合性强、电气距离近的节点划分至同一集群,而集群之间的电气耦合性较弱,进而实现群内节点电压的快速高效调节。采用智能算法对复杂网络进行集群划分时,合理选择评价划分结果优劣的指标是提高集群划分效果的关键环节。
1.1 模块度指标
复杂网络中的集群结构通常由功能相近或性质相似的网络节点组成,其实质是网络节点间物理、化学或社会作用关系的区域耦合。同一集群内部的节点之间应具有较强的相似性,Newman[14]提出模块度ρ的概念并将其拓展到加权网络分区中,用以衡量复杂网络的集群划分结果,模块度的定义如下:
(1)
式中:Avw为电力网络当中节点v、w之间连边权重;m为电力网络所有边的权重之和;kv为连接节点v的所有边权重之和;kw为连接节点w的所有边权重之和;cv和cw分别为节点v和w所在社团编号,当节点v,w属于同一社团时,δ(cw,cv)=1,否则δ(cw,cv)=0。
复杂网络中节点间连边的权重值Avw由节点之间的电气距离决定。节点间的电气距离可衡量网络中两节点之间电气耦合紧密程度,表示为
ΔV=SVQΔQ。
(2)
式中:SVQ为无功电压灵敏度矩阵;ΔV和ΔQ分别为节点电压幅值变化量和节点无功变化量。矩阵SVQ中第v行第w列元素Svw表示节点w无功功率变化单位值对应节点v电压的变化值,令电压灵敏度为αvw[14],表达式为
(3)
式(3)表示节点w无功功率变化单位值时其自身电压变化值与节点v电压变化值之比,αvw越大表明节点w电压变化对节点v电压变化的影响越小,即两节点间电气距离越远。
为保证节点v与节点w之间的距离唯一,定义节点v和w之间的电气距离dvw为
dvw=dwv=-lg(αvw·αwv)。
(4)
由此定义节点v和w之间连边的权重为
Avw=1-dvw/max d。
(5)
式中:max d表示网络各节点电气距离矩阵d中所有元素的最大值。由式(5)可以看出:当节点v与节点w之间电气距离小时,两节点间的联系更为紧密,两节点间所连边的权重值更大,由此可计算集群划分结果的模块度。
1.2 群内源荷无功匹配度指标
目前,大规模分布式电源并网分层群调群控策略的控制架构可划分为群间协调优化层和集群内部自治层,其调控优化策略由群间协调策略和群内自治策略两部分构成[15]。为降低网络损耗的影响,在进行集群划分时,集群内部的无功功率供应能力应尽可能满足无功就地平衡的需求,减少跨集群的无功传递,基于此定义集群的群内源荷无功匹配度指标如下:
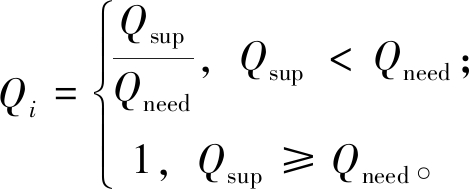
(6)
(7)
式中:Qi为集群i的群内源荷无功匹配度;Qsup为集群内部节点的无功功率供应值;Qneed为集群内部节点的无功功率的需求值;c为集群个数;定义所划分区域配电网的c个集群的平均无功平衡度φQ为其群内源荷无功匹配度指标。
1.3 群内源荷有功匹配度指标
同理,为实现分布式光伏的就地消纳,降低能量传输过程中出现的网损,应减少集群间的有功传递量。同理定义群内源荷有功匹配度指标如下:
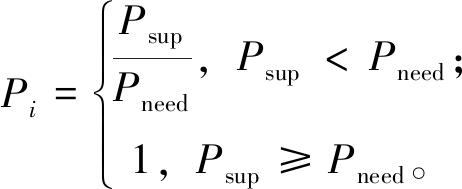
(8)
(9)
式中:Pi为集群i的群内源荷有功匹配度指标;Psup为集群内部节点的有功功率供应值;Pneed为集群内部节点的有功功率的需求值;c为集群个数;定义所划分区域配电网的c个集群的平均群内源荷有功匹配度φP为群内源荷有功匹配度指标。
综上,将模块度指标、源荷有功和无功匹配度指标加权组合提出评价集群划分优劣区域配电网的综合性能指标F:
F=αρ+βφP+γφQ。
(10)
式中:α、β、γ均为权重系数,α+β+γ=1。基于单一指标模块度ρ使用粒子群优化算法对含有分布式电源的区域配电网进行集群划分时,算法所得目标函数适应度值即为集群划分结果的模块度值ρ;采用综合指标进行集群划分时算法所得目标函数适应度值即为集群划分结果的综合指标F。
2 改进粒子群优化算法
粒子群优化算法(PSO)属于群体智能优化算法,此算法源于对鸟群捕食的行为研究。其基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。PSO算法利用无质量的粒子来模拟鸟群中的鸟,粒子具有速度和位置2个属性。
2.1 经典粒子群优化算法
将粒子群优化算法应用至分布式电源集群划分,粒子的位置即为划分结果。设待划分的复杂电网节点数为D,则粒子的位置与速度均为D维粒子。第i个粒子在经过n次迭代后的位置可记为
(11)
式中:![]() 为第n次迭代时d节点的集群编号。若xid=xie,e为复杂电网D个节点中的任一节点,则节点d与节点e被划分在同一集群内。
为第n次迭代时d节点的集群编号。若xid=xie,e为复杂电网D个节点中的任一节点,则节点d与节点e被划分在同一集群内。
第i个粒子在经过n次迭代后的速度可记为
(12)
式中:![]() 为节点d在第n次迭代时的集群编号变化量。
为节点d在第n次迭代时的集群编号变化量。
在粒子迭代寻优过程中,定义每个粒子在前n次迭代中的个体最优位置Pbest和所有粒子中的全局最优位置Gbest,则第i个粒子在n+1次迭代寻优后的速度和位置公式为
(13)
(14)
式中:T为惯性常数;c1、c2为随机生成的学习因子;r1、r2为0~1之间的随机生成的参数。
速度更新公式(13)主要由3部分组成(等号右侧3项),第1部分为记忆项,表示历史状态下的速度对当前状态下速度的影响程度;第2部分为个体认知项,是表征粒子当前位置到局部最优位置之间的距离,表示粒子基于自身经验将要进行的寻优动作;第3部分是群体认知项,是表征粒子当前位置到全局最优位置之间的距离,表示粒子基于群体经验将要进行的寻优动作。根据第n+1次寻优结果寻找当前全局最优解,并依据式(13)、式(14)在寻优过程中不断调整粒子的速度和位置,依次迭代搜寻到最优结果。
2.2 改进离散二进制粒子群优化(BPSO)算法
传统PSO算法中的c、r因子将导致集群编号出现非整数情况,为此使用BPSO算法[16]制定粒子速度与位置更新策略。首先定义BPSO算法所需的sigmoid函数以及f(x)如下:
(15)
(16)
对所有分布式电源节点进行集群划分,需要赋予节点不同的集群编号,当划分集群数目超过2个,则不满足BPSO算法的定义。为了将集群划分与BPSO算法相结合,第i个粒子中节点d的速度更新方法为
(17)
式中:T为惯性权重常数;![]() 为粒子i的节点d在n+1次迭代时位置的变化量;
为粒子i的节点d在n+1次迭代时位置的变化量;![]() 为粒子i的节点d在第n次迭代时寻优到的局部最优位置;
为粒子i的节点d在第n次迭代时寻优到的局部最优位置;![]() 为粒子i的节点d在第n次迭代时寻优到的全局最优位置;⊙为同或运算,当粒子集群编号相同时取1,集群编号不同时取0。
为粒子i的节点d在第n次迭代时寻优到的全局最优位置;⊙为同或运算,当粒子集群编号相同时取1,集群编号不同时取0。
位置更新是改进PSO算法的最重要的一步,位置更新很大程度上受速度更新的影响。当粒子迭代后速度较小为0时,意味着粒子依据记忆项、个体认知项和群体认知项得到的信息为保持当前位置不变,无须进行位置的修改;当粒子迭代后速度较大为1时,则应该对粒子位置进行修改来寻找最优值。基于此,第i个粒子中节点d的位置更新方法为
(18)
式中:![]() 为粒子i的d节点在n+1次迭代时的集群编号;
为粒子i的d节点在n+1次迭代时的集群编号;![]() 为粒子i的m节点在n+1次迭代时的集群编号;m节点为与d节点相连任意1个节点。
为粒子i的m节点在n+1次迭代时的集群编号;m节点为与d节点相连任意1个节点。
利用式(18)对粒子位置进行更新,可以达到粒子在速度值为0时,保持当前位置不变,继续进行迭代寻优;而当速度为1时,粒子便会更改自己位置,更改方式为将粒子与在拓扑结构上直接相连的邻居节点划分为同一集群,然后进行迭代寻优。此位置更新公式符合集群划分原则。
2.3 基于惯性权重线性递减策略的改进BPSO算法
为探究式(13)中记忆项惯性权重的变化对粒子群寻优过程及寻优结果的影响,基于模块度指标采用离散二进制粒子群算法对IEEE33节点系统进行集群划分,并分别设置惯性权重T=0.4、0.7、0.9,所得粒子群寻优过程中适应度与迭代次数关系曲线如图1所示。
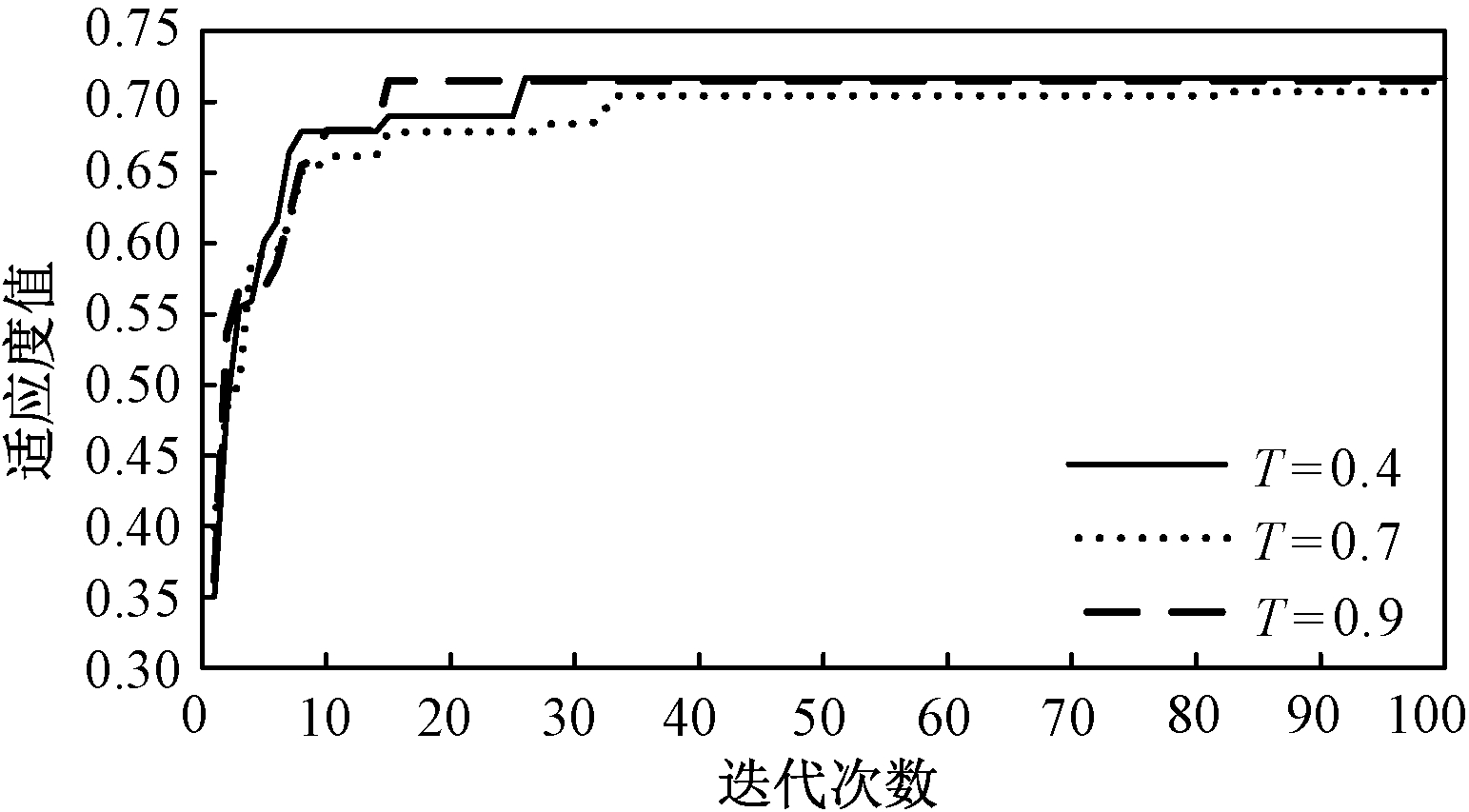
图1 T为不同常数时适应度值变化
Figure 1 Variation of fitness value when T is different constants
由图1可知,使用粒子群算法进行寻优时,当惯性权重T分别为0.4、0.7、0.9,所得适应度值分别为0.721 0、0.700 2、0.719 6,集群划分结果所得适应度值的大小对应集群划分结果的优劣程度,即适应度值越大,集群划分效果越好。当T=0.4时,集群划分所得适应度值最大,收敛速度适中;增加惯性权重值至0.7,集群划分效果与收敛速度都有不同程度的下降;继续增加惯性权重至0.9,集群划分效果与收敛速度均有所改善。惯性权重的变化会影响粒子群算法的收敛速度与集群划分效果,且集群划分效果与惯性权重无明显规律。因此为了平衡粒子的寻优能力,本文采用权重线性递减策略对算法的惯性权重进行动态调整,调整公式如下:
T=Tbegin-(Tbegin-Tfinal)g/gmax。
(19)
式中:T∈[Tfinal,Tbegin];Tbegin为初始惯性权重系数;Tfinal为最终惯性权重系数;gmax为总共迭代次数;g为当前迭代次数。
将式(19)代入式(17)可得
(20)
基于模块度指标使用惯性权重动态改变的BPSO算法对IEEE33节点进行集群划分,所得结果如图2所示。由图2可知,惯性权重保持不变时,在T=0.4时可取得较高的适应度值0.721 0;当惯性权重动态变化时,最终所得适应度值为0.734 1,比惯性权重为常数时(T=0.4、0.7、0.9)所得适应度值提高了1.8%、4.8%和2%,所得划分结果均优于惯性权重为常数值的划分结果。因此,本文采用惯性权重线性递减的BPSO算法进行集群划分。
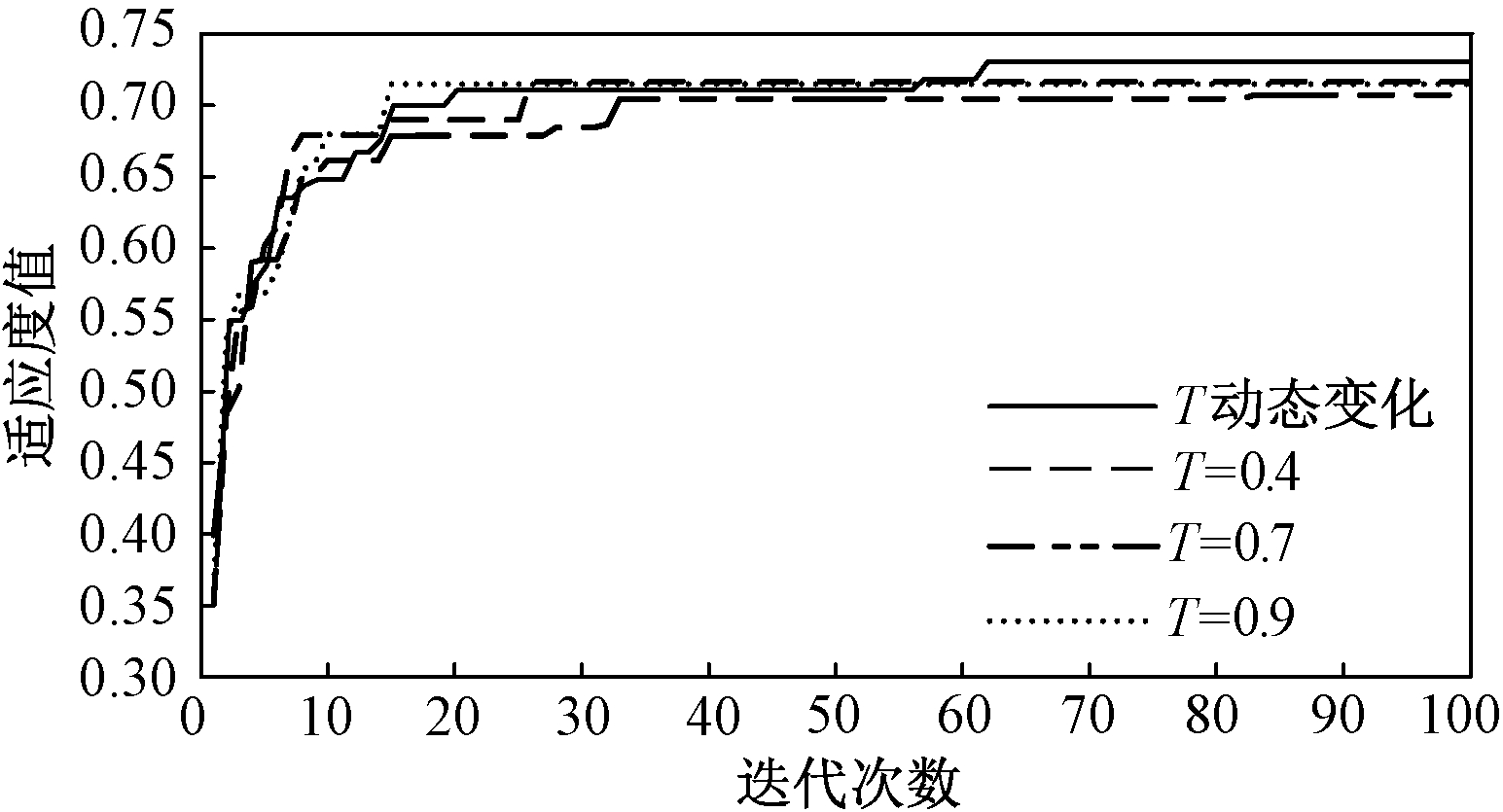
图2 T动态变化后适应度值的优化结果
Figure 2 Graph of optimization results of adaptation degree values after dynamic changes of T
2.4 算法流程
本文以模块度指标、源荷有功和无功匹配度指标加权组合的综合指标作为粒子寻优的适应度函数,应用惯性权重动态变化的改进BPSO算法对分布式光伏大规模接入的配电网节点进行集群划分,通过粒子位置与速度的不断变化完成适应度函数值的迭代寻优。具体过程如下。
(1)输入需要进行集群划分网络的拓扑结构、各支路阻抗值、负荷节点功率、光伏节点出力等系统信息。
(2)采用牛顿拉夫逊方法对该网络进行潮流计算,提取出雅可比矩阵中的无功电压灵敏度矩阵,计算电气距离矩阵和权重矩阵,构造加权网络。
(3)设定粒子群算法相关参数的数值,需要设置的参数有粒子个数、迭代次数、惯性权重值最大值、惯性权重值最小值、学习因子值等。
(4)依照式(10)计算各粒子的适应度函数值,将各粒子当前位置的适应度值分别与局部最优粒子适应度值、全局最优粒子适应度值作比较,将适应度值大的粒子作为局部最优粒子与全局最优粒子。
(5)根据式(19)更新粒子的惯性权重值。
(6)判断是否达到设置的迭代次数,如果未达到,则继续进行迭代;如果达到,则输出划分结果。
3 算例分析
采用提出的基于综合指标和惯性权重动态变化的改进BPSO算法对分布式电源接入的IEEE33节点系统、某县域10 kV实际馈线系统进行集群划分,并着重分析综合指标体系以及惯性权重动态变化等因素对集群划分结果的影响。
3.1 IEEE33节点算例分析
IEEE33节点配电系统结构如图3所示,此系统中负荷节点32个[17],含光伏电源节点15个,光伏安装总容量为5.368 4 MW,网络所需总负荷为(3 715+j2 300) kVA。
在改进的BPSO算法中设置粒子数为50,学习因子c1=c2=1.49,Tbegin=0.9,Tfinal=0.4,迭代次数设为100次。按照上述参数设置对该系统进行集群划分。
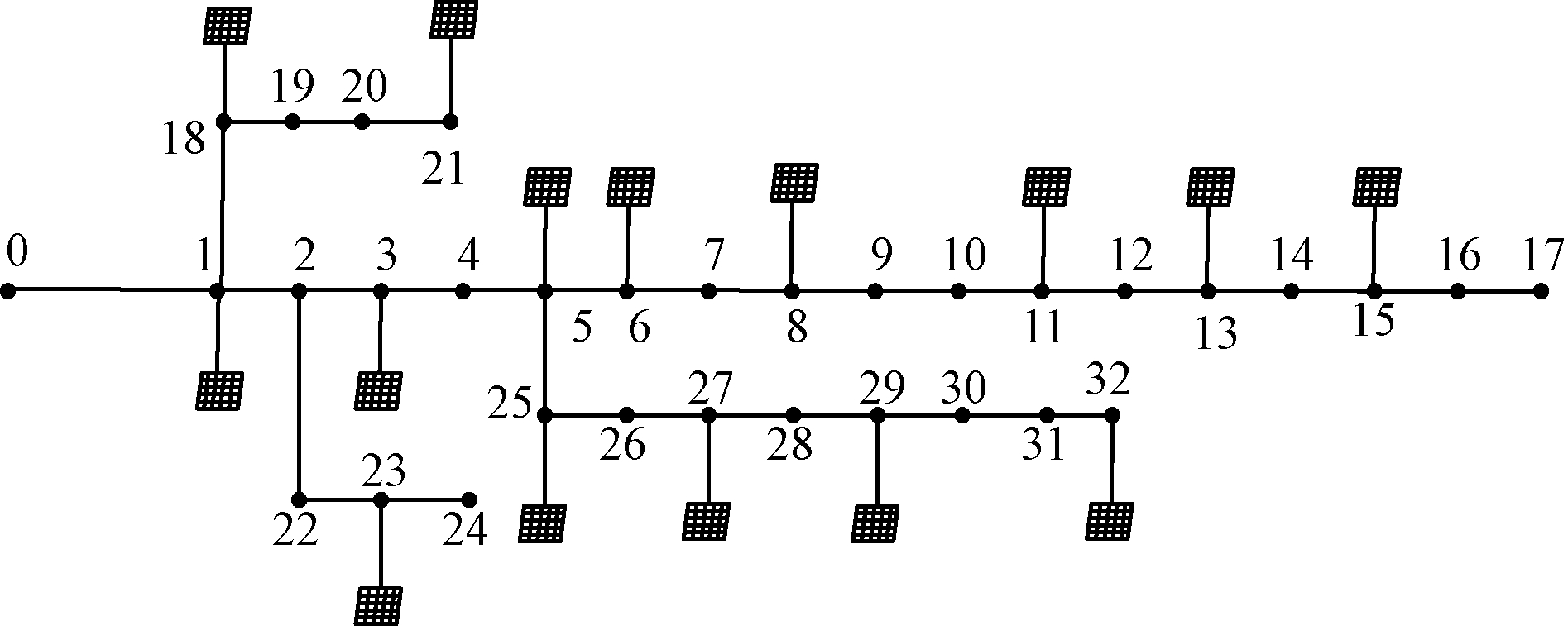
图3 IEEE33节点光伏接入拓扑图
Figure 3 Photovoltaic access topology diagram of IEEE33 nodes
3.1.1 指标权重对集群划分的影响
上文提出的适应度函数即综合指标考虑模块度、群内源荷有功匹配度、群内源荷无功匹配度3个指标,并给2个指标赋予了一定的权重。每个指标被赋予的权重大小可能会受主观因素影响,为了研究不同指标权重情况下的集群划分效果,设置某一指标相对其余两个更为重要的指标来进行赋权,划分完成后所得结果如表1所示。(1号赋权方式中模块度所占比重最大;2号赋权方式中源荷有功匹配度所占权重最大;3号赋权方式中源荷无功匹配度权重最大)。
由表1可知,2号赋权方式下,其有功匹配度指标值为1,即表明集群内部可提供的有功容量可以充分满足群内负荷的有功需求,虽然1号与2号的φP指标值相同,但2号有着更高的模块度与无功匹
表1 指标权重对集群划分影响
Table 1 Impact of indicator weights on cluster division

赋权方式FαβγρφPφQc1号0.800.50.30.20.6910.7962号0.880.30.50.20.7110.8163号0.810.30.20.50.640.990.835
配度,即划分结果当中划分节点之间的电气耦合性最好,便于后续电网集群控制,并且群内光伏电源可提供无功容量可充分匹配负荷的无功需求。而3号的φQ值指标值最高,虽然集群内部提供的无功容量可以很好地满足群内负荷的无功需求,但其另外2个指标值均低于1号和2号,集群划分效果不佳。
当模块度所占权重较大时,综合指标适应度值为0.80;当群内有功匹配度所占权重较大时,综合指标适应度值为0.88;群内无功匹配度所占权重较大时,适应度值为0.81。对比可知,2号赋权方式集群划分适应度值最高,综合考虑3种赋权方式,2号赋权方式集群划分效果最佳,为此本文采用2号赋权方式进行集群划分。集群划分结果(0节点为平衡节点,不参与集群划分)如图4所示。
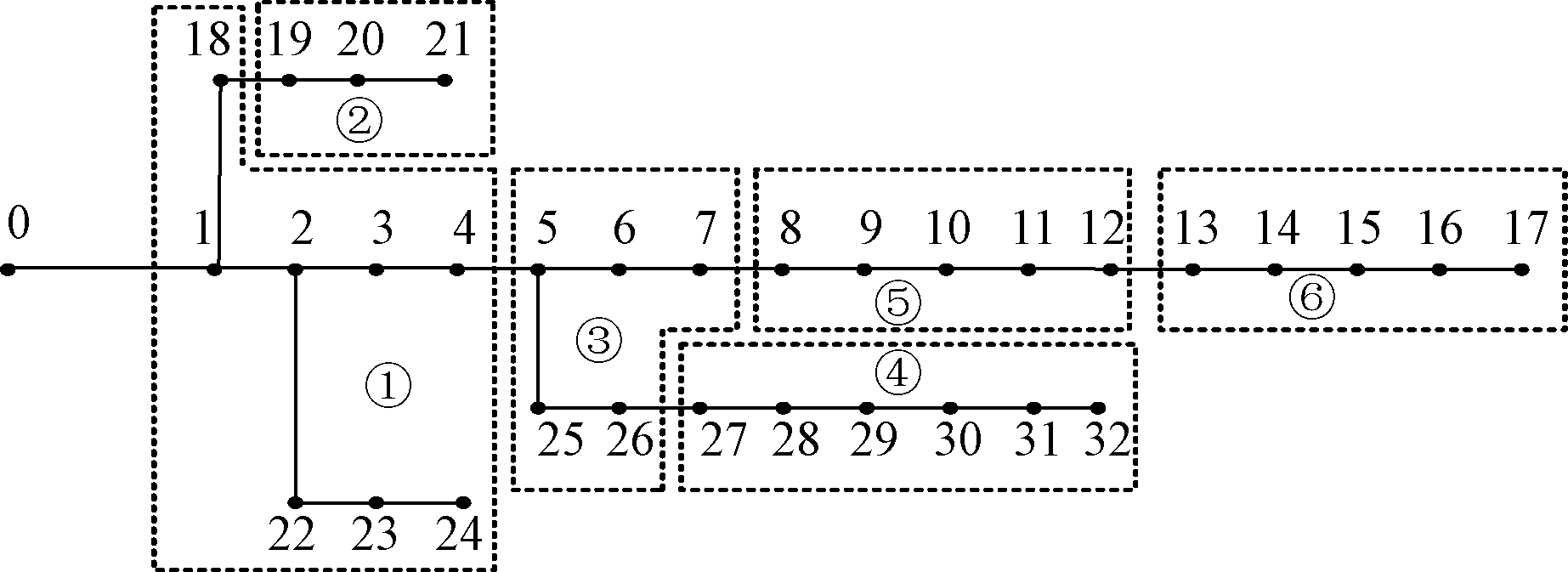
图4 IEEE33节点基于综合指标集群划分结果图
Figure 4 Result diagram of IEEE33 nodes cluster division based on comprehensive indicators
由此可见,需进行集群划分的不同分布式电源接入的配电网系统对应不同最优权重,需要针对具体系统结构及参数进行权重优化。
3.1.2 指标类型对集群划分的影响
目前大部分集群划分研究均以模块度指标为标准进行划分,为探究基于综合指标进行集群划分方法的有效性,本节分别用2种方法(方法1的集群划分指标仅考虑模块度指标;方法2的集群划分指标综合考虑模块度指标、群内源荷有功匹配度指标和群内源荷无功匹配度指标)进行集群划分,并对划分结果进行对比分析。所得结果如表2所示。
表2 指标类型对集群划分影响
Table 2 Impact of indicator types on cluster partition

方法FρφPφQc10.720.720.790.64720.880.711.000.816
由表2可知,单一指标划分所得集群个数为7,综合指标划分所得集群个数为6。综合指标划分所得模块度下降1.39%,但其划分所得F、φP、φQ指标均有大幅度提升,其中综合指标F提升22.22%,群内有功匹配度φP提升26.58%,群内无功匹配度φQ提升26.56%。由此可见,基于综合指标的集群划分方法综合考虑模块度、有功和无功匹配度3个因素,其划分结果如图5所示。

图5 IEEE33节点基于模块度指标集群划分结果图
Figure 5 Result diagram of cluster partitioning of IEEE33 nodes based on modularity index
3.1.3 惯性权重动态变化对集群划分的影响
由2.3节及文献[13]可知,基于单一模块度指标对配电网节点进行集群划分,采用定值惯性权重为0.4时集群划分模块度最大,且惯性权重动态变化可进一步改善集群划分模块度。本节基于综合指标使用2种方法(方法1惯性权重为常量0.4,方法2惯性权重动态变化)对配电网节点进行集群划分,研究惯性权重动态变化对划分结果的影响。所得结果见表3和图6。
由表3可知,方法2对模块度的改善影响最大,方法2的模块度比方法1提高4.41%,即用方法2进行划分,集群内部各节点之间耦合性更好。2种方法划分结果中无功平衡度亦提升1.25%。
表3 惯性权重动态变化对适应度值影响
Table 3 Influence of dynamic change of inertia weight on fitness value

方法FρφPφQc10.870.6810.80520.880.7110.816
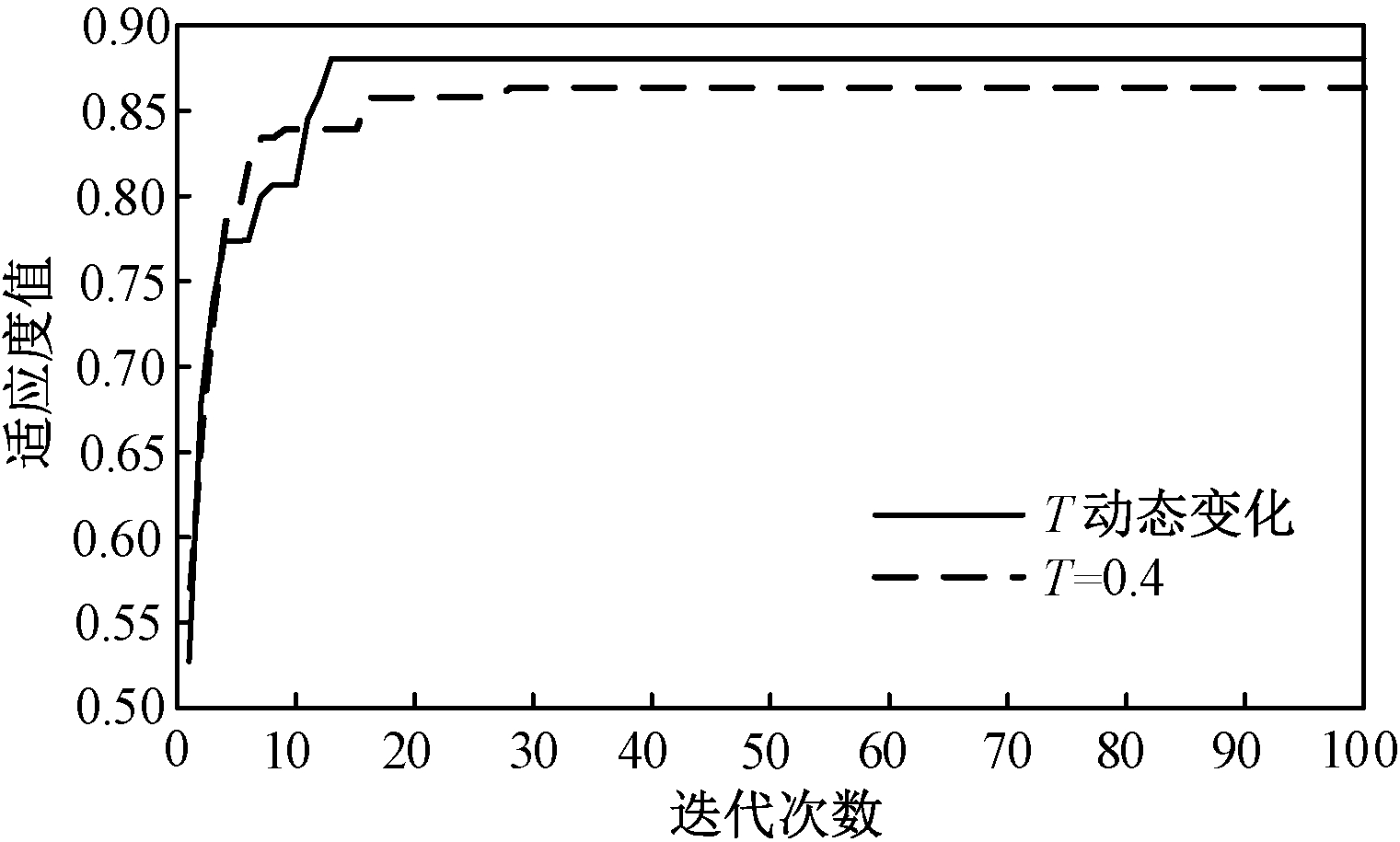
图6 基于综合指标划分不同情况下的适应度值变化
Figure 6 Variation of adaptation values in different cases when divided based on the composite index
由图6可知,当T保持为0.4不变时,基于综合指标进行集群划分所得适应度值为0.87;当T动态变化时所得适应度值为0.88,适应度值提高了1.15%,即基于综合指标进行集群划分时,惯性权重动态变化可进一步提升集群划分效果。
3.2 某县域10 kV馈线系统算例分析
采用线性权重动态变化的改进BPSO算法对某县域10 kV馈线110节点系统进行集群划分。此系统包含负荷节点109个,光伏接入节点16个,光伏安装总容量为1.732 3 MW,网络所需总负荷为(1 642+j918) kVA。馈线系统结构及光伏接入情况如图7所示。设置粒子数为50,学习因子c1=c2=1.49,Tbegin=0.9,Tfinal=0.4,迭代次数设为100次,指标权重按照赋权方式2设定。
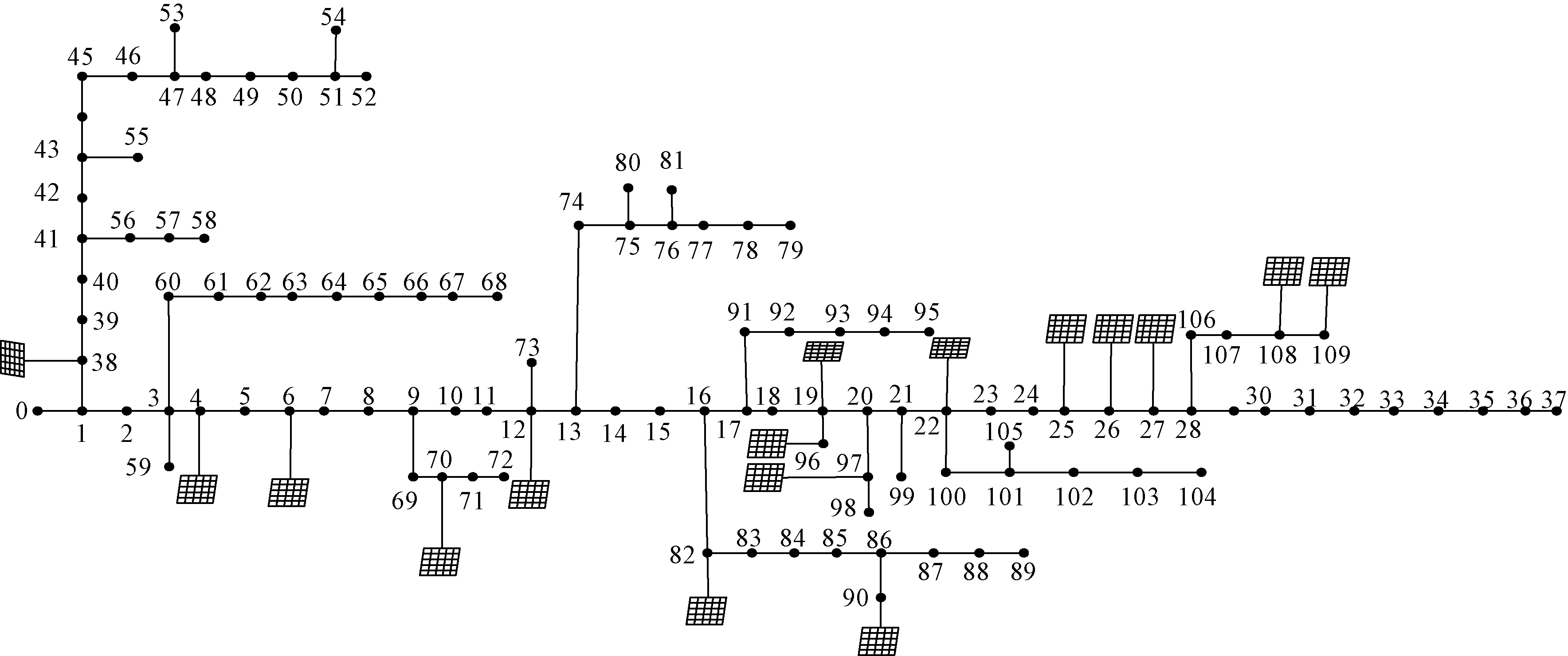
图7 某县域10 kV 110节点光伏接入拓扑图
Figure 7 Photovoltaic access topology diagram of 10 kV 110 nodes in a county
3.2.1 指标类型对集群划分的影响
本节基于2种方法(方法1基于单一模块度指标进行划分;方法2基于综合指标体系进行划分)对此配网节点进行集群划分所得结果见图8和表4。
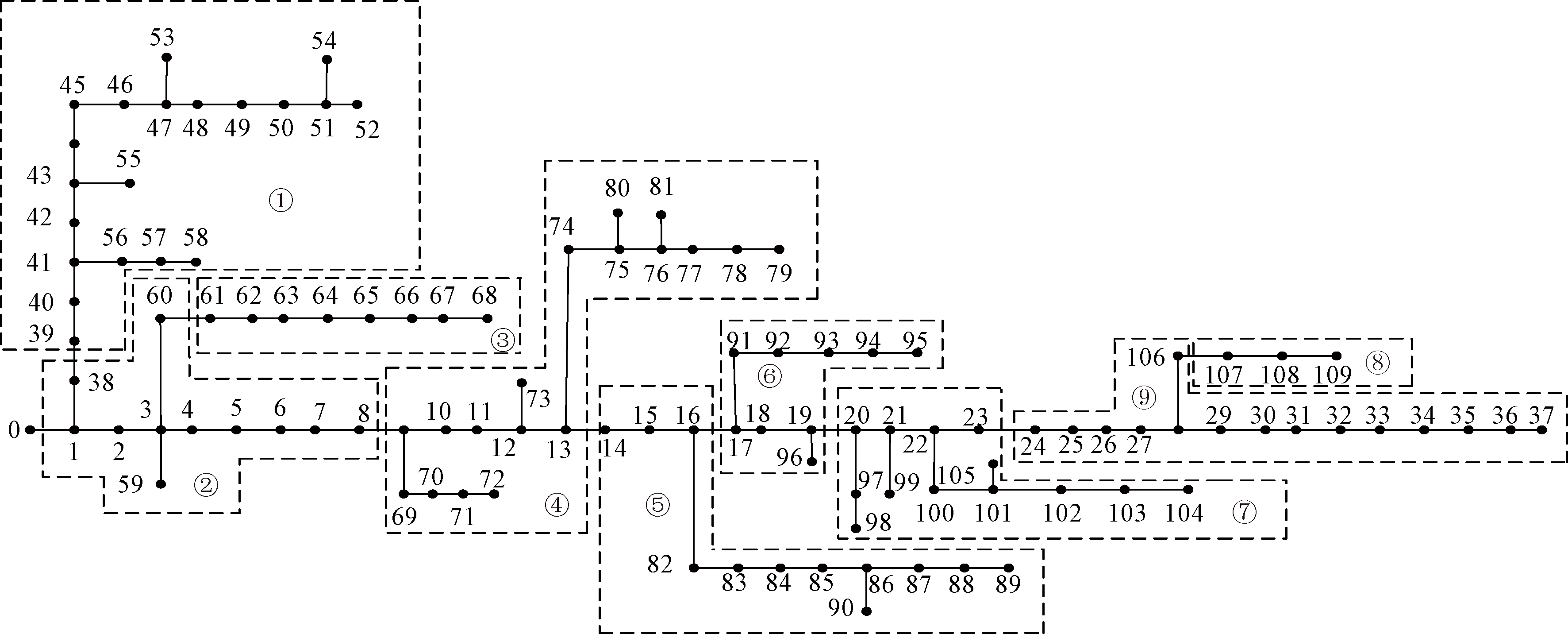
图8 110节点基于综合指标集群划分结果图
Figure 8 Result diagram of 110 nodes cluster division based on comprehensive indicators
由图8与表4可知,方法1集群划分所得集群个数为10,方法2集群划分所得集群个数为9。虽然方法2所得模块度相比方法1下降了6.10%,但通过方法2进行集群划分所得F、φP、φQ指标分别提升18.03%、36.00%、31.58%。方法2所得集群划分结果大幅度提高了群内源荷有功与无功的匹配度,可减小各集群之间有功、无功的流动量,从而降低网损。
表4 指标类型对集群划分影响
Table 4 Influence of indicator types on cluster partition

方法FρφPφQc10.610.820.500.571020.720.770.680.759
3.2.2 惯性权重动态变化对集群划分的影响
由3.1节可知,基于综合指标对配电网IEEE33节点进行集群划分,惯性权重动态变化可改善集群划分结果。本节基于综合指标使用2种方法(方法1惯性权重为常量0.4;方法2惯性权重动态变化)对实际配电网110节点进行集群划分,研究惯性权重动态变化对实际配电网集群划分结果的影响,所得结果如表5所示。
表5 惯性权重动态变化对适应度值影响
Table 5 Influence of dynamic change of inertia weight on fitness value

方法FρφPφQc10.700.760.650.741020.720.770.680.759
由表5可知,当T保持为0.4不变时,基于综合指标进行集群划分所得适应度值为0.70;当T动态变化时,所得适应度值为0.72,适应度值提高了2.86%。在实际配网中,惯性权重动态改变对3个指标值均有不同程度的改善,方法2集群划分结果的模块度值、群内源荷有功匹配度值与群内源荷无功匹配度值分别比方法1提高1.32%、4.62%、1.35%,即用方法2进行划分集群内部各节点之间耦合性更好,且各集群内部的功率平衡效果更优。
4 结论
本文在模块度划分标准基础上,引入群内源荷有功匹配度与群内源荷无功匹配度,提出一种基于综合指标和改进BPSO算法的集群划分方法,并以IEEE33节点、某10 kV实际馈线系统为例进行集群划分,对所得结果进行分析可得以下结论。
(1)与仅依靠模块度进行集群划分相比,将本文所提集群划分方法应用至IEEE33节点系统,所得结果中φP和φQ分别提高了26.58%、26.56%;而将此方法应用至某县域110节点实际配网系统中,所得结果中φP和φQ分别提高了36.00%、31.58%。即基于综合性能指标利用改进的BPSO算法进行集群划分,在考虑系统各节点电气耦合性的同时,也会充分考虑划分所得集群内部源荷之间的功率匹配程度,通过集群内部各节点间的相互配合,减少功率在群间的流动,最大程度地实现功率就地平衡,从而改善集群划分结果。
(2)与惯性权重为常数时相比,基于综合指标将惯性权重动态变化BPSO算法应用至IEEE33节点系统,所得结果中ρ和φQ分别提高了4.41%、1.25%;而将此方法应用至某县域110节点实际配网系统中,所得结果中ρ、φP、φQ分别提高了1.32%、4.62%、1.35%。即本文所提的改进BPSO算法可优化粒子的寻优过程,使粒子在迭代更新过程中寻优到更佳的集群划分结果。
[1] 国家统计局.中华人民共和国2021年国民经济和社会发展统计公报[EB/OL].(2022-02-28)[2022-10-12].http:∥www.stats.gov.cn/xxgk/sjfb/zxfb2020/202202/t20220228_1827971.html.
National Bureau of Statistics .Statistical bulletin of national economic and social development in 2021. [EB/OL]. (2022-02-28)[2022-10-12]. http:∥www.stats.gov.cn/xxgk/sjfb/zxfb2020/202202/t20220228_1827971.html.
[2] 史如新, 王德顺, 余涛, 等. 基于NARX神经网络-小波分解光伏发电功率预测[J]. 郑州大学学报(工学版), 2020, 41(6):79-84.
SHI R X, WANG D S, YU T, et al. Prediction of photovoltaic power generation based on NARX neural network-wavelet decomposition[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(6):79-84.
[3] 高平平. 考虑灵活性的分布式发电集群划分方法研究[D]. 合肥: 合肥工业大学,2020.
GAO P P. Research on partition method of distributed power generation cluster considering flexibility[D]. Hefei: Hefei University of Technology,2020.
[4] 张跃. 基于分布式发电与微网的一种新型电力集群网络技术研究[D]. 青岛: 青岛科技大学,2010.
ZHANG Y. Research on a new power cluster network technology based on distributed generation and microgrid[D]. Qingdao: Qingdao University of Science &Technology,2010.
[5] 薛峰, 常康, 汪宁渤. 大规模间歇式能源发电并网集群协调控制框架[J]. 电力系统自动化, 2011, 35(22):45-53.
XUE F, CHANG K, WANG N B. Coordinated control frame of large-scale intermittent power plant cluster[J]. Automation of Electric Power Systems, 2011, 35(22):45-53.
[6] 魏震波. 复杂网络社区结构及其在电网分析中的应用研究综述[J]. 中国电机工程学报, 2015, 35(7):1567-1577.
WEI Z B. Overview of complex networks community structure and its applications in electric power network analysis[J]. Proceedings of the CSEE, 2015, 35(7):1567-1577.
[7] 龚尚福, 陈婉璐, 贾澎涛. 层次聚类社区发现算法的研究[J]. 计算机应用研究, 2013, 30(11):3216-3220, 3227.
GONG S F, CHEN W L, JIA P T. Survey on algorithms of community detection[J]. Application Research of Computers, 2013, 30(11):3216-3220, 3227.
[8] 鲍威, 朱涛, 赵川, 等. 基于聚类分析的三阶段二级电压控制分区方法[J]. 电力系统自动化, 2016, 40(5): 127-132.
BAO W, ZHU T, ZHAO C, et al. A three-stage network partition method for secondary voltage control based on agglomerative analysis[J]. Automation of Electric Power Systems, 2016, 40(5): 127-132.
[9] 胡雪凯, 尹瑞, 时珉, 等. 基于改进粒子群算法的分布式光伏集群划分与无功优化策略[J]. 电力电容器与无功补偿, 2021, 42(4):14-21.
HU X K, YIN R, SHI M, et al. Distributed photovoltaic cluster partition and reactive power optimization strategy based on improved particle swarm optimization algorithm[J]. Power Capacitor &Reactive Power Compensation, 2021, 42(4):14-21.
[10] 魏震波, 刘俊勇, 程飞, 等. 利用社区挖掘的快速无功电压分区方法[J]. 中国电机工程学报, 2011, 31(31):166-172.
WEI Z B, LIU J Y, CHENG F, et al. Fast power network partitioning method in mvar control space based on community mining[J]. Proceedings of the CSEE, 2011, 31(31):166-172.
[11] 杨秀媛, 董征, 唐宝, 等. 基于模糊聚类分析的无功电压控制分区[J]. 中国电机工程学报, 2006, 26(22):6-10.
YANG X Y, DONG Z, TANG B, et al. Power network partitioning based on fuzzy clustering analysis[J]. Proceedings of the CSEE, 2006, 26(22):6-10.
[12] 丁明, 刘先放, 毕锐, 等. 采用综合性能指标的高渗透率分布式电源集群划分方法[J]. 电力系统自动化, 2018, 42(15):47-52, 141.
DING M, LIU X F, BI R, et al. Method for cluster partition of high-penetration distributed generators based on comprehensive performance index[J]. Automation of Electric Power Systems, 2018, 42(15):47-52, 141.
[13] 于琳, 孙莹, 徐然, 等. 改进粒子群优化算法及其在电网无功分区中的应用[J]. 电力系统自动化, 2017, 41(3):89-95, 128.
YU L, SUN Y, XU R, et al. Improved particle swarm optimization algorithm and its application in reactive power partitioning of power grid[J]. Automation of Electric Power Systems, 2017, 41(3):89-95, 128.
[14] NEWMAN M E J. Analysis of weighted networks[J]. Physical Review E,2004,70(5): 1-9.
[15] 梁志峰, 叶畅, 刘子文, 等. 分布式电源集群并网调控: 体系架构与关键技术[J]. 电网技术, 2021, 45(10): 3791-3802.
LIANG Z F, YE C, LIU Z W, et al. Grid-connected regulation of distributed power clusters: architecture and key technologies[J]. Power System Technology, 2021, 45(10): 3791-3802.
[16] 张军, 张新慧, 高震, 等. 基于改进二进制粒子群算法的孤岛划分方法[J]. 电网与清洁能源, 2022, 38(7):54-62.
ZHANG J, ZHANG X H, GAO Z, et al. An island division method based on improved binary particle swarm optimization algorithm[J]. Advances of Power System &Hydroelectric Engineering, 2022, 38(7):54-62.
[17] 于琳. 主动配电网多目标规划及控制分区研究[D]. 济南: 山东大学,2017.
YU L. Research on multi-objective planning and control partition of active distribution network[D]. Jinan: Shandong University,2017.