实际工程应用中会涉及许多约束多目标优化问题[1](constrained multi-objective optimization problem,CMOP),这些问题不仅需要优化多个目标,而且需要满足各种类型的约束。约束在搜索空间中会形成不可行区域,这给算法的求解带来了巨大的挑战,因此,解决CMOP比解决无约束的多目标优化问题(multi-objective optimization problem, MOP)更困难[2-3]。
虽然现有的约束多目标进化算法在处理具有小规模决策变量的CMOP方面表现出了良好的性能,但随着决策变量的增加,其有效性会因“维度灾难”而急剧退化[4]。大规模约束多目标优化问题 (large-scale constrained multi-objective optimization problem,LCMOP)也很常见,例如飞行安全系统的优化问题[5]、时变比误差估计问题[6]、深度神经网络参数优化问题等[7]。然而,相关学者对LCMOP的研究较少。He等[8]将固定数量的邻域解与参考向量相关联,以此来构建子种群。在每个子种群中,利用竞争粒子群的策略来生成子代。Zhang等[9]针对供应链网络优化问题,提出了一种双种群的进化算法:第一个种群用于解决原始的复杂约束优化问题,并且使用提出的线性修复算子来提高种群的可行性;第二个种群用于解决抽象的无约束问题。Wang等[10]提出了一种基于动态种群的约束多目标进化算法,种群的规模在进化过程中逐渐缩小,这将有利于在进化的早期阶段对决策空间进行充分探索。
以上算法虽然可以初步解决LCMOP,但算法的收敛速度较慢,在很多LCMOP上依旧找不到可行解,因此,大规模多目标优化是一个具有挑战性的领域,主要面临着以下难题。
(1) 随着搜索空间的增加,LCMOP的可行域会变得更小,使得种群难以满足约束条件,从而无法找到这些可行区域。
(2) 变量间的耦合更为严重,会给算法优化带来更大的困难。
(3) 当LCMOP具有许多离散可行域或者不可行区域,种群易陷入局部最优。这不仅会降低种群的收敛速度,也会严重损失种群的多样性。
为了克服以上难题,本文设计了一种自适应两阶段的约束多目标进化算法(adaptive two-stage constrained multi-objective evolutionary algorithm, ATCMEA),在不同的阶段自适应地优化不同的变量。对于第一阶段,算法在不考虑任何约束的前提下,自适应地对部分变量进行优化,以帮助种群更好地逼近无约束帕累托前沿;对于第二阶段,算法将所有的变量整体进行优化,采用ε约束处理方法引导种群向帕累托前沿收敛。此外,存档种群作为最终输出种群,用于保存可行解,并不断更新以提高其收敛性和多样性。与其他6种算法相比,在37个测试函数上的实验结果表明了所提算法的优越性。
1 相关背景及工作
1.1 相关背景
不失一般性,一个大规模约束多目标优化问题可以描述为
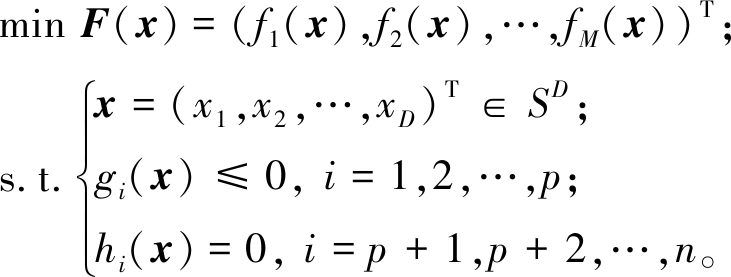
(1)
式中:F(x)为目标函数;M为目标函数数量;x为D维决策空间SD中的一个决策向量,通常当D≥100时,被称为大规模优化问题;g(x)和p分别为不等式约束和它的数量;h(x)和n分别为等式约束和它的数量。
为了计算x总的约束违反度,等式约束一般通过松弛参数δ转换为不等式约束:
|hi(x)|-δ≤0, i=p+1,p+2,…,n 。
(2)
之后,使用以下公式计算每个约束的违反度:
(3)
最后,x总的约束违反度由以下公式计算得到:
(4)
式中:当G(x)=0时,x为可行解,否则为不可行解。给定两个可行解xa与xb,对任意j∈(1,2,…,M),fj(xa)≤fj(xb),并且存在k∈(1,2,…,M),使得fk(xa)<fk(xb),则称解xa帕累托支配解xb。如果一个解不被任何解所支配,那么该解被称为帕累托最优解。LCMOP的目标是获得一组约束帕累托最优解集(constrained Pareto set,CPS)。在目标空间中,CPS映射为约束帕累托前沿(constrained Pareto front,CPF)。此外,将不考虑约束的帕累托前沿称为无约束帕累托前沿(unconstrained Pareto front,UPF)。
1.2 相关工作
近年来,各种新型的约束多目标算法被陆续提出,主要包括基于双阶段的方法和基于多种群的方法。
基于双阶段的方法将CMOP转化为两阶段优化问题,利用两个进化阶段来平衡目标和约束。Fan等[11]提出了一种推拉搜索的框架(push and pull search, PPS),在第一阶段,种群不考虑任何约束条件,仅优化目标,将种群推向无约束帕累托前沿;在第二阶段,种群考虑所有的约束和目标,并采用改进的ε约束处理方法将种群拉向约束帕累托前沿。Ma等[12]在此基础上提出了一种新的多阶段算法(multi-stage constrained multi-objective optimization, MSCMO)。与PPS不同的是,在第二阶段,MSCMO逐步添加约束,以利用更多不可行解的信息来维持种群的多样性。这类方法在相应进化阶段有不同的侧重点,大大降低了问题的优化难度。其缺点是第一阶段探索到的有希望的个体无法在第二阶段得到充分利用。
基于多种群的方法将CMOP转化为协同优化问题,使用多个种群分别搜索可行解与不可行解,以协同解决问题。Tian等[13]提出了一种协同进化框架,一个种群用于解决原始的CMOP,另一个种群解决无约束的辅助问题。两个种群在环境选择过程中通过共享后代种群来实现协同进化。Wang等[14]提出了一种多种群的协同差分进化框架,这样每个子种群仅优化一个单独的目标以及所有的约束。同时,存档种群不断保存并更新所得到的约束非支配解,逐步逼近CPF。此外,进化多任务[15](evolutionary multi-tasking,EMT)是最近提出的一种新的优化模式,其目的在于同时优化多个不同但相关的任务。通过任务间的知识迁移,以提高算法在每个任务上的求解能力[16]。受此启发,Qiao等[17]通过创建简单的辅助任务,将CMOP转化为一个多任务优化问题。在实现的算法例子中,第一个任务是原始的CMOP,另一个是从原始CMOP中提取出的MOP。同时,定义了两类知识并提出了一种新的知识匹配方法,以提高知识迁移的有效性。这类方法利用多个种群,有效地对约束和目标进行了平衡,然而如何更有效地更新和利用辅助种群仍然需要深入研究。
以上两类新型的约束多目标算法具有不同的特点,并且已经较好地解决了小规模约束多目标优化问题。然而,当解决LCMOP时,这些算法往往收敛较慢并且难以找到可行域。为了有效解决LCMOP,本文提出了一种新的自适应两阶段的大规模约束多目标算法。通过在两个阶段使用不同的决策变量优化方法,提高算法的收敛性。
2 算法描述
本文提出了一种自适应两阶段约束多目标算法来解决LCMOP,进化阶段如图1所示。如图1(a)所示,在第一阶段,所提算法在不考虑任何约束的前提下专注于搜索两个目标f1与f2。为了充分探索目标空间找到更精确的UPF,提出了一种决策变量自适应优化的策略,即在满足相应条件下,自适应地优化收敛性与多样性变量;在第二阶段,所有的变量将同时被优化,并且ε约束处理技术被用来引导种群向CPF收敛,如图1(b)所示。
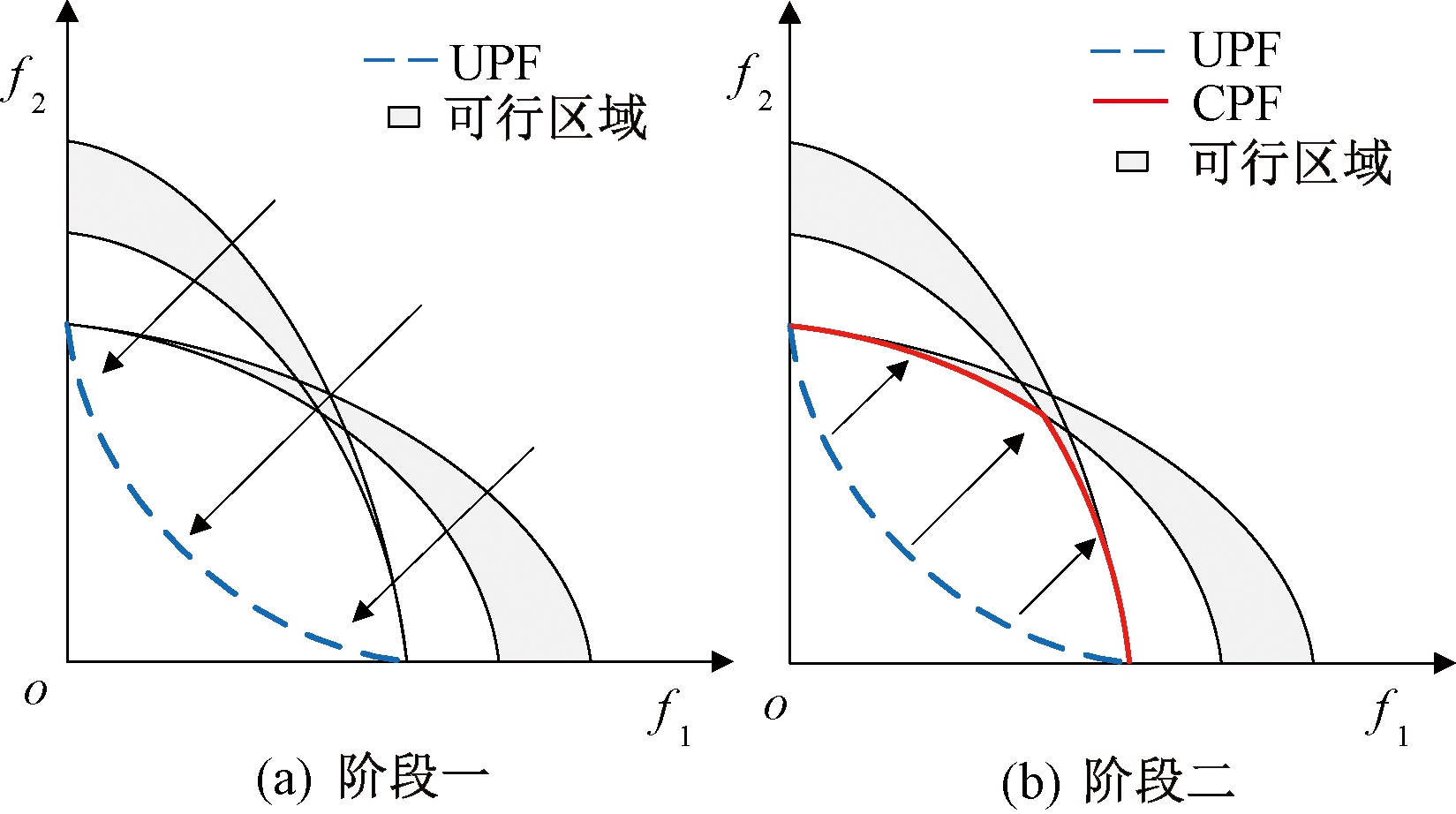
图1 进化阶段示意图
Figure 1 Schematic diagram of evolution stage
2.1 变量自适应优化策略
在处理小规模优化问题时,之前的大多数进化算法通常将所有决策变量作为一个整体进行优化。然而,由于LCMOP变量维度很高,决策空间搜索范围更大,若仍然把所有的变量视为一个整体并进行优化,算法非常容易陷入局部最优并且难以找到可行域。因此,受文献[18]的启发,本文提出了一种自适应的进化策略来对变量进行优化。
Zhang等[19]利用聚类分析将决策变量分为两类:多样性变量和收敛性变量,并基于此提出了大规模多目标进化算法(large-scale many-objective evolutionary algorithm, LMEA)来迭代优化两种变量,以平衡收敛性和多样性。此方法变量分类精度高、算法效果好且优化时间短,因此本文采取LMEA来对变量进行分类。
该方法首先挑选几个候选解,对每个解中所有变量分别执行数次扰动。将变量值进行归一化后,计算每条拟合线与超平面法线之间的角度。之后根据角度来对决策变量进行聚类,将变量分为两个集:具有较小角度平均值的变量被归为收敛性变量集(CV);其余变量则被归为多样性变量集(DV)。此外,由于大多数变量会归为CV,CV中变量较多,因此需再对CV进行相关性分析,将其划分为l个子组来进一步降低优化难度[18-19]。设φ(x)为连续微分函数,如果∃x、a1、a2、b1、b2满足如下条件,则两个决策变量xi与xj相互作用[19]。
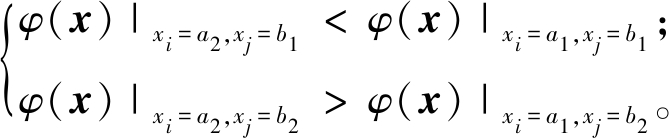
(5)
需要注意的是l的大小由变量之间的交互作用决定。具体来说,每个变量与子组中的至少一个变量相互作用。如果变量之间没有交互作用,则每个变量都是一个子组;而如果所有变量都相互作用,则只有一个子组。所以,l的取值为[1,|CV|]。
将变量分组后,LMEA交替对收敛性变量和多样性变量进行优化。但在每一次交替中,其都需要对收敛性变量优化10轮,这将耗费大量的计算资源。为了进一步节约资源,同时充分对目标空间进行搜索,ATCMEA在相应的阶段对不同的变量自适应地进行优化。
图2给出了变量自适应的优化过程。在第一阶段,首先固定多样性变量,对(D-K)个收敛性变量进行优化,满足条件后进行切换,只对K个多样性变量进行优化;第二阶段属于进化的中后期阶段,将着力寻找CPF,而约束与绝大多数的变量都有关,因此将整体优化所有的变量。
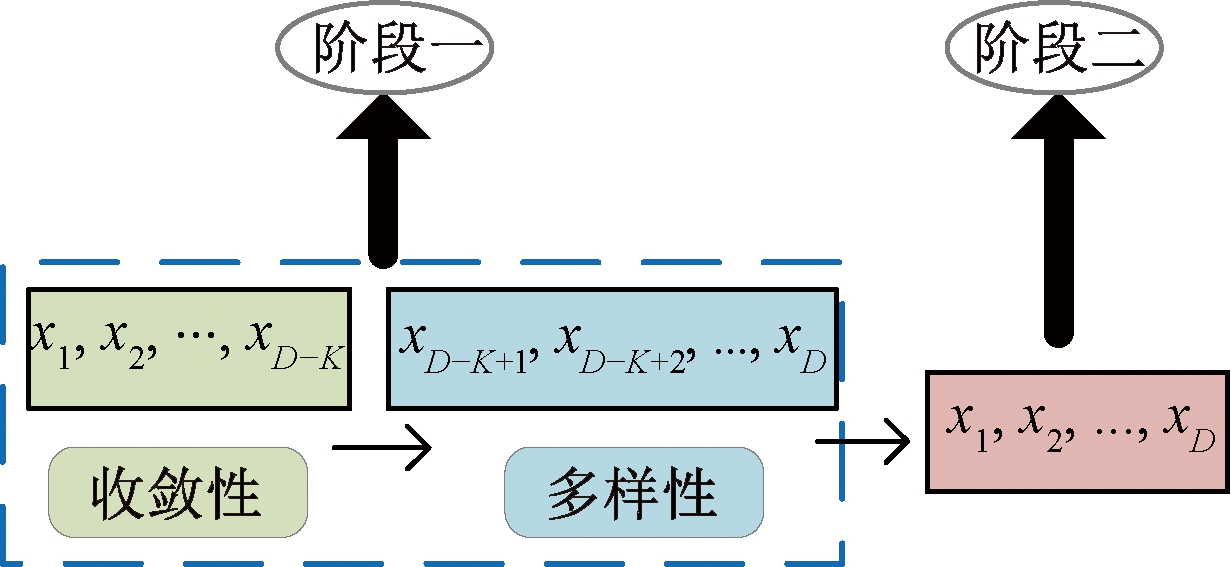
图2 变量优化过程
Figure 2 Variable optimization process
2.2 ATCMEA的第一阶段
在第一阶段,所有的约束将被忽略,专注于寻找UPF。在将决策变量分为收敛性变量与多样性变量后,由于2类变量性质不同,对其分别进行优化。
在两目标MW6问题上[20]对其中的两个决策变量分别执行数次扰动后得到的散点图如图3所示。其中,红色点为选取的初始解,蓝色点为固定其余变量只对一维变量进行扰动产生的解。此时,图3(a)中的变量被视为收敛性变量,因为当对该变量扰动时,生成的解基本是被一一支配的,即优化这个变量时,对种群收敛性影响较大;而图3(b)中的变量被视为多样性变量,对其扰动后生成的解基本是互相非支配的关系,即优化这部分变量时,对种群的多样性影响较大。
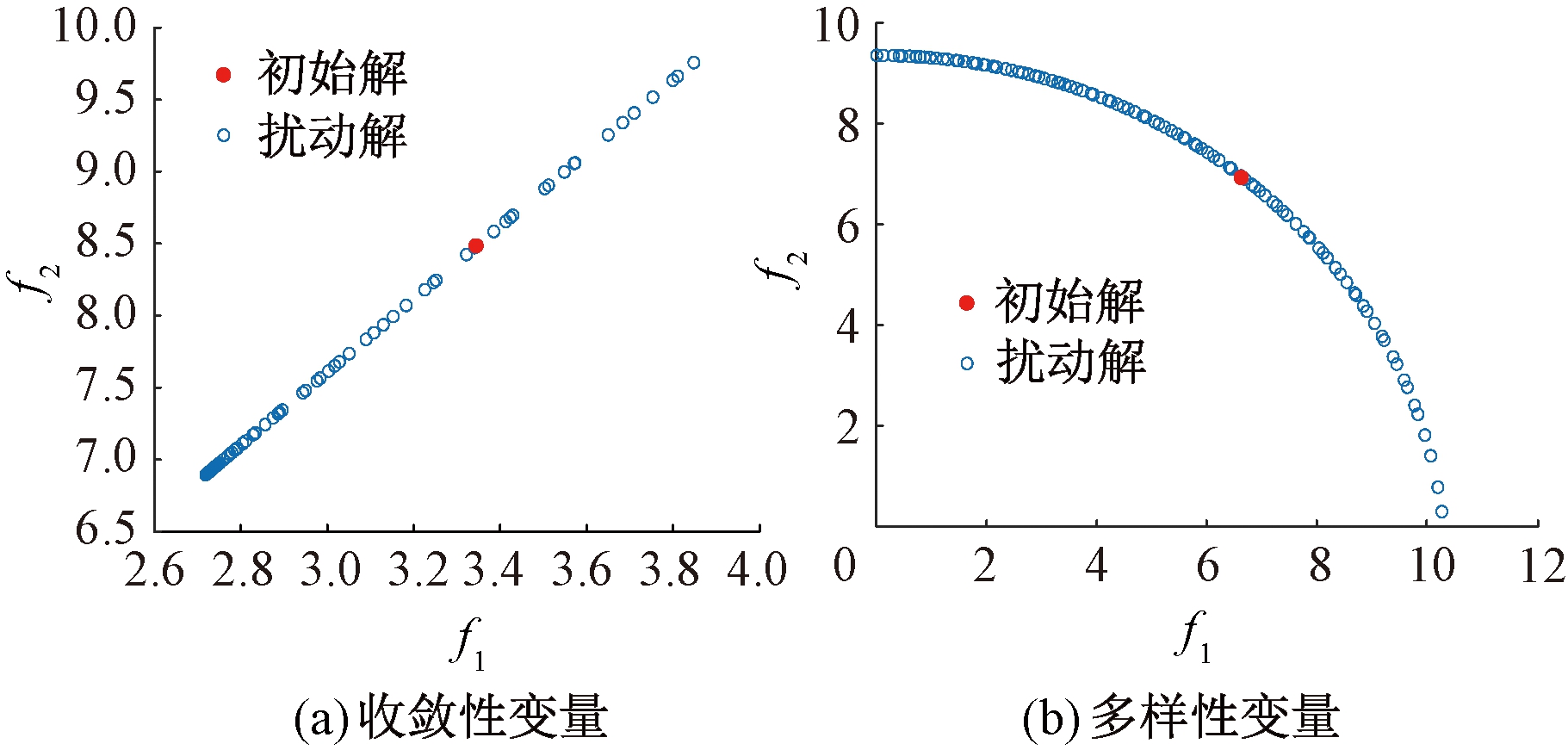
图3 两种不同类型的变量
Figure 3 Two different types of variables
因此,在第一阶段,算法先对收敛性变量进行优化,旨在全力探索目标空间,使其快速逼近UPF。之后固定收敛性变量,为了获得均匀分布的种群,对多样性变量单独优化。第一阶段算法流程如下。
Step 1 初始化种群P。
Step 2 初始化外部存档R,令R=P。
Step 3 基于决策变量聚类的方法,将变量划分为收敛性变量集CV与多样性变量集DV。
Step 4 对收敛性变量进行相关性分析,将其划分为l个子组。
Step 5 固定DV,对CV的每一个子组依次执行如下操作:产生成子种群O,将种群P与O合并为S后更新,输出下一代种群P。
Step 6 所有CV子组优化一轮后,得到后代OC,将OC与R合并后更新存档。
Step 7 如果满足相应的切换条件,则跳到Step 8,否则跳转至Step 3。
Step 8 固定CV,只优化DV,生成子种群OD,将P与OD合并为S后更新,输出下代种群P。
Step 9 将OD与R合并后更新存档。
Step 10 如果该种群满足切换条件,则第一阶段结束,否则跳至Step 7。
其中,在Step 5的更新中,该阶段是对收敛性变量进行优化,所以当且仅当子代候选解在非支配排序中具有较小的层数或者具有相同的非支配层数,但到理想点的欧氏距离较小时,才认为其比父代候选解更优,即具有更好的收敛质量。
在Step 8的更新中,首先对S进行非支配排序,之后的环境选择包括以下两步:①选择前(z-1)个前沿的候选解,其中z是满足|S1∪S2∪…∪Sz|>|P|的最小值(S1,S2,…,Sz分别代表第1,2,…,z层的个体);②根据Sz中候选解在目标空间中的夹角,依次选择剩余的解,直到达到种群规模|P|。
在Step 6与Step 9中,存档作为最终的输出种群,只对可行解进行保存,并利用SPEA2[21](strength Pareto evolutionary algorithm Ⅱ)的环境选择来对存档进行更新,从而不断提高其收敛性与多样性。Step 7与Step 10中的切换需要满足如下两个条件。
条件(1) :当前种群进化代数满足T代;
条件(2):T代后种群在每个目标上的平均值与上一代的变化值小于给定阈值α。
平均值的计算公式为
(6)
(7)
首先利用式(6)将目标值归一化,其中x为种群P的一个解;fi(x)为解x在第i个目标上的原始值, f′i(x)为解x在第i个目标上归一化后的值;![]() 与
与![]() 为种群在第i个目标上原始值的最大和最小值。之后利用式(7)计算均值,其中,N为种群P中的个体数;
为种群在第i个目标上原始值的最大和最小值。之后利用式(7)计算均值,其中,N为种群P中的个体数;![]() 即为种群P在第i个目标上的平均值。
即为种群P在第i个目标上的平均值。
条件(2)的计算公式为
(8)
式中:![]() 与
与![]() 分别代表当前和上一代的平均值;α为一个阈值,用于衡量种群的稳定程度。
分别代表当前和上一代的平均值;α为一个阈值,用于衡量种群的稳定程度。
条件(1)给出了种群最小的进化代数,为了保证种群能够充分进化,在此算法中将T设为50;满足条件(2)则说明当前种群波动较小,取值相对稳定,将阈值α设为0.01。
虽然优化收敛性变量与多样性变量的终止条件一致,但两个阶段用于判断的目的不同:优化收敛性变量是为了更充分地探索目标空间,使其快速逼近UPF,因此只计算位于非支配排序第一层的个体的均值;而第二阶段对多样性变量进行优化的目的是让种群能够在UPF上更均匀地分布,因此判断时需计算整个种群的均值。
2.3 ATCMEA的第二阶段
在第二阶段,考虑所有的约束对决策变量整体进行优化。为了更好地探索可行区域,采用ε约束处理技术将种群从UPF拉回CPF。之所以采用ε约束处理技术是因为其可以保留一些有希望的不可行解来探索未检测到的可行区域。其中约束放松参数εt计算公式[22]为
(9)
式中:tmax为第二阶段的最大代数;β为控制εt下降比例的参数,设为0.5;e0为第二阶段初始种群的最大约束违反度值。
第二阶段算法流程如下。
Step 1 将第一阶段终止时的种群和存档设为初始种群P与外部存档R。
Step 2 根据种群P计算初始最大约束违反度ε0,令t=0。
Step 3 对变量整体优化,生成子代O,将P与O合并为S后应用ε约束处理技术来对其更新,得到下一代种群P。
Step 4 将O与R合并后更新存档。
Step 5 t=t+1,根据式(9)对ε值进行更新。
Step 6 判断是否达到设定的最大评价次数,若达到,则算法终止并输出外部存档R,否则跳至Step 3。
其中Step 3中的种群更新方式与外部存档可行解更新方式保持一致。
3 实验设置和结果
为了验证所提算法ATCMEA在LCMOP上的性能,选择CCMO[13]、PPS[11]、MSCMO[11]、DPSEA[10]、LMOCSO[23]和POCEA[8]这6个具有代表性的约束多目标算法在LIRCMOP[24]、DASCMOP[25]和MW[20]3个测试集上进行对比。
3.1 实验参数设置
种群大小设为100,函数最大评价次数设为10 000×D,实验中D的取值分别为100、150和200。为了公平比较,对比算法中的参数与原始文献中保持一致。所有的实验均是在多目标优化平台PlatEMO[26]上实现。
3.2 评价指标
选取可行率FR和反向世代距离IGD作为评价指标。FR是算法至少获得一个可行解的运行次数与总运行次数的比率[27],FR越大,证明算法找到可行解的次数也越多,其解决大规模约束多目标问题的能力也越强。IGD指标衡量的是所求得最佳前沿近似解集到真实Pareto前沿中的点之间最小距离的平均值[23],IGD越小,表明测试算法的收敛性和多样性越好。
3.3 实验结果及分析
3.3.1 100维问题上的结果及分析
表1给出了决策变量100维的情况下,所有算法在3个基准问题测试集上的IGD与FR。在比较时,先比较可行率,可行率一致则比较IGD指标,并将最佳结果以灰色底色进行标记。“NaN”表示相应的算法无法在30次运行中每一次都能获得可行解,即FR≠100%,在这种情况下,呈现形式为NaN(FR);当FR=100%时,呈现形式为IGD均值(方差)。使用Wilcoxon秩和检验在显著性水平为0.05下比较两种算法是否有显著性差异。
表1 7种算法在100维问题上的IGD及FR
Table 1 IGD and FR of seven algorithms on 100 dimensional problems
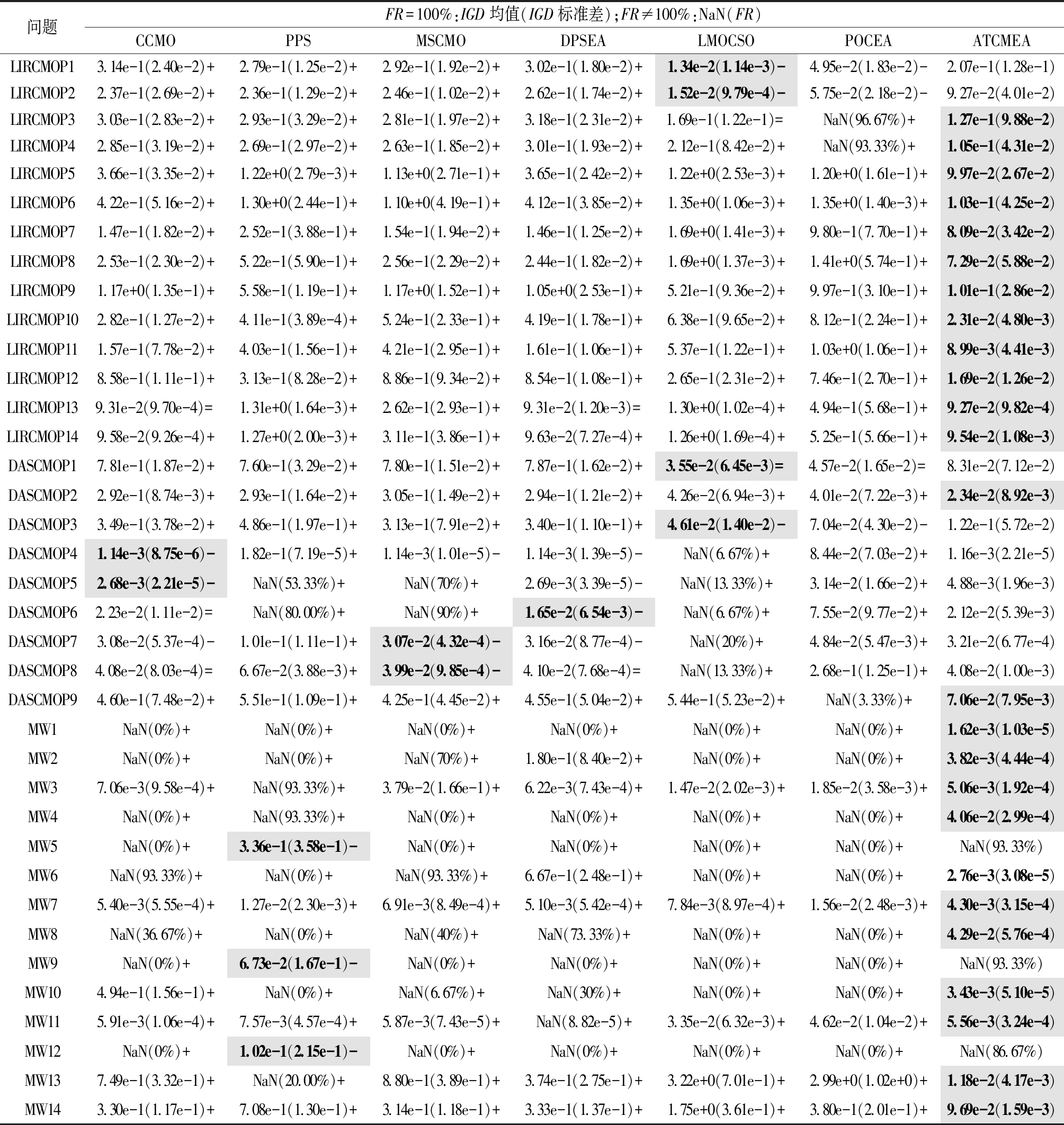
问题FR=100%:IGD均值(IGD标准差);FR≠100%:NaN(FR)CCMOPPSMSCMODPSEALMOCSOPOCEAATCMEALIRCMOP13.14e-1(2.40e-2)+2.79e-1(1.25e-2)+2.92e-1(1.92e-2)+3.02e-1(1.80e-2)+1.34e-2(1.14e-3)-4.95e-2(1.83e-2)-2.07e-1(1.28e-1)LIRCMOP22.37e-1(2.69e-2)+2.36e-1(1.29e-2)+2.46e-1(1.02e-2)+2.62e-1(1.74e-2)+1.52e-2(9.79e-4)-5.75e-2(2.18e-2)-9.27e-2(4.01e-2)LIRCMOP33.03e-1(2.83e-2)+2.93e-1(3.29e-2)+2.81e-1(1.97e-2)+3.18e-1(2.31e-2)+1.69e-1(1.22e-1)=NaN(96.67%)+1.27e-1(9.88e-2)LIRCMOP42.85e-1(3.19e-2)+2.69e-1(2.97e-2)+2.63e-1(1.85e-2)+3.01e-1(1.93e-2)+2.12e-1(8.42e-2)+NaN(93.33%)+1.05e-1(4.31e-2)LIRCMOP53.66e-1(3.35e-2)+1.22e+0(2.79e-3)+1.13e+0(2.71e-1)+3.65e-1(2.42e-2)+1.22e+0(2.53e-3)+1.20e+0(1.61e-1)+9.97e-2(2.67e-2)LIRCMOP64.22e-1(5.16e-2)+1.30e+0(2.44e-1)+1.10e+0(4.19e-1)+4.12e-1(3.85e-2)+1.35e+0(1.06e-3)+1.35e+0(1.40e-3)+1.03e-1(4.25e-2)LIRCMOP71.47e-1(1.82e-2)+2.52e-1(3.88e-1)+1.54e-1(1.94e-2)+1.46e-1(1.25e-2)+1.69e+0(1.41e-3)+9.80e-1(7.70e-1)+8.09e-2(3.42e-2)LIRCMOP82.53e-1(2.30e-2)+5.22e-1(5.90e-1)+2.56e-1(2.29e-2)+2.44e-1(1.82e-2)+1.69e+0(1.37e-3)+1.41e+0(5.74e-1)+7.29e-2(5.88e-2)LIRCMOP91.17e+0(1.35e-1)+5.58e-1(1.19e-1)+1.17e+0(1.52e-1)+1.05e+0(2.53e-1)+5.21e-1(9.36e-2)+9.97e-1(3.10e-1)+1.01e-1(2.86e-2)LIRCMOP102.82e-1(1.27e-2)+4.11e-1(3.89e-4)+5.24e-1(2.33e-1)+4.19e-1(1.78e-1)+6.38e-1(9.65e-2)+8.12e-1(2.24e-1)+2.31e-2(4.80e-3)LIRCMOP111.57e-1(7.78e-2)+4.03e-1(1.56e-1)+4.21e-1(2.95e-1)+1.61e-1(1.06e-1)+5.37e-1(1.22e-1)+1.03e+0(1.06e-1)+8.99e-3(4.41e-3)LIRCMOP128.58e-1(1.11e-1)+3.13e-1(8.28e-2)+8.86e-1(9.34e-2)+8.54e-1(1.08e-1)+2.65e-1(2.31e-2)+7.46e-1(2.70e-1)+1.69e-2(1.26e-2)LIRCMOP139.31e-2(9.70e-4)=1.31e+0(1.64e-3)+2.62e-1(2.93e-1)+9.31e-2(1.20e-3)=1.30e+0(1.02e-4)+4.94e-1(5.68e-1)+9.27e-2(9.82e-4)LIRCMOP149.58e-2(9.26e-4)+1.27e+0(2.00e-3)+3.11e-1(3.86e-1)+9.63e-2(7.27e-4)+1.26e+0(1.69e-4)+5.25e-1(5.66e-1)+9.54e-2(1.08e-3)DASCMOP17.81e-1(1.87e-2)+7.60e-1(3.29e-2)+7.80e-1(1.51e-2)+7.87e-1(1.62e-2)+3.55e-2(6.45e-3)=4.57e-2(1.65e-2)=8.31e-2(7.12e-2)DASCMOP22.92e-1(8.74e-3)+2.93e-1(1.64e-2)+3.05e-1(1.49e-2)+2.94e-1(1.21e-2)+4.26e-2(6.94e-3)+4.01e-2(7.22e-3)+2.34e-2(8.92e-3)DASCMOP33.49e-1(3.78e-2)+4.86e-1(1.97e-1)+3.13e-1(7.91e-2)+3.40e-1(1.10e-1)+4.61e-2(1.40e-2)-7.04e-2(4.30e-2)-1.22e-1(5.72e-2)DASCMOP41.14e-3(8.75e-6)-1.82e-1(7.19e-5)+1.14e-3(1.01e-5)-1.14e-3(1.39e-5)-NaN(6.67%)+8.44e-2(7.03e-2)+1.16e-3(2.21e-5)DASCMOP52.68e-3(2.21e-5)-NaN(53.33%)+NaN(70%)+2.69e-3(3.39e-5)-NaN(13.33%)+3.14e-2(1.66e-2)+4.88e-3(1.96e-3)DASCMOP62.23e-2(1.11e-2)=NaN(80.00%)+NaN(90%)+1.65e-2(6.54e-3)-NaN(6.67%)+7.55e-2(9.77e-2)+2.12e-2(5.39e-3)DASCMOP73.08e-2(5.37e-4)-1.01e-1(1.11e-1)+3.07e-2(4.32e-4)-3.16e-2(8.77e-4)-NaN(20%)+4.84e-2(5.47e-3)+3.21e-2(6.77e-4)DASCMOP84.08e-2(8.03e-4)=6.67e-2(3.88e-3)+3.99e-2(9.85e-4)-4.10e-2(7.68e-4)=NaN(13.33%)+2.68e-1(1.25e-1)+4.08e-2(1.00e-3)DASCMOP94.60e-1(7.48e-2)+5.51e-1(1.09e-1)+4.25e-1(4.45e-2)+4.55e-1(5.04e-2)+5.44e-1(5.23e-2)+NaN(3.33%)+7.06e-2(7.95e-3)MW1NaN(0%)+NaN(0%)+NaN(0%)+NaN(0%)+NaN(0%)+NaN(0%)+1.62e-3(1.03e-5)MW2NaN(0%)+NaN(0%)+NaN(70%)+1.80e-1(8.40e-2)+NaN(0%)+NaN(0%)+3.82e-3(4.44e-4)MW37.06e-3(9.58e-4)+NaN(93.33%)+3.79e-2(1.66e-1)+6.22e-3(7.43e-4)+1.47e-2(2.02e-3)+1.85e-2(3.58e-3)+5.06e-3(1.92e-4)MW4NaN(0%)+NaN(93.33%)+NaN(0%)+NaN(0%)+NaN(0%)+NaN(0%)+4.06e-2(2.99e-4)MW5NaN(0%)+3.36e-1(3.58e-1)-NaN(0%)+NaN(0%)+NaN(0%)+NaN(0%)+NaN(93.33%)MW6NaN(93.33%)+NaN(0%)+NaN(93.33%)+6.67e-1(2.48e-1)+NaN(0%)+NaN(0%)+2.76e-3(3.08e-5)MW75.40e-3(5.55e-4)+1.27e-2(2.30e-3)+6.91e-3(8.49e-4)+5.10e-3(5.42e-4)+7.84e-3(8.97e-4)+1.56e-2(2.48e-3)+4.30e-3(3.15e-4)MW8NaN(36.67%)+NaN(0%)+NaN(40%)+NaN(73.33%)+NaN(0%)+NaN(0%)+4.29e-2(5.76e-4)MW9NaN(0%)+6.73e-2(1.67e-1)-NaN(0%)+NaN(0%)+NaN(0%)+NaN(0%)+NaN(93.33%)MW104.94e-1(1.56e-1)+NaN(0%)+NaN(6.67%)+NaN(30%)+NaN(0%)+NaN(0%)+3.43e-3(5.10e-5)MW115.91e-3(1.06e-4)+7.57e-3(4.57e-4)+5.87e-3(7.43e-5)+NaN(8.82e-5)+3.35e-2(6.32e-3)+4.62e-2(1.04e-2)+5.56e-3(3.24e-4)MW12NaN(0%)+1.02e-1(2.15e-1)-NaN(0%)+NaN(0%)+NaN(0%)+NaN(0%)+NaN(86.67%)MW137.49e-1(3.32e-1)+NaN(20.00%)+8.80e-1(3.89e-1)+3.74e-1(2.75e-1)+3.22e+0(7.01e-1)+2.99e+0(1.02e+0)+1.18e-2(4.17e-3)MW143.30e-1(1.17e-1)+7.08e-1(1.30e-1)+3.14e-1(1.18e-1)+3.33e-1(1.37e-1)+1.75e+0(3.61e-1)+3.80e-1(2.01e-1)+9.69e-2(1.59e-3)
注:符号“+”、“-”及“=”分别表示ATCMEA明显好于、明显差于和相似于对比算法,下同。
从表1中可以看出,在IGD方面,ATCMEA在37个测试函数中有25个表现最好。对于其余算法,大都只在0~4个测试函数中取得最佳结果。经Wilcoxon秩和检验,对于所有的测试函数,ATCMEA分别在第31、34、34、31、32、33个函数上的性能显著优于CCMO、PPS、MSCMO、DPSEA、LMOCSO和POCEA。此外,ATCMEA在90%以上函数中的FR都能达到100%;相反,其余6个对比算法可行率则较差,尤其在MW问题集上,存在独立运行30次,每次都未找到可行解的情况。原因在于MW问题集具有约束条件难,可行区域狭窄且收敛困难等特征。随着决策变量维度的扩增,MW问题集变得更加困难,而本文提出的ATCMEA能很好地解决大规模MW问题。
3.3.2 150维及200维问题上的结果及分析
为了进一步验证算法在解决大规模约束多目标问题上的性能,表2给出了ATCMEA在100维、150维及200维问题上的Wilcoxon测试结果。显然,对于每一种对比算法,在IGD指标上“+”的数量都远远大于“-”的数量,这充分证明了ATCMEA在不同维度测试函数上的显著优越性。
表2 ATCMEA与其他算法优劣性比较
Table 2 Comparison of adrantages and disadvantages between ATCMEA and other algorithms
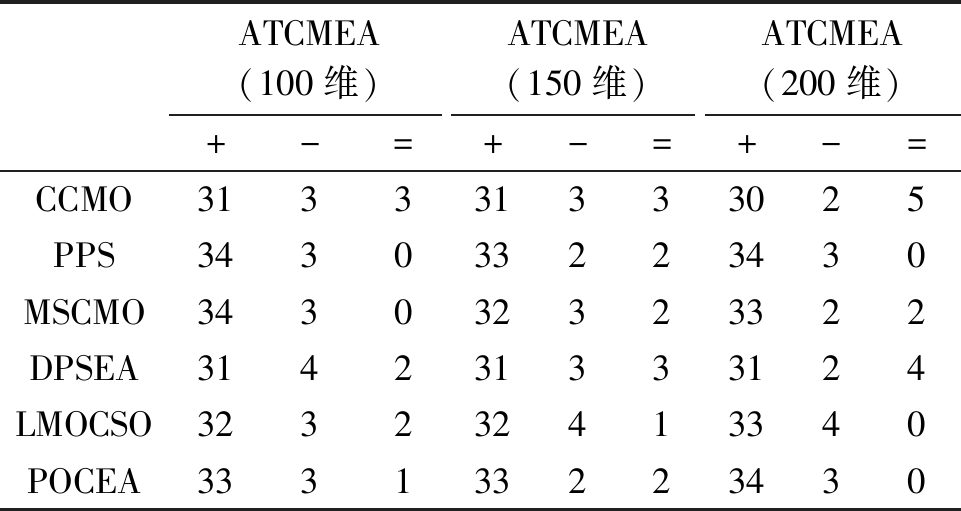
ATCMEA(100维)ATCMEA(150维)ATCMEA(200维)+-=+-=+-=CCMO313331333025PPS343033223430MSCMO343032323322DPSEA314231333124LMOCSO323232413340POCEA333133223430
与此同时,图4给出了算法获得100%可行率的问题数量占总测试函数数量的比例。可以看出,提出的ATCMEA能在最大比例问题上获得100%可行率,说明其可以解决绝大多数的大规模约束多目标测试函数,验证了所提算法不仅可以获得收敛性和多样性均较好的解集,并且具有较好的鲁棒性。
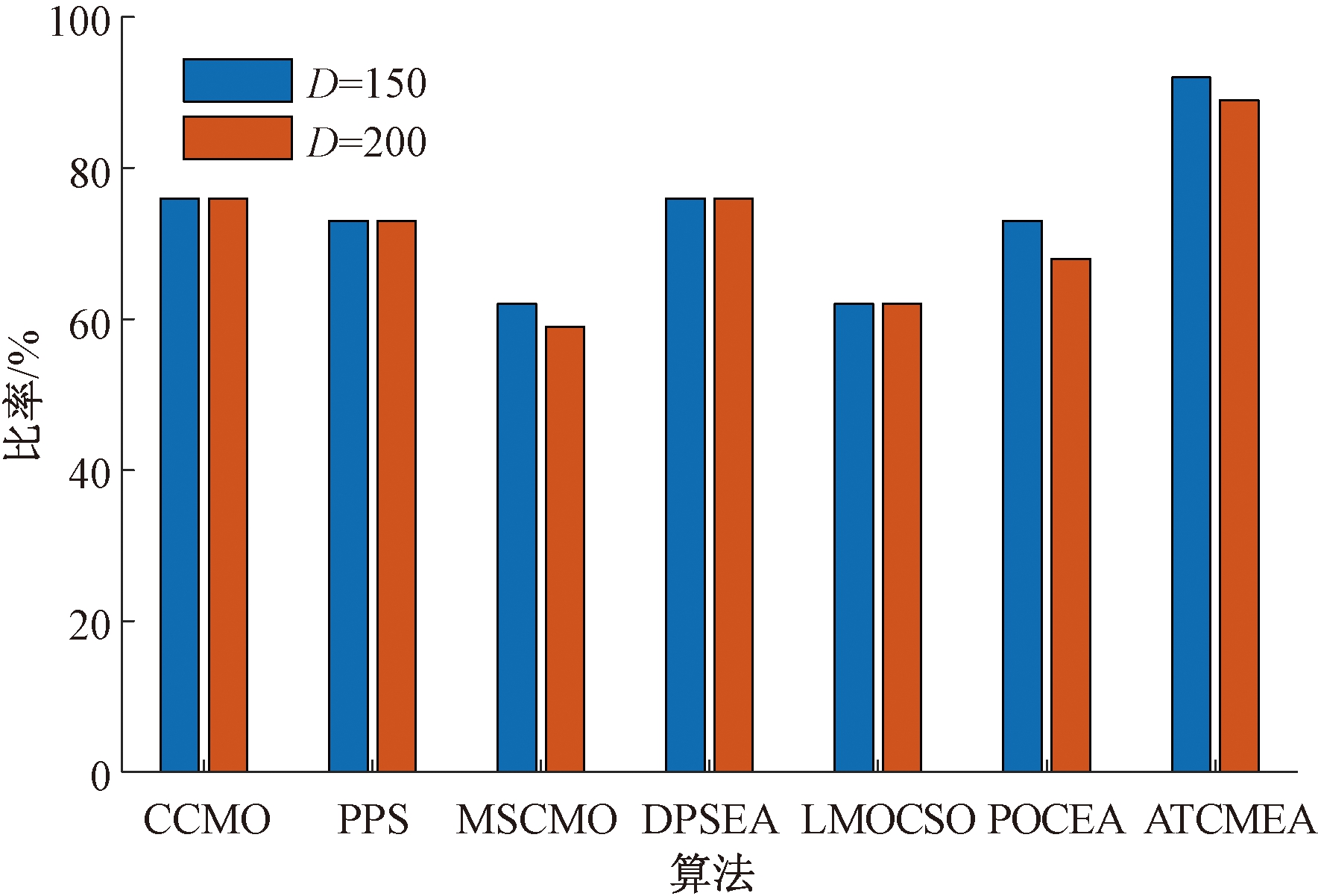
图4 算法可行率为100%问题所占比例
Figure 4 Percentage of problems with 100% feasibility of the algorithms
3.3.3 算法收敛速度及时间
图5给出了ATCMEA和其他算法在3个选定问题(即LIRCMOP11、DASCMOP9和MW7)上200维时的IGD的收敛曲线,由于POCEA在DASCMOP9上始终无法获得可行解,因此图5(b)中没有展示其结果。由图5可以看出,与其他算法相比,ATCMEA实现了更快的收敛,当处理具有复杂可行区域的LIRCMOP时,这种优势尤为显著。

图5 算法的收敛曲线
Figure 5 Convergence curves of the algorithms
表3给出了7种算法在37个100维问题上的平均运行时间排名,ATCMEA排名第2,说明所提算法不仅运行时间较短,而且获得了更为突出的效果。
表3 算法运行时间排名
Table 3 Running time ranking of algorithms
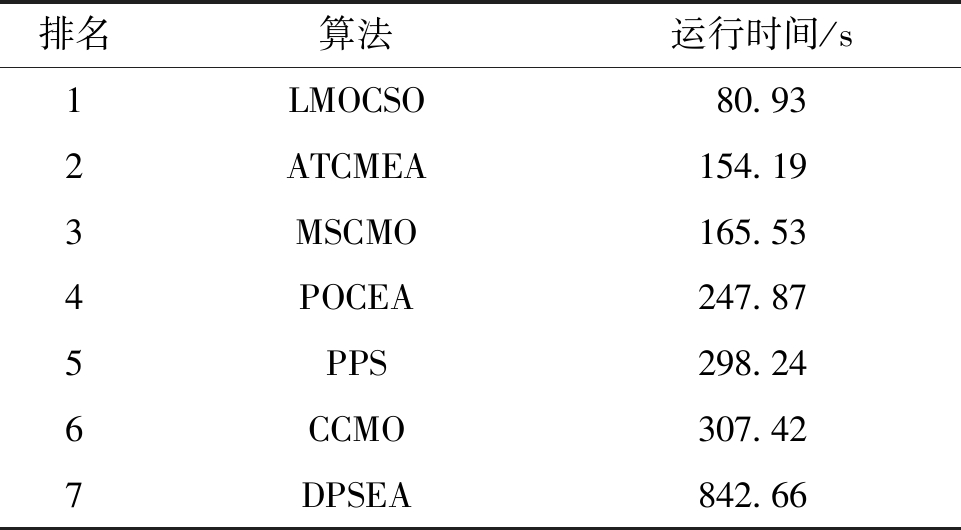
排名算法运行时间/s1LMOCSO80.932ATCMEA154.193MSCMO165.534POCEA247.875PPS298.246CCMO307.427DPSEA842.66
4 结论
(1)针对大规模约束多目标优化问题,提出了一种自适应两阶段的进化算法(ATCMEA)。算法采用两阶段的框架来平衡约束和目标,同时,为了降低高维变量带来的优化难度,结合变量聚类这一技术,对部分变量自适应优化。
(2)在3个不同维度的测试问题上均进行了实验,并给出了算法的收敛曲线及运行时间。实验结果表明,相比于其他先进的约束多目标优化算法,提出的算法具有较好的获得可行解的能力,并且可以获得收敛性及多样性均较好的解集,有效地解决了大规模约束多目标优化问题。
(3) 大规模约束多目标优化问题目前仍是一个较新且较难的领域,所提出的算法虽然在大部分测试集上取得了良好性能,但在部分MW问题上效果不佳,还有很大改进空间。此外随着维度的扩增,约束与目标之间的冲突将更加难以解决。因此,大规模约束多目标优化领域是未来一个重要的研究方向。
[1] 李二超, 李进. 两阶段三存档集约束优化算法(TSDA)[J]. 郑州大学学报(工学版), 2018, 39(6): 23-29.
LI E C, LI J. Constraint optimization algorithm with two-stage and three-archive[J]. Journal of Zhengzhou University (Engineering Science), 2018, 39(6): 23-29.
[2] 华一村, 刘奇奇, 郝矿荣, 等. 非规则Pareto前沿面多目标进化优化算法研究综述[J]. 郑州大学学报(工学版), 2021, 42(1): 1-8.
HUA Y C, LIU Q Q, HAO K R, et al. A survey of evolutionary algorithms for multi-objective optimization problems with irregular Pareto fronts[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(1): 1-8.
[3] 史非凡, 史旭华. 基于参考向量的自适应约束多目标进化算法[J]. 计算机应用, 2022, 42(2): 542-549.
SHI F F, SHI X H. Adaptive reference vector based constrained multi-objective evolutionary algorithm[J]. Journal of Computer Applications, 2022, 42(2): 542-549.
[4] 梁静, 刘睿, 瞿博阳, 等. 进化算法在大规模优化问题中的应用综述[J]. 郑州大学学报(工学版), 2018, 39(3): 15-21.
LIANG J, LIU R, QU B Y, et al. A survey of evolutionary algorithms for large scale optimization problem[J]. Journal of Zhengzhou University (Engineering Science), 2018, 39(3): 15-21.
[5] EVERSON R M, FIELDSEND J E. Multiobjective optimization of safety related systems: an application to short-term conflict alert[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(2): 187-198.
[6] HE C, CHENG R, ZHANG C J, et al. Evolutionary large-scale multiobjective optimization for ratio error estimation of voltage transformers[J]. IEEE Transactions on Evolutionary Computation, 2020, 24(5): 868-881.
[7] TIAN Y, ZHANG X Y, WANG C, et al. An evolutionary algorithm for large-scale sparse multiobjective optimization problems[J]. IEEE Transactions on Evolutionary Computation, 2020, 24(2): 380-393.
[8] HE C, CHENG R, TIAN Y, et al. Paired offspring generation for constrained large-scale multiobjective optimization[J]. IEEE Transactions on Evolutionary Computation, 2021, 25(3): 448-462.
[9] ZHANG X, MA Z B, DING B W, et al. A coevolutionary algorithm based on the auxiliary population for constrained large-scale multi-objective supply chain network[J]. Mathematical Biosciences and Engineering, 2022, 19(1): 271-286.
[10] WANG B C, SHUI Z Y, FENG Y, et al. Evolutionary algorithm with dynamic population size for constrained multiobjective optimization[J]. Swarm and Evolutionary Computation, 2022, 73: 101104.
[11] FAN Z, LI W J, CAI X Y, et al. Push and pull search for solving constrained multi-objective optimization problems[J]. Swarm and Evolutionary Computation, 2019, 44: 665-679.
[12] MA H P, WEI H Y, TIAN Y, et al. A multi-stage evolutionary algorithm for multi-objective optimization with complex constraints[J]. Information Sciences, 2021, 560: 68-91.
[13] TIAN Y, ZHANG T, XIAO J H, et al. A coevolutionary framework for constrained multiobjective optimization problems[J]. IEEE Transactions on Evolutionary Computation, 2021, 25(1): 102-116.
[14] WANG J H, LIANG G X, ZHANG J. Cooperative differential evolution framework for constrained multiobjective optimization[J]. IEEE Transactions on Cybernetics, 2019, 49(6): 2060-2072.
[15] GUPTA A, ONG Y S, FENG L. Multifactorial evolution: toward evolutionary multitasking[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(3): 343-357.
[16] CHEN K, XUE B, ZHANG M J, et al. An evolutionary multitasking-based feature selection method for high-dimensional classification[J]. IEEE Transactions on Cybernetics, 2022, 52(7): 7172-7186.
[17] QIAO K J, YU K J, QU B Y, et al. An evolutionary multitasking optimization framework for constrained multiobjective optimization problems[J]. IEEE Transactions on Evolutionary Computation, 2022, 26(2): 263-277.
[18] MA X L, LIU F, QI Y T, et al. A multiobjective evolutionary algorithm based on decision variable analyses for multiobjective optimization problems with large-scale variables[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(2): 275-298.
[19] ZHANG X Y, TIAN Y, CHENG R, et al. A decision variable clustering-based evolutionary algorithm for large-scale many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2018, 22(1): 97-112.
[20] FAN Z, LI W J, CAI X Y, et al. Difficulty adjustable and scalable constrained multiobjective test problem toolkit[J]. Evolutionary Computation, 2020, 28(3): 339-378.
[21] ZITZLER E, LAUMANNS M, THIELE L. SPEA2: improving the strength Pareto evolutionary algorithm[EB/OL].(2001-05-10)[2022-06-13].https:∥doi.org/10.3929/ethz-a-004284029.
[22] WANG B C, LI H X, LI J P, et al. Composite differential evolution for constrained evolutionary optimization[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019, 49(7): 1482-1495.
[23] TIAN Y, ZHENG X T, ZHANG X Y, et al. Efficient large-scale multiobjective optimization based on a competitive swarm optimizer[J]. IEEE Transactions on Cybernetics, 2020, 50(8): 3696-3708.
[24] FAN Z, LI W J, CAI X Y, et al. An improved epsilon constraint-handling method in MOEA/D for CMOPs with large infeasible regions[J]. Soft Computing, 2019, 23(23): 12491-12510.
[25] MA Z W, WANG Y. Evolutionary constrained multiobjective optimization: test suite construction and performance comparisons[J]. IEEE Transactions on Evolutionary Computation, 2019, 23(6): 972-986.
[26] TIAN Y, CHENG R, ZHANG X Y, et al. PlatEMO: a MATLAB platform for evolutionary multi-objective optimization educational forum[J]. IEEE Computational Intelligence Magazine, 2017, 12(4): 73-87.
[27] YU K J, LIANG J, QU B Y, et al. Dynamic selection preference-assisted constrained multiobjective differential evolution[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(5): 2954-2965.