交叉路口是城市路网中重要的节点与枢纽,也是城市道路交通安全和拥堵频发的瓶颈点[1-5]。随着具备联网功能和完全自动驾驶车辆(connected and automated vehicles,CAV)的出现,在降低交叉路口交通事故和缓解拥堵方面,将发挥革命性作用[6]。目前,针对CAV的交叉路口管理系统研究主要分为两类:①在传统交通信号控制系统基础上,利用CAV获得高精度交通数据,对信号控制系统相位和相序方案进行调整来满足智能车辆的通行需求;②抛弃传统的信号控制方式,实现针对全自动驾驶车辆调度的无信号交叉路口管理模式。
在基于CAV的改进传统信号控制系统研究中,Li等[7]介绍了基于CAV信号控制系统的全局规划、局部规划以及自组织控制模式,通过数据分析,给出上述模式适用的不同交通情况。Guo等[8]将CAV获得数据集成到信号控制系统中,根据CAV状态信息对相位和相序进行优化,来提升交叉路口的通行效率。
虽然上述研究成果能够在一定程度上提高CAV的通行效率,然而信号控制系统本质是为人类驾驶车辆服务,对于可以精确控制的CAV而言,执行效率仍然过低。因此,一些研究机构开始着眼于未来,研究适用于CAV的交叉路口控制系统,其中起步较早的是德克萨斯大学奥斯丁分校Stone团队开发的自治交叉路口管理系统(autonomous intersection management,AIM)[9],研究者设计了性能较为优秀的先来先服务(first come first served, FCFS)控制策略。并在此基础上,相继提出了多种高效的控制策略[10],包括支持人类驾驶车辆的FCFS-light控制策略和考虑紧急车辆通行的FCFS-emerg策略等。Vasirani等[11]也在AIM系统中以竞价拍卖为核心思想,设计了基于组合拍卖的交叉路口控制策略。
随后,基于车辆集中调度方式,Mahbub等[12]提出了在状态和控制双约束条件下进行有效调度的交叉路口控制策略。Xu等[13]基于蒙特卡洛搜索方法,提出了协同驾驶控制策略,提高了交叉路口的通行效率。Zhu等[14]通过预测车辆可能到达延迟,建立了基于准确预测车辆到达时间的交叉路口控制策略。刘明剑等[15]提出了基于禁忌搜索的交叉路口控制策略,通过消减车辆间冲突关系,来提升交叉路口的吞吐量。常玉林等[16]提出了基于蚁群算法的控制策略,通过分析交叉路口车流量情况,能够更加准确地搜索到车辆的最优行驶路径。Pei等[17]提出了一种基于动态规划的多车协作控制策略。吴伟等[18]建立了基于混合整数线性规划的交叉口控制策略。
利用分布式控制方式,蒋阳升等[19]提出了一种基于虚拟车队的时序调度模型,实现了交叉路口调度的全局优化。Gonz
lez等[20]提出了一种多车分布式协作管理系统,该系统通过引入明确的规则,让车辆遵守规则来提高通行效率。Yesilyurt等[21]通过共享车辆在交叉路口中期望占据的行驶区域以及它们的预计到达时间,来协调车辆间通行顺序。
也有学者利用深度学习方法开展了交叉路口调度的研究,Zhang等[22]提出了一种基于卷积神经网络的框架来预测不同车流密度下的车辆平均等待时间,进而选择耗时最少的方案作为调度策略。
FCFS目前仍然为一种高效的交叉路口控制策略,但FCFS控制策略缺乏对未来交叉路口车流量变化的考量,容易发生死锁,决策过程中也存在一定的盲目性,不利于实现交叉路口中车辆吞吐量的最大化需求。交通信号控制策略是针对人类驾驶车辆设计的策略,对于能够精确控制的CAV而言,存在执行效率过低的问题;基于启发式算法的交叉路口控制策略在车流量密度较大时容易陷入局部最优,无法进一步提升交叉路口的通行效率。
为了解决上述交叉路口控制策略存在的问题,本文提出了一种基于最大团自治交叉路口控制策略,在保证系统实时性需求的前提下,提高了交叉路口的通行效率,最后通过仿真实验证明了控制策略的有效性与可靠性。
1 问题描述与建模
自治交叉路口控制系统是服务于具备完全自动驾驶功能CAV的交叉路口控制系统。首先,CAV进入交叉路口区域,开始向路侧单元发送预约通过交叉路口的请求;其次,路侧单元根据接收到的预约请求信息,模拟出车辆的行驶轨迹;再次,控制系统依据相应控制策略,给出CAV在交叉路口中的通行顺序;最后,CAV驶离交叉路口区域,中断与路侧单元之间通信。交叉路口控制系统如图1所示。
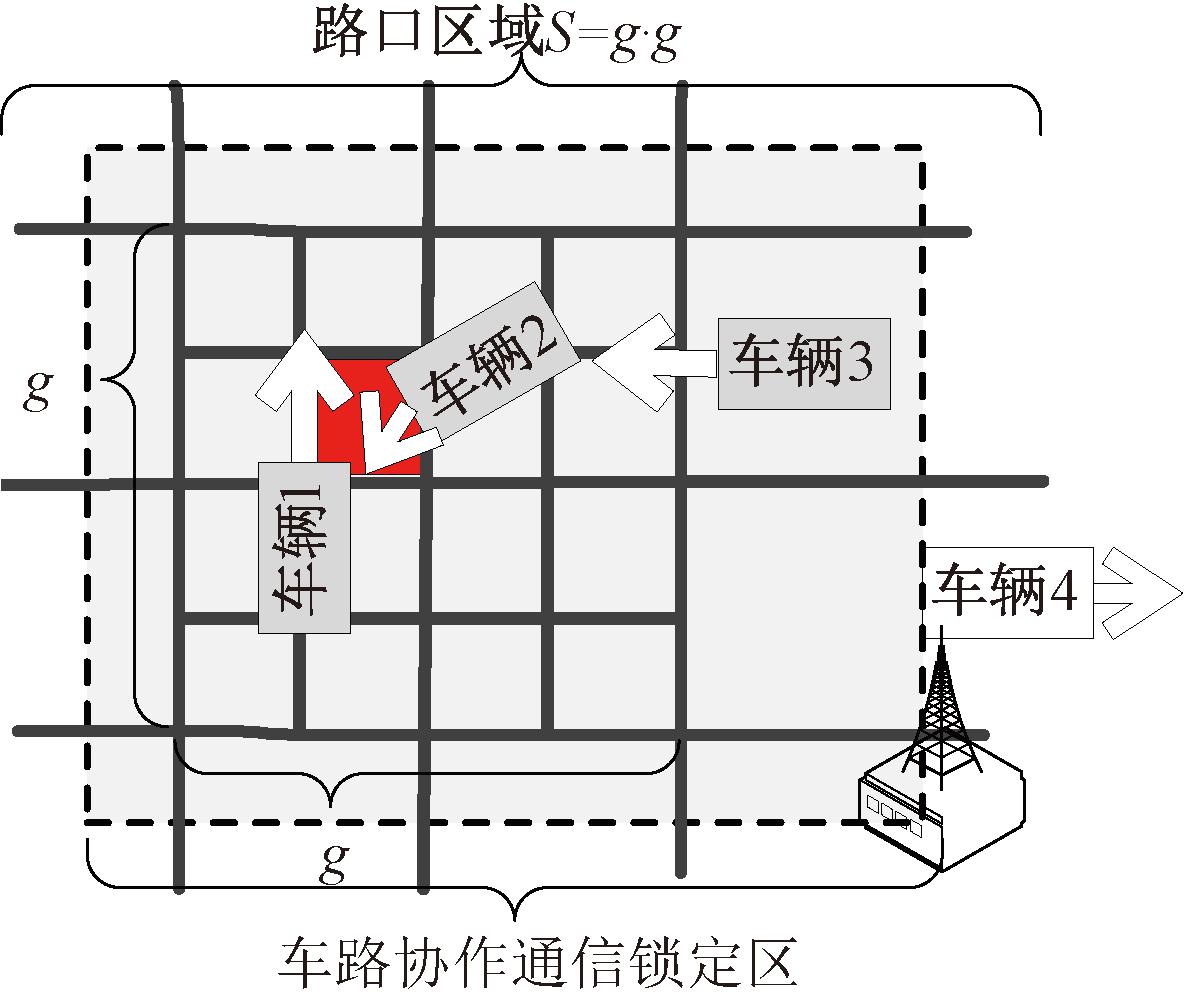
图1 交叉路口控制系统
Figure 1 Intersection control system
1.1 自治交叉路口控制系统的处理机制
(1) 交叉路口空间区域划分机制。将矩形的交叉路口空间区域S进行网格化划分处理,划分为g2个二维空间小区域网格。划分之后路口的第i个小区域网格为si,那么整个交叉路口S可以看作是由si组成的有限集合,如图1所示。
S={si|1≤i≤g2,g∈N+}。
(1)
(2) 交叉路口时间批处理机制。定义整个交叉路口控制系统的离散时间域为T,将其等量切分后每个处理周期为Ti,整个控制系统的时间轴T是由批处理周期Ti组成的无限集合:
T={T1,T2,…,Ti,Ti+1,…,Tk}。
(2)
在每一个批处理周期Ti,自治交叉路口控制系统接收到预约过交叉路口的车辆请求集合为R:
R={vi|1≤i≤n,m∈N+}。
(3)
从R集合中选取可以通过交叉路口的车辆请求集合为Rac:
Rac={vi|1≤i≤m≤n,n、m∈N+},Rac⊆R。
(4)
1.2 控制系统建模
为了提高自治交叉路口的通行效率,并保证行车安全,需要确保在每一个批处理周期,预约通过交叉路口的任意两辆车之间均不存在冲突关系,即车辆vi和vj(i≠j)在交叉路口行驶过程中,任意时刻均不能占用相同的一个或一组小网格交叉路口空间区域。
通过以上分析,建立每个批处理周期自治交叉路口求解的目标函数f,即在集合R选取最大车辆预约请求集合max Rac:
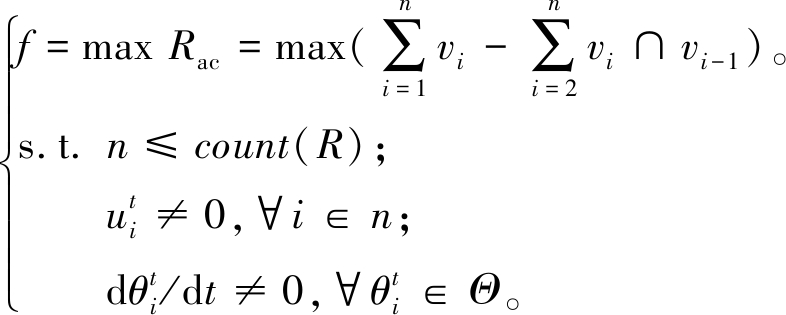
(5)
式中:
代表每次从R中选取要处理的车辆集合;
代表选取集合中存在冲突的情况;
代表车辆在交叉路口行驶过程中不能出现停车行为;
代表车辆行驶方向不能更改,即在进入路口前已经确定驶入和驶出交叉路口方向;Θ代表所有方向集合。
2 求解算法
2.1 基于最大团的自治交叉路口控制问题描述
基于第1节分析的车辆间的冲突关系可以建立车辆间冲突关系图,即节点(CAV)以及弧(车辆间的冲突关系)组成的冲突关系图G=(V,E),其中V为图G中车辆预约请求集合Rall的车辆节点集;E则为车辆冲突关系的集合,即存在预约请求冲突关系的车辆节点之间有边连接。自治交叉路口控制系统流程如图2所示。
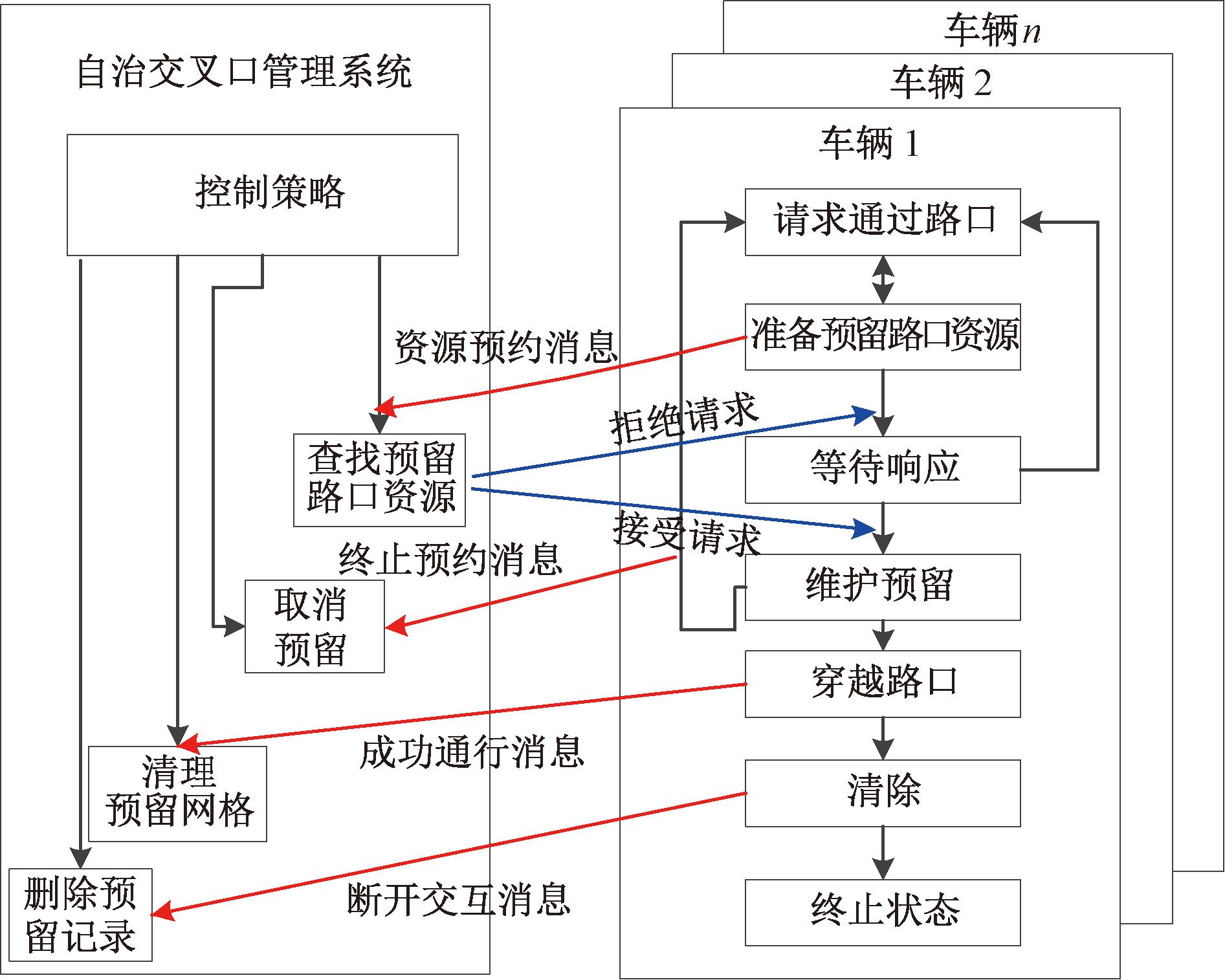
图2 控制系统整体流程
Figure 2 Overall process of control system
在目标函数f中,寻找最大接受集合max Rac的本质是要寻找最大无冲突车辆对数。因此可以将建立的冲突关系图G进行转换,得到其补图
其节点集合V仍然是预约请求集合Rall的车辆节点集合;
可以理解为将任意2个不存在冲突车辆节点进行连接的相容关系边集合。在非冲突关系图
中,定义一个完全子图
完全子图不唯一,其中V*为中点的子集;E*为
边集的子集。
基于上述分析,可以将本问题看作多类资源组合优化问题,而最大团理论是对此类问题进行描述和求解的有效方式[23-24]。在图
中包含车辆节点数最多的完全子图为控制系统需要寻找的最大团
满足节点个数
因此控制系统的目标函数f,依据某种策略,在非冲突关系图中,找到一个包含车辆节点最大完全子图使得每一个控制周期内交叉路口的吞吐量最大。
2.2 基于最大团的自治交叉路口控制策略
该控制策略输入量为车辆非冲突关系图
输出量为本周期内求解的最大团,此时求解的团应包含本周期内预约最多无冲突车辆数目。NDMC控制策略寻找最大团的过程共分为3个子阶段,每个阶段目标均要判断是否找到包含设定请求数目为tc大小的团(tc≤count(R)),如果找到则结束算法,并输出tc数目集合,否则进行下一个阶段的搜索,如果最终没有找到大小为tc数目的团,则输出目前找到的最优结果。
寻找最大相容车辆节点集合max Rac的3个子阶段如下。
(1) 随机选择车辆预约请求节点阶段:随机从集合中选择一个车辆预约请求节点,对选择车辆节点性质没有倾向性。
(2) 选择最大度的车辆预约请求节点阶段:从集合中选择一个具有最大度的车辆预约请求结点(初始时计算)。
(3) 选择惩罚节点阶段:加入节点惩罚机制,使得搜索过程多样化,避免搜索停滞,基于贪心算法,越频繁加入当前团的点,则在未来选择过程中越不容易被重新选择。
本文研究的控制策略的每一个选择阶段均设定最大外部循环次数和选择次数,当达到最大循环次数或者最大选择次数时输出结果。设系统当前接收车辆的集合为
即找到当前团的大小,集合A0为和当前团
中所有点都邻接的点的集合,集合A1为和当前团中除一个点外于都连接的所有点的集合,集合U为中加入一个
中的点,中被删除的那个不满足团条件的点的集合,U初始时为空。
在算法每个子阶段的外部循环中设置内部循环,条件满足
和U的交集不为
则内部一直进行循环,内部循环主要包括2个部分。①内部子循环,根据传入函数(3个阶段不同的节点选择策略),从中选择一个点加入到中,更新内部循环次数,若
结束整个算法,重置U为空;②内部选择条件,如果和U的交集不为
则执行如下过程:根据传入函数(3个阶段不同的选择策略),从
和U的交集中选择一个点v加入到
中并删除和v不邻接的点,以满足团的条件,将中所有和v不邻接的点集合Rv加入到U中,U=U+Rv,更新选择次数。内部循环体结束后,更新外部循环次数,更新惩罚值,并加入扰动策略,随机选择一个点,加入当前团中,并删除其中不满足条件的点。
NDMC控制策略3个子阶段运行完成之后,输出最终接受车辆数集合Rac,即本周期内找到的最大接受请求车辆集合。
3 实验与分析
为了对本研究提出的基于最大团的自治交叉路口控制策略的准确性和执行效率进行验证,在开源自治交叉路口仿真平台AIM[12]中,设定在平衡与不平衡2种车流量情况下对NDMC控制策略、FCFS控制策略、基于禁忌搜索控制策略(Tabu)[15]以及交通信号控制策略(traffic-light)的性能进行了对比评估。
3.1 实验仿真设定
(1)仿真参数设定。在AIM系统中,设定一个双向六车道正方形交叉路口区域(g=12)[12],单条车道宽度设定为3.25 m;生成车辆数量分布服从泊松分布,交通流分布服从Greenshields模型,车辆行驶速度依据车流量变化进行调整;交通路口通信范围为以交叉路口中心点位半径的300 m区域;车型为2种并按照2点分布生成(小型车尺寸为4.30 m×2.35 m,生成概率为0.8;大型车尺寸为10.0 m×2.5 m,生成概率为0.2)。控制系统的时间仿真步为0.02 s,时间片的划分与仿真步保持一致,系统批处理周期为2 s,实验的执行时间均为1 h。
(2)仿真性能评估指标。①车辆平均等待时间。车辆在交叉路口中以当前行驶状态通行所花费的平均时间为
其中,n为自治车辆的总数;
为车辆在拥堵情况下实际通过交叉路口所花费时间;
为车辆理想状态下以当前状态通过交叉路口所花费时间。②交叉路口的车辆完成数。在单位时间内(1 h)安全通过交叉路口的CAV总数。
3.2 平衡车流下控制策略性能评估实验
在AIM仿真平台中,平衡车流量情况表示进入交叉路口4个方向上车流量基本相当。
(1)车辆排队情况分析。交叉路口各个驶入方向上车辆到达服从数学期望λ相一致的泊松分布,不失一般性,λ分别取值为0.100、0.125、0.150、0.175。统计2 min内交叉路口中车辆的排队情况。如图3所示,NDMC控制策略当λ取值为0.100、0.125、0.150时排队总数低于26辆;而当λ=0.175时,车辆排队数呈增加趋势,但也维持在80辆之内,显示出了较强的鲁棒性。
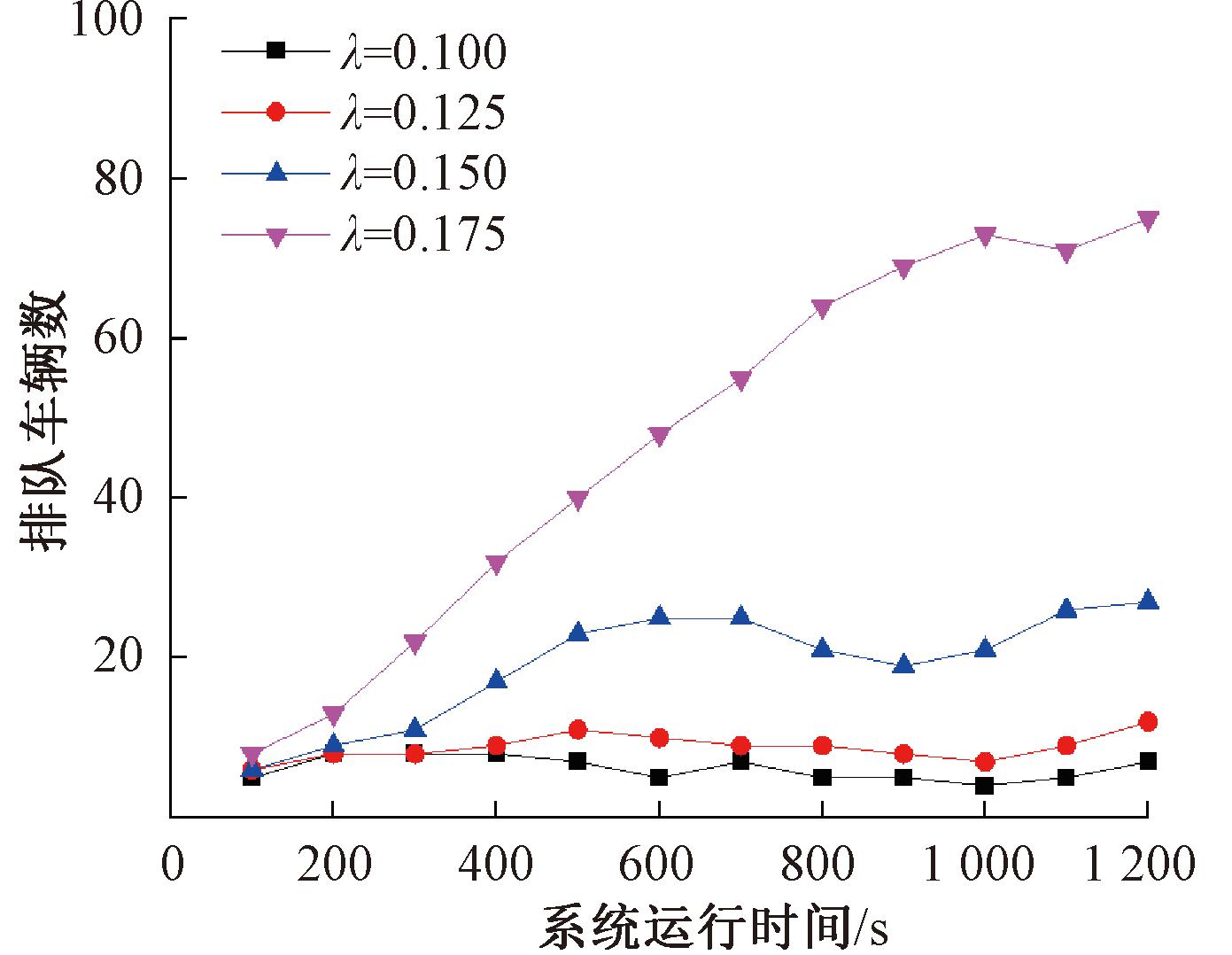
图3 服从泊松分布取不同λ值的车辆排队长度对比
Figure 3 Following Poisson distribution λ value of vehicle queue length comparison
(2)平衡车流量情况下对比情况。在每个交叉路口进入方向的每条车道起始处依据泊松分布生成车流,车辆密度ω从0辆/h变化到2 500辆/h,车辆前进方向依据交通规则基础上按照随机规则生成(如最右侧车道,车辆有直行或右转弯2种前进方向)。交通信号控制策略采用固定的相位配时方案,如表1所示。
表1 传统交通信号控制的相位配时
Table 1 Phase time in traditional traffic signal control
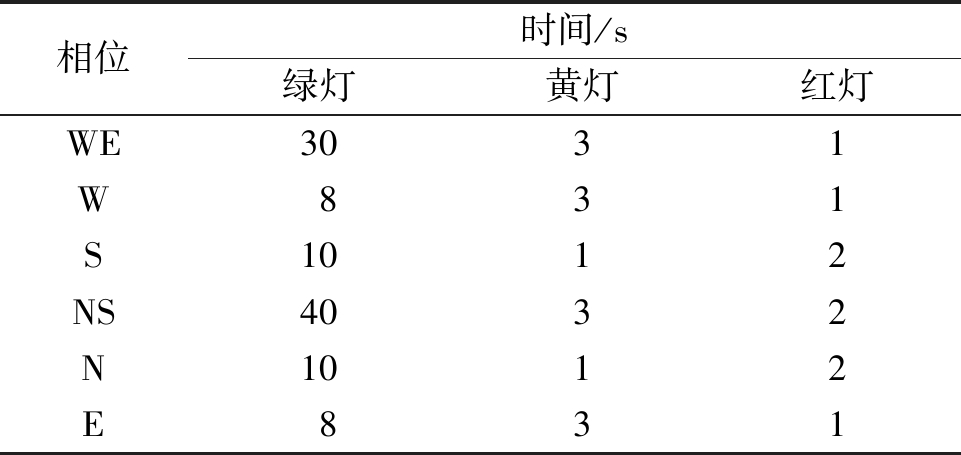
相位时间/s绿灯黄灯红灯WE3031W831S1012NS4032N1012E831
图4为本文策略与其他策略性能对比情况。如图4(a)所示,随着车流量密度增加,FCFS控制策略发生死锁次数也随之增加,车辆完成数方面增加较为缓慢,当车流量密度小于500 辆/h时,NDMC控制策略与其他策略性能基本相当;当车辆密度大于1 000辆/h时,NDMC控制策略优于其他策略。当车流量密度小于240辆/h时,NDMC控制策略与其他策略的平均等待时间均维持在可接受范围内;当流量密度超过300辆/h时,FCFS控制策略的平均等待时间出现了大幅度增加;当车辆密度超过2 000辆/h时,NDMC控制策略的平均等待时间低于其他控制策略。
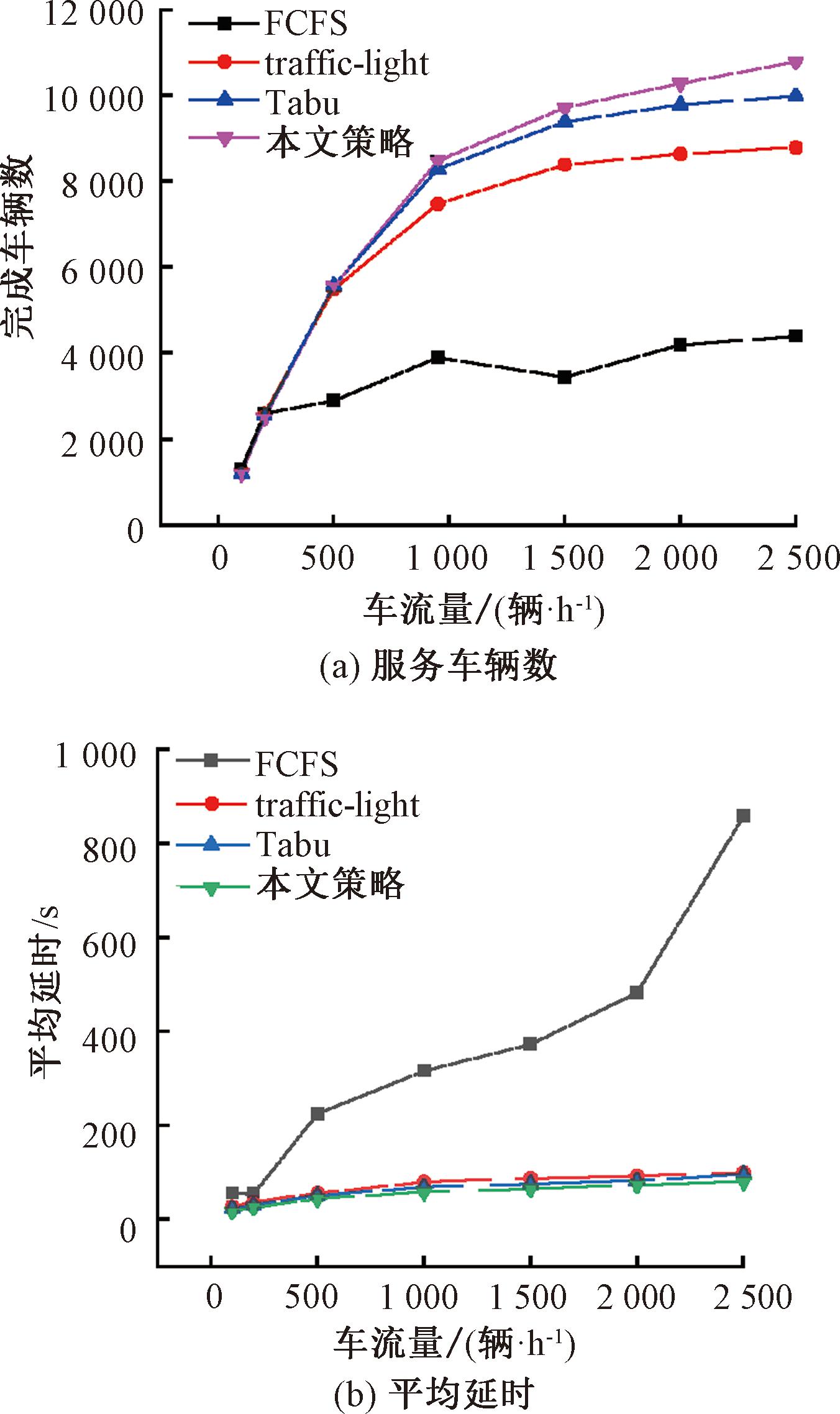
图4 平衡车流下不同策略性能对比情况
Figure 4 Performance comparison of different strategies under balanced traffic flow
随后,在平衡车流量情况下,对NDMC控制策略服务车辆数和拒绝车辆数情况进行评估,如图5所示。NDMC控制策略服务车辆数即车辆完成数随着车流量密度增加呈现出增加趋势,当车辆密度大于1 000辆/h时,增加趋势减缓;拒绝车辆数也随着车辆密度增加而提高,当车辆密度为2 500辆/h时,拒绝的车辆数为3 656辆次,呈现出逐渐增加趋势。这是因为随着车流量密度增加,每个周期内请求数在增多,导致每个周期找到最优解即最大团的效率逐步降低。
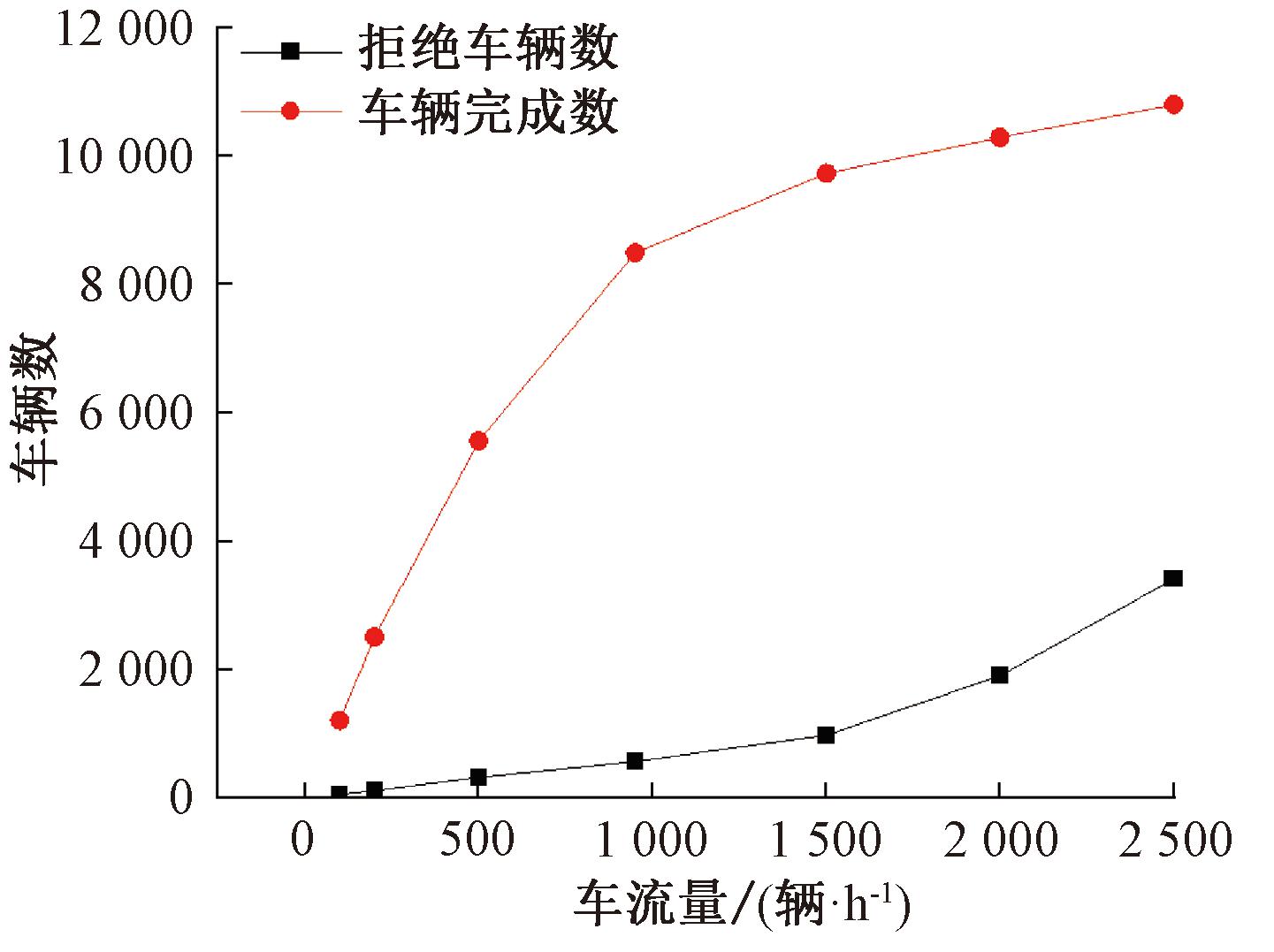
图5 车辆完成数和拒绝数对比分析
Figure 5 Comparison and analysis of the number of vehicles completed and rejected
3.3 不平衡车流下控制策略性能评估实验
在交叉路口东西进入方向车流量ω从0辆/h变化到2 500辆/h,南北两进入方向的车流量密度维持1 500辆/h,其他参数设置与平衡车流下实验设置相同。
图6为不平衡车流下车辆平均等待时间。如图6(a)所示,FCFS策略的车辆平均等待时间指标受不平衡车流影响最为明显。当车辆密度超过500辆/h时,本文策略和Tabu控制策略性能基本相当,优于其他控制策略;当车辆密度超过1 600辆/h时,NDMC策略平均等待时间要低于其他策略。图6(b)绘制了NDMC和FCFS控制策略在交叉路口南北方向和东西方向上的车辆平均等待时间对比情况。在NDMC控制策略中,南北方向车辆产生的平均等待时间高于东西方向车辆所产生平均等待时间,但仍然优于FCFS控制策略。
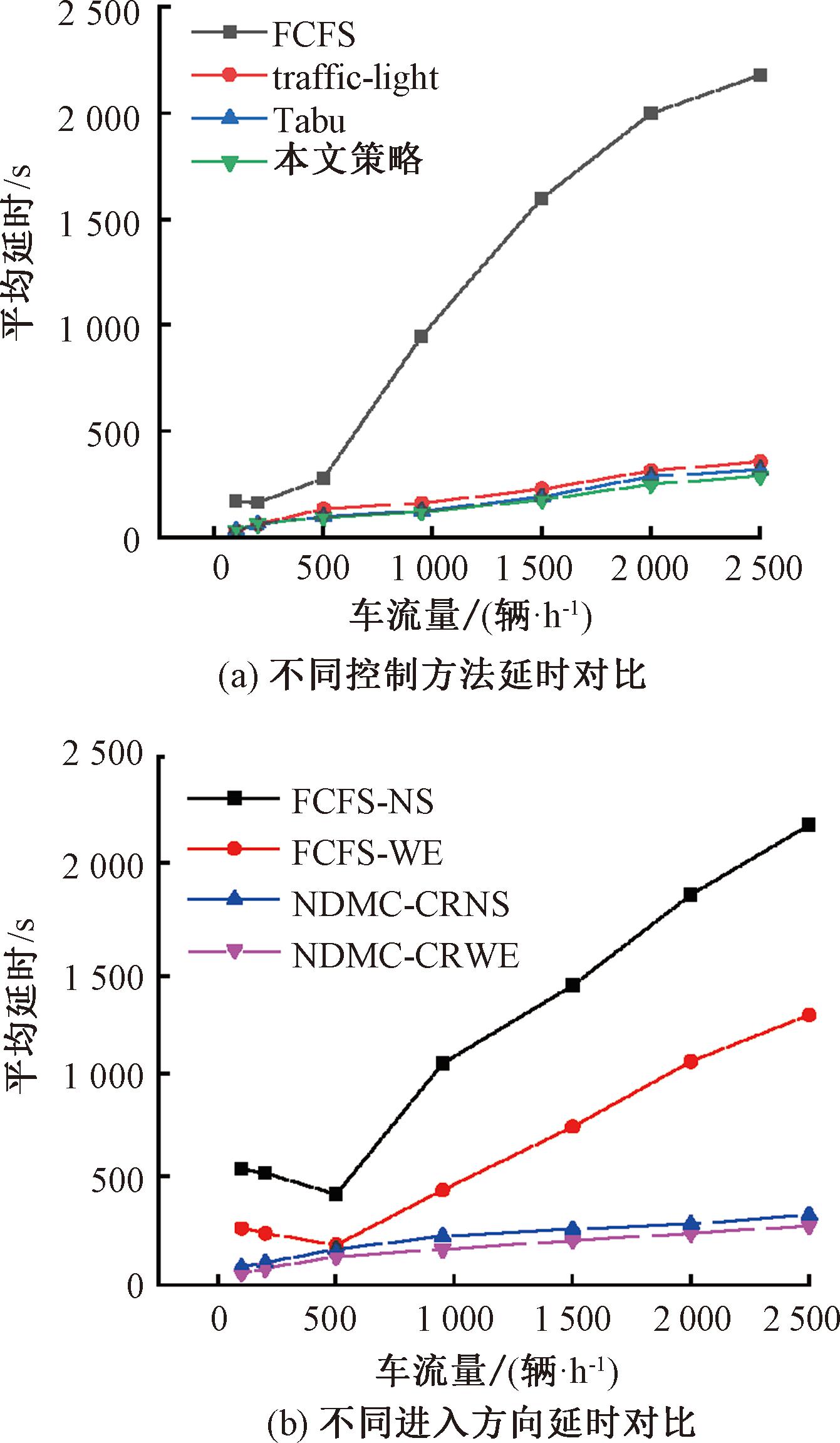
图6 不平衡车流下车辆平均等待时间对比
Figure 6 Average delays of the vehicles in unbalanced traffic
综上,为了对本文控制策略的执行效率进行评估,首先,评估了服从泊松分布不同λ取值的车辆排队长度的变化情况,证明该策略有较强鲁棒性;其次,与FCFS、Tabu和traffic-light控制策略在车辆完成数和车辆平均等待时间2个方面进行了对比评估,实验结果表明:本文控制策略性能均优于上述控制策略。证明了本文路口控制策略的有效性与可靠性。
4 结论
本文基于最大团理论提出了一种自治交叉路口控制策略。首先,对车辆在交叉路口中行驶的时空轨迹进行建模;其次,根据车辆间的时空行驶轨迹建立车辆间的冲突关系模型,并将车辆间冲突关系抽象成图;最后,通过在每个批处理周期内求解冲突关系图中最大团的补集作为接受车辆预约请求集合,使得在单位时间内更多车辆能够通过交叉路口,达到降低车辆平均延时和提高交叉路口吞吐量的目标。
与当前研究成果相比,本研究的工作主要体现在两个方面:①为了降低自治交叉路口控制系统的计算复杂度,将路口区域进行网格化处理,同时将控制系统时间轴进行切分,划分成等量批处理周期;②使用最大团理论来求解自治交叉路口控制问题,该方法自适应能力强,在不同车流量情况均能获得较优的解,能使得更多车辆安全通过交叉路口。
本文是在系统运行正常和通信理想情况下进行相关研究,没有考虑了车辆发生故障无法移动以及通信不畅等情况,因此未来工作设计一种在无线通信环境下仍能高效运行的路口控制策略,在更加趋近于真实交叉路口的交通环境中保证行车安全,提高自治交叉路口的通行效率。
[1] 高德软件有限公司. 2021年度中国主要城市交通分析报告[R]. 北京:高德地图交通大数据,2022.
AMAP. 2021 China′s major urban traffic analysis report[R]. Beijing: Gaode Transportation Big Data, 2022.
[2] 张雪妍, 贺锋. 基于累积前景理论的组合出行交通分配模型[J]. 郑州大学学报(工学版), 2020, 41(3): 91-96.
ZHANG X Y, HE F. Traffic assignment model with combined modes based on cumulative prospect theory[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(3): 91-96.
[3] 龙雪琴, 王瑞璇, 王晗. 考虑出行者不同理性程度的拥堵交通流分配方法[J]. 交通运输系统工程与信息, 2023, 23(1): 216-223.
LONG X Q, WANG R X, WANG H. Traffic flow assignment method considering travelers′ different rational degree under congestions[J]. Journal of Transportation Systems Engineering and Information Technology, 2023, 23(1): 216-223.
[4] 岳昊, 刘晓玲, 孟晓雨, 等. 拥堵道路网的静态交通流非均衡分配方法[J]. 北京交通大学学报, 2017, 41(3): 1-6.
YUE H, LIU X L, MENG X Y, et al. A non-equilibrium method to solve static traffic assignment problem at the congested road network[J]. Journal of Beijing Jiaotong University, 2017, 41(3): 1-6.
[5] 张新洁, 关宏志, 赵磊, 等. 有限理性视野下出行者出行方式选择分层Logit模型研究[J]. 交通运输系统工程与信息, 2018, 18(6): 110-116.
ZHANG X J, GUAN H Z, ZHAO L, et al. Nested logit model on travel mode choice under boundebly rational view[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(6): 110-116.
[6] HOU Y F, SELIMAN S M S, WANG E S, et al. Cooperative and integrated vehicle and intersection control for energy efficiency (CIVIC-E2)[J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(7): 2325-2337.
[7] LI L, WEN D, YAO D Y. A survey of traffic control with vehicular communications[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(1): 425-432.
[8] GUO Q Q, LI L, BAN X G. Urban traffic signal control with connected and automated vehicles: a survey[J]. Transportation Research Part C: Emerging Technologies, 2019, 101: 313-334.
[9] DRESNER K, STONE P. A multiagent approach to autonomous intersection management[J]. Journal of Artificial Intelligence Research, 2008, 31: 591-656.
[10] CARLINO D, BOYLES S D, STONE P. Auction-based autonomous intersection management[C]∥16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013). Piscataway:IEEE, 2014: 529-534.
[11] VASIRANI M, OSSOWSKI S. A market-inspired approach for intersection management in urban road traffic networks[J]. Journal of Artificial Intelligence Research, 2012, 43: 621-659.
[12] MAHBUB A M I, MALIKOPOULOS A A. Conditions for state and control constraint activation in coordination of connected and automated vehicles[C]∥2020 American Control Conference (ACC). Piscataway:IEEE, 2020: 436-441.
[13] XU H L, ZHANG Y, LI L, et al. Cooperative driving at unsignalized intersections using tree search[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(11): 4563-4571.
[14] ZHU M J, LI X, HUANG H Y, et al. LICP: a look-ahead intersection control policy with intelligent vehicles[C]∥2009 IEEE 6th International Conference on Mobile Adhoc and Sensor Systems. Piscataway:IEEE, 2009: 633-638.
[15] 刘明剑, 谭国真, 魏欣, 等. 基于禁忌搜索的交叉路口自治车辆调度方法[J]. 中国公路学报, 2016, 29(2): 123-129.
LIU M J, TAN G Z, WEI X, et al. Autonomous vehicle scheduling method based on tabu search at intersections[J]. China Journal of Highway and Transport, 2016, 29(2): 123-129.
[16] 常玉林, 汪小渟, 张鹏. 改进蚁群算法在交通分配模型中的应用[J]. 郑州大学学报(工学版), 2017, 38(2): 41-44, 49.
CHANG Y L, WANG X T, ZHANG P. Modified ant colony algorithm and its application on traffic assignment model[J]. Journal of Zhengzhou University (Engineering Science), 2017, 38(2): 41-44, 49.
[17] PEI H X, FENG S, ZHANG Y, et al. A cooperative driving strategy for merging at on-ramps based on dynamic programming[J]. IEEE Transactions on Vehicular Technology, 2019, 68(12): 11646-11656.
[18] 吴伟, 刘洋, 马万经. 自动驾驶环境下面向交叉口自由转向车道的交通控制模型[J]. 中国公路学报, 2019, 32(12): 25-35.
WU W, LIU Y, MA W J. Intersection traffic control model for free-turning lane in connected and autonomous vehicle environment[J]. China Journal of Highway and Transport, 2019, 32(12): 25-35.
[19] 蒋阳升, 蒋浩然, 姚志洪, 等. 基于虚拟车队的自动交叉路口车辆时序优化模型[J]. 中国公路学报, 2022, 35(8): 291-303.
JIANG Y S, JIANG H R, YAO Z H, et al. Vehicle schedule optimization model for autonomous intersection based on virtual platoon[J]. China Journal of Highway and Transport, 2022, 35(8): 291-303.
[20] GONZ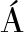
LEZ C L, ZAPOTECATL J L, GERSHENSON C, et al. A robustness approach to the distributed management of traffic intersections[J]. Journal of Ambient Intelligence and Humanized Computing, 2020, 11(11): 4501-4512.
[21] YESILYURT A Y, TUNC I, SOYLEMEZ M T. A reservation method for multi-agent system intersection management with energy consumption considerations[J]. IFAC-PapersOnLine, 2021, 54(2): 246-251.
[22] ZHANG J, JIANG X, LIU Z Y, et al. A study on autonomous intersection management: planning-based strategy improved by convolutional neural network[J]. KSCE Journal of Civil Engineering, 2021, 25(10): 3995-4004.
[23] PULLAN W. Approximating the maximum vertex/edge weighted clique using local search[J]. Journal of Heuristics, 2008, 14(2): 117-134.
[24] PULLAN W. Approximating the maximum vertex/edge weighted clique using local search[J]. Journal of Heuristics, 2008, 14(2): 117-134.