空间矢量脉宽调制技术(space vector pulse width modulation, SVPWM)具有母线电压利用率高、开关损耗少、输出谐波成分小等优点[1]。基于SVPWM的矢量控制方法以及直接转矩控制方法已经在高性能电机控制场合得到了广泛应用[2-3]。
SVPWM算法属于实时算法,更快的计算速度有利于提高最大开关频率与转速、减少控制延时。孙鹤旭等[4]对SVPWM算法进行改进,提出了一种基于120°AB坐标系的SVPWM算法,以互差120°的基本矢量为基,构建非正交坐标系,在该坐标系下计算速度有所提高,但增加了铜损耗。齐昕等[5]基于DSP平台,利用一个压缩变换将基础电压矢量由60°压缩至45°,可以快速地判断扇区,该方法提高了计算速度,同时减少了内存空间的使用量。FPGA灵活性高,其搭载的算法在本质上属于硬件电路,适合运行对实时性要求较高的算法。Benedetto等[6]基于FPGA提出了一种SVPWM的硬件结构,预先计算α-β平面1/6区域的标准化停留时间,存储于由LUT构成的优化后的内存之中,基于查表法的思想,只需输入若干参数即可完成三相占空比的计算,效果与常规方法相同,但是计算速度更快。
以往的研究大多针对SVPWM计算过程中的某个步骤进行优化,优化效果不佳。本文从整体出发,提出一种将零矢量分散的七段式SVPWM算法在FPGA中快速高效实现的硬件架构,以兼顾模拟控制器的实时性和数字控制器的输出精度。该硬件架构整体考虑了Clarke逆变换与SVPWM算法之间的对称性和FPGA并行计算的特点,灵活使用时序逻辑与组合逻辑,充分挖掘可以复用的计算步骤,将多个环节视为一个整体,来完成占空比计算与PWM的输出。在逻辑资源消耗方面,使用了1次乘法运算和若干加法与逻辑运算。在计算速度方面,采用了3次时钟的上下边沿触发,并在2个时钟周期内完成计算。在PWM输出方面,陈增禄等[7]、刘健等[8]在FPGA中实现了自然采样方法,证明自然采样较规则采样具有更佳的谐波水平,因此,本文亦选择自然采样作为PWM的输出方式,来提高SVPWM算法的整体性能。
为了证明该硬件架构的效果,本文进行了行为级仿真与实物验证。通过行为级仿真评估了该架构的计算速度以及输出效果,并给出了该硬件结构在不同平台下的资源使用情况。通过实物验证,给出了接入逆变器与滤波器后实际测量输出波形。
1 SVPWM的原理
在三相两电平逆变器中,每个半桥的上下桥臂开关状态互补,可以用1 bit表示,整个逆变器共有23个状态,构成SVPWM算法中的8个基本矢量。由基本矢量组成的平面如图1所示,U0与U7为零矢量,U1至U6为非零矢量。在任意时刻,控制器的指令将映射至某一基本矢量,在一个微小的周期Ts内,控制器交替发出基本矢量,由于电感绕组对电流具有惯性,可以按照式(1)等效合成任意方向的参考电压。
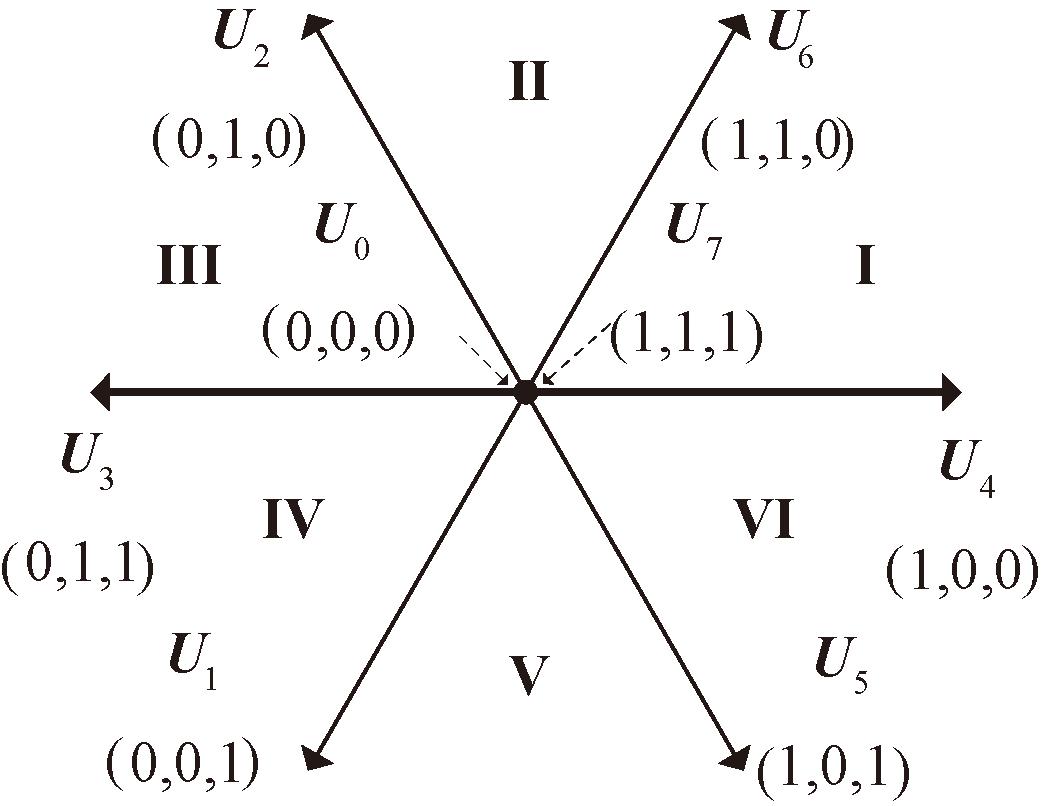
图1 基本矢量平面
Figure 1 Basic vector plane
![]() Urefdt=
Urefdt=![]() Uidt+
Uidt+![]() Ujdt+
Ujdt+![]() U0,7dt。
U0,7dt。
(1)
式中:Uref为参考电压,Ui与Uj为Uref所在扇区的2个非零矢量。为了能够方便地在控制器中计算,需将式(1)简化为式(2)的形式:
(2)
本文采用七段式SVPWM,以第I扇区为例,其合成方式如图2、3所示。其中,图2的基本矢量合成图与图3的PWM波形在形状上严格按照比例对应,共同表示七段式SVPWM的典型运行原理。显然,该典型运行原理可以拆解为一系列计算步骤,但其实现方式无法脱离具体的控制器平台。传统的SVPWM一般部署于DSP之中,而在DSP中运行SVPWM尚有以下不足之处:①DSP按照拆解好的计算步骤串行执行指令,这决定了系统的实时性能不如并行的硬件结构;②DSP中输出高精度的PWM主要依赖于定时器外设,一般使用规则采样法进行PWM的输出,难以实现自然采样;③DSP中的定时器外设的数量是有限的,难以满足任意多的PWM通道的需求,而且当通道数量较多时,多个通道之间难以实现较为精确的同步。
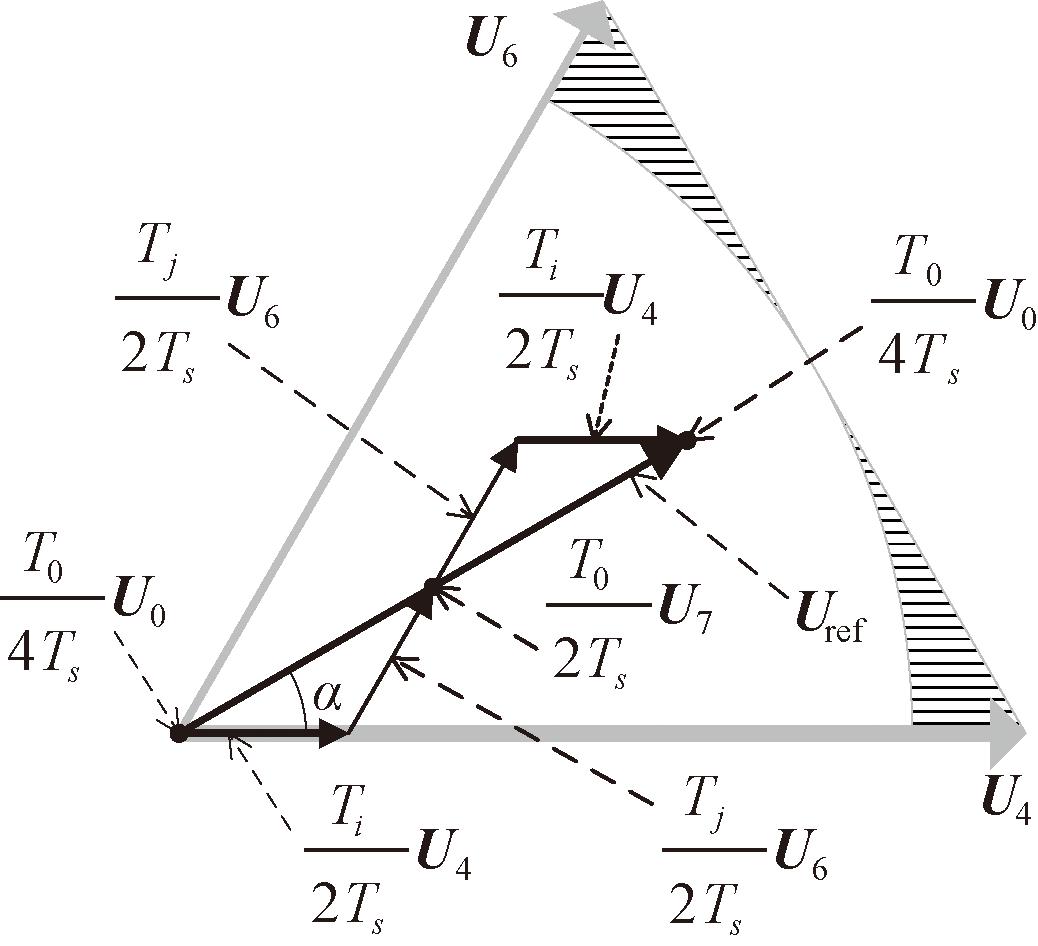
图2 七段式矢量合成方式
Figure 2 7-segment vector synthesis mode
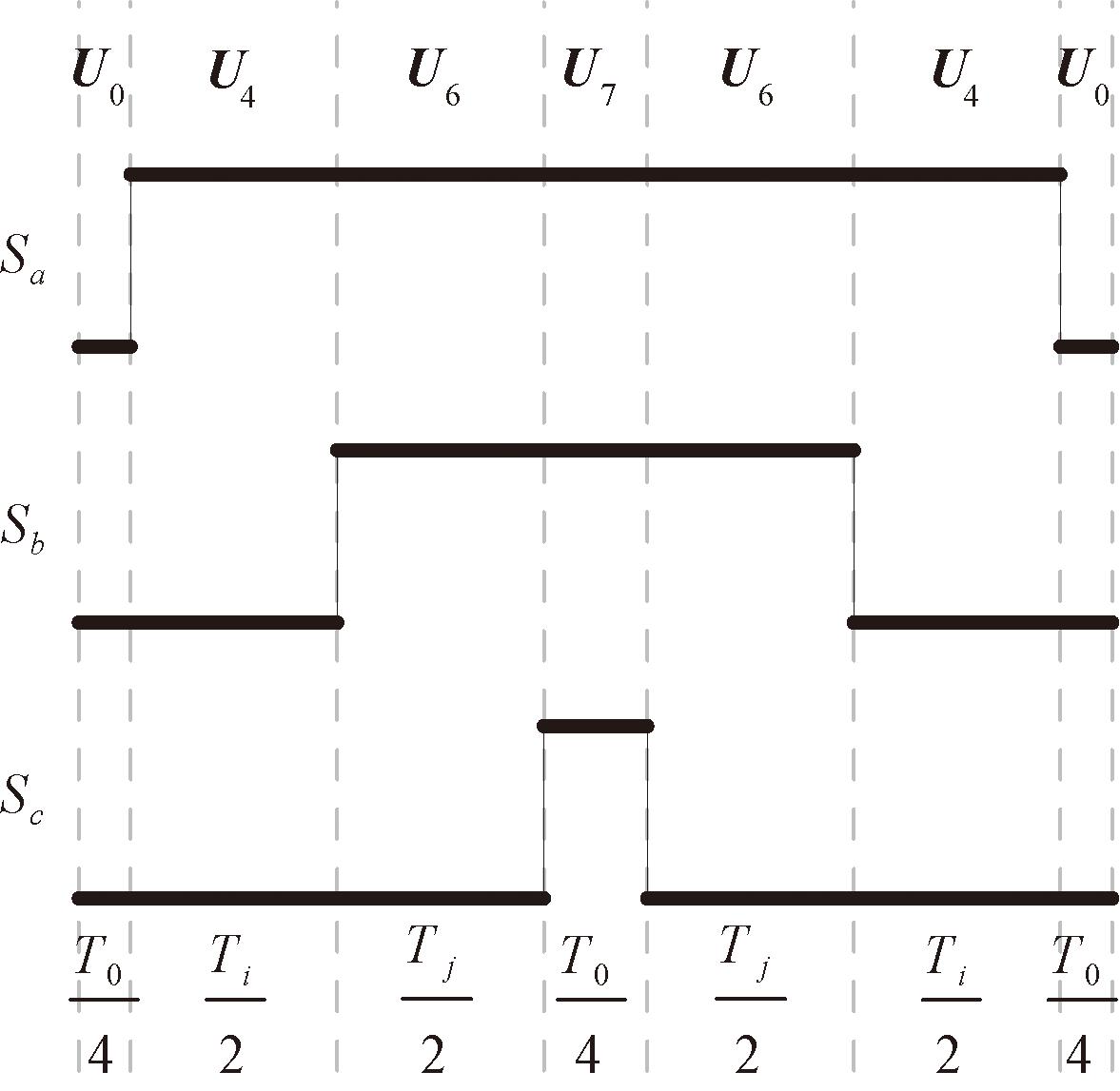
图3 七段式矢量合成的PWM波形
Figure 3 PWM waveform of 7-segment vector synthesis
2 SVPWM的硬件优化算法
所述硬件结构分为3个部分,分别为占空比计算、溢出保护、PWM比较生成,这3个部分密不可分,在设计阶段各部分的参数放在一起考虑。
2.1 占空比计算
首先需要定义输入变量、输出变量以及中间变量的精度与数据格式。由于在FPGA中浮点计算的代价比较大,因此需要将诸多变量先标幺化,再定点化。本文将输入变量定义为直角坐标系下的ALPHA、BETA,用来表示目标矢量Uref。为了便于计算,先将二者的输入范围标幺化为[-1,1),再将其定点化为Q11格式。ALPHA与基本矢量U4同方向,具体的映射关系见图4。
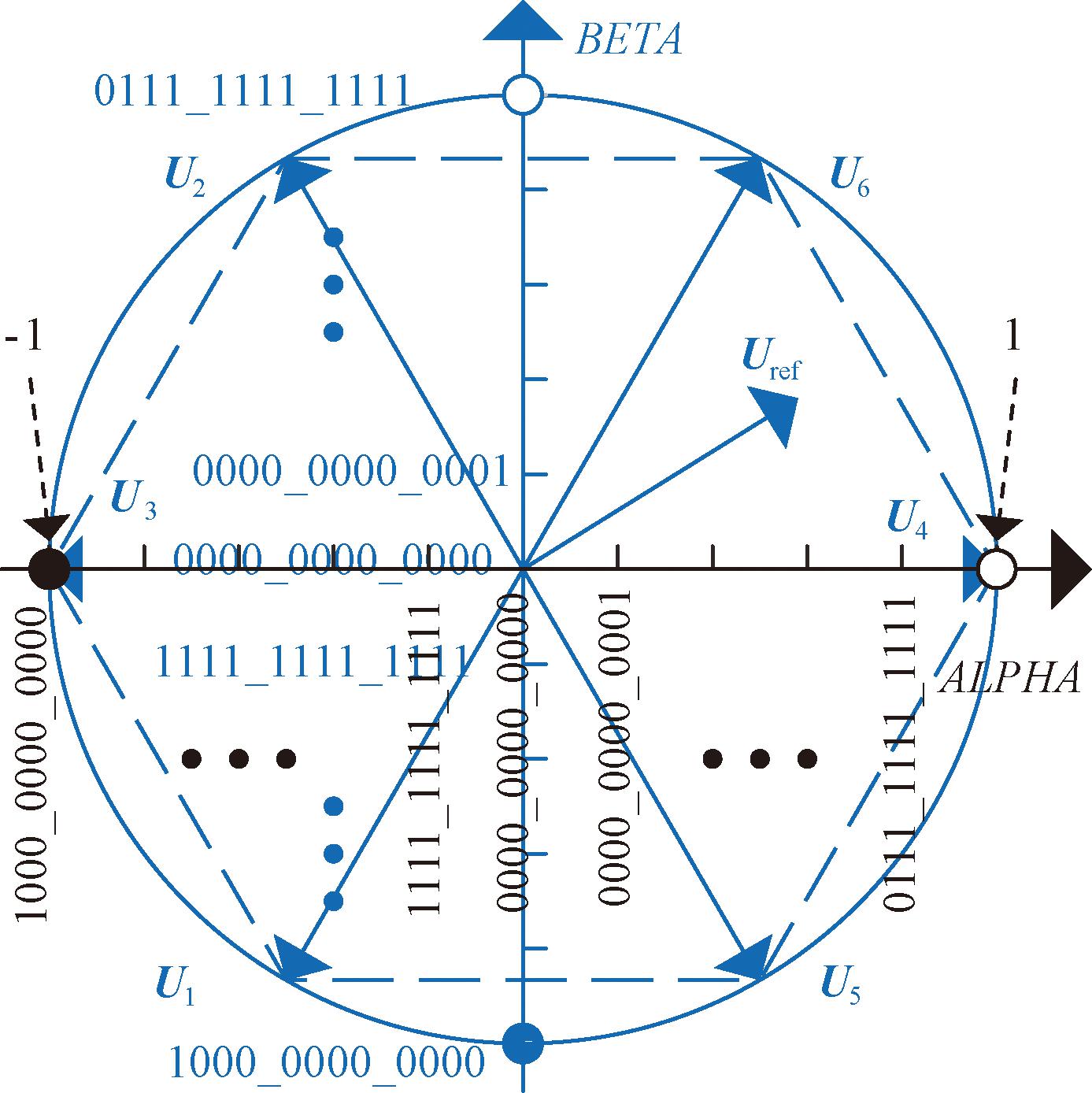
图4 输入变量之间的映射关系
Figure 4 Mapping relationship between input variables
本文将输出变量定义为TA0、TB0、TC0,均为13 bit有符号数,其中低12位定义为占空比。当Uref未超出图4中六边形输入范围时,TA0、TB0、TC0的符号位将会始终保持为0,只有在超出该范围时,符号位才发生逆转,利用这一特性,在后文设计溢出保护功能。其余变量的数据格式见表1。
表1 三相占空比计算过程中的主要变量
Table 1 Main variables during duty factor calculation
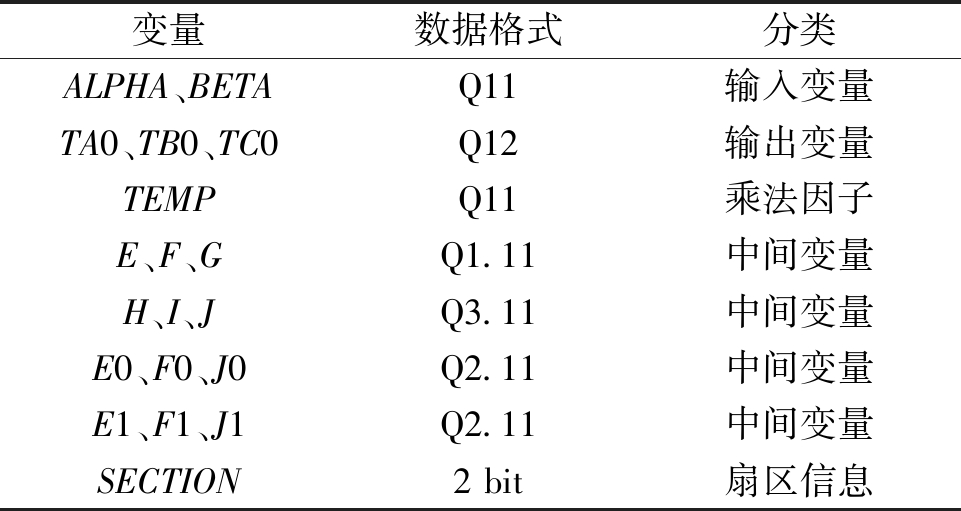
变量数据格式分类ALPHA、BETAQ11输入变量TA0、TB0、TC0Q12输出变量TEMPQ11乘法因子E、F、GQ1.11中间变量H、I、JQ3.11中间变量E0、F0、J0Q2.11中间变量E1、F1、J1Q2.11中间变量SECTION2 bit扇区信息
TA0、TB0、TC0的计算可以分为以下3个步骤。
步骤1 ALPHA、BETA经过调整后的Clarke逆变换得到中间变量E、F、G与扇区信息SECTION,该结构如图5所示。
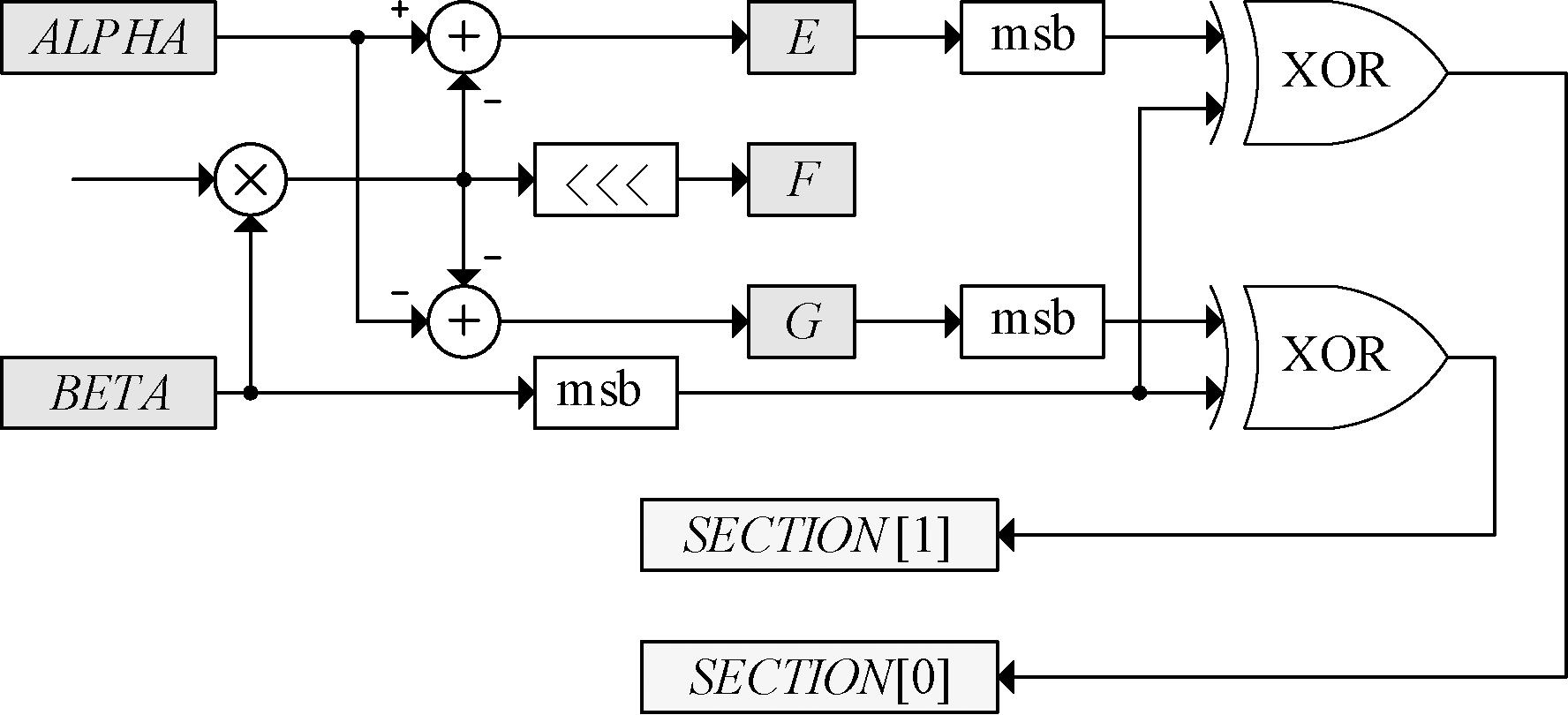
图5 Clarke逆变换与扇区信息
Figure 5 Inverse Clarke transform and sector information
中间变量E、F、G的计算遵循式(3)的变换规则:首先将ALPHA与BETA沿45°线翻转;其次进行Clarke逆变换;最后放缩一定倍数,以简化计算。
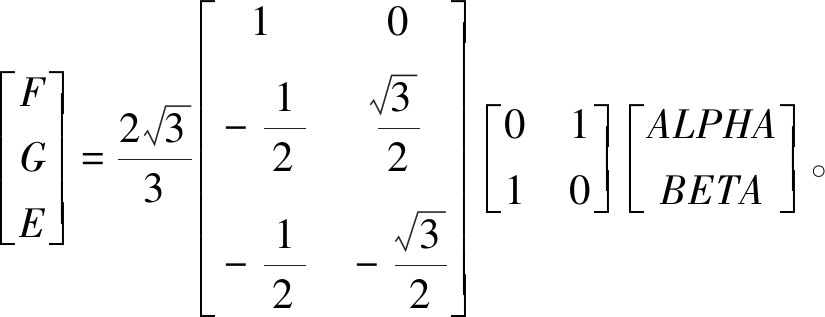
(3)
为了便于在FPGA中实现,式(3)按照式(4)、(5)的方式拆分成1个常数乘法、2个加法和1个移位计算。
(4)

(5)
同时,可以通过2个异或运算得到扇区信息,其计算方式见式(6),该部分利用变量的符号位,在FPGA中的计算代价较小。
(6)
步骤2 由E、F、G生成3组直接包含占空比信息的中间变量,如图6所示。
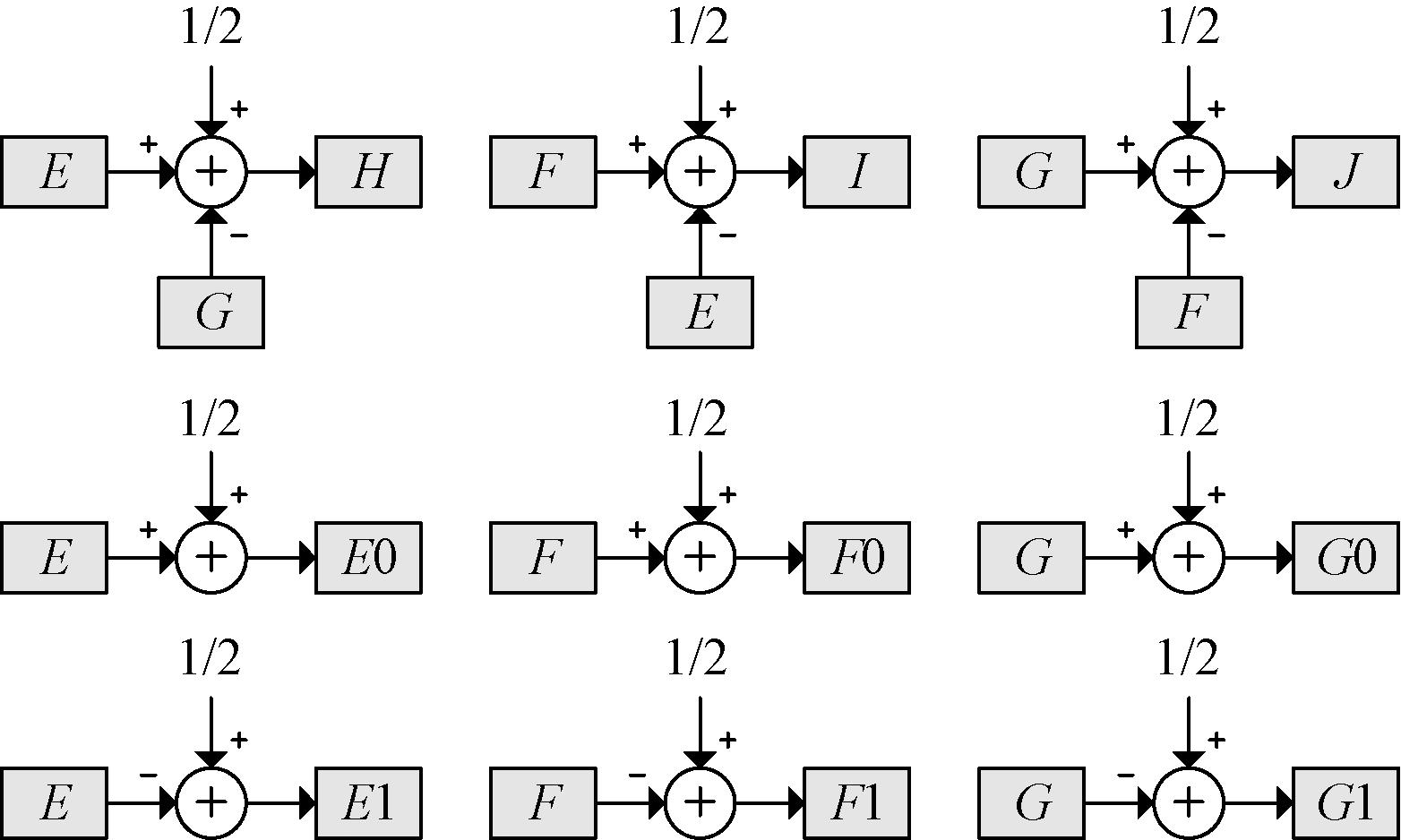
图6 中间变量
Figure 6 Intermediate variables
该部分生成了9个中间变量H、I、J、E0、E1、F0、F1、G0、G1,均由步骤1中的E、F、G变量通过加法运算获得。这9个变量同时进行计算,但是其中只有3个变量是真正的占空比。
步骤3 根据获得的扇区信息,从3组中间变量中筛选出未经过溢出保护的含有符号信息的占空比,如图7所示。
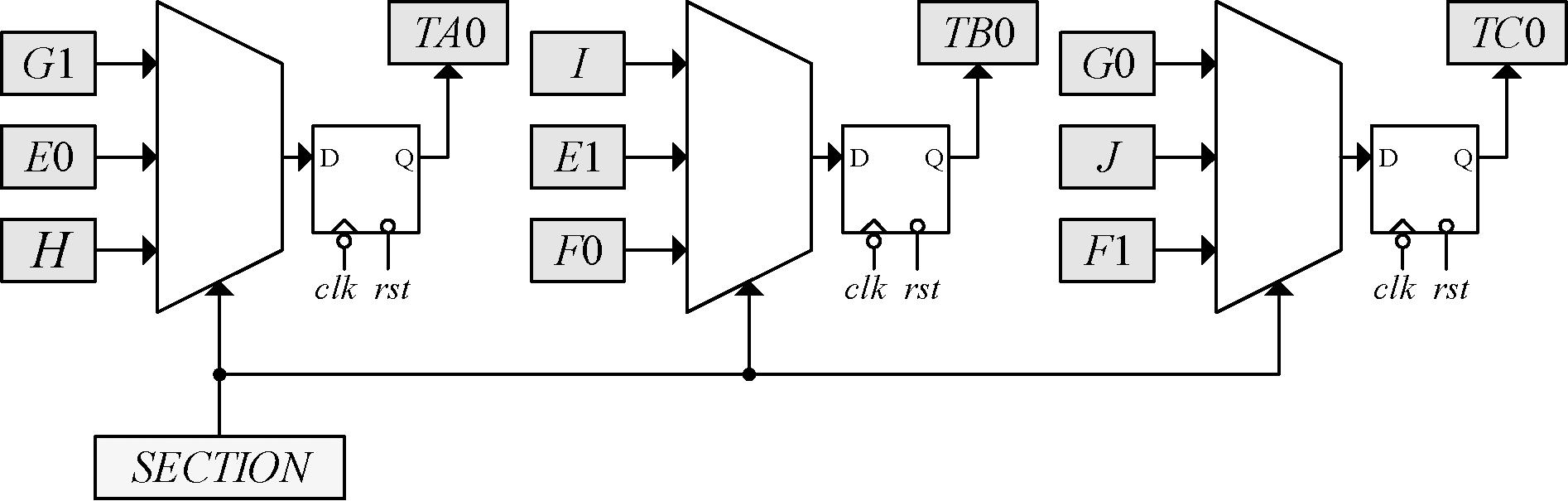
图7 从中间变量中选出占空比
Figure 7 Select duty ratio from intermediate variables
该部分在步骤2中获得的9个中间变量中筛选出占空比,其筛选的依据为第一部分获得的2 bit扇区信息。其中的多路器具有22个分支,其中一个分支为默认选项。由于步骤1中的变换并非等幅值变换,因此可以将TA0、TB0、TC0强制按照Q12格式读取,这使得其最终结果恢复为真正结果。
整体来看,上述3个步骤主要由组合逻辑构成,TA0、TB0、TC0在这一小结作为输出(并非最终的占空比输出),只使用了1次下降沿触发,与之对应,ALPHA、BETA在时钟的上升沿触发。这种交错的时钟边沿触发提高了计算速度,保证了数据的稳定。
2.2 溢出保护
由于并非所有的输入变量都能处于线性调制范围,因此需要对其加以限制。由前文可知TA0、TB0、TC0均为13 bit的有符号数,而真正的占空比只能是无符号数,本文利用其符号位来使输出得到钳位。以TA0为例,当TA0的符号位为0时,只需将数值位传递给TA即可,当TA0的符号位由0上升为1时,则使TA取TA0在时间上最近的一个未溢出的数值位,当TA0的符号位由1恢复至0时,恢复数值位的传递。上述过程可以由式(7)、(8)所示的时间序列表示。
(7)
(8)
为了将以上思路应用于FPGA中,以TA为例可以将式(7)、(8)转变成图8所示的结构。与TA0、TB0、TC0的下边沿触发方式相对应,TA、TB、TC采用时钟上边沿触发。
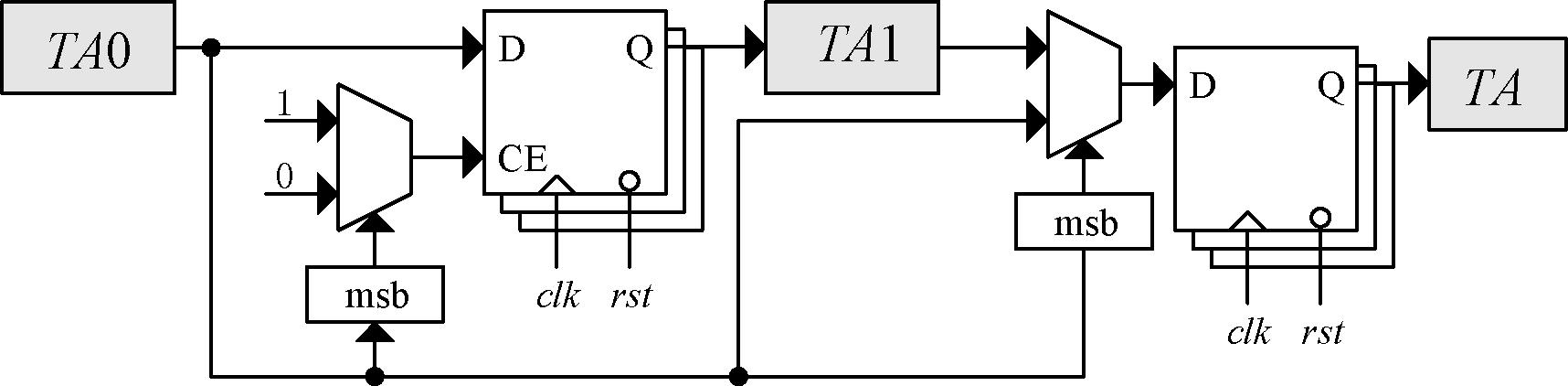
图8 溢出保护
Figure 8 Overflow protection
2.3 PWM比较生成
将三相占空比与三角载波进行比较,便能生成PWM。目前常用的生成方法为规则采样法,该方法在三角载波的固定位置对占空比信号进行采样,在半个或1个载波周期内保持不变,从而便于和三角载波比较,这种方式往往应用于DSP之中,而自然采样则全过程进行比较,这种方式适合于在模拟控制器中实现,图9展示了两种采样方式输出PWM的对比结果。

图9 2种采样方式对比
Figure 9 Comparison of two sampling methods
虽然规则采样法在实现过程中具有一定的简便性,但是自然采样法在谐波水平方面比规则采样法要更为优越[9]。DSP中常见的定时器外设难以实现自然采样,而FPGA本身具有高度的灵活性,可以设计出具有差异化功能的定时器,从而实现自然采样,本文据此设计了图10的硬件结构。其中,三角载波由计数器CNT产生,主频频率为100 MHz,CNT的位数L决定了fcarrier的大小:
(9)
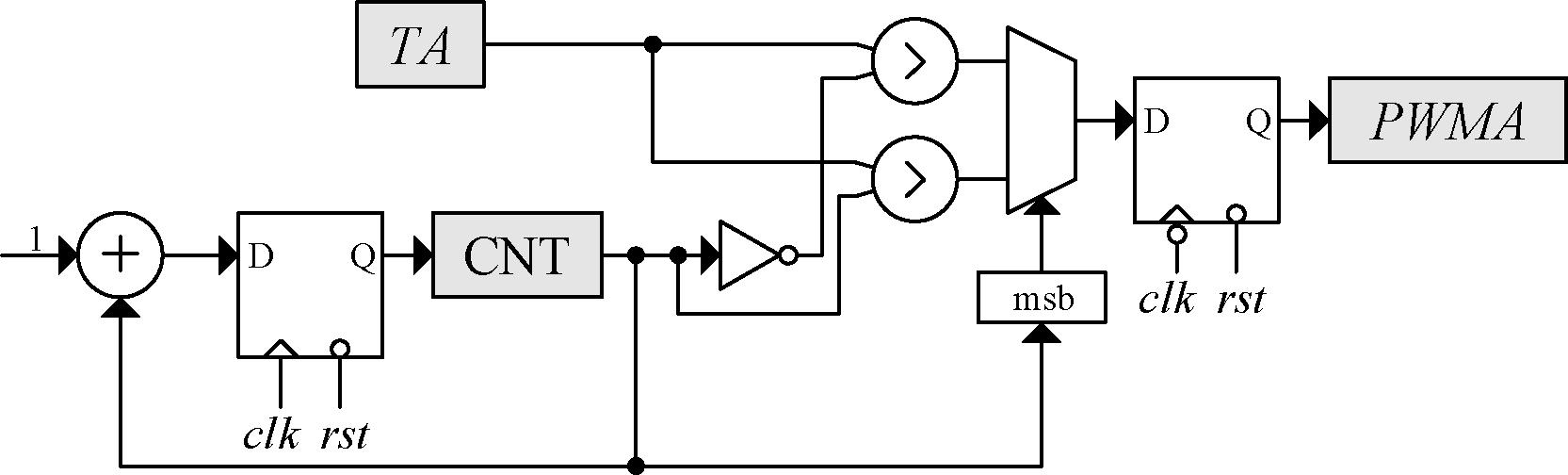
图10 自然采样
Figure 10 Natural sampling
当L为13时,载波频率为12.207 kHz,此时PWM分辨率可以达到12 bit。由于载波频率与PWM分辨率R不能同时无限制上升(R<L-1),过高的占空比精度将无法体现为PWM分辨率,因此前文只采用12 bit作为最终的占空比精度,这也有利于节省逻辑资源。
3 仿真与验证
3.1 行为级仿真
仿真方案如图11所示,使用Vivado软件,采用CORDIC算法模块作为激励信号源[10],产生幅值为1的一对正交的正弦信号,经过一定衰减后输入SVPWM模块,通过观测SVPWM的输入量与输出量来验证SVPWM,该行为级仿真可以证明本文所述硬件结构在功能上的可行性。
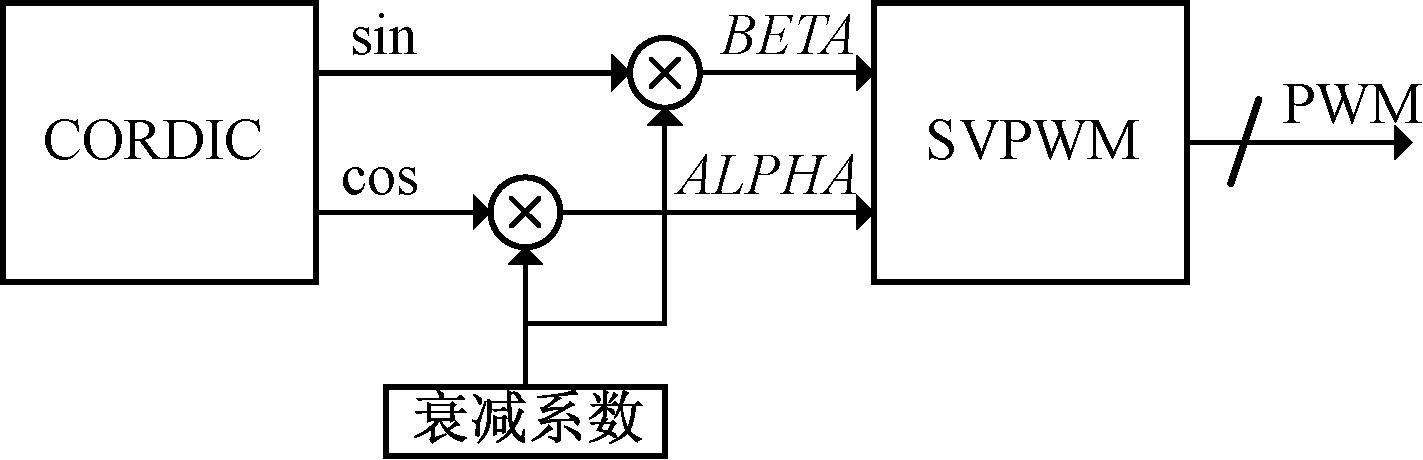
图11 仿真方案
Figure 11 Simulation scheme
首先,对于线性调制范围,设置衰减系数为0.5,其仿真结果如图12所示。观察输入的ALPHA与BETA的波形,以及占空比TA、TB、TC的波形,可以看出该硬件结构在线性范围内符合预期。
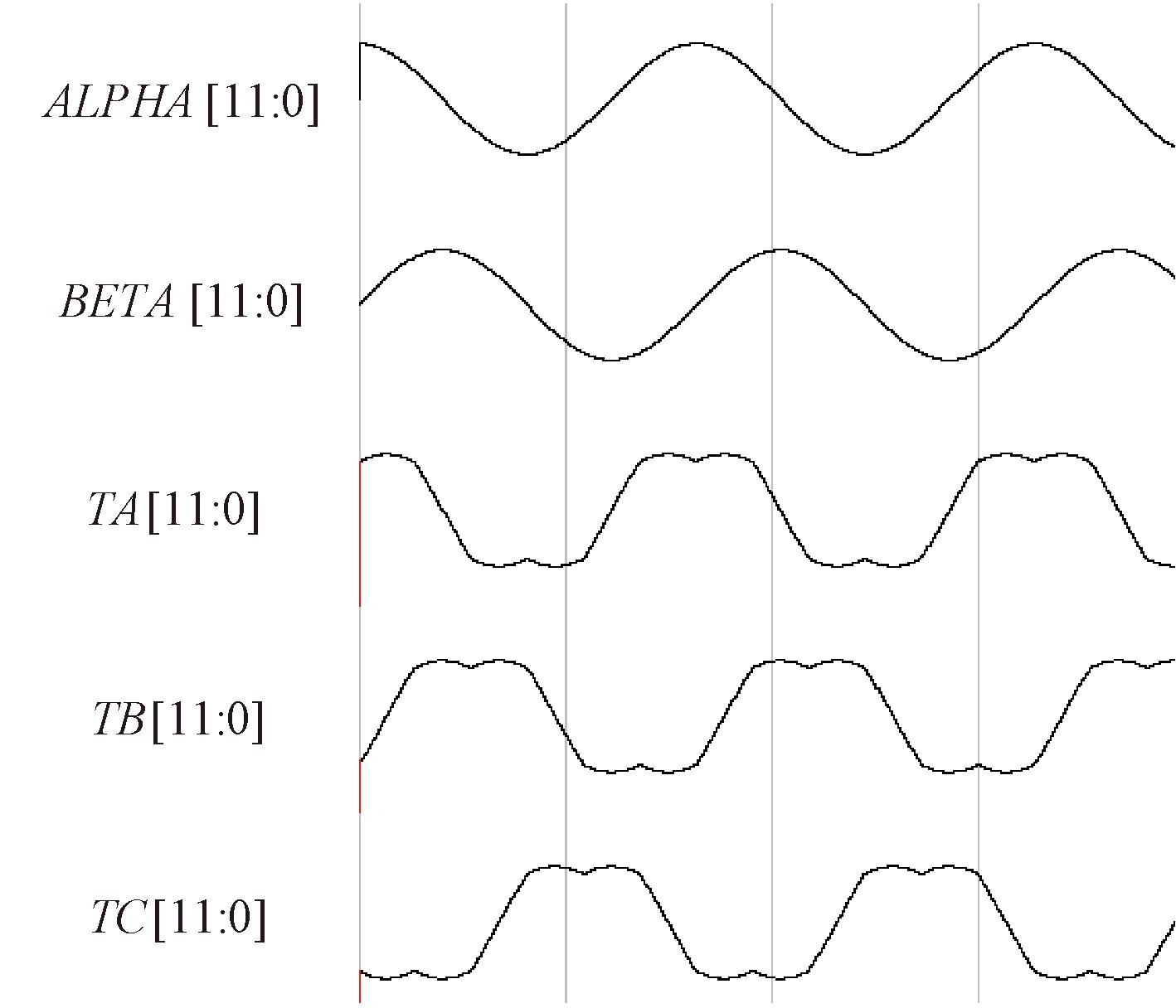
图12 SVPWM的输出结果
Figure 12 Output results of SVPWM
当衰减系数大于0.866时,参考矢量便超出了线性调制范围,此时溢出保护发生作用。为了能较好地观察到预期波形,本文以衰减系数0.93为例,其仿真结果如图13所示。可以看出,当占空比在达到最大值后受到钳位,据此可以证明该硬件结构中的溢出保护功能是有效的。
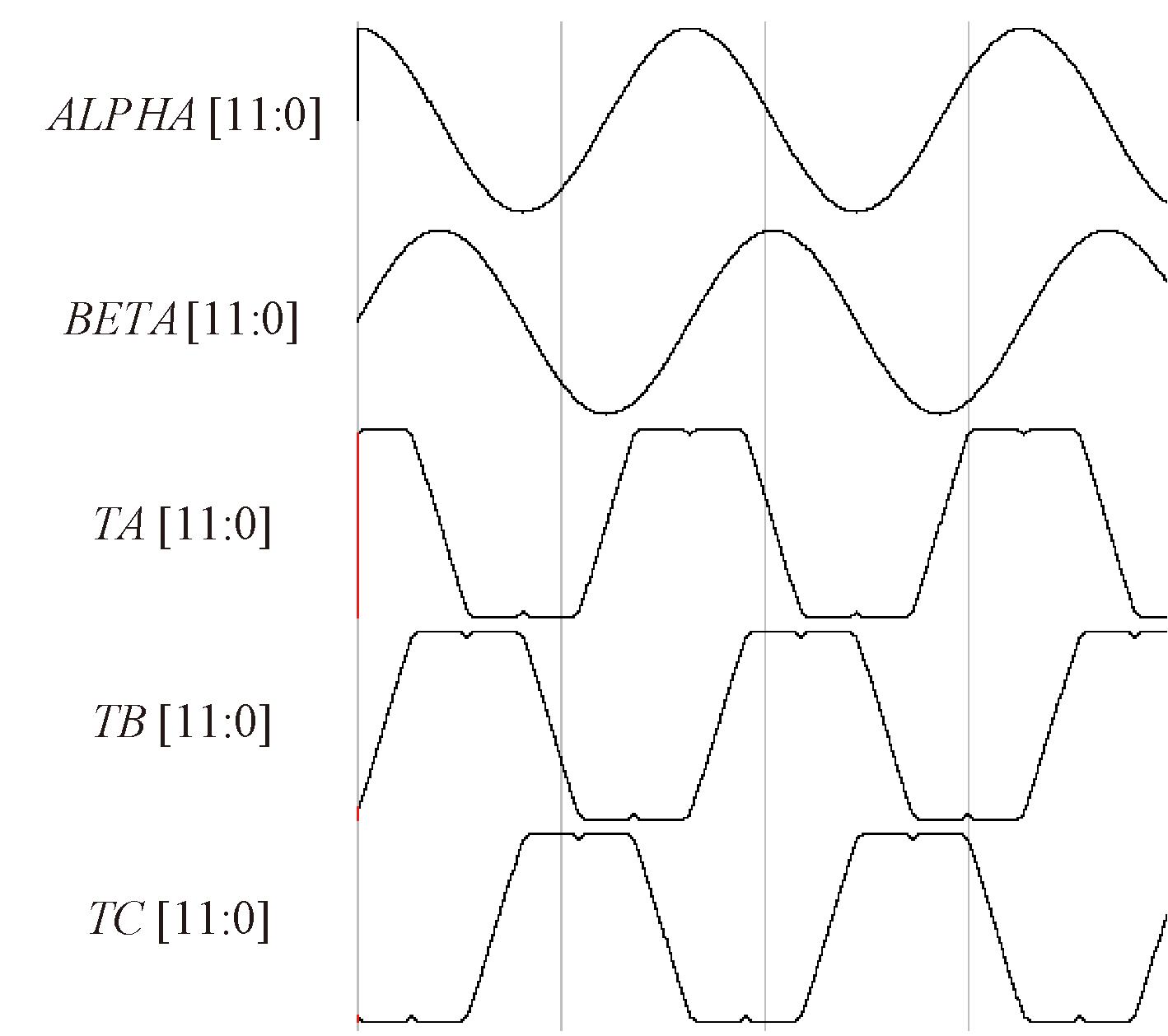
图13 溢出保护功能生效
Figure 13 Overflow protection takes effect
以上部分验证了SVPWM的主要功能,接下来验证该硬件结构的计算速度。从输入ALPHA和BETA开始,到输出三路PWM结束,其时序如图14所示。输入的参考矢量模为0.5,从0°开始逆时针旋转,输出的PWM以零矢量U7作为开头,其值为(1,1,1)。可以看出,该硬件架构在2个时钟周期内完成了整个计算过程,当时钟频率为100 MHz时,该算法造成的延迟为15 ns,其实时性已接近于模拟控制器的效果。表2给出了二电平七段式SVPWM在不同平台、不同方法下的计算速度对比。
表2 计算速度对比
Table 2 Calculation speed comparison

算法计算时间平台本文算法1.5个时钟周期(15 ns@100 MHz)FPGA文献[11]算法8.83 μsDSP文献[12]算法30个时钟周期FPGA文献[13]算法1.38 μsFPGA
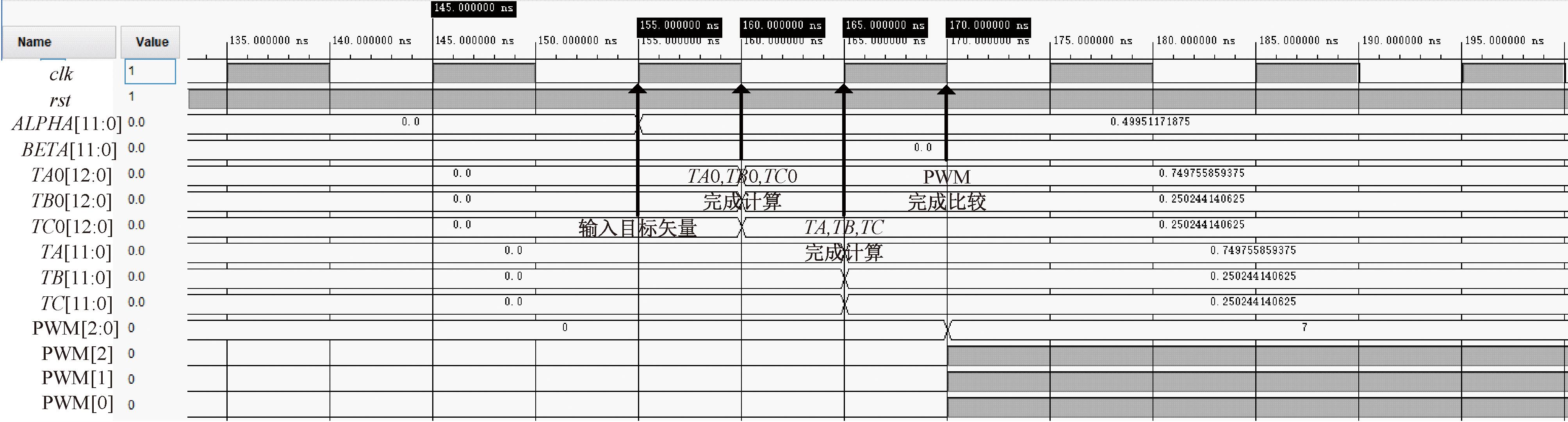
图14 评估计算速度的时序图
Figure 14 Key sequence diagram for evaluating computing speed
为了评估所述硬件架构的资源利用水平,将所述算法使用不同的EDA软件部署于不同FPGA平台之中,得到其资源使用情况如表3所示。其中ZYNQ为Xilinx公司的FPGA;CycloneIV为Inter公司的FPGA;GW1NR为高云半导体公司的FPGA。虽然不同型号的FPGA资源使用量略有不同,但是LUT资源使用量均保持在300个左右,节省了逻辑资源。
表3 资源使用情况
Table 3 Utilization of resources on the chip
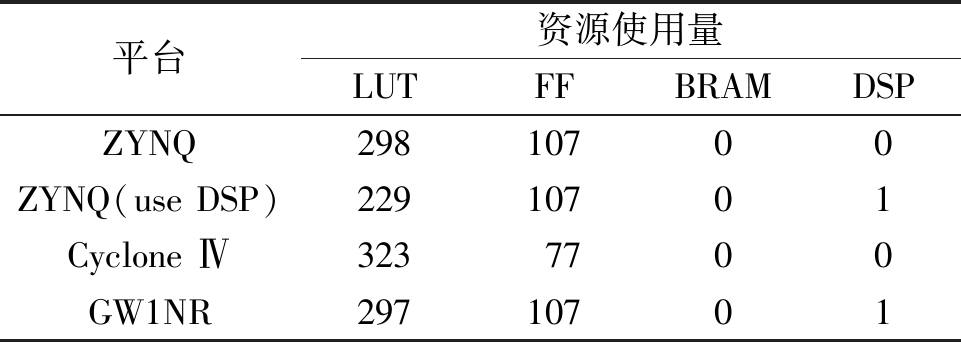
平台资源使用量LUTFFBRAMDSPZYNQ29810700ZYNQ(use DSP)22910701Cyclone Ⅳ3237700GW1NR29710701
3.2 实物验证
本文设计了两个实物验证方案,分别验证输出的端电压、线电流。三相逆变器采用ZYNQ系列的xc7z020为主控,母线电压为24 V,在主控芯片中应用本文的SVPWM模块和CORDIC模块,死区功能通过模拟方法实现。
实物验证方案一:验证SVPWM的端电压。为了能观测到与图12仿真相似的马鞍形信号,需要对输出的PWM进行合适的滤波,其具体参数如下:输入的参考电压Uref的模为0.5、转速为11.921 r/s、PWM频率为97.656 kHz、输出PWM的分辨率为9 bit。采用三相LC滤波,滤波电感L为5 mH、滤波电容为20 μF。输出效果如图15(a)所示(A相),可见经过LC滤波后,其实测波形与仿真波形较为一致。
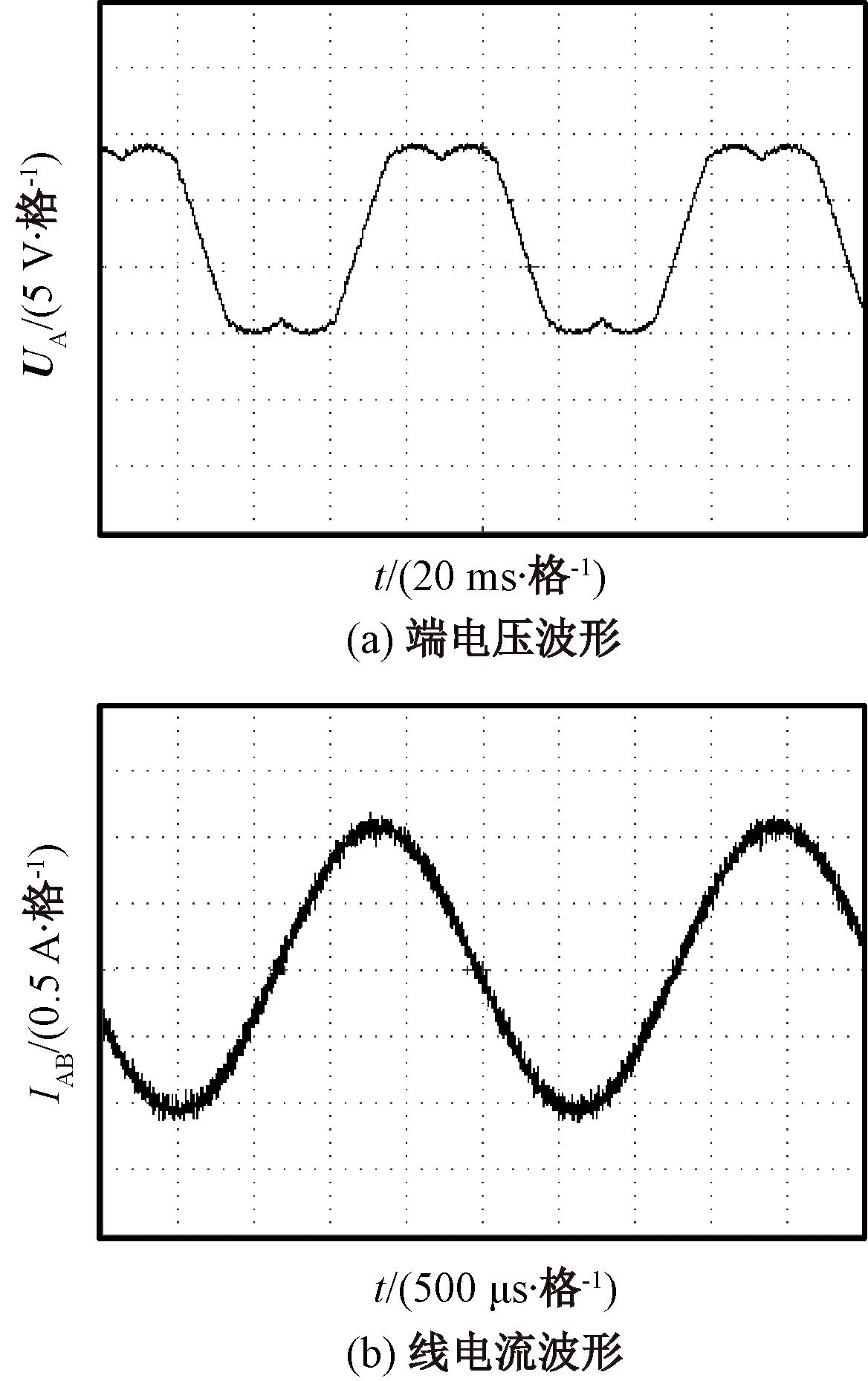
图15 端电压与线电流
Figure 15 Terminal voltage and line current
实物验证方案二:验证SVPWM的线电流。该验证方案期望获得一个较为标准的正弦电流信号波形,采集方案为“采样电阻+隔离运放”。具体参数如下:Uref的模为0.5,转速为381.470 r/s、PWM频率为48.828 kHz、输出PWM的分辨率为10 bit,采用三相LC滤波器,滤波电感L为44 mH,滤波电容为20 μF。将A相线与B相线接入10 Ω的阻性负载,观测其中电流,如图15(b)所示,可见本文的SVPWM算法较好的执行了输入指令。
4 结论
本文基于FPGA平台设计了一种SVPWM的硬件架构,该架构主要目的在于提高二电平七段式SVPWM的调制速度和输出质量,同时尽可能降低计算资源利用水平。
(1)利用了FPGA的并行能力,在100 MHz的主频下,能够在15 ns内完成SVPWM的调制,速度较快。这有利于降低系统的延时,提高实时性。
(2)当输入超过线性范围时,能够做到占空比钳位,提高了系统的安全性。
(3)实现了自然采样法,降低了输出PWM的误差,理论上可以提高输出PWM的质量。
(4)针对FPGA平台做出了特殊优化,使得资源使用量较少,整体上只用了1个乘法器,有利于在单个平台中实现更多的功能。
本文对以上功能进行了仿真与实物试验,试验结果表明该硬件结构是可行的。
[1] 高莹, 谢吉华, 陈浩. SVPWM的调制及谐波分析[J]. 微特电机, 2006, 34(7):10-12,25.
GAO Y, XIE J H, CHEN H. Modulation and harmonic analysis of SVPWM[J]. Small &Special Electrical Machines, 2006, 34(7):10-12,25.
[2] 曹原, 尉乔南. 静止同步补偿器新型双闭环控制策略研究[J]. 郑州大学学报(工学版), 2015, 36(4):19-23.
CAO Y, YU Q N. Research on a novel double closed loops control method of STATCOM[J]. Journal of Zhengzhou University (Engineering Science), 2015, 36(4):19-23.
[3] 白国长, 吴贺松, 郑鹏. 基于立方型转矩分配函数的SRM直接转矩控制[J]. 郑州大学学报(工学版), 2022, 43(1):48-54.
BAI G C, WU H S, ZHENG P. Direct torque control of switched reluctance motor based on cubic torque sharing function[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(1):48-54.
[4] 孙鹤旭, 荆锴, 董砚, 等. 基于120°坐标系的SVPWM算法研究[J]. 电工技术学报, 2016, 31(5): 52-59.
SUN H X, JING K, DONG Y, et al. Research of SVPWM algorithm based on 120° coordinates system[J]. Transactions of China Electrotechnical Society, 2016, 31(5): 52-59.
[5] 齐昕, 王冲, 周晓敏, 等. 一种低硬件资源消耗快速SVPWM算法[J]. 电机与控制学报, 2014, 18(4): 31-38.
QI X, WANG C, ZHOU X M, et al. Low hardware resource consumption fast SVPWM algorithm[J]. Electric Machines and Control, 2014, 18(4): 31-38.
[6] BENEDETTO L D, DONISI A, LICCIARDO G D, et al. Implementation of hardware architecture for SVPWM with arbitrary parameters[J]. IEEE Access, 2022, 10: 32381-32393.
[7] 陈增禄, 毛惠丰, 周炳根, 等. SPWM数字化自然采样法的理论及应用研究[J]. 中国电机工程学报, 2005, 25(1): 32-37.
CHEN Z L, MAO H F, ZHOU B G, et al. A study on theory and application of digital natural sampling based SPWM[J]. Proceedings of the CSEE, 2005, 25(1): 32-37.
[8] 刘健, 张号, 曾华, 等. 基于FPGA技术的三电平自然采样SPWM全数字化理论研究与实现[J]. 中国电机工程学报, 2017, 37(5): 1498-1506.
LIU J, ZHANG H, ZENG H, et al. Theoretical research and realization of three-level natural sampling SPWM full digitization based on FPGA technology[J]. Proceedings of the CSEE, 2017, 37(5): 1498-1506.
[9] HOLMES D G, MCGRATH B P. Opportunities for harmonic cancellation with carrier-based PWM for a two-level and multilevel cascaded inverters[J]. IEEE Transactions on Industry Applications, 2001, 37(2): 574-582.
[10] 蔡权利, 高博, 龚敏. 基于FPGA的CORDIC算法实现[J]. 电子器件, 2018, 41(5)1242-1246, 1256.
CAI Q L, GAO B, GONG M. Implementation of CORDIC algorithm based on FPGA[J]. Chinese Journal of Electron Devices, 2018, 41(5)1242-1246, 1256.
[11] 王光, 王旭东, 马骏杰, 等. 一种快速SVPWM算法及其过调制策略研究[J]. 电力系统保护与控制, 2019, 47(3): 136-145.
WANG G, WANG X D, MA J J, et al. A fast SVPWM algorithm and its overmodulation strategy[J]. Power System Protection and Control, 2019, 47(3): 136-145.
[12] 吴春, 陈子豪, 傅子俊. 永磁同步电机全速范围无位置传感器控制及FPGA实现[J]. 电机与控制学报, 2020, 24(7): 121-129.
WU C, CHEN Z H, FU Z J. Sensorless control of permanent magnet synchronous machines in full speed range and FPGA implementation[J]. Electric Machines and Control, 2020, 24(7): 121-129.
[13] 周京华, 王晨, 张新雷, 等. FPGA全数字电力电子变换控制器设计[J]. 电机与控制学报, 2021, 25(8): 99-112.
ZHOU J H, WANG C, ZHANG X L, et al. Design of FPGA full digital power electronic conversion controller[J]. Electric Machines and Control, 2021, 25(8): 99-112.