近年来,中国新能源发展迅速,风电、光伏装机规模均居世界首位[1]。但是,基于逆变器接口的新能源使得电力系统的电力电子化特性明显[2],随着新能源在局部电网中装机占比的提升,电力系统抗扰能力持续下降[3]。为此,国内外学者针对新能源并网逆变器提出了虚拟同步发电机(virtual synchronous generator,VSG)控制策略[4-5],通过在控制程序中引入转子运动方程和励磁系统模型,使并网逆变器可以自发地为系统提供必要的惯性和阻尼支撑,从而提升高比例新能源电力系统的抗扰能力和稳定水平[6]。
VSG的输出电压可以根据控制参数及所带负荷自行建立,能方便地实现从并网到离网的模式切换。而当VSG由离网向并网模式切换时,需要进行预同步控制以避免出现较大的电流冲击,甚至硬件设备损坏[7]。
与传统同步发电机相似,VSG的预同步过程也包括幅值同步、频率同步和相位同步3个环节。目前,现有文献多侧重相位预同步控制方法研究,如文献[7-9]通过计算VSG与电网电压的相位偏差并通过比例-积分(PI)反馈控制调节相位差至零;文献[10-11]通过构建虚拟电流或虚拟功率作为相位调节的反馈量;文献[12-13]将相位偏差表示为dq坐标系下并网开关两侧电压分量的差值,并将其反馈至输出频率以实现相位调节。在幅值及频率预同步控制方面,现有研究通常将VSG与电网电压的幅值及频率偏差经PI反馈后实现预同步控制[10],而较少关注幅值及频率同步方式对VSG并网后输出功率的影响。实际中,若VSG在并网前的输出功率与并网后稳态工作点对应的输出功率不一致,仅通过PI反馈消除幅值及频率偏差的预同步控制方式会导致VSG在预同步控制环节退出运行后出现输出功率跃变现象。王浩等[14]在VSG并网后切换为传统电流源控制并采用恒定的内环dq轴电流指令实现并网前后功率一致,但该方法改变了VSG的运行特性且在切换期间易出现电流冲击。施永等[15]通过构建能量管理系统对VSG并网后的输出功率进行调整,但受制于控制指令的响应延时无法完全消除并网时刻的功率跃变。此外,当VSG向小容量微电网并网时,由于微电网频率扰动及机械开关动作延时等原因,VSG在并网时刻较难与电网电压达到完全同步状态,因此仍可能出现一定的功率扰动。
针对以上问题,本文基于VSG的基本控制结构对其稳态输出特性进行了分析,提出了通过调整VSG的有功及无功输出参考值实现电压频率及幅值同步的控制方法,并使得VSG并网后稳态工作点对应的输出功率与并网前一致,避免了预同步控制环节退出运行后VSG的输出功率跃变。同时,针对非理想情况下VSG向微电网并网时出现的功率扰动,引入自适应惯性实现同步过程中功率振荡的抑制。基于MATLAB/Simulink构建了仿真分析模型,验证了所提方法的有效性。
1 VSG的基本控制原理
VSG的基本控制结构包括虚拟转速调节器(有功-频率控制环节)、虚拟励磁调节器(无功-电压控制环节)和同步发电机的电磁模型。为简化建模和参数计算过程,通常将复杂的同步发电机电磁模型简化,并在VSG控制结构中引入电压电流内环控制器以提升其动态响应性能[16]。
1.1 有功-频率控制环节
传统同步发电机可以通过释放或者吸收转子中的动能与电网进行能量交互。假设发电机转子的极对数为1,其转子运动方程可表示为
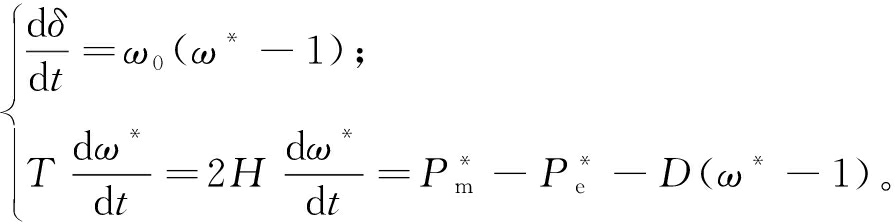
(1)
式中:δ和ω分别为同步发电机的功角和输出电压角频率;ω0为电网同步角频率;T为惯性时间常数;D为等效阻尼系数;Pm、Pe分别为输入的机械功率和输出的电磁功率;上标*表示标幺值。
图1为VSG的有功-频率控制框图,包含了式(1)所示的转子运动方程以模拟传统同步发电机的惯性和阻尼特性。机械功率Pm采用式(2)所示的下垂控制,用以实现功率调节和一次调频,其中K表示VSG的单位调节功率[17]。
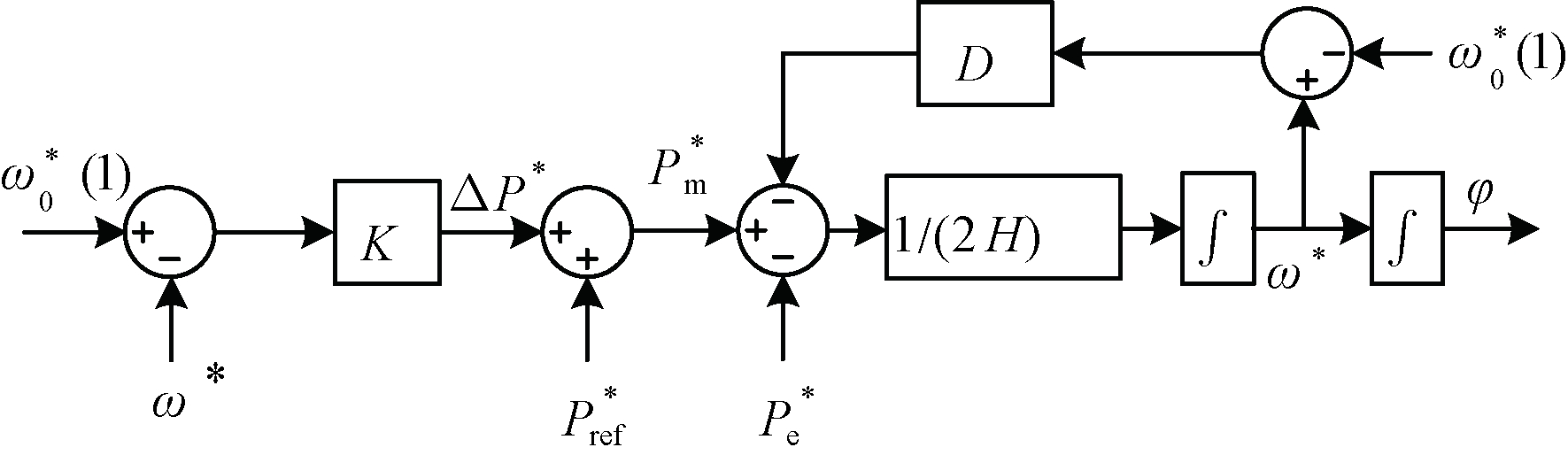
图1 VSG的有功-频率控制框图
Figure 1 Power and frequency regulation diagram
of the VSG
(2)
1.2 无功-电压控制环节
VSG的无功-电压控制环节主要用于模拟传统同步发电机的励磁调节特性[6],如图2所示。
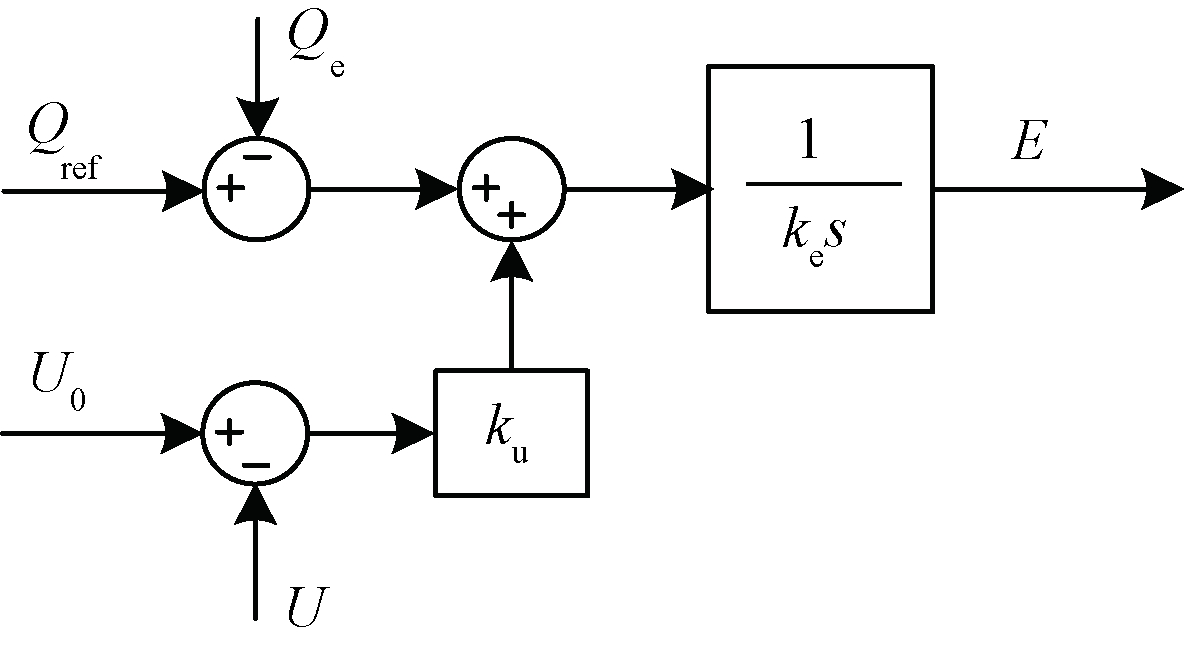
图2 VSG的无功-电压控制框图
Figure 2 Reactive power and voltage regulation
diagram of the VSG
图2中,U、U0分别为VSG输出电压的实际值和额定值;Qe、Qref分别为VSG输出的无功功率及其参考值;ku为无功-电压下垂系数,ke为调压系数;E为VSG的内电势幅值。
根据图2可得VSG的电压控制方程为
(3)
由VSG的内电势幅值E和相位φ可得VSG的三相内电势为
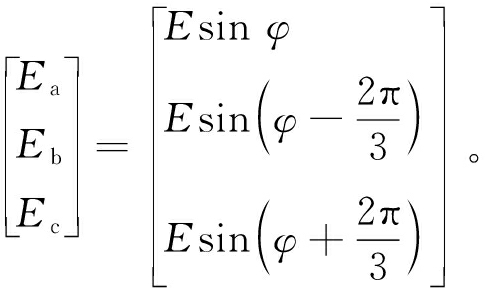
(4)
1.3 VSG的基本控制结构
根据VSG有功-频率控制环节及无功-电压控制环节的建模分析,可得VSG的基本控制结构如图3所示[17]。
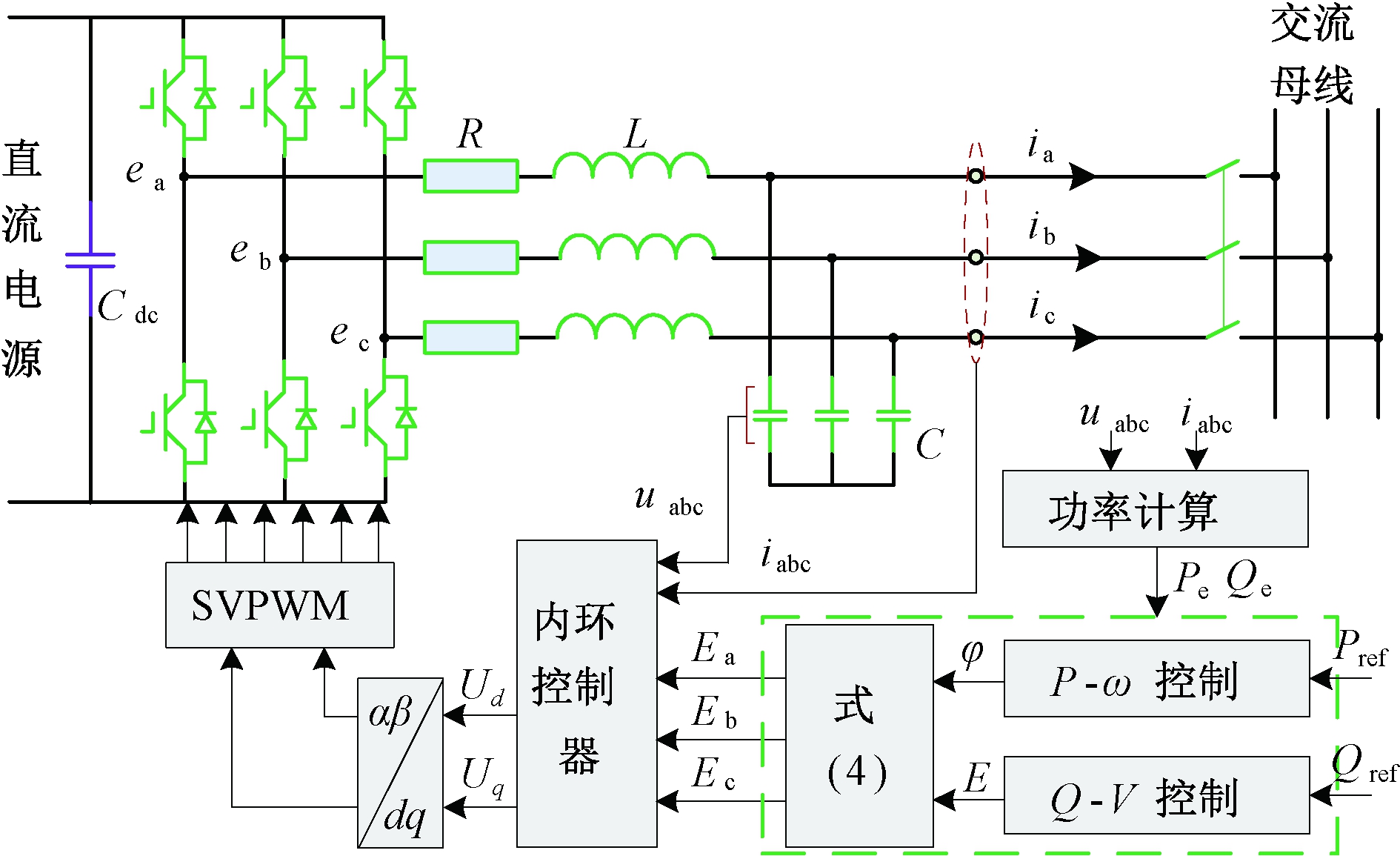
图3 VSG基本控制结构
Figure 3 Control structure of the VSG
图3中,Cdc为直流侧稳压电容;R、L分别为滤波电路的电阻和电感,C为滤波电容;uabc、iabc分别为VSG的输出电压和电流;Pe、Pref分别为VSG输出的有功功率及其参考值;Eabc、eabc分别为VSG的三相内电势及桥臂中点平均输出电压;Ud、Uq分别为内环控制器的d、q轴输出分量。
2 VSG的稳态功频输出特性
设系统稳态运行时频率变化为0,有dω/dt=0。将式(2)代入式(1)并化简,得到VSG的静态输出功率Pe与参考值Pref及频率偏差Δω的数值关系:
Pe=Pref-ω0(ω*-1)(K+D)=Pref-Δω(K+D)。
(5)
由式(5)可得VSG的静态功频特性曲线,如图4所示。图4中,ω0为VSG输出功率等于Pref时对应的额定频率,ωmax为VSG空载运行时对应的最大频率。
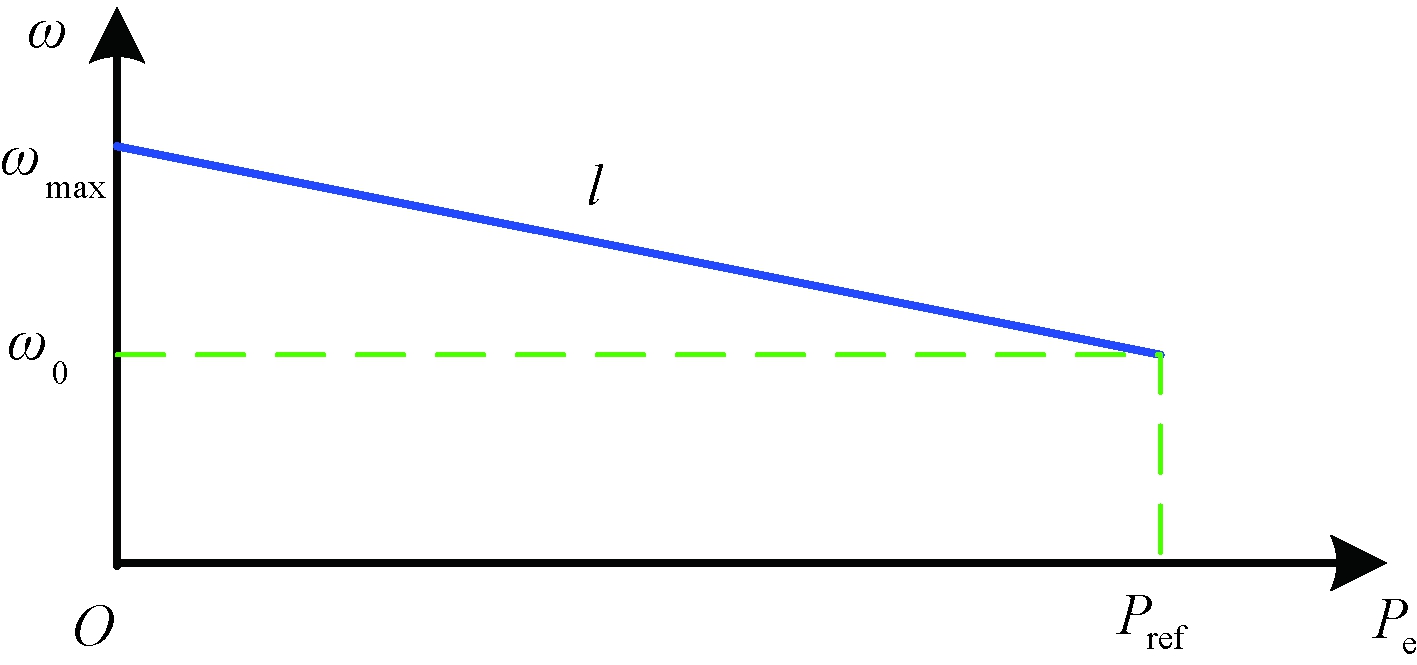
图4 VSG的静态功频特性曲线
Figure 4 Static power frequency characteristic
curve of the VSG
(6)
当VSG离网运行时,其输出功率Pe与本地负载PL相等,由式(5)可知,通过调整输出功率参考值Pref可以调节VSG离网运行时的频率偏差Δω,且只有Pref与本地负载功率PL相等时,频率偏差才为0。
当VSG并网运行时,其输出电压被电网电压钳位,若电网频率为额定值,VSG输出电压的频率偏差Δω也将为0,由式(5)可知,VSG并网时的稳态输出功率Pe将等于参考值Pref。因此,Pref决定了VSG并网后稳态工作点对应的输出功率,通过调整Pref可以对VSG并网后的输出功率Pe进行调节。
综上,在VSG由离网向并网模式切换的预同步过程中,可以根据离网运行时本地负载功率PL对VSG的输出参考值Pref进行调整,使VSG的输出频率与电网频率同步,并使得VSG并网后稳态工作点对应的输出功率与并网前一致,避免VSG并网后的有功输出跃变。
同理,在VSG预同步过程中可以根据本地无功负载功率QL调整其无功输出参考值Qref,使VSG输出电压的幅值与电网电压同步。为简化分析,本文仅基于有功负载开展讨论。
3 VSG的预同步控制方法
3.1 基于功率匹配的预同步控制步骤
根据VSG的静态功频输出特性,本文提出一种考虑VSG并网后稳态工作点的预同步控制方法,如图5所示,具体步骤如下。
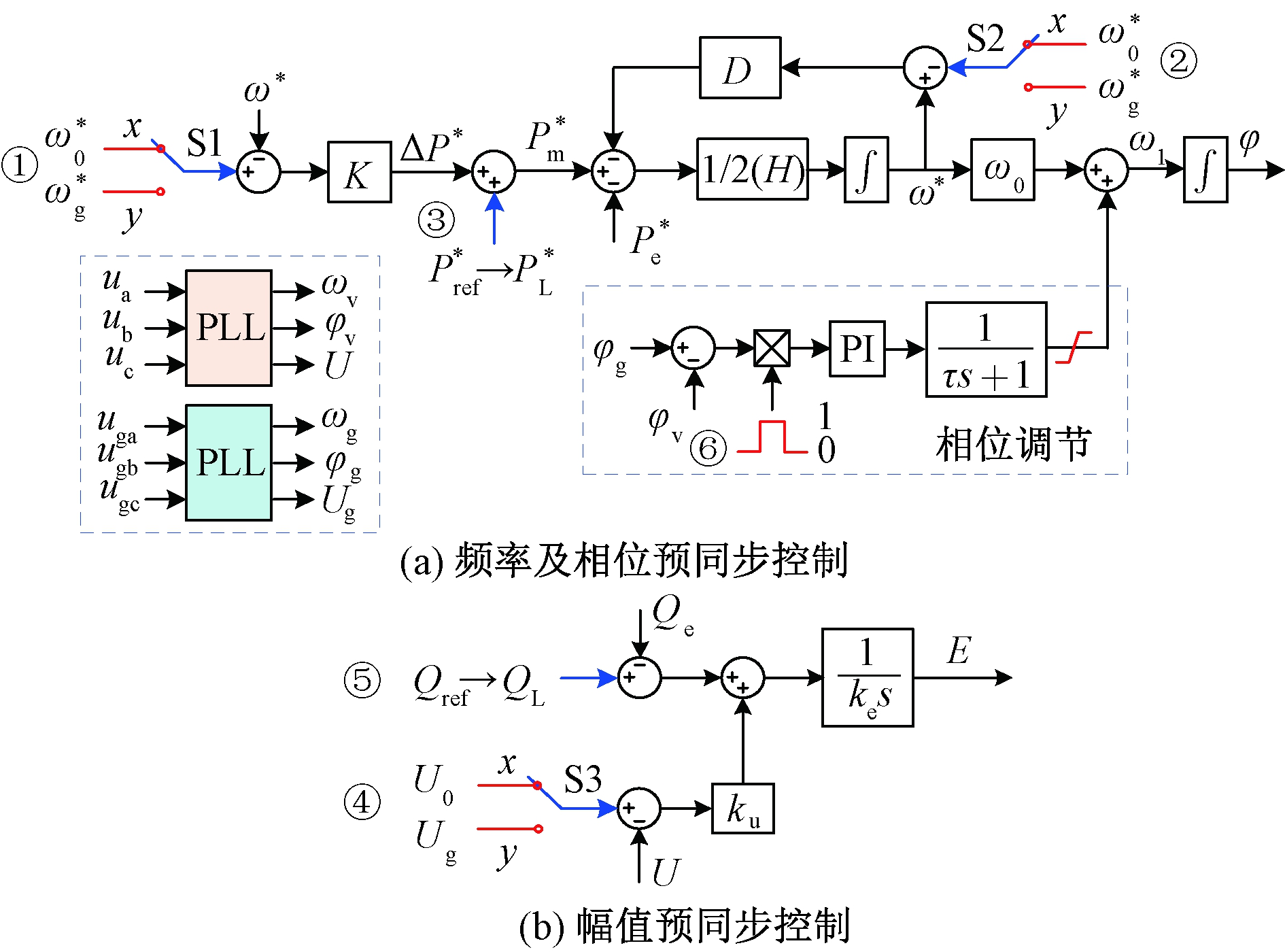
图5 VSG预同步控制方法
Figure 5 Pre-synchronization control method of the VSG
步骤1 通过锁相环获取电网电压的频率、幅值和相位信息。
步骤2 将有功控制环中的频率参考值由额定频率ω0切换为电网频率ωg(即开关S1、S2由位置x切换为位置y),根据本地有功负载功率PL调整有功输出参考值Pref,即设定Pref=PL,使VSG的输出频率与电网频率一致。
步骤3 将无功控制环中的电压参考值由额定值U0切换为电网电压Ug(即开关S3由位置x切换为位置y),根据本地无功负载功率QL调整无功输出参考值Qref,即设定Qref=QL,使VSG输出的电压幅值与电网电压一致。
步骤4 将VSG输出电压与电网电压的相位差经PI控制器后叠加到有功环节的输出频率ω上以实现相位同步。考虑到初始相位差的反馈量可能为[0,2π]的任意值,为避免VSG输出电压畸变,本文在PI控制器后增加了一个惯性环节[10],以平滑相位差反馈量的作用效果。待相位差满足并网标准后,闭合VSG的并网开关。
步骤5 VSG并网后,将其输出电压的频率及幅值参考值重新切换为额定值并退出相位预同步环节,使VSG恢复主动参与系统功率调节的能力。
3.2 自适应惯性的选取方法
当VSG向小容量微电网并网时,由于微电网频率扰动及并网开关等环节的时间延迟,VSG经预同步控制并网时难以与电网电压完全同步,在并网后仍可能出现功率振荡现象。因此,本文将自适应惯性引入VSG并网后的同步过程,以抑制VSG在非理想情况下并网后的功率振荡[18-19]。
VSG并网运行时受小扰动偏离稳态工作点后,其功角及频率将出现一个阻尼振荡过程,如图6所示。为便于分析,将一个震荡周期划分为图6所示的4个区间[19]。当VSG偏离稳态运行点时(区间①和区间③),采用较大的惯性时间常数可减小VSG的频率变化率和频率偏差;而当VSG向稳态工作点运行时(区间②和区间④),采用较小的惯性时间常数可加速VSG回归稳态工作点。结合不同区间的频率偏差及频率变化率的正负号,可得表1所示的VSG自适应惯性选取规则。
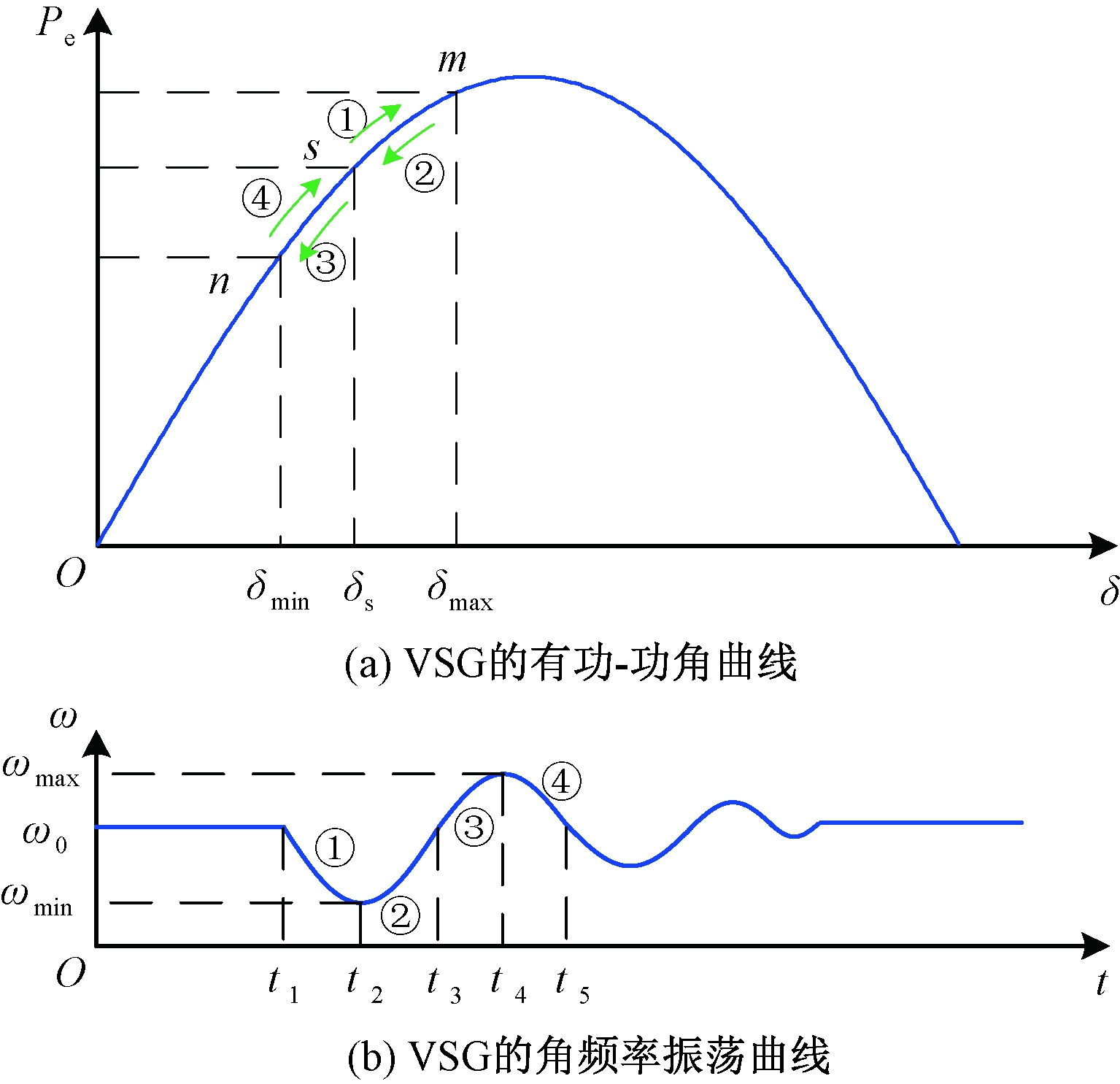
图6 VSG的有功-功角曲线及频率振荡曲线
Figure 6 Power-angle curve and angular frequency
oscillation curve of the VSG
表1 VSG自适应惯性选取规则
Table 1 Selection method of self-adaptive inertia
for the VSG
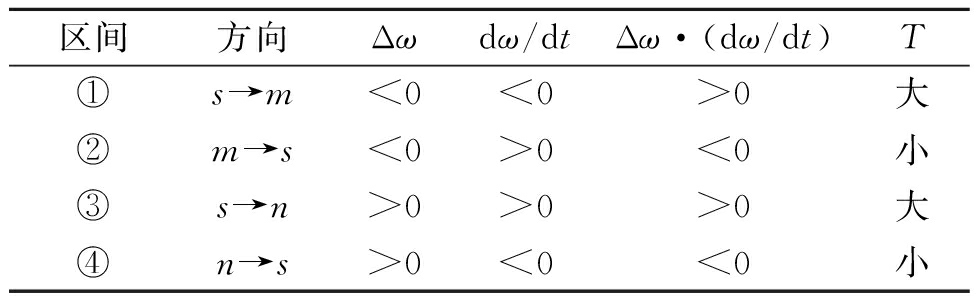
区间方向Δωdω/dtΔω·(dω/dt)T①s→m<0<0>0大②m→s<0>0<0小③s→n>0>0>0大④n→s>0<0<0小
惯性时间常数直接影响VSG的动态响应特性和运行稳定性,其选取方法可参考文献[20]。为简化控制,本文将VSG的惯性时间常数设置为一个较大值Tmax和一个较小值Tmin,并分别设置频率偏差和频率变化率的判断阈值,以避免2个参数在零值附近引起误判。这样,VSG的自适应惯性可表示为
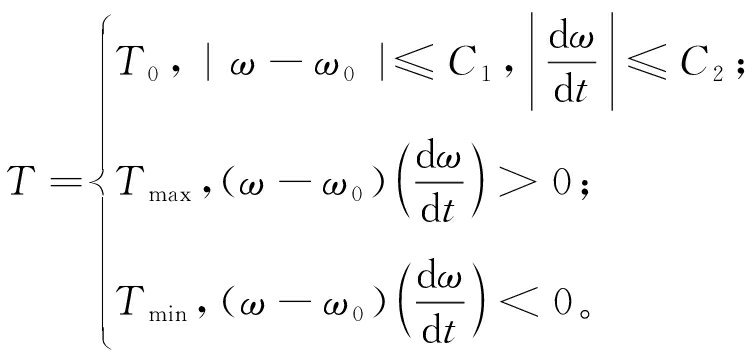
(7)
4 仿真验证
为验证所提控制方法的有效性,基于MATLAB/Simulink构建了图7所示的VSG预同步并网仿真模型。其中,柴油发电机组(diesel generator,DG)额定功率为100 kW,是微电网中的主导电源,负责完成系统的二次调频;负载PL1=60 kW、PL2=40 kW;VSG额定功率为100 kW,初始输出功率参考值为1,惯性时间常数T0=6 s,其他主要参数如表2所示。
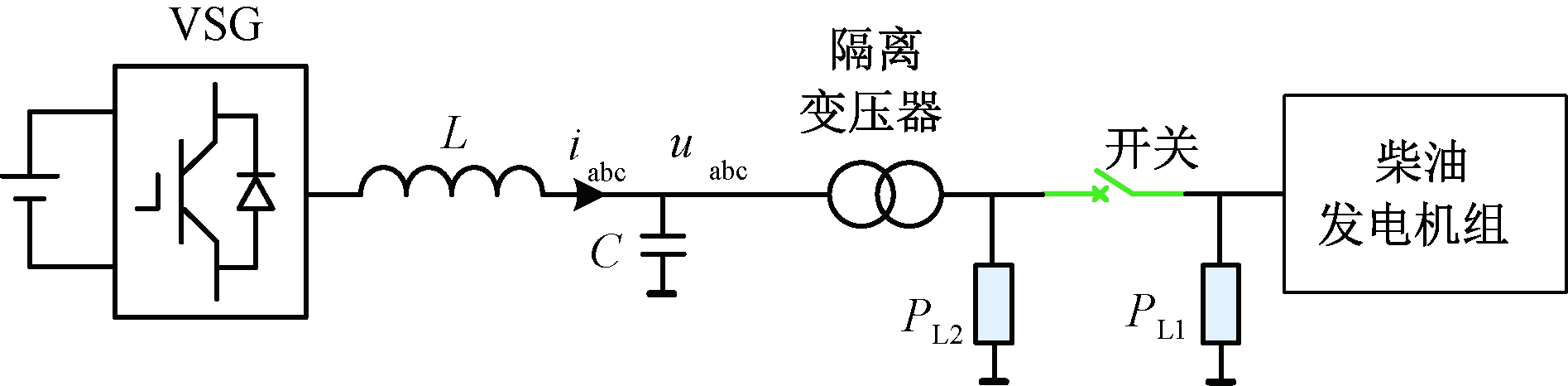
图7 VSG预同步并网仿真模型
Figure 7 Simulation model of pre-synchronization
control for the VSG
表2 仿真模型主要参数
Table 2 Parameters of the simulation model
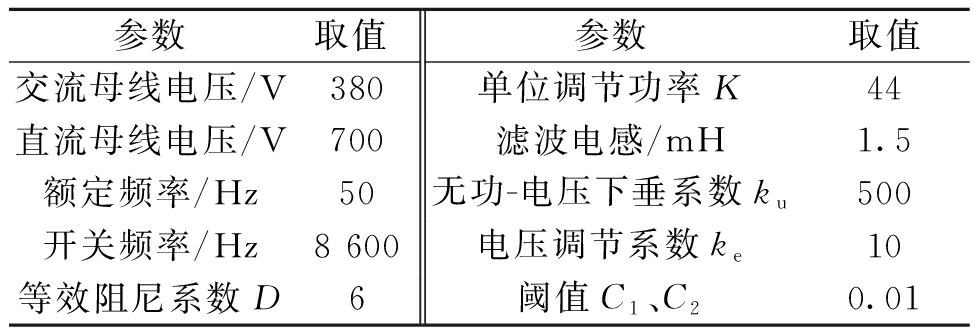
参数取值参数取值交流母线电压/V380单位调节功率K44直流母线电压/V700滤波电感/mH1.5额定频率/Hz50无功-电压下垂系数ku500开关频率/Hz8 600电压调节系数ke10等效阻尼系数D6阈值C1、C20.01
4.1 预同步控制方法的有效性验证
初始状态下,VSG带负载PL2独立运行。按照本文提出的预同步控制方法对VSG输出电压的频率、幅值和相位进行预同步控制,当相位偏差小于1×10-3 rad时并网,仿真得到VSG与柴油发电机组的输出电压波形如图8所示、输出功率及频率波形如图9所示。同时,设置对照组仿真结果如图10所示,对照组采用常规PI闭环反馈实现VSG输出电压与电网电压的频率和幅值同步,即分别将频率偏差和幅值偏差经PI控制器后反馈至VSG的频率和电压控制环节,对照组相位同步方法与本文所提方法一致。
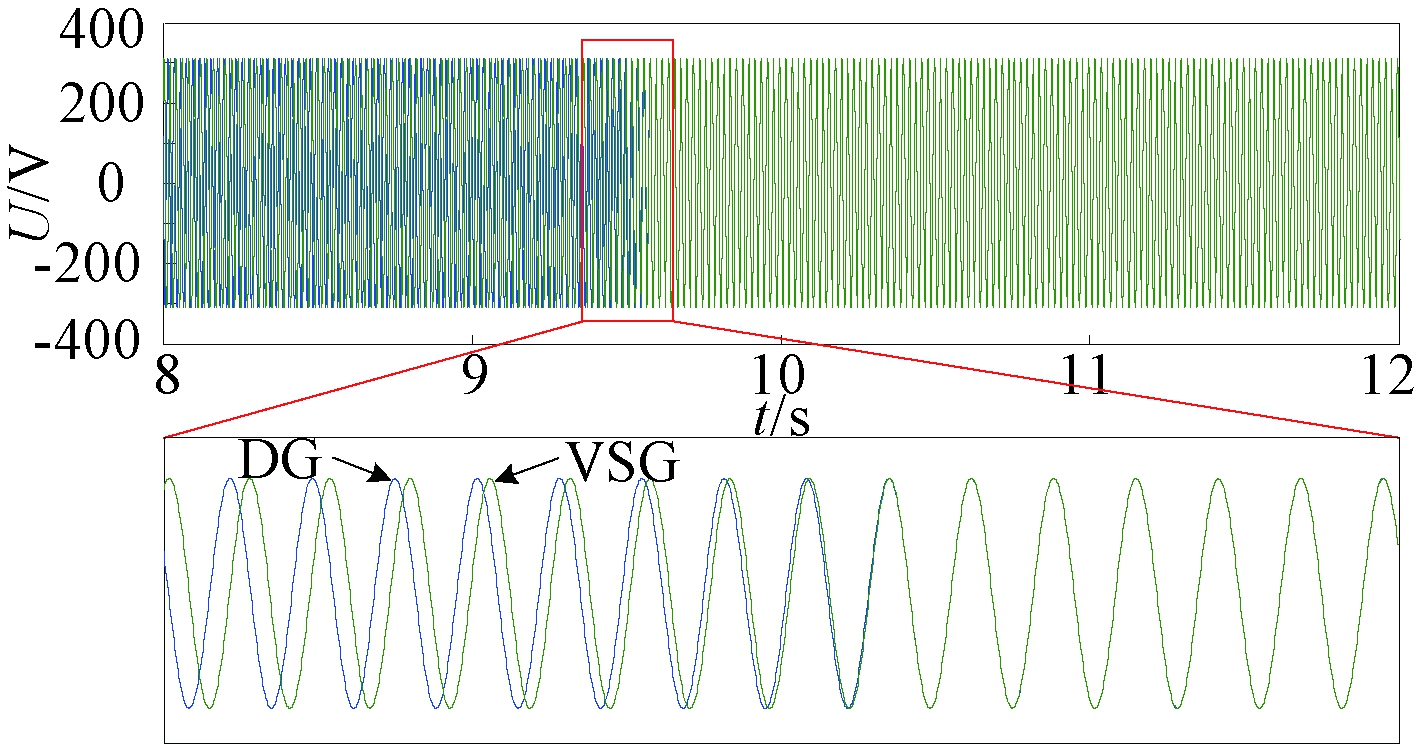
图8 VSG与柴油发电机组输出电压波形
Figure 8 Voltage waveform of the VSG and the diesel
generator
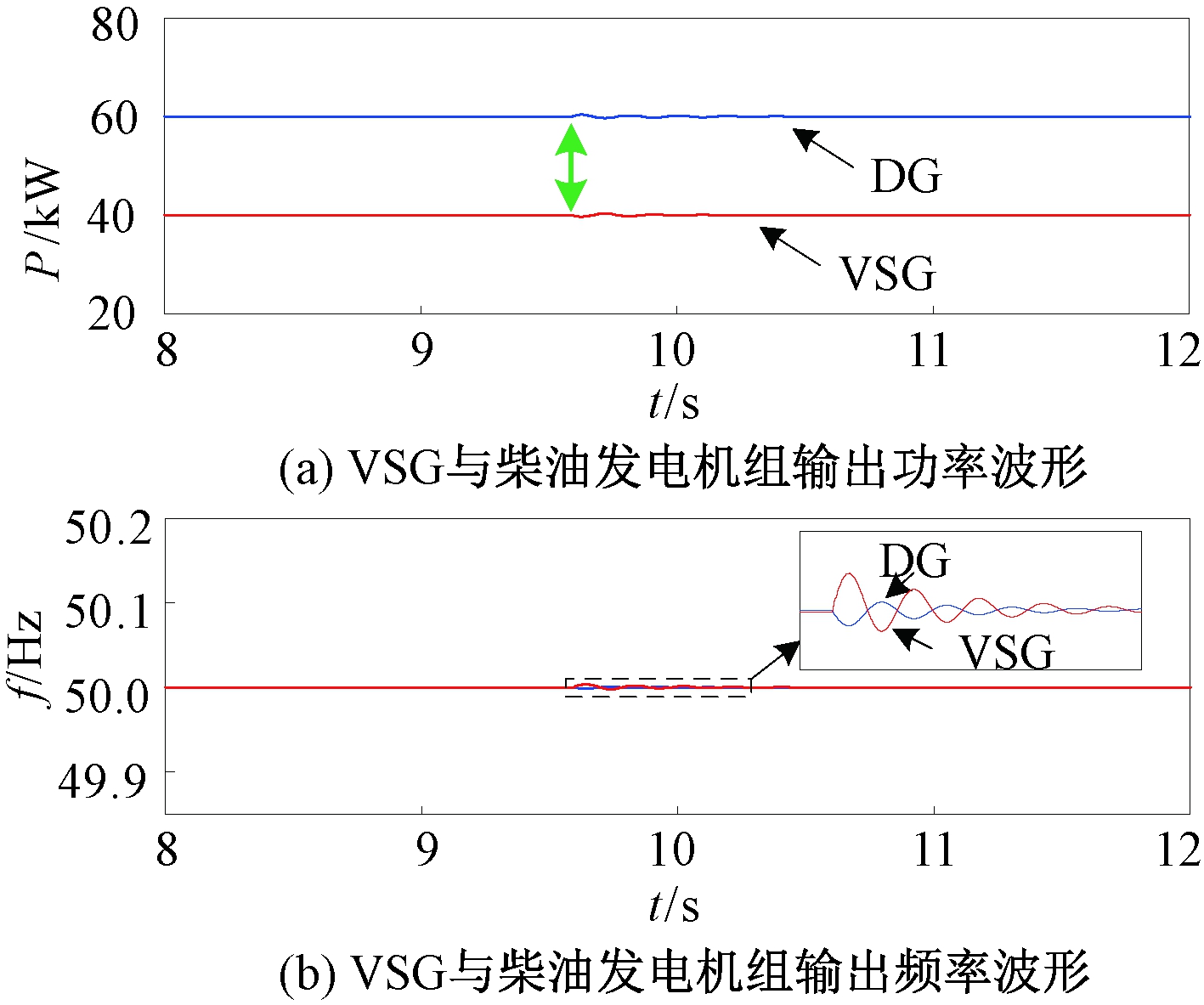
图9 本文预同步控制方法仿真结果
Figure 9 Simulation results with the proposed method
in this paper
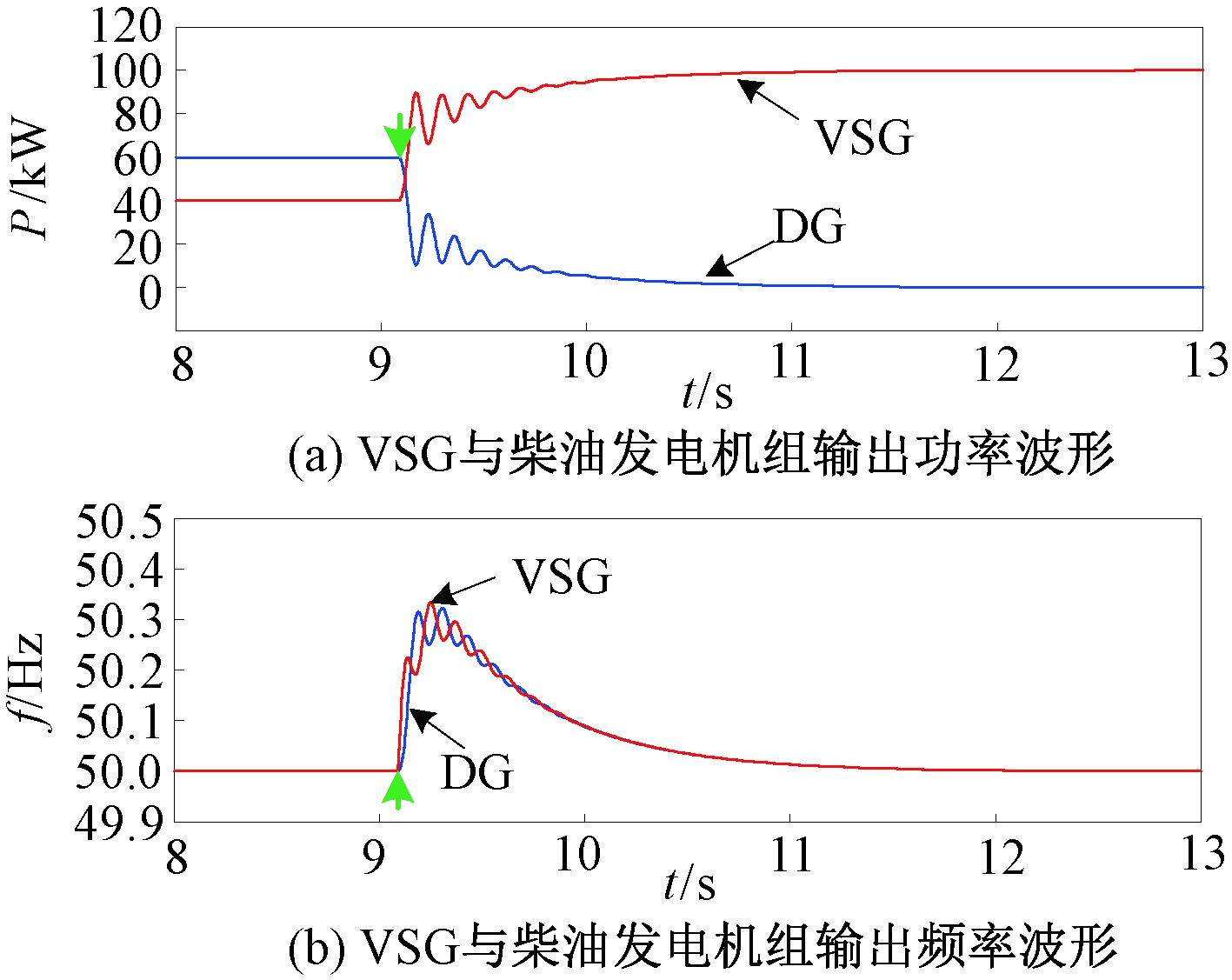
图10 对照组仿真结果
Figure 10 Simulation results of the control group
对比图9和图10可以看出:①对照组采用PI反馈控制虽然使VSG输出电压的幅值和频率与电网电压同步,但由于VSG在并网前的输出功率(40 kW)与并网后稳态工作点对应的输出功率(100 kW)不一致,导致VSG在并网后出现输出功率跃升现象,柴油发电机组输出功率下降、系统频率升高。当柴油发电机组完成二次调频后,系统频率恢复至50 Hz,VSG的输出功率由40 kW稳定至100 kW。②VSG采用本文控制方法并网时,根据本地负载功率调整其输出功率参考值,一方面使得VSG输出电压的幅值和频率与电网电压同步,另一方面也将VSG并网后稳态工作点对应的输出功率由100 kW调节为40 kW,使之与VSG并网前的输出功率一致,避免了VSG在并网后的输出功率跃变,同步过程中仅出现微小的功率和频率振荡。
4.2 自适应惯性控制方法的有效性验证
由于微电网频率波动及开关延时等原因,VSG在并网时刻较难与电网电压保持完全同步。本部分仿真模型中,将各种非理想因素归一化为并网时刻的相位偏差。初始状态下,VSG仍带负载PL2独立运行。按照本文提出的预同步控制方法对VSG输出电压的频率、幅值和相位进行预同步控制,当相位偏差小于0.05 rad时并网。VSG采用恒定惯性(T0=6 s)时的仿真结果如图11所示,引入式(7)所示自适应惯性(Tmax=10 s,T0=6 s,Tmin=2 s)后的仿真结果如图12所示。
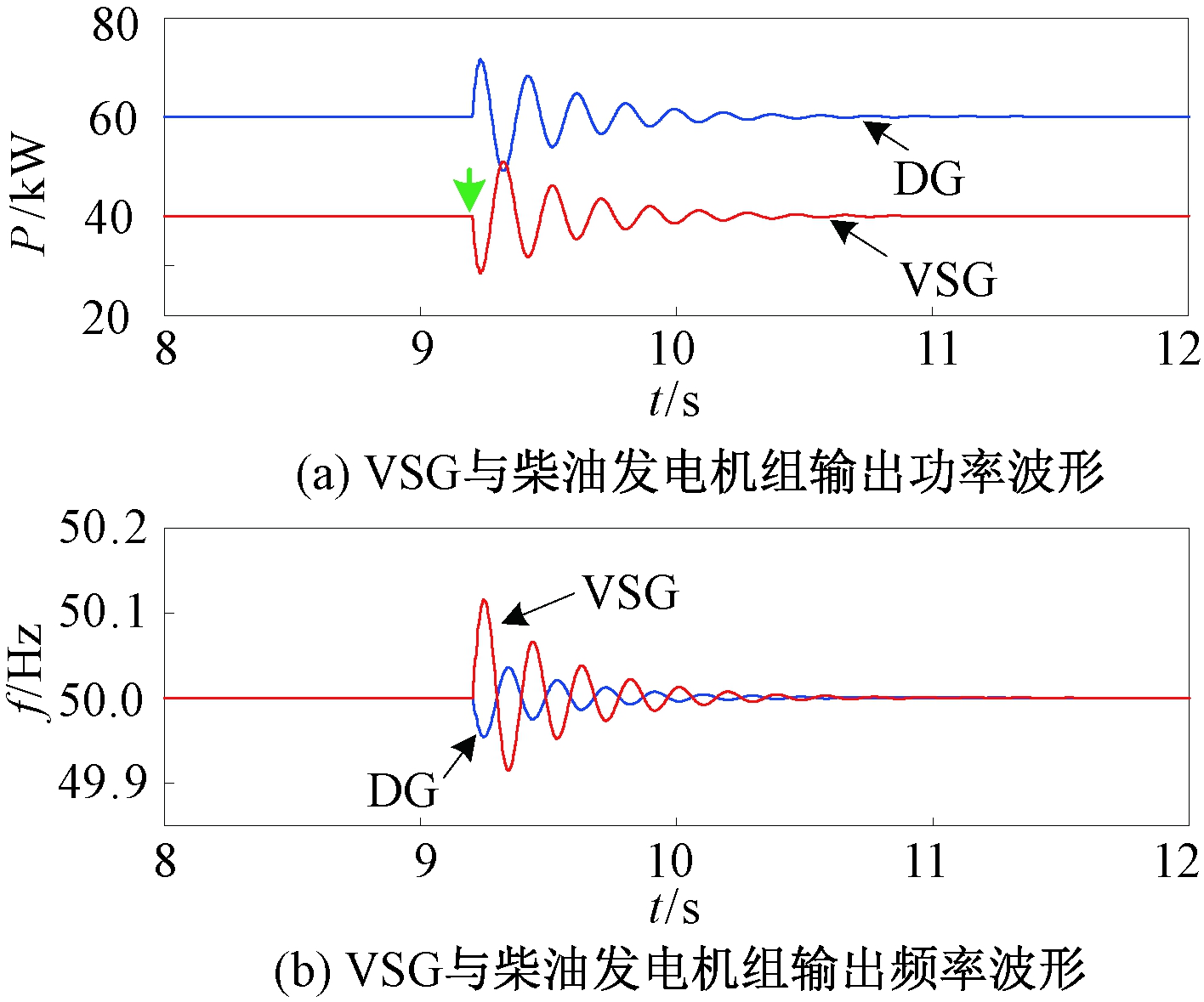
图11 VSG采用恒定惯性时仿真结果
Figure 11 Simulation results when the VSG with
constant inertia
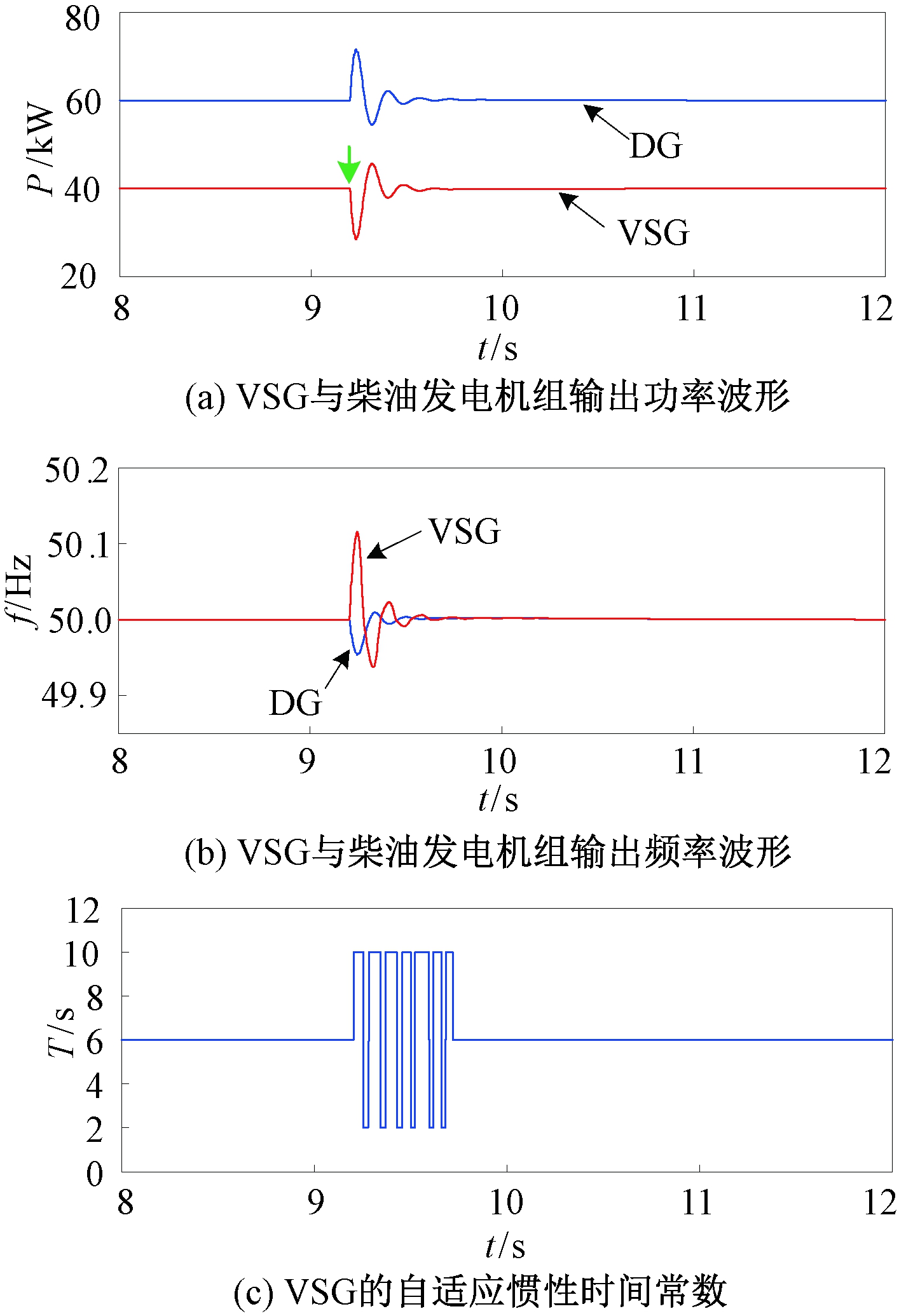
图12 VSG采用自适应惯性时仿真结果
Figure 12 Simulation results when the
VSG with self-adaptive inertia
对比图11和图12可以看出:①VSG在非完全同步情况下并网后,并网时刻出现功率冲击并在同步过程中出现较为严重的功率和频率振荡,约1.5 s后达到稳态;②引入本文提出的自适应惯性后,VSG的惯性时间常数根据频率偏差及频率变化率的正负自适应调整,使得VSG在相同条件下并网后的功率和频率振荡次数减少,同步过程缩短至0.6 s左右。因此,本文提出的自适应惯性有助于提升VSG在非理想情况下并网后的稳定能力。
5 结论
(1)VSG可以自行建立输出电压,因此由离网向并网模式切换时需要进行预同步控制,以避免VSG输出电压与电网电压偏差造成的电流冲击。
(2)将电网电压的频率和幅值设定为VSG的输出电压参考值,通过调整VSG的输出功率参考值与本地负载功率一致,可使VSG输出电压的幅值和频率与电网电压同步,并使得VSG并网后稳态工作点对应的输出功率与并网前一致,避免并网后的功率跃变。
(3)根据VSG的频率偏差及频率变化率引入自适应的惯性时间常数,可抑制VSG在非理想情况下并网后的振荡过程,提升VSG并网运行时的稳定能力。
(4)VSG作为可再生能源的并网接口,其输出功率与风电、光伏等可再生能源实际出力的协同控制以及直流侧储能单元的配置方案将是后续的研究重点。
[1] 韩冬, 解红叶. 水电水利规划设计总院发布《中国可再生能源发展报告2018》[J]. 水力发电, 2019(8): 46.
HAN D, XIE H Y. Hydropower planning and design institute released “China renewable energy development report 2018”[J]. Water Power, 2019(8): 46.
[2] 王金凤, 张惠惠, 祝方圆. 基于典型场景集的高比例风电系统运行灵活性评估[J]. 郑州大学学报(工学版), 2021, 42(6): 93-98.
WANG J F, ZHANG H H, ZHU F Y. Evaluation of system operational flexibility of high proportion wind power system based on the typical scene set[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(6): 93-98.
[3] 章健, 张玉晓, 熊壮壮, 等. 计及DR的新能源配电网电压无功协调优化[J]. 郑州大学学报(工学版), 2020, 41(2): 61-66.
ZHANG J, ZHANG Y X, XIONG Z Z, et al. Voltage reactive power coordination optimization of distributed new energy network considering DR[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(2): 61-66.
[4] ZHONG Q C, WEISS G. Synchronverters: inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.
[5] XIONG L S, ZHUO F, WANG F, et al. Static synchronous generator model: a new perspective to investigate dynamic characteristics and stability issues of grid-tied PWM inverter[J]. IEEE Transactions on Power Electro-nics, 2016, 31(9): 6264-6280.
[6] 邢鹏翔, 付立军, 王刚, 等. 改善微电网频率动态响应的虚拟同步发电机强化惯量控制方法[J]. 高电压技术, 2018, 44(7): 2346-2353.
XING P X, FU L J, WANG G, et al. Control strategy of virtual synchronous generator with enhanced inertia for improving dynamic frequency response of microgrid[J]. High Voltage Engineering, 2018, 44(7): 2346-2353.
[7] 柴伦, 李岚, 李冰, 等. 基于改进虚拟同步发电机的预同步并网策略[J]. 可再生能源, 2019, 37(7): 1015-1020.
CHAI L, LI L, LI B, et al. Strategy of pre-synchronized grid-connection based on improving virtual synchronous generator[J]. Renewable Energy Resources, 2019, 37(7): 1015-1020.
[8] 徐晓宁, 周雪松. 微网脱/并网运行模式平滑切换控制策略[J]. 高电压技术, 2018, 44(8): 2754-2760.
XU X N, ZHOU X S. Control strategy for smooth transfer between grid-connected and island operation for micro grid[J]. High Voltage Engineering, 2018, 44(8): 2754-2760.
[9] 柴秀慧, 张纯江, 赵晓君, 等. 基于自恢复下垂的分布式电源主动同步控制及参数优化[J]. 电力系统自动化, 2020, 44(19): 128-133.
CHAI X H, ZHANG C J, ZHAO X J, et al. Self-recovery droop based active synchronization control and parameter optimization of distributed generator[J]. Automation of Electric Power Systems, 2020, 44(19): 128-133.
[10] 魏亚龙, 张辉, 孙凯, 等. 基于虚拟功率的虚拟同步发电机预同步方法[J]. 电力系统自动化, 2016, 40(12): 124-129, 178.
WEI Y L, ZHANG H, SUN K, et al. Pre-synchronization method of virtual synchronous generator using virtual power[J]. Automation of Electric Power Systems, 2016, 40(12): 124-129, 178.
[11] 颜湘武, 王德胜, 贾焦心. 基于分散式微电网的虚拟同步发电机无通信预同步并网方案[J]. 电工技术学报, 2019, 34(19): 4143-4153.
YAN X W, WANG D S, JIA J X. Non-communication pre-synchronization scheme of VSGs based on decentra-lized microgrids[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4143-4153.
[12] 聂志强, 梁晖, 罗浩, 等. 基于非线性下垂控制的单模式微网并/离网无缝切换技术[J]. 电网技术, 2016, 40(5): 1371-1378.
NIE Z Q, LIANG H, LUO H, et al. Single mode grid-connected/islanded microgrid seamless transition based on nonlinear droop control technology[J]. Power System Technology, 2016, 40(5): 1371-1378.
[13] 耿昊翔, 王维俊, 唐帅, 等. 基于无锁相环的虚拟同步发电机离并网切换控制策略研究[J]. 电机与控制应用, 2021, 48(9): 90-95.
GENG H X, WANG W J, TANG S, et al. Research on off-grid/on-grid switching control strategy of virtual synchronous generator without PLL[J]. Electric Machines &Control Application, 2021, 48(9): 90-95.
[14] 王浩, 郝正航, 陈卓, 等. 基于虚拟同步发电机的储能逆变器控制策略及无缝切换技术[J]. 科学技术与工程, 2022, 22(9): 3594-3600.
WANG H, HAO Z H, CHEN Z, et al. Control strategy and seamless switching technology of energy storage inver-ter based on virtual synchronous generator[J]. Science Technology and Engineering, 2022, 22(9): 3594-3600.
[15] 施永, 赖纪东, 苏建徽, 等. 微网系统运行模式平滑切换控制策略[J]. 电力系统自动化, 2016, 40(8): 85-91.
SHI Y, LAI J D, SU J H, et al. Control strategy of seamless transfer for microgrid operation mode[J]. Automation of Electric Power Systems, 2016, 40(8): 85-91.
[16] 宋琼, 张辉, 孙凯, 等. 多微源独立微网中虚拟同步发电机的改进型转动惯量自适应控制[J]. 中国电机工程学报, 2017, 37(2): 412-424.
SONG Q, ZHANG H, SUN K, et al. Improved adaptive control of inertia for virtual synchronous generators in islanding micro-grid with multiple distributed generation units[J]. Proceedings of the CSEE, 2017, 37(2): 412-424.
[17] 邢鹏翔, 贾璇悦, 许长清, 等. VSG低电压穿越的特性分析及控制方法研究[J]. 电网与清洁能源, 2022, 38(8): 130-137, 143.
XING P X, JIA X Y, XU C Q, et al. A study on characteristic analysis and control methods of low voltage ride through for the VSG[J]. Power System and Clean Energy, 2022, 38(8): 130-137, 143.
[18] LI D D, ZHU Q W, LIN S F, et al. A self-adaptive inertia and damping combination control of VSG to support frequency stability[J]. IEEE Transactions on Energy Conversion, 2017, 32(1): 397-398.
[19] 于晶荣, 孙文, 于佳琪, 等. 基于惯性自适应的并网逆变器虚拟同步发电机控制[J]. 电力系统保护与控制, 2022, 50(4): 137-144.
YU J R, SUN W, YU J Q, et al. Virtual synchronous generator control of a grid-connected inverter based on adaptive inertia[J]. Power System Protection and Control, 2022, 50(4): 137-144.
[20] WU H, RUAN X B, YANG D S, et al. Small-signal modeling and parameters design for virtual synchronous generators[J]. IEEE Transactions on Industrial Electro-nics, 2016, 63(7): 4292-4303.