面板对堤坝发挥着防渗和防冲刷的重要作用,由于荷载变化会引起堤坝体不均匀沉降,导致面板与垫层变形不协调,从而出现堤坝面板脱空[1]。面板脱空轻则会引起面板开裂,严重时将会产生渗漏通道,影响堤坝的安全性能[2-3]。因此,需要及时对堤坝面板脱空进行检测和修复。高聚物注浆技术具有对堤坝扰动小、施工便捷、抗震抗裂、与土体协调变形能力强、无污染等优点,已被应用于堤坝渗漏病害修复工程[4]。目前,高聚物注浆技术的研究主要集中于高聚物材料特性[5]及高聚物防渗墙力学特性[6],在高聚物注浆修复效果评价方面研究较少。郭成超等[7]采用高密度电法对高聚物防渗墙的完整性进行了无损检测,对检测出的缺陷断面进行了现场开挖验证。但是,高聚物注浆修复堤坝面板脱空病害的效果评判仍缺乏深入研究。
探地雷达作为一种检测和识别地下目标的有效手段,与其他常规的地下探测方法相比,具有费用低、速度快、过程连续、范围广、分辨率高、操作方便灵活、无须开挖等优点,探测结果能够实时反映目标物内部结构分布。Liu等[8]采用三维探地雷达对道路空洞进行了检测,结果表明,根据三维探地雷达数据集可以估计空洞深度、水平尺寸和高度;Feng等[9]采用有限元时域和有限差分时域的混合算法,对隧道衬砌多缺陷模型进行了探地雷达正演模拟,为实际工程中探地雷达图像解释提供了理论指导;徐浩等[10]采用探地雷达对不同钢筋层数面板下的脱空病害进行探测,得到了不同钢筋层数面板下脱空病害的典型图谱和瞬时相位图;张杨等[11]采用GPRMAX对不同堤坝隐患进行探地雷达正演模拟,得出了不同形态、构造位置和电性参数的隐患的探地雷达剖面图。但是,探地雷达电磁波在高聚物注浆修复面板脱空堤坝中的波场特征尚未揭示。
因此,针对高聚物修复堤坝面板脱空病害效果缺乏有效评价方法的问题,基于时域有限差分法(finite-difference time-domain,FDTD)和完全匹配层(perfectly matched layers,PML)边界条件[12],建立不同修复程度下高聚物注浆修复的探地雷达电磁波计算模型,分析雷达中心频率面板脱空修复程度及脱空区域大小、面板厚度及配筋等因素对高聚物注浆修复面板脱空的探地雷达波场特征的影响,从而为评判堤坝面板脱空病害高聚物注浆修复效果提供依据。
1 基本原理
1.1 探地雷达原理
在工程探测中,探地雷达电磁波在传播过程中遇到不同介电特性的介质(如空洞、裂缝、材料分界面等)时,其传播路线、反射波形及幅值会发生改变,根据接收到的反射回波信号的波形、双程走时及幅值,从而对堤坝体的内部构造进行识别,达到探测坝体病害的目的[11]。
根据电磁波理论,高频电磁波在均匀、各向同性介质中的传播规律服从Maxwell方程组,在国际单位制下Maxwell方程组[13]可写为
(1)
(2)
▽·D=ρ;
(3)
▽×B=0。
(4)
式中:E为电场强度矢量,V/m;H为磁场强度矢量,A/m;B为磁感性强度矢量,T;D为电位移矢量,C/m2;J为电密度矢量,A/m2;ρ为电荷密度,C/m3。
1.2 正演方法
基于Yee氏网格[14]模型,采用FDTD对TM模式下的电磁波进行离散[15],可得
(5)
(6)
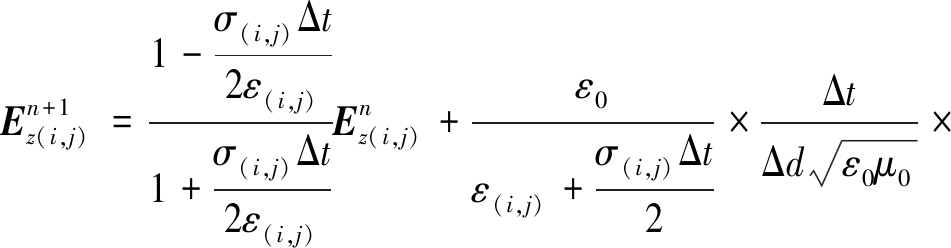
(7)
式中:ε0为初始介电常数;μ0为初始磁导率;σ为电导率;Δt为时间;Δd为空间步长;i、j分别为x、y方向的网格步数;σ(i,j)、ε(i,j)分别为Yee氏元胞中(i,j)处的电导率和介电常数;![]() 为nΔt时刻在Yee氏元胞中(i,j)处的z方向电场分量;
为nΔt时刻在Yee氏元胞中(i,j)处的z方向电场分量;![]() 分别为(n+1/2)Δt时刻在Yee氏元胞中(i,j+1/2)处的x、y方向磁场分量。
分别为(n+1/2)Δt时刻在Yee氏元胞中(i,j+1/2)处的x、y方向磁场分量。
PML边界条件[16]是在计算域截断边界处设置一种特殊的非物理的吸收介质层,使入射波不发生反射,直接穿过分界面进入PML层,且进入PML层的透射波能迅速衰减。对于TM型电磁波,其FDTD方法在PML中差分格式[17]为
(8)
(9)
(10)
(11)
式中:ε为介电常数;μ0为初始磁导率;σx、σy分别表示x和y方向的电导率;![]() 分别表示x、y方向的等效磁阻率;Ezx、Ezy为Ez的2个子分量。
分别表示x、y方向的等效磁阻率;Ezx、Ezy为Ez的2个子分量。
采用FDTD方法求解Maxwell方程组时,为保证解的稳定性,时空步长需要满足CFL条件[18-19],即时间步长Δt与空间步长Δx、Δy需满足如下关系:
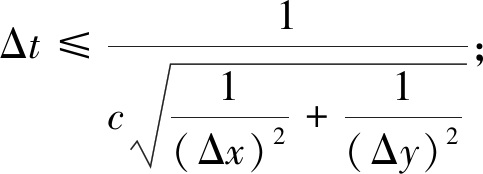
(12)
(13)
式中:c为光速;λ为电磁波传递过程中的最小波长;T为电磁波信号周期。
2 计算模型
高聚物修复的面板脱空堤坝模型如图1所示,模型尺寸为4.0 m×2.5 m。根据堤坝实际结构,堤坝体模型分为混凝土面板和黏土两层,堤坝内部各介质的介电参数如表1所示,非磁性介质相对磁导率为1,磁损耗为0。为了满足FDTD稳定性条件和数值色散条件的要求,正演模拟参数如表2所示。
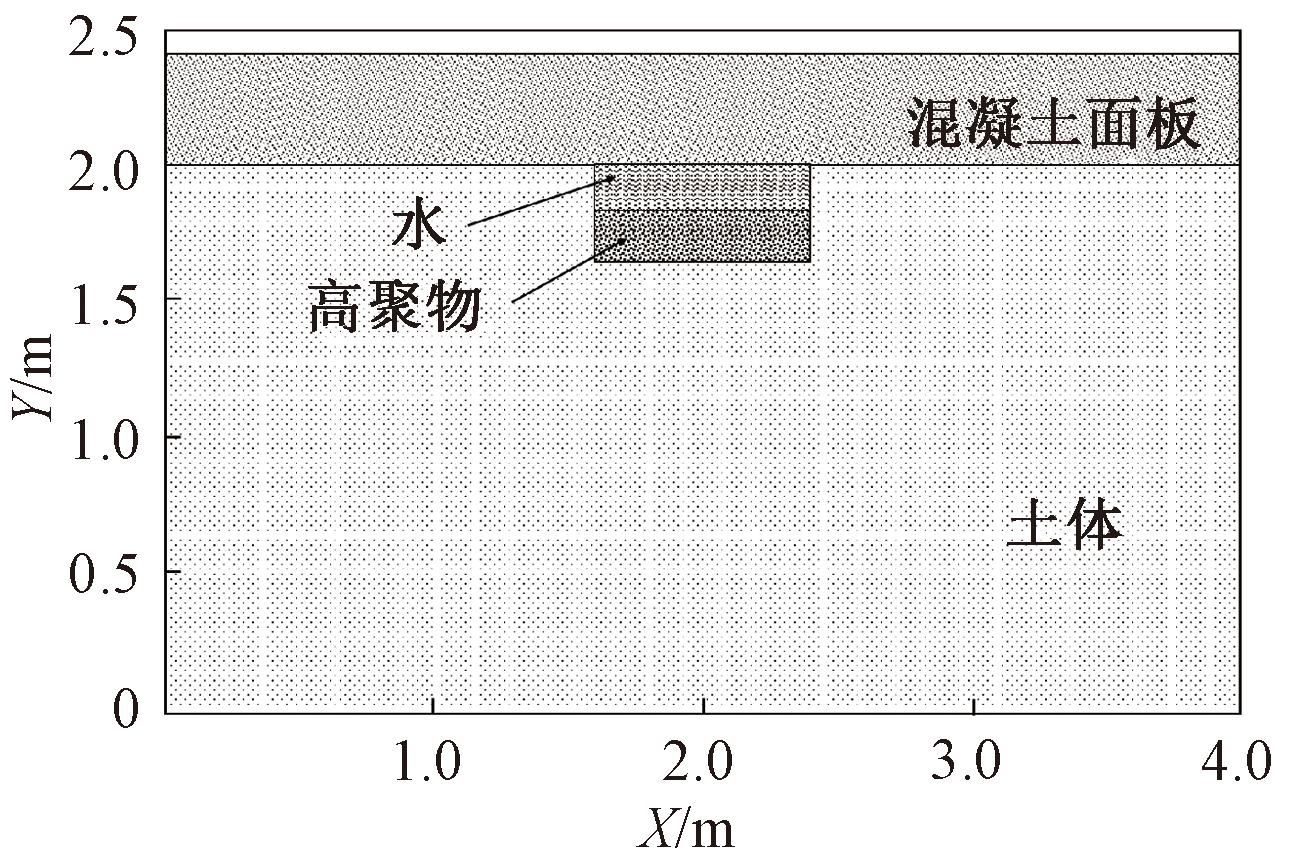
图1 含高聚物修复的堤坝面板脱空模型
Figure 1 Face disengaging models of dam during polymer repair
表1 堤坝内部介质介电参数
Table 1 Dielectric parameters inside dam
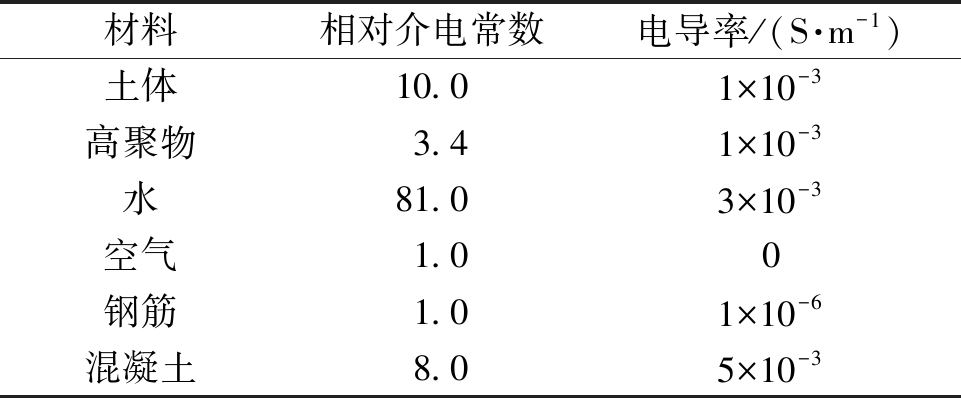
材料相对介电常数电导率/(S·m-1)土体10.01×10-3高聚物3.41×10-3水81.03×10-3空气1.00钢筋1.01×10-6混凝土8.05×10-3
表2 FDTD正演模拟参数
Table 2 Parameters of FDTD forward simulation
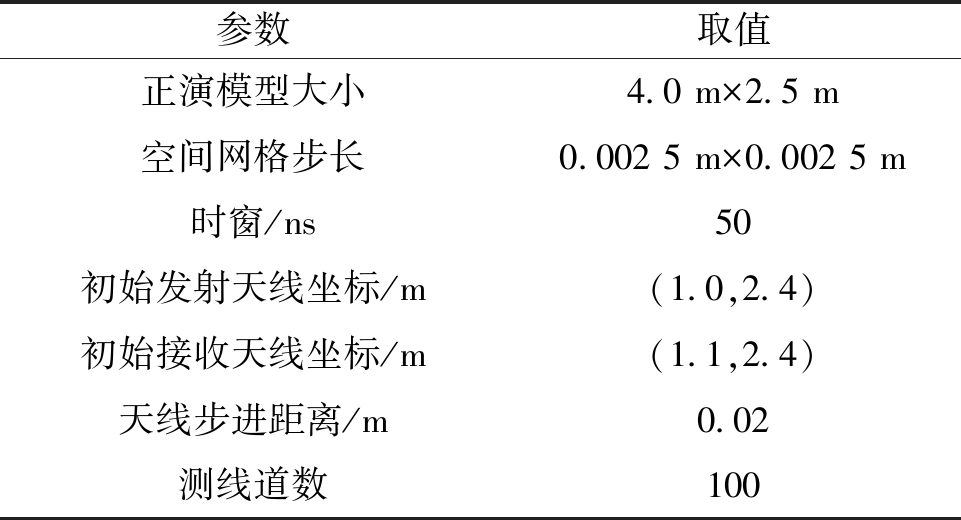
参数取值正演模型大小4.0 m×2.5 m空间网格步长0.002 5 m×0.002 5 m时窗/ns50初始发射天线坐标/m(1.0,2.4)初始接收天线坐标/m(1.1,2.4)天线步进距离/m0.02测线道数100
3 正演模拟
3.1 激励源中心频率
为了对比激励源中心频率对判断堤坝面板脱空高聚物修复效果的影响,将Ricker子波中心频率分别设置为200、500、900、1 600 MHz,如图2所示。混凝土面板厚度为40 cm,脱空区域面积为0.8 m×0.35 m。

图2 不同激励源中心频率堤坝面板脱空探地雷达正演剖面图
Figure 2 Forward simulation profiles of GPR for face disengaging models with different excitation source center frequencies
在图2中,探地雷达正演剖面图分辨率随着中心频率增大而逐渐升高,图像分层越来越明显,杂波和绕射波也随之增加。中心频率为200 MHz的探地雷达剖面图中,反射波形分辨率较低,难以清晰分辨各分界面;中心频率为500 MHz的探地雷达剖面图中,各介质分界面的反射水平线,杂波和绕射波幅值增大;中心频率为900 MHz的探地雷达剖面图中绕射波和杂波较少,可以判断脱空区域修复过程中的介质分界面分布情况;中心频率为1 600 MHz的探地雷达剖面图中,反射波形分辨率最高,但杂波和绕射波分辨率也增大,脱空区域下部分界面图像被杂波和绕射波干扰。为获得理想的图片分辨率,应该选取合适的激励源中心频率。因此,综合考虑堤坝面板脱空区域大小、深度和配筋等因素,下文正演模拟中激励源中心频率采用900 MHz。
3.2 脱空区修复程度
建立修复前、修复50%和完全修复后的面板脱空堤坝模型,如图3所示。堤坝面板厚度为40 cm,脱空区域面积为0.8 m×0.35 m。
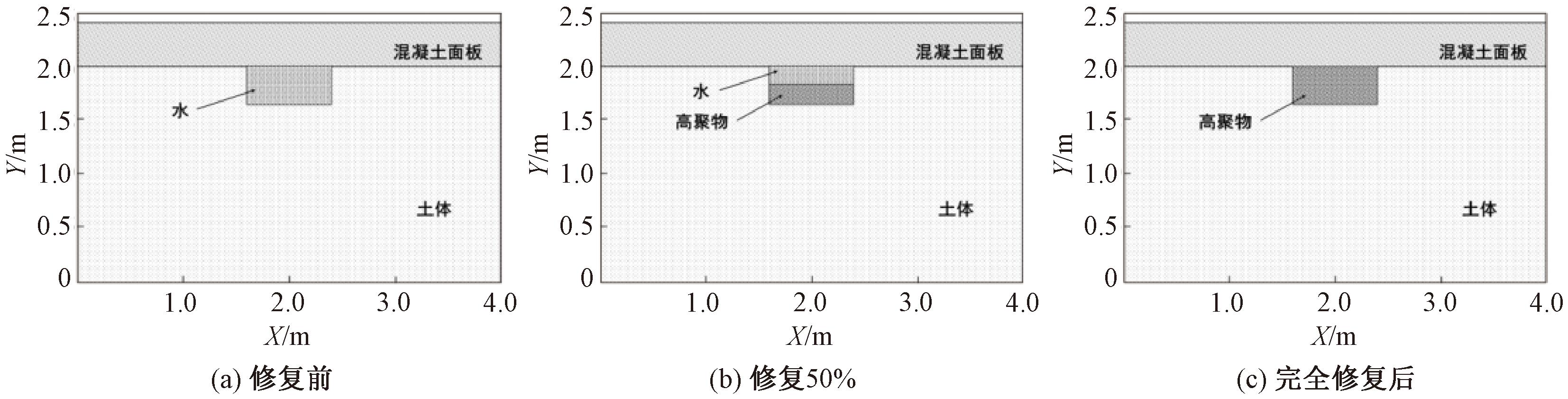
图3 不同高聚物修复程度下的堤坝面板脱空模型
Figure 3 Face disengaging models of dam with different degree of polymer repair
图4为不同高聚物修复程度下的堤坝面板脱空探地雷达正演剖面图。由图4可知,修复前与完全修复后图像均呈现两簇水平状反射线,修复前正演图像水平线顶端幅值大于完全修复后水平线顶端幅值,且修复前两簇水平线间隔时间明显大于完全修复后间隔时间;修复50%正演模拟图像呈现三簇水平状反射线。因此,可以通过正演模拟图中反射线的簇数、幅值大小、传递时间间隔来判断高聚物在堤坝面板脱空区域中的充填情况。
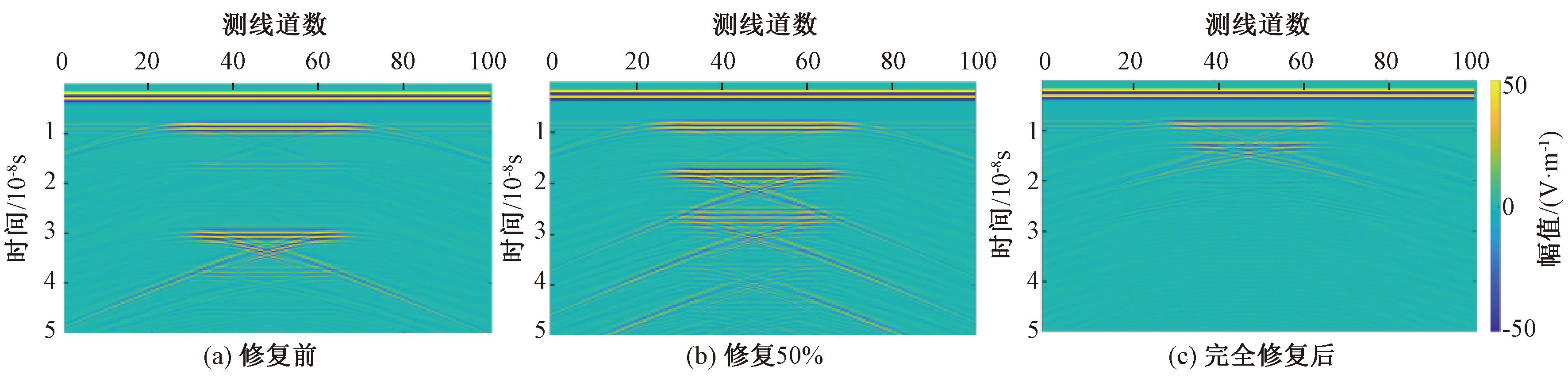
图4 不同高聚物修复程度下的堤坝面板脱空探地雷达正演剖面图
Figure 4 Forward simulation profiles of GPR for face disengaging models with different degree of polymer repair
3.3 脱空区几何尺寸
堤坝面板脱空探测过程中,会遇到不同几何尺寸的脱空区域,假定脱空区域为矩形,分析不同脱空长度和脱空深度的堤坝正演模拟图像特征。
3.3.1 不同脱空长度
为了对比脱空长度对高聚物修复面板脱空堤坝波场特征的影响,混凝土面板厚度为30 cm,矩形脱空区域分别设为0.3 m×0.35 m、0.5 m×0.35 m、0.8 m×0.35 m和1.0 m×0.35 m,模型分布如图3(c)所示。
图5为不同脱空长度的脱空模型探地雷达剖面图。由图5可知,随着脱空区域长度的增加,探地雷达剖面图中产生的水平状界面反射波增长,脱空区域分层现象更加明显,可以清晰看出高聚物完全修复后的脱空区域上下分界面。

图5 不同脱空长度的脱空模型探地雷达剖面图
Figure 5 Forward simulation profiles of GPR for face disengaging models with different model lengths
3.3.2 不同脱空深度
为了对比脱空深度对高聚物修复面板脱空堤坝波场特征的影响,混凝土面板厚度为30 cm,矩形脱空区域分别设为0.8 m×0.2 m、0.8 m×0.3 m、0.8 m×0.4 m和0.8 m×0.45 m,模型分布如图3(c)所示。
图6为不同脱空深度的脱空模型探地雷达正演剖面图。由图6可知,随着脱空区域深度方向尺寸增大,探地雷达剖面图水平状反射线之间时间间隔逐渐增大,脱空区域存在衍射波和绕射波也逐渐分散,有利于清晰展现脱空区域完全修复后的上下反射界面。因此,随着脱空区域深度增大,剖面图中脱空区域上下界面更加清晰,有利于高聚物修复结果的判别。根据脱空区域上下界面之间的电磁波双程走时,通过计算所得的模拟脱空深度与实际脱空深度相近。

图6 不同脱空深度的脱空模型探地雷达正演剖面图
Figure 6 Forward simulation profiles of GPR for face disengaging models with different model depths
3.4 堤坝面板厚度
为了对比混凝土面板厚度对高聚物修复面板脱空堤坝波场特征的影响,堤坝面板混凝土厚度分别设置为20、30、40、50 cm,脱空区域面积为0.8 m×0.35 m,模型分布如图3(c)所示。
图7为不同厚度混凝土面板的脱空模型探地雷达正演模拟图。由图7可知,面板脱空模型在高聚物完全修复后呈现两簇明显的平板状反射线,顶端反射幅值大,随着深度增加幅值逐渐减小。由图7(a)和图7(b)可知,在面板脱空修复区域出现很多绕射波和衍射波,由于绕射波和衍射波的影响,在高聚物注浆修复区域,面板脱空区域下界面水平状反射线被分割开。由图7(c)、7(d)可以看出,随着面板厚度增加,在面板脱空修复区域绕射波和衍射波幅值减小,可以识别面板与高聚物、高聚物与土体垫层之间的反射界面。

图7 不同厚度混凝土面板的脱空模型探地雷达正演模拟图
Figure 7 Forward simulation profiles of GPR for face disengaging models with different thickness concrete slabs
3.5 面板配筋
为了对比面板配筋对高聚物修复面板脱空堤坝波场特征的影响,对无钢筋和含钢筋堤坝面板脱空模型进行数值模拟。混凝土面板厚度为30 cm,单层钢筋埋深为15 cm,钢筋间距为40 cm,钢筋半径为14 mm,矩形脱空区域为0.8 m×0.35 m,如图8所示。
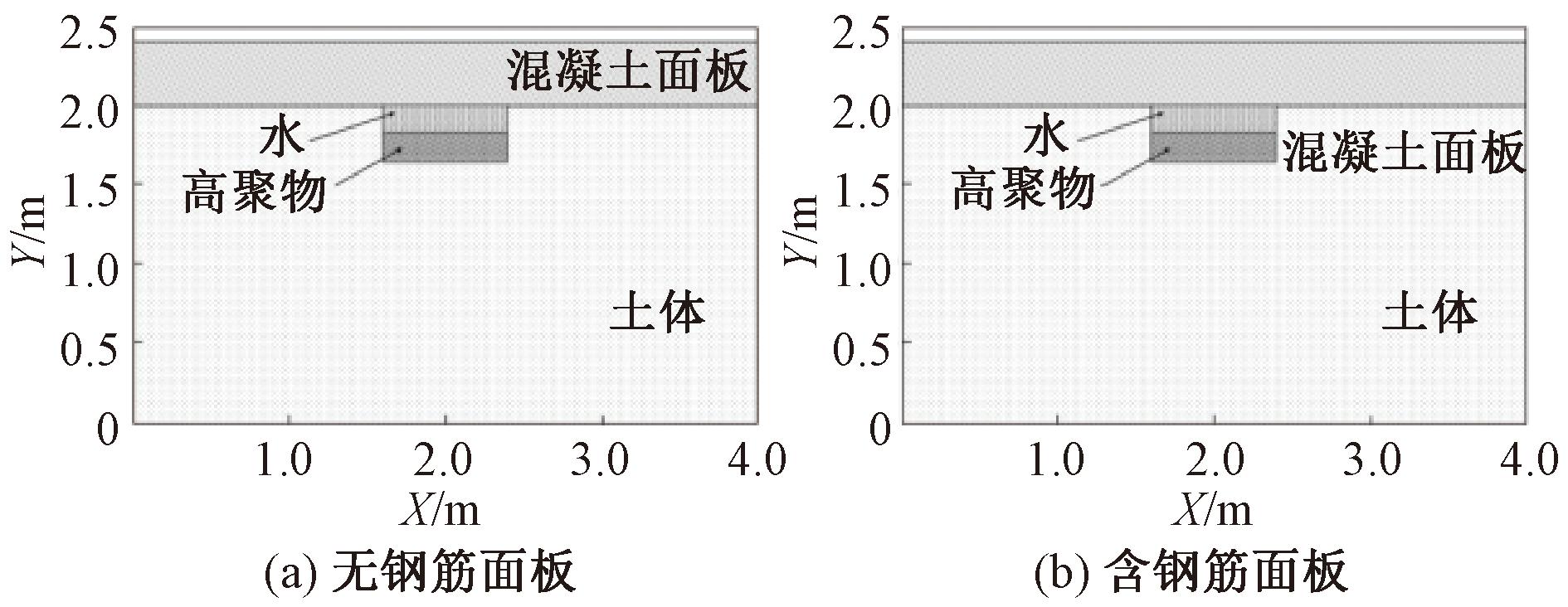
图8 不同配筋面板的脱空模型示意图
Figure 8 Face disengaging models of dam with different reinforcement layers
图9为面板配筋的脱空模型探地雷达正演剖面图。由图9(a)可知,在无钢筋面板脱空区域被高聚物完全修复状态下,探地雷达可以清晰显示脱空区域的上下界面,并根据探地雷达电磁波双程走时推断实际脱空区域深度。由图9(b)可知,由于钢筋介电常数远大于混凝土和土体介电常数,探地雷达发射的电磁波遇到钢筋时将产生能量较强的绕射波,强绕射波将脱空区域上下分界面的反射波分割开,但还存在脱空隐患的上下界面,可以通过探地雷达识别脱空病害。
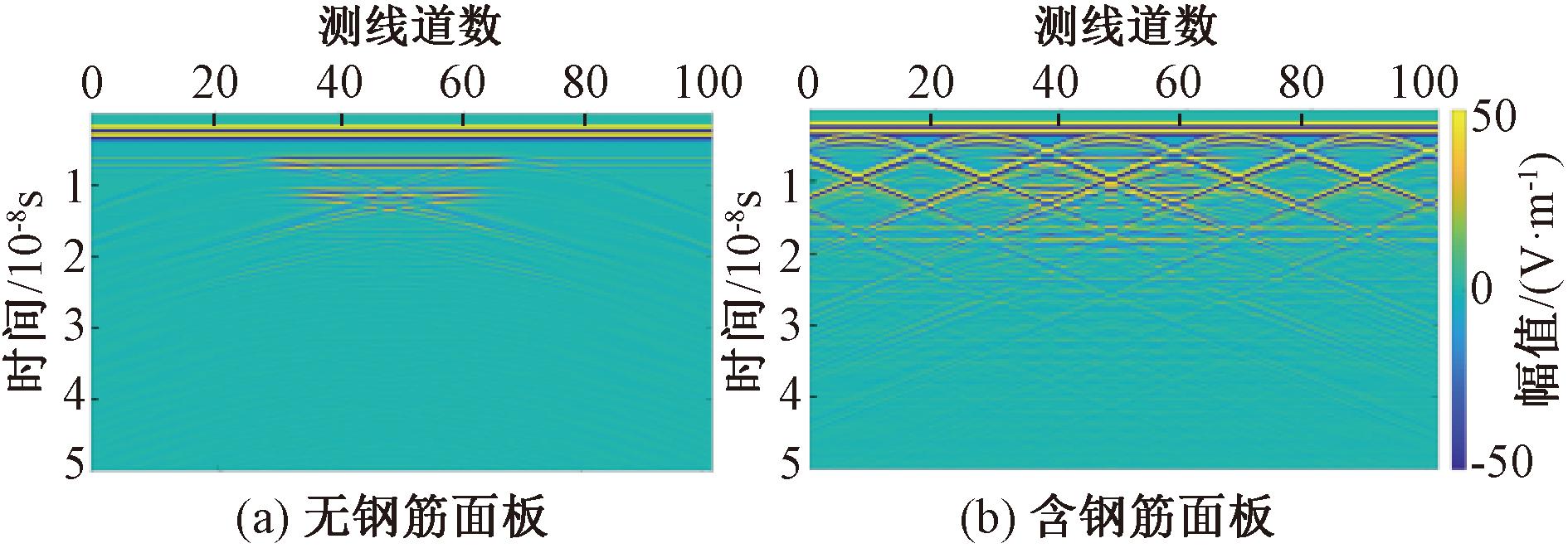
图9 面板配筋的脱空模型探地雷达正演剖面图
Figure 9 Forward simulation profiles of GPR for face disengaging models with different reinforcement layers
4 结论
(1)根据高聚物注浆修复面板脱空堤坝的探地雷达剖面图中的反射波尺寸、幅值大小以及反射波之间的传递时间间隔,能有效判断堤坝面板脱空区域的高聚物注浆修复效果。
(2)随着激励源中心频率增大,探地雷达剖面图分辨率逐渐增加,脱空区域分界面可以清晰显示,但是激励源中心频率越大,杂波和绕射波也随之增加,影响数据分析,在实际探测过程中应选择合适的激励源中心频率进行探测。
(3)随着脱空区域长度增加,探地雷达剖面图中产生的水平状界面反射波增长,脱空区域分层现象更加明显,可以清晰看出脱空区域上下分界面;随着脱空区域深度增大,探地雷达剖面图水平状反射线之间时间间隔逐渐增大,剖面图中脱空区域上下界面更加清晰,有利于高聚物修复结果的判别。
(4)随着堤坝面板厚度增加,在面板脱空修复区域绕射波和衍射波幅值减小,可以识别面板与高聚物、高聚物与土体垫层之间的反射界面。
(5)探地雷达发射的电磁波遇到钢筋时将产生能量较强的绕射波,强绕射波将脱空区域上下分界面的反射波分割开,难以判断反射波的水平长度。
[1] 张丙印, 师瑞锋. 流变变形对高面板堆石坝面板脱空的影响分析[J]. 岩土力学, 2004, 25(8): 1179-1184.
ZHANG B Y, SHI R F. Influence of creeping on separation between concrete slab and cushion layer in high concrete face rock-fill dam[J]. Rock and Soil Mechanics, 2004, 25(8): 1179-1184.
[2] 李宗坤, 宋子元, 葛巍, 等. 基于模糊集理论的土石坝开裂破坏风险分析[J]. 郑州大学学报(工学版), 2020, 41(5): 55-59.
LI Z K, SONG Z Y, GE W, et al. Risk analysis of cracking failure of earth-rock dam based on fuzzy set theory[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(5): 55-59.
[3] 葛巍, 焦余铁, 洪辛茜, 等. 基于AHP-BN法的溃坝生命损失风险评价[J]. 郑州大学学报(工学版), 2021, 42(3): 8-12.
GE W, JIAO Y T, HONG X Q, et al. Risk assessment of life loss caused by dam breach based on AHP-BN method[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(3): 8-12.
[4] 王复明, 李嘉, 石明生, 等. 堤坝防渗加固新技术研究与应用[J]. 水力发电学报, 2016, 35(12): 1-11.
WANG F M, LI J, SHI M S, et al. New seepage-proof and reinforcing technologies for dikes and dams and their applications[J]. Journal of Hydroelectric Engineering, 2016, 35(12): 1-11.
[5] LI M J, FANG H Y, DU M R, et al. The behavior of polymer-bentonite interface under shear stress[J]. Construction and Building Materials, 2020, 248: 118680.
[6] FANG H Y, ZHANG H, XUE B H, et al. Coordination characteristics analysis of deformation between polymer anti-seepage wall and earth dam under traffic load[J]. Water, 2022, 14(9): 1442.
[7] 郭成超, 杨建超, 石明生, 等. 高密度电法在高聚物防渗墙检测中的应用研究[J]. 地球物理学进展, 2019, 34(2): 709-716.
GUO C C, YANG J C, SHI M S, et al. Application of high density electrical method in detection of polymer cutoff wall[J]. Progress in Geophysics, 2019, 34(2): 709-716.
[8] LIU H, SHI Z S, LI J H, et al. Detection of road cavities in urban cities by 3D ground-penetrating radar[J]. GEOPHYSICS, 2021, 86(3): WA25-WA33.
[9] FENG D S, WANG X, ZHANG B. Specific evaluation of tunnel lining multi-defects by all-refined GPR simulation method using hybrid algorithm of FETD and FDTD[J]. Construction and Building Materials, 2018, 185: 220-229.
[10] 徐浩, 刘江平, 余信江. 大坝面板脱空地质雷达波场数值模拟与瞬时属性分析[J]. 中南大学学报(自然科学版), 2021, 52(2): 489-497.
XU H, LIU J P, YU X J. Numerical simulation of dam face disengaging ground penetrating radar wave field and instantaneous attribute analysis[J]. Journal of Central South University (Science and Technology), 2021, 52(2): 489-497.
[11] 张杨, 周黎明, 肖国强. 堤防隐患探测中的探地雷达波场特征分析与应用[J]. 长江科学院院报, 2019, 36(10): 151-156.
ZHANG Y, ZHOU L M, XIAO G Q. Analysis and application of wave field of ground penetration radar in defect detection of embankment[J]. Journal of Yangtze River Scientific Research Institute, 2019, 36(10): 151-156.
[12] WARREN C, GIANNOPOULOS A, GRAY A, et al. A CUDA-based GPU engine for gprMax: open source FDTD electromagnetic simulation software[J]. Computer Physics Communications, 2019, 237: 208-218.
[13] LAX M, NELSON D F. Maxwell equations in material form[J]. Physical Review, 1976, 13(4): 1777-1784.
[14] YEE K E. Numerical solution of initial boundary value problems involving maxwell′s equations in isotropic media[J]. IEEE Transactions on Antennas and Propagation, 1966, 14(3): 302-307.
[15] CHEN H W, HUANG T M. Finite-difference time-domain simulation of GPR data[J]. Journal of Applied Geophysics, 1998, 40(1/2/3): 139-163.
[16] BERENGER J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200.
[17] 马月红. 时域有限差分法及其在电磁波测井正演问题中应用[D]. 秦皇岛: 燕山大学, 2007.
MA Y H. FDTD method and its application to simulation of electromagnetic well-logging tool response[D]. Qinhuangdao: Yanshan University, 2007.
[18] LEI J W, XUE B H, FANG H Y, et al. Forward analysis of GPR for underground pipes using CUDA-implemented conformal symplectic Euler algorithm[J]. IEEE Access, 2020, 8: 205590-205599.
[19] LEI J W, FANG H Y, XUE B H, et al. A parallel conformal symplectic Euler algorithm for GPR numerical simulation on dispersive media[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5.