随着中国国民经济的提高和交通运输行业的快速发展,车型日益复杂化并且车辆数量也在持续增加,导致车辆荷载成为威胁既有大型桥梁运营安全的重要因素[1]。因此,建立准确合理的车辆荷载效应极值模型成为在役大型桥梁结构安全性评估和可靠度研究的关键所在[2]。然而,车辆荷载受到多种因素的影响,具有随机性大、时变性强等特点,导致车辆荷载效应及其分布也具有高度不确定性[3]。如何建立更加准确有效的荷载效应极值预测模型,一直是相关领域研究的热点与重点[4]。
Xia等[5]用Gumbel分布拟合相对较短时间内记录的车辆荷载极值,并用其拟合分布来推断长期的荷载效应极值;Obrien等[6]针对实际车辆荷载具有非平稳随机的特点,假定作用过程可以分解为若干个短期平稳过程,并采用GEV(generalised extreme value distributions)分布对其进行拟合,进而得到实际车辆荷载的效应极值模型;Zhou等[7]在桥梁车辆荷载受多种因素影响而不满足独立同分布时,提出混合超阈值法的GPD(generalised pareto distribution)模型来预测车辆荷载效应极值,得出更加准确合理的预测结果;周军勇等[8]分析混合超阈值方法的难点,并解决了样本数据独立性检验、阈值选取以及参数修正等重要问题。
GEV模型在数据选择时一个区组只取其最大值,不能很好地利用数据分布尾部的已有信息,样本数据利用不经济[9]。GPD模型虽然能充分利用数据中的有效信息,但是模型不包含时间信息,不能体现车辆荷载的时变特性[10]。基于此,本文将2种模型结合起来,建立一种更加符合实际车辆荷载效应极值的概率模型,从而保障既有大型桥梁的运营安全。
1 极值理论及极值模型
1.1 广义极值分布与区组最大值模型
荷载效应建模的理论基础是极值统计理论[11]。令Mn=max(X1,X2,…,Xn) ,X1,X2,…,Xn为独立同分布的随机变量,分布函数为F(x)。如果存在常数列{an>0}和{bn} ,当n→∞时,使得
(1)
成立,其中H(x)为非退化的分布函数,引入位置参数μ和尺度参数σ,可以采用统一的表达形式[12]:
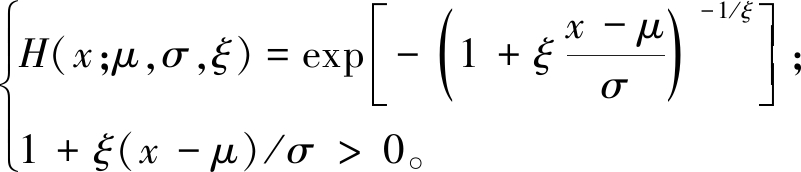
(2)
式中:μ、ξ∈R;σ>0;H为广义极值分布;ξ为形状参数。当ξ=0时,H表示Gumbel分布。当ξ>0时,H表示Fréchet分布。当ξ<0时,对应Weibull分布。
根据以上理论,若样本数量充足,则各组数据的最大值服从GEV分布,并且利用这些极值数据构建区组最大值模型[13]。
1.2 广义Pareto分布与超阈值模型
如果随机变量X的分布函数为
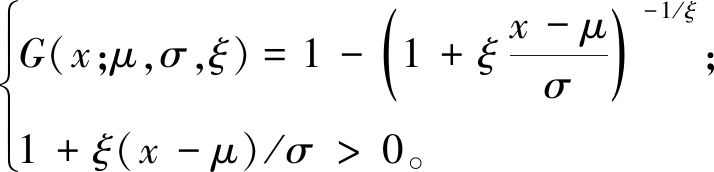
(3)
则称X服从广义Pareto分布,其中μ∈R为位置参数;σ>0为尺度参数;ξ∈R为形状参数。根据形状参数ξ的不同,广义Pareto分布也有3种表示形式:Pareto Ⅰ型、Ⅱ型和Ⅲ型分布。
在样本数量较小,或不能按天或月划分时段长度时,为了充分利用数据中的极值信息,有时需要考虑超过某个很大值(称为阈值)的所有数据,并利用这些数据进行建模,即超阈值模型[14]。
2 区组超阈值模型
2.1 模型的提出和建立
区组超阈值模型将上述2种模型相结合,只需要在建立观测序列的超阈值模型后,根据GP分布参数得到GEV分布参数,然后根据不同时段长度上最大值分布参数之间的关系实现不同时段长度上荷载效应最大值的分布预测。这与原有的超阈值建模步骤组合形成了区组超阈值模型完整的建模步骤[15]。
2.2 阈值选择
阈值u的选择是采用阈值模型进行超阈值建模时的关键,u的大小直接决定着有效样本的数量。本文采用平均剩余寿命图,对于大于某一合理阈值u0的阈值u,样本平均超出量函数是u的线性函数,由以下点集构成:
(4)
式中:nu为超出阈值u的次数,平均剩余寿命图应近似为线性。因此,若图中某一阈值u0以后剩余寿命斜率能保持不变,则这个点通常可以作为一个合理的阈值。
2.3 模型检验
通常采用概率图、分位数图、重现水平图以及概率密度图来评估拟合的GP分布的质量[16]。
(1)概率图。对于随机变量X,给定阈值u,记按照从小到大重排序后的超出量为y(1)≤y(2)≤…≤y(k),拟合的超阈值模型为![]() 则称由下述点集构成的图形为概率图(又称P-P图)。
则称由下述点集构成的图形为概率图(又称P-P图)。
(5)
(2)分位数图。假定![]() 则分位数图(又称Q-Q图)由下列点集构成:
则分位数图(又称Q-Q图)由下列点集构成:
(6)
(3)重现水平图。在极值分析中,所谓T的重现水平u(T)就是要求在T时间内,超过阈值u(T)的平均次数为1,此时要求每年只有一个观测值[17]。假定一形状参数和尺度参数分别为ξ和σ的GP分布是随机变量X对阈值u的超阈值分布。在极值建模中,xm为m次观测的回归水平。如果每年有ny次观测,则N年重现水平就是m=Nny次观测的重现水平。因此,N年的重现水平为
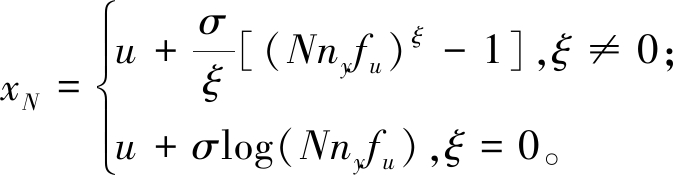
(7)
由点集{(log m,xm)}构成的轨迹图称为重现水平图。
2.4 参数估计
在对极值进行统计建模时,点过程描述为超阈值模型转换为最大值模型提供了方法。概率知识表明,当n很大且p接近于0时,可以用均值为np的泊松分布来近似含有参数n和p的二项分布[18]。因此,假定稀有事件发生次数的序列由参数为λ的泊松过程控制,那么,在时间间隔T内事件发生的次数NT服从均值为λT的泊松分布,即
Pr{NT=k}=[(λT)ke-λT]/k!,k=0,1,2,…。
(8)
当已知GP分布参数ξ、σ和u时,可求得相应的GEV分布参数ξ、σ、μ:
σ=σ*λξ;
(9)
(10)
2种分布的形状参数ξ保持不变,且上述GEV分布的时间尺度为单位时间。如果求时间间隔为T的GEV分布参数,由式(8)可知,相应的泊松分布参数为λT,则用λT代替式(9)~(10)中的λ即可得到时间间隔为T的GEV分布的分布参数:
σT=σ*(λT)ξ;
(11)
(12)
式中:形状参数ξ仍然保持不变。
3 实例应用
3.1 工程实例简介
本文主要工作围绕某大型斜拉桥结构健康监测系统的监测数据展开。该斜拉桥健康监测系统在主梁上共安装50个钢纵向应变传感器,其中,本文应用的钢纵向应变传感器在主跨跨中截面布置及其编号如图1所示。
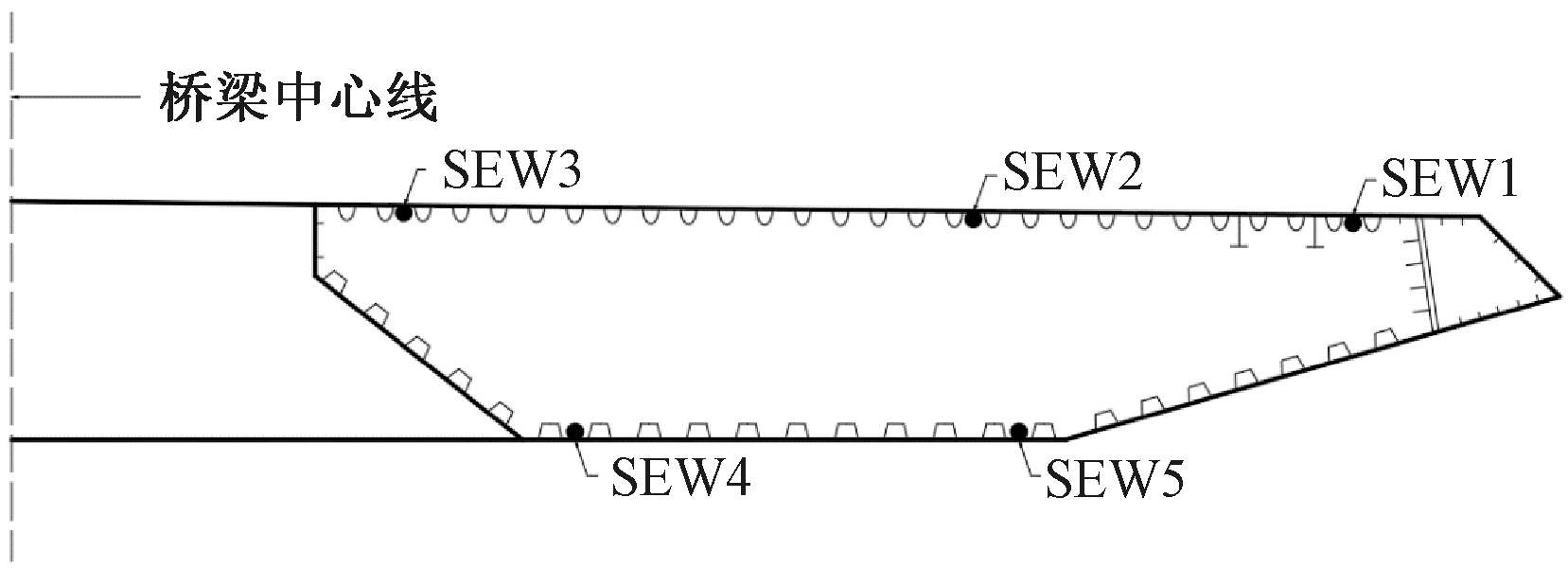
图1 跨中截面钢纵向应变布置图及其编号
Figure 1 Layout diagram and number of steel longitudinal strain sensors in mid-span
3.2 监测数据的预处理
在对数据进行分析研究之前,需要对原始监测数据进行预处理。传感器失效不工作或者是不能正常工作主要造成以下3类异常情况:①传感器能够正常输出数据,但是输出结果为超过正常幅度的不合理极大值或者是极小值;②传感器能够输出信息,但是输出信息为非数值;③传感器不能正常输出信息,造成一段数据的缺失。这些非正常情况都会影响后续研究工作的顺利进行,因此需要进行剔除[19]。本文所采用数据均为处理后数据。
3.3 车辆荷载效应时变极值模型
根据区组超阈值模型建模方法,首先以传感器SEW2在1 a内的车辆荷载纵向应变为例来说明超阈值模型建模的具体过程,然后给出其他钢纵向应变传感器的超阈值模型建模结果,并且所有钢纵向应变建模样本时长均为1 a。
首先,根据平均剩余寿命图选择合理阈值。钢纵向应变传感器SEW2的车辆荷载纵向应变的剩余寿命图及其95%置信区间如图2所示。图 2显示,点u=30附近,平均剩余寿命曲线有个折角,因此,可以初步判断最小合理阈值u0=30。进一步对不同阈值下的超阈值模型进行K-S检验,得到最小合理阈值u0=29。图3给出了超阈值概率fu=P(X>u)随阈值u的变化曲线。随着阈值u的增大,超阈值概率fu迅速减小,超阈值的离散性也显著增大,因此,为了保证模型的可靠性,合理的阈值选择区间可取[29,45]。
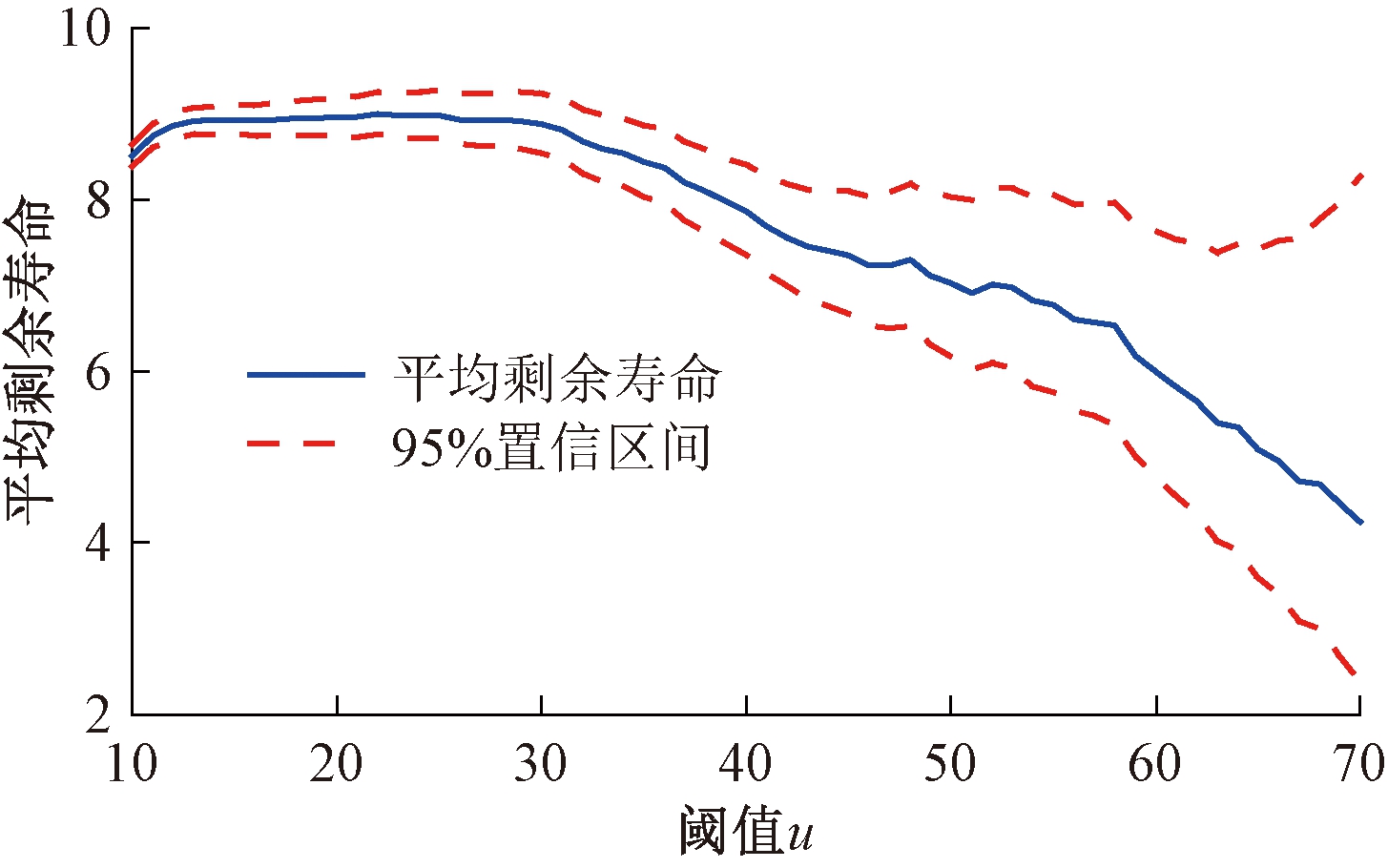
图2 SEW2的车辆荷载应变的平均剩余寿命图
Figure 2 MRL plot for vehicle load strain of SEW2
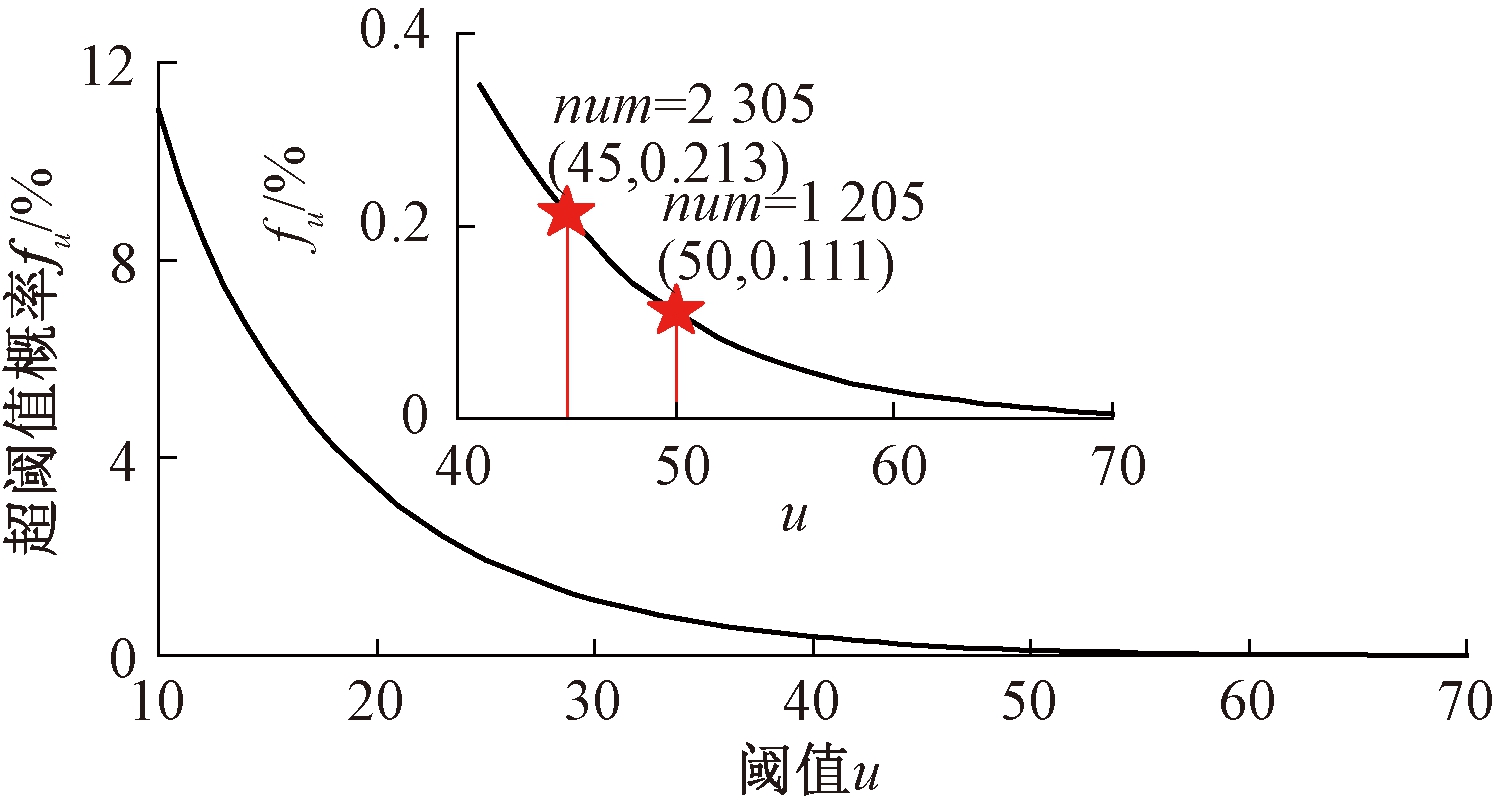
图3 超阈值概率图
Figure 3 Probability of exceeding threshold plot
其次,采用u=35对相应的车辆荷载应变进行超阈值建模,结果如图4所示。P-P图和Q-Q图均具有非常好的线性,经验概率密度和拟合的GP密度函数也非常吻合。重现水平图显示,由观测样本得到的经验重现水平所描绘的点也均在重现水平的置信度为95%的置信区间内。
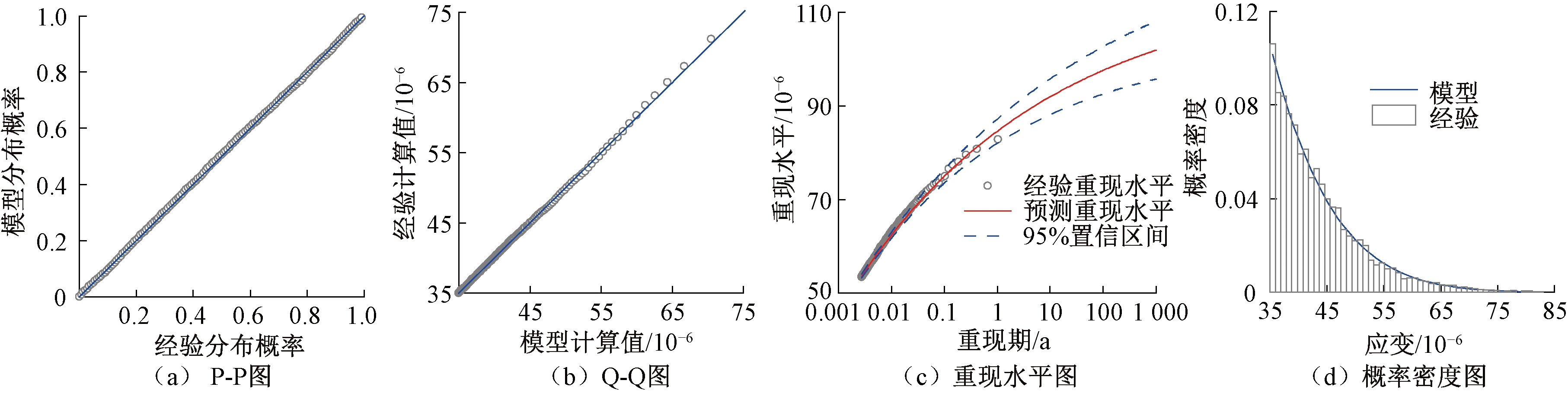
图4 SEW2车辆荷载应变超阈值模型诊断
Figure 4 Diagnostic plots of the GPD model for SEW2
再次,模型诊断图给出了GP分布对经验概率密度直方图的完美拟合。因此,采用GP分布拟合车辆荷载压应变对u=35的超出量分布是合理的,此时,GP模型分布参数的极大似然估计为![]() 相应的对数似然函数值为
相应的对数似然函数值为![]() 和
和![]() 的协方差矩阵近似为[0.000 1,-0.001 2,-0.001 2,0.022 3]。
的协方差矩阵近似为[0.000 1,-0.001 2,-0.001 2,0.022 3]。
最后,按照上述过程对其他钢纵向应变传感器位置处的车辆荷载应变进行超阈值模型建模。本文在选择阈值u0时,均对不同阈值的超出量的GP分布拟合做了K-S检验[20]。选择能通过GP分布拟合的K-S检验的最小阈值作为u0,各应变传感器处车辆荷载应变的平均剩余寿命及所选最小合理阈值如图5所示。
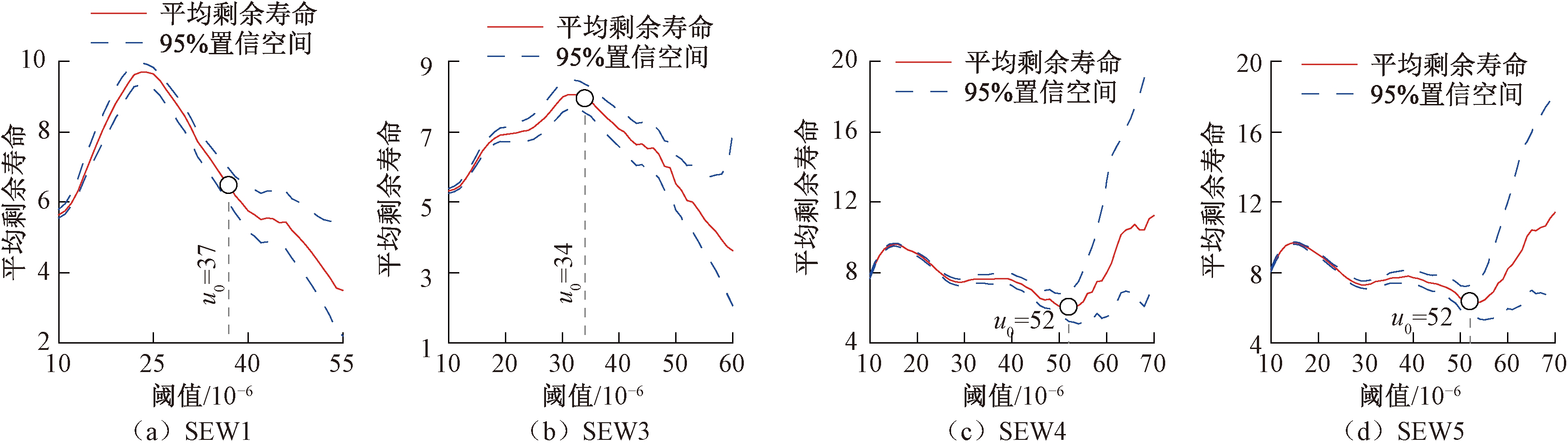
图5 传感器车辆荷载应变的平均剩余寿命图
Figure 5 MRL plot for vehicle load strain of sensors
根据传感器SEW2的建模步骤,对每一处钢纵向应变传感器的车辆荷载应变,选择一合适的阈值,如表1所示。
表1 车辆荷载应变超阈值模型
Table 1 Fitted GPD model parameters
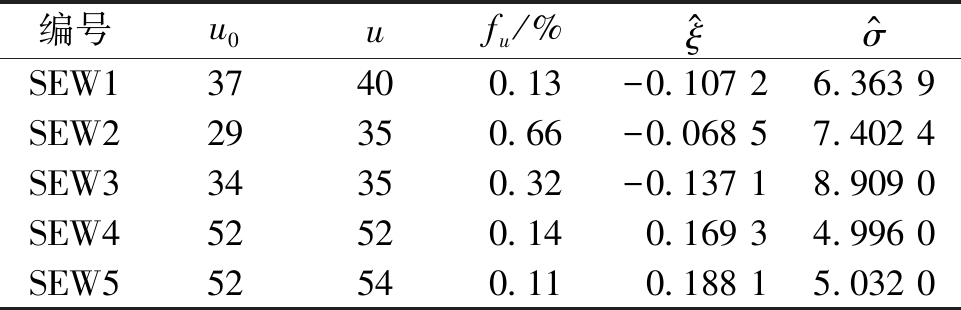
编号u0ufu/%ξ^σ^SEW137400.13-0.107 26.363 9SEW229350.66-0.068 57.402 4SEW334350.32-0.137 18.909 0SEW452520.140.169 34.996 0SEW552540.110.188 15.032 0
根据所建立的GP模型,建立SEW1、SEW3、SEW4、SEW5车辆荷载纵向应变的模型诊断图,分别如图6~9所示。4幅图中的Q-Q图、P-P图都具有非常良好的线性,虽然在P-P图中拟合直线的尾部有个别点稍偏离直线,但是这些偏离直线的点对应的较大车辆荷载应变是由超重车所引起的,而超重车为个别现象,且具有较大的随机性,因此不影响所拟合模型的合理性。
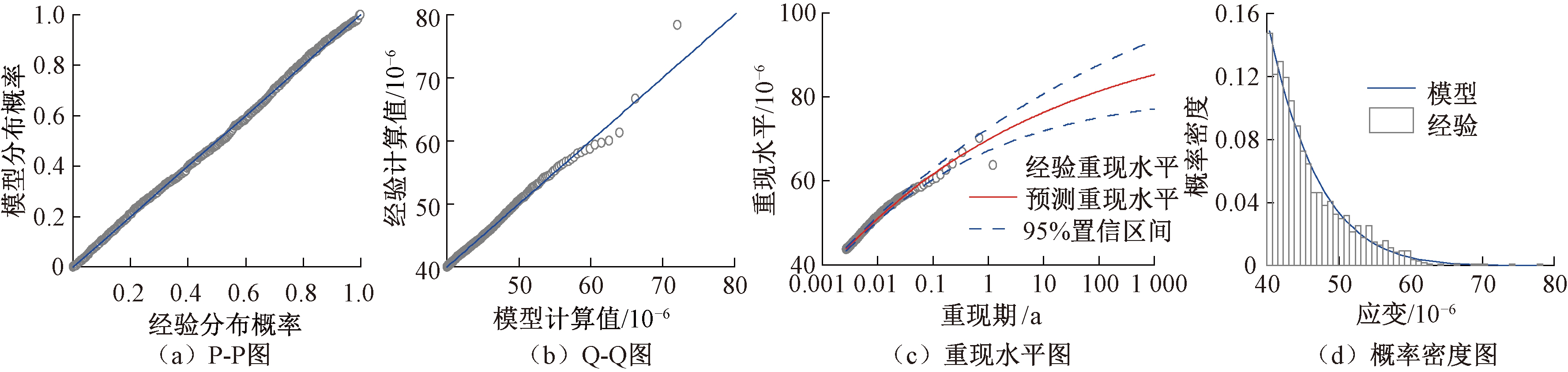
图6 SEW1车辆荷载应变超阈值模型诊断图
Figure 6 Diagnostic plots of the GPD model for SEW1
在图6和图7给出的重现水平图中,由于顶板车辆荷载纵向应变的超阈值分布形状参数ξ的估计值是负值,因此相应的分布支撑就有上限值,故重现水平图也应渐进地趋于某个有限值,所以重现水平曲线也显示了GP模型的合理性。由于底板车辆荷载纵向应变的超阈值分布形状参数ξ的估计值是正值,则相应的分布支撑的上界无限,故重现水平曲线也应该是趋于无穷大的,如图8和图9中的重现水平图所示,但是这显然是不合理的,因为车辆荷载应变是不可能无限增大的,由此说明采用GP模型的过分外推并不可靠。本文结合所研究桥梁的设计使用年限,外推到100 a的重现水平。最后,4幅图的密度曲线的估计均与经验直方图有很好的吻合。各拟合的GP分布的分布参数估计值如表1所示。根据该模型参数可以很方便地得到车辆荷载纵向应变的概率密度函数,即图4和图6~9各模型诊断图中的概率密度图。
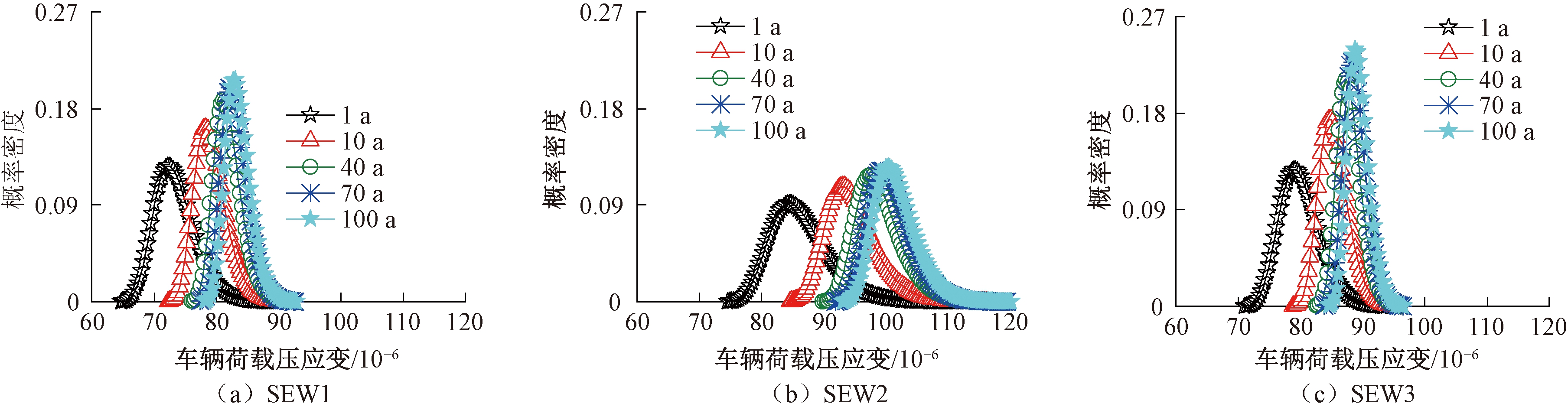
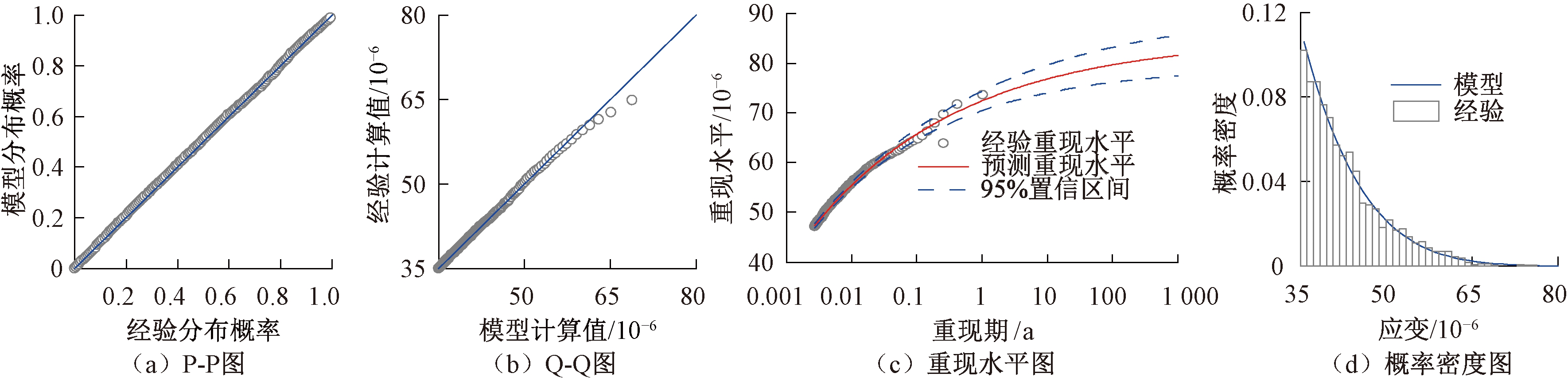
图7 SEW3车辆荷载应变超阈值模型诊断图
Figure 7 Diagnostic plots of the GPD model for SEW3
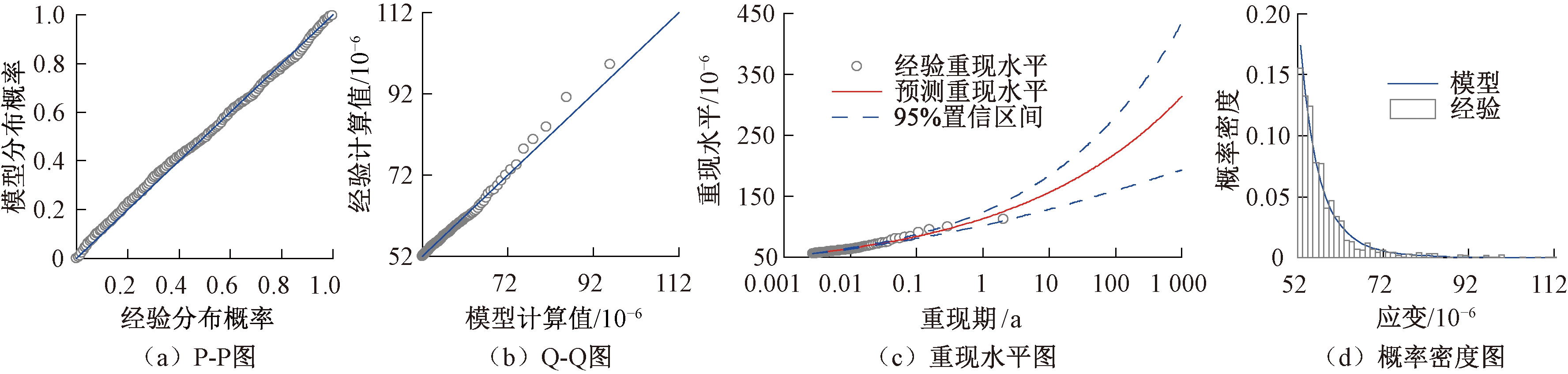
图8 SEW4车辆荷载应变超阈值模型诊断图
Figure 8 Diagnostic plots of the GPD model for SEW4
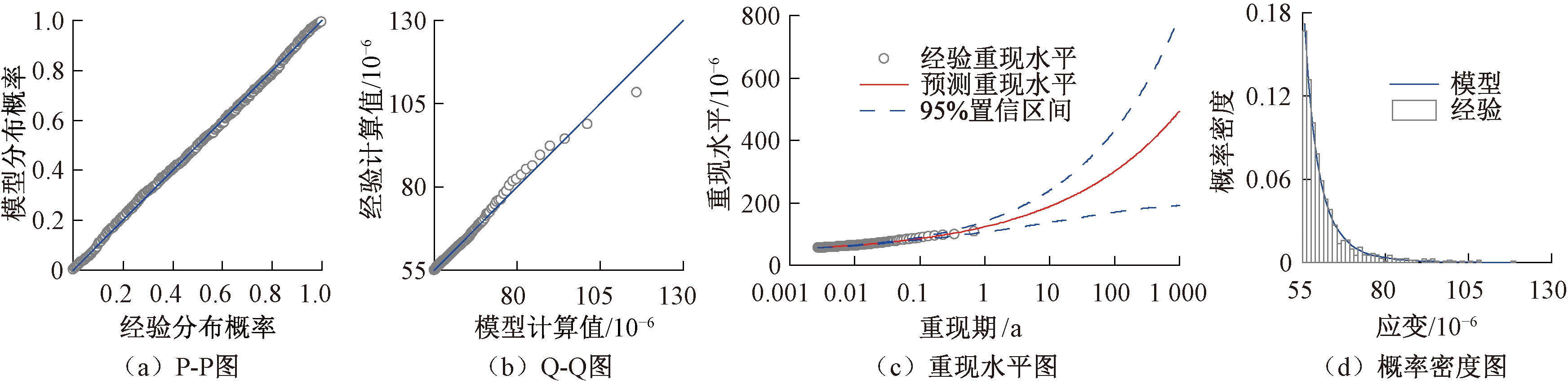
图9 SEW5车辆荷载应变超阈值模型诊断
Figure 9 Diagnostic plots of the GPD model for SEW5
根据式(9)~(10),利用表1所给数据即可求得车辆荷载应变的年最大值分布参数(GEV分布),结果见表2。表2显示,顶板车辆荷载应变极大值模型的形状参数小于0,而底板的形状参数大于0,因此,由经典极值理论可知,顶板车辆荷载应变的最大值服从Fréchet分布,而底板车辆荷载应变的最大值服从Weibull分布。
表2 车辆荷载应变年最大值分布参数
Table 2 Distribution parameters of annual maximum for vehicle load strain
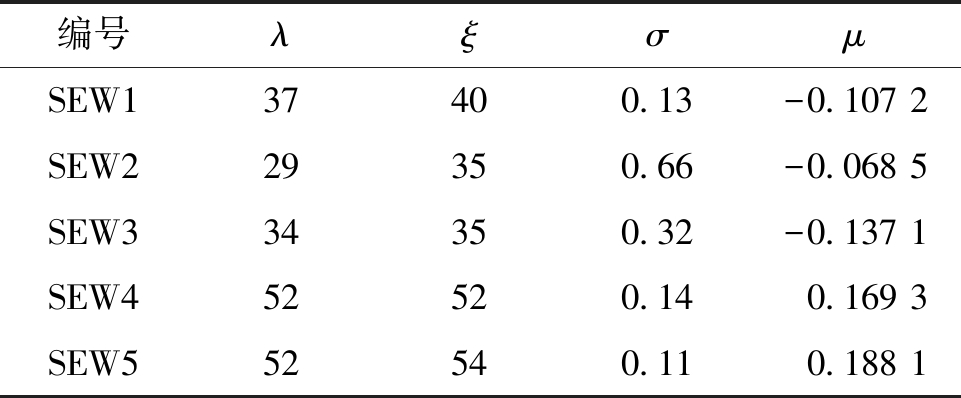
编号λξσμSEW137400.13-0.107 2SEW229350.66-0.068 5SEW334350.32-0.137 1SEW452520.140.169 3SEW552540.110.188 1
式(11)~(12)给出了时间长度为T时的GEV分布参数,将表2中年最大值分布参数代入这2个公式可得到任意时间长度T内车辆荷载应变最大值的GEV分布参数,跨中截面车辆荷载应变在100 a内的最大值分布的概率密度的变化过程如图10所示。
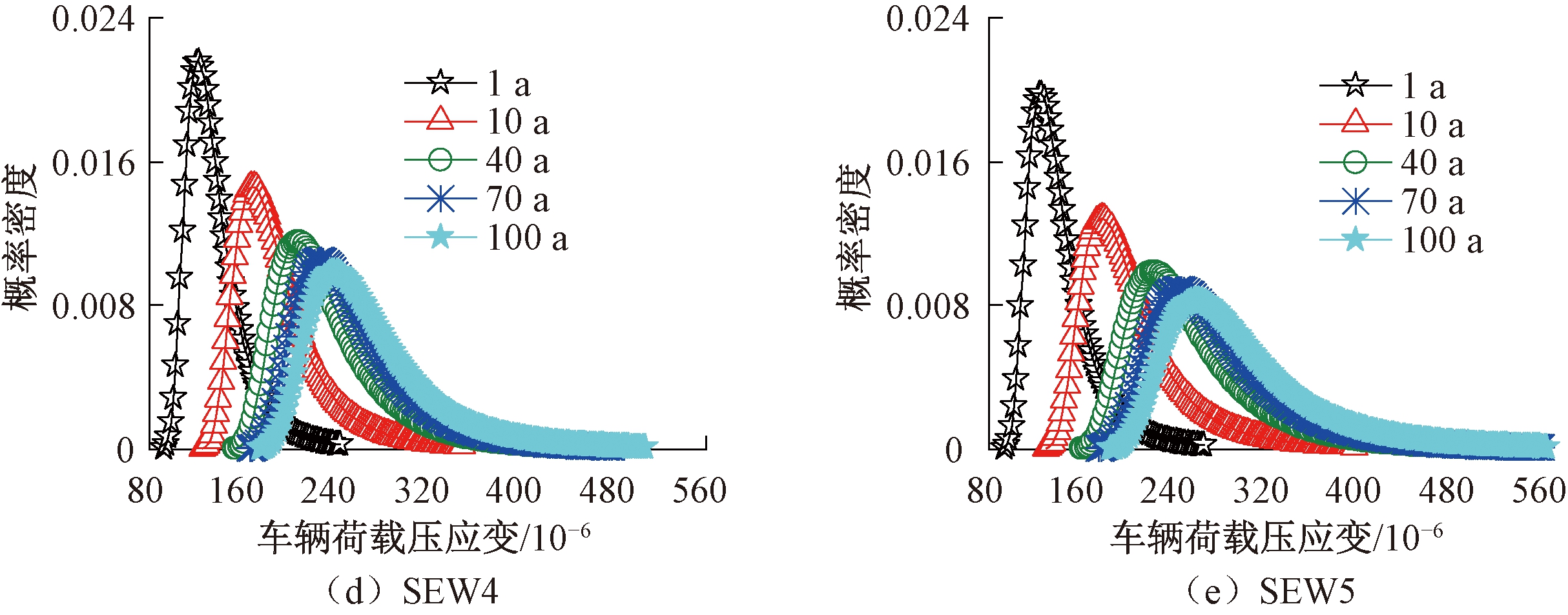
图10 年限T内车辆荷载应变的概率密度
Figure 10 Probability density of vehicle load strain in T years
由图10可知,随着预测年限T的增大,车辆荷载应变最大值分布向右移动,但是相同时间间隔内移动的幅度越来越小,最后趋于稳定,这显然是合理的,因为无论统计年限有多大,车辆荷载应变都不可能无限制地增大。
4 结论
(1)GP分布的形状参数、尺度参数和阈值与GEV分布的形状参数、尺度参数和位置参数可由一个二维的非齐次泊松过程组成的点过程参数λ联系起来。
(2)结合工程实例的样本数据,对钢纵向应变传感器SEW1、SEW2、SEW3、SEW4和SEW5在1 a内的车辆荷载纵向应变进行区组超阈值模型建模,并对模型进行验证,结果表明模型能够和数据完美拟合,证明了模型的优良性。
(3)采用区组超阈值模型过分外推并不可靠,车辆荷载应变不可能无限增大。因此,不能盲目外推极长重现期的重现水平。根据桥梁使用年限,本文外推了10、40、70、100 a车辆荷载应变的概率密度,为桥梁运营期的安全性及可靠性评估提供了一定的依据。
[1] 鲁乃唯, 刘扬, MOHAMMAD N. 交通量持续增长下大跨桥梁时变极值外推分析[J]. 工程力学, 2018, 35(7): 159-166.
LU N W, LIU Y, MOHAMMAD N. Extrapolation of time-variant extreme effect on long-span bridge considering steadily growing traffic volume[J]. Engineering Mechanics, 2018, 35(7): 159-166.
[2] 中华人民共和国交通运输部. 公路桥涵设计通用规范: JTG D60—2015[S]. 北京: 人民交通出版社, 2015.
Ministry of Transport of the People′s Republic of China General specifications for design of highway bridges and culverts: JTG D60—2015[S]. Beijing: China Communications Press, 2015.
[3] GU Y M, LI S L, LI H, et al. A novel Bayesian extreme value distribution model of vehicle loads incorporating de-correlated tail fitting: theory and application to the Nanjing 3rd Yangtze River Bridge[J]. Engineering Structures, 2014, 59: 386-392.
[4] OBRIEN E J, ENRIGHT B, GETACHEW A. Importance of the tail in truck weight modeling for bridge assessment[J]. Journal of Bridge Engineering, 2010, 15(2): 210-213.
[5] XIA M, CAI C S, PAN F, et al. Estimation of extreme structural response distributions for mean recurrence intervals based on short-term monitoring[J]. Engineering Structures, 2016, 126: 121-132.
[6] OBRIEN E J, BORDALLO-RUIZ A, ENRIGHT B. Lifetime maximum load effects on short-span bridges subject to growing traffic volumes[J]. Structural Safety, 2014, 50: 113-122.
[7] ZHOU X Y, SCHMIDT F, TOUTLEMONDE F, et al. A mixture peaks over threshold approach for predicting extreme bridge traffic load effects[J]. Probabilistic Engineering Mechanics, 2016, 43: 121-131.
[8] 周军勇, 石雪飞, 阮欣. 多事件混合影响的桥梁车辆荷载效应组合极值预测[J]. 哈尔滨工业大学学报, 2018, 50(9): 11-18.
ZHOU J Y, SHI X F, RUAN X. Composite extrema prediction of multi-event driven bridge traffic load effects[J]. Journal of Harbin Institute of Technology, 2018, 50(9): 11-18.
[9] LEAHY C, OBRIEN E, O′CONNOR A. The effect of traffic growth on characteristic bridge load effects[J]. Transportation Research Procedia, 2016, 14: 3990-3999.
[10] OBRIEN E J, SCHMIDT F, HAJIALIZADEH D, et al. A review of probabilistic methods of assessment of load effects in bridges[J]. Structural Safety, 2015, 53: 44-56.
[11] COLES S. An introduction to statistical modeling of extreme values[M]. London: Springer Press, 2001.
[12] HU P, ZHOU X, ZHOU Z Y. On the modelling of maximum field distribution within reverberation chamber using the generalized extreme value theory[C]∥2020 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO). Piscataway:IEEE, 2021: 1-4.
[13] XIA H W, NI Y Q, WONG K Y, et al. Reliability-based condition assessment of in-service bridges using mixture distribution models[J]. Computers &Structures, 2012, 106/107: 204-213.
[14] LIU M, FRANGOPOL D M, KIM S. Bridge safety evaluation based on monitored live load effects[J]. Journal of Bridge Engineering, 2009, 14(4): 257-269.
[15] VAN DE VYVER H. A multiscaling-based intensity-duration-frequency model for extreme precipitation[J]. Hydrological Processes, 2018, 32(11): 1635-1647.
[16] SHAO Y H, WU J M, LI M. Study on quantile estimates of extreme precipitation and their spatiotemporal consistency adjustment over the Huaihe River Basin[J]. Theoretical and Applied Climatology, 2017, 127(1): 495-511.
[17] LIU Y C, HUO X L, LIU Y, et al. Analyzing streamflow extremes in the upper Ürümqi River with the generalized Pareto distribution[J]. Environmental Earth Sciences, 2015, 74(6): 4885-4895.
[18] HOSSAIN I, IMTEAZ M, KHASTAGIR A. Study of various techniques for estimating the generalised extreme value distribution parameters[J]. IOP Conference Series: Materials Science and Engineering, 2021, 1067(1): 012065.
[19] 翟科玮, 杜朝伟, 郑凤玺, 等. 在役钢筋混凝土T形梁桥承载能力的模糊随机评估法[J]. 郑州大学学报(工学版), 2017, 38(4): 88-93.
ZHAI K W, DU C W, ZHENG F X, et al. Load bearing capacity of existing highway RC T beam bridge based on fuzzy stochastic comprehensive evaluation[J]. Journal of Zhengzhou University (Engineering Science), 2017, 38(4): 88-93.
[20] 梁岩, 张卓航, 班亚云, 等. 多跨连续梁-刚构桥地震易损性分析[J]. 郑州大学学报(工学版), 2023, 44(1): 96-102.
LIANG Y, ZHANG Z H, BAN Y Y, et al. Seismic fragility analysis of multi-span continuous girder-rigid frame bridges[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(1): 96-102.