磁流变阻尼器(magnetorheological damper,MRD)是一种利用磁流变效应提供可控阻尼的半主动控制器件,具有阻尼可控、功耗低、响应迅速等特点,能够对结构起到良好的减振作用[1-2]。MRD在桥梁工程中的应用较多,主要目的为实现对斜拉索的振动控制。在国内,2006年至2013年间,李金海[3]、曹宏[4]、瞿伟廉等[5]分别将MRD应用于山东滨州黄河大桥、长沙洪山大桥和岳阳洞庭湖大桥;2015年,国外学者Weber等[6]成功将MRD应用于俄罗斯岛大桥。MRD在建筑工程中的应用较少,日本将40 t MRD先后成功应用于博物馆和Keio大学建筑中[7]。
MRD对电流变化具有极高的灵敏度,电流变化的瞬间MRD阻尼力同时发生改变,因此,可通过改变供给电流的大小实时控制MRD阻尼力。近年来,学者利用MRD这一特性,将MRD应用于混凝土抗震结构以提高其抗震性能,减小地震作用下的结构响应[8-12]。相对于钢筋混凝土抗震结构,CFRP筋混凝土抗震结构可以有效减小震后残余变形,但是耗能能力相对较低[13-14]。通常采用增设耗能元件提高抗震结构的耗能能力,但是传统的耗能元件如屈曲约束支撑、软钢阻尼器及摩擦阻尼器等在受力时将产生塑性变形或永久性偏位,进而增加结构变形[15-16]。因此,在CFRP筋混凝土抗震结构中采用传统耗能元件虽然耗能能力有所提高,但是结构变形恢复性能将受到耗能元件变形的限制,无法发挥残余变形较小的优势。MRD可通过调节电流提高结构耗能且不增加残余变形,是CFRP筋混凝土抗震结构理想的耗能元件。在结构受力时增大电流提高MRD阻尼力,以提高结构的耗能能力;在结构卸载或荷载为0 kN时减小或关闭电流降低阻尼力,以降低或消除MRD对结构恢复功能的限制,实现不增大结构的残余变形。
目前,对于MRD-CFRP筋混凝土柱及剪力墙抗震性能已开展了相关的试验研究[8,10],研究表明,MRD对CFRP筋混凝土柱及剪力墙抗震性能影响较大,但是理论分析研究较少,限制了MRD在抗震结构中的应用。为开展MRD-CFRP筋混凝土柱及剪力墙抗震性能理论分析,需要首先开展MRD力学性能方面的研究。轴向往复荷载作用下MRD力学性能虽有少量试验研究成果[17],但是未考虑加载速率和电流控制方式对MRD阻尼力影响。因此,为深入研究MRD力学性能,本文将开展轴向往复荷载作用下MRD力学性能试验研究,同时考虑峰值点位移、电流大小、加载速率和电流控制方式的影响,最后提出轴向往复荷载作用下MRD阻尼力-位移曲线计算模型。
1 试验概况
1.1 MRD设计概况及工作原理
图1为MRD示意图,本文试验采用课题组制作的四线圈剪切阀式磁流变阻尼器,外部形状为圆柱体,外部缸筒高为596 mm,直径为150 mm;活塞杆直径为40 mm,行程为±40 mm。MRD内部的多级活塞有4个凹槽,每个凹槽缠绕漆包线,采用环氧树脂密封进行绝缘处理;多级活塞两端分别与活塞杆连接并穿过缸筒内部,一端活塞杆与试验装置或其附属连接件相连,另一端引出铜线与直流电源箱相连。磁流变液采用自制方法获得,其组分主要包括铁粉、硫酸钠和液体石蜡等。
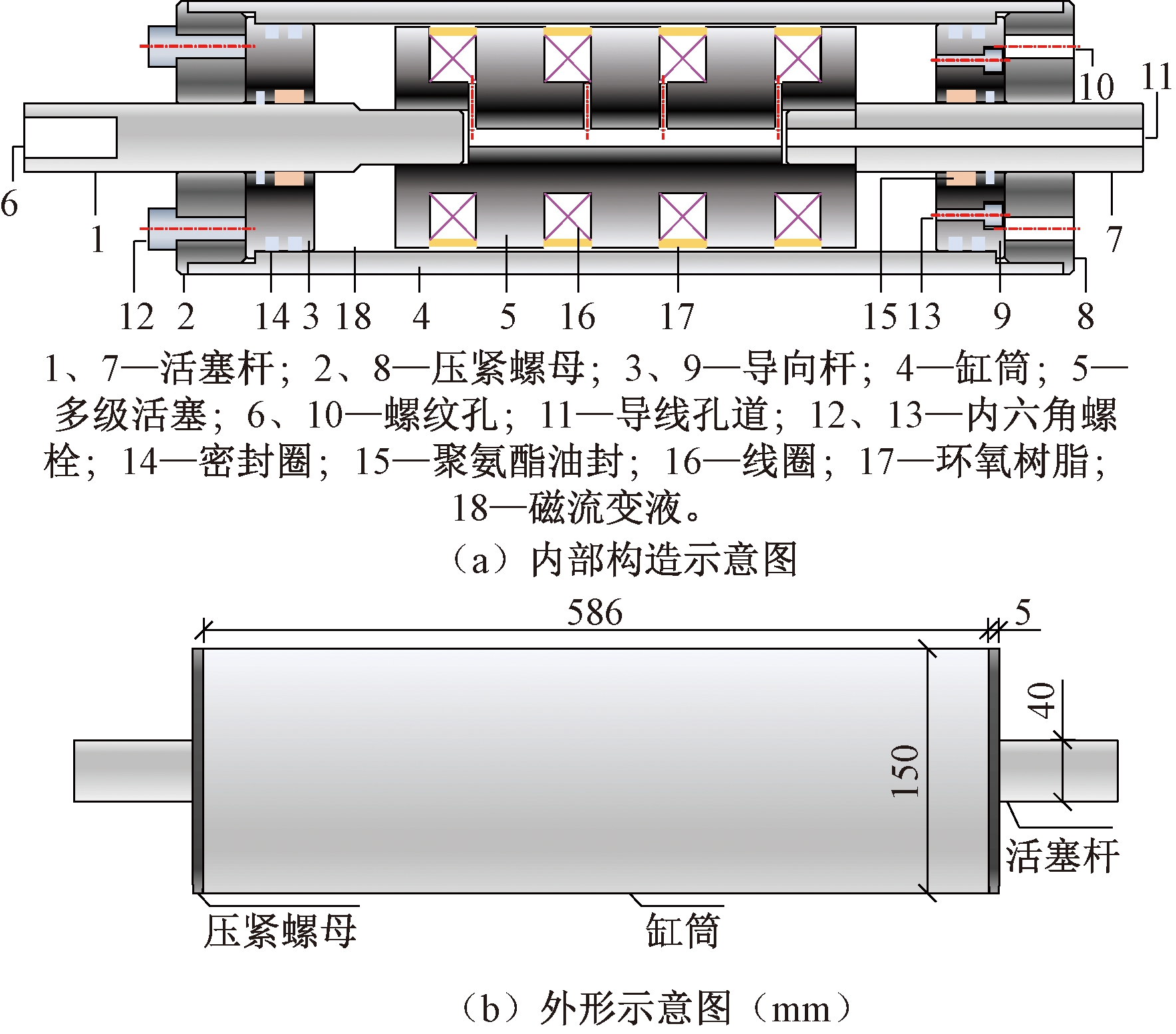
图1 MRD示意图
Figure 1 MRD schematic diagram
MRD加载过程中,活塞与缸体发生相对运动,挤压磁流变液并使其流过缸体与活塞间的间隙,调节电流可使MRD内部磁场强度改变,磁流变液黏度也随之改变[18],进而可控制阻尼力大小。
1.2 加载装置
图2为加载装置。加载设备为MTS拉力试验机,最大荷载为±200 kN,行程为±50 mm。将MRD和拉力试验机牢固连接后,MTS拉力试验机对MRD施加轴向往复荷载。
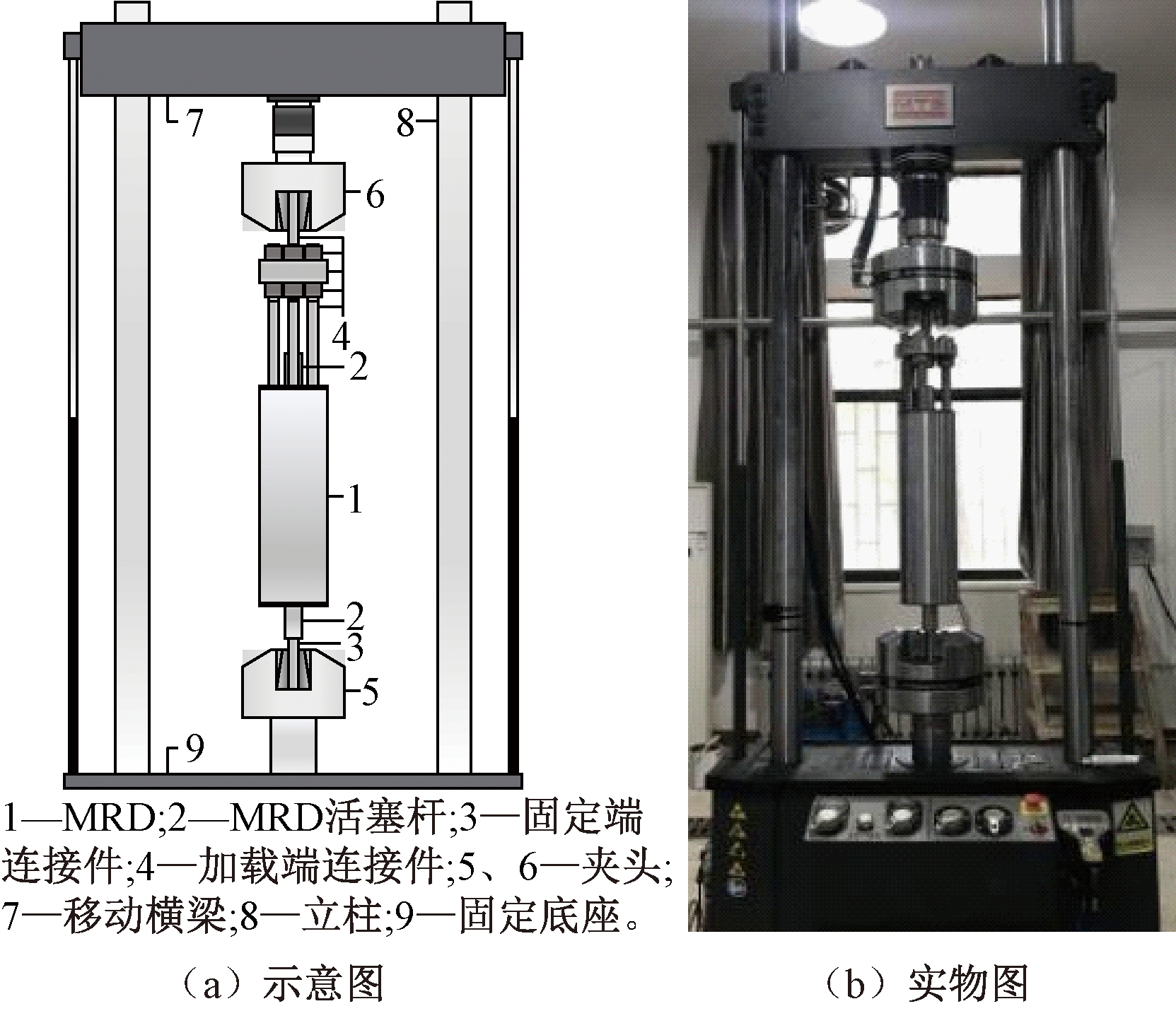
图2 MRD轴向往复荷载试验装置
Figure 2 MRD axially cyclic loading test device
1.3 加载制度
轴向往复荷载作用下MRD力学性能试验采用位移控制加载,具体加载制度如下。
(1)电流大小I和峰值点位移ΔM的影响。分别进行4组不同峰值点位移ΔM、不同电流大小I的MRD力学性能试验,各组试验加载速率v均为1.0 mm/s。4组试验峰值点位移ΔM分别为±5、±10、±20及±40 mm,每组试验均包含8个加载等级,每级进行1次往复加载,各级循环峰值点位移ΔM相同,对应的电流I分别为0、0.04、0.08、0.12、0.16、0.20、0.24、0.28 A。4组试验分别命名为I-5、I-10、I-20和I-40,加载制度如图3(a)所示。
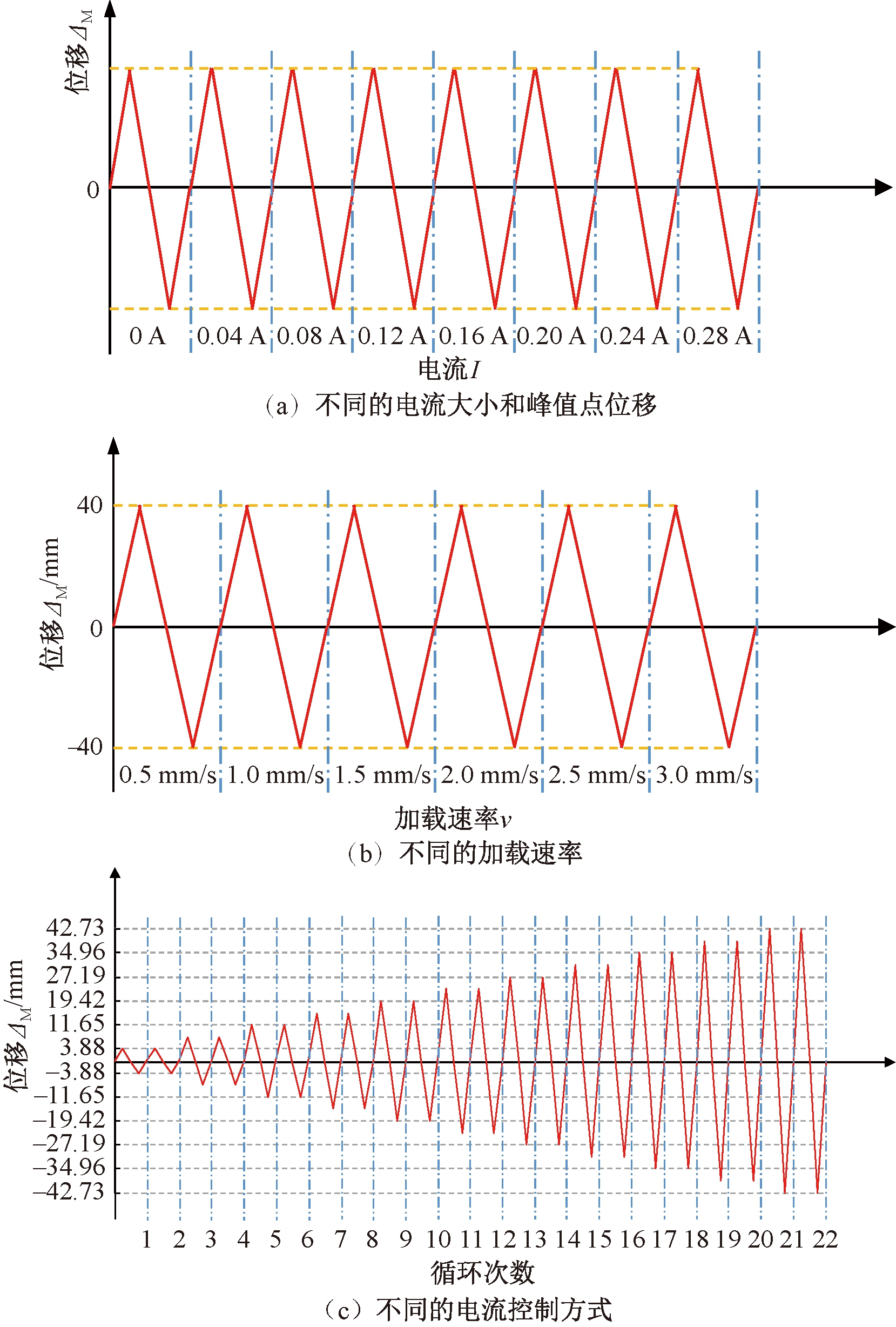
图3 加载制度
Figure 3 Loading system
(2)加载速率v的影响。进行3组不同加载速率v的MRD力学性能试验,同时考虑了电流大小I的影响。每组试验均包含6个加载等级,每级进行1次往复加载,各级峰值点位移均为± 40 mm,每级循环加载速率分别为0.5、1.0、1.5、2.0、2.5、3.0 mm/s。每组试验电流大小I保持不变,但3组试验电流大小I不同,分别为0 、0.14 和0.28 A,3组试验分别命名为V-0、V-0.14和V-0.28,加载制度如图3(b)所示。
(3)电流控制方式的影响。分别进行4组不同电流控制方式的MRD力学性能试验。结合混凝土结构拟静力试验,试验中各级循环峰值点位移以±3.88 mm为级差逐级增加。每组试验均包含11个加载等级,每级进行2次往复循环加载。4组试验分别命名为M-0、M-0.28、M-P和M-S,其中试验M-0全程关闭电流;试验M-0.28全程保持通电,电流大小为0.28 A;试验M-P在每级循环峰值点位移处断电1次,随后继续保持通电,电流大小为0.28 A;试验M-S在每次循环在峰值点向0 mm加载过程中,加载至1/3峰值点位移处断电1次,随后继续保持通电,电流大小仍为0.28 A。加载制度如图3(c)所示。
2 试验结果与分析
2.1 电流大小对MRD阻尼力的影响
图4为试验I-5、I-10、I-20和I-40的MRD阻尼力-位移曲线图。由图4可知,由于MRD制作时磁流变液未充满阻尼器,自0 kN加载时,初始位移4~5 mm荷载增长较小,斜率趋近于零,接近于水平线,该阶段为初始位移段。随后曲线进入荷载增长段,即初始位移段之后的2~3 mm加载段,该阶段荷载急剧增加,斜率急剧增大。该阶段结束后曲线进入荷载稳定段,荷载稳定段初期时荷载略微下降,随着位移的增大,阻尼力保持稳定状态。由于试件制作缺陷以及试验I-5的峰值点位移较小,试验I-5不具备明显的荷载稳定段,呈现捏拢现象。加载至峰值点后卸载,卸载段斜率趋向于无穷大,荷载急剧下降,但位移几乎不变。
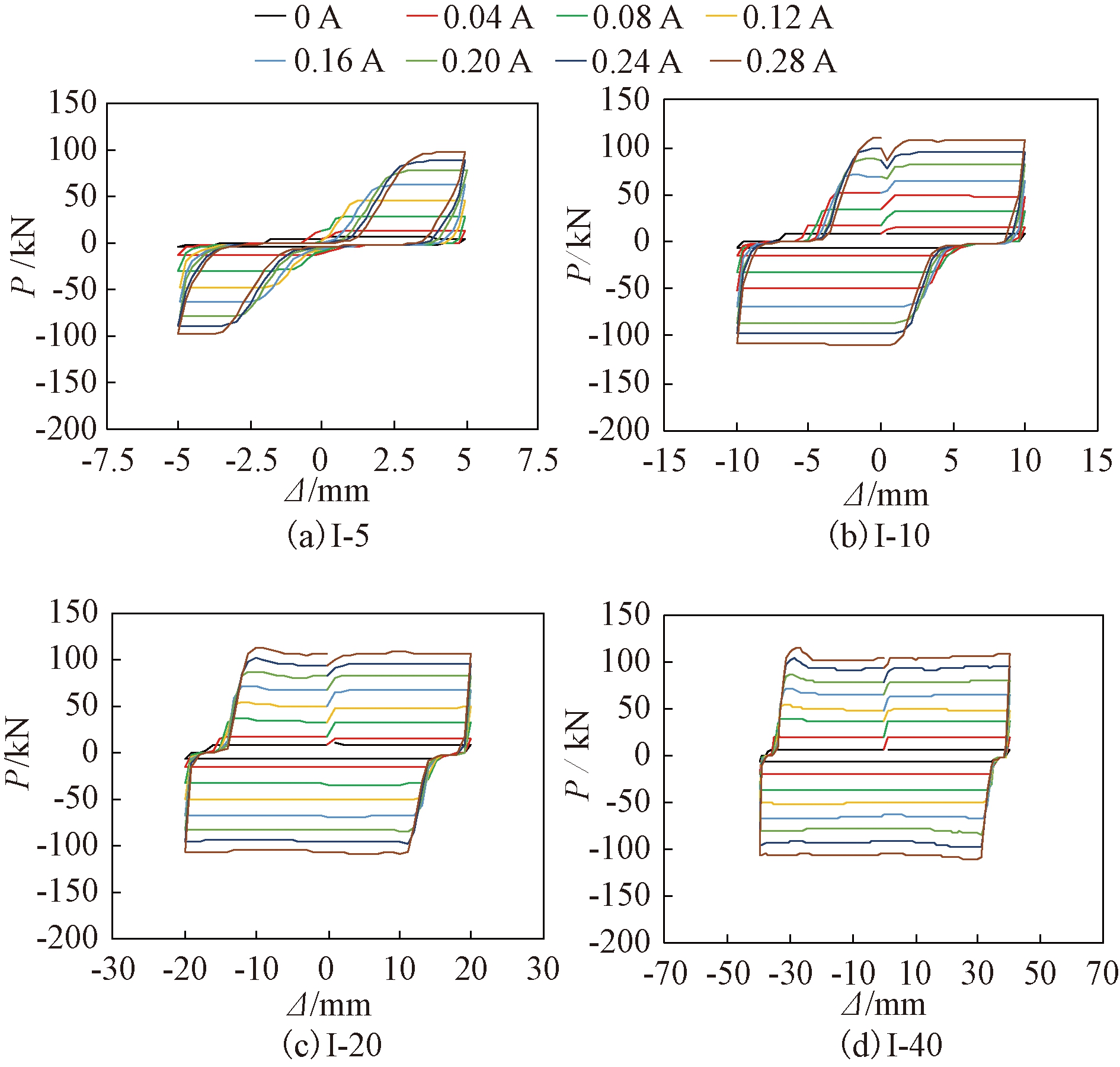
图4 不同电流大小下MRD阻尼力-位移曲线
Figure 4 MRD damping force-displacement curves with different currents
图5为试验I-5、I-10、I-20和I-40各级循环正、反向峰值点阻尼力随电流大小变化关系图。由图5可知,I为0~0.28 A时,峰值点阻尼力随电流大小的增大而提高。I为0.04 A时的峰值点阻尼力相对0 A时提高较小;I为0.04~0.20 A时,峰值点阻尼力随着I的增大显著提高;0.20 A以后,曲线斜率略微降低,说明MRD峰值点阻尼力增幅放缓。整体而言,I为0~0.28 A时,峰值点阻尼力基本随电流大小呈线性增长,电流每提高0.04 A,峰值点阻尼力可提高16 kN。
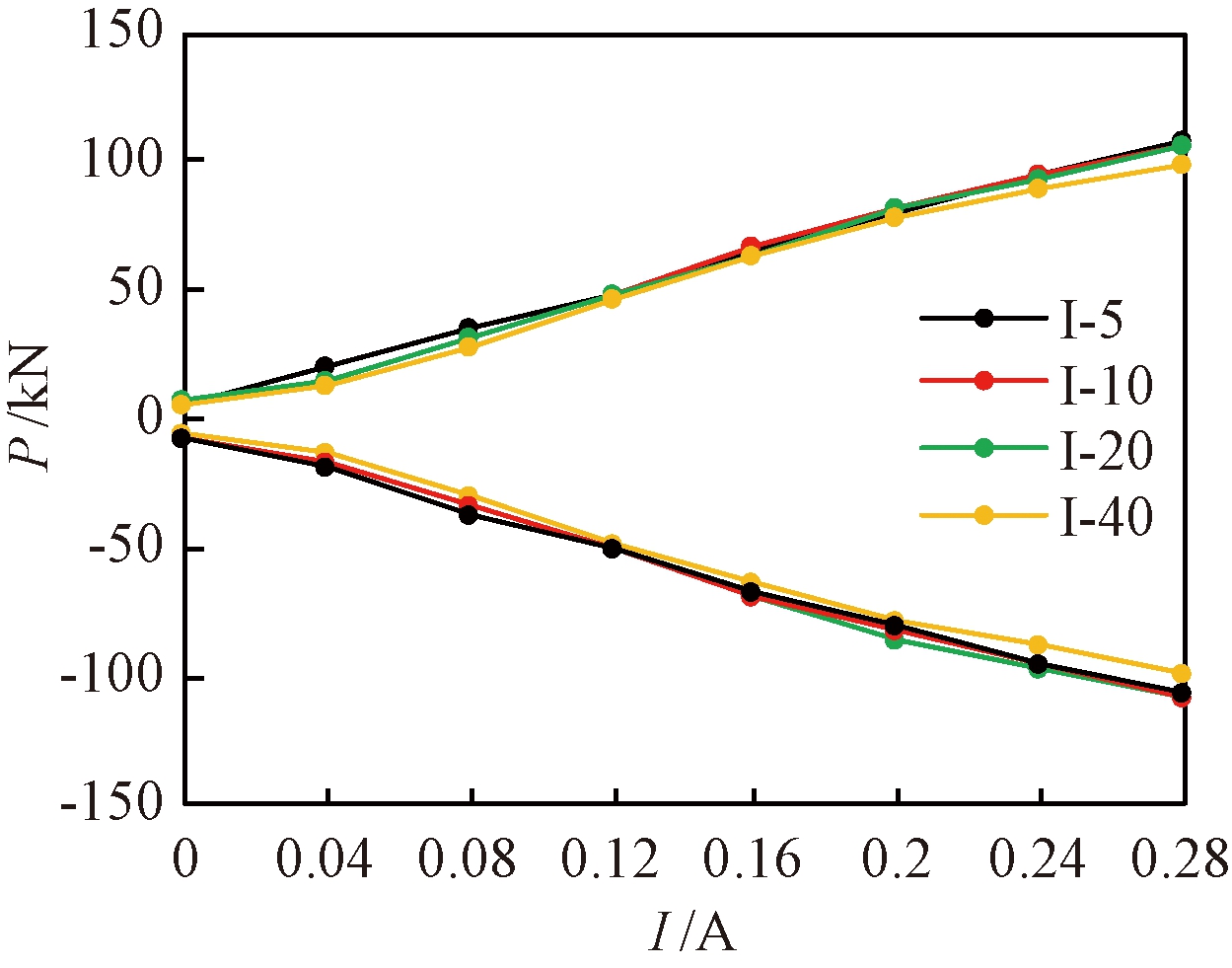
图5 峰值点阻尼力随电流大小变化关系
Figure 5 Relationship between damping force and current at peak point in each cycle
2.2 峰值点位移对MRD阻尼力的影响
根据试验I-5、I-10、I-20和I-40的试验结果,绘制了相同电流大小、不同峰值点位移下的MRD阻尼力-位移曲线图,如图6所示。图6(a)、6(b)、6(c)及6(d)电流大小分别为0、0.08、0.16、0.28 A。由图6可知,峰值点位移为40 mm且电流大小相同时,试验I-40各级循环的峰值点阻尼力高于I-5、I-10、I-20,试验I-20和I-10峰值点阻尼力基本相同,试验I-5峰值点阻尼力最低。相同的电流大小和加载速率下,峰值点位移小于10 mm时,MRD阻尼力较小,在峰值点位移大于10 mm时,MRD阻尼力基本维持稳定状态。说明峰值点位移小于初始位移时,峰值点阻尼力较小,大于初始位移时,峰值点阻尼力较为稳定。
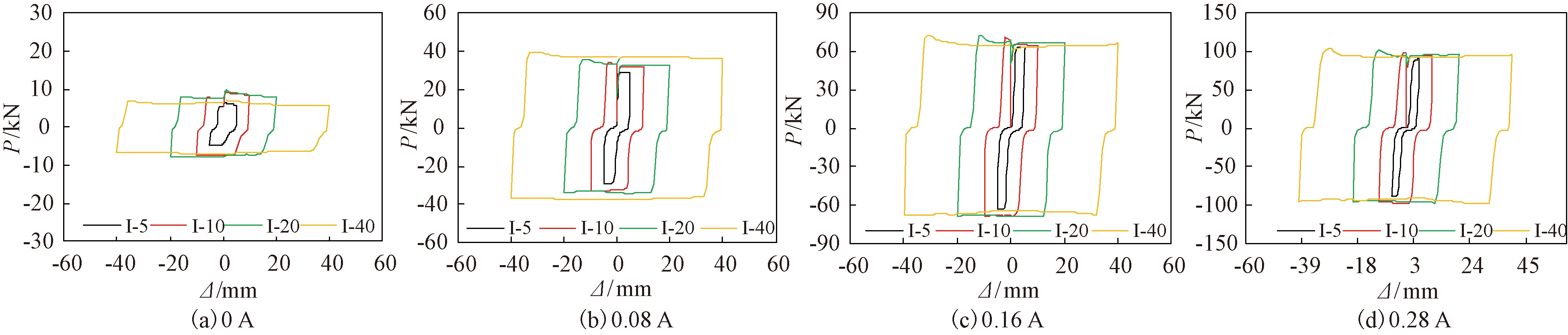
图6 不同峰值点位移下MRD阻尼力-位移曲线
Figure 6 MRD damping force-displacement curves at different peak displacements
2.3 加载速率对MRD阻尼力的影响规律
图7为试验V-0、V-0.14和V-0.28的MRD阻尼力-位移曲线图。由图7可知,MRD阻尼力随加载速率增大而增长。当I为0 A时,加载速率每提高0.5 mm/s,正向峰值点阻尼力提高1.6~1.9 kN,反向峰值点阻尼力提高1.7~2.1 kN;当I为0.14 A时,加载速率每提高0.5 mm/s,正向峰值点阻尼力提高2.0~4.2 kN,反向峰值点阻尼力提高2.6~4.4 kN;当I为0.28 A时,加载速率每提高0.5 mm/s,正向峰值点阻尼力提高1.3~7.1 kN,反向峰值点阻尼力提高3.1~8.9 kN。
2.4 电流控制方式对MRD性能的影响
图8为试验M-0、M-0.28、M-P和M-S的MRD阻尼力-位移曲线图。由图8可知,试验中关闭电流,随后再次供给电流且电流大小为0.28 A时,MRD在加载较短位移后,阻尼力仍然可以稳定在100 kN左右。图8(b)与8(c)曲线相似,但是由实测数据分析可知,M-P的卸载段由峰值点阻尼力急剧降至0 kN,而M-0.28则由峰值点阻尼力缓慢降至0 kN,M-P卸载段斜率相对于M-0.28更趋近于无穷大。由M-S可知,在加载过程中关闭电源,MRD将瞬间降至0 A时的阻尼力,继续通电,加载较短位移后阻尼力可重新达到稳定状态。
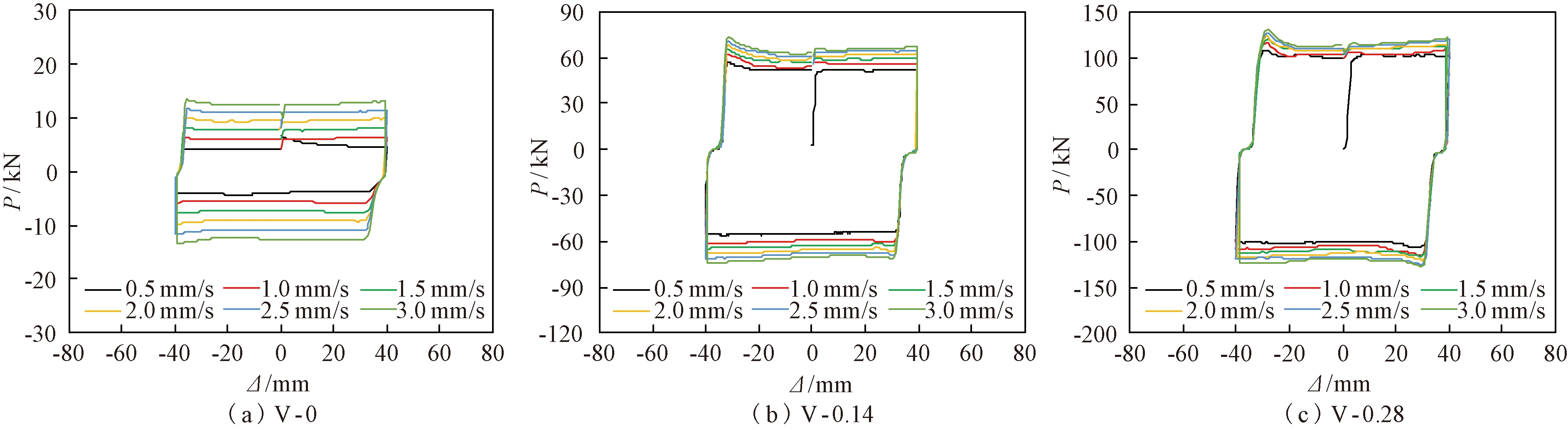
图7 不同加载速率下MRD阻尼力-位移曲线
Figure 7 MRD damping force-displacement curves with different loading rates
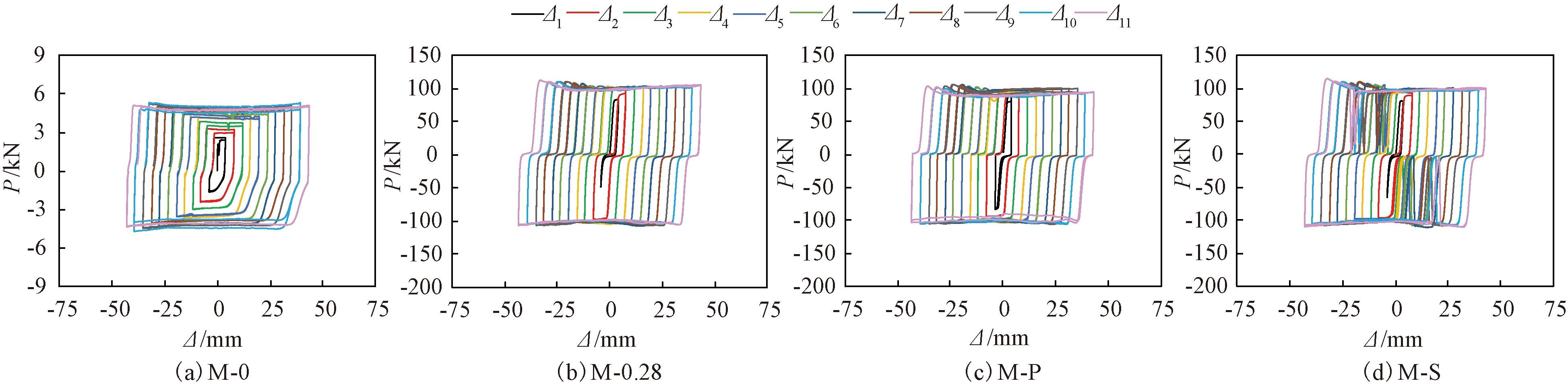
图8 不同电流控制方式下MRD阻尼力-位移曲线
Figure 8 MRD damping force-displacement curves under different current control modes
3 MRD阻尼力-位移曲线计算模型
3.1 模型简化
MRD阻尼力-位移试验曲线滞回环呈中心对称,正、反向曲线特征相似。图9为阻尼力-位移曲线滞回环简化模型,假设正、反向曲线完全中心对称。以图9正向加载曲线(A-B-C-D-(E)-A′)为例,曲线可分为4个阶段,即初始位移段(AB段)、荷载增长段(BC段)、荷载稳定段(CD段)、卸载段(D(E)A′段)。各阶段基本特征如下:初始位移段和荷载稳定段内阻尼力随着位移的增大变化较小;卸载段内位移变化较小;荷载增长段内阻尼力基本随位移呈线性增长。因此,可将AB段和CD段简化为水平段,D(E)A′段简化为斜率无穷大的竖直段,BC段简化为斜率为K的直线段。另外,对于D(E)A′段,若关闭电流,则曲线由卸载点首先降低至点E处,随后卸载至点A′;若保持电流不变,则曲线由卸载点直接降低至点A′处。
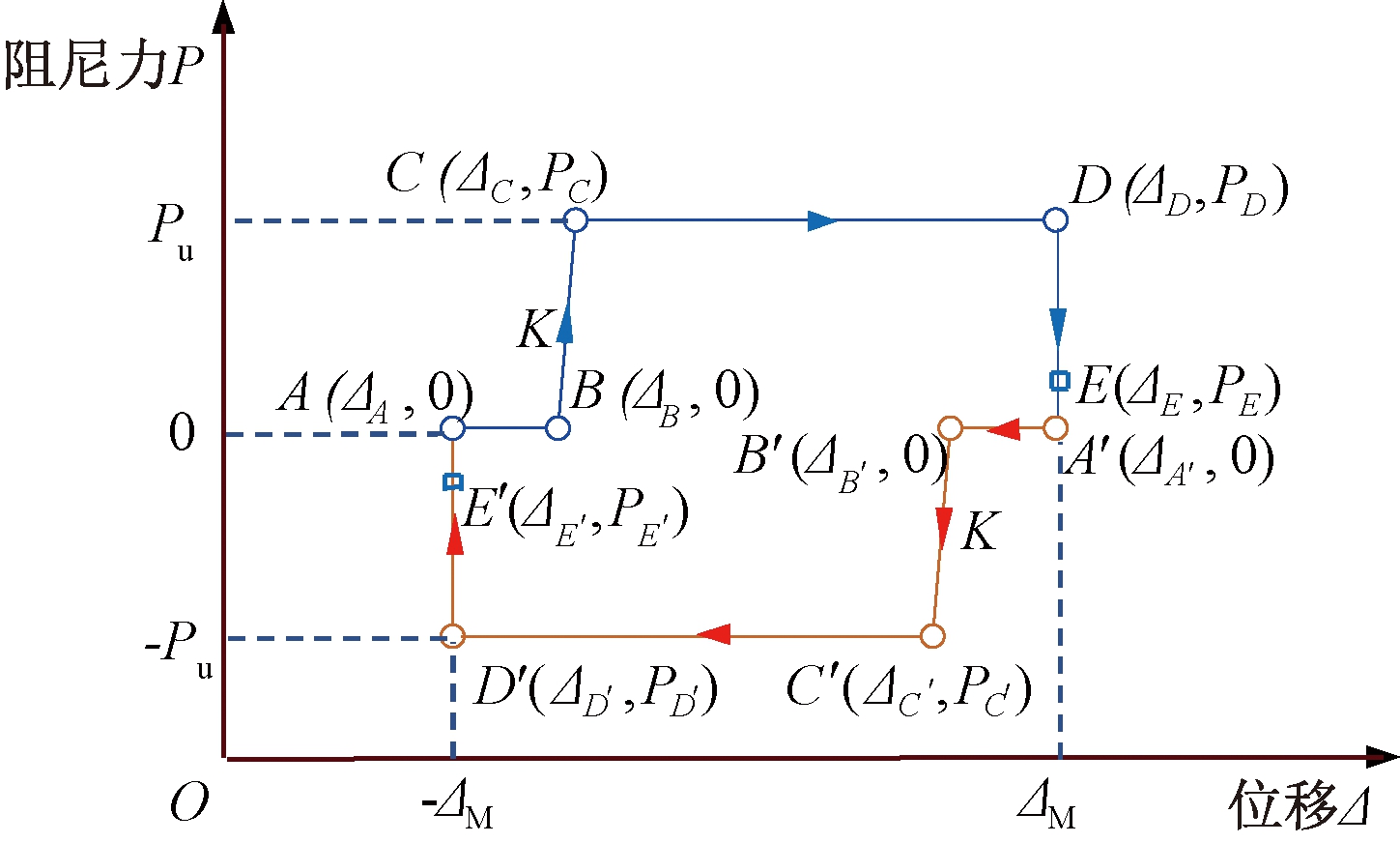
图9 滞回环简化模型
Figure 9 Simplified hysteretic model
3.2 MRD峰值点阻尼力计算式
通过对各组试验每级循环正、反向峰值点阻尼力试验值的回归分析,得到峰值点阻尼力Pu与电流I和加载速率v的计算式:
Pu=364.78I+6.33v+0.024。
(1)
图10为峰值点阻尼力计算值与试验值对比图,Pu,c为计算值,Pu,t为试验值。由图10可知,计算值与试验值吻合较好,误差为1%~8%。
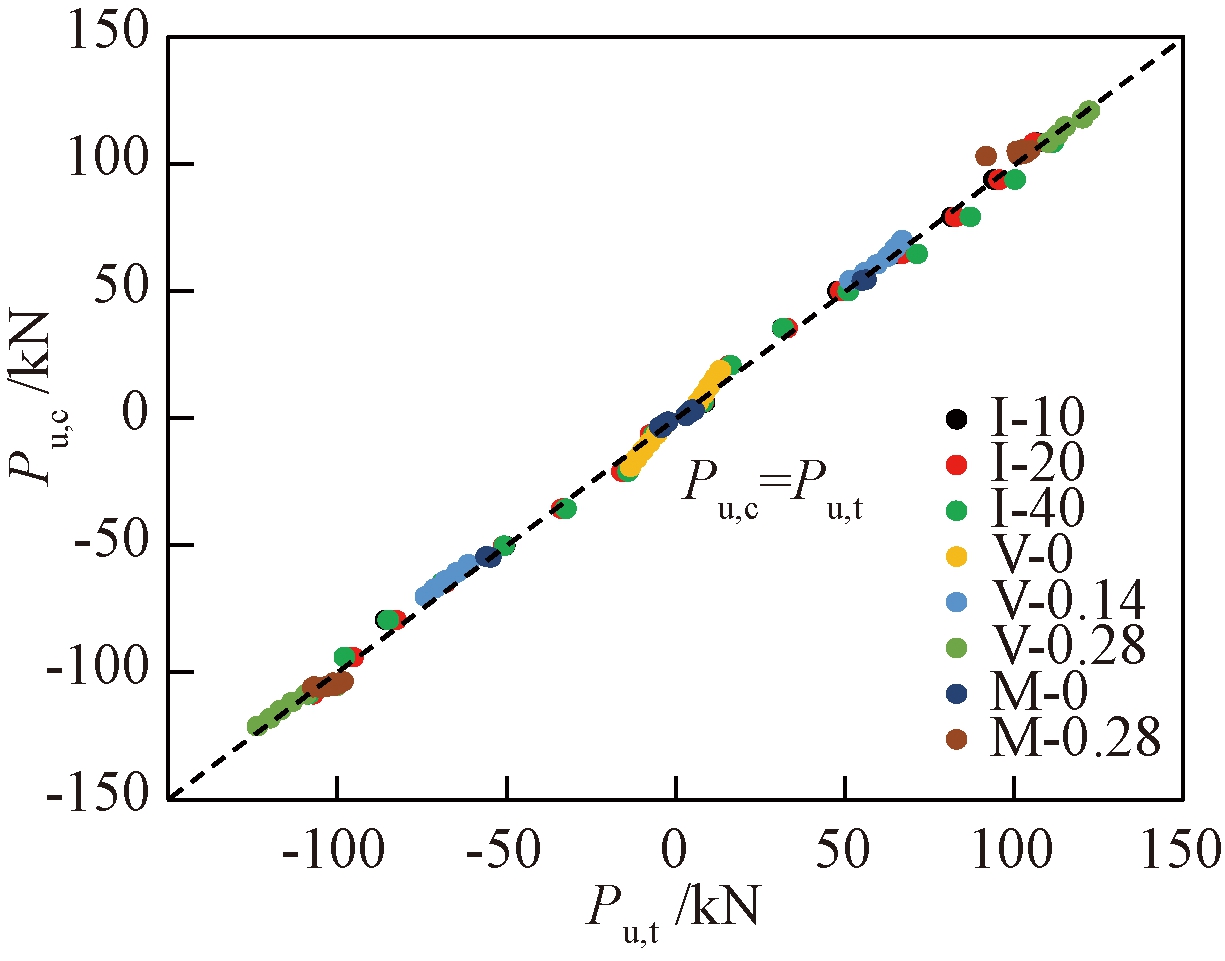
图10 峰值点阻尼力计算值和试验值对比
Figure 10 Comparison between calculated and test values of damping force at peak point
3.3 特征点和特征曲线计算式
(1)荷载增长段。图11分别为各组试验每级循环荷载增长段B、C点处位移ΔB、ΔC与峰值点位移ΔM分布关系图。由图11可知,ΔB、ΔC基本随ΔM线性增长。通过线性拟合,分别得到ΔB和ΔC计算式:
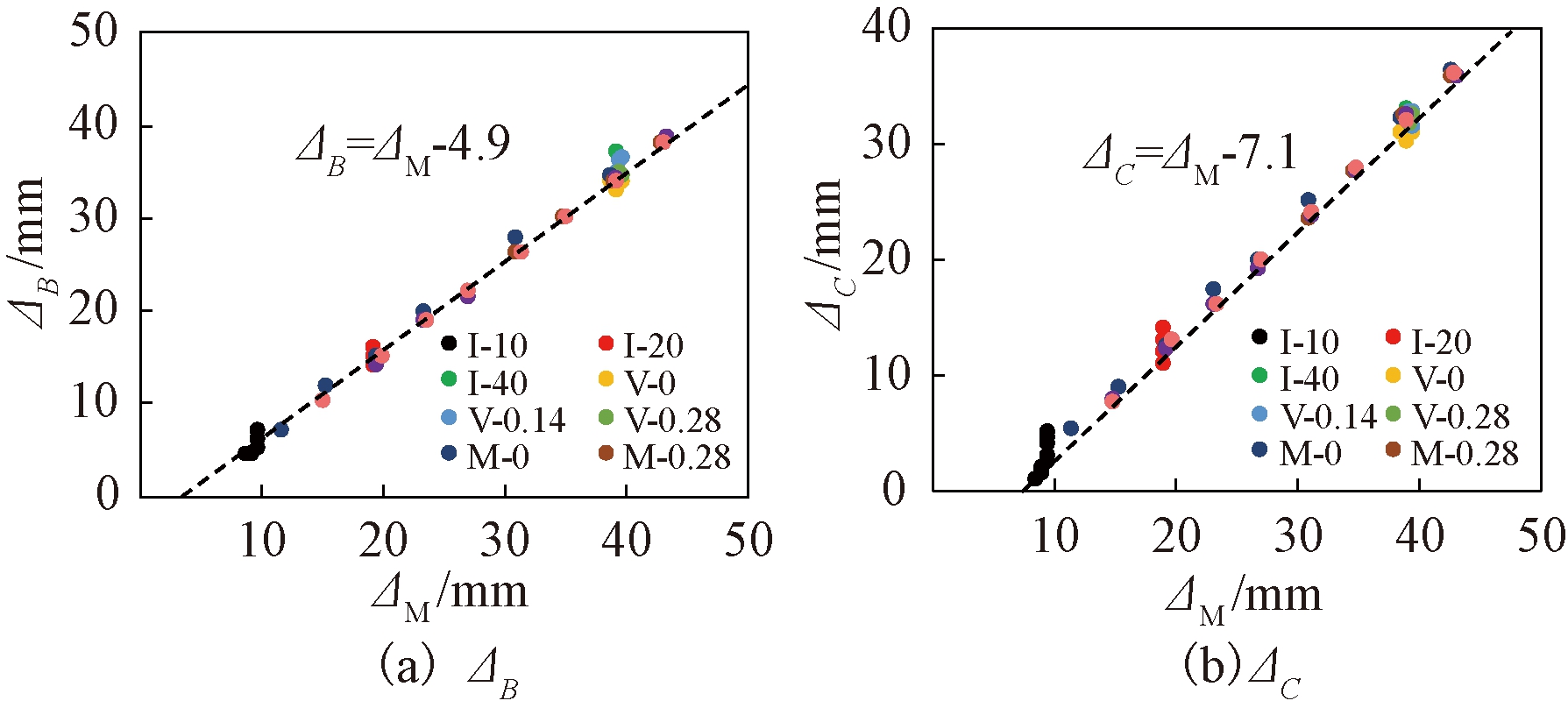
图11 ΔB、ΔC与ΔM分布关系
Figure 11 Relationship between ΔB, ΔC and ΔM
ΔB=ΔM-4.9;
(2)
ΔC=ΔM-7.1。
(3)
根据直线方程,由式(1)、(2)和(3)可得到荷载增长段斜率K计算式,即
K=165.80I+2.88v+0.01。
(4)
(2)关闭电流时阻尼力及再加载段。图12分别为相同加载等级下试验M-P和M-S关闭电流时MRD阻尼力与试验M-0峰值点阻尼力关系图,Pp和Ps分别为M-P和M-S关闭电流时阻尼力,Pu,0为M-0各级循环峰值点阻尼力。由图12可知,Pp和Ps与Pu,0相差较小,说明试验过程中如关闭电流,阻尼力将瞬间降低至0 A时的阻尼力,因此,断电处阻尼力,即图9中E点处阻尼力可近似为0 A时阻尼力,结合式(1),可得到关闭电流时阻尼力计算式:
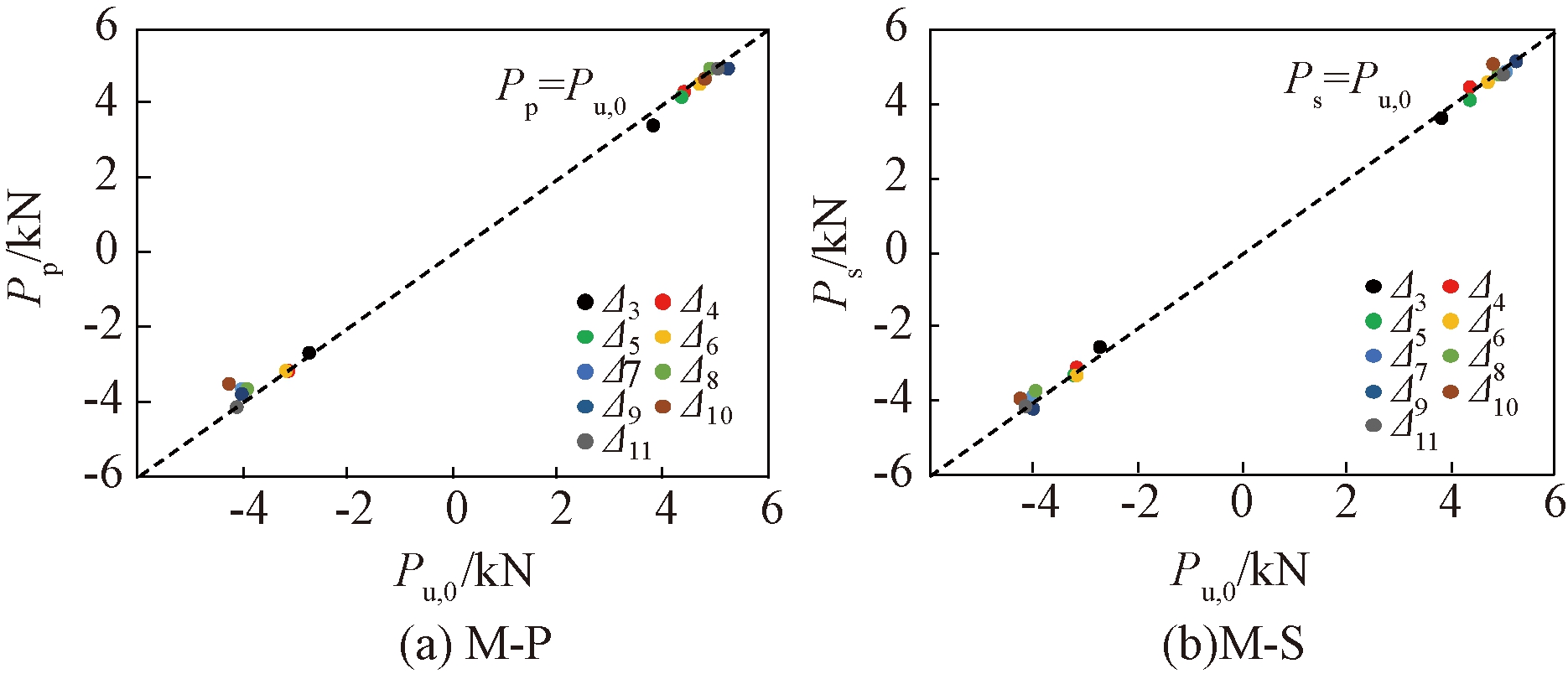
图12 关闭电流时阻尼力Pp、Ps与Pu,0关系
Figure 12 Relationship between Pp, Ps and Pu,0
PE=6.33v+0.024。
(5)
图13为试验M-S同级循环断电后再加载段斜率Ks与荷载增长段斜率K关系图。由图13可知,MRD关闭电流后,再供给相同大小的电流,Ks与K较为接近,因此,可近似认为Ks与K相等,可采用式(4)进行Ks的计算。
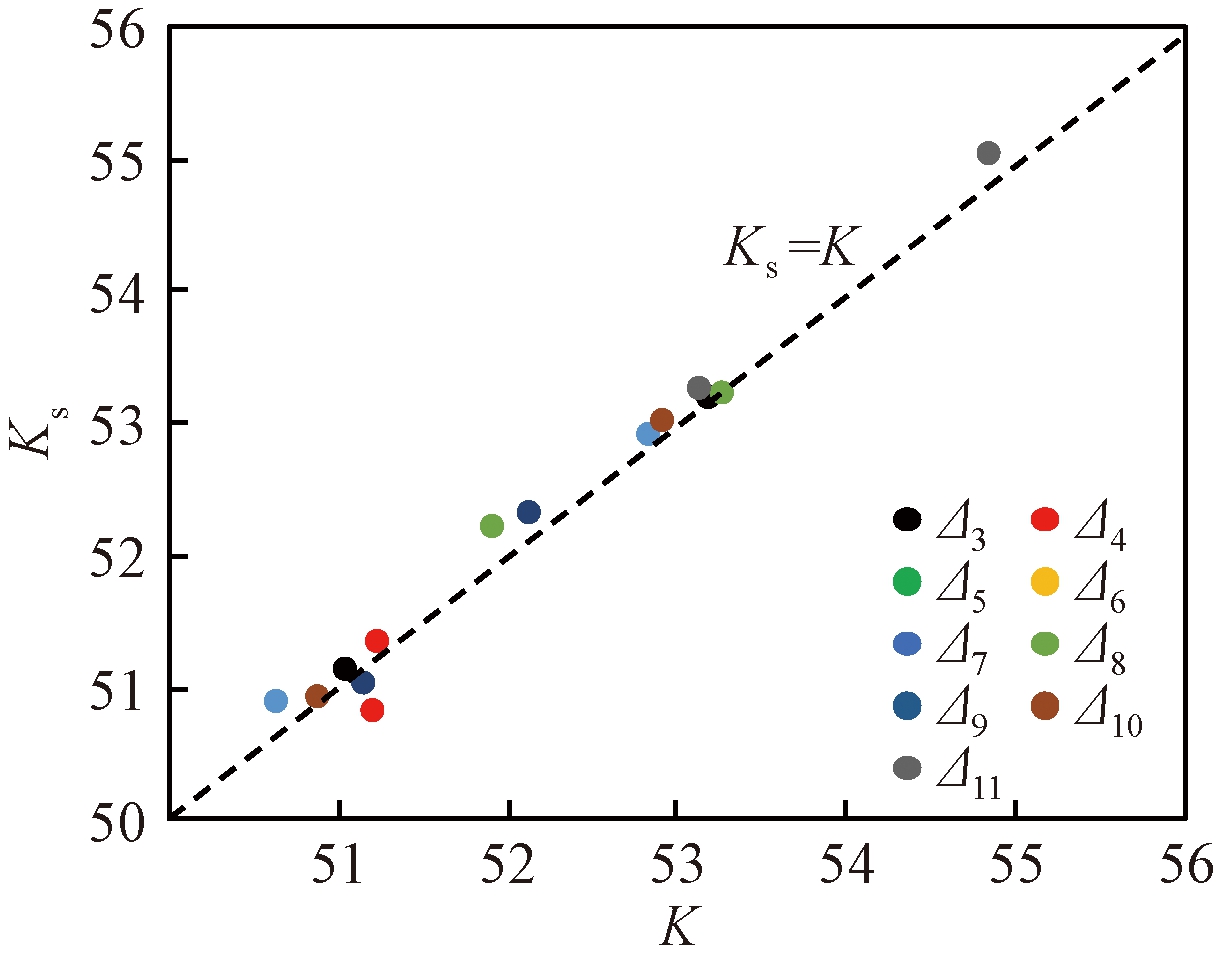
图13 断电再加载段斜率Ks与荷载增长段斜率K关系
Figure 13 Relationship between Ks of re-loading phase after closing current and slope K of load increasing phase
4 模型验证
图14为试验I-40、V-0.28、M-P和M-S计算曲线和试验曲线对比图,虚线代表计算曲线,实线代表试验曲线。由图14可知,计算曲线与试验曲线具有较高的吻合度。图15为各级循环耗能计算值Ec与试验值Et对比图,其中试验M-S和M-P各级耗能试验值取2次循环的平均值。由图15可知,Ec与Et的比值为0.93~1.15,误差较小。
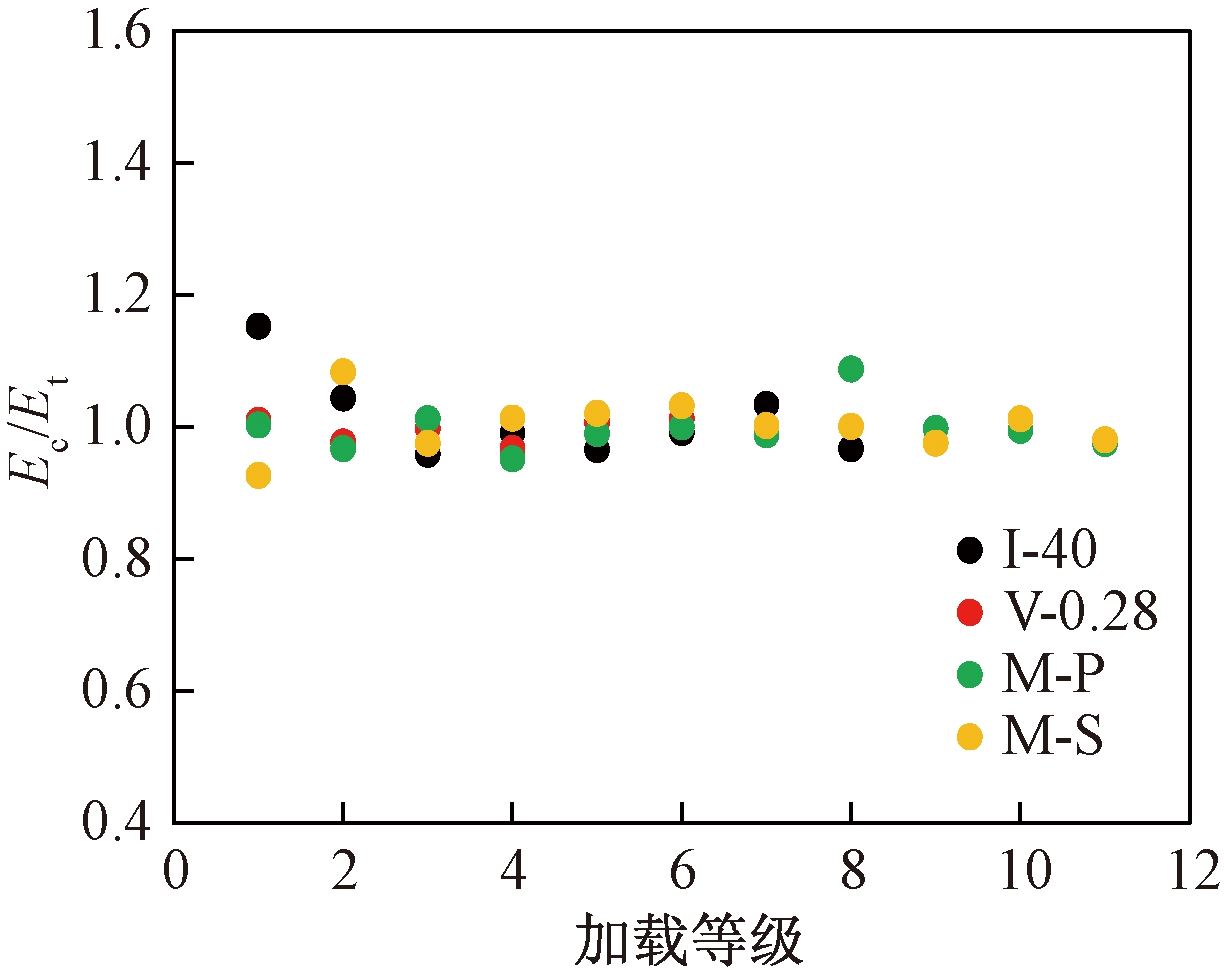
图15 耗能计算值Ec与试验值Et对比
Figure 15 Comparison between calculated value Ec and test value Et of energy dissipation
综上所述,本文提出的计算模型在计算轴向往复荷载作用下MRD阻尼力-位移曲线时具有较高的精确度,且能够很好地描述不同电流大小、位移幅值、加载速率和电流控制方式对MRD力学性能的影响。
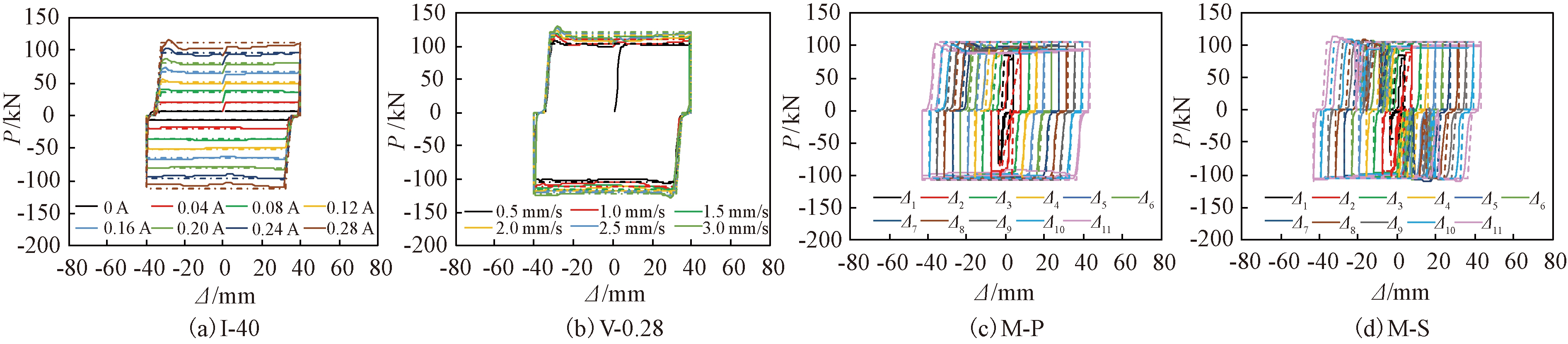
图14 计算曲线与试验曲线对比
Figure 14 Comparison between calculated and test curve
5 结论
本文进行了轴向往复荷载作用下MRD力学性能试验,分析了电流大小、峰值点位移、加载速率和电流控制方式对MRD阻尼力的影响规律。
(1)相同峰值点位移和加载速率下,当电流大小为0.04~0.20 A时,MRD峰值点阻尼力随电流大小基本呈线性增长;当电流大小为0.20~0.28 A时,MRD峰值点阻尼力增长幅度逐渐减小。
(2)相同的电流大小和加载速率下,当峰值点位移小于初始位移时,峰值点阻尼力较小,大于初始位移时,峰值点阻尼力较为稳定。
(3)相同的电流大小和峰值点位移下,MRD峰值点阻尼力随着加载速率的增大而增大。
(4)在加载过程中关闭电流,MRD阻尼力瞬间降至0 A时的阻尼力,若继续供给电流,MRD阻尼力在较短的加载位移内仍能达到该电流大小下的阻尼力状态,且再加载段与荷载增长段斜率近似相等。
(5)本文提出的计算模型在计算轴向往复荷载作用下MRD阻尼力-位移曲线时具有较高的精确度,能够很好地描述不同电流大小、峰值点位移、加载速率和电流控制方式下MRD阻尼力-位移曲线变化规律。
[1] BAHAR A, POZO F, ACHO L, et al. Parameter identification of large-scale magnetorheological dampers in a benchmark building[J]. Computers &Structures, 2010, 88(3/4): 198-206.
[2] 杨岗, 李芾, 赖森华, 等. 基于磁流变阻尼器的高速受电弓模糊半主动控制[J]. 科学技术与工程, 2020, 20(11): 4534-4539.
YANG G, LI F, LAI S H, et al. Semi-active control of fuzzy for high-speed pantograph using MRD[J]. Science Technology and Engineering, 2020, 20(11): 4534-4539.
[3] 李金海. 磁流变液及其智能阻尼器的研究与应用[D]. 哈尔滨: 哈尔滨工业大学, 2006.
LI J H. Research and application of magnetorheological fluid and its intelligent damper[D]. Harbin: Harbin Institute of Technology, 2006.
[4] 曹宏. 磁流变阻尼器在拉索减振中的应用研究[D]. 长沙: 湖南大学, 2006.
CAO H. The research on the application of MR damper in cable vibration mitigation[D]. Changsha: Hunan University, 2006.
[5] 瞿伟廉, 秦顺全, 涂建维, 等. 武汉天兴洲公铁两用斜拉桥主梁和桥塔纵向列车制动响应智能控制的理论与关键技术[J]. 土木工程学报, 2010, 43(8): 63-72.
QU W L, QIN S Q, TU J W, et al. Theory and crucial technologies of intelligent control for responses in deck and towers of Wuhan Tianxingzhou cable-stayed bridge subjected to train braking[J]. China Civil Engineering Journal, 2010, 43(8): 63-72.
[6] WEBER F, DISTL H. Amplitude and frequency independent cable damping of Sutong Bridge and Russky Bridge by magnetorheological dampers[J]. Structural Control and Health Monitoring, 2015, 22(2): 237-254.
[7] FUJITANI H, SODEYAMA H, TOMURA T, et al. Development of 400 kN magnetorheological damper for a real base-isolated building[J].Proceedings of SPIE,2003, 5052: 265-276.
[8] 赵军, 王培培, 冯益博, 等. 配置MRD的CFRP筋混凝土柱抗震性能试验[J]. 建筑科学与工程学报, 2020, 37(4): 23-31.
ZHAO J, WANG P P, FENG Y B, et al. Experiment on seismic performance of CFRP reinforced concrete column with MRD[J]. Journal of Architecture and Civil Engineering, 2020, 37(4): 23-31.
[9] FU W Q, ZHANG C W, LI M, et al. Experimental investigation on semi-active control of base isolation system using magnetorheological dampers for concrete frame structure[J]. Applied Sciences, 2019, 9(18): 3866.
[10] 张香成, 陈娜, 罗芳, 等. 铅-磁流变阻尼器在减震结构中的位置优化[J]. 郑州大学学报(工学版), 2018, 39(2): 44-49.
ZHANG X C, CHEN N, LUO F, et al. Position optimization of lead magnetroheological damper in energy dissipation structural[J]. Journal of Zhengzhou University (Engineering Science), 2018, 39(2): 44-49.
[11] LI J, MEI Z, CHEN J B, et al. Experimental investigations of stochastic control of randomly base-excited structures[J]. Advances in Structural Engineering, 2012, 15(11): 1963-1975.
[12] 王蒂, 黄平明. 超大跨度斜拉桥纵向减震耗能塔、梁连接装置研究[J]. 郑州大学学报(工学版), 2008, 29(4): 112-115, 144.
WANG D, HUANG P M. Research on deck-tower connection of super long-span cable-stayed bridge[J]. Journal of Zhengzhou University (Engineering Science), 2008, 29(4): 112-115, 144.
[13] 王作虎, 罗义康, 刘杜, 等. CFRP筋-高强钢筋/高强混凝土柱的抗震性能[J]. 复合材料学报, 2021, 38(10): 3463-3473.
WANG Z H, LUO Y K, LIU D, et al. Seismic behavior of high-strength concrete columns reinforced with CFRP tendons and high-strength steels[J]. Acta Materiae Compositae Sinica, 2021, 38(10): 3463-3473.
[14] ZHAO J, REN W B, RUAN X H, et al. Experimental study on the seismic performance of columns reinforced by the CFRP bar and sheet[J]. Applied Composite Materials, 2021, 28(4): 1291-1313.
[15] 王静峰, 王新乐, 李贝贝, 等. 屈曲约束支撑装配式混凝土框架结构抗震性能试验研究[J]. 土木工程学报, 2018, 51(12): 72-80.
WANG J F, WANG X L, LI B B, et al. Experimental studies on seismic performance of prefabricated concrete frame structures with buckling-restrained braces[J]. China Civil Engineering Journal, 2018, 51(12): 72-80.
[16] 马立威, 张海宾, 王燕. 转动型摩擦阻尼器试验研究与理论分析[J]. 防灾减灾工程学报, 2021, 41(5): 1001-1011.
MA L W, ZHANG H B, WANG Y. Experimental research and theoretical analysis of rotational friction damper[J]. Journal of Disaster Prevention and Mitigation Engineering, 2021, 41(5): 1001-1011.
[17] ZHANG X C, WU G B, ZHAO J. Quasi-static mechanical properties and mechanical model of MRD[J]. Journal of Civil and Environmental Engineering, 2020, 42(3): 46-53.
[18] 祝世兴, 杨丽昆, 魏戬, 等. 基于改进Bingham模型的磁流变阻尼器力学建模及试验研究[J]. 重庆理工大学学报(自然科学), 2021, 35(4): 254-264.
ZHU S X, YANG L K, WEI J, et al. Modeling and experimental study of magnetorheological damper based on improved Bingham model[J]. Journal of Chongqing University of Technology (Natural Science), 2021, 35(4): 254-264.