生物电信号是由复杂生命体发出的不稳定的自然信号[1],属于强噪声背景下的低频微弱信号。对于大多数的生物电信号如心电、脑电、眼电等,主要频带在50 Hz以内。生物电信号在采集、放大、模数转换中常会受到各类信号干扰,其中基线漂移与工频干扰的分量尤为明显。工频干扰的模型由50 Hz的正弦信号及其谐波组成[2],幅值一般同生物电信号幅值相当或更强。为避免有用信号淹没在噪声中,精准去除工频干扰和保留更多有用信号是预处理中十分重要的一步。
研究学者提出了各种抑制工频干扰的方法,主要包括固定频率滤波[3]和自适应滤波[4]两类。当工频频率由于不同发电机和变压输电等发生偏移时,虽然增大固定频率滤波器的带宽也能滤除这部分干扰信号,但容易丢失原本就微弱的有用信息,因此自适应滤波器在生物电信号的预处理中很有必要。自适应滤波能根据输入、输出及原参量信号按照一定准则修改滤波参数,使得滤波器能够适应不同信号,常见的自适应滤波主要有最小均方误差滤波(least mean square, LMS)[5]、递推最小二乘滤波(recursive least square, RLS)[6]以及演变算法等[7],此类自适应方法信号跟随性好,但运算需要反复迭代,容易发生误差反复传播的现象,致使滤波器稳定性不高、收敛速度较慢。根据信号频域离群点检测捕捉实际工频,可直接修正陷波器的中心频率,各类参数无需多次循环递归,能够避免由于迭代产生的误差反复传播带来的稳定性问题,具有简单易行、运行效率高、精准性高等优势。
无论是固定频率滤波还是自适应滤波,都是在全频域下进行处理,容易对邻近频带的有用信号造成影响[8]。经验模态分解(empirical mode decomposition,EMD)可以根据信号特点自适应获取基函数和分解层次,对分解后的各局部分量进行单独处理,保证非滤波频段内信号不受影响,从而保留更多有效信号。Rilling等[9]基于经验模态分解的滤波特性提出了构造滤波器组的方法,最大限度保留信号的非线性和非平稳性;邹清等[10]利用EMD获取心电信号局部特征,对指定固有模态函数进行硬阈值滤波处理,有效去除了工频噪音等干扰。但是,单独使用EMD滤波时无法调整滤波参数,因此需要与自适应的算法相结合,才能保证不同情况下滤波的优异性。
本文提出了一种新型工频自适应抑制方法,使用基于频率密度的局部离群因子(local outlier factor based on frequency density,FLOF)算法与经验模态分解对信号进行去噪。该方法首次将局部离群因子算法拓展到频域,克服了常规自适应滤波器稳定性差等问题,并与经验模态分解进行结合,保留更多有用信号。首先,根据FLOF得出信号各时刻实际工频及工频偏移时刻,并根据偏移时刻对信号进行分段,结合不同信号段内实际工频调整陷波器的中心频率,实现自适应滤波的效果;其次,利用EMD对每段信号进行分解,根据EMD分解特点找到工频所属的局部特征分量,用分量滤波替代全信号滤波,仅对含噪特征分量进行处理能够保留更多有用信息。
1 联合FLOF与EMD的工频干扰抑制方法
1.1 基于频率密度的局部离群算法
局部离群因子(local outlier factor,LOF)算法属于异常点检测算法中的一种,该算法中每个对象的离群度用局部离群因子来表示,使用局部离群因子刻画对象成为离群点的可能性,对应的局部离群因子值越高,其作为离群点的可能性越大[11]。衡量一个数据点的异常程度,并不取决于完全数据点的绝对局部密度,而是取决于数据点与周围邻近的数据点的相对密度[12],该算法兼顾局部离群点和全局离群点,避免因数据分布不均匀、密度不同而发生误判。
局部可达密度lrdk(o)表示数据点在全局范围内的异常程度。定义对象o的局部可达密度为k距离邻域内所有数据对象平均可达距离的倒数,局部可达密度lrdk(o)可表示为
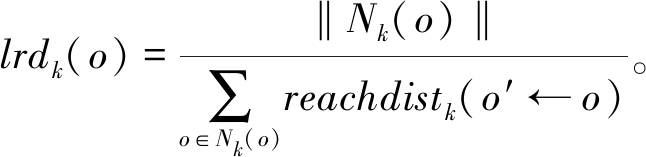
(1)
式中:Nk(o)表示对象o的 k距离邻域;o′∈Nk(o);reachdistk(o←o′)表示从对象o到对象o′的可达距离。
局部离群点因子LOFk(o)为该点在k近邻范围内的异常程度。对象o的局部离群点因子LOFk(o)的数学表达式为
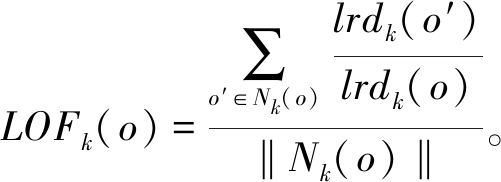
(2)
当工频发生偏移时,信号的频谱、均值、方差等统计特征发生变化,由一种分布状态变成另一种分布状态[13]。因此,可将局部离群因子算法运用于频域领域,关联频率和幅值,结合频谱分布和局部离群点因子算法捕捉实际工频,调整滤波器参数,实现自适应滤波。
首先对信号进行短时傅里叶变换,频谱矩阵表示为

(3)
式中:t为时间刻度的输出变量;f为频率刻度的输出变量;dt,f表示短时傅里叶变换后t时间变量和f频率变量下的幅值。
定义LOFk(o,O)为对象o在数据集O内的局部离群点因子,序列LDt为t时刻下序列Dt的局部离群因子:
LDt(f)=LOFk(dt,f,Dt)。
(4)
当LDt(f)达到最大时,对应的f为实际工频傅里叶变换后的频率变量,即可知t时刻实际工频的数值大小。
当信号频谱分布在低频部分幅度与噪音幅度差异明显时,在频域上运用LOF算法效果良好,但当低频部分幅度与噪音幅度大体相当,运用LOF算法时会产生虚假的离群点,错误识别工频偏移。采用滑动窗口模型,检测每个频率点一定邻域内的局部离群点因子大小,可避免虚假离群点的产生。滑动窗口指用一组固定长度的窗口从长序列的起点滑动到终点,对窗口内的数据分别进行处理并依次记录。设定一个宽度固定为Lwin的滑动窗口,综合算法精度及效率设置窗口对应频率为10 Hz,该窗口沿着t时刻下的频率序列向右滑动,步长为1,滑动到数据的频率序列末端。t时刻下的频谱图、窗口大小和移动方向如图1所示。
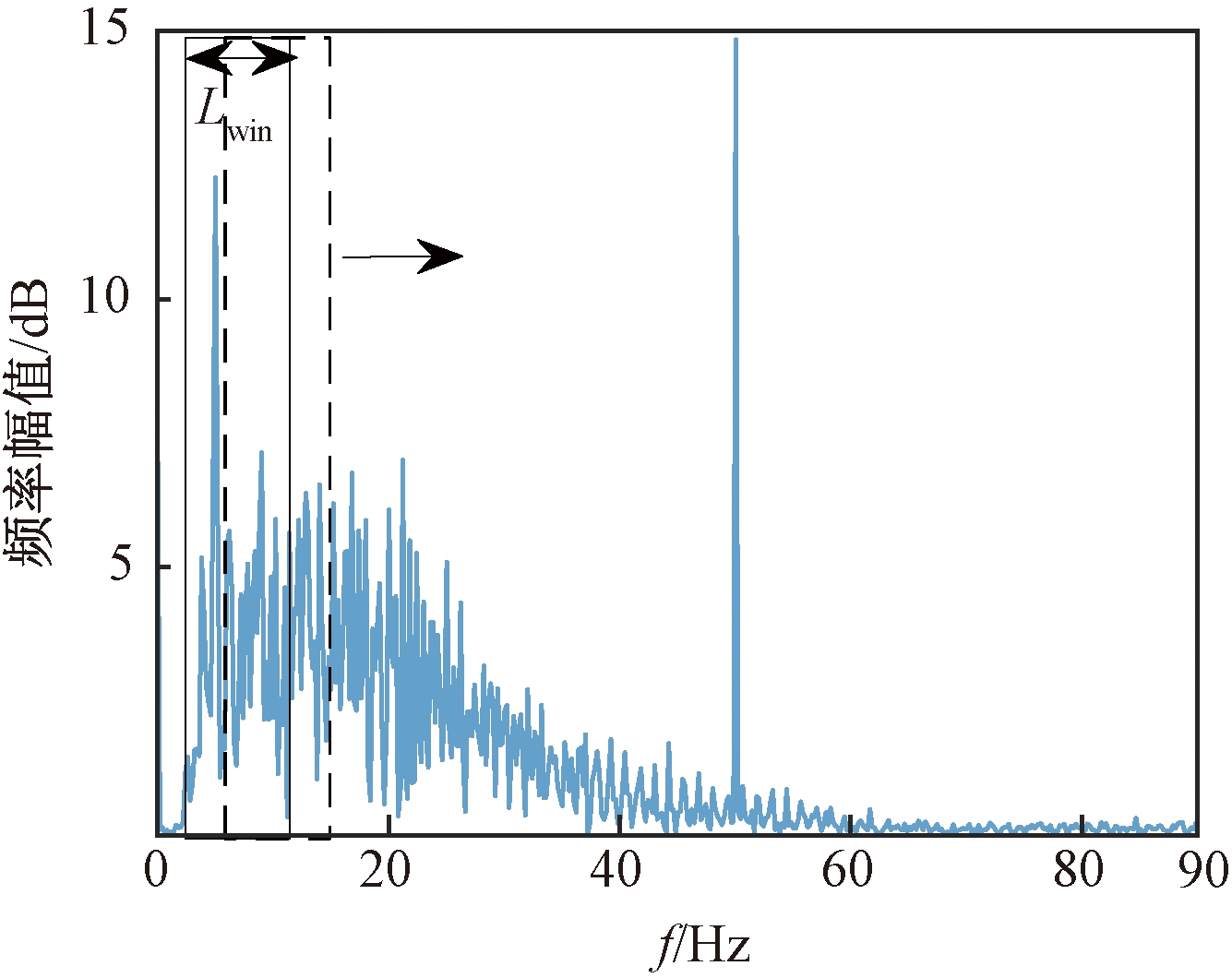
图1 t时刻下频谱图
Figure 1 Lower spectrum at time t
t时刻下第i次滑动序列表示为![]() :
:
(5)
式中:1≤i≤q-Lwin+1。
在每一次窗口滑动中,计算序列在该窗口范围内的局部离群因子,则t时刻下第i次滑动窗口序列对应的局部离群因子为
(6)
式中:f′为窗口序列中的点数,1≤f′≤Lwin。
取窗口序列f′=1时的局部离群因子作为窗口首端对应频率点在全局范围的局部离群因子,即基于频率密度的局部离群因子定义为
(7)
当工频随着时间发生偏移时,可由式(7)捕捉各时刻的实际瞬时工频,并根据偏移时刻划分信号区间,使用各区间内瞬时工频的平均值作为该段内陷波器的中心频率,修正滤波器参数,从而达到自适应滤波的效果。
1.2 局部分量滤波
经验模态分解EMD基于数据时域局部特征,把复杂的数据分解成有限的几个内蕴模式函数分量(intrinsic mode function,IMF)。分解得到的函数分量由高频到低频进行排列,最低频分量通常为原始信号的趋势项或残差,最高频分量为噪声。由于分解不再依赖基函数,因此分解更为高效,适合用来分析非平稳非线性的时变过程[14-15]。
生物电信号是一种带有强噪音的微弱信号,使用EMD能精准地对信号特定局部分量进行分析,避免对不属于该频段的分量信号造成影响,实现最大均方误差最小化,即去噪后的信号是原始信号的近似最优估计,在去除噪音的同时最大程度保留有效信号。局部分量滤波首先利用EMD将信号分解成多个IMF内蕴模式函数分量,再根据IMF分量频率排序特点找到工频所属分量,然后根据已知的陷波频率对该分量进行滤波,最后将各分量重构。局部分量滤波流程见图2。
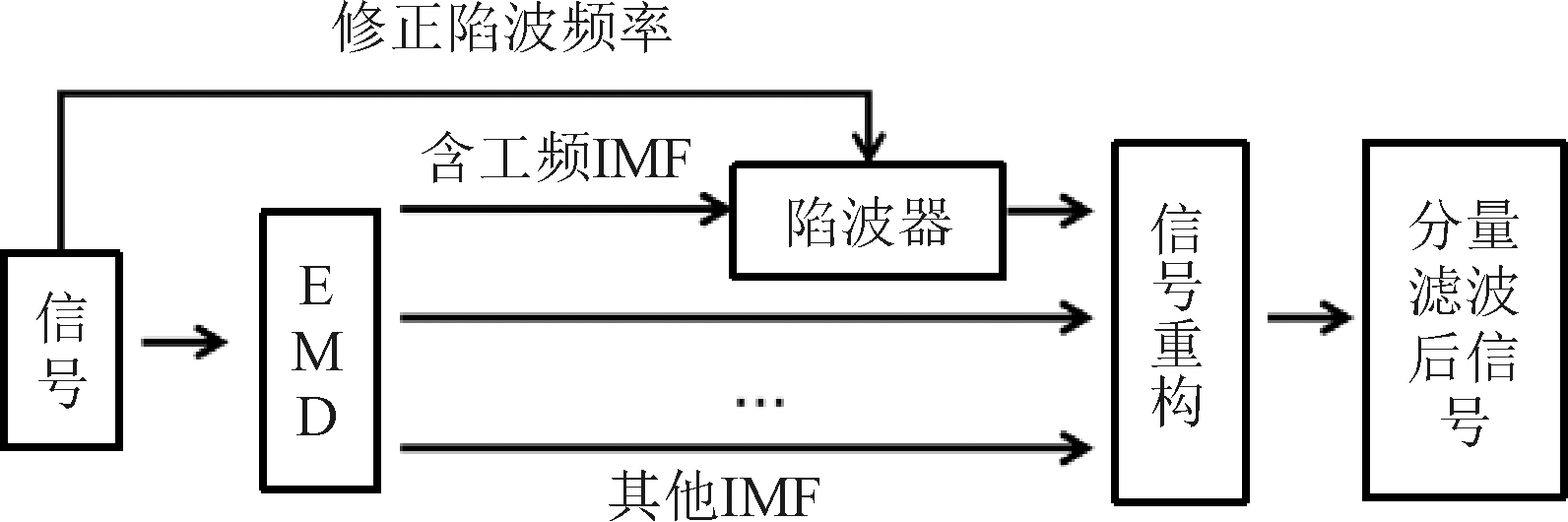
图2 局部分量滤波流程
Figure 2 Local component filtering flow
1.3 FLOF与EMD结合方式
本文将FLOF与EMD相结合实现自适应滤波,去除工频信号干扰。FLOF的自适应解决了信号由于外界或者本身原因引起的非平稳过程,弥补了EMD局部分量滤波固定滤波频率的缺陷;EMD局部分量滤波在FLOF自适应上,增强了有用信号的保留程度。2种方式结合使用,有效地提高了信号工频滤波效果,同时兼具稳定性高、自适应能力好、精准度强等优势。
FLOF与EMD联合去噪处理方法步骤如下。首先,通过短时傅里叶变换将信号转换到时频域,再使用FLOF算法,根据滑动窗口模型找到每一时刻下的频率的突变点,即工频信号实际频率sfn。同时综合时序上实际工频频率,找到信号突变时刻,将信号分成区间信号1~n多个部分。其次,利用经验模态分解将每部分区间信号分解成多个固有模态,找到IMF中工频所属分量并根据FLOF检测到的短时噪音频率进行局部分量滤波。最后,将处理后的各区间信号进行组合。整体流程见图3。
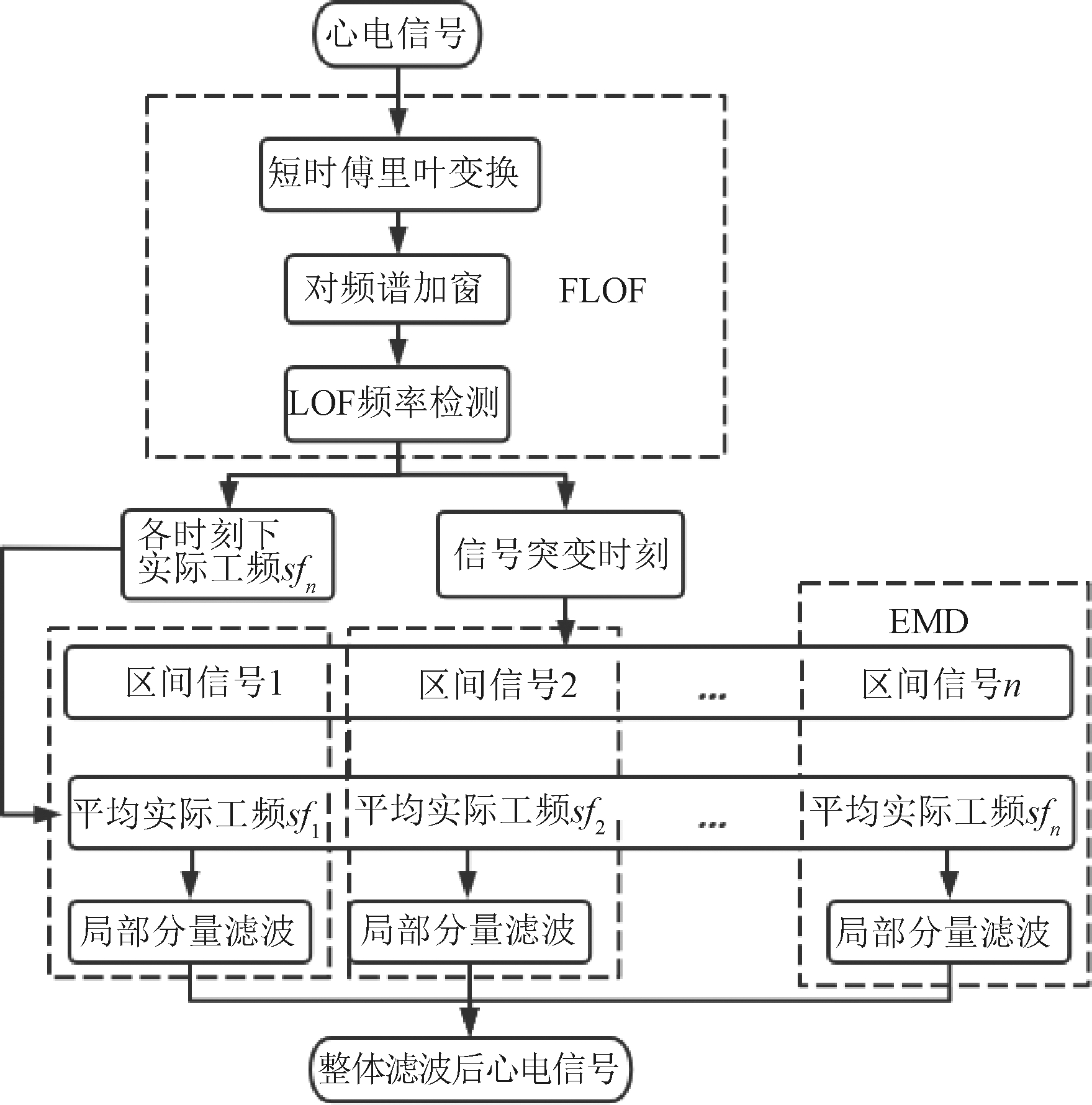
图3 去噪处理整体流程图
Figure 3 Overall flow chart of denoising processing
2 分析与讨论
心电信号作为生物电研究热点,具有获取方便、数据库齐全等优势,因此本文以心电信号为例,对自适应滤波方法进行分析。MIT-BIH心律失常数据库是国际公认三大标准心电库之一,包括48组30 min的Ⅱ导联心电信号片段,近年应用较为广泛。本文选择噪声含量较少的第101号数据[16]作为实验的原始心电数据。心电信号频率为0.05~100 Hz,该组信号采样频率fs为360 Hz,截取15 s的数据,前5 s、中间5 s、后5 s分别混入50.0、49.5、50.5 Hz的频率分量,同时在整个时间周期内混入白噪声。纯净及混合后的心电信号如图4所示。
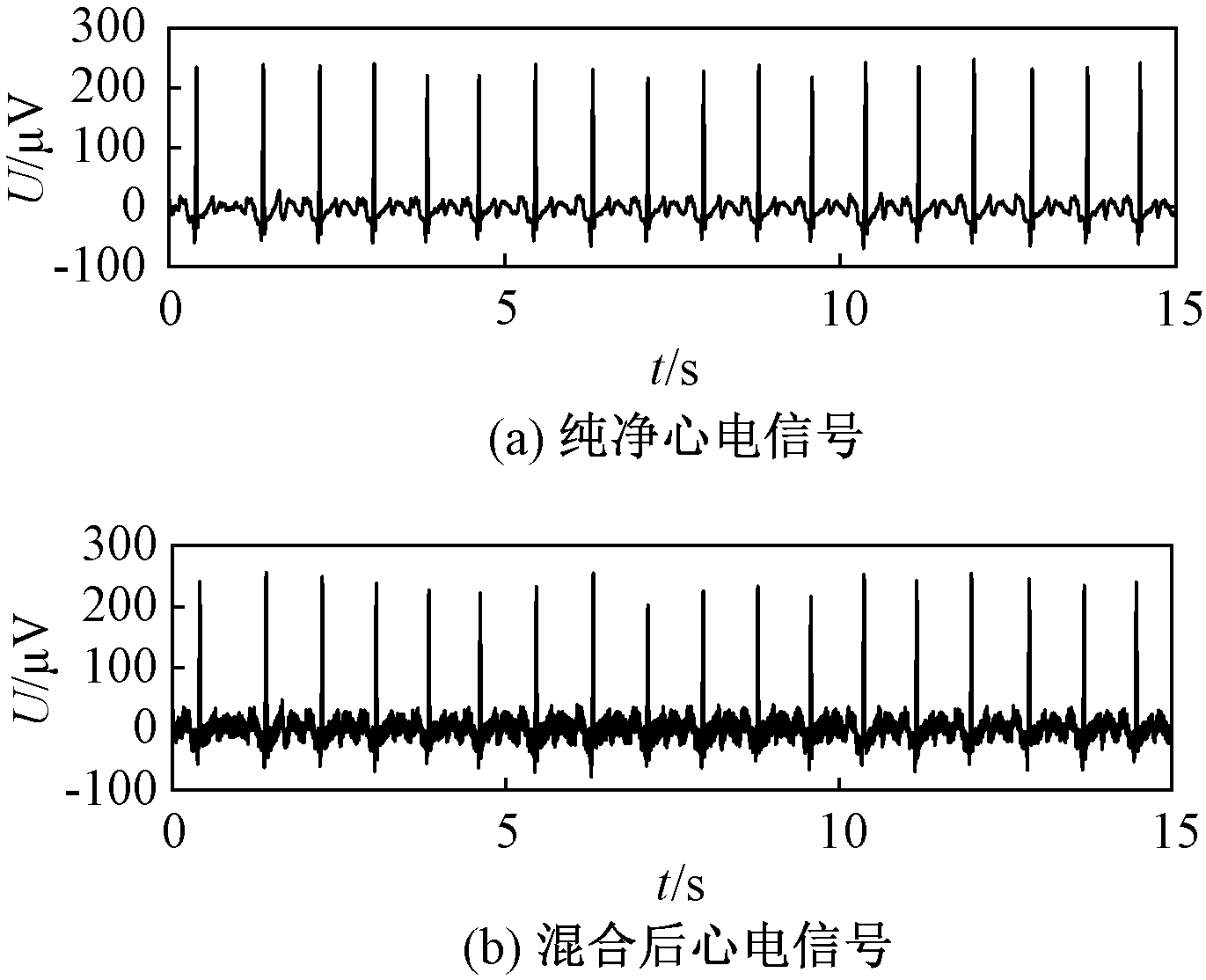
图4 原始信号
Figure 4 Original signals
2.1 FLOF的突变频率与突变时间检测
图5为某时刻下LOF算法和FLOF算法的检测结果,纵坐标局部离群因子表示对应算法计算得出的不同频率点异常程度。从图5 (a)可以明显看出,运用LOF算法在低频部分会搜索到几个虚假的离群点。使用滑动窗口后,FLOF结合了频率这一变量,就能避免此类情况,从而找到该时刻下对应的突变频率。
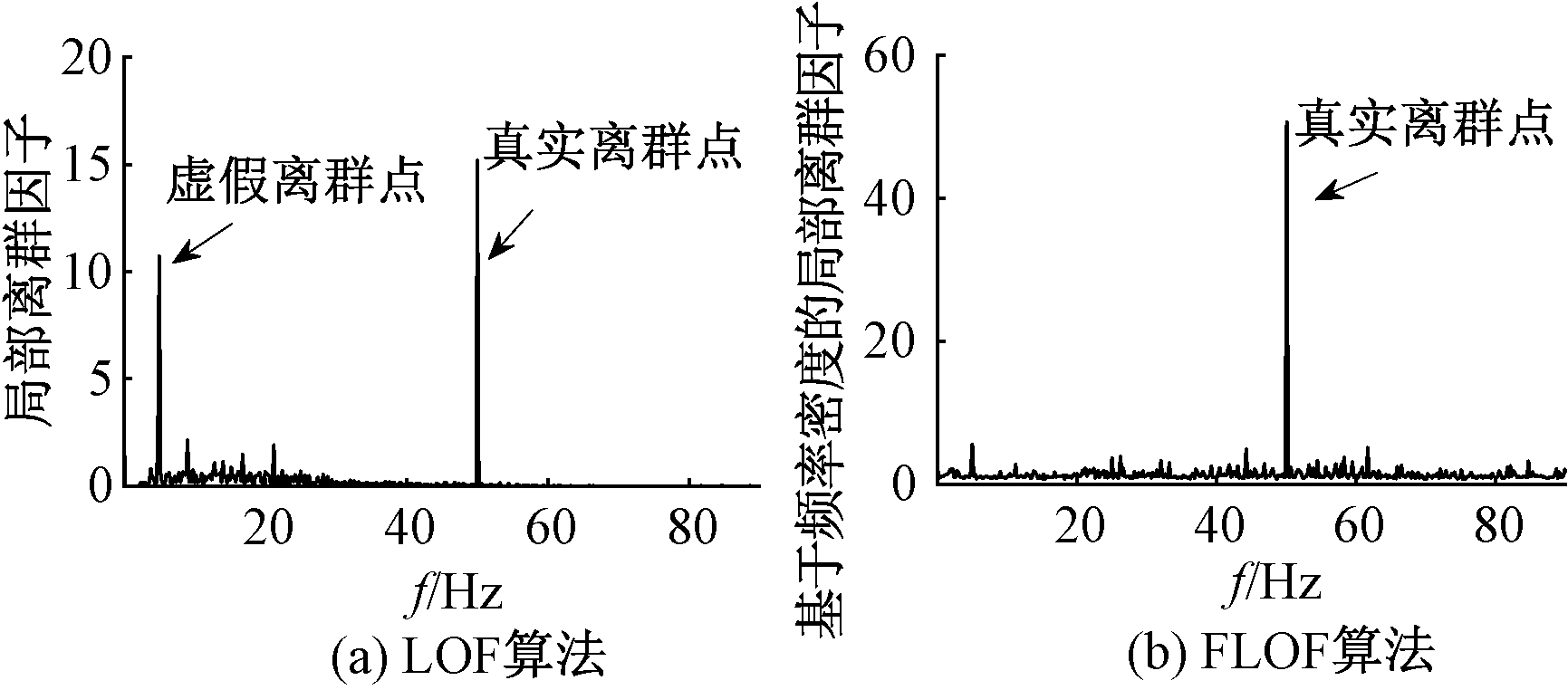
图5 LOF算法和FLOF算法的检测结果
Figure 5 Detection results of LOF and FLOF
根据每一时刻下离群值检测,就能得到整个时间段内的异常频率,即实际工频噪音频率,其波动图如图6所示。由图6实际工频噪音频率波动图可以看出,心电信号中第5、10 s为突变时刻,信号被分成3部分。以每一部分的平均实际工频值当作该段时间内的短时噪音频率,可知这3部分的短时噪音频率分别为49.991 3、49.504 9、50.507 9 Hz。在后续滤波时保留2位小数。
2.2 滤波性能分析
图7为基于FIR陷波器单时段下结合EMD滤波前后的频谱图。为了使实验结果具有对照性,两种滤波方式采用的陷波器的带宽和衰减倍数均相同。使用EMD滤波后50 Hz处幅值与FIR滤波效果基本无差异,但50 Hz周边频率点更加接近于原始信号幅值,因此在保证滤波效果的同时能更多地保留有用信号。
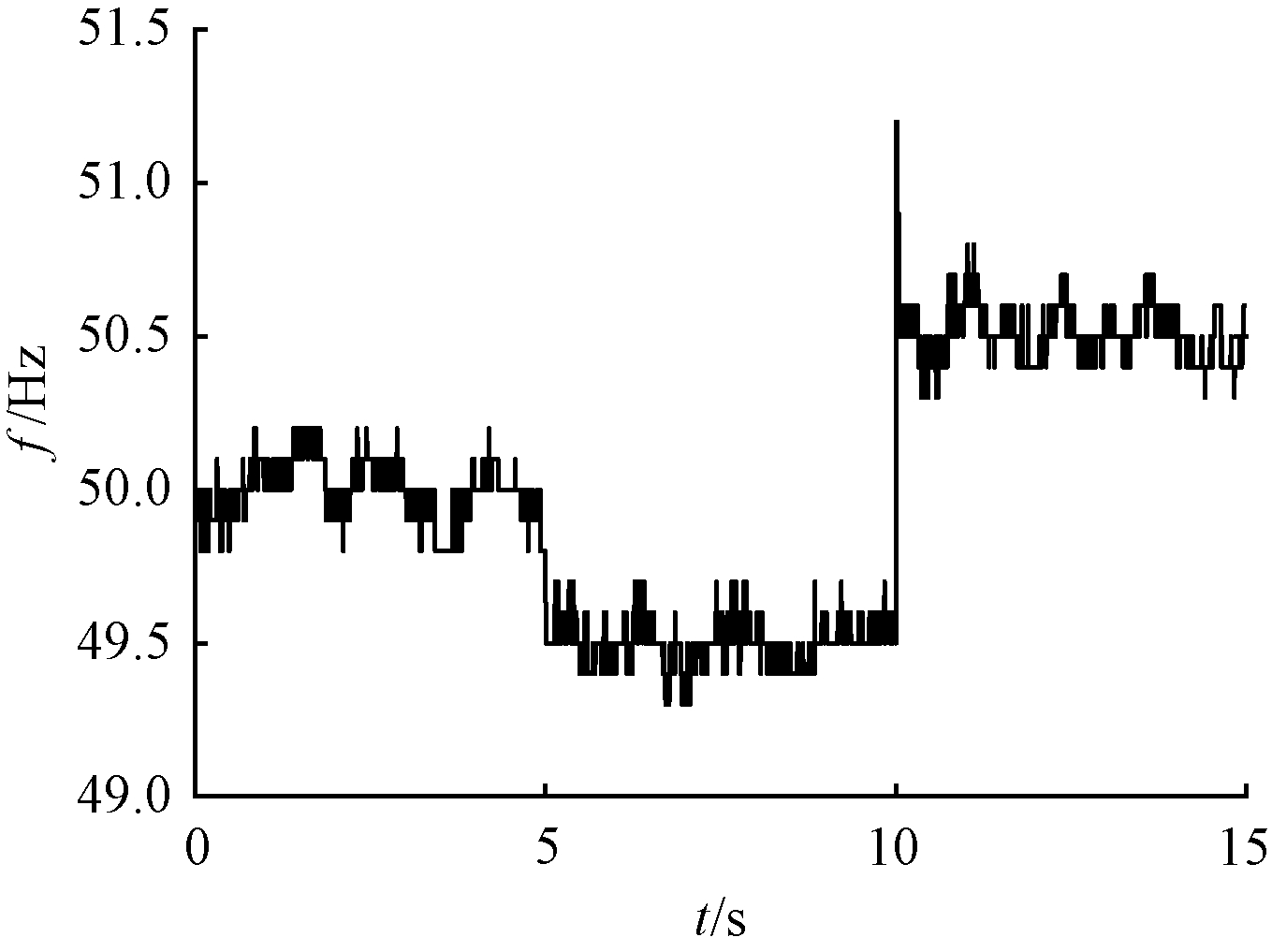
图6 实际工频噪音频率波动图
Figure 6 Frequency fluctuation diagram of actual power frequency noise
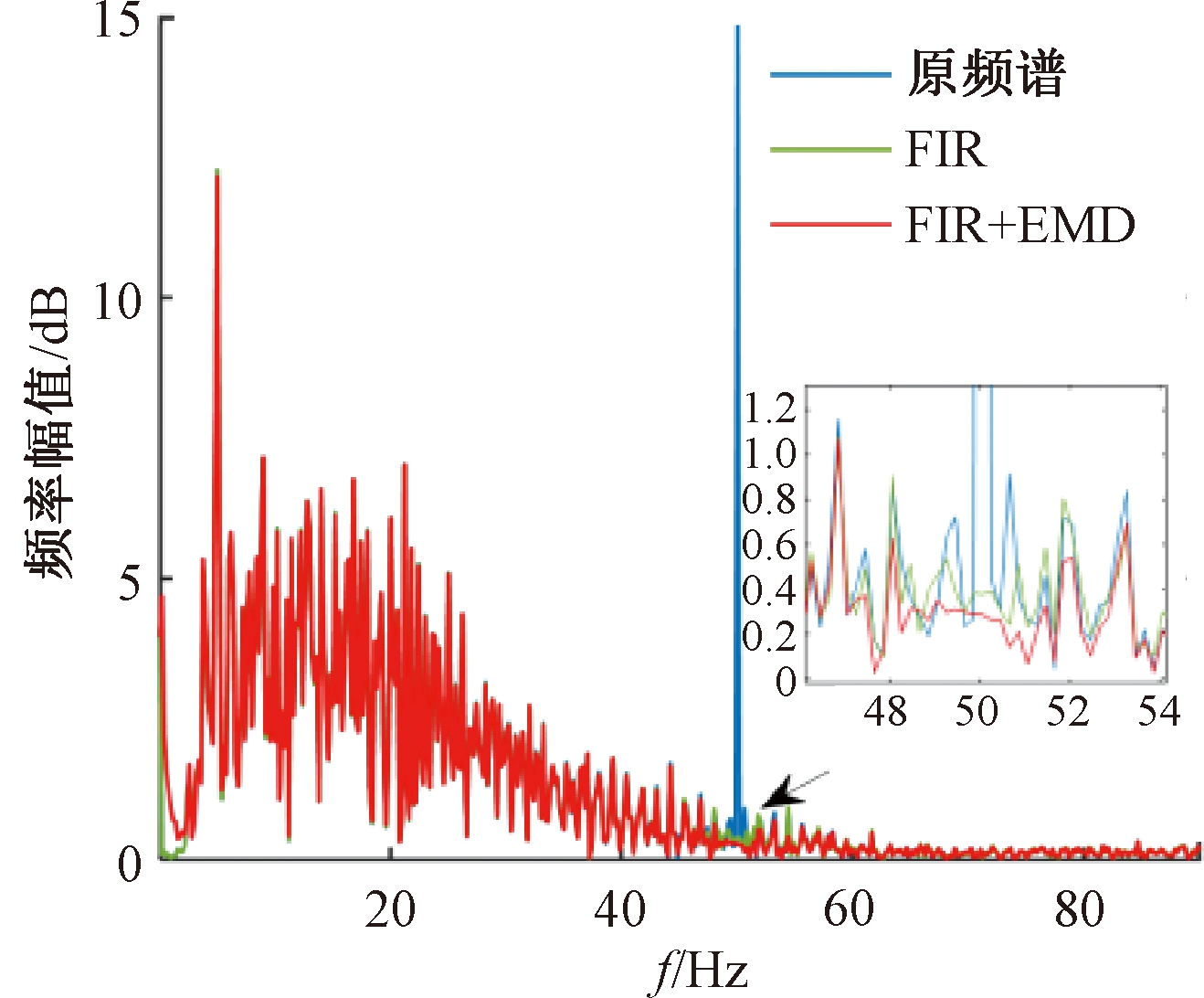
图7 使用EMD滤波前后频谱图
Figure 7 Spectrum before and after using filter
图8 (a)为纯净信号和FIR滤波后信号细节对比图,图8 (b)为纯净信号和本文方法滤波信号细节对比图。可以看出,两种方法在前5 s滤波效果基本一致,但在5 s后工频信号发生偏移,固定中心频率的去噪方式去噪效果变差,而采用本文方法能够检测出实际工频信息,在整个时间段内具有自适应的去噪效果。
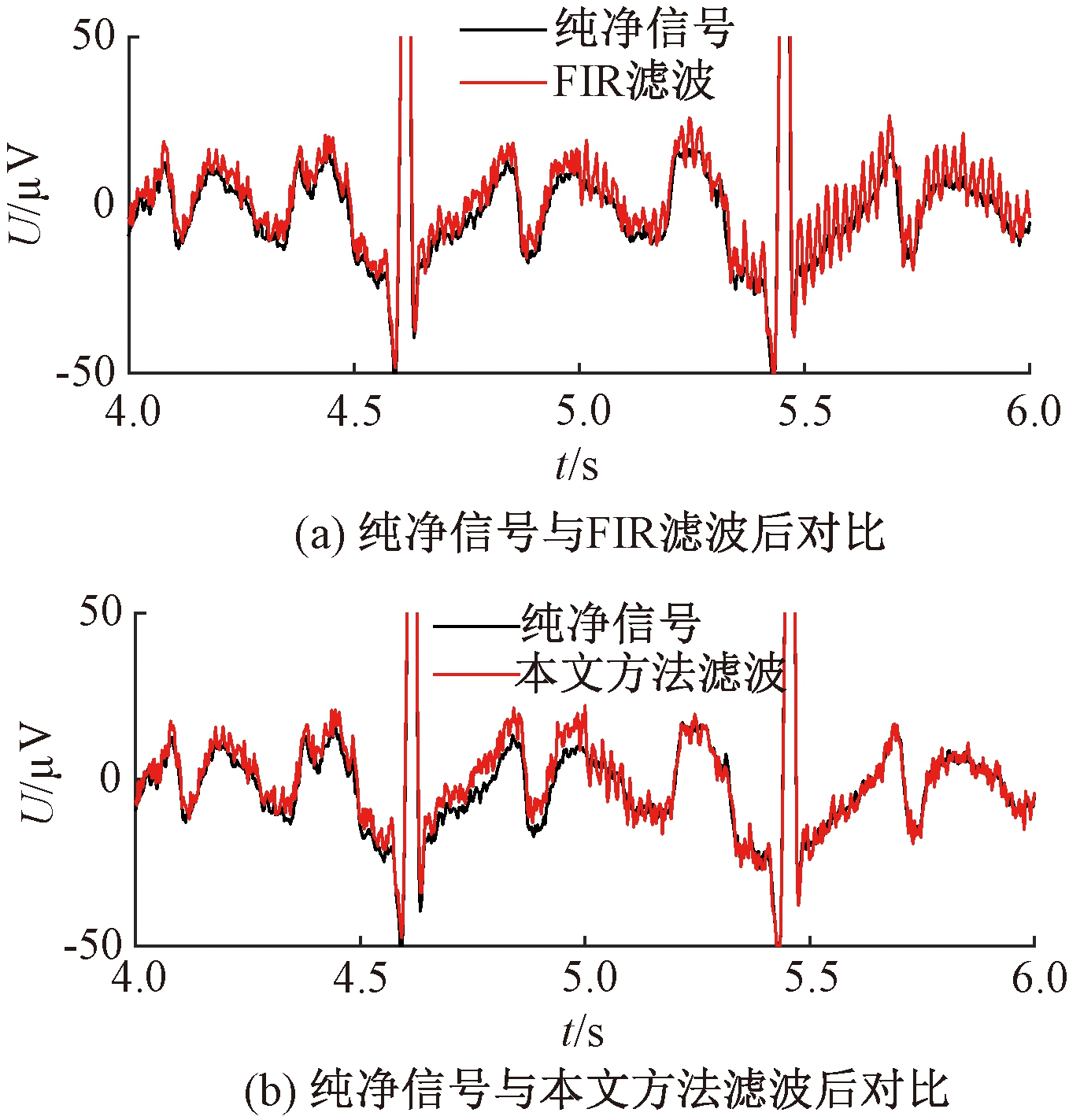
图8 信号细节对比
Figure 8 Signal detail comparison
2.3 不同滤波方法下性能对比
采用3种评估标准来评估滤波结果的性能,包括信噪比、均方根误差、相似度。信噪比是衡量降噪程度最直观的一个量,信噪比越大说明信号中包含的噪声越少、降噪效果越好。均方根误差是反映估计量与被估计量之间差异程度的一种度量,用于衡量滤波后信号与纯净信号间的差异。相似度计算采用的是Pearson相关系数,用于衡量纯净信号与滤波后信号波形的相似程度,相关系数的绝对值越接近1,相关度越强,相关系数的绝对值越接近于0,相关度越弱。信噪比用于衡量滤波方法的去噪效果,均方根误差用于衡量滤波方法滤波后与原信号的接近程度,相似度用于衡量滤波后信号的整体形变情况。信噪比SNR、均方根误差RMSE、相似度SIM公式计算如式(8)~(10)所示。
(8)
(9)
(10)
式中:x为含噪信号;x′为纯净信号;N为信号长度;‖·‖ 2表示“·”对应的二范数;Cov表示协方差;σ为标准差。
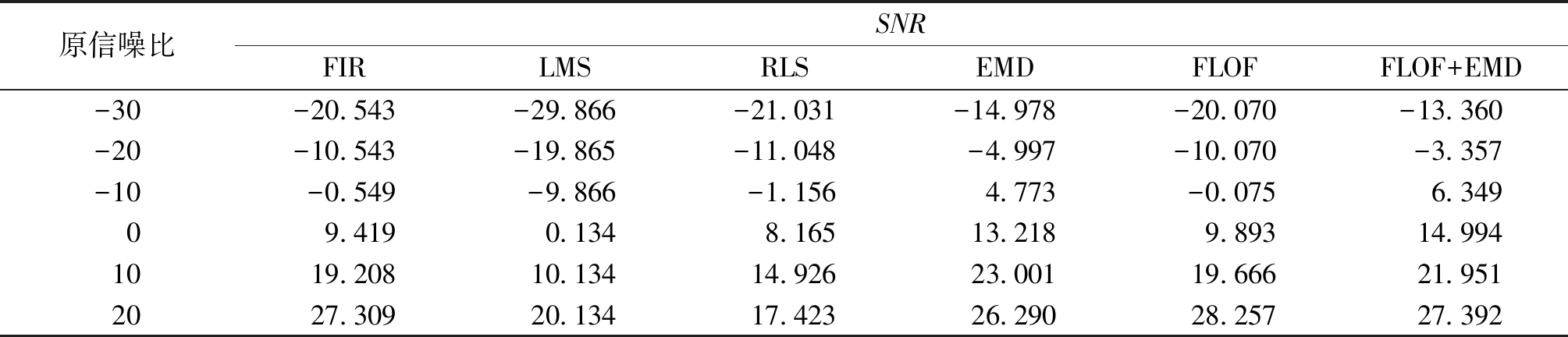
表1~3为信号在不同原信噪比和滤波方法去噪后的信噪比、均方根误差、相似度的对照情况。从同一信噪比不同滤波方式来看,本文方法与其他滤波器相比效果较好。以原信噪比-30 dB为例,FLOF相较于常规自适应LMS、RLS滤波方法,在信噪比、均方根误差、相似度方面滤波效果均更优。同时,EMD滤波均方根误差在大多数情况下远小于FIR、LMS、RLS、FLOF,因此去噪后的信号与原始信号更为接近,能够保留更多的有用信号。将EMD与FLOF相结合后,与单独使用这两种方法相比具有更优异的表现,相较于自适应滤波器LMS和RLS,信噪比提升16.266、7.671 dB,均方根误差减小16.017、4.388 dB,相似度提升0.200、0.013。结果表明,本文所提方法滤波效果与不同滤波器相比均有一定提升,验证了本文方法的有效性。
表1 信号在不同信噪比和滤波方法去噪后的信噪比对比
Table 1 SNR comparison of signals after denoising under different SNR and filtering methods dB
原信噪比SNRFIRLMSRLSEMDFLOFFLOF+EMD-30-20.543-29.866-21.031-14.978-20.070-13.360-20-10.543-19.865-11.048-4.997-10.070-3.357-10-0.549-9.866-1.1564.773-0.0756.34909.4190.1348.16513.2189.89314.9941019.20810.13414.92623.00119.66621.9512027.30920.13417.42326.29028.25727.392
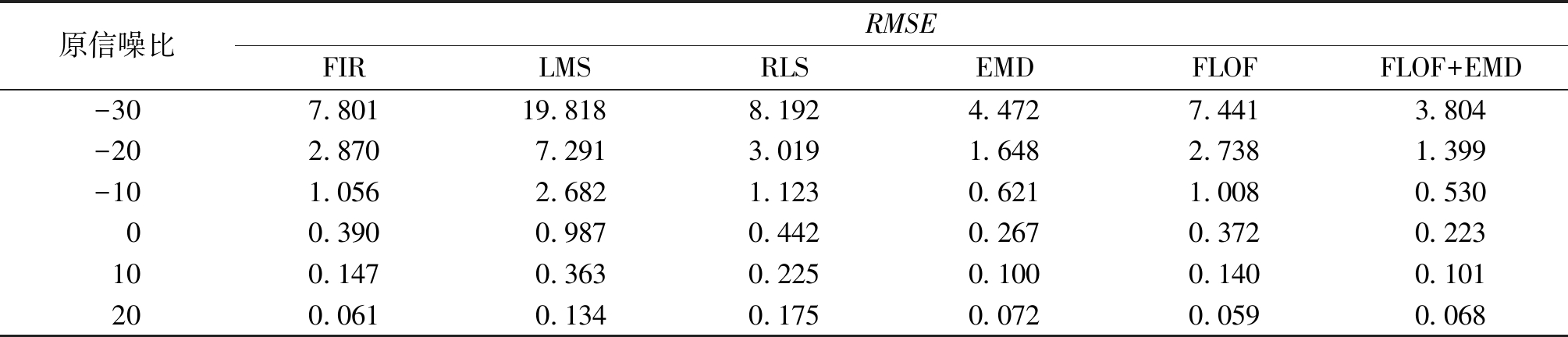
表2 信号在不同信噪比和滤波方法去噪后的均方根误差对比
Table 2 RMSE comparison of signals after denoising under different SNR and filtering methods dB
原信噪比RMSE FIRLMSRLSEMDFLOFFLOF+EMD-307.80119.8188.1924.4727.4413.804-202.8707.2913.0191.6482.7381.399-101.0562.6821.1230.6211.0080.53000.3900.9870.4420.2670.3720.223100.1470.3630.2250.1000.1400.101200.0610.1340.1750.0720.0590.068
表3 信号在不同信噪比和滤波方法去噪后的相似度对比
Table 3 SIM comparison of signals after denoising under different SNR and filtering methods

原信噪比/dBSIMFIRLMSRLSEMDFLOFFLOF+EMD-300.2160.0520.2390.2150.2530.252-200.5180.1420.5600.5160.5810.579-100.8550.3650.8730.8490.8890.88300.9760.7300.9710.9660.9820.977100.9960.9460.9880.9960.9970.997200.9990.9920.9900.9980.9990.998
在同一滤波方式下,相较于表1~3中的FIR、LMS、RLS和EMD等常规滤波方法,本文方法在不同信噪比下均有较好表现。低信噪比的信号结合FLOF与EMD滤波方法的优势后,滤波效果尤为明显;但随着原信噪比的升高,EMD带来的滤波优势逐渐减小,这是由于高信噪比信号中含噪较少,EMD运算引入误差趋于稳定,给滤波器带来的一些不良影响。但实际工作中信号中混入的工频噪声强度一般较大,因此本文的滤波方法也可以进行较好处理。
3 结论
本文在LOF的基础上,提出了一种基于频率密度的局部离群因子和EMD结合的心电信号滤波方法。将突变点检测引入信号处理的频域中,通过基于频率密度的异常值点检测找到工频的实际频率及变化时刻,并根据不同时间段内的实际工频频率修改陷波器中心频率进行去噪,提高滤波的实时性与准确性。统计结果表明:本文方法各项评估指标均优于常规的自适应滤波方法,在不同的信噪比下均具有较好的去噪效果,滤波后的信号在信噪比、均方根误差、信号相似度上均有较好表现。
[1] 刘彬, 马少华, 闫广宇. 生物医学信号相似性分析方法的研究[J]. 医疗装备, 2017, 30(14): 50-51.
LIU B,MA S H,YAN G Y.Research on similarity analysis methods for biomedical signals[J]. Medical Equipment, 2017, 30(14):50-51.
[2] GUEZGOUZ D, CHARIAG D E, RAINGEAUD Y, et al. Modeling of electromagnetic interference and PLC transmission for loads shedding in a microgrid[J]. IEEE Transactions on Power Electronics, 2011, 26(3): 747-754.
[3] 张文伟, 底青云, 耿启立, 等. 基于数字递归陷波的多通道瞬变电磁法周期噪声去除研究[J]. 物探与化探, 2020, 44(2):278-289.
ZHANG W W, DI Q Y, GENG Q L, et al. The removal of MTEM periodic noise based on digital recursive notching[J]. Geophysical and Geochemical Exploration, 2020, 44(2):278-289.
[4] 雷文平, 宋圣霖, 郝旺身, 等. 基于FV-FBE的滚动轴承故障诊断研究[J]. 郑州大学学报(工学版), 2020, 41(5): 82-86.
LEI W P, SONG S L, HAO W S, et al. Fault diagnosis of rolling bearing based on FV-FBE[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(5): 82-86.
[5] 刘军. 重力异常频率域分离方法及应用[J]. 物探与化探, 1998, 22(6): 446-451, 445.
LIU J. The frequency field separation technique of gravity anomalies and its application[J]. Geophysical and Geochemical Exploration, 1998, 22(6): 446-451, 445.
[6] 谷晓彬, 冯国英, 刘建. 自适应滤波算法在微弱振动测量中的应用[J]. 红外与激光工程, 2016, 45(4): 0417003.
GU X B, FENG G Y, LIU J. Application of adaptive filtering algorithm in the weak vibration measurement[J]. Infrared and Laser Engineering, 2016, 45(4): 0417003.
[7] 彭良广, 林金朝, 庞宇, 等. 基于自适应滤波的可穿戴式心电信号检测系统[J]. 电子技术应用, 2017, 43(9): 17-21.
PENG L G, LIN J Z, PANG Y, et al. Wearable system based on adaptive filter for monitoring ECG signal[J]. Application of Electronic Technique, 2017, 43(9): 17-21.
[8] 任杰, 杨双龙, 王俊翔, 等. 迭代ICA与LEVKOV联合的瞬态响应工频干扰抑制方法[J]. 电子测量与仪器学报, 2021, 35(12): 37-44.
REN J, YANG S L, WANG J X, et al. Anti-power interference method of combining iterative ICA and LEVKOV for transient response[J]. Journal of Electronic Measurement and Instrumentation, 2021, 35(12): 37-44.
[9] RILLING G, FLANDRIN P. One or two frequencies? the empirical mode decomposition answers[J]. IEEE Transactions on Signal Processing, 2008, 56(1): 85-95.
[10] 邹清, 汤井田, 唐艳. Hilbert-Huang变换应用于心电信号消噪[J]. 中国医学物理学杂志, 2007, 24(4): 309-312.
ZOU Q, TANG J T, TANG Y. Hilbert-Huang transform for ECG de-noising[J]. 中国医学物理学杂志, 2007, 24(4):309-312.
[11] 邹云峰, 张昕, 宋世渊, 等. 基于局部密度的快速离群点检测算法[J]. 计算机应用, 2017, 37(10):2932-2937.
ZOU Y F, ZHANG X, SONG S Y, et al. Fast outlier detection algorithm based on local density[J]. Journal of Computer Applications, 2017, 37(10):2932-2937.
[12] 薛明志, 陈商玥, 高强. 基于k-medoids聚类算法的低压台区线损异常识别方法[J]. 天津理工大学学报, 2021, 37(1):26-31.
XUE M Z, CHEN S Y, GAO Q. Recognition method of line loss anomaly in low-voltage station area based on k-medoids clustering algorithm[J]. Journal of Tianjin University of Technology, 2021, 37(1):26-31.
[13] 方海超. 脉冲噪声环境中基于GSP的噪声信号突变点检测技术研究[D]. 南京: 南京邮电大学,2021.
FANG H C. Research on detection technology of noise signal abrupt point based on GSP in impulsive noise environment[D]. Nanjing: Nanjing University of Posts and Telecommunications,2021.
[14] 徐晓刚, 徐冠雷, 王孝通, 等. 经验模式分解(EMD)及其应用[J]. 电子学报, 2009, 37(3):581-585.
XU X G, XU G L, WANG X T, et al. Empirical mode decomposition and its application[J]. Acta Electronica Sinica, 2009, 37(3):581-585.
[15] 赵雯雯, 曾兴雯. 一种新的EMD去噪方法[J]. 电子科技, 2008, 21(5): 30-32, 36.
ZHAO W W, ZENG X W. A new signal denoising method based on empirical mode decomposition(EMD)[J]. Electronic Science and Technology, 2008, 21(5): 30-32, 36.
[16] 杨承金, 聂春燕, 王慧宇, 等. 基于小波改进阈值的肌电干扰降噪研究与效果评估[J]. 电子测量技术, 2021, 44(22): 80-86.
YANG C J, NIE C Y, WANG H Y, et al. Research of noise reduction algorithm and effect evaluation about EMG interference based on improved wavelet threshold[J]. Electronic Measurement Technology, 2021, 44(22): 80-86.