聚类[1-2]的根本目的是将对象按照某种相似或距离规则进行划分,使得簇内对象距离尽可能小,簇间对象之间距离尽可能大。因此,聚类的核心问题是衡量对象之间的距离或相似度。当对象是数值数据,常用欧氏距离和马氏距离等来衡量对象之间的距离;当对象是分类数据[3],属性值是类别属性而不是数字,常用汉明距离及其变体[4]来度量。但这些距离度量只能单独运用于数值数据或者分类数据,不能用来衡量同时具有数值属性和分类属性的异构属性数据对象之间的距离[5]。由于异构属性数据难以处理,常被编码成纯数值数据或离散化成纯分类数据进行处理,但编码和离散化过程会在一定程度上曲解数据的原始信息,进而影响聚类结果。
因此,许多学者利用异构属性数据的数据特征来定义距离,Huang[6]分别运用汉明距离和欧式距离定义分类和数值属性值之间的距离,并用一个权重来平衡2种属性的差异。Huang等[7]提出的自动加权的k-Means聚类算法(WKM),不再用一个权重来平衡2种属性的差异,而是用拉格朗日子乘子法得到最优权重来衡量属性之间关系。之后,Ienco等[8]提出了基于上下文的分类数据距离度量;Jian等[9]对非独立同分布分类数据提出了耦合相似度量(coupled metric similarity,CMS)。这些距离度量[10-11]都可以与k-Prototypes算法[6]结合,运用于异构属性数据中。但是,如图1所示,分类属性由有序属性和标称属性构成,这些距离度量将分类属性中的有序属性[10]当作标称属性对待,没有区分有序属性,导致有序属性的等级结构信息被忽略,难以在含有有序属性的数据集上取得理想的聚类效果。
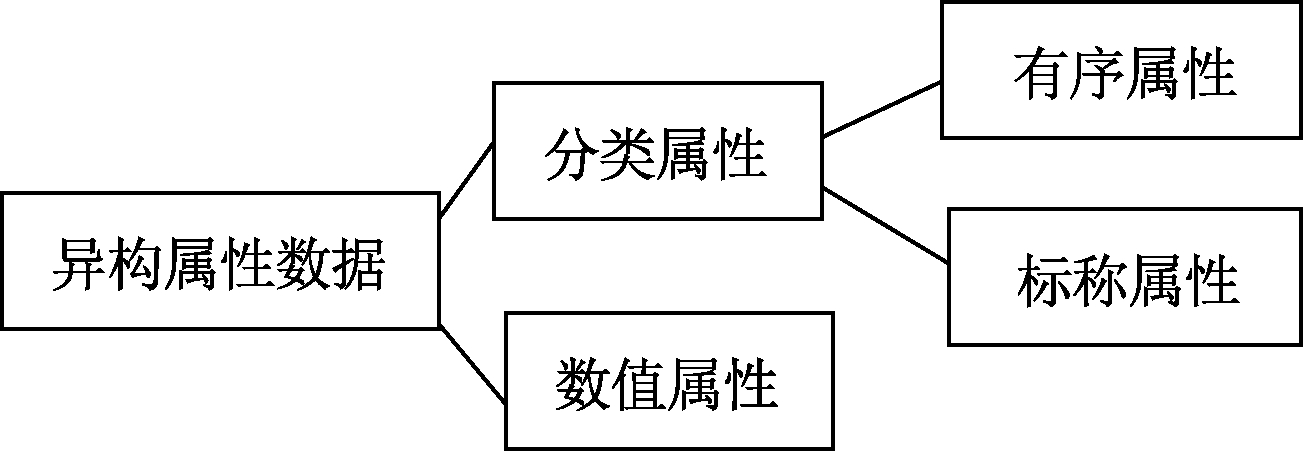
图1 异构属性数据的属性构成
Figure 1 Attribute composition of heterogeneous-attribute data
将有序属性的取值按等级排列后用连续的整数1,2,…,n来编码,并利用数值属性的度量方法来度量属性值之间的距离,是一种最为常见的有序属性处理方法。然而数字编码的方式同样会丢失有序属性中的数据分布特征。近年来,Zhang等[11-12]分别从信息熵和图论的角度定义了区分有序属性的分类数据统一距离度量(unified distance metric,UDM)和可学习加权的分类数据距离度量。虽然这些距离度量也可以与k-Prototypes等混合数据聚类算法结合,运用于含有数值属性的异构属性数据,但是它们并没有提出可以同时处理两种异构属性数据的办法。
与此同时,同一个属性对不同簇的重要性是不一样的,大部分的聚类算法平等地对待每一个属性,这在一定程度上具有不合理性。子空间聚类则较好地解决了这一类问题,它根据数据的子空间而不是整个数据空间将数据对象分组到集群中。例如Cheung等[13]利用簇内对象的信息熵来量化属性对簇的贡献;Jia等[14]提出的属性权重OCIL 算法(attribute-weighted OCIL algorithm,WOCIL)利用不同属性的聚类区分能力和簇内紧凑性来设定加权方案。但是,这些权重定义方案同样没有区分有序属性。
针对现有的异构属性数据距离度量没有区分分类属性中的有序属性而导致信息缺失、聚类效果不理想的问题,本文提出了一种新的异构属性数据距离度量,并基于此距离度量得到一种新的异构属性数据子空间聚类算法(subspace clustering algorithm for heterogeneous-attribute data,SCAH)。
1 相关工作
大部分数据集都包含分类属性和数值属性,其中分类属性可分为有序属性和标称属性,有序属性和标称属性的区别是有序属性的类别属性值之间具有等级关系。例如:学生成绩这一有序属性,它的属性值分别是优秀、良好、及格、不及格,很明显这些属性值之间具有等级关系。
现有的异构属性数据的距离定义和权重定义都是为标称属性和数值属性而设计,未能区分分类属性中有序属性的等级结构特点,Zhang等[11-12]提出的分类数据距离度量,很好地解决了这个问题。其解决方案是:当给定同个属性下2个属性值ar,m和ar,h的距离公式为dist(ar,m,ar,h),如果这个属性为有序属性,且属性值的等级从高到低排列分别为ar,1,…ar,m,…,ar,h,…,ar,vr。为了突出有序属性的等级结构特征,dist(ar,m,ar,h)只需要转变为![]() 即可。这个解决方案虽然仅在纯分类数据距离度量中运用,但是可以将其扩展到异构属性数据中。
即可。这个解决方案虽然仅在纯分类数据距离度量中运用,但是可以将其扩展到异构属性数据中。
2 本文方法
给定异构属性数据集X的n个对象和d个属性分别为x1,x2,…,xn和A1,A2,…,Ad,对任意对象xm可记为![]() 其中
其中![]() 表示第m个对象中Ai的属性值,i=1,2,…,d,m=1,2,…,n。d个属性中前dc个属性为分类属性,后du个属性为数值属性,d=dc+du。其中分类属性前do个属性表示有序属性,后dn个属性表示标称属性,dc=do+dn。分类属性Ar的属性值由{ar,1,ar,2,…,ar,vr}构成。当Ar为有序属性,其属性值之间等级关系从高到低可表示成:ar,1≻ar,2≻…≻ar,vr,符号“≻”表示左边属性值等级高于右边属性值。若n个对象被划分成k个簇,分别用C1,C2,…,Ck表示,X的每个对象都属于k个簇中的一个。对任意一个簇的簇中心记为
表示第m个对象中Ai的属性值,i=1,2,…,d,m=1,2,…,n。d个属性中前dc个属性为分类属性,后du个属性为数值属性,d=dc+du。其中分类属性前do个属性表示有序属性,后dn个属性表示标称属性,dc=do+dn。分类属性Ar的属性值由{ar,1,ar,2,…,ar,vr}构成。当Ar为有序属性,其属性值之间等级关系从高到低可表示成:ar,1≻ar,2≻…≻ar,vr,符号“≻”表示左边属性值等级高于右边属性值。若n个对象被划分成k个簇,分别用C1,C2,…,Ck表示,X的每个对象都属于k个簇中的一个。对任意一个簇的簇中心记为![]() 其中,
其中,![]() 表示第j个簇第m个属性的中心。当
表示第j个簇第m个属性的中心。当![]() 是第j个簇中第m个属性中频率最高的属性值;当
是第j个簇中第m个属性中频率最高的属性值;当![]() 是第j个簇中第m个属性的均值。
是第j个簇中第m个属性的均值。
如表1所示,对象是x1,x2,…,x6,其中 x1=(↑,□,1.0)。属性分别是A1,A2,A3,它们分别代表有序属性、标称属性和数值属性,且A1的属性值由{↑,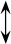 ,↓}构成,令属性值的等级关系为↑≻
,↓}构成,令属性值的等级关系为↑≻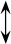 ≻↓,A2的属性值由{□,△}构成。
≻↓,A2的属性值由{□,△}构成。
表1 异构属性数据集实例
Table 1 Example of heterogeneous-attribute data
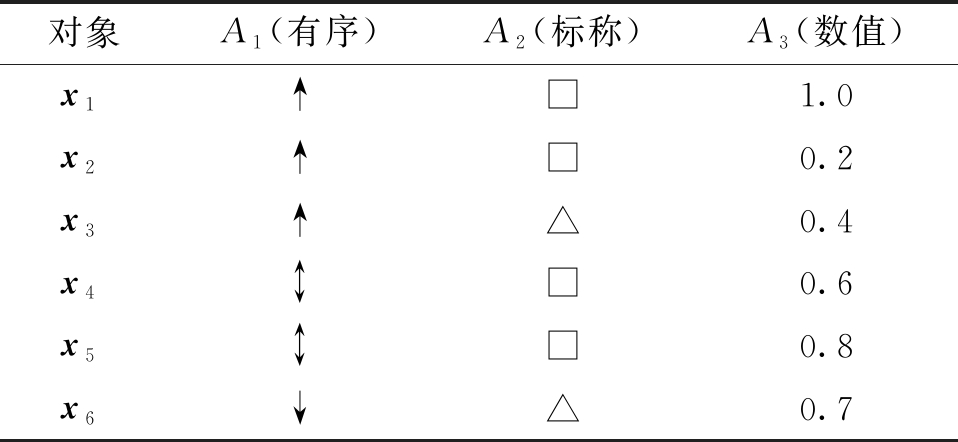
对象A1(有序)A2(标称)A3(数值)x1↑□1.0x2↑□0.2x3↑△0.4x4↕□0.6x5↕□0.8x6↓△0.7
聚类的目的是通过式(1)的最小化目标函数得到最优的划分Q*:
(1)
其中Q=qij是一个n×k的矩阵,满足条件:![]() 且 qij∈{0,1},i=1,2,…,n,j=1,2,…,k。dist(xi,Cj)为xi与Cj的距离,xi与Cj的距离相当于xi的每一个属性值与Cj簇中心的距离和。由于分类数据的属性值代表样本的重要特征,数值数据更关注数据的整体效果[14],所以利用权重来衡量不同属性对簇的影响,则有
且 qij∈{0,1},i=1,2,…,n,j=1,2,…,k。dist(xi,Cj)为xi与Cj的距离,xi与Cj的距离相当于xi的每一个属性值与Cj簇中心的距离和。由于分类数据的属性值代表样本的重要特征,数值数据更关注数据的整体效果[14],所以利用权重来衡量不同属性对簇的影响,则有
(2)
式中:![]() 表示分类属性中第r个属性值与
表示分类属性中第r个属性值与![]() 的距离公式;
的距离公式;![]() 表示数值属性中第s个属性值与
表示数值属性中第s个属性值与![]() 的距离。权重
的距离。权重![]() 为一个k×d的矩阵,j=1,2,…,k,r=1,2,…,d。式(2)中
为一个k×d的矩阵,j=1,2,…,k,r=1,2,…,d。式(2)中![]() 表示Cj中第r个属性的影响,
表示Cj中第r个属性的影响,![]() 表示Cj第s个数值属性的影响,且满足条件:
表示Cj第s个数值属性的影响,且满足条件:
(3)
因此问题的关键有2个:①定义分类属性2个值之间的距离![]() 和数值属性2个值之间的距离
和数值属性2个值之间的距离![]() ②定义权重W。对于这两个问题的解决方案分别在2.1和2.2节中进行介绍。
②定义权重W。对于这两个问题的解决方案分别在2.1和2.2节中进行介绍。
2.1 属性值之间的距离定义
首先定义分类属性下的距离![]() 若
若![]() 则有
则有
(4)
因为distc(ar,m,ar,h)需要定义同一属性下2个属性的属性值之间的距离,而同一属性下的2个属性值之间的距离不仅与这个属性有关,还与其他分类属性有关系[8,11],也就是说ar,m和ar,h的距离不仅与Ar有关系,还与其他属性有关系。用ψr,t(ar,m,ar,h)表示Ar属性值ar,m和ar,h在At属性中的距离,t=1,2,…,dc。当ar,m和ar,h相同时,ψr,t(ar,m,ar,h)=0;当ar,m和ar,h不相同时,用![]() 和
和![]() 分别表示Ar属性值为ar,m和ar,h的条件下,在At属性值为at,1,at,2,…,at,vt的概率分布列,其中
分别表示Ar属性值为ar,m和ar,h的条件下,在At属性值为at,1,at,2,…,at,vt的概率分布列,其中![]() 表示Ar的属性值为ar,m的条件下At属性值为vt的概率。
表示Ar的属性值为ar,m的条件下At属性值为vt的概率。
当At为标称属性时,其距离可用其差异和![]() 来表示,同时为了使距离的取值范围在[0,1],应除以2,因此当At为标称属性时,这2个概率分布列的距离如定义1所示。
来表示,同时为了使距离的取值范围在[0,1],应除以2,因此当At为标称属性时,这2个概率分布列的距离如定义1所示。
定义1 若At为标称属性,![]() 与
与![]() 这2个概率分布列的距离可定义为
这2个概率分布列的距离可定义为![]()
当At为有序属性时,若用定义1的公式来定义距离,则[1,0,0,0]和[0,1,0,0]之间的距离与[1,0,0,0]和[0,0,1,0]之间的距离都等于1,也就是说当这个概率分布列分别代表着有序属性值的优秀、良好、及格和不及格时,它意味着优秀与良好的差距和优秀与及格的差距是一样的,很明显定义1中的公式并不能用来衡量有序属性值之间的距离,所以文献[12]定义并解释了有序属性的2个概率分布列的距离,有序属性的概率分布列的距离如定义2所示。
定义2 若At为有序属性,![]() 与
与![]() 这2个概率分布列的距离可定义为
这2个概率分布列的距离可定义为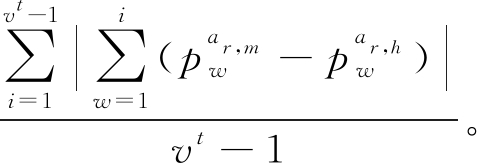
则ψr,t(ar,m,ar,h)可记为
ψr,t(ar,m,ar,h)=
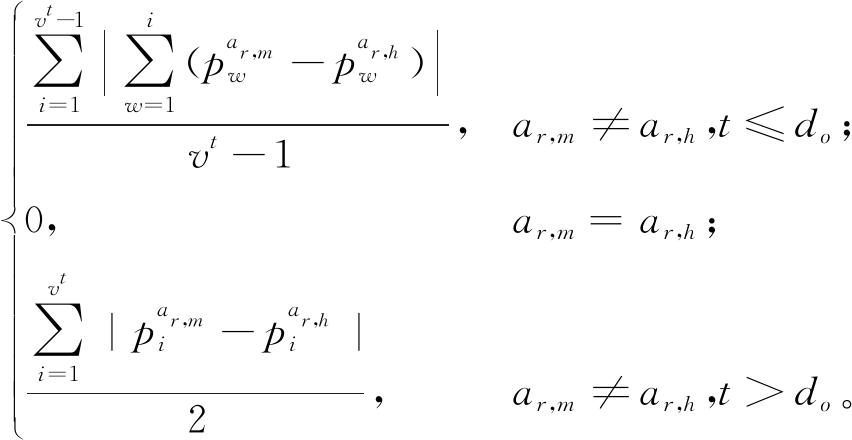
(5)
ψr,t(ar,m,ar,h)代表Ar的属性值ar,m和ar,h在At属性中的影响。对ψr,t(ar,m,ar,h)求和并求均值就是Ar的属性值ar,m和ar,h之间的距离。同时为了突出Ar为有序属性时的等级结构,利用相关工作中的解决方案,则distc(ar,m,ar,h)可表示为
distc(ar,m,ar,h)=
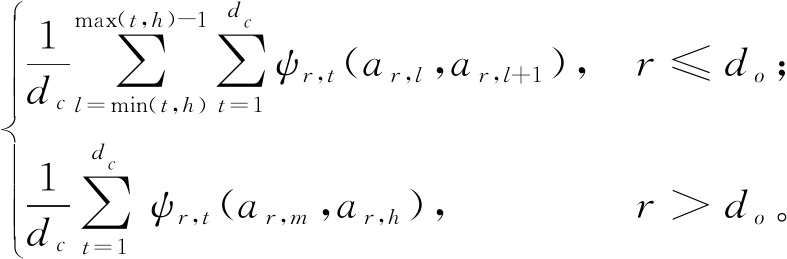
(6)
对于![]() 可直接运用经典的欧氏距离来计算两个数值
可直接运用经典的欧氏距离来计算两个数值![]() 和
和![]() 的距离。则
的距离。则
(7)
如表1数据集,A1属性值为“↑”的条件下A2属性值分别为“□”和“△”的概率分布列为[2/3,1/3];A1属性值为“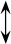 ”的条件下A2属性值分别为“□”和“△”的概率分布列为[1,0]。因A2为标称属性,则由式(5)可得ψ1,2(↑,
”的条件下A2属性值分别为“□”和“△”的概率分布列为[1,0]。因A2为标称属性,则由式(5)可得ψ1,2(↑,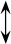 )=1/3,ψ1,1(↑,
)=1/3,ψ1,1(↑,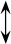 )=1/2,同理有ψ2,1(□,△)=1/4,ψ2,2(□,△)=1。则由式(6)可得distc(↑,
)=1/2,同理有ψ2,1(□,△)=1/4,ψ2,2(□,△)=1。则由式(6)可得distc(↑,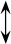 )=5/12,distc(□,△)=5/8。
)=5/12,distc(□,△)=5/8。
2.2 动态权重的定义
在同一个数据集中,一个属性对不同簇的重要程度可能不一样,不同的属性对同一个簇的重要程度也可能不一样。所以权重矩阵W需要研究第r个属性对簇Cj贡献,记为![]() 在量化第r个属性对簇Cj贡献时,考虑簇间差异和簇内距离这2个因素[14]。令第r个属性对簇Cj的簇间差异为
在量化第r个属性对簇Cj贡献时,考虑簇间差异和簇内距离这2个因素[14]。令第r个属性对簇Cj的簇间差异为![]() 它衡量了属性Ar区分簇Cj与其他簇的能力;令第r个属性对簇Cj的簇内距离为
它衡量了属性Ar区分簇Cj与其他簇的能力;令第r个属性对簇Cj的簇内距离为![]() 它评估了属性Ar的簇Cj是否具有紧凑的结构。
它评估了属性Ar的簇Cj是否具有紧凑的结构。
首先测量簇间差异![]() 令P1(r,j)和P2(r,j)分别为Ar在簇Cj内外的统计信息。
令P1(r,j)和P2(r,j)分别为Ar在簇Cj内外的统计信息。
当Ar为分类属性,常用簇内外的概率分布列的距离来表示簇间差异,定义1和定义2分别区分了标称属性和有序属性的概率分布列的距离,所以定义1和定义2同样可以量化分类属性簇内外概率分布的差异。令Ar在簇Cj内外的概率分布列分别为![]() 用Ho(P1(r,j),P1(r,j))表示Ar为有序属性时簇Cj的内外差异,则
用Ho(P1(r,j),P1(r,j))表示Ar为有序属性时簇Cj的内外差异,则
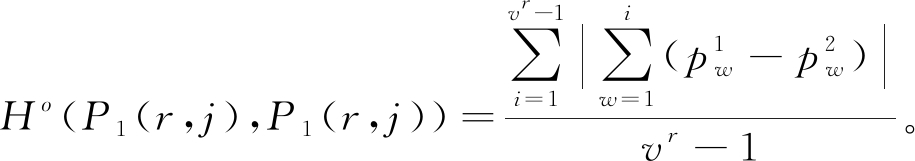
(8)
用Hn(P1(r,j),P1(r,j))表示Ar是标称属性时簇Cj的内外差异,则
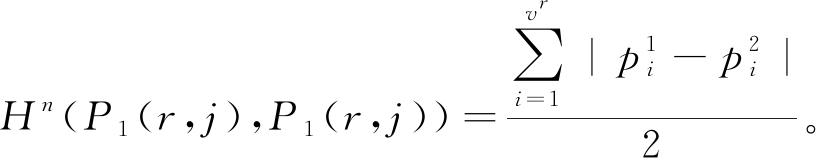
(9)
当Ar为数值属性,海林格距离[14-15]可以量化数值属性的簇间差异,令簇Cj内外的统计信息分别是![]() 其中
其中![]() 分别表示簇Cj内外Ar属性的均值。
分别表示簇Cj内外Ar属性的均值。![]() 和
和![]() 分别表示簇Cj内外Ar属性的方差,用Hu(P1(r,j),P1(r,j))表示当Ar为数值属性时簇Cj的内外差异,则
分别表示簇Cj内外Ar属性的方差,用Hu(P1(r,j),P1(r,j))表示当Ar为数值属性时簇Cj的内外差异,则
Hu(P1(r,j),P1(r,j))=
(10)
因此![]() 可记为
可记为

(11)
然后,属性Ar在簇Cj的簇内距离![]() 可以通过属性Ar的簇Cj的平均对象簇距离来估计,平均对象簇距离越小,代表了这个簇划分效果的越好,则
可以通过属性Ar的簇Cj的平均对象簇距离来估计,平均对象簇距离越小,代表了这个簇划分效果的越好,则
(12)
其中:
![]()
(13)
最后,对于![]() 和
和![]() 当
当![]() 越大,
越大,![]() 越小时代表了第r个属性对簇Cj贡献越大;当
越小时代表了第r个属性对簇Cj贡献越大;当![]() 越小,
越小,![]() 越大时代表了第r个属性对簇Cj贡献越小,则
越大时代表了第r个属性对簇Cj贡献越小,则
(14)
式中:![]() 和
和![]() 的取值范围都是
的取值范围都是![]() 是为了防止分母等于0,所以
是为了防止分母等于0,所以![]() 的取值范围为[0,1]。则属性权重
的取值范围为[0,1]。则属性权重![]() 可定义为
可定义为
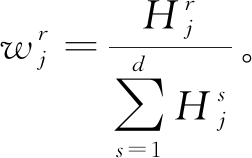
(15)
如表1所示,若所有对象分为C1、C2两簇,分别为{x1,x2,x3}和{x4,x5,x6},则这两簇的簇中心分别为(↑,□,8/15)和(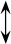 ,□,7/10),A1在簇C1内外的统计信息分别是P1(1,1)=[1,0,0],P2(1,1)=[0,2/3,1/3],则利用式(8)、(11)求得簇间差异
,□,7/10),A1在簇C1内外的统计信息分别是P1(1,1)=[1,0,0],P2(1,1)=[0,2/3,1/3],则利用式(8)、(11)求得簇间差异![]() 利用公式(12)求得簇内距离
利用公式(12)求得簇内距离![]() 并利用式(14)得属性A1对簇C1贡献
并利用式(14)得属性A1对簇C1贡献![]()
2.3 SCAH算法
在2.1节中定义了![]() 和
和![]() 距离公式,2.2节中的权重定义利用了簇间差异
距离公式,2.2节中的权重定义利用了簇间差异![]() 和簇内距离
和簇内距离![]() 这两个因素量化了属性对簇的贡献
这两个因素量化了属性对簇的贡献![]() 将属性值之间的距离和权重联立后得到一种新的异构属性数据距离度量:
将属性值之间的距离和权重联立后得到一种新的异构属性数据距离度量:
(16)
其中,![]() 和
和![]() 如式(6)和(7)所示,权重
如式(6)和(7)所示,权重![]() 和
和![]() 如式(15)所示。
如式(15)所示。
现讨论式(6)和式(16)的性质。对于同一属性的属性值ar,m,ar,h,ar,s,式(6)满足以下性质:
(1)distc(ar,m,ar,h)≥0;
(2)当ar,m=ar,h时,distc(ar,m,ar,h)=0;
(3)distc(ar,m,ar,h)=distc(ar,h,ar,m);
(4)distc(ar,m,ar,h)≤distc(ar,m,ar,s)+
distc(ar,s,ar,h)。
对于任意数据对象xi、xj、xt,式(16)也满足以下性质:
(1)dist(xi,xj)≥0;
(2)当xi=xj时,dist(xi,xj)=0;
(3)dist(xi,xj)=dist(xj,xi);
(4)dist(xi,xj)≤dist(xi,xt)+dist(xt,xj)。
由于式(6)满足距离度量的条件,式(16)也满足距离度量的条件,因此式(16)中的dist(xi,Cj)是一个距离度量。
最后利用式(16)提出了新的子空间聚类算法SCAH。SCAH的迭代步骤如下。
步骤1 输入数据集X和k、do、dc、d;
步骤2 从X随机选取k个对象u1,u2,…,uk作为簇中心,初始化权重![]()
步骤3 令Cj=∅,j=1,2,…,k;
步骤4 利用式(16)计算对象xi,i=1,2,…,n与uj(j=1,2,…,k)的距离dist(xi,uj);
步骤5 记![]()
Cj∪{xi};
步骤6 重复步骤4~5,直到所有样本划分完成;
步骤7 更新C1,C2,…,Ck的簇中心;
步骤8 利用式(8)~(15)更新权重W;
步骤9 重复步骤4~8,直到C1,C2,…,Ck不再改变,输出簇C1,C2,…,Ck。
3 实验部分
为了验证SCAH的有效性,使用了11个真实数据集,在3个聚类效果评估指标上与6个异构数据聚类算法进行比较,设计了3个实验来验证SCAH在异构属性数据集的有效性。
3.1 实验设置
11个数据集都来自UCI机器学习数据库,其中包含5个纯分类数据、3个纯数值数据和3个异构属性数据,所有数据集缺失的对象都被删除。do、dn、du分别表示有序属性、标称属性和数值属性的属性个数,n表示数据集的对象个数。数据集的具体信息如表2所示。
表2 数据集属性说明
Table 2 Statistics of the 11 data sets
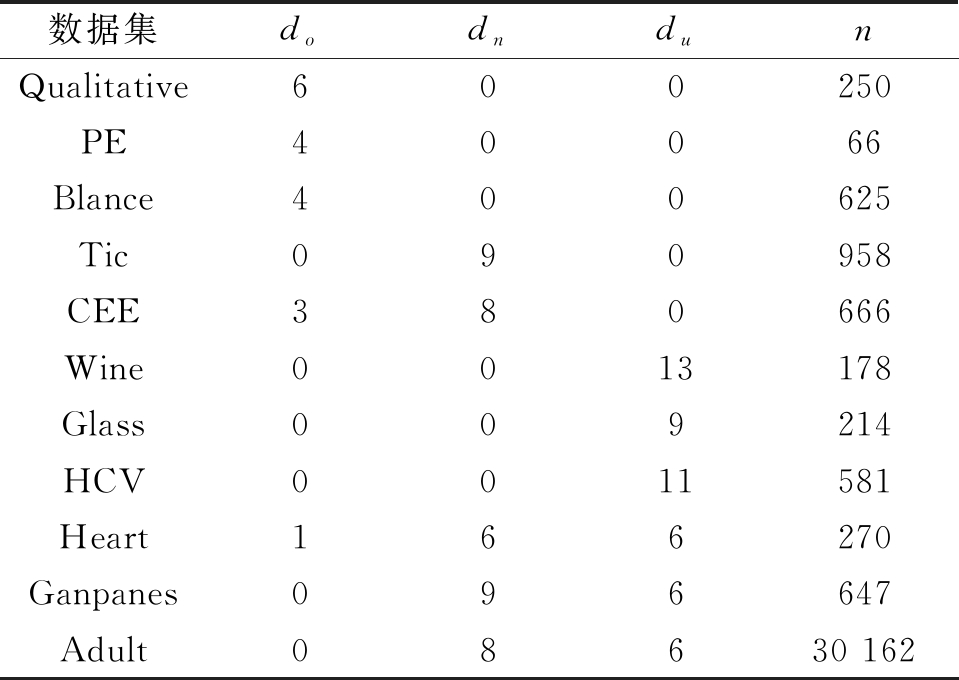
数据集dodndunQualitative600250PE40066Blance400625Tic090958CEE380666Wine0013178Glass009214HCV0011581Heart166270Ganpanes096647Adult08630 162
分别利用3个聚类指标来衡量聚类的效果,它们是聚类精度(CA),调整的兰德指数(ARI)和归一化信息(NMI)。公式分别为
(17)
ARI=(RI-E(RI))/(max(RI)-E(RI));
(18)
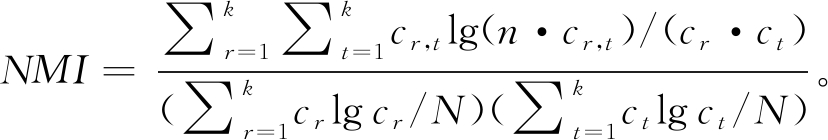
(19)
式中:ci表示第i个数据的真实标签;map(li)为映射到真实标签后的预测标签值,当ci=map(li),δ(ci,map(li))=1,当ci≠map(li),δ(ci,map(li))=0;E(RI)、max(RI)为RI的均值和最大值;k、cr、ct和cr,t分别表示类标签的数量,预测标签值为r的数量,真实标签值为t的数量和同时满足预测标签值为r,真实标签值为t的数量。NMI从信息理论角度来衡量预测标签和真实标签的一致性。CA和NMI的取值范围都为[0,1];ARI的取值范围为[-1,1]。当指标值越大,代表聚类的效果越好。
为了验证SCAH的聚类效果,将SCAH分别与传统的聚类算法、经典的聚类算法和前沿的聚类算法进行比较。其中WKM[7]是异构属性数据聚类算法里比较常用的算法,可作为传统的聚类算法来比较;WOCIL[14]是经典的异构属性数据子空间聚类算法;CMS[9]和UDM[11]是较为前沿的分类数据距离度量,将它们分别与k-Prototypes算法和WOCIL算法结合得到的KP+CMS算法、KP+UDM算法、WOCIL+ CMS算法和WOCIL+UDM算法,且 KP+UDM和WOCIL+UDM是区分了有序属性的聚类算法。
实验一利用纯分类属性数据来验证SCAH在分类数据集中的有效性;实验二利用纯数值属性数据验证SCAH在数值数据集中的有效性;实验三利用异构属性数据集来验证SCAH在异构属性数据集中的有效性。为了保证实验的公平,这6个聚类算法都随机选取k个聚类中心,其中k是从数据集的标签中获取的,并重复10次后用聚类指标的平均值和标准差作为实验结果,用“平均值±标准差”来表示,其中效果最好的数值用黑体来表示。当ARI为负数时,用“-”来表示。由于KP+CMS和KP+UDM在纯数值数据中的结果是一样的,同时WOCIL+ CMS和WOCIL+UDM在纯数值数据中的结果与WOCIL是一样的,所以KP+UDM、WOCIL+ CMS和WOCIL+UDM的实验结果不在表4列出。具体实验结果如表3~5所示。
3.2 实验分析
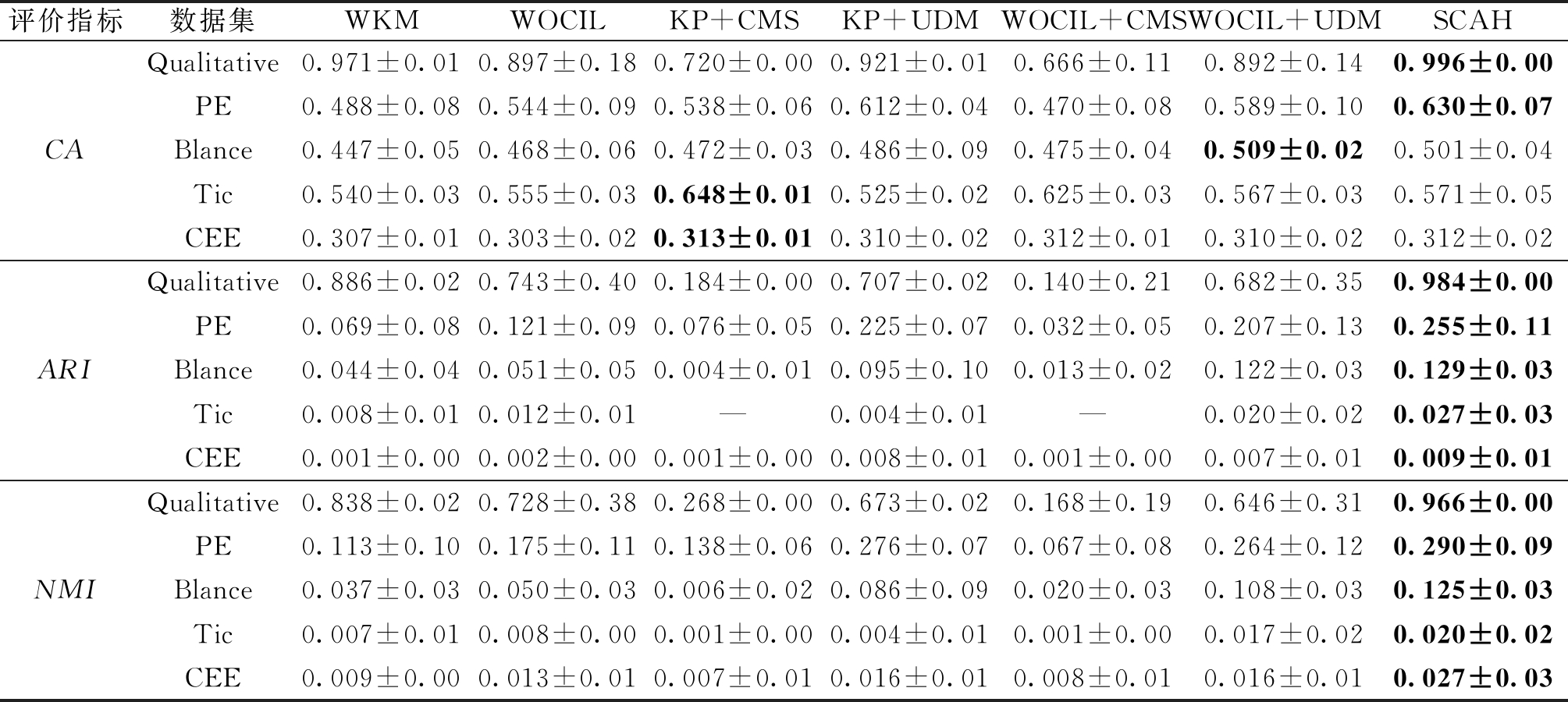
实验一的结果如表3所示,在只有有序属性的分类数据集Qualitative、PE和Blance中,整体上来说SCAH的聚类效果是最好的,特别是与WKM、WOCIL、KP+CMS和WOCIL+ CMS的实验结果相比,SCAH的效果非常显著,这表明了在分类数据中区分有序属性是有效的。在只有标称属性的分类数据集Tic中,SCAH的聚类效果也较好,但是CA的结果没有KP+CMS好,这是因为SCAH的最大优势是衡量有序属性的距离。在CEE中,SCAH的聚类效果仍是最好的。综上所述,SCAH区分有序属性和标称属性的距离定义和权重定义在纯分类数据中是有效的。
表3 不同算法在纯分类属性数据集上的聚类效果
Table 3 Experimental results of different heterogeneous-attribute data clustering algorithms on categorical data sets
评价指标数据集WKMWOCILKP+CMSKP+UDMWOCIL+CMSWOCIL+UDMSCAHCAQualitative0.971±0.010.897±0.180.720±0.000.921±0.010.666±0.110.892±0.140.996±0.00PE0.488±0.080.544±0.090.538±0.060.612±0.040.470±0.080.589±0.100.630±0.07Blance0.447±0.050.468±0.060.472±0.030.486±0.090.475±0.040.509±0.020.501±0.04Tic0.540±0.030.555±0.030.648±0.010.525±0.020.625±0.030.567±0.030.571±0.05CEE0.307±0.010.303±0.020.313±0.010.310±0.020.312±0.010.310±0.020.312±0.02ARIQualitative0.886±0.020.743±0.400.184±0.000.707±0.020.140±0.210.682±0.350.984±0.00PE0.069±0.080.121±0.090.076±0.050.225±0.070.032±0.050.207±0.130.255±0.11Blance0.044±0.040.051±0.050.004±0.010.095±0.100.013±0.020.122±0.030.129±0.03Tic0.008±0.010.012±0.01—0.004±0.01—0.020±0.020.027±0.03CEE0.001±0.000.002±0.000.001±0.000.008±0.010.001±0.000.007±0.010.009±0.01NMIQualitative0.838±0.020.728±0.380.268±0.000.673±0.020.168±0.190.646±0.310.966±0.00PE0.113±0.100.175±0.110.138±0.060.276±0.070.067±0.080.264±0.120.290±0.09Blance0.037±0.030.050±0.030.006±0.020.086±0.090.020±0.030.108±0.030.125±0.03Tic0.007±0.010.008±0.000.001±0.000.004±0.010.001±0.000.017±0.020.020±0.02CEE0.009±0.000.013±0.010.007±0.010.016±0.010.008±0.010.016±0.010.027±0.03
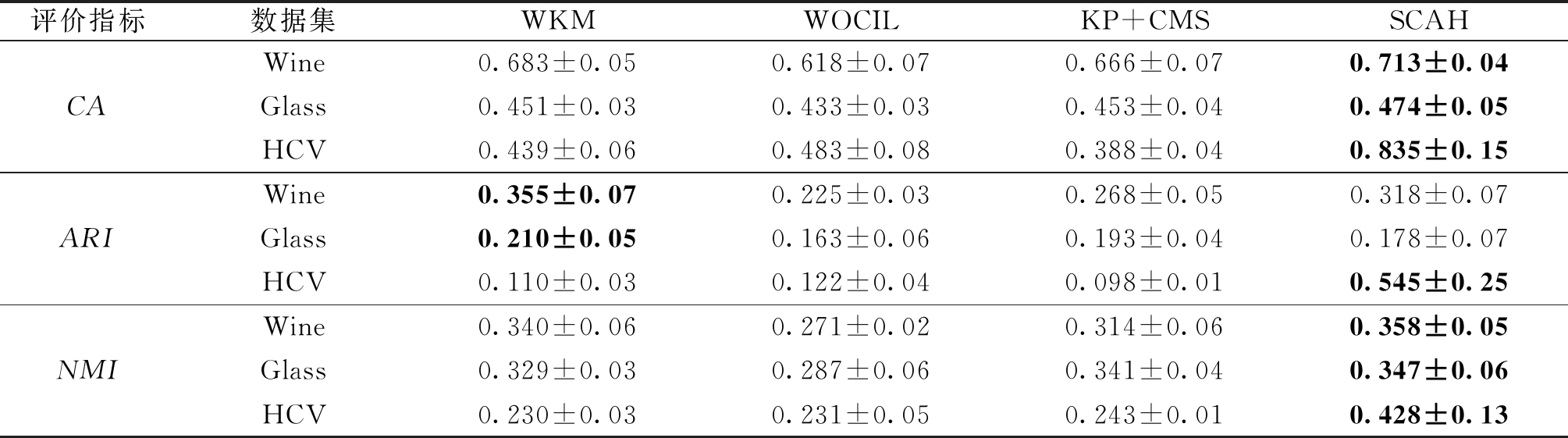
实验二是验证SCAH在纯数值数据中的有效性,如表4所示。其中WKM、KP+CMS和 SCAH的区别是权重的定义。SCAH的聚类效果总体上来说是比较好的,这是因为WKM的最优权重容易陷入局部最优,并不能真正表示属性的重要性。SCAH的效果比WOCIL好的原因是SCAH同时利用数值属性数据的信息和对象与簇内外之间的统计信息这2个角度来定义的距离,比WOCIL更能衡量数值属性值的真实距离。所以SCAH适用于纯数值属性的数据集。
表4 不同算法在纯数值属性数据集上的聚类效果
Table 4 Experimental results of different heterogeneous-attribute data clustering algorithms on numerical data sets
评价指标数据集WKMWOCILKP+CMSSCAHCAWine0.683±0.050.618±0.070.666±0.070.713±0.04Glass0.451±0.030.433±0.030.453±0.040.474±0.05HCV0.439±0.060.483±0.080.388±0.040.835±0.15ARIWine0.355±0.070.225±0.030.268±0.050.318±0.07Glass0.210±0.050.163±0.060.193±0.040.178±0.07HCV0.110±0.030.122±0.040.098±0.010.545±0.25NMIWine0.340±0.060.271±0.020.314±0.060.358±0.05Glass0.329±0.030.287±0.060.341±0.040.347±0.06HCV0.230±0.030.231±0.050.243±0.010.428±0.13
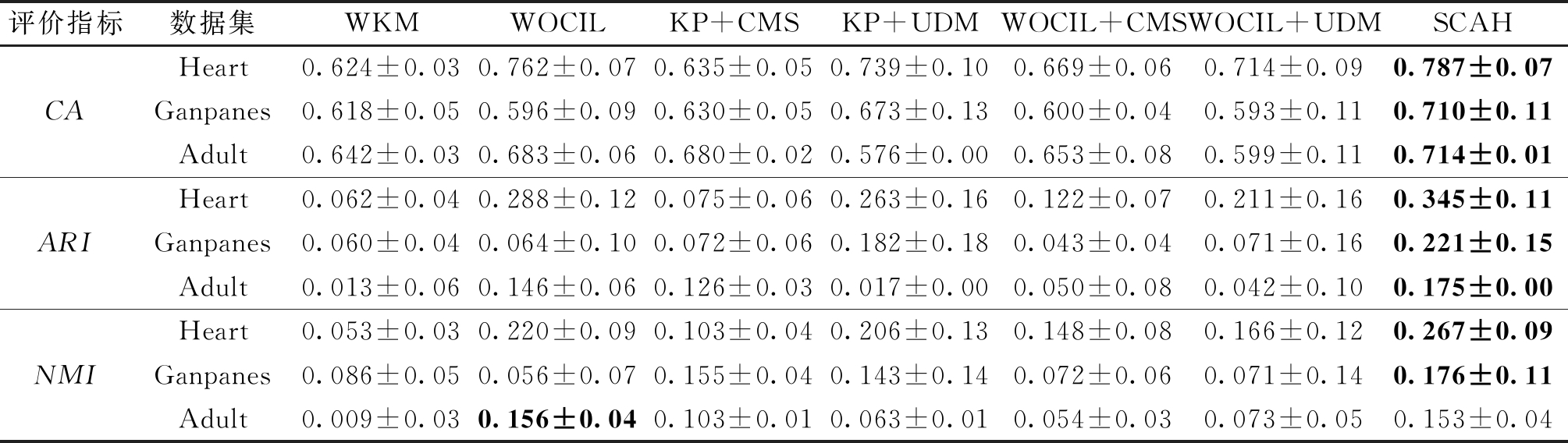
实验三的结果如表5所示,在既有分类属性和数值属性的数据集中,整体上来说SCAH的聚类效果是最好的,这表明了SCAH区分有序属性、标称属性、数值属性的距离定义和动态权重的结合能更好地量化异构属性数据的距离,更能为异构数据集找到最佳的分区。
表5 不同算法在异构属性数据集上的聚类效果
Table 5 Experimental results of different heterogeneous-attribute data clustering algorithms on heterogeneous-attribute data sets
评价指标数据集WKMWOCILKP+CMSKP+UDMWOCIL+CMSWOCIL+UDMSCAHCAHeart0.624±0.030.762±0.070.635±0.050.739±0.100.669±0.060.714±0.090.787±0.07Ganpanes0.618±0.050.596±0.090.630±0.050.673±0.130.600±0.040.593±0.110.710±0.11Adult0.642±0.030.683±0.060.680±0.020.576±0.000.653±0.080.599±0.110.714±0.01ARIHeart0.062±0.040.288±0.120.075±0.060.263±0.160.122±0.070.211±0.160.345±0.11Ganpanes0.060±0.040.064±0.100.072±0.060.182±0.180.043±0.040.071±0.160.221±0.15Adult0.013±0.060.146±0.060.126±0.030.017±0.000.050±0.080.042±0.100.175±0.00NMIHeart0.053±0.030.220±0.090.103±0.040.206±0.130.148±0.080.166±0.120.267±0.09Ganpanes0.086±0.050.056±0.070.155±0.040.143±0.140.072±0.060.071±0.140.176±0.11Adult0.009±0.030.156±0.040.103±0.010.063±0.010.054±0.030.073±0.050.153±0.04
综上所述,实验结果表明了SCAH不仅适用于异构属性数据集,也适用于纯分类属性和纯数值属性的数据集。同时实验也表明:SCAH中区分有序属性、标称属性、数值属性的距离定义和动态权重对于异构属性数据聚类的有效性。
4 结论
本文基于新的距离度量提出了一种新的异构属性数据子空间聚类算法SCAH。与现有的异构属性聚类算法相比,①SCAH的属性值之间的距离定义和动态权重的定义都区分了有序属性的结构特征,更能充分地利用异构属性数据的统计信息;②将距离公式和动态权重联合后,使SCAH在聚类过程能更好地利用距离公式和动态权重协作搜索到更优的样本划分;③SCAH不仅在异构属性数据中有优异的聚类效果,在纯分类数据和数值数据中也有优异的聚类效果,通过在11个种类各异的真实数据集上的对比实验,验证了SCAH的有效性。
[1] 姜鸣, 赵红宇, 刘学良. 一种基于聚类分析的自适应步态检测方法[J]. 郑州大学学报(工学版), 2017, 38(3): 63-67.
JIANG M, ZHAO H Y, LIU X L. An adaptive gait detection method based on clustering analysis[J]. Journal of Zhengzhou University (Engineering Science), 2017, 38(3): 63-67.
[2] 王军芬,刘培跃,董建彬,等.用于分割无损检测图像的快速模糊C均值算法[J].郑州大学学报(工学版),2022,43(6):42-48.
WANG J F, LIU P Y, DONG J B, et al. Fast fuzzy C means algorithm for segmentation of non-destructive testing image[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(6):42-48.
[3] AGRESTI A. An introduction to categorical data analysis[M]. New York:John Wiley & Sons, 2018.
[4] HAMMING R W. Error detecting and error correcting codes[J]. The Bell System Technical Journal, 1950, 29(2): 147-160.
[5] AHMAD A, KHAN S S. Survey of state-of-the-art mixed data clustering algorithms[J]. IEEE Access,2019,7: 31883-31902.
[6] HUANG Z X. Clustering large data sets with mixed numeric and categorical values[C]//Proceedings of the First Pacific-Asia Conference on Knowledge Discovery and Data Mining.New York:Springer,1997: 21-34.
[7] HUANG J Z, NG M K, RONG H Q, et al. Automated variable weighting in k-means type clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(5): 657-668.
[8] IENCO D, PENSA R, MEO R. From context to distance: learning dissimilarity for categorical data clustering[J]. ACM Transactions on Knowledge Discovery From Data, 2012, 6,(1): 1-25.
[9] JIAN S L, CAO L B, LU K, et al. Unsupervised coupled metric similarity for non-IID categorical data[J]. IEEE Transactions on Knowledge and Data Engineering, 2018, 30(9): 1810-1823.
[10] AGRESTI A. Analysis of ordinal categorical data[M]. Hoboken: Wiley, 2010.
[11] ZHANG Y Q, CHEUNG Y M. A new distance metric exploiting heterogeneous interattribute relationship for ordinal-and-nominal-attribute data clustering[J]. IEEE Transactions on Cybernetics, 2022, 52(2): 758-771.
[12] ZHANG Y Q, CHEUNG Y M. Learnable weighting of intra-attribute distances for categorical data clustering with nominal and ordinal attributes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(7): 3560-3576.
[13] CHEUNG Y M, JIA H. Categorical-and-numerical-attribute data clustering based on a unified similarity metric without knowing cluster number[J]. Pattern Recognition, 2013, 46(8): 2228-2238.
[14] JIA H, CHEUNG Y M. Subspace clustering of categorical and numerical data with an unknown number of clusters[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(8): 3308-3325.
[15] OOSTERHOFF J, VAN ZWET W R. A note on contiguity and hellinger distance[EB/OL].(2011-01-01)[2022-03-12]. https://doi.org/10.1007/978-1-4614-1314-1_6.