约束满足问题(constraint satisfaction problem, CSP)[1]又称约束网络,在计算机科学、数学和物理学等学科中占据重要地位。CSP在许多领域(如模式识别、交通规划和人机交互等领域)中发挥着重要的作用。从旅行商、图着色等经典问题到神经网络、图像识别等大型应用问题,都可以转化为CSP问题进行求解。
布尔可满足性问题(boolean satisfiability problem, SAT)是CSP问题的子问题,同时也是一个NP完全(NP-complete)问题[2]。现阶段,解决SAT问题的算法有完备算法、非完备算法及组合算法。近年来这3类算法都取得了一些研究成果,如DPLL(davis putnam logemann loveland)算法[3]、消息传送算法[4]、演化计算算法[5]等。然而,针对大规模问题实例、难满足问题实例等,多数求解器无能为力。研究发现,SAT问题的求解难度与其结构特征紧密联系。因此,研究SAT问题的结构特征对设计求解SAT问题的高效算法具有十分重要的意义。其中,相变、树宽、结构熵、DNA折纸术是研究SAT问题结构特征的4种常用度量模型。本文也将对上述4种度量模型的概念及其相关应用展开综述。首先,对相关知识进行介绍;其次,对4种度量模型的基本概念、相关原理及其在SAT问题的应用进行介绍;再次,指出研究SAT问题结构特征面临的挑战及研究方向;最后,总结全文。
1 相关知识
1.1 SAT问题
若干个文字的析取构成一个子句[6],记为C=L1∨L2∨…∨Ln,若干子句的合取构成一个合取范式(conjunctive normal form, CNF)公式,记为F=C1∧C2∧…∧Cm,SAT判定问题指是否存在一组指派能够使CNF公式为真。
1.2 因子图
给定CNF公式F=C1∧C2∧…∧Cm,其中,子句为C1,C2,…,Cm,变元为x1,x2,…,xn,为方便表示,将xi简记为i。公式F能够表示为一个二部网络G=(C∪X,E),G称为因子图,如图1所示。图1中的一侧以布尔变元集为变元节点(图1中用圆形表示),而另一侧以子句集为子句节点(图1中用矩形表示)。因子图中的实边和虚边包含CNF公式的2种不同的信息。

图1 因子图
Figure 1 Factor graph
实边:(Ci,j)∈E⟺变元xi在子句Ci中正出现。
虚边:(Ci,j)∈E⟺变元xi在子句xi中负出现。
例:对于一个CNF公式,F=(![]() x1∨x2∨x3)∧(
x1∨x2∨x3)∧(![]() x1∨x2∨
x1∨x2∨![]() x3)∧(x2∨
x3)∧(x2∨![]() x3∨
x3∨![]() x4)={a1,a2,a3}的因子图G=(C∪X,E)。
x4)={a1,a2,a3}的因子图G=(C∪X,E)。
2 解空间
聚类是指将数据空间实体划分,把相似实体划分为一个簇。同一类簇的任意2个点的距离小于不同簇的任意2个点间的距离[7]。目前已有部分研究者用聚类研究SAT问题解空间的性质。Mezard等[8]证明XOR-SAT问题中存在解聚类成簇的现象;Maneva等[9]引入覆盖的概念,进一步证明随机k-SAT问题(子句长度为k)解空间的聚类现象。接着,Achlioptas等[7]证明了聚类的存在性;莫孝玲等[6]分析研究了CNF公式赋值空间的可满足解的聚类现象。CNF公式赋值空间中存在可满足解聚类现象,并且随着约束密度的变化可满足解聚类的个数也发生变化。
k-SAT问题是研究较多的一类SAT问题。自从统计物理学家利用复本对称破缺平均场理论预测出k-SAT问题的解空间在临界约束密度结构上发生定性改变后,各个领域的研究人员开始通过概率分析、算法分析、数理统计等方法对k-SAT问题的结构特征进行大量研究,尝试找出k-SAT问题的难解本质。解空间被划分为许多子空间,这种突变现象被称为簇集相变。
相变研究SAT问题解空间的分布情况,观察满足与不可满足之间的变化规律,即解的临界特征。随机k-SAT问题是SAT问题的子问题。对于随机k-SAT问题的实例产生模型G(n,k,m),统计结果表明,子句约束密度α=m/n(m为子句数,n为变元数)是一个关键的参数,该参数刻画了随机k-SAT问题解的临界特征和实例的难解程度。然而,对于正则SAT问题,子句约束密度恒为常数,该参数已无法反映正则SAT问题的相变现象。近年来,研究人员利用一阶矩和二阶矩证明了SAT相变问题。一阶矩方法的理论依据是马尔可夫不等式[10],通过一阶矩方法可得到随机CNF公式高概率不可满足判定条件。一阶矩引理如下。
引理1 设X为随机变量且为非负整数值,对任意的a>0,都有
(1)
使用方差估计特定随机事件发生概率的方法称为二阶矩方法,该方法的理论依据是切比雪夫不等式[11]。二阶矩引理如下。
引理2 如果X为随机变量且为非负整数值,那么
p(X=0)≤p(|X-E[X]|≥E[X])≤
(2)
当前,对相变性质的研究主要集中于k-NAESAT[12]、Regular 2-SAT[13]以及Regular NAE-SAT[14]等具有特殊结构的SAT问题的确切相变点。张明明等[15]发现在规模较小的情况下,正则3-SAT问题的相变点有偏移现象,并从变元自由度的角度给出定性解释。周锦程等[16]不但证明严格随机正则(3,s)-SAT问题可满足临界点的上界,而且给出的严格随机正则(3,s)-SAT实例产生模型可以构造在相变点s=11处的随机3-SAT难解实例。王永平等[17]使用一阶矩方法,研究出取定s的严格d-正则随机(3,2s)-SAT问题的可满足临界值的一个下界。进一步,周锦程等[18]又以覆盖总数作为一阶矩方法的随机变量,获得随机正则(k,r)-SAT问题可满足临界值点的一个最紧致界。Ding等[14]研究了随机(d,k)-NAE-SAT问题的相变,并给出一个关于变元出现次数d的相变控制参数。综述至此发现,关于规则问题相变的证明技术主要基于一阶矩和二阶矩。然而,使用二阶矩时需要处理一个高阶无穷小量,这是困难的,因此,还有大量的开放问题未获得严格的相变点。
3 树宽
随着SAT问题研究的不断深入,基于图论的方法成为重要的研究方法之一,图结构的特殊性质和表达能力在SAT问题研究中得到应用。这些图结构的性质逐渐成为探索SAT问题难解本质和设计SAT问题求解算法的重要方法之一。聂国霞等[19]将CNF公式转化成因子图,通过研究因子图的结构和性质,进而研究CNF公式的可满足性。因为子句和变元之间的复杂联系,所以SAT实例存在潜在的结构特征。刘纯[20]也将SAT实例表示为图模型,利用数据挖掘技术分析子句和子句之间以及变元之间的潜在结构信息。
1972年,Bertele等[21]首次引入树宽(tree width),后来,Arnborg等[22]确定任意图的树宽本身就是一个NP难问题。20世纪80年代发展起来的图子式理论是重要的图理论分支。Fellows等[23]在1988年就研究了图子式理论在算法分析与设计中的应用。树分解是将给定图G的节点集合V划分,使图G尽可能地划分为树形结构,通过研究树的结构信息来刻画原图的一些性质。树宽是衡量图树分解程度好坏的指标。正如Enright等[24]的研究表明,如果随机组合2个非常简单的层,每个层由n个顶点的路径组成,那么所生成的网络的树宽将以高概率随n增长。
无向图的树宽是G的所有树分解中的宽度最小值。图的树宽和弦图关系密切,借助弦图可给出树宽的等价定义,即图G的树宽为其所有超弦图H中最小的一个最大团减1。
虽然树分解的结构是树宽的经典表现形式,但如果树分解的形式是受限制的,则许多问题可以用动态规划来描述和解决。路径分解是树分解的另一个版本,它应用了一些动态规划算法的定义,换言之,图的路径分解是动态规划算法的重要组成部分。因此,图G的路径分解是G的树分解,其中底层的树T是一条路径。
人工智能、数据库和逻辑电路设计等领域的诸多实际应用通常采用启发式算法构造树分解。在以往的研究中,构造树分解的启发式方法一般有2类。一类是基于消点序的启发式搜索算法。所谓消点(也可以称为消元)是指删除无向图G中的某个节点v以及与v相连的边,同时在剩下的图中添加一些边,使得v原来的邻节点构成一个三角剖分。通过在初始的图G中逐个消元的方法可以生成G的一个消点序,根据这个消点序便能构造出图G的一个树分解。由于消点序的选择存在一定的随机性,因此,不同的消元顺序可以得到不同的树分解。此外,由于求解最优消元顺序是一个NP难问题,研究者常采用启发式方法求解图的消点序。如最小度搜索算法(minimum degree search)[25]、最大势搜索算法(maximum cardinality search)及其改进算法[26]、最小缺边搜索算法(minimum deficiency search)[27]等。另一类是基于割集的启发式搜索算法,即通过在初始图中找到某些割集来构造树分解。所谓割集是指在无向图G=(V,E)中,若存在E′⊆E使得p(G-E′)>p(G),且对于任意的E″⊂E′,均有p(G-E″)>p(G),则称E′为G的边割集,简称为割集。基于割集的方法来构造图G的树分解的过程相较于利用消点序的方法更复杂,但Amir[28]验证了基于割集的方法在一些问题研究中更为有效。
事实上,树分解在众多研究领域一直都有着重要的用途。Arnborg等[29]利用树分解来求解组合优化问题;Koster等[30]讨论了利用树分解解决计算生物学的问题;Zhao等[31]探讨了利用树分解来解决社交网络问题。
随着研究的不断深入,Adcock等[32]引入特殊的树形结构,将正则CNF公式的因子图转换为树形结构,并证明随机正则(3,r)-SAT问题的可能相变点。莫孝玲等[6]通过引入树分解技术,将CNF公式的因子图分解为一棵树。谢志新等[33]提出一种度量命题公式结构特征的树宽算法,并给出不同规模随机实例算法收敛时的树宽充分条件。
4 结构熵
信息传播算法[34]是否收敛取决于因子图的结构。近年来,随着实例集不断增大,因子图的结构也变得复杂。由于信息熵可以度量不确定性,是概率分布的静态度量方法。在信息论中,根据概率分布选择节点,则熵值反映了确定节点代码所需的平均信息量。所以,在通信领域中,信息熵只测量点与点之间的单个信息。在此基础上,Li等[35]首次提出结构熵。结构熵被定义为节点编码所需的最小总位数,该节点可通过随机游走来访问。与信息熵不同,结构熵是一种能够反映网络复杂性的动态度量方法,因此,结构熵弥补了信息熵的缺陷。不确定信息最小化是实现网络结构熵度量过程中遵循的基本原则。为保证因子图不确定信息最小化,对因子图进行精确的社区结构划分。
Newman等[36]于2004年首次提出模块度,模块度能定量地评估不同社区划分算法结果的准确度以及评价网络中社区结构的质量。虽然模块度有着清晰的定义,但无法识别小规模的社区结构,即存在分辨率[37]的问题。基于模块度的社区发现算法有GN算法、Louvain算法、FN算法[36]等。其实最初设计模块度的目的是用来对GN算法进行质量评估。随着研究的不断深入,该模型得到研究人员的普遍认可,于是,衍生出大量与模块度相关的算法。Rotta等[38]对Louvain算法加入更多层次的细化阶段。Blondel等[39]提出图折叠算法(gragh folding algorithm),该算法也称为模块性优化算法,因为该算法具有时间复杂度低的特点,所以相关研究人员认为它是目前性能最佳的社区划分算法。
4.1 二维结构熵
若一个具有n个节点、m个变量的图G=(V, E)是带权无向连通图,V为图G中的顶点集,E为图G中的边集。设P={X1,X2,…,XL}为节点集合V的划分。
定义划分P的结构熵如下:
(3)
式中:L为划分P中的划分个数;nj为Xj中的顶点数;![]() 为社区Xj中第 i个节点的度数;Vj=Vol(Xj);gj为社区Xj与其他社区相连的边数。二维结构熵定义为
为社区Xj中第 i个节点的度数;Vj=Vol(Xj);gj为社区Xj与其他社区相连的边数。二维结构熵定义为
H2(G)=min{Hp(G)}。
(4)
4.2 K维结构熵
对于无向连通图G=(V,E),假设T为社区模块树,定义编码树的结构熵如下:
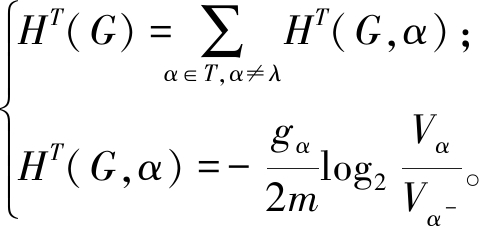
(5)
式中:m=|E|;Vα为Tα中所有节点的度数之和,即集合Tα的体积;gα为从Tα内的节点到Tα外的节点的边数。连通图G的K维结构熵定义:
HK(G)=minT:h(T)≤K{HT(G)}。
(6)
其中T在G的所有编码树高度不高于维度K。
对于非连通图G的K维结构熵定义如下:
(7)
式中:Vol(Gj)为Gj的体积;G1,G2,…,GL为图G的所有连通分支。
K维结构信息是网络动态复杂性的一个指标,衡量网络交互、通信、操作等的复杂性。指标满足可加性、局部性、稳健性、局部和增量可计算性等基本属性。Brooks[40]将结构信息的量化问题列为计算机科学面临的三大挑战之首。Liu等[41]证明,结构信息是冯·诺依曼图熵的一个很好的近似,同时实现了可证明的精度、可扩展性和可解释性。熵测度起源于量子信息论,用于描述密度矩阵表示的量子系统的混合性。Braunstein等[42]首次使用冯·诺依曼图熵通过将缩放拉普拉斯矩阵视为密度矩阵来衡量图的复杂性。众所周知,拉普拉斯谱包含图的多尺度结构的丰富信息,因此,熵在复杂网络分析和模式识别的下游任务中得到广泛应用。
当前对结构熵的应用研究已经取得了一些成果。网络中各种行为的不确定性是网络复杂性的本质。Li等[35]的研究表明,最小化二维结构熵是检测网络自然社区结构的原则,并用K维结构熵度量K维网络的动态复杂性。Zhang等[43]发现解决命题公式的困难程度与d公式的结构熵大小有关,公式的压缩信息越小,求解公式就越困难。其次,提出了一种λ-近似策略来近似大型公式的结构熵。牛进等[44]提出了WPLPA算法,并基于二维结构熵提出命题公式的结构熵度量模型,给出BP算法收敛的充分条件,之后又利用结构熵表示命题公式的结构信息,给出WP算法收敛的充分条件。限于篇幅,不再一一赘述。
5 DNA折纸术
DNA折纸术是利用碱基互补配对原则和DNA分子所具有的结构特征,将一条较长的DNA单链(通常称为脚手架链)的特定区域进行折叠,并用较短的DNA片段(通常称为订书钉链)加以固定,构造出预期的纳米图案或结构。最终得到的结构大小、形状取决于特殊的订书钉链。与传统DNA自组装技术相比,DNA折纸术更容易组合出结构稳定、精密度高及可控性高的纳米结构,并且具有组装速度快、生物毒性较低、易于操作、纳米可寻址性和可编程性等优点。随着分子生物学、热力学及电子学技术的不断发展,DNA自组装的形式从一维到二维再到三维,在NP问题中起到不可或缺的作用。
1994年,Adleman教授[45]首次利用DNA分子实验解决了有向图的哈密顿问题。次年,Lipton[46]在Adleman的实验基础上,给出一种解决可满足性问题的DNA计算模型。2000年,Sakamoto等[47]利用DNA分子自组装,为可满足性问题的求解提供一种新方法。2002年,Braich等[48]利用DNA折纸术成功地解决了变量n=20的3-SAT问题。次年,张凤月等[49]首次提出了一种利用荧光标记的策略,解决了可满足问题。周康等[50]在2009年提出了解决可满足性问题的闭环DNA算法;Xiao等[51]在2013年给出了可满足性问题的DNA计算模型。2017年,马莹等[52]利用微流路芯片高压凝胶电泳,给出了可满足性问题的生物芯片DNA计算模型。2020年,陈哲[53]给出了一个利用动态DNA计算模型去解决3-SAT问题的方法。2021年,麻晶晶等[54]提出了一种利用DNA折纸术解决可满足性问题的DNA计算模型。
上述利用DNA求解的可满足性问题,几乎都不是大规模可满足性问题。然而,随着人工智能的发展,可满足性问题的规模越来越大,因此,找出基于DNA折纸术求解大规模可满足性问题的算法是值得研究的。
6 讨论与展望
首先,对各种SAT问题结构度量模型的优缺点进行总结和分析;其次,对各种模型在SAT问题上未来可能的应用进行讨论。表1总结了研究SAT问题结构的各种度量模型的优缺点。
表1 研究SAT结构特征的各种度量模型的优缺点
Table 1 The advantages and disadvantages of various measurement models for studying the structural characteristics of SAT
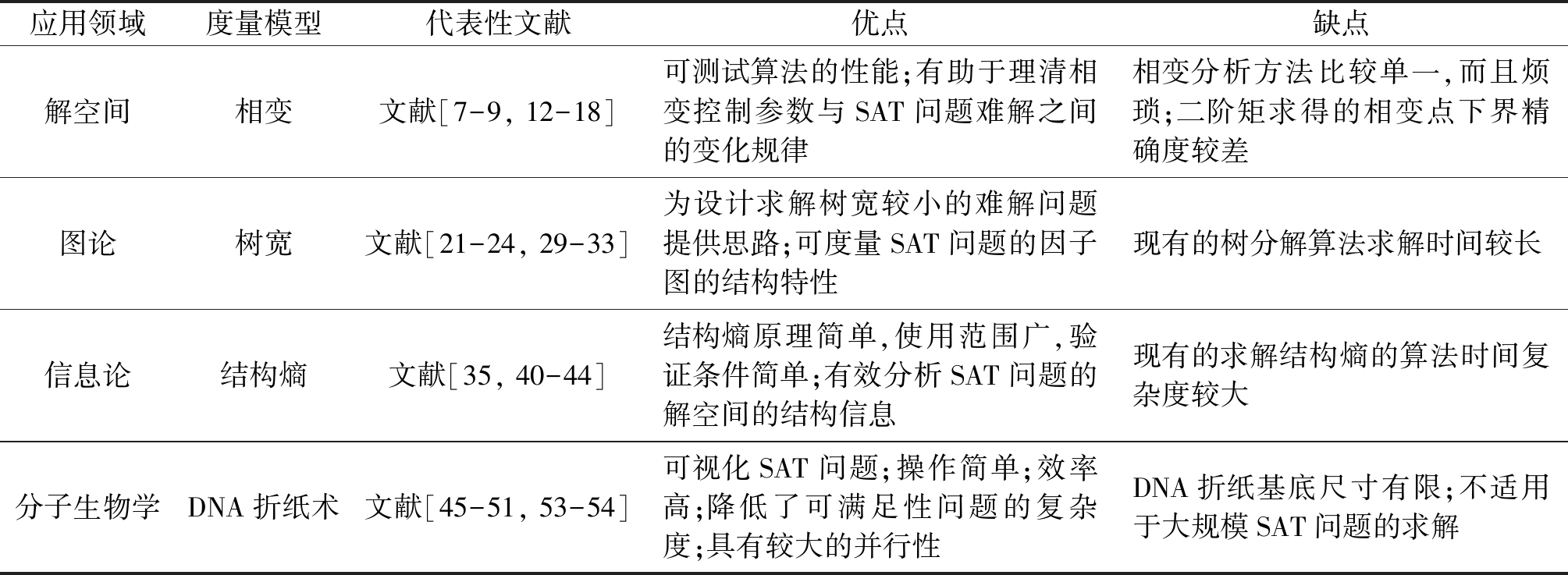
应用领域度量模型代表性文献优点缺点解空间相变文献[7-9, 12-18]可测试算法的性能;有助于理清相变控制参数与SAT问题难解之间的变化规律相变分析方法比较单一,而且烦琐;二阶矩求得的相变点下界精确度较差图论树宽文献[21-24, 29-33]为设计求解树宽较小的难解问题提供思路;可度量SAT问题的因子图的结构特性现有的树分解算法求解时间较长信息论结构熵文献[35, 40-44]结构熵原理简单,使用范围广,验证条件简单;有效分析SAT问题的解空间的结构信息现有的求解结构熵的算法时间复杂度较大分子生物学DNA折纸术 文献[45-51, 53-54]可视化SAT问题;操作简单;效率高;降低了可满足性问题的复杂度;具有较大的并行性DNA折纸基底尺寸有限;不适用于大规模SAT问题的求解
相变、树宽、结构熵和DNA折纸术等结构度量模型使可满足性问题的求解有了长足的发展,但仍存在许多值得深入研究的问题,主要包括以下方面。
(1)相变分析方面。深入研究一阶矩和局部最大值方法,探索相变点的精确上界。在运用二阶矩方法得到可满足性问题相变点的下界时,往往需要刻画组合解的空间结构,并且要处理一个关于常数1的高阶无穷小量问题,这是困难的。因此,探寻新方法(小子图条件)能够得到更优的下界。
(2)结构熵度量模型方面。计算模块度和结构熵本质上就是对图节点进行划分,现有结构熵的计算算法时间复杂度较高,可以利用性能较好的社区划分算法思想改进现有的结构熵计算方法。结构熵是度量图结构信息的有效方法,设计一种高效的基于结构熵指导的SAT求解器具有非凡意义。
(3)树分解算法方面。针对CNF公式实例的因子图,分析及比较现有树分解算法,提高SAT问题实例的因子图的树分解算法求解效率。
(4)DNA折纸术方面。深入研究DNA折纸计算模型,探索新的基于DNA求解SAT问题算法,改善DNA折纸术在超大规模的SAT问题效果。
(5)混合使用结构度量模型方面。深入理解命题公式的结构熵度量模型原理,建立结构熵与相变之间的详细变化规律,并分析基于结构熵的信息传播算法的收敛性。
(6)结构度量模型内在联系方面。深入理解相变、树宽、结构熵和DNA折纸术度量模型的内部度量原理,找出它们的内在联系,并分析出它们各自度量适用的SAT问题类型。
(7)信息传播算法的收敛性方面。信息传播算法的性能取决于命题公式的结构特征,因此,建立结构度量模型与信息传播算法收敛性之间的关系有重要意义。
(8)结构特征方面。根据可满足性问题的结构特征,优化已有SAT求解器,给出求解SAT问题的高效算法,并分析算法的收敛性及近似度等性能。
7 结语
自1991年以来,SAT问题受到研究人员的广泛关注,其在人工智能、密码学、数学、计算机科学等领域具有重要实际价值。本文重点研究SAT问题的结构特征,将结构度量模型划分为相变、树宽、结构熵、DNA折纸术,并概述总结了上述4种结构度量模型及其在SAT问题上的应用。最后,对未来研究SAT问题的结构特征可能面临的挑战及研究方向进行了讨论与展望。
[1] DYER M, FRIEZE A, MOLLOY M. A probabilistic analysis of randomly generated binary constraint satisfaction problems[J]. Theoretical Computer Science, 2003, 290(3): 1815-1828.
[2] VIZEL Y, WEISSENBACHER G, MALIK S. Boolean satisfiability solvers and their applications in model checking[J]. Proceedings of the IEEE, 2015, 103(11): 2021-2035.
[3] DAVIS M, PUTNAM H. A computing procedure for quantification theory[J]. Journal of the ACM, 1960, 7(3): 201-215.
[4] ZHAO C Y, ZHOU H J, ZHENG Z M, et al. A message-passing approach to random constraint satisfaction problems with growing domains[J]. Journal of Statistical Mechanics: Theory and Experiment, 2011, 2011(2): P02019.
[5] WANG H F, FAN H, LI F L. Quantum algorithm for solving some discrete mathematical problems by probing their energy spectra[J]. Physical Review A, 2014, 89: 012306.
[6] 莫孝玲, 许道云. CNF公式赋值空间上可满足解的概率性质[J]. 计算机科学与探索, 2018, 12(11): 1852-1861.
MO X L, XU D Y. Probabilistic properties of satisfiable solutions on space of assignments for CNF formula[J]. Journal of Frontiers of Computer Science and Technology, 2018, 12(11): 1852-1861.
[7] ACHLIOPTAS D, COJA-OGHLAN A, RICCI-TERSENGHI F. On the solution-space geometry of random constraint satisfaction problems[J]. Random Structures &Algorithms, 2011, 38(3): 251-268.
[8] MEZARD M, RICCI-TERSENGHI F, ZECCHINA R. Two solutions to diluted p-spin models and XORSAT problems[J]. Journal of Statistical Physics, 2003, 111(3): 505-533.
[9] MANEVA E, SINCLAIR A. On the satisfiability threshold and clustering of solutions of random 3-SAT formulas[J]. Theoretical Computer Science, 2008, 407(1/2/3): 359-369.
[10] MITZENMACHER M, UPFAL E. 概率与计算[M].冉启康等译. 北京: 机械工业出版社,2020.
MITZENMACHER M, UPFAL E. Probability and computing[M]. RAN Q K, et al. Translated. Beijing: China Machine Press, 2020.
[11] HARDY G H, LITTLEWOOD J E, P LYA G. Inequalities: a mathematical olympiad approach[M]. Cambridge: Cambridge University Press, 1952.
LYA G. Inequalities: a mathematical olympiad approach[M]. Cambridge: Cambridge University Press, 1952.
[12] COJA-OGLAN A, PANAGIOTOU K. Catching the k-NAESAT threshold[C]∥Proceedings of the Forty-fourth Annual ACM Symposium on Theory of Computing. New York: ACM, 2012: 899-908.
[13] BOUFKHAD Y, DUBOIS O, INTERIAN Y, et al. Regular random k-SAT: properties of balanced formulas[J]. Journal of Automated Reasoning, 2005, 35(1): 181-200.
[14] DING J, SLY A, SUN N K. Satisfiability threshold for random regular NAE-SAT[J]. Communications in Mathematical Physics, 2016, 341(2): 435-489.
[15] 张明明, 许道云. 正则3-SAT问题的相变现象[J]. 计算机科学, 2016, 43(4): 33-36.
ZHANG M M, XU D Y. Phase transition phenomenon of regular 3-SAT problem[J]. Computer Science, 2016, 43(4): 33-36.
[16] 周锦程, 许道云, 卢友军. 随机正则(k,r)-SAT问题的可满足临界[J]. 软件学报, 2016, 27(12): 2985-2993.
ZHOU J C, XU D Y, LU Y J. Satisfiability threshold of the regular random(k,r)-SAT problem[J]. Journal of Software, 2016, 27(12): 2985-2993.
[17] 王永平, 许道云. 取定s的严格d-正则随机(3, 2s)-SAT问题的可满足临界[J]. 软件学报, 2021, 32(9): 2629-2641.
WANG Y P, XU D Y. Satisfiability threshold of strictly d-regular random(3,2s)-SAT problem for fixed s[J]. Journal of Software, 2021, 32(9): 2629-2641.
[18] 周锦程, 许道云, 卢友军. 基于1RSB的正则(k,r)-SAT问题可满足临界[J]. 华中科技大学学报(自然科学版), 2017, 45(12): 7-13.
ZHOU J C, XU D Y, LU Y J. Satisfiability threshold of regular(k,r)-SAT problem via 1RSB theory[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2017, 45(12): 7-13.
[19] 聂国霞, 秦永彬, 许道云. 基于因子图求解(3, 4=)-CNF公式类下可满足问题[J]. 计算机与数字工程, 2013, 41(5): 686-689.
NIE G X, QIN Y B, XU D Y. Based on the factor graph for solving satisfiability problem of (3, 4=)-CNF formula class[J]. Computer &Digital Engineering, 2013, 41(5): 686-689.
[20] 刘纯. 基于聚类的SAT实例结构分析[D]. 武汉: 华中科技大学, 2015.
LIU C. The structural analysis of SAT instance based on clustering[D]. Wuhan: Huazhong University of Science and Technology, 2015.
[21] BERTELE U, BRIOSCHI F. Nonserial dynamic programming[M]. New York: Academic Press, 1972.
[22] ARNBORG S, CORNEIL D G, PROSKUROWSKI A. Complexity of finding embeddings in a k-tree[J]. SIAM Journal on Algebraic Discrete Methods, 1987, 8(2): 277-284.
[23] FELLOWS M R, LANGSTON M A. Nonconstructive tools for proving polynomial-time decidability[J]. Journal of the ACM, 1988, 35(3): 727-739.
[24] ENRIGHT J, MEEKS K. Deleting edges to restrict the size of an epidemic: a new application for treewidth[J]. Algorithmica, 2018, 80(6): 1857-1889.
[25] 雷莹. 树分解算法在可满足性问题中的应用研究[D]. 贵阳: 贵州大学, 2020.
LEI Y. Tree decomposition algorithm and application for the SAT[D]. Guiyang: Guizhou University, 2020.
[26] TARJAN R E, YANNAKAKIS M. Simple linear-time algorithms to test chordality of graphs, test acyclicity of hypergraphs, and selectively reduce acyclic hypergraphs[J]. SIAM Journal on Computing, 1984, 13(3): 566-579.
[27] HELL P, KIRKPATRICK D G. Algorithms for degree constrained graph factors of minimum deficiency[J]. Journal of Algorithms, 1993, 14(1): 115-138.
[28] AMIR E. Approximation algorithms for treewidth[J]. Algorithmica, 2010, 56(4): 448-479.
[29] ARNBORG S, PROSKUROWSKI A. Linear time algorithms for NP-hard problems restricted to partial k-trees[J]. Discrete Applied Mathematics, 1989, 23(1): 11-24.
[30] KOSTER A M C A, VAN HOESEL S P M, KOLEN A W J. Solving partial constraint satisfaction problems with tree decomposition[J]. Networks, 2002, 40(3): 170-180.
[31] ZHAO J Z, MALMBERG R L, CAI L M. Rapid ab initio prediction of RNA pseudoknots via graph tree decomposition[J]. Journal of Mathematical Biology, 2008, 56(1): 145-159.
[32] ADCOCK A B, SULLIVAN B D, MAHONEY M W. Tree decompositions and social graphs[J]. Internet Mathematics, 2016, 12(5): 315-361.
[33] 谢志新, 王晓峰, 于卓, 等. 基于树宽的警示传播算法收敛性分析[J]. 计算机应用研究, 2022, 39(10): 3061-3064, 3077.
XIE Z X, WANG X F, YU Z, et al. Convergence analysis of warning propagation algorithm based on tree width[J]. Application Research of Computers, 2022, 39(10): 3061-3064, 3077.
[34] 程亚南, 王晓峰, 刘凇佐, 等. 一种求解旅行商问题的信息传播算法[J]. 郑州大学学报(理学版), 2022, 54(3): 52-58.
CHENG Y N, WANG X F, LIU S Z, et al. An information propagation algorithm for solving traveling salesman problem[J]. Journal of Zhengzhou University (Natural Science Edition), 2022, 54(3): 52-58.
[35] LI A S, PAN Y C. Structural information and dynamical complexity of networks[J]. IEEE Transactions on Information Theory, 2016, 62(6): 3290-3339.
[36] NEWMAN M E J, GIRVAN M. Finding and evaluating community structure in networks[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2004, 69(2): 026113.
[37] 成科扬, 荣兰, 蒋森林, 等. 基于深度学习的遥感图像超分辨率重建方法综述[J]. 郑州大学学报(工学版), 2022, 43(5): 8-16.
CHENG K Y, RONG L, JIANG S L, et al. Overview of methods for remote sensing image super-resolution reconstruction based on deep learning[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(5): 8-16.
[38] ROTTA R, NOACK A. Multilevel local search algorithms for modularity clustering[J]. ACM Journal of Experimental Algorithmics, 2011, 16(2):1-27.
[39] BLONDEL V D, GUILLAUME J L, LAMBIOTTE R, et al. Fast unfolding of communities in large networks[J]. Journal of Statistical Mechanics: Theory and Experiment, 2008, 2008(10): P10008.
[40] BROOKS J F P. Three great challenges for half-century-old computer science[J]. Journal of the ACM, 2003, 50(1): 25-26.
[41] LIU X C, FU L Y, WANG X B, et al. On the similarity between Von Neumann graph entropy and structural information: interpretation, computation, and applications[C]∥IEEE Transactions on Information Theory. Piscataway: IEEE, 2022: 2182-2202.
[42] BRAUNSTEIN S L, GHOSH S, SEVERINI S. The Laplacian of a graph as a density matrix: a basic combinatorial approach to separability of mixed states[J]. Annals of Combinatorics, 2006, 10(3): 291-317.
[43] ZHANG Z J, XU D Y, ZHOU J C. A structural entropy measurement principle of propositional formulas in conjunctive normal form[J]. Entropy, 2021, 23(3): 303.
[44] 牛进, 王晓峰, 左逢源, 等. 基于二维结构熵的置信传播算法收敛性分析[J]. 计算机应用研究, 2021, 38(7): 2032-2036, 2043.
NIU J, WANG X F, ZUO F Y, et al. Convergence analysis of belief propagation algorithm based on two-dimensional structural entropy[J]. Application Research of Computers, 2021, 38(7): 2032-2036, 204.
[45] ADLEMAN L M. Molecular computation of solutions to combinatorial problems[J]. Science, 1994,266(5187): 1021-1024.
[46] LIPTON R J. Using DNA to solve NP-complete problems[J]. Science. 1995,268:542-545.
[47] SAKAMOTO K, GOUZU H, KOMIYA K, et al. Molecular computation by DNA hairp information[J]. Science, 2000,288(5469):1223-1226.
[48] BRAICH R S, CHELYAPOV N, JOHNSON C, et al. Solution of a 20-variable 3-SAT problem on a DNA computer[J]. Science, 2002, 296(5567): 499-502.
[49] 张凤月, 殷志祥, 许进. DNA芯片在0-1规划问题中的应用[J]. 生物化学与生物物理进展, 2003, 30(3): 412-415.
ZHANG F Y, YIN Z X, XU J. Application of DNA chip on 0-1 planning problem[J]. Progress in Biochemistry and Biophysics, 2003, 30(3): 412-415.
[50] 周康, 魏传佳, 刘朔, 等. 可满足性问题的闭环DNA算法[J]. 华中科技大学学报(自然科学版), 2009, 37(7): 75-78.
ZHOU K, WEI C J, LIU S, et al. Closed circle DNA algorithm for SAT problem[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2009, 37(7): 75-78.
[51] XIAO J H, XU J. The DNA computation model based on giant magnetoresistance for SAT problem[J]. Chinese Journal of Computers, 2014, 36(4): 829-835.
[52] 马莹, 殷志祥, 方欢. 可满足性问题生物芯片DNA算法[J]. 计算机应用研究, 2017, 34(8): 2310-2311, 2367.
MA Y, YIN Z X, FANG H. DNA computation model based on biochips for satisfiability problem[J]. Application Research of Computers, 2017, 34(8): 2310-2311, 2367.
[53] 陈哲. 基于DNA计算的可满足性问题的模型研究[D]. 淮南: 安徽理工大学, 2020.
CHEN Z. Research on the model of satisfiability based on DNA computing[D]. Huainan: Anhui University of Science &Technology, 2020.
[54] 麻晶晶, 许进. 基于DNA折纸术求解图的顶点着色问题的方法[J]. 电子与信息学报, 2021, 43(6): 1750-1755.
MA J J, XU J. A method for the graph vertex coloring problem based on DNA origami[J]. Journal of Electronics &Information Technology, 2021, 43(6): 1750-1755.