真实世界中存在着大量的网络结构,如社交网络、生物蛋白质网络、引文网络、交通网络、化学分子网络等[1-2]。采用复杂网络分析方法对这些网络结构进行研究有助于人们更好地挖掘隐藏在网络数据中的规律[3]。而网络结构具有数据规模较大、结构稀疏等特性,无法直接用网络分析方法进行分析。网络表示学习将深度学习拓展到了网络数据分析,旨在学习网络节点低维向量表示的方法,并保留网络拓扑结构和节点属性[4]。将节点表示成低维、实值、稠密的向量形式,使得到的向量表示在向量空间中具有表示以及推理的能力[5]。得到的向量表示可以运用到下游任务中,如链路预测、节点分类、社区发现、个性化推荐等[6-7]。
符号网络是一种包含正、负对立关系的二维网络,正关系包括朋友、支持、喜欢等积极关系;负关系包括敌人、反对、讨厌等消极关系[8]。在符号网络学习节点嵌入过程中,正向边、负向边以及边的方向都会对学习节点嵌入造成很大的挑战[9]。对此,研究者们利用符号网络中的社会学理论(结构平衡理论和地位理论)对网络结构进行建模来正确区分正负边,并结合图神经网络或深度学习来学习节点嵌入,这些方法在符号网络嵌入领域也取得了最优性能[10-11]。但上述方法都是从节点层面关注节点邻居的影响,忽视了路径信息这一特征。在路径层面,节点与邻居之间链路不同方向和符号构成复杂的路径,这些不同的路径也会对节点嵌入造成影响。
本文提出了SNEDA方法(signed network embedding via dual attention mechanism),通过划分不同的motif来捕捉路径信息(链路不同方向和符号),用节点级注意力学习每个motif下节点之间的影响,用路径级注意力学习不同motif之间的权重,基于重要motif选择性的聚合邻居信息,得到节点的向量表示。得到的向量表示不仅融合了节点邻居的信息,同时也融合了网络结构信息,实验证明SNEDA模型可以提升节点嵌入的质量。
1 理论知识
定义1 度中心性(degree centrality,DC)。DC是在网络中刻画节点中心性最直接的度量指标。一个节点的度越大,就意味着这个节点的度中心性越高,说明在网络中这个节点越重要。节点的度中心性为
(1)
式中:Ndegree表示节点的度;n表示节点的个数。
1.1 结构平衡理论
(1)结构平衡三角形。通过三角形3条边的符号之积来判定三角形是否结构平衡。若为正,则该三角形结构平衡;否则不平衡[12]。研究表明,在真实社交网络结构中平衡三角形的数目远大于结构不平衡的三角形数量,且不平衡网络结构随着时间推移逐渐向平衡网络结构演化[13]。
(2)结构平衡环。如果一个L-环(L≥3)包含偶数条负边,则该L-环结构是平衡的,否则结构是不平衡的[14]。图1为结构平衡理论示意图。
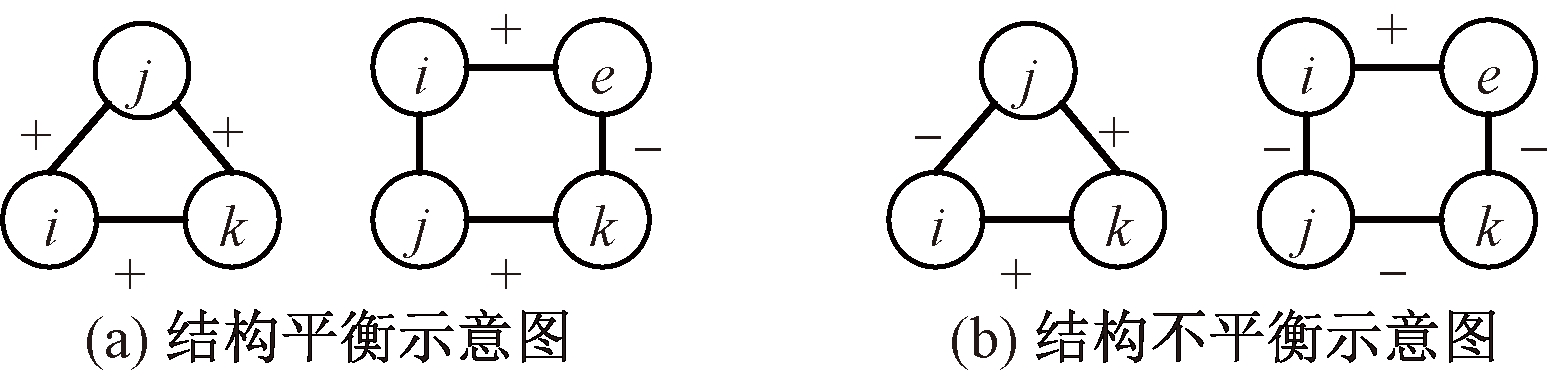
图1 结构平衡理论示意图
Figure 1 Schematic diagram of structural balance theory
1.2 社会地位理论
Leskovec等[15]提出适用于有符号网络的社会地位理论。该理论认为如果有一条正的边从节点i指向节点j,则节点i比j社会地位高,若有一条节点i指向节点j的负向边,则j比i社会地位高,且这种地位高低具有传递性。图2为地位平衡理论示意图。
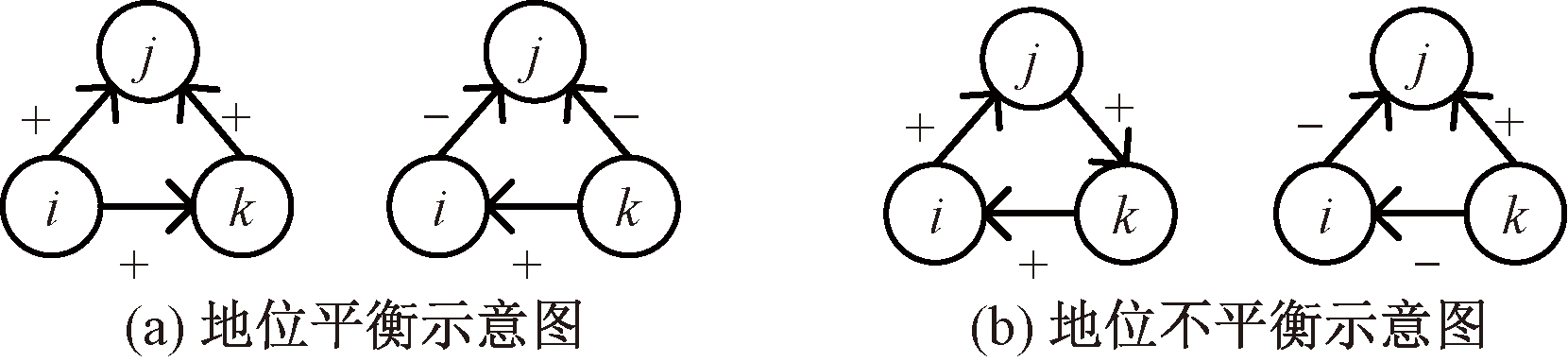
图2 地位平衡理论示意图
Figure 2 Schematic diagram of status balance theory
1.3 网络模体(network motif)
在真实的社交网络中,用户节点的链接行为受邻居节点影响,且不同的邻居会造成不同的影响。依据链路不同的方向和符号,将节点与邻居之间不同的路径划分不同的motif,如图3所示。节点j是节点i的一阶邻居,共有4种不同的motif,节点k是节点i的二阶邻居,共有16种不同的motif。
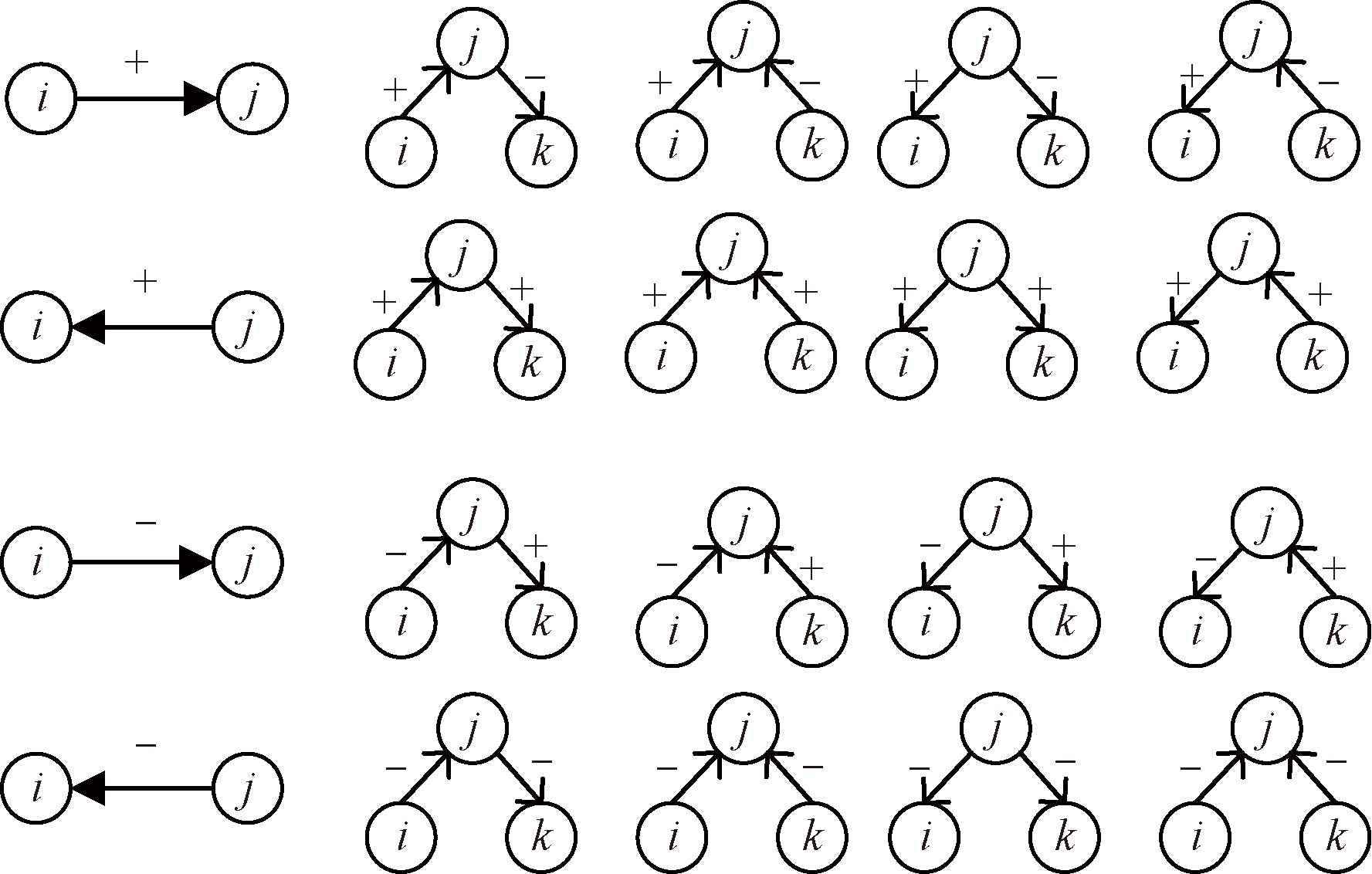
图3 符号网络中20种不同的模体
Figure 3 20 different motifs in the signed network
2 SNEDA模型
SNEDA模型的框架如图4所示,由5部分组成。首先,通过节点邻居采样得到节点的一阶和二阶邻居信息;其次,依据不同的motif划分得到不同的邻居集合;再次,在每个motif下用节点级注意力来学习节点之间的权重,得到特定的节点嵌入;从次,使用路径级注意力来学习不同motif的重要性,基于重要motif汇聚节点邻居信息得到最终的向量表示;最后,通过链路预测实验来检测模型节点嵌入的质量。
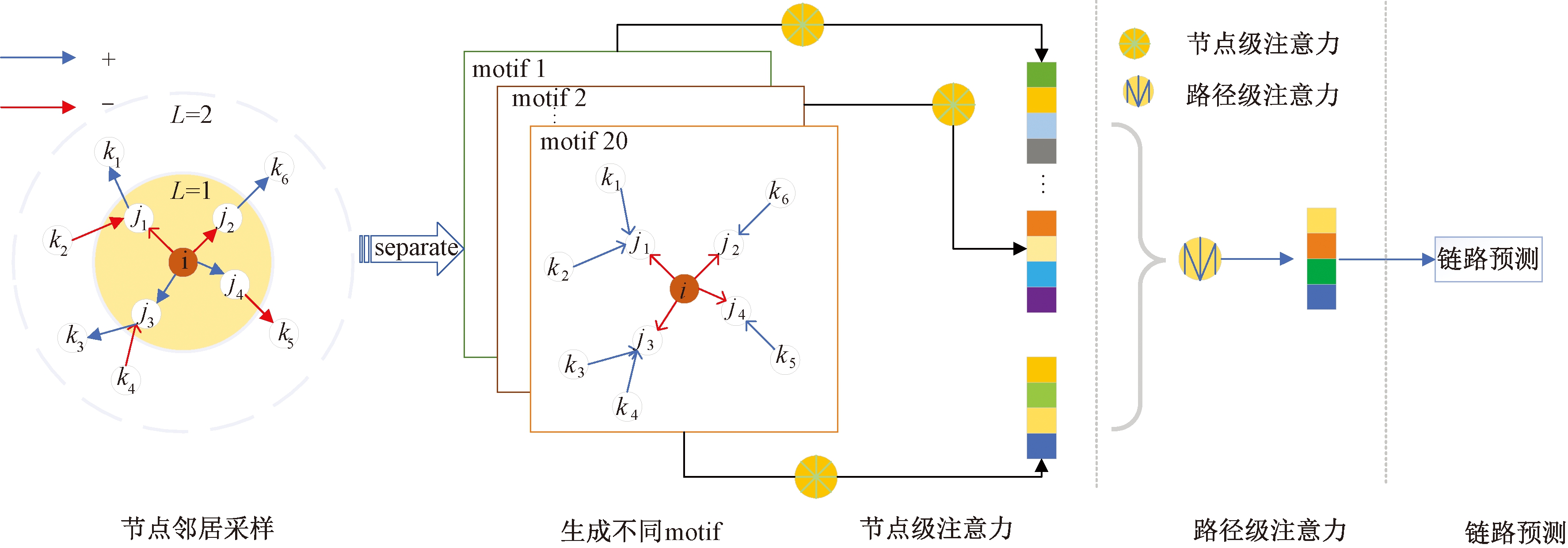
图4 SNEDA模型图
Figure 4 Illustratiion of SNEDA model
2.1 产生节点在不同motif下的向量表示
为了消除链路方向和链路符号不同造成节点不同的影响,将节点与邻居之间相同的链路划分为一种motif,每一种motif都独立使用自注意力机制学习节点之间的权重。节点i和节点j经过路径φ连接,节点j在φ模式下对节点i的影响力为
(2)
式中:attnode表示执行节点级注意力的深度神经网络;φ表示不同motif的集合;hi和hj表示节点i和j的特征向量;注意力系数![]() 表示在某个motif下节点j对节点i的重要性,
表示在某个motif下节点j对节点i的重要性,![]() 是非对称的,即
是非对称的,即![]() 这表明节点i对节点j的重要性与节点j对节点i的重要性是不对等的。
这表明节点i对节点j的重要性与节点j对节点i的重要性是不对等的。
在得到节点对之间的重要性后,用softmax函数对其权重进行归一化处理:
(3)
式中:σ表示激活函数;![]() 表示在某个motif下节点对的注意力系数;
表示在某个motif下节点对的注意力系数;![]() 表示在某个motif下节点i的邻居集合;
表示在某个motif下节点i的邻居集合;![]() 表示在某个motif下节点的注意力向量;[]和
表示在某个motif下节点的注意力向量;[]和![]() 表示连接操作(concatenation)。
表示连接操作(concatenation)。
通过汇聚节点的邻居信息及其相关系数得到节点Vi新的向量表示:
(4)
式中:![]() 表示在某个motif下节点i的向量表示;
表示在某个motif下节点i的向量表示;![]() 表示在某个motif下节点对的注意力系数。在给定的20种motif下分别进行学习,得到节点i不同motif下的特征向量集合
表示在某个motif下节点对的注意力系数。在给定的20种motif下分别进行学习,得到节点i不同motif下的特征向量集合![]()
2.2 融合不同的motif
节点级注意力学习得到的节点嵌入只反映节点层面信息。为了学习更加全面的节点嵌入,需要融合更加丰富的路径信息,将路径按照方向和正负信息划分不同的motif,通过路径级注意力学习不同motif的重要性,基于重要motif汇聚节点邻居信息得到节点的向量表示, 如图4(路径级注意力部分)所示。
节点级注意力学习到的节点嵌入作为输入,每个motif学习权重为
Bφ1,Bφ2,…,Bφ20=attpath(hφ1,hφ2,…,hφ20)。
(5)
式中: attpath表示执行路径注意力的深度神经网络,在每个motif下的attpath参数是共享的;Bφm表示学习得到不同motif的权重。
将节点级注意力学习到的节点嵌入进行非线性变化,利用节点层面注意力机制学习到的特定向量和路径层面注意力向量q计算相似度,以此衡量不同语义向量的重要性,每个motif的重要性由wφi表示:
(6)
式中:W和b分别为可训练参数矩阵和偏差向量;q为路径向量;所有motif的嵌入都共享以上参数。在得到各motif的重要性后,用softmax函数对其进行归一化处理:
(7)
式中:Bφi表示motif的权重,Bφi越高,表示该motif越重要,对于不同的motif,可能有着不用的权重。通过学习得到不同motif的权重系数,得到最终的目标节点嵌入:
(8)
式中:Bφi表示学习得到的motif权重系数;![]() 表示在某个motif下节点i的向量表示。
表示在某个motif下节点i的向量表示。
2.3 链路预测
通过链路预测实验来验证模型学习节点嵌入的质量,经过SNEDA模型学习得到每个节点的向量表示,将训练集中的节点向量表示作为节点特征输入到二分类模型中进行链路预测的实验。为了更好地学习模型参数,SNEDA模型采用交叉熵作为损失函数,定义如下:
(9)
式中:C为用来调节正向连接和负向连接数量的比例;N(u)+为节点u正链接的所有邻居集合;N(u)-为节点u负链接的所有邻居集合。该函数反映朋友的嵌入是相似的,而敌人的嵌入是不相似,通过不断减少交叉熵损失loss来更新模型参数,经过多次优化,当loss趋于稳定时得到节点的最终向量表示。算法1是SNEDA模型算法。
算法1 SNEMA算法流程。
输入:符号网络图G、节点特征hi、节点
集合V;
输出:节点向量最终表示Zi。
① procedure begin:
② for each Vi∈V:
得到节点i的邻居集合{φ0,φ1,…,φm};
for each φi∈{φ0,φ1,…,φm} do :
用式(3)计算权重系数![]()
用式(4)计算节点的嵌入![]()
end for
end for
③ 得到每个motif下的节点嵌入:![]()
④ 用式(6)和(7)计算权重系数motif的重要性;
⑤ 学习到不同motif的重要性后,汇聚这些信息得到节点i的最终向量表示![]()
⑥ 通过式(9)来计算损失值;
⑦ 通过反向传播计算梯度来更新模型参数;
⑧ end procedure。
3 实验
实验中所有代码使用Pytorch编程语言编写,电脑配置为cpu i7-6700六核十二线程,内存12 GB,显卡AMD R7 2 GB。
3.1 数据集描述
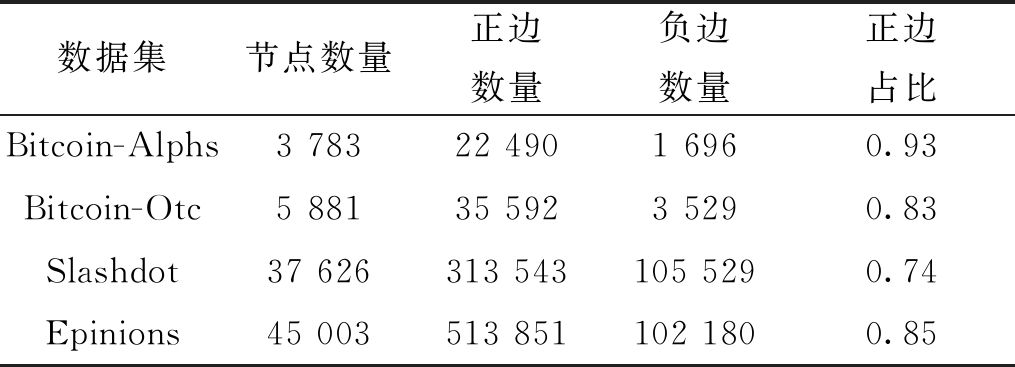
在实验中采用4个真实的社交网络数据集Bitcoin-Alphs、Bitcoin-Otc、Slashdot和Epinions,表1是对数据集的统计信息,这些数据都可以从Stanford Large Network Dataset网站中下载。
表1 4个数据集统计信息
Table 1 Statistics of four datasets
数据集节点数量正边数量负边数量正边占比Bitcoin-Alphs3 78322 4901 6960.93Bitcoin-Otc5 88135 5923 5290.83Slashdot37 626313 543105 5290.74Epinions45 003513 851102 1800.85
Bitcoin-Alphs和Bitcoin-Otc是在Alpha和Otc的平台上使用比特币进行交易的人际关系网络。
Slashdot是一个科技新闻的网站。新闻可以由网站所有的用户提供,用户在这里可以选择自己的朋友和敌人,将朋友看作是正关系,敌人看作是负关系。
Epinions是一个消费者评论网站。用户可以通过另外一个用户提供评价产品的质量来决定是否信任该用户。将信任的关系看作正关系,将不信任的关系看作是负关系。
3.2 基准方法
(1)DeepWalk[16]:针对无符号网络设计了一种基于随机游动的网络嵌入方法。这里将网络中的负向链接当成正向链接处理,将整个符号网络看成无符号网络。
(2)SiNE[17]:利用符号网络的特性用随机游走的方法对节点采样建模来获得节点嵌入。
(3)SiGAT[18]:提供了特定的结构模式,利用GAT对每个模式下的节点进行学习。
(4)SGCN[19]:利用结构平衡理论通过图卷积层聚合和传播信息,生成节点嵌入。
(5)SNEA[20]:利用自注意机制学习节点之间的权重系数,用平衡理论聚合高阶信息对节点进行嵌入。
(6)SDGNN[21]:基于社会学中的结构平衡理论设计了一种新的信息传播和聚合机制,并且利用了一种平均采样的理论来学习节点嵌入。
3.3 链路预测实验
通过链路预测实验来验证SNEDA模型学习节点嵌入的质量。随机选取80%的连边作为训练集,这些连边经过SNEDA模型会产生节点的向量表示;剩余的20%的连边作为测试集。将训练集中的节点向量表示作为节点特征,输入到二分类逻辑回归模型中进行实验。将Accuracy、Macro-F1、F1、AUC作为评估指标对连边符号预测结果进行验证。这些指标数值越高,表示连边符号预测结果越准确。
SNEDA方法与基线方法实验对比结果如表2所示,SNEDA在4个数据集上的各项评价指标大多优于基准方法。忽视负链接直接用于表示学习的DeepWalk方法性能表现最差,说明负向链接在很大程度上影响符号网络表示的质量;SiNE首次用社会学理论对符号网络进行建模,取得了不错的实验效果,表明基于社会学理论对符号网络建模的可行性;SiGAT方法用多头注意力通过聚合一阶邻居的信息学习得到目标节点嵌入;SNEA基于平衡理论聚合节点的高阶邻居信息,用注意力机制学习节点对之间不同的权重;相较于之前的方法,SNEDA方法考虑节点之间不同路径的影响,并用双重注意力层捕捉节点和路径的影响。从表2实验结果看,链路预测准确率有了明显的提升,实验结果表明基于重要motif选性地聚合邻居信息能够提升链路预测的准确率。
表2 SNEDA和其他算法在4个数据集上的实验结果
Table 2 Experimental results of SNEDA and other algorithms on four datasets
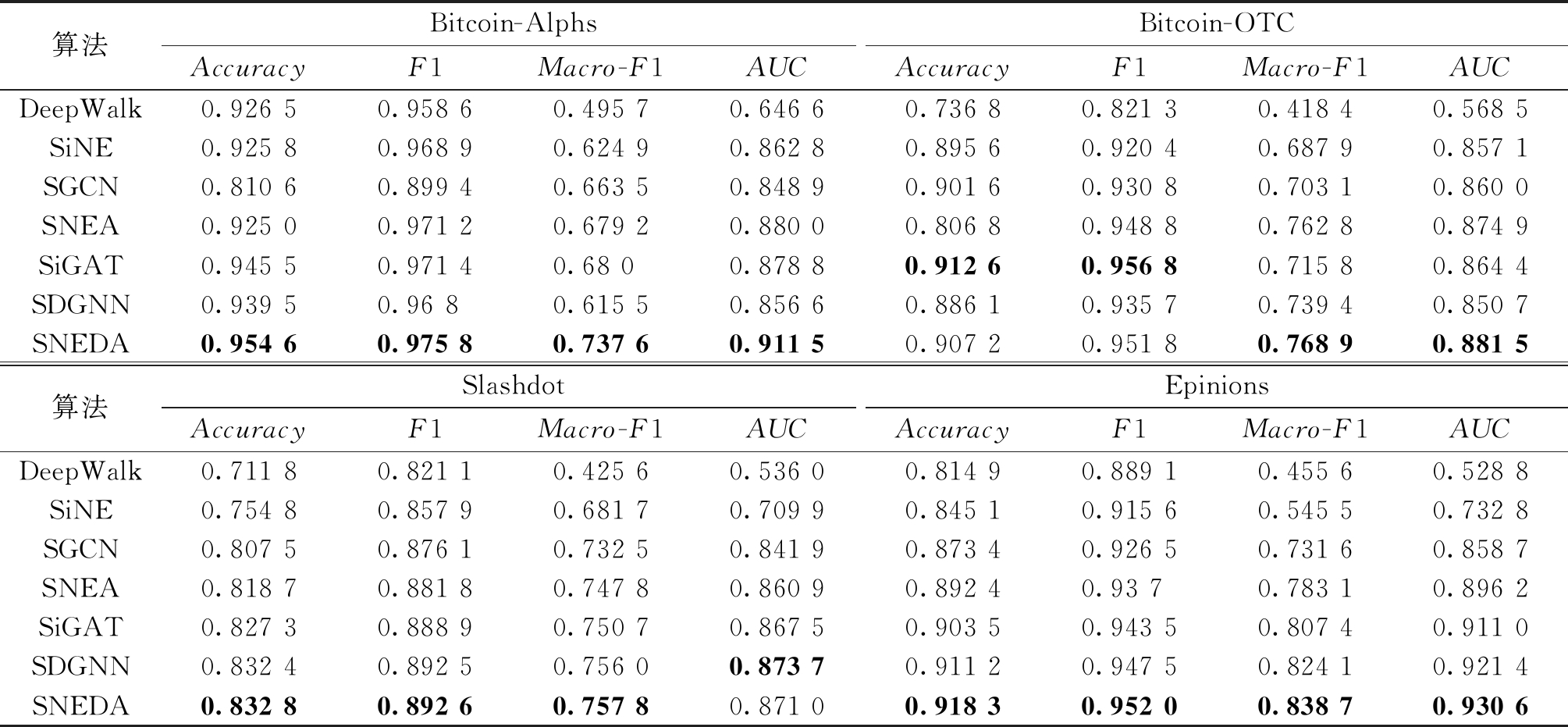
算法Bitcoin-AlphsBitcoin-OTCAccuracyF1Macro-F1AUCAccuracyF1Macro-F1AUCDeepWalk0.926 50.958 60.495 70.646 60.736 80.821 30.418 40.568 5SiNE0.925 80.968 90.624 90.862 80.895 60.920 40.687 90.857 1SGCN0.810 60.899 40.663 50.848 90.901 60.930 80.703 10.860 0SNEA0.925 00.971 20.679 20.880 00.806 80.948 80.762 80.874 9SiGAT0.945 50.971 40.68 00.878 80.912 60.956 80.715 80.864 4SDGNN0.939 50.96 80.615 50.856 60.886 10.935 70.739 40.850 7SNEDA0.954 60.975 80.737 60.911 50.907 20.951 80.768 90.881 5算法SlashdotEpinionsAccuracyF1Macro-F1AUCAccuracyF1Macro-F1AUCDeepWalk0.711 80.821 10.425 60.536 00.814 90.889 10.455 60.528 8SiNE0.754 80.857 90.681 70.709 9 0.845 10.915 60.545 50.732 8SGCN0.807 50.876 10.732 50.841 90.873 40.926 50.731 60.858 7SNEA0.818 70.881 80.747 80.860 90.892 40.93 70.783 10.896 2SiGAT0.827 30.888 90.750 70.867 50.903 50.943 50.807 40.911 0SDGNN0.832 40.892 50.756 00.873 70.911 20.947 50.824 10.921 4SNEDA0.832 80.892 60.757 80.871 00.918 30.952 00.838 70.930 6
3.4 模型超参数分析
SNEDA模型有2个重要参数控制实验的效果,分别是节点向量d和路径向量q。本节将通过实验分析超参数对 SNEDA模型性能的影响。选取Bitcoin-Alpha作为实验数据集,在分析特定的超参数时,其他参数值设置为默认值。图5给出了 SNEDA模型在不同参数下符号链路预测性能AUC值。图5(a)和5(b)表示随着训练轮次的增加,loss值逐渐减小,AUC增大,然后逐渐收敛,最后趋于稳定。图5(c)显示节点向量d对实验结果的影响,可以看到向量维度在20时效果达到最优,随着维度的增加,实验效果反而有所降低,这可能由于过拟合导致的。图5(d)展示了路径向量q对实验性能的影响,当向量q=64时,效果达到最佳,随着向量维度的增加,效果反而降低。
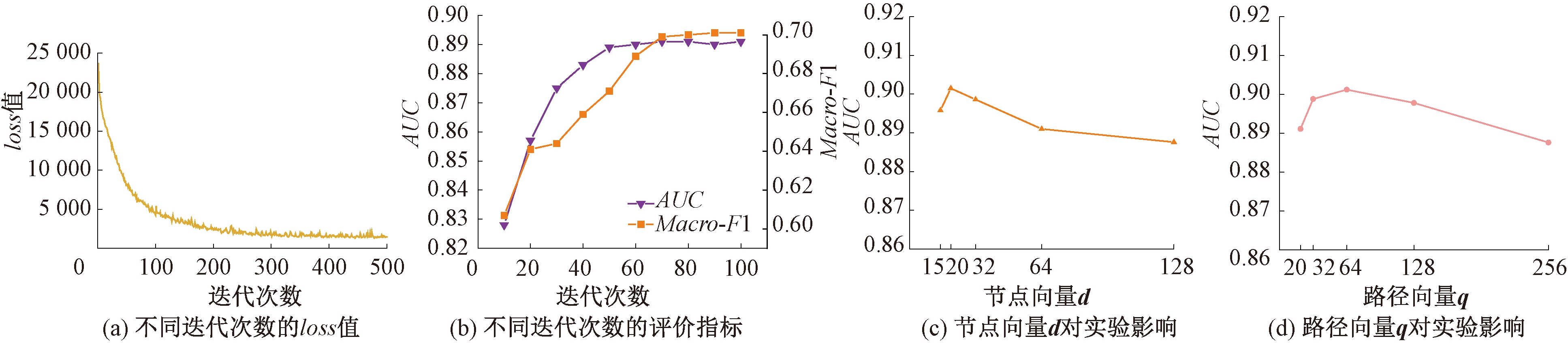
图5 SNEMA模型超参数分析
Figure 5 SNEMA model hyperparametric analysis
4 结论
(1)SNEDA模型由2层注意力机制组成,节点级注意力关注节点层面的信息,学习节点与邻居之间不同的权重;路径级注意力捕捉路径层面的信息,学习不同motif之间的重要性。基于重要motif选择性地聚合邻居信息,学习得到节点的低维向量表示。
(2)通过SNEDA模型的学习,节点的特征信息同时包含邻居信息和路径信息,使得节点的向量表示更加完整、丰富。与基准方法相比,SNEDA在链路预测任务中取得了更好的效果,说明结合路径层面的信息有助于提高节点嵌入的质量。
在未来工作中,将考虑采样更高阶的邻居,比如用随机游走的方式或者用GraphSAGE的采样方式,以此来补全节点向量表示的完整性。
[1] 任磊, 杜一, 马帅, 等. 大数据可视分析综述[J]. 软件学报, 2014, 25(9): 1909-1936.
REN L, DU Y, MA S, et al. Visual analytics towards big data[J]. Journal of Software, 2014, 25(9): 1909-1936.
[2] BORSBOOM D, DESERNO M K, RHEMTULLA M, et al. Network analysis of multivariate data in psychological science[EB/OL]. (2021-08-19)[2022-03-16].https://doi.org/10.1038/s43586-021-00055-w.
[3] ZHOU J Y, LIU L, WEI W Q, et al. Network representation learning: from preprocessing, feature extraction to node embedding[J]. ACM Computing Surveys, 2023, 55(2): 1-35.
[4] CUI P, WANG X, PEI J, et al. A survey on network embedding[J]. IEEE Transactions on Knowledge and Data Engineering, 2019, 31(5): 833-852.
[5] 涂存超, 杨成, 刘知远, 等. 网络表示学习综述[J]. 中国科学: 信息科学, 2017, 47(8): 980-996.
TU C C, YANG C, LIU Z Y, et al. Network representation learning: an overview[J]. Scientia Sinica Informationis, 2017, 47(8): 980-996.
[6] 高岳林, 杨钦文, 王晓峰, 等. 新型群体智能优化算法综述[J]. 郑州大学学报(工学版), 2022, 43(3): 21-30.
GAO Y L, YANG Q W, WANG X F, et al. Overview of new swarm intelligent optimization algorithms[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(3): 21-30.
[7] 郑建兴, 郭彤彤, 申利华, 等. 基于评论文本情感注意力的推荐方法研究[J]. 郑州大学学报(工学版), 2022, 43(2): 44-50, 57.
ZHENG J X, GUO T T, SHEN L H, et al. Research on recommendation method based on sentimental attention of review text[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(2): 44-50, 57.
[8] 程苏琦, 沈华伟, 张国清, 等. 符号网络研究综述[J]. 软件学报, 2014, 25(1): 1-15.
CHENG S Q, SHEN H W, ZHANG G Q, et al. Survey of signed network research[J]. Journal of Software, 2014, 25(1): 1-15.
[9] CHEN J, ZHONG M, LI J, et al. Effective deep attributed network representation learning with topology adapted smoothing[J]. IEEE Transactions on Cybernetics, 2022, 52(7): 5935-5946.
[10] WU Z H, PAN S R, CHEN F W, et al. A comprehensive survey on graph neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(1): 4-24.
[11] ZHANG Z W, CUI P, ZHU W W. Deep learning on graphs: a survey[J]. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(1): 249-270.
[12] HEIDER F. Attitudes and cognitive organization[J]. The Journal of Psychology, 1946, 21(1): 107-112.
[13] 刘苗苗, 扈庆翠, 郭景峰, 等. 符号网络链接预测算法研究综述[J]. 计算机科学, 2020, 47(2): 21-30.
LIU M M, HU Q C, GUO J F, et al. Survey of link prediction algorithms in signed networks[J]. Computer Science, 2020, 47(2): 21-30.
[14] ANCHURI P, MAGDON-ISMAIL M. Communities and balance in signed networks: a spectral approach[C]//2012 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining. Piscataway:IEEE,2012: 235-242.
[15] LESKOVEC J, HUTTENLOCHER D, KLEINBERG J. Predicting positive and negative links in online social networks[C]//Proceedings of the 19th International Conference on World Wide Web. New York: ACM, 2010: 641-650.
[16] PEROZZI B, AL-RFOU R, SKIENA S. DeepWalk: online learning of social representations[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2014: 701-710.
[17] WANG S H, TANG J L, AGGARWAL C, et al. Signed network embedding in social media[C]//Proceedings of the 2017 SIAM International Conference on Data Mining. Philadelphia: Society for Industrial and Applied Mathematics, 2017: 327-335.
[18] DERR T, MA Y, TANG J L. Signed graph convolutional networks[C]//2018 IEEE International Conference on Data Mining. Piscataway: IEEE,2018: 929-934.
[19] LI Y, TIAN Y, ZHANG J W, et al. Learning signed network embedding via graph attention[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, 34(4): 4772-4779.
[20] HUANG J J, SHEN H W, HOU L, et al. Signed graph attention networks[C]//Artificial Neural Networks and Machine Learning-ICANN 2019: Workshop and Special Sessions. Cham: Springer, 2019: 566-577.
[21] HUANG J J, SHEN H W, HOU L, et al. SDGNN: learning node representation for signed directed networks[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2021, 35(1): 196-203.