磨削具有较高的材料去除能力和加工精度,普遍应用于难切削材料的轴类零件加工生产中,尤其是在零件的最终加工阶段,需要保证较好的表面完整性和精确的公差,磨削工艺是实现这一目的的最优加工方法。磨削加工过程中影响加工质量的参数较多,其中磨削力是与磨削参数和磨削质量相关的重要过程变量,常常被用来对磨削质量进行分析和预测。因此,建立科学有效的磨削力理论模型,对磨削力的预测及实际加工生产中的参数选择具有十分重要的意义[1]。
近年来,国内外许多学者在影响磨削力的加工参数和预测模型等方面对磨削力进行了诸多研究。Maeng等[2]将磨削分为摩擦、耕犁和切屑3个阶段磨削力的模型,预测的力与小接触面积的磨削过程吻合较好,但与大接触面积的实验结果略有偏差。Zhou等[3]使用了BP和GABP两种模型分别预测钛基复合材料在深磨过程中的磨削力,结果表明,GABP与传统回归模型和BP模型相比具有更好的预测精度。詹友基等[4]对纳米硬质合金GU092为主的3种硬质合金磨削力进行实验研究,并使用RBF神经网络对磨削力进行预测,其误差在5%以下。Li等[5]根据磨粒与材料的接触摩擦力、塑性变形、剪切应变效应3个关键因素建立了平面磨削三段式的磨削力模型,并使用分段比例法求解该模型,最终得到法向和切向磨削力的预测误差分别为13.6%和9.8%。马少奇[6]利用锥形磨粒等效模型,计算了动态切削刃密度,并结合塑性堆积和材料去除机理,建立了不同磨削阶段的磨削力预测模型,并使用分段比例法求解模型待求系数,该模型法向和切向磨削力的预测误差分别为8.7%和11.8%。Jamshidi等[7]通过考虑磨粒与工件之间的微观相互作用,针对平面磨削建立了一种考虑不同磨削阶段的磨削力预测模型,该模型切向磨削力和法向磨削力的预测误差分别为12%和![]() 等[8]使用回归分析和遗传算法来求解外圆磨削切削力模型,结果表明,这两种方法均可用于切削力建模,遗传算法略有优势,相比回归分析方法所求解的模型精度提高34%。
等[8]使用回归分析和遗传算法来求解外圆磨削切削力模型,结果表明,这两种方法均可用于切削力建模,遗传算法略有优势,相比回归分析方法所求解的模型精度提高34%。
近年来业内关于磨削的研究较多,并且建立起了多种磨削力模型,但针对磨削力理论模型的预测误差都普遍偏高,基本都处在10%~15%,对实际工程实践的参考意义有限。目前求解模型时大多使用分段计算法或列方程组直接计算各个待求系数,不仅计算量大且其精度也无法保证。本文在现有磨削理论模型的基础上,基于遗传算法优化的非线性优化函数(genetic algorithm-lsqnonlin,GA-LSQ)求解模型待求系数,对磨削力的预测及实际加工生产中的参数优化提供参考。
1 模型分类及选取
目前国内外学者对于磨削力的模型研究方法众多,其大致可分为4类:基于力学模型基础的解析法[5-6]、基于实验的经验方法[8-10]、有限元分析法[11]、人工智能预测模型[12]。本文主要针对前两种建模方法进行求解。
解析法是通过分析磨削过程中的材料去除机理,剪切应变效应和磨粒分布、形状等建立磨削力的解析模型。通过解析法所建立的磨削力模型主要分为外圆、平面、内圆、成形磨削等,而目前的磨削力模型研究大多集中于外圆和平面,对内圆的研究很少。经验模型法主要通过建立加工参数和磨削力的非线性指数函数关系来预测磨削力的大小,优点在于简单实用、适用范围广。
目前学者在建立磨削力模型时将过程参数(磨粒形状、磨粒密度、磨粒方向,摩擦系数等)都通过公式推导而整合转化成最终的待求参数k(k1,k2,…)的形式,即将多个过程参数通过乘积最终转化为一个待求参数。为验证本文计算方法的普适性,分别对Li等[5]建立的平面磨削力模型、马少奇[6]建立的外圆横向磨削力模型、赵静雯[13]建立的成形磨削力模型、蔡卫星等[14]建立的超声磨削力模型以及![]() 等[8]建立的外圆纵向磨削力模型进行相应的计算验证,误差均在10%以下。因此本文所提出的计算方法对不同形式的解析、经验模型都同样适用。
等[8]建立的外圆纵向磨削力模型进行相应的计算验证,误差均在10%以下。因此本文所提出的计算方法对不同形式的解析、经验模型都同样适用。
为论述计算方法的详细求解过程以文献[5-6,8]模型作为算法验证对象,根据原文献实验获得并划分的训练集及验证集数据进行求解验证。3种磨削力模型形式与具体参数如表1所示。
表1 模型形式参数表
Table 1 Table of model formal parameters
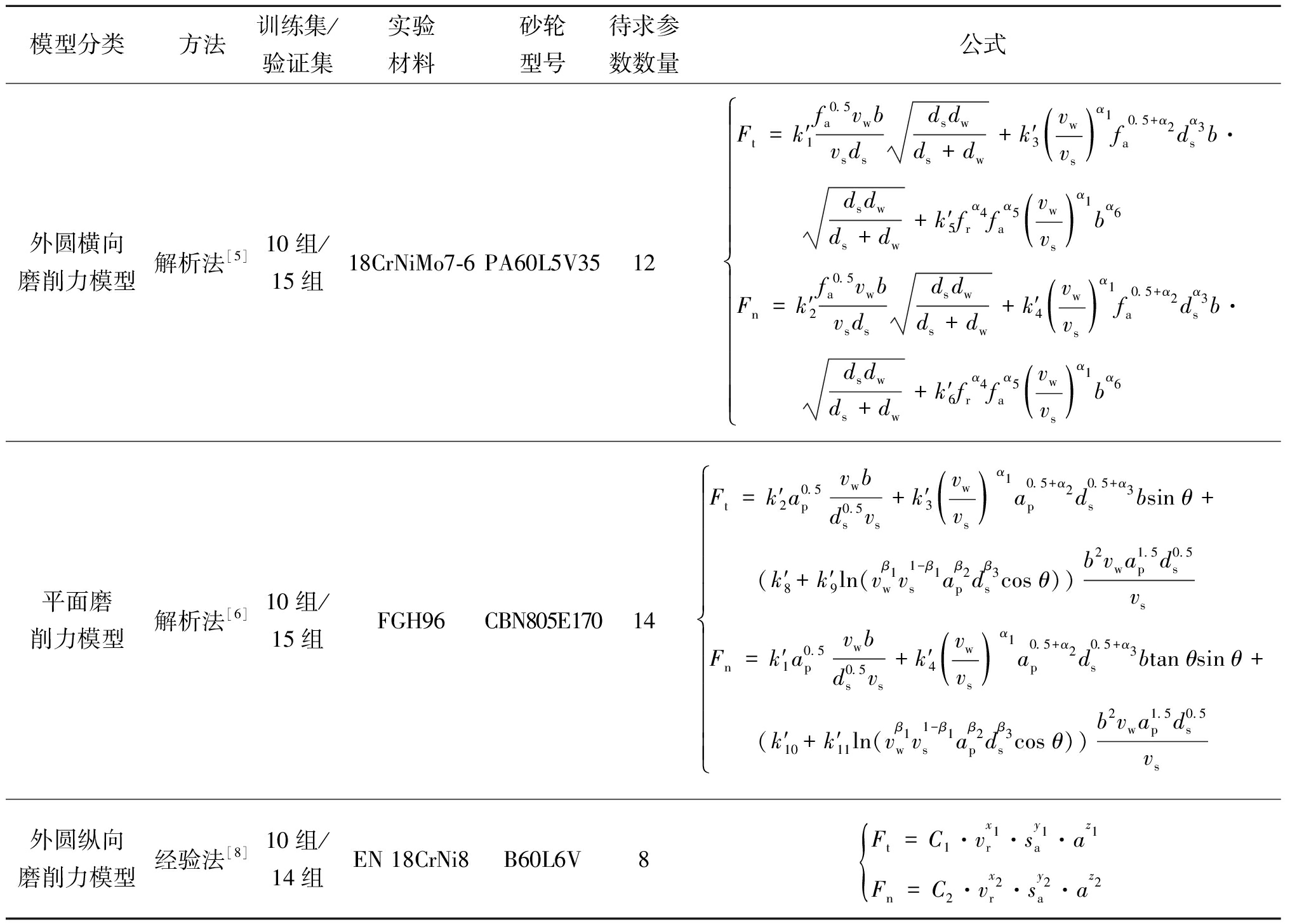
模型分类方法训练集/验证集实验材料砂轮型号待求参数数量公式外圆横向磨削力模型解析法[5]10组/15组18CrNiMo7-6PA60L5V3512Ft=k′1f0.5avwbvsdsdsdwds+dw+k′3vwvs()α1f0.5+α2adα3sb· dsdwds+dw+k′5fα4rfα5avwvs()α1bα6Fn=k′2f0.5avwbvsdsdsdwds+dw+k′4vwvs()α1f0.5+α2adα3sb· dsdwds+dw+k′6fα4rfα5avwvs()α1bα6ìîíïïïïïïïïïïïï平面磨削力模型解析法[6]10组/15组FGH96CBN805E17014Ft=k′2a0.5pvwbd0.5svs+k′3vwvs()α1a0.5+α2pd0.5+α3sbsinθ+ (k′8+k′9ln(vβ1wv1-β1saβ2pdβ3scosθ))b2vwa1.5pd0.5svsFn=k′1a0.5pvwbd0.5svs+k′4vwvs()α1a0.5+α2pd0.5+α3sbtanθsinθ+ (k′10+k′11ln(vβ1wv1-β1saβ2pdβ3scosθ))b2vwa1.5pd0.5svsìîíïïïïïïïïïï外圆纵向磨削力模型经验法[8]10组/14组EN 18CrNi8B60L6V8Ft=C1·vx1r·sy1a·az1Fn=C2·vx2r·sy2a·az2{
2 外圆横向磨削力模型求解
本文主要针对外圆横向磨削力理论模型的求解过程进行说明。为了准确预测分析各个磨削参数对磨削力的影响效果,必须较好地拟合出公式中的各个待求系数,本文基于遗传算法优化非线性优化函数(GA-LSQ)针对上述公式进行非线性回归分析。
2.1 遗传算法
遗传算法(GA)是一种基于生物进化原理构想出来的仿生算法,模拟基因重组与进化的自然过程,把待解决问题的参数变成二进制码或其他进制即基因,若干基因组成一个染色体(个体)[15]。该算法将随机产生的一代染色体作为候选解并计算其适应度,采用优胜劣汰的方法选择个体进行选择、交叉、变异等遗传操作,保留适应度高的染色体作为新一代种群,向着更优解的方向进化,最终获得最优的一组染色体,从而达到某种预定的优化收敛指标,具有多参数、多组合和随机性强的寻优特点。遗传算法的具体计算步骤如下。
步骤1 对磨削力公式的待求系数采用实数编码的方式进行编码。由外圆磨削力公式可得待求系数为12个,故染色体个体编码长度为12,从而得到种群中初始染色体。
步骤2 遗传算法适应度函数取若干组数据误差的二范数作为适应度函数S,其误差越小,适应度函数值越小[16]。
步骤3 使用轮盘赌算法在当前种群中选择适应度较高染色体进行复制,进一步产生新的种群。
步骤4 根据适应度函数,使用轮盘赌算法在当前种群中选择适应度较高染色体作为父代染色体进行选择、交叉、变异等遗传操作,在新产生的一代种群中选择适应度高的染色体作为下一代种群,染色体编码的基因选择概率px[17]为
(1)
fx=k/Fx。
(2)
式中:Fx为个体x的适应度值;N为种群染色体数量;k为常数。
步骤5 第k条染色体Akj与第l条染色体Alj之间在j处发生的交叉操作的方法如下:
(3)
式中:α为[0,1]的随机数。
步骤6 第k个染色体中的第l个基因akl的变异过程如下:
(4)
(5)
式中:amax为基因akl中的最大值;amin为基因akl中的最小值;r2为随机数;g为当前时刻的迭代数;Gmax为最大迭代数;r为[0,1]中的随机数。
遗传算法每次迭代就相当于完成了选择、交叉和变异等操作,经过迭代,误差逐渐降低直到满足优化目标,获得相应个体的最优适应度,从而得到最优系数组合并作用于非线性优化函数。其算法流程图如图1所示。
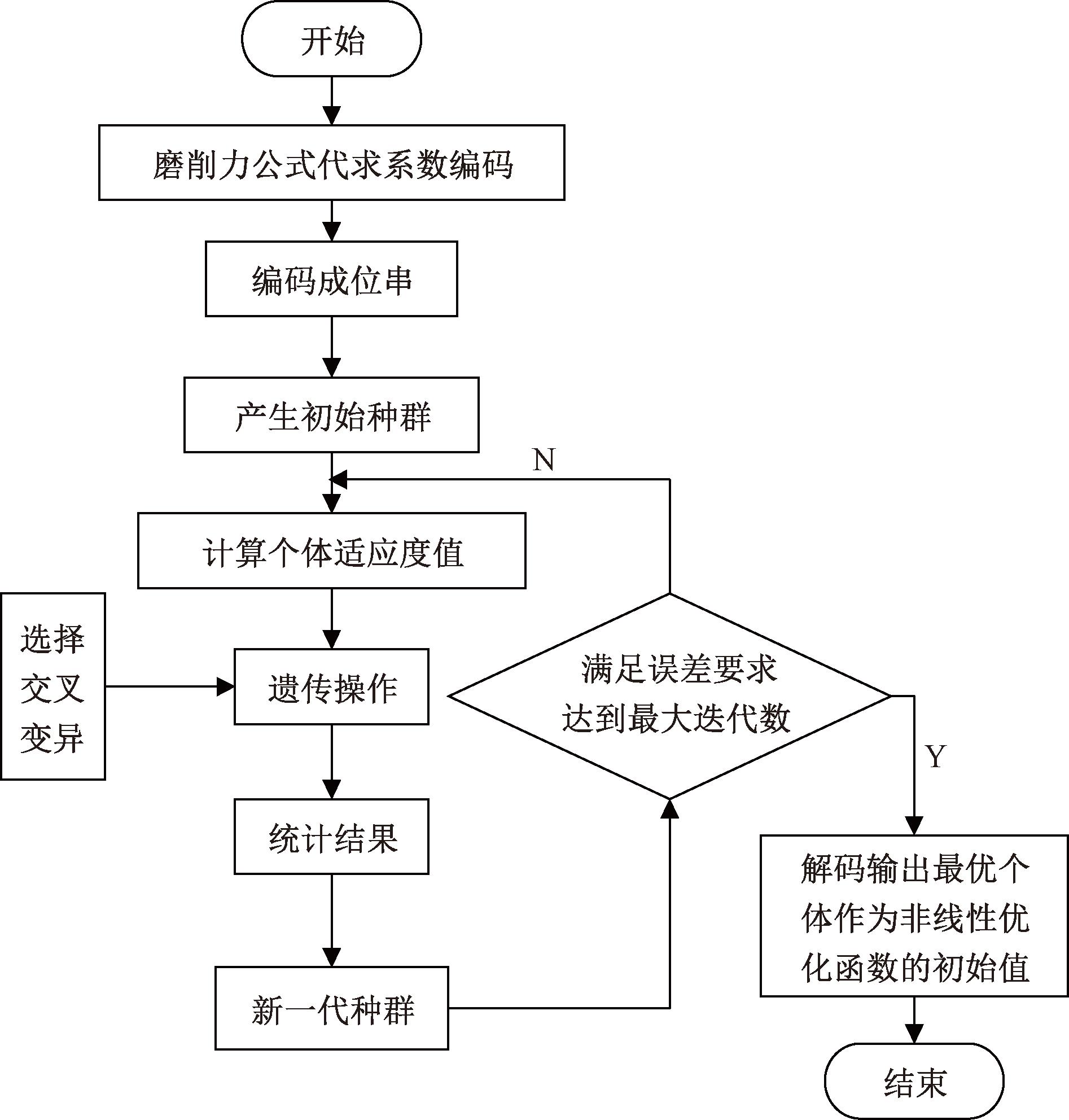
图1 遗传算法流程图
Figure 1 Genetic algorithm flow chart
2.1.1 确定适应度函数
在遗传算法计算过程中,适应度函数对算法输出的染色体起着至关重要的作用。选取外圆横向模型中10组实验得到的数据如表2所示。
表2 系数确定实验表[6]
Table 2 Coefficient determination test sheet[6]
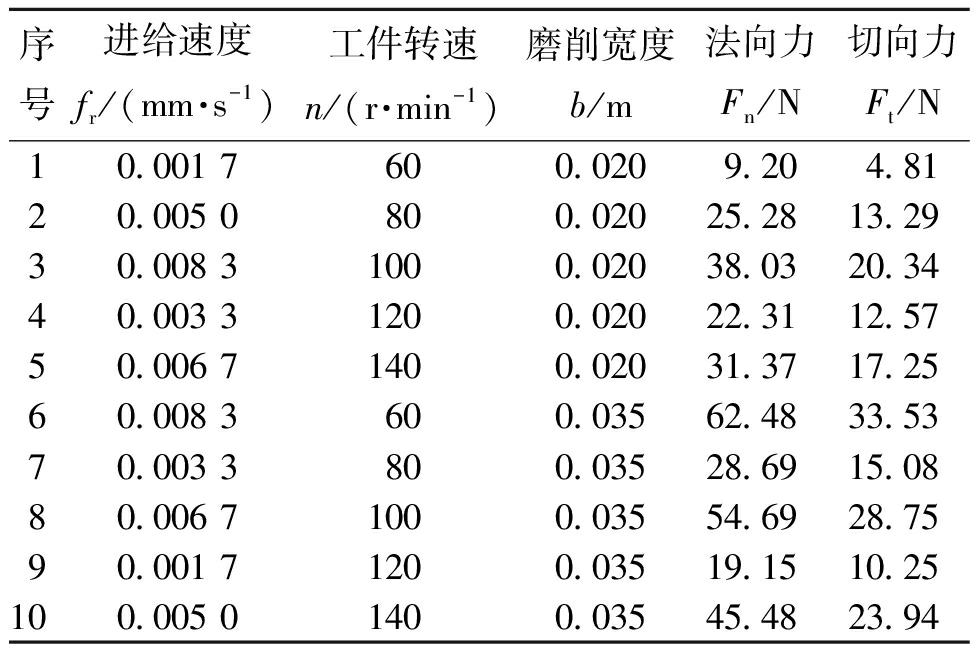
序号进给速度fr/(mm·s-1)工件转速n/(r·min-1)磨削宽度b/m法向力Fn/N切向力Ft/N10.001 7600.0209.204.8120.005 0800.02025.2813.2930.008 31000.02038.0320.3440.003 31200.02022.3112.5750.006 71400.02031.3717.2560.008 3600.03562.4833.5370.003 3800.03528.6915.0880.006 71000.03554.6928.7590.001 71200.03519.1510.25100.005 01400.03545.4823.94
若![]() 取误差的二范数‖δi‖2。在求解磨削力模型的系数时,误差的二范数越小,预测区间越窄,其预测的精度就越高,所以选择文献[6]模型中10组数据误差的二范数作为适应度函数S:
取误差的二范数‖δi‖2。在求解磨削力模型的系数时,误差的二范数越小,预测区间越窄,其预测的精度就越高,所以选择文献[6]模型中10组数据误差的二范数作为适应度函数S:
(6)
式中:yi为每次实验磨削力的实际值;![]() 为每次实验磨削力的拟合值。
为每次实验磨削力的拟合值。
2.1.2 参数设置
本文使用MATLAB R2020a作为仿真实验工具,遗传算法迭代次数设置为100。为了进一步提高迭代进化效率,根据磨削力公式进行试算,为参数设定上下限,其中k′1,k′2,…,k′6取值为1 000 000~10 000 000,α1,α2,…,α6取值为-20~20。对于具体实现遗传算法的操作而言,初始种群个数N、交叉概率Pc、变异概率Pm这些参数偏大或偏小都会对寻优结果造成影响。为了能够获得最好的个体,首先要确定最佳的参数组合,因此设计一组3因素5水平的正交参数表进行遗传算法各参数寻优。种群个数5水平分别为80、90、100、110、120;交叉概率5水平分别为0.40、0.45、0.50、0.55、0.60;变异概率5水平分别为0.02、0.04、0.06、0.08、0.10。
由上述正交实验寻优结果可得,当遗传算法参数的组合为N=110、Pc=0.55、Pm=0.04时,其对应的最优适应度变化曲线如图2所示。在迭代次数达到81后,目标的适应度值收敛到最优结果。遗传算法搜寻到10组实验数据最小误差的二范数S的结果为8.05。对应该参数下搜寻到的外圆横向磨削力模型参数组合k′1,k′2,…,k′6分别为9 991 050.41、5 741 027.33、1 963 086.61、1 416 058.29、2 759 136.77、5 746 585.79,α1,α2,…,α6分别为0.3、3.46、3.03、0.84、0.70、0.85。

图2 遗传算法寻优适应度曲线
Figure 2 Optimizing fitness curve by genetic algorithm
2.1.3 非线性优化函数(lsqnonlin)
将遗传算法得出的最优系数组合作为非线性拟合函数的初始值,进一步求解最优系数组合。非线性优化函数求解公式系数最优组合的原理为搜索10组误差范数的最小值,相应数字模型为已知函数矩阵F(X)=[f1(x),f2(x),…fn(x)]T,求X使得![]() 其中
其中![]() 每一代残差返回值为
每一代残差返回值为![]() 结果如图3所示。
结果如图3所示。
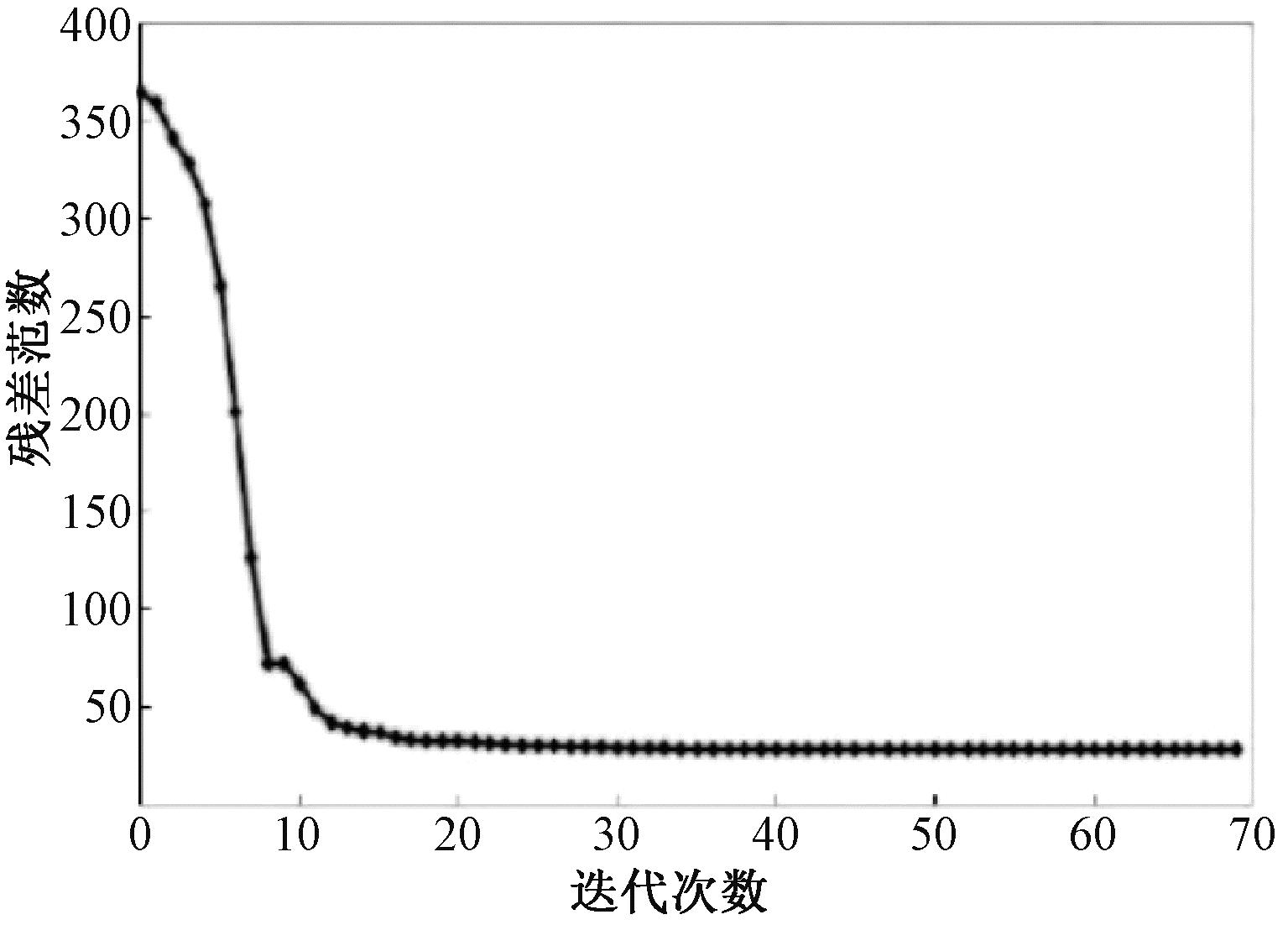
图3 非线性优化函数残差迭代曲线
Figure 3 Nonlinear optimization function residual iteration curve
从图3可以看出,在迭代达到62之后,非线性优化函数收敛到最优结果28.4。非线性优化函数搜寻到10组实验数据的最小残差值为8.05。最终得到外圆横向磨削力模型系数的最优组合k′1,k′2,…,k′6分别为4 105 391.76、7 131 411.89、3 819 675.5、2 593 089.88、1 000 021.34、2 283 679.89,α1,α2,…,α6分别为0.57、0.96、-2、0.39、0.62、0.86。
最终得到的外圆磨削力优化模型如式(7)所示。

(7)
3 外圆横向磨削力模型预测结果及分析
为了探究基于遗传算法的非线性优化函数求出的系数组合的准确性,将文献[6]中15组实验数据代入到外圆磨削力模型中,计算模型预测值并与实验得出的实际值进行比较来验证该方法的拟合效果。曲线拟合效果通常可以用决定系数R2来评价[18]:
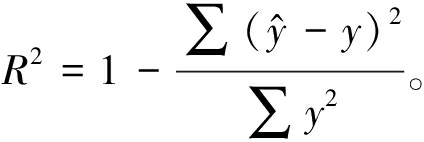
(8)
式中:![]() 为预测值;y为实验值。
为预测值;y为实验值。
表3为外圆横向磨削力模型各组预测数据的误差对比。其验证数据对比见图4,其中下标1、2分别对应本文模型与文献[6]模型,Fn 、Ft 分别表示法向磨削力和切向磨削力。下文规则同上。
表3 外圆横向磨削力模型验证实验表
Table 3 Cylindrical transverse grinding force model validation test table
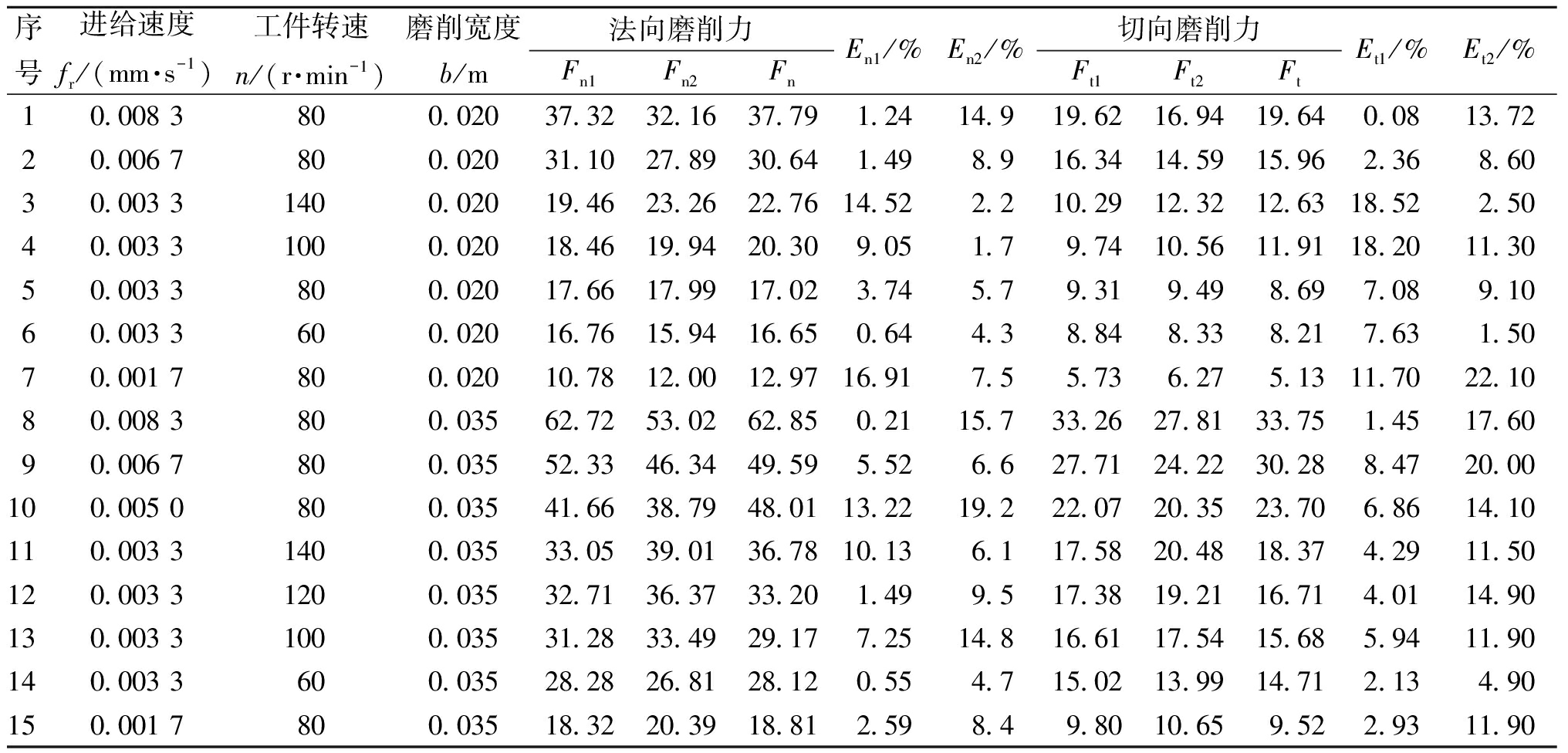
序号进给速度fr/(mm·s-1)工件转速n/(r·min-1)磨削宽度b/m法向磨削力Fn1Fn2FnEn1/%En2/%切向磨削力Ft1Ft2FtEt1/%Et2/%10.008 3800.02037.3232.1637.791.2414.919.6216.9419.640.0813.7220.006 7800.02031.1027.8930.641.498.916.3414.5915.962.368.6030.003 31400.02019.4623.2622.7614.522.210.2912.3212.6318.522.5040.003 31000.02018.4619.9420.309.051.79.7410.5611.9118.2011.3050.003 3800.02017.6617.9917.023.745.79.319.498.697.089.1060.003 3600.02016.7615.9416.650.644.38.848.338.217.631.5070.001 7800.02010.7812.0012.9716.917.55.736.275.1311.7022.1080.008 3800.03562.7253.0262.850.2115.733.2627.8133.751.4517.6090.006 7800.03552.3346.3449.595.526.627.7124.2230.288.4720.00100.005 0800.03541.6638.7948.0113.2219.222.0720.3523.706.8614.10110.003 31400.03533.0539.0136.7810.136.117.5820.4818.374.2911.50120.003 31200.03532.7136.3733.201.499.517.3819.2116.714.0114.90130.003 31000.03531.2833.4929.177.2514.816.6117.5415.685.9411.90140.003 3600.03528.2826.8128.120.554.715.0213.9914.712.134.90150.001 7800.03518.3220.3918.812.598.49.8010.659.522.9311.90
说明:下标1 和2 分别对应本文和文献[6]模型,E为误差。
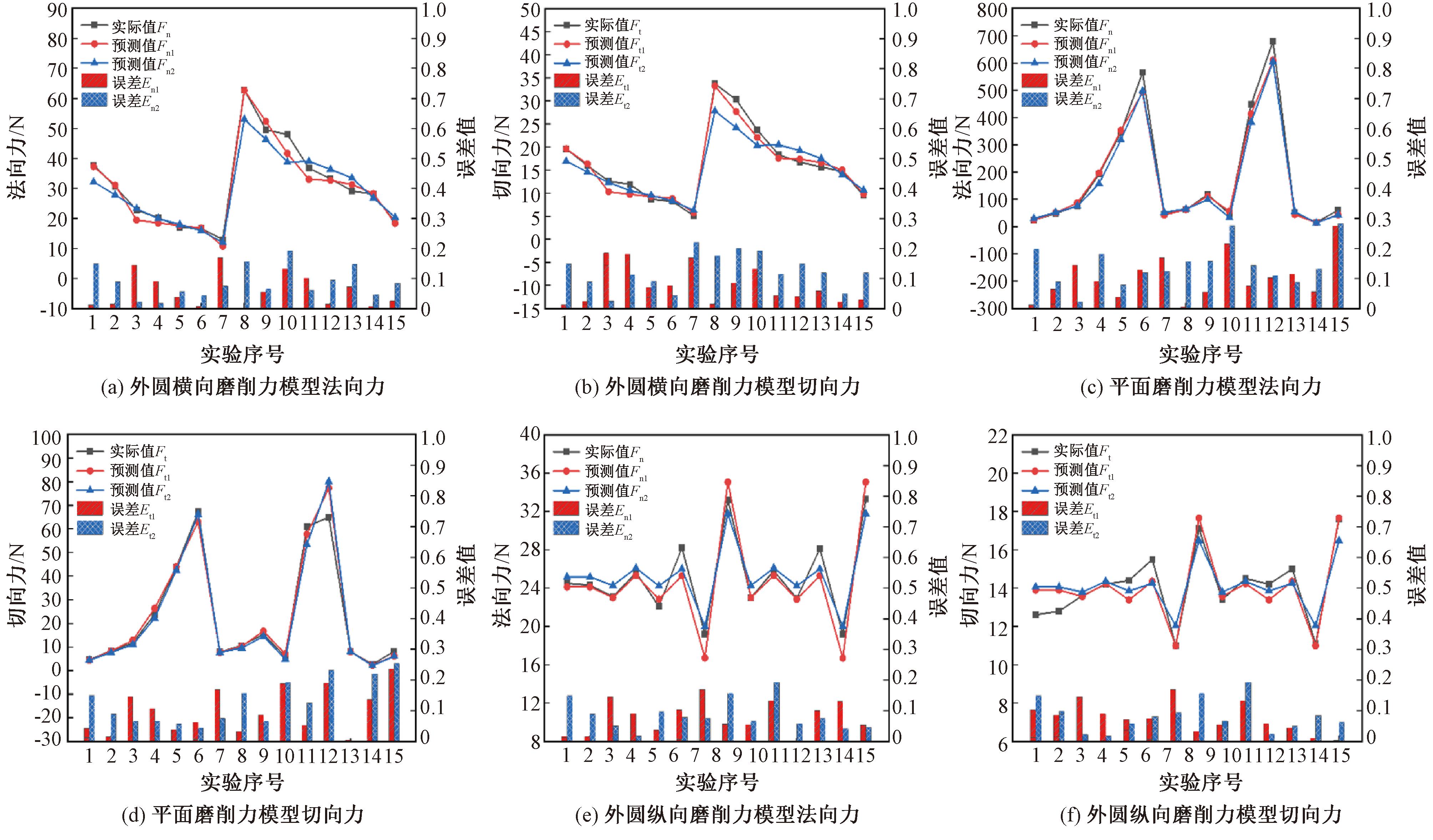
图4 3种模型各组验证数据对比图
Figure 4 Comparison of validation data of each group in three models
计算得到外圆横向磨削法向和切向磨削力公式预测结果的决定系数R2分别为0.994 9和0.995 2,较接近1。通过外圆横向磨削得到法向磨削力和切向磨削力的平均预测误差分别为5.90%和 6.78%,相比于原文中的模型误差分别降低了32.18%、42.54%,具体如图4(a)、4(b)所示。
4 平面磨削力模型与外圆纵向磨削力模型预测结果及分析
平面模型、外圆纵向磨削力模型优化过程本文在此并不详细叙述。本文方法与文献[5,8]方法关于模型的误差对比如图4(c)~4(f)所示,得到法向磨削力平均预测误差分别为9.13%、3.23%,切向磨削力的平均预测误差分别为8.36%、3.69%,相比于文献[5,8]中的模型,法向力预测误差分别降低32.87%、38.48%,切向磨削力预测误差分别降低14.69%、31.54%。可见这种计算待求系数的方法同时适用于平面磨削力模型与外圆纵向磨削力模型,并且能起到一定的优化作用。
最终通过基于遗传算法的非线性优化函数求解平面磨削力模型、外圆纵向磨削力模型如式(9)、(10)所示。

(9)
(10)
表4为3种模型预测数据的误差对比。可以看出,使用本文所提出的模型优化方法绝大部分误差小于文献[5,8]模型,决定系数均高于相关文献模型,因此可以认为本文所提出的优化方法对不同磨削力模型优化结果都较为适用。
表4 3种模型验证误差表
Table 4 Table of validation errors of three models
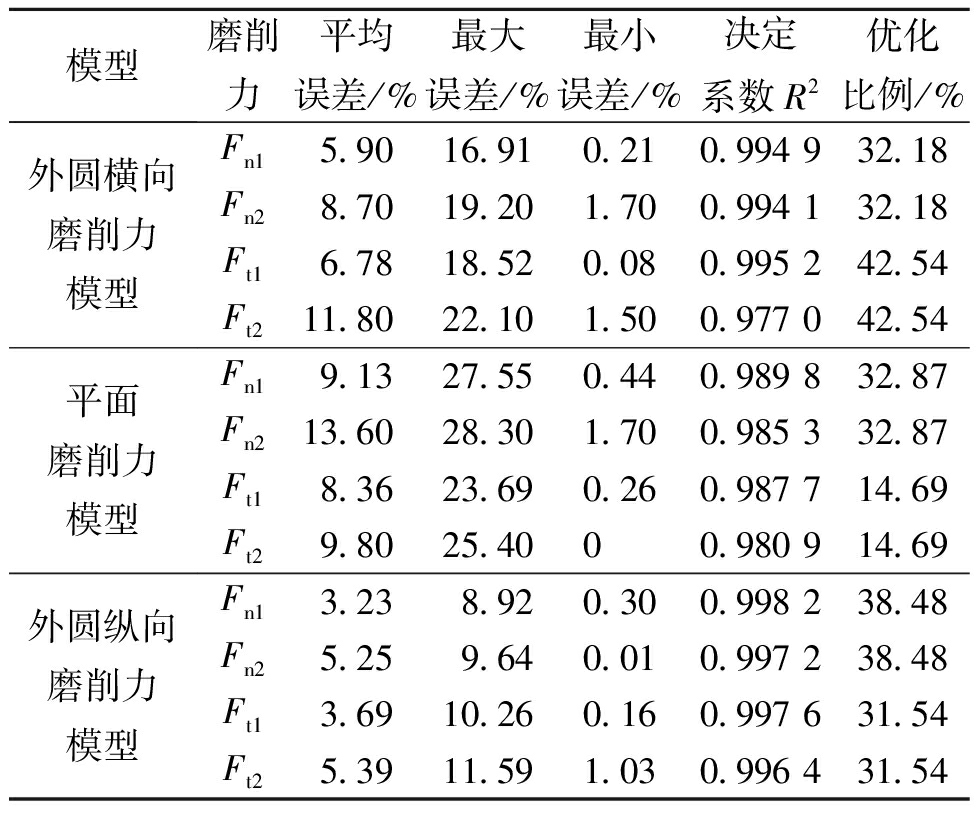
模型磨削力平均误差/%最大误差/%最小误差/%决定系数R2优化比例/%外圆横向磨削力模型平面磨削力模型外圆纵向磨削力模型Fn15.9016.910.210.994 932.18Fn28.7019.201.700.994 132.18Ft16.7818.520.080.995 242.54Ft211.8022.101.500.977 042.54Fn19.1327.550.440.989 832.87Fn213.6028.301.700.985 332.87Ft18.3623.690.260.987 714.69Ft29.8025.4000.980 914.69Fn13.238.920.300.998 238.48Fn25.259.640.010.997 238.48Ft13.6910.260.160.997 631.54Ft25.3911.591.030.996 431.54
5 结论
(1)将外圆横向磨削力模型、平面磨削力模型和外圆纵向磨削力模型的磨削实验结果与理论推导相结合并通过GA-LSQ算法经过多点搜索对参数集进行处理,从而得到输出的最优系数组合。从优化的模型中可直接得出各加工参数与磨削力的关系,通过控制磨削力从而进一步提高表面质量。
(2)本文方法具有普遍适用性,针对平面磨削力模型、外圆横向磨削力模型、成形磨削力模型、外圆纵向磨削力模型等进行了相应的计算验证,预测的模型误差均在10%以下。
(3)在外圆横向磨削力模型、平面磨削力模型和外圆纵向磨削力模型中,其法向磨削力预测误差分别为5.90%、9.13%、3.23%,切向磨削力的预测误差分别为6.78%、8.36%、3.69%,磨削力的预测精度提高了14.69%~42.54%。
[1] PATNAIK DURGUMAHANTI U S, SINGH V, VENKATESWARA RAO P. A new model for grinding force prediction and analysis[J]. International Journal of Machine Tools and Manufacture, 2010, 50(3): 231-240.
[2] MAENG S J, LEE P A, KIM B H, et al. An analytical model for grinding force prediction in ultra-precision machining of WC with PCD micro grinding tool[J]. International Journal of Precision Engineering and Manufactu-ring-Green Technology, 2020, 7(6): 1031-1045.
[3] ZHOU H, DING W F, LI Z, et al. Predicting the grin-ding force of titanium matrix composites using the genetic algorithm optimizing back-propagation neural network model[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2019, 233(4): 1157-1167.
[4] 詹友基, 左振, 许永超, 等. 纳米晶硬质合金的磨削力实验与预测[J]. 材料与冶金学报, 2022, 21(6): 448-455.
ZHAN Y J, ZUO Z, XU Y C, et al. Experiment and prediction of grinding force of nanosized cemented carbide[J]. Journal of Materials and Metallurgy, 2022, 21(6): 448-455.
[5] LI B K, DAI C W, DING W F, et al. Prediction on grinding force during grinding powder metallurgy nickel-based superalloy FGH96 with electroplated CBN abrasive wheel[J]. Chinese Journal of Aeronautics, 2021, 34(8): 65-74.
[6] 马少奇. 18CrNiMo7-6钢外圆磨削力及表面完整性研究[D]. 郑州: 郑州大学, 2021.
MA S Q. Research on grinding force and surface integrity of 18CrNiMo7-6 steel in cylindrical grinding[D]. Zhengzhou: Zhengzhou University, 2021.
[7] JAMSHIDI H, GURTAN M, BUDAK E. Identification of active number of grits and its effects on mechanics and dynamics of abrasive processes[J]. Journal of Materials Processing Technology, 2019, 273: 116239.
[8] KOVA P, PUCOVSKY V,
P, PUCOVSKY V, ![]() M, et al. Cutting force during grinding determined by regression analysis and genetic algorithms[J]. Key Engineering Materials, 2016, 686: 13-18.
M, et al. Cutting force during grinding determined by regression analysis and genetic algorithms[J]. Key Engineering Materials, 2016, 686: 13-18.
[9] GUO M X, LI B Z, DING Z S, et al. Empirical modeling of dynamic grinding force based on process analysis[J]. The International Journal of Advanced Manufacturing Technology, 2016, 86(9): 3395-3405.
[10] MISHRA V K, SALONITIS K. Empirical estimation of grinding specific forces and energy based on a modified Werner grinding model[J]. Procedia CIRP, 2013, 8: 287-292.
[11] SU Y H, LIN B, CAO Z C. Prediction and verification analysis of grinding force in the single grain grinding process of fused silica glass[J]. The International Journal of Advanced Manufacturing Technology, 2018, 96(1): 597-606.
[12] AMAMOU R, BEN FREDJ N, FNAIECH F. Improved method for grinding force prediction based on neural network[J]. The International Journal of Advanced Manufacturing Technology, 2008, 39(7/8): 656-668.
[13] 赵静雯. 圆柱形疲劳试样V型缺口成形磨削工艺优化研究[D]. 郑州: 郑州大学, 2022.
ZHAO J W. Optimization study on cylindrical fatigue specimen V-notch of forming grinding process[D]. Zhengzhou: Zhengzhou University, 2022.
[14] 蔡卫星, 周伟华, 张峰. 21NiCrMo5H齿轮钢超声磨削力建模研究[J]. 现代制造工程, 2020(4): 113-118.
CAI W X, ZHOU W H, ZHANG F. Research on the grinding force model of ultrasonic grinding for 21NiCrMo5H[J]. Modern Manufacturing Engineering, 2020(4): 113-118.
[15] 赵庆岩, 黎杰, 吴顺, 等. 基于遗传算法优化的机械臂动态矩阵预测控制[J]. 郑州大学学报(工学版), 2020, 41(1): 32-37.
ZHAO Q Y, LI J, WU S, et al. Dynamic matrix predictive control of manipulators based on genetic algorithms[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(1): 32-37.
[16] 秦娜, 刘凡, 刘亚龙, 等. 基于遗传算法优化BP神经网络的钛合金旋转超声磨削力预测[J]. 中国科技论文, 2017, 12(10): 1128-1131, 1156.
QIN N, LIU F, LIU Y L, et al. Prediction of grinding force in rotary ultrasonic grinding of titanium alloy based on BP neural network optimized by genetic algorithm[J]. China Sciencepaper, 2017, 12(10): 1128-1131, 1156.
[17] 欧阳海滨, 全永彬, 高立群, 等. 基于混合遗传粒子群优化算法的层次路径规划方法[J]. 郑州大学学报(工学版), 2020, 41(4): 34-40.
OUYANG H B, QUAN Y B, GAO L Q, et al. Hierarchical path planning method for mobile robots based on hybrid genetic particle swarm optimization algorithm[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(4): 34-40.
[18] 张翔, 王应刚, 陈泓谕, 等. 基于BP神经网络与遗传算法的固结磨具制作工艺参数优化[J]. 表面技术, 2022, 51(2): 358-366.
ZHANG X, WANG Y G, CHEN H Y, et al. Optimization of fixed-abrasive tool development parameters based on BP neural network and genetic algorithm[J]. Surface Technology, 2022, 51(2): 358-366.