近年来,国内外学者对智能车辆的轨迹跟踪控制问题进行了大量的研究。目前常用的轨迹跟踪控制算法主要有滑模控制、预瞄控制、模糊控制以及模型预测控制(MPC)等。李印祥等[1]、张家旭等[2]、李渊等[3]建立了包含系统加性不确定性的汽车弯道超车路径变积分滑模跟踪模型,并利用在环仿真系统验证了模型的有效性。聂枝根等[4]、寇发荣等[5]设计了轨迹预瞄前馈和状态反馈结合的横向控制方式,实现了对智能汽车变道动态轨迹和航向角良好的跟踪。赵伟等[6]基于模糊控制算法,提出了控制载重汽车保持行驶轨迹的控制策略,有效提高了载重汽车曲线行驶的循迹能力。
相对于其他控制算法,MPC具有很好的鲁棒性和抗干扰性,能够利用被控对象现在和过去的输入和输出偏差,预测未来的输入和输出[7-9];同时能够解决多约束问题,将约束条件添加到目标函数,滚动优化确定当前的最优控制目标值。Falcone等[10]基于模型预测控制算法提出了一种用于控制自动驾驶汽车中的主动前转向(AFS)系统的控制方法,实现了在湿滑的道路上以尽可能高的进入速度更好地循迹。Wu等[11]、张维刚等[12]、由智恒[13]考虑控制执行器约束和车辆动态稳定性约束,设计了通过主动转向和四轮独立驱动/制动的MPC轨迹跟踪控制器,避免了车辆在紧急工况下出现因地面不能提供足够侧向力而引起的车辆失稳现象。Zhang等[14]针对受输入约束的扰动自主地面车辆(AGVs)轨迹跟踪问题,基于递归最小二乘(RLS)和鲁棒性约束,提出了一种自适应学习模型预测控制(AL-MPC)方案,并通过数值算例和对比研究证明了该方法的有效性。Yuan等[15]基于LQR-MPC算法提出了一种用于轨迹跟踪控制系统的横向和纵向耦合控制器,实现了在跟踪期望轨迹的同时,最小化横向跟踪偏差。王艺等[16-17]、王银等[18]为了解决智能车辆的自主转向问题,提出了一种变参数的智能网联汽车路径跟踪控制方法,实现了不同速度和不同道路线形下的跟踪控制。虽然上述研究在给定的环境下都取得了不错的跟踪效果,但许多研究未充分考虑低附着情况下的车辆动力约束,对MPC控制器内控制参数的研究大多停留在单一控制参数的研究,轨迹跟踪依旧存在控制精度和控制稳定性问题。
为提高智能车辆在低附着环境下轨迹跟踪控制的准确性和稳定性问题,以智能车辆主动转向控制为研究对象,在现有模型预测控制算法的基础上,添加轮胎侧偏角约束,并同时优化控制器的时域参数,设计轨迹跟踪控制器,实现稳定精确的跟踪控制。
1 轨迹跟踪控制
1.1 车辆动力学模型
考虑车辆的行驶环境和转向时的稳定性,选择考虑轮胎滑移的车辆动力学模型描述车辆运动。如图1所示,XOY为大地坐标系,xoy为车身坐标系。其中,Fcf、Fcr分别为前、后轮侧向力;Flf、Flr分别为前、后轮纵向力;a和b分别为前、后轮到车辆质心的距离;δf为前轮转向角;φ为车辆横摆角;
为横摆角速度;αf和αr分别为前后轮侧偏角;β为质心侧偏角;Vf、Vr和V分别为车身坐标系中前、后轮和质心位置的速度。
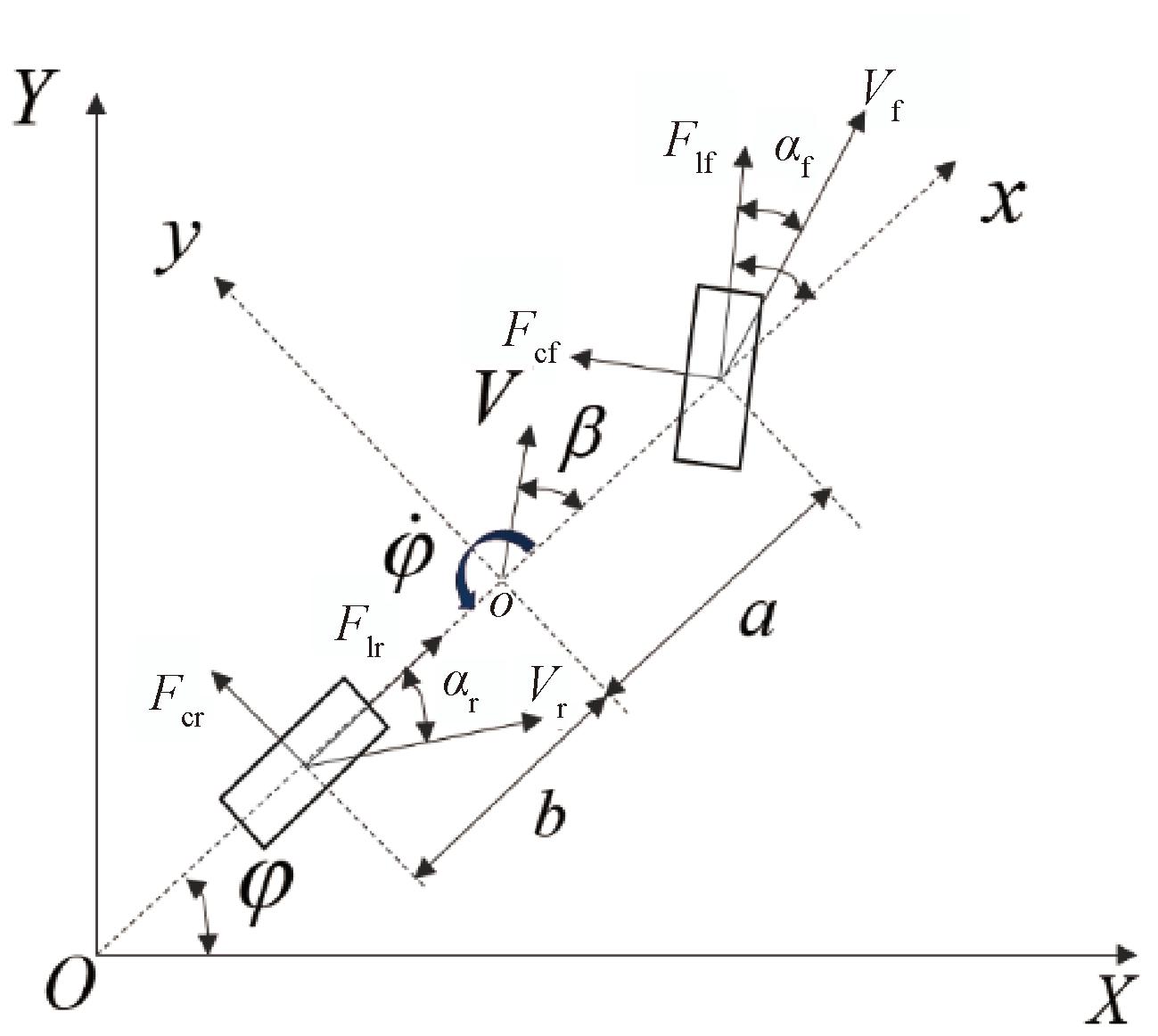
图1 车辆动力学模型
Figure 1 Vehicle dynamics model
根据牛顿第二定律,在小角度假设和线性轮胎模型假设下,结合车身坐标转换公式,最终得到车辆动力学模型为
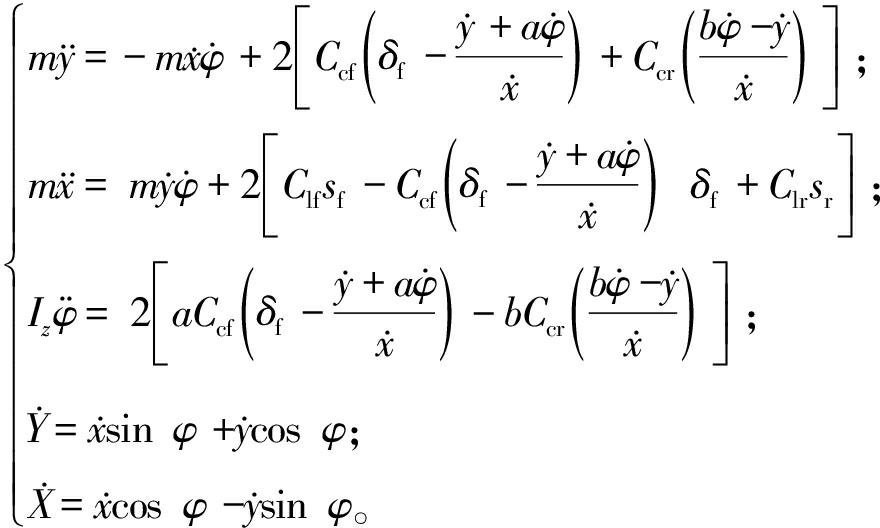
(1)
式中：m为车辆整备质量;Iz为车辆绕z轴的转动惯量;
和
分别为车辆在XOY坐标系中纵向和横向速度;
和
分别为车辆在xoy坐标系中纵向和横向速度;Ccf和Ccr分别前轮和后轮侧偏刚度;Clf和Clr分别为前轮和后轮纵向刚度;sf和sr分别为前轮和后轮滑移率,取值均为0.2。
选取状态量
控制量u=[δf]。
1.2 MPC控制器设计
1.2.1 预测模型
根据式(1)建立非线性车辆动力学状态方程：
(2)
式中：
为控制输出量,
为输出矩阵,
设当前时刻的状态量和控制量分别为ξ0、u0,非线性模型如下：
(3)
对任意点(ξ0,u0)进行泰勒展开,只留一阶项：
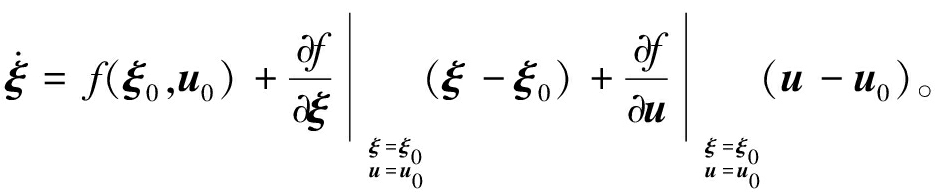
(4)
将式(4)、(3)相减,并采用前向欧拉法进行离散化,可得离散化状态方程：
(5)
式中：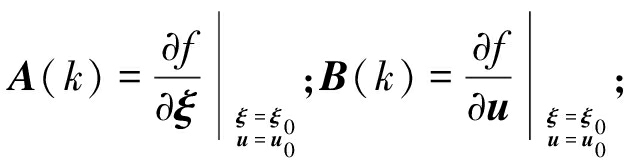
ξ(k)为k时刻车辆的状态量;u(k)为k时刻控制输入量;Ck为输出矩阵。
为减小误差,引入增量模型,将式(5)中控制量改写成控制增量的形式,如式(6)所示：
(6)
式中：
其中ξ(k|k)为车辆在k时刻的状态量,u(k-1|k)为车辆在k-1的控制输入量;Δu(k|k)=u(k|k)-u(k-1|k)表示k时刻控制增量;
对整个预测时域内控制输出进行迭代,得到k时刻输出矩阵表达式为
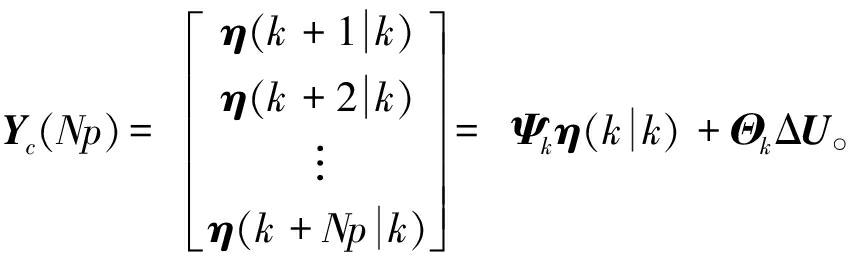
(7)
式中：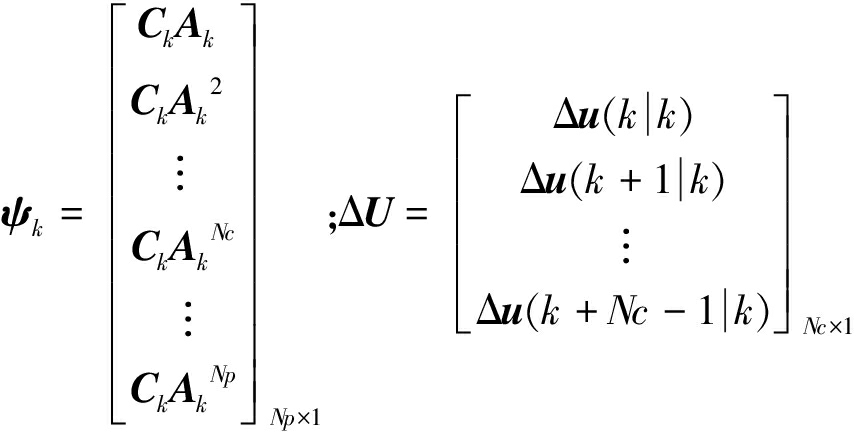
;
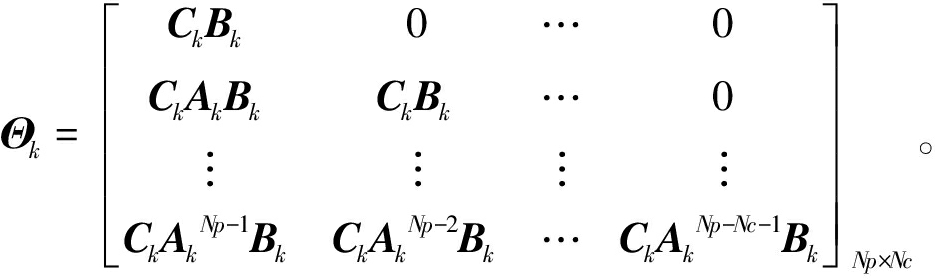
1.2.2 目标函数与约束条件
为了保证车辆能够迅速且稳定地跟踪目标轨迹,以前轮转向角增量作为目标函数的控制量,定义轨迹跟踪模型预测控制优化目标函数为
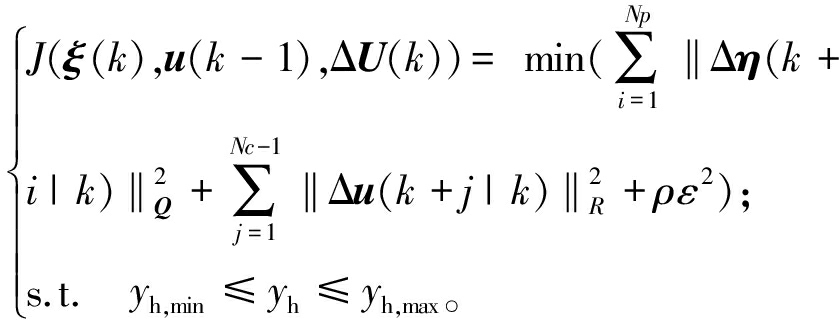
(8)
式中：Δη(k+i|k)=η(k+i|k)-Y(k+i|k)为预测时域内实际输出与已知参考轨迹之差;ρ为权重系数;ε为松弛因子;Q和R分别为输出权重矩阵和控制量权重矩阵;yh包括前轮转角约束|δfmax|≤10°、|Δδfmax|≤0.847°和质心侧偏角约束|βmax|≤5°;yh,min、yh,max分别为硬约束的最小值和最大值。
由于动力学模型是在线性轮胎模型假设下建立的,因此需要对轮胎侧偏角进行限制,使轮胎的受力在线性稳定区域内,以保证车辆在低附着极限工况下运动时的安全性。
轮胎侧偏角与车辆纵向速度
车辆横向速度
横摆角速度以及前轮转角δf之间的关系如下：
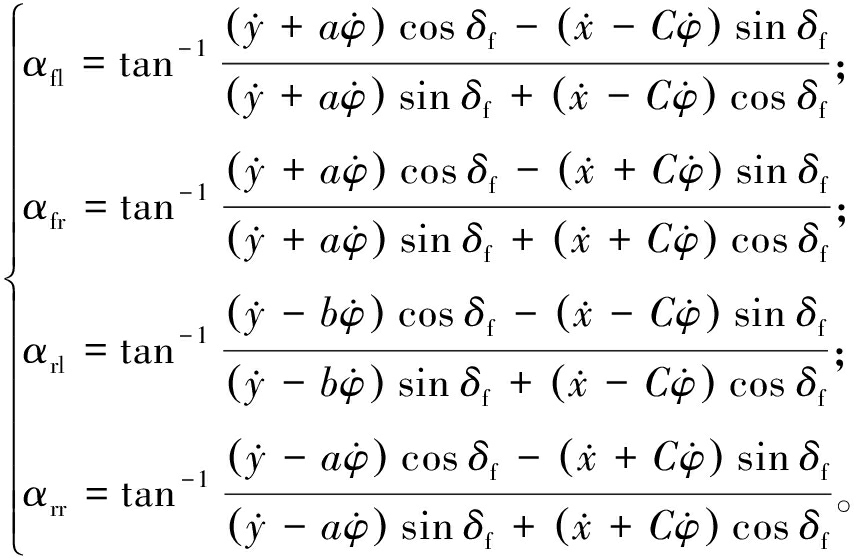
(9)
将式(9)进行线性化和离散化,方法与1.2.1节预测模型一样,得到离散线性时变模型：
(10)
式中：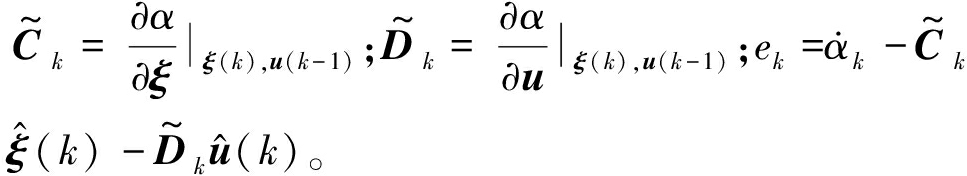
将
和
代入到目标函数中得到
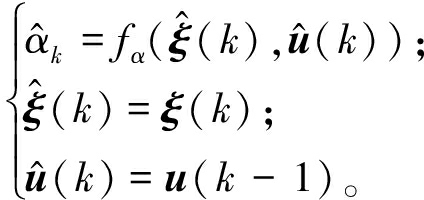
(11)
轮胎侧偏角约束条件为
αmin-ε≤αk≤αmax+ε。
(12)
式中：αmin、αmax分别轮胎侧偏角的最大值和最小值。
将目标函数转化成二次规划的标准矩阵形式,结合约束条件利用内点法进行最优求解,转化形式如下：
[ΔU(k)T,ε]THk[ΔU(k)T,ε]+Gk[ΔU(k)T,ε]。
(13)
式中：Hk为正定的Hessian矩阵,
滚动优化求解,得到控制时域内的控制增量ΔU=[Δu*(k)Δu*(k+1)…Δu*(k+Nc-1)],将控制增量序列的第1个当前时刻的控制量(即前轮转角)输入被控车辆,重复上述过程,最终实现轨迹跟踪控制。
为验证上述添加轮胎侧偏角约束的MPC控制器在极限工况下的有效性,搭建MATLAB/SimuLink与CarSim联合仿真平台进行仿真分析。其中,在CarSim中选择Class-C型车辆作为被控车辆模型,车辆基本参数如表1所示。结合相关文献,在SimuLink中搭建MPC控制器,通过调试得到控制器的基本参数如表2所示。
表1 车辆基本参数
Table 1 Basic vehicle parameters
参数取值m/kg1 723Iz/(kg·m2)4 175a/m1.232b/m1.468Ccf、Clf/(N·rad-1)66 900Ccr、Clr/(N·rad-1)62 700
在CarSim仿真平台设置冰雪路面,路面附着系数值均为0.2,纵向速度设置为108 km/h,参考路径选择双移线实验工况,模拟超车工况。对添加侧偏角约束的MPC控制器和未添加侧偏角约束的MPC控制器进行对比。仿真对比效果如图2(a)～2(c)所示。
表2 控制器基本参数
Table 2 Basic parameters of the controller
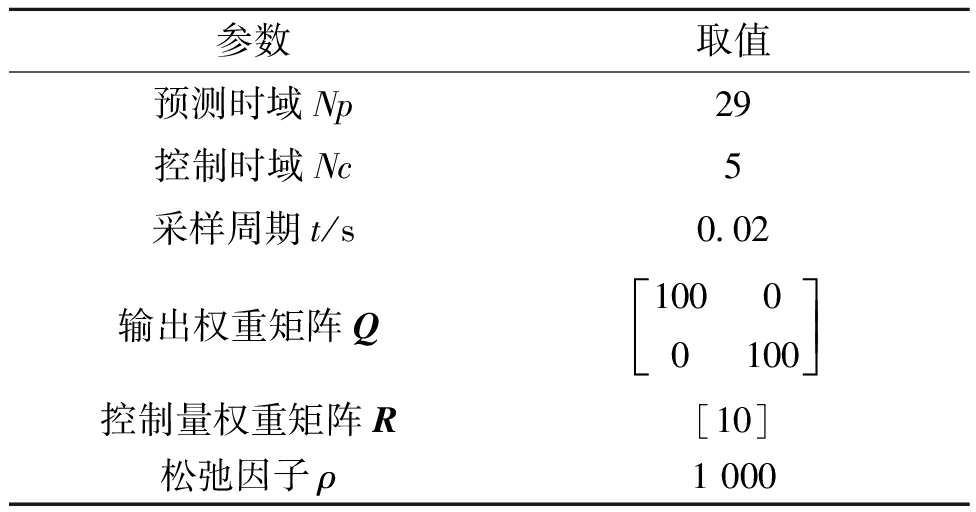
参数取值预测时域Np29控制时域Nc5采样周期t/s0.02输出权重矩阵Q10000100éëêêùûúú控制量权重矩阵R[10]松弛因子ρ1 000
从图2可以看出,不考虑侧偏约束的控制器在跟踪过程中出现了有明显的振荡现象,车辆行驶稳定性较差,轮胎侧偏角也超过了稳定范围,轮胎模型的适应性变差。而考虑侧偏角约束的控制器能够较好地实现跟踪控制,产生的横向偏差也较小,有效改善了控制器行驶的稳定性。
图2 路径跟踪和侧偏角变化对比
Figure 2 Comparison of path tracking and sideslip angle change
2 自适应时域参数MPC控制器设计
控制构架主要由两部分构成：线性时变(LTV)MPC控制器设计和自适应时域参数控制器设计,如图3所示。基于接收的规划轨迹信息,结合1.2.2节目标函数和车辆动力学约束条件,采用LTV-MPC求解最优前轮转向角δf,输入到被控车辆,得到当前车辆状态,作为自适应时域参数控制器的输入,根据当前车速优化得到最优时域参数,输入到控制器的预测模型中,重复上述步骤,最终实现避撞轨迹跟踪控制。上文已经完成了轨迹跟踪控制器的建立,下文将对自适应时域参数控制器进行设计。
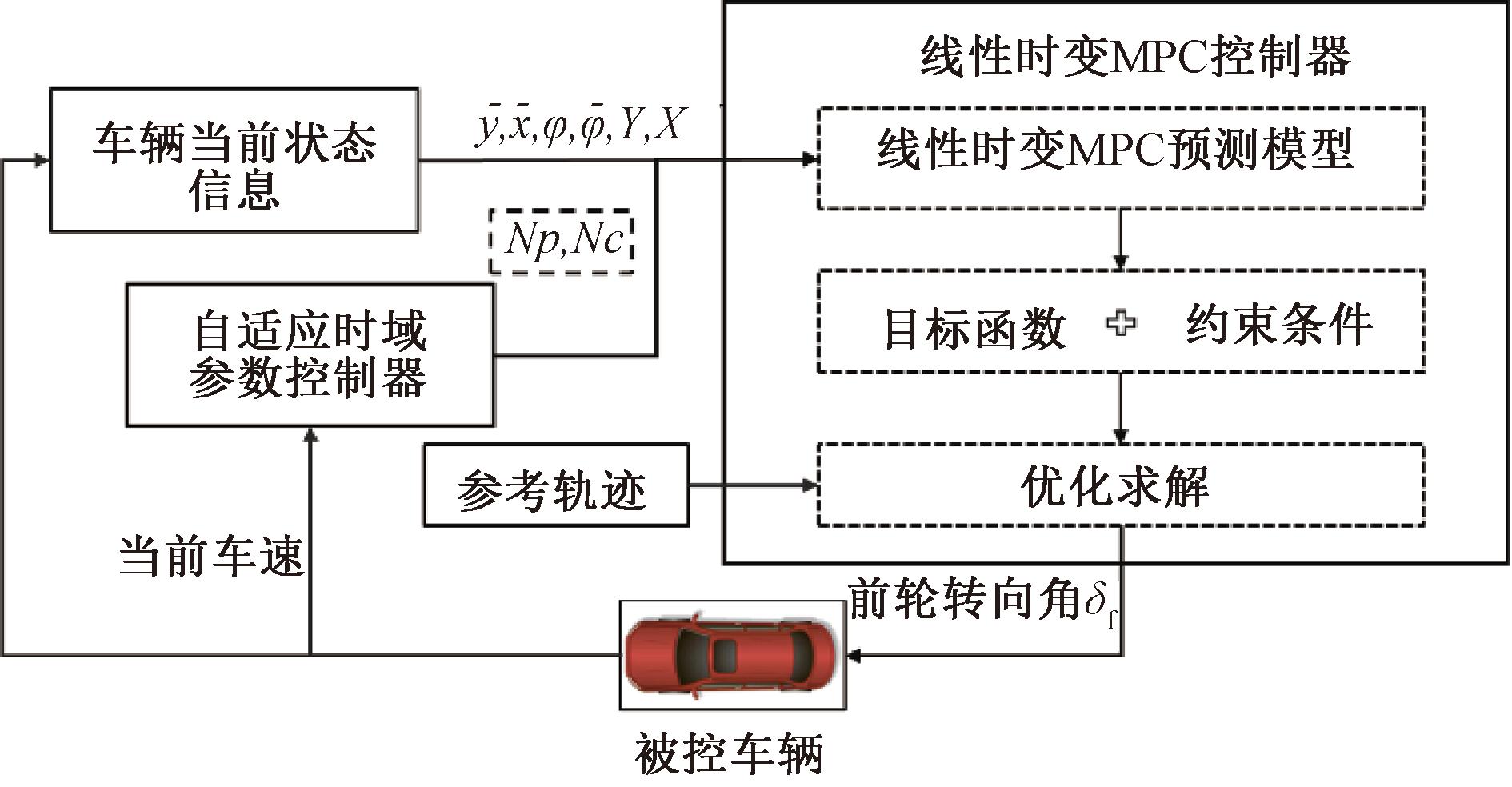
图3 自适应时域参数MPC控制器构架
Figure 3 Architecture of adaptive time domain parameter MPC controller
2.1 分析Np和Nc参数对控制器的影响
模型预测控制器主要包括：采样时间T、Np、Nc这3个控制参数,三者选取的数值不同,控制器产生的控制效果也有所不同。本文主要分析预测时域和控制时域的变化对控制器跟踪效果影响。
为了直观地看出不同预测时域和控制时域对车辆跟踪控制器的影响,设计了3组仿真测试,速度设置为72 km/h,全局参考轨迹选择双移线,仿真结果如图4所示。
图4 72 km/h时路径跟踪效果对比图
Figure 4 Comparison of path tracking effects at 72 km/h
从图4(a)中可以看出,车辆在72 km/h速度行驶时,控制器在不同控制时域取值下的控制效果有了明显差异,控制时域取值较小时,控制器在跟踪控制时出现了超调现象,车辆的行驶稳定性受到一定影响,从图4(b)也可以看出产生了较大的横向偏差。当预测时域固定,控制时域变大时,控制效果有所改善,避免了超调,横向误差也较小。当控制时域参数固定时,可以发现预测时域Np=25时,车辆跟踪控制产生的横向偏差较小,控制效果更好。
2.2 最优Np和Nc的选择
为了确定不同速度下最优的Np和Nc,以18 km/h作为速度间隔,车速设置为36～108 km/h,预测时域Np设置为15～30,控制时域Nc设置为1～5,对跟踪控制器进行离线仿真实验,总实验组数为400组。同时,为了保证控制器参数的有效性、防止出现车辆控制失效情况,对预测时域参数和控制时域参数进行如下有效筛选：①选取参数能够保证控制器有效运行;②选取参数满足所设定的约束条件,保证行驶安全;③选取参数保证控制器的实时性,求解时间小于采样时间T。基于以上筛选条件,得到有效仿真实验组168组。
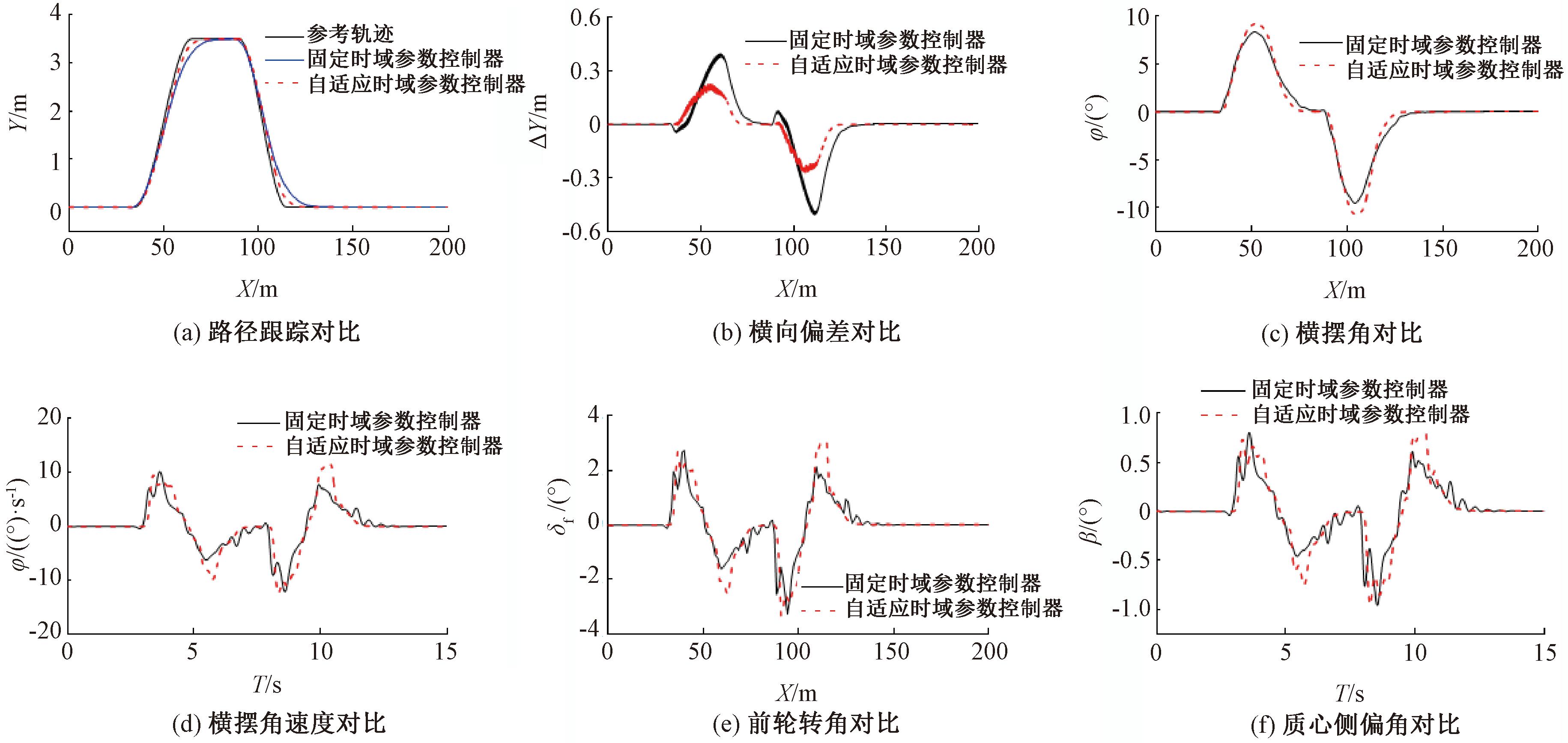
图5 40 km/h时车辆跟踪控制效果对比
Figure 5 Comparison of vehicle tracking control effects at 40 km/h
以最大横向偏差、平均横向偏差、横向偏差方差作为衡量控制精度指标,最大质心侧偏角和最大横摆角速度作为衡量车辆稳定性指标,利用TOPSIS法评价出不同速度下预测时域和控制时域的最优取值,并将车速与相应的最优预测时域参数和控制时域参数进行样条插值拟合,得到基于车速变化的时域参数控制律如式(14)所示,用于轨迹跟踪控制设计。
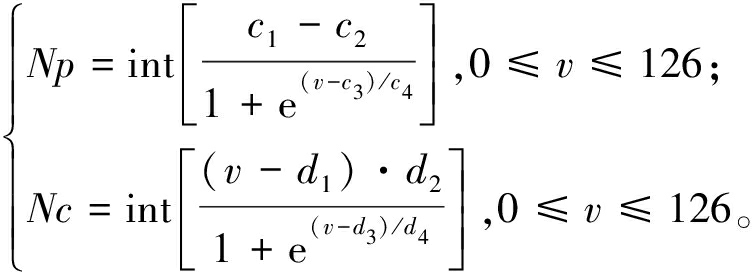
(14)
式中：ci和di(i=1,2,3,4)分别为预测时域拟合系数和控制时域拟合系数;v表示车辆在大地坐标系中的纵向车速,即
3 仿真验证
上述实验研究了不同预测时域参数和控制时域参数对控制器的影响,完成了自适应时域参数控制器的设计。为了验证自适应时域参数MPC控制器的跟踪性能,在双移线工况下与2.1节固定时域控制器进行仿真对比,仿真车速分别选取40 km/h和80 km/h为代表车速,仿真结果如图5和图6所示。
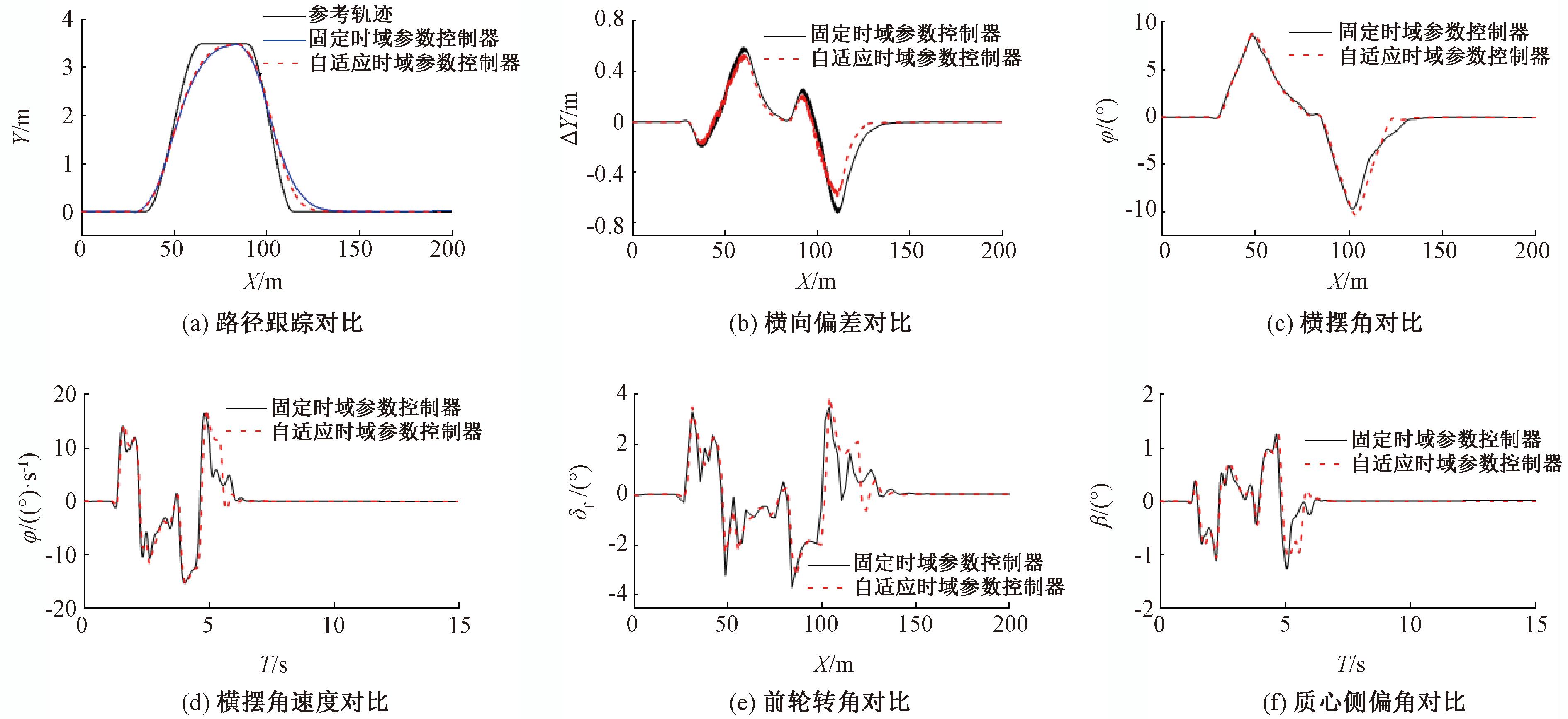
图6 80 km/h时车辆跟踪控制效果对比
Figure 6 Comparison of vehicle tracking control effects at 80 km/h
从图5和图6可以看出,在不同速度下,自适应控制器的路径跟踪效果要优于固定时域参数控制器。在车速为40 km/h时,固定时域参数控制器的最大横向偏差为396.439 mm,而自适应时域参数MPC控制器的最大横向偏差为224.669 mm,控制精度提高了43.3%。两者的横摆角、横摆角速度、前轮转角以及质心侧偏角相差不大,都满足约束条件。当速度达到80 km/h时,自适应时域参数控制器的横向偏差依旧小于固定时域参数控制器,保证了控制精度。此时,自适应时域参数控制器的最大横摆角速度和最大质心侧偏角也小于固定时域参数控制器,说明在高速工况下,自适应时域参数控制器的控制效果更好,车辆行驶的稳定性更好。
4 结论
(1)添加轮胎侧偏角约束的MPC控制器能够有效约束车辆轮胎侧偏角在稳定范围内变化,保证了车辆在极限工况下行驶的稳定性,从而提高车辆行驶安全性。
(2)相对于固定时域MPC控制器,自适应时域参数的MPC控制器在横向偏差上有明显改善,有效提高了跟踪控制精度,并且质心侧偏角变化也在约束范围内,保证了车辆在不同速度下行驶的稳定性。
[1] 李印祥, 王凯. 基于滑模控制的汽车主动换道避障研究[J]. 车辆与动力技术, 2018(2)： 26-30, 35.
LI Y X, WANG K. Research on vehicle obstacle avoi-dance based on synovium control[J]. Vehicle &Power Technology, 2018(2)： 26-30, 35.
[2] 张家旭, 周时莹, 施正堂, 等. 采用滑模条件积分的无人驾驶汽车弯道超车路径规划与跟踪控制[J]. 控制理论与应用, 2021, 38(2)： 197-205.
ZHANG J X, ZHOU S Y, SHI Z T, et al. Path planning and tracking control for corner overtaking of driverless vehicle using sliding mode technique with conditional integrators[J]. Control Theory &Applications, 2021, 38(2)： 197-205.
[3] 李渊, 马戎, 付维平. 智能车辆的滑模轨迹跟踪控制[J]. 测控技术, 2012, 31(9)： 71-74.
LI Y, MA R, FU W P. Sliding mode control for trajectory tracking of intelligent vehicle[J]. Measurement &Control Technology, 2012, 31(9)： 71-74.
[4] 聂枝根, 王万琼, 赵伟强, 等. 基于轨迹预瞄的智能汽车变道动态轨迹规划与跟踪控制[J]. 交通运输工程学报, 2020, 20(2)： 147-160.
NIE Z G, WANG W Q, ZHAO W Q, et al. Dynamic trajectory planning and tracking control for lane change of intelligent vehicle based on trajectory preview[J]. Journal of Traffic and Transportation Engineering, 2020, 20(2)： 147-160.
[5] 寇发荣, 杨慧杰, 张新乾, 等. 采用状态反馈的无人车路径跟踪横向控制[J]. 机械科学与技术, 2022, 41(1)： 143-150.
KOU F R, YANG H J, ZHANG X Q, et al. A lateral control strategy for unmanned vehicle path tracking using state feedback[J]. Mechanical Science and Technology for Aerospace Engineering, 2022, 41(1)： 143-150.
[6] 赵伟, 王宁宁, 段燕燕, 等. 载重汽车曲线行驶智能循迹控制仿真研究[J]. 郑州大学学报(工学版), 2015, 36(2)： 10-13.
ZHAO W, WANG N N, DUAN Y Y, et al. The simulation study of the truck curve traveling intelligent traction control[J]. Journal of Zhengzhou University (Enginee-ring Science), 2015, 36(2)： 10-13.
[7] WANG H, HUANG Y J, KHAJEPOUR A, et al. Crash mitigation in motion planning for autonomous vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(9)： 3313-3323.
[8] BRUSCHETTA M, MARAN F, BEGHI A. A fast implementation of MPC-based motion cueing algorithms for mid-size road vehicle motion simulators[J]. Vehicle System Dynamics, 2017, 55(6)： 802-826.
[9] PRACH A, KAYACAN E. An MPC-based position controller for a tilt-rotor tricopter VTOL UAV[J]. Optimal Control Applications and Methods, 2018, 39(1)： 343-356.
[10] FALCONE P, BORRELLI F, TSENG H E, et al. Linear time-varying model predictive control and its application to active steering systems： stability analysis and experimental validation[J]. International Journal of Robust and Nonlinear Control, 2008, 18(8)： 862-875.
[11] WU H D, SI Z L, LI Z H. Trajectory tracking control for four-wheel independent drive intelligent vehicle based on model predictive control[J]. IEEE Access, 2020,8： 73071-73081.
[12] 张维刚, 张朋, 韦昊, 等. 一种基于LTVMPC改进的无人驾驶汽车路径跟踪控制算法[J]. 湖南大学学报(自然科学版), 2021, 48(10)： 67-73.
ZHANG W G, ZHANG P, WEI H, et al. An improved path tracking control algorithm for autonomous vehicle based on LTVMPC[J]. Journal of Hunan University (Natural Sciences), 2021, 48(10)： 67-73.
[13] 由智恒. 基于MPC算法的无人驾驶车辆轨迹跟踪控制研究[D]. 长春： 吉林大学, 2019.
YOU Z H. Research on model predictive control-based trajectory tracking for unmanned vehicles[D]. Changchun： Jilin University, 2019.
[14] ZHANG K W, SUN Q, SHI Y. Trajectory tracking control of autonomous ground vehicles using adaptive learning MPC[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(12)： 5554-5564.
[15] YUAN T F, ZHAO R C. LQR-MPC-based trajectory-tracking controller of autonomous vehicle subject to coupling effects and driving state uncertainties[J]. Sensors, 2022, 22(15)： 5556.
[16] 王艺, 蔡英凤, 陈龙, 等. 基于模型预测控制的智能车辆路径跟踪控制器设计[J]. 汽车技术, 2017(10)： 44-48.
WANG Y, CAI Y F, CHEN L, et al. Design of intelligent vehicle path tracking controller based on model predictive control[J]. Automobile Technology, 2017(10)： 44-48.
[17] 王艺, 蔡英凤, 陈龙, 等. 基于模型预测控制的智能网联汽车路径跟踪控制器设计[J]. 机械工程学报, 2019, 55(8)： 136-144, 153.
WANG Y, CAI Y F, CHEN L, et al. Design of intelligent and connected vehicle path tracking controller based on model predictive control[J]. Journal of Mechanical Engineering, 2019, 55(8)： 136-144, 153.
[18] 王银, 张灏琦, 孙前来, 等. 基于自适应MPC算法的轨迹跟踪控制研究[J]. 计算机工程与应用, 2021, 57(14)： 251-258.
WANG Y, ZHANG H Q, SUN Q L, et al. Research on trajectory tracking control based on adaptive MPC algorithm[J]. Computer Engineering and Applications, 2021, 57(14)： 251-258.