目前,随着汽车电动化和智能化相关技术的飞速发展,人们对汽车行驶的安全性和可靠性提出了更高的要求,车辆主动安全被视为重要环节[1-2]。近年来,线控制动系统引起了广泛关注,其中电子机械制动(electronic mechanical braking, EMB)系统最为理想。EMB系统制动响应快,可实现车轮制动力矩的独立控制[3],且便于与其他车辆主动安全系统进行集成控制,对改善车辆的主动安全具有积极作用[4]。
迅速准确地获知路面附着信息和提高执行器控制器的鲁棒性,对提高车辆稳定性和行驶安全性具有积极作用[5-6]。在路面识别方面,He等[7]提出了一种基于拉格朗日插值法的路面识别算法,并通过仿真实验分析验证了该算法的有效性;潘辉等[8]利用滑移率及减速度特征参数的变化进行路面识别;邱明明等[9]采用了一种基于计算机视觉的路面辨识方法,经实验验证具有良好的识别精度和实时性。此外,控制器设计的优劣在很大程度上影响着车辆的制动效果,比例-积分-微分(PID)控制、模糊控制和滑模控制(SMC)等常应用到防抱死制动系统(anti-lock braking system, ABS)控制中。王国微等[10]运用了模糊控制和预测控制理论设计ABS控制器,提高了制动效果;Peng等[11]基于模糊滑模控制方法设计了EMB控制器以控制滑移率,通过实验验证相比于PID控制和滑模控制,模糊滑模算法的鲁棒性、对不同路面工况的适应性及制动效果更好。
然而,线控制动控制的相关研究多采用固定滑移率验证,较少考虑不同路面附着的差异性,同时传统逻辑门限控制方式存在逻辑复杂和难以适应不同路面工况的缺点。首先,本文以EMB系统为平台设计ABS控制策略,考虑到路面附着信息和控制器鲁棒性影响ABS控制效果,以及实际中车速难以准确获取和路面识别精度要求,设计了路面识别算法获知路面附着信息,输出最佳滑移率;其次,基于滑模控制理论设计EMB系统控制器,旨在控制实际滑移率维持在最佳滑移率附近;最后,通过仿真验证所提路面识别方法的实时性和准确性,并分析逻辑门限控制、模糊PID控制和积分滑模控制下ABS控制策略的制动控制效果。
1 EMB系统描述及建模
基于路面识别的EMB系统ABS控制系统框图如图1所示,上层控制包括制动意图和路面识别模块,研究重点为ABS控制策略,故仿真制动意图为紧急制动,在紧急制动工况下将路面识别输出结果最佳滑移率λopt作为目标滑移率λref;下层控制包括控制器模型和制动器模型,设计了基于滑模控制理论的控制器跟踪目标滑移率λref,得到EMB制动器所需要的电机电枢电流Ia,进而获得车轮所需的制动力矩Tb。
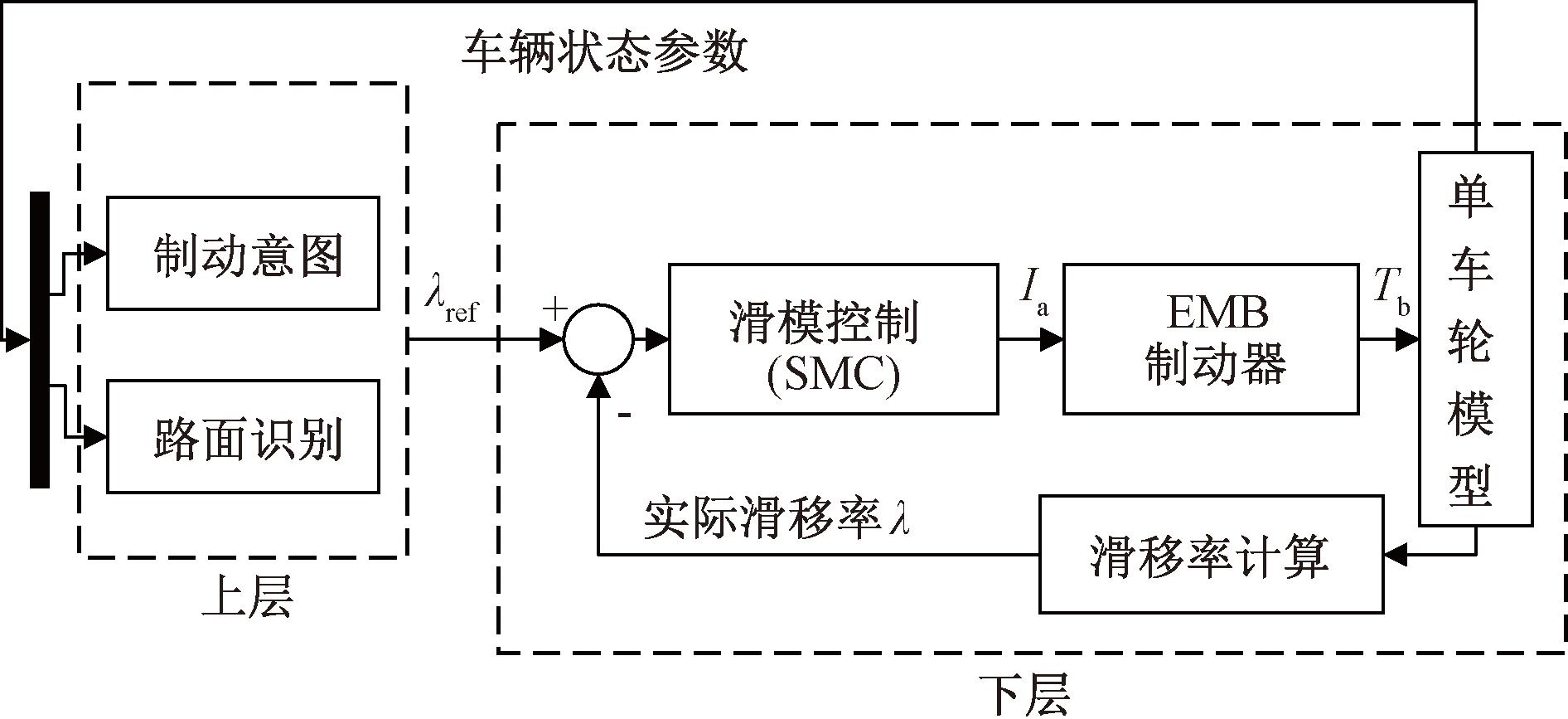
图1 ABS控制系统框图
Figure 1 ABS control system block diagram
1.1 单车轮模型
EMB系统4个车轮可以独立控制制动,其运动特性类似,为简化分析,忽略轴荷转移的影响,以下采用单车轮制动模型研究问题[9],制动时单车轮受力分析如图2所示。
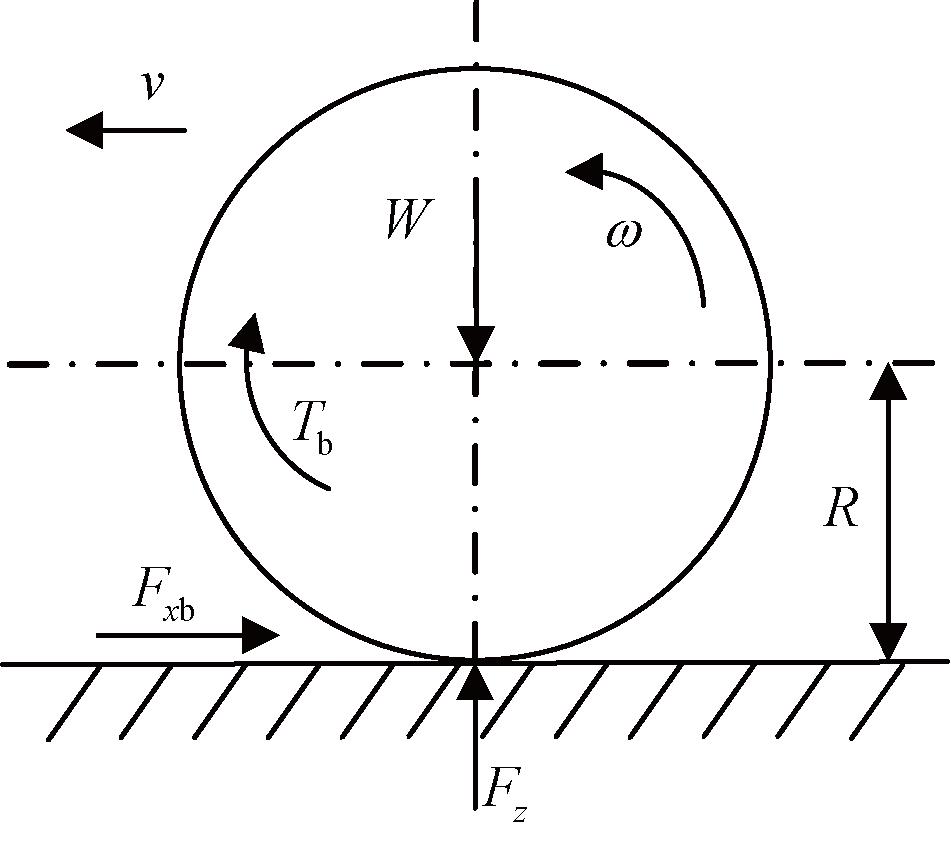
图2 单车轮制动受力分析
Figure 2 Force analysis of single wheel braking
分析轮胎受力,其动力学方程为
(1)
(2)
(3)
滑移率的定义为
(4)
式中：m为1/4车辆总质量,kg;v为轮心速度,m/s;W为车轮垂直载荷,N;Fxb为地面制动力,N;J为车轮转动惯量,kg·m2;R为轮胎半径,m;Tb为制动器制动力矩,N·m;μ为轮胎纵向利用附着系数;Fz为地面对车轮的法向作用力,N;ω为车轮角速度,
为车轮角减速度,rad/s2;λ为滑移率。
1.2 轮胎-路面模型
根据研究需要选用Burckhardt轮胎模型来描述车辆制动时的纵向路面附着关系[10],该模型给出了μ与λ的关系：
μ(λ)=c1(1-e-c2λ)-c3λ。
(5)
式中：c1、c2与c3为各种典型路面的拟合参数值。各种典型路面的拟合参数值见文献[10]。
1.3 EMB制动器模型
EMB制动器结构形式为浮动钳盘式,制动执行器结构包括驱动电机、行星齿轮机构、滚珠丝杠机构和制动盘,制动时施加给车轮的制动力矩Tb为
(6)
(7)
式中：Te为电机电磁转矩,N·m;KT为电机力矩系数,N·m/A;Ia为电机电枢电流,A;Ts为电机摩擦力矩,N·m;Kb为制动器输出力矩系数;ix为行星齿轮传动比;ηx为行星齿轮机械效率;ηs为滚珠丝杠机械效率;μb为制动盘摩擦系数;rb为制动盘有效半径,m;Ph为滚珠丝杠导程,m。
2 路面识别算法设计
轮胎作为车辆与道路接触的载体,传递着车辆运动所需的力和力矩。在制动过程中受到轮胎和地面不同程度打滑的影响,车辆受到的切向力是有限的,其纵向制动力最大值Fxbmax为
Fxbmax=μmaxFz。
(8)
式中：μmax为峰值附着系数。
在制动过程中,由单车轮制动模型,即式(2)和式(3)获得车轮纵向利用附着系数为
(9)
式中：制动器制动力矩Tb由测得电机电枢电流后通过EMB制动器模型即式(6)、(7)获取;车轮角减速度
通过轮速传感器测得角速度后差分得到。
制动时利用附着系数随车轮角减速度的变化曲线如图3所示。由图3(a)可知,以湿沥青路面紧急制动为例,在路面附着达到利用附着系数峰值点时,车轮进入非稳定区域,且车轮角减速度发生了急剧变化;由图3(b)可知,各典型路面下利用附着系数μ和车轮角减速度的关系曲线变化规律相似且都满足“先增后减”的变化趋势,即根据
数值发生正负变化时,此时可以进行峰值附着系数估计。
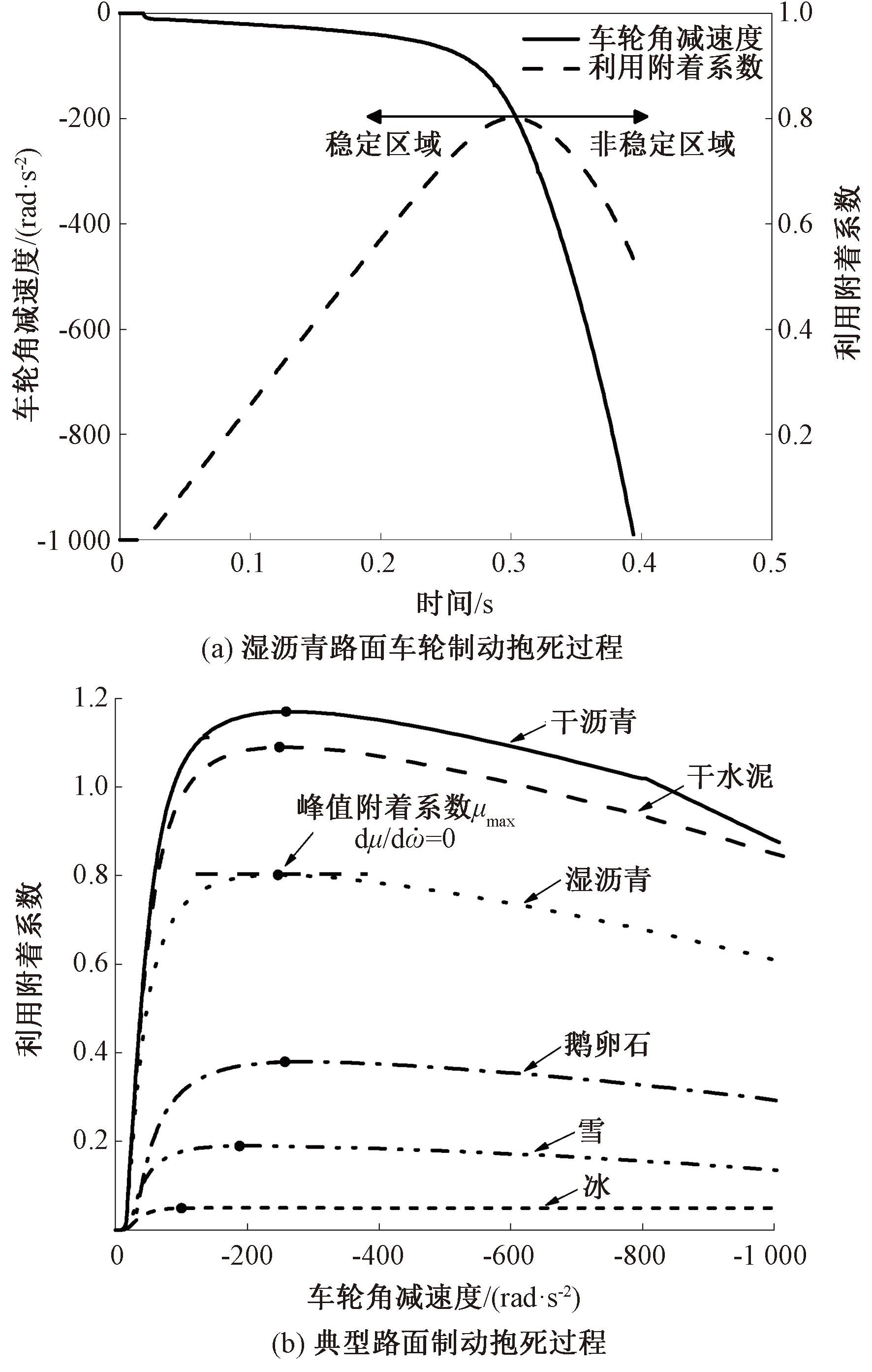
图3 制动时利用附着系数和车轮角减速度的变化曲线
Figure 3 Variation curve between adhesion coefficient and wheel angle deceleration braking
在实际应用时,获取k时刻前一采样周期δ(k-1)、当前采样周期δ(k)的两个δ采样值,根据δ(k)=0或者δ(k-1)·δ(k)<0来判断利用附着系数达到峰值,则此时获取峰值附着系数估计值
路面识别算法整体逻辑流程框图如图4所示,其中Flag为是否到达利用附着系数峰值点的标志位;μi为由各典型路面μ-λ曲线分别计算得到的利用附着系数。
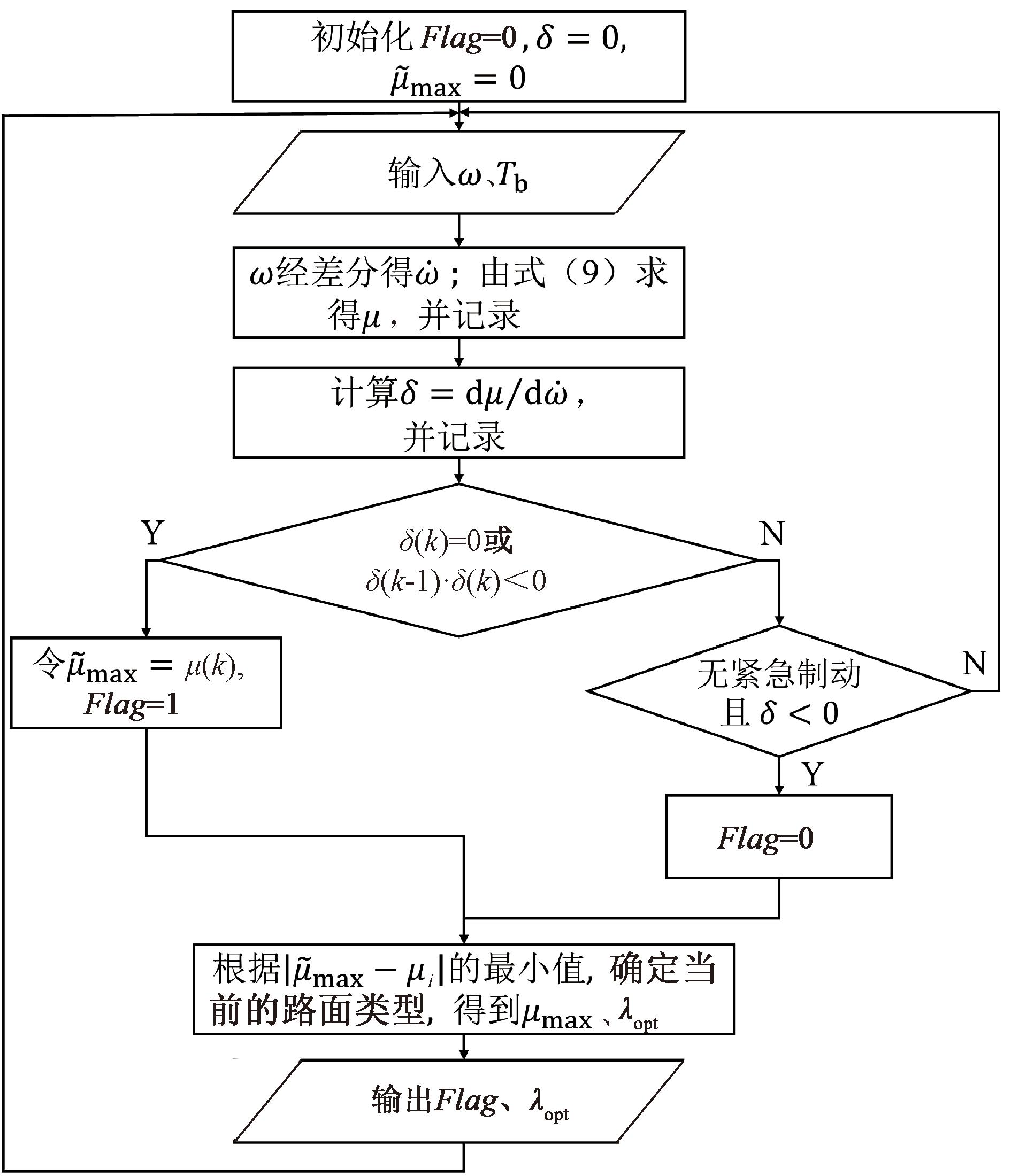
图4 路面识别算法逻辑流程框图
Figure 4 Road recognition algorithm logic flow diagram
3 基于SMC的ABS滑移率控制
ABS系统具有非线性、时变和不确定的特性,此外ABS系统使用场景常处于车辆行驶极端状态,且路面情况复杂多变,要求ABS系统控制满足响应快速、抵抗外界干扰能力强。滑模控制优点在于对参数变化不敏感、有效抑制外部干扰和响应快速等,常用于非线性控制系统中,故选用滑模控制理论设计EMB控制器。
根据路面识别算法输出结果,控制策略旨在将车轮的实际滑移率维持在最佳滑移率λopt附近,故设定ABS控制器的跟踪误差为
e=λopt-λ。
(10)
为了提高系统稳定性和鲁棒性引入积分,设计切换函数为
s=e(t)+c
e(τ)dτ。
(11)
式中：c为大于0的常数;t为时间。
对式(11)求导得
(12)
将式(1)～(4)、式(6)和式(7)代入式(12)中整理得
(13)
这里选择指数趋近律：
(14)
式中：ε为切换增益,k为系数,二者均大于0;sgn(·)为符号函数。
同时,设定电机电枢电流Ia为EMB控制器的控制输入,用u表示,联立式(13)和式(14)得到滑模控制器的控制律为
(15)
定义Lyapunov函数为
(16)
对式(16)求导后,将式(13)、(15)代入得
故可证明系统渐进稳定。
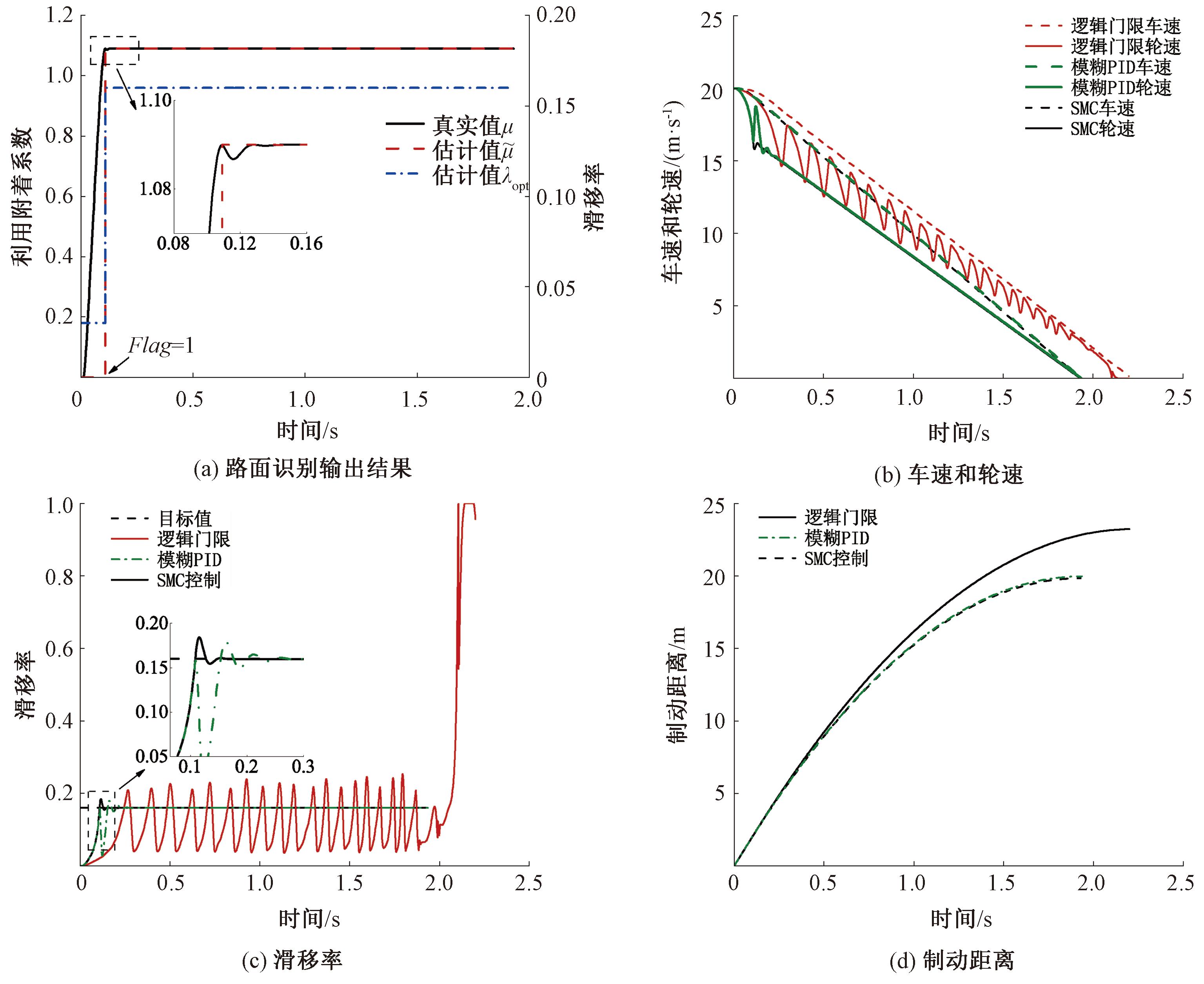
图5 干水泥路面紧急制动仿真结果
Figure 5 Simulation results of emergency braking on dry cement condition
4 仿真验证
4.1 仿真条件
在MATLAB/Simulink中搭建1/4车辆仿真模型,设定仿真工况为制动初始速度为20 m/s的紧急制动工况,首先分别选取干水泥和雪路面作为目标路面进行单路面条件仿真;再进行变路面条件仿真,包括在雪路面开始制动1 s后进入湿沥青路面和在干水泥路面开始制动1 s后进入雪路面。仿真采用文献[12]中参数进行不同路面条件下紧急制动工况仿真分析研究。
4.2 仿真结果分析
4.2.1 单路面条件
以干水泥路面制动工况分析为例,如图5所示。由图5(a)可知,在t=0.109 s获得峰值附着系数估计值,Flag标志位从0更新为1,同时估算出最佳滑移率为0.16。当Flag=1时,为保证制动效果,此时ABS控制介入,控制系统实时进行最佳滑移率跟踪控制。制动过程如图5(b)～5(d)所示,可知在SMC控制和模糊PID控制下,车速和轮速几乎同步减速到0,车轮未发生抱死现象。在跟踪滑移率方面,SMC控制波动较小且快速平稳地趋于目标值,而模糊PID控制波动大且达到目标值的响应时间较慢,传统制动系统逻辑门限控制仅能在设定的滑移率门限值附近调节,出现震荡现象无法有效地将各路面的最佳滑移率最大化使用。从制动时间、制动距离以及制动响应效果等角度分析,与逻辑门限控制和模糊PID控制相比,SMC控制效果更好。所设计SMC控制策略相较于传统逻辑门限控制,在单路面条件制动工况下制动时间减少了11.89%,制动距离缩短了12.7%。
其他典型单路面条件下的仿真结果与干水泥路面条件下的控制效果具有相似性：在单路面条件下路面识别方法可以迅速且准确地识别出最佳滑移率,满足紧急制动下路面识别对准确度和响应时间的要求;所设计的积分滑模可以平稳跟踪滑移率且具有良好的控制品质。
4.2.2 变路面条件
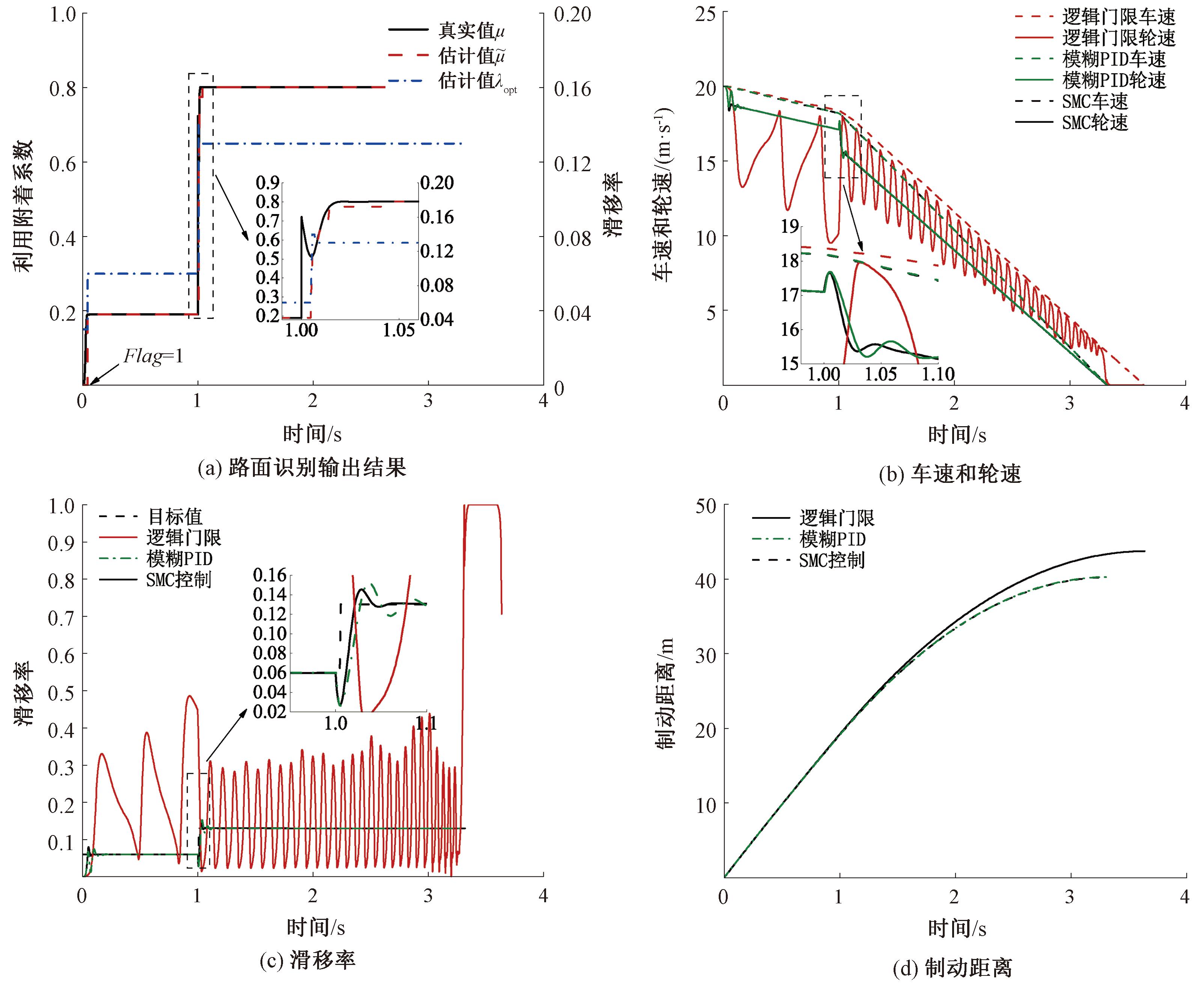
图6 雪路面到湿沥青路面紧急制动仿真结果
Figure 6 Simulation results of emergency braking from snow condition to wet asphalt condition
以雪路面到湿沥青路面工况分析为例,如图6所示。其路面识别结果如图6(a)所示,分别在t=0.044 s和t=1 s时迅速估算出雪路面和湿沥青路面的峰值附着系数,进而获得对应的最佳滑移率;在t=0.044 s时,ABS开始介入,进行滑移率控制。制动过程如图6(b)～6(d)所示,在路面发生变化时,相比于模糊PID,SMC控制对路面变化的适应性更强,且滑移率控制波动小,能迅速平稳过渡到稳定状态,传统逻辑门限控制仅能在设定的滑移率门限值附近调节,无法有效利用最佳滑移率。由图6可知,与模糊PID、逻辑门限控制相比,SMC控制没有出现明显震荡现象,在ABS介入时和切换路面时达到稳定所需时间更少,可以有效应对外界状态变化,具有更好的制动效果。所设计的SMC控制策略相较于逻辑门限控制,在变路面条件工况下制动时间减少了17.8%,制动距离缩短了19.9%。
干水泥路面到雪路面紧急制动仿真结果与上述变路面工况下的控制效果具有相似规律：路面识别方法对变路面条件具有较强的适应性,且识别响应快、识别准确度高;所设计的积分滑模可以快速地应对变路面条件下的紧急制动工况。
此外由各路面仿真结果可知,在Flag标志位更新为1之前,路面识别输出最佳滑移率的结果为0.03,这是因为在利用附着系数未达到峰值时没有进行路面识别,故此时峰值附着系数估计值为0,根据路面识别算法输出结果为冰路面,即最佳滑移率的结果为0.03,但此时Flag未更新为1,表明车轮制动状态仍属于稳定区域,ABS控制不会介入,该现象符合路面识别算法逻辑。
5 结论
(1)考虑到不同路面制动时路面附着存在差异性,提出了基于峰值附着系数的路面识别算法用于估计路面信息。该算法实时性好且计算量小,仿真结果表明：在不同路面条件下可以迅速且准确获知当前路面附着信息,满足紧急制动工况下对路面识别精度和响应时间的要求。
(2)与模糊PID和逻辑门限控制相比,所设计的积分滑模控制器具有很好的鲁棒性,有效地将实际滑移率控制在最佳滑移率处,同时对不同路面工况变化的适应性强,提高了制动效果。在单路面条件下制动时间减少了11.89%,制动距离缩短了12.7%;在变路面条件下制动时间减少了17.8%,制动距离缩短了19.9%。
[1] 张三川, 马啸. 基于轨迹加权预测的主动避撞安全距离模型及算法[J]. 郑州大学学报(工学版), 2022, 43(3)： 104-110.
ZHANG S C, MA X. A safe distance model and algorithm for active collision avoidance based on weighted prediction of trajectory[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(3)： 104-110.
[2] 王丙琛, 司怀伟, 谭国真. 基于深度强化学习的自动驾驶车控制算法研究[J]. 郑州大学学报(工学版), 2020, 41(4)： 41-45, 80.
WANG B C, SI H W, TAN G Z. Research on autopilot control algorithm based on deep reinforcement learning[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(4)： 41-45, 80.
[3] MENG B M, YANG F F, LIU J G, et al. A survey of brake-by-wire system for intelligent connected electric vehicles[J]. IEEE Access, 2020, 8： 225424-225436.
[4] ZHANG L, ZHANG Z Q, WANG Z P, et al. Chassis coordinated control for full X-by-wire vehicles-a review[J].Chinese Journal of Mechanical Engineering, 2021, 34(1)： 1-25.
[5] LIU Y H, et al. Estimation of tire-road friction coefficient based on combined APF-IEKF and iteration algorithm[J]. Mechanical Systems and Signal Processing, 2017, 88： 25-35.
[6] ZAREIAN A, AZADI S, KAZEMI R. Estimation of road friction coefficient using extended Kalman filter, recursive least square, and neural network[J]. Proceedings of the Institution of Mechanical Engineers, Part K： Journal of Multi-Body Dynamics, 2016, 230(1)： 52-68.
[7] HE R, ZHANG L W. Interval recognition algorithm of the pavement surface condition based on Lagrange interpolation method[J]. Mathematical Problems in Enginee-ring, 2020, 2020： 1-8.
[8] 潘辉, 李礼夫. 基于路面识别的汽车ABS滑模控制方法的研究[J]. 现代制造工程, 2011(2)： 43-47.
PAN H, LI L F. The research of ABS′ sliding-mode control method based on road automatic identification[J]. Modern Manufacturing Engineering, 2011(2)： 43-47.
[9] 邱明明, 曹龙凯, 黄康, 等. 基于视觉识别的线控制动压力滑模控制[J]. 汽车工程, 2021, 43(1)： 68-76, 85.
QIU M M, CAO L K, HUANG K, et al. Brake by wire pressure sliding mode control based on visual recognition[J]. Automotive Engineering, 2021, 43(1)： 68-76, 85.
[10] 王国微, 尹安东. 基于神经网络路面识别的电动汽车ABS控制研究[J]. 合肥工业大学学报(自然科学版), 2020, 43(7)： 878-883.
WANG G W, YIN A D. Research on ABS control of electric vehicle based on road recognition using neural network[J]. Journal of Hefei University of Technology (Natural Science), 2020, 43(7)： 878-883.
[11] PENG X Y, JIA M F, HE L, et al. Fuzzy sliding mode control based on longitudinal force estimation for electro-mechanical braking systems using BLDC motor[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(1)： 142-151.
[12] 尘帅, 王吉忠, 郑龙月, 等. 基于制动意图的线控制动系统滑模变结构控制[J]. 济南大学学报(自然科学版), 2019, 33(5)： 425-430, 438.
CHEN S, WANG J Z, ZHENG L Y, et al. Sliding mode variable structure control of brake-by-wire system based on braking intention[J]. Journal of University of Jinan (Science and Technology), 2019, 33(5)： 425-430, 438.