盾构法已成为中国城市地铁建设的主要施工技术,隧道施工普遍使用土压平衡盾构,土压平衡盾构具有适用地层范围广、出土率大等特点,掘进过程中能够有效维持土体稳定从而降低对地表变形的影响。在实际工程中,盾构掘进参数的设置主要依靠盾构司机的经验确定,缺乏科学的预测参数设定,这对工程质量和施工安全不利。合理、科学地设定盾构掘进参数能够有效提高盾构机对地层的适应性以及盾构施工效率。
近年来,国内外学者对掘进参数与地质参数、地表变形的关系以及掘进参数的内在规律等方面进行了一系列的探索和研究。司翔宇等[1]、孙捷城等[2]通过盾构施工现场实测数据,研究了盾构法施工中的掘进参数间相关性及其对地表沉降的影响,总结了盾构掘进参数变化与地表沉降之间的规律。杨果林等[3]、周振梁等[4]基于实际工程采集的盾构施工记录数据,对盾构掘进参数在不同地层中的分布情况及变化规律进行统计分析,提出考虑地层条件的掘进速度预测模型。宋克志等[5]、朱合华等[6]通过模糊数学原理,运用模型试验方法对掘进参数存在的内在变化规律进行了分析和研究。
鉴于此,本文结合佛山地铁3号线逢沙站-创意园站区间隧道工程,详细分析了土压平衡盾构穿越软土地层时盾构掘进参数内在变化规律,并建立了掘进速度预测模型。
1 工程概况
1.1 工程背景
佛山地铁3号线逢沙站—创意园站区间隧道工程左、右线盾构均由创意园站始发,逢沙站接收。区间起讫里程Z(Y)DK12+463.505—Z(Y)DK14+422.200,全长约1 959 m,管片内径与宽度分别为5.4 m和1.5 m,盾构外径约6 m。每隔500 m左右设置一座联络通道,共设置3座联络通道,埋深约18.5 m。隧道左、右线中心轴线间距约14 m,盾构外径约6 m,开挖面约30 m2,拱顶覆土埋深8.67~21.88 m,轨面埋深13.49~26.70 m。采用2台德国海瑞克S-870复合式土压平衡盾构机进行隧道盾构掘进施工作业。
1.2 工程水文地质条件
根据现场勘察情况,逢沙站-创意园站区间隧道工程场地地层由第四系地层与基岩组成,勘察范围内主要分布的地层有:淤泥质土、淤泥质中粗砂、淤泥质粉细砂、粉质黏土等。本区间线位范围内地表水体发育,多次与河涌斜交,稳定地下水位埋深为0.2~2.0 m。此类地层具有含水量大、流塑性大、扰动后自稳性差、易产生弹塑性变形等特点。选取该工程具有代表性的地层分布及标高,如图1所示。
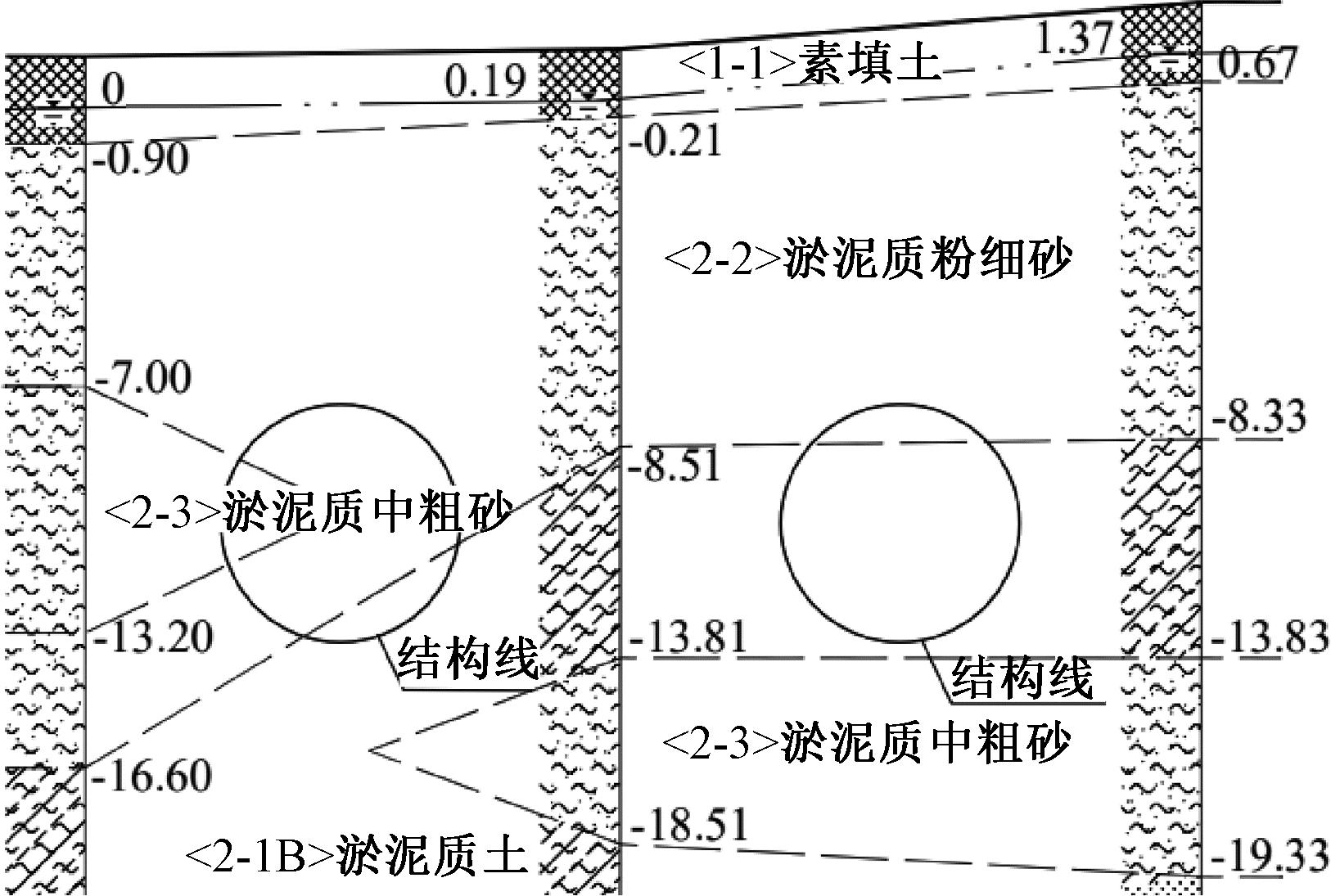
图1 工程地质横断面图(m)
Figure 1 Cross-sectional view of engineering geology(m)
2 掘进参数数理统计分析
2.1 数据选取及预处理
根据逢沙站—创意园站区间右线掘进台账采集的数据,确定拼装环号1~1 311环为研究对象。盾构机掘进参数数据的自动保存频率为1次/min,本文以1次/5 min调取数据,并用于分析计算,共调取27 464组数据样本。
为了保证数据均为正常掘进状态下采集,将部分非正常掘进状态的数据删除,其中包括拼接状态、机械损坏状态、停机状态、刀盘空转状态等[7]。为了保证数据的可靠性,在剔除非正常掘进状态数据的基础上再过滤部分异常数据。首先为了消除参数变量之间的量纲效应,按照式(1)将所有数据进行归一化处理,然后利用拉依达准则[4](3σ准则)删除异常值。
(1)
式中:aij为原始参数变量数据;bij为标准化处理后的参数变量数据。
经过数据清洗后,剔除了12 821组数据,其中包括4 089组非正常掘进状态下的数据和8 732组异常数据,最终选取数据为14 643组。
2.2 数据描述
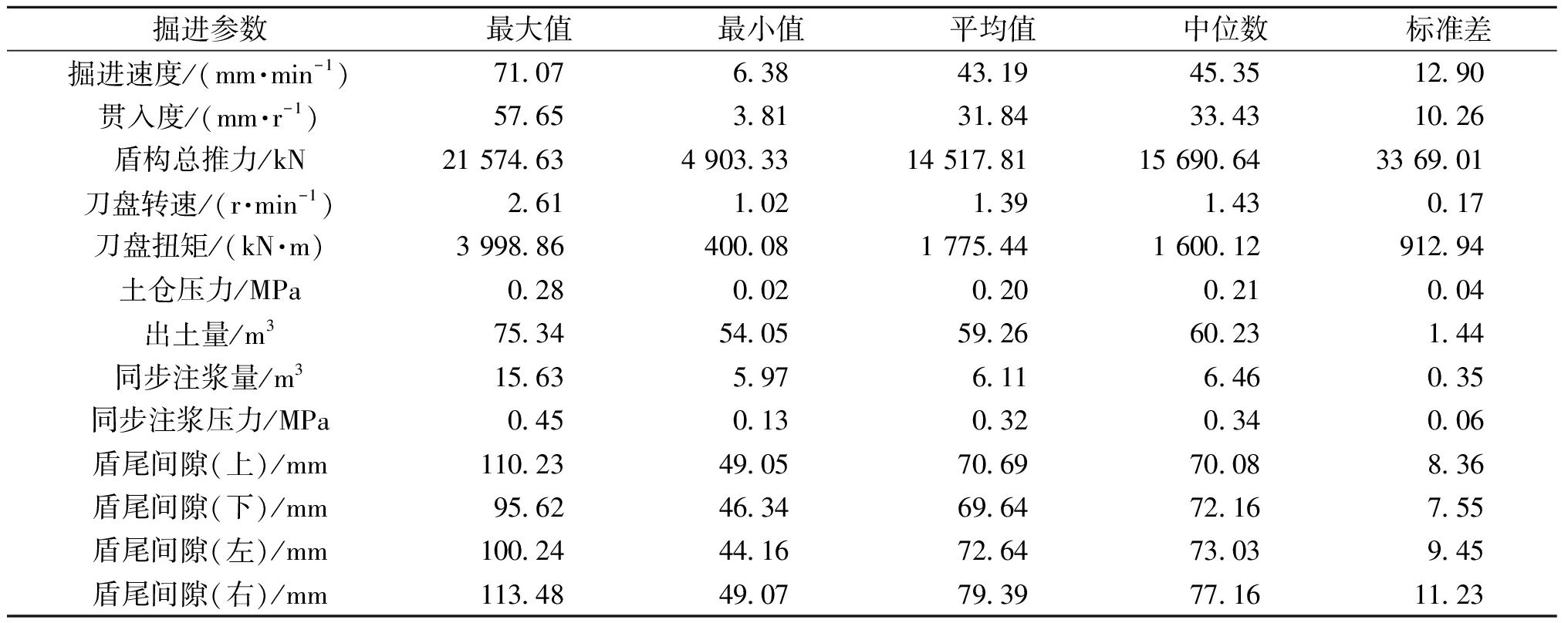
对预处理后的14 643组数据进行数理统计分析,统计结果如表1所示。观察数据统计分析结果可以发现,盾构总推力的平均值为14 517.81 kN,在4 903.33~21 574.63 kN之间变化,由于本工程为软土地层,刀盘所受的反推力较大[8],而刀盘上水平推力引起的反推力是影响盾构总推力的主要组成部分[2],因此本工程的盾构总推力平均值相比于其他工程较大。
除此以外,掘进速度、贯入度、土仓压力平均值相比于其他工程均较大,最主要的原因还是由于软土地层地质情况导致。与深圳地铁16号线天健花园站-龙城中路站左线区间盾构隧道工程[7]各盾构掘进参数对比可知,佛山地铁工程中掘进速度、贯入度、盾构总推力、土仓压力这4个掘进参数的平均值明显大于深圳地铁工程,而刀盘转速和刀盘扭矩的平均值均小于深圳地铁工程。在相对较软弱的地层,通常采用较低的刀盘转速和刀盘扭矩,以减少刀盘对地层的扰动;当围岩强度较高时,岩石硬度越大,刀盘受到的阻力越大,刀盘转速和刀盘扭矩也相应增大[9]。
表1 掘进参数数理统计分析结果(n=14 643)
Table 1 Results of mathematical statistical analysis of boring parameters(n=14 643)
掘进参数最大值最小值平均值中位数标准差掘进速度/(mm·min-1)71.076.3843.1945.3512.90贯入度/(mm·r-1)57.653.8131.8433.4310.26盾构总推力/kN21 574.634 903.3314 517.8115 690.6433 69.01刀盘转速/(r·min-1)2.611.021.391.430.17刀盘扭矩/(kN·m)3 998.86400.081 775.441 600.12912.94土仓压力/MPa0.280.020.200.210.04出土量/m375.3454.0559.2660.231.44同步注浆量/m315.635.976.116.460.35同步注浆压力/MPa0.450.130.320.340.06盾尾间隙(上)/mm110.2349.0570.6970.088.36盾尾间隙(下)/mm95.6246.3469.6472.167.55盾尾间隙(左)/mm100.2444.1672.6473.039.45盾尾间隙(右)/mm113.4849.0779.3977.1611.23
绘制各掘进参数的统计分布直方图,以掘进速度的频数分布直方图为例,如图2所示。
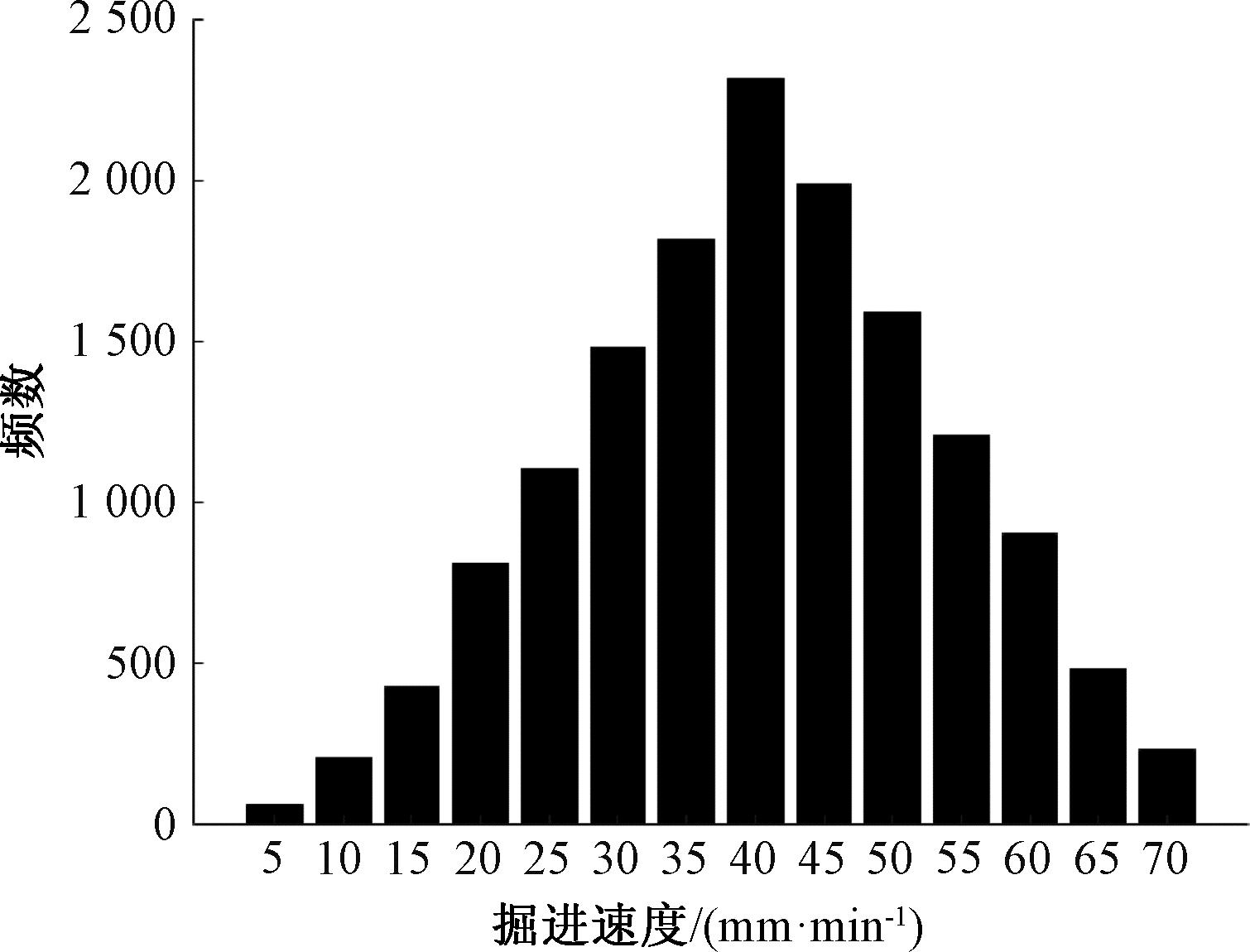
图2 掘进速度频数分布直方图
Figure 2 Statistical histogram of driving speed frequency
为验证各掘进参数是否服从正态分布,对各掘进参数的频数分布进行正态性检验,采用K-S检验法,同样以掘进速度为例,检验过程如下。
(1)原假设H0:X~N(μ,σ2);备择假设H1:X不服从N(μ,σ2),μ为43.19,σ2为166.41。
(2)在α=0.05的显著性水平下,检验临界值为![]() 拒绝域为
拒绝域为![]() 取14 643。
取14 643。
(3)计算经验分布函数Fn(xi)和理论分布函数值F0(xi),Dn=sup|Fn(xi)-F0(xi)|=0.010 8,由于![]() 所以
所以![]() 接受原假设,可认为掘进速度样本数据服从正态分布。
接受原假设,可认为掘进速度样本数据服从正态分布。
经过正态性检验可知掘进速度、贯入度、盾构总推力、刀盘转速、刀盘扭矩、盾尾间隙(上、下、左、右)符合正态分布的程度较高;土仓压力、出土量、同步注浆压力、同步注浆量符合正态分布的程度较低。
正常掘进过程中,土仓压力主要由施工人员操作来控制土仓内渣土量、土壤改良系统以及仓内气压,受人为操作影响较大[10],导致出现正态分布程度较低的情况;而掘进速度、刀盘转速、刀盘扭矩主要受地质条件和机械自身工作性能的客观条件限制,所以整体呈正态分布程度较高。
3 掘进参数相关性分析
由于该工程地质为软土地层,且每环的盾构掘进参数变化较小,为简化计算分析,取每环各掘进参数的平均值作为该环的代表值。为验证各掘进参数间是否具有相关性,首先做出各参数随环号序列变化的曲线,发现部分掘进参数具有相似的变化趋势,然后将具有相似性的掘进参数变化曲线放在同一图中进行对比,如图3所示,可以很直观地看到掘进速度与贯入度、盾构总推力与刀盘扭矩、土仓压力与同步注浆压力的变化趋势相近,盾尾间隙(左)与盾尾间隙(右)的变化趋势相反。
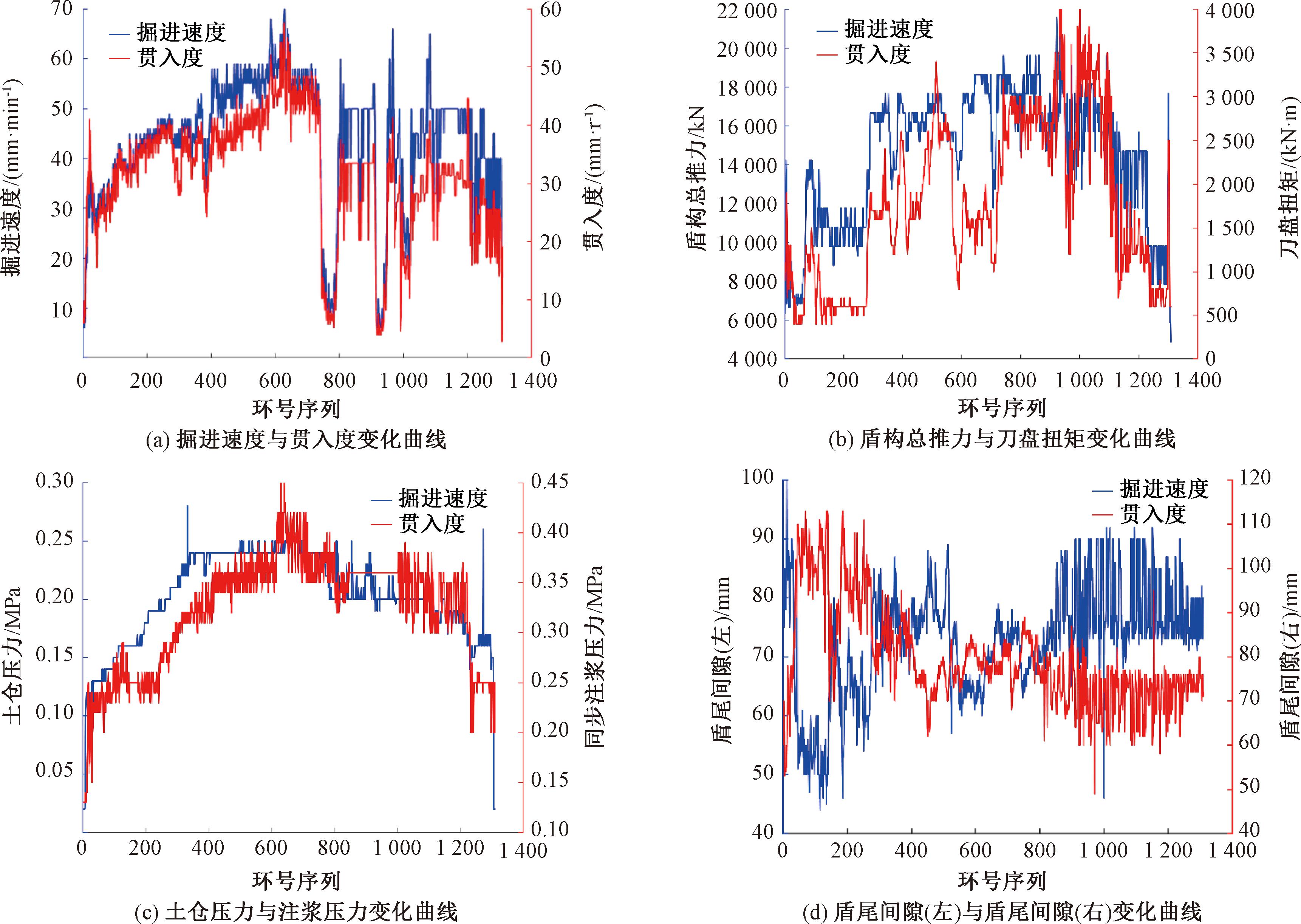
图3 各掘进参数的变化曲线对比图
Figure 3 Comparison chart of change curve of each boring parameter
Pearson相关性分析通过计算变量之间的相关系数r来分析两者的关系,r的绝对值越接近1,则变量间相关性越大,正号为正相关,负号为负相关。利用MATLAB软件对13个掘进参数进行Pearson相关性分析,计算的相关系数矩阵如图4所示。
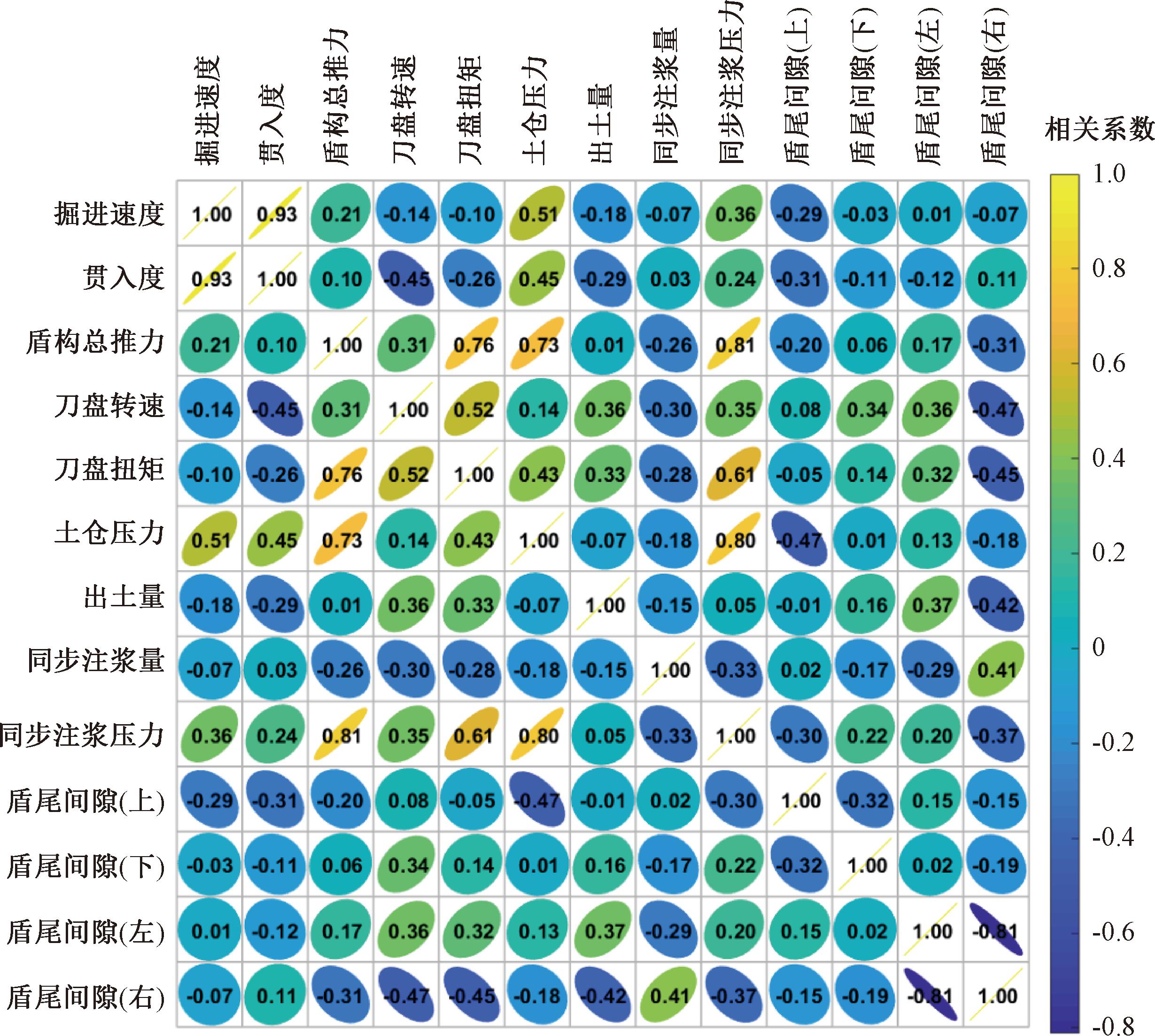
图4 掘进参数间Pearson相关系数矩阵图
Figure 4 Map of Pearson correlation coefficient matrix between boring parameters
掘进速度与贯入度线性相关性极强,贯入度的物理意义为刀盘每转的刀盘切入深度,从一定程度上反映了盾构施工地层的可掘性与机械作业水平[3],通过提高贯入度可以明显加快掘进速度。
4 掘进速度影响因素分析
由图4可知,掘进速度与除贯入度外其余掘进参数的Pearson相关系数值均较小,最大的相关系数值为0.51,因此无法通过线性分析确定其余掘进参数影响掘进速度的程度。参数变量数据之间具有高度非线性,传统意义上的线性分析方法无法计算变量间非线性关系。而基于互信息的特征选择算法可以反映出参数变量间的非线性关系。当参数变量之间的互信息值越大时,也就代表它们之间的相互耦联性越强[11]。
根据数据预处理得到的1 311×13实测数据矩阵,采用MATLAB软件计算12个掘进参数变量与掘进速度的互信息值,再按照互信息值从大到小进行排序,计算结果如表2所示。
理论上与掘进速度互信息值越大,其与掘进速度关联程度的概率分布“贡献率”越大[12]。根据表2的结果,可以筛选与掘进速度非线性相关性较高的参数变量。
表2 掘进速度与其余掘进参数互信息值
Table 2 Value of the mutual information between the driving speed and the remaining boring parameters
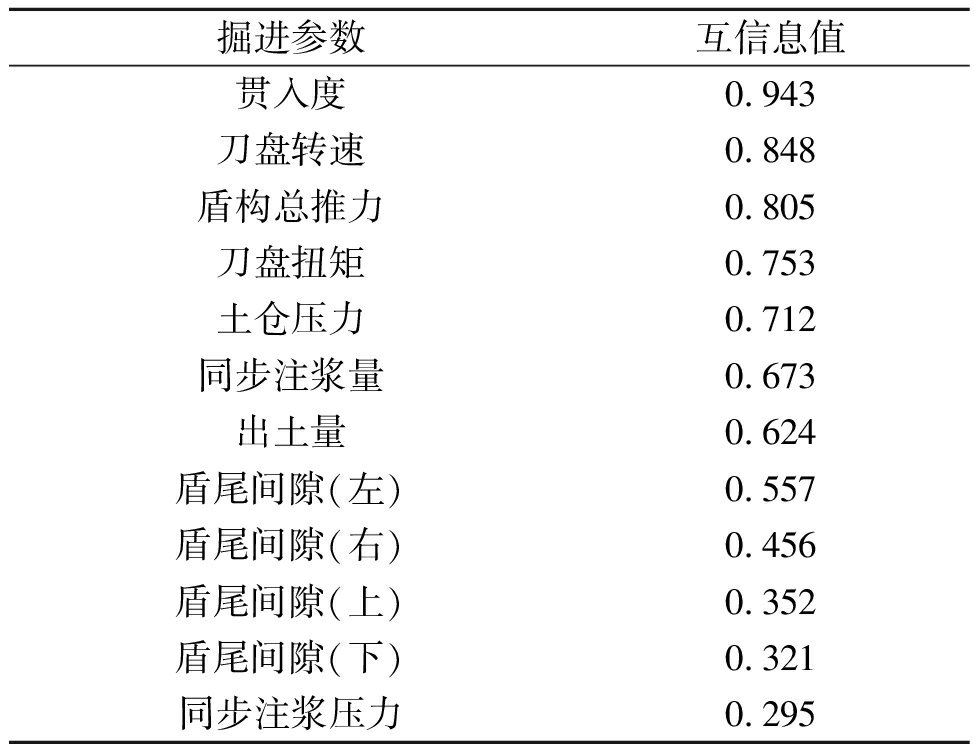
掘进参数互信息值贯入度0.943刀盘转速0.848盾构总推力0.805刀盘扭矩0.753土仓压力0.712同步注浆量0.673出土量0.624盾尾间隙(左)0.557盾尾间隙(右)0.456盾尾间隙(上)0.352盾尾间隙(下)0.321同步注浆压力0.295
5 掘进速度预测模型
在实际工程中,为了防止延误工期和降低成本,其中一项重要的指标就是掘进效率,而影响掘进效率的主要因素是掘进速度,因此对掘进速度的预测具有重要的现实意义。
5.1 模型选择与样本划分
由于掘进速度与除贯入度外其余掘进参数均具有较强的非线性相关关系,因此需要考虑采用非线性模型对掘进速度进行预测。机器学习因其适应性强、预测精度高等优点在处理非线性问题时具有独特优势,本文拟采用随机森林、BP神经网络等机器学习算法建立掘进速度预测模型。
由表2可知各掘进参数与掘进速度关联程度的大小,本文将0.5作为特征选取的判断阈值,取前8个参数变量作为掘进速度预测的特征参量。本文将前918环掘进数据设定为训练集,将后393环(即919~1 311环)掘进数据设定为测试集。
5.2 随机森林回归预测模型
5.2.1 模型建立与求解
随机森林的基本思想是利用Bootstrap重抽样方法从原始样本中抽取多个样本,对每个Bootstrap样本构建决策树,然后将所有决策树预测平均值作为最终预测结果[13]。决策树的数量对掘进速度预测精度的影响较大,决策树数量太少,预测误差会变大;决策树数量太多,计算量会剧增,当决策树到达一定数量后,预测精度提升会很少[14]。经过计算推演可知,决策树数量取100较为合适。
5.2.2 结果分析
通过对918个训练集随机采样,构建出100个采样集,基于采样集构建100棵决策树作为掘进速度预测模型的弱学习器,最后对100棵决策树的掘进速度预测结果求解算术平均值作为最终预测结果。训练集和测试集数据的实测值与预测值的对比如图5、6所示。掘进速度在训练集和测试集上的随机森林回归预测模型评价指标对比,如表3所示。由表3可知,测试集上的预测精度略次于训练集。
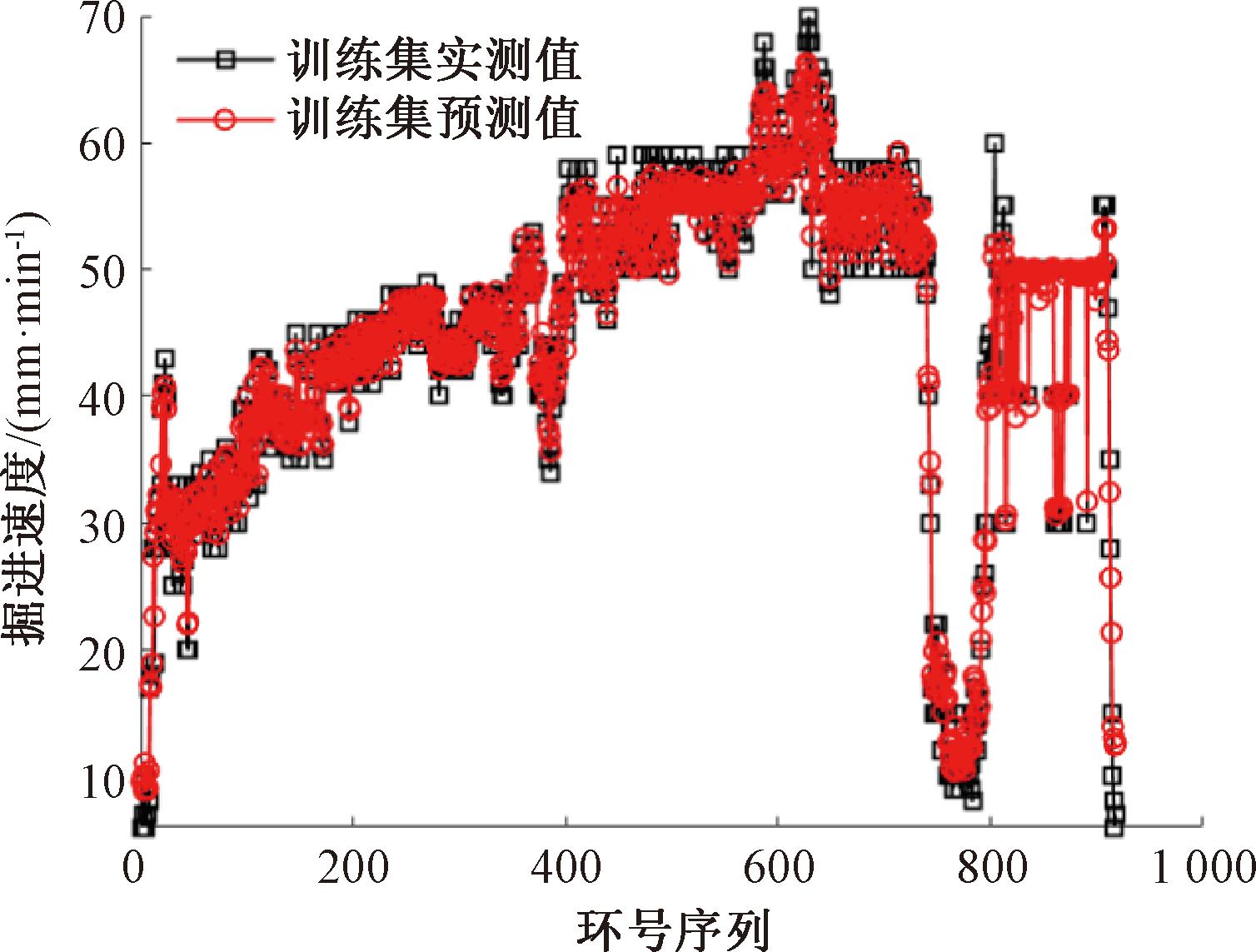
图5 随机森林回归模型在训练集上的预测
Figure 5 Prediction on the training set of RFR model
5.3 基于遗传算法优化BP神经网络预测模型
5.3.1 模型建立与求解
BP神经网络适合解决非线性问题,但是BP神经网络容易出现收敛速度慢以及陷入局部最优解等问题。可利用遗传算法(GA)对BP神经网络初始权值和阈值进行优化分析,通过选择、交叉、变异等操作不断迭代得到最优的BP神经网络初始权值和阈值,最后利用BP神经网络进行局部寻优,从而得到具有全局最优解的BP神经网络预测值。
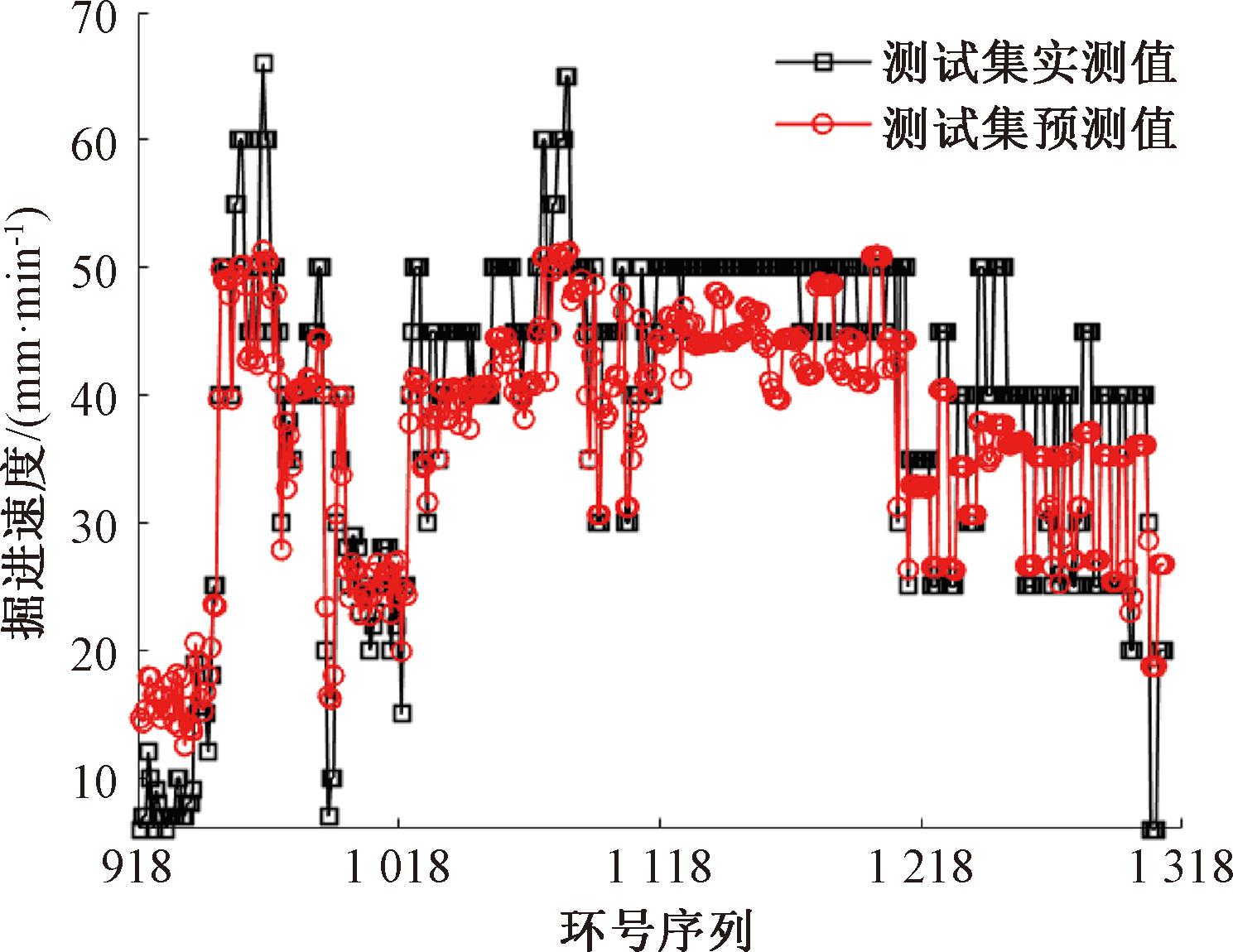
图6 随机森林回归模型在测试集上的预测
Figure 6 Prediction on the test set of RFR model
表3 RFR预测模型评价指标
Table 3 Evaluation indicators of RFR prediction model

数据集R2RMSEMAE训练集0.9861.5581.139测试集0.8715.0384.055
在该模型中,BP神经网络的输入层有8个节点,隐含层有8个节点,输出层有1个节点,共有8×8+8×1=72个权值,8+1=9个阈值,所以遗传算法个体编码长度为72+9=81。
遗传算法的4个初始参数:种群规模为50,终止进化代数为300,交叉概率为0.5,变异概率为0.001。BP神经网络训练过程中,涉及3个网络进化参数的设定,分别为迭代次数、学习率、训练误差目标,经过对参数的不断调试,最终确定3个进化参数依次为5 000、0.1、0.000 01。
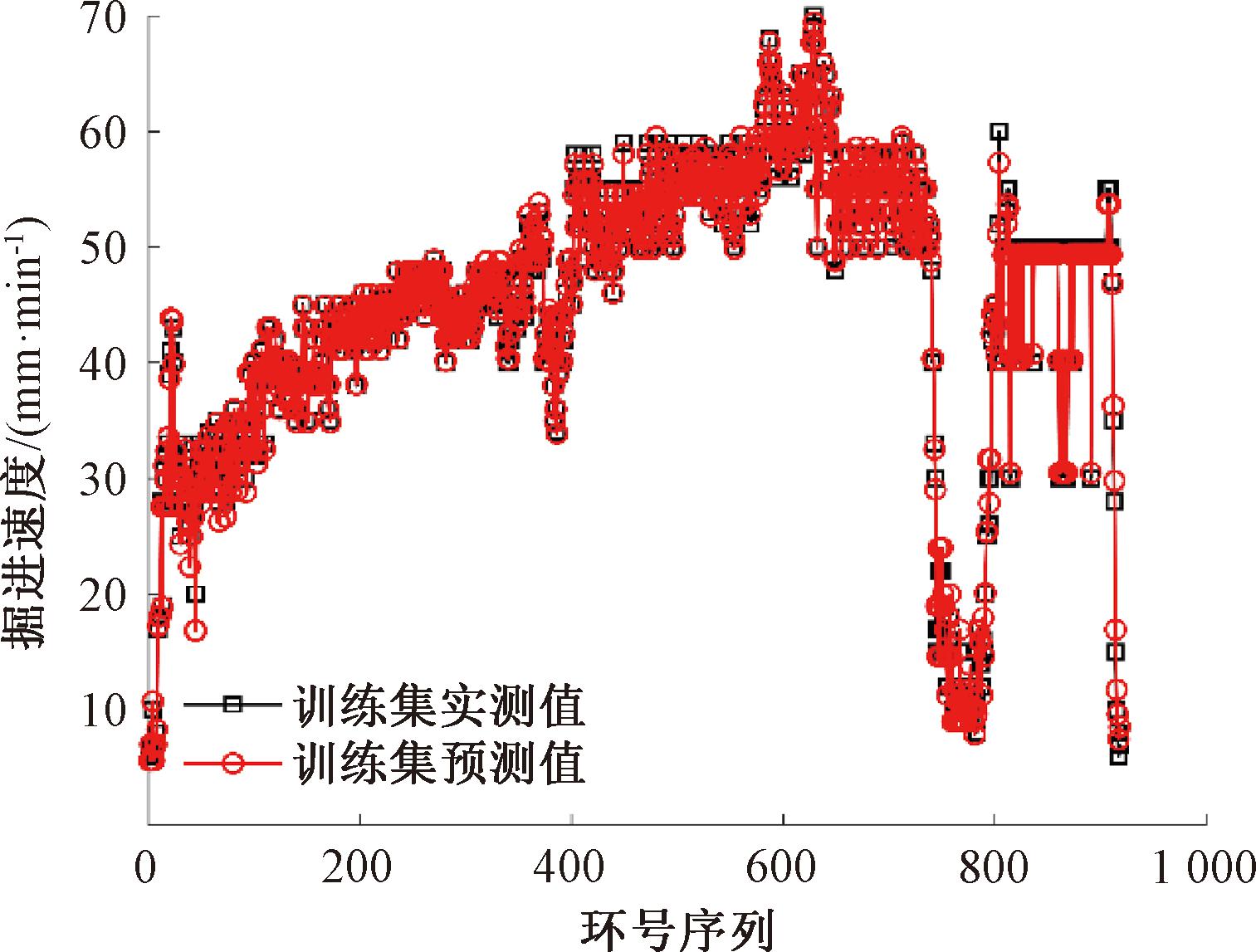
图7 BP-GA模型在训练集上的预测
Figure 7 Prediction on the training set of BP-GA model
5.3.2 结果分析
做出训练集和测试集数据的实测值与预测值的对比图,如图7、8所示。掘进速度在训练集和测试集上的基于遗传算法优化BP神经网络预测模型评价指标对比,如表4所示。
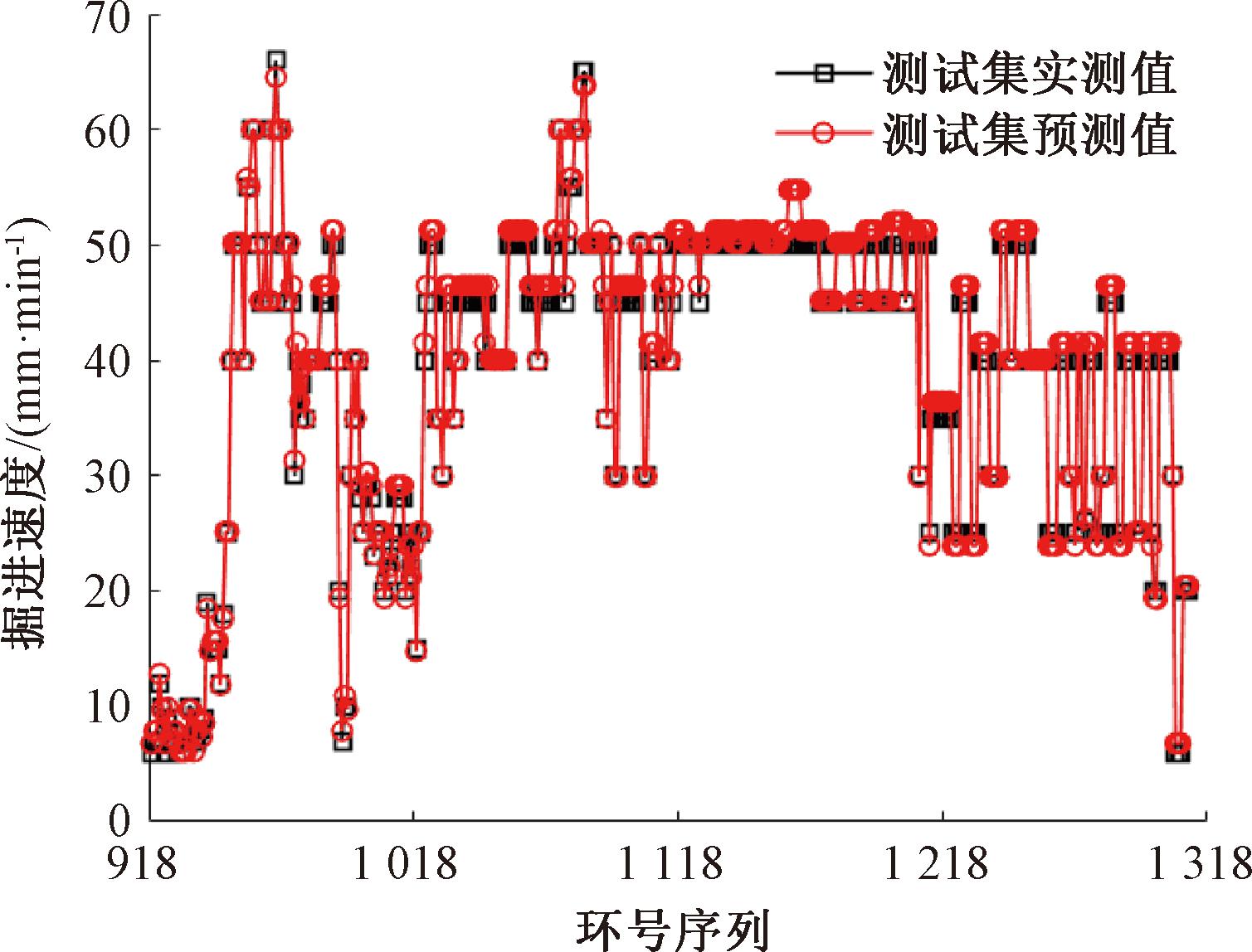
图8 BP-GA模型在测试集上的预测
Figure 8 Prediction on the test set of BP-GA model
表4 BP-GA预测模型评价指标
Table 4 Evaluation indicators of BP-GA prediction model

数据集R2RMSEMAE训练集0.9960.7890.554测试集0.9911.2440.822
6 结论
影响盾构掘进参数的因素有很多,其中主要包含地质条件和参数内在规律,本文在软土地层条件下研究参数内在规律对掘进参数的影响,得出如下结论。
(1)软土地层条件导致本工程掘进速度、贯入度、盾构总推力等掘进参数相比于其他硬岩地层工程较大;在相对软弱的地层,通常采用较低的刀盘转速和刀盘扭矩,以减少刀盘对地层的扰动。
(2)掘进速度等掘进参数符合正态分布的程度较高;土仓压力等掘进参数符合正态分布的程度较低。
(3)由掘进参数间Pearson相关系数知,掘进速度与贯入度存在极强正相关关系。
(4)随机森林回归预测模型和基于遗传算法优化BP神经网络预测模型均能较好地预测掘进速度,基于遗传算法优化BP神经网络预测模型的预测精度略优于随机森林回归预测模型。
与已有类似研究相比,本文率先提出分别建立随机森林回归预测模型和基于遗传算法优化BP神经网络预测模型,对掘进速度进行预测,并对模型预测结果量化和可视化。此模型不仅可以预测掘进速度,对其他掘进参数的预测也是可行的。本研究仍存在不足之处:现场收集到的参数变量较少,影响掘进速度的因素不全;没有考虑地层条件改变对掘进参数的影响。地层条件和参数内在规律对掘进参数的共同影响作用将是下一步研究的主要工作。
[1] 司翔宇,杨平,邵光辉,等. 隧道盾构施工参数对地表沉降影响的实测研究[J]. 湖南大学学报(自然科学版), 2008, 35(11): 167-170.
SI X Y,YANG P,SHAO G H, et al. Site monitoring research on ground surface subsidence of tunnel induced by shield construction parameters[J]. Journal of Hunan University(Natural Sciences), 2008, 35(11): 167-170.
[2] 孙捷城, 王国富, 路林海, 等. 厚冲积地层盾构掘进参数设定及地表变形规律研究[J]. 防灾减灾工程学报, 2018, 38(3): 487-497.
SUN J C, WANG G F, LU L H, et al. Study on parameters setting of EPB shield driving and laws of surface deformation in thick alluvial clay[J]. Journal of Disaster Prevention and Mitigation Engineering, 2018, 38(3): 487-497.
[3] 杨果林, 张沛然, 陈亚军, 等. 长沙典型地层土压平衡盾构掘进参数及表现预测[J]. 中南大学学报(自然科学版), 2020, 51(8): 2069-2080.
YANG G L, ZHANG P R, CHEN Y J, et al. Excavation parameters and performance prediction of earth pressure balance shield in typical strata of Changsha[J]. Journal of Central South University (Science and Technology), 2020, 51(8): 2069-2080.
[4] 周振梁, 谭忠盛, 李宗林, 等. 一种基于数据挖掘的掘进速度预测模型[J]. 应用基础与工程科学学报, 2021, 29(5): 1201-1219.
ZHOU Z L, TAN Z S, LI Z L, et al. A data mining based prediction model for penetration rate[J]. Journal of Basic Science and Engineering, 2021, 29(5): 1201-1219.
[5] 宋克志, 袁大军, 王梦恕. 基于盾构掘进参数分析的隧道围岩模糊判别[J]. 土木工程学报, 2009, 42(1): 107-113.
SONG K Z, YUAN D J, WANG M S. Fuzzy identification of surrounding rock conditions based on analysis of shield tunneling data[J]. China Civil Engineering Journal, 2009, 42(1): 107-113.
[6] 朱合华, 徐前卫, 廖少明, 等. 土压平衡盾构法施工参数的模型试验研究[J]. 岩土工程学报, 2006, 28(5): 553-557.
ZHU H H, XU Q W, LIAO S M, et al. Experimental study on working parameters of EPB shield machine[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(5): 553-557.
[7] 李锟, 田管凤, 马宏伟, 等. 土压平衡盾构掘进参数相关性分析及预测模型[J]. 科学技术与工程, 2021, 21(9): 3814-3821.
LI K, TIAN G F, MA H W, et al. Correlation analysis and prediction model of boring parameters of earth pressure balance shield[J]. Science Technology and Engineering, 2021, 21(9): 3814-3821.
[8] 张延杰. 成都富水砂卵石地层EPB盾构土体改良技术及掘进参数研究[D]. 西安: 西安建筑科技大学, 2019.
ZHANG Y J. Research on the tunneling parameters and soil improvement technique of the EPB shield tunneling in water-rich sandy cobble layer of Chengdu city[D]. Xi′an: Xi′an University of Architecture and Technology, 2019.
[9] 沈翔, 袁大军, 吴俊, 等. 复杂地层条件下盾构掘进参数分析及预测[J]. 现代隧道技术, 2020, 57(5): 160-166.
SHEN X, YUAN D J, WU J, et al. Analysis and prediction of driving parameters of shield tunnelling in complex strata[J]. Modern Tunnelling Technology, 2020, 57(5): 160-166.
[10] 赵博剑, 周建军, 谭忠盛, 等. 复合地层盾构掘进参数及其与地层相关性分析[J]. 土木工程学报, 2017, 50(增刊1): 140-144.
ZHAO B J, ZHOU J J, TAN Z S, et al. Variation of shield boring parameters and correlation analysis in mixed ground[J]. China Civil Engineering Journal, 2017, 50(S1): 140-144.
[11] RAHMANIAN M, MANSOORI E G. An unsupervised gene selection method based on multivariate normalized mutual information of genes[J]. Chemometrics and Intelligent Laboratory Systems, 2022, 222: 104512.
[12] ZHOU S B, WANG T, HUANG Y J. Feature screening via mutual information learning based on nonparametric density estimation[J]. Journal of Mathematics, 2022, 2022: 7584374.
[13] 李爱民, 王海隆, 许有成. 优化随机森林算法的城市湖泊DOC质量浓度遥感反演[J]. 郑州大学学报(工学版), 2022, 43(6): 90-96. LI A M, WANG H L, XU Y C. Remote sensing retrieval of urban lake DOC concentration based on optimized random forest algorithm[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(6): 90-96.
[14] PAN Y B, ZHU X L. Application of HMM and ensemble learning in intelligent tunneling[J]. Mathematics, 2022,10(10): 1778.