具有高效、清洁、环保等优点的电动汽车(electric vehicel,EV)在推进绿色低碳发展、二氧化碳排放尽早达峰等方面发挥了重要作用,近年来其保有量迅速增长[1]。2021年中国电动汽车数量达到794万辆,充电桩保有量为261.7万台,但实际公共充电桩数仅有114.7万台,远未实现“车桩1∶1”预设目标[2],预计未来需建设更多的充电站来满足EV用户的充电需求。在此背景下,EV充电站的合理规划建设显得尤为重要。
充电站作为一种为用户提供充电服务的公共设施,EV充电负荷的时空分布直接影响其建设位置和容量配置。从国内外学者的相关研究来看,EV充电负荷时空分布受交通状况[3]、环境温度[4]、用户出行特性[5]以及里程焦虑[6]等多种因素的影响。赵书强等[7]基于出行链理论来模拟用户出行规律,通过蒙特卡洛方法对电动汽车充电负荷进行预测。宋雨浓等[8]考虑道路红绿灯位置影响建立一种按步长仿真的车辆时空转移模型。张美霞等[9]考虑多源信息实时交互,构建基于后悔理论的充电站选择模型得到充电站充电负荷信息。
充电站规划问题涉及充电站经营者[10]、EV用户[11]和配电网[12]等多个相关利益主体。藏海祥等[13]在多种场景下对EV用户充电需求进行预测,建立综合考虑用户侧与非用户侧双方利益的多目标规划模型。陈静鹏等[14]基于用户出行需求,构建以EV用户空驶成本最小为目标的选址定容规划模型。但是现有研究对EV充电负荷的时空分布特性以及充电站规划问题的研究仍存在以下局限。
(1)上述文献虽然考虑了交通路网约束,但是对交通拥堵的时变特性分析不足,亦弱化了车速和环境温度的实时变化对单位里程耗电量的影响。
(2)以往的研究大多先预测出EV充电负荷的时空分布,在充电站规划时假设用户就近选择充电站进行充电,并没有具体分析不同EV用户的动态充电需求,得到的充电站充电负荷信息会有误差。
(3)目前在充电站规划时考虑EV用户充电满意度的研究尚不完善,用户充电满意度主要由前往充电站的时间损失、电量损耗及站内排队时间决定。
针对以上分析,本文提出一种考虑用户动态充电需求的电动汽车充电站规划方法。首先基于EV用户出行特性、实时交通信息、环境温度以及里程焦虑等因素,通过改进Dijkstra算法模拟EV出行过程,建立考虑用户动态充电需求的充电站选择模型;然后,采用M/M/c排队论方法对充电站进行容量配置,建立以充电站建设运维成本和EV用户经济损失之和最小为目标的充电站规划模型;最后,以某市主城区部分实际道路情况为规划区域验证本文所提方法的有效性与合理性。
1 电动汽车用户出行特性
1.1 基于出行链方式的私家车出行特征
出行链可以很好地模拟电动私家车的出行过程,出行链就是围绕人的所有出行活动构成一个完整的出行链条,从起始点出发,在一定时间顺序上依次经过若干目的地,最后到达终点,结束全部出行的过程[7]。本文以家作为私家车用户的起点和终点,所构成的3种出行链如图1所示,假设3种出行链的概率分别为52.8%、24.1%、23.1%[14]。
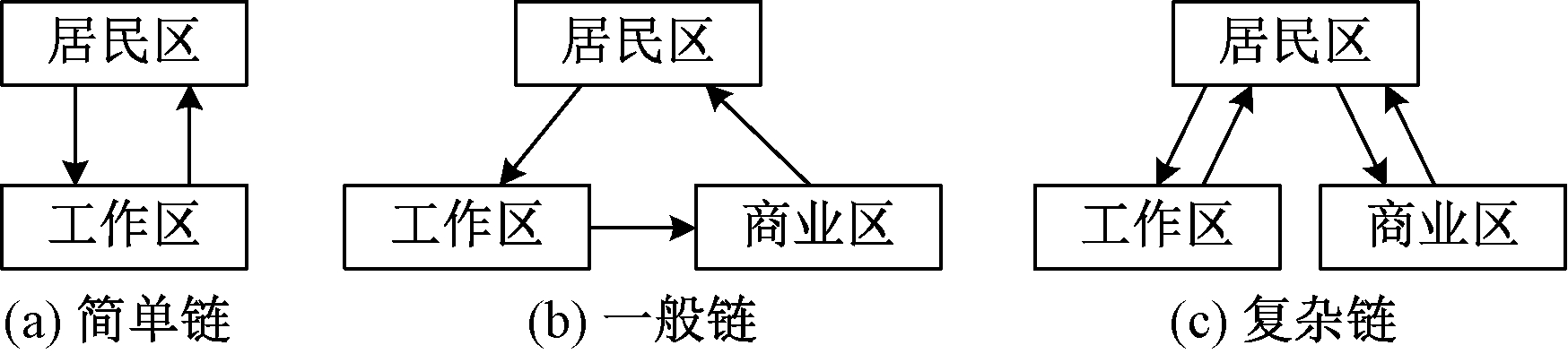
图1 典型出行链结构
Figure 1 Typical travel chain structure
根据美国交通部居民出行数据统计结果[14],私家车用户第一次出行时刻和下班时刻均服从正态分布[7],在商业区的停留时间服从广义极值分布[7]。
1.2 基于出行概率矩阵的出租车出行特征
当前出租车的运营模式主要实行轮班制,车辆由多名司机轮班驾驶运营。出租车在早上6点换班时间的出行概率最大,其目的地由乘客决定,具有很强的不确定性和随机性,采用OD(origin-destination)分析法来描述出租车的出行特征。OD分析是一种广泛应用于道路规划和交通仿真的方法,通过调查统计可以确定出租车出行起讫点分布规律,从各时段城市路网节点的OD概率矩阵得到电动出租车的出行目的地[6]。
2 动态交通路网
2.1 静态交通路网
根据图论的原理来描述交通路网拓扑结构特征,图G=(V, E)表示路网的拓扑结构图,V为路网中所有节点的集合{1,2,…,n},即道路的起止点或交叉口;E为路网中所有路段的集合。在图2交通路网拓扑结构中,道路都为双行道,采用道路长度对交通路网图量化赋值,其静态交通路网拓扑结构可由式(1)矩阵D表示。
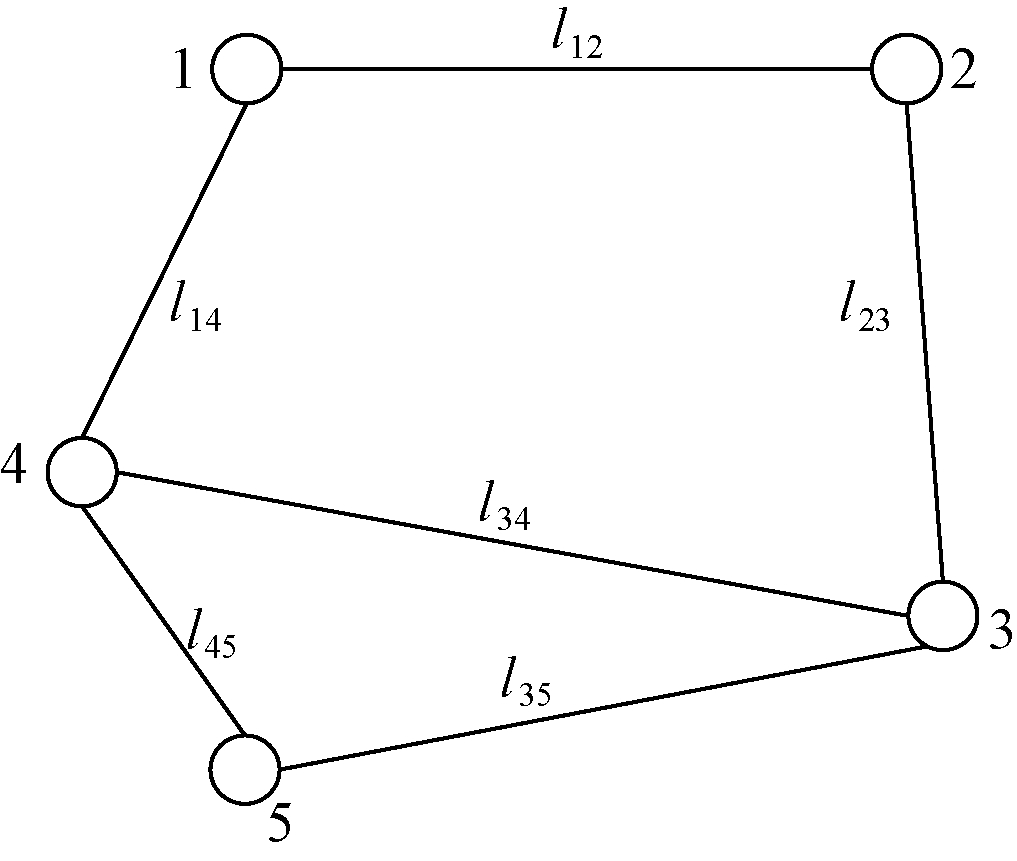
图2 交通路网拓扑结构
Figure 2 Road network topology matrix
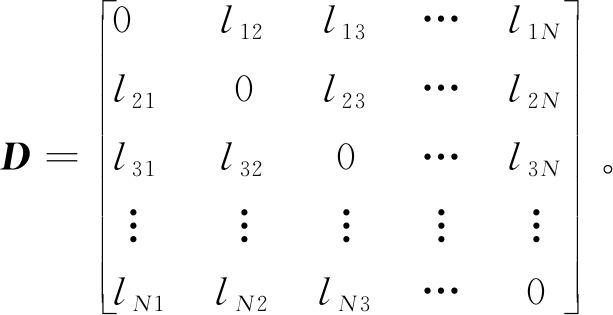
(1)
式中:N为交通路网中道路节点总数量;lij(i,j=1,2,…,N且i ≠ j)为路网中直连道路ij的长度,当两节点没有道路直接连通时,lij的取值为inf。矩阵D中的元素值由道路长度构成,不随时间变化,故称之为静态交通路网。
2.2 动态交通路网架构
交通路网中道路在不同时刻的拥堵情况完全不同,不同道路等级的EV平均行驶速度可由式(2)计算:
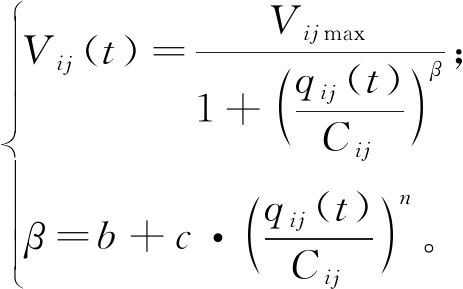
(2)
式中:Vijmax为路段ij的零流速度;qij(t)为t时刻路段ij的车流量;Cij为道路ij的最大通行能力,与道路等级成正比;qij(t)与Cij的比值为t时刻路段饱和度;β为经验系数;不同等级道路的相关系数b、c、n的取值参考文献[6]。
由式(2)可知t时刻车辆在道路ij上的通行耗时可表示为
Tij(t)=lijVij(t)-1。
(3)
把静态交通路网模型中矩阵D的元素lij替换为lijVij(t)-1,形成新的矩阵Dt,可间接反映时段t车辆在交通路网中任一条道路上的通行耗时,Dt即为考虑道路等级和实时车流量的动态交通路网模型,如式(4)所示。
Dt=
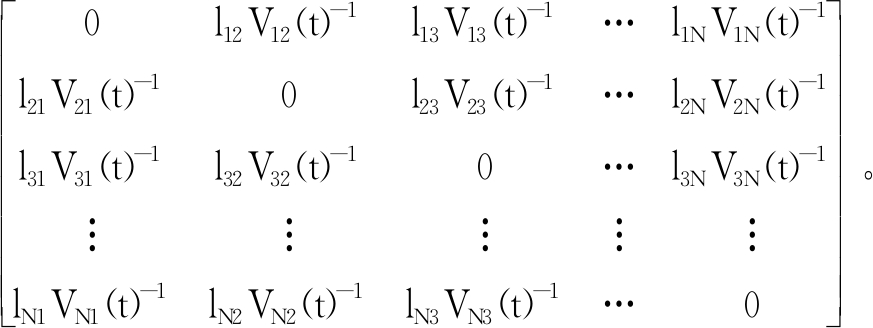
(4)
3 充电站需求模型
3.1 最短耗时出行路径规划
利用蒙特卡洛方法为EV用户抽取起讫点后,从起始点有多种行驶路径可以到达目的地,通常情况下EV用户会选择耗时最短的出行路线。传统的Dijkstra算法常用于解决网络图论模型的最短路径规划问题,基本思想是利用静态交通路网矩阵D,以式(5)为目标函数,在所有可能的R中求出令L值最小的行驶路线[8]:
(5)
式中:R表示路径所含道路集合;L为路径R的总长度。
在传统Dijkstra算法思想的基础上,结合不同时刻的动态交通路网矩阵Dt,以式(6)中L′值最小为目标,求得最短耗时出行路径:
(6)
3.2 实时单位里程功耗
(1)交通-能耗关系。交通拥堵在影响车辆行驶速度的同时会导致车辆频繁地制动和启动,从而增加耗电量。基于实时交通拥堵情况建立单位里程耗电量模型[8],单位里程耗电量可由式(7)计算:
(7)
式中:![]() 为不同道路等级下的单位里程耗电量;an为不同道路等级的交通能耗系数[8]。
为不同道路等级下的单位里程耗电量;an为不同道路等级的交通能耗系数[8]。
(2)温度-能耗关系。环境温度的变化会对电池的性能产生影响,空调系统的使用也会产生额外耗电量。本文引入式(8)来表示车辆单位里程耗电量与环境温度之间的函数关系[8]:
(8)
式中:T为环境温度;ωT为不同环境温度下的单位里程耗电量;bn为温度能耗系数[8]。
(3)综合能耗。由温度-能耗关系可知,在20 ℃时车辆的单位里程耗电量最小,以ω20为基准,定义温度T时耗电量比kT为
(9)
(10)
综合考虑交通和温度的影响,实时单位里程耗电量可以用式(10)计算。
3.3 动态充电需求判断
车辆t时刻剩余电量Capt可由式(11)计算:
(11)
式中:![]() 为t-1时刻路段ij的实时单位里程耗电量。当t时刻电动汽车电量满足以下特征时,产生充电需求。
为t-1时刻路段ij的实时单位里程耗电量。当t时刻电动汽车电量满足以下特征时,产生充电需求。
(1)对私家车来说,出行链结构比较固定,当车辆开始下一段行程前,判断当前电量是否满足出行所需电量。式(12)为判断私家车t时刻电量是否满足下段行程出行所需电量。
Capt≤Capij。
(12)
式中:Capij为下一次出行所需电量。
(2)对于出租车,停车时间较短,考虑到出租车司机的里程焦虑不同,设置SOC阈值服从[0.15,0.30]均匀分布。式(13)为判断t时刻出租车电量是否达到用户的心理充电阈值。
Capt≤Capc。
(13)
式中:Capc为用户充电阈值电量。
3.4 考虑用户动态需求的充电站选择模型
当用户产生充电需求时,先分析EV用户动态充电需求信息,由改进的Dijkstra算法计算从充电需求点前往充电站j和充电完成后前往目的地的行程时间之和,充电站选择模型可表示为
(14)
式中:FTj为选择充电站j时的综合行程时间;R1和R2分别为用户从充电需求点前往充电站和补电之后前往目的地的最短耗时路径集合。EV用户会选择综合行程时间最短的充电站,充电站需求模型框架如图3所示。
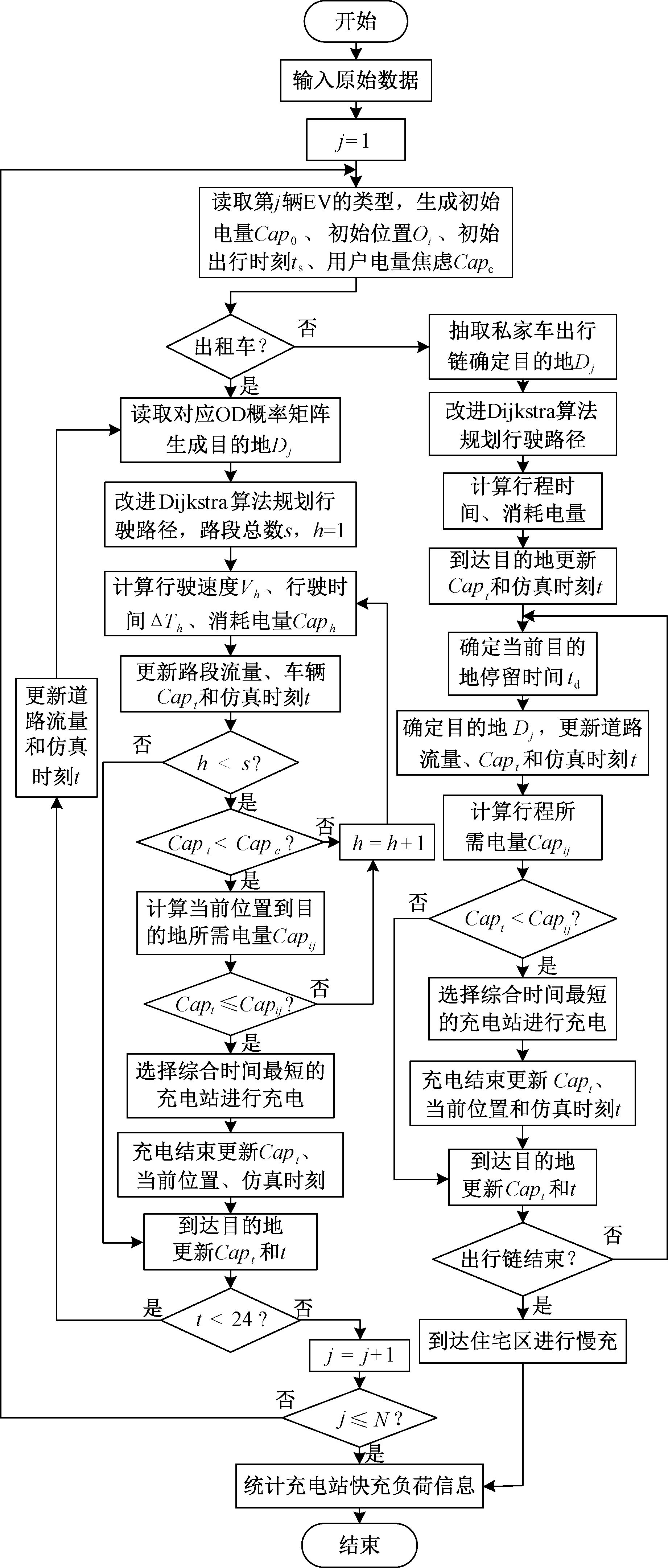
图3 充电站需求模型流程图
Figure 3 Flow chart of charging station demand model
F=F1+F2。
4 充电站规划策略
4.1 目标函数
建设EV充电站时不仅要考虑充电站经营者的投资成本,同时要兼顾提供充电服务过程中的用户满意度[2]。本文考虑充电站经营者与EV用户双方利益具有同等重要性,建立充电站选址定容优化模型,以充电站年化总经济成本最低为目标函数,如式(15)所示:
(15)
式中:F为充电站年化总经济成本;F1为充电站年建设运维成本;F2为用户年化经济损失。
(1)充电站年建设运维成本。充电站的年建设运维成本包括年建设成本和年运维成本,计算公式为
(16)
f(Nchj)=Cj+qNchj。
(17)
式中:M为充电站数量;Nchj为充电站j内充电桩的数量;r0为充电站平均折旧率;ys为充电站最高使用年限;f(Nchj)为充电站建设成本函数;Cj为第j个充电站的固定投资成本;q为单个充电桩购买及土地租金等相关费用。
Cyj为第j个充电站的年运维成本,充电站的运维成本与日运行容量成正比[2],充电站的年运维成本为
Cyj=(k1+k2)CaprpjTy。
(18)
式中:k1为员工工资比例系数;k2为并网成本比例系数;Caprpj为第j个充电站日运行容量。
(2)用户年化经济损失。综合考虑用户前往充电站的路途耗时、站内排队时间和充电路途电量损耗,用式(19)计算用户年化经济损失:
(19)
式中:Cwj为EV用户从充电需求点前往第j个充电站的路途时间成本;Cmj表示第j个充电站内的用户排队时间成本;Cccj为用户从充电需求点行驶至第j个充电站的电量损耗成本。其中:
(20)
式中:Cuat为用户的单位时间等效经济损失;Jcsj为选择到第j个充电站充电的充电需求点集合。
本文基于M/M/c排队论方法来计算车主排队等待时间。假设车辆到达充电站的过程服从泊松分布[15],以每小时在充电站接受服务的充电车辆作为参数λ,则用户平均等待时间Wq为
(21)
(22)
(23)
式中:p为充电桩服务强度;μ为每个充电桩1 h能完成充电服务的车辆数。在第j个充电站接受充电服务的EV用户排队时间成本Cmj可表示为
(24)
式中:Wqk为k时刻充电站j内的平均排队时间;λk为充电站j内k时刻的充电车辆数。
用户前往第j个充电站产生的路途电量损耗成本Cccj为
(25)
式中:Cjg为用户充电单价;Capij表示从充电需求点到第j个充电站所耗费的电量。
4.2 充电站容量配置
以充电站的系统单位总费用(系统服务成本与等待成本之和)最小为目标,建立充电站容量配置优化模型:
min F(Nchj)=CsNchj+CuatLs;
(26)
(27)
式中:Cs为单位时间内每个充电桩的使用成本;Ls为单位时间的平均队长;p<1是式(27)成立的必要条件。
4.3 约束条件
(1)充电桩配置约束。
Nchmin≤Nchj≤Nchmax。
(28)
式中:Nchmin、Nchmax分别为充电站内充电桩最小和最大配置数量。
(2)排队等待时间约束。
Wq≤Wmax。
(29)
式中:Wmax为排队等待时间的最大值。
(3)充电站覆盖强度约束。为了避免用户前往充电站行驶的距离过长和充电站分布过于集中,相邻2个充电站之间的距离Lj,j+1应不大于充电站服务半径的2倍[15]。
Rs≤Lj,j+1≤2Rs。
(30)
式中:Rs为充电站的服务范围;Lj,j+1为节点j和节点j+1之间的实际距离。
4.4 求解流程
在求解过程中,首先,依据建设充电站数量M,列出候选充电站站址组合,筛选出满足式(30)约束的候选站址组合,利用蒙特卡洛方法通过充电站需求模型动态模拟,得到候选站址组合的充电站快充需求信息;其次,基于排队论方法,采用粒子群算法以式(26)值最小为目标对充电站进行容量配置,过程须满足式(28)和式(29)的约束条件;最后,根据式(15)~(25)计算各充电站候选站址组合年化总经济成本F,求得该模型充电站站址组合及容量的最优规划。
5 算例分析
5.1 参数设置
以图4所示某城区部分主要道路为规划区域,该区域共分为居民区、商业区和工业区,包含29个道路节点和49条道路,各道路参数见文献[7]。本文假设该区域中共有8 000辆电动私家车,2 000辆电动出租车,算例所用的电动出租车电池额定容量60 kWh,私家车电池额定容量24 kWh。初始出行时电池荷电状态服从正态分布(0.6,0.12),充电站充电功率为60 kW,充电效率为0.9,充电站选址定容模型相关参数设置如表1所示。
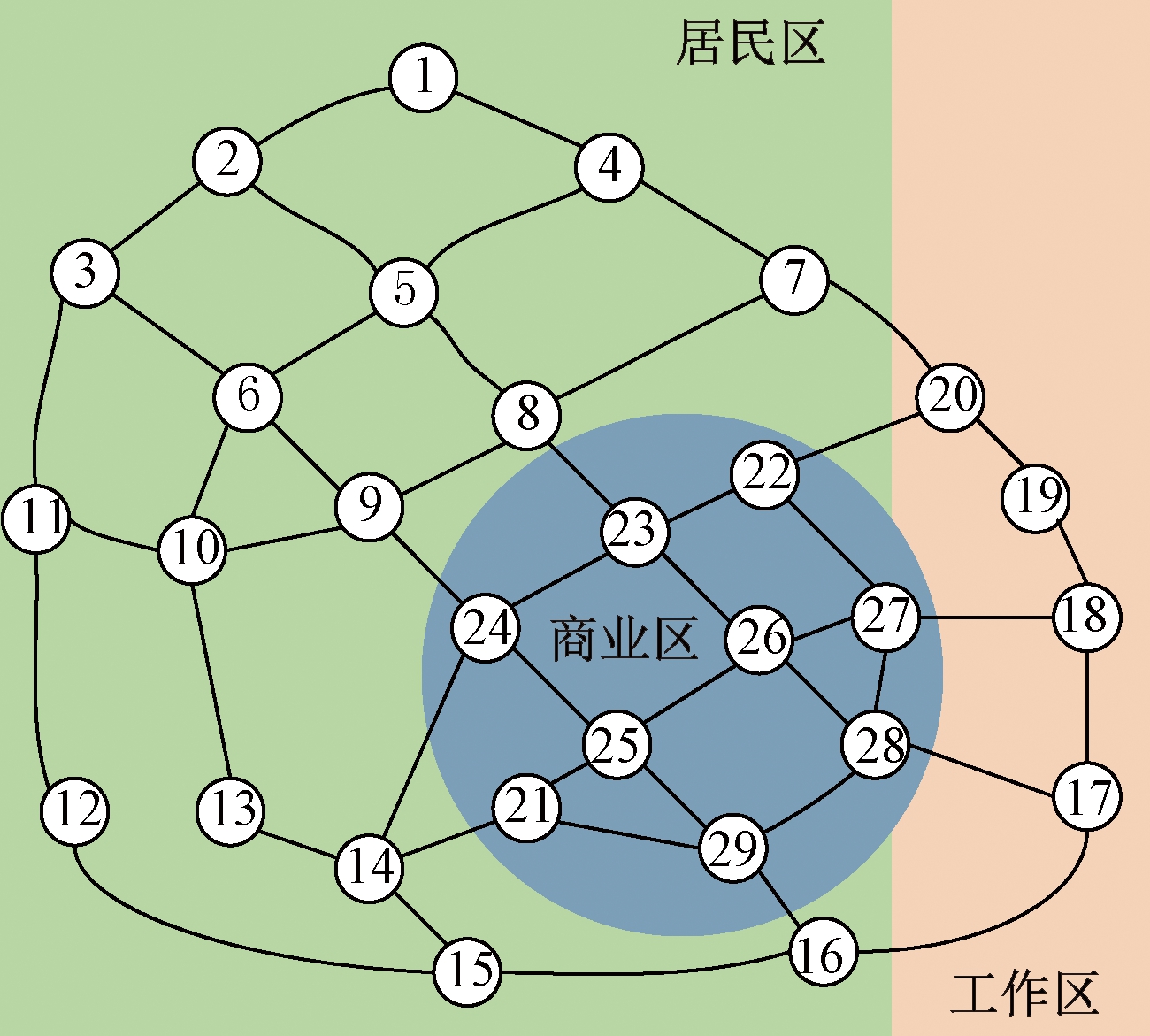
图4 规划区域部分主干道示意图
Figure 4 Schematic diagram of main road in planning area
表1 充电站选址定容参数
Table 1 Charging station location and capacity parameters
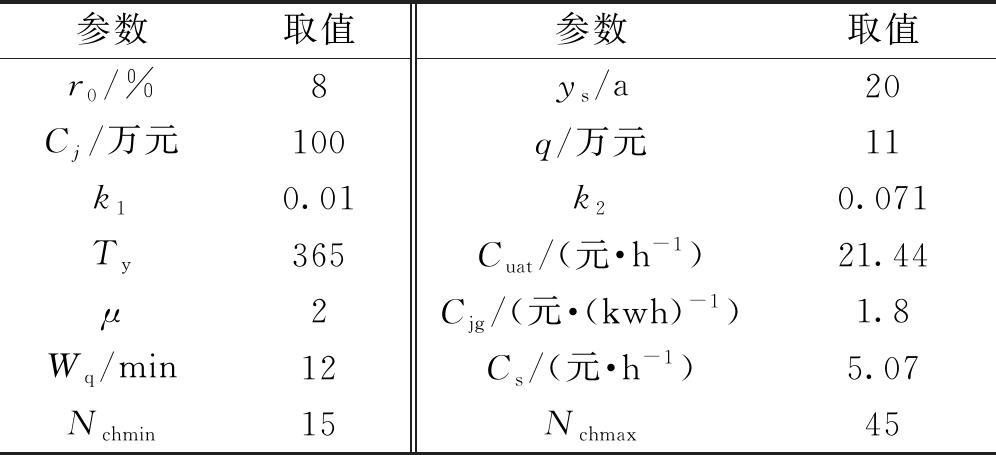
参数取值参数取值r0/%8ys/a20Cj/万元100q/万元11k10.01k20.071Ty365Cuat/(元·h-1)21.44μ2Cjg/(元·(kwh)-1)1.8Wq/min12Cs/(元·h-1)5.07Nchmin15Nchmax45
5.2 规划结果及分析
规划区域充电站建设数量设置为5~8座,对应充电站综合年化经济成本如表2所示。
从表2可以看出,随着充电站建设数量的增多,充电站年建设成本呈增加趋势,因为充电站建设数量增多,导致充电站的固定投资成本、充电桩的购买和安装成本都相应增加。充电站年运维成本相近,因为区域内车辆数固定,充电站日运行容量变化不大。充电路途耗时成本、耗电成本和排队时间成本呈减小趋势,是因为更多的充电站投入使用,增加了用户充电的便利度,减少EV用户前往充电站的行驶时间、损耗电量和排队时间,同时提升了用户充电满意度。当规划区域建设6座充电站时,充电站综合年化总经济成本最低,为598.13万元。
表2 充电站综合年化经济成本
Table 2 Comprehensive annualized economic cost of charging stations

充电站数量/座充电站年建设成本/万元充电站年运维成本/万元年充电路途耗时成本/万元年排队时间成本/万元年充电路途耗电成本/万元年化总经济成本/万元5223.7498.38123.5074.4593.31613.386237.1397.39109.8569.5384.23598.137259.2099.36105.8866.0880.11610.638290.9198.5394.3660.4571.90616.15
5.3 最优充电站位置和容量
给建设的6座充电站编号为CS1~CS6,最优充电站建设位置、充电桩配置数如表3所示。从表3结合图4可以看出,充电站位置分布均匀,站间距离合适,能很好地为整个区域提供快充服务。图5为快充需求时空分布图,从图5看出,快充需求数在14:00~15:00出现第一个峰值,快充点分布比较均匀,主要因为出租车在经历一上午的寻客和载客后电量不足;在20:00~21:00出现另一个峰值,快充需求点集中在从工作区和商业区回居民区的道路节点,私家车用户下班或经历商业活动之后电量不满足下段行程所需电量,因此产生快充需求。
表3 最优站址组合规划结果
Table 3 Optimal site combination planning results

充电站编号道路节点充电桩数量CS1719CS21027CS31433CS41836CS52322CS62921
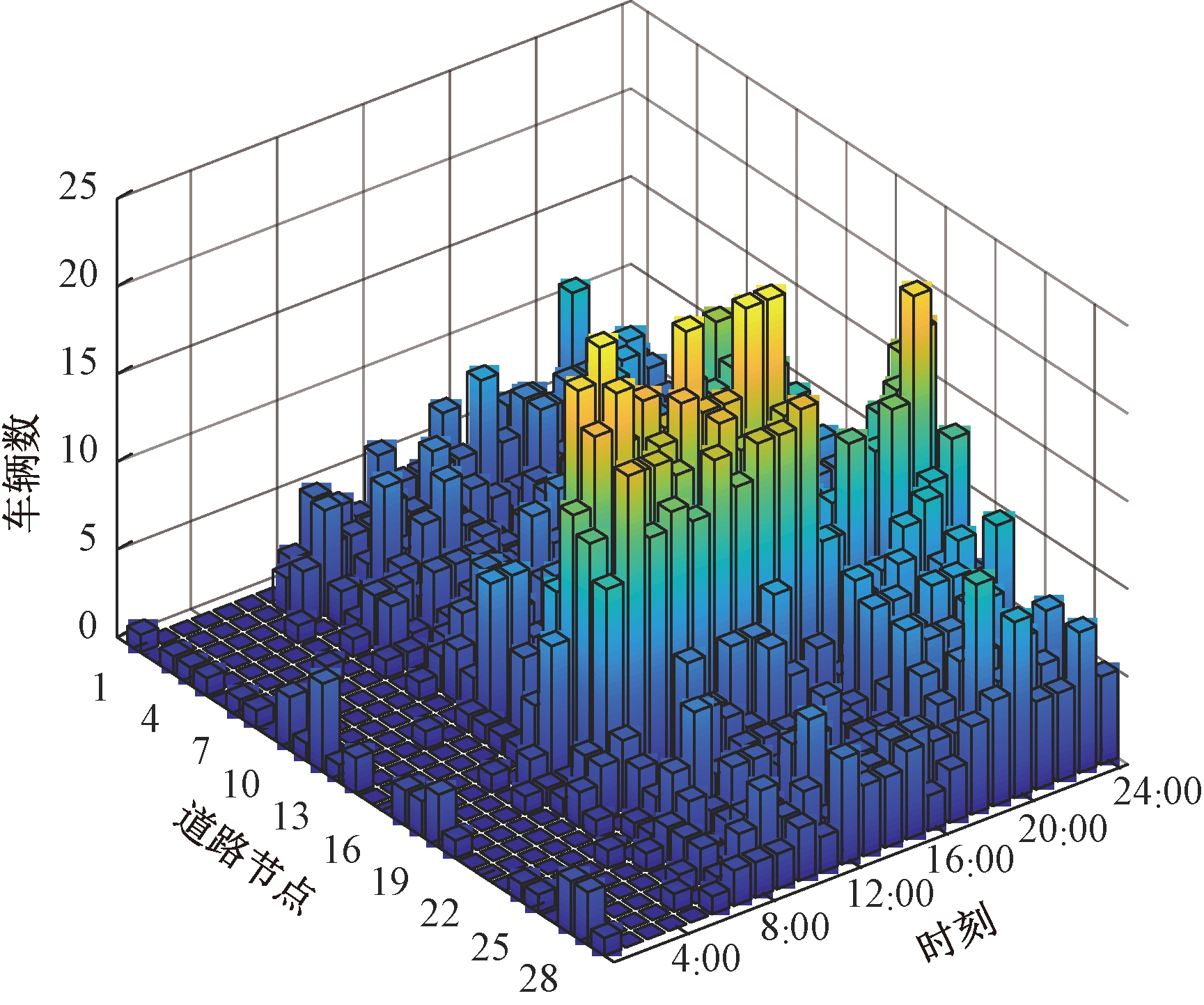
图5 快充需求时空分布
Figure 5 Space-time distribution of fast charging demand
图6为充电站CS1~CS6一天的充电车辆数分布图,从图6中看出,选择在充电站CS2、CS3、CS4进行补电的车辆数较多,因为充电需求点大多分布在从商业区和工作区返回居民区的路上,EV用户选择综合行程时间最短的充电站,这些充电站位于居民区和工作区的重要道路节点,也是出租车接送客路线和私家车回居民区路线主要经过节点。图7为充电站快充负荷分布图,从图7可以看出,充电负荷的分布特性和EV用户充电行为相一致,充电站CS2、CS3、CS4服务的车辆数量较多。从图8充电站综合年化经济成本中看出,充电站的年排队等待时间成本并不高,因为这些充电站有更多的充电桩,减少用户排队时间,在一定程度上反映了充电站容量配置方法的合理性。充电站的建设运维成本、EV用户的路途耗时和电量损耗成本均与充电站容量及服务车辆数呈正相关,证明了本文提出的充电站选址定容模型的合理性。
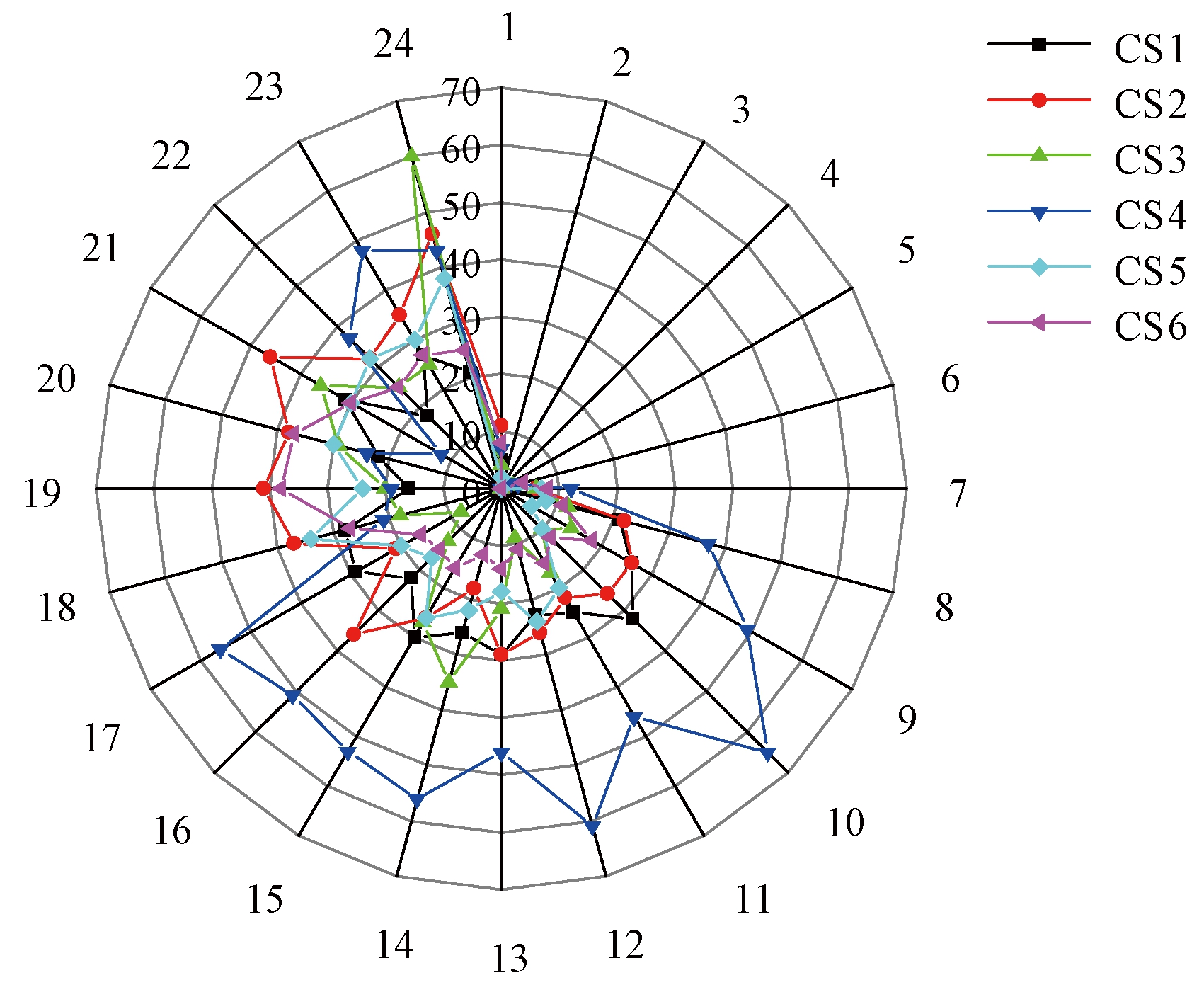
图6 充电车辆数
Figure 6 Number of charging electric vehicles
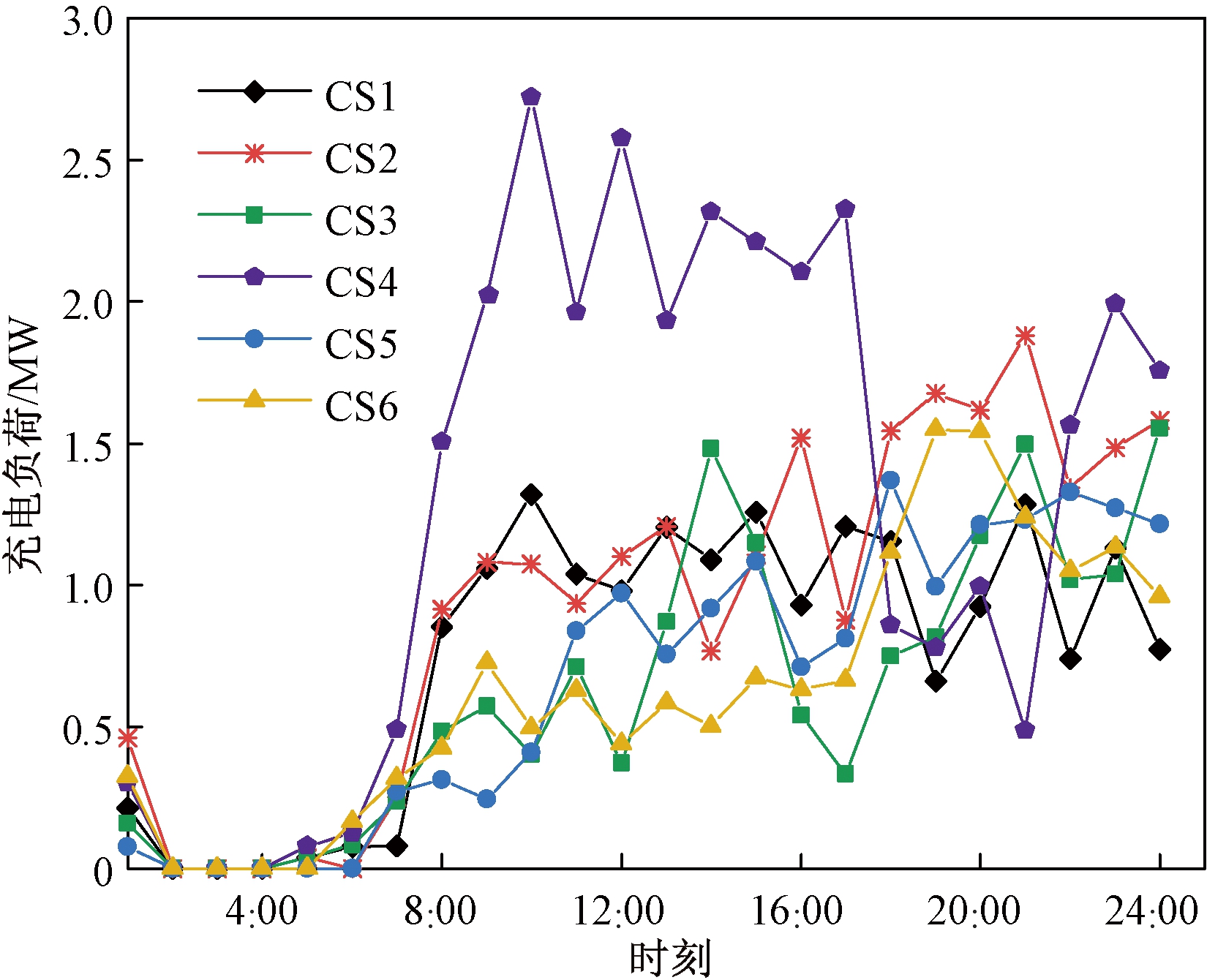
图7 充电站快充负荷
Figure 7 Fast charging at charging station
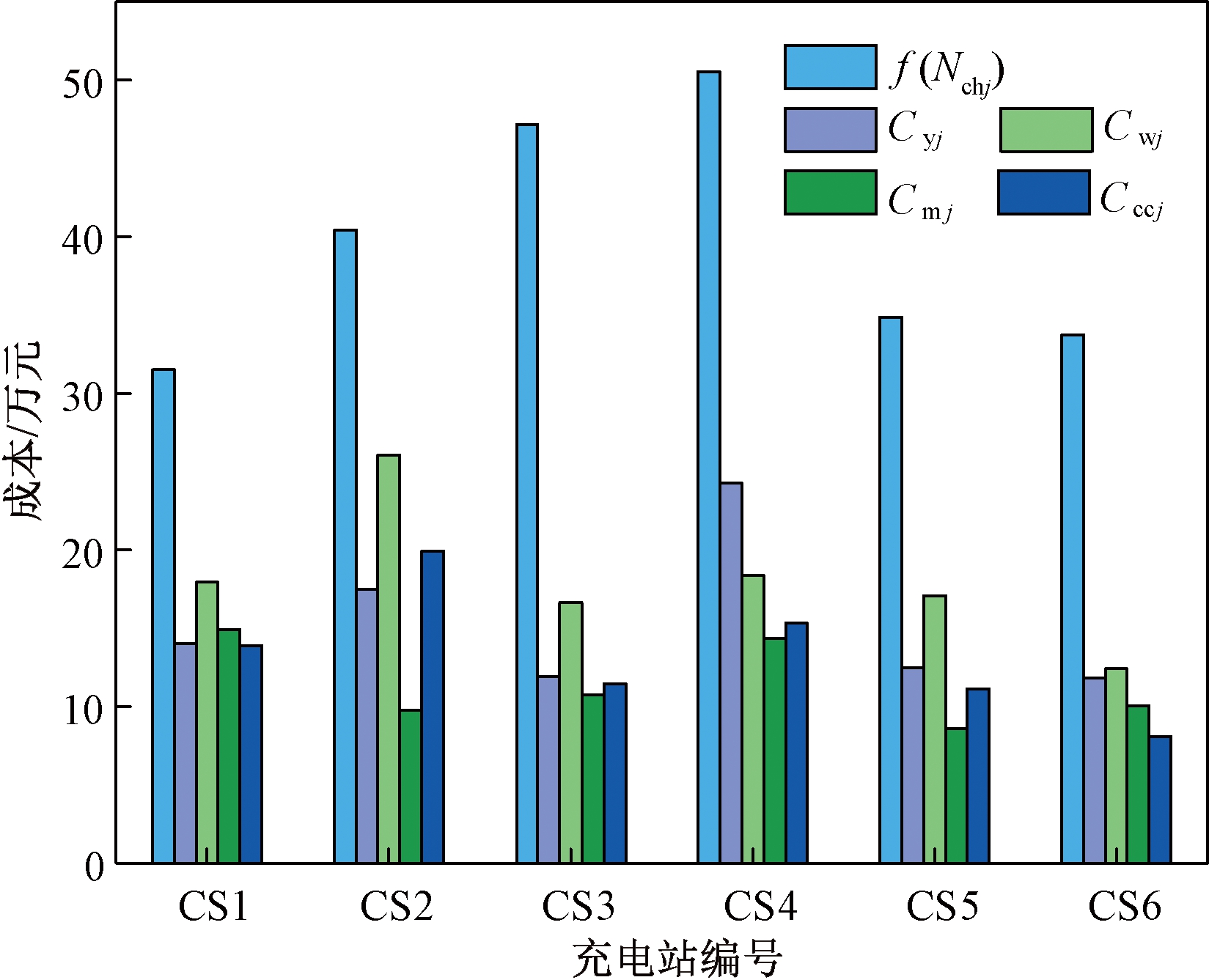
图8 充电站综合年化经济成本
Figure 8 Annualized economic cost of charging station
5.4 充电站选择行为对比结果分析
为了分析用户选择充电站行为对规划结果的影响,设置如下方案。
方案1:采用本文所提充电站选择方法。
方案2:用户在选择充电站时只考虑距离因素。
以建设6个充电站为例,规划对比结果如表4所示,从表4可以看出,方案2中充电站主要分布在各功能区车流量较大的道路节点,附近的充电需求车辆较多,用户在选择充电站时只考虑距离因素,同一时段充电车辆前往同一充电站的几率增加。充电站建设道路节点18和22位于工作区和商业区,EV用户出行活动频率较高,产生的快充需求车辆数也随之增多,充电站内充电桩配置也相对较多。
表4 不同方案规划结果
Table 4 Planning results of different schemes

方案最优充电站选址最优充电桩数量充电站综合年化成本/万元f(Nchj)CyjCwjCmjCccjF用户补电后年路途成本/万元17,10,14,18,23,2919,27,33,36,22,21237.1397.39109.8569.5384.23598.1375.2125,13,16,18,21,2226,19,17,39,22,43247.0996.11115.1165.4187.16610.88164.77
方案2中充电站年建设成本相比方案1增加9.96万元,因为总充电桩数量增多,虽然EV用户年排队时间成本减少4.12万元,但用户年路途耗时和路途电量损耗成本相比方案1都增加了,用户选择距离最近的充电站,没有考虑路段交通拥堵的影响,前往充电站路程花费的时间和损耗电量不一定就少。用户在充电站补电后前往目的地的年路途成本为164.77万元,对比方案1增加89.56万元,充电站年化总经济成本F也比方案1高,证明本文提出的选择综合行程时间最短的充电站方法的优势,使EV用户规避交通拥堵路段,以最短的行程时间到达目的地,减少了用户的时间和电量损失成本。
5.5 不同规划目标结果分析
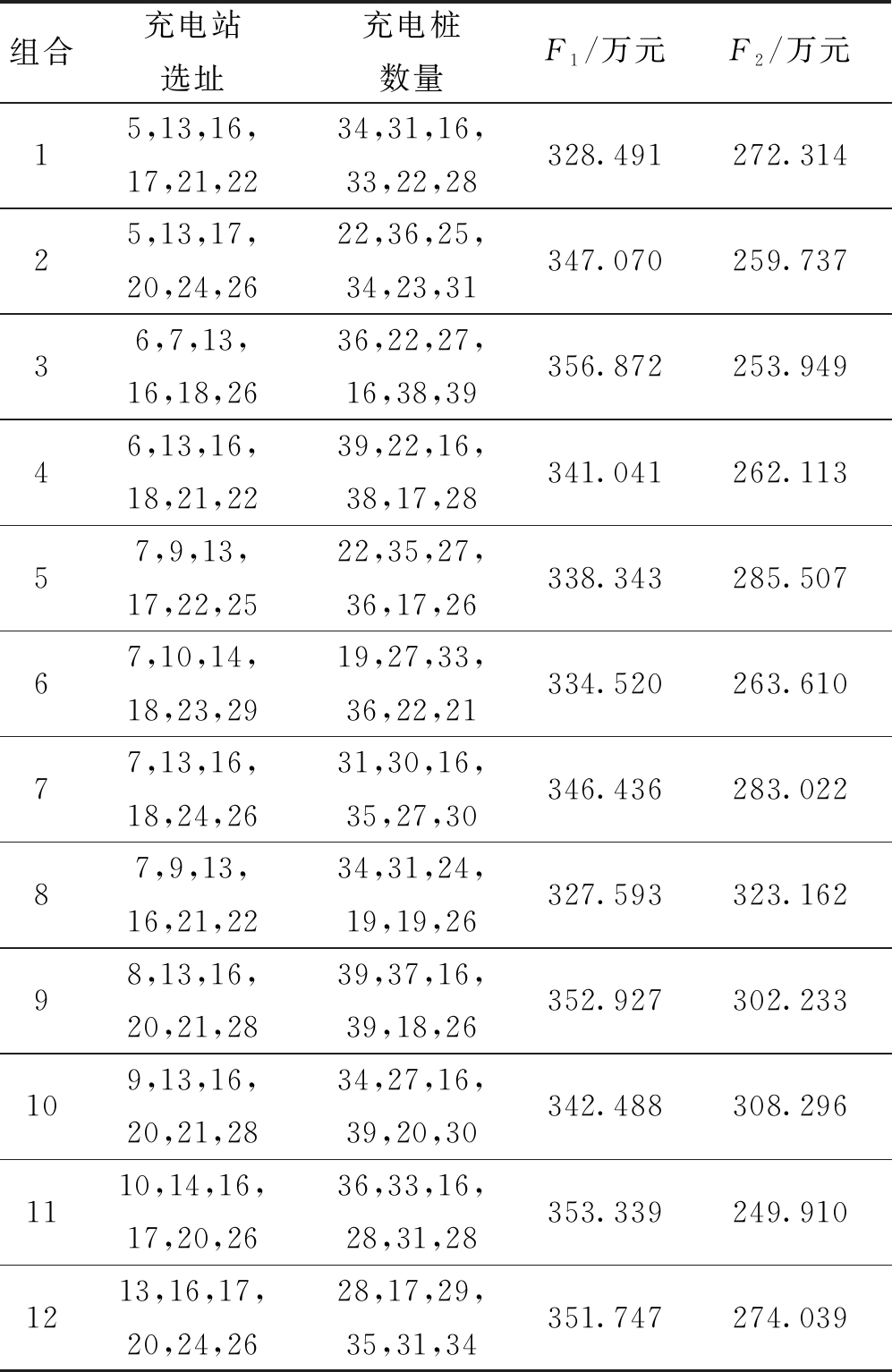
为了分析充电站投资成本和用户经济损失对规划结果的影响,以建设6个充电站为例,表5展示了12个典型充电站候选站址组合规划结果。图9为典型组合综合年化经济成本图。
由表5可知,在充电站规划时只考虑EV用户利益时方案11为最优解,用户年经济损失成本为249.910万元,充电站年建设运维成本为353.339万元。单独考虑充电站投资方利益时方案8为最优解,充电站年建设维行成本为327.593万元,用户年经济损失成本为323.162万元。
本文提出的考虑充电站经营者和EV用户双方利益具有同等重要性,结合表5和图9可知,方案6是本文所提模型的最优解方案,方案6的充电站建设成本、用户前往充电站的时间和电量损失成本、排队时间成本相比其他方案都不是最低的,但是该方
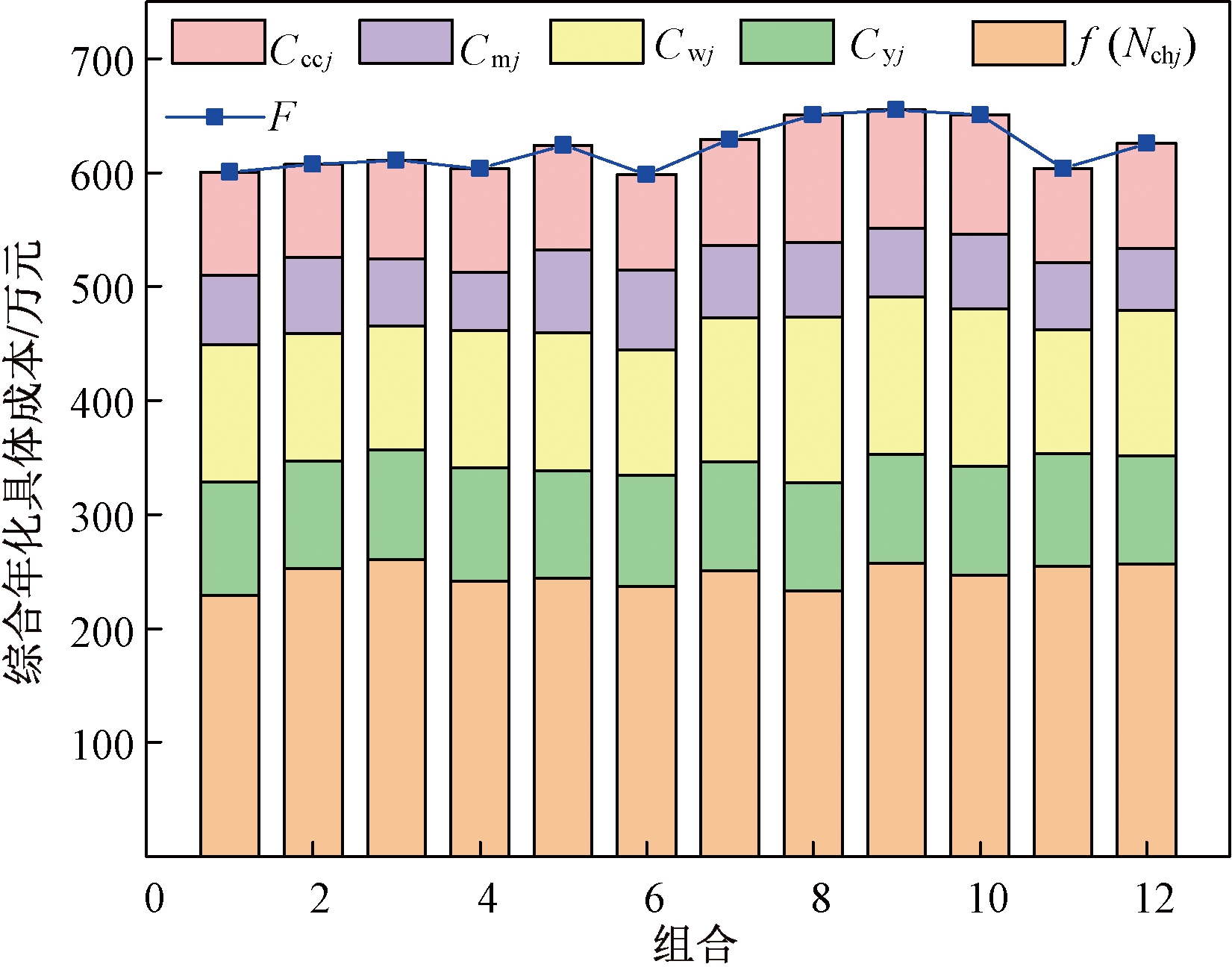
图9 典型组合综合年化经济成本
Figure 9 Typical portfolios combine annualized economic costs
表5 典型站址组合规划结果
Table 5 Typical site combination planning results
组合充电站选址充电桩数量F1/万元F2/万元15,13,16,17,21,2234,31,16,33,22,28328.491272.31425,13,17,20,24,2622,36,25,34,23,31347.070259.73736,7,13,16,18,2636,22,27,16,38,39356.872253.94946,13,16,18,21,2239,22,16,38,17,28341.041262.11357,9,13,17,22,2522,35,27,36,17,26338.343285.50767,10,14,18,23,2919,27,33,36,22,21334.520263.61077,13,16,18,24,2631,30,16,35,27,30346.436283.02287,9,13,16,21,2234,31,24,19,19,26327.593323.16298,13,16,20,21,2839,37,16,39,18,26352.927302.233109,13,16,20,21,2834,27,16,39,20,30342.488308.2961110,14,16,17,20,2636,33,16,28,31,28353.339249.9101213,16,17,20,24,2628,17,29,35,31,34351.747274.039
案综合年化总经济成本F为598.13万元,是各方案中最具有优势的,证明本文所提模型的优势性,充分保障了充电站经营者与EV用户双方利益。
6 结论
本文提出考虑用户动态充电需求的电动汽车充电站规划方法,并以某市主城区部分实际道路情况为规划区域进行仿真分析,得出以下主要结论。
(1)建立考虑用户动态充电需求的充电站选择模型分析用户实际充电需求信息,EV用户选择综合行程时间最短的充电站,规避拥堵路段,在充电完成后快速前往目的地,减少EV用户经济损失。
(2)以充电站年化总经济成本最低为优化目标,充电站建设运维成本和EV用户经济损失成本之和较低,规划的充电站建设位置和充电桩数量配置比较合理,符合实际情况,充分保障了双方利益,证明了本文所提模型的合理性和可行性。
[1] SUN S Y, YANG Q, YAN W J. Optimal temporal-spatial PEV charging scheduling in active power distribution networks[EB/OL]. (2017-09-19)[2022-03-17].https://doi.org/10.1186/541601-017-0065-x.
[2] 严干贵, 刘华南, 韩凝晖, 等. 计及电动汽车时空分布状态的充电站选址定容优化方法[J]. 中国电机工程学报, 2021, 41(18): 6271-6284.
YAN G G, LIU H N, HAN N H, et al. An optimization method for location and capacity determination of charging stations considering spatial and temporal distribution of electric vehicles[J]. Proceedings of the Csee, 2021, 41(18): 6271-6284.
[3] 李晓辉, 李磊, 刘伟东, 等. 基于动态交通信息的电动汽车充电负荷时空分布预测[J]. 电力系统保护与控制, 2020, 48(1): 117-125.
LI X H, LI L, LIU W D, et al. Spatial-temporal distribution prediction of charging load for electric vehicles based on dynamic traffic information[J]. Power System Protection and Control, 2020, 48(1): 117-125.
[4] YAN J, ZHANG J, LIU Y Q, et al. EV charging load simulation and forecasting considering traffic jam and weather to support the integration of renewables and EVs[J]. Renewable Energy, 2020, 159: 623-641.
[5] 张琳娟, 许长清, 王利利, 等. 基于OD矩阵的电动汽车充电负荷时空分布预测[J]. 电力系统保护与控制, 2021, 49(20): 82-91.
ZHANG L J, XU C Q, WANG L L, et al. OD matrix based spatiotemporal distribution of EV charging load prediction[J]. Power System Protection and Control, 2021, 49(20): 82-91.
[6] 邵尹池, 穆云飞, 余晓丹, 等. “车-路-网”模式下电动汽车充电负荷时空预测及其对配电网潮流的影响[J]. 中国电机工程学报, 2017, 37(18): 5207-5219, 5519.
SHAO Y C, MU Y F, YU X D, et al. A spatial-temporal charging load forecast and impact analysis method for distribution network using EVs-traffic-distribution model[J]. Proceedings of the Csee, 2017, 37(18): 5207-5219, 5519.
[7] 赵书强, 周靖仁, 李志伟, 等. 基于出行链理论的电动汽车充电需求分析方法[J]. 电力自动化设备, 2017, 37(8): 105-112.
ZHAO S Q, ZHOU J R, LI Z W, et al. EV charging demand analysis based on trip chain theory[J]. Electric Power Automation Equipment, 2017, 37(8): 105-112.
[8] 宋雨浓, 林舜江, 唐智强, 等. 基于动态车流的电动汽车充电负荷时空分布概率建模[J]. 电力系统自动化, 2020, 44(23): 47-56.
SONG Y N, LIN S J, TANG Z Q, et al. Spatial-temporal distribution probabilistic modeling of electric vehicle charging load based on dynamic traffic flow[J]. Automation of Electric Power Systems, 2020, 44(23): 47-56.
[9] 张美霞, 孙铨杰, 杨秀. 考虑多源信息实时交互和用户后悔心理的电动汽车充电负荷预测[J]. 电网技术, 2022, 46(2): 632-645.
ZHANG M X, SUN Q J, YANG X. Electric vehicle charging load prediction considering multi-source information real-time interaction and user regret psychology[J]. Power System Technology, 2022, 46(2): 632-645.
[10] LIU Y B, XIANG Y, TAN Y Y, et al. Optimal allocation model for EV charging stations coordinating investor and user benefits[J]. IEEE Access, 2018,6: 36039-36049.
[11] SADEGHI-BARZANI P, RAJABI-GHAHNAVIEH A, KAZEMI-KAREGAR H. Optimal fast charging station placing and sizing[J]. Applied Energy, 2014, 125: 289-299.
[12] 张忠会, 刘故帅, 熊剑峰, 等. 基于谱聚类算法的城市充换电站分布决策[J]. 郑州大学学报(工学版), 2017, 38(5): 32-38.
ZHANG Z H, LIU G S, XIONG J F, et al. The application of spectral clustering algorithm to distributive decision for charging and battery swap station[J]. Journal of Zhengzhou University (Engineering Science), 2017, 38(5): 32-38.
[13] 臧海祥, 舒宇心, 傅雨婷, 等. 考虑多需求场景的城市电动汽车充电站多目标规划[J]. 电力系统保护与控制, 2021, 49(5): 67-80.
ZANG H X, SHU Y X, FU Y T, et al. Multi-objective planning of an urban electric vehicle charging station considering multi demand scenarios[J]. Power System Protection and Control, 2021, 49(5):67-80.
[14] 陈静鹏, 艾芊, 肖斐. 基于用户出行需求的电动汽车充电站规划[J]. 电力自动化设备, 2016, 36(6): 34-39.
CHEN J P, AI Q, XIAO F. EV charging station planning based on travel demand[J]. Electric Power Automation Equipment, 2016, 36(6): 34-39.
[15] 姜欣, 冯永涛, 熊虎, 等. 基于出行概率矩阵的电动汽车充电站规划[J]. 电工技术学报, 2019, 34(增刊1): 272-281.
JIANG X, FENG Y T, XIONG H, et al. Electric vehicle charging station planning based on travel probability matrix[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 272-281.