作为压缩/喷射制冷循环系统的关键装置,两相喷射器可有效回收流体流动过程中的节流损失,提高系统性能。但是两相喷射器偏低的效率制约了系统性能进一步提高。为解决这一问题,众多研究者分别从理论模型[1-4]、数值模拟[5-7]和实验研究[8-10]等方面对喷射器流场、性能及结构尺寸的影响进行了研究,取得了一系列成果。
Sriveerakul等[11]、Ruangtrakoon等[12]、Chen等[13]发现在临界状态下,喷射器混合室出口附近存在低压区,这阻碍了喷射器内流体流动,降低了其性能。为此,相关研究者提出在临界喷射器内部流场低压区域增加介质旁路通道来改善流体流动,提高设备性能。Chen等[13]研究发现,当旁路进口中心位置到混合室进口的长度与混合室长度之比为1.1时,旁路喷射器获得最大引射系数,与传统喷射器相比,旁路喷射器的引射系数增加了9.65%。之后,Chen等[14]进一步分析了旁路进口宽度的影响,结果显示,旁路进口宽度为0.8~1.6 mm时,相较于无旁路喷射器,设备性能最大可提高34.88%。Tang等[15]通过研究,建议当喷射器处于设计工况(临界状态)时,在混合室等面积段上设置旁路进口;当处于非设计工况(亚临界状态)时,在混合室等面积段和扩压室上设置旁路进口。之后,Tang等[16]研究发现旁路存在最优的进口位置、宽度和角度使得喷射器性能最优。Bodys等[17]以CO2为工质,研究了旁路进口角度对旁路喷射器的影响,结果表明:与传统喷射器相比,当旁路角度为19°时,喷射器的引射系数提高了36.9%。后来Bodys等[18]又研究了旁路进口位置对旁路喷射器的影响,得到了与Chen等[19]相似的结论。
综上所述,目前关于旁路喷射器的研究主要集中于临界状态下的两相喷射器,通过在扩压室进口附近的流场低压区引入旁路流体来改善流体流场分布,提高喷射器的性能。在课题组所研究的双温压缩/喷射制冷系统中[10,19-20],在大部分工况条件下,两相喷射器处于亚临界状态,不存在临界状态下的流场低压区。为此,在Tang等[15-16]以及前期大量模拟工作基础上,提出在混合室和扩压室连接处增加旁路进口,引入高压旁路流体,通过促进喷射器混合室内混合流体流动来提高喷射器性能。本文对以R134a为工质的亚临界旁路喷射器进行研究,分析旁路进口几何形状尺寸和工况参数对其性能和内部流场的影响,探究最佳旁路结构尺寸和工质工况参数。
1 计算模型
1.1 数值模型
在课题组前期的实验研究中[10],所研究的亚临界两相喷射器喷嘴进口为过冷液体,引射室进口为过热蒸汽。过冷液体在经过主喷嘴时降压膨胀发生相变,故在对两相喷射器的模拟中设置两相流模型和两相流声速模型。
(1)两相流模型。选取两相非均相混合模型捕捉喷射器内部的相变效应。稳态条件下,质量方程、动量守恒、能量守恒以及与第二相守恒相对应的附加平流方程如下:
(1)
(2)
(3)
(4)
式中:ρ为混合流体的密度,kg/m3;u为速度,m/s;p为压力,kPa;τ为雷诺应力;▽为哈密顿算子;keff为有效热导率,W/(m·K);T为开氏温度,K;i、j表示方向;E为内能,J/kg;Q表示相变过程中传递的能量J/kg;m表示相变过程中传递的质量,kg。
(2)两相流声速模型。采用冻结声速模型来计算气液两相流体的声速,计算公式[21]为
(5)
式中:ρv、ρl分别为气相密度、液相密度,kg/m3;αv为气相体积分数;cv、cl分别为气相和液相声速,m/s。
1.2 几何模型
所研究的两相旁路喷射器主体尺寸结构是基于课题组前期设计使用的两相喷射器,其结构尺寸见表1。由于目前文献中尚未有确切的计算公式用来指导计算旁路尺寸,因此借鉴文献[13]的喷射器旁路几何尺寸来设置本文中喷射器旁路的初始尺寸,将旁路初始角度设为90°,进口初始宽度设为2 mm,设置旁路后的两相喷射器结构如图1所示。在后续研究中,通过改变旁路的角度和宽度探寻旁路结构与喷射器主体结构的最佳配比,分析两者对喷射器内部流场的影响规律,获得具有高引射效率的旁路喷射器。

图1 旁路喷射器几何结构
Figure 1 Geometric schematic diagram of two-phase bypass ejector
表1 旁路喷射器的几何尺寸
Table 1 Geometric parameters of bypass ejector
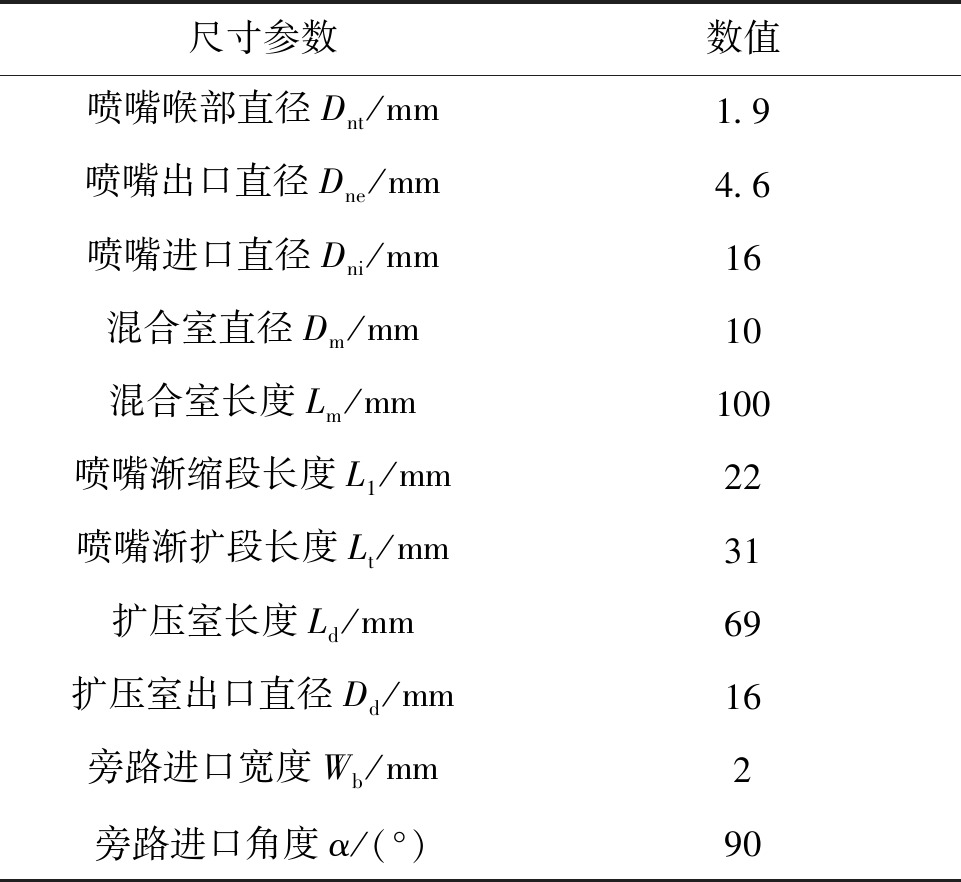
尺寸参数数值喷嘴喉部直径Dnt/mm1.9 喷嘴出口直径Dne/mm4.6 喷嘴进口直径Dni/mm16 混合室直径Dm/mm10 混合室长度Lm/mm100 喷嘴渐缩段长度L1/mm22 喷嘴渐扩段长度Lt/mm31 扩压室长度Ld/mm69 扩压室出口直径Dd/mm16 旁路进口宽度Wb/mm2 旁路进口角度α/(°)90
1.3 数值模拟方法及边界条件
采用Ansys Fluent 19.2对两相旁路喷射器的数值进行计算。采用Realizable k-ε湍流模型[22]基于压力求解器,使用二阶迎风格式的空间离散格式,近壁处采用了标准壁面函数法。喷嘴进口、引射室进口和旁路进口均为压力进口,出口为压力出口。假设旁路进口压力为488.50 kPa,其他边界条件为文献[17]中实验测得的数据,其中喷嘴进口压力为1 354.83 kPa,引射室进口压力为38.97 kPa,扩压室出口压力为418.50 kPa,工质为R134a。
1.4 网格无关性验证
本文采用ICEM软件进行网格划分,对网格数目分别为1.2×105、1.6×105、2.1×105、2.6×105、3.4×105的模型进行了计算,发现当网格数目超过2.1×105时,更加细化的网格对模型预测结果影响不大,因此本文采用的计算网格数量为2.1×105。
1.5 模型验证
将喷射器引射率的数值模拟结果与文献[20]中的实验结果进行对比,验证模拟结果的准确性,如表2所示,数值模拟结果误差为-1.52 %~4.03 %,表明本文所使用的数值模型准确性较好。
表2 数值模拟结果与实验结果对比
Table 2 Comparison between numerical simulation results and experimental results
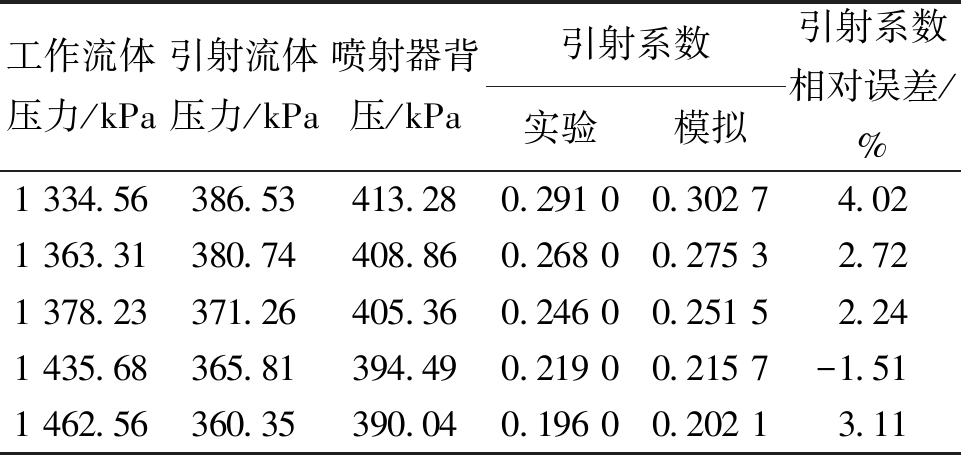
工作流体压力/kPa引射流体压力/kPa喷射器背压/kPa引射系数实验模拟引射系数相对误差/%1 334.56386.53413.280.291 0 0.302 7 4.021 363.31380.74408.860.268 0 0.275 3 2.72 1 378.23371.26405.360.246 0 0.251 5 2.241 435.68365.81394.490.219 0 0.215 7 -1.511 462.56360.35390.040.196 0 0.202 1 3.11
2 结果与讨论
2.1 旁路进口角度的影响
研究旁路进口角度影响时,保持旁路喷射器的其他结构尺寸和工况参数不变。图2为旁路喷射器引射系数、质量流量随旁路角度的变化图,其中,μ为引射系数,ms,mp和mb分别是引射流体、工作流体和旁路进口流体质量流量。随着旁路角度的增加,工作流体质量流量几乎不变,旁路进口流体质量流量增加,引射流体流量先增加后缓慢减小,喷射器引射系数先增加后减小。在本研究范围内,当旁路进口角度为15°时,喷射器引射系数最大。其中,当旁路进口角度从90°降低至15°时,引射系数从-0.52增加到0.38;当旁路进口角度从15°降低到5°时,引射系数从0.38降到0.35。
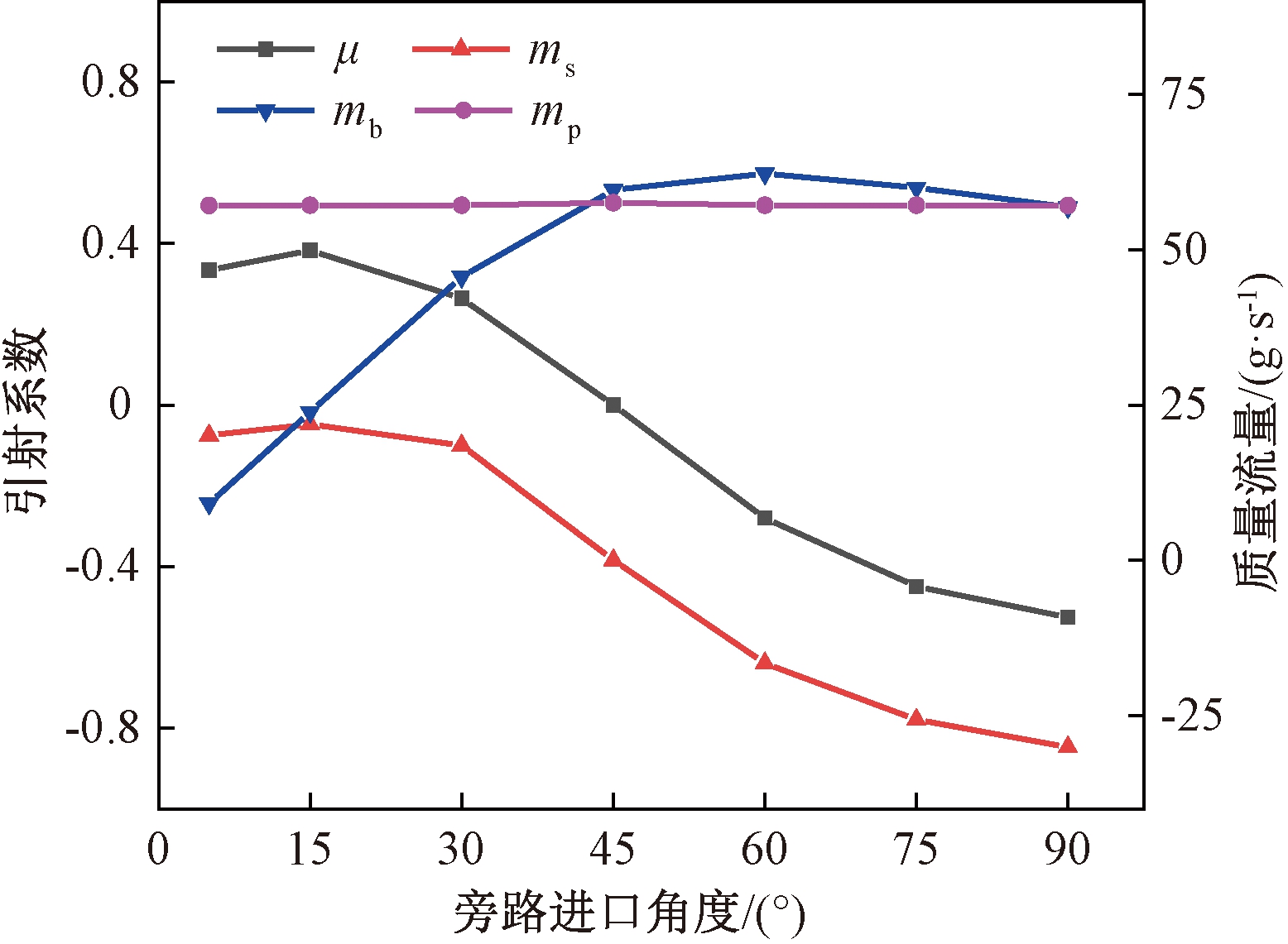
图2 旁路喷射器引射系数和质量流量随旁路进口角度的变化
Figure 2 Profiles of entrainment ratio and mass flow as a function of bypass inlet angle with the angle of bypass inlet
图3和图4分别为喷射器轴向压力和轴向马赫数分布图。喷射器内马赫数在喷嘴出口附近大于1,说明旁路喷射器处于亚临界状态,即工作流体质量流量不随旁路进口角度的变化而变化。当旁路进口角度从90°降低至15°时,混合室内混合流体压力降低(见图3),速度增加(见图4),混合流体质量流量增加。同时,工作流体质量流量基本保持不变,即混合流体质量流量增加主要是引射流体质量流量增加所致,因此喷射器引射系数增加。当旁路进口角度从15°减小至5°时,混合流体压力和速度基本保持不变,即混合流体质量流量变化较小。在工作流体质量流量基本不变的前提下,引射流体流量变化较小,所以旁路喷射器的引射系数变化较小。
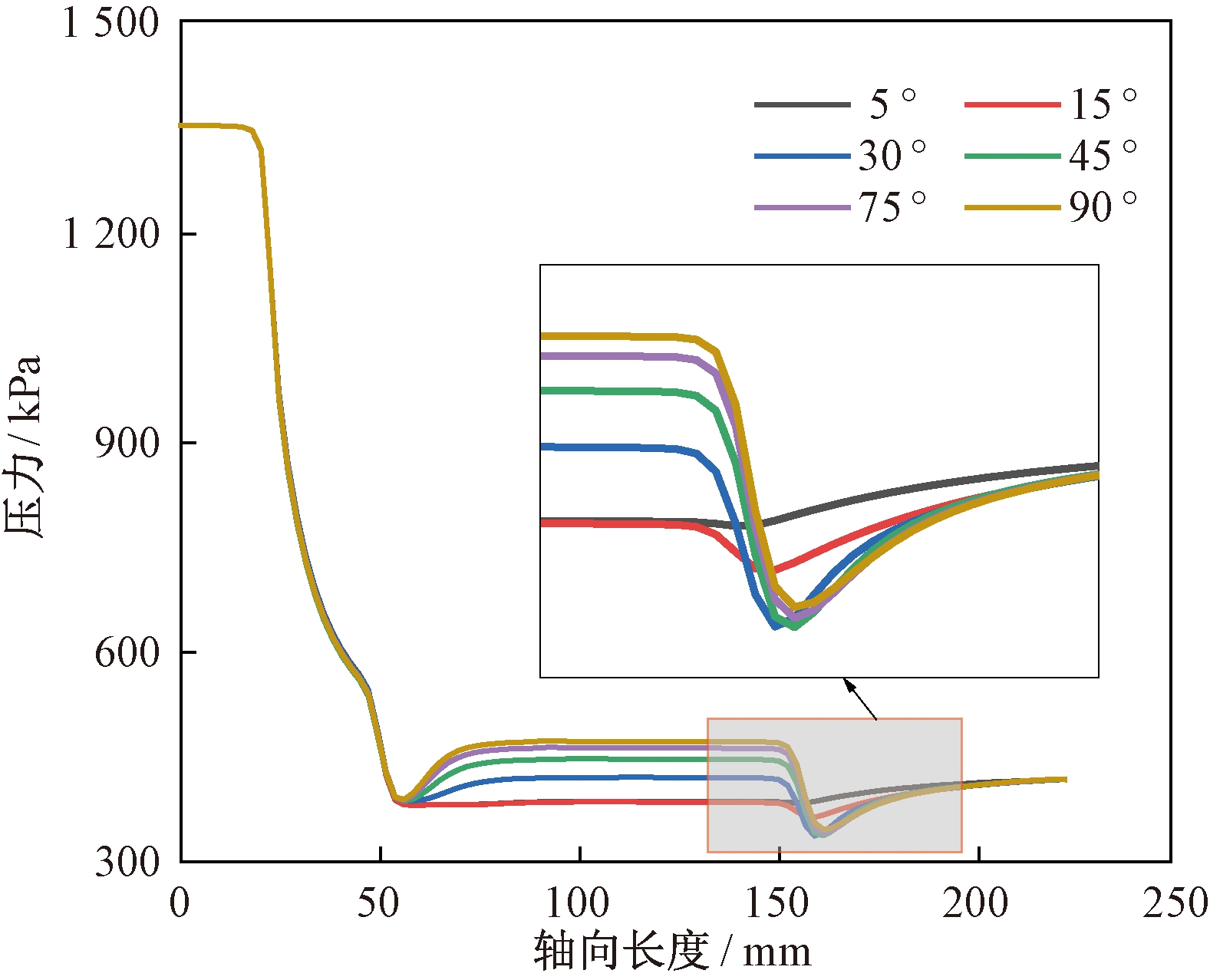
图3 旁路喷射器轴向压力分布
Figure 3 Axis pressure distribution of bypass ejector
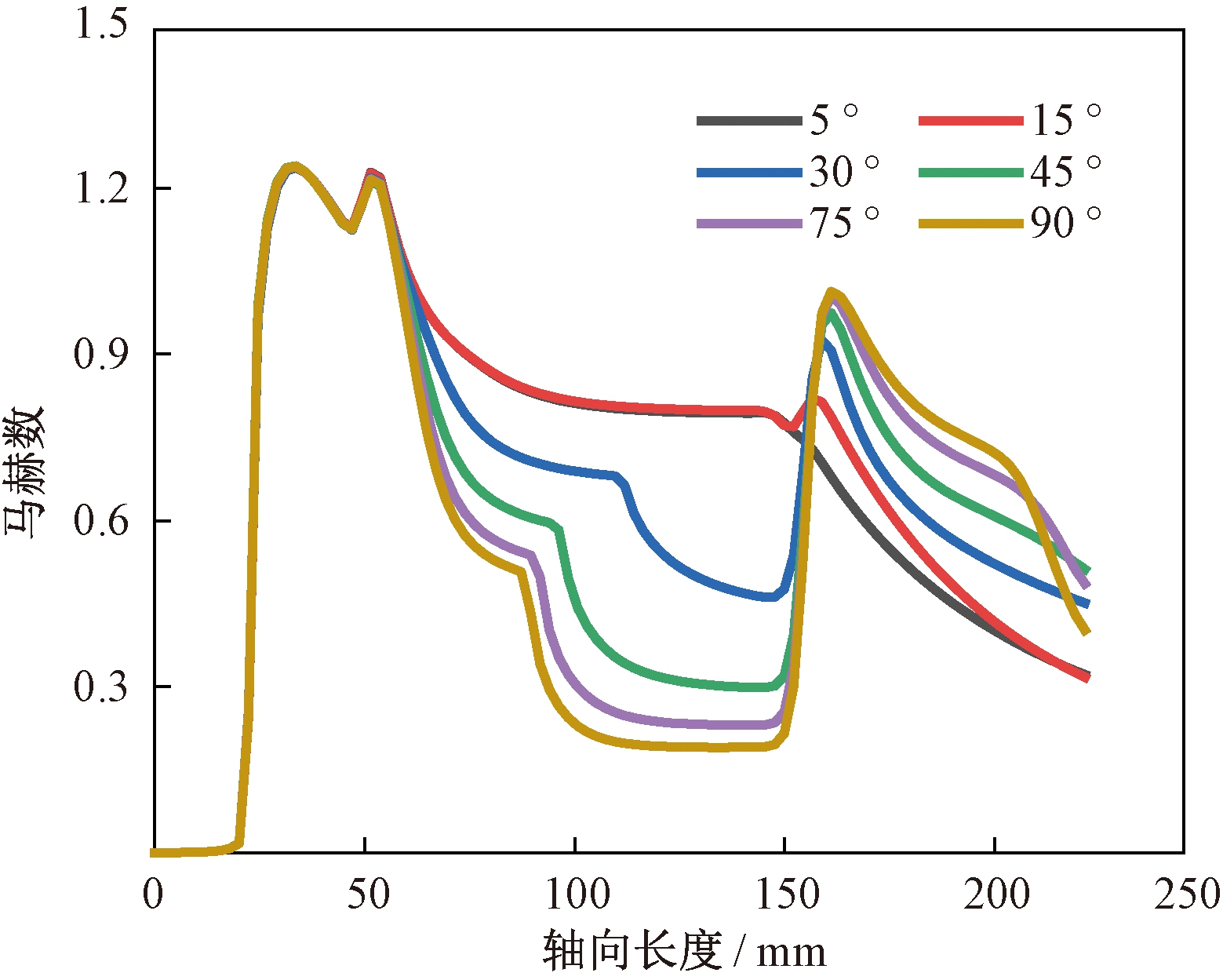
图4 旁路喷射器轴向马赫数分布
Figure 4 Axis Mach number distribution of bypass ejector
2.2 旁路进口宽度的影响
在最优旁路进口角度下,保持喷射器其他结构尺寸和工况参数不变,研究旁路进口宽度对喷射器性能的影响。结果如图5所示。随着旁路进口宽度增加,喷射器引射系数先增加后减小。当旁路进口宽度为3 mm时,喷射器引射系数达到最大,此时旁路进口宽度为最优旁路进口宽度。其中,当旁路进口宽度从1 mm增加至3 mm时,引射系数从0.35增加到0.40,增加幅度为14.3%;旁路进口宽度从3 mm增加至5 mm时,引射系数从0.40降低到0.37,降低幅度为7.5%。
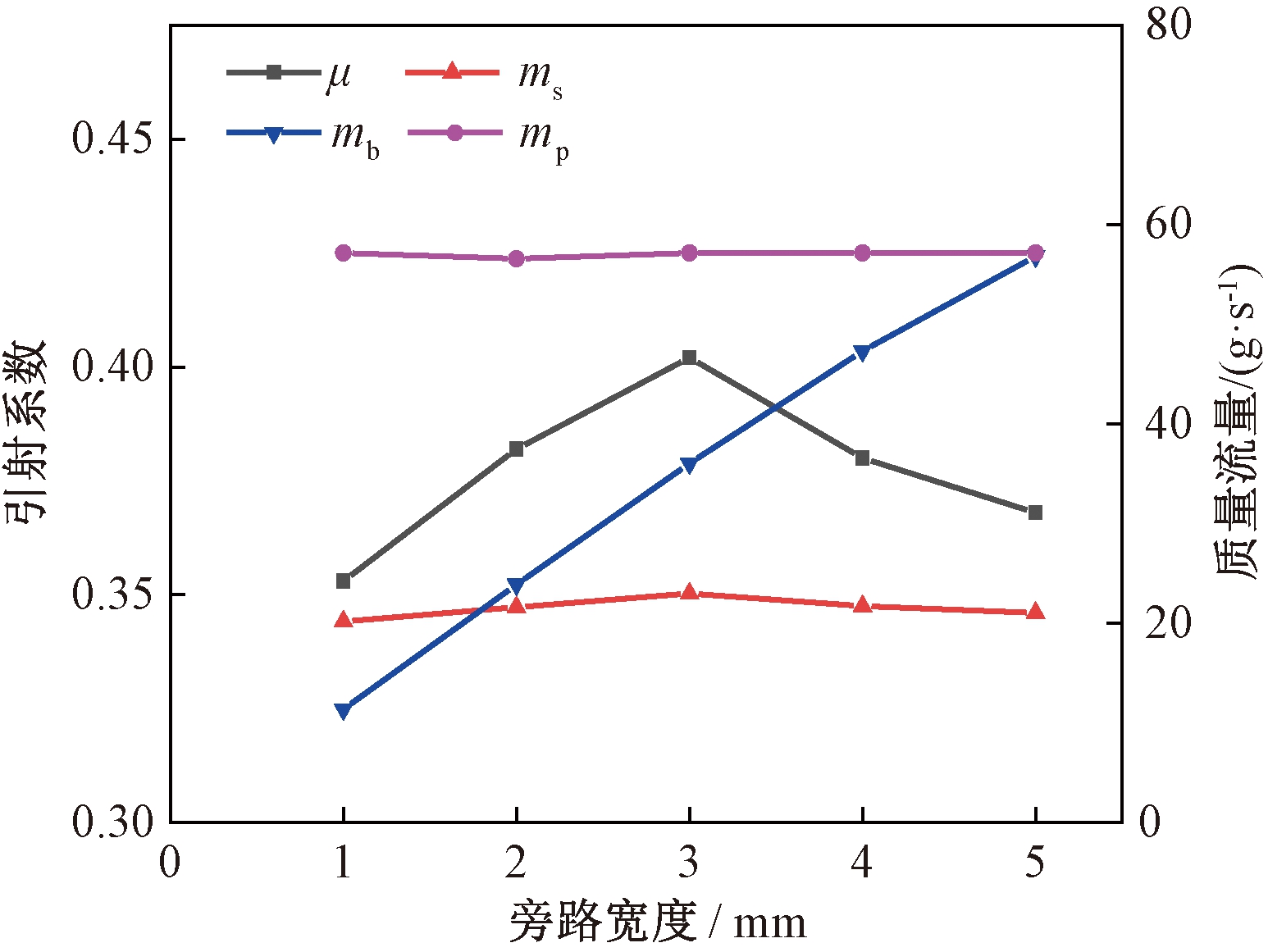
图5 旁路喷射器引射系数和质量流量随旁路宽度的变化
Figure 5 Profiles of entrainment ratio and mass flow rate as a function of bypass inlet width
分析喷射器轴向压力分布和马赫数分布可知(见图6、7),当旁路进口宽度从1 mm增加至3 mm时,混合室内混合流体压力降低,速度增加,混合流体质量流量增加。当旁路进口宽度从3 mm增加至5 mm时,混合室内混合流体压力升高,速度降低,混合流体质量流量降低。同时,从图7可知,喷射器内马赫数在喷嘴出口附近大于1,喷射器处于亚临界状态,即工作流体质量流量不随旁路进口宽度的变化而变化,所以混合流体质量流量的变化主要是引射流体质量流量变化所致,这是该过程中引射系数先增加后减小的原因。
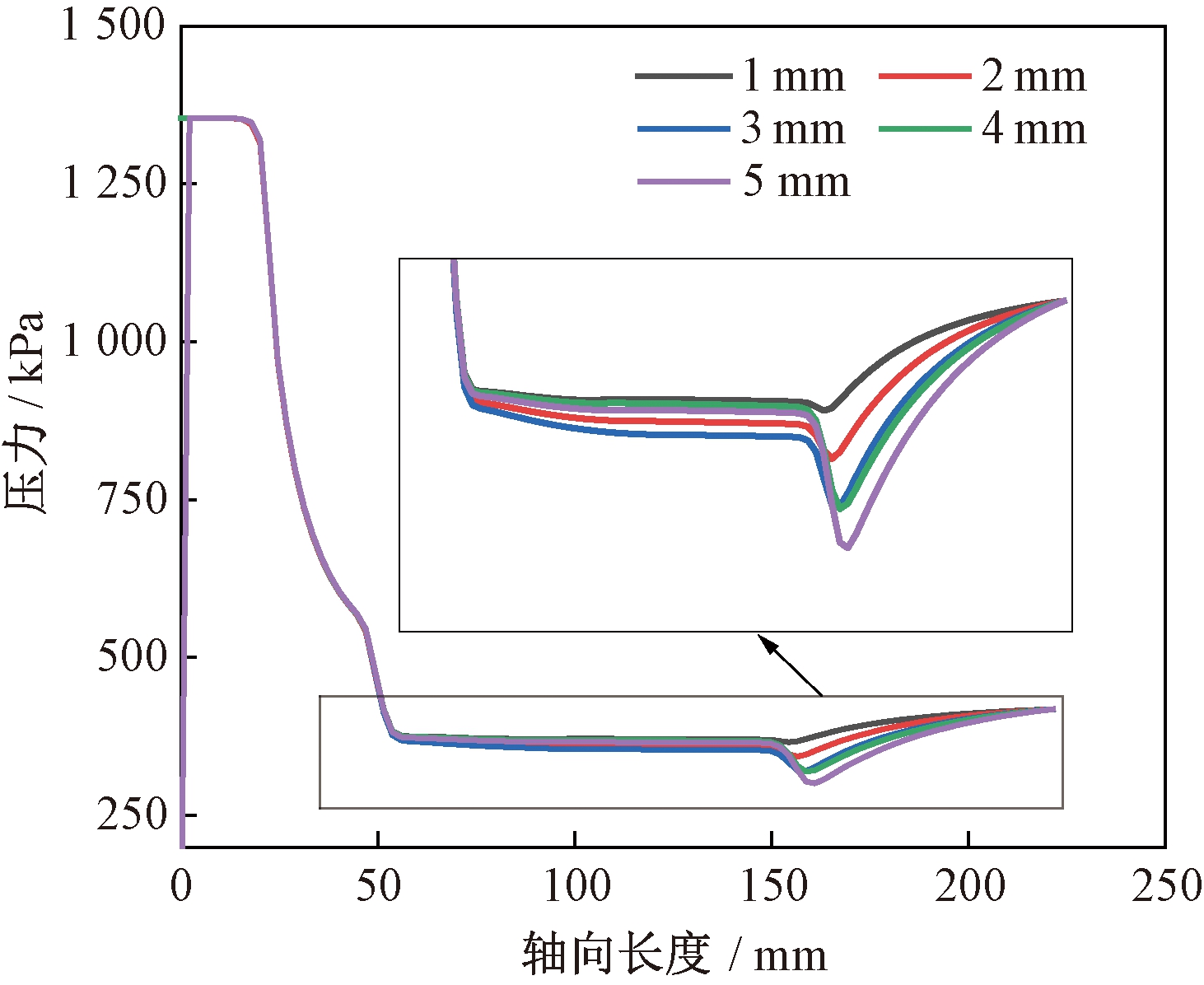
图6 旁路喷射器内轴向压力分布
Figure 6 Axis pressure distribution of bypass ejector
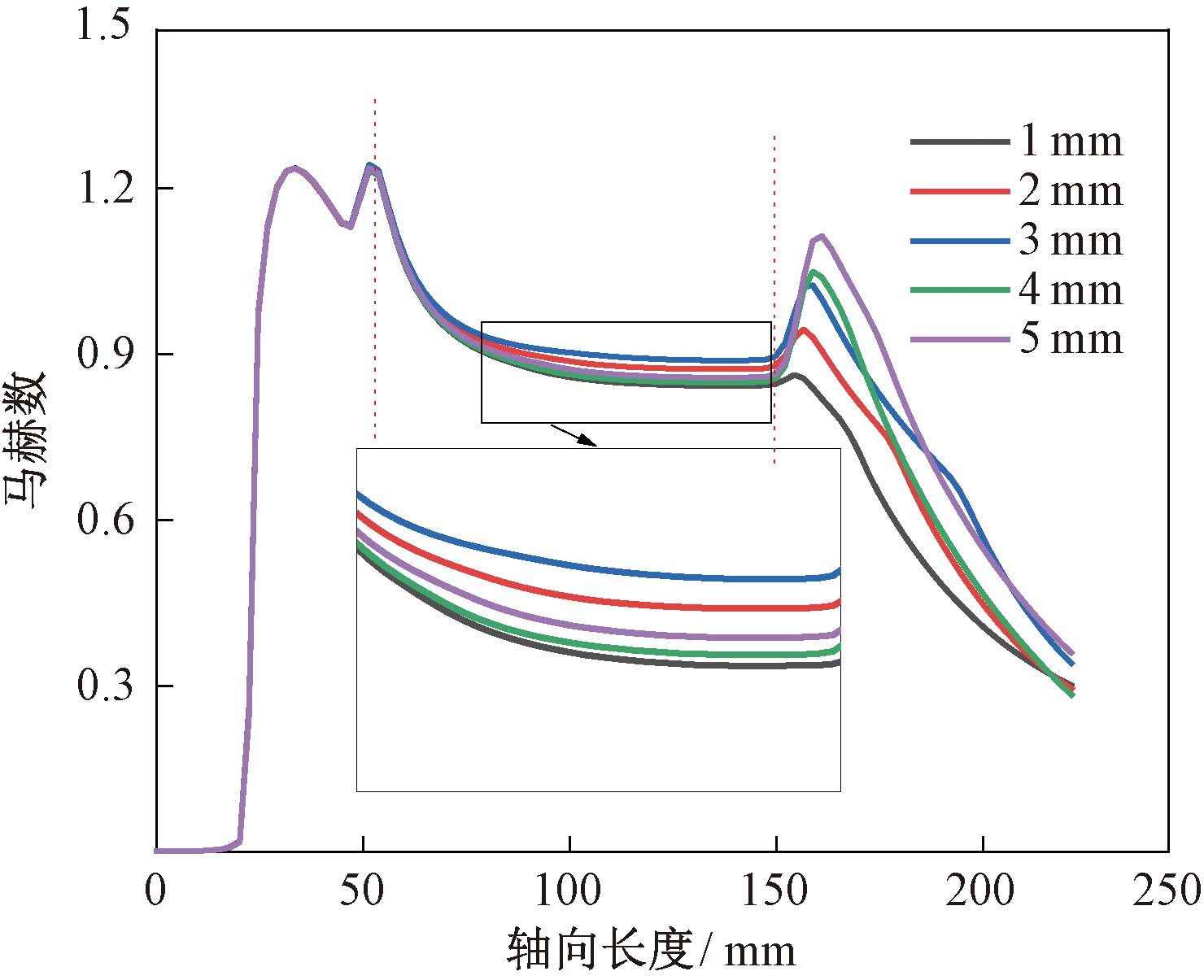
图7 旁路喷射器内轴向马赫数分布
Figure 7 Axis Mach number distribution of bypass ejector
2.3 旁路进口压力的影响
在最优旁路进口角度和宽度下,保持喷射器其他几何结构尺寸和工况参数不变,研究旁路进口压力对两相旁路喷射器引射系数和质量流量的影响。结果如图8所示。随着旁路进口压力的增加,工作流体质量流量不变,旁路进口流体质量流量增加,引射流体质量流量和喷射器引射系数都先增加后减小。当旁路进口压力为618.5 kPa时,喷射器的引射系数最大。其中,当旁路进口压力从468.5 kPa增加到618.5 kPa,引射系数从0.35增加到0.64,增加了82.9%。当旁路进口压力618.5 kPa增加到718.5 kPa,引射系射系数从0.64降低到0.44,降低了31.3%。
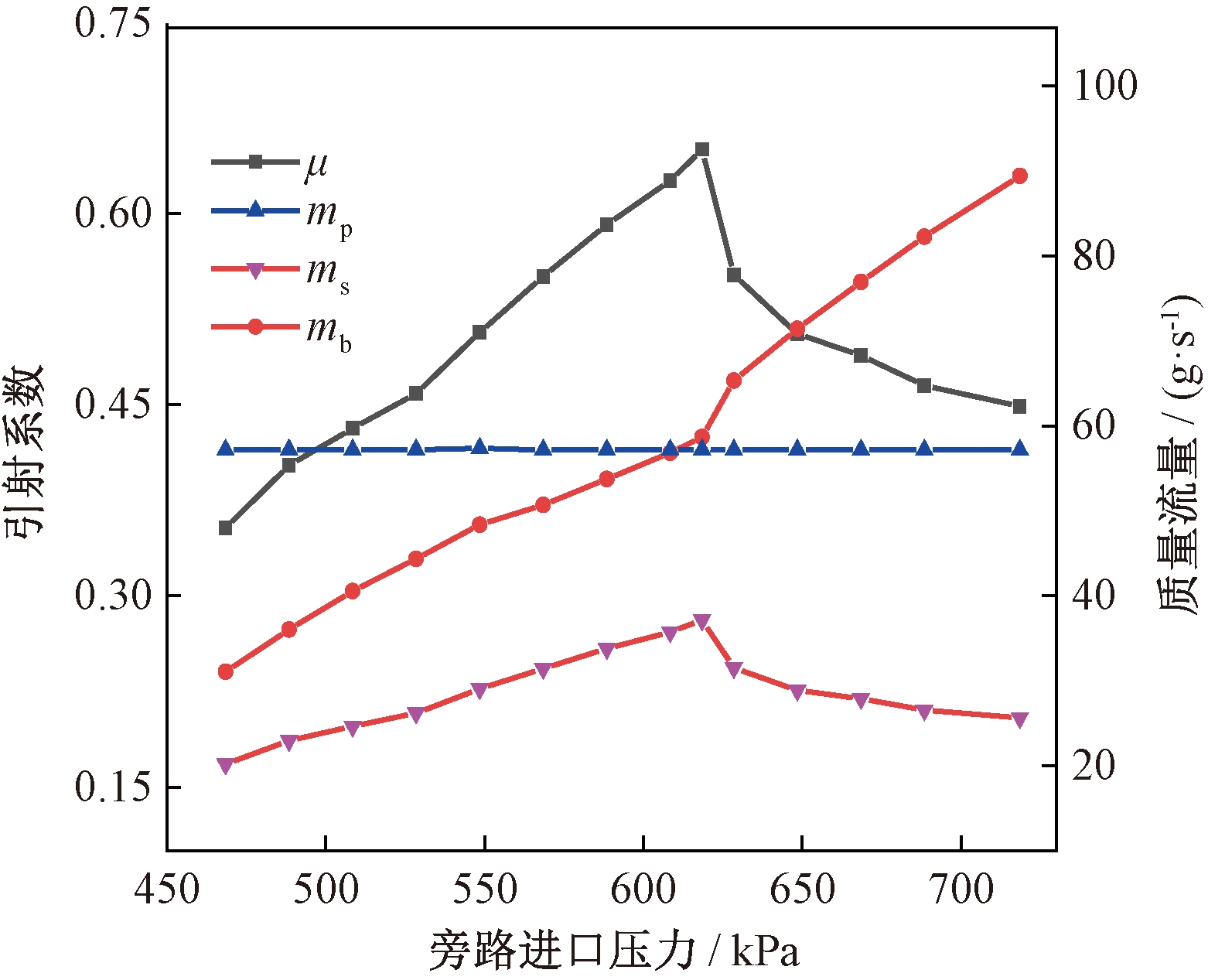
图8 旁路喷射器的引射系数和质量流量随旁路进口压力的变化
Figure 8 Profiles of entrainment ratio and mass flow rate as a function of bypass inlet pressure
2.4 旁路喷射器与传统喷射器的性能对比
保持喷射器其他结构参数和工况参数相同,改变喷嘴出口压力,将旁路喷射器与传统喷射器的性能进行对比,其中旁路喷射器的旁路进口角度、宽度和进口压力分别设置为15°、3 mm、618.5 kPa,结果见图9。两喷射器的质量流量和引射系数变化趋势相似,其中随着喷嘴出口压力增加,工作流体质量流量基本保持不变,引射流体质量流量和引射系数降低。相同出口压力下,与传统两相喷射器相比,旁路喷射器的引射系数提高了25.7%~56.8%,其中在较低出口压力下,旁路喷射器引射系数提高幅度更大。
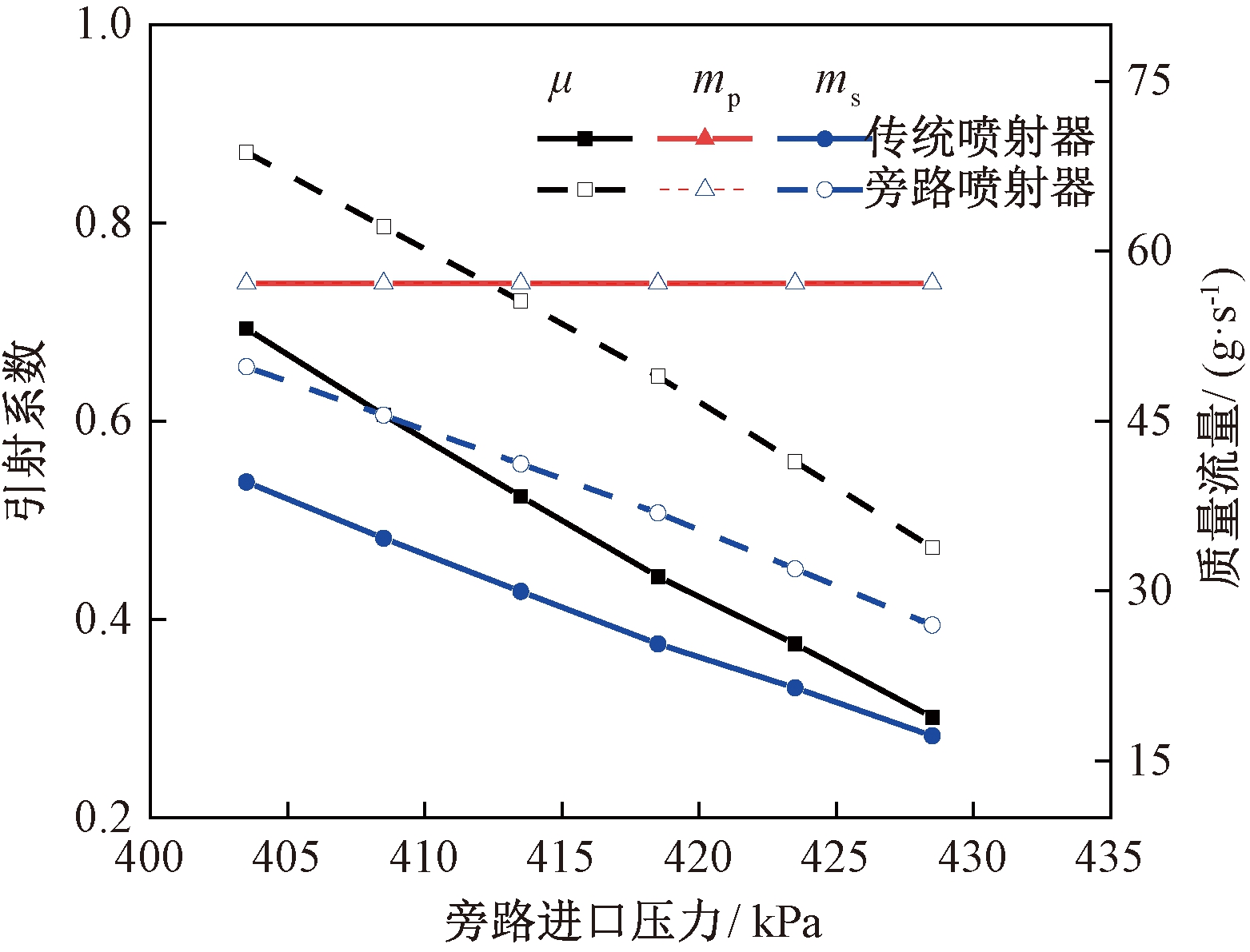
图9 旁路喷射器和传统喷射器引射系数随出口压力的变化
Figure 9 Entrainment ratio of bypass ejector and conventional ejector varies with outlet pressure
分析传统喷射器和旁路喷射器内轴向压力分布和马赫数分布(见图10、11)可知,出口压力相同时,传统喷射器和旁路喷射器的喷嘴内部压力和马赫数变化相同,在喷嘴出口处马赫数都大于1,说明两喷射器都处于亚临界状态。与传统喷射器相比,旁路喷射器在混合室内压力更低速度更高,混合室内流体质量流量更大,由于两喷射器工作流体质量流量基本相同,所以旁路喷射器引射流体质量流量较高,引射系数较大。
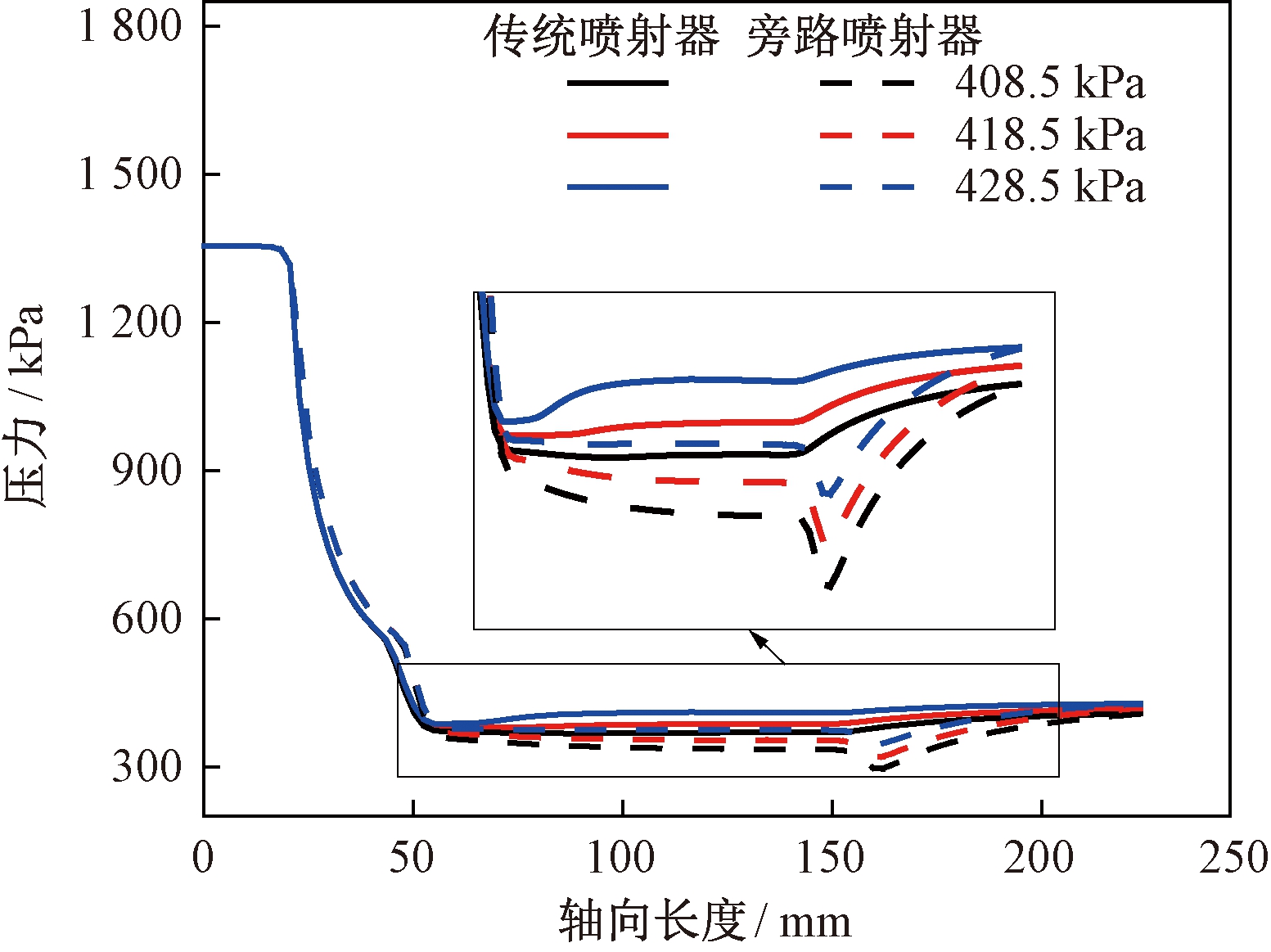
图10 旁路喷射器和传统喷射器轴向压力分布
Figure 10 Axis pressure distribution of bypass ejector and traditional ejector
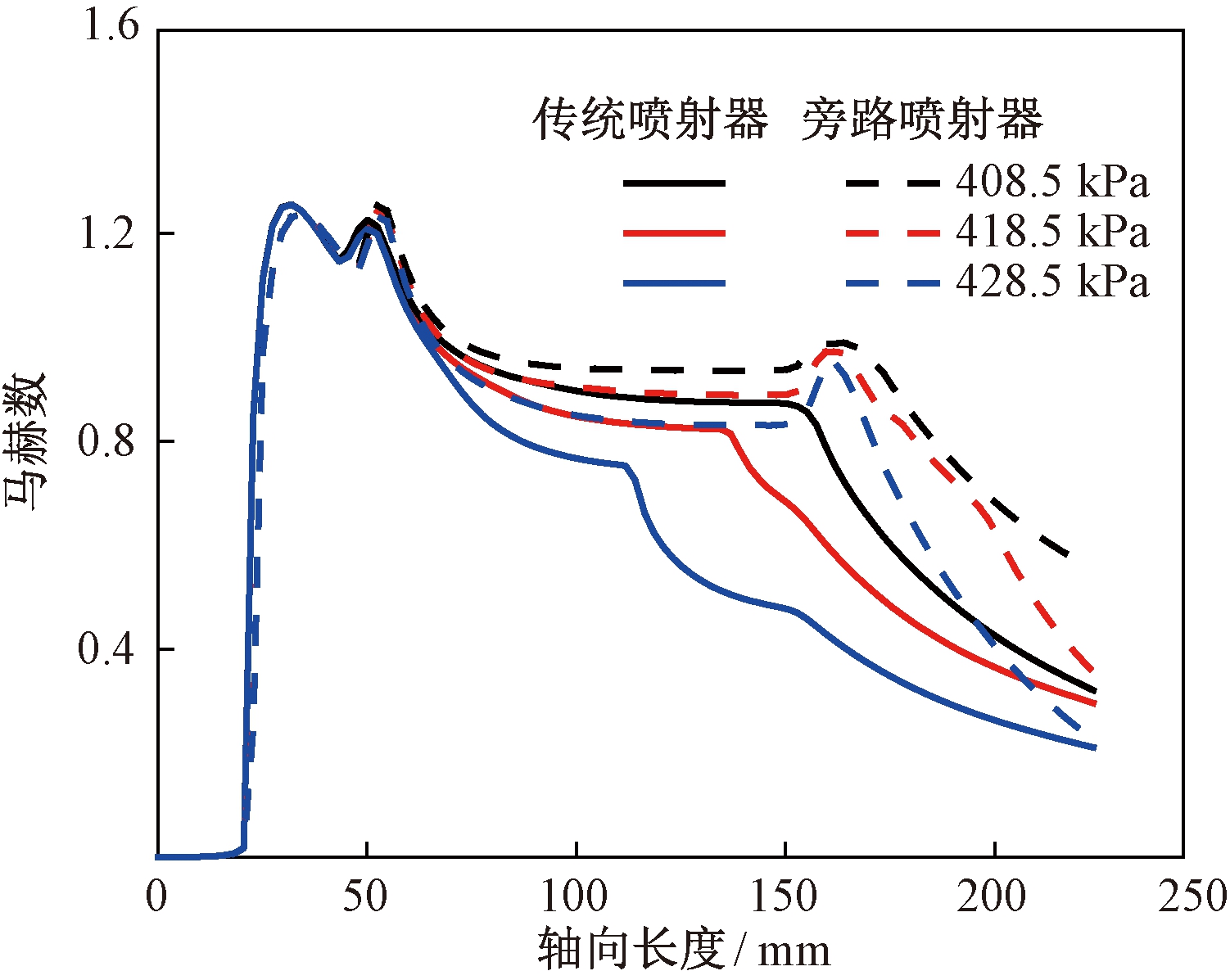
图11 旁路喷射器和传统喷射器轴向马赫数分布
Figure 11 Axial Mach number distribution for bypass ejector and traditional ejector
3 结论
(1)喷射器结构尺寸及工况条件固定时,引射系数随旁路进口角度、旁路进口宽度、旁路进口压力的增加先增加后减小。
(2)存在最优的旁路进口角度、进口宽度和最优旁路进口压力,使喷射器的引射效率最大。在本文的研究范围内,最优旁路进口角度为15°,进口宽度为3 mm,最优旁路进口压力为618.5 kPa。
(3)工况相同时,最佳旁路结构尺寸和旁路进口压力下,旁路喷射器的引射系数较传统喷射器提高了25.7%~56.8%。
[1] KEENAN J H, NEUMANN E P. A simple air ejector[J]. Journal of Applied Mechanics, 1942, 9(2): A75-A81.
[2] MUNDAY J T, BAGSTER D F. A new ejector theory applied to steam jet refrigeration[J]. Industrial &Engineering Chemistry Process Design and Development, 1977, 16(4): 442-449.
[3] HUANG B J, CHANG J M, WANG C P, et al. A 1-D analysis of ejector performance[J]. International Journal of Refrigeration, 1999, 22(5): 354-364.
[4] BARTA R B, DHILLON P, BRAUN J E, et al. Design and optimization strategy for ejectors applied in refrigeration cycles[J]. Applied Thermal Engineering, 2021, 189: 116682.
[5] FU W N, LIU Z L, LI Y X, et al. Numerical study for the influences of primary steam nozzle distance and mixing chamber throat diameter on steam ejector performance[J]. International Journal of Thermal Sciences, 2018, 132: 509-516.
[6] DONG J M, HU Q Y, YU M Q, et al. Numerical investigation on the influence of mixing chamber length on steam ejector performance[J]. Applied Thermal Engineering, 2020, 174: 115204.
[7] WU Y F, ZHAO H X, ZHANG C Q, et al. Optimization analysis of structure parameters of steam ejector based on CFD and orthogonal test[J]. Energy, 2018, 151: 79-93.
[8] ZHU Y H, WANG Z C, YANG Y P, et al. Flow visualization of supersonic two-phase transcritical flow of CO2 in an ejector of a refrigeration system[J]. International Journal of Refrigeration, 2017, 74: 354-361.
[9] LITTLE A B, GARIMELLA S. Shadowgraph visualization of condensing R134a flow through ejectors[J]. International Journal of Refrigeration, 2016, 68: 118-129.
[10] 史海路, 刘华东, 魏新利, 等. 喷嘴距对喷射器及双蒸发压缩/喷射制冷系统性能的影响研究[J]. 高校化学工程学报, 2019, 33(2): 321-328.
SHI H L, LIU H D, WEI X L, et al. Effects of nozzle exit position on the performance of ejector and bi-evaporator compression/ejection refrigeration system[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(2): 321-328.
[11] SRIVEERAKUL T, APHORNRATANA S, CHUNNANOND K. Performance prediction of steam ejector using computational fluid dynamics: part 2, flow structure of a steam ejector influenced by operating pressures and geometries[J]. International Journal of Thermal Sciences, 2007, 46(8): 823-833.
[12] RUANGTRAKOON N, THONGTIP T, APHORNRATANA S, et al. CFD simulation on the effect of primary nozzle geometries for a steam ejector in refrigeration cycle[J]. International Journal of Thermal Sciences, 2013, 63: 133-145.
[13] CHEN W X, CHEN H Q, SHI C Y, et al. A novel ejector with a bypass to enhance the performance[J]. Applied Thermal Engineering, 2016, 93: 939-946.
[14] CHEN W X, HUANG C X, CHONG D T, et al. Numerical assessment of ejector performance enhancement by means of combined adjustable-geometry and bypass methods[J]. Applied Thermal Engineering, 2019, 149: 950-959.
[15] TANG Y Z, LIU Z L, LI Y X, et al. Performance improvement of steam ejectors under designed parameters with auxiliary entrainment and structure optimization for high energy efficiency[J]. Energy Conversion and Ma-nagement, 2017, 153: 12-21.
[16] TANG Y Z, LIU Z L, SHI C, et al. A novel steam ejector with pressure regulation to optimize the entrained flow passage for performance improvement in MED-TVC desalination system[J]. Energy, 2018, 158: 305-316.
[17] BODYS J, SMOLKA J, BANASIAK K, et al. Performance improvement of the R744 two-phase ejector with an implemented suction nozzle bypass[J]. International Journal of Refrigeration, 2018, 90: 216-228.
[18] BODYS J, SMOLKA J, PALACZ M, et al. Experimental and numerical study on the R744 ejector with a suction nozzle bypass[J]. Applied Thermal Engineering, 2021, 194: 117015.
[19] 魏新利, 王中华, 耿利红, 等. 压缩制冷系统节流损失及应对方案研究[J]. 郑州大学学报(工学版), 2015, 36(3): 68-72.
WEI X L, WANG Z H, GENG L H, et al. Study on the throttling losses in CRS and solutions[J]. Journal of Zhengzhou University (Engineering Science), 2015, 36(3): 68-72.
[20] 耿利红. 双蒸发压缩/喷射制冷系统及两相喷射器的研究[D]. 郑州: 郑州大学, 2017.
GENG L H. Study on bi-evaporator compression/ejection refrigeration system and two-phase ejector[D]. Zhengzhou: Zhengzhou University, 2017.
[21] 孔珑. 流体力学[M]. 北京: 高等教育出版社, 2003.
KONG L.Hydromechanics[M]. Beijing: Higher Education Press, 2003.
[22] BARTOSIEWICZ Y, AIDOUN Z, MERCADIER Y. Numerical assessment of ejector operation for refrigeration applications based on CFD[J]. Applied Thermal Engineering, 2006, 26(5/6): 604-612.