目标跟踪是计算机视觉领域中的一个重要研究方向。运动目标跟踪算法按照工作原理可分为生成式方法和判别式方法,而相关滤波算法是一种判别式跟踪方法[1],它通过循环移位来产生训练样本,并在傅里叶域中进行计算,大大提高了算法效率,因此,得到了广泛研究。Bolme 等[2]提出最小输出平方和误差 (minimum output sum of squared error,MOSSE)算法,并首次引入相关滤波进行图像跟踪。Henriques等[3]提出循环结构内核 (circulant structure of tracking-by-detection with kernel,CSK)跟踪器,随后又改进了CSK跟踪器,提出了多通道特征的核相关滤波器(kernelized correlation filter,KCF)[4]。基于目标尺度变化问题,Danelljan等[5]提出快速区分尺度空间跟踪(fast discriminative scale space tracker,fDSST)算法,引入一种基于尺度金字塔的相关滤波器来检测尺度变化,实现相关滤波与尺度滤波相结合。
针对跟踪过程中的目标遮挡问题,目前大部分的改进侧重点在搜集更多目标特征,从而在跟踪中得到较大的目标响应。Li等[6]通过融合CN特征和HOG特征,提出尺度自适应多特征滤波算法(scale adaptive with multiple feature tracker,SAMF)。Bertinetto等[7]提出互补学习的跟踪方法Staple,通过2种互补特征因子颜色直方图和HOG特征进行融合。除此之外,还有一些其他针对目标遮挡问题的跟踪算法。Kalal等[8]提出跟踪学习检测算法(tracking learning detection,TLD),引入学习和检测概念,通过先验知识实现对目标的长期跟踪。陈丽萍等[9]通过在核相关滤波中加入高置信度判断以及重检机制来实现长时目标跟踪。潘振福等[10]将峰值旁瓣比作为跟踪目标检测的标准,在跟踪失败时通过目标检测器在图像中重新检测目标。上述方法虽然可以在一定程度上处理遮挡问题,但是仍然存在一些不足。第一,许多算法无法判断出目标遮挡的具体程度,并且采用固定的学习率不能自适应地更新模型。第二,在目标遮挡情况下,这些算法单纯依靠外观模型,忽略了目标的运动信息。
本文在KCF目标跟踪算法的框架基础上,提出一种抗遮挡的目标跟踪算法。首先,传统KCF算法缺少对跟踪结果的遮挡检测,为了评估跟踪结果的可靠性,算法引入响应的峰值旁瓣比来判断遮挡类型。其次,针对KCF算法采用固定学习率进行模型更新而导致跟踪漂移的问题,算法实现根据遮挡类型来自适应改变学习率参数。当目标被部分遮挡时,自适应降低目标模型更新的学习率,减少背景或者遮挡物对目标模型的影响;当严重遮挡发生时,停止目标模型的更新。最后,为了解决KCF算法在遮挡场景中丢失跟踪目标的问题,算法加入卡尔曼滤波(Kalman filter,KF)构建运动模型来预测严重遮挡下的目标位置。
1 核相关滤波算法原理
核相关滤波算法首先提取目标的样本特征;其次利用循环矩阵生成大量训练样本;再次通过高斯滤波器计算目标区域和待测区域的相关响应值,最大响应值位置即是目标中心;最后选择新目标区域的特征来更新目标模型。
KCF 算法以岭回归方式训练滤波器,假设训练样本为xi,其目的是寻找一个目标分类器f(xi)=wTxi,使得滤波器期望输出yi和训练样本xi之间的均方误差函数最小,即
(1)
式中:λ为正则化参数;w为分类器权重系数,w的最优解[4]为
w=(XTX+λI)-1XTy。
(2)
式中:X为数据矩阵;I为单位矩阵;y为期望目标回归矩阵。
利用循环矩阵和傅里叶变换性质,式(1)在频域中的解为
(3)
式中:⊙为元素的点积;
为x的离散傅里叶变换;
为的复共轭。
为了解决非线性问题,在岭回归方法中引入核函数k(x,z′)=〈φ(x),φ(z′)〉,则权重系数w在高维空间中表示为
其中φ(xi)是指将样本xi映射到高维空间。
找到w的最佳值等同于找到α的最佳值,其中α计算公式为
α=(K+λI)-1y。
(4)
式中:K为由Ki,j=k(xi,xj)组成的核矩阵。基于循环结构和快速傅里叶变换(FFT),矩阵α变换为
(5)
式中:kxx为核矩阵K第1行元素组成的向量。
输出响应计算公式为
(6)
式中:F-1为离散傅里叶逆变换;f(z)为输出响应值,其最大值就是待跟踪目标所在位置。
KCF目标跟踪算法采用线性插值并且以固定的学习率对模型进行更新,更新方式如下:
(7)
式中:γ为学习率;αt、xt和αt-1、xt-1分别表示第t帧和第t-1帧的参数和目标模板。
在KCF目标跟踪算法的更新公式(7)中,学习率γ是一个固定值,但是当目标遇到遮挡时,若仍然按照固定的学习率γ对模型进行更新,就会学习到遮挡物特征,导致在后续跟踪过程中将此遮挡物作为跟踪目标,造成跟踪失败。为了解决这个问题,本文在KCF跟踪的框架基础上引入了遮挡判断机制、模型自适应更新策略以及遮挡情况下的卡尔曼滤波预测估计。
2 改进的核相关滤波算法
原有的核相关滤波算法不能适应目标尺度变化,当目标尺度发生变化时,滤波器在更新时会引入更多的背景信息。为了能够实现自适应尺度变化,原算法引入Danelljan等[5]提出的尺度估计方法。本文的遮挡处理框架由遮挡检测方法、KCF基本跟踪器和卡尔曼滤波预测模块组成。由遮挡检测方法确定遮挡类型。在非遮挡和部分遮挡的情况下,KCF基本跟踪器使用目标可见部分的外观信息来估计目标位置;在严重遮挡情况下,运行卡尔曼滤波预测模块,使用目标的运动模型来预测目标位置。算法流程如图1所示。
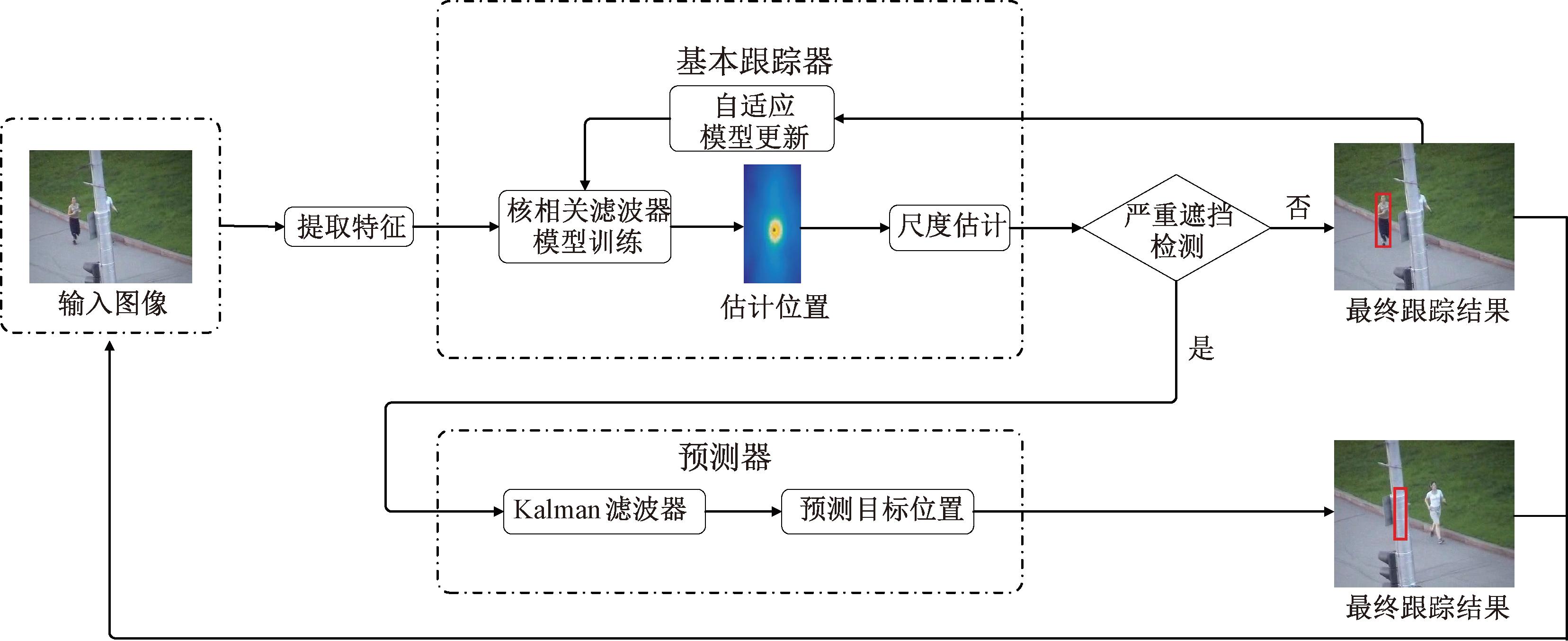
图1 基于改进的核相关滤波目标跟踪算法流程
Figure 1 Process of target tracking algorithm based on improved kernel correlation filtering
2.1 遮挡检测方法
当遮挡情况发生时,遮挡检测方法在基本跟踪器和预测系统中起着重要作用。基本跟踪器借助物体的外观模型来实现跟踪,而预测系统借助物体的运动模型来估计目标位置[11]。在MOSSE跟踪器中[2],响应的峰值旁瓣比 PSR可以用来评估目标跟踪状态以及受遮挡的程度。在本文中引入了PSR作为跟踪质量评估的标准,第t帧PSR为
(8)
式中:max(ft(z))为第t帧响应的峰值;μt和δt分别为第t帧响应的平均值和标准偏差。
在正常条件下跟踪目标时,每帧的PSR通常在20～60。当严重遮挡发生时,PSR下降到7以下,基于PSR范围获得固定阈值以估计遮挡状态[12]。但是并不是所有序列的PSR都在20～60,当目标快速移动或者具有低分辨率时,其PSR保持在低值。因此采用固定阈值来估计目标遮挡状态是不合理的。
在本文中,与单独在一帧中考虑PSR不同,假设在前几帧不发生遮挡的情况下,将前N帧PSR的平均值μ作为遮挡检测的标准(在本文中设置N=10),分别定义0.25μ和0.75μ为低阈值TL和高阈值TH,μ和当前帧的PSR差值为d。当d<TL时,当前帧中没有遮挡,此时μ根据当前帧中的PSR值进行更新,运行基本跟踪器;当TL≤d≤TH时,目标处于部分遮挡状态,运行基本跟踪器,并使用2.2节提出的方法更新目标外观模型;当d>TH时,目标被严重遮挡,停止更新模型,通过预测器来估计目标位置。
在前几帧没有被遮挡的情况下,所选模板和搜索窗口之间的相关性较高,所以前几帧上的PSR具有最大值。当目标完全没有被遮挡时,需要更新μ,所以μ是所有帧中的最大值,即PSRt≤μ。这一条件将体现在2.2节的模型自适应更新上。
2.2 自适应模型更新
在KCF算法中,目标模型的学习率是固定值。当目标被遮挡时,模型中的遮挡信息会被更新,导致跟踪失败[12]。本文使用自适应学习率代替固定学习率来更新外观模型:
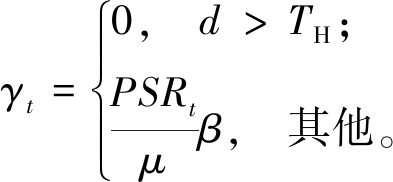
(9)
式中:学习率参数γt根据式(8)中计算的PSRt自适应地改变;β为一个常数,通常设置为0.025,可以提高目标跟踪性能[5]。
当目标被严重遮挡时,学习参数设置为0;否则,自适应更新外观模型。根据2.1节描述,在所有帧中PSRt≤μ,即
所以在目标被部分遮挡情况下,γt<β;当目标没有被遮挡时,PSRt≈μ,γt≈β。
2.3 卡尔曼滤波预测跟踪算法
KCF目标跟踪算法基于目标在上一帧中所处位置的特征相似性来搜索目标在当前帧中的位置,没有利用目标的运动信息,并过分依赖特征最大响应值来确定目标位置[13]。而KF对运动目标具有良好的运动约束,可以有效地减少跟踪失败[13]。因此,基于KCF跟踪框架,可以将KF视为运动信息的补充,KF通过对目标状态的测量和预测来估计其当前状态。跟踪目标的运动状态方程为
xk=Fkxk-1+wk;
(10)
yk=Hkxk+vk。
(11)
式中:xk和yk分别为k时刻的目标状态向量和观测向量,
和y代表目标中心位置的横纵坐标,dx和dy分别代表运动目标水平和竖直方向的速度;Fk为状态矩阵;Hk为观测矩阵;wk为过程噪声;vk为观测噪声。wk和vk为均值为0、协方差分别为Qk和Rk的高斯白噪声。Fk和Hk分别定义为
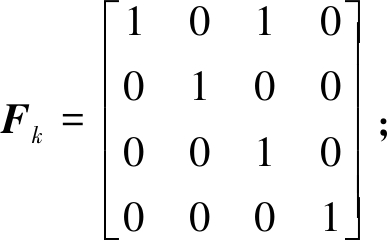
(12)
(13)
KF算法可分为2个步骤:预测步骤和更新步骤。
预测步骤为
(14)
(15)
式中:
表示在k时刻预测的目标状态向量;Pk|k-1表示k时刻状态预估计的协方差矩阵。
更新步骤为
(16)
(17)
Pk|k=(I-KkHk)Pk|k-1。
(18)
式中:Kk为卡尔曼增益;
为k时刻估计的目标状态向量;Pk|k为k时刻状态预估计的协方差矩阵。过程噪声的Qk值较大,设Qk=0.1I,I为4×4的单位矩阵,而观测噪声的Rk值较小,设Rk=10-6I,I为2×2的单位矩阵[14]。
2.4 算法步骤
步骤1 根据第1帧中的目标信息,完成核相关滤波器及其相关参数的初始化。
步骤2 在待检测图像区域中提取目标HOG特征,根据式(6)得到目标位置PtKCF。
步骤3 使用Danelljan等[5]提出的方法估计目标的尺度,根据式(8)计算响应的PSRt值。
步骤4 根据前N帧的PSR值计算μ,分别计算出TH和TL;并通过前N帧的目标位置来初始化卡尔曼滤波器。
步骤5 根据式(8)计算t←N+1帧的PSRt的值,并计算d。①若目标未被遮挡,即d<TL,重复步骤2和步骤3,并以当前帧的PSRt的值更新μPSR;②若目标被部分遮挡,即TL≤d≤TH,重复步骤2和步骤3,根据式(9)更新学习率,根据式(7)更新KCF外观模型;③若目标被严重遮挡,即d>TH,停止更新KCF模型,利用卡尔曼滤波器预测目标,根据式(17)得到预测位置PtKF,并根据式(16)～(18)更新卡尔曼滤波器。
步骤6 设置t←t+1,重复步骤5,直至视频序列结束。
3 实验结果与分析
3.1 环境设置
为了评估本文算法,实验均在Intel(R)Core(TM)i5-1135G7,主频2.4 GHz,内存16 GB的计算机上进行验证,采用MATLAB R2018b作为实验仿真平台。在OTB-2013数据集[15]上采用一次通过评估对跟踪器进行评估,使用基于中心位置误差的距离精度和基于重叠率的成功率作为跟踪器的评估标准。距离精度DP表示中心位置误差低于某个阈值的正确跟踪帧数百分比。重叠成功率OS表示边界框重叠率超过一定阈值的帧数百分比,使用曲线下面积AUC来衡量跟踪器性能。帧率FPS表示视频总帧数与所消耗时间的比值。在实验中,选择20像素为精度阈值,0.5为重叠阈值。
本文算法的参数设置与KCF算法一致,使用4×4的单元大小提取HOG特征,直方图方向为9,采样窗口大小为最初区域的1.5倍,正则化参数λ=10-4,高斯核带宽σ=0.5。尺度相关滤波器参数设置与DSST算法[5]一致,如2.2节设置β为0.025。
3.2 跟踪性能分析
为了验证本文算法的有效性,选取OTB-2013数据集中的36组彩色视频序列进行测试,并将本文KCF-KF算法与SAMF[6]、STAPLE[7]、KCF[4]、TLD[8]4种经典目标跟踪算法进行比较。表1为5种算法的性能指标,KCF-KF算法的距离精度和重叠成功率分别为0.796和0.692,均为最佳值。KCF-KF算法的帧率为31.2帧/s,虽然算法速度有所下降,但仍然满足实时性要求。图2为 KCF-KF算法与其他4种传统算法的精度和成功率曲线对比图。
表1 5种跟踪算法的性能指标
Table 1 Performance metrics of five tracking algorithms
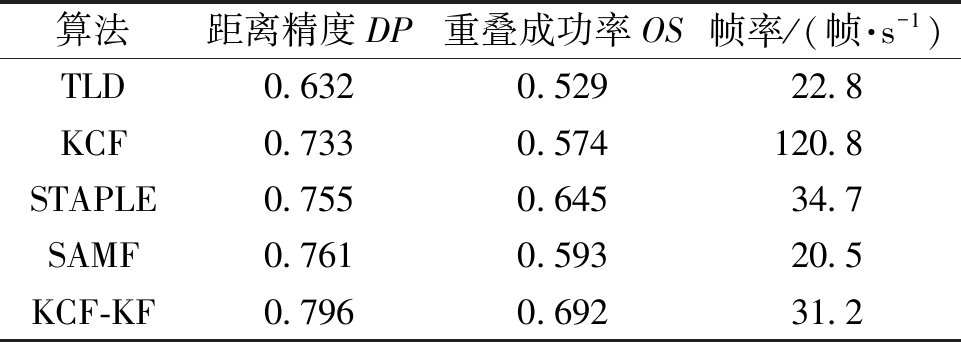
算法距离精度DP重叠成功率OS帧率/(帧·s-1)TLD0.6320.52922.8KCF 0.7330.574120.8STAPLE0.7550.64534.7SAMF0.7610.59320.5KCF-KF0.7960.69231.2
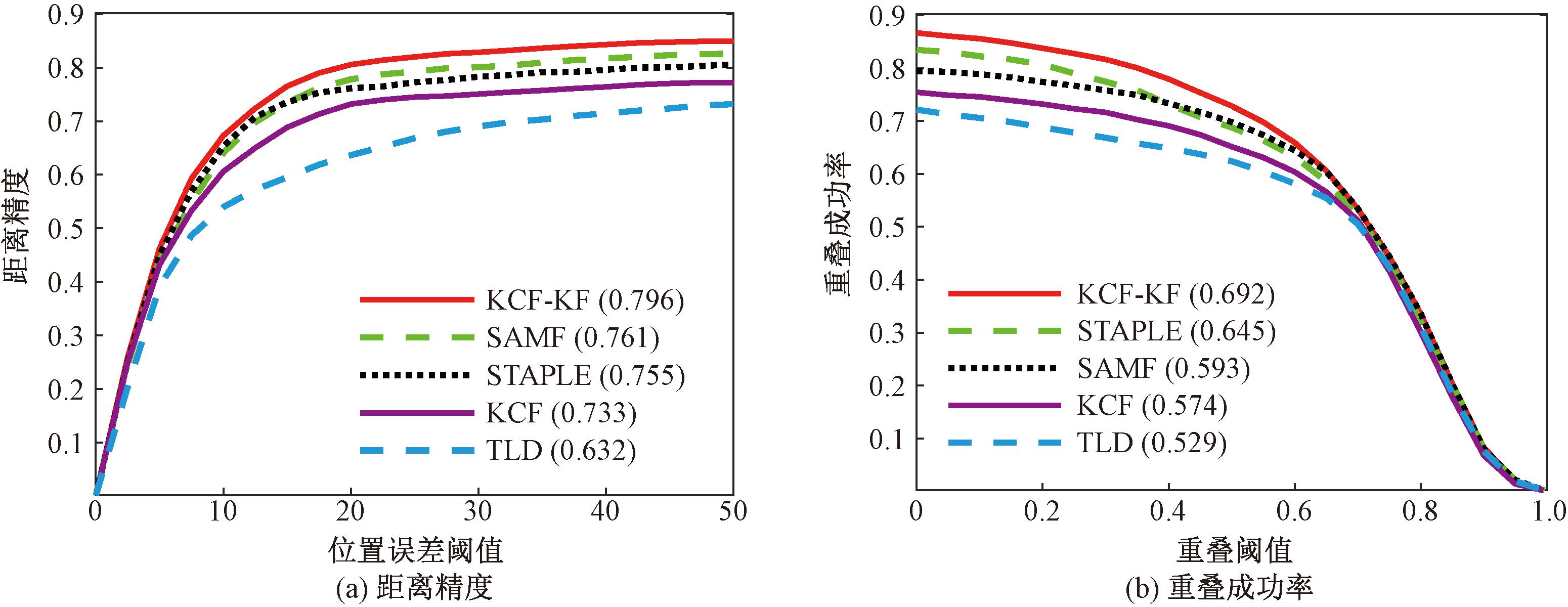
图2 不同跟踪算法的精度曲线和成功率曲线
Figure 2 Accuracy curve and success rate curve of different tracking algorithms
为了更直观地展示KCF-KF算法在遮挡情况下的跟踪性能,选取jogging1、lemming、soccer、tiger1、woman 5组具有遮挡属性的视频序列,将KCF-KF算法与SAMF、Staple、KCF、TLD 4种算法进行实验对比,跟踪结果如图3所示。在jogging1视频序列中,面临的主要挑战为遮挡。当目标在第72帧被严重遮挡后,KCF、SAMF、STAPLE 3种算法均存在跟踪漂移,TLD算法通过在线检测机制,可以在第98帧目标变得完全可见后重新定位目标。KCF-KF算法中由于加入卡尔曼滤波来预测目标位置,可以在目标被严重遮挡的帧中,通过估计目标位置达到准确跟踪。在lemming视频序列中,运动目标在左右快速移动时被遮挡,第337帧被严重遮挡。当目标离开遮挡区域后,KCF、SAMF、Staple、TLD 4种算法均丢失了目标,只有KCF-KF算法在第396帧准确跟踪目标。在soccer视频序列中,背景复杂且目标颜色与背景颜色相似,在跟踪过程中容易学习到太多的背景信息。从图3(c)的结果中可以看到,相比于其他4种算法,只有KCF-KF算法能够有效跟踪目标。在tiger1视频序列中,目标经历遮挡、光照变化和尺度变化等干扰。SAMF算法、STAPLE算法和KCF-KF算法都能够跟踪目标,但从图3(d)的跟踪结果看出,KCF-KF算法对目标位置的估计更加准确。在woman视频序列中,目标从第565帧被长时间遮挡,KCF-KF算法在模型更新模块实现了学习率自适应,能够优化更新模型,从图3(e)中可以看出,KCF-KF算法跟踪效果最好。综合几种算法在具有遮挡属性视频序列上的跟踪效果,KCF-KF算法能够解决目标被遮挡时跟踪失败的问题,性能最佳。
图3 不同算法在遮挡视频序列上的跟踪结果
Figure 3 Tracking results of different algorithms on occluded video sequences
4 结论
本文在传统KCF算法的基础上,对其抗遮挡能力不足的问题进行改进,实现了一种核相关滤波和卡尔曼滤波预测结合的抗遮挡图像目标跟踪方法。算法通过遮挡判别模块判断目标的遮挡状态,并对模型更新机制进行了优化,能够自适应更新模型的学习率。此外,还增加了一个卡尔曼滤波预测模块,当目标被严重遮挡时,使用位置预测模块来定位目标。相比于传统跟踪算法,所提算法在抗遮挡方面具有更好的性能。在未来的工作中,可将研究重点放在提取更丰富的目标特征上,进一步完善算法的性能。
[1] 孟晓燕, 段建民. 基于相关滤波的目标跟踪算法研究综述[J]. 北京工业大学学报, 2020, 46(12): 1393-1416.
MENG X Y, DUAN J M. Advances in correlation filter-based object tracking algorithms:a review[J].Journal of Beijing University of Technology,2020,46(12):1393-1416.
[2] BOLME D S, BEVERIDGE J R, DRAPER B A, et al. Visual object tracking using adaptive correlation filters[C]∥2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE,2010:2544-2550.
[3] HENRIQUES J F, CASEIRO R, MARTINS P, et al. Exploiting the circulant structure of tracking-by-detection with kernels[C]∥Proceedings of the 12th European Conference on Computer Vision. New York: ACM, 2012: 702-715.
[4] HENRIQUES J F, CASEIRO R, MARTINS P, et al. High-speed tracking with kernelized correlation filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596.
[5] DANELLJAN M, H
GER G, KHAN F S, et al. Discriminative scale space tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(8): 1561-1575.
[6] LI Y, ZHU J K. A scale adaptive kernel correlation filter tracker with feature integration[C]∥Computer Vision-ECCV 2014 Workshops. Cham: Springer, 2015: 254-265.
[7] BERTINETTO L, VALMADRE J, GOLODETZ S, et al. Staple: complementary learners for real-time tracking[C]∥2016 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway:IEEE,2016:1401-1409.
[8] KALAL Z, MIKOLAJCZYK K, MATAS J. Tracking-learning-detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(7): 1409-1422.
[9] 陈丽萍, 王铭羽, 杨文柱, 等. 基于改进核相关滤波的长时目标跟踪算法[J]. 郑州大学学报(工学版), 2020, 41(3): 32-36.
CHEN L P, WANG M Y, YANG W Z, et al. An improved kernelized correlation filter for long-term target tracking[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(3): 32-36.
[10] 潘振福, 朱永利. 使用PSR重检测改进的核相关目标跟踪方法[J]. 计算机工程与应用, 2017, 53(12): 196-202.
PAN Z F, ZHU Y L. Improvement for tracker with kernelized correlation filters with PSR redetection[J]. Computer Engineering and Applications, 2017, 53(12): 196-202.
[11] CHEN H, ZHANG W G, YAN D H. Robust visual tracking with reliable object information and Kalman filter[J]. Sensors (Basel), 2021, 21(3): 889.
[12] YUAN Y, CHU J, LENG L, et al. A scale-adaptive object-tracking algorithm with occlusion detection[J]. EURASIP Journal on Image and Video Processing, 2020, 2020(1): 7.
[13] LI F Q, DONG E Z, YANG S. An improved object tracking algorithm combining LCT kernel correlation filtering and Kalman prediction[C]∥2021 China Automation Congress (CAC). Piscataway: IEEE, 2021:877-882.
[14] 刘耀胜,廖育荣,林存宝,等.基于特征融合与抗遮挡的卫星视频目标跟踪方法[J].北京航空航天大学学报,2022,48(12):2537-2547.
LIU Y S,LIAO Y R,LIN C B, et al. Feature-fusion and anti-occlusion based target tracking method for satellite videos[J].Journal of Beijing University of Aeronautics and Astronautics,2022,48(12):2537-2547.
[15] WU Y, LIM J, YANG M H. Online object tracking: a benchmark[C]∥2013 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway:IEEE, 2013:2411-2418.