连续倒塌指偶然荷载作用下,初始局部破坏沿构件传递导致结构发生整体倒塌或是与初始破坏不成比例的大规模倒塌。1968年Roman Point公寓倒塌首次引起工程界对连续倒塌的关注。近年来也发生了多起RC框架结构的倒塌,如1995年美国默拉联邦政府办公楼遭遇爆炸袭击,导致框架底部中柱破坏进而造成倒塌[1]。
国内外学者对RC框架结构连续倒塌下的受力机制进行了深入研究。Su等[2]通过轴向约束的梁柱子结构倒塌试验得出压拱效应可显著提高结构的弯曲承载力。何庆锋等[3]探究了结构在倒塌大变形下的悬索机制,提出承载力的简化计算方法。Lim等[4]进一步讨论了轴向约束以及转动约束对悬链效应的影响。Yu等[5]研究了跨高比、梁配筋率对压拱与悬链承载力的影响。陈伟宏等[6]分析了失效柱的楼层位置及梁配筋率对平面框架抗倒塌性能的影响。
工程中常需要考虑框架的空间作用。Qian等[7]通过空间“十”字形框架中柱移除试验,指出当考虑结构空间效应时,抗倒塌承载力提高近1倍。Rashidian等[8]将平面框架扩展为“T”字型空间框架以探究横向梁的作用,结果表明,横向梁只承受弯曲作用,不能发挥压拱机制及悬链机制作用。Lim等[9]通过空间框架连续倒塌试验显示:由于横向梁的作用,纵向两跨梁发生了扭转变形与平面外位移,但加载柱头产生的扭转作用并不会对结构的承载力产生影响。张望喜等[10]在空间子结构试验中也发现底筋未断裂一侧的梁在悬链阶段出现明显扭转裂缝,但在其对装配整体式结构倒塌分析中[11]得出:空间框架结构的抗倒塌承载力小于平面框架结构与横向梁的叠加,扭转产生了不利效应,这与Lim等[9]的结论有所不同。
由前述研究可知,考虑横向梁扭转作用的RC框架抗连续倒塌性能的研究还较为匮乏,且不同学者[9,11]得出的结论也不一致,故而扭转对RC框架连续倒塌的影响机制有待进一步研究。鉴于此,本文采用有限元软件LS-DYNA建立RC框架精细化模型,在对混凝土构件受扭试验以及框架连续倒塌试验模型验证的基础上,分别研究平衡扭转及协调扭转作用下RC框架结构抗连续倒塌的受力性能。
1 模型建立与验证
1.1 单元类型
混凝土采用缩减积分的8节点实体单元(SOLID164),该单元内部只有一个积分点,相比于全积分单元能够提高计算效率,但会造成单元的一种零能模式,也就是沙漏模态,因此需设置合适的沙漏系数来保证计算结果的可靠性,取值依据为沙漏能小于结构总内能的10%。根据Weng等[12]的数值模拟,积分方式采用Flanagan-Belytschko刚度形式,沙漏系数取0.002。钢筋采用2×2高斯积分形式的2节点Hughes-Liu单元(BEAM161)。
根据Qian等[13]的有限元分析,将钢筋内置于混凝土中使其具有较好的模拟精度。传统的钢筋与混凝土共节点法的建模方式较为复杂,采用耦合法能够更高效地将钢筋嵌入混凝土中,通过设置关键字*CONSTRAINED_LAGRANGE_IN_SOLID实现模拟。
1.2 材料本构模型
混凝土性能模拟采用连续面帽盖模型(CSCM),该模型能够有效地模拟低围压下混凝土的力学性能,如损伤演化、剪切膨胀、剪切压实、约束效应以及应变率效应[14],因而被广泛应用于倒塌模拟。CSCM的屈服面由剪切破坏面和硬化帽盖面组成,如图1(a)所示。LS-DYNA提供了2种CSCM模型:简化的3参数模型(*MAT_CSCM_CONCRETE)以及自定义参数模型(*MAT_CSCM)。简化的CSCM模型只需输入无侧限抗压强度fc、最大骨料粒径Ag以及单位。采用简化的3参数CSCM模型会使得模拟承载力高于实验值,特别是RC梁受扭试件,因此本文采用全参数的自定义CSCM模型。根据材料本构模型开发者的建议,当模拟值偏大时,可以将混凝土的受拉断裂能Gft降至默认值的80%[15]。由于RC梁在受扭过程中剪切破坏明显,框架在连续倒塌中梁端截面处剪力也很大,将混凝土剪切断裂能Gfs取为受拉断裂能的50%(默认情况下Gfs=Gft)[16]。
材料模型如图1所示。钢筋采用塑性随动硬化模型(*MAT_PLASTIC_KINEMATIC),该模型应力-应变关系如图1(b)所示。加载所用钢板以及支座处垫块均采用弹性材料进行模拟。
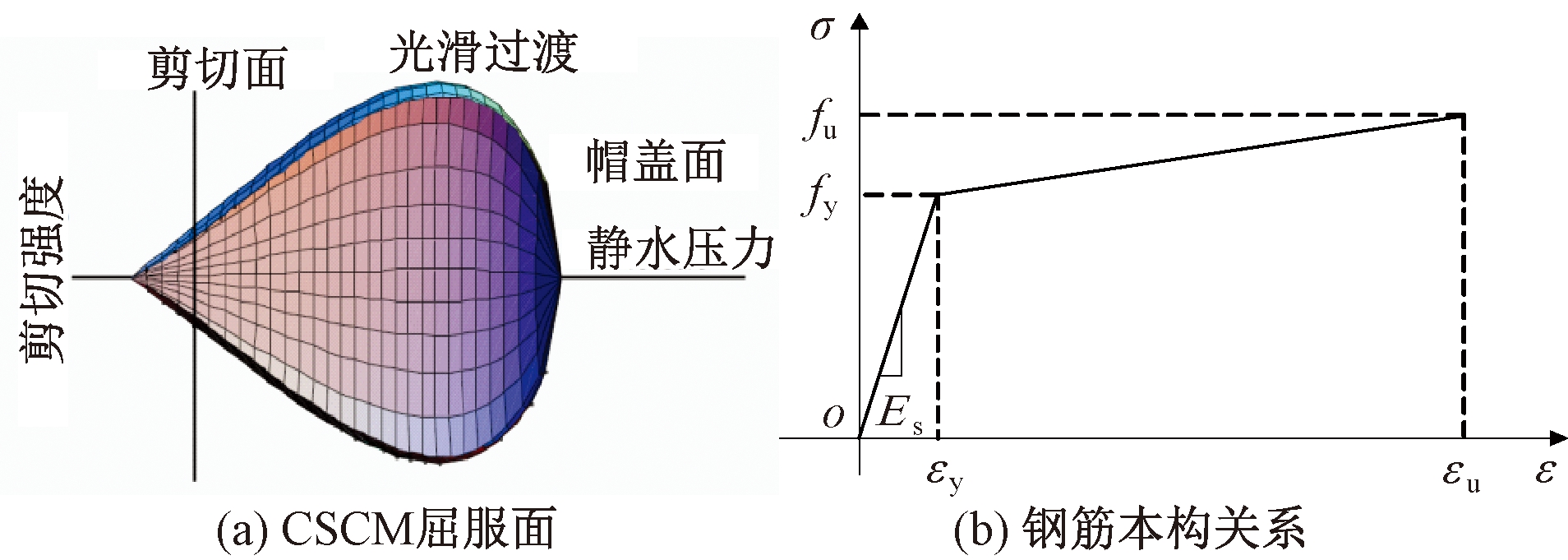
图1 材料模型
Figure 1 Material models
1.3 单元删除准则
连续倒塌分析需要考虑结构在大变形下的受力特点,因此定义合适的单元删除准则可以避免单元畸变。RC结构在移除柱时,破坏形态为压拱阶段梁端垂直裂缝的开展以及悬链阶段沿梁整个跨度上裂缝的发展,故采用最大主应变作为混凝土单元的删除准则。根据Pham等[16]的数值分析,取失效时的最大主应变为0.1。钢筋单元在达到极限应变时自动删除,模型验证中钢筋的极限应变取试验实测值。
1.4 模型验证
分别选取梁受扭试件A095c、B080a、B110a[17]及连续倒塌试件B3[18]、RC-H[10]进行模型验证,B080a、B3、RC-H试件的几何尺寸及配筋如图2所示。受扭试件扭矩-转角曲线模拟结果与试验对比如图3所示。模型能够较好地模拟梁开裂与破坏,峰值扭矩与转角吻合良好。连续倒塌构件的模拟结果对比如图4所示。压拱承载力与悬链承载力吻合度均较好,钢筋的断裂位置也与试验保持一致。说明本文建模合理、计算准确。
2 结构设计与建立
根据中国规范的要求设计一栋6层框架,平面设计为4×4跨,跨度均为6 m,层高均为3.6 m,抗震设防烈度为7度(0.15g),场地类别为Ⅱ类,地震设计分组为第1组。楼面和屋面的恒荷载为5.0 kN/m2,活荷载为2.0 kN/m2。混凝土采用C40,钢筋采用HRB400。选取底层外围梁柱子结构为分析模型,由于模型左右对称,图5给出了半边结构的几何尺寸及配筋。
3 扭转作用下RC平面框架抗倒塌分析
为了探究扭转对RC平面框架抗连续倒塌性能的影响,首先在失效的中柱柱头上施加一扭矩T,而后对结构进行竖向位移加载,扭矩在竖向位移加载过程中保持恒定,模型细节如图6所示。施加的扭矩值分别为梁跨中截面受扭承载力的40%、80%、120%、160%(实际分配到单跨梁上的扭矩为梁抗扭承载力的20%、40%、60%、80%),研究不同扭矩对结构抗倒塌性能的影响。值得注意的是,扭矩的存在会使柱头发生转动,此时在柱顶施加竖向荷载将产生附加扭矩,附加扭矩随着竖向荷载的增加而增大。因此,为保证加载过程中扭矩的恒定,在中柱节点的中心处施加扭矩与竖向位移。
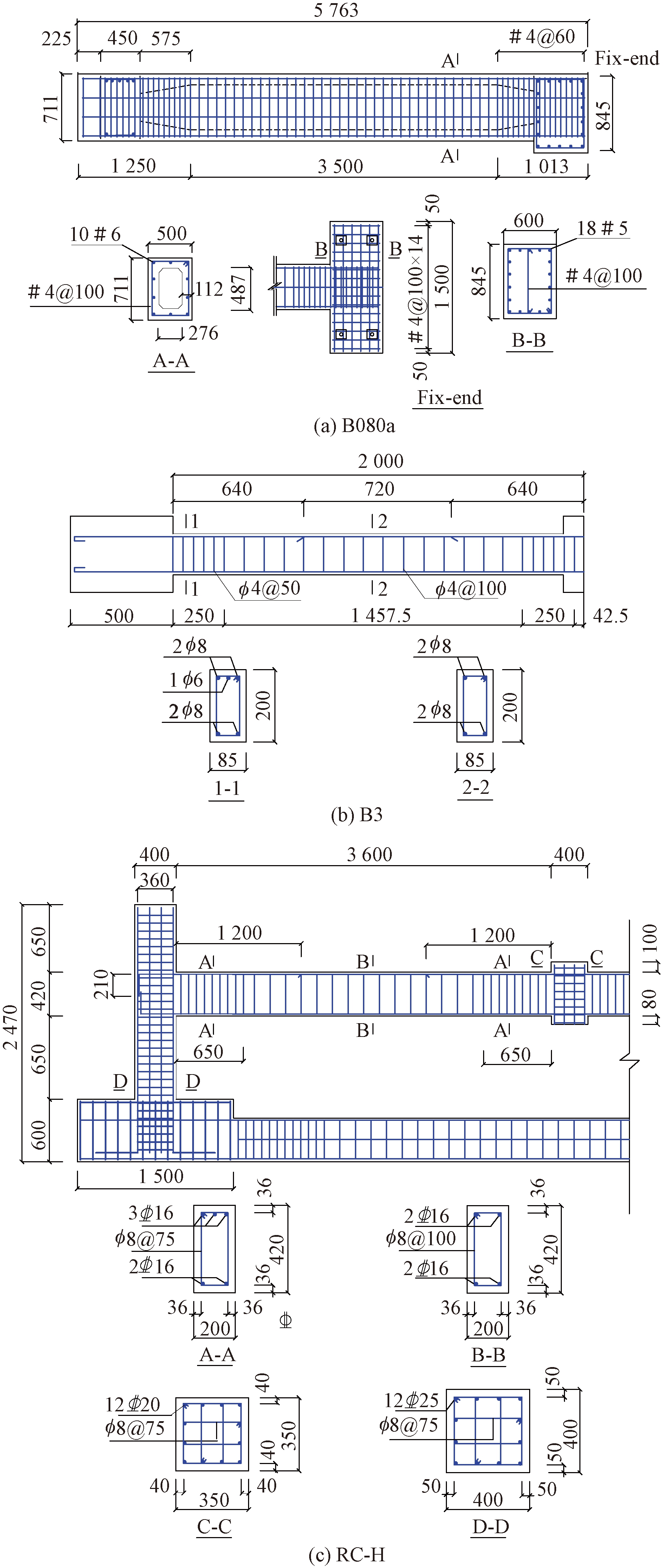
图2 试件几何尺寸及配筋(mm)
Figure 2 Dimensions and reinforcements of specimens(mm)
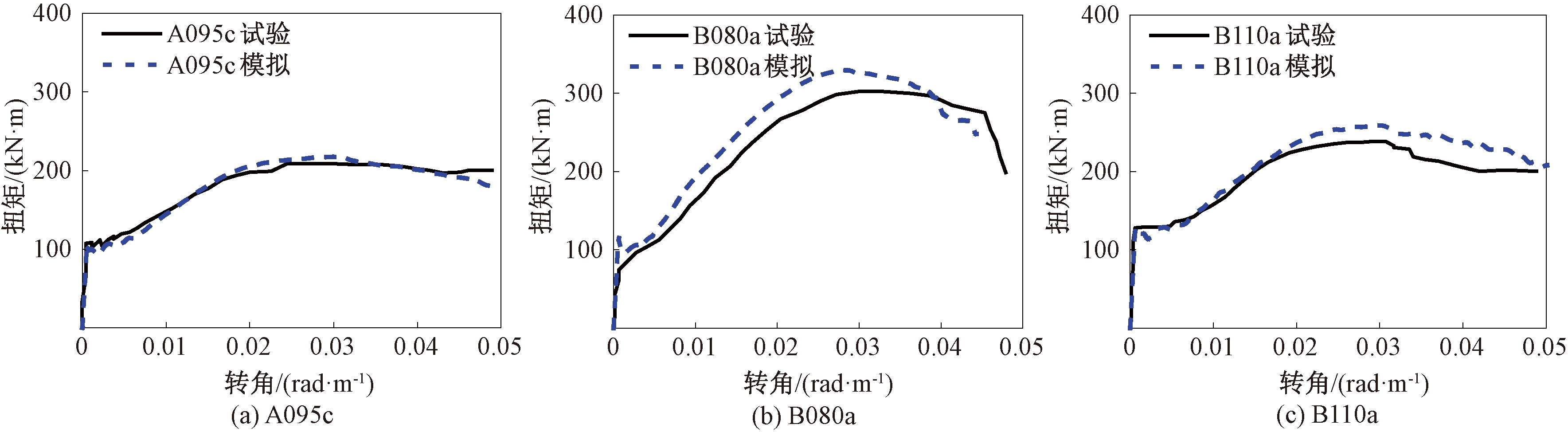
图3 受扭构件试验与模拟扭矩-转角曲线
Figure 3 Tested and simulated torque-twist curves of torsional specimens
3.1 受力机制分析
各级扭矩下框架的竖向荷载-中柱位移曲线如图7(a)所示。分析中极限位移取0.2倍单侧梁的跨度。竖向位移加载初期,承载力由梁端的抗弯承载力提供,随着位移的增大,柱端约束效应明显,未受扭构件在竖向位移为74.4 mm时达到压拱峰值。之后压拱失稳,承载力有所下降,中柱端梁顶部和边柱端梁底部混凝土逐渐被压碎退出工作。随着梁中轴力由压力转变为拉力,结构受力从压拱阶段向悬链阶段转换,荷载-位移曲线再次上升,混凝土受拉裂缝逐渐由梁端向梁中开展,最终结构在梁底纵筋发生断裂时达到峰值承载力,此时梁段上混凝土已严重开裂基本退出工作,梁顶纵筋受拉屈服。受扭构件同样经历了从压拱机制向悬链机制的转变,但随着扭矩的增加,结构的压拱承载力逐渐减小,单跨梁所受扭矩为截面抗扭承载力的20%、40%、60%、80%时,压拱承载力分别降低了0.5%、3.4%、10.9%、15.6%,但达到压拱峰值时的位移相差较小,在6%以内。各构件之间钢筋的断裂有显著的差别,随着扭矩的增大,悬链线阶段梁底钢筋的断裂位移呈现先减小后增大的趋势。无扭矩构件在达到极限位移时梁顶部钢筋未发生断裂,而受扭构件均发生了梁顶钢筋的断裂,且随着扭矩的增大钢筋断裂不断提前。特别地,当施加扭矩达到80%时,梁顶钢筋会先于底部钢筋断裂,这是因为柱头的平面外转角过大,导致梁底纵筋相对于中柱形心有向外侧移动的趋势,钢筋位置的偏离使得梁底纵筋应力发展变缓。框架梁的轴力-中柱竖向位移曲线如图7(b)所示,在竖向位移较小时,各扭矩百分比下框架梁均为受压状态,且随着扭矩的增大,梁中最大轴压力不断减小;达到压拱承载力峰值后,梁中轴力逐渐减小,减小速度随扭矩的增大而增加。

图4 连续倒塌构件试验与模拟荷载-位移曲线
Figure 4 Tested and simulated load-displacement curves of progressive collapse specimens
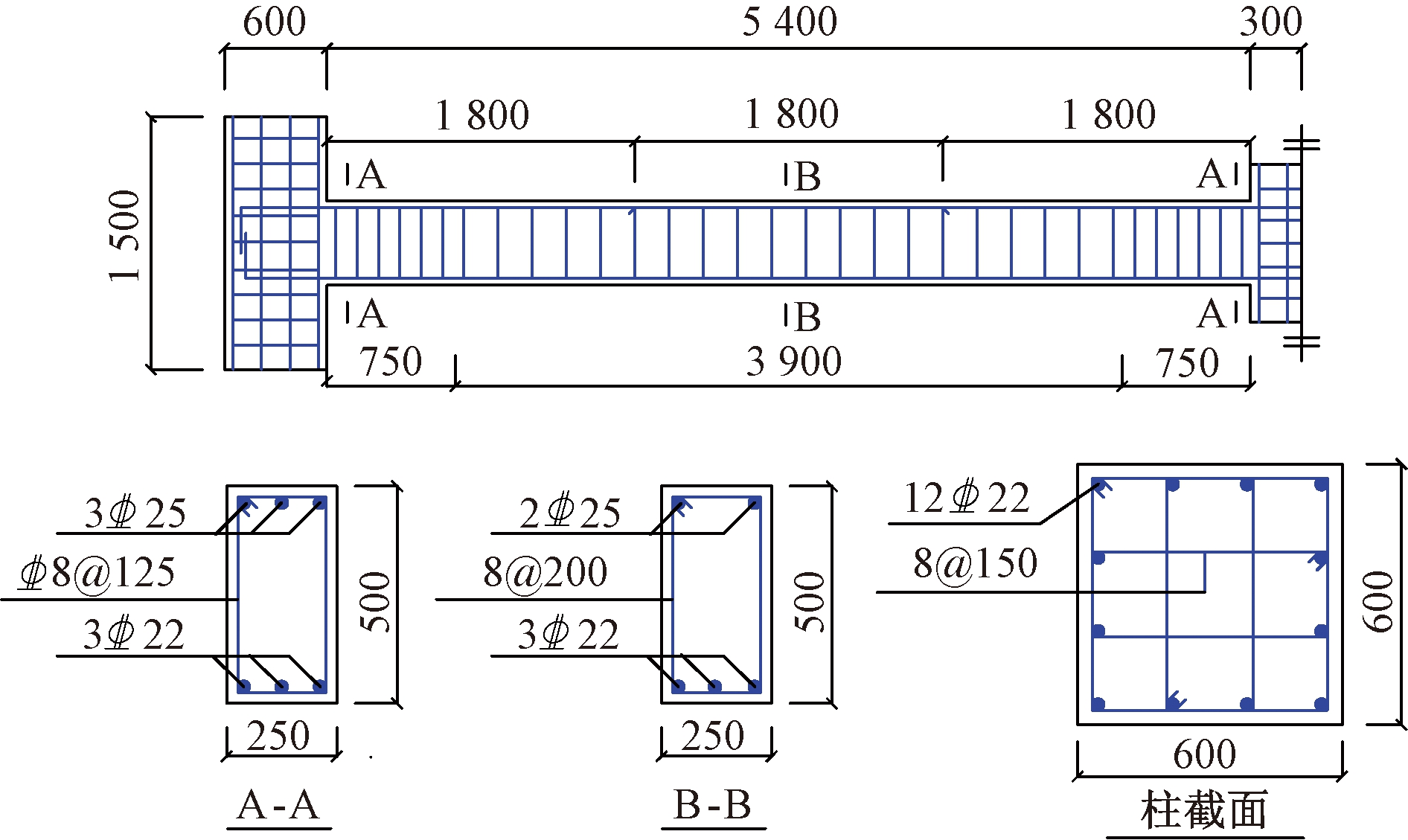
图5 分析模型尺寸及配筋(mm)
Figure 5 Dimension and reinforcement details of model(mm)
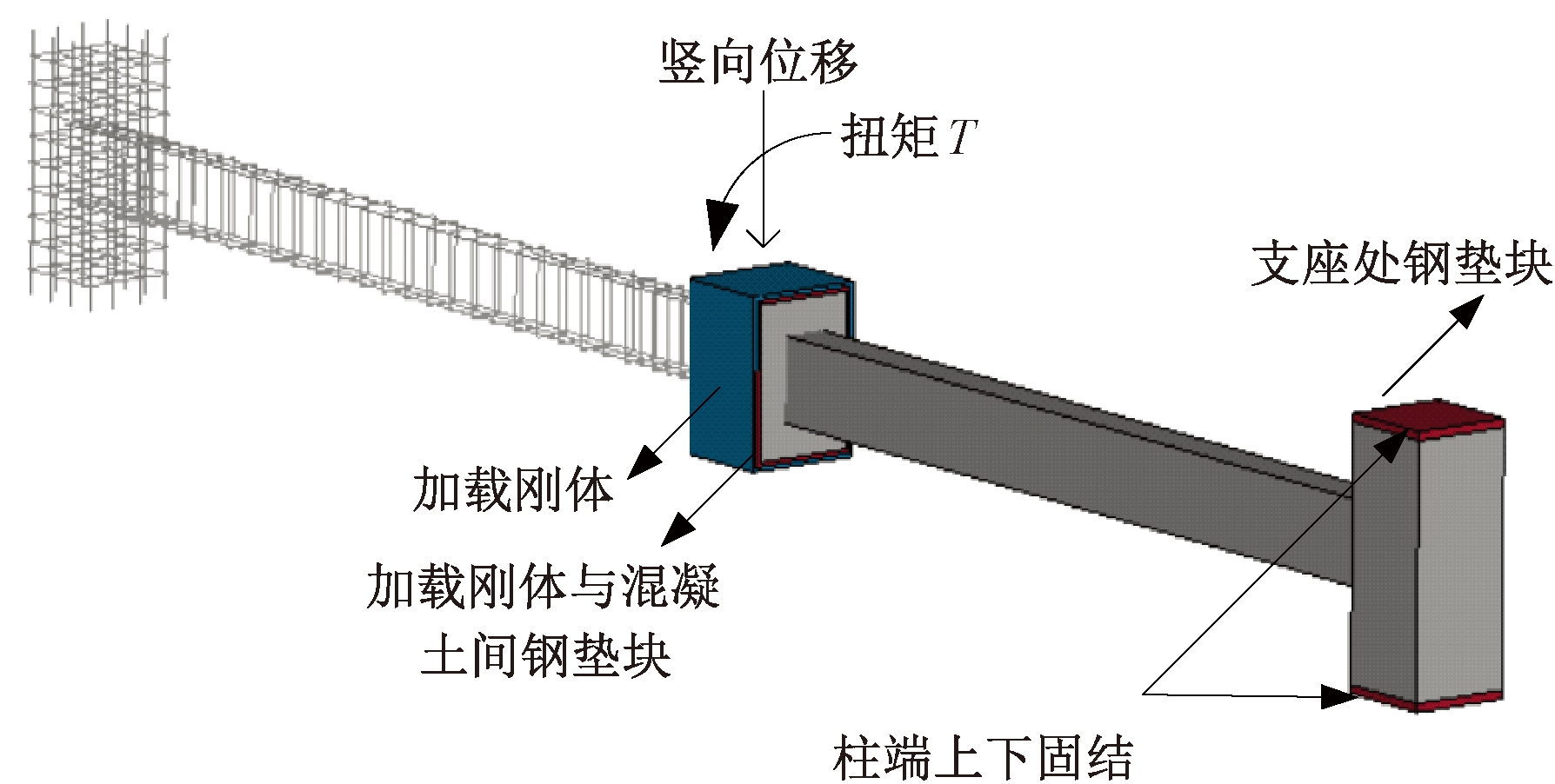
图6 模型细节
Figure 6 Detailed model
采用有效塑性应变可以反映混凝土的损伤程度[14],无扭矩构件与扭矩为60%构件破坏时的有效塑性应变对比如图8所示,由图8可以看出,后者由于柱头的平面外转动,混凝土的损伤呈斜向开展。

图7 荷载-位移曲线与轴力-位移曲线
Figure 7 Load-displacement curve and axial force-displacement curve
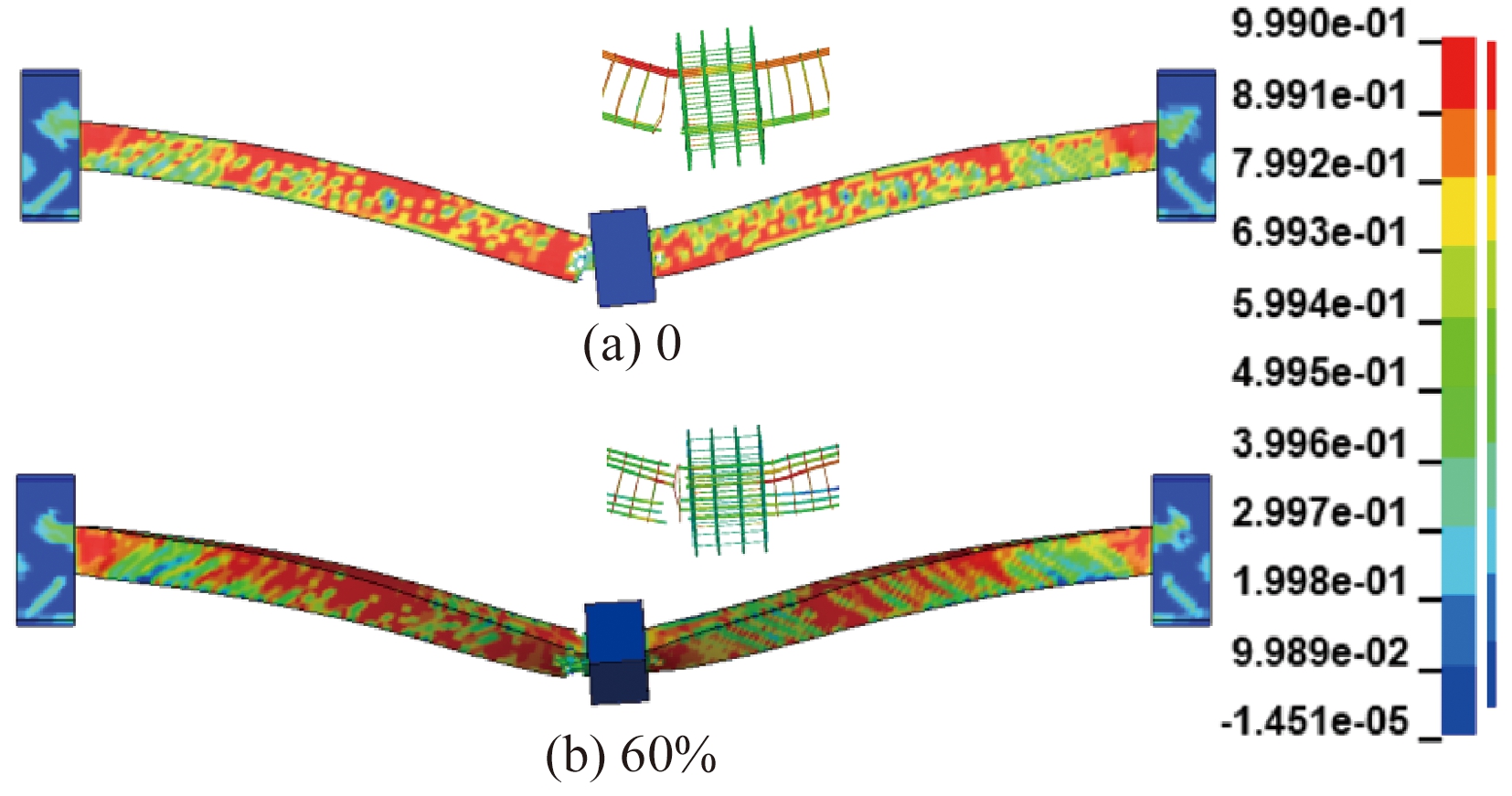
图8 极限位移下破坏形态对比
Figure 8 Comparison of failure patten under limit displacement
3.2 钢筋应变分析
钢筋是RC框架抗连续倒塌的重要受力组成部分,以往试验[6-7]表明,在倒塌过程中,靠近中柱的梁端底部钢筋和靠近边柱的梁端顶部钢筋会先后发生断裂。当对失效柱柱头不进行平面内转动约束时,构件最终会发生中柱端梁顶部钢筋的断裂[19]。因此对该3个重要位置的钢筋受力进行分析,钢筋名称及对应位置如图9所示。
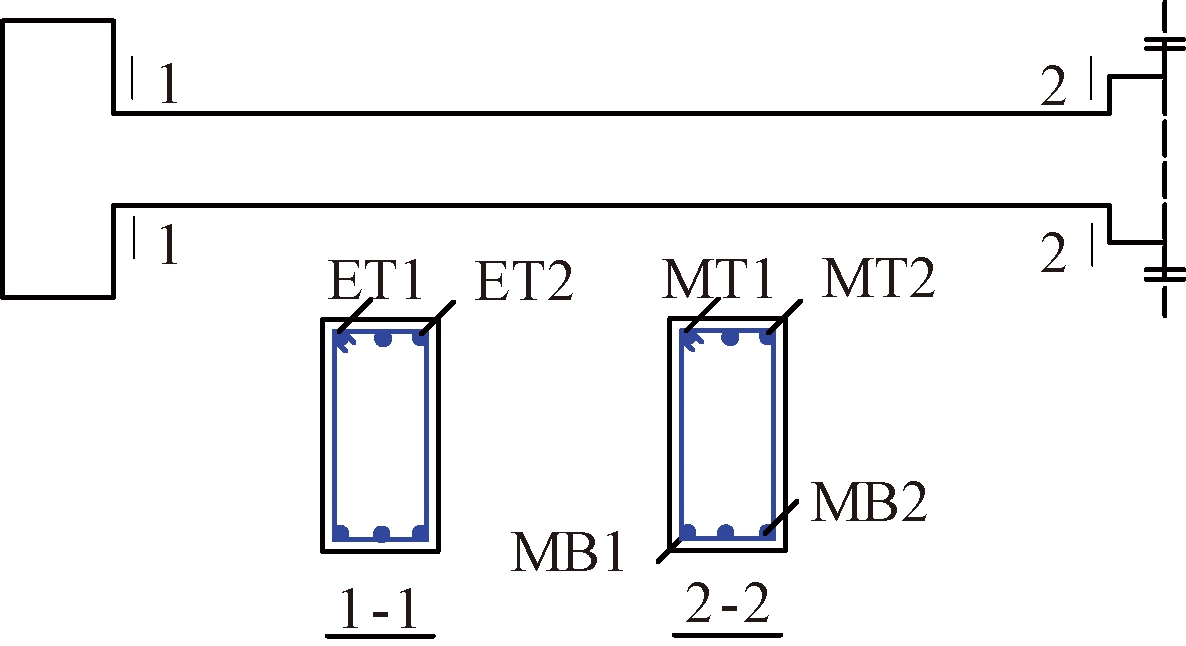
图9 钢筋名称示意图
Figure 9 Schematic diagram of reinforcements
图10为钢筋应变对比,图10(a)对比了各构件在压拱峰值时的钢筋应变,受扭构件虽然承受额外的扭矩作用,但中柱端梁底纵筋MB1、MB2的应变却随着扭矩的增大而降低。此现象的原因有2点:一是结构按照抗震设计,纵筋配置较多,在扭转作用下受扭纵筋和受扭箍筋的强度比远大于发生适筋破坏的限值,故施加初始扭矩后承载力主要由箍筋承担,纵筋应变很小;二是由于柱头的平面外转动,钢筋相对于中柱形心位置有所改变,受拉纵筋MB1、MB2的应变减小,受压纵筋MT1、MT2由压转拉的趋势增强。随着中柱竖向位移的增大,扭矩使柱头的平面外转角不断增大,进而对中柱两端梁纵筋受力产生较大影响。图10(b)对比了悬链后期各构件竖向位移为800 mm时的钢筋应变,此时在小扭矩下MB1的应变随着扭矩的增大不断增大,当扭矩百分比由40%增大到80%时,由于中柱转角过大,应变发展变缓。MT1受柱头转动影响相对于中柱形心有向下的位移,即向受拉区移动,故应变不断增大。边柱端梁顶钢筋ET1、ET2的应力受扭转的影响较小,各构件的应变差别不大,这是因为梁端箍筋加密区抗扭刚度更大,梁受扭变形较大处位于箍筋非加密段。
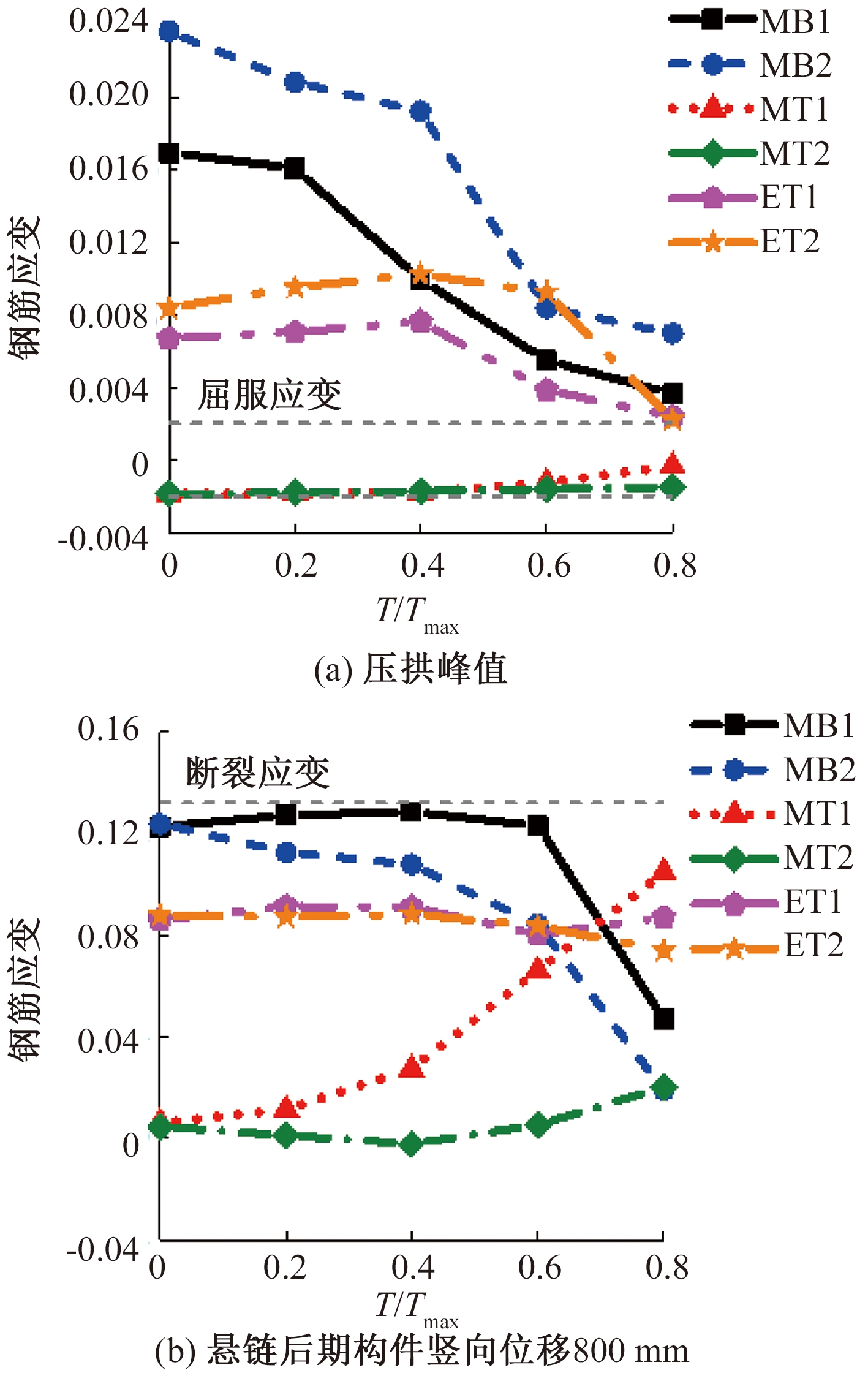
图10 钢筋应变对比
Figure 10 Strain comparison of reinforcements
3.3 抗震构造措施的影响
本文框架按照7度(0.15g)设防,当考虑抗震构造措施(梁端加密区箍筋间距为125 mm)时,梁柱子结构在纯扭作用下破坏发生在箍筋非加密段,此时纵筋受力较大位置与连续倒塌纵筋主要受力位置不同,而当不考虑抗震构造措施(即框架梁整个跨度上箍筋间距均为200 mm)时,结构受扭破坏更靠近中柱。对梁端箍筋非加密构件采取前述相同的方法分析,其荷载-位移曲线如图11所示,在梁所受扭矩为抗扭承载力的20%及40%时,梁底纵筋断裂位移并未提前太多,当扭矩达到60%后就不会发生断裂。造成此现象的原因是相同的初始扭矩下,不考虑抗震构造的构件在竖向位移加载过程中中柱转角要明显高于考虑抗震构造的构件,如图12所示,中柱的过大转动使得MB1的应力发展变缓,如图13所示,ET1的应变在后期要明显高于箍筋加密构件,是因为此时梁沿全长抗扭刚度相同,中柱绕着支座梁端部转动。
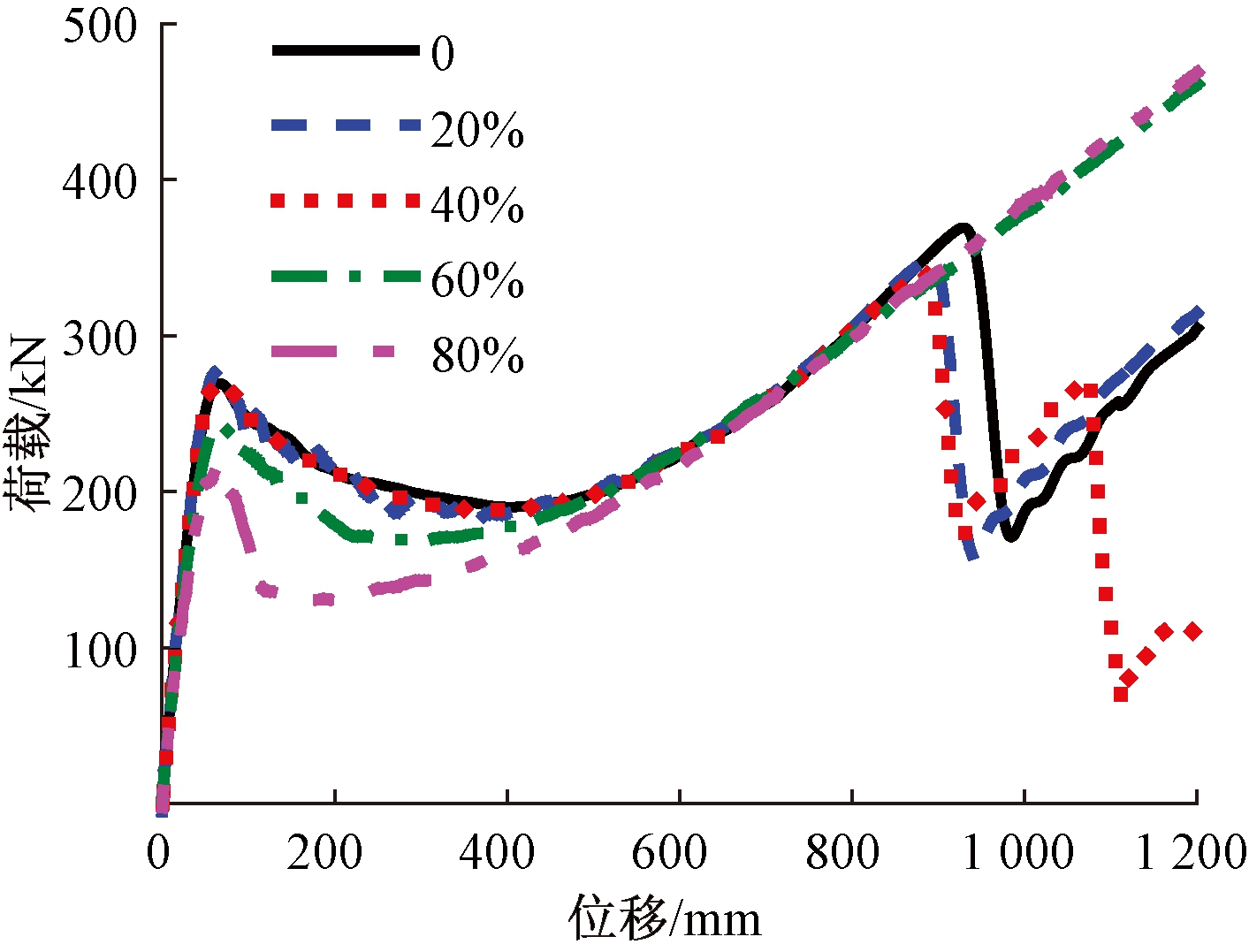
图11 荷载-位移曲线
Figure 11 Load-displacement curve
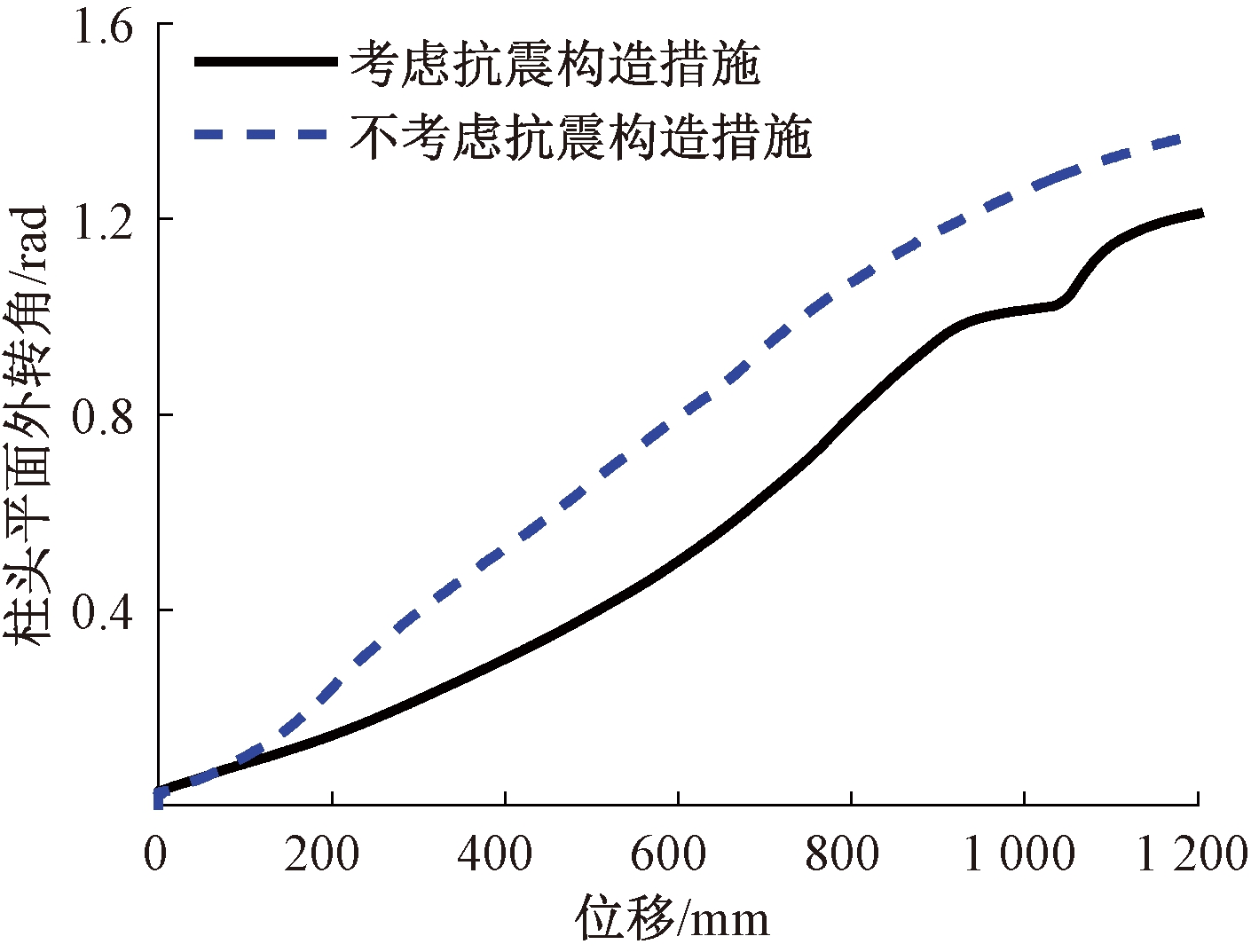
图12 中柱转角
Figure 12 Rotation of middle column
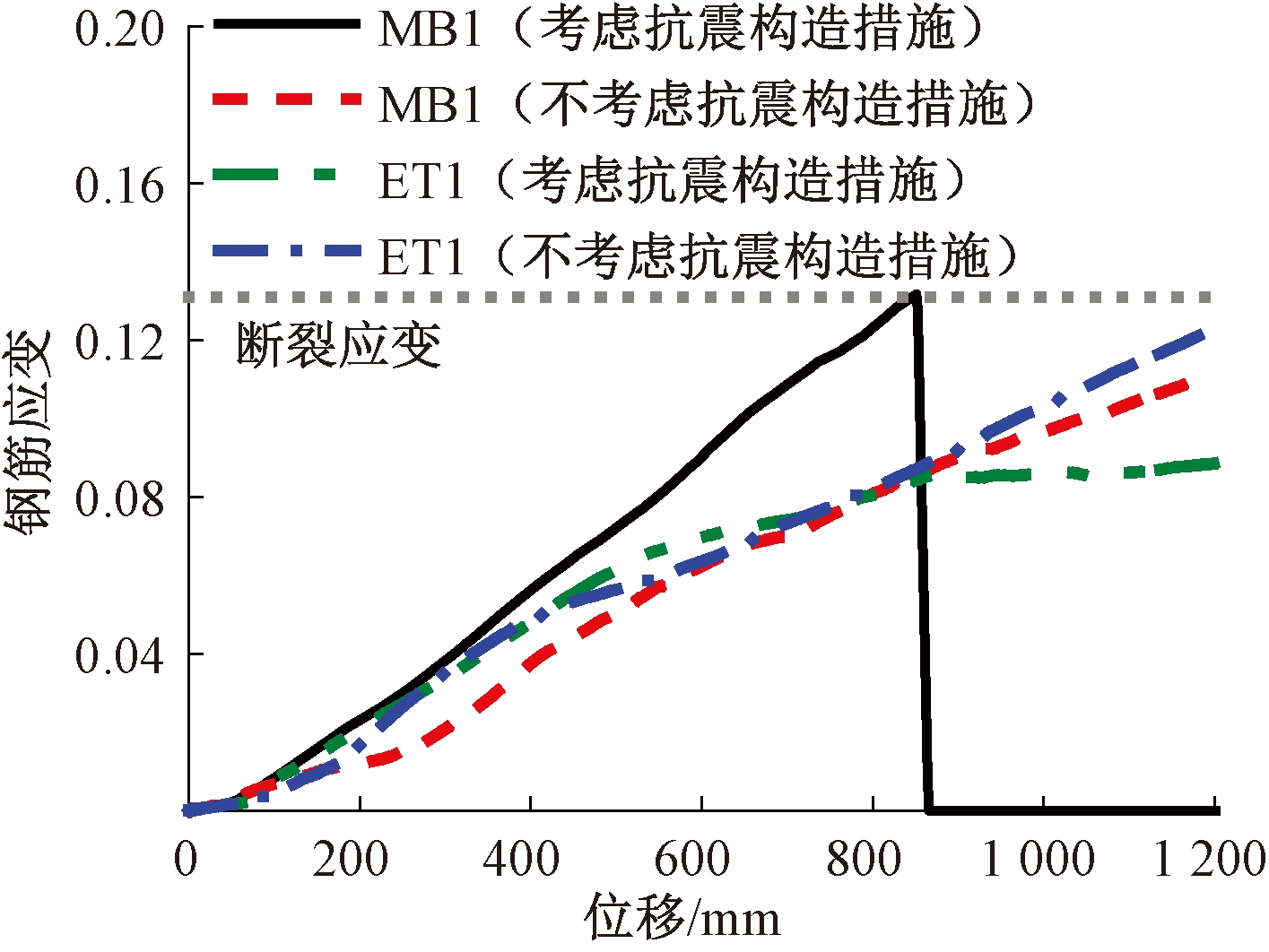
图13 MB1、ET1应变
Figure 13 Strain of MB1 and ET1
4 RC空间框架抗倒塌分析
4.1 空间框架抗倒塌承载力分析
当框架的失效柱是边柱时,需要考虑与边柱相连的横向梁的影响,有研究[8-10]表明,空间框架中只有平面内的双跨梁可以有效开展压拱机制与悬链机制,横向梁对承载力的贡献只有弯曲作用,其弯曲变形会带动失效柱发生平面外转动,从而使得平面内梁受扭。为了明确该条件下扭转的影响,对空间T型框架子结构进行连续倒塌分析,单跨结构的尺寸和配筋与前述相同,同时为了探究扭转是否会降低空间框架的抗倒塌承载力,对组成其相应的平面框架和横向梁也进行了分析,其荷载-位移曲线如图14所示。在钢筋断裂前空间框架的抗倒塌承载力基本等于其对应的平面框架和横向梁承载力的叠加,但横向梁的作用使得空间框架梁底纵筋的断裂相比于平面框架会提前,这与平面框架中施加较小的扭时破坏规律相似。
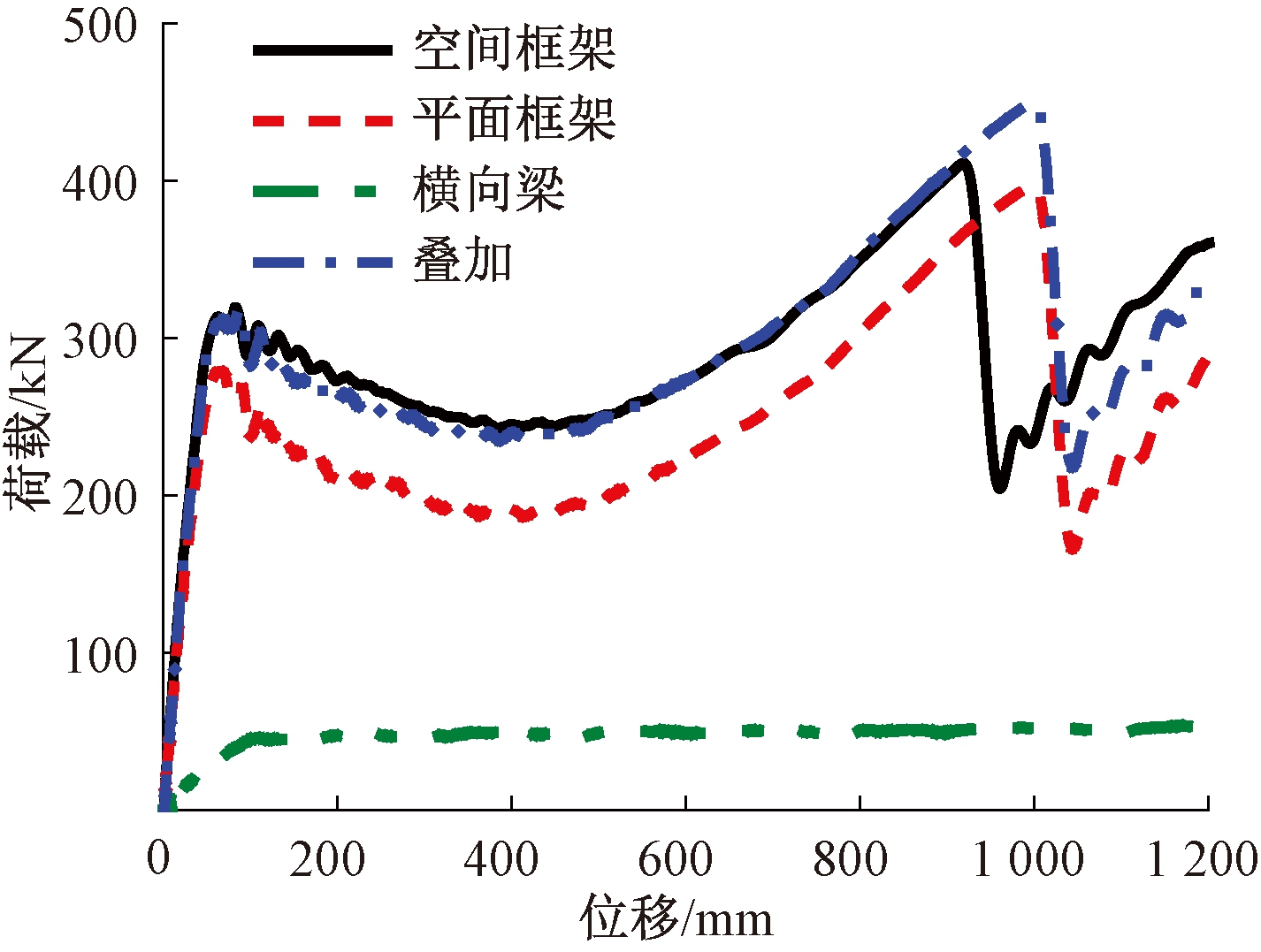
图14 倒塌承载力-位移曲线
Figure 14 Collapse capacity-displacement curve
图15为平面框架中模型编号为20%、40%的构件梁中扭矩与空间框架中平面内梁扭矩的对比。在平面框架失效柱上施加扭矩,倒塌过程中梁截面扭矩基本保持恒定状态,受扭特征是平衡扭转。而空间框架中平面内梁的受扭特征是协调扭转,梁中扭矩首先随着横梁抗弯承载力的增大而增加,在弯曲纵筋屈服后基本保持恒定,当结构进入到悬链线阶段后,由于横向梁的弯曲刚度不断下降,扭矩不断降低,因而横向梁的影响程度是有限的。
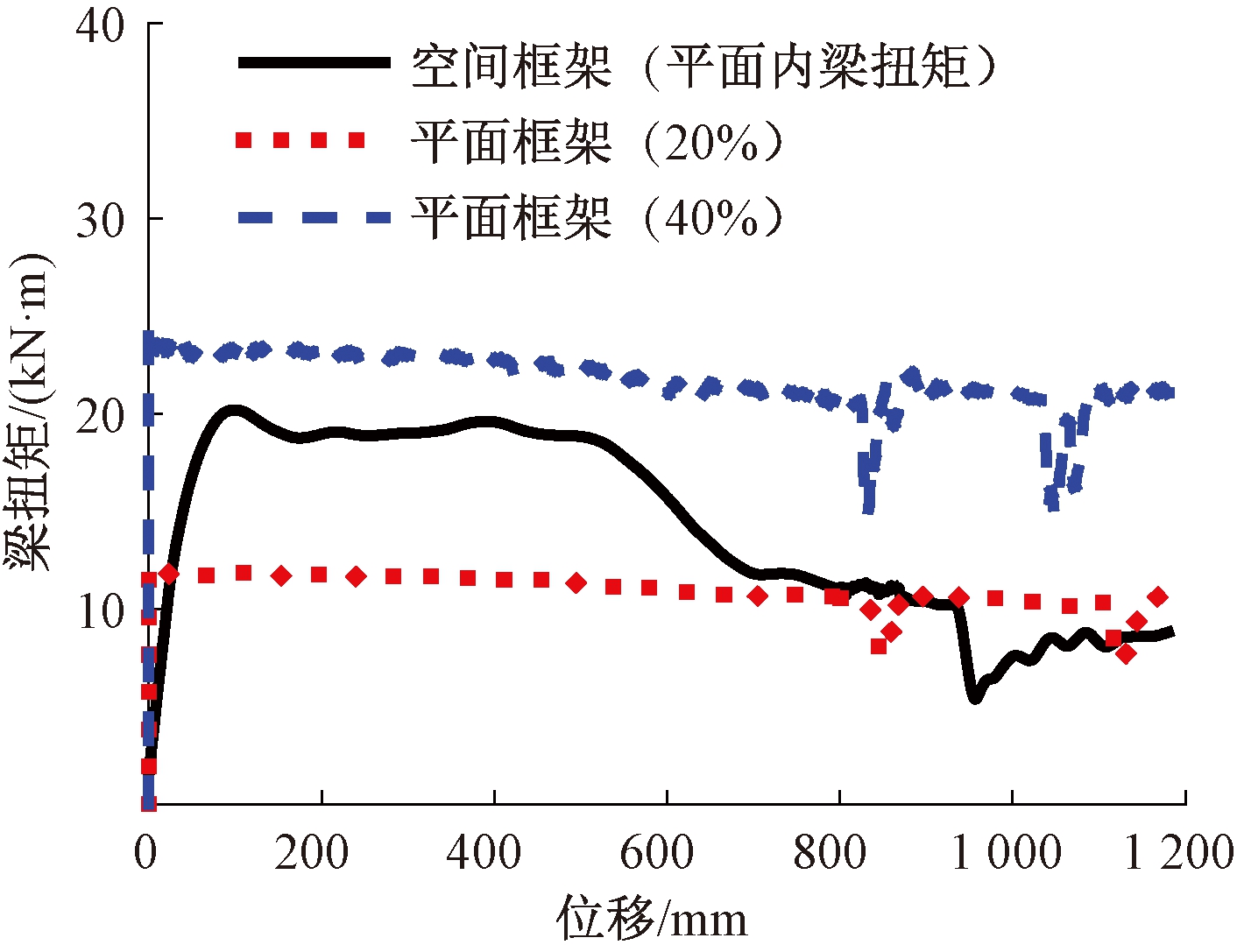
图15 梁扭矩对比
Figure 15 Comparison of torque in the beams
4.2 子结构选取的影响
为了更直接反映柱子的影响并分析柱子的受力形态,建立了空间子结构的整体模型,整体模型中平面内取一整榀框架,平面外取单跨。柱子取一层柱底至上层柱反弯点处,柱底采用固定约束,与失效柱相邻的柱约束柱顶水平方向位移,远离失效柱的柱子不做额外约束处理,仅考虑其自身对主要受力跨的约束作用。本文框架平面设计为4×4跨,因此分别分析了结构边跨第2根柱和第3根柱失效2种情况,以讨论柱失效位置及周边结构约束作用的影响。对2种情况下的结构进行竖向位移加载分析,并同时对组成其相应的平面框架和悬臂梁进行分析,荷载位移曲线如图16所示。扭转效应使钢筋提前断裂的不利作用受梁端约束条件的影响,约束越强,钢筋断裂越提前。图17为结构最终的破坏形态,2种情况下与失效柱相邻的平面内柱在柱底以及梁柱节点处出现了较为明显的损伤,柱底部外侧纵筋以及梁顶部柱内侧纵筋都受拉屈服,梁顶部位置的柱外侧纵筋受压也较为显著,但未屈服;由于顶部水平约束的作用,二层柱在结构悬链机制发展下沿柱高出现拉裂缝。值得注意的是,当失效柱是第2根柱时,左侧边柱没有周边结构的约束,梁柱节点处以及上层柱的损伤要明显高于另一侧柱子。2种柱失效工况下,平面外柱都只在梁柱节点处有轻微的损伤,柱身受力不明显。

图16 结构承载力-位移曲线
Figure 16 Structural capacity-displacement curve
《建筑结构抗倒塌设计规范》(CECS 392:2014)对拆除构件法下拆柱位置和拆柱方法进行了相关规定,但是对结构的空间效应鲜有提及,根据本文的分析结果,对于承受较大扭矩的结构如悬挑结构,需要特别考虑扭矩对连续倒塌的不利影响,同时当空间框架失效柱是边柱时,需要考虑横向梁对平面内梁的作用,对抗倒塌有较高要求的结构构件也需关注柱子的受力状态。
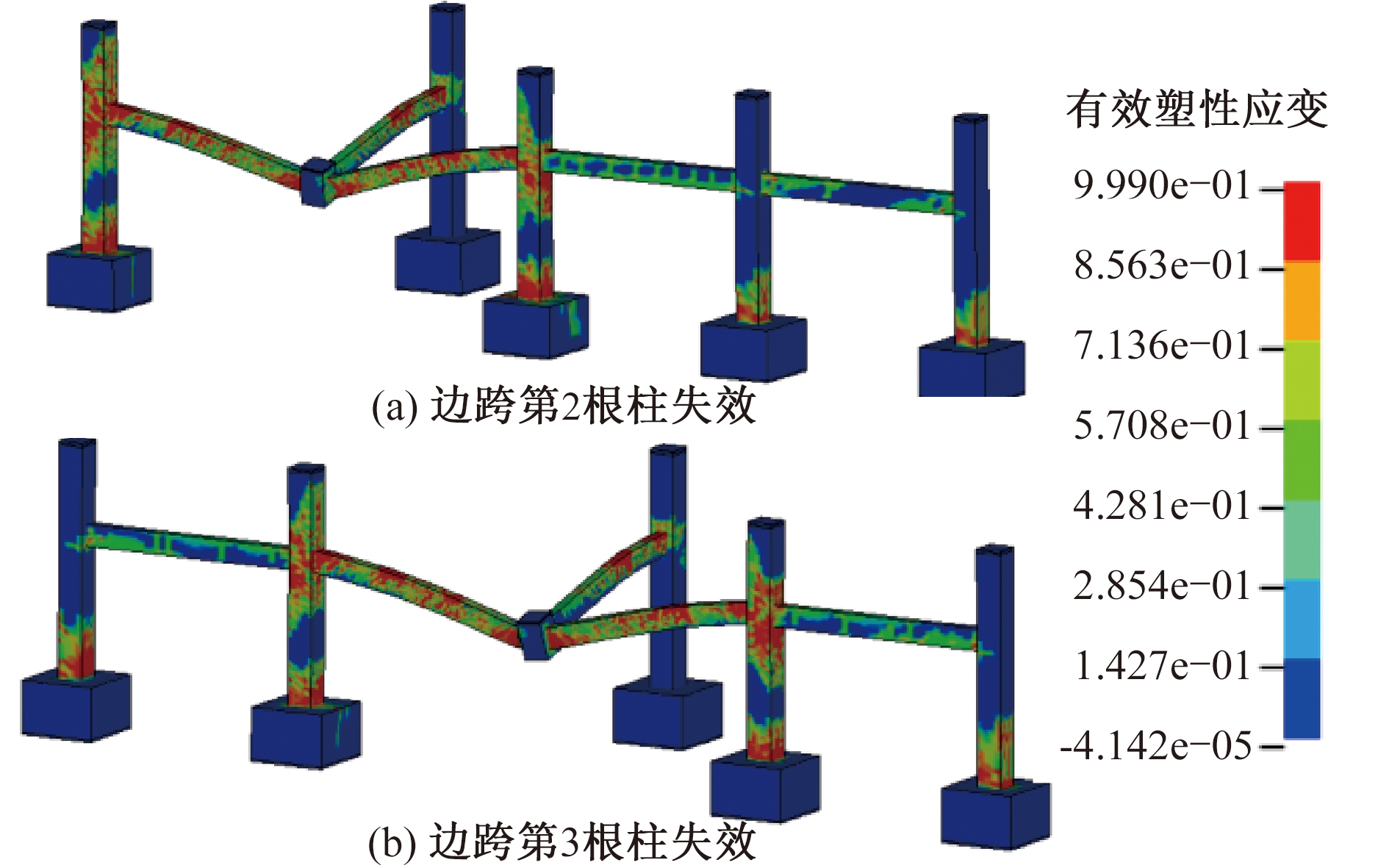
图17 2种情况下结构最终破坏形态
Figure 17 Final failure pattern of structure in two cases
5 结论
本文采用有限元软件LS-DYNA对考虑扭转作用的RC框架结构抗连续倒塌性能进行了研究,在验证计算模型准确性的基础上,讨论了不同扭矩作用下平面框架抗连续倒塌的受力特点,分析了空间框架的抗倒塌性能,得到以下主要结论。
(1)相比于不受扭构件,施加扭矩的构件在连续倒塌时同样经历了从压拱阶段到悬链线阶段的转变,当梁所受扭矩为梁截面抗扭承载力的20%、40%、60%及80%时,压拱承载力分别降低了0.5%、3.4%、10.9%、15.6%;随着扭矩的增大,结构的悬链作用不断提前。
(2)不同扭矩作用下结构纵筋的断裂有明显差别,当扭矩较小时,扭转作用使得中柱端梁底钢筋的断裂不断提前,但在大扭矩下失效柱头的平面外转动过大会导致其应力发展变缓;中柱端梁顶钢筋的断裂随着扭矩的增大不断提前。
(3)当不考虑抗震构造措施时,纯扭作用下纵筋的受力最大位置靠近中柱,与连续倒塌作用下纵筋主要受力位置相同,而扭矩作用并未使钢筋提前断裂更为显著,因为随着梁所受扭矩的增加,在相同竖向位移下,不考虑抗震构造措施构件的中柱平面外转角也随之增大,使得其中柱两端的梁底纵筋应变减小,从而延缓了梁底纵筋的断裂。
(4)空间框架连续倒塌时,横向梁的弯曲作用会使平面内梁受扭,但其提供的扭矩会随着横向梁抗弯刚度的下降而不断降低,在梁底钢筋断裂前,空间框架的抗倒塌承载力基本等于其对应的平面框架和横向梁承载力的叠加。
[1] SOZEN M A, THORNTON C H, CORLEY W G, et al. The Oklahoma City bombing: structure and mechanisms of the murrah building[J]. Journal of Performance of Constructed Facilities, 1998, 12(3): 120-136.
[2] SU Y P, TIAN Y, SONG X S. Progressive collapse resistance of axially-restrained frame beams[J]. ACI Structural Journal, 2009, 106(5): 600-607.
[3] 何庆锋, 易伟建. 考虑悬索作用钢筋混凝土梁柱子结构抗倒塌性能试验研究[J]. 土木工程学报, 2011, 44(4): 52-59.
HE Q F, YI W J. Experimental study of the collapse-resistant behavior of RC beam-column sub-structures considering catenary action[J]. China Civil Engineering Journal, 2011, 44(4): 52-59.
[4] LIM N S, TAN K H, LEE C K. Effects of rotational capacity and horizontal restraint on development of catenary action in 2-D RC frames[J]. Engineering Structures, 2017, 153: 613-627.
[5] YU J, TAN K H. Structural behavior of RC beam-column subassemblages under a middle column removal scenario[J]. Journal of Structural Engineering, 2013, 139(2): 233-250.
[6] 陈伟宏, 刘方豪, 乔泽惠, 等. 钢筋混凝土框架抗倒塌性能影响因素分析[J]. 郑州大学学报(工学版), 2021, 42(2): 31-36, 104.
CHEN W H, LIU F H, QIAO Z H, et al. Analysis on factors affecting the capability of collapse of reinforced concrete[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(2): 31-36, 104.
[7] QIAN K, LI B, MA J X. Load-carrying mechanism to resist progressive collapse of RC buildings[J]. Journal of Structural Engineering, 2015, 141(2): 04014107.
[8] RASHIDIAN O, ABBASNIA R, AHMADI R, et al. Progressive collapse of exterior reinforced concrete beam-column sub-assemblages: considering the effects of a transverse frame[J]. International Journal of Concrete Structures and Materials, 2016, 10(4): 479-497.
[9] LIM N S, TAN K H, LEE C K. Experimental studies of 3D RC substructures under exterior and corner column removal scenarios[J]. Engineering Structures, 2017, 150: 409-427.
[10] 张望喜, 王雄, 刘精巾, 等. 现浇与装配整体式混凝土空间框架子结构的抗连续倒塌性能试验对比研究[J]. 建筑结构学报, 2020, 41(7): 81-90.
ZHANG W X, WANG X, LIU J J, et al. Experimental comparative study on progressive collapse behavior of cast-in-place and monolithic precast concrete spatial frame substructures[J]. Journal of Building Structures, 2020, 41(7): 81-90.
[11] 张望喜, 吴昊, 张瑾熠, 等. 装配整体式混凝土框架子结构防连续倒塌空间受力性能试验研究[J]. 土木工程学报, 2020, 53(5): 42-56, 64.
ZHANG W X, WU H, ZHANG J Y, et al. Experimental test on progressive collapse resistance of the spatial behavior of integrated precast concrete frame substructures[J]. China Civil Engineering Journal, 2020, 53(5): 42-56, 64.
[12] WENG Y H, QIAN K, FU F, et al. Numerical investigation on load redistribution capacity of flat slab substructures to resist progressive collapse[J]. Journal of Building Engineering, 2020, 29: 101109.
[13] QIAN K, CHENG J F, WENG Y H, et al. Effect of loading methods on progressive collapse behavior of RC beam-slab substructures under corner column removal scenario[J]. Journal of Building Engineering, 2021, 44: 103258.
[14] YU J, LUO L Z, LI Y. Numerical study of progressive collapse resistance of RC beam-slab substructures under perimeter column removal scenarios[J]. Engineering Structures, 2018, 159: 14-27.
[15] MURRAY Y D, ABUODEH A Y, BLIGH R P. Evaluation of LS-DYNA concrete material model 159[R]. Washington DC: Federal Highway Administration, 2007.
[16] PHAM A T, TAN K H, YU J. Numerical investigations on static and dynamic responses of reinforced concrete sub-assemblages under progressive collapse[J]. Engineering Structures, 2017, 149: 2-20.
[17] JENG C H, PENG S F, CHIU H J, et al. New torsion experiment on large-sized hollow reinforced concrete beams[J]. ACI Structural Journal, 2014, 111(6): 1469-1480.
[18] REN P Q, LI Y, LU X Z, et al. Experimental investigation of progressive collapse resistance of one-way reinforced concrete beam-slab substructures under a middle-column-removal scenario[J]. Engineering Structures, 2016, 118: 28-40.
[19] DENG X F, LIANG S L, FU F, et al. Effects of high-strength concrete on progressive collapse resistance of reinforced concrete frame[J]. Journal of Structural Engineering, 2020, 146(6): 04020078.