相关研究表明人是导致交通事故的主要原因,由于人的操作不当造成的事故占总交通事故的95.30%[1],而无人驾驶汽车不需要驾驶员的参与,可以大大减少此类事故的发生。汽车避开障碍物顺利进行路径规划是实现无人驾驶的重要基础。
目前局部路径规划算法主要分为4类:基于采样的方法、基于图搜索法、基于离散优化以及人工势场法的方法[2]。1986年Khatib首次提出人工势场法[3],并广泛应用于机器人避障领域,后来因其反应速度快、实时性高被用于汽车路径规划领域。但传统人工势场容易陷入局部最优点以及出现目标不可达问题,许多学者针对局部最优问题提出改进方案,例如,Li等[4]重新定义潜在函数进行改进;于振中等[5]提出填平势场法;Huang等[6]提出“沿边走”策略的改进方案;徐飞[7]通过设置中间虚拟目标点进行改进;Fedele等[8]利用引力势场与螺旋斥力场的切换策略进行改进。这些改进虽然能够克服机器人产生的局部最优问题,但针对交通环境行驶的汽车还有待进一步改进。范玉龙等[9]通过设置虚拟障碍物提供逃逸力进行改进;张三川等[10]通过在汽车与障碍物异侧增加附加力进行改进。这些方法虽能够克服局部最优点,但未考虑汽车行驶时对路径曲率的要求,容易在障碍物附近出现路径曲率过大的情况。王树凤等[11]构建新型障碍物虚拟力场模型,并建立局部目标点实现汽车超车路径规划;谭宝成等[12]通过调节障碍物势场作用范围提高规划路径的平滑度;胡丹丹等[13]通过构建虚拟区域以及重构物理势能力场解决换道过程中局部最优问题。这些单一改进势场模型的方法,难以克服传统人工势场共线问题,缩小了人工势场法的适用场景范围。
针对以上改进方法的不足,本文从汽车安全性与稳定性出发,通过偏转斥力,解决传统人工势场合力为零的问题;设计新的斥力函数解决传统人工势场规划路径振荡、曲率过大问题。仿真表明,改进的人工势场可以避免局部最优点,规划的避障路径曲率小且平缓,安全性更高、稳定性更好。
1 传统人工势场
无人驾驶汽车在行车区间首先通过感知系统获得自车位置、航向角以及障碍物的位置信息,然后把这些信息传递给规划层。人工势场主要利用斥力与引力的合力来引导汽车下一步的行车方向。
目标产生的引力势场可表示为[10]
(1)
式中:ρ(q, qg)为矢量,方向从汽车指向目标点,大小为汽车位置q和目标点位置qg之间的距离;η为引力增益系数;引力势场对汽车产生的引力始终指向目标点,引力的大小为引力势场的负梯度,即
Fatt(q)=-grad(Uatt(q))=-ηρ(q, qg)。
(2)
当汽车进入障碍物斥力影响范围时,障碍物对汽车产生斥力势场,可表示为[10]
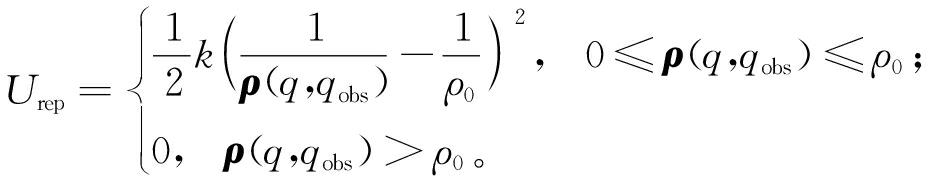
(3)
式中:k为斥力增益系数;ρ(q, qobs)为矢量,方向从障碍物指向汽车,大小为汽车位置q和障碍物位置qobs之间的距离;ρ0表示障碍物对汽车产生作用的最大距离;斥力大小为斥力势场的负梯度,即
Frep(q)=
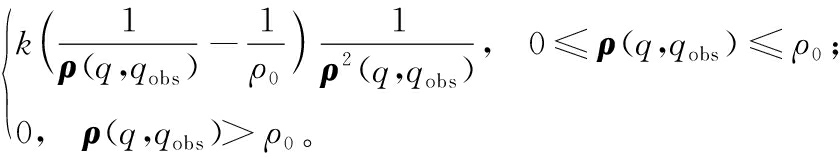
(4)
当汽车受到n个障碍物的同时作用,其所受的斥力为各障碍物斥力的矢量和,斥力大小为
(5)
因此,汽车在传统人工势场下的汽车所受到的引力与斥力的合力的大小为
(6)
2 改进斥力模型的人工势场
2.1 斥力偏转方向
为避免汽车陷入局部最优点,根据汽车与道路边界以及障碍物与汽车速度的关系来确定斥力偏转方向,进而在偏转方向上偏转角度α,规定传统人工势场斥力方向角度为0°。规定障碍物与道路边界之间的距离L0为汽车可通行距离,根据常见的车道标准宽度,L0取3.5 m。当障碍物与道路边界距离小于等于L0时,汽车不能从障碍物与道路边界之间通过,此时障碍物斥力偏转方向有2种,如图1所示:当汽车位置处于位置1时表示障碍物靠近道路上边界,斥力逆时针偏转;处于位置2时表示障碍物靠近道路下边界,斥力顺时针偏转。当障碍物与道路边界距离大于L0时,如位置3和4所示,此时应根据汽车速度方向与障碍物相对位置关系确定偏转方向。位置3表示汽车速度方向在障碍物上方,斥力顺时针偏转;位置4表示汽车速度方向在障碍物下方,斥力逆时针偏转。
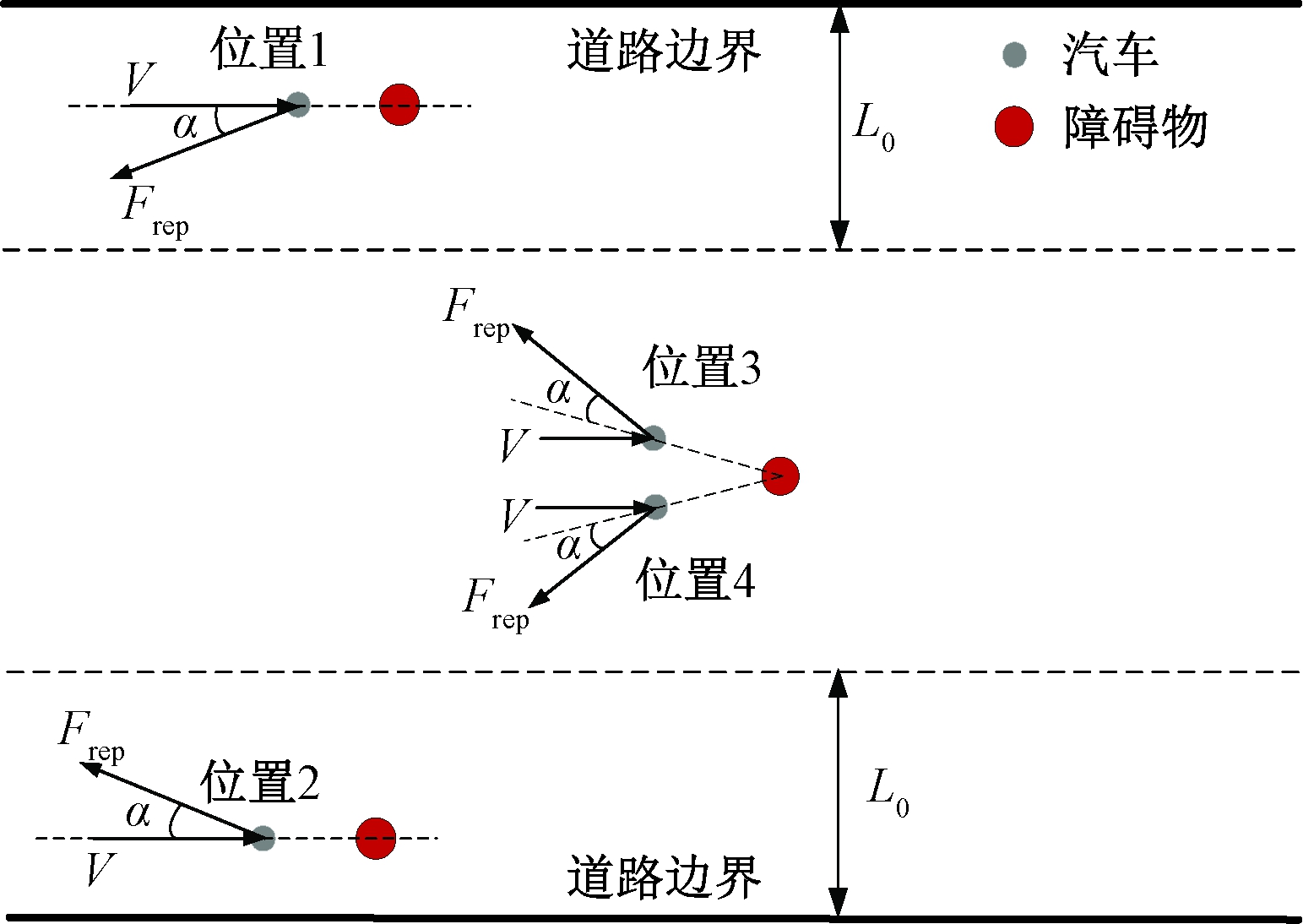
图1 斥力的偏转方向
Figure 1 The direction of deflection of repulsion
2.2 斥力大小
汽车主动避撞有转向避撞和制动避撞2种方式[14]。本文只研究主动避撞下局部路径规划。在避撞的时候要考虑行车速度以及路面附着条件等,假设道路上汽车行驶速度为V,障碍物速度为V0,车身长度为L1,车身几何中心代表其实际位置,单个车轮的制动力为Fbra,汽车总重为m。要避免汽车与障碍物发生碰撞,应使汽车在进行行为决策时汽车与前方障碍物的距离至少为[15]
(7)
根据障碍物斥力势场的定义,汽车与障碍物的距离为ρ0时,障碍物开始对汽车产生斥力。
为保证汽车能够平稳避开障碍物,避免出现振荡点,根据对数函数的性质以及人工势场理论,改进后的斥力大小为
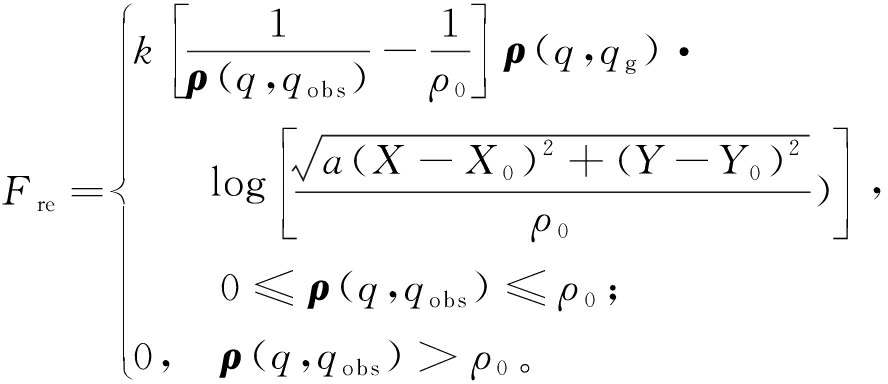
(8)
式中:斥力增益因子k由避障最大侧向偏移量和最小碰撞安全距离决定,本文k=2.3;a为纵向相对距离调节因子,a决定斥力大小在纵向和横向的变化速率,0<a≤1,本文a=0.1;(X0, Y0)和(X, Y)分别表示障碍物qobs和汽车q的位置坐标分量。如图2所示,汽车受到了障碍物1斥力Frep和目标点引力Fatt的作用。
在现实行车过程中,常常见到2个障碍物的距离较近,他们之间的距离不能满足汽车的正常通行条件的情况,如图2中障碍物2和障碍物3。这时假设障碍物之间的距离为l,允许通过汽车的2个障碍物之间的最小距离为l0,根据单车道宽度可取l0=3.5 m。当l<l0时,可在2个障碍物连线中点处构造一个虚拟障碍物,用虚拟障碍物代替2个相邻障碍物产生的斥力,如图2所示。
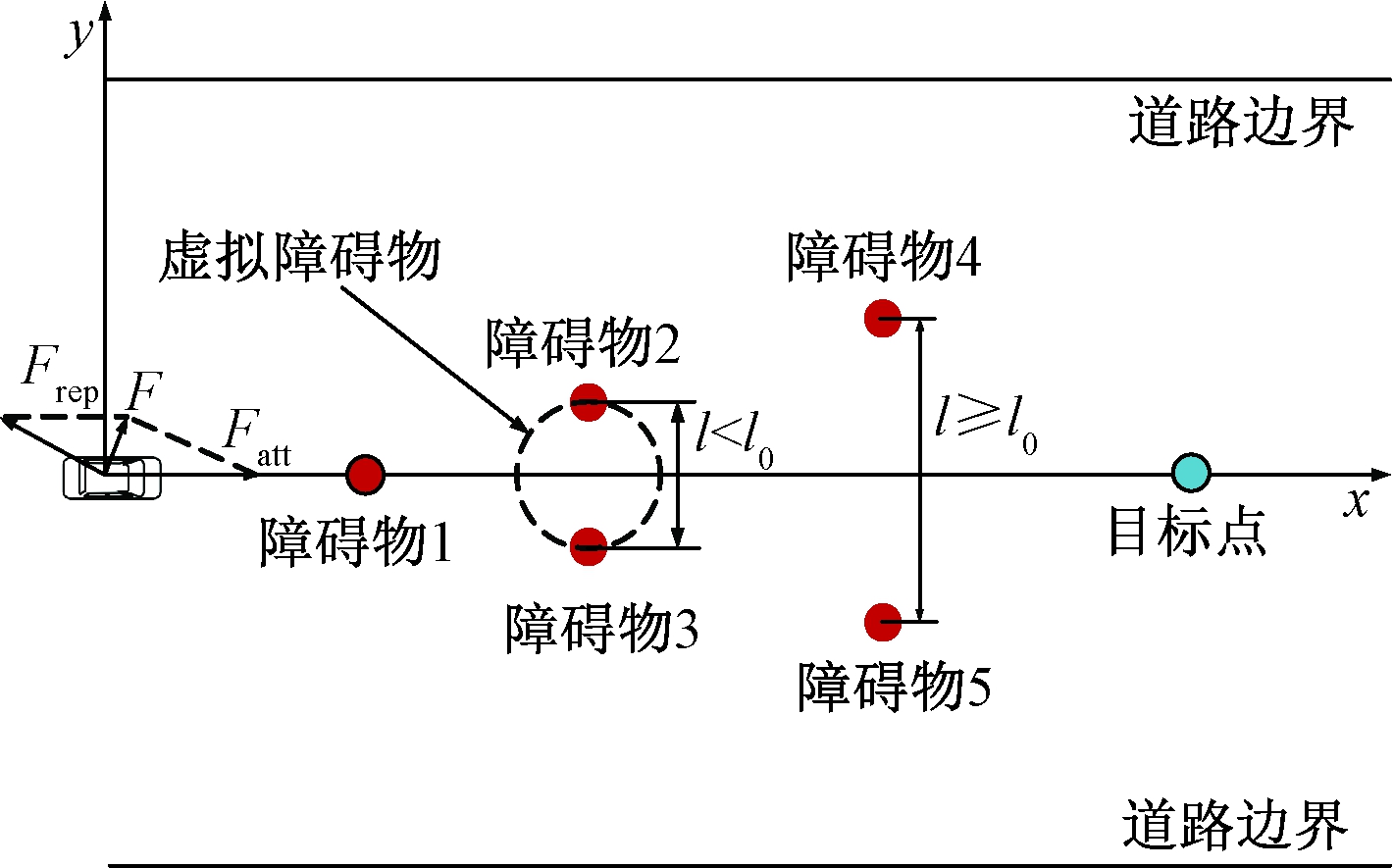
图2 汽车在改进斥力模型的人工势场中的受力情况
Figure 2 The vehicle forces in the artificial potential
field of the modified repulsive model
2.3 道路边界斥力
汽车在避障的过程中可以穿越车道分界线,但不能与道路两侧边界发生碰撞,汽车与道路边界距离越近,危险程度越高。以车辆行驶参考线为x轴,垂直于参考线为y轴建立坐标系,如图2所示,车辆起点位置为坐标原点,可设计道路边界斥力函数为
(9)
式中:w1为道路边界约束的安全系数;D1表示汽车行驶参考线与道路左侧边界距离;D2表示参考线与道路右侧边界距离;d表示汽车宽度。
3 算法验证与仿真结果分析
3.1 算法设计
改进斥力模型的人工势场局部路径规划算法流程如图3所示。汽车接收到前方障碍物与目标点的位置信息后,开始计算与障碍物的距离、障碍物和道路边界的距离以及速度方向与障碍物的相对位置关系,确定斥力偏转方向,计算合力;确定下一步的位置信息,判断下一位置是否到达目标点,如果到达目标点则局部路径规划算法完成;如果没到达目标位置,修正当前位置信息,继续计算此位置的合力,进行下一步位置信息计算,判断是否到达目标点,重复以上步骤,直至到达目标点。
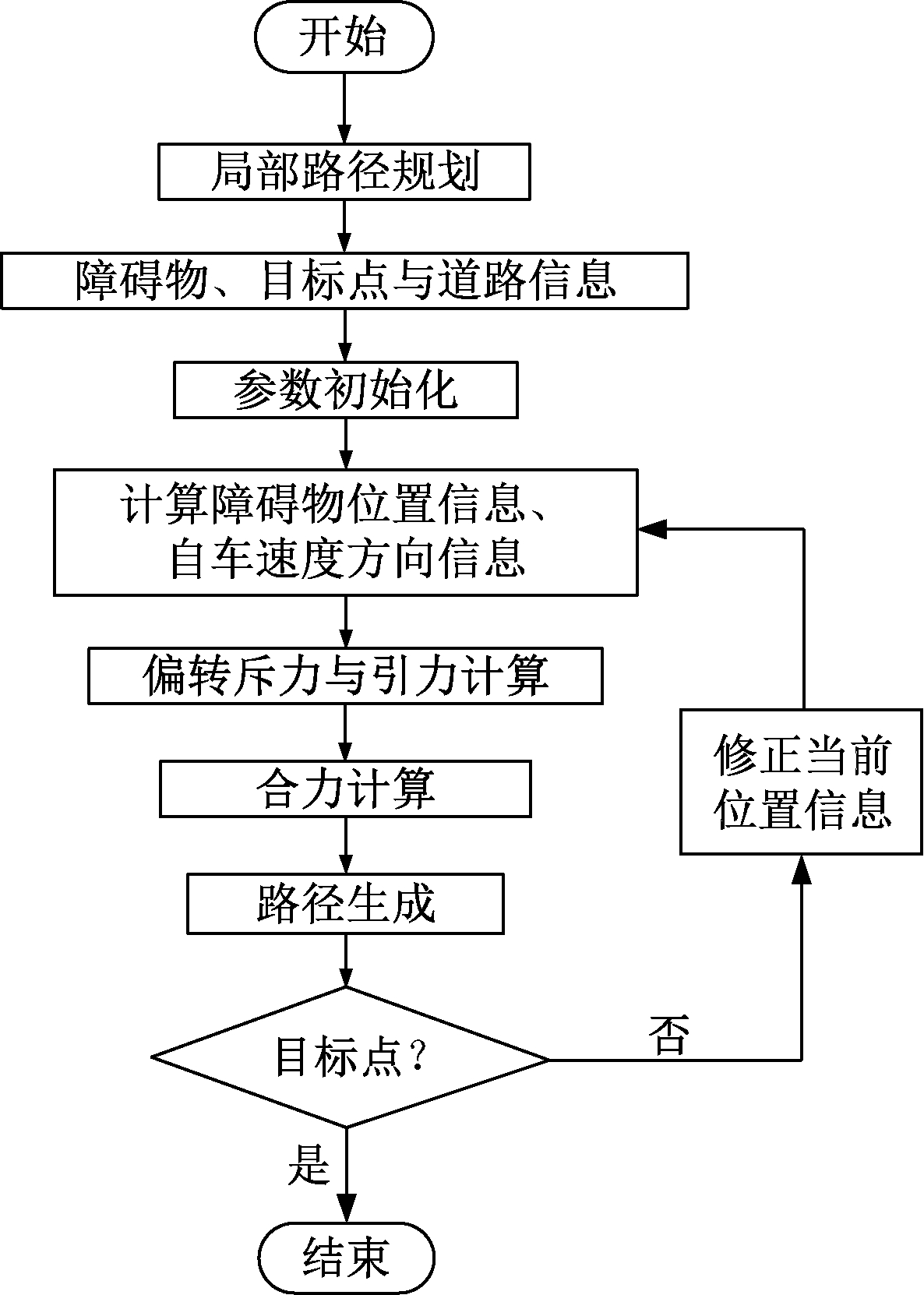
图3 改进斥力模型的人工势场算法流程
Figure 3 Flow chart of improved artificial potential
field algorithm for repulsive model
3.2 偏转角度的选取
如图2所示,障碍物4和5的距离l≥l0时,此时不需构建虚拟障碍物,汽车可以从2个障碍物中间顺利通过,如果斥力偏转角度过小,汽车可能由于存在局部最优点无法正常通过;在l=l0时,此时能通过障碍物的斥力偏转角度为最小偏转角度。
为确定最小偏转角度,设定以下仿真条件:障碍物2和障碍物3距离3.5 m,道路附着条件良好,仿真道路为车道宽3.5 m同向三车道,中间车道中心线为汽车行驶参考中心线,道路边界约束的安全系数w1=0.5,起点位于坐标原点,障碍物位置(50,1.75),(50,-1.75),目标点位置(100, 0)。仿真结果表明:当偏转角度α≥36°时,汽车速度为20 m/s,可顺利通过障碍物到达目标点。
为进一步确定偏转角度,选取单个障碍物位于(50,0)、偏转角度α∈[36°,50°]变化下进行仿真计算。从汽车主动安全出发,把安全性指标QS[10]、路径曲率k、最大侧向偏移量及路径总转角作为评价指标。图4给出了路径曲率峰值和路径总转角的变化,可以看出,当偏转角度36°≤α≤42°时,曲率峰值不变,路径总转角在逐渐增加;α>42°以后增加速率加快。由此可见,36°≤α≤42°时曲率峰值和路径总转角指标好且稳定。图5为安全性指标与最大侧向偏移量的变化,随着偏转角度的增加,其安全性指标和最大侧向偏移量在缓慢减小,36°≤α≤42°时安全性指标值变化了0.03,最大侧向偏移量变化0.03,说明此范围内安全性指标与最大侧向偏移量好且稳定性高。
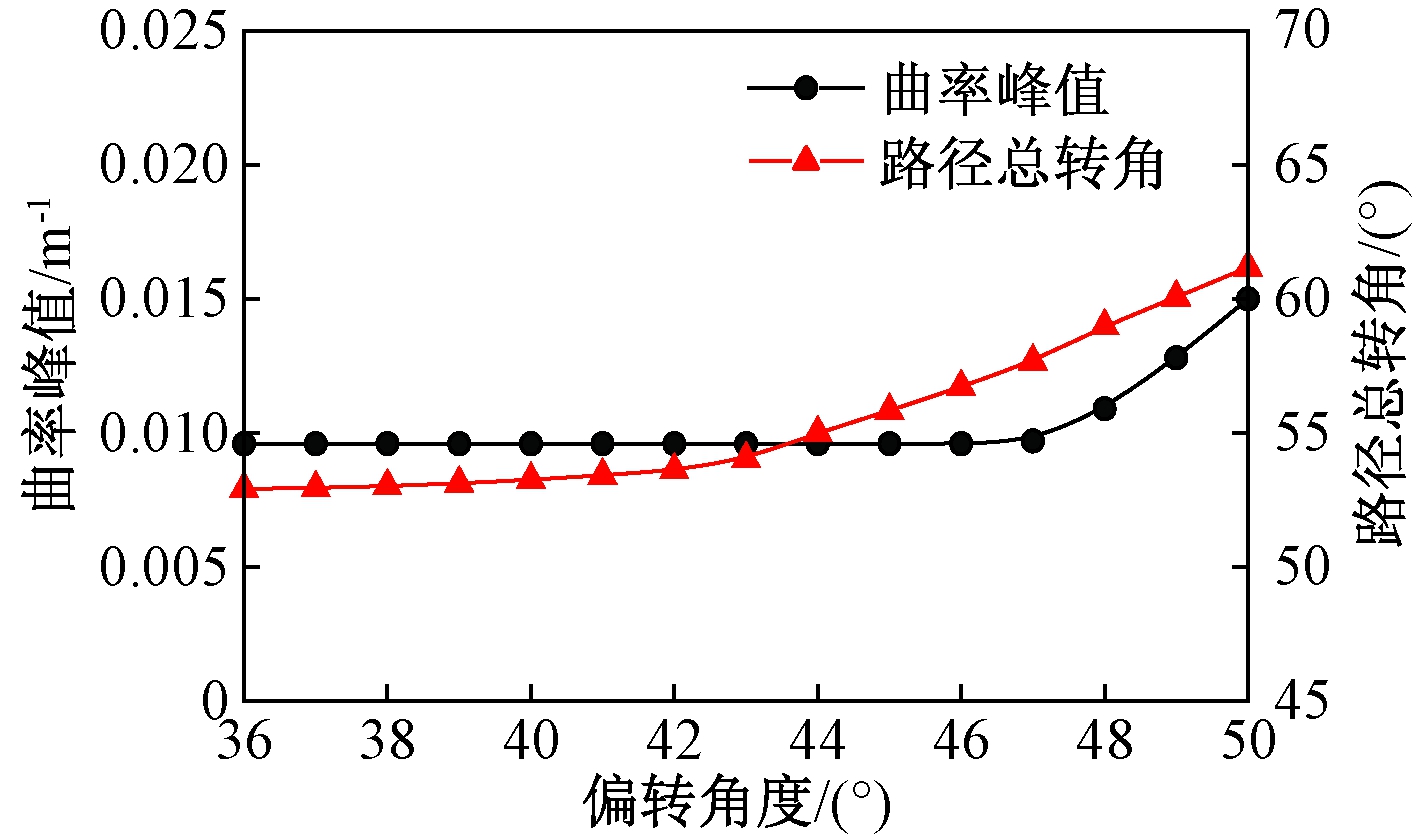
图4 不同偏转角度的曲率峰值与路径总转角
Figure 4 Curvature peak of different rotation angle
and total rotation angle of path
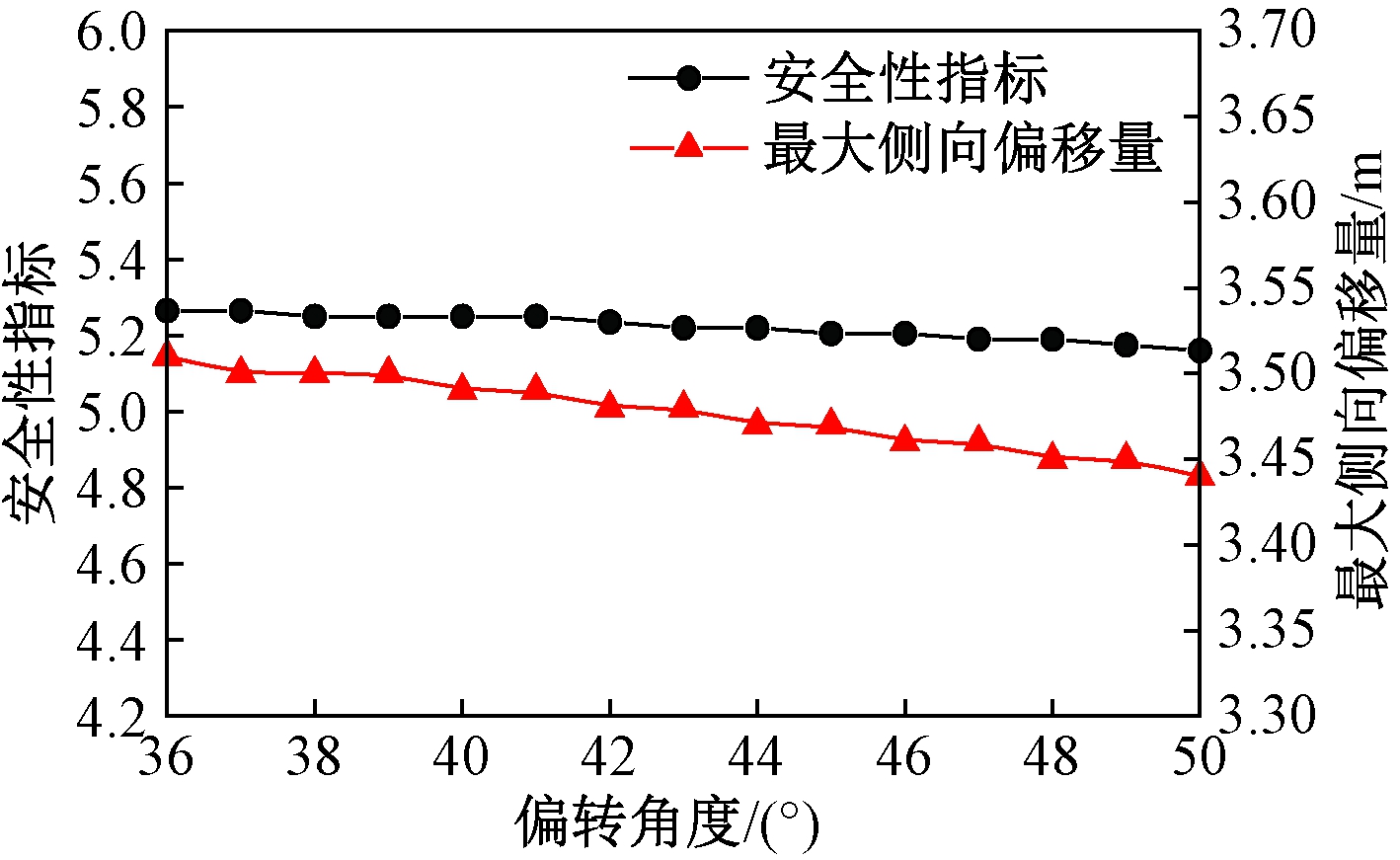
图5 不同偏转角度的安全性指标与最大侧向偏移量
Figure 5 Safety index and maximum lateral deviation
at different deflection angles
3.3 局部路径规划仿真
如前文所述,当36°≤α≤42°时规划的局部路径具有稳定性高、安全性好的特点,这里选择偏转角度α=40°来对自动驾驶车辆进行局部路径规划仿真计算。道路参数以及车辆参数选取与3.2节相同,图6(a)和6(b)分别为单一障碍物与相近障碍物2种行驶环境下的路径规划结果。从图6中可以看出,不论哪种行驶条件,传统人工势场方法都很容易陷入局部最优点,导致路径规划失败,而改进斥力模型方法可以正确地规划出完整的局部路径。因此,当选择合适的偏转角时,改进斥力模型方法可以有效解决路径规划中出现局部最优的问题。
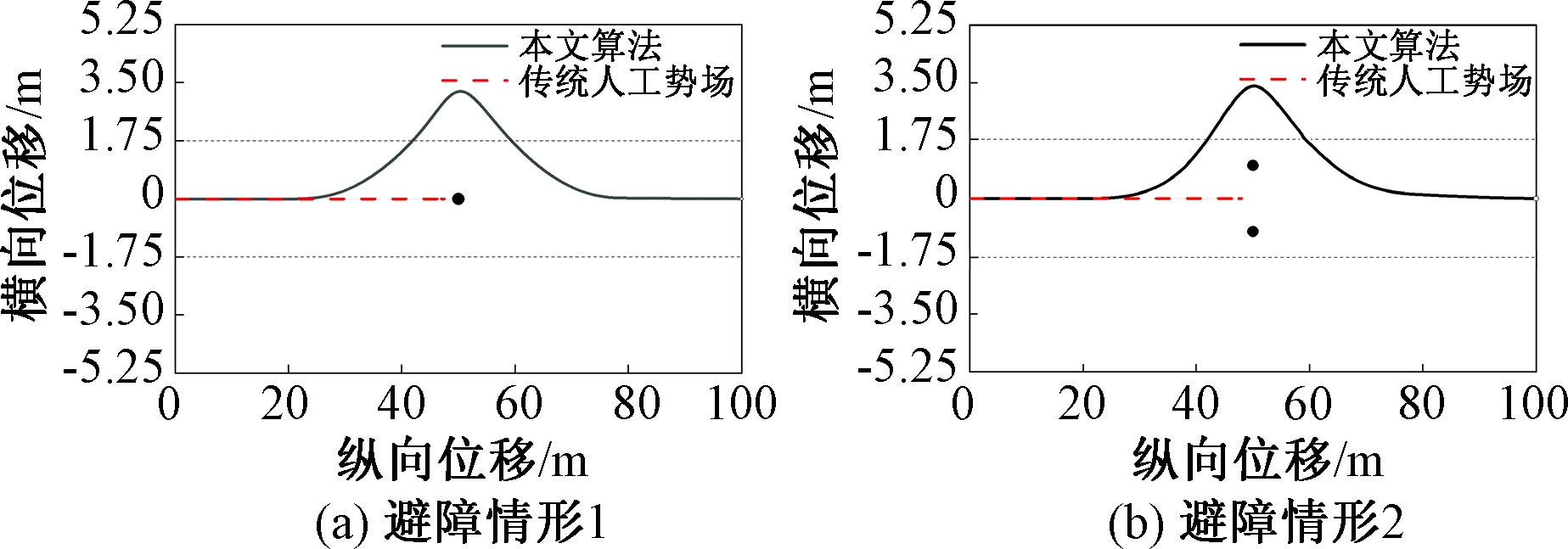
图6 路径对比图
Figure 6 Path contrast diagram
多障碍物环境是自动驾驶中经常出现的情形,该环境下科学的局部路径规划对于车辆自动驾驶实现具有重要意义。下面针对该环境进行局部路径规划,仿真中道路参数以及车辆参数选取与3.2节相同,车道长度取200 m。汽车起点坐标为(0,0),多个障碍物坐标分别为(30,-0.5)、(60,3)、(100,-1)、(100,1)、(140,3.5)、(140,-3.5)和(170,1),目标点坐标为(200,0)。图7为3种算法的局部路径和路径曲率的对比,3种算法分别为传统人工势场算法、文献[10]算法及本文算法。
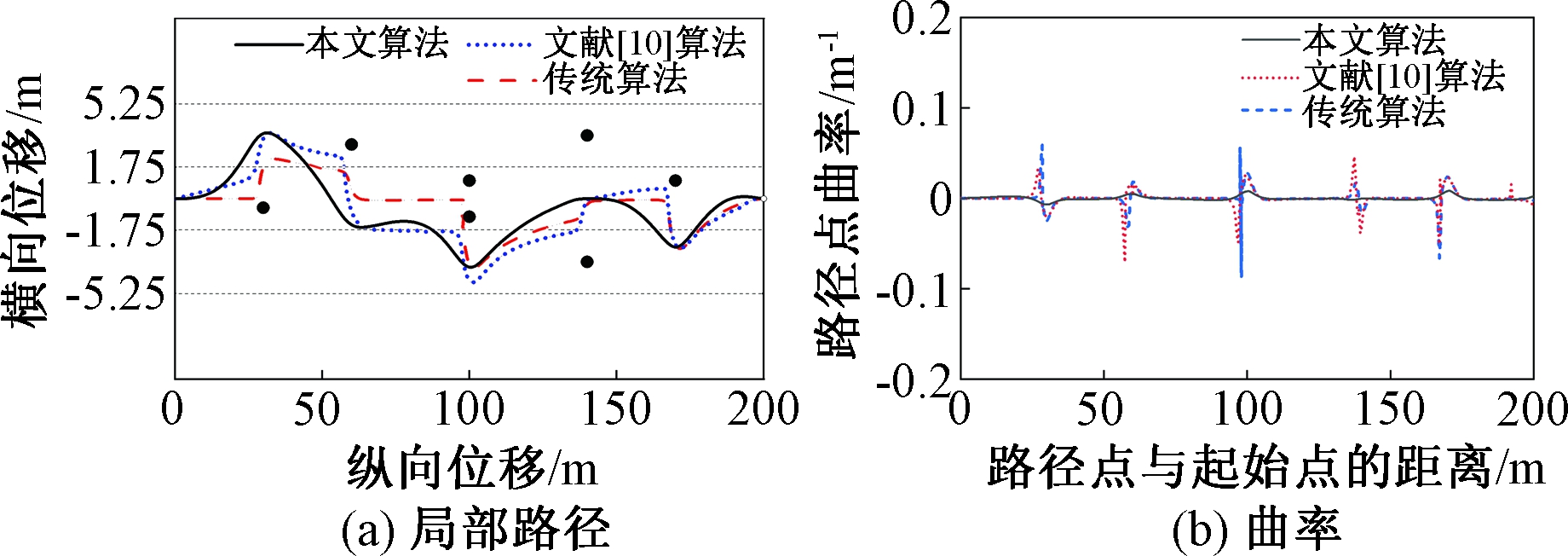
图7 3种算法的局部路径和曲率
Figure 7 Local path and path curvature of
three algorithms
由图7可以看出,传统的人工势场路径存在局部振荡点,文献[10]算法存在大转角路径点,本文改进算法能克服这些不足,改进效果明显。
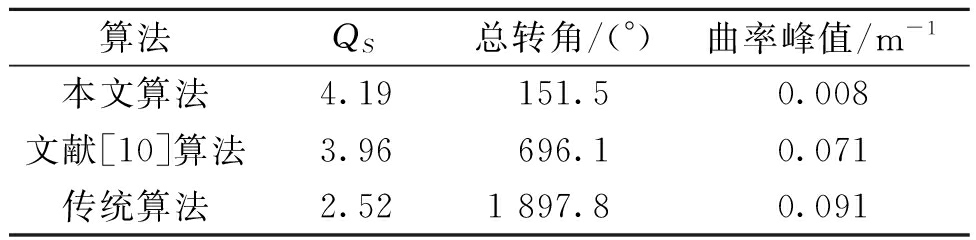
表1给出了采用3种不同算法进行局部路径规划的性能评价指标值。可以看出,相较于传统算法和文献[10]算法,本文算法在安全性指标QS上提高明显,分别提高了1.67和0.23;路径总转角以及曲率峰值显著下降,路径总转角分别降低了1 746.3°和544.6°,路径曲率峰值减小到0.008 m-1,可见改进斥力模型方法能有效提高行驶安全性。
表1 3种算法性能评价指标值
Table 1 Performance evaluation index values of
three algorithms
算法QS总转角/(°)曲率峰值/m-1本文算法4.19151.50.008文献[10]算法3.96696.10.071传统算法2.521 897.80.091
4 结论
(1)根据汽车速度方向与障碍物位置以及汽车位置与道路边界之间的关系,确定斥力偏转方向以及偏转角度,当选择合适的偏转角时,改进斥力模型方法可以有效解决路径规划中出现局部最优的问题。
(2)在斥力偏转的基础上,结合对数函数性质以及人工势场理论设计新的斥力函数,把避障安全距离引入到斥力场作用范围中,在斥力函数中引入对数函数以及纵向相对距离调节因子,可使规划的路径曲率峰值以及路径总转角显著下降,提高行驶的安全性指标。
(3)基于改进斥力模型的人工势场局部路径规划方法不仅可以克服局部最优点,而且规划的路径稳定性更好、安全性更高,因此可以为车辆自动驾驶局部路径规划技术的实现提供理论支持。
[1] 宁世发, 冯忠祥. 道路交通事故成因分析[J]. 交通标准化, 2006, 34(10): 152-155.
NING S F, FENG Z X. Analysis on the cause of road traffic accidents[J]. Communications Standardization, 2006, 34(10): 152-155.
[2] 彭晓燕, 谢浩, 黄晶. 无人驾驶汽车局部路径规划算法研究[J]. 汽车工程, 2020, 42(1): 1-10.
PENG X Y, XIE H, HUANG J. Research on local path planning algorithm for unmanned vehicles[J]. Automotive Engineering, 2020, 42(1): 1-10.
[3] KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[J]. The International Journal of Robotics Research, 1986, 5(1): 90-98.
[4] LI G H, YAMASHITA A, ASAMA H, et al. An efficient improved artificial potential field based regression search method for robot path planning[C]∥2012 IEEE International Conference on Mechatronics and Automation. Piscataway: IEEE, 2012: 1227-1232.
[5] 于振中, 闫继宏, 赵杰, 等. 改进人工势场法的移动机器人路径规划[J]. 哈尔滨工业大学学报, 2011, 43(1): 50-55.
YU Z Z, YAN J H, ZHAO J, et al. Mobile robot path planning based on improved artificial potential field me-thod[J]. Journal of Harbin Institute of Technology, 2011, 43(1): 50-55.
[6] HUANG Y Q, HU H, LIU X Q. Obstacles avoidance of artificial potential field method with memory function in complex environment[C]∥2010 8th World Congress on Intelligent Control and Automation. Piscataway: IEEE, 2010: 6414-6418.
[7] 徐飞. 基于改进人工势场法的机器人避障及路径规划研究[J]. 计算机科学, 2016, 43(12): 293-296.
XU F. Research on robot obstacle avoidance and path planning based on improved artificial potential field method[J]. Computer Science, 2016, 43(12): 293-296.
[8] FEDELE G, D′ALFONSO L, CHIARAVALLOTI F, et al. Obstacles avoidance based on switching potential functions[J]. Journal of Intelligent &Robotic Systems, 2018, 90(3/4): 387-405.
[9] 范玉龙, 黄波, 周仟, 等. 基于改进人工势场法的小车避障路径规划研究[J]. 软件导刊, 2021, 20(7): 38-42.
FAN Y L, HUANG B, ZHOU Q, et al. Research on vehicle obstacle avoidance path planning based on improved artificial potential field method[J]. Software Guide, 2021, 20(7): 38-42.
[10] 张三川, 明珠. 基于主动安全的改进人工势场局部路径规划研究[J]. 郑州大学学报(工学版), 2021, 42(5): 32-36, 55.
ZHANG S C, MING Z. Research on improved local path planning of artificial potential field based on active safety[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(5): 32-36, 55.
[11] 王树凤, 张钧鑫, 刘宗锋. 基于改进人工势场法的智能车辆超车路径规划研究[J]. 汽车技术, 2018(3): 5-9.
WANG S F, ZHANG J X, LIU Z F. A research on overtaking lane planning for intelligent vehicles based on improved artificial potential field method[J]. Automobile Technology, 2018(3): 5-9.
[12] 谭宝成, 崔佳超. 改进人工势场法在无人车避障中的应用[J]. 西安工业大学学报, 2014, 34(12): 1007-1011, 1017.
TAN B C, CUI J C. Application of improved artificial potential field method in intelligent collision avoidance system on structured road[J]. Journal of Xi′an Technological University, 2014, 34(12): 1007-1011, 1017.
[13] 胡丹丹, 张琪. 基于PER-APF算法的无人驾驶汽车换道轨迹规划[J]. 计算机测量与控制, 2022, 30(6): 229-234, 241.
HU D D, ZHANG Q. Lane changing trajectory planning of driverless vehicle based on PER-APFAlgorithm[J]. Computer Measurement &Control, 2022, 30(6): 229-234, 241.
[14] 来飞, 黄超群, 董红亮. 智能汽车自动紧急避撞系统的安全距离模型及其对比分析[J]. 重庆理工大学学报(自然科学), 2020, 34(9): 39-46.
LAI F, HUANG C Q, DONG H L. Safety distance model and comparative analysis for intelligent vehicle emergency collision avoidance system[J]. Journal of Chongqing University of Technology (Natural Science), 2020, 34(9): 39-46.
[15] 冀杰, 姬鹏, 彭和, 等. 面向车辆主动避撞的三维虚拟危险势能场设计[J]. 汽车工程, 2016, 38(9): 1065-1071, 1079.
JI J, JI P, PENG H, et al. Design of 3D virtual dange-rous potential field for vehicle active collision avoidance[J]. Automotive Engineering, 2016, 38(9): 1065-1071, 1079.