无线传感器网络(wireless sensor network,WSN)是由许多感知节点所构成的一种网络[1],应用在对数据精确度比较敏感的医疗和战区监控中。由于其本身存在固有的局限性和脆弱性,易受到各种形式的攻击[2],比较典型的内部攻击有污水池攻击、虫洞攻击、选择性转发攻击等。认证、加密等方法只能防御来自网络外部的入侵和攻击,针对被妥协的内部恶意节点和故障节点,建立安全可靠的攻击检测算法是非常有必要的。
Fang等[3]采用改进的贝叶斯与信誉评估的WSN模型,通过调用一个适应性遗忘因子来减弱过去行为的影响,提高了模型的动态性和准确性。Ram等[4]以消息成功率、节点运行时间、正确性和公平性等参数作为信任度量,利用模糊逻辑处理不确定性,对不精确数据的容忍度高。Kurdi等[5]提出了基于主观逻辑的轻量级信任管理算法,能以较低的执行时间和较高的可扩展性生成准确的信任信息。Busi等[6]采用加权D-S理论计算间接信任,利用传感器数据的中值计算数据可信度,能够在更大的时间窗内检测报文丢弃攻击。Yin等[7]根据相邻节点的相应行为估计直接和间接信任值,采用熵权法确定合适的权重值提高信任量化的有效性,保证评价的客观性。尹荣荣等[8]利用云简化逆向算子对节点的间接信任值和直接信任值进行计算,采用正态云模型的隶属度函数进行推荐信任值的计算,解决信任误判问题。秦丹阳等[9]将WSN中所有节点的推荐信任、直接信任和激励因子三者相结合,利用多目标决策计算每个信任度影响因素的权重,以较低的开销抵御多种攻击。
以上文献均在一定程度上利用推荐信任、直接信任等评价指标来区分恶意节点和正常节点,但仍然存在以下问题:判断节点间信任存在主观性和模糊性,不可信推荐节点影响对间接信任的评估结果;信任值增难减易性质带来的局限性;如何选择合适的权重值和信任阈值,信任模型对攻击检测速度与精度的效率问题。
针对上述问题,本文搭建了一种融合多指标的WSN动态信任评估预测模型FSEPM(dynamic trust evaluation model integrating fuzzy comprehensive evaluation mechanism and similarity measure theory)。该模型利用模糊综合评判对直接信任分配权重,改善主观分配权重所带来的问题;采用贴近度理论对不同的推荐节点赋予权重,提高推荐信任评估的可靠性;借助加权因子对综合信任值分配权重,避免人为因素的干预;采用自适应权值动态更新综合信任值,加快恶意节点信任值的下降速度;通过信任值预测模型,将预测结果与实际信任值进行差值运算,与信任阈值对比快速检测出恶意节点,保障无线传感器网络的安全性,延长网络生命周期,实现数据的可靠传输。
1 信任评估模型
1.1 直接信任
1.1.1 通信行为信任
本文利用Beta分布对节点信誉进行拟合,得到节点的信誉reputationij符合Beta(α+1,β+1)。节点通信行为信任DTBij可以用信誉分布的统计期望表示,即
(1)
(2)
(3)
式中:αij和βij分别为节点间历史正常和非正常通信次数;Δαij和Δβij分别为在Δt时间内节点正常和非正常通信次数;κ为信誉维护函数,主要维护当前时段节点的通信行为对信誉值的影响,减少节点历史行为对信誉值的影响;θ为常数,用来确定κ作用范围;q∈[0,1]为异常弱化因子;Nint表示由于入侵因素引起节点非正常通信次数;Ndet表示网络中非正常通信总次数。
1.1.2 模糊权重
为改善主观分配权重所带来的问题,本文利用模糊综合评判[10]对直接信任分配权重。
设U={u1,u2,u3}为被评价对象的3种评价因素集合,u1、u2、u3分别表示数据发送率、节点剩余能量、处理延迟。V={v1,v2,v3}为评价者对被评价对象的评价等级的模糊集合,v1、v2、v3分别表示不可信、不确定、可信。A=(a1,a2,a3)为权重分配模糊向量,其中am分别代表第m个因素的权重,m=1,2,3且a1+a2+a3=1,为降低权重分配的主观性,满足精度要求,参考三标度法建立判断尺度表可以求得a1=0.633 4,a2=0.260 5,a3=0.106 1。再将各因素归一化到[0,1]内,将3种评价因素作为输入变量,代入梯形隶属度函数,得到隶属度矩阵R,梯形隶属度函数如图1所示。
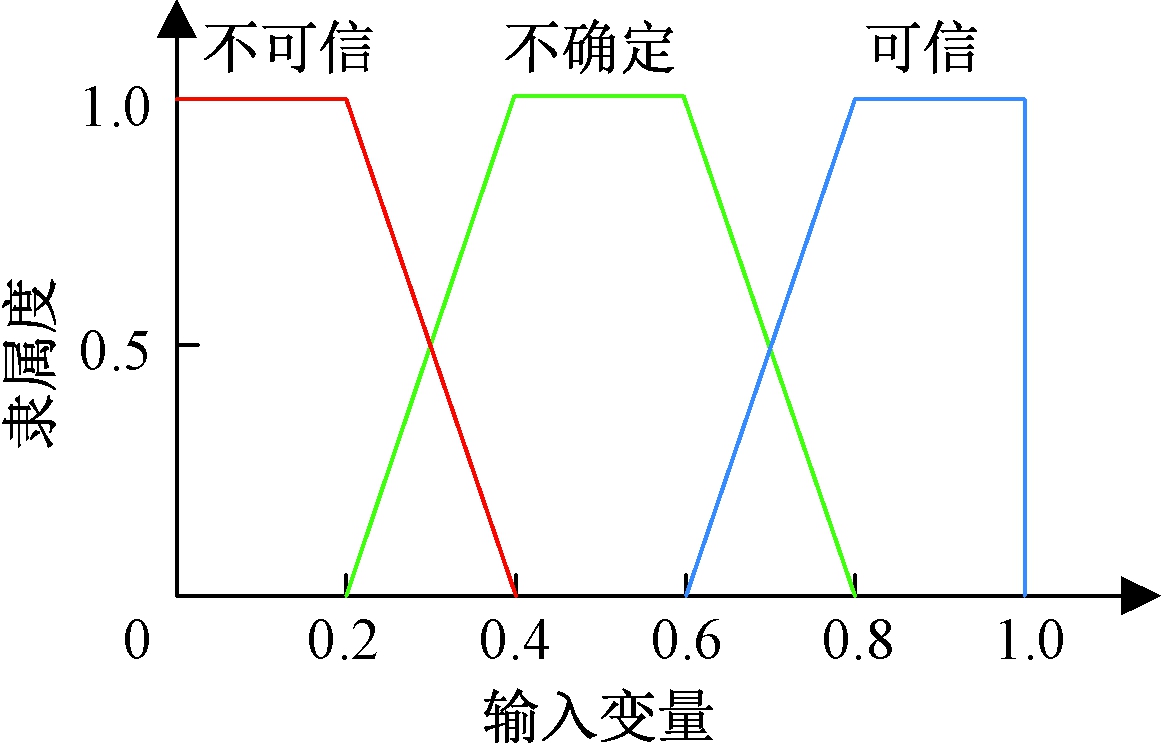
图1 梯形隶属度函数图
Figure 1 Graph of the trapezoidal
membership function
确定评价因素权向量A与隶属度矩阵R后,本文采用加权平均型的乘法-有界算子,将U上的模糊向量A利用模糊变化变成V上的模糊向量B,具体计算过程为

[b1,b2,b3]。
(4)
式中:∘为模糊综合评判中的合成算子;bm为在信任评价模糊子集vm中被评价节点的隶属程度。
权重ωij为
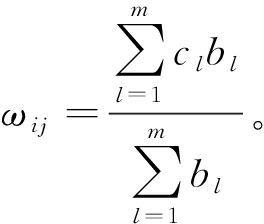
(5)
式中:cl为信任等级,参考模糊向量单值法,将不可信、不确定、可信3个信任等级定义为c1=0.2、c2=0.5、c3=0.9。
1.1.3 直接信任值
节点的直接信任计算公式为
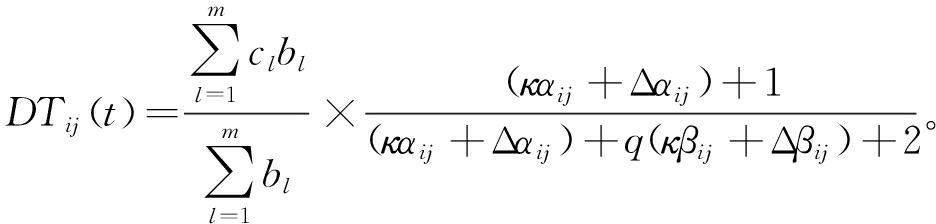
(6)
1.2 间接信任
节点的间接信任值由推荐节点(两节点间的公共邻居节点)计算得出。由于推荐节点也存在不可信现象,本文采用贴近度理论对不同的推荐节点赋予权重,提高推荐信任评估的可靠性。图2为推荐信任图。如图2所示,节点i向在其通信半径内的邻居节点广播一个查询信息用来获得节点j的推荐信任值,推荐节点k收到节点i的广播信息后,将它对节点j的直接信任值返回给节点i。假设有n个推荐节点,相应的有n个推荐信任![]() 其中
其中![]()
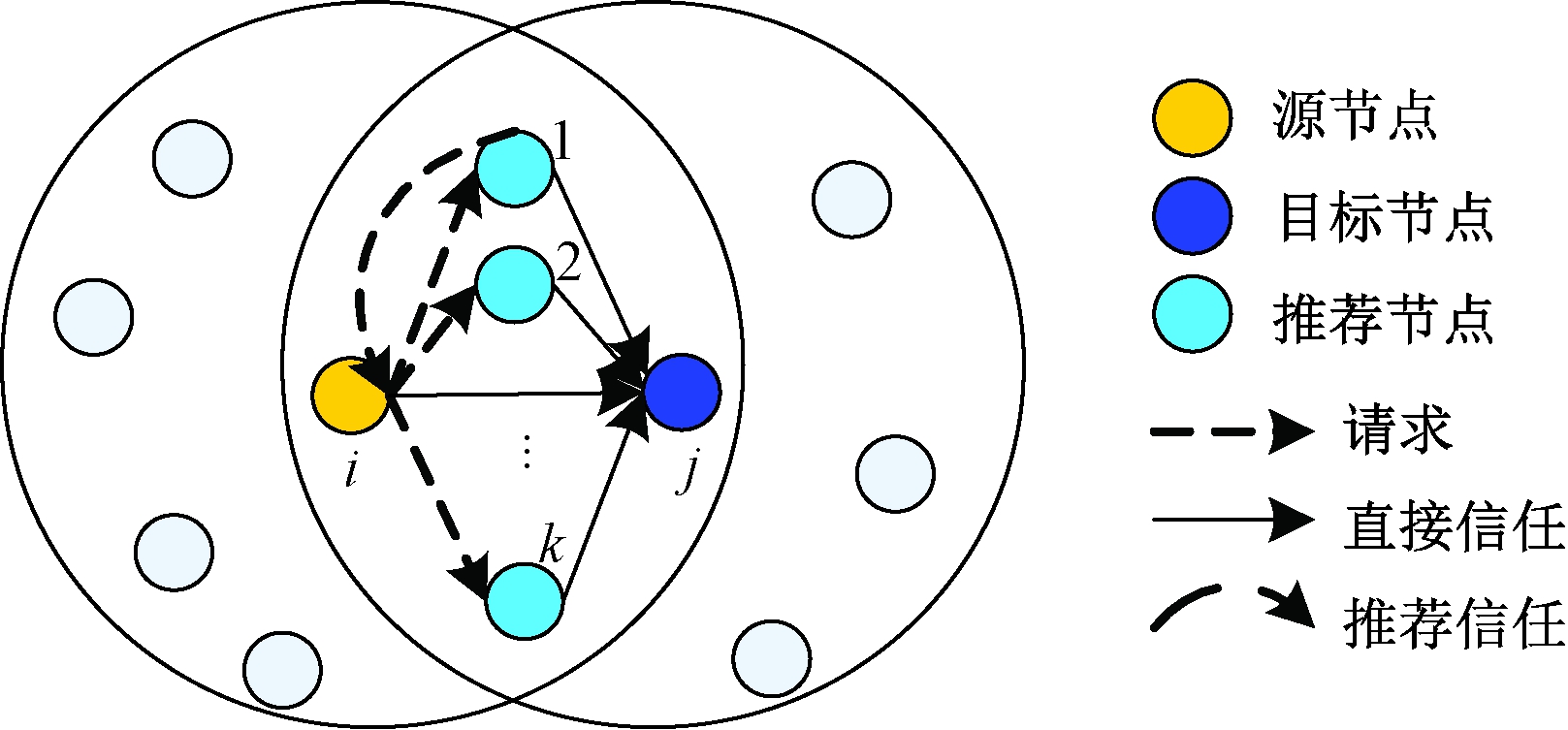
图2 推荐信任图
Figure 2 Recommended trust graph
本文采用离散型最小-平均贴近度,计算各推荐节点的交互贴近度为
(7)
推荐节点的交互贴近度![]() 越小,推荐节点的信任程度就越低,越可能是来自恶意节点的虚假推荐,计算间接信任时不考虑此类推荐节点。设置贴近度界限值ε,将贴近度
越小,推荐节点的信任程度就越低,越可能是来自恶意节点的虚假推荐,计算间接信任时不考虑此类推荐节点。设置贴近度界限值ε,将贴近度![]() 的推荐节点滤除。将
的推荐节点滤除。将![]() 的节点加入到可信推荐节点集合S中,于是,各推荐节点的权重σk可通过集合S中贴近度归一化计算得到:
的节点加入到可信推荐节点集合S中,于是,各推荐节点的权重σk可通过集合S中贴近度归一化计算得到:
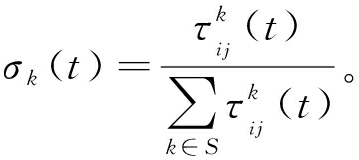
(8)
因此,由式(9)计算可得到间接信任:
(9)
1.3 综合信任
为提高信任模型的检测精度,综合信任值由节点的间接信任值与直接信任值进行加权求和得到,公式如下:
CTij(t)=γDTij(t)+(1-γ) ITij(t)。
(10)
式中:γ∈(0,1]为加权因子,其大小由直接信任值以及间接信任中的变量共同确定。
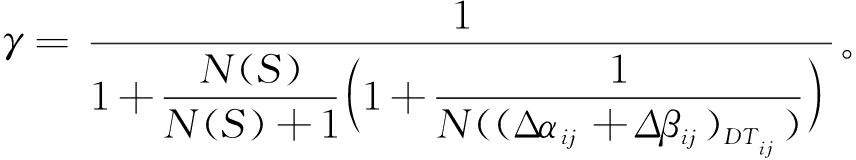
(11)
式中:N((Δαij+Δβij)DTij)表示在直接信任中Δt时间内正常和非正常通信的总交互次数;N(S)表示在可信推荐节点集合中推荐节点的个数。
2 信任值预测模型
2.1 信任值更新
信任值更新时,将上一周期的综合信任值CTij(t-1)加到更新计算中,可以使信任值的迭代上升速度变缓,恶意节点的信任值下降速度加快,此时综合信任值![]() 计算公式如下:
计算公式如下:
(12)
(13)
式中:ΔCTij=CTij(t)-CTij(t-1);λ为自适应权值;η表示权值λ对信任差ΔCTij的敏感程度,本文选取η=10。当信任值上升,信任差ΔCTij>0时,λ>0.5,即t-1时刻的信任值的权值更大,会更多地考虑前一周期的信任值,信任值的增长速度减缓;反之,当信任差ΔCTij<0时,λ<0.5,此时将会更多地考虑当前周期的信任值,使得信任值的整体下降速度加快。
2.2 信任值预测
综合信任值是基于不同时间收集的数据,将数据看作一个时间序列,并随时间变化。信任值不断更新,信任数据存在相关性,由于各个时间序列数值不是独立的,所以可以通过过去时刻的数据推断出未来时刻的数据。因此,可依据窗口中信任数据的相关性搭建信任值预测模型。
利用正常状态的数据建立预测模型,与当前状态对比。本文借助AR(auto-regressive)模型处理信任数据[11-12],与其他模型相比,本文采用的模型处理速度较快且整体运算量较低,非常适合WSN异常检测环境。采用滑动时间窗对综合信任值进行预测。图3为滑动时间窗口。
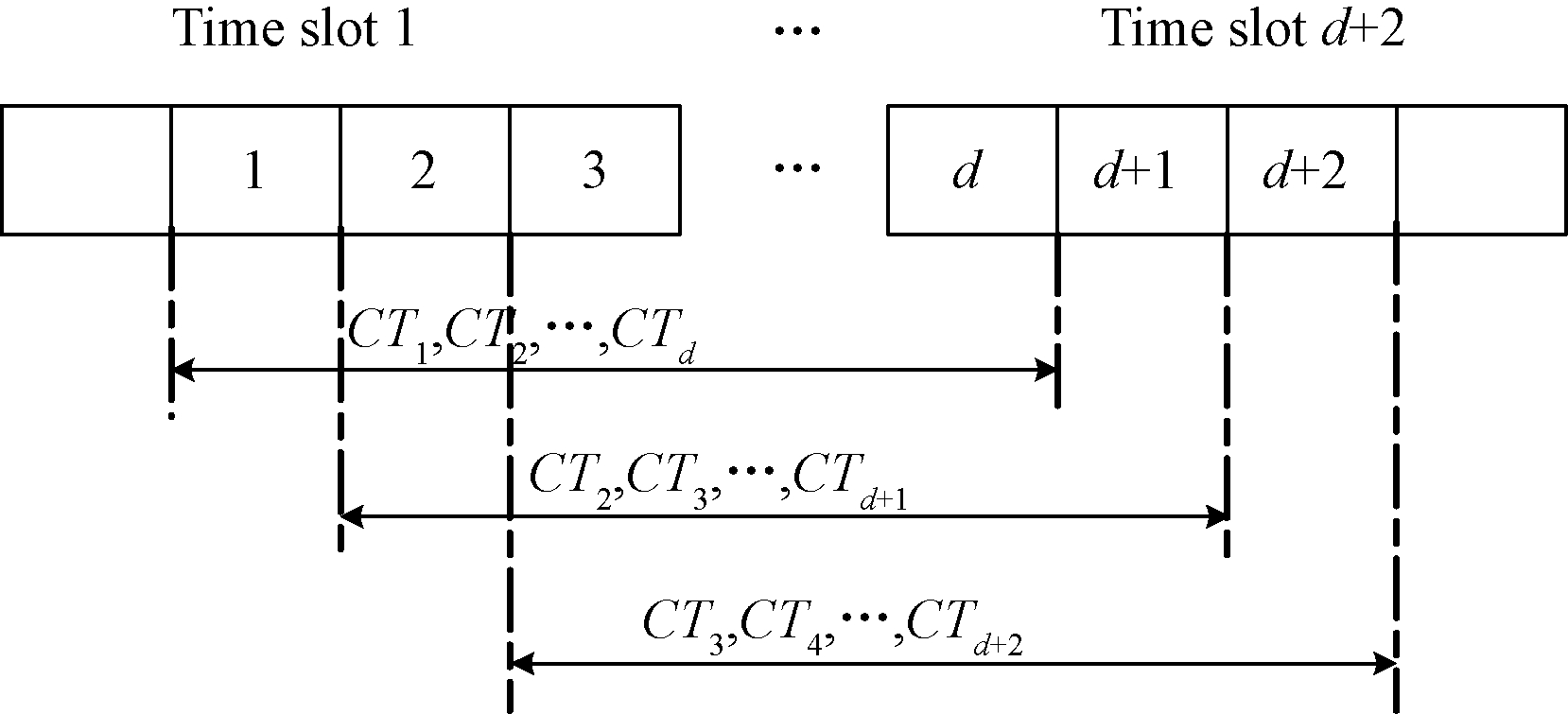
图3 滑动时间窗口
Figure 3 Slide the time window
如图3所示,随着信任值数据的不断更新,时间窗口不断向后进行迭代,通过窗口采集到d个时间序列{CT1,CT2,…,CTd},并建立AR(p)模型,预测CTd+1。采用最小二乘法估计AR(p)模型的未确定参数。采用AR(2)模型预测信任值,AR(2)模型的表达式如下:
CTd+v=φ1CTd+v-1+φ2CTd+v-2+ed+v。
(14)
式中:φ1、φ2为AR(2)模型的未确定参数;ed+v为干扰项,本文中正常节点信任值缓慢上升,可令ed+v=0,v为滑动变量,v=0,1,…,W(W=迭代周期-d-1)。AR(2)模型中的未确定参数可以被CTd+v所估算。计算过程为
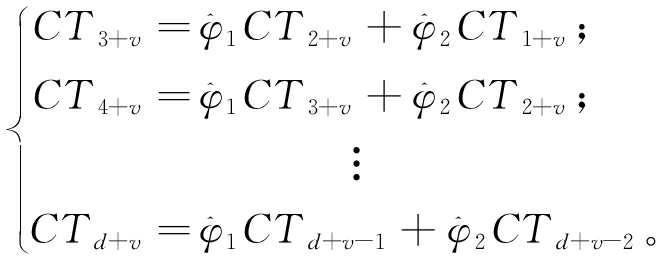
(15)
通过最小二乘法估算,得出估算数值![]() 流程如下:
流程如下:
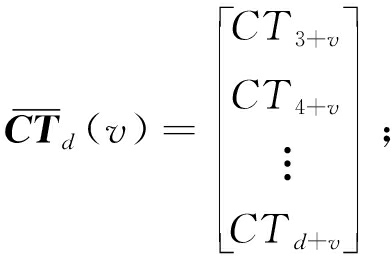
(16)
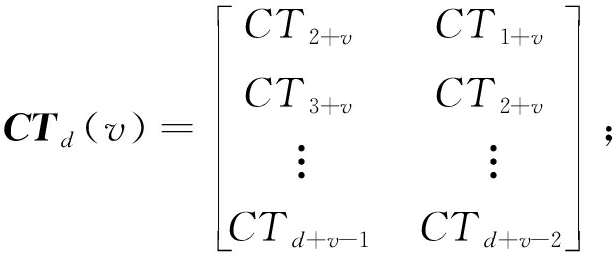
(17)
(18)
得到的单步预测模型为
(19)
最后,比较预测信任值和实际信任值的差值是否超过信任阈值,超出则判定为恶意节点。
FSEPM信任模型包括直接信任模块、间接信任模块、信任集成模块、信任更新模块和信任预测模块,流程图如图4所示。
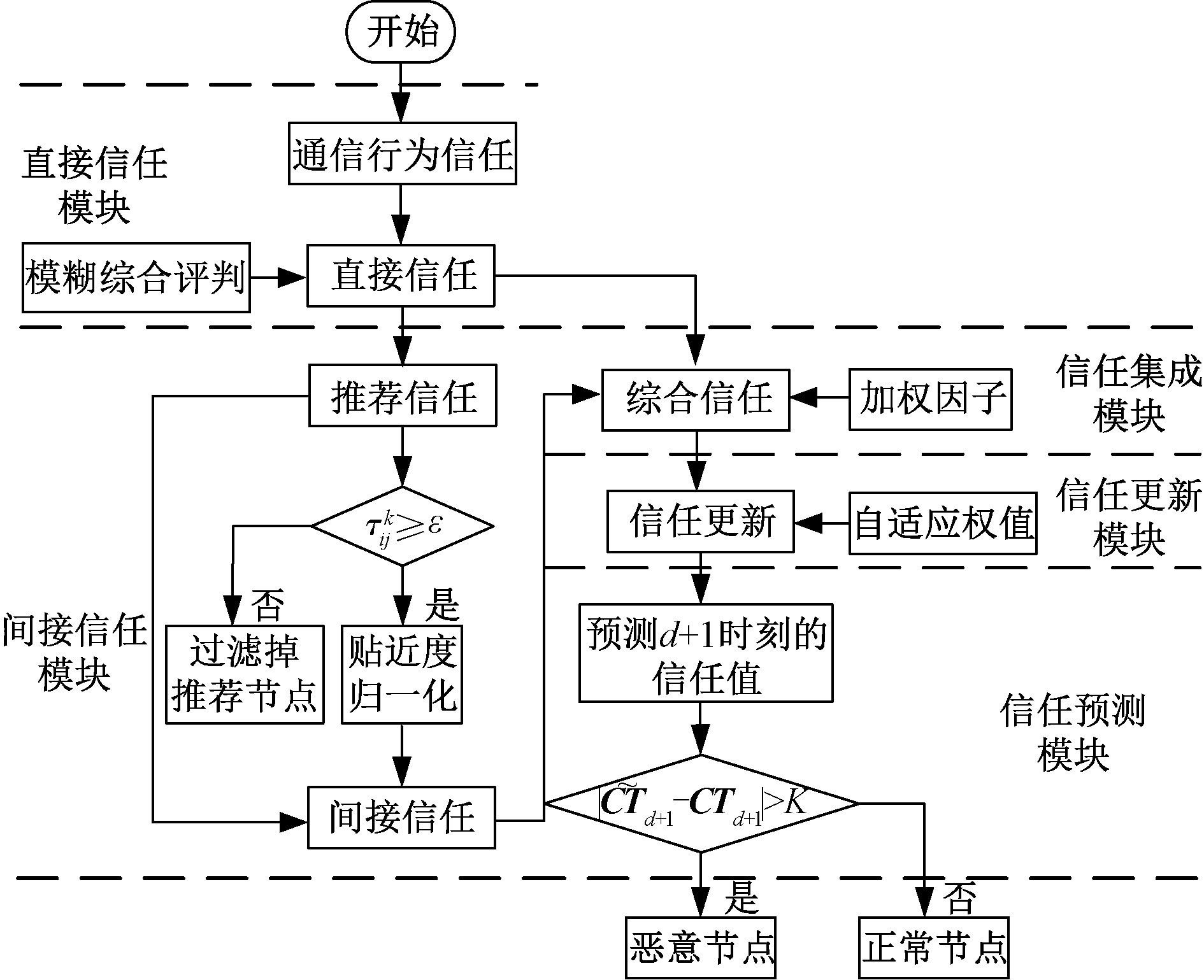
图4 FSEPM模型流程图
Figure 4 FSEPM model flow chart
3 仿真分析
本文采用MATLAB2020b来搭建仿真环境,定义正常节点数据转发率为0.9~1.0,恶意节点以0.1~0.5的概率丢弃数据包,每进行一次迭代后评估一次所有节点的信任值,将一次迭代所需时间分成若干个时间段,每个时间段进行一次转发率的记录。选取不同恶意节点比例分析性能,详细参数如表1所示。
表1 仿真参数
Table 1 Simulation parameters
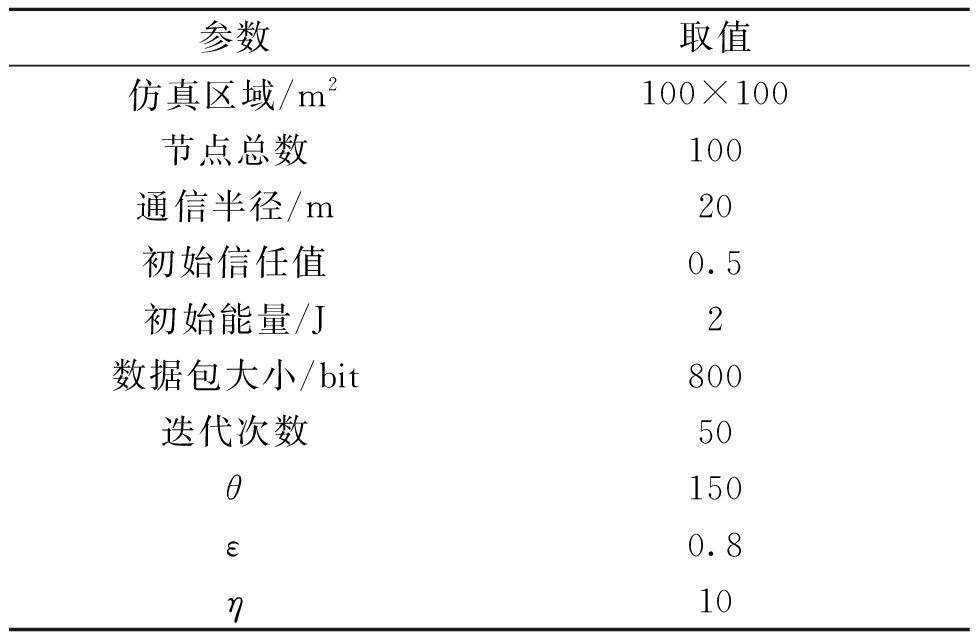
参数取值仿真区域/m2100×100节点总数100通信半径/m20初始信任值0.5初始能量/J2数据包大小/bit800迭代次数50θ150ε0.8η10
3.1 检测方法有效性验证
3.1.1 恶意节点信任值分析
图5为恶意节点信任值变化曲线。如图5所示,在不同恶意节点比例下,对网络中恶意节点在每个时间段所得到的信任值取平均值,随着恶意行为次数的累积,信任值总体呈下降趋势,通过对信任值进行分析,为信任评估检测提供参考。
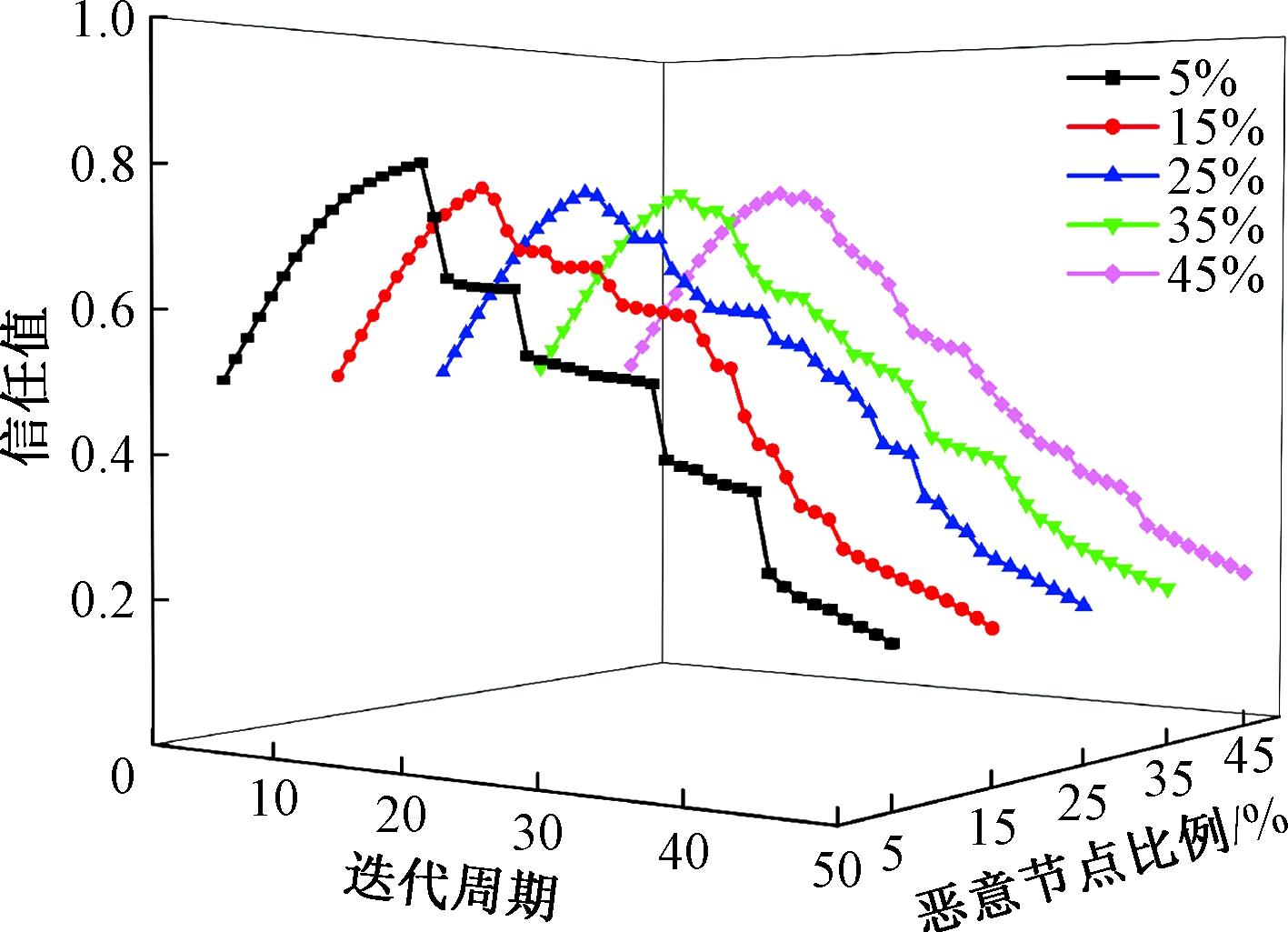
图5 恶意节点信任值变化曲线
Figure 5 Malicious node trust value change curve
3.1.2 信任阈值的选取
本文采用检测率DR和误检率FPNR对算法性能进行评价,公式如下:
(20)
(21)
图6为信任阈值对检测率和误检率的影响。由图6(a)可以看出,随着信任阈值的增加,检测率从0.30开始呈下降趋势,在不同的恶意节点比例场景下,当信任阈值在[0,0.30]时,所有的恶意节点能够被有效识别,检测率达到1;随着信任阈值由0.30提高到0.50,恶意节点被识别的个数在减少,出现明显的漏检,导致恶意节点检测率快速减小。由图6(b)可以看出,当信任阈值由0增加到0.50时,误检率先骤减,在达到一定阈值后逐渐上升;在信任阈值为[0.15,0.30]时,误检率达到最低;当阈值大于0.30后,误检率增高,恶意节点所占比例越大,误检率的增加速度越快,直到达到峰值。综合考虑检测率和误检率实验结果,选取[0.15,0.30]作为本文信任评估模型的信任阈值的取值范围。根据正态分布的3σ原则,数值分布在[μ-3σ,μ+3σ]内的概率为99.7%,μ=0.225,σ=0.025。基于该原则,取正态分布x=μ对称轴为信任阈值K,则K取0.225。
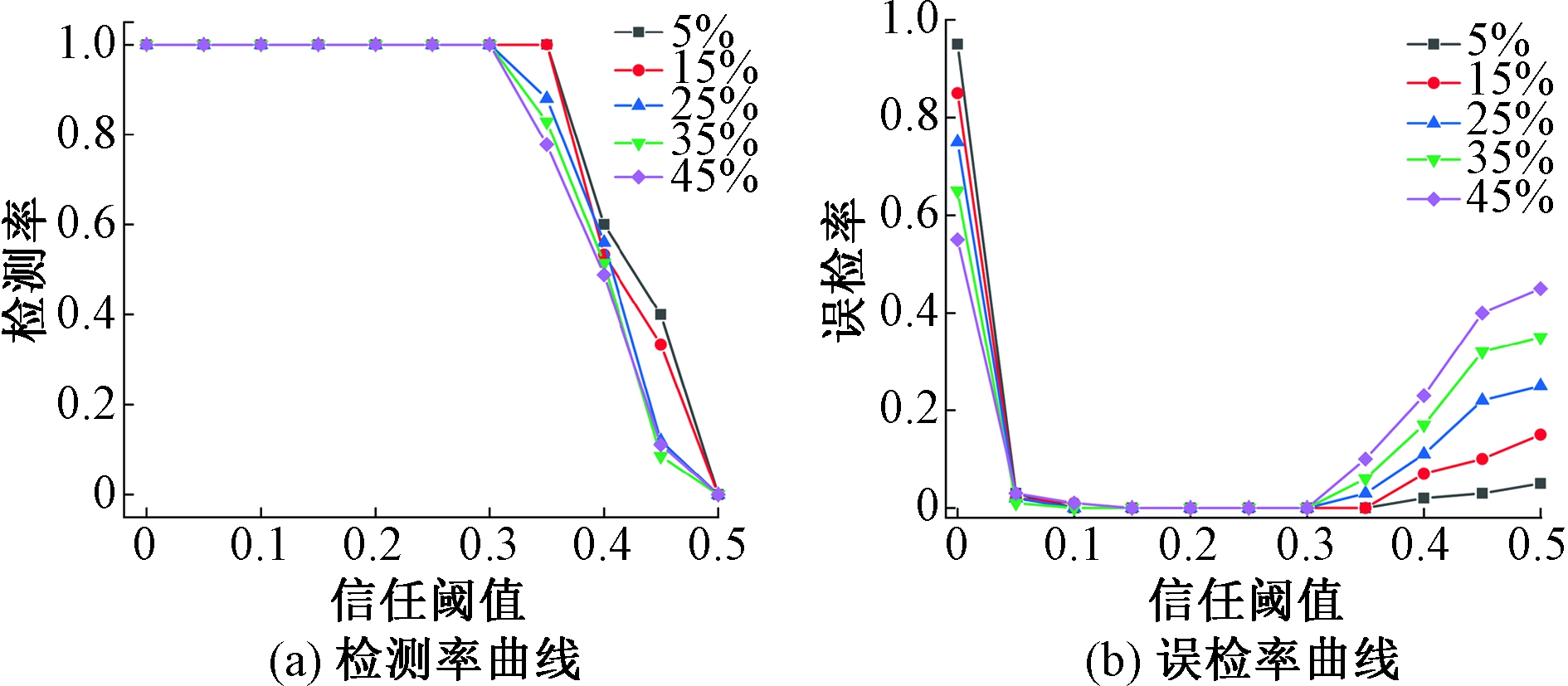
图6 信任阈值对检测率、误检率的影响
Figure 6 Effect of trust threshold on detection
rate and false detection rate
3.2 本文检测方法与其他方法的性能对比分析
在MATLAB平台上进行性能评估和安全评估,将BTMS[13]、ATSDA[14]和FSEPM模型进行比较。
3.2.1 信任值分析
图7为正常节点和恶意节点的信任值比较。由图7可以看出,对于正常节点之间的综合信任,BTMS信任值的增长速度要快于其他2种算法;在ATSDA中,由于开始时受到惩罚因素和调节函数的影响,信任值的增长速度比BTMS算法要慢;FSEPM将历史因素加入到信任值更新中,其信任值的增长速度慢于BTMS和ATSDA,可有效避免短时间内信任的迅速提升。另一方面,对于恶意节点之间的综合信任,由于FSEPM的信任差ΔCTij<0,λ会更接近0,此时更多考虑当前时刻的信任值,导致更新后的节点信任值更小,综合信任值比其他算法的综合信任值下降更快,可更准确评估节点之间的信任,敏锐反映节点交互行为的变化。
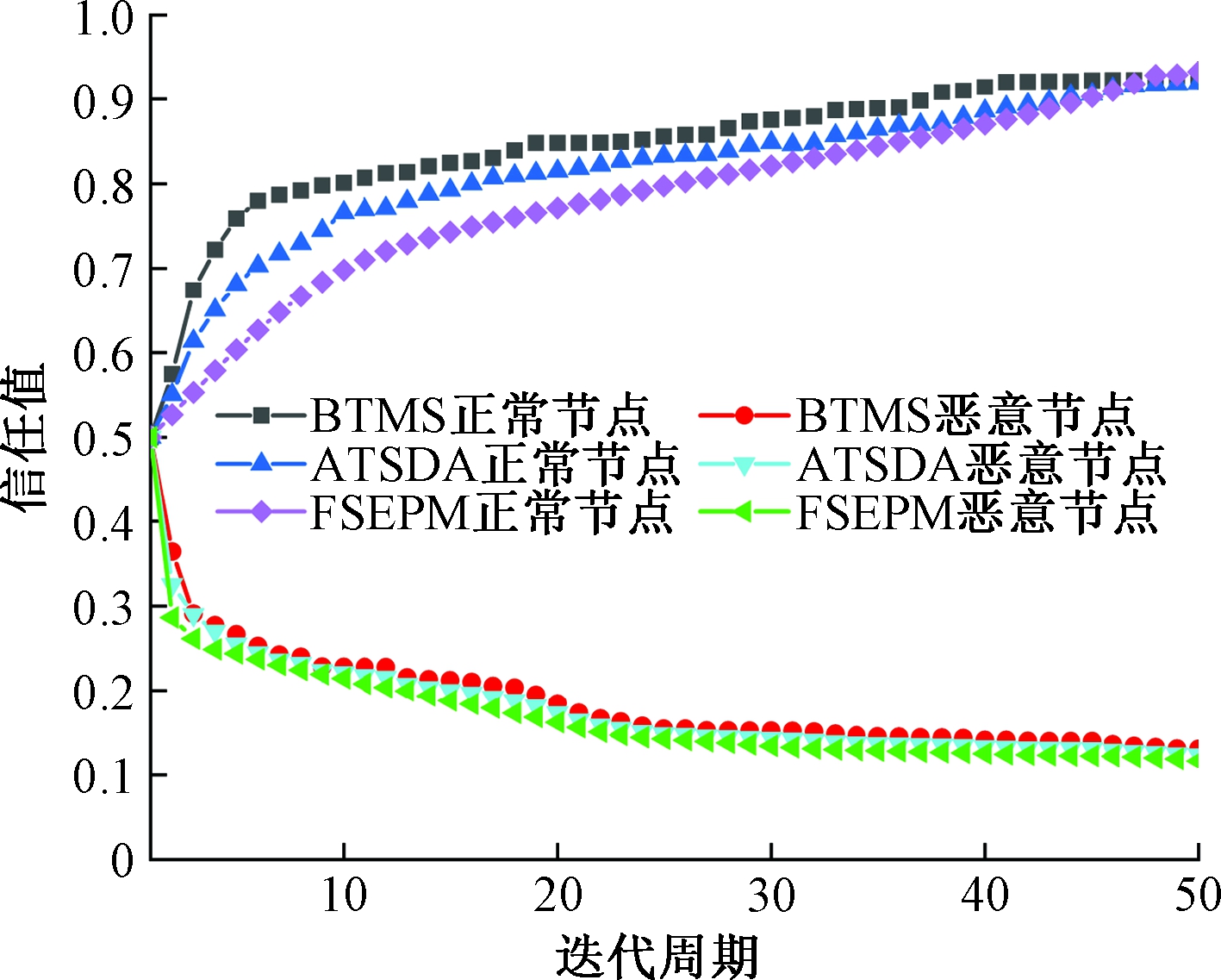
图7 正常节点和恶意节点的信任值比较
Figure 7 Comparison of trust value for normal node
and malicious node
3.2.2 检测率和误检率的对比分析
图8为不同恶意节点比例对检测率和误检率的影响。由图8(a)可以看出,4种信任模型的检测率都随着恶意节点比例的增加呈下降趋势。计算综合信任时,在BTMS模型中,直接信任未超出信任阈值时,才考虑直接信任和间接信任;在ATSDA模型中,很难确定节点间交互次数阈值,从而影响节点的信任值确定和检测准确性。而FSEM模型与FSEPM模型以模糊综合评判和贴近度对信任值分配权重,利用直接信任和推荐信任中的因素对综合信任分配权重,降低人为分配权重给评估模型带来的影响,减轻了决策者的负担,增强了模型的普适性,使检测结果更准确。
由图8(b)可以看出,随着恶意节点占比的逐渐增加,4种方法的误检率呈上升趋势。BTMS和ATSDA模型仅通过节点间交互行为判断节点的信任值,而FSEM和FSEPM模型综合考虑了节点的多指标变化情况判定节点状态,但由于信任值增难减易的特性,影响对节点性质的判断速度。因此,本文FSEPM模型是以信任值为数据构建的预测模型,能够将预测信任值与实际信任值相差较大的节点快速找出,识别出恶意节点,使得检测结果更加准确。结果表明,FSEPM具有较强的信任评估能力和检测攻击能力。
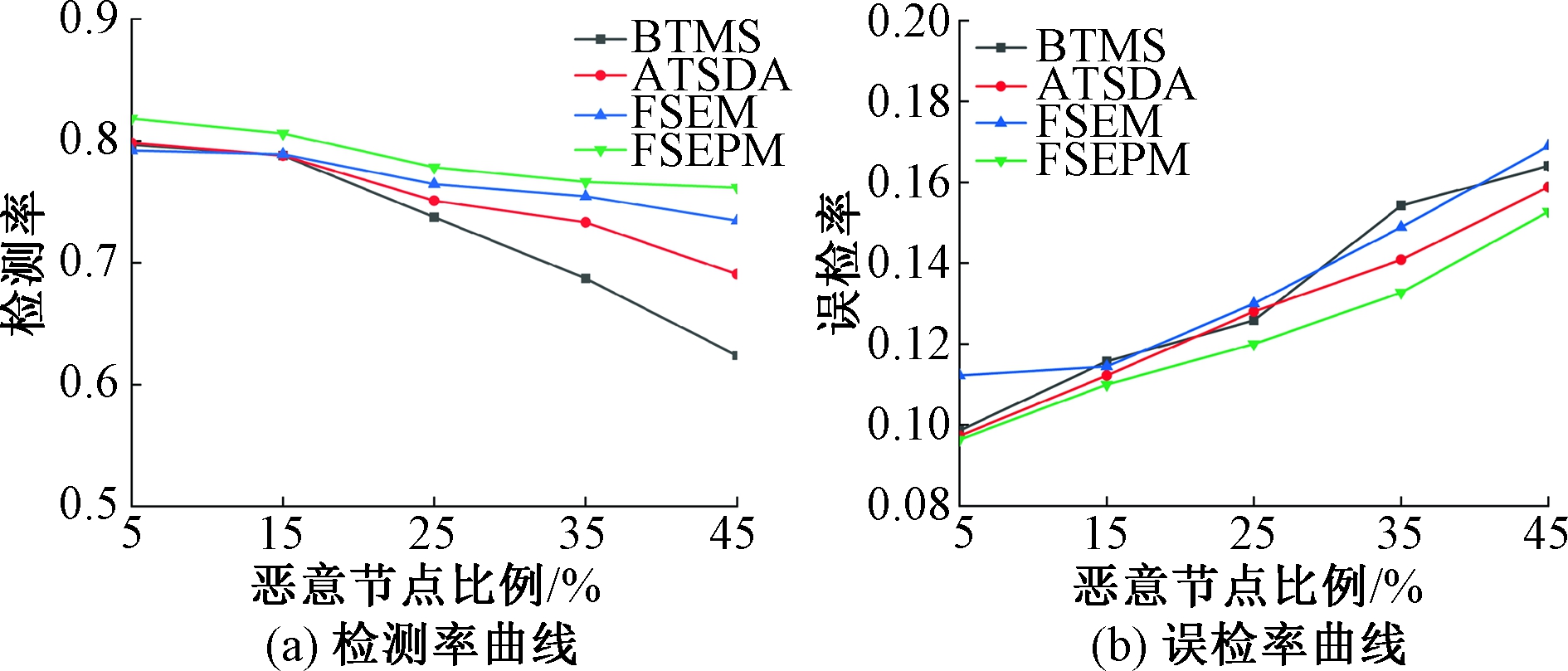
图8 恶意节点比例对检测率和误检率的影响
Figure 8 Effect of malicious node ratios on detection
rate and false detection rate
3.2.3 不同攻击的检测率对比分析
图9为不同信任模型下的攻击检测率。由图9可以看出,FSEPM模型在污水池攻击、虫洞攻击、选择性转发攻击和开关攻击这4种典型攻击中的检测率仍高于BTMS和ATSDA模型。因此,FSEPM模型能够提高WSN的安全性,及时准确地发现并检测出恶意节点,将恶意节点在全网隔离,降低网络损耗,延长网络生命周期,实现数据的可靠传输。
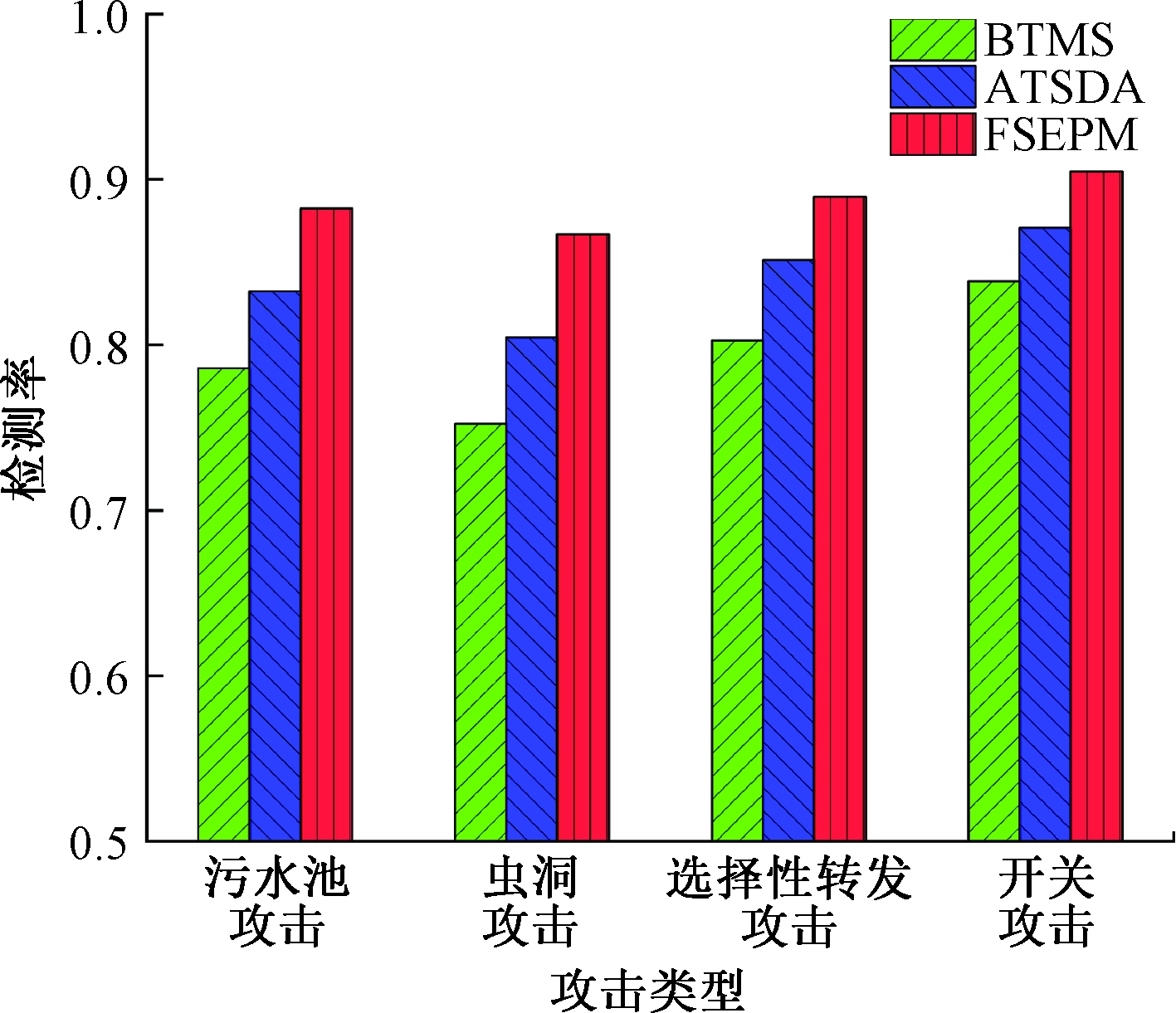
图9 不同信任模型下的攻击检测率
Figure 9 Attack detection rate with different trust models
4 结论
本文针对WSN安全问题,提出一种融合多指标的WSN动态信任评估预测模型。该模型首先采用模糊综合评判对直接信任值分配权重,改善主观分配权重带来的问题,同时利用贴近度理论计算间接信任,不考虑虚假推荐;其次,运用直接信任和间接信任变量得出自适应权值计算综合信任;最后,采用AR预测模型将预测信任值和实际信任值进行差值运算,与信任阈值比较检测出恶意节点。仿真结果表明,本文提出的FSEPM模型相较于其他模型具有明显优势,WSN中恶意节点的信任值下降程度明显,结合预测模型能有效检测出恶意节点,模型检测率较高,误检率较低。WSN在攻击检测方面还有待进一步研讨,下一阶段将针对污水池攻击方式完善信任评估模型,提升FSEPM模型的实用性及网络的安全性。
[1] 李建坡, 张庆华, 张展图, 等. 基于拥塞控制的无线传感器网络能耗优化路由算法[J]. 东北电力大学学报, 2020, 40(4): 69-74.
LI J P, ZHANG Q H, ZHANG Z T, et al. Congestion control and energy optimization routing algorithm for wireless sensor networks[J]. Journal of Northeast Electric Power University, 2020, 40(4): 69-74.
[2] 张安琳, 张启坤, 黄道颖, 等. 基于CNN与BiGRU融合神经网络的入侵检测模型[J]. 郑州大学学报(工学版), 2022, 43(3): 37-43.
ZHANG A L, ZHANG Q K, HUANG D Y, et al. Intrusion detection model based on CNN and BiGRU fused neural network[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(3): 37-43.
[3] FANG W D, ZHANG C L, SHI Z D, et al. BTRES: beta-based trust and reputation evaluation system for wireless sensor networks[J]. Journal of Network and Computer Applications, 2016, 59: 88-94.
[4] RAM P V, LATHA P. Fuzzy trust protocol for malicious node detection in wireless sensor networks[J]. Wireless Personal Communications, 2017, 94(4): 2549-2559.
[5] KURDI H, ALFARIES A, AL-ANAZI A, et al. A lightweight trust management algorithm based on subjective logic for interconnected cloud computing environments[J]. The Journal of Supercomputing, 2019, 75(7): 3534-3554.
[6] BUSI R V, VENKATARAMAN S, NEGI A. Communication and data trust for wireless sensor networks using D-S theory[J]. IEEE Sensors Journal, 2017, 17(12): 3921-3929.
[7] YIN X Q, LI S N. Trust evaluation model with entropy-based weight assignment for malicious node′s detection in wireless sensor networks[J]. EURASIP Journal on Wireless Communications and Networking, 2019, 2019: 198.
[8] 尹荣荣, 张文元, 杨绸绸, 等. 基于简化云与K/N投票的选择性转发攻击检测方法[J]. 电子与信息学报, 2020, 42(12): 2841-2848.
YIN R R, ZHANG W Y, YANG C C, et al. A selective forwarding attack detection method based on simplified cloud and K/N voting model[J]. Journal of Electronics &Information Technology, 2020, 42(12): 2841-2848.
[9] 秦丹阳, 贾爽, 杨松祥, 等. 基于信任感知的无线传感器网络安全路由机制研究[J]. 通信学报, 2017, 38(10): 60-70.
QIN D Y, JIA S, YANG S X, et al. Research on trust sensing based secure routing mechanism for wireless sensor network[J]. Journal on Communications, 2017, 38(10): 60-70.
[10] 滕志军, 杜春秋, 孙汇阳, 等. 融合节点信誉度和路径跳数的WSNs虫洞攻击检测策略[J]. 哈尔滨工业大学学报, 2021, 53(8): 64-71, 131.
TENG Z J, DU C Q, SUN H Y, et al. A wormhole attack detection strategy integrating node creditworthiness and path hops in WSNs[J]. Journal of Harbin Institute of Technology, 2021, 53(8): 64-71, 131.
[11] 王秋惠. 基于空间自回归模型的电力系统中长期负荷特性分析与预测[J]. 东北电力大学学报, 2021, 41(3): 118-123.
WANG Q H. The characteristic analysis and forecasting of mid-long term load based on spatial autoregressive model[J]. Journal of Northeast Electric Power University, 2021, 41(3): 118-123.
[12] 陈浩杰, 黄锦, 左兴权, 等. 基于宽度&深度学习的基站网络流量预测方法[J]. 郑州大学学报(工学版), 2022, 43(1): 7-13.
CHEN H J, HUANG J, ZUO X Q, et al. Base Station network traffic prediction method based on wide &deep learning[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(1): 7-13.
[13] FENG R J, HAN X N, LIU Q, et al. A credible Bayesian-based trust management scheme for wireless sensor networks[J]. International Journal of Distributed Sensor Networks, 2015, 11(11): 678926.
[14] 叶正旺, 温涛, 刘振宇, 等. 基于信任模型的WSNs安全数据融合算法[J]. 东北大学学报(自然科学版), 2019, 40(6): 789-794.
YE Z W, WEN T, LIU Z Y, et al. An algorithm of trust-based secure data aggregation for wireless sensor networks[J]. Journal of Northeastern University (Natural Science), 2019, 40(6): 789-794.