近年来,由于全球气候和能源问题日渐突出,人们对制冷领域的节能和环保提出了新的要求[1]。越来越多的人将目光从传统的压缩制冷技术转向绿色环保的电热(electrocaloric,EC)制冷技术[2]。
根据制冷过程的实现原理可将现有电热制冷装置分为基于热再生的电热制冷装置和基于热开关的电热制冷装置。在基于热再生的电热制冷装置中,液(固)态载热体在驱动力作用下在冷热端之间往复流动,将冷端的热量带到热端来实现制冷。例如,Guo等[3]通过膜片驱动器驱动流体在多层三元聚合物材料P(VDF-TrFE-CFE)(聚偏氟乙烯-三氟乙烯-氯氟乙烯)构成的流道内来回流动,将冷端的热量带到热端来实现制冷。在两端温差为5 K的条件下,单个制冷元件的制冷功率密度(CPD)为4.59 W/cm2,这是在目前公开文献中同工况下电热制冷装置中所能实现的比较高的制冷功率密度。但是流体工质流动过程会存在流动损失以及流体工质因本身比热容会消耗一部分能量导致功率降低。而机械热开关的电热制冷装置通过导热体中间的运动来代替流体流动实现对热流动方向的控制。理论上导热体中间可以消除流动损失,并能够减少因导热体自身温度变化造成的热损失,因此具有较大的提高制冷功率密度的潜力。
但目前已有的基于机械热开关结构设计的装置的制冷功率密度依然较低,并未充分体现机械热开关的优势。例如,Ma等[4]利用柔性P(VDF-TrFE-CFE)薄膜和静电驱动机制设计了一种电热制冷装置。当电场为66.7 MV/m时,CPD仅为29.7 mW/cm2。Wang等[5]设计了由多层陶瓷电容器组成的电热模块堆叠而成的环形制冷装置,当温度跨度为5.2 K时,最大制冷功率密度才达到135 mW/cm2。因此通过创新的结构设计,发挥热开关优势,进一步提升制冷功率密度是今后机械热开关式制冷结构的发展趋势。
针对上述问题,利用P(VDF-TrFE-CFE)(未拉伸)这种材料高温变、柔软的优势,本研究提出了一种带状电热制冷结构。该结构具有模块化特点,并具有良好的可扩展性。通过模拟方法对其制冷单元的制冷性能进行了研究,证明了其优良的制冷性能,同时还简要说明了提高制冷性能的设计原则。
1 装置设计
1.1 工作原理
该装置的概念模型如图1所示,它的结构由热端蓄热器、电热模块、带状结构、步进电机、电极、冷端蓄热器组成。蓄热器和电极均由外部支架结构所固定,并与带状结构接触良好。该制冷模型中的电热模块每隔一定距离嵌在带状橡胶结构中,形成电热制冷带。工作时,步进电机带动电热制冷带,让电热模块依次通过由电极、热端蓄热器和冷端蓄热器组成的制冷单元组,从而实现连续制冷。通过调整步进电机转速及图1中所示虚拟区域改变制冷单元组数可以适应不同的制冷功率需求。其中每个电热模块经过这样一个制冷单元就完成通电极化、放热、断电去极化、吸热4个阶段。①极化:在tp时间内,对电热模块施加电场,即从0增加到Emax,电热模块极化升温并向热端移动;②放热:在th时间,电热模块开始接触热端,向热端蓄热器释放热量并继续移动;③去极化:在td时间,施加在电热模块上的电场被移除,电场从Emax下降到0,电热模块退极化降温并向冷端移动;④吸热:在tc时间内,电热模块开始接触冷端,从冷端蓄热器吸收热量。在一个周期中电压及温度变化如图2所示。
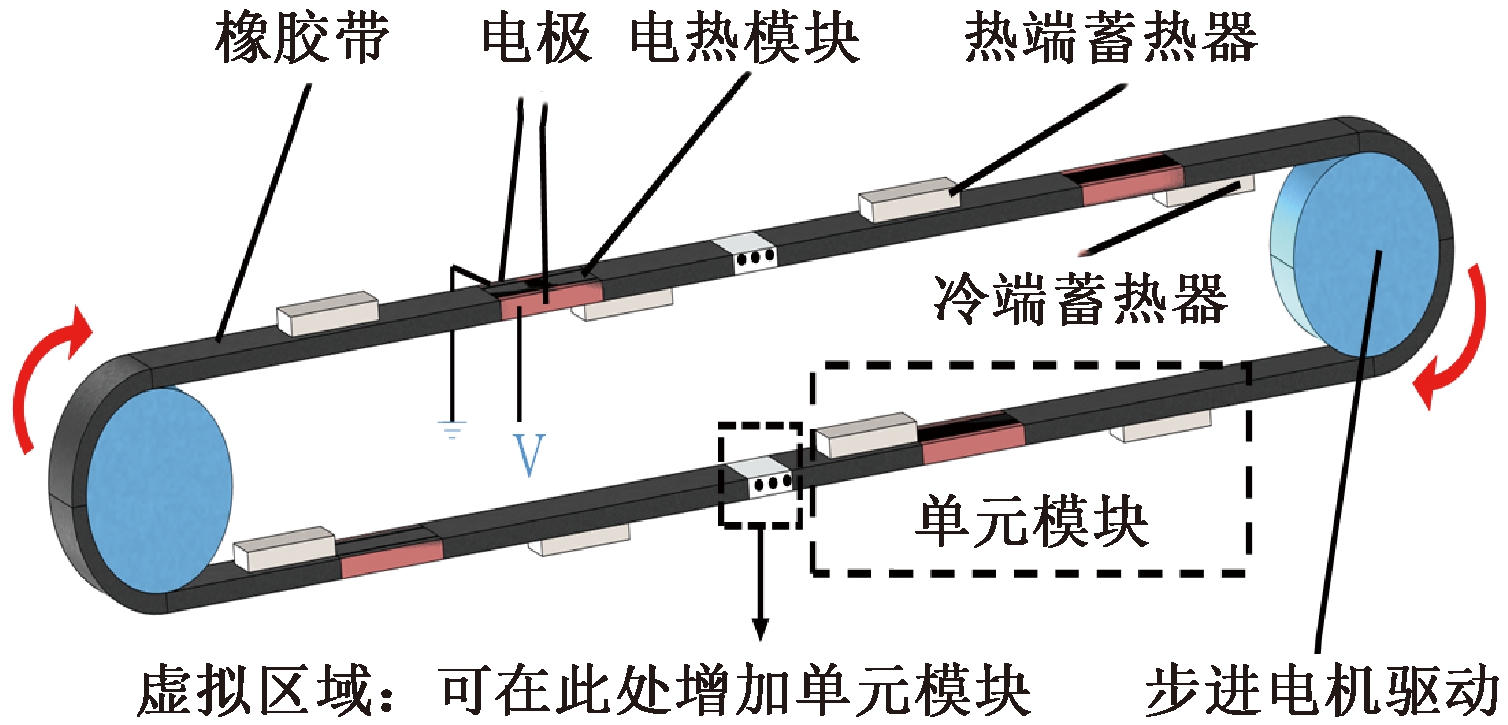
图1 电热制冷装置的概念模型
Figure 1 Conceptual model of electrocaloric cooling device
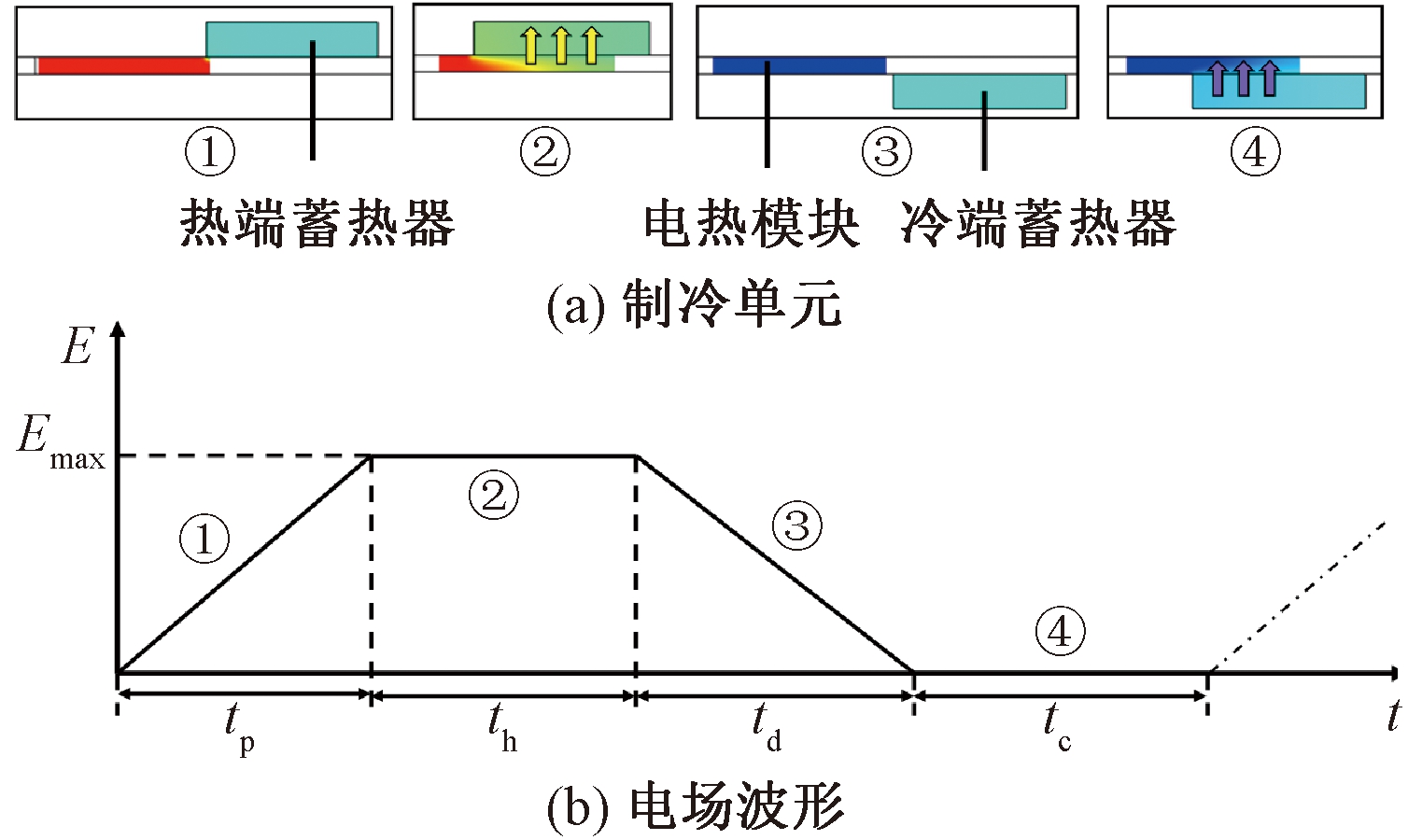
图2 制冷单元制冷过程及电场波形示意图
Figure 2 Schematic diagram of refrigeration process and electric field waveform of cooling unit
在制冷带移动方向可以设置多个制冷单元,多个电热模块重复这样的循环,可以连续地把热量从冷端带到热端,达到连续制冷的目的。该结构通过电热模块移动实现热开关的作用,同时与其他结构相比减少了中间导热体(载热体)因温度变化带来的热损失。
1.2 制冷单元设计计算
由上述原理可知,电热模块内电场的施加与撤去由其自身移动实现,而电场变化的各个阶段的时间长短由电热模块的移动速度v、长度LEC和冷(热)端蓄热器在电热模块移动方向的尺寸LR、冷端蓄热器和热端蓄热器之间的距离LCH共同决定。各阶段时间与移动速度之间的关系如下:
(1)
(2)
tp=td;
(3)
th=tc;
(4)
tp+th+td+tc=τ。
(5)
式中:s为制冷单元之间的距离;τ为电场周期。
在本研究中,电热材料采用P(VDF-TrFE-CFE)三元聚合物,因为这种材料具有接近20 K的高温变[6]。表1提供了模拟中使用的蓄热器、EC模块的相关材料物性,为方便横向对比,采用与文献[7]相同的物性。
表1 组件的属性参数
Table 1 Parameters and properties of components

组件密度ρ/(kg·m-3 )热导率k/(W·m-1·K-1)比热c/(J·kg-1·K-1)EC 模块1 8000.21 500蓄热器8 00016500
对于电热模块,为了实现标准的布雷顿循环过程,其长度LEC应与蓄热器的长度LR保持一致,这里设定为1 mm;电热模块与热端蓄热器的初始距离设定为1 mm;冷热端蓄热器之间的距离LCH为其长度的两倍,即2 mm;制冷单元之间的距离s是LEC的6倍,即6 mm。另外,计算其厚度时要兼顾受到电场强度和热传导的影响,根据文献可知,其厚度由热穿透厚度[8]δ决定,热穿透厚度的定义为[9]
(6)
式中:f表示工作频率,Hz;k表示热导率,W/(m·K);ρ为密度,kg/m3;c为比热,J/(kg·K)。对于电热模块在温度为298.15 K、工作频率为1 Hz时的热穿透厚度为0.15 mm。因此,电热模块的厚度dEC设定为0.1 mm,蓄热器的厚度dR设定为0.2 mm。
2 制冷单元模型的建立
2.1 几何模型
由图1可知,由于垂直于模块运动方向(x方向)的z方向的尺寸对装置制冷功率密度研究没有影响,因此将其简化为一个二维问题,其二维几何模型如图3所示,由于模拟不研究电场分布,因此可忽略电极。简化模型中包含一个电热模块、一个热端蓄热器和一个冷端蓄热器。
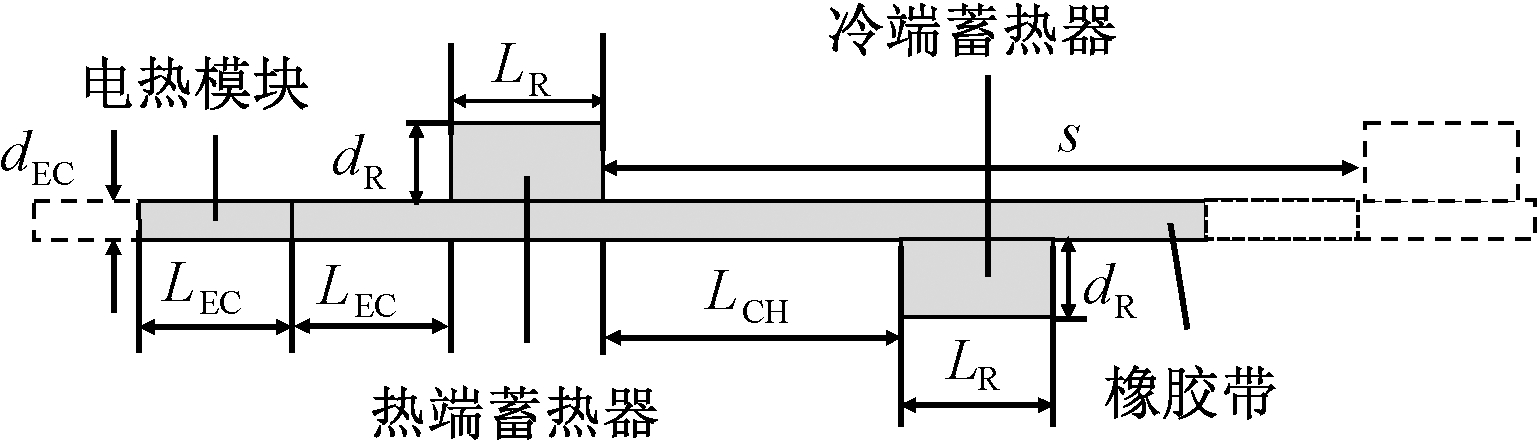
图3 电热制冷单元的二维几何模型
Figure 3 Two dimensional geometric model of electrocaloric refrigeration unit
同时需要说明的是,为简化计算,模拟在以下假设条件下进行。
(1)忽略热辐射;
(2)忽略电极的影响;
(3)电热材料的物理参数在工作温度范围内是恒定的。
(4)接触处没有热阻;
(5)除冷端和热端之外的表面为绝热状态。
2.2 数学模型
模拟中EC模块的控制方程为
(7)
式中:T表示电热模块温度,K;t为时间,s;Q为热源项,W/m3。
热源项Q可以用以下表达方式表示:
(8)
式中:E为电热材料内电场强度,MV/m;S为熵,J/K。熵和电场之间的关系可以从实验中得到[10]。对于P(VDF-TrFE-CFE),式(8)中S和E之间的关系可以拟合为
S=C1E2+C2E。
(9)
式中:C1=-2.83×10-15 J·m2/(kg·K·V2);C2=-6.85×10-8 J·m/(kg·K·V)。当接近室温时,三元聚合物所产生的绝热温变基本不受环境温度的影响,也即在280~330 K式(9)有效[10]。模拟中,制冷单元所处环境温度设定为298.15 K。热端温度设定为比环境温度稍高,模拟中取定值TH=301.15 K。冷端温度根据温度跨度取值进行变化。温度跨度为热端和冷端的温度差,模拟中取值为3~15 K,间隔2 K。
2.3 性能指标
(1)制冷功率密度CPD。在模拟中固定热端和冷端温度,它表示冷端单位时间单位面积上的热通量。
(10)
式中:dEC为EC模块的厚度,mm;τ为电场周期,s;ΔTc为EC模块在吸热过程中的平均温度变化,K。
(2)制冷性能系数COP。
(11)
式中:QC和QH分别表示一个循环过程中冷端吸收的总热量和热端释放的总热量,J。
(12)
式中:COPc为卡诺循环的热效率;TC和TH分别表示冷端温度和热端温度,K。
2.4 模拟方法可靠性验证
(1)热源项准确性验证。为验证模拟中热源项的准确性,利用式(8)和(9),在与文献[10]相同条件下计算得到绝热温变,并与文献[10]中的实验值进行比较,如图4所示。由图4可见,两者误差很小。另当电场强度为160 MV/m时,绝热温度变化与文献[11]相比误差约为2.3%。
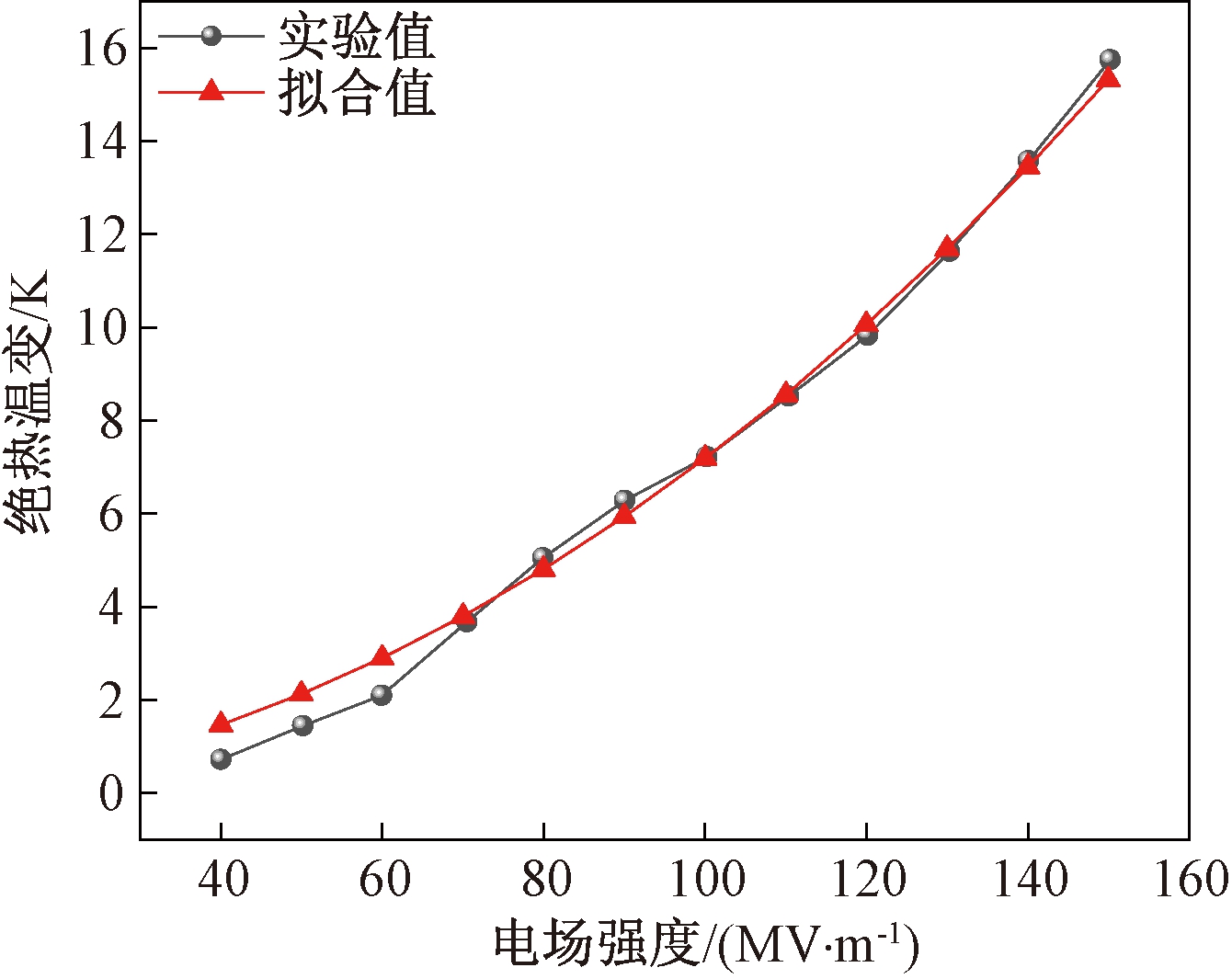
图4 电热模块温度跨度实验值和拟合值的对比
Figure 4 Comparison of experimental and fitted values of temperature span of EC module
此外,借助MATLAB对式(8)进行编程计算,得到1 s内热源产生的热量为19.22 MJ/m3,和文献[12]中的理论公式计算值19.37 MJ/m3基本相同。
(2)模拟方法可靠性验证。利用本研究所用模拟方法及热源项对文献[7]中的模型进行模拟计算,模拟结果与原文献中的实测温度数据对比如图5所示。由图5可见,利用本文中的模拟方法所得到的结果与文献[7]数据误差在5%以内。
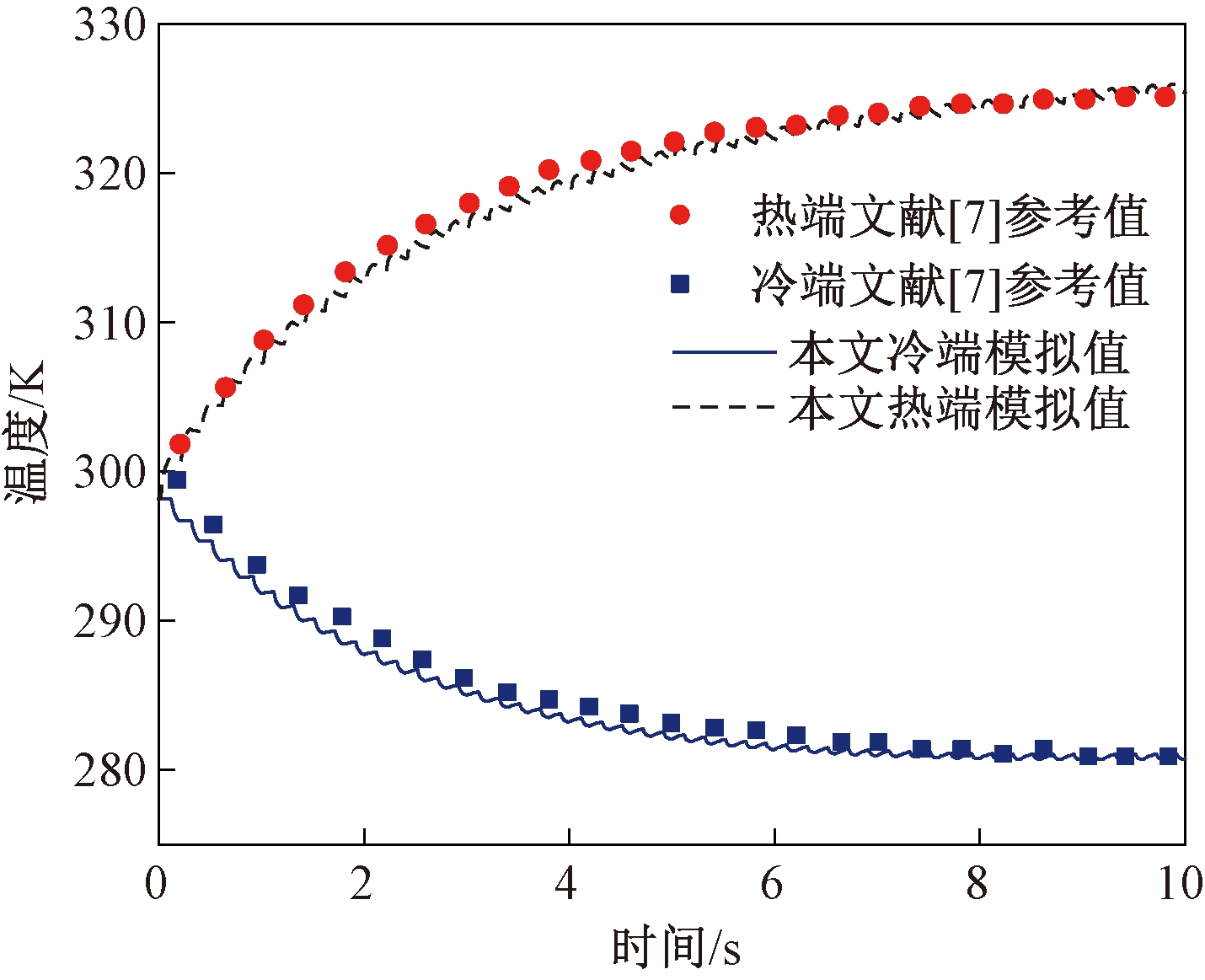
图5 模型数据验证对比
Figure 5 Comparison diagram of model data verification
综上,本研究所采用的模拟方法可行。利用该方法模拟了在温度跨度为5 K、电场强度为150 MV/m的情况下,本研究所提出的带状电热制冷装置的CPD达到了6.02 W/cm2,高于文献[3]中的4.59 W/cm2,同时COP/COPc为22.6%,高于文献[3]中的17.4%。
3 结果和讨论
根据前面制冷单元的设计计算可知,需要选取极化时间tp、移动速度v、电热模块长度LEC和温度跨度(TH-TC)作为变量,研究这些因素对制冷单元性能的影响。此外,电场强度是电热制冷的一个重要影响因素,本文取值为120、140和160 MV/m,均小于薄膜的最大允许电场400 MV/m。
3.1 电热模块极化时间的影响
图6显示了极化时间tp对CPD的影响。由图6可见,在场强为160 MV/m、冷端温度为294.15 K时,CPD随着tp的变化而变化。首先,随着移动速度v的增加,CPD也增加。根据式(1)和式(10),冷热端蓄热器距离一定时,v越大,电场周期τ越小,此时CPD越大。其次,在v一定时,CPD变化趋势以0.2τ 时刻为分界点分为两个阶段:tp<0.2τ时CPD基本不变;tp>0.2τ时CPD出现波动。原因是在一定的移动速度下,电热模块在施加电场的时间内是绝热的。根据式(2),可以计算得出电热模块完成极化过程的临界时间是0.17τ≈0.2τ。在这个时间点之前,电热模块已经完成了绝热升温过程,温度已经达到一个恒定值,这导致CPD基本保持不变。然而,当tp>0.2τ时,电热模块在接触热端之前没有完成绝热升温过程,影响下一步与冷端蓄热器的热交换,导致CPD出现一定程度的变化。值得一提的是,当tp>0.2τ时,其过程不再属于布雷顿循环的讨论范围。因此,为获得较高的CPD,电极长度应大于电热模块在极化时间内移动的距离。
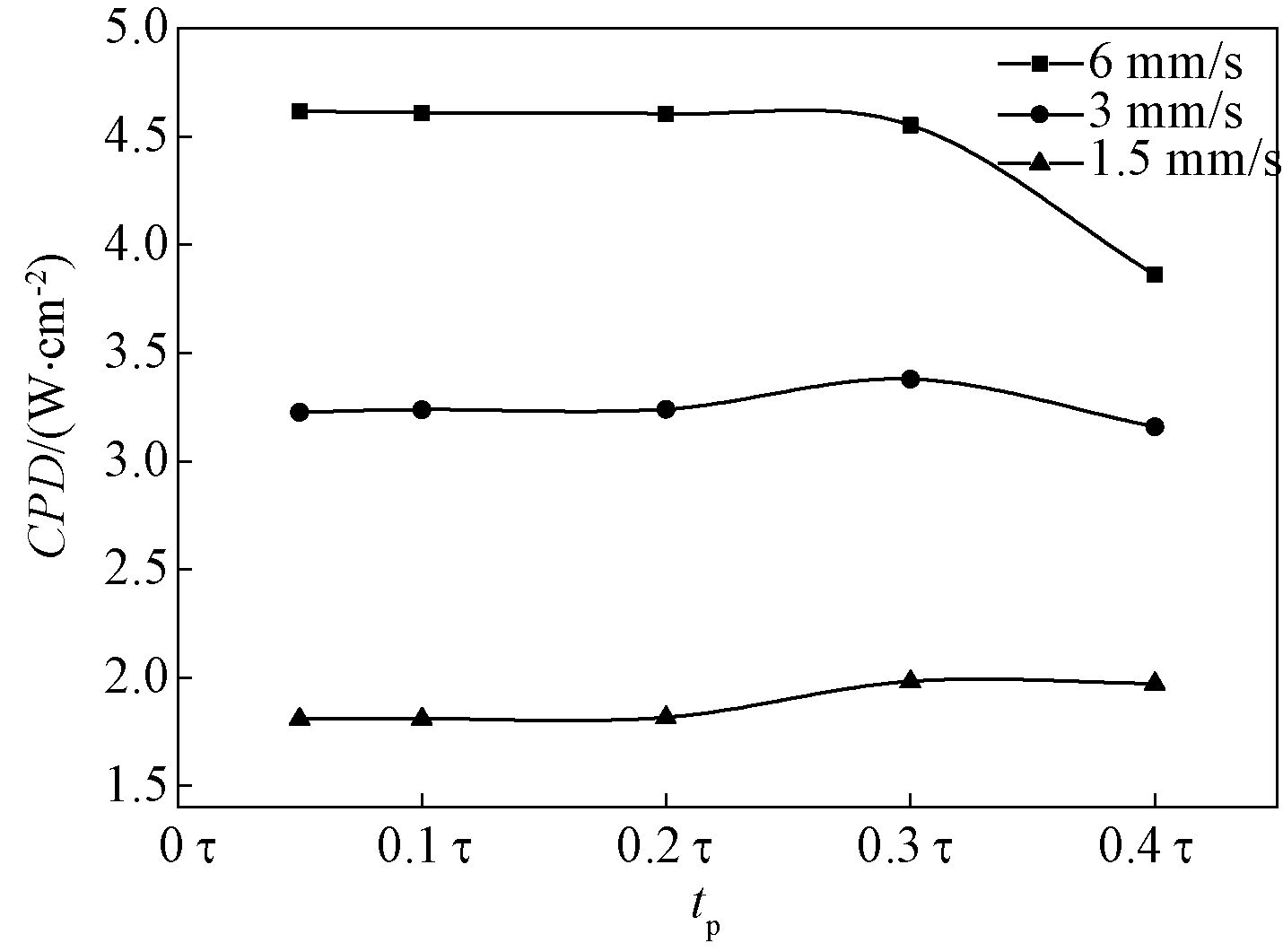
图6 CPD随极化时间tp变化趋势
Figure 6 Trend of CPD with polarization time tp
3.2 电热模块移动速度的影响
当tp为0.1τ、Tc为294.15 K、电场强度为160 MV/m时,电热模块的移动速度v对CPD的影响如图7所示。由图7可见,CPD随着v的增加而增加。当v超过6 mm/s后,CPD依然随着v的增加而增大,但增速减小。
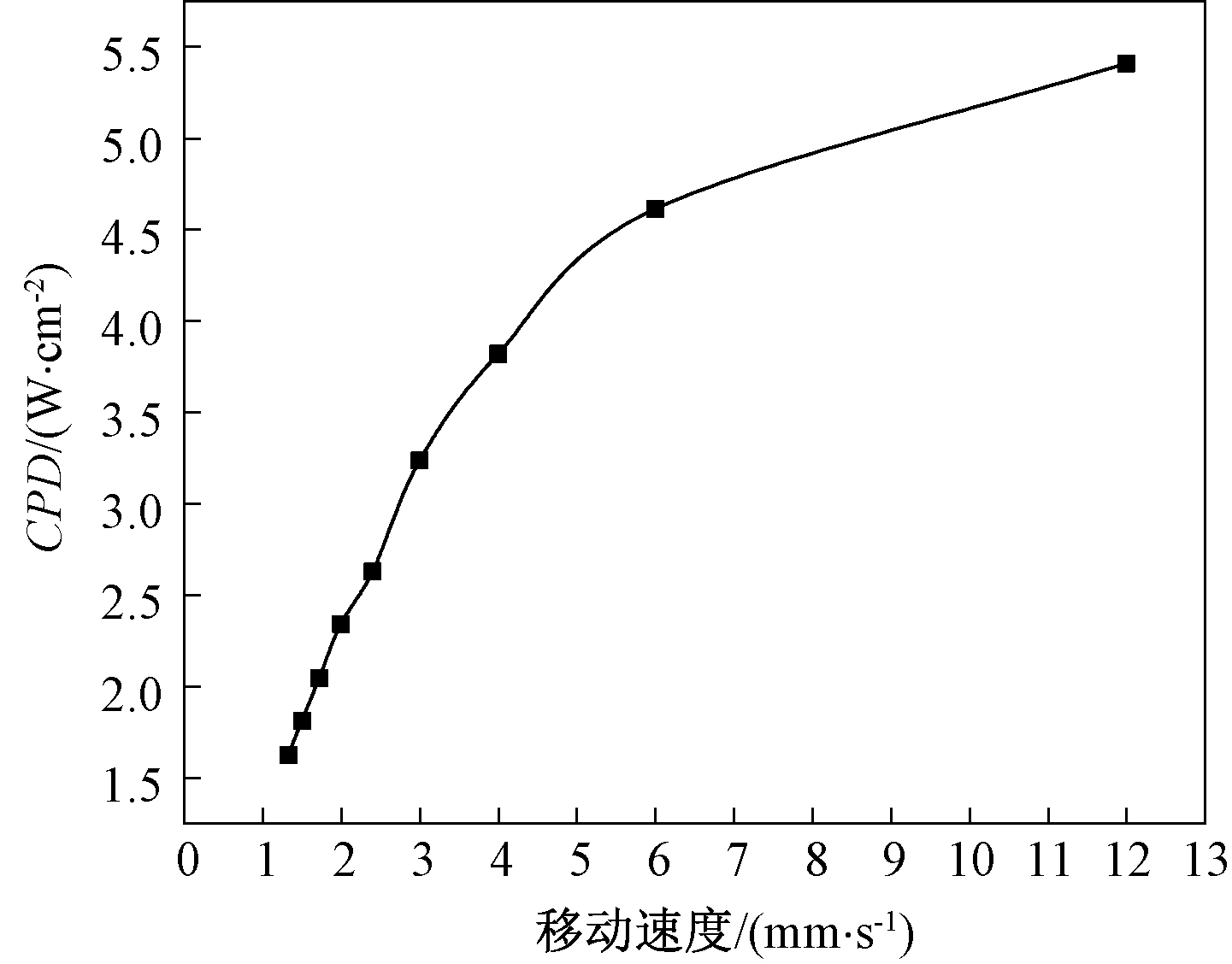
图7 CPD与电热模块移动速度的关系
Figure 7 CPD versus EC module moving speed
根据热穿透厚度定义式(6),通过增加v来提高CPD受到电热模块厚度的限制,因此不能无限地提高EC模块速度来增加CPD。虽然根据式(10),增加电热模块的厚度可以增大CPD,但从热穿透厚度的定义来看,当v增加时,根据式(6),会导致热穿透厚度减小,那么它需要更多的时间来实现充分的热交换。在该研究中,冷热两端的蓄热器的厚度设定为固定值0.2 mm,因此CPD与v之间并不是严格的线性关系。
因此,在实际的结构设计中首先要保证电热模块的厚度要在所施加移动速度对应的热穿透厚度范围内,这样能确保电热模块与蓄热器之间能够进行充分的热交换;其次,在保证能够充分换热的基础上,尽量采用较大的v以获得可观的CPD。
3.3 电热模块长度的影响
图8显示了当tp为0.1τ、Tc为294.15 K、电场强度为160 MV/m时,电热模块的长度LEC对装置CPD的影响。由图8可见,CPD随着LEC的增加而逐渐增加。因为随着LEC的增加,一方面,电热模块的总热容量增加,这导致它在冷端蓄热器吸收的热量相应地增加;另一方面,电热模块与冷热端蓄热器之间的热交换时间增加。电热模块与冷热端蓄热器之间的充分的热交换导致CPD的增加。这是因为在τ一定时,热交换过程中热量的增加或者热交换时间的增加会导致ΔTc的增加。根据式(10),CPD也随之不断增加。
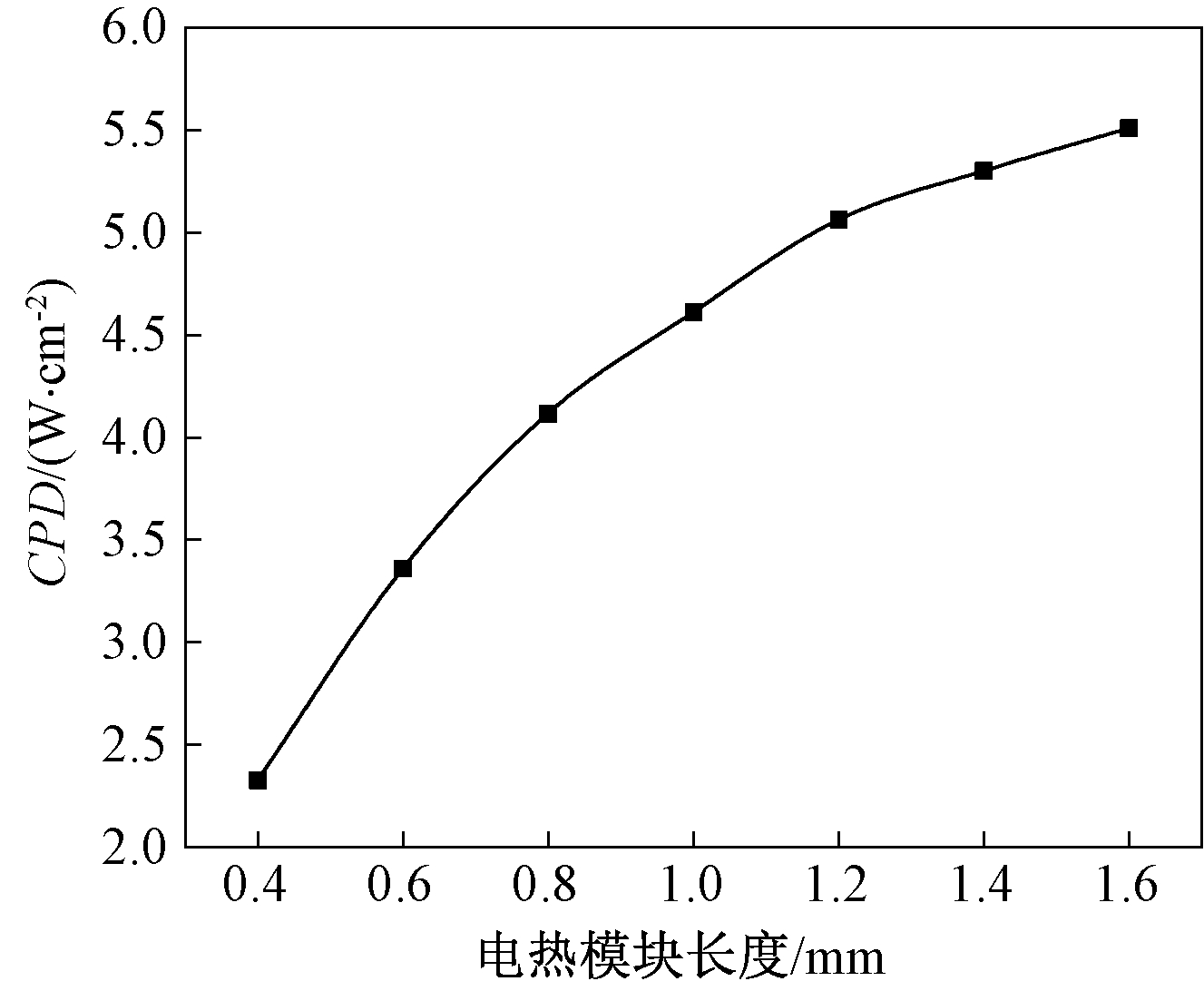
图8 CPD与电热模块长度的关系
Figure 8 CPD versus length of EC module
在结构设计中,当冷热端蓄热器距离一定时,在确保布雷顿循环过程的条件下,采用的电热模块越长,获得的CPD越大。因此,在其他条件不变时,在设计中尽量采用较长的电热模块以获得最优的CPD。
3.4 温度跨度的影响
温度跨度即冷端和热端的边界温度差,是影响制冷性能的一个重要因素。在热端边界温度固定为301.15 K、v为6 mm/s的情况下,电场强度分别设置为120、140和160 MV/m,温度跨度对CPD、COP和COP/COPc的影响如图9所示。
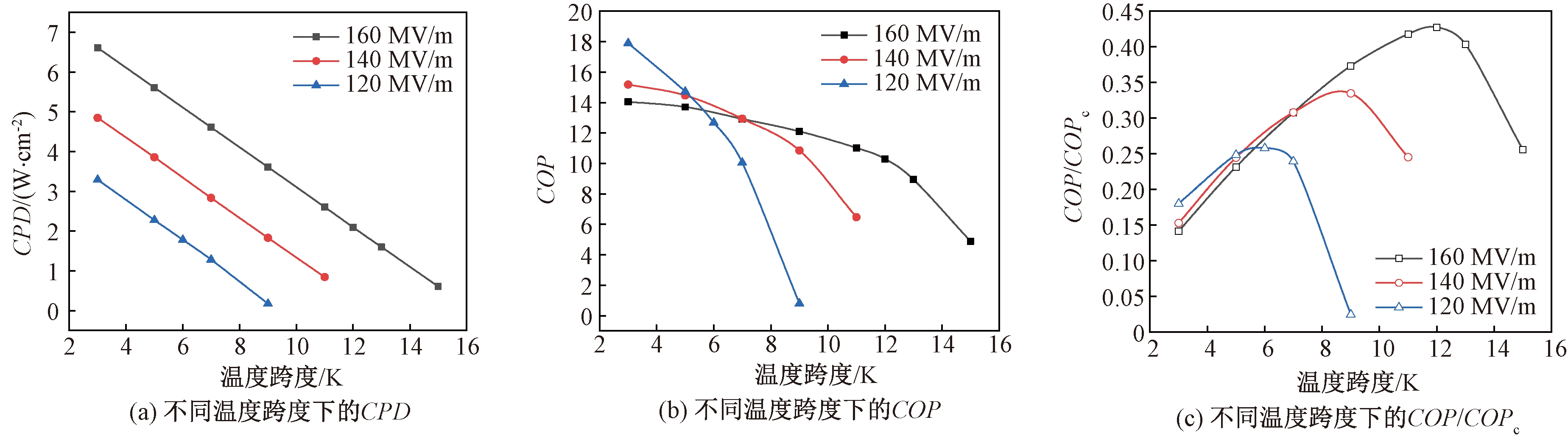
图9 CPD、COP和COP/COPc与温度跨度的变化关系
Figure 9 CPD, COP and COP/COPc versus temperature span
从图9中可以发现,随着温度跨度的增加,CPD线性下降。随着电场强度的增加,CPD线性增加。因为电热模块的最大绝热温度变化是由电场强度决定的。比如,当施加的电场强度达到120 MV/m时,可应用于该设备的最大有效温度跨度约为9 K。超过最大温度跨度后,几乎没有冷负荷。对于施加的电场强度达到140 MV/m和160 MV/m,最大温度跨度分别为13 K和15 K。
4 结论
数值模拟研究表明该结构的制冷性能相比现有电热制冷装置有明显提高。主要结论如下。
(1)提高电热模块移动速度、增加电热模块长度并辅以相应的电极长度,可以提高制冷功率。但在结构设计中首先要保证电热模块的厚度要在所施加移动速度对应的热穿透厚度范围内,以确保电热模块与蓄热器之间能够进行充分的热交换。
(2)在本研究范围内,温度跨度为3 K、电场强度为160 MV/m时,装置制冷功率达到最大值6.61 W/cm;电场强度为120、140、160 MV/m时,最大温度跨度分别为9 K、13 K、15 K,但此时的制冷功率为0;COP随温度跨度的增加而降低;不同电场强度下,COP/COPc的峰值所对应的温度跨度为6 K、9 K、12 K。
[1] 魏新利,王中华,耿利红,等.压缩制冷系统节流损失及应对方案研究[J].郑州大学学报(工学版),2015,36(3):68-72.
WEI X L, WANG Z H, GENG L H, et al. Study on the throttling losses in CRS and solutions[J]. Journal of Zhengzhou University (Engineering Science), 2015,36(3):68-72.
[2] SUN Z M, WANG Q M, SLAUGHTER W S. A solid-state refrigeration based on electrocaloric effect: device and its analytical model[J]. Journal of Applied Physics, 2018, 124(6): 064503.
[3] GUO D Z, GAO J S, YU Y J, et al. Design and modeling of a fluid-based micro-scale electrocaloric refrigeration system[J]. International Journal of Heat And Mass Transfer, 2014, 72: 559-564.
[4] MA R J, ZHANG Z Y, TONG K, et al. Highly efficient electrocaloric cooling with electrostatic actuation[J]. Science, 2017, 357(6356): 1130-1134.
[5] WANG Y D, ZHANG Z Y, USUI T, et al. A high-performance solid-state electrocaloric cooling system[J]. Science, 2020, 370(6512): 129-133.
[6] 李海波, 姜倩, 徐小农, 等. 基于热开关的铁电制冷新结构及数值模拟[J]. 低温工程, 2016(5): 51-56.
LI H B, JIANG Q, XU X N, et al. A new structure of electrocaloric effect refrigeration based on thermal switch and numerical calculation[J]. Cryogenics, 2016(5): 51-56.
[7] GU H M, CRAVEN B, QIAN X S, et al. Simulation of chip-size electrocaloric refrigerator with high cooling-power density[J]. Applied Physics Letters, 2013, 102(11): 112901.
[8] HOLMAN J P. Heat transfer, tenth edition[M]. New York: McGraw-Hill Companies, Inc., 2010.
[9] GUO D Z, GAO J S, MCGAUGHEY A J H, et al. Design and evaluation of a MEMS-based stirling microcooler[J]. Journal of Heat Transfer, 2013, 135(11): 111003.
[10] LI X Y, QIAN X S, LU S G, et al. Tunable temperature dependence of electrocaloric effect in ferroelectric relaxor poly(vinylidene fluoride-trifluoroethylene-chlorofluoroethylene terpolymer[J]. Applied Physics Letters, 2011, 99(5): 052907.
[11] SHI J Y, LI Q, GAO T Y, et al. Numerical evaluation of a kilowatt-level rotary electrocaloric refrigeration system[J]. International Journal of Refrigeration, 2021, 121: 279-288.
[12] APREA C, GRECO A, MAIORINO A, et al. A comparison between different materials in an active electrocaloric regenerative cycle with a 2D numerical model[J]. International Journal of Refrigeration, 2016, 69: 369-382.
[13] CHEN Q, CHU B J, ZHOU X, et al. Effect of metal-polymer interface on the breakdown electric field of poly(vinylidene fluoride-trifluoroethylene-chlorofluoroethylene) terpolymer[J]. Applied Physics Letters, 2007, 91(6): 062907.