0 引言
钢管混凝土结构具有优越的力学性能，已经在国内外得到广泛的应用[1-2]。钢管混凝土异形柱具备承载力高、塑性性能好、施工方便、结构布置灵活等优点。同钢筋混凝土异形柱相比，在结构承载力和刚度相同的前提下，钢管混凝土异形柱可以做到截面更小。框架节点是梁和柱传递弯矩和剪力的纽带，处于复杂应力状态，其力学性能在建筑结构中至关重要，节点的损坏将导致严重的后果。目前钢管混凝土异形柱-钢梁节点结构形式有：内隔板全焊接节点、外加强环板节点及外肋环板节点等[3]，节点形式少，难以满足工程实际多样性的需求；异形柱截面尺寸较小，内部焊接钢板后，不能保证核心混凝土的浇筑质量；外加强环板节点凸出墙体，可能出现露梁露柱的情况，不符合异形柱设计的理念。
恢复力模型是弹塑性时程分析的基础，对结构的地震反应分析结果有着重要影响，国内外学者对钢管混凝土柱-钢梁节点的恢复力模型进行了大量试验研究。其中,张月等[4]基于耗能螺栓连接钢管混凝土梁柱节点的低周往复加载试验，建立了新型装配式节点的恢复力模型。王先铁等[5]针对带楔形装置的自复位方钢管混凝土柱-钢梁节点进行了拟静力试验，提出了带楔形装置自复位节点的简化恢复力模型。郏书朔等[6]依据试验结果，提出了单边高强螺栓连接节点恢复力模型，采用四参数幂函数模型拟合节点骨架曲线，给出了节点在弹性阶段和弹塑性阶段滞回曲线恢复力模型。赵毅等[7]基于劲性环梁式钢管混凝土柱-钢筋混凝土梁节点的低周往复荷载试验及ABAQUS有限元数值模拟结果，考虑刚度退化的影响，提出了劲性环梁式钢管混凝土节点的三折线恢复力模型。唐榕等[8]通过对2个矩形钢管再生混凝土柱-工字型钢梁框架边节点在低周反复荷载下进行的拟静力试验，建立了该类型节点的恢复力模型。曾磊等[9]进行了5榀比例为1∶4的不同混凝土强度等级及不同轴压比的框架中节点低周反复加载试验，建立了该节点考虑刚度退化的三线型恢复力模型。王文达等[10]通过分析影响钢管混凝土框架结构荷载-位移骨架曲线的因素，得到了框架结构的恢复力模型。
因此，本文提出一种新型侧板连接T形钢管混凝土柱-钢梁节点，侧板平贴于节点域，高于工字梁并沿其轴线方向外伸一定距离，能够达到节点不突出墙面、柱子与墙体平齐的效果，如图1所示。侧板对节点核心区起到约束加强的作用，可以在一定程度上提高节点的强度。与传统钢管混凝土梁柱节点相比，这种节点形式与内隔板全焊接节点相比，具有钢管连续贯通可以保证核心混凝土浇筑时的连续性和均匀性的优点；与外加强环板节点相比，具有避免梁柱节点凸出墙体增加建筑整体美观性、便于室内家具布置的优点，故该节点构造形式不仅具有构造简单、便于施工、传力明确还兼顾整体美观的特点。
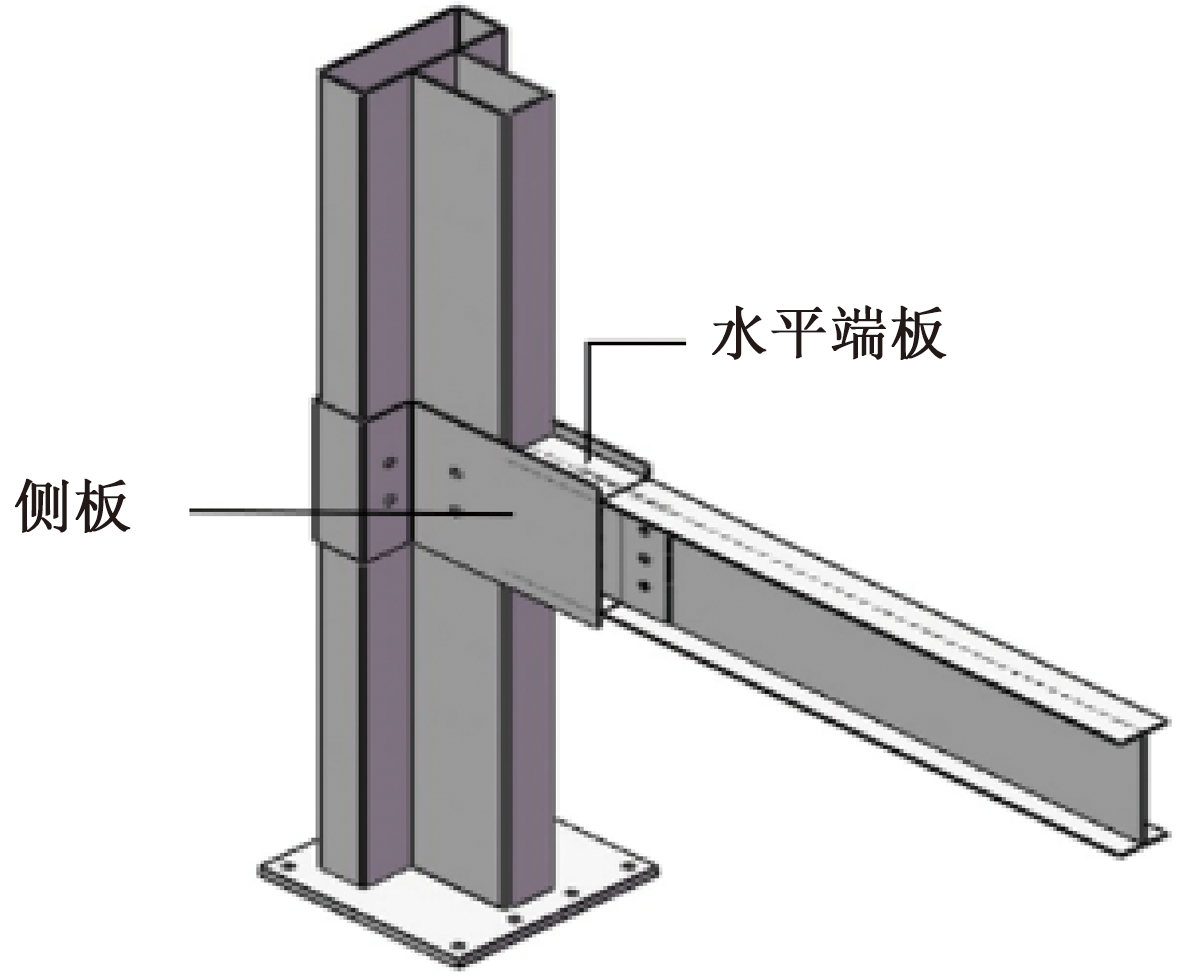
图1 节点构造形式
Figure 1 Structural form of specimen
本文通过低周往复加载试验对有无侧板、侧板长度、有无约束拉杆和不同轴压比4种影响因素下的7个侧板连接T形钢管混凝土柱-钢梁节点的抗震性能进行研究，基于试验结果建立此类节点的恢复力模型，为节点及其结构在弹塑性地震反应分析时提供理论参考。
1 试验概况
1.1 试件设计与制作
通过拟静力试验对7个侧板连接T形钢管混凝土柱-钢梁节点试件进行研究。其中T形钢管混凝土柱由矩形钢管和U形槽钢焊接而成。T形钢管混凝土柱与工字型钢梁通过上端板与下端板组成的短钢梁焊接在一起。试件尺寸参数如图2和表1所示。钢材为Q235钢，混凝土强度等级为C40。
表1 试件设计参数
Table 1 Design parameters of specimen
试件编号侧板尺寸水平端板尺寸竖向端板尺寸轴压比约束拉杆JD1300 mm×318 mm×4 mm100 mm×100 mm×4 mm250 mm×100 mm×4 mm0.2有JD2350 mm×318 mm×4 mm150 mm×100 mm×4 mm250 mm×150 mm×4 mm0.2有JD3400 mm×318 mm×4 mm200 mm×100 mm×4 mm250 mm×200 mm×4 mm0.2有JD4300 mm×318 mm×4 mm100 mm×100 mm×4 mm250 mm×100 mm×4 mm0.2无JD5100 mm×100 mm×4 mm250 mm×100 mm×4 mm0.2有JD6300 mm×318 mm×4 mm100 mm×100 mm×4 mm250 mm×100 mm×4 mm0.4有JD7300 mm×318 mm×4 mm100 mm×100 mm×4 mm250 mm×100 mm×4 mm0.6有
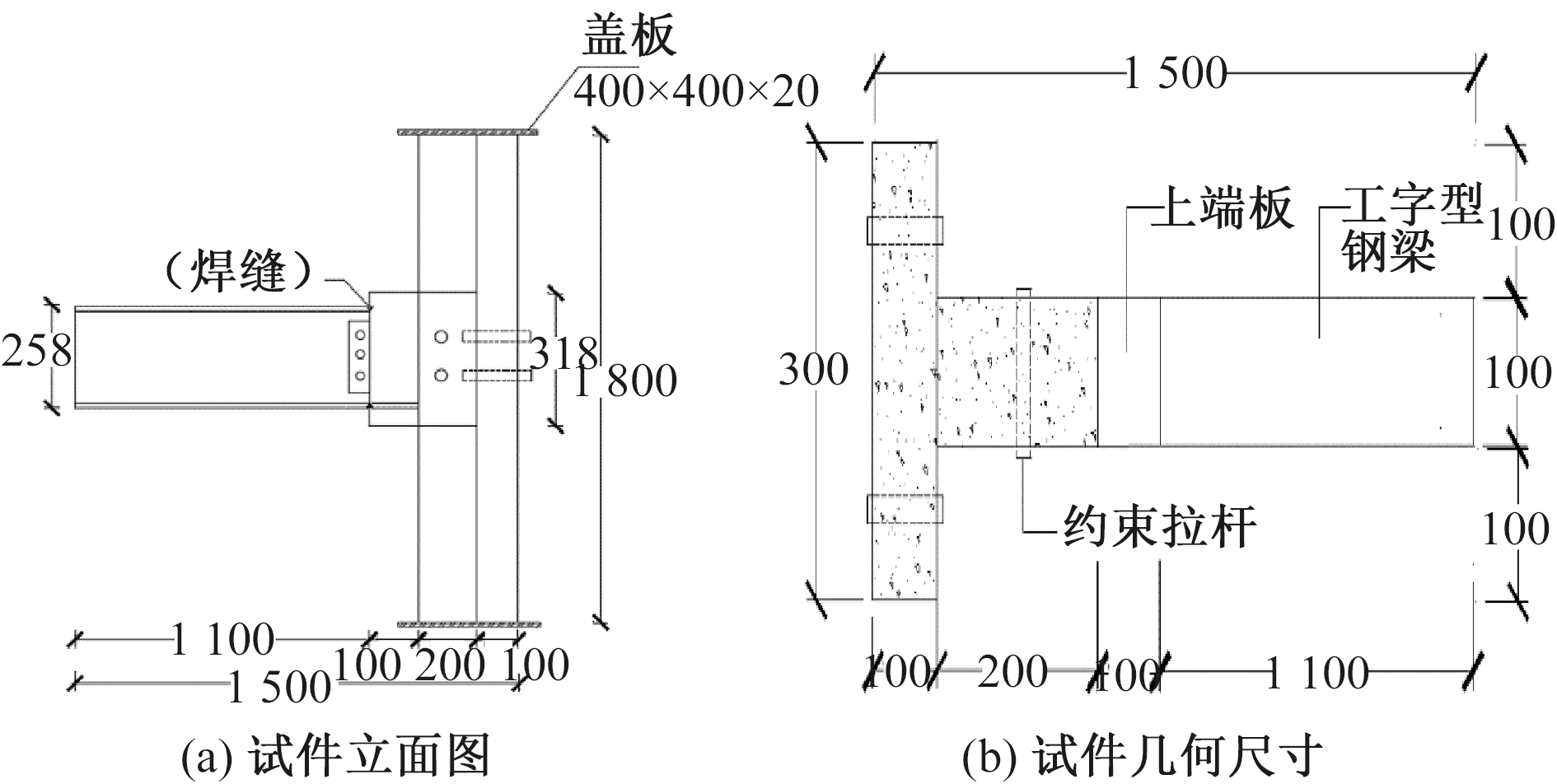
图2 试件几何尺寸(mm)
Figure 2 Geometric dimension of specimen(mm)
1.2 加载装置及加载制度
为模拟试件在地震作用下的受力情况，在柱端千斤顶处设置滑动滚轴，柱底端设置铰支座，梁端设置链杆与铰支座连接，加载装置如图3所示。
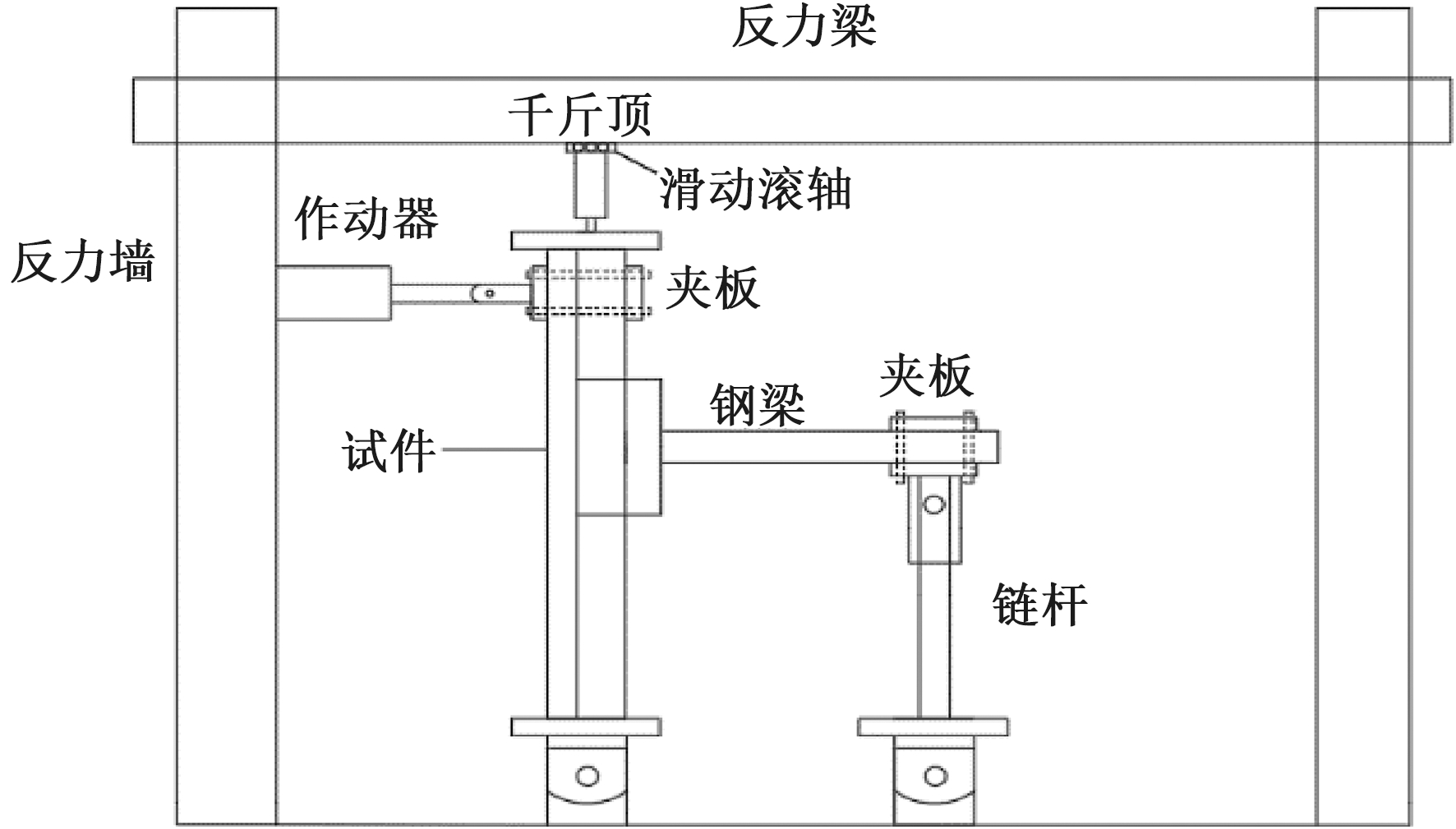
图3 加载装置图
Figure 3 Loading device diagram
2 试验现象及破坏模式
从图4可以看出，节点破坏主要有两种模式：梁铰破坏模式和柱铰破坏模式。
图4 节点破坏模式
Figure 4 Failure mode of node
产生梁铰破坏的试件均为侧板连接T形钢管混凝土柱-钢梁节点试件，它们在整个加载过程中具有相似的破坏历程。在荷载加载初期，试件均处于线弹性发展阶段，钢材和混凝土具有稳定的承载能力，能够承受外部荷载。随着荷载的增加，在侧板端部的工字型钢梁上下翼缘开始产生局部屈曲，并在受拉过程中产生细微裂纹，随着循环加载的不断进行，裂纹逐渐延伸并反复闭合，最终进入塑性阶段，此时工字型钢梁的上翼缘产生撕裂破坏，如图4(a)所示。产生柱铰破坏的是试件JD5，此试件在节点核心区没有设置侧板。采用的加载方式和加载制度与其他试件相同，产生的试验现象却不同。试件屈服后T形钢管混凝土柱与上端板连接处的焊缝首先发生了开裂，随着往复加载的持续进行，钢管混凝土柱与上、下端板连接处的竖向焊缝也依次开裂，最终破坏如图4(b)所示。可以看出，由于侧板对节点核心区的加强作用，节点破坏模式发生了改变，最终的破坏形式由柱铰破坏转变为梁铰破坏，符合建筑结构设计所要求的“强柱弱梁”设计原则。
3 确定骨架曲线
3.1 滞回曲线分析
图5为各试件的荷载-位移滞回曲线。从图5中可以看出：①各试件的滞回曲线符合节点设计要求，没有出现明显的捏缩现象。②相同条件下侧板连接的T形钢管混凝土柱-钢梁节点试件的极限承载力明显大于不带侧板连接的节点试件，并且带侧板连接节点试件的极限承载力受轴压比影响较为明显，随着轴压比的增大，极限荷载分别增加了23%和42%。③约束拉杆对试件极限承载力没有影响。④与基准试件相比，侧板长度对试件的承载力无明显影响。
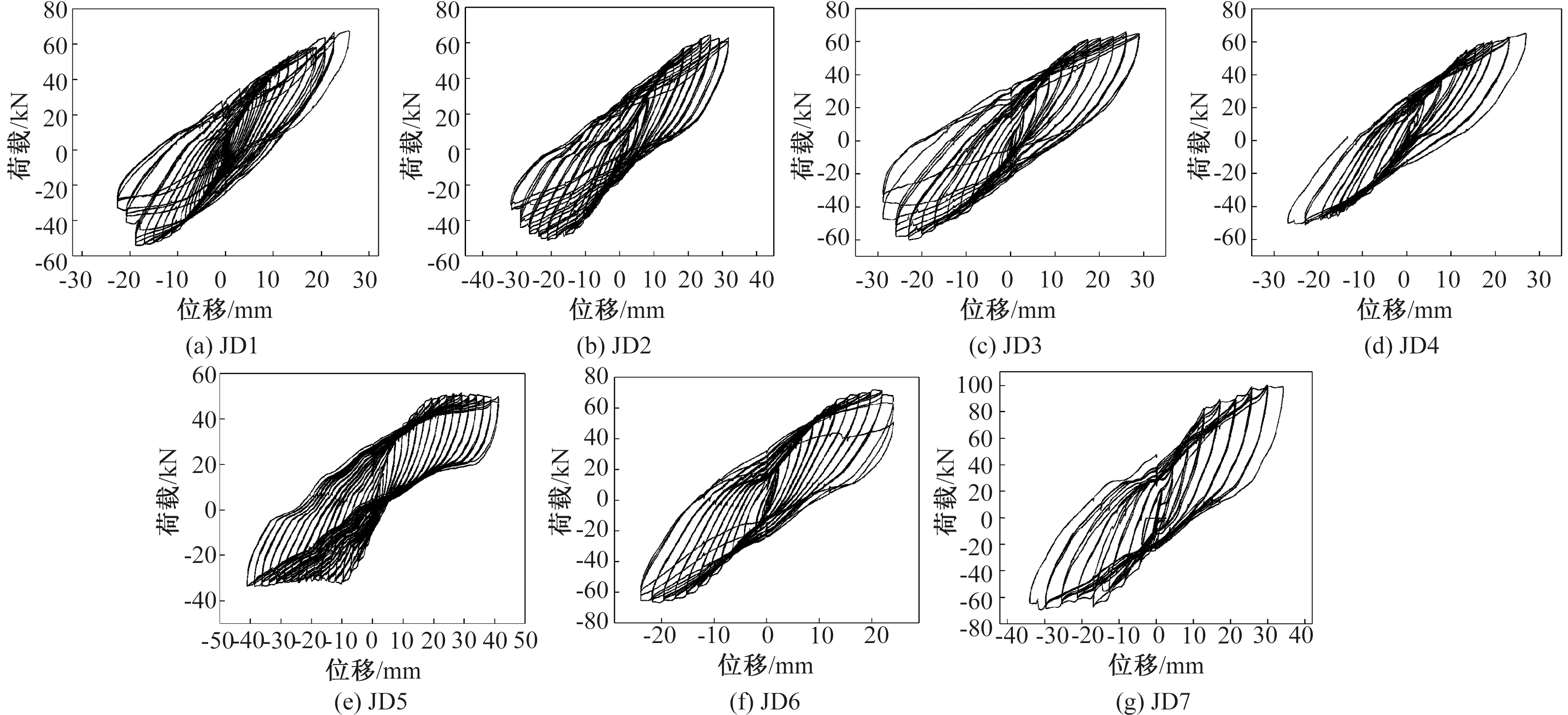
图5 各试件的荷载-位移滞回曲线
Figure 5 Load displacement hysteretic curves of each specimen
3.2 骨架曲线对比
图6为7个侧板连接T形钢管混凝土柱-钢梁节点试件滞回曲线中各级加载的峰值点所对应的荷载和位移确定骨架曲线。在加载初期，试件整体具有一定的稳定性，能够承受外部荷载，处于弹性阶段。随着荷载及往复循环的增加，试件产生局部裂纹，从而产生损伤，试件从弹性阶段进入弹塑性阶段，试验加载方式改为位移控制加载，随着加载位移的不断增大，试件局部产生屈曲，微小裂缝继续扩展，试件所能承受的外部荷载增长率开始降低，因此，骨架曲线逐渐趋于平缓。后期随着加载的进行，加载位移继续增大，试件内部开始产生较大变形，负向方向上所能承受的荷载逐渐降低，当降低到极限荷载的85%时便立即停止试验。
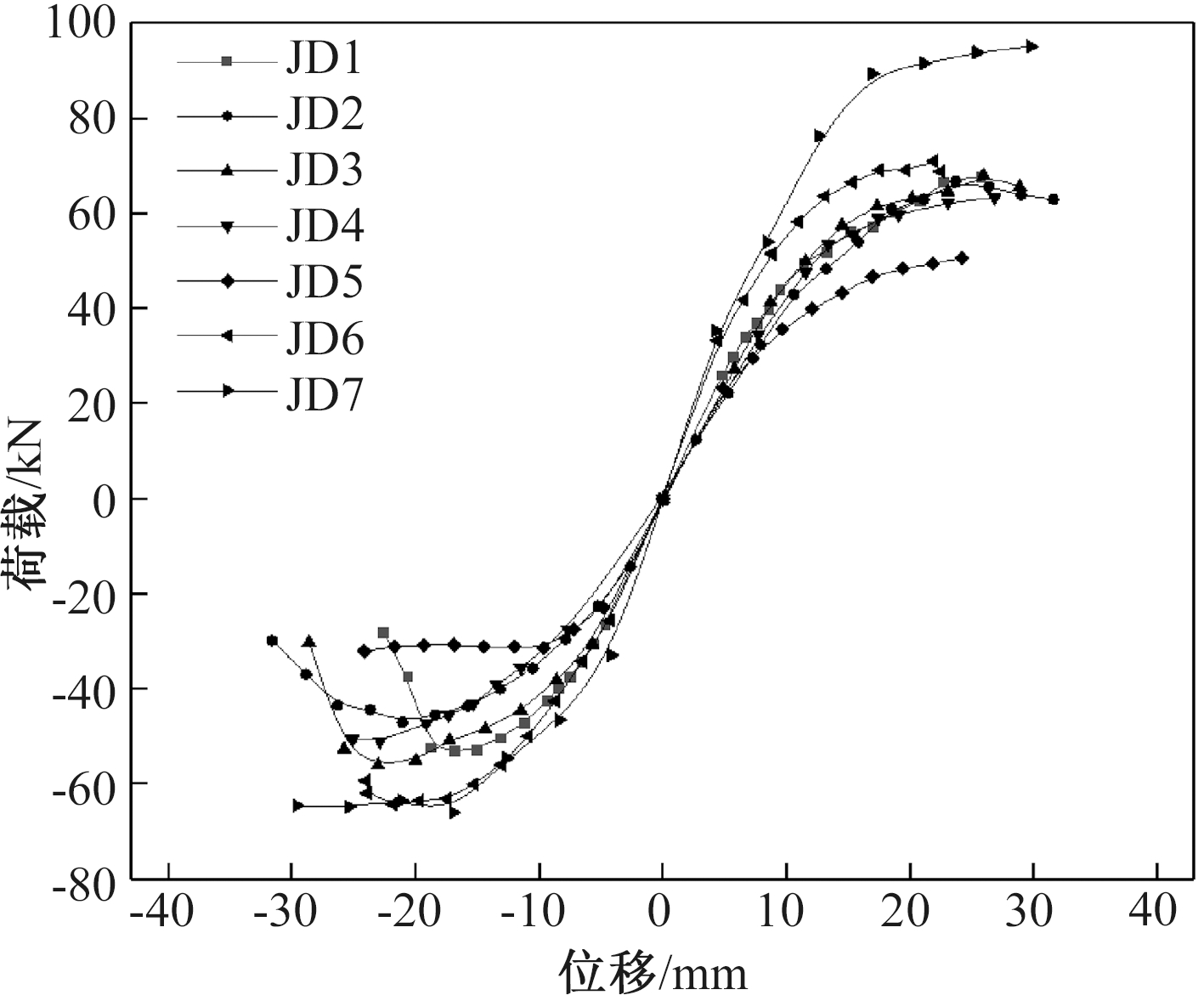
图6 各个试件骨架曲线对比图
Figure 6 Comparison of skeleton curves of each specimen
4 恢复力模型
侧板连接T形钢管混凝土异形柱-钢梁节点的抗震性能良好，能够满足在高烈度地区使用的要求。恢复力模型是结构构件抗震性能在结构弹塑性地震反应中的具体体现，为了使得新型节点在高烈度地区推广应用，本节对该节点的恢复力模型进行研究。
4.1 确定骨架曲线模型
由于各试件在不同阶段的特征值存在较大差异，很难得到其中规律，本文利用极限荷载Pu和其所对应的位移Δu无量纲化处理各个试件骨架曲线，得到无量纲骨架曲线，如图7所示。
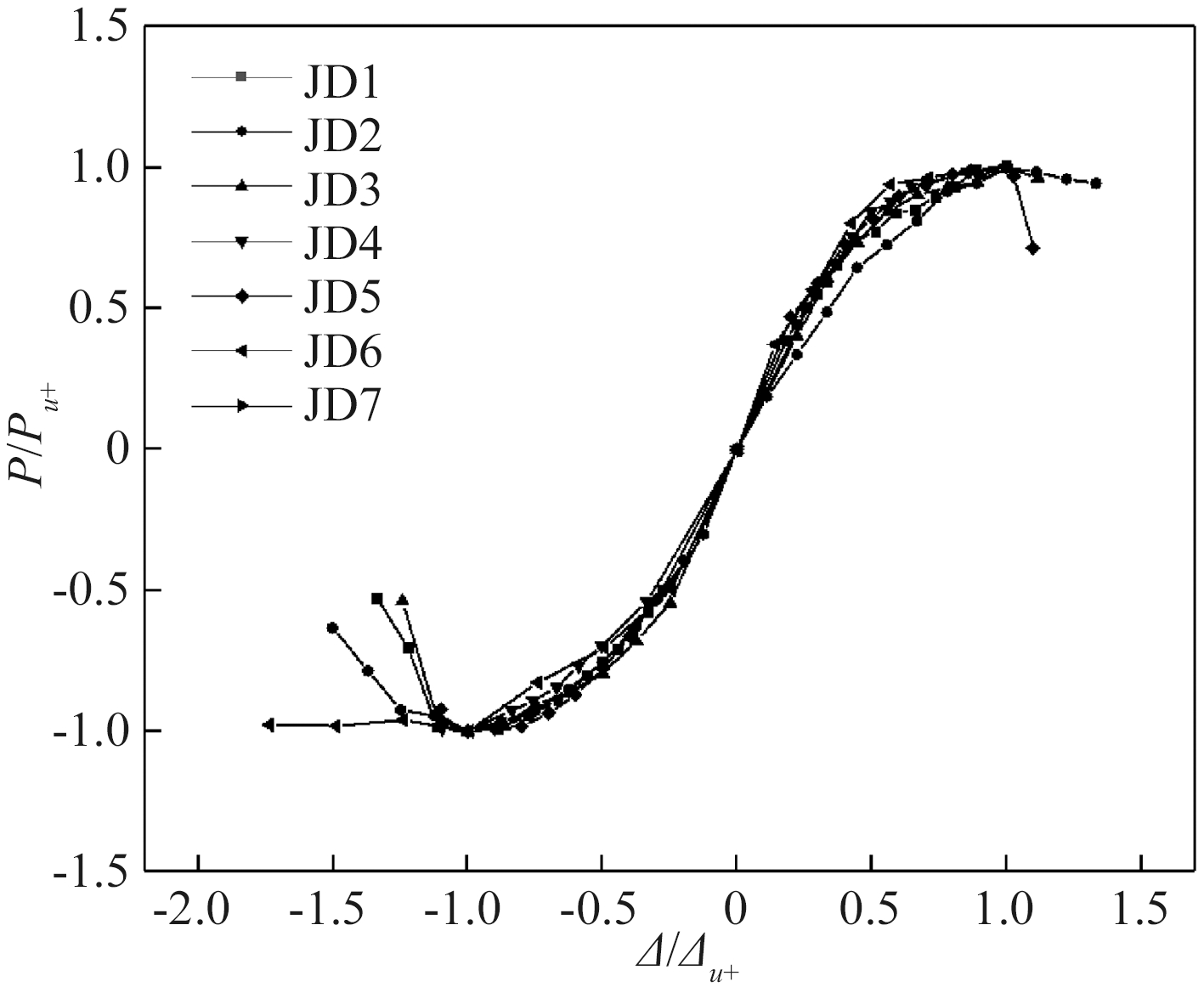
图7 无量纲骨架曲线
Figure 7 Dimensionless skeleton curve
由图7分析可知，试件在加载过程中分为弹性阶段、弹塑性阶段及破坏阶段，故采用三折线型骨架曲线模型，如图8所示。图中A点和A′点分别为正、负向加载的屈服点；B点和B′点分别为正、负向加载的峰值点；C与C′点分别为正、负向破坏点。
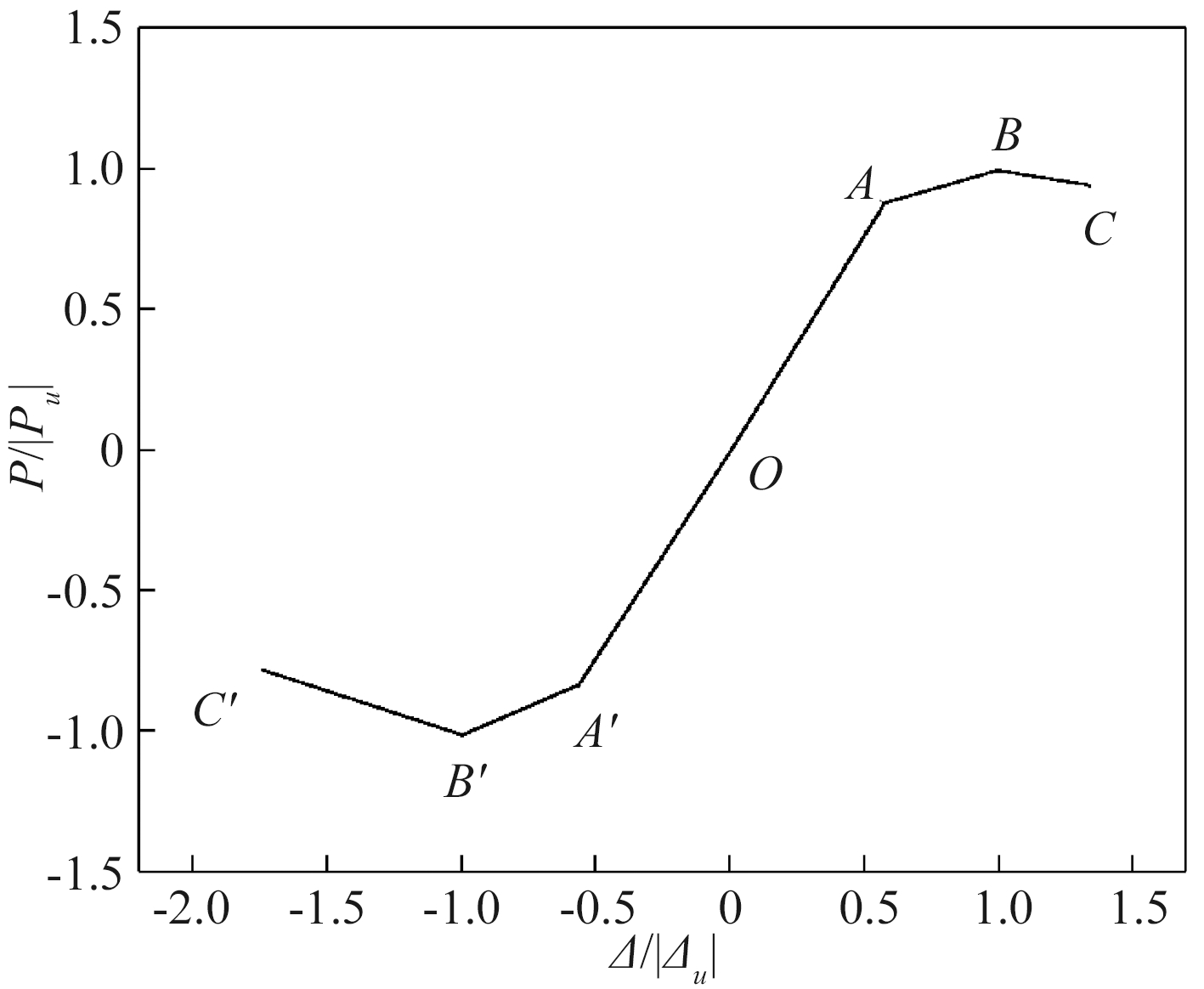
图8 三折线型骨架曲线模型
Figure 8 Three fold skeleton curve model
利用回归方程计算侧板连接T形钢管混凝土柱-钢梁节点试件的骨架曲线，与试验结果进行对比，如图9所示。从图9中可以看出两者较为吻合，能够较好地说明在外部荷载作用下侧板连接节点的荷载-位移曲线发展阶段，同时也验证了此模型的正确性。
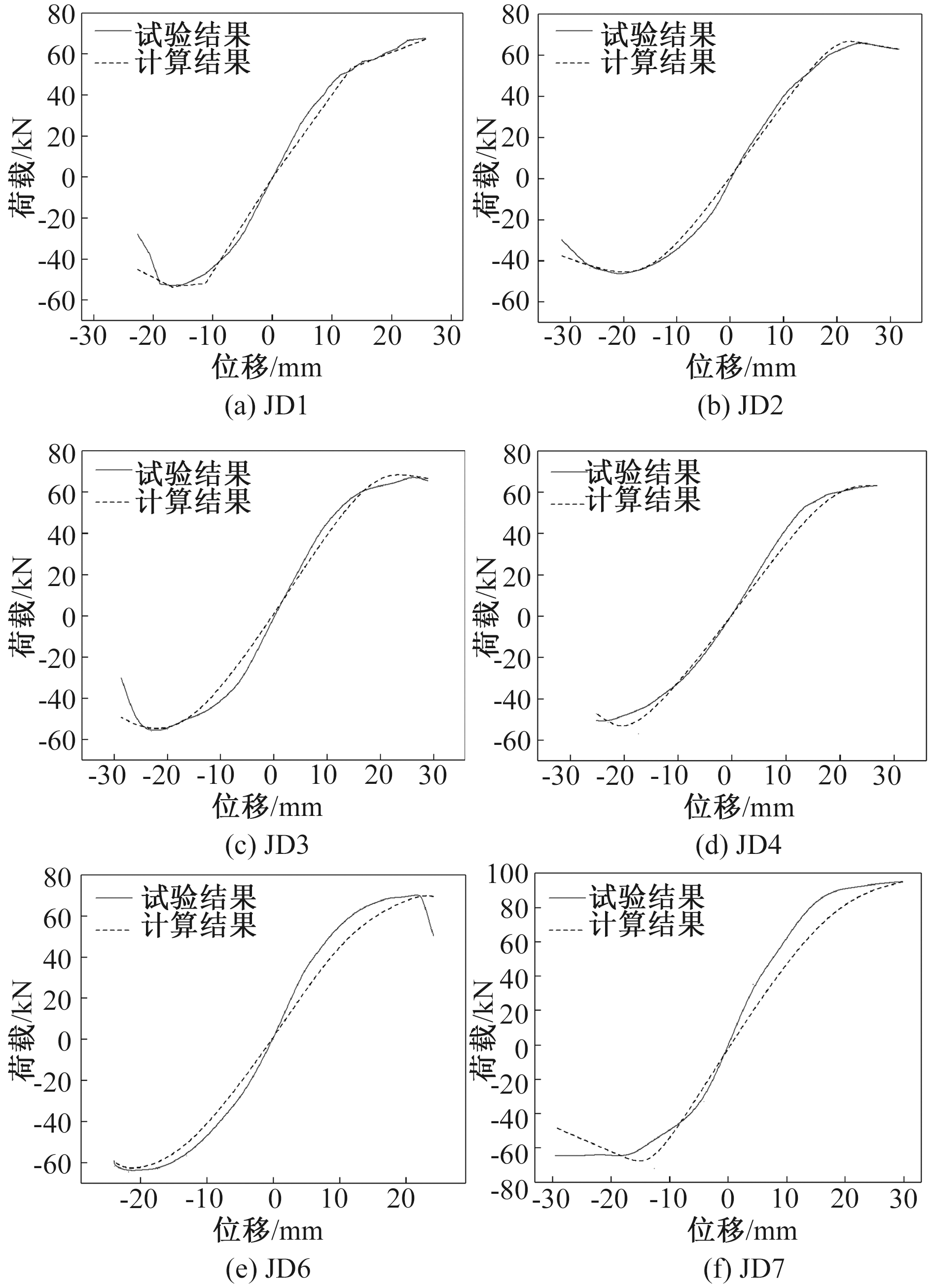
图9 骨架曲线对比图
Figure 9 Skeleton curve comparison chart
4.2 刚度退化
从试验结果可以看出，试验过程中试件的刚度存在一定程度的退化。为了对试件的刚度退化进行分析，本文采用试件在加载或卸载过程中滞回曲线的斜率K来进行表示。K0表示节点的初始刚度，K1 和K4分别表示正向荷载作用时节点的卸载刚度和加载刚度，K2 和K3分别表示负向荷载作用时节点的卸载刚度和加载刚度，其中Δ1、Δ2分别为正向和反向卸载时所对应的位移，Δu为峰值荷载所对应的位移。图10展示了试验过程中试件各个阶段的刚度退化曲线。
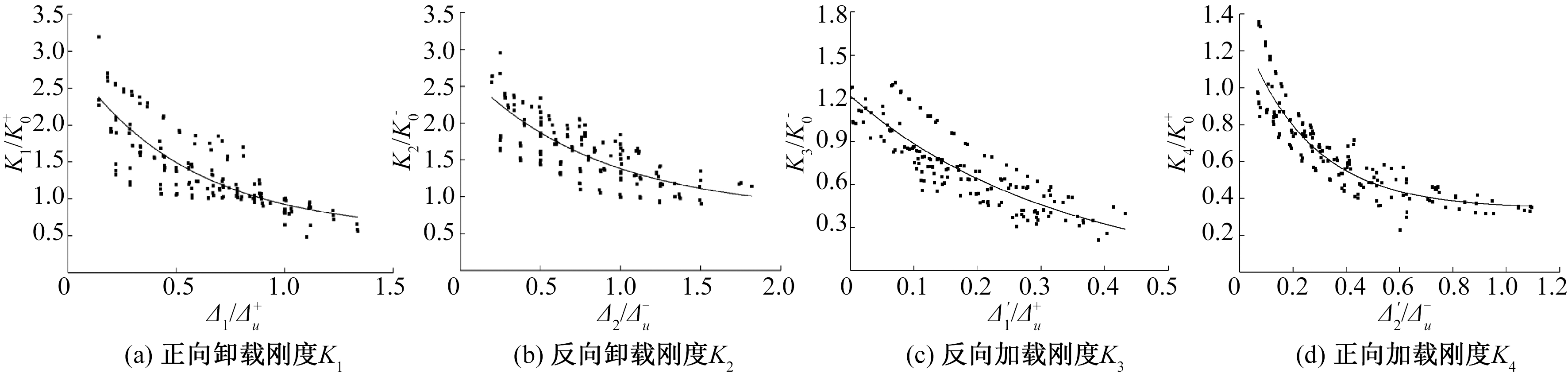
图10 刚度退化曲线
Figure 10 Stiffness degradation curve
其中正向卸载刚度K1与初始刚度K0+之间的关系为
(1)
反向卸载刚度K2与初始刚度K0-的关系为
(2)
反向加载刚度K3与初始刚度K0-的关系为
(3)
正向加载刚度K4与初始刚度K0+的关系为
(4)
4.3 滞回规则
从试验得到的滞回曲线可以看出，在低周往复荷载作用下试件刚度不断退化，采用三线退化型恢复力模型能够较好地反映试件荷载和位移的关系，如图11所示。
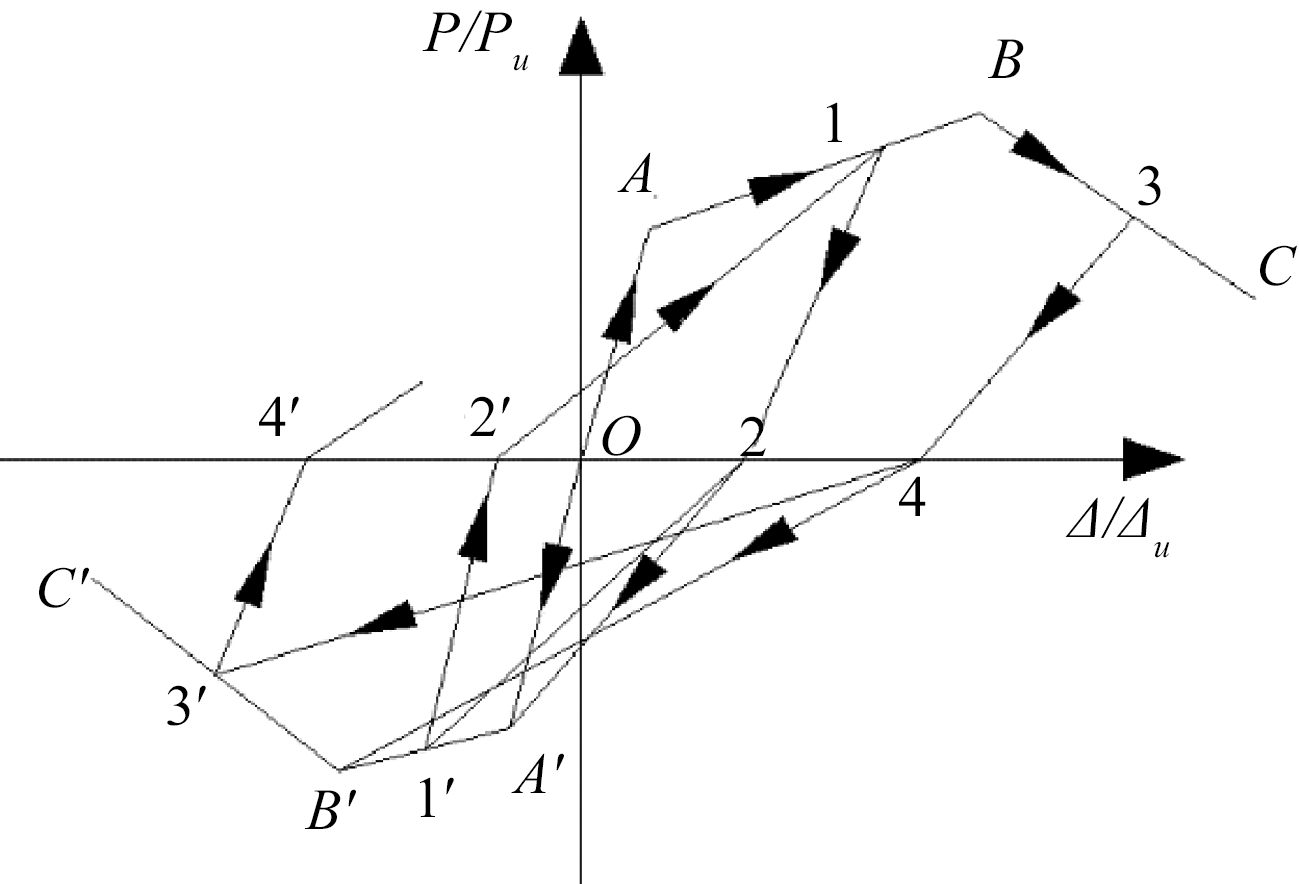
图11 刚度退化三线型恢复力模型
Figure 11 Stiffness degradation trilinear restoring force model
在初始阶段，刚度为弹性刚度
和
加载至A点(A′点)，节点试件开始屈服，加载达到极限荷载B点(B′点)之前，加载路线为O—A—1，卸载路线沿1—2，此时卸载刚度为K1；进行反向加载时，加载路线为2—A′—1′，此时加载刚度为K3；反向卸载路线为1′—2′，此时卸载刚度K2，至此完成一个滞回循环。在达到极限荷载之后，沿O—A—B—3进行加载，卸载路线为3—4，反向加载路线为4—B′—3′，卸载路线为3′—4′。在加载初期，试件刚度较大，残余位移基本可以忽略不计，处于弹性阶段；试件达到屈服阶段之后，残余位移(O2与O2′之间的距离)明显增大，不能忽略；当试件节点达到峰值荷载以后，残余位移(O4与O4′之间的距离)继续增大，表明结构内部出现严重损伤而不能继续承受较大荷载。
4.4 恢复力模型验证
根据骨架曲线结合上述刚度退化规律与滞回规则，构建侧板连接T形钢管混凝土柱-钢梁节点的恢复力模型，并与试验结果进行对比验证，结果如图12所示。
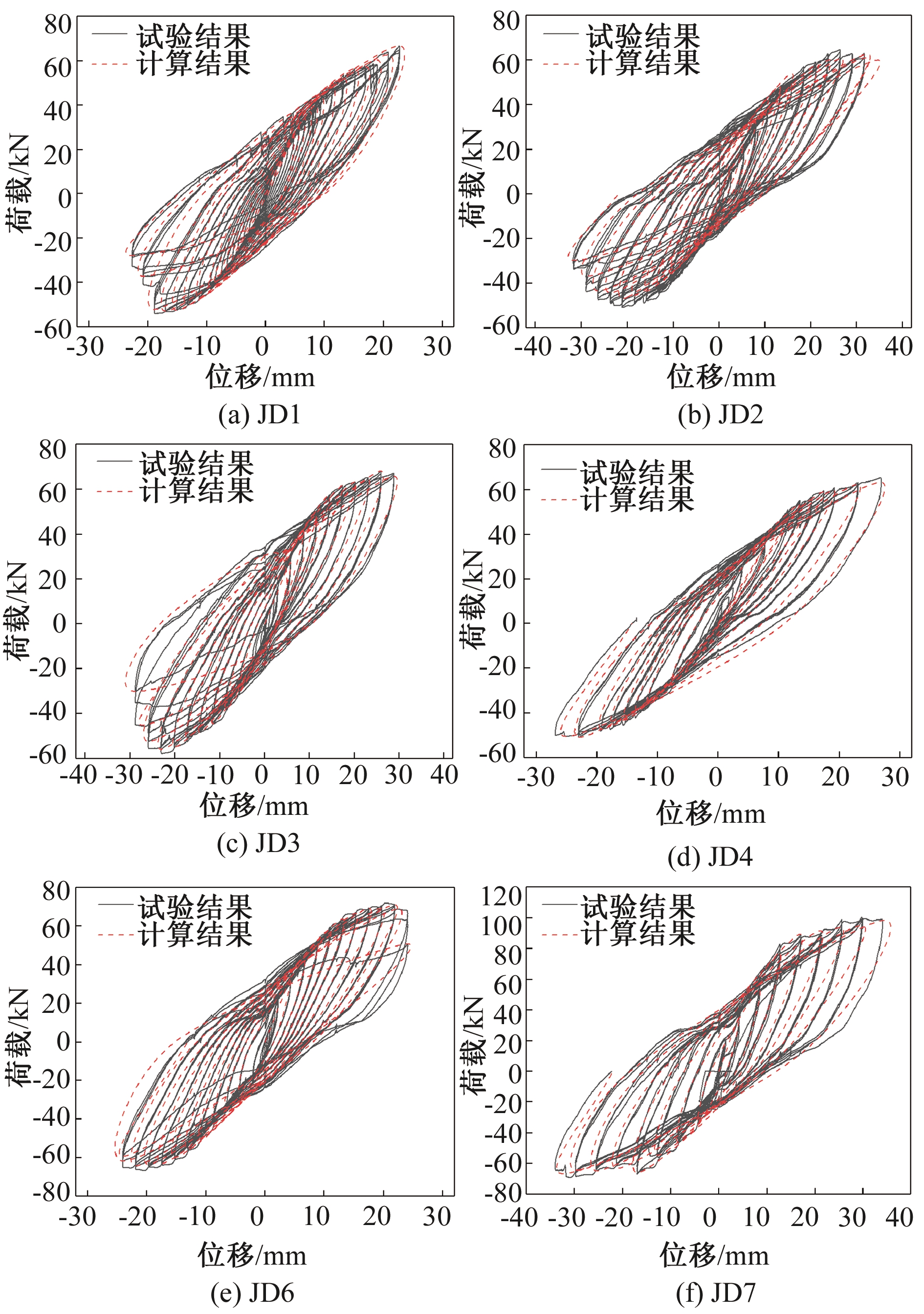
图12 滞回曲线计算结果与试验结果对比
Figure 12 Hysteresis curves compared with experimental results
由图12可知，新型侧板连接T形钢管混凝土异形柱-钢梁节点恢复力模型较好地反映了该节点的滞回特性，经过计算得到的滞回曲线与试验所得吻合良好，此节点恢复力模型可为以后该类节点的试验研究和工程应用提供理论基础。
5 结论
(1)在节点核心区采用侧板连接的方式能够明显提高T形钢管混凝土柱-钢梁节点试件的承载能力和耗能能力等各项抗震性能指标，约束拉杆与侧板长度对试件的承载力影响并不明显。
(2)轴压比较大的试件在受到外部荷载作用时所能承受的荷载也较大，并且在加载后期，随着加载位移的不断增大，试件最终破坏时承载力没有产生明显下降。
(3)利用滞回规则与刚度退化规律建立了侧板连接T形钢管混凝土柱-钢梁节点的恢复力模型，计算得到的滞回曲线与试验得到的滞回曲线吻合较好。
[1] 王景玄, 杨永, 沈亚军. 钢管混凝土组合框架-填充墙结构抗连续倒塌分析[J]. 郑州大学学报(工学版), 2021, 42(2): 19-24.
WANG J X, YANG Y, SHEN Y J. Progressive collapse analysis of composite planar frame with CFST columns and full-height infill walls[J]. Journal of Zhengzhou university (engineering science), 2021, 42(2): 19-24.
[2] 赵毅, 静行. 钢管混凝土柱-RC梁节点受力性能数值模拟[J]. 低温建筑技术, 2014, 36(12): 42-44.
ZHAO Y, JING X. Numerical simulation of mechanical behavior of concrete filled steel tubular column-RC beam joints [J]. Low temperature architecture technology, 2014, 36(12): 42-44.
[3] 叶全喜, 郝放, 薛炳勇, 等. 钢管混凝土异形柱及相关梁柱节点构造研究综述[J]. 北京工业大学学报, 2021, 47(9): 1083-1094.
YE Q X, HAO F, XUE B Y, et al. Review on configurations of concrete-filled steel tubular (CFST) special-shaped columns and corresponding beam-column joints[J]. Journal of Beijing university of technology, 2021, 47(9): 1083-1094.
[4] 张月,李冬生.耗能螺栓连接装配式钢管混凝土梁柱节点恢复力模型研究[EB/OL].(2020-11-26)[2021-07-21].http:∥kns.cnki.net.zzulib.vpn358.com/kns8/defaultresult/index.
ZHANG Y,LI D S. Research on Restoring Force Model of Assembled Concrete Filled Steel Tube Beam-Column Joint Connected by Energy Dissipation Bolt[EB/OL].(2020-11-26)[2021-07-21].http:∥kns.cnki.net.zzulib.vpn358.com/kns8/defaultresult/index.
[5] 王先铁, 谢川东, 罗遥, 等. 带楔形装置的自复位方钢管混凝土柱-钢梁节点抗震性能试验研究[J]. 建筑结构学报, 2021, 42(9): 52-61.
WANG X T, XIE C D, LUO Y, et al. Experimental study on seismic behavior of self-centering concrete-filled square steel tubular column-steel beam frame joint with wedge-shaped device[J]. Journal of building structures, 2021, 42(9): 52-61.
[6] 郏书朔, 王燕, 王修军, 等. 矩形钢管柱与H型钢梁单边螺栓连接节点的抗震性能与恢复力模型研究[J]. 建筑结构学报, 2020, 41(5): 168-179.
JIA S S, WANG Y, WANG X J, et al. Seismic behavior and restoring force model of connections between rectangular tubular columns and H-shaped beams using single direction bolts[J]. Journal of building structures, 2020, 41(5): 168-179.
[7] 赵毅, 边亚东, 王爱勤, 等. 劲性环梁式钢管混凝土节点恢复力模型[J]. 混凝土与水泥制品, 2016(8): 58-62.
ZHAO Y, BIAN Y D, WANG A Q, et al. Restoring force model of steel reinforced ring-beam steel tube filled concrete joint[J]. China concrete and cement products, 2016(8): 58-62.
[8] 唐榕, 张阳阳, 朱凯. 钢管再生混凝土柱-钢梁框架边节点恢复力模型研究[J]. 长江大学学报(自科版), 2016, 13(31): 67-72.
TANG R, ZHANG Y Y, ZHU K. Study on restoring force model of joints in the composite frame with recycled concrete-filled steel tubular column and steel beam[J]. Journal of Yangtze university (natural science edition), 2016, 13(31): 67-72.
[9] 曾磊, 许成祥, 郑山锁, 等. 型钢高强高性能混凝土框架节点P-Δ恢复力模型[J]. 武汉理工大学学报, 2012, 34(9): 104-108.
ZENG L, XU C X, ZHENG S S, et al. Research on restoring force model of SRHSHPC frame joints[J]. Journal of Wuhan university of technology, 2012, 34(9): 104-108.
[10] 王文达, 韩林海. 钢管混凝土框架实用荷载-位移恢复力模型研究[J]. 工程力学, 2008, 25(11): 62-69.
WANG W D, HAN L H. Research on practical resilience model of load versus displacement for concrete filled steel tubular frame[J]. Engineering mechanics, 2008, 25(11): 62-69.