在超宽带(UWB)定位系统中,亟待解决的问题是提高测距精度和测量范围以满足具体应用场景的需要。在视距(LOS)信号场景,目前常采用的UWB定位模式一般基于飞行时间差(TOF) [1-2]、到达时间(TOA)[3-4]或到达时间差(TDOA) [5-6],通过测量的距离构建非线性方程,采用Fang算法[5]、Chan算法[6]或Taylor算法[7-13]求解非线性方程组,得到标签坐标。其中Taylor迭代定位算法具有精度高、计算收敛快等优点,但该方法需要一个初始粗定位置,因此,测距与Taylor迭代联合定位成为目前UWB定位技术的研究热点。姜志鹏等[6]利用TOA测距得到TDOA双曲线方程,然后采用Chan-Taylor算法求解标签坐标;由于传统的TOA需要严格的时钟同步,因此, Liu等[7]、高健等[8]分别通过一次和三次TOF测距得到TDOA双曲线方程,提高了定位精度,尤其是文献[8]的定位精度比文献[6]的定位精度提升了20%。由于TDOA双曲线的性质,靠近双曲线渐近线的点误差小,反之误差大[13],因此王磊等[9]采用全质心-TDOA联合定位,该方法利用了质心算法对距离误差敏感度小的优势,改善了部分初始粗定位置的坐标;任晓奎等[14]提出一种加权质心定位算法用于WSN网络中的RSSI测距;祖明浩等[15]对质心定位引入修正因子从而改善了粗定位精度。然而上述质心定位算法都忽略了多个圆不相交的情况,因此,本文将在TOF测距的基础上,引入加权质心算法计算标签的初始值,并采用TDOA Taylor迭代得到标签的最终位置。与现有UWB定位算法相比,本文所提方法避免了传统TOA测距需要的严格时钟同步,而且能够处理标签位于某个基站边缘或者大噪声环境带来的定位坐标求解问题。
1 算法描述
TOF-LOS定位方程为
(1)
式中:xn为第n个基站的横坐标;yn为第n个基站的纵坐标;Rn为第n个基站到标签的距离。为提高测距精度,本文采用TOF双向测距法
测距时,标签向基站发送测距请求信号,到达基站反应一段时间,再给标签反馈测距信号,最终得到标签到基站的测距时间为
(2)
式中:T1为总的测距时间;T2为基站反应时间。则标签到基站的距离为
Rn=C×T。
(3)
式中:C为光速。
已知Rn,求解式(1)常采用质心算法。图1给出了三基站TOF质心定位示意图,以每一个基站为圆心,以基站到标签距离为半径可以得到3个圆。理论上3个圆的交点就是所求的标签坐标,但是噪声的存在导致3个圆不一定会相交于一点。图1中圆A、圆B、圆C共有6个交点,其中交点E、F、G覆盖区域的质心记为点O,该质心坐标等于E、F、G三点坐标的横坐标和纵坐标的平均值。在上述计算过程中,圆B和圆C有2个交点,而圆A到交点E的距离最小,从而可确定用于计算质心的交点E,同理确定交点F和G。
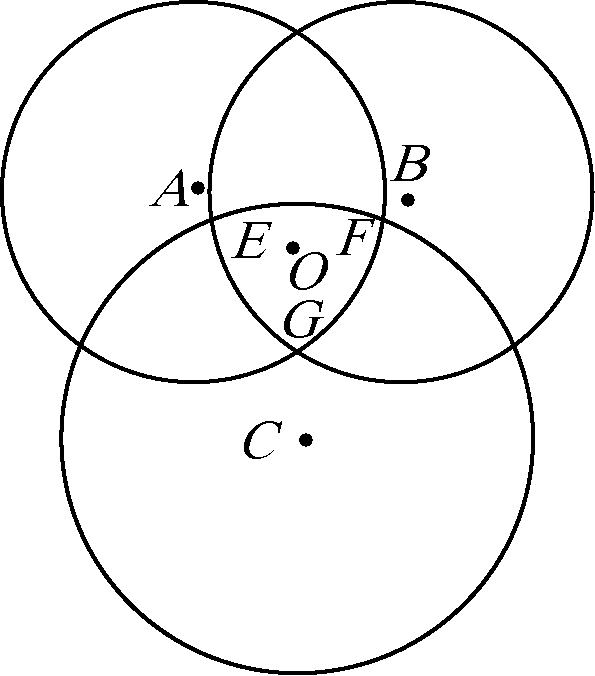
图1 TOF质心定位
Figure 1 TOF centroid location
当噪声较为严重时,会出现3个圆无法两两相交的情况,如图2所示。图2中圆C与另外2个圆没有交点,此时需采用加权质心算法,将3个圆的圆心依次连接,在ΔABC的AB边上选取一点D,使其满足
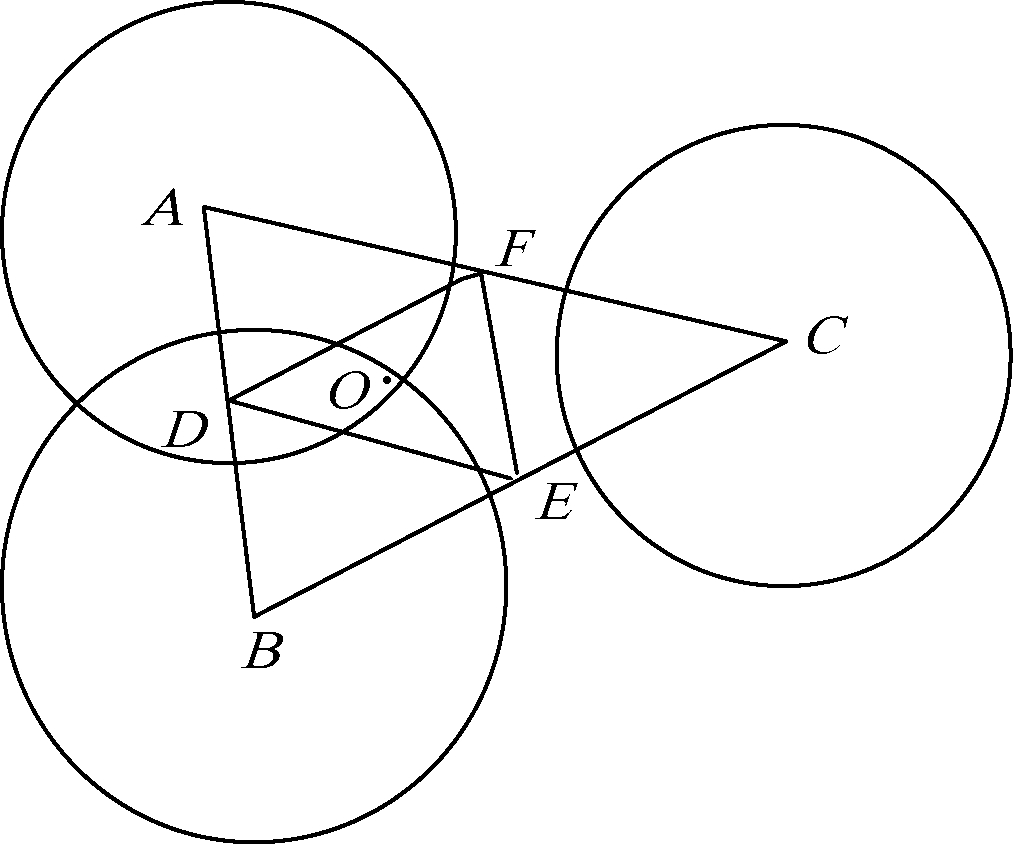
图2 TOF加权质心定位
Figure 2 TOF weighted centroid location
(4)
式中:RA、RB分别为圆A、圆B的半径。同理可得E、F的坐标位置。由此可以构建ΔDEF,其质心即为标签坐标O。
以O点作为标签粗定位置,对TDOA双曲线方程组进行Taylor级数展开,保留展开式前两项,从而将非线性方程组转变为线性方程组,其最优解即为标签坐标。假设标签粗定位置O点坐标为(xl,yl),经过Taylor算法迭代求得的最优标签坐标为(xo,yo),它们满足关系式:
(5)
式中:Δx和Δy分别为横纵方向的误差。
构建以第1个基站为参考的双曲线方程:
(6)
在(xl,yl)处将式(6)进行泰勒级数展开,可得
Rn-R1=Rn,1。
(7)
式(7)用矩阵形式描述为
Z-Aφ=r。
(8)
式中:r为误差矢量;Z为关于Rn,i的标量矩阵;A为关于Rn和xl的标量矩阵;φ为位置偏差。采用最小二乘法可求得位置偏差:
φ=[Δx,Δy]T=
ATQ-1Z。
(9)
其中,Q为TDOA测量误差的协方差矩阵,每次递归求解时目标节点不断更新:
(10)
设置阈值ε,满足
|Δx|+|Δy|≤ε。
(11)
当误差满足式(11)时,停止迭代,输出最终的标签估计位置。
2 仿真实验
在LOS条件下选择4个UWB基站,坐标分别为A(0,0)、B(100,0)、C(0,100)、D(100,100),其示意图如图3所示。标签真实坐标为(x,y),标签接收来自各个基站的信号,信道噪声服从N(0,δ2)。为验证所提联合定位算法的可行性,仿真实验对比分析了基于TOF的加权质心定位算法(记为TOF)、Qin等[4]提出的TDOA定位算法(记为TOA-TDOA)、Zhang等[5]提出的TOF-TDOA联合定位算法(记为TOF-TDOA),评估指标包括均方根误差(RMSE)、算法复杂度、定位散点图等。
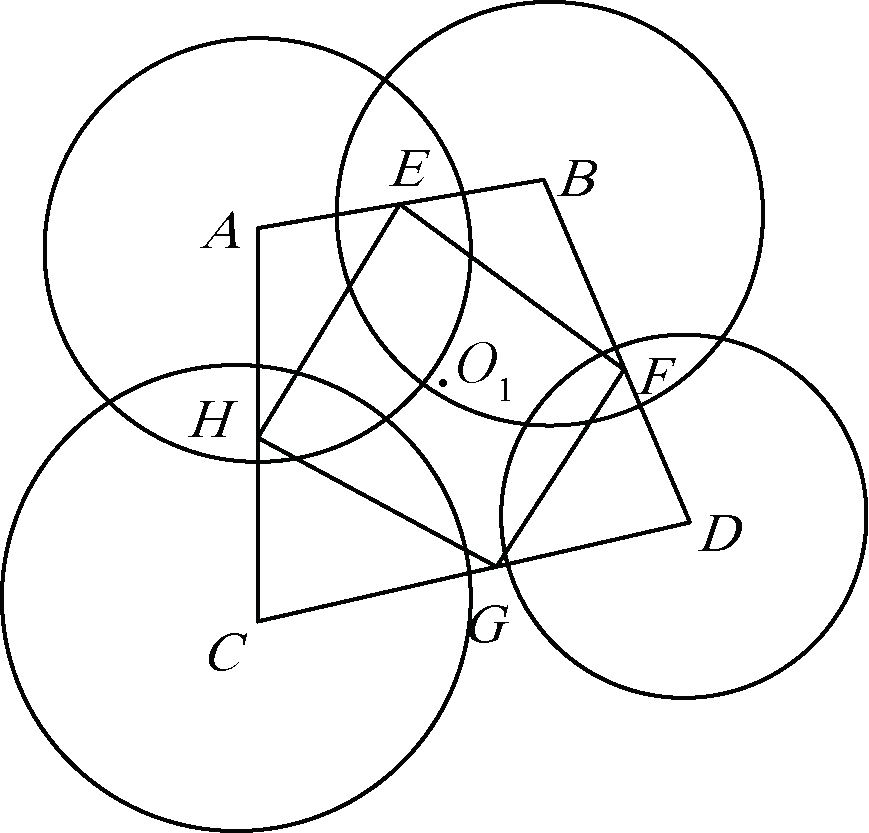
图3 四基站加权质心定位
Figure 3 Four base station weighted centroid location
(1)基于TOF的加权质心定位算法(TOF)。利用TOF测距,得到标签到基站的距离Rn,代入式(1)所示的TOF-LOS定位方程,可得定位方程组:
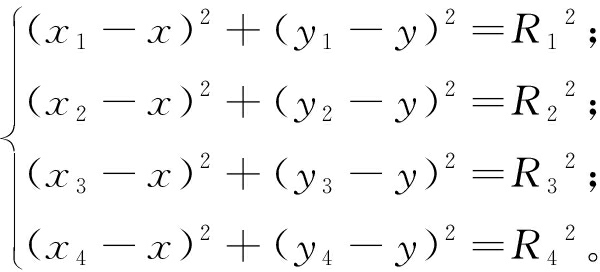
(12)
式中:R1、R2、R3、R4分别为基站A、B、C、D到标签的距离。
以每一个基站为圆心,基站到标签距离为半径可以得到4个圆。理论上4个圆的交点就是所求的标签坐标。当存在噪声时,这4个圆不一定会相交于一点(图3)。将圆心A、B、C、D依次连接,得到四边形ABCD,在边AB上选取一点E,使其满足
(13)
由此可得E的坐标位置。同理可得F、G、H的坐标位置。基于此,构建新的四边形EFGH,其质心O1即为标签坐标。Ol记为(xo1,yo1),则
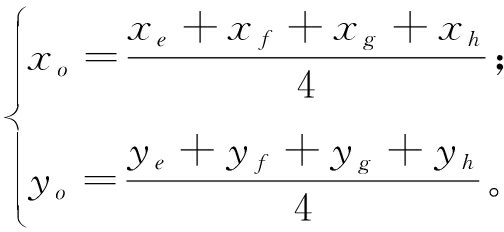
(14)
式中:xe、xf、xg、xh分别为E、F、G、H的横坐标;ye、yf、yg、yh 分别为E、F、G、H的纵坐标。
(2)TOA-TDOA定位算法(TOA-TDOA)[4]。TDOA定位算法利用TOA测距,得到基站到标签的距离ri;以基站A作为参考基站,将基站B、C、D到标签的距离与基站A到标签的距离作差,得到TDOA双曲线方程组:
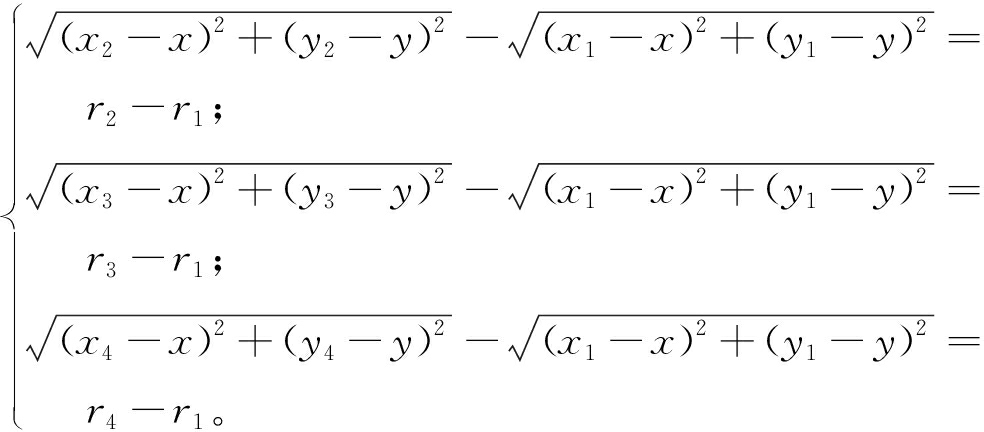
(15)
式中:r1、r2、r3、r4分别为基站A、B、C、D到标签的距离。
将式(15)平方并展开可得
(16)
式中:
将式(16)转换为矩阵形式可得
HV=L。
(17)
式中:H=[x,y,r1]T;V为与xn,1、yn,1、rn,1有关的标量矩阵;L为与rn,1和Kn有关的标量矩阵。
采用Chan算法[16]求解式(17),即采用2次加权最小二乘法(WLS)求解,得到标签的初始粗定位置,记为(xh,yh),其中第1次WLS可得
H=(VTφ-1V)-1Vφ-1L。
(18)
式中:φ为测量误差的协方差矩阵。
第2次WLS可得
H′=(V′TW-1V′)-1VW-1L′。
(19)
式中: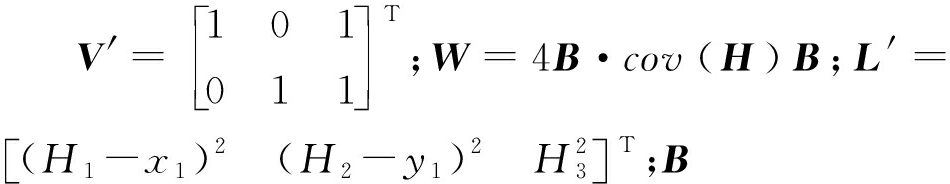
为L′元素的对角矩阵。
则(xh,yh)为
(20)
将该坐标代入式(7)进行Taylor迭代得到最终的标签坐标位置O2,记为(xo2,yo2)。
(3)TOF-TDOA定位算法(TOF-TDOA)[5]。通过TOF测距得到基站到标签的距离,再以基站A作为参考基站,B、C、D基站到标签的距离与A基站到标签的距离作差,得到式(15)所示的TDOA双曲线方程组,最后采用Chan-Taylor算法求解得到最终的标签坐标位置O3,记为(xo3,yo3)。
根据以上3种算法的标签最终估计位置(xoi,yoi),i=1,2,3,可计算定位标签位置估计均方根误差RMSE:
(21)
式中:n为实验仿真次数。
2.1 噪声对定位性能的影响
为验证本文算法在大噪声环境下的性能,将噪声方差分别设置为0.10、0.25、0.50、0.75和1.00,标签真实坐标为(87,35),实验仿真1 000次,迭代阈值设置为0.001。图4为本文算法和TOF、TOA-TDOA[4]、TOF-TDOA[5]的定位均方根误差RMSE。
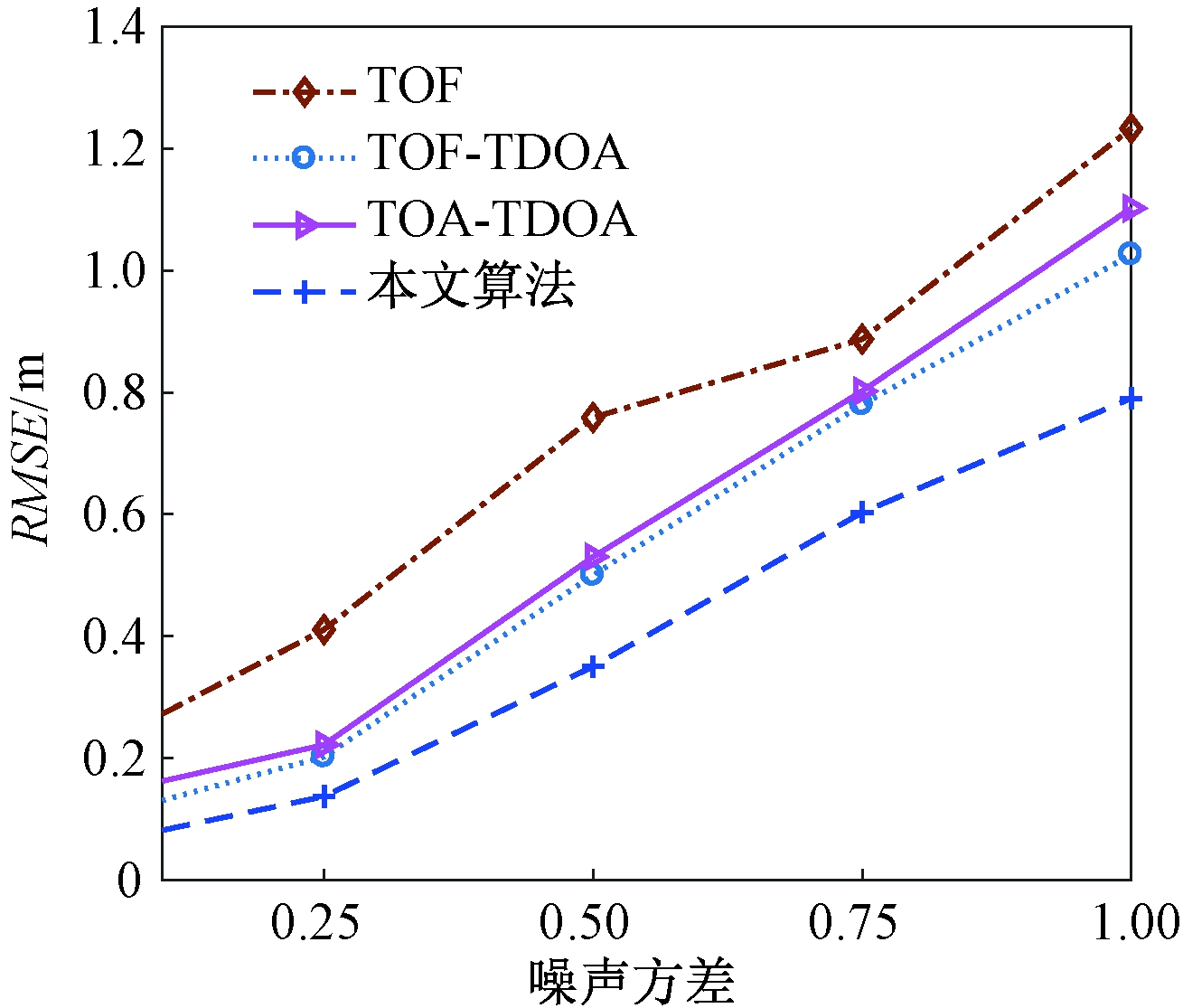
图4 不同噪声下的定位精度
Figure 4 Positioning accuracy with different noises
由图4可知,4种算法的定位精度随噪声方差成正比变化,且本文算法定位精度最高。当噪声方差等于0.75时,本文算法的定位精度比TOF、TOF-TDOA和TOA-TDOA分别提升了30.1%、25.6%和25.8%,此时,TOF、TOF-TDOA和TOA-TDOA算法的定位误差已经超过0.6 m。
2.2 标签位置对定位性能的影响
将噪声方差设置为0.4,随机生成5个标签位置:(50,49)、(90,99)、(89,72)、(3,12)、(68,63),其中(50,49)、(68,63)为远离双曲渐近线的标签,(90,99)、(89,72)、(3,12)为靠近基站的标签。理论上,在上述标签位置定位性能会受到限制。与TOF、TOF-TDOA和TOA-TDOA相比,本文算法的RMSE如图5所示。本文算法与TOF-TDOA、TOA-TDOA的单次定位时间如图6所示。
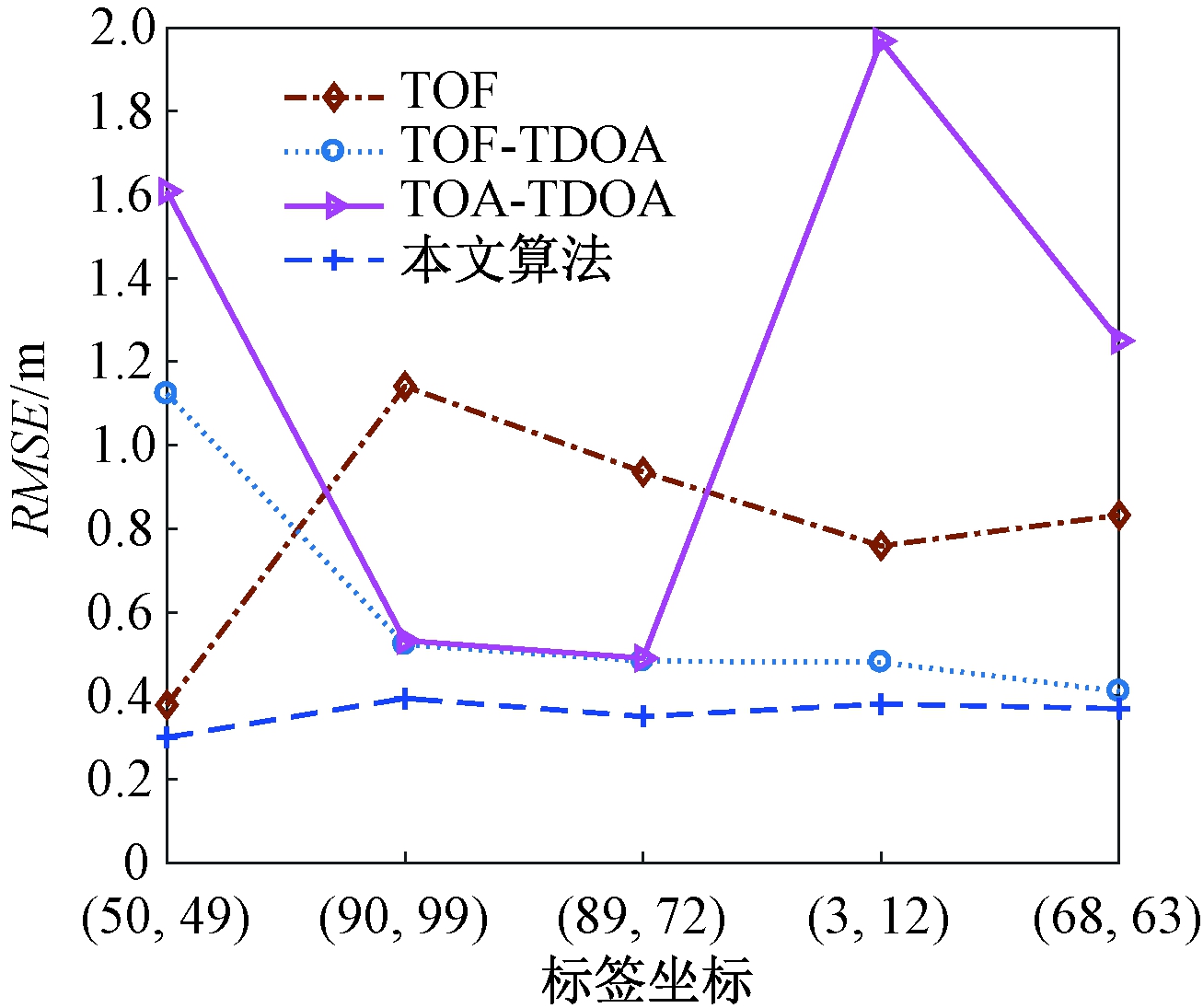
图5 不同标签坐标对应的定位精度
Figure 5 Positioning accuracy with
different tag coordinates
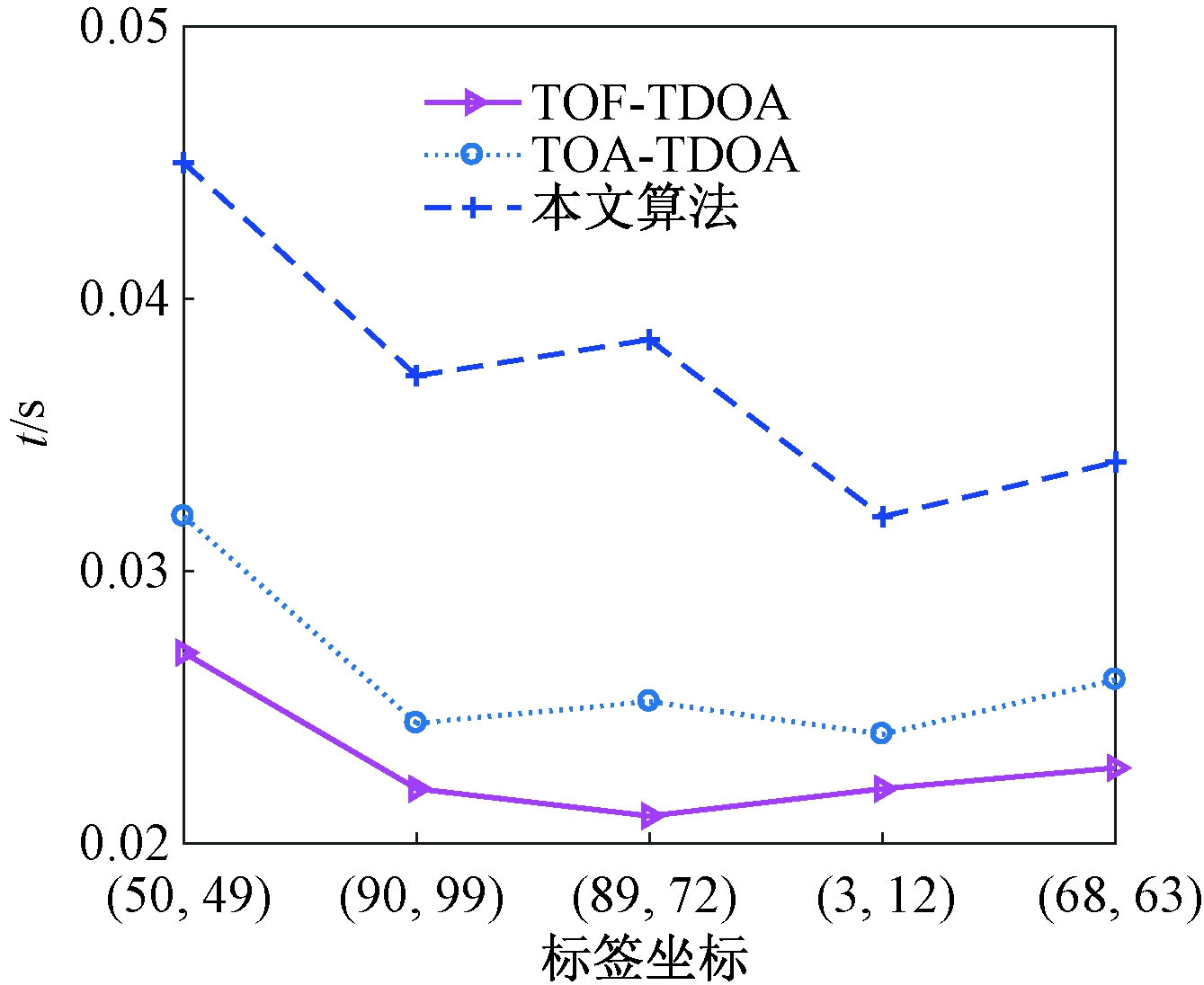
图6 定位算法运行时间对比分析
Figure 6 Positioning time of the proposed algorithm
由图5可知,不管标签远离双曲渐近线还是靠近基站,本文算法均能够提供稳定的定位性能,其定位均方误差曲线随标签位置变化的波动最小。当标签位于基站边缘时,与TOF-TDOA相比,本文算法的定位精度平均提高26%,而TOA-TDOA的定位误差已经超过1.6 m。当标签远离双曲线渐近线时,本文算法的定位误差在0.4 m以内。
由图6可知,在算法复杂度方面,本文算法与TOA-TDOA、TOF-TDOA的迭代次数相同,但本文算法的平均定位时间为0.036 s,比TOF-TDOA增加了0.013 s,这是由于增加初始标签坐标计算导致的,但是仍满足UWB室内实时定位的需求。
2.3 标签定位散点图分析
由上述实验可知,本文算法的优势是能够在大噪声环境以及标签位于基站附近或者偏离双曲线渐近线的位置保证较好的定位性能。
为进一步验证本文所提算法估计的标签位置分布情况,本文算法与TOF、TOF-TDOA、TOA-TDOA的标签位置估计散点图如图7所示。实验中选取偏离双曲线渐近线位置的标签,其真实位置为(60,35),噪声方差为0.8,实验仿真200次。
由图7可知,在大噪声条件下,本文算法计算得到的标签位置坐标基本分布在同一区域,围绕真实坐标呈现较好的聚集性,而TOF、TOF-TDOA、TOA-TDOA标签定位坐标分布较为发散,有部分定位坐标已经严重失真。
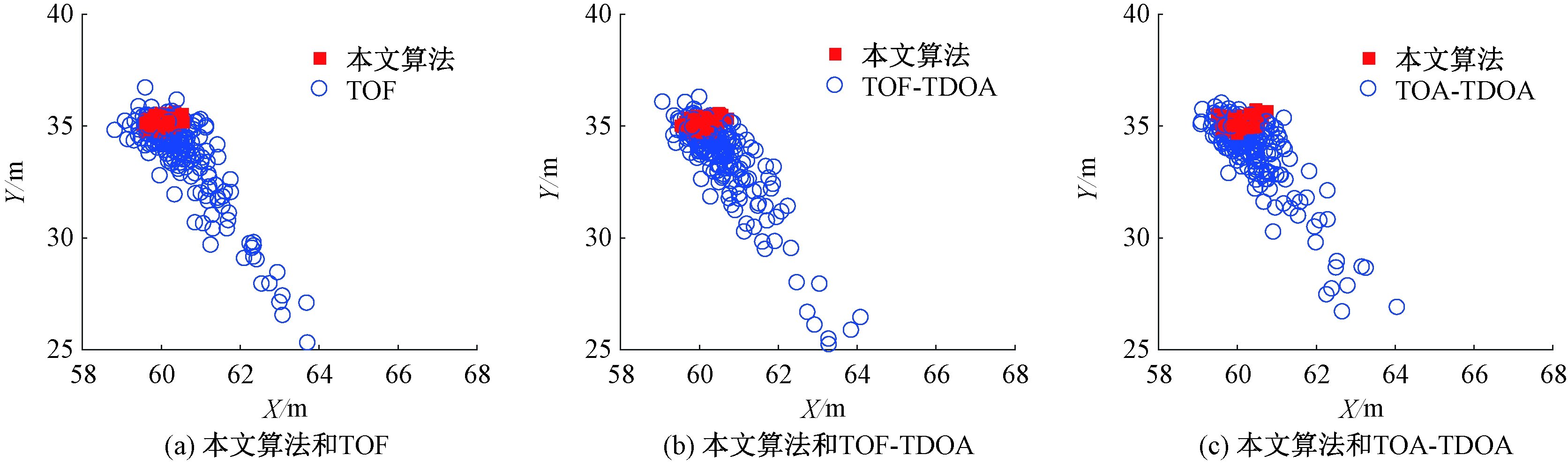
图7 本文所提算法与其他方法的标签定位散点图对比分析
Figure 7 Positioning tag scatter of the proposed algorithm compared with others
3 结论
(1)针对大噪声环境或者标签位于基站边缘的情况,以不同基站为圆心的定位圆两两不相交导致的TOF非线性定位方程无法求解的问题,引入加权质心算法求解标签初始位置。
(2)以标签初始位置为定位方程解的初值,采用Taylor迭代求解标签最终坐标。仿真实验表明,本文算法对噪声强度变化并不敏感,其定位精度保持在0.4 m以内;与其他算法相比,本文算法能够有效改善定位精度,尤其是在大噪声环境或者标签位于基站边缘或偏离双曲线渐近线的场景。
[1] MOON S, YOUN W. A novel movable UWB localization system using UAVs[J]. IEEE Access, 2022, 10: 41303-41312.
[2] JANG B J. Principles and trends of UWB positioning technology[J]. The Journal of Korean Institute of Electromagnetic Engineering and Science, 2022, 33(1): 1-11.
[3] ZHANG S, YANG J, ZHANG L, et al. A research on UWB precise positioning algorithm using TOA algorithm of two-way ranging[J].Journal of Aeronautics, Astronautics and Aviation, 2022, 54(4): 375-391.
[4] QIN X F, XIA B, DING T, et al. An improved Cuckoo search localization algorithm for UWB sensor networks[J]. Wireless Networks, 2021, 27(1): 527-535.
[5] ZHANG F Y, YANG L, LIU Y H, et al. Design and implementation of real-time localization system (RTLS) based on UWB and TDoA algorithm[J]. Sensors, 2022, 22(12): 1-23.
[6] 姜志鹏, 陈正宇, 刘影,等. TOA定位算法非线性优化问题研究[J]. 传感技术学报, 2015, 28(11): 1716-1719.
JIANG Z P, CHEN Z Y, LIU Y, et al. Study on nonlinear optimization for TOA location algorithm[J]. Chinese Journal of Sensors and Actuators, 2015, 28(11): 1716-1719.
[7] LIU C, BAI F, WU C. A joint positioning algorithm of TDOA and TOF based on ultra-wideband[J]. Journal of Physics, 2021, 2031(1): 1-8.
[8] 高健, 陆阳, 李庆巧,等. 采用三次通信的TOF与TDOA联合定位算法[J]. 电子测量与仪器学报, 2020, 34(3): 66-73.
GAO J, LU Y, LI Q Q, et al. TOF and TDOA joint positioning algorithm using three communications [J]. Journal of Electronic Measurement and Instrumentation, 2020, 34(3): 66-73.
[9] 王磊, 李鹏涛, 贾宗璞. 基于全质心-Taylor的UWB室内定位算法[J]. 传感器与微系统, 2017, 36(6): 146-149.
WANG L, LI P T, JIA Z P. UWB indoor localization algorithm based on full centroid and Taylor[J]. Transducer and Microsystem Technologies, 2017, 36(6): 146-149.
[10] WANG N, YUAN X L, MA L X, et al. Research on indoor positioning technology based on UWB[C]∥2020 Chinese Control and Decision Conference (CCDC). Piscataway: IEEE, 2020: 2317-2322.
[11] 陈小斯, 沈重, 周群, 等. 基于TDOA算法的差分UWB室内定位系统研究[J]. 现代电子技术, 2018, 41(6): 45-49.
CHEN X S, SHEN C, ZHOU Q, et al. Research on differential UWB indoor positioning system based on TDOA algorithm[J]. Modern Electronics Technique, 2018, 41(6): 45-49.
[12] 张勇, 高光辉, 郭一楠, 等. 融合差分进化和Taylor级数的超宽带定位解算方法[J]. 郑州大学学报(工学版), 2020, 41(1): 70-74, 82.
ZHANG Y, GAO G H, GUO Y N, et al. Ultra-wideband positioning solution method based on differential evolution and Taylor series[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(1): 70-74, 82.
[13] MAZRAANI R, SAEZ M, GOVONI L, et al. Experimental results of a combined TDOA/TOF technique for UWB based localization systems[C]∥2017 IEEE International Conference on Communications Workshops (ICC Workshops). Piscataway: IEEE, 2017: 1043-1048.
[14] 任晓奎, 于百川, 李岩. 基于RSSI的加权质心定位算法的改进[J]. 传感器与微系统, 2021, 40(11): 150-153.
REN X K, YU B C, LI Y. Improvement of weighted centroid localization algorithm based on RSSI[J]. Transducer and Microsystem Technologies, 2021, 40(11): 150-153.
[15] 祖明浩, 荣宪伟. 基于内三角形质心修正——Taylor的UWB室内定位算法[J]. 哈尔滨师范大学自然科学学报, 2018, 34(6): 42-47.
ZU M H, RONG X W. UWB indoor localization algorithm based on inner triangle centroid correction and Taylor[J]. Natural Science Journal of Harbin Normal University, 2018, 34(6): 42-47.
[16] 郑飞, 郑继禹. 基于TDOA的CHAN算法在UWB系统LOS和NLOS环境中的应用研究[J]. 电子技术应用, 2007, 33(11): 110-113, 132.
ZHENG F, ZHENG J Y. Application research of TDOA based CHAN algorithm under the circumstances of LOS and NLOS in UWB system[J]. Application of Electronic Technique, 2007, 33(11): 110-113, 132.