岩体由岩石和结构面两部分组成,但岩体的变形和破坏主要受到结构面控制。结构面的抗剪强度特性是岩体的重要力学性质之一,将直接影响岩体工程的安全。针对结构面的抗剪强度特性,国内外学者从不同方面展开了大量的研究。在结构面表面形态方面,Barton[1]研究了结构面表面形态对结构面抗剪强度的影响;张清照等[2]、周辉等[3]探讨了不同形态(起伏角)的锯齿形结构面的强度及变形规律。在尺寸效应方面,Bandis等[4]根据结构面抗剪强度直剪试验结果,给出了抗剪强度尺寸效应的定性描述;Bahaaddini等[5]基于数值计算分析了岩体节理抗剪强度的尺寸效应。在结构面充填特征方面,Indraratna等[6]探究了节理充填度与抗剪强度的关系;孙辅庭[7]探究了岩样结构面注浆前后的剪切规律。在结构面连通率方面,Lajtai[8]研究了共面非贯通节理岩体的剪切特性;陈庆芝等[9]研究了不共面非贯通节理岩体的特性。
风化程度是影响结构面抗剪强度特性的主要因素之一。Ismail等[10]、Ram等[11]发现风化程度显著影响节理的抗剪强度。Woo等[12]通过节理面壁抗压强度和残余摩擦角来评价节理风化过程中抗剪强度的演化规律。Özvan等[13]发现风化作用会导致花岗岩节理的节理表面粗糙度增加,但表面粗糙度的增加并没有导致抗剪强度的提高,相反,不连续面抗剪强度显著降低。
针对锯齿形结构面的抗剪强度特性,学者们[2-3,14-15]探讨了锯齿形结构面形态(起伏角)的剪切强度和剪切变形的规律,并建立了锯齿形结构面剪切强度估算模型。众所周知,风化作用普遍存在于自然界中,会对岩体结构面剪切特性产生不利影响。现有研究发现,随着风化程度的增加,岩体结构面抗剪强度降低。现有研究仅针对锯齿形结构面的抗剪强度以及起伏角建立锯齿形结构面抗剪强度公式,但并未考虑风化程度这一因素。因此,通过风化模拟试验制备不同风化程度的锯齿形结构面试样,开展结构面直剪试验探讨风化程度对锯齿形结构面抗剪强度特性的影响规律,以此建立风化作用下灰岩锯齿形结构面抗剪强度估算模型,对于在岩体工程中快速获取灰岩风化锯齿形结构面抗剪强度特性具有重要意义。
1 样品制备
从现场选取新鲜的灰岩岩样作为试验材料,加工成起伏角为15°、25°、35°、45°的锯齿形结构面试样,单锯齿长度L为4 cm,试样尺寸为100 mm×100 mm×50 mm,部分锯齿形结构面试样如图1所示。

图1 锯齿形结构面试样
Figure 1 Sawtooth structural plane sample
根据锯齿形结构面起伏角的大小,将其分为4组,每组12个试样,共计48个试样,结构面形态模拟方案如表1所示。
表1 结构面形态模拟方案
Table 1 Structural plane shape simulation scheme

试验组别试样编号起伏角/(°)试样个数1 1-1^1-12#151222-1^2-12#251233-1^3-12#351244-1^4-12#4512
2 锯齿形结构面风化模拟试验
2.1 试验方案
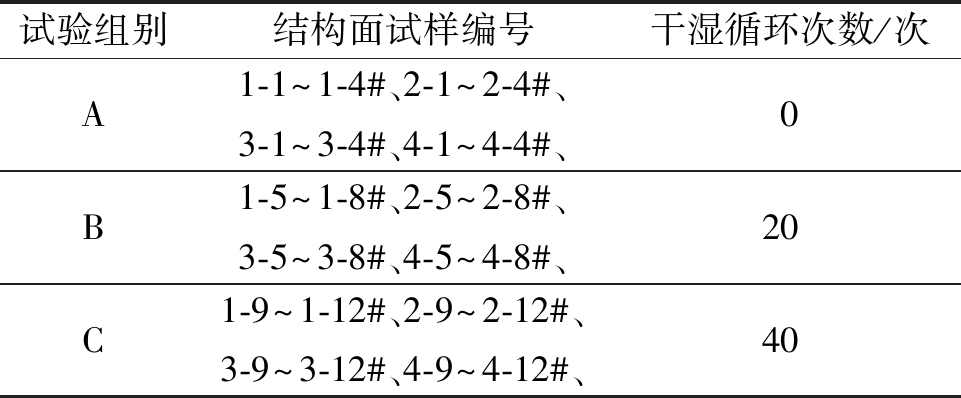
在研究风化程度对锯齿形结构面抗剪强度特性的影响规律之前,需要利用结构面风化模拟试验制备不同风化程度结构面的试样。相同起伏角大小的结构面试样选取4个试样,4种结构面共计16个为1组,共3组(A、B、C组),3组试样分别进行0、20、40次的浸泡-干燥循环试验,锯齿形结构面试样的风化模拟试验方案如表2所示。
表2 锯齿形结构面风化试验方案
Table 2 Weathering test scheme of limestone structural plane
试验组别结构面试样编号干湿循环次数/次A1-1^1-4#、2-1^2-4#、3-1^3-4#、4-1^4-4#、0B1-5^1-8#、2-5^2-8#、3-5^3-8#、4-5^4-8#、20C1-9^1-12#、2-9^2-12#、3-9^3-12#、4-9^4-12#、40
本次结构面风化模拟试验按以下试验方法进行:采用先浸泡,再干燥的循环模式,一次循环试验为利用Na2SO4溶液[16]作为浸泡环境,持续24 h;然后在烘箱里干燥12 h,烘烤温度控制为105~110 ℃,以此为一次循环试验[17]。
2.2 试验结果
利用风化模拟试验制备了不同风化程度的锯齿形结构面试样,为了对结构面的风化程度进行判定,需要对其进行波速测试获取波速比,根据《公路工程地质勘查规范》(JTG C20—2011)[18],对结构面风化程度进行试验,结果如图2所示。
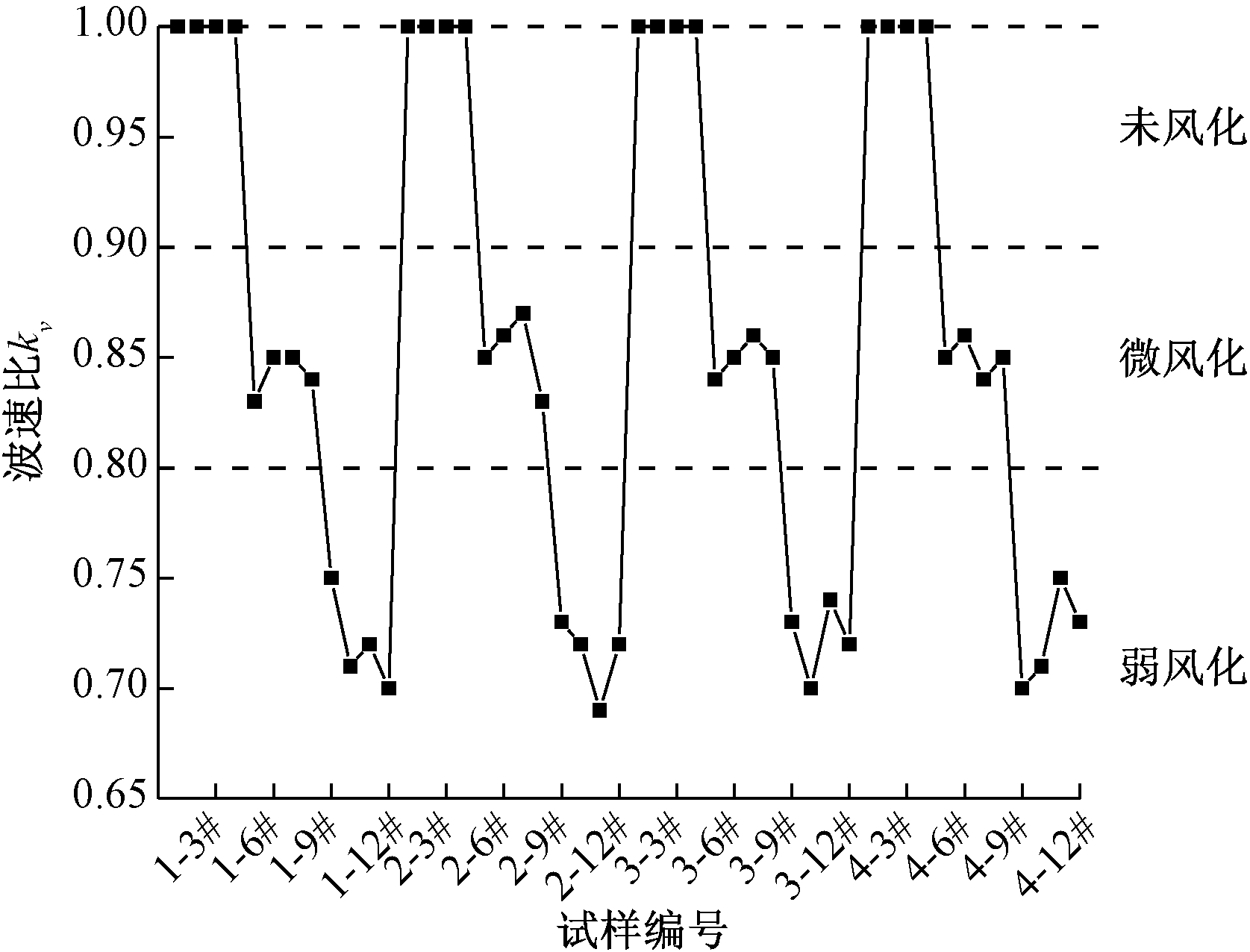
图2 灰岩结构面风化试验结果
Figure 2 Weathering test results of limestone structural plane
2.3 结构面风化机理浅析
岩体中的结构面会为各种风化提供作用通道,从而使风化作用沿结构面向内部发展,导致岩体结构及抗剪强度特性劣化[19],如图3所示。水化学环境对岩体的作用包括物理和化学两方面的影响。在物理方面,水会对岩体内颗粒界面产生润滑作用,破坏矿物颗粒之间的连接[20],同时水压力会对微裂隙等缺陷产生劈裂作用等;在化学方面,水化学溶液会与矿物成分发生化学反应,出现物质改变,并溶解一些矿物,导致岩体微孔隙、微裂隙等微细观结构发生变化,宏观上表现为岩体抗剪强度特性的改变。
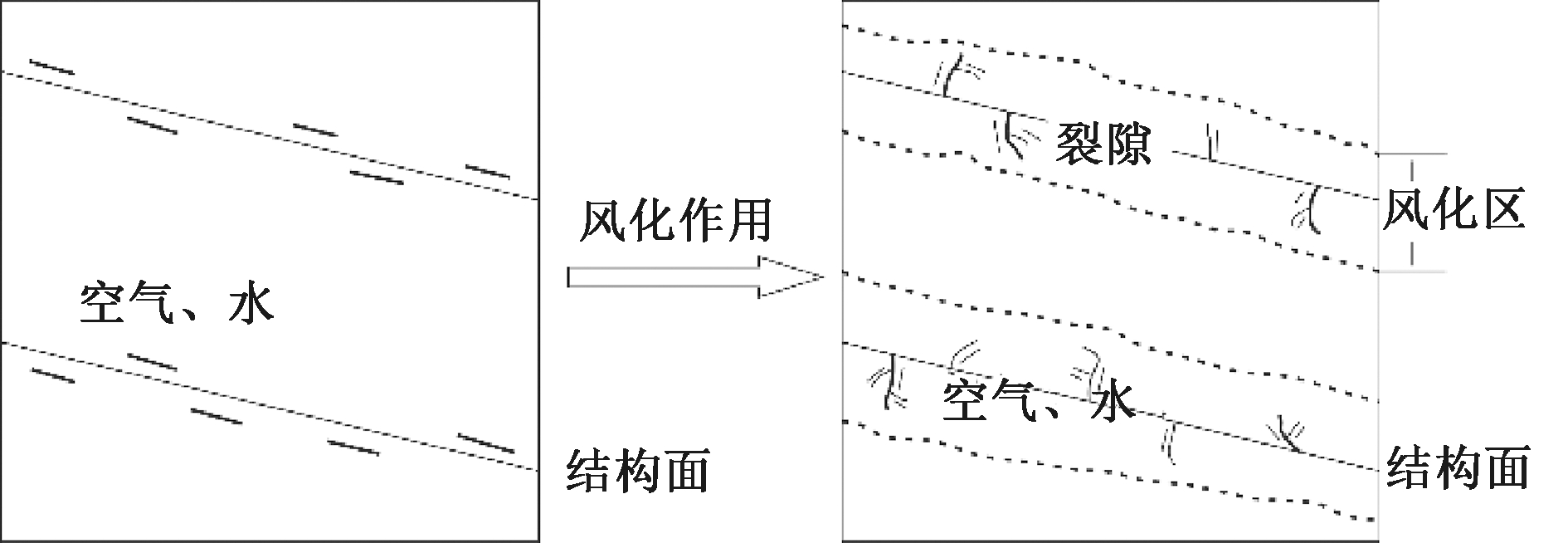
图3 岩体结构面风化示意图
Figure 3 Weathering diagram of rock structural plane
3 锯齿形结构面抗剪强度试验
3.1 试验方案
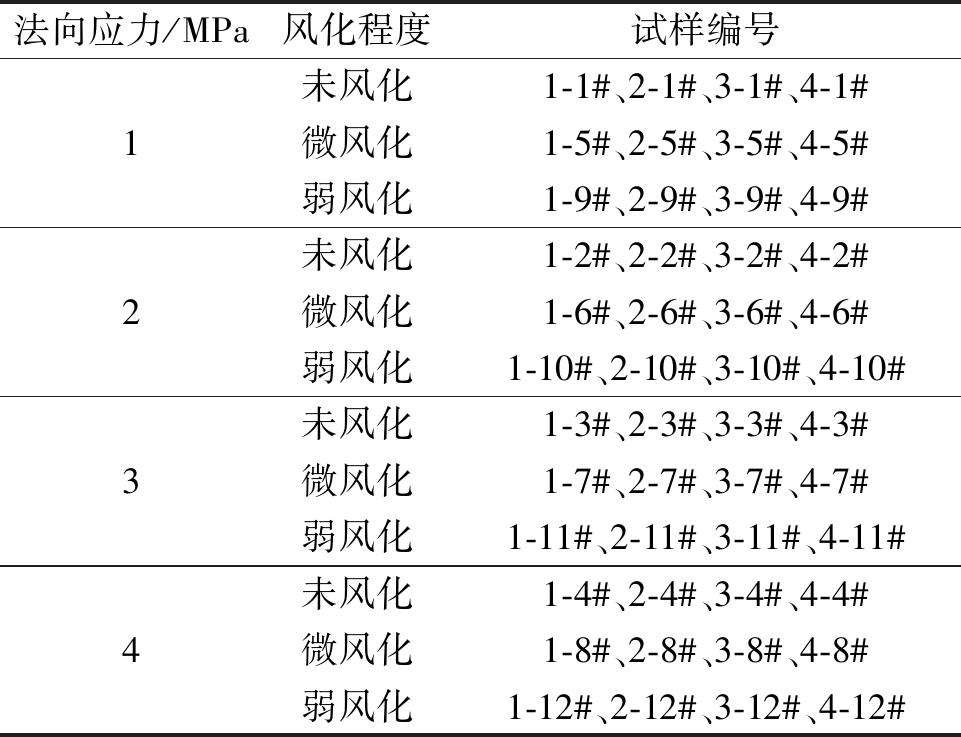
以结构面风化试验的结果为基础,考虑起伏角、风化程度与法向应力3个变量,开展室内结构面直剪试验,试验方案如表3所示。
表3 锯齿形结构面剪切试验方案
Table 3 Test scheme of serrated structural plane
法向应力/MPa风化程度试样编号1未风化1-1#、2-1#、3-1#、4-1#微风化1-5#、2-5#、3-5#、4-5#弱风化1-9#、2-9#、3-9#、4-9#2未风化1-2#、2-2#、3-2#、4-2#微风化1-6#、2-6#、3-6#、4-6#弱风化1-10#、2-10#、3-10#、4-10#3未风化1-3#、2-3#、3-3#、4-3#微风化1-7#、2-7#、3-7#、4-7#弱风化1-11#、2-11#、3-11#、4-11#4未风化1-4#、2-4#、3-4#、4-4#微风化1-8#、2-8#、3-8#、4-8#弱风化1-12#、2-12#、3-12#、4-12#
此次结构面直剪试验采用如图4所示的携带式岩土力学多功能试验仪。将不同风化程度结构面的试样利用一定配比的混凝土(水泥、干砂、水的质量比为1∶2∶0.5)浇筑成150 mm×150 mm×150 mm的标准试样,然后放入内模尺寸与试样大小相同的剪切盒中进行试验。

图4 携带式岩土力学多功能试验仪
Figure 4 Portable multifunctional rock tester
采用推剪法进行试验,施加预定法向应力并保持不变,分阶段施加剪切载荷,记录每次剪切载荷下的剪切位移,最终记录试验破坏时的剪切压力,仪器归置。
3.2 锯齿形结构面剪切位移特征
采用本文试验设计方案可得到不同起伏角锯齿形结构面在不同法向应力条件下的剪切应力-剪切位移曲线,以起伏角为35°的锯齿形结构面为例,如图5所示。
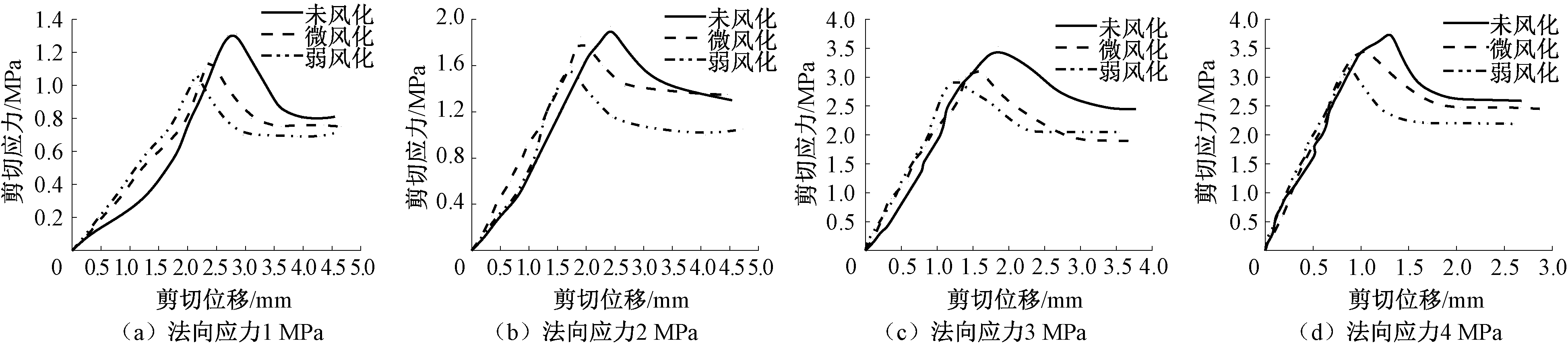
图5 锯齿形结构面剪切应力与剪切位移的关系曲线
Figure 5 Relationship between shear stress and shear displacement of sawtooth structural plane
由图5可知,随着剪切位移的增加,剪切应力首先呈近似线性增长,达到峰值剪切应力后开始跌落,最终保持近似水平恒定的趋势,表现为峰值剪断型曲线。随着风化程度的增加,线性增长阶段的曲线斜率大致相同,说明风化程度对曲线的斜率并无影响。而相同起伏角大小条件下,随着法向应力的增加,峰值剪切应力相应增加,但线性增长阶段的曲线斜率不同。当法向应力较低时,锯齿首先会发生爬坡效应然后才被剪断,从而造成剪切位移明显增大,曲线斜率较小。当法向应力增大时,爬坡效应逐渐减小,最终会基本消失,曲线斜率明显加大。
3.3 风化程度对锯齿形结构面抗剪强度的影响
干湿循环模拟风化作用改变了岩体结构面的微细观结构特性,破坏了岩体颗粒或晶体间的连接,结构面变得更加脆弱,致使其力学特性随之发生变化。不同风化程度灰岩锯齿形结构面抗剪强度试验结果如图6所示。
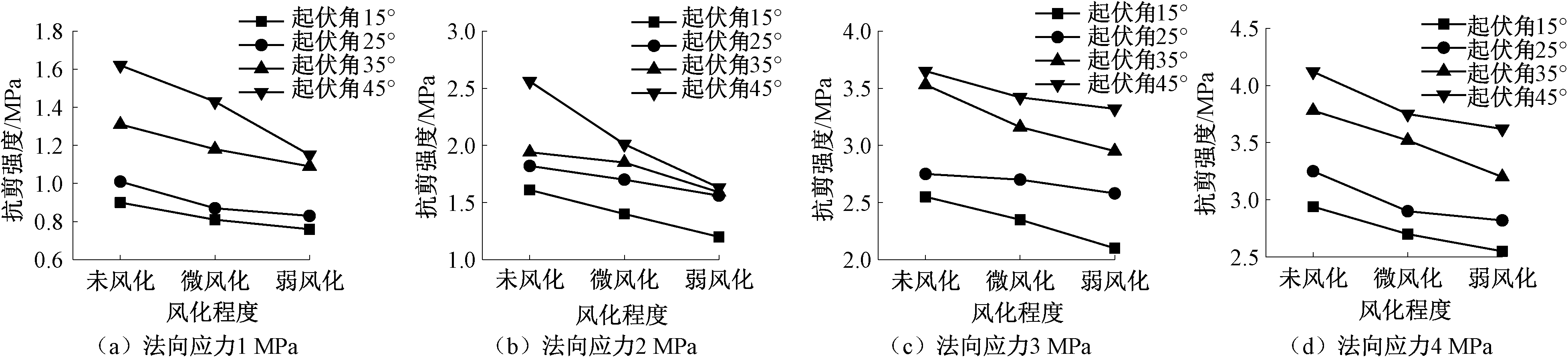
图6 锯齿形结构面抗剪强度曲线
Figure 6 Shear strength curves of sawtooth structural plane
由图6可知,在相同法向应力下,结构面抗剪强度与风化程度呈负相关。同样,结构面起伏角越大,其结构面抗剪强度越大。经计算,相对于起伏角15°未风化结构面,微风化组平均抗剪强度降低9.76%,弱风化组平均抗剪强度降低17.99%;而起伏角为25°和35°的结构面劣化程度相似,与未风化试样相比,起伏角为25°和35°的微风化组平均抗剪强度分别降低了8.26%与7.98%,起伏角为25°和35°的弱风化组平均抗剪强度降低了12.88%与12.12%;与起伏角为45°的未风化结构面相比,微风化组平均抗剪强度降低了9.76%,弱风化组平均抗剪强度降低了21.63%。
结合图5可知,锯齿形结构面残余抗剪强度与风化程度之间并无明显的规律,可能是由于当锯齿被剪断后不同破裂面的粗糙程度不同,导致摩擦系数不同,从而影响了残余抗剪强度的大小。
3.4 风化程度对锯齿形结构面抗剪强度的影响
风化作用对岩体结构面抗剪强度特性的影响最直观的表现是结构面抗剪强度的降低,而结构面的抗剪强度受控于其参数黏聚力c及摩擦角φ。根据上述锯齿形结构面的室内直剪试验结果,得到锯齿形结构面抗剪强度参数,如表4所示。
表4 不同风化程度下灰岩锯齿形结构面力学参数
Table 4 Values of mechanical parameters of sawtooth structural plane of limestone in different weathering degrees
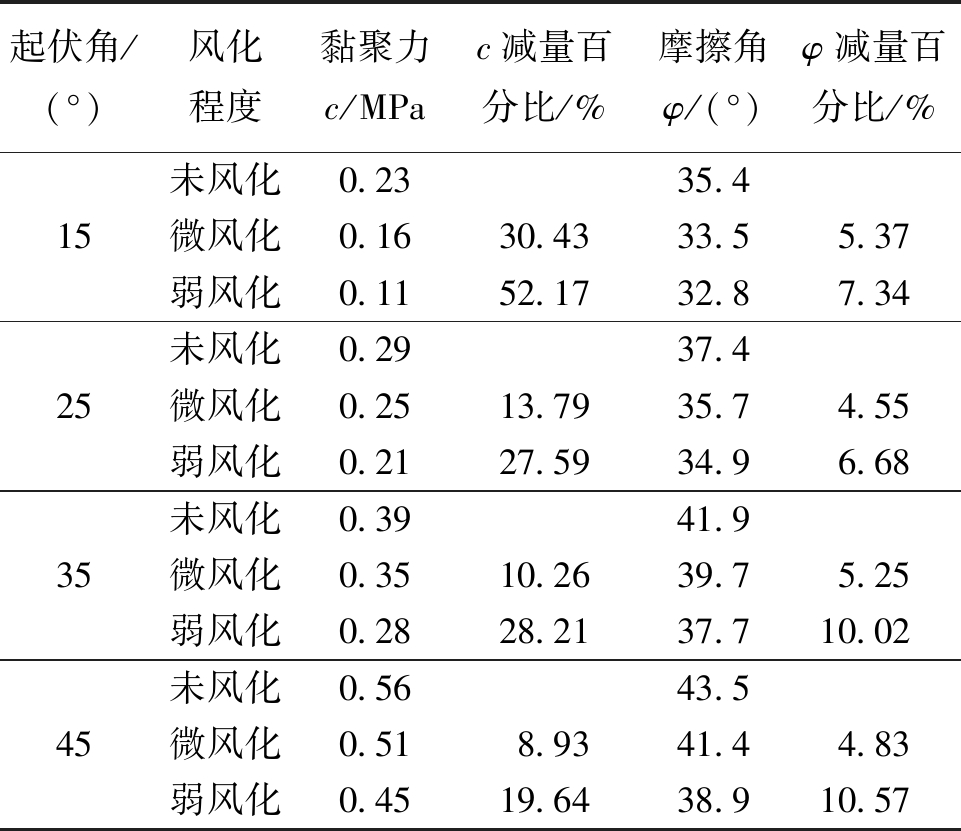
起伏角/(°)风化程度黏聚力c/MPac减量百分比/%摩擦角φ/(°)φ减量百分比/%15未风化0.2335.4微风化0.1630.4333.55.37弱风化0.1152.1732.87.3425未风化0.2937.4微风化0.2513.7935.74.55弱风化0.2127.5934.96.6835未风化0.3941.9微风化0.3510.2639.75.25弱风化0.2828.2137.710.0245未风化0.5643.5微风化0.518.9341.44.83弱风化0.4519.6438.910.57
从表4可以看出,结构面的黏聚力和摩擦角均随着风化程度的增大而减小。总体上,黏聚力减量百分比均随着起伏角的增大而减小,说明结构面起伏角越大,其黏聚力对风化作用越不敏感,这是由于起伏角较小的锯齿形结构面在剪切过程中会发生爬坡效应,锯齿的尖端发生剪断,而起伏角较大时,爬坡效应逐渐消失,结构面破坏时,整个锯齿从根部被剪断。同时因为风化作用是一个由表及里的过程,锯齿尖端厚度较薄,容易受到风化作用的影响,因此强度参数受风化作用劣化严重,而锯齿根部厚度较厚,越往里受到风化的影响越小,表现为更小的劣化程度,但起伏角为25°时,弱风化程度的黏聚力劣化程度小于起伏角为35°的情况,其原因可能为试验过程以及试样的误差。而无论何种风化程度的结构面,其摩擦角减量百分比随着起伏角的增加均无明显变化,说明结构面摩擦角对起伏角大小不敏感。
4 风化锯齿形结构面抗剪强度估算模型
4.1 模型建立
为快速获取风化锯齿形结构面的力学特性与强度参数,需建立求解其抗剪强度的数学模型。结构面的抗剪强度特性主要受结构面自身摩擦阻力和两壁岩石强度控制。在上述的试验结果中,结构面的抗剪强度由风化程度、起伏角i、法向应力σ这3个参数决定。其中,摩擦阻力与起伏角和法向应力有关,而岩壁强度JCS由风化作用决定。因此,可将起伏角、σ/JCS作为自变量建立求解抗剪强度(τ)的数学关系表达式,设函数关系式如下:
τ=F(i,σ/JCS)。
(1)
由于风化程度是一个定性的判定结果,不能清楚地量化数学关系,所以采用波速比这一定量判定风化程度的指标代替风化程度,通过回弹试验建立回弹值与波速比的关系,如图7所示。拟合结果为
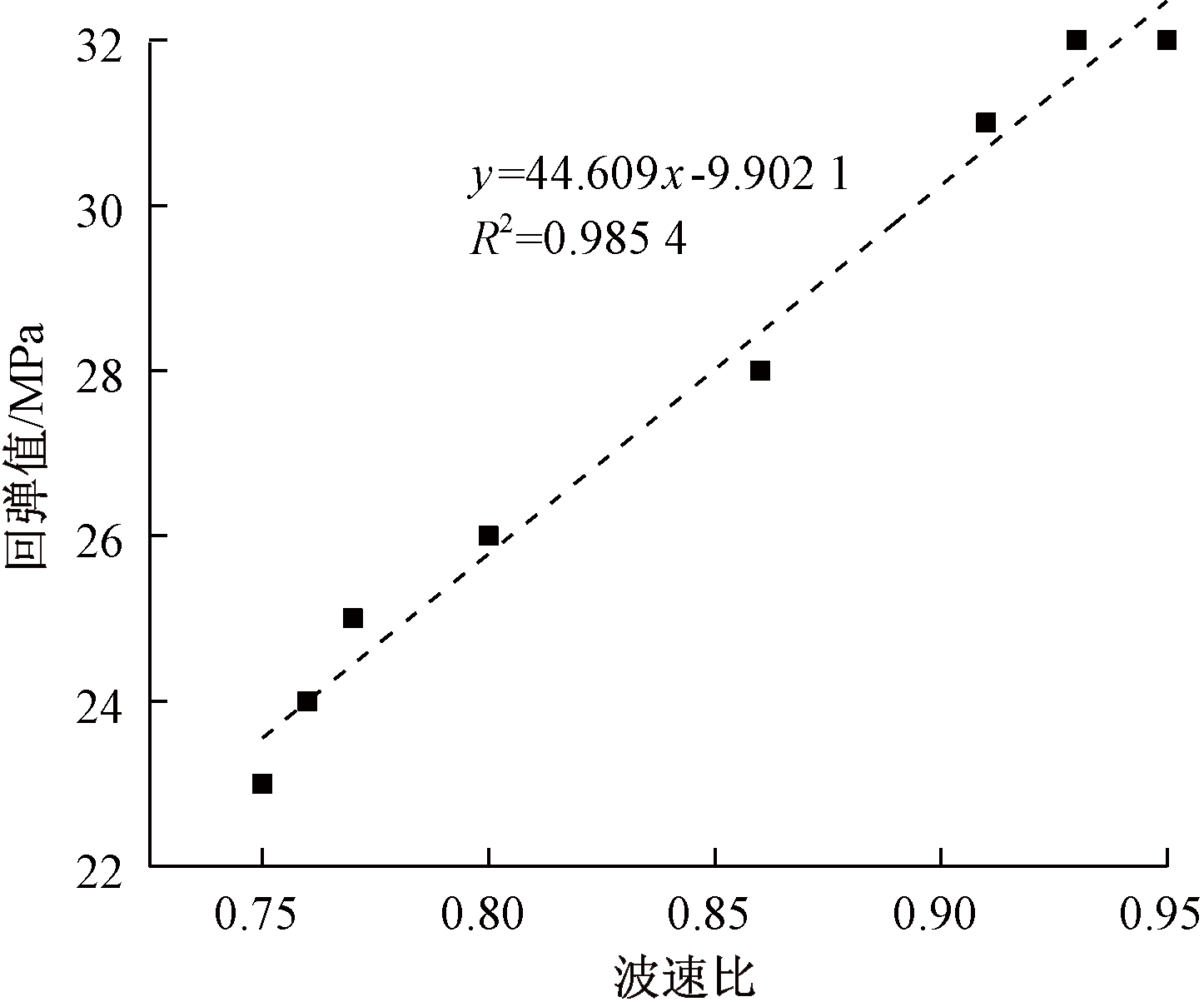
图7 波速比kv与岩壁强度回弹值关系曲线
Figure 7 Relationship curve between wave velocity ratio kv and rock wall strength rebound value
Re=44.609kv-9.902 1。
(2)
式中:kv为波速比;Re为回弹值,MPa。
岩壁强度可以依据回弹值进行估算[1],计算式为
lg JCS=0.000 863γdRe+1.01。
(3)
式中:JCS为岩壁强度,MPa;Re为回弹值,MPa;γd为岩石干密度。
因此,将式(2)代入到式(3)中,即可求解岩壁强度:
JCS=100.000 863γd(44.609kv-9.902 1)+1.01。
(4)
根据室内试验结果,利用MATLAB软件建立与起伏角及σ/JCS相关的风化锯齿形结构面抗剪强度估算模型:
τ=-209(σ/JCS)2+0.16iσ/JCS+
46σ/JCS+0.018i-0.5。
(5)
式中:i为结构面起伏角,(°);σ为法向应力,MPa;τ为结构面抗剪强度,MPa;JCS为岩壁强度,MPa。
4.2 模型验证
为验证上述风化锯齿形结构面抗剪强度估算模型的准确性,选取试验建模数据的模型计算值与试验值进行误差分析。检验指标根据相对误差Δ及平均相对误差δ来评估模型的准确性:
(6)
(7)
式中:n为试验组数。
图8为抗剪强度模型值与实测值对比。可以看出,模型值与计算值相对误差最大为22.74%,平均相对误差为9.52%,效果良好。因此,该模型具有良好的可靠性,可快速有效地估算风化作用下灰岩锯齿形结构面的抗剪强度。
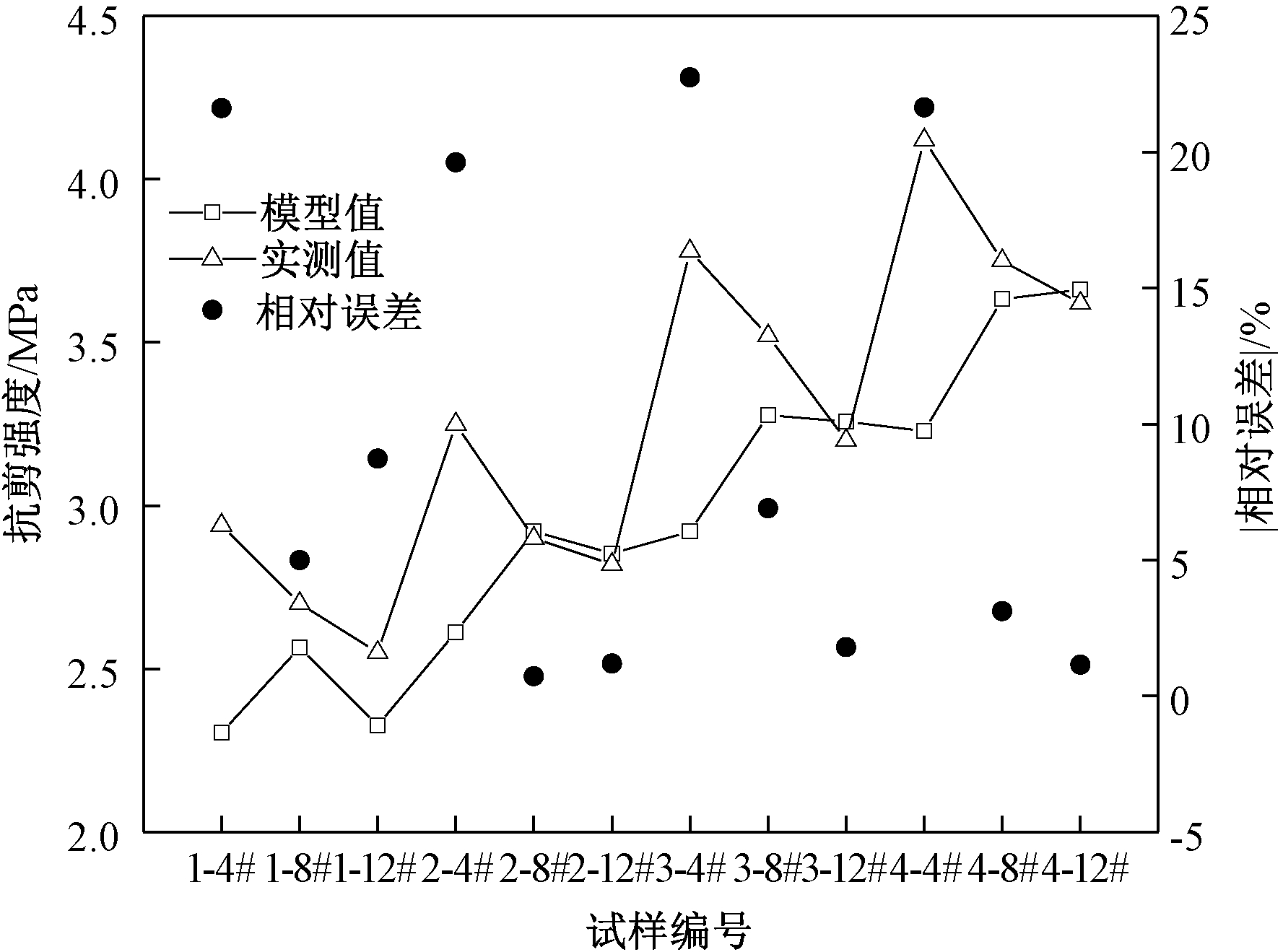
图8 抗剪强度模型值与实测值对比
Figure 8 Comparison of shear strength model values and measured values
5 结论
(1)锯齿形结构面的剪切应力-剪切位移曲线先近似线性增加,达到峰值剪切应力后跌落,最后基本趋于稳定,保持一定的残余抗剪强度,表现为峰值剪断型。
(2)随着风化程度的增加,灰岩锯齿形结构面抗剪强度呈现减小的趋势,其抗剪强度参数发生不同程度的劣化,黏聚力的劣化程度大于摩擦角。
(3)基于模型试验结果,建立了风化锯齿形结构面抗剪强度估算模型,其检验效果良好,为快速准确获取并评价灰岩风化锯齿形结构面抗剪强度特性提供了一种简便易行的方法。
[1] BARTON N. Review of a new shear-strength criterion for rock joints[J]. Engineering Geology, 1973, 7(4): 287-332.
[2] 张清照, 沈明荣, 丁文其. 结构面在剪切状态下的力学特性研究[J]. 水文地质工程地质, 2012, 39(2): 37-42.
ZHANG Q Z, SHEN M R, DING W Q. Study on the mechanical properties of rock mass discontinuity under shear condition[J]. Hydrogeology &Engineering Geology, 2012, 39(2): 37-42.
[3] 周辉, 程广坦, 朱勇, 等. 大理岩规则齿形结构面剪切特性试验研究[J]. 岩土力学, 2019, 40(3): 852-860.
ZHOU H, CHENG G T, ZHU Y, et al. Experimental study of shear deformation characteristics of marble dentate joints[J]. Rock and Soil Mechanics, 2019, 40(3): 852-860.
[4] BANDIS S, LUMSDEN A C, BARTON N R. Experimental studies of scale effects on the shear behaviour of rock joints[J]. International Journal of Rock Mechanics and Mining Sciences &Geomechanics Abstracts, 1981, 18(1): 1-21.
[5] BAHAADDINI M, HAGAN P C, MITRA R, et al. Scale effect on the shear behaviour of rock joints based on a numerical study[J]. Engineering Geology, 2014, 181: 212-223.
[6] INDRARATNA B, PREMADASA W, BROWN E T, et al. Shear strength of rock joints influenced by compacted infill[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 70: 296-307.
[7] 孙辅庭. 张拉型硬岩节理三维形貌表征及其灌浆前后抗剪强度特性试验研究[D]. 武汉: 武汉大学, 2015.
SUN F T. Experimental research on three-dimensional joint morphology quantification and shear strength property of tensile hard rock joints with and without cement grouting[D]. Wuhan: Wuhan University, 2015.
[8] LAJTAI E Z. Shear strength of weakness planes in rock[J]. International Journal of Rock Mechanics and Mining Sciences &Geomechanics Abstracts, 1969, 6(5): 499-515.
[9] 陈庆芝, 刘远明, 朱爱军, 等. PFC2D模拟研究不同工况的异面非贯通节理对岩体力学性质的影响[J]. 水利水电技术, 2019, 50(4): 190-199.
CHEN Q Z, LIU Y M, ZHU A J, et al. PFC2D-based simulative study on influence from non-penetrative heterogeneous joint under various working conditions on mechanical properties of rock mass[J]. Water Resources and Hydropower Engineering, 2019, 50(4): 190-199.
[10] ISMAIL K M A, MOHD-NORDIN M M, Md HASAN A S, et al. Shear strength behaviour of rock joint material influenced by different weathering grade[J]. Journal of Physics: Conference Series, 2019, 1349(1): 012069.
[11] RAM B K, BASU A. Shear behavior of unfilled-planar quartzitic rock joints with reference to weathering grade of joint surfaces[J]. Rock Mechanics and Rock Engineering, 2019, 52(10): 4113-4121.
[12] WOO I, FLEURISSON J A, PARK H J. Influence of weathering on shear strength of joints in a porphyritic granite rock mass in Jechon area, South Korea[J]. Geosciences Journal, 2010, 14(3): 289-299.
[13] ÖZVAN A, DINÇER ![]() ACAR A, et al. The effects of discontinuity surface roughness on the shear strength of weathered granite joints[J]. Bulletin of Engineering Geology and the Environment, 2014, 73(3): 801-813.
ACAR A, et al. The effects of discontinuity surface roughness on the shear strength of weathered granite joints[J]. Bulletin of Engineering Geology and the Environment, 2014, 73(3): 801-813.
[14] 唐雯钰, 林杭. 不同锯齿高度对软弱结构面剪切特性的影响[J]. 中南大学学报(自然科学版), 2017, 48(5): 1300-1307.
TANG W Y, LIN H. Influence of dentate discontinuity height on shear properties of soft structure plane[J]. Journal of Central South University (Science and Technology), 2017, 48(5): 1300-1307.
[15] JAEGER J C. Friction of rocks and stability of rock slopes[J]. Géotechnique, 1971, 21(2): 97-134.
[16] 朱立平. 建筑物风化与地貌学研究[J]. 地理科学进展, 1997, 16(1): 62-70.
ZHU L P. Building weathering and the geomorphology study[J]. Progress in Geography, 1997, 16(1): 62-70.
[17] 刘新荣, 李栋梁, 王震, 等. 酸性干湿循环对泥质砂岩强度特性劣化影响研究[J]. 岩石力学与工程学报, 2016, 35(8): 1543-1554.
LIU X R, LI D L, WANG Z, et al. The effect of dry-wet cycles with acidic wetting fluid on strength deterioration of shaly sandstone[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(8): 1543-1554.
[18] 中华人民共和国交通运输部. 公路工程地质勘察规范: JTG C20—2011[S]. 北京: 人民交通出版社, 2011.
Ministry of Transport of the People′s Republic of China. Code for highway engineering geological investigation: JTG C20—2011[S]. Beijing: China Communications Press, 2011.
[19] 孙雁军, 阳军生, 张箭, 等. 风化花岗岩地层隧道衬砌裂损分析与处理研究[J]. 郑州大学学报(工学版), 2017, 38(4): 78-83.
SUN Y J, YANG J S, ZHANG J, et al. The effect of weathered granites on the highway tunnel lining[J]. Journal of Zhengzhou University (Engineering Science), 2017, 38(4): 78-83.
[20] 王军祥. 岩石弹塑性损伤MHC耦合模型及数值算法研究[D]. 大连: 大连海事大学, 2014.
WANG J X. Study on elastoplastic damage and MHC coupling model of rock and numerical algorithm[D]. Dalian: Dalian Maritime University, 2014.