随着网络通信、智能控制、云计算和智能传感器技术的飞速发展,信息物理系统(cyber physical systems, CPSs)应运而生[1]。信息物理系统是一个更庞大更高级更智能化的网络控制系统(network control systems, NCSs),它借助控制技术、高速通信与智能计算实现对外界环境信息的采集、分析、计算和智能控制[2]。信息物理系统的典型架构如图1所示,可以看出,信息物理系统由物理节点层、网络传输层、智能控制层组成[3]。随着系统规模和传感器节点数量的增加,通过网络传输的信号可能会出现信息传输不完全的现象,这种现象极有可能导致系统错乱。
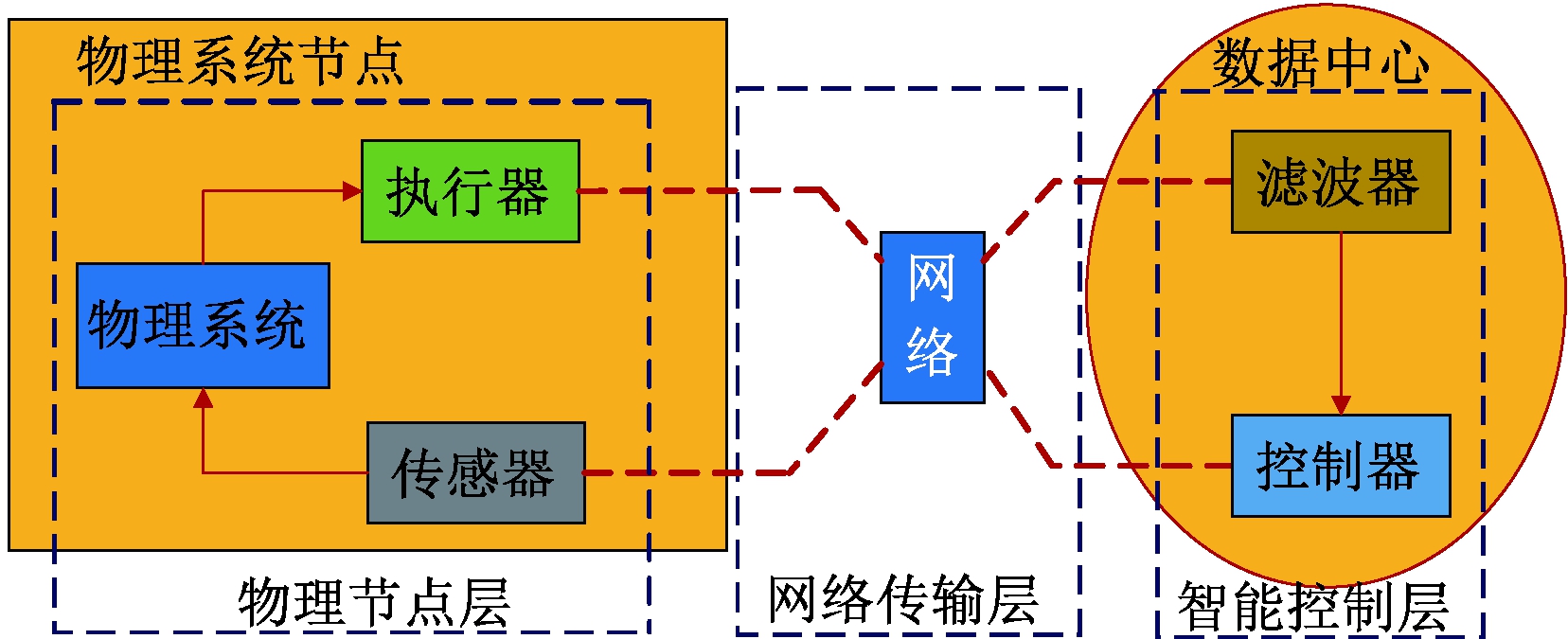
图1 信息物理系统典型架构
Figure 1 Typical architecture of cyber physical systems
滤波也叫状态估计,滤波问题在目标识别、信息处理和控制领域都有着重要的研究意义。为了适应系统模型的不确定性,H∞滤波器得以推广。在外界存在干扰和系统模型具有不确定性的情况下,H∞滤波可以使H∞范数最小或小于一个给定值,因此,H∞滤波在自动控制、模式识别、目标跟踪、信号处理等领域得到了广泛的关注[4]。
对于丢包情况下的滤波问题,目前已有大量的研究成果。Liu等[5]考虑了多通道时延、数据包丢失情况下的网络控制系统H2/H∞滤波问题。Sun等[6]构造了一个描述随机多步时延和丢包现象的新模型,为线性离散时间随机系统设计了最优化的线性估计器。然而,现有的大部分研究成果考虑的丢包形式往往都是单包丢失,对于连续随机多包丢失的研究较少,将其与量化误差同时考虑的研究更少。因此,连续随机多数据包丢失和量化误差同时存在情况下的H∞滤波问题具有重要的研究意义。
作为传统移位算子的改进,Delta算子模型能够有效克服移位算子高速采样时的缺点,且采样速率越高,系统性能越好。
基于以上讨论,本文采用Delta算子离散化方法,重点研究了连续随机多数据包丢失和量化误差同时存在情况下的信息物理系统H∞滤波问题。
1 问题描述
1.1 Delta算子离散化方法
Delta算子离散化方法可以将连续时间系统和离散时间系统建立为统一的模型[7]。目前,Delta算子已广泛应用于计算机高速信号处理、宽带通信、数字采样控制等领域[8]。Delta算子的定义如下:
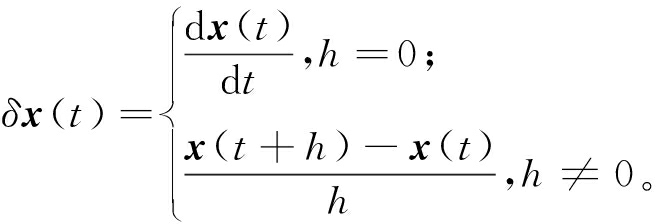
(1)
式中:h表示采样周期。
1.2 系统模型构建
图2为具有量化误差和连续随机多数据包丢失的信息物理系统滤波架构。式(2)为基于Delta算子离散化的信息物理系统模型:
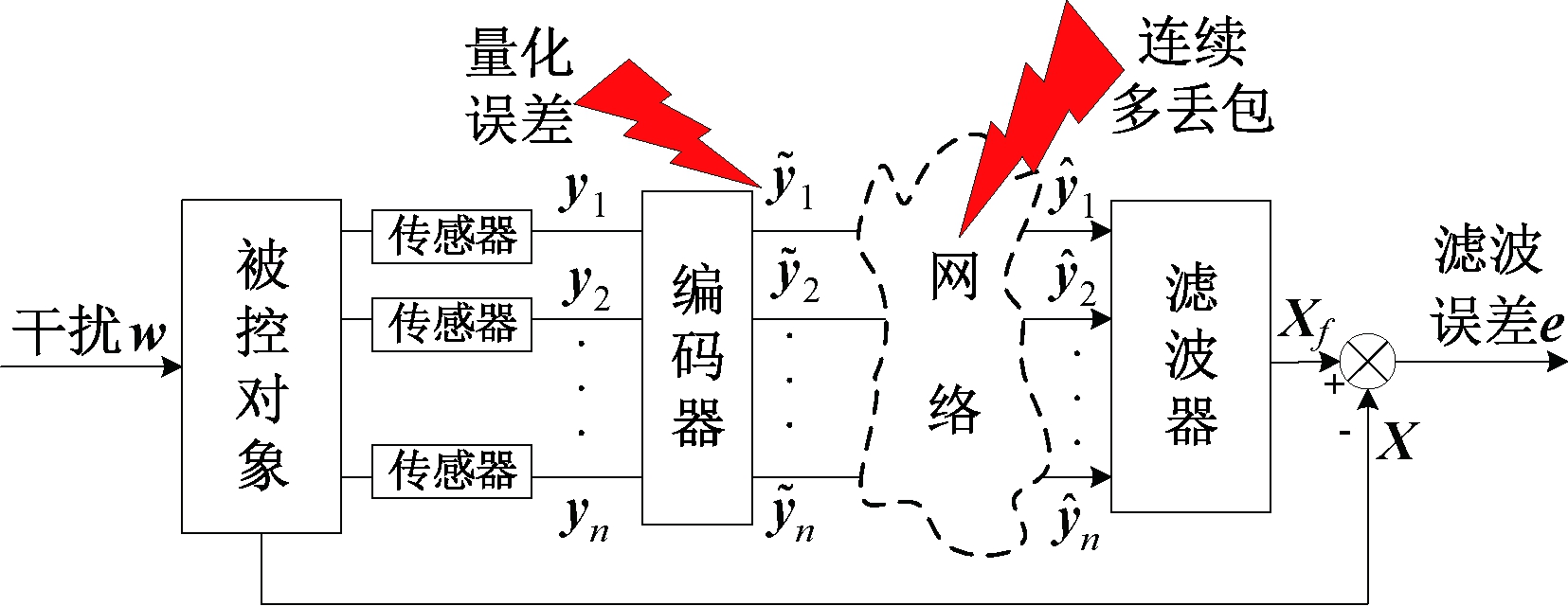
图2 信息物理系统滤波架构
Figure 2 Filtering architecture of cyber physical systems
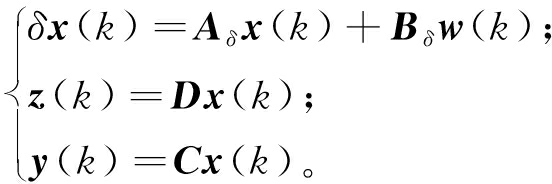
(2)
式中:x(k)∈Rm为状态向量;y(k)∈Rl为测量输出;z(k)∈Rn为待估计状态向量x(k)的线性组合;w(k)∈Rp为属于l2[0,∞)的外界干扰;Aδ、Bδ、C、D均为具有适当维数的常数矩阵。
(1)考虑量化误差。假设在信号编码解码环节产生量化误差,目前广泛使用的量化器有放大缩小量化器和对数量化器,本文考虑时不变的对数量化器,量化器q(v)定义如下:
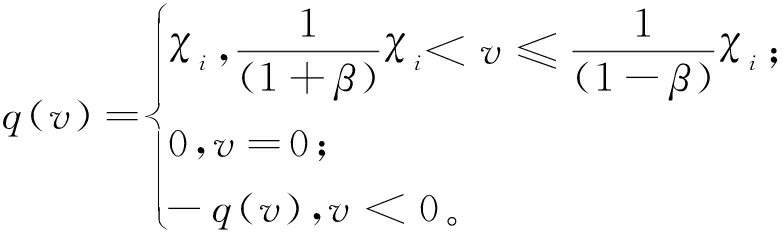
(3)
式中:β=(1-ρ)/(1+ρ),ρ为量化密度; χi={± χi:χi=ρiχ0,i=±1,±2,±3,…}∪{± χ0}∪{0},0<ρ<1, χ0>0。
由文献[9]可知,经过量化器的量化误差信号为
(4)
式中:‖Δk‖≤β。
(2)连续随机多数据包丢失现象。数据包通过网络传输,在第k个采样时刻,数据发生单丢包现象,可建模如下:
(5)
式中:
为可能的量化误差传输信号;
为滤波器接收到的信号;随机变量α(k)∈R在0和1之间取值且满足Bernoulli分布。
随机变量α(k)的分布概率如下:
(6)
式中:
为已知的正数。
在信息物理系统中,连续随机多丢包现象更符合实际情况。基于随机单丢包模型,连续随机多数据包丢失可建模如下:
(7)
式中:N为最大丢包数;αi(k)∈[0,1]且满足Bernoulli分布。当αi(k)全为1时,
表示丢包数达到N个;当αi(k)全为0时,
(k)表示数据包没有发生丢失;当遇到第1个为0的αi(k)时,
表示数据包丢失达到i-1个。其中,当最大丢包数N取1时,模型退化为单数据包丢失模型。为方便后续计算,本文假设任何时间段内数据包丢失的概率不随时间变化,即αi(k)取1的概率与i无关,并且随机变量αi(k)之间是互不相关的,由此可得
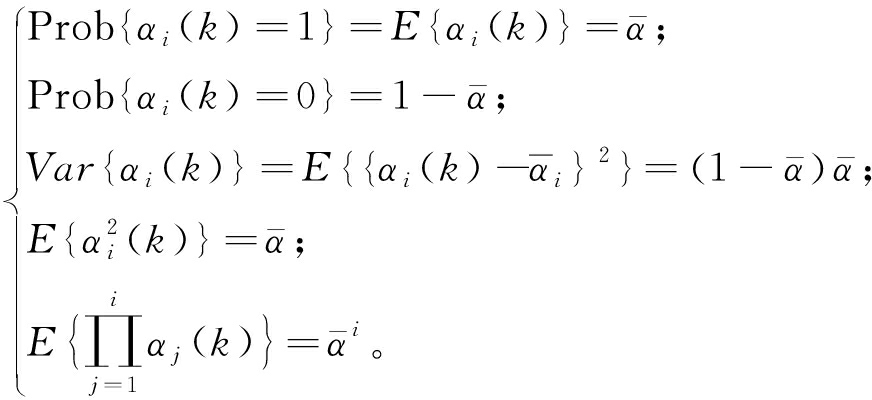
接下来,考虑如下形式的H∞滤波器:
(8)
式中:xf(k)∈Rm为滤波器状态向量;
为网络传输后可能发生随机多数据包丢失或量化误差的信号,同时也是滤波器的输入信号;zf(k)∈Rn为z(k)的估计,同时也是滤波器的输出信号;Af、Bf、Cf为待求的滤波器参数。
由式(2)、(4)、(7)和(8)可得滤波误差系统模型:
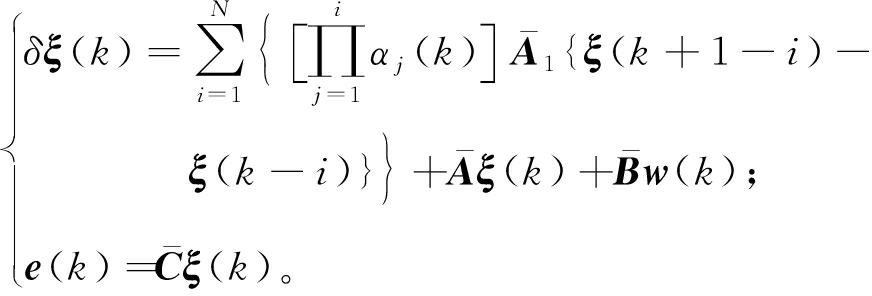
(9)
式中:e(k)为滤波误差;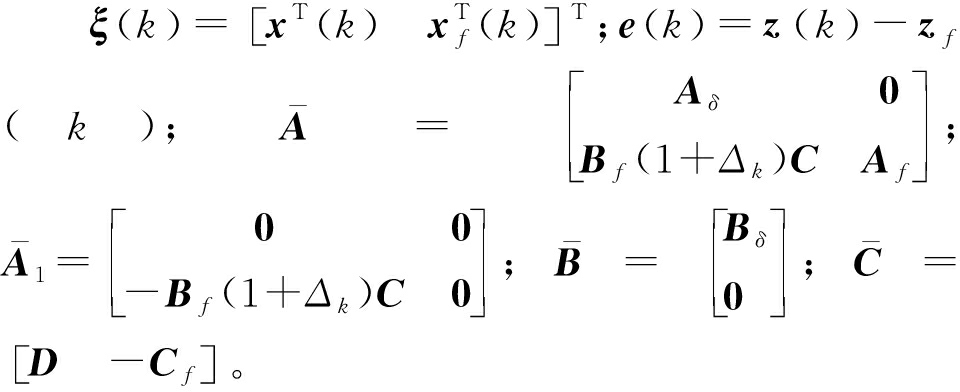
基于以上模型建立的过程,设计一个H∞滤波器,并计算其相关滤波器参数使其满足以下2个条件:①在外界干扰噪声为0时,滤波误差系统满足渐近稳定性;②当初始条件为0时,滤波误差系统具有给定的H∞性能。
2 滤波器设计
展示主要结果之前先给出系统满足渐近稳定性和H∞性能的2个定义。
定义1 考虑如式(2)所示的Delta算子系统,若在Delta域内存在Lyapunov泛函V(x(k))满足以下条件,则系统是渐近稳定的[10]:①在初始状态x(k)=0时,V(x(k))≥0;②在非初始状态下,δV(x(k))<0。
定义2 给定大于0的标量γ,如果在零初始条件下,式(2)所示的Delta算子系统满足下面2个条件,则系统具有H∞性能[11-12]:①在外界干扰噪声为0时,系统满足稳定性;②当初始条件为0,即x(0)=0时,有
其中,γ表示H∞性能指数,反映了系统抵抗外界扰动和模型不确定性的能力。
定理1 考虑大于0的标量γ,如果存在矩阵
使不等式(10)成立,则系统(式(9))是渐近稳定的,同时满足给定的H∞性能。
(10)
式中:
表示单位矩阵;*表示在对称矩阵中的对称项。
证明 首先定义η(k)=ξ(k+1)-ξ(k)。由式(9)可得
(11)
令
并选择如式(12)所示的Lyapunov函数:
V(k)=V1k{Φ(k)}+V2k{Φ(k)}+V3k{Φ(k)}。
(12)
式中:
V1k{Φ(k)}=ξT(k)Pξ(k);
P=PT>0;P2=P2T>0;P3=P3T>0;U=[In0n]。
分别对上述Lyapunov泛函进行微分可得
E{V1(k+1){Φ(k+1)|Φ(k)}}-E{V1k{Φ(k)}}=
E{V2(k+1){Φ(k+1)|Φ(k)}}-E{V2k{Φ(k)}}=ξT(k)ZTQZξ(k)-ξT(k-N)ZTQZξ(k-N);
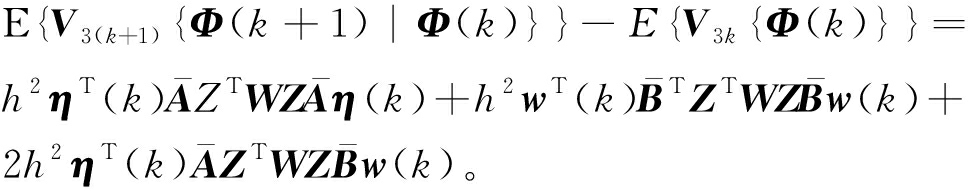
由以上微分可得
δV(k)=E{V{Φ(k+1)|Φ(k)}}-E{V{Φ(k)}}
≤ΘT(k)ΩΘ(k)。
(13)
式中:
Ωij=0。
由Schur补引理和式(10)可知,存在一个常数
<0使得下式成立:
E{V{Φ(k+1)|Φ(k)}}-E{V{Φ(k)}}<
-ξT(k)ξ(k)=-ξ(k)2。
由定义1知滤波误差系统(式(9))满足渐近稳定性,则H∞性能为
δV{Φ(k)}+E{eT(k)e(k)}-γ2E{wT(k)w(k)}≤
γ2wT(k)w(k)=E{ΘT(k)ΛΘ(k)}。
(14)
式中:
Λ0i=Ω0i;Λiw=Ωiw;Λij=Ωij;
Λww=Ωww-γ2I;Λow=Ω0w。
将矩阵Λ进行2次Schur变换,式(10)是Λ<0的充分条件,由Λ<0可知:
δV{Φ(k)}+E{eT(k)e(k)}-
γ2E{wT(k)w(k)}<0。
(15)
由于系统是渐近稳定的,可得
eT(k)e(k)-γ2wT(k)w(k)<0。
(16)
由定义2知,滤波误差系统(式(9))具有H∞性能,H∞性能指数为γ。定理得证。
定理2 考虑大于0的标量γ,如果存在矩阵R=RT>0、S=ST>0、P=PT>0、P2=P2T>0、P3=P3T>0和实矩阵H1、H2、H3使矩阵不等式(17)成立,则系统(式(9))是渐近稳定的,同时满足给定的H∞性能。
(17)
式中:
φ5=R(hAδ+I)+hH1(1+Δk)C+hH3+S-R;
φ6=R(hAδ+I)+hH1(1+Δk)C;
l=N1/2;φ4i=haiH2(1+Δk)C。
滤波器的系数可表示如下:
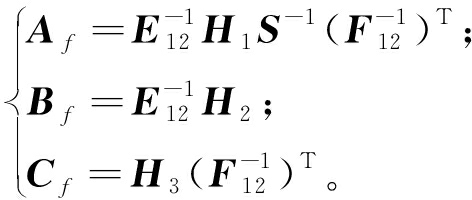
(18)
对于H∞性能的优化问题,可以考虑取多组合适的矩阵
求解LMI得到多组γ值,并取其最优的γ值。
证明 定义矩阵P、P-1、Z1和Z2分别为
由以上定义可以计算得到下式成立:
接下来对矩阵进行全等变换,用diag{Z1 I I Z1 I … I Z1 I I}、diag{I I I I S I … I S I I P2}先后对式(10)进行全等变换,在第1次全等变换结束后需要将矩阵
展开后再进行第2次全等变换。为了得到一个标准的LMI,矩阵中的非线性项
必须转化为线性项,本文采用如下转换方法。
考虑
可得
接下来,使用
分别替代可得式(17)。另外,转换H1、H2、H3可得到式(18)。由于LMI(式(17))中加入了新的矩阵
使用MATLAB求解时需先给出合适且固定的矩阵
如果不等式是可解的,那么
成立,再根据
所以非奇异矩阵E12、F12必定是存在的,因此,滤波器的参数一定可以通过式(18)求得。定理得证。
3 实验结果与分析
为验证滤波器有效性,考虑如下目标追踪系统:
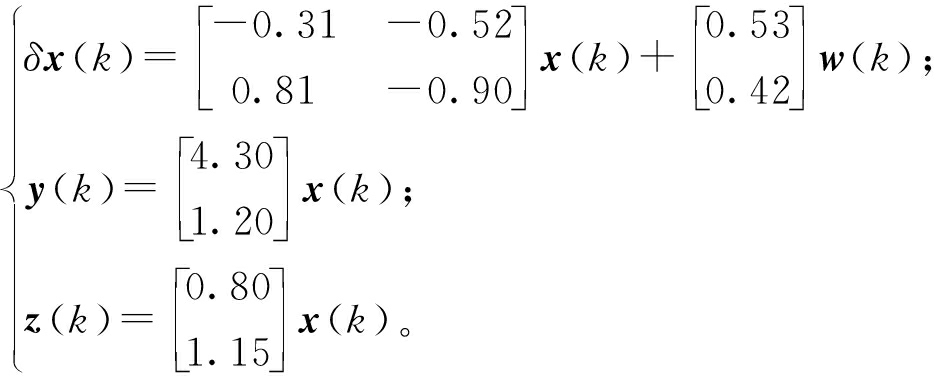
其中,x(k)由目标的位置量和速度量组成,取x(k)的初始值为
仿真中令h=10-4,干扰信号w(k)=0.5exp(-0.1k)sin(0.01πk),且E{w(k)}=0。量化器q(v)的参数设定为χ0=1.3,ρ=0.75。由式(4)知Δk≤α=0.142 9,实验中,借助MATLAB工具,将量化噪声的阈值α代入LMI来求解滤波器参数,并假设最大丢包数为2和3这2种情况,如表1所示。
表1 2种情况下滤波器参数及H∞性能指标
Table 1 Filter parameters and H∞performance index in two cases
最大丢包数AfBfCfγ2-0.313 7 -4.519 00.092 7 0.896 2-0.545 5-0.109 5-0.000 7-0.008 2T1.256 83-0.313 8 -4.518 20.092 7 0.896 1-0.114 5-0.022 9-0.000 6-0.008 2T1.258 4
最大丢包数为
其中,α1(k)=0.5,α2(k)=0.5。
最大丢包数为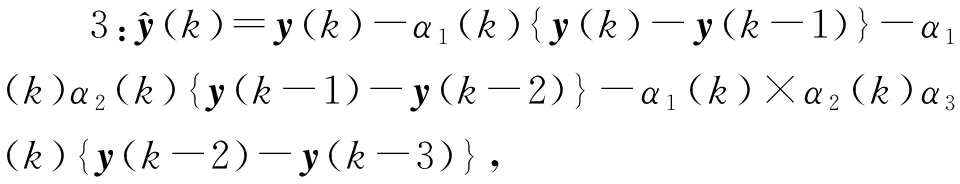
其中,α1(k)=0.2,α2(k)=0.2,α3(k)=0.2。
在MATLAB 8.3的环境下进行仿真实验,仿真结果如图3所示。
图3 γ值随N变化图
Figure 3 Variation of γ value with N
图3表示H∞性能指标γ随最大丢包数N变化图(1≤N≤5)。由图3可知,随着最大丢包数的增加,γ值有所增大。此现象反映了数据包丢失会对系统性能产生影响,且数据包丢失越严重对系统造成的影响越大,但在N=5时,系统仍满足渐近稳定性和H∞性能。此外,对于使系统稳定的最大丢包数上限问题值得后续深入研究。表1描述了数据最大丢包数为2和3时的滤波器参数及H∞性能指标。从表1中可以看出,最大丢包数为2和3时系统具有H∞性能,对应的H∞指标分别为1.256 8、1.258 4。
图4表示最大丢包数为2时,滤波误差系统响应曲线图。图5表示真实量z(k)和估计量zf(k)的状态曲线。从图4、5中可以看出,数据包在100个采样点遭受不同程度的丢包。在数据包发生多丢包的情况下,滤波误差e(k)仍在第30个采样点附近得到了有效收敛。表明在干扰w(k)下,系统满足渐近稳定性,并且在指定H∞性能指标γ=1.256 8下,估计量zf(k)能够有效地估计出真实量z(k)的状态。
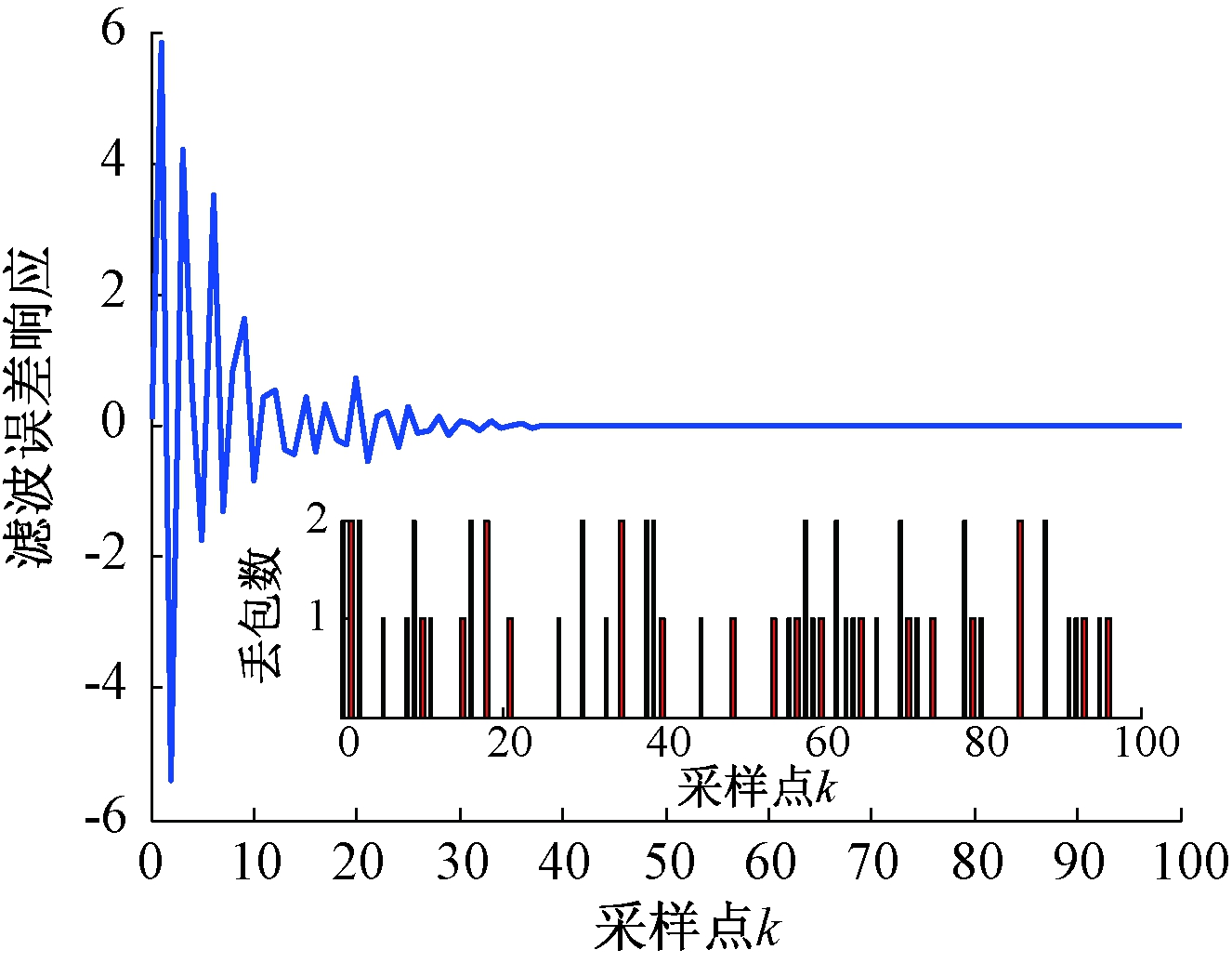
图4 情况1的滤波误差系统响应
Figure 4 The filter error system response of case 1
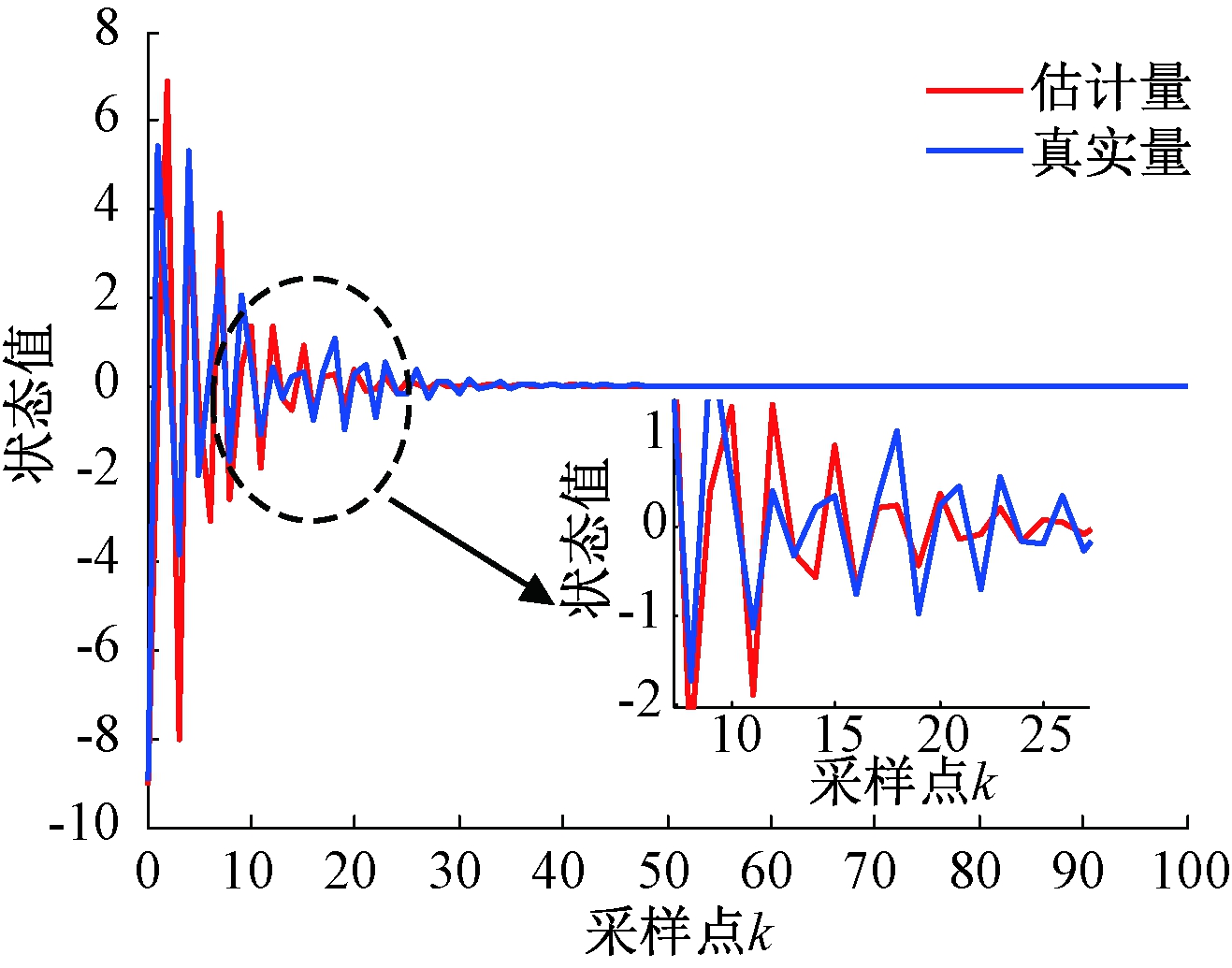
图5 情况1的z(k)和zf(k)
Figure 5 z(k) and zf(k) of case 1
图6表示最大丢包数为3时的滤波误差系统响应,图7表示真实量z(k)和估计量zf(k)的状态。由图可知,在100个采样点数据发生随机多数据包丢失,最大丢包数为3的情况下滤波误差e(k)在第30个采样点附近得到了有效收敛,系统满足渐进稳定,并且在干扰w(k)下,估计量zf(k)在指定的H∞性能指标下能够有效地估计出真实量z(k)的状态。综上所述,本文设计的H∞滤波器是有效的。
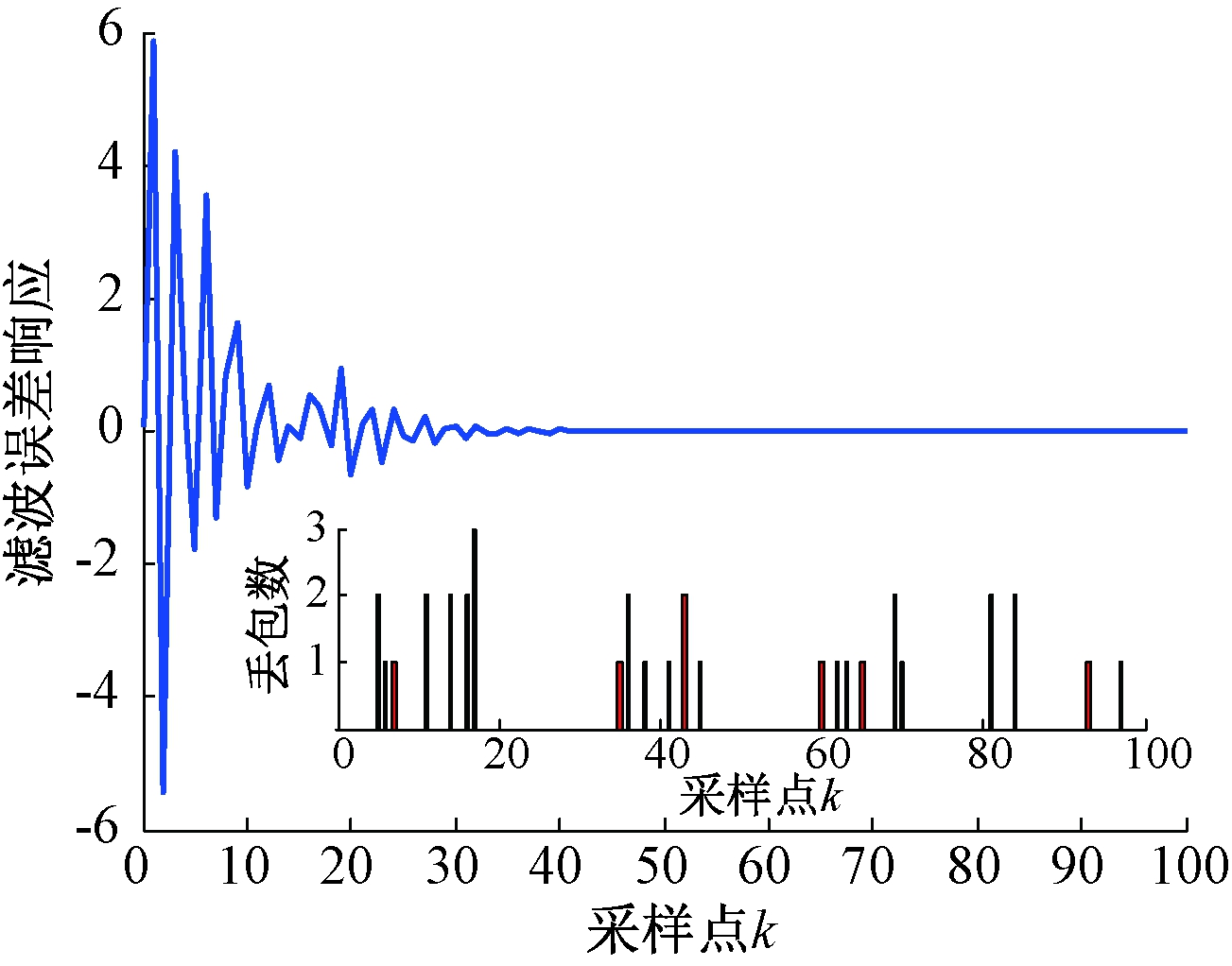
图6 情况2的滤波误差系统响应
Figure 6 The filter error system response of case 2
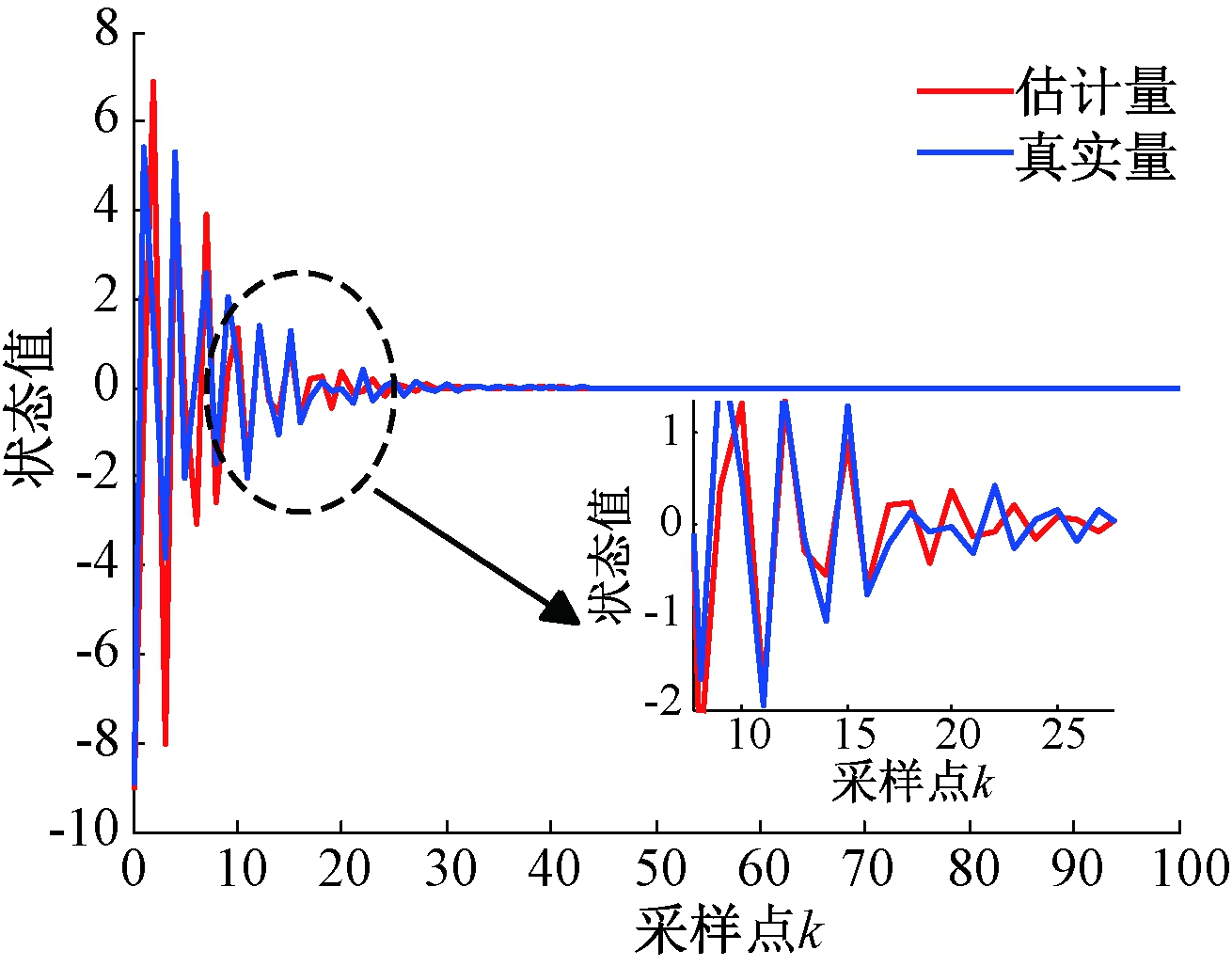
图7 情况2的z(k)和zf(k)
Figure 7 z(k) and zf(k) of case 2
4 结论
本文考虑了由网络信道固有因素和通信设备缺陷造成的随机多数据包丢失和量化误差现象。其中,连续随机多数据包丢失发生在信号的网络传输环节,量化误差发生在数据包进行网络传输前的编码环节。构建的连续随机多数据包丢失模型既包含单丢包也包含多丢包,具有一般性。基于Delta算子离散化方法,利用Lyapunov函数、Schur补引理及LMI得到使系统满足渐近稳定的H∞滤波器。最后,仿真结果表明,在最大丢包数为2和3 2种情况下滤波误差系统是渐近稳定的,且满足指定的H∞性能。
[1] OLOWONONI F O, RAWAT D B, LIU C M. Resilient machine learning for networked cyber physical systems: a survey for machine learning security to securing machine learning for CPS[J]. IEEE Communications Surveys &Tutorials, 2021, 23(1): 524-552.
[2] BANDYSZAK T, DAUN M, TENBERGEN B, et al. Orthogonal uncertainty modeling in the engineering of cyber-physical systems[J]. IEEE Transactions on Automation Science and Engineering, 2020, 17(3): 1250-1265.
[3] HAN D. Constrained remote state estimation: a stochastic scheduling approach[D]. Hong Kong:Hong Kong University of Science and Technology,2015.
[4] BAIDOO E, HU J R, ZHAN L. Kalman filtering method for sparse off-grid angle estimation for bistatic multiple-input multiple-output radar[J]. IET Radar, Sonar &Navigation, 2020, 14(2): 313-319.
[5] LIU M J, ZHANG D J. H2/H∞ filtering for delta operator networked systems with multi-channel delay, packet dropout and sequence disorder[C]∥2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC). Piscataway: IEEE, 2020: 4460-4465.
[6] SUN S L, XIAO W D. Optimal linear estimators for systems with multiple random measurement delays and pa-cket dropouts[J]. International Journal of Systems Science, 2013, 44(2): 358-370.
[7] MIDDLETON R, GOODWIN G. Improved finite word length characteristics in digital control using delta operators[J]. IEEE Transactions on Automatic Control, 1986, 31(11): 1015-1021.
[8] GOODWIN G C, LEAL R L, MAYNE D Q, et al. Rapprochement between continuous and discrete model ref-erence adaptive control[J]. Automatica, 1986, 22(2): 199-207.
[9] FU M Y, XIE L H. The sector bound approach to quantized feedback control[J]. IEEE Transactions on Automatic Control, 2005, 50(11): 1698-1711.
[10] YANG H J. Analysis and synthesis of delta operator systems[M]. Berlin: Springer, 2012.
[11] 俞立. 鲁棒控制: 线性矩阵不等式处理方法[M]. 北京: 清华大学出版社, 2002.
YU L. Robust control: linear matrix inequality method[M]. Beijing: Tsinghua University Press, 2002.
[12] 张端金, 王钟堃. 具有丢包的未知转移概率Markov跳变系统鲁棒H∞滤波[J]. 郑州大学学报(工学版), 2021, 42(6): 1-6, 41.
ZHANG D J, WANG Z K. Robust H∞ filtering for Mar-kov jump systems with unknown transition probabilities and packet dropouts[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(6): 1-6, 41.