近几年随着经济的迅速发展，居民对于小汽车的需求量不断增加，停车难问题不断凸显。为了解决因需求时空差异化而导致的车位利用率低问题，共享停车理念被提出并广泛实施。对于共享停车运营模式会产生如何配置最优停车场位置以及如何提高运营商的运营收益等问题。
在出行停车选择及泊位分配方面，国内外学者进行了不同程度的研究。对于出行停车选择，张雪妍等[1]通过利用累积前景理论，在随机交通网络中，分析了组合出行下的随机用户均衡条件。Hassine等[2]提出了多项logit模型，该模型通过对城市中驾驶员停车类型的选择和相关因素的显示偏好调查获得相关数据。Wang等[3]综合考虑不同层级城市的差异，研究车位拥有者共享车位的意愿。田丽君等[4]基于出行者的出行方式选择，考虑不同方式的出行时间不确定性建立出行方式选择模型。Fang等[5]针对出行用户的出行需求和出行选择，对出行方式进行灰色关联建模与分析。
在停车泊位分配方面，Shao等[6]以运营商利润最大为目标建立整数规划模型，并进行供给匹配。在泊位分配的基础上，Jiang等[7]建立了出行用户在不同时段的停车概率函数，并且将随机规划模型转化为期望模型。Wang等[8]提出了一种解决共享停车预约用户出行时间不确定性的预定和分配模型。张水潮等[9]研究了预约需求下的运营平台供给匹配方法。姚恩建等[10]以共享停车泊位利用率最大化为目标建立模型，对停车供给进行匹配。Lai等[11]设计了一种新型共享停车模式并且探讨了该模式的市场设计问题。胥晶晶[12]建立包括共享停车泊位分配和泊车路径诱导的停车模型。段满珍等[13]通过研究出行用户停车诱导服务问题提出了以居住区为背景的共享停车泊位匹配模型。
虽然上述文献已经运用不同方法研究出行用户停车选择和共享停车泊位分配，但是缺乏从出发地到目的地完整出行链的角度研究停车选择及泊位分配；对于停车选择，已有文献忽略考虑出行者早于预约时间到达停车位的可能，会导致其停车巡航时间增加。本文首先基于在给定的共享停车和非共享停车供给下，出行者的停车选择表现为最小化问题，进一步针对不同停车方式的出行用户构建停车选择均衡模型，对均衡状态下的共享停车用户，从共享停车运营商角度出发，考虑其购买停车位成本、停车位运营管理费用、拒绝用户请求造成的损失以及出售停车位获取的收入，建立0-1泊位分配整数规划模型，出行选择模型与泊位分配模型之间通过决策变量建立关联，最终通过实例求解来完善共享停车泊位供需匹配模式。
1 停车选择均衡及泊位分配模型
1.1 问题描述
本文首先建立考虑非共享停车和共享停车的停车选择均衡模型，即在给定的共享停车和非共享停车供应条件下，没有用户可以通过单方面改变停车选择来降低自己的总出行成本，从而确定最优的停车场停车。对于选择共享停车方式的用户，为了对其请求匹配合适的共享停车泊位，进一步以运营商利润最大为目标，建立0-1整数规划模型来对停车位预约请求进行分配。泊位分配过程主要涉及3组决策机构：需要停车位的出行用户、可提供车位的泊位拥有者，以及停车共享平台运营商。图1展示了P1、P2、P3这3个共享停车位的空闲时段，其中阴影部分表示泊位拥有者对车位的占用时段，白色部分表示空闲时段即可出租时段。用户停车后可步行至目的地，具体停车过程如图2所示。
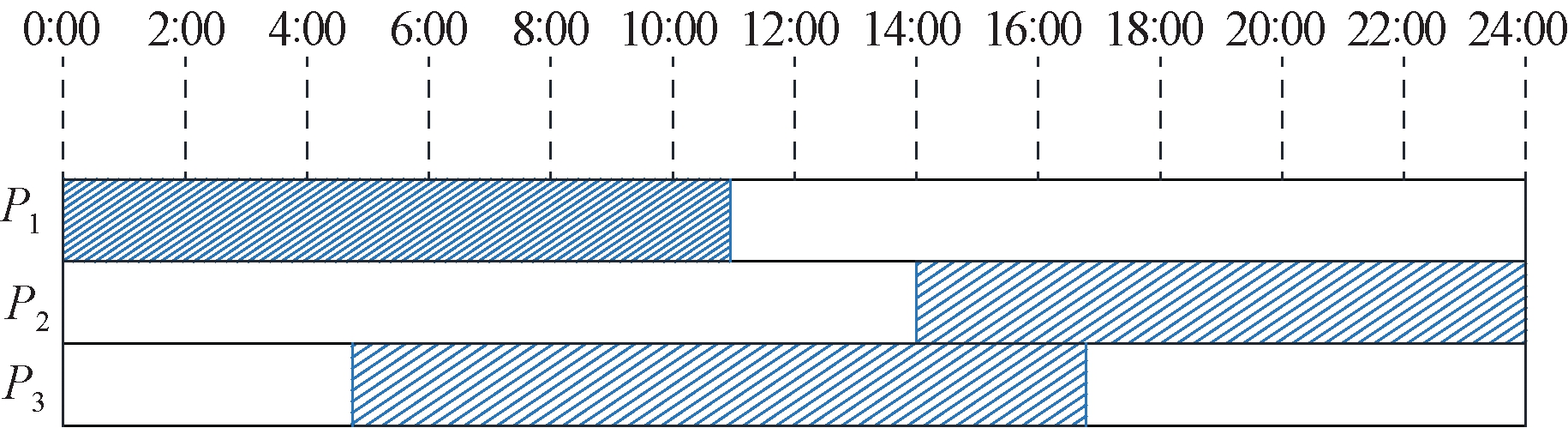
图1 停车位可共享时段示意图
Figure 1 Schematic diagram of shared period of berth
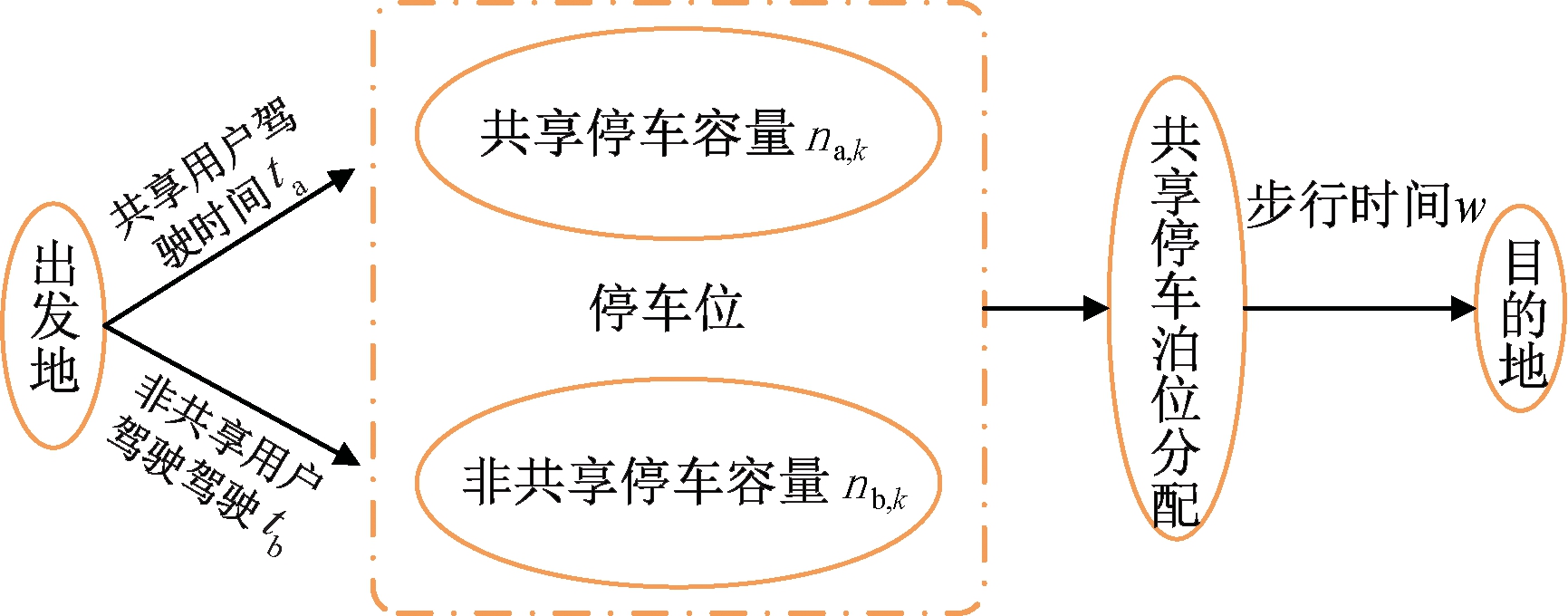
图2 用户停车选择示意图
Figure 2 Schematic diagram of user parking selection
1.2 停车选择均衡模型
每天有d个出行者从出发地到目的地，出行者需要在目的地附近找到合适的停车场，停车场可归类为非共享停车和共享停车，停车场被定义为k∈{1,2,…,K}。从出发地到停车场k的行驶时间为tk，从k到目的地的步行时间为wk，旅行者可以选择非共享停车场或共享停车场，令a表示用户选择的停车方式是共享停车，b表示用户选择的停车方式是非共享停车，设在位置k有共享的停车场数量为na,k，非共享停车的数量为nb,k。
当出行者在位置k选择共享停车时，开车到位置k，然后步行到目的地，其个人旅行费用为
Ca,k=α(tk+ta,k)+c(wk)+γa,k。
(1)
式中：γa,k为k位置共享停车价格；c(wk)为从停车点到目的地的步行成本；ta,k为共享停车巡航时间，包括访问时间和早到惩罚时间。因为共享停车中，出行者存在早于预约时间到达停车位的可能，导致其停车巡航时间增加，因此共享停车巡航时间可以定义为
ta,k=tav+(tor-tac)。
(2)
式中：tav为选择共享停车位的平均访问时间；tor为出行者的停车位预约时间；tac为出行者实际到达停车位的时间。
当出行者在位置k选择非共享停车时，开车到位置k寻找停车位，然后步行到目的地，非共享停车用户旅行费用为
Cb,k=α(tk+tb,k)+c(wk)+γb,k。
(3)
式中：tk为出行者从起点到停车点的行车时间；γb,k为非共享停车价格；tb,k为非共享停车点的巡航时间。
进一步定义非共享停车的巡航时间tb,k。对于位置k的非共享停车，旅客所面临的停车占用率为
sb,k=fb,k/nb,k。
(4)
式中：fb,k为选择k位置非共享停车的出行者数量；nb,k为k位置非共享停车容量。
k位置非共享停车的巡航时间为该位置停车占用率函数，即
tb,k=h(sb,k)。
(5)
在明确出行流量以及停车供给流量条件下，停车选择均衡问题可以通过求解最小化所有出行用户的出行总费用解决：
(6)
约束条件为
(7)
(8)
fi,k≥0,∀k∈{1,2,…,K}；
(9)
fa,k≤na,k,∀k∈{1,2,…,K}；
(10)
fb,k≤nb,k,∀k∈{1,2,…,K}。
(11)
式中： fa和fb分别为共享停车流向量和非共享停车流向量。式(7)表示总停车流量约束;式(8)表示共享停车流量约束;式(9)表示选择共享停车和非共享停车的流量不小于0;式(10)、(11)分别表示共享、非共享停车流量满足供给约束。
1.3 泊位分配整数规划模型
泊位分配模型的供需决策分配会影响用户的出行选择。泊位分配模型从共享停车运营商的角度出发，对共享停车泊位供需进行匹配，泊位分配模型和出行选择模型之间通过匹配决策变量建立联系。为了对其请求匹配合适的共享停车泊位，进一步考虑停车场如何实现利润最大化。将共享车位的每日计划分为多个时段q。假设N表示可共享泊位的集合，n∈N；引入0-1决策变量dnq表示运营商在时段q是否租用停车位n，取值如下：
(12)
假设m表示用户的预约申请，m∈M，M代表所有的出行预约申请用户。引入0-1决策变量anm表示停车请求m是否分配到共享泊位n,取值如下：
(13)
运用决策变量xmq表示时段q请求m的状态：
(14)
因此得到共享停车位占用矩阵，其元素znq=anm·xmq,n=1,2,…,N,q=1,2,…,Q。其中znq表示时段q泊位n是否被占用，若被占用znq=1，否则znq=0。
在共享泊位分配过程中，运营商需要根据出行者所申请停车的时间以及空间进行决策。运用pr、pd和py分别表示运营商租用车位单时段的价格、出行者预约车位单时段的价格和运营商运营管理车位单时段的价格。假设这3个价格在所有车位的所有时段都是恒定不变的。为了提高运营商的运营收益以及保证用户获得较高的满意度，这里考虑了因特殊因素影响而拒绝用户请求所带来的负面影响，因此引入拒绝请求惩罚系数β来减少负面影响。基于以上分析建立以运营商的收益最大化为目标的泊位分配0-1整数规划模型为
(15)
式中：等号右边第1项为运营商接受停车请求获得的收入；第2项为运营商租用停车位空闲时间段的成本；第3项为运营商因拒绝出行者请求带来的潜在损失；第4项为共享停车平台运营商对购买的车位进行管理运营产生的费用。
约束条件为
(16)
zmnq≠zjnq,j=1,2,…,J;
(17)
znq≤dnq,n=1,2,…,N,q=1,2,…,Q。
(18)
式中：znq,amn,dnq∈{0,1},n=1,2,…,N。式(16)表示每一个出行者预约请求最多分配一个停车位；式(17)表示两个出行者预约申请不能在同一时间段被分配到同一个停车位；式(18)表示每一个停车位在每一个时间段只容纳一辆车。
2 算法求解
针对停车选择均衡模型，定义ηa和ηb分别为在给定条件下使用共享停车位的用户da的最大出行成本和使用非共享停车位的用户db的最小出行成本，同时设计下降算法进行求解，算法流程图如图3所示。
步骤1(初始化)：设置非共享停车总流量的初始上界
和一个下界
步骤2(更新总停车流的分配)：令
和da=d-db。
步骤3(非共享停车流量分配)：以步骤2中给定的db开始，使用Frank-Wolfe算法求解模型非共享停车部分，设i=b，并且确定ηb。
步骤4(共享停车流分配)：以步骤2中给定da开始，使用单纯形法求解模型共享停车部分，并确定ηa。
步骤5(收敛检验)：如果
且为正值，停止并返回当前解，否则，转到步骤6。
步骤6(更新停车流边界
和
如果ηb>ηa，令
和
否则令
和
然后转到步骤2。
对共享停车泊位分配的0-1整数规划模型，本文将供需数据输入到软件MATLAB中进行求解。
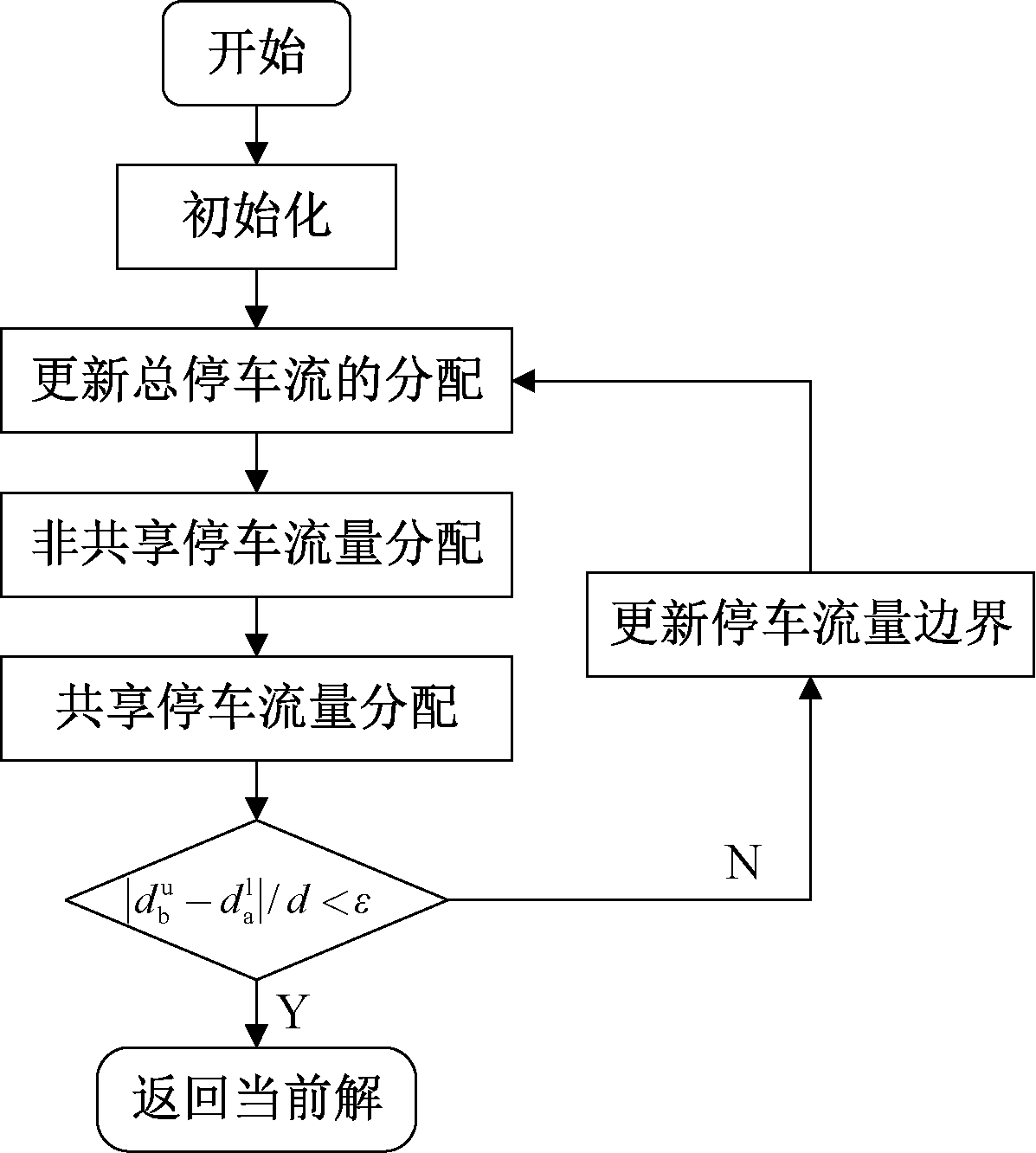
图3 算法流程图
Figure 3 Algorithm flow chart
3 算例分析
3.1 泊位分配整数规划模型验证
首先对于本文所提共享停车泊位分配整数规划模型的有效性进行验证。共享停车平台运营商购买车位的费用为2元/时段，出售给停车需求用户为每时段5元，平台对购买车位进行运营管理的费用为每时段2元，平台拒绝用户请求造成的潜在影响为每时段2元。供给车位由P1、P2、P3、P4和P5组成，共享时段分别为[9∶30,18∶30],[11∶00,19∶30],[8∶00,10∶30]、[12∶30,17∶30],[9∶00,18∶00],[9∶30,20∶00]。车位请求信息如表1所示。
表1 停车需求用户预约信息
Table 1 Parking demand information of user reservation
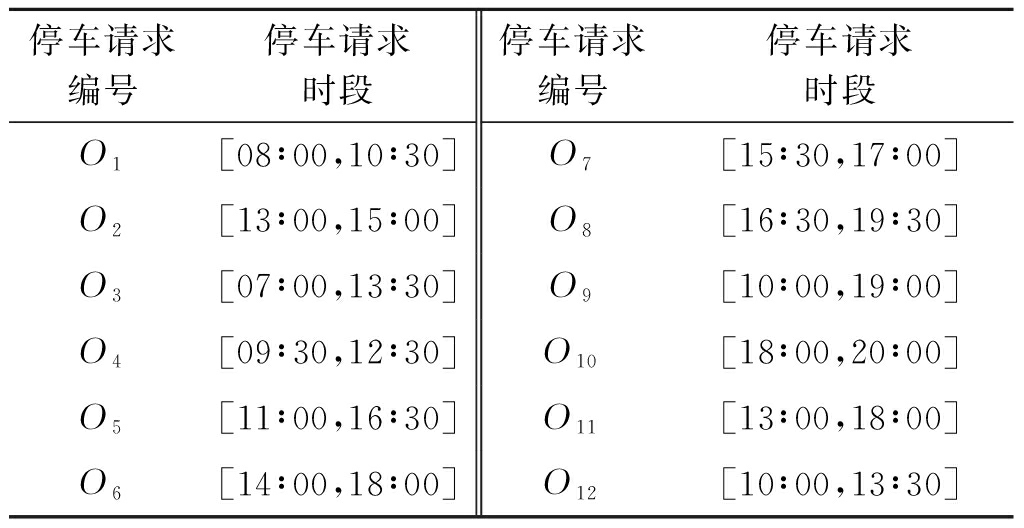
停车请求编号停车请求时段停车请求编号停车请求时段O1[08∶00,10∶30]O7[15∶30,17∶00]O2[13∶00,15∶00]O8[16∶30,19∶30]O3[07∶00,13∶30]O9[10∶00,19∶00]O4[09∶30,12∶30]O10[18∶00,20∶00]O5[11∶00,16∶30]O11[13∶00,18∶00]O6[14∶00,18∶00]O12[10∶00,13∶30]
共享停车平台运营商对需求信息和供给信息进行匹配，最终得到满足约束条件的方案，如图4所示。可以看出，总共12个停车请求，其中有10个停车请求被接受，2个停车请求被拒绝，停车请求的接受率达83%。因此本文所提共享泊位分配模型可在提高泊位利用率的前提下使运营商获取最大利润。
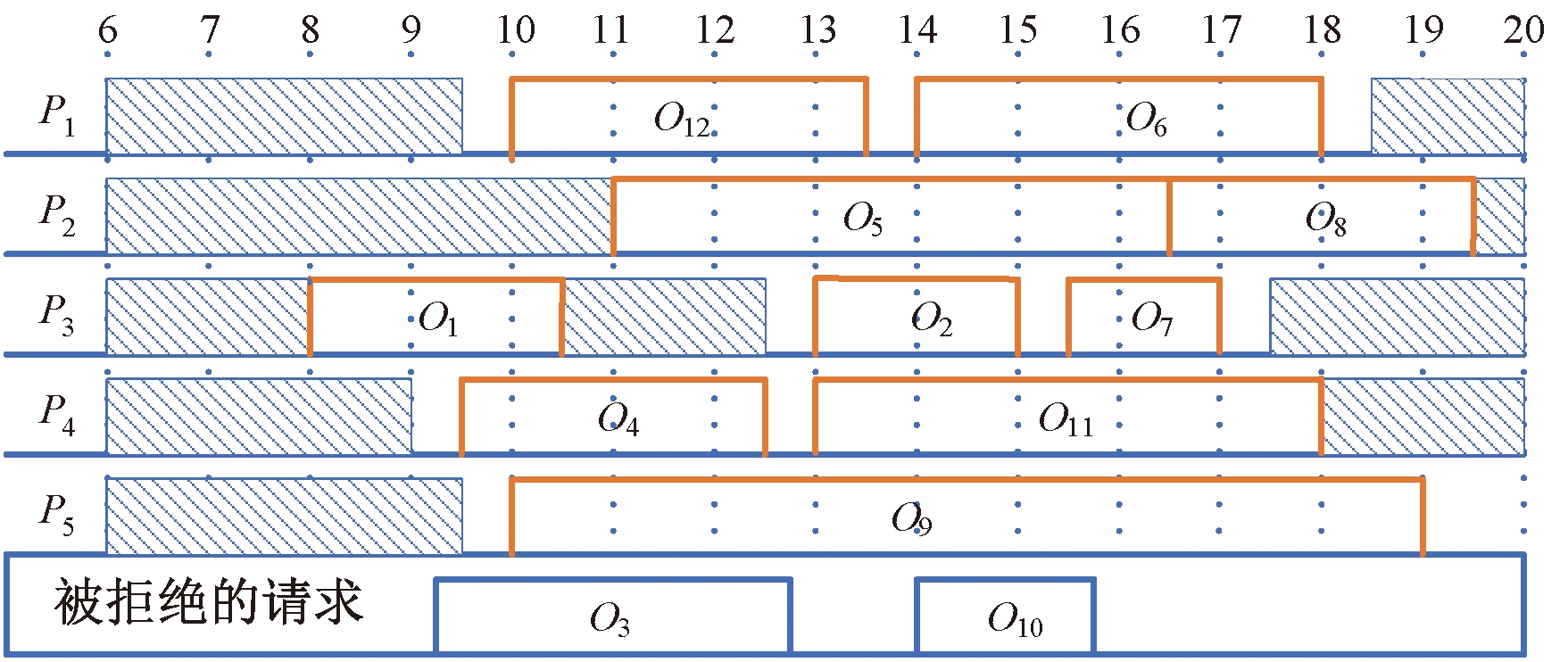
图4 共享停车请求分配结果
Figure 4 Shared parking request allocation results
3.2 用户出行选择及泊位分配分析
本文借助常州市金坛区吾悦广场附近部分路网及数据进行测试。华城二村作为用户出行的出发地，吾悦广场作为用户出行的目的地，金城花苑、景潭花园3区、景潭花园E区、徐塘新村和左邻右里为提供共享停车位区域，将5个区域分别设定为K1、K2、K3、K4和K5，总需求d=3 000个，出行用户的驾驶速度和步行速度分别为v=25 km/h和vw=5 km/h。停车区域的数据如表2所示。为了便于计算，将研究区域简化为1个算例网络示意图如图5所示。
表2 停车区域基础数据
Table 2 Basic data of parking area
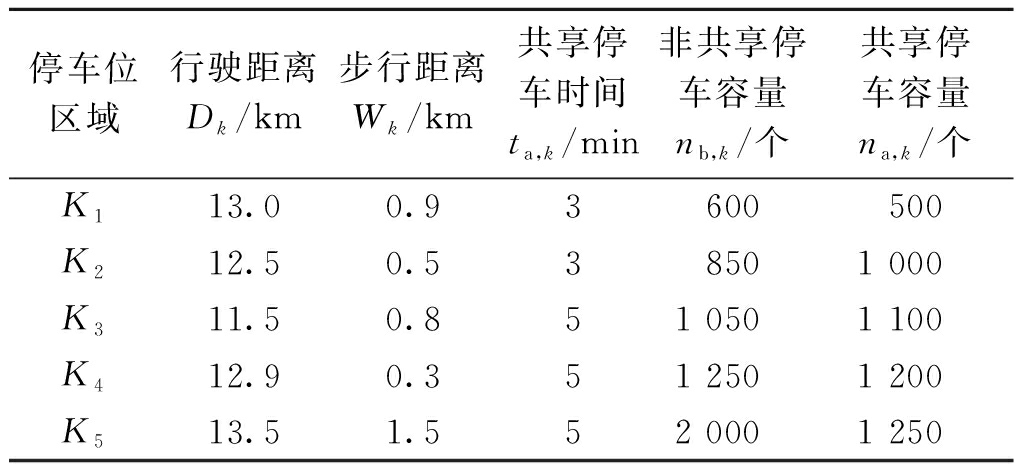
停车位区域行驶距离Dk/km步行距离Wk/km共享停车时间ta,k/min非共享停车容量nb,k/个共享停车容量na,k/个K113.00.93600500K212.50.538501 000K311.50.851 0501 100K412.90.351 2501 200K513.51.552 0001 250
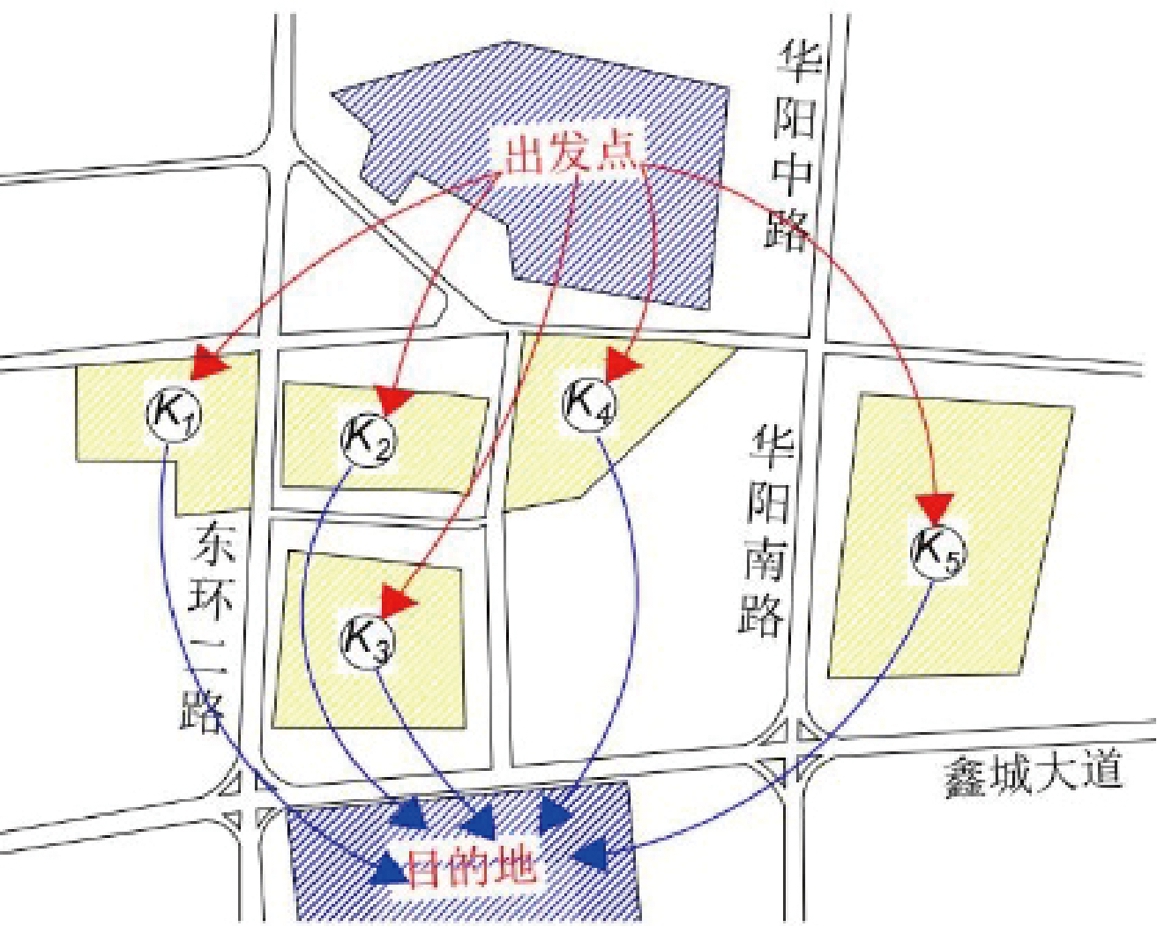
图5 算例网络图
Figure 5 Example network diagram
设计非共享停车巡航时间函数：h(fb,k)=εkδ/(1-fb,k/nb,k)，其中，εk=5表示在区域k中寻找一个空闲停车位所花费的平均时间，δ<1为调整因素。
从出发地到位置k的驾驶时间定义为tk=Dk/v，从位置k到目的地的步行时间定义为wk=Wk/vw。为验证算法的收敛性，定义变量
其中e随着非共享停车流量上界和下界的变化而变化。从图6可以看出，变量e随着迭代次数的增加不断减少，逐渐趋向于0，非共享停车流量的上界与下界逐渐接近并且最终趋于一致，共享停车选择流量与非共享停车选择流量逐渐趋向于均衡。图7描述了在出行费用最小及运营商收益最大情况下，各个停车场的停车流量随迭代次数发生的变化。从图7中可以看出，停车场K3和K4承担的流量相对较高，K1和K5分担的流量相对较低。这是因为K1和K5行驶距离和步行距离都比较远，出行用户更倾向于选择行驶距离和步行距离近的区域停车。
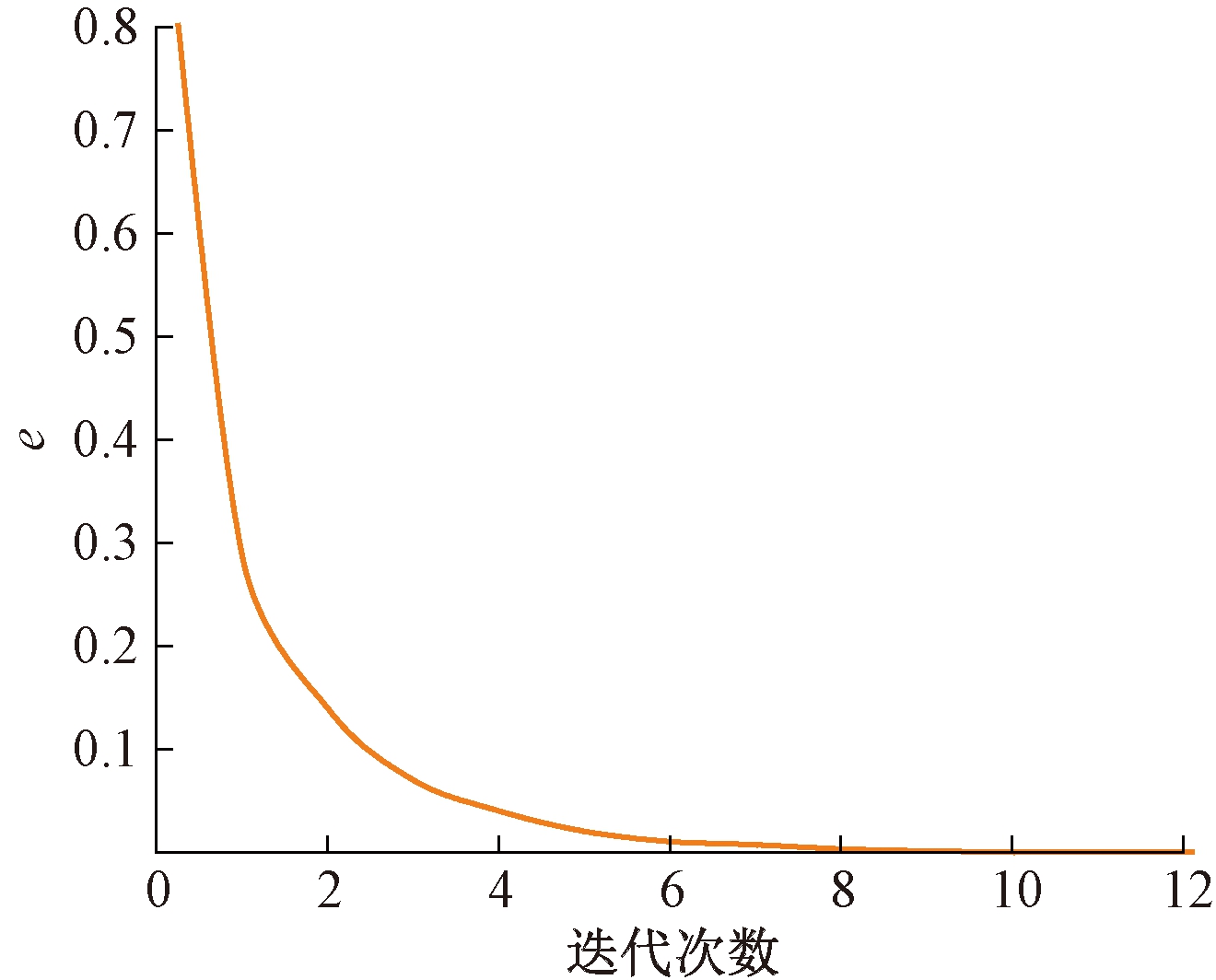
图6 收敛验证
Figure 6 Convergence verification
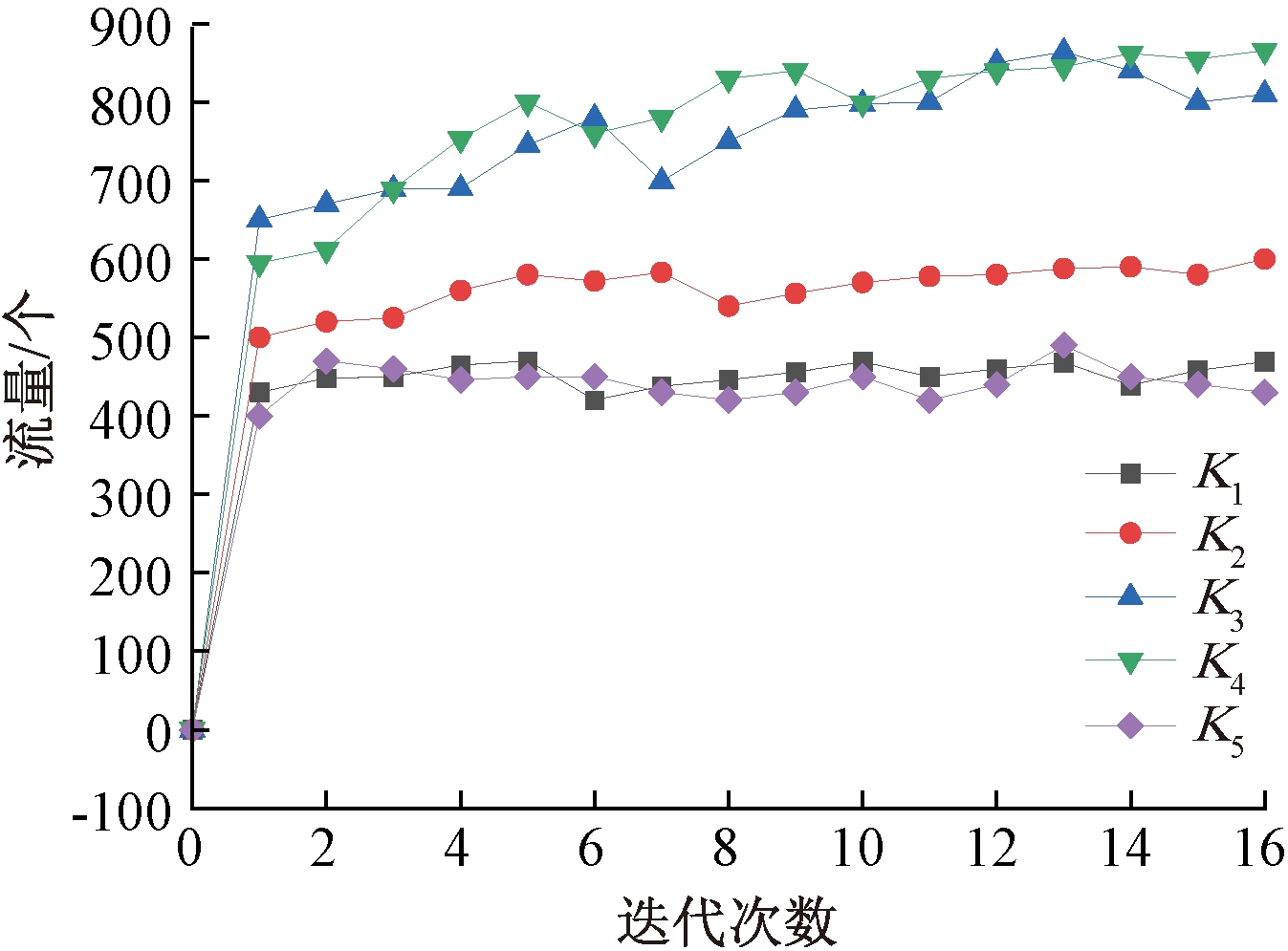
图7 停车流量变化
Figure 7 Parking flow change
为了进一步分析模型特性，假设在平台运营时间内，共享停车需求用户驾驶车辆到达停车位时间服从泊松分布，停车需求时间服从负指数分布，该负指数的均值为3 h，同时提出运营商利润指标对模型求解的方案的合理性进行量化评价，表达如式(19)。为了控制指标的变化，停车需求的变化范围设为0到1 000个。
(19)
图8描述了在出行费用最小化情况下，共享停车运营平台获得的利润随着请求数量的变化而发生的变化。从图8中可以看出停车区域K2、K3和K4随着需求的增加增长速度较快，当需求达到800个时，利润增长趋势放缓。这是因为模型中设置了拒绝用户惩罚费用，随着需求的增加，停车场满足用户预约需求的泊位减少，部分预约用户被拒绝。而K1和K5增加速度缓慢。这是因为K1和K5区域距离目的地的驾驶距离和步行距离较远，因此出行用户更倾向于选择距离近的停车场停车。图9描述了随着停车请求规模的变化，共享停车与非共享停车流量的演化过程。共享停车与非共享停车流量与请求规模呈正相关，当请求高于800个时，非共享停车流量增加的趋势高于共享停车。这是因为部分共享出行用户的预约与停车场泊位供给无法匹配而被拒绝。因此在此供给规模下，预约请求达到800个时，既可以使运营商获得较高利润，又可以提高共享停车与非共享停车流量之间的平衡性。
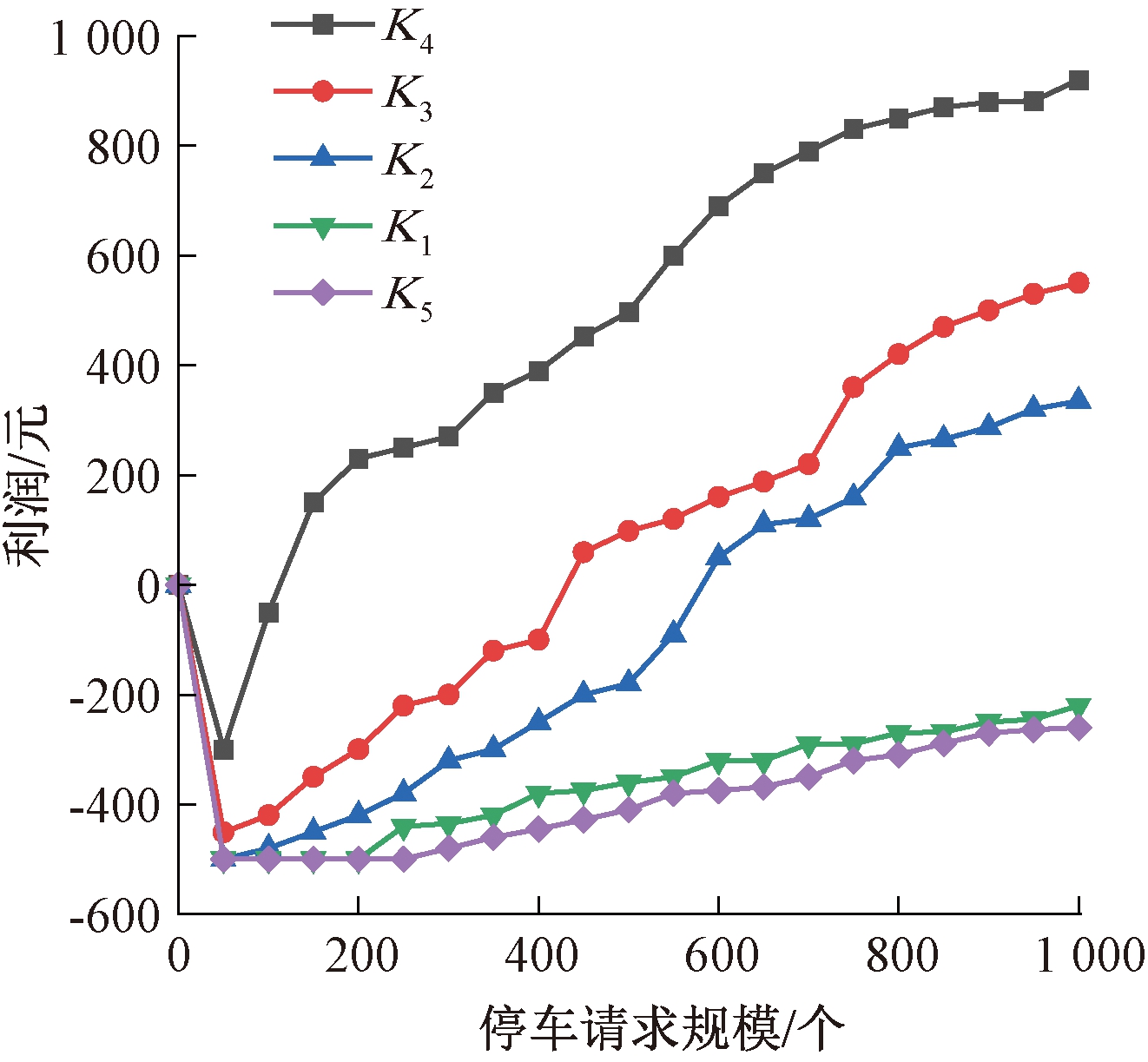
图8 出行费用最小化下平台的利润
Figure 8 Profit of the platform with the minimization of travel expenses
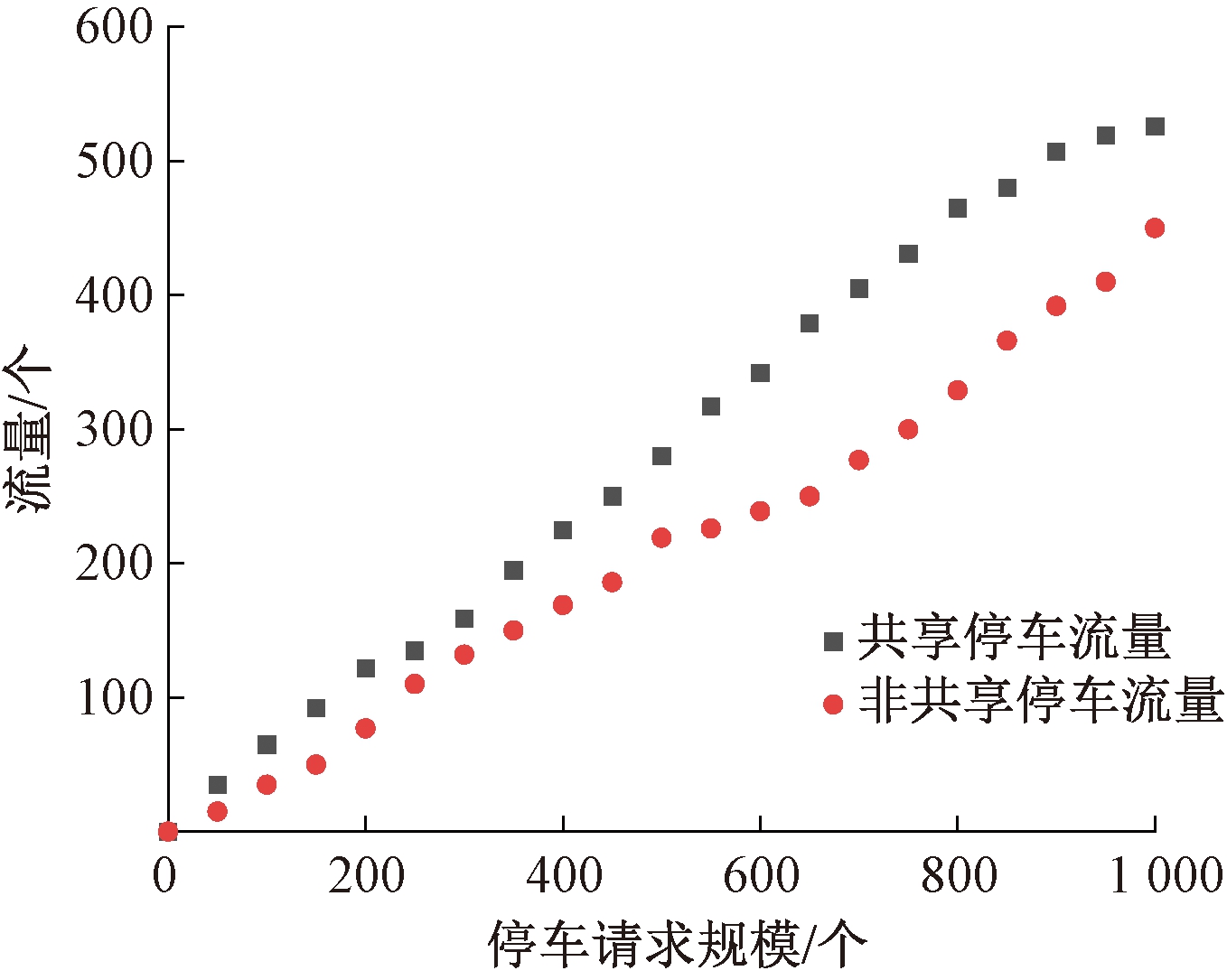
图9 共享停车与非共享停车流量演化
Figure 9 Shared parking and non-shared parking flow evolution
4 结论
本文从用户出发地到目的地完整出行链角度，研究停车选择及泊位分配，并结合常州市金坛区部分路网作为实际算例进行研究。利用共享停车泊位分配决策变量将泊位分配模型和用户出行模型建立联系。建立的共享停车泊位分配模型中，停车请求的接受率可以达到83%。同时得出出行用户更加倾向于选择行驶距离和步行距离更短的停车场。合理的停车请求规模既可以使运营商获得较高利润，又可以提高共享停车与非共享停车流量之间的平衡性。对于接下来的研究可以考虑从用户角度建立共享停车泊位分配整数规划目标函数，结合用户出行路网交通流量不确定性进行深入研究。
[1] 张雪妍, 贺锋. 基于累积前景理论的组合出行交通分配模型[J]. 郑州大学学报(工学版), 2020, 41(3): 91-96.
ZHANG X Y, HE F. Traffic assignment model with combined modes based on cumulative prospect theory[J]. Journal of Zhengzhou university (engineering science), 2020, 41(3): 91-96.
[2] HASSINE S B, MRAIHI R, LACHIHEB A, et al. Modelling parking type choice behavior[EB/OL]. (2021-09-22)[2022-03-20]. https://www.sciencedirect.com/science/article/pii/S2046043021000721.
[3] WANG A G, GUAN H Z, QIN Z T, et al. Study on the intention of private parking space owners of different levels of cities to participate in shared parking in China[J]. Discrete dynamics in nature and society, 2021, 2021: 1-16.
[4] 田丽君, 杨茜, 黄海军, 等. 基于累积前景理论的出行方式选择模型及实证[J]. 系统工程理论与实践, 2016, 36(7): 1778-1785.
TIAN L J, YANG Q, HUANG H J, et al. The cumulative prospect theory-based travel mode choice model and its empirical verification[J]. Systems engineering-theory & practice, 2016, 36(7): 1778-1785.
[5] FANG S S, YAO X S, ZHANG J Q, et al. Grey correlation analysis on travel modes and their influence factors[J]. Procedia engineering, 2017, 174: 347-352.
[6] SHAO C Y, YANG H, ZHANG Y, et al. A simple re-servation and allocation model of shared parking lots[J]. Transportation research part C: emerging technologies, 2016, 71: 303-312.
[7] JIANG B W, FAN Z P. Optimal allocation of shared parking slots considering parking unpunctuality under a platform-based management approach[J]. Transportation research part E: logistics and transportation review, 2020, 142: 102062.
[8] WANG S F, LI Z H, XIE N. A reservation and allocation model for shared-parking addressing the uncertainty in dri-vers′ arrival/departure time[J]. Transportation research part C: emerging technologies, 2022, 135: 103484.
[9] 张水潮, 蔡逸飞, 黄锐, 等. 基于预约需求的共享停车平台泊位分配方法[J]. 交通运输系统工程与信息, 2020, 20(3): 137-143, 162.
ZHANG S C, CAI Y F, HUANG R, et al. Shared parking space allocation method considering reservation demand[J]. Journal of transportation systems engineering and information technology, 2020, 20(3): 137-143, 162.
[10] 姚恩建, 张正超, 张嘉霖, 等. 居住区共享泊位资源优化配置模型及算法[J]. 交通运输系统工程与信息, 2017, 17(2): 160-167.
YAO E J, ZHANG Z C, ZHANG J L, et al. A model and algorithm for optimization of the utilization of residential shared parking slots[J]. Journal of transportation systems engineering and information technology, 2017, 17(2): 160-167.
[11] LAI M H, CAI X Q, HU Q. Market design for commute-driven private parking lot sharing[J]. Transportation research part C: emerging technologies, 2021, 124: 102915.
[12] 胥晶晶. 考虑泊位共享的居住区停车预约分配模型研究[D]. 西安: 长安大学, 2019.
XU J J. Study on parking reservation allocation model in residential area of considering berth sharing[D]. Xi′an: Chang′an University, 2019.
[13] 段满珍, 杨兆升, 张林, 等. 个性化诱导下的居住区共享停车泊位分配模型[J]. 东北大学学报(自然科学版), 2017, 38(2): 174-179.
DUAN M Z, YANG Z S, ZHANG L, et al. Parking spaces allocation model of residential areas sharing parking based on personalized guidance[J]. Journal of northeastern university (natural science), 2017, 38(2): 174-179.