高速插针机是电子工业中常用的一种机械装置,其功能是实现快速的元件接头引线的连接。插针机构是高速插针机中最为关键的机构,一般采用圆柱凸轮机构实现插针头的快速往复运动。工作过程中,凸轮滚子与沟槽之间的接触受力十分复杂,深入研究其接触应力的计算方法、进而实现疲劳寿命预测十分重要。
董九志等[1]根据推针块位置变化的轨迹对高速插针机中凸轮轮廓曲线进行优化,实现了插针机构的性能提升。许勇坚[2]采用图谱对凸轮插针机的运动各个阶段进行计算和分析。毛璐瑶等[3]研究了插针机片式凸轮箱在高速运转时的振动,发现弹簧是限制其高速运转的主要因素。Li等[4]设计了一种基于耦合圆柱凸轮机构的机械接口,并分析了该接口的故障模式和故障原因。Sun等[5]利用两个共轭圆柱凸轮对弹簧进行非线性驱动,从而实现假膝的规律动作。包钊华等[6]建立了不同的凸轮曲线模型,并分析比较了不同凸轮曲线的运动学和机械特性。尹建军等[7]对某打结机咬绳机构中的线接触圆柱凸轮进行设计,并对圆柱凸轮的接触力和接触疲劳强度进行分析。崔永杰等[8]设计了一种基于圆柱凸轮的植距可调秧苗末端执行器,通过耦合模拟单因素试验研究了各试验因素对执行端变形量的影响。王小增[9]基于弹性力学理论得到了偏心圆柱凸轮液力连接过程中的各方向受力与变形特征。陈立伟[10]对圆柱凸轮的曲线进行设计与优化,得出符合工况的凸轮曲线方程,并对系统进行静力学和动力学仿真分析。薛珊等[11]基于赫兹接触理论,应用多体动力学仿真软件对圆柱凸轮进行了接触仿真,得到了运动状态曲线和接触力曲线。张超洋[12]对含有冗余结构的大小滚子圆柱凸轮机构和双层滚子圆柱凸轮机构进行了建模与动力学仿真分析。魏俊杰等[13]建立双滚子螺旋运动的圆柱凸轮机构模型,通过仿真软件求解其动力学性能。徐一村等[14]将推杆轮廓离散化,利用离散后的多个接触点生成多条曲线并取交集运算,得到了较理想的凸轮轮廓曲线。
通过上述研究可知,目前针对圆柱凸轮机构的力学研究主要是基于软件仿真的机构静力学与动力学分析,但这样的研究无法对凸轮机构的凸轮滚子-沟槽力学性能进行精确的计算。为此,本文以高速插针机构中的圆柱凸轮滚子为研究对象,运用有关力学知识对其进行分析,构建运动学和力学模型,通过数值计算方法对其力学性能及疲劳寿命进行深入研究。
1 圆柱凸轮滚子力学分析
1.1 插针机构的组成及工作原理
插针机构的结构原理如图1所示,其工作原理如下。同步带轮转动带动凸轮轴匀速转动,圆柱凸轮与凸轮轴通过键联接,当凸轮轴转动时,圆柱凸轮与凸轮轴同步转动。圆柱凸轮沟槽内嵌有凸轮滚子,滚子连接在滚子连接件上,滚子连接件安装在直线导轨的滑块上,滚子连接件上方装有U形槽滚子。圆柱凸轮转动时,带动滚子、滚子连接件、滑块及U形槽滚子整体左右往复运动。U形槽滚子嵌在U形块的U形槽中。U形块、连接块、推杆及插针四者静连接,推杆装配在滑槽中。当U形槽滚子左右往复运动时,推动右侧的U形块、连接块、推杆及插针整体做相同的运动,从而实现插针动作。圆柱凸轮旋转1圈,完成1次插针动作。
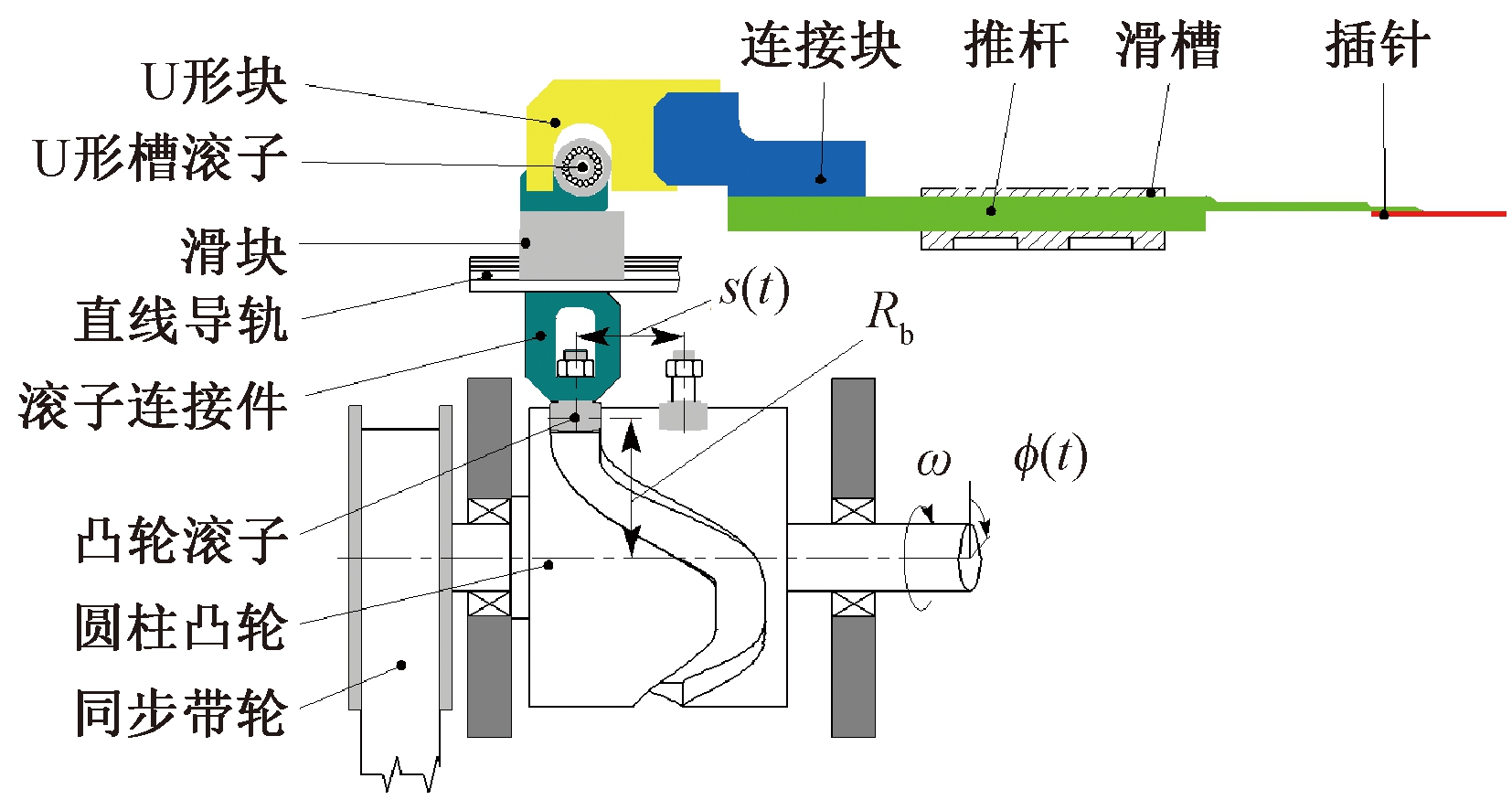
图1 插针机构的组成
Figure 1 Composition of the pin insertion mechanism
1.2 圆柱凸轮机构从动件运动规律与惯性力
如图1所示,凸轮转动1圈过程中,将凸轮近休止角的初始时刻记为t=0,设从动件在t时刻位移为s(t),速度为v1(t),加速度为a(t),凸轮转动角速度为恒定值ω,凸轮的转角φ(t)=ωt,存在函数关系:
s(t)=f[φ(t)] ;
(1)
(2)
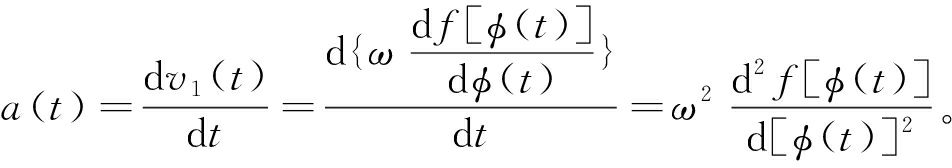
(3)
高速插针机中插针机构的圆柱凸轮机构满足正弦加速度运动规律,根据文献[15]可计算出从动件在t时刻的加速度a(t)。对a(t)进行一次积分与二次积分,并引入边界条件,即可得从动件速度v1(t)与位移s(t)。根据牛顿第二定律可推导插针机构从动件的惯性力。假设凸轮滚子、滚子连接件、滑块、U形槽滚子及与四者相互静连接的连接件的总质量为M1,U形块、连接块、推杆、插针及与四者相互静连接的连接件的总质量为M2,则从动件所受的总惯性力I(t)为
I(t)=(M1+M2)·a(t)。
(4)
1.3 圆柱凸轮机构的力学模型构建
在进行力学分析之前,假设:(1)高速插针机正常工作时,凸轮轴转速恒定不变;(2)分析机构运动学特性时,不考虑机构的弹性变形;(3)不考虑凸轮滚子与轨道在加工过程产生的几何误差;(4)凸轮滚子与沟槽间的接触变形在弹性范围之内;(5)凸轮滚子在沟槽内进行的是纯滚动,不考虑其相对滑动。
如图2所示,F1(t)为直线导轨所受的横向摩擦力;F2(t)为推杆所受的横向摩擦力;F3(t)为针孔对针的横向摩擦力;Fx(t)为圆柱凸轮沟槽对凸轮滚子力的横向分力。规定图2标注的Fx(t)、I(t)、F3(t)的方向分别为该力的正方向,当Fx(t)计算结果为正(负)时,表明凸轮滚子与其左侧(右侧)的沟槽表面接触并受力。当I(t)计算结果为正(负)时,表明从动件惯性力与图示方向相同(相反)。推程阶段的插针入孔过程F3(t)>0,其余时间段F3(t)=0。回程阶段F1(t)与F2(t)均为反向,即分别为-F1(t)与-F2(t)。
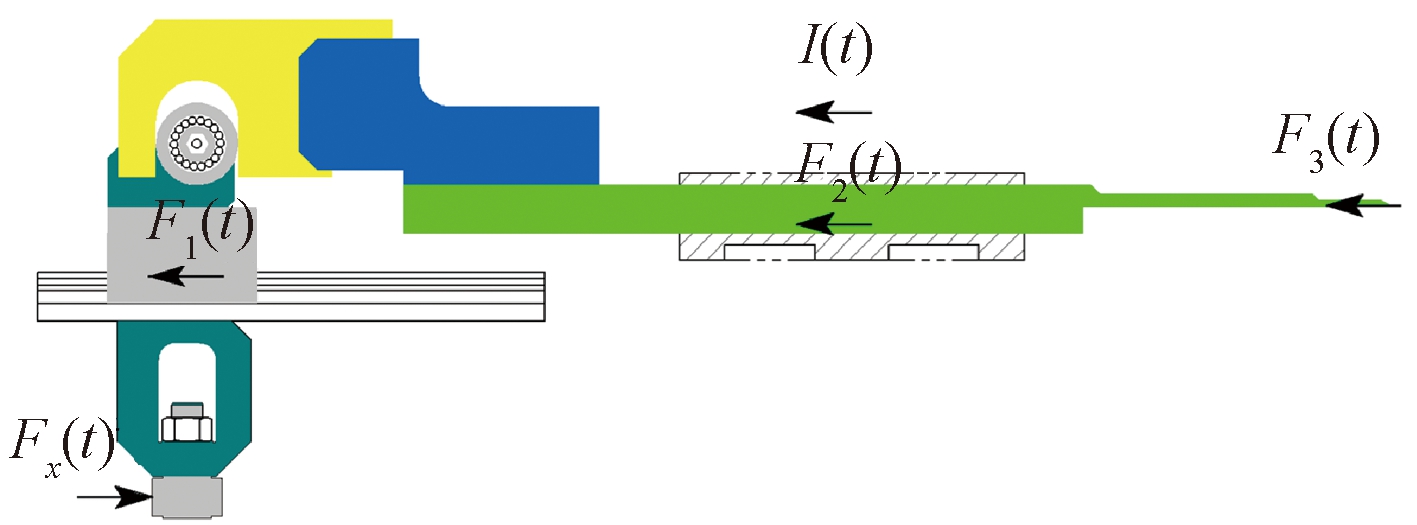
图2 凸轮从动件的水平方向的力学分析
Figure 2 Mechanical analysis of cam follower in horizontal direction
推程时有
Fx(t)=F1(t)+F2(t)+F3(t)+I(t) 。
(5)
回程时有
Fx(t)=-F1(t)-F2(t)+I(t) 。
(6)
如图3所示,将圆柱凸轮沟槽在基圆半径Rb处按圆周方向展开,展开后圆周方向长度为凸轮基圆周长2πRb,圆柱凸轮的旋转运动可等效为展开后的沟槽以某一速度水平向左运动。通过反转法等效为沟槽静止、凸轮滚子在沟槽中纯滚动。等效后滚子中心水平向右的速度v2(t)与等效前沟槽水平向左的速度大小相等,即v2(t)=Rbω。图3中,v(t)表示滚子中心合速度;v1(t)表示从动件平移速度;FC(t)表示凸轮沟槽对滚子的接触力,该力的方向是曲面在接触点处的公法线方向;压力角α(t)为v1(t)与FC(t)的夹角,和曲面在接触点的切线与横轴正方向的夹角相等或互补,即
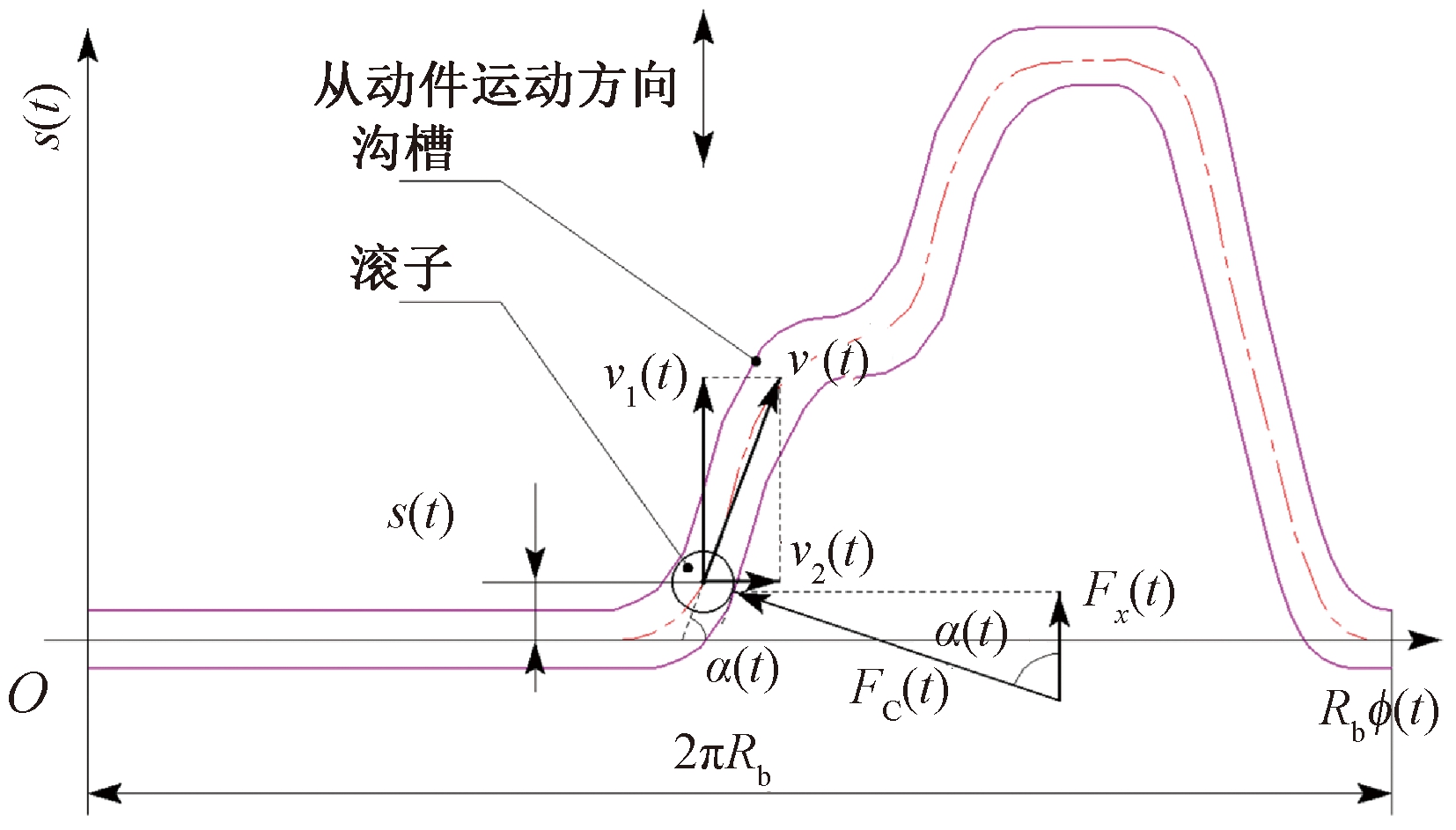
图3 圆柱凸轮的展开图
Figure 3 An expansion of a cylindrical cam
(7)
将凸轮沟槽对滚子的接触力FC(t)分解到从动件运动方向的分力Fx(t),即
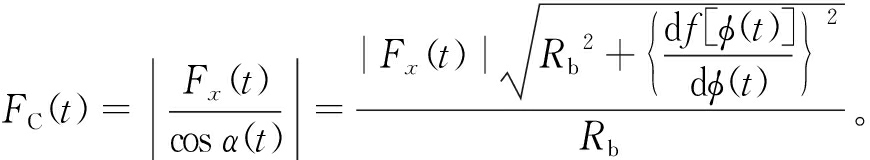
(8)
由式(7)推导出滚子中心合速度v(t):
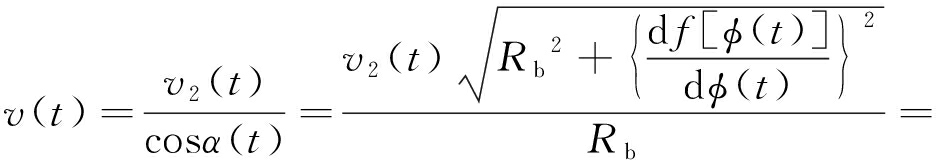
(9)
凸轮滚子与沟槽之间的接触形式为两圆柱面间的线接触,采用赫兹接触公式计算出凸轮转动1圈过程中每一时刻凸轮滚子与沟槽受力接触点的最大接触应力。假设ρ1为滚子曲率半径,ρ2(t)为凸轮滚槽在接触点的曲率半径,b为线接触的长度,μ1与μ2分别为滚子与沟槽的接触面泊松比,E1与E2分别为滚子与沟槽的接触面弹性模量,由图3可知,凸轮的曲率半径ρ2(t)可通过圆柱凸轮的展开图的曲线方程求出:
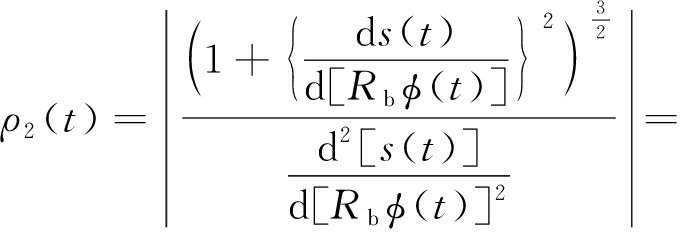
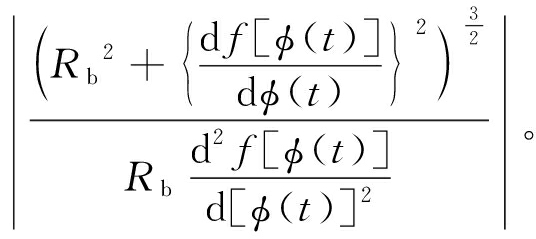
(10)
则圆柱凸轮机构滚子与沟槽受力接触点的最大接触应力σHmax(t)为
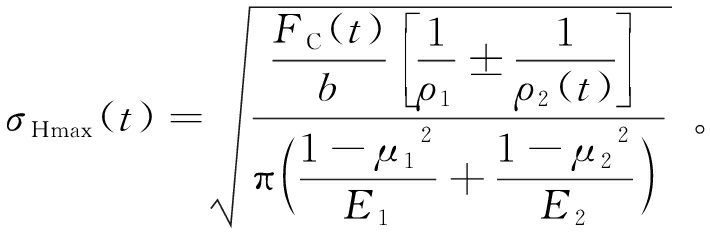
(11)
由图3可以看出,凸轮滚子整个阶段均与凹面接触,故式(11)中“±”取“-”。
如图4所示,将凸轮滚子在滚槽中的空间运动转化为只考虑滚子中心走过路程的一维运动,建立凸轮滚子在沟槽内的运动几何模型。凸轮转动1圈后滚子中心走过的距离L为
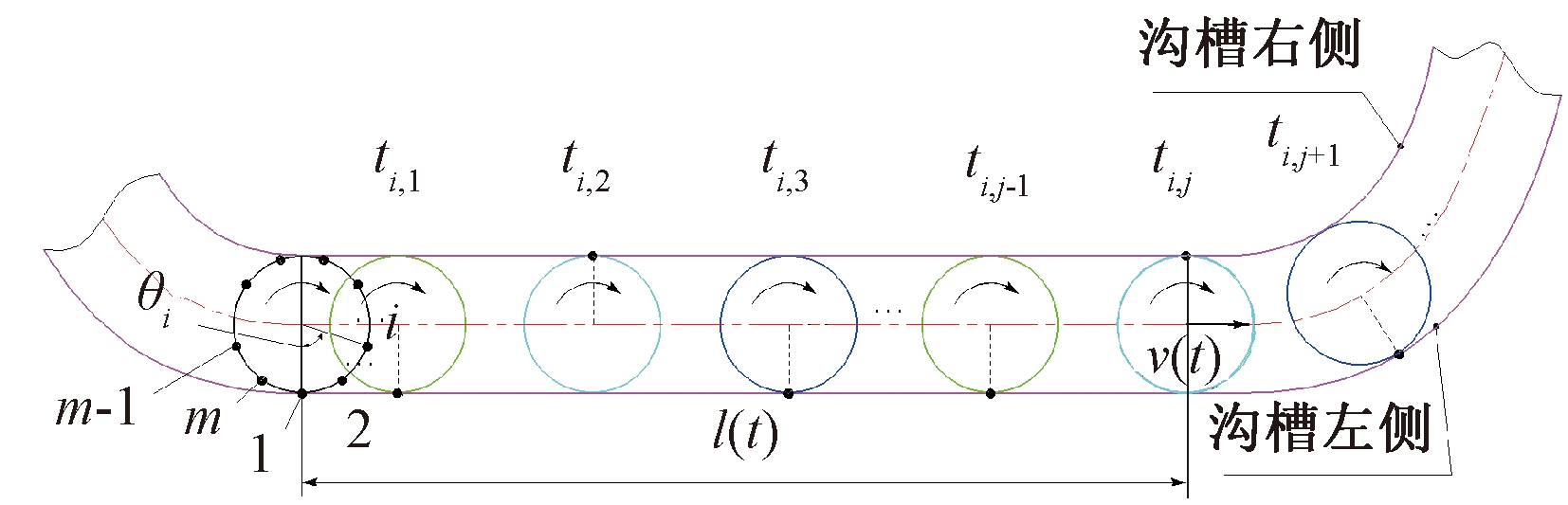
图4 滚子运动几何模型
Figure 4 Geometric motion model of a roller
(12)
凸轮转动1圈过程中,t时刻滚子中心走过的距离l(t)为
l(t)=![]() v(t)dt。
v(t)dt。
(13)
将凸轮滚子圆周方向离散化,均分为m等分,从最低点逆时针方向依次标记为1,2,3,…,i-1,i,i+1,…,m-1,m。其中,第i个点与竖直方向夹角为θi,即θi=2π(i-1)/m。假设凸轮滚子上i点与沟槽第j次接触时间为ti,j,已知l(ti,j)可通过式(13)反求ti,j。从图4可以看出,当j为奇数时,滚子上i点与沟槽的左侧接触;当j为偶数时,滚子上i点与沟槽的右侧接触。结合图2,当j为奇数(偶数),且此时Fx(ti,j)为正(负)时,则通过式(11)计算该点此时最大接触应力![]() 否则该点与沟槽侧面之间不接触或者接触但受力点在其对面θi±π位置,此时
否则该点与沟槽侧面之间不接触或者接触但受力点在其对面θi±π位置,此时![]()
1.4 圆柱凸轮机构滚子疲劳寿命预测
圆柱凸轮机构滚子接触面疲劳损伤可视作是变应力作用下的接触疲劳问题,可采用Miner线性疲劳累积损伤理论[16],计算凸轮旋转1圈后,滚子上任意点i的累积损伤率Qi为
(14)
式中:Qi,j为凸轮旋转1圈后滚子上i点第j次接触时的单次接触损伤率;m为随材料和应力而定的指数,N0为循环基数,根据文献[17]受接触应力时m取6,N0取107;σr为循环基数N0对应的接触应力,根据文献[18]当硬度为60 HRC时,σr取2 450 MPa。当凸轮滚子上i点第p次接触后,剩下的路程不足以完成该点下一次接触时(即L-l(ti,p)<πρ1时),对式(14)中Qi,j的累加操作结束,Qi为凸轮旋转1圈后滚子上i点第1次到第p次接触产生的累积损伤率。
凸轮转动1圈后,凸轮滚子圆周上的点产生的累积损伤各不相同。出于安全考虑,将凸轮旋转1圈后滚子圆周上累积损伤率最大的点作为危险点,并基于Miner线性疲劳累积损伤理论计算该危险点的疲劳寿命,以该危险点的寿命作为滚子的疲劳寿命:
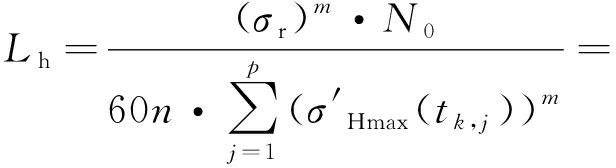
(15)
式中:Lh为滚子接触疲劳寿命,h;n为凸轮转速,r/min;滚子圆周方向上第k点为危险点。
2 算例分析
2.1 参数确定
以某型号高速插针机为研究对象,其插针机构从动件运动特性如表1所示,其中(0,31π/36]为近休止角,(31π/36,43π/36]为推程角1,(43π/36,14π/9]为推程角2,(14π/9,29π/18]为远休止角,(29π/18,2π]为回程角。推程1、2及回程均满足正弦加速度运动规律。由文献[15]中正弦加速度运动规律,计算该从动件的位移-转角关系,根据φ(t)=ωt,结合式(1)~(3)就可以求出s(t)、v(t)与a(t),结合式(4)即可求出I(t)。
表1 圆柱凸轮机构从动件运动特性
Table 1 Motion characteristics of follower of cylindrical cam mechanism
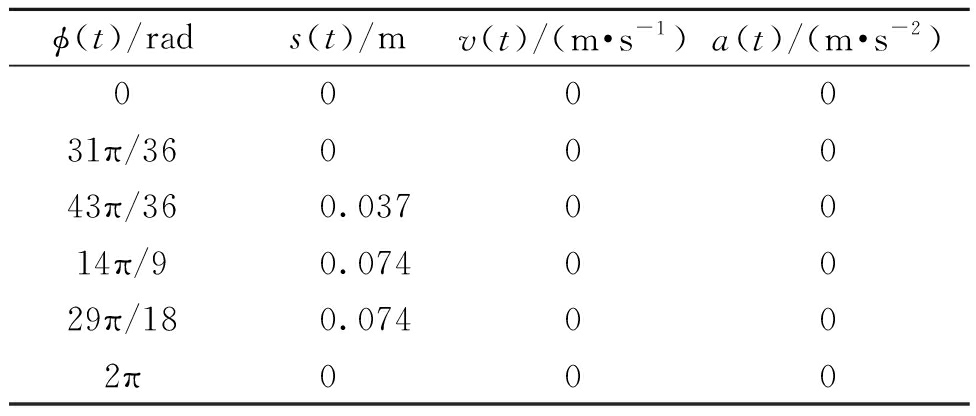
ϕ(t)/rads(t)/mv(t)/(m·s-1)a(t)/(m·s-2)00 0031π/3600043π/360.0370014π/90.0740029π/180.074002π000
圆柱凸轮机构从动件所受的阻力包括直线导轨所受的横向摩擦力F1(t)、推杆所受的横向摩擦力F2(t)和针孔对针的横向摩擦力F3(t)。实测得到F1(t)与F2(t)的总和约为8.3 N,F3(φ)满足式(16),再由φ(t)=ωt即可求出F3(t)。圆柱凸轮机
构的其他参数如表2所示。
表2 圆柱凸轮机构的参数
Table 2 Parameters of cylindrical cam mechanism

参数数值组合体1质量M1/kg1.25组合体2质量M2/kg1.00圆柱凸轮直径Db/mm134凸轮转速n/(r·min-1)600凸轮滚子直径D1/mm22.0凸轮滚子与沟槽接触长度b/mm12.0凸轮滚子接触面弹性模量E1/MPa2.08×105滚子接触面泊松比μ10.30沟槽接触面弹性模量E2/MPa2.18×105沟槽接触面泊松比μ20.28

(16)
2.2 算例分析
根据式(1)~(3),设凸轮转动速度n为600 r·min-1,计算出凸轮转动1圈时凸轮从动件的位移、速度、加速度、惯性力,并绘制其变化曲线,如图5所示。可以看出,位移、速度、加速度满足正弦加速度运动规律。
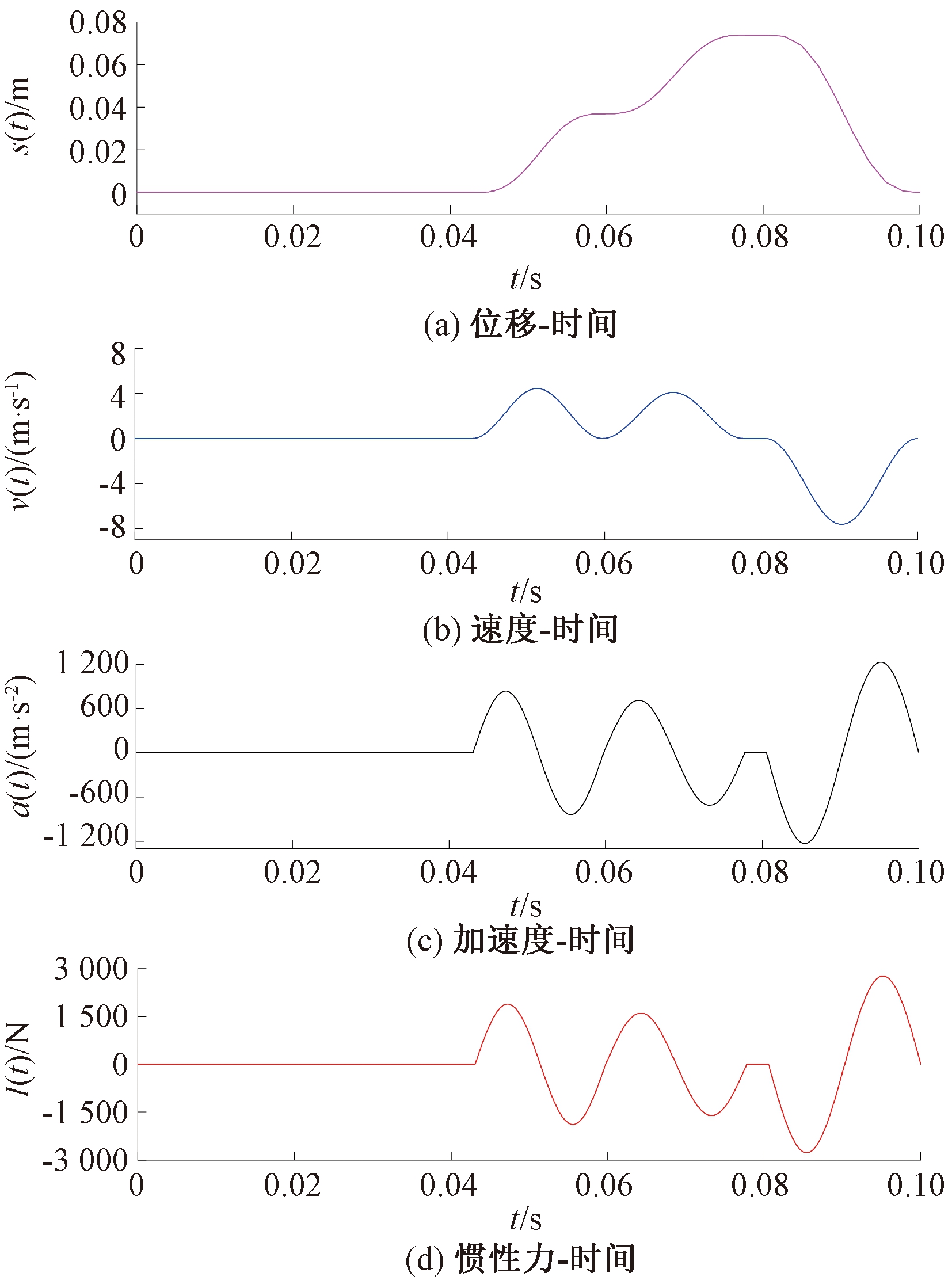
图5 凸轮转动1圈从动件的位移、速度、加速度及惯性力
Figure 5 Displacement, velocity, acceleration and inertia force of the follower as cam rotates one circle
图6所示为凸轮转动1圈过程中凸轮滚子与沟槽接触点的最大接触应力随时间的变化。可以看出,0.086 61 s时的最大接触应力达到最大值1 168 MPa,此时凸轮转角为311°48′。
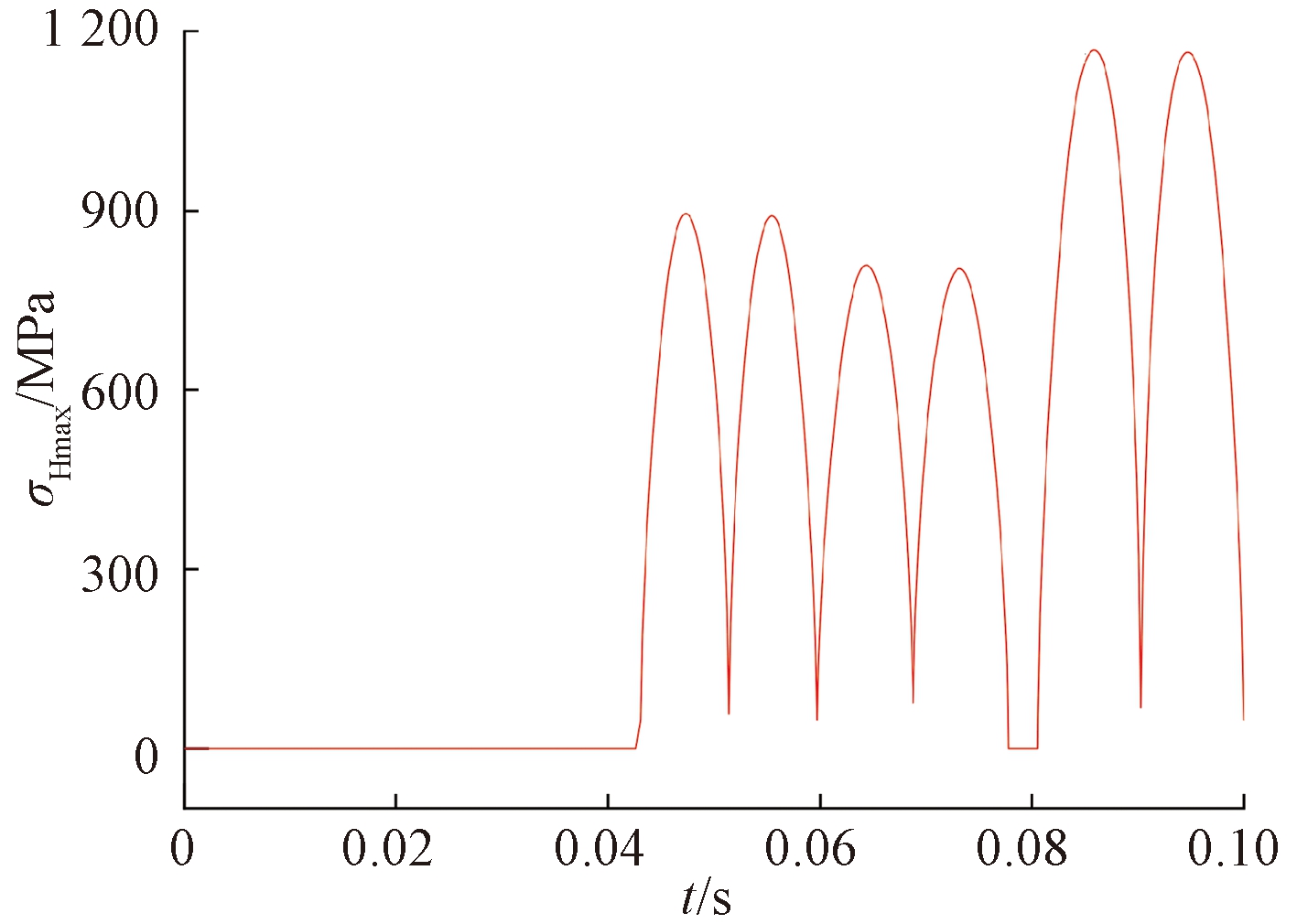
图6 凸轮转动1圈接触点的最大接触应力
Figure 6 Maximum contact stress of contact point when cam rotates one circle
凸轮滚子直径取IKO公司标准凸轮随动器典型的7种滚子直径,其余参数见表2,根据式(15)研究圆柱凸轮直径对滚子接触疲劳寿命的影响,如图7所示。可以看出,当圆柱凸轮直径增大时,各组滚子的接触疲劳寿命均有所提升。以凸轮滚子直径D1=22 mm组为例,当凸轮直径为50 mm时凸轮滚子的疲劳寿命为22 510 h;当凸轮直径增大到140 mm时凸轮滚子的疲劳寿命随之增加到191 341 h。
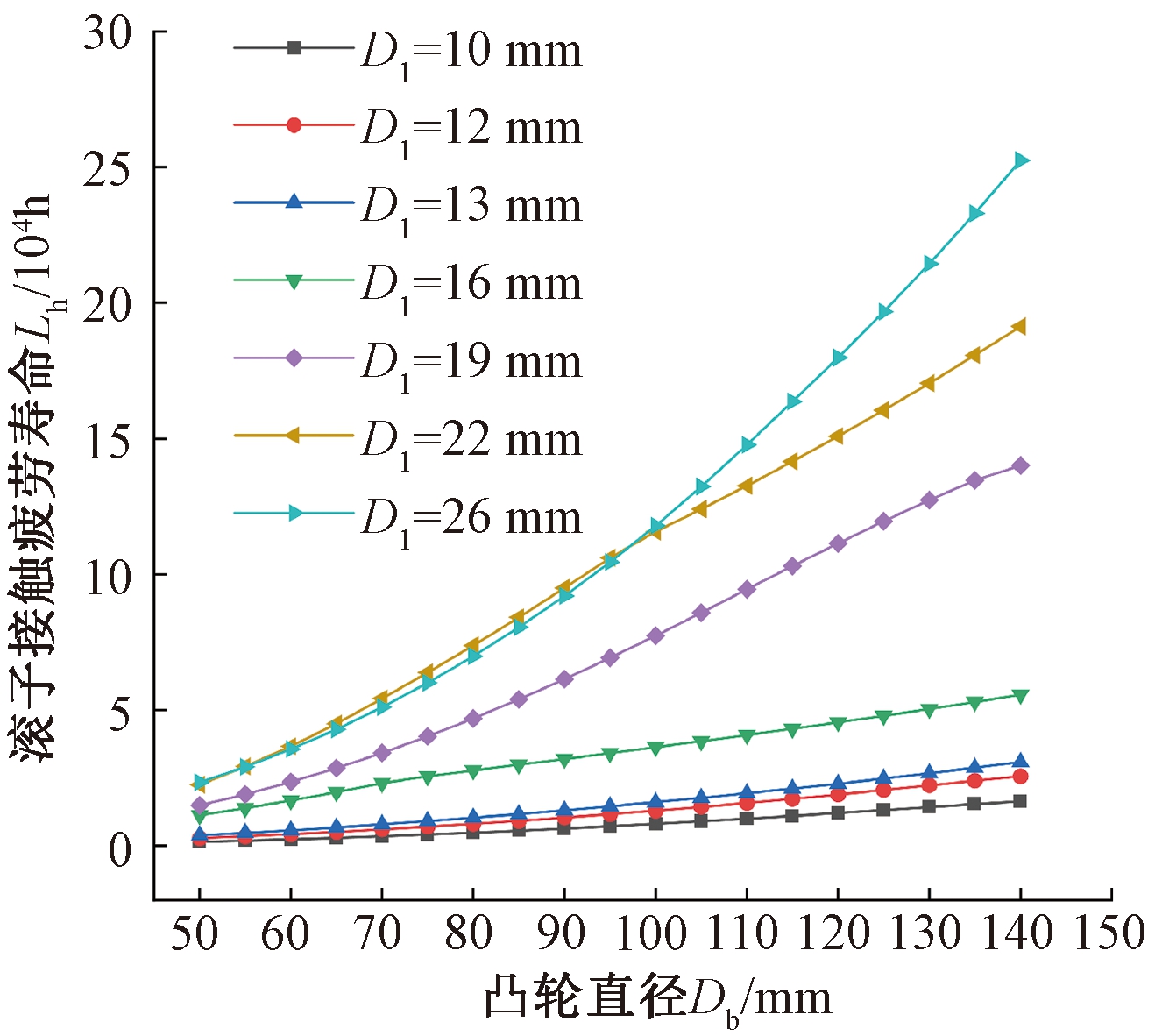
图7 滚子疲劳寿命随圆柱凸轮直径变化曲线
Figure 7 Variation curve of roller fatigue life with diameter of cylindrical cam
图8所示为凸轮滚子与沟槽接触长度对疲劳寿命的影响规律。可以看出,当接触长度增大时,各组滚子的接触疲劳寿命均有所提升。以凸轮滚子直径D1=22 mm组为例,当接触长度为5 mm时凸轮滚子的疲劳寿命为12 919 h,当接触长度增大到15 mm时凸轮滚子的疲劳寿命随之增加到348 804 h。
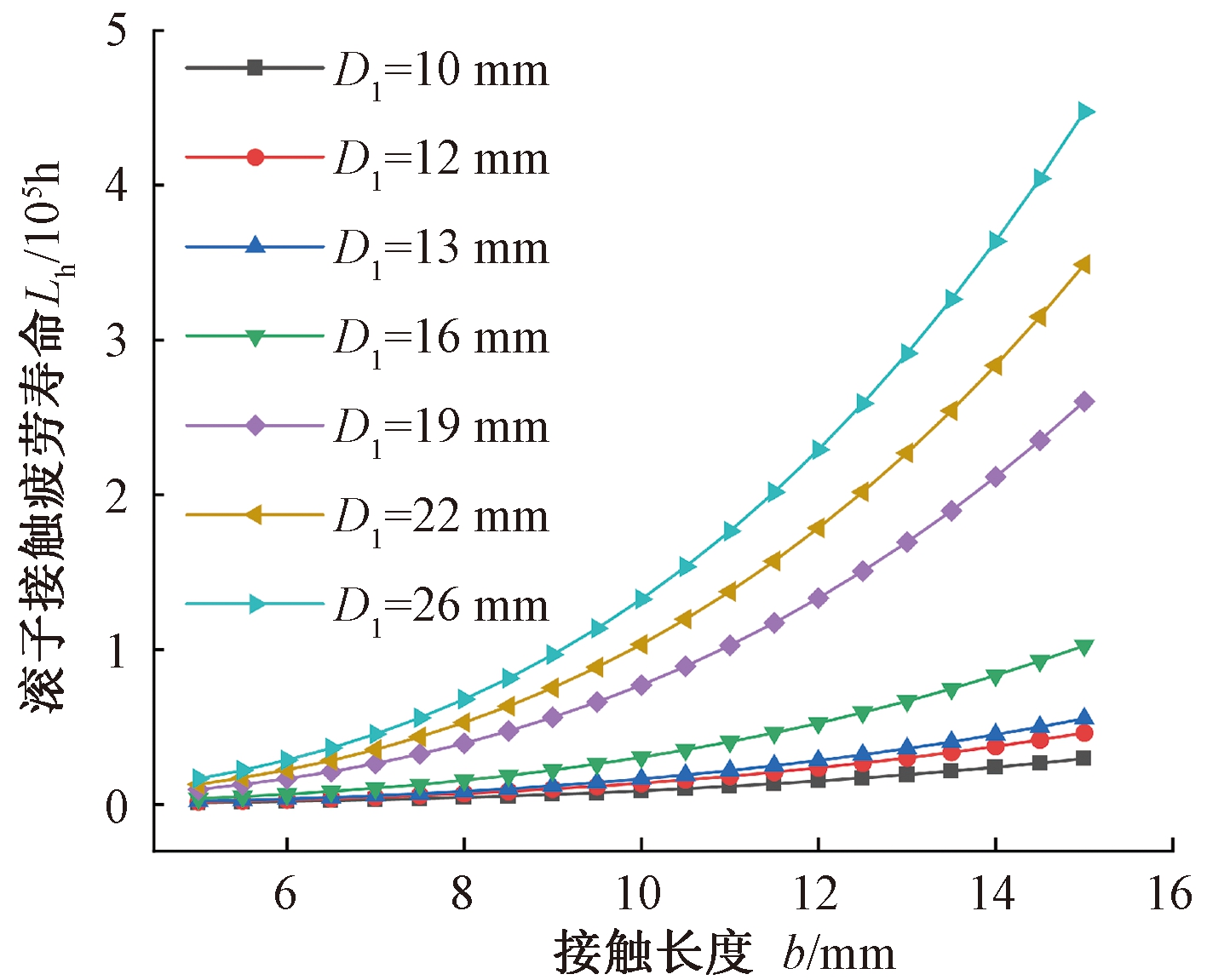
图8 滚子疲劳寿命随接触长度变化曲线
Figure 8 Variation curve of roller fatigue life with contact length
图9所示为凸轮转速对凸轮滚子疲劳寿命的影响。可以看出,凸轮转速增大时,滚子接触疲劳寿命迅速降低。以凸轮滚子直径D1=22 mm组为例,当凸轮转速为600 r·min-1时凸轮滚子的疲劳寿命为178 588 h;当凸轮转速增大到1 300 r·min-1时凸轮滚子的疲劳寿命随之降低到801 h。
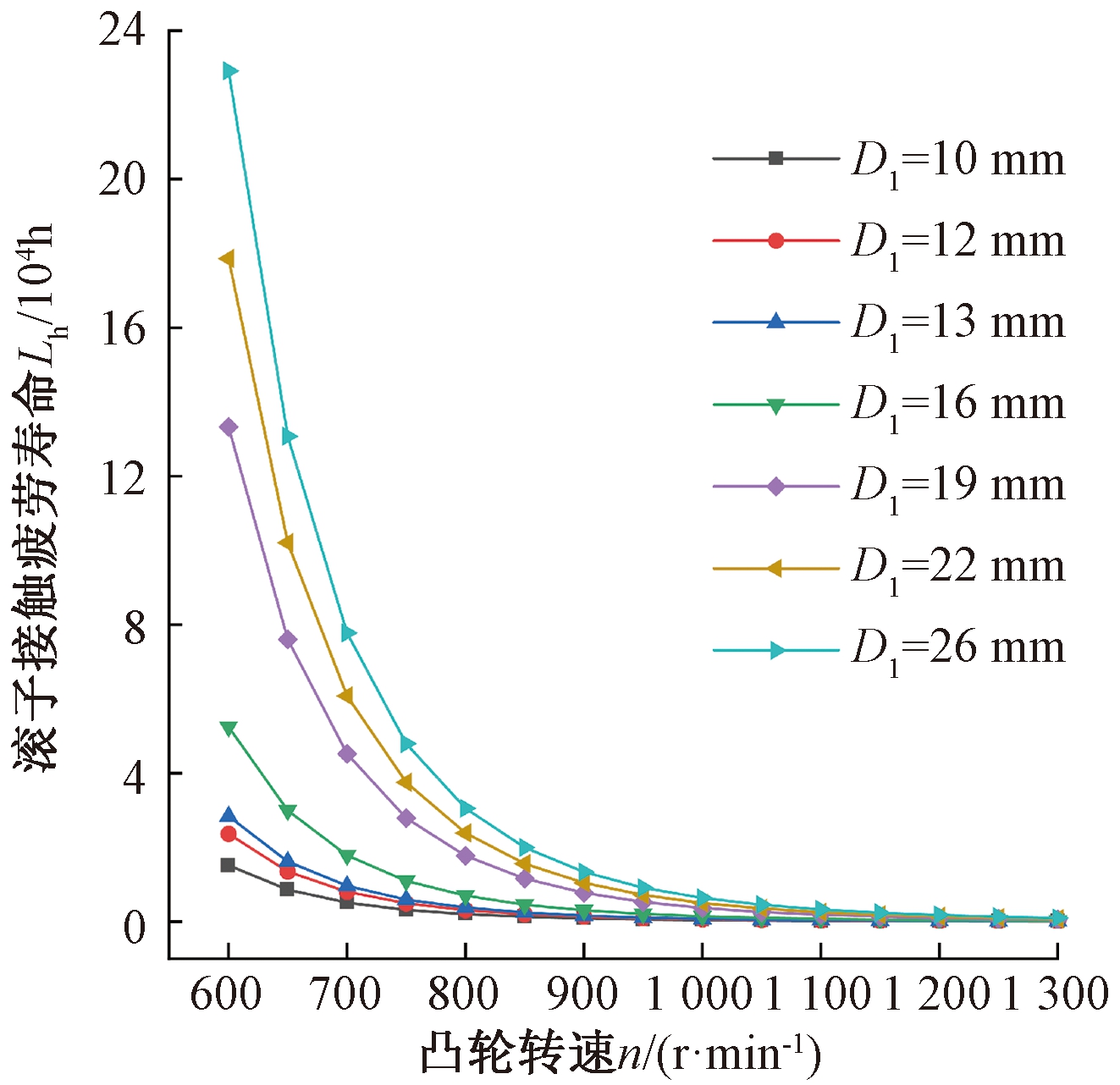
图9 滚子疲劳寿命随凸轮转速变化曲线
Figure 9 Variation curve of roller fatigue life with cam rotation speed
3 结论
(1)以高速插针机为研究对象,在凸轮转动1周过程中,对其插针机构的插针动作进行了力学分析,建立了凸轮滚子-沟槽的力学模型。推导了从动件在正弦加速度运动规律下凸轮运动位移、速度、加速度公式,并计算出从动件的惯性力。实现了凸轮转动1圈过程中,凸轮滚子与沟槽的受力接触点在每一时刻的最大接触应力计算。根据Miner线性疲劳累积损伤理论,将凸轮转动1圈后凸轮滚子圆周方向上各点每次接触产生的疲劳损伤率进行叠加,计算出累积损伤率。比较各点的累积损伤率,找出损伤率最大的点,并将其作为危险点,提出了凸轮滚子寿命预测的定量计算方法。
(2)以某型号高速插针机的插针机构为算例,研究了凸轮滚子-沟槽力学特性,绘制出从动件在凸轮转动1圈过程中的位移、速度、加速度以及惯性力曲线。计算出凸轮转动1圈过程中,凸轮滚子与沟槽的最大接触应力达到最大值时对应的时间、凸轮转角以及最大接触应力。研究了7种典型凸轮滚子直径下,圆柱凸轮直径、凸轮滚子与沟槽的接触长度以及凸轮转速对凸轮滚子疲劳寿命的影响,绘制了相关规律的变化曲线。计算结果表明:控制其他变量一定时,当凸轮滚子直径从10 mm增大到26 mm时凸轮滚子的接触疲劳寿命随之增大了14.1倍;当凸轮直径从50 mm增大到140 mm时疲劳寿命随之增大了7.5倍;当接触长度从5 mm增大到15 mm时疲劳寿命随之增大了26.0倍;当凸轮转速从600 r·min-1增大到1 300 r·min-1时疲劳寿命随之降低为原来的0.449%。
[1] 董九志, 宋宗建, 陈云军, 等. 预制体缝合针稳定性分析及插刺机构改进设计[J]. 纺织学报, 2019, 40(10): 171-176.
DONG J Z, SONG Z J, CHEN Y J, et al. Stability analysis of suture needle of prefabricated parts and improvement of inserting mechanism[J]. Journal of Textile Research, 2019, 40(10): 171-176.
[2] 许勇坚. 浅谈图谱分析法在凸轮插针机的应用[J]. 中国设备工程, 2018(21): 150-151.
XU Y J. Application of atlas analysis method in cam pin inserting machine[J]. China Plant Engineering, 2018(21): 150-151.
[3] 毛璐瑶, 张华伟, 刘辉, 等. 基于虚拟样机的片式凸轮箱性能改善研究[J]. 机械设计与制造, 2020(7): 200-204.
MAO L Y, ZHANG H W, LIU H, et al. Research on performance improvement of chip cam box based on virtual prototyping[J]. Machinery Design &Manufacture, 2020(7): 200-204.
[4] LI J H, LIU Z J, WANG D P, et al. Fault mode analysis and reliability optimization design of a mechanical interface based on cylindrical cam mechanisms[J]. Eksploa-tacja I Niezawodnosc-maintenance and Reliability, 2020, 22(4): 715-723.
[5] SUN Y X, TANG P, ZHENG J, et al. Optimal design of a nonlinear series elastic actuator for the prosthetic knee joint based on the conjugate cylindrical cam[J]. IEEE Access, 2019,7: 140846-140859.
[6] 包钊华, 吴明晖, 周围. 旋转式吹瓶机开合模凸轮槽优化研究[J]. 轻工机械, 2020(4): 64-68.
BAO Z H, WU M H, ZHOU W. Optimization of cam curve groove for opening and closing die of rotary bottle blowing machine[J]. Light Industry Machinery, 2020(4): 64-68.
[7] 尹建军, 陈亚明, 张万庆. 打结器咬绳机构线接触凸轮设计与载荷分析[J]. 农业机械学报, 2016, 47(7): 224-231.
YIN J J, CHEN Y M, ZHANG W Q. Line-contact cam design and load analysis of rope-biting mechanism of knotter[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(7): 224-231.
[8] 崔永杰, 卫咏哲,丁辛亭, 等. 基于圆柱凸轮的株距可调式取苗末端执行器设计与试验[J]. 农业机械学报,2022,53(01),104-114,122.
CUI Y J, WEI Y Z, DING X T, et al. Design and experiment of adjustable spacing end-effector based on cylindrical cam[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022,53(1): 104-114, 122.
[9] 王小增. 偏心圆柱凸轮与轴管液力连接应力和变形分析[J]. 机械设计, 2019, 36(2): 88-95.
WANG X Z. Analysis on hydro-joining stress and deformation of eccentric cylindrical cam and tube[J]. Journal of Machine Design, 2019, 36(2): 88-95.
[10] 陈立伟. 基于圆柱凸轮机构的模块化航天器接口研究[D]. 大连: 大连海事大学, 2017.
CHEN L W. The research on interface of modular spacecraft based on cylindrical cam[D]. Dalian: Dalian Maritime University, 2017.
[11] 薛珊, 徐龙, 赵运来, 等. 基于Adams与RecurDyn的机械结构Hertz接触仿真对比分析[J]. 长春理工大学学报(自然科学版), 2016, 39(4): 73-77, 86.
XUE S, XU L, ZHAO Y L, et al. Comparative analysis of Hertz contact simulation based on Adams and RecurDyn[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2016, 39(4): 73-77, 86.
[12] 张超洋. 冗余结构圆柱凸轮机构的研究[D]. 西安: 陕西科技大学, 2017.
ZHANG C Y. Research on cylindrical cam mechanism with redundant structure[D]. Xi′an: Shaanxi University of Science &Technology, 2017.
[13] 魏俊杰, 朱家诚, 杨徐, 等. 双螺旋线圆柱凸轮机构的设计与分析[J]. 机械设计与制造, 2021(9): 207-210, 215.
WEI J J, ZHU J C, YANG X, et al. Design and analysis of double helix cylindrical cam mechanism[J]. Machi-nery Design &Manufacture, 2021(9): 207-210, 215.
[14] 徐一村, 张磊. 基于ADAMS的平底从动件凸轮轮廓曲线设计[J]. 郑州大学学报(工学版), 2020, 41(3): 42-46.
XU Y C, ZHANG L. Design of cam profile curve of flat bottom follower based on ADAMS[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(3): 42-46.
[15] 孙桓,陈作模,葛文杰. 机械原理[M]. 北京: 高等教育出版社, 2013.
SUN H, CHEN Z M, GE W J. The principle of machines and mechanisms[M]. Beijing: Higher Education Press, 2013.
[16] MINER M A. Cumulative damage in fatigue[J]. Journal of applied mechanics, 1945, 12(3): A159-A164.
[17] 安琦, 顾大强. 机械设计[M]. 北京: 科学出版社, 2016.
AN Q, GU D Q. Mechanical design[M]. Beijing: Science Press, 2016.
[18] 甄妮, 安琦. 考虑滚珠尺寸误差时滚珠螺旋副的受力和寿命分析[J]. 华东理工大学学报(自然科学版), 2017, 43(5): 724-732.
ZHEN N, AN Q. Analysis of stress and fatigue life of ball screw with considering dimension errors of balls[J]. Journal of East China University of Science and Technology (Natural Science Edition), 2017, 43(5): 724-732.