盲源分离是在未知源信号的先验信息及信道参数的情况下,仅利用传感器接收到的观测信号对源信号进行恢复的过程[1-3]。由Hyvärinen等[4-5]提出的快速独立成分分析(fast independent component analysis, FastICA)是目前最常用的盲源分离算法。FastICA的使用前提是观测信号个数不小于源信号个数,并且需要已知源信号个数。而在实际工程应用中,由于受到设备器材、配置成本等条件的限制,仅能接收到单通道信号。只有一个观测信号时无法直接使用FastICA进行盲源分离,处理此问题常用的方法是首先将单通道信号升维,构建虚拟多通道信号,再通过FastICA对虚拟多通道信号进行源信号的恢复。
由于使用FastICA对源信号进行恢复必须正确给出源信号个数,在源信号个数未知时算法失效,因此如何有效估计盲源信号个数是盲源分离的关键点,也是盲源分离效果好坏的关键前提。目前比较常用的源数估计算法包括两种:一种为基于矩阵分析的源数估计算法,如主成分分析(principle component analysis, PCA)[6]、奇异值分解(singular value decomposition, SVD)[7]等;另一种为基于信息论的源数估计算法,如Akaike[8]提出的赤池信息准则(Akaike information criterion, AIC)、Rissanen[9]提出的最小描述长度准则(minimum description length, MDL)等。虽然这些算法在实际应用中被广泛使用,但AIC算法得到的估计结果不具有一致性,MDL算法在低信噪比条件下误差率较高[10]。由于在实际应用中,采集到的信号通常会受到多种噪音和干扰的影响,因此提出一种有较强抗噪性的源数估计算法具有重要意义。
为此,本文提出了一种新的基于信息熵指标的源数估计算法,无须知道源信号的先验信息,直接通过计算分离得到的估计源信号的信息熵来度量源信号的信息量大小,从而确定源信号的个数。本文使用总体经验模态分解(ensemble empirical mode decomposition, EEMD)[11]对单通道观测数据进行升维处理,再使用FastICA算法分解得到估计源信号。计算估计源信号的信息熵,从而确定源信号个数。
1 基于信息熵的源数估计
1.1 信息熵基本理论
1948年Shannon[12]在信息科学领域提出信息熵(entropy)的概念,来描述信源的不确定性。不确定性越大,系统包含的混合信息源的信息量越大。
随机变量的连续熵定义如式(1)所示:
(1)
式中:f(x)为随机变量X的概率密度。
随机变量X和Y的联合熵定义如式(2)所示:
(2)
式中:f(x,y)为随机变量X和Y的联合概率密度。
引理1 若变量X和Y是相互独立的,则联合熵等于独立熵之和[13]:
H(X,Y)=H(X)+H(Y)。
(3)
推论1 联合熵不小于其中任意变量的熵:
H(X,Y)≥max(H(X),H(Y))。
(4)
本文使用信息熵来估计源数,理论分析如下。
假设源信号个数为n,第i个源信号的概率密度函数为fi(x),根据式(1)得到第i个源信号的信息熵为
(5)
由于源信号之间彼此独立,根据引理1得到n个源信号的平均信息熵如式(6)所示:
(6)
根据推论1得
(7)
由FastICA分解得到的各源信号是相互独立的,独立信号混合到一起,其联合熵比较大。在引理1和推论1的基础上如果能分解出相对纯净的独立信号,则平均信息熵会降低。因此迭代地增加盲源估计个数,随着个数的增加,分离的信号会越来越纯净,进而信号平均信息熵越来越低,当过分解时(估计源数大于真实源数),分离结果会出现杂乱的噪声信号,熵值又会呈现增加的趋势。故当源数估计正确时,分离源信号不含有其他源的信息,估计源信号的平均信息熵会达到最小,由此得到最小熵值对应的个数即为最佳源数,如式(8)所示:
(8)
基于以上分析,本文提出基于平均信息熵最小的盲源个数估计算法。
1.2 基于GMM的源信号概率密度拟合
为了计算源信号的信息熵,需要已知信号的概率密度函数。由于信号的概率密度未知且较为复杂,无法得到其精确的表达式,根据统计理论,任何一个随机变量的分布都可以用高斯混合模型(Gaussian mixed model, GMM)去逼近[14]。因此本文使用GMM来拟合估计源信号的概率密度函数。
GMM数学解析式如式(9)所示:
(9)
式中:K为GMM模型中子模型的个数;αk为变量x属于第k个子模型的概率,
为第k个子模型的参数;φ(x|θk)为第k个子模型的概率密度函数,如式(10)所示:
(10)
式中各参数通常使用期望最大化算法(expectation maximum, EM)[15]迭代计算得到。
通过GMM得到源信号的概率密度,则信息熵进一步可以写成数学期望如式(11)所示:
=E(-ln f(x|θ))。
(11)
1.3 基于MCMC的信号熵值计算
在1.2节中,通过GMM可以得到源信号的概率密度。由于所求信息熵的积分函数是一个复杂的混合模型,无法求得式(8)的精确值。为了解决复杂积分求解问题,本文使用马尔可夫链蒙特卡罗(Markov chain Monte Carlo, MCMC)算法[16]近似计算其期望。MCMC的理论基础为大数定律:当样本容量足够多时,样本均值以概率1收敛于数学期望。本文应用此定律来近似计算期望。根据MCMC算法,首先生成1组服从目标分布的随机样本,然后通过计算其样本均值代入式(11)进行估算。
对于用于计算积分的随机样本,本文使用Metropolis-Hastings(M-H)算法进行采样[17-18],得到服从目标分布的样本点。
M-H采样算法步骤如下。
输入:抽样的目标分布的密度函数f(x|θ)、建议分布函数q(x,y);
输出:f(x|θ)的随机样本{xm+1,xm+2,…,xn};
参数:收敛步数m、迭代步数n。
① 随机初始化x0;
② For i=1,2,…,n;
从建议分布q(x,xi-1)随机生成样本xi
计算接受概率:
从均匀分布U(0,1)中生成样本u
if α(xi,xi-1)≤u
return (xi-1)
else
return (xi)
得到样本{xm+1,xm+2,…,xn}。为了保证样本的收敛性,删去前m个样本,得到目标分布的样本{xm+1,xm+2,…,xn}。
③ end
基于M-H采样算法得到服从目标分布f(x|θ)的随机样本{xm+1,xm+2,…,xn},将这些样本用来计算函数-ln f(x|θ)的均值,如式(12)所示:
(12)
1.4 基于信源信息熵最小的单通道盲源数估计算法
输入:单通道观测信号数据x、分解的源信号的最大维数m、GMM模型高斯分布的个数K、M-H采样的样本个数l;
输出:源信号个数
① 使用EEMD将单通道观测信号x分解重构成虚拟多通道信号X;
② For n=2,3,…,m;
使用FastICA对X进行分解,得到n维估计源信号
For p=1,2,…,n
用GMM拟合源信号Yn的概率密度函数:
使用M-H采样得到目标分布
的样本:
使用采样得到的样本计算平均信息熵:
end
end
③ 选择
中数值最小的元素所对应的n的取值,即为最佳源数:
2 仿真实验
参考文献[19]中的仿真数据实验,通过R软件生成正弦信号s1(t)、余弦信号s2(t)、幅值调制信号s3(t)这3个源信号,信号的表达式如下式所示:
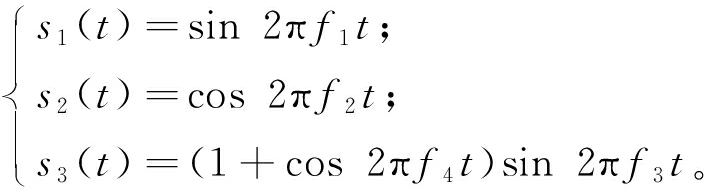
(13)
式中各信号的参数如下:f1=50 Hz、 f2=25 Hz、 f3=100 Hz、 f4=15 Hz,采样时间为0.5 s,采样频率为1 024 Hz,各源信号时域曲线如图1所示。
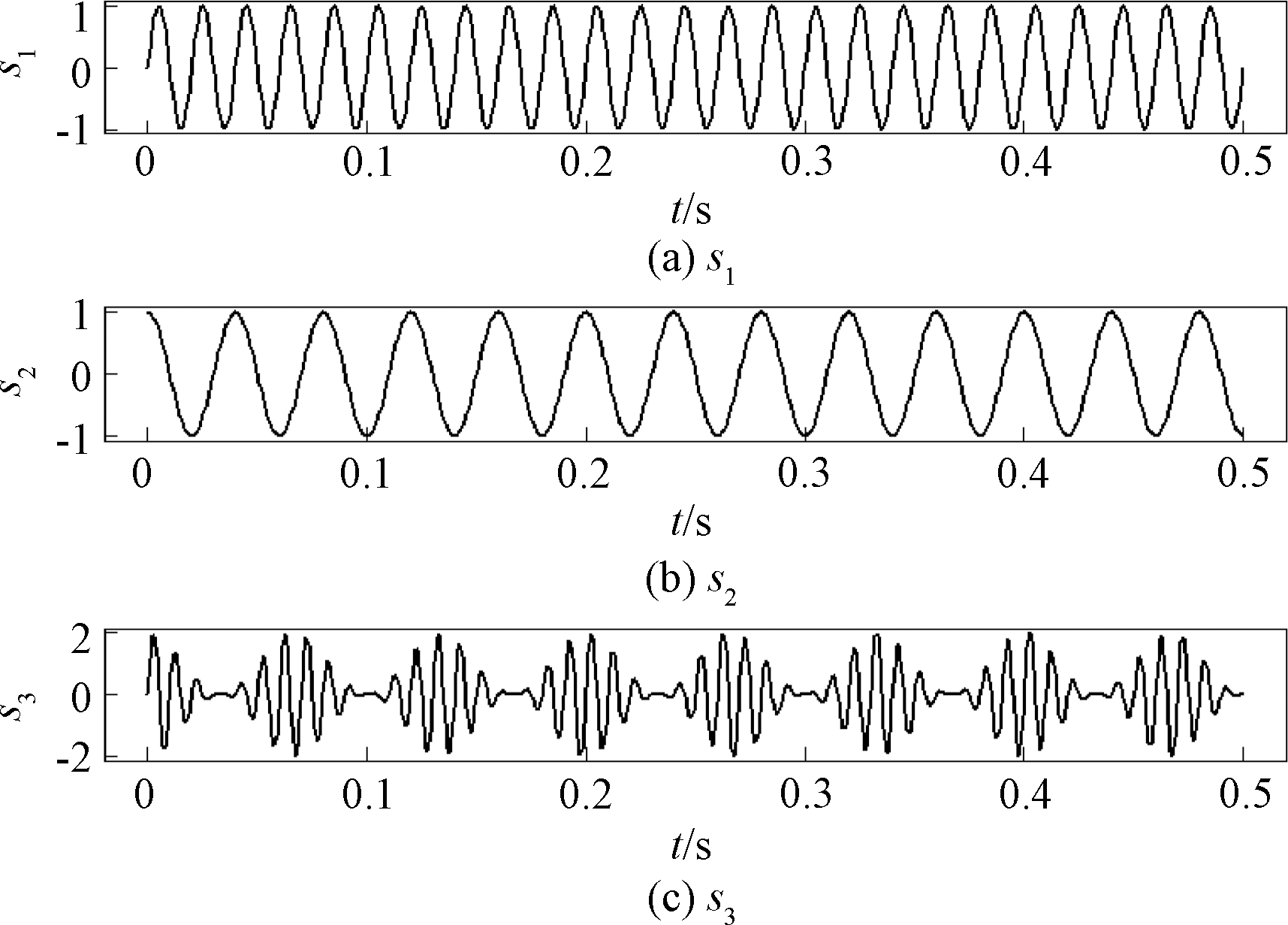
图1 仿真源信号时域曲线
Figure 1 Time-domain curves of simulated source signals
将源信号[s1,s2,s3]乘以一个1×3的服从均匀分布U(0,1)的随机矩阵,并添加高斯白噪声,混合成一个单通道信号x(t),时域曲线如图2所示。
图2 仿真观测信号时域曲线
Figure 2 Time-domain curve of simulated observed signal
将单通道观测信号x(t)使用EEMD分解成具有多个不同瞬时频率的IMF分量,并根据式(14)的Pearson相关系数公式,计算得到IMF分量和x(t)的相关系数,根据式(14)计算的相关系数如表1 所示。
表1 IMF分量与观测信号的相关系数
Table 1 Correlation coefficient between separated signals and observed signals
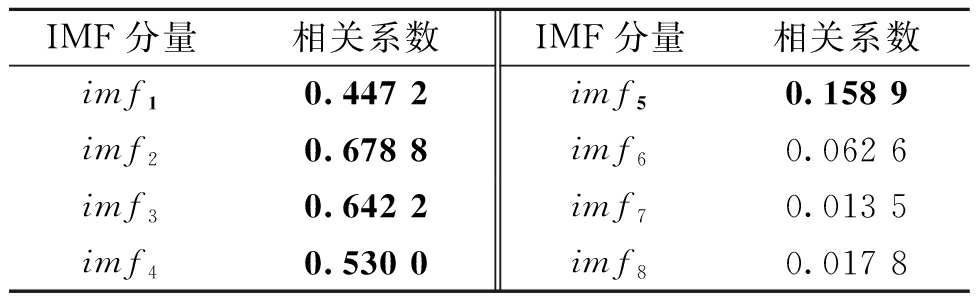
IMF分量相关系数IMF分量相关系数imf10.447 2imf50.158 9imf20.678 8imf60.062 6imf30.642 2imf70.013 5imf40.530 0imf80.017 8
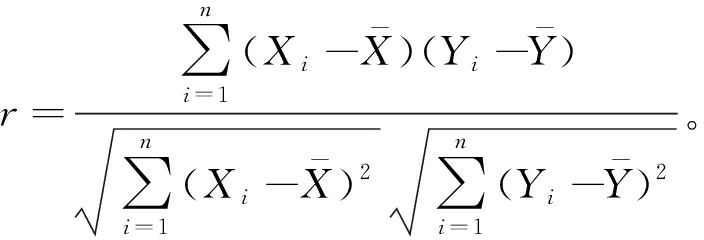
(14)
由式(15)计算IMF分量的相关系数累计贡献率R,选择累计贡献率超过阈值η(本文选择阈值为η=90%)的各分量和x(t)组成新的观测信号X(t)。
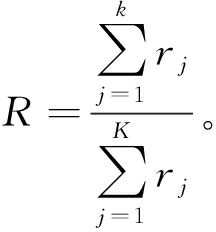
(15)
式中:ri为按降序排列的第i个相关系数;K为分量总个数。根据累计贡献率,最终选择了5个IMF分量和x(t)重构成新的观测信号X(t)=[x(t),imf2,imf3,imf4,imf1,imf5]T。
由于FastICA要求源信号个数不大于观测信号个数,因此选择源数从2到6。为了降低随机误差的影响,共进行仿真实验50次,分别计算出这50次实验中不同可能源数下的估计源信号的平均信息熵值,结果如图3所示。
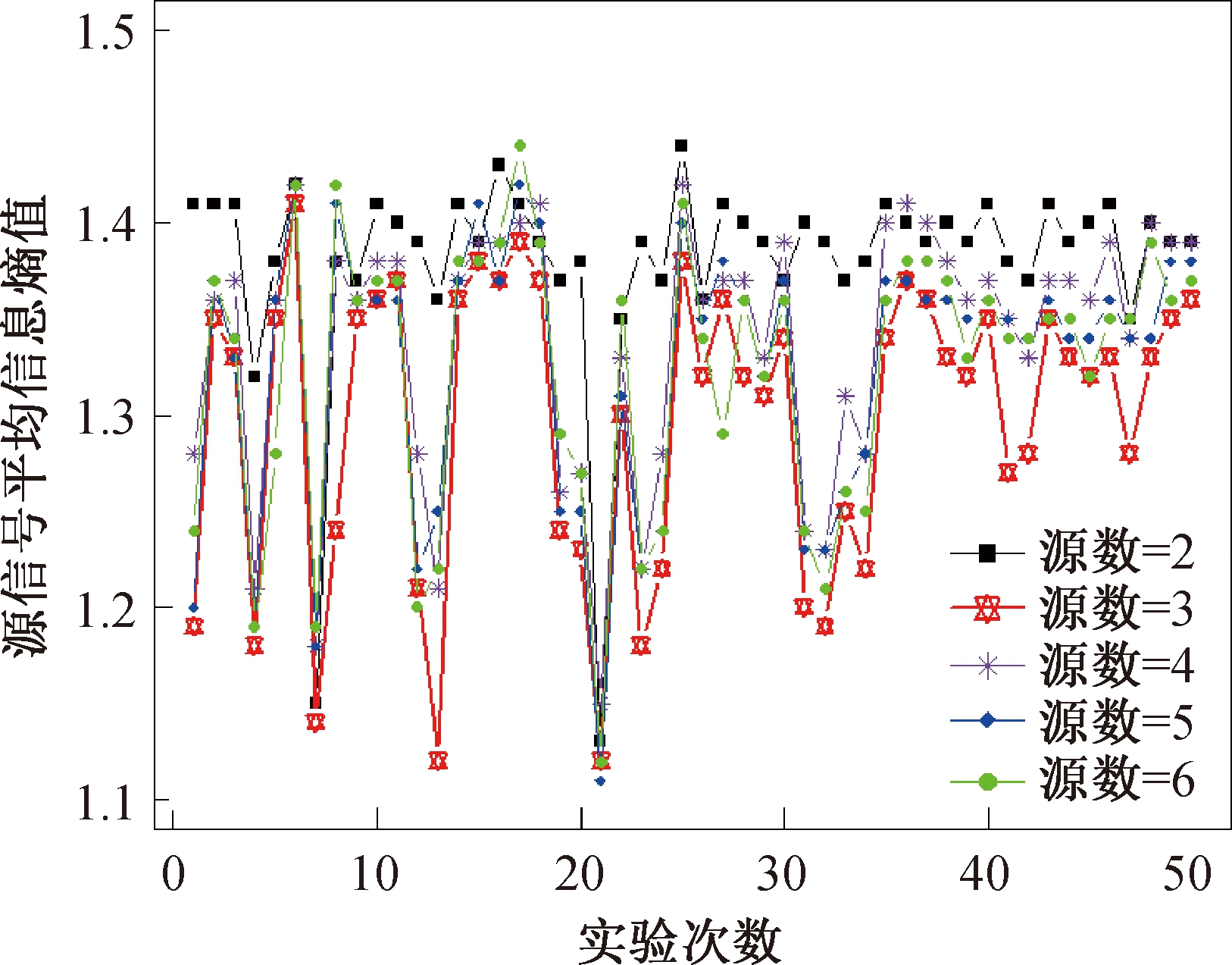
图3 50次实验下不同源数的源信号平均信息熵值
Figure 3 Average information entropy of the source signals with different source numbers in 50 experiments
图3中当源信号个数为3时,计算得到的估计源信号信息熵值最小,因此认为源信号的最佳个数为3。结果表明,本文提出的基于信息熵的源数估计算法估计得到的最佳源数和设定的仿真源信号个数相等。在50次实验中成功次数为46,得到本文源数估计算法的估计准确率为92%。
根据以上实验结果选择源信号个数为3,并使用FastICA算法对盲源信号进行恢复,得到估计源信号如图4所示。
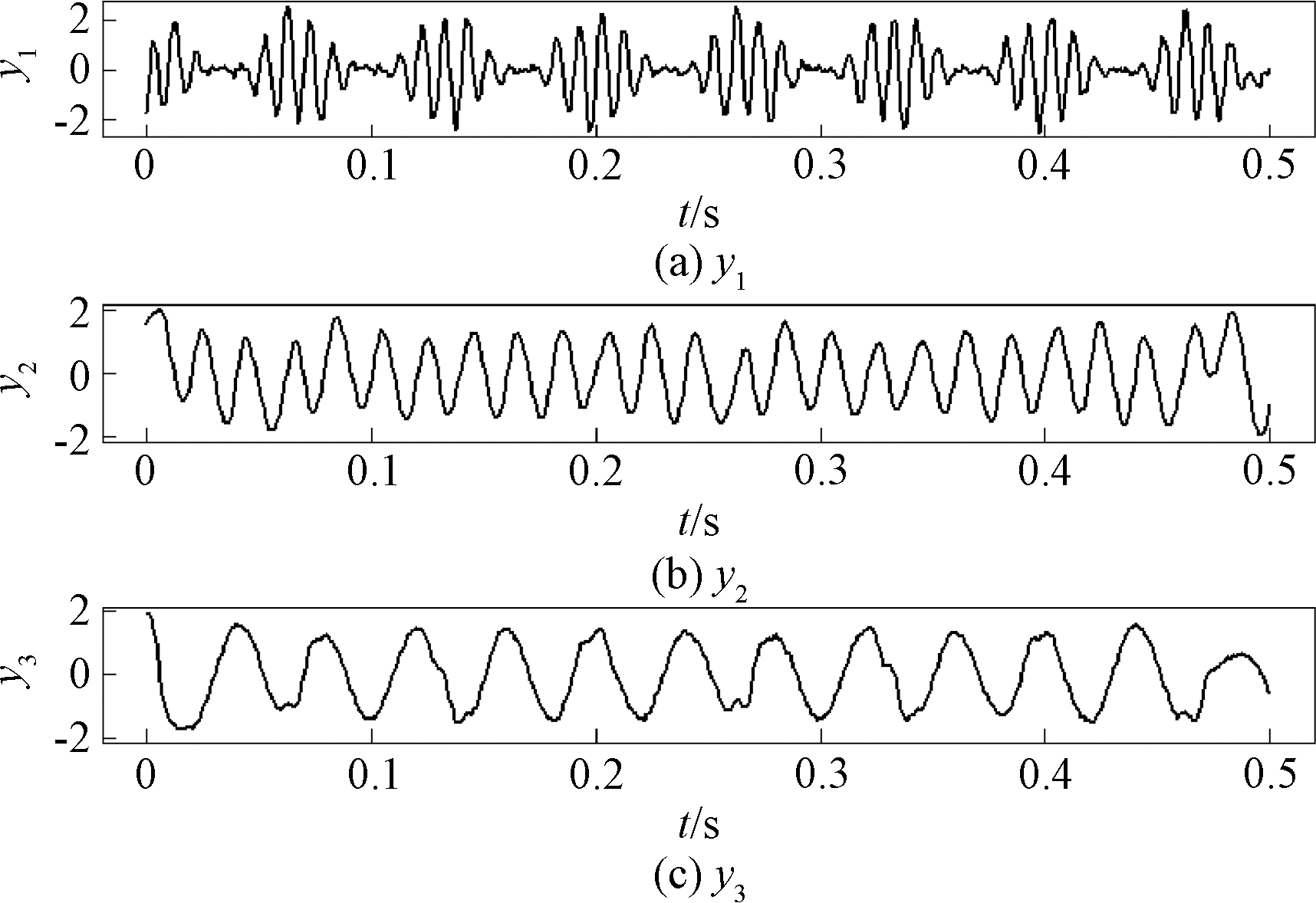
图4 仿真信号的估计信号时域曲线
Figure 4 Estimated signals′ time-domain curves of simulated signals
为考察本文算法对源信号的估计效果,根据式(14)计算估计信号与源信号之间的Pearson相关系数,结果如表2所示。
表2 估计信号和源信号相关系数
Table 2 Correlation coefficient between estimated signals and source signals
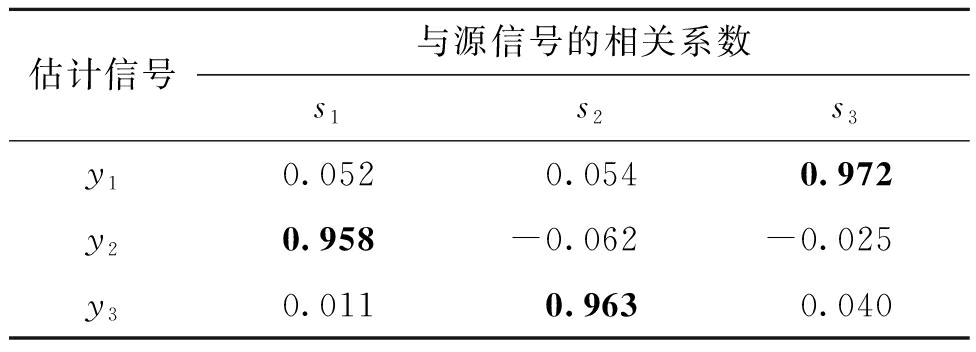
估计信号与源信号的相关系数s1s2s3y10.0520.0540.972y20.958-0.062-0.025y30.0110.9630.040
由图4和表2结果可知,分离得到的估计源信号和仿真源信号的波形非常接近,且估计源信号和仿真源信号之间的相关系数绝对值均大于0.9。结果表明,本文提出的基于信息熵最小的源数估计算法估计能够精确地估计出盲源个数,为EEMD和FastICA算法能够有效分离混合信号得到目标信号奠定了基础。
为了进一步验证算法的可靠性,将仿真实验设置为3个源、4个源、5个源和6个源混合的4种情况,并使用上述算法对分离结果的源信号平均信息熵值进行计算,结果如图5所示。
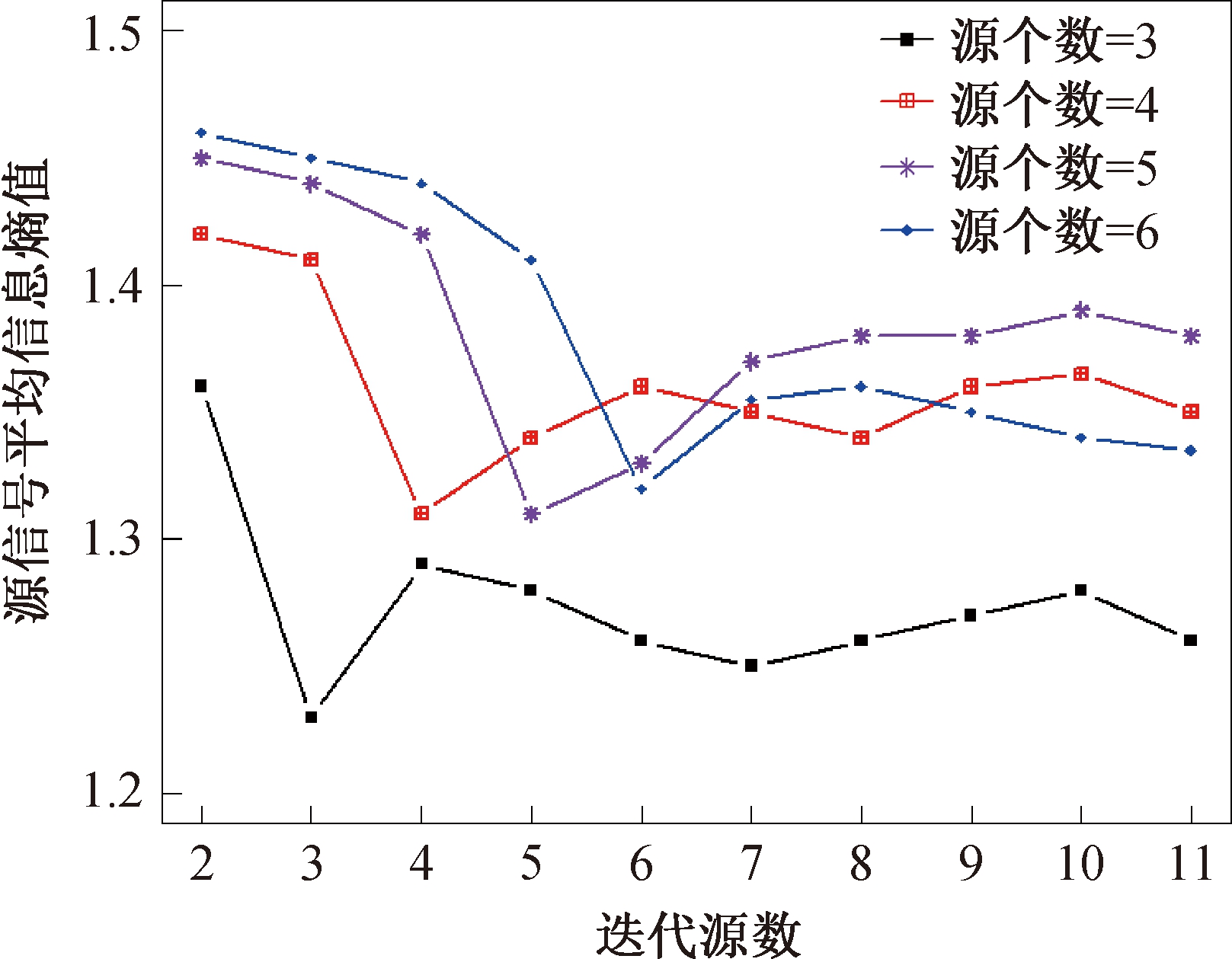
图5 4种情况下源信号的平均信息熵值
Figure 5 Average information entropy of the source signals in 4 cases
图5结果表明,当迭代源数等于真实源数时,估计源信号的平均信息熵会达到最小,进一步说明了本文提出的基于信息熵最小的源数估计算法的有效性。
实验结果证明,当估计源数小于真正源数时,随着迭代源数增加,源信号的平均信息熵值减小;而当迭代源数大于真正源数时,源信号的平均信息熵值又在增大;只有当平均信息熵达到最小时,对应迭代源数则为正确源数。
3 与传统源数估计算法的对比实验
为验证本文算法的鲁棒性和高估计准确率,将本文算法与传统源数估计算法PCA和AIC进行对比。由于噪声能量会影响算法的性能,故在仿真实验中,通过考察不同估计算法随信噪比(SNR)的变化来分析其估计准确性能。为便于分析,实验以算法的估计准确率为性能的评价指标,以估计正确频率表示各算法的估计准确率A如式(16)所示:
(16)
式中:n为估计正确次数;N为模拟总次数。
数据采用第2节的仿真信号,设置SNR为-10～10 dB,步长为1 dB,进行1 000次模拟实验,计算不同信噪比下各算法的估计准确率,得到实验结果如图6所示。
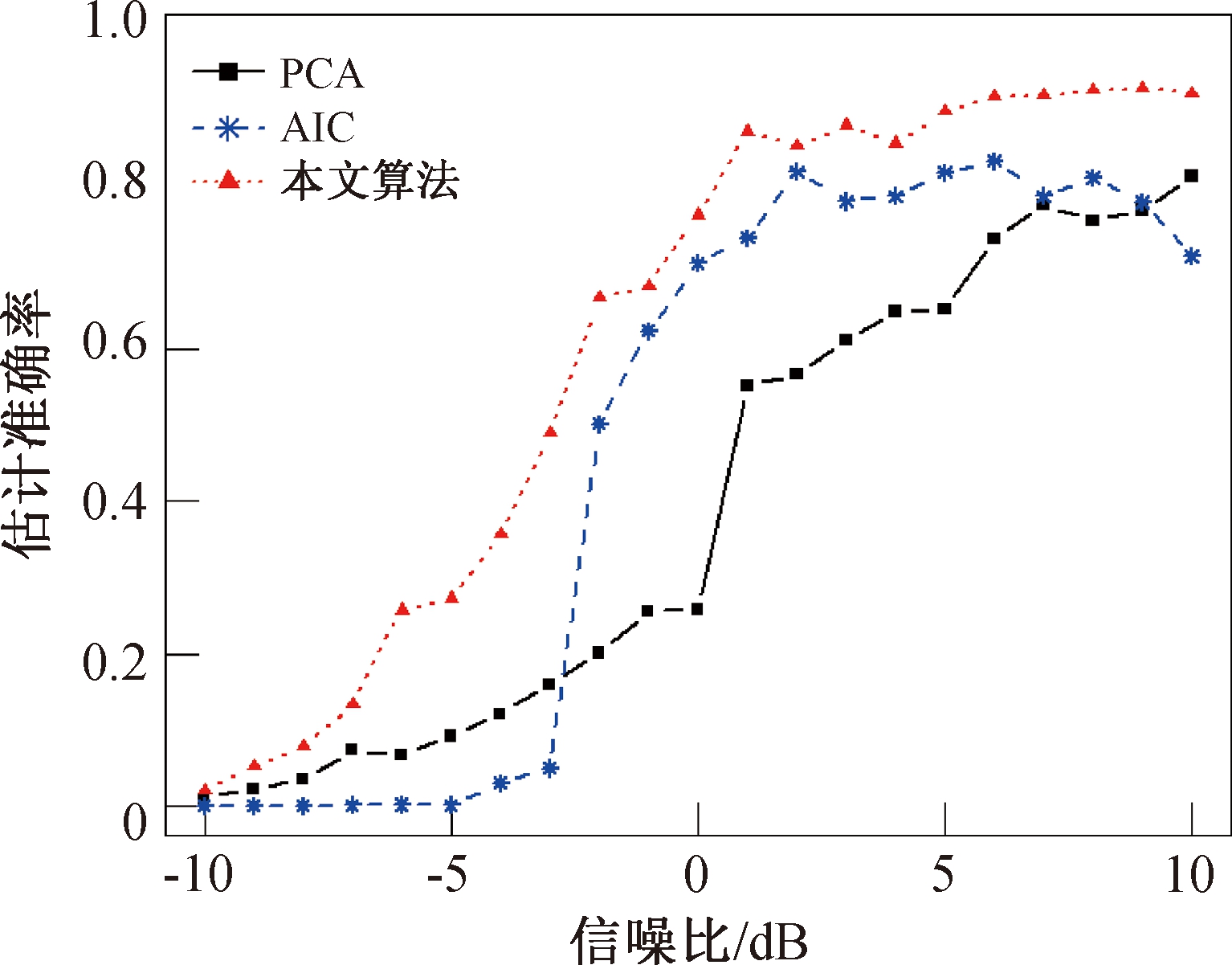
图6 3种算法的估计准确率随信噪比变化的情况
Figure 6 Variation of 3 algorithms′ accuracy with different SNR
由图6知,在高斯噪声环境中,当SNR在-10～-7 dB之间时,本文算法和PCA算法的估计准确率均高于AIC算法,且本文算法比另外两种算法的准确率都要高;当SNR大于-7 dB时,本文算法和AIC算法的估计准确率均高于PCA;但当SNR逐渐增大时,AIC算法的估计准确率会呈现下降趋势,估计结果不具有一致性。本文算法整体表现性能均高于另外两种算法,且最终估计准确率稳定在94%左右,因此本文算法更具有鲁棒性,且估计准确率更高。
4 算法在TETRA通信信号中的验证
通信信号在日常传输过程中,经常会受到不同类型干扰信号的干扰[20]。为了保证通信正常,需要对混有干扰的数据进行目标信号提取,从而达到将目标信号与干扰分开的目的。使用TETRA手持电台发射信号进行实时采集,并对其进行频谱搬移变为基带信号。信号参数为TETRA通信信号采样率为9.21 MHz,中心频率为0 Hz,信号带宽为25 kHz,幅值为1 V,采样时长为9 999/9 210 s。叠加两类通信干扰信号:单音干扰和宽带线性扫频干扰信号。干扰信号参数为单音干扰信号中心频率为1 kHz、幅值为1 V;宽带线性扫频干扰信号的起始频率为5 Hz,截止频率为100 Hz,扫频斜率为95 Hz/s,信号幅度为1 V。
首先基于本文提出的源数估计算法估计出源信号个数,然后结合EEMD和FastICA将源信号分离出来。混有干扰的TETRA信号如图7所示。
图7 混有干扰信号的TETRA观测信号时域曲线
Figure 7 Time-domain curve of TETRA observation signal with interference signals
将观测信号进行EEMD分解,计算IMF分量和TETRA信号的Pearson相关系数如表3所示。
表3 IMF分量与观测信号的相关系数
Table 3 Correlation coefficients between IMF components and observed signal
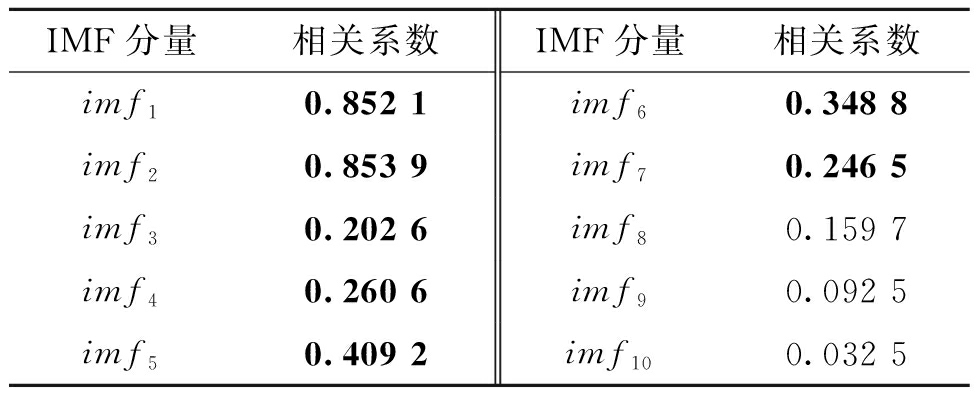
IMF分量相关系数IMF分量相关系数imf10.852 1imf60.348 8imf20.853 9imf70.246 5imf30.202 6imf80.159 7imf40.260 6imf90.092 5imf50.409 2imf100.032 5
计算IMF分量的相关系数累计贡献率,得到imf1～imf7分量的累计贡献率超过90%,故选择这7个IMF分量和x(t)组成新的观测信号,即X(t)=[x(t),imf2,imf1,imf5,imf6,imf4,imf7,imf3]T,使用FastICA对X(t)进行盲源分离,通过本文算法计算得到的源信号平均信息熵值如表4所示。
表4 估计源信号平均信息熵值
Table 4 Average information entropy of the estimated source signals
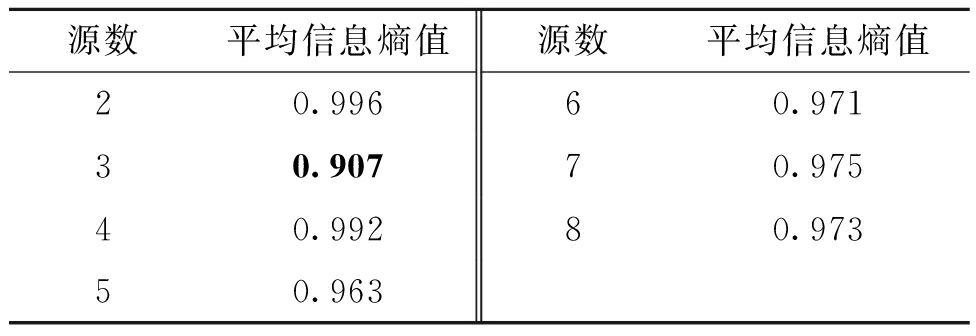
源数平均信息熵值源数平均信息熵值20.99660.97130.90770.97540.99280.97350.963
根据表4结果,当源信号个数为3时,估计源信号平均信息熵值最小,因此得到源信号的最佳个数为3。确定源信号个数后,再使用FastICA算法,得到TETRA信号盲分离结果如图8所示。
图8 TETRA信号盲分离结果
Figure 8 BSS result of TETRA signal
计算分离得到的估计信号与源信号之间的Pearson相关系数,如表5所示。
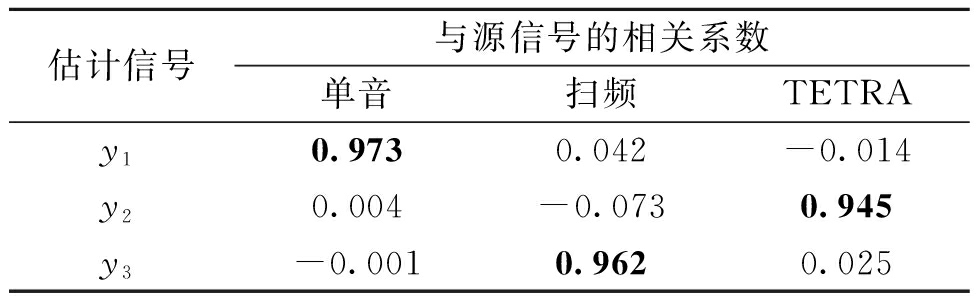
表5 估计信号和源信号相关系数
Table 5 Correlation coefficient between estimated signals and source signals
估计信号与源信号的相关系数单音扫频TETRAy10.9730.042-0.014y20.004-0.0730.945y3-0.0010.9620.025
根据表5结果可知,估计信号y1对应了单音干扰信号,y2对应了TETRA通信信号,y3对应了扫频干扰信号,相关系数均达到0.9以上。结果验证了本文提出的基于信源信息熵最小的单通道盲源数估计算法的有效性,能准确获取盲源信号个数。
5 结论
本文通过对估计源信号的分布信息进行估计,提出了一种将信息熵作为评价指标的盲源信号源数估计算法。该算法运用递归的方式检验不同可能盲源数下通过FastICA分离得到的信号的信息量,通过分析和比较信息熵,筛选出最佳的盲源数作为真实盲源数的估计值。文中的算法充分利用了源信号的信息特征,进而给出了源信号个数估计的算法。基于仿真数据和真实数据的数字实验结果也验证了本文算法的有效性和较强的抗噪性,为源数未知条件下的盲源分离提供了有效技术支持。
[1] 付卫红, 周新彪, 农斌. 单通道盲源分离的研究现状与展望[J]. 北京邮电大学学报, 2017, 40(5): 1-11.
FU W H, ZHOU X B, NONG B. The research of SCBSS technology: survey and prospect[J]. Journal of Beijing University of Posts and Telecommunications, 2017, 40(5): 1-11.
[2] AKHAVAN S, SOLTANIAN-ZADEH H. Blind separation of sparse sources from nonlinear mixtures[J]. Digital Signal Processing, 2021, 118: 103220.
[3] OURDOU A, GHAZDALI A, LAGHRIB A, et al. Blind separation of instantaneous mixtures of independent/dependent sources[J]. Circuits, Systems, and Signal Processing, 2021, 40(9): 4428-4451.
[4] HYV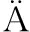
RINEN A, OJA E. A fast fixed-point algorithm for independent component analysis[J]. Neural Computation, 1997, 9(7): 1483-1492.
[5] HYV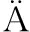RINEN A, OJA E. Independent component analysis: algorithms and applications[J]. Neural Networks, 2000, 13(4/5): 411-430.
[6] 陈韬伟, 金炜东. 基于主成分分析的雷达辐射源信号数量估计[J]. 西南交通大学学报, 2009, 44(4): 501-506.
CHEN T W, JIN W D. Radar emitter number estimation based on principal component analysis[J]. Journal of Southwest Jiaotong University, 2009, 44(4): 501-506.
[7] GAO L Y, LIU M Z, YUE J Y, et al. Source number estimation based on improved singular value decomposition at low SNR[C]∥2019 IEEE 9th International Conference on Electronics Information and Emergency Communication. Piscataway: IEEE, 2019:1-4.
[8] AKAIKE H. A new look at the statistical model identification[J]. IEEE Transactions on Automatic Control, 1974, 19(6): 716-723.
[9] RISSANEN J. Modeling by shortest data description[J]. Automatica, 1978, 14(5): 465-471.
[10] JIANG B, LU A N, XU J. An improved signal number estimation method based on information theoretic criteria in array processing[C]∥2019 IEEE 11th International Conference on Communication Software and Networks (ICCSN). Piscataway: IEEE, 2019: 193-197.
[11] ZHANG G D, ZHOU H M, WANG C J, et al. Forecasting time series albedo using NARnet based on EEMD decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(5): 3544-3557.
[12] SHANNON C E. A mathematical theory of communication[J]. Bell System Technical Journal, 1948, 27(3): 379-423.
[13] GOUR G, TOMAMICHEL M. Entropy and relative entropy from information-theoretic principles[J]. IEEE Transactions on Information Theory, 2021, 67(10): 6313-6327.
[14] SABETSARVESTANI Z, RENNA F, KIRALY F, et al. Source separation with side information based on Gaussian mixture models with application in art investigation[J]. IEEE Transactions on Signal Processing, 2020, 68: 558-572.
[15] YU L, YANG T Y, CHAN A B. Density-preserving hierarchical EM algorithm: simplifying Gaussian mixture models for approximate inference[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(6): 1323-1337.
[16] OSMUNDSEN K K, KLEPPE T S, OGLEND A. MCMC for Markov-switching models—Gibbs sampling vs. marginalized likelihood[J]. Communications in Statistics: Simulation and Computation, 2021, 50(3): 669-690.
[17] HASTINGS W K. Monte Carlo sampling methods using Markov chains and their applications[J]. Biometrika, 1970, 57(1): 97-109.
[18] 张双圣, 强静, 刘汉湖, 等. 基于拉丁超立方抽样的改进型多链DRAM算法求解地下水污染反问题[J]. 郑州大学学报(工学版), 2020, 41(3): 72-78.
ZHANG S S, QIANG J, LIU H H, et al. Improved multi-chain DRAM algorithm based on Latin hypercube sampling for inverse problems of underground water pollution[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(3): 72-78.
[19] 纪林章, 庄海滔, 程道来, 等. 基于EEMD和FastICA的单通道背景声舱音盲源分离[J]. 应用技术学报, 2021, 21(1): 62-67, 74.
JI L Z, ZHUANG H T, CHENG D L, et al. Blind source separation of single-channel background sound cockpit voice based on EEMD and FastICA[J]. Journal of Technology, 2021, 21(1): 62-67, 74.
[20] 谭志良, 毕军建, 徐立新, 等. 一种多干扰条件下非连续通信信号自适应消噪方法: CN104394109B[P]. 2015-08-26.
TAN Z L, BI J J, XU L X, et al. Adaptive denoising method of non-continuous communication signal under multi-interference condition: CN104394109B[P]. 2015-08-26.