作为一种能量转换装置,固体氧化物燃料电池(SOFC)可以直接将化学能转化为电能[1],转换过程不受限于卡诺循环,具有高效环保和燃料灵活性强等优点,受到了广泛的关注[2]。根据其结构的不同,SOFC可以分为平板式、管式和瓦楞式。其中,瓦楞式SOFC采取了波纹状的PEN(阳极-电解质-阴极)设计,增大了电化学反应面积、提高了输出性能,具有很好的应用前景。
瓦楞式SOFC作为一种较为新颖的结构,由于其较高的输出性能引起了广泛关注。Hwang等[3]对瓦楞式SOFC的气体质量分数分布等进行了研究,结果表明,电极和连接体接触区域气体扩散较为困难。Stygar等[4]比较了瓦楞式SOFC在不同流动方式下的温度分布,结果表明,逆流流动时温度分布更加均匀。瓦楞式SOFC和平板式SOFC运行上存在一定差异,许多学者对两者的性能进行了对比分析。Yang等[5]的研究表明,沿流动方向,平板式SOFC温度梯度要高于瓦楞式SOFC。Ramírez-Minguela等[6]对平板式和瓦楞式SOFC进行了对比,结果表明,两者的物质摩尔分数分布和电流密度分布趋势均相似,但瓦楞式SOFC具有更低的平均温度。以上研究表明,瓦楞式SOFC相较于平板式SOFC性能更佳,具有较好的应用前景。而前人对于瓦楞式SOFC结构优化研究较少。Ramírez-minguela等[7]详细讨论了电解质厚度对瓦楞式SOFC性能的影响,发现其对热力学不可逆的预测有着强烈的影响。靳遵龙等[8]研究了流道夹角对瓦楞式SOFC性能的影响,发现流道夹角为135°时性能最佳。Huang等[9]研究了结构参数对平板式和瓦楞式两种构型SOFC性能的影响,发现结构参数对两种SOFC都有较大的影响,但该研究仅对电化学性能进行了研究,缺乏对温度分布的分析。
结构参数对瓦楞式SOFC的物质传输、电化学反应以及热量传递等运行性能均有着较大影响。肋覆盖下的区域由于扩散受到限制导致较低的物质摩尔分数分布和电流密度分布,对其研究很有必要;同时,较薄的阴极会导致较大的浓差极化,选取一个合适的阴极厚度对于提升瓦楞式SOFC性能至关重要。为了解决上述问题,本文对瓦楞式SOFC的肋宽和阴极厚度进行了优化设计。利用COMSOL软件建立了三维瓦楞式SOFC模型,耦合了流体流动、传热传质和电化学反应,并对其进行了计算。通过定量分析气体的摩尔分数分布、浓差极化、性能曲线和温度分布来更好地研究肋宽和阴极厚度对瓦楞式SOFC性能的影响。
1 模型与方法
1.1 模型描述
考虑到瓦楞式SOFC结构的高度对称性,为了节约计算时间,选取电池堆栈的一个重复单元作为计算区域。如图1所示,该模型由阳极、阴极、电解质、两个连接体以及两个梯形流道组成。电池的阳极材料为 Ni-YSZ,阴极材料为 LSM-YSZ,电解质材料为YSZ。电池的长度为80 mm,宽度为4 mm,阳极电极、电解质、阴极电极的厚度分别为0.50、0.05、0.25 mm。
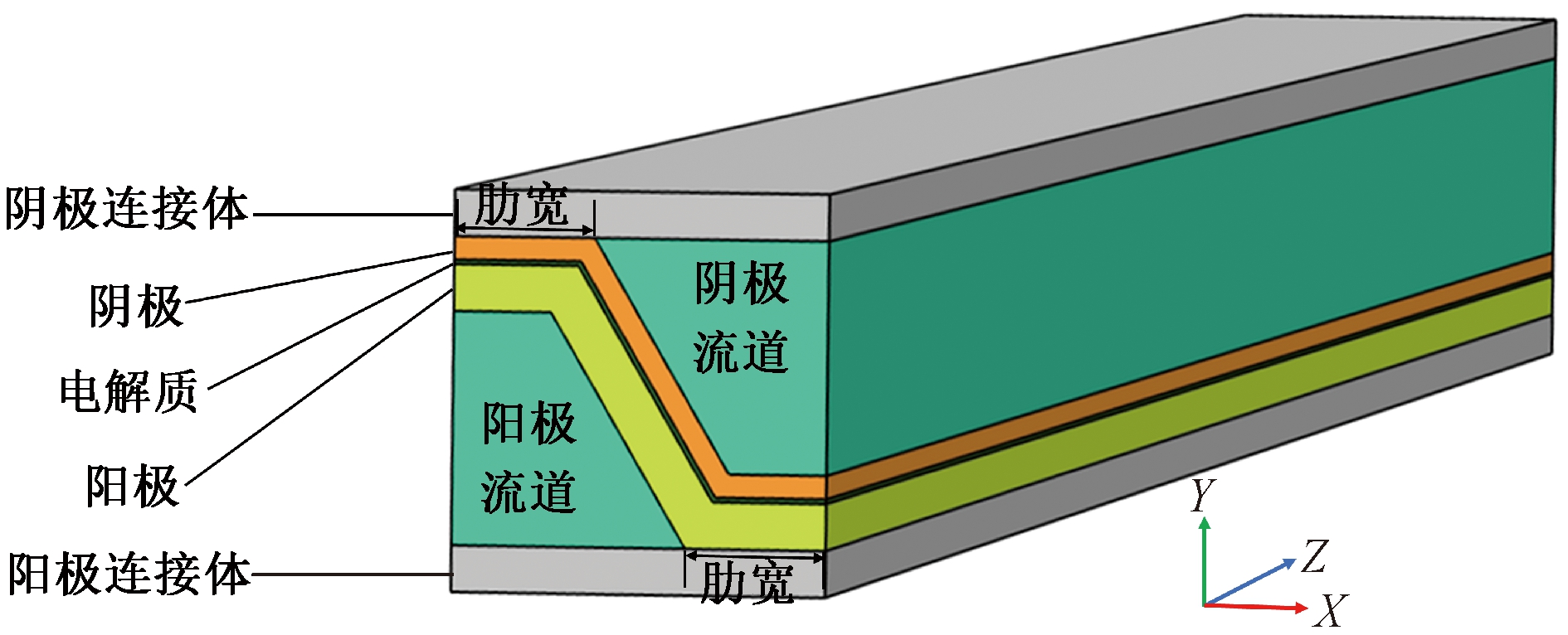
图1 瓦楞式SOFC结构示意图
Figure 1 Schematic diagram of the MOLB-type SOFC
本文考虑了8个模型来研究结构参数对瓦楞式SOFC性能的影响,如表1所示。这些模型的差异是肋宽和阴极厚度不同,而其他参数均相同。
表1 各个模型的结构参数
Table 1 Structural parameters of each model mm
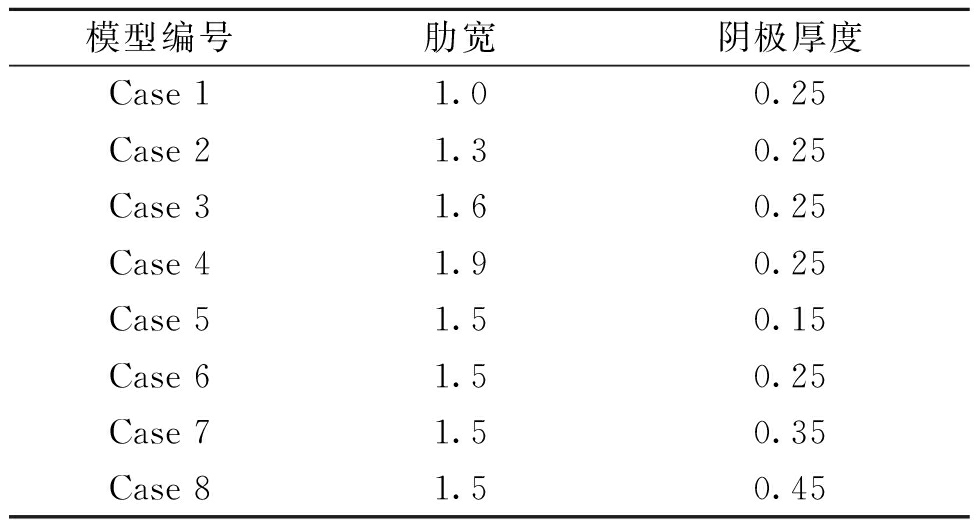
模型编号肋宽阴极厚度Case 11.00.25Case 21.30.25Case 31.60.25Case 41.90.25Case 51.50.15Case 61.50.25Case 71.50.35Case 81.50.45
1.2 模型假设
为了简化SOFC模型,使用了以下假设:SOFC稳态运行;流体为层流流动;流体为不可压缩理想气体;多孔电极均匀且各向同性。
1.3 控制方程
该模型耦合了流体流动、传热传质、电化学反应,采用以下守恒方程来描述这些传递现象。
1.3.1 质量守恒方程
流体流动区域包括气体通道和多孔电极。质量守恒方程可以描述为
(1)
式中:ρ为混合气体的密度,kg·m-3;u为流体的流速,m·s-1。
1.3.2 动量守恒方程
考虑摩擦项,流体在多孔介质中流动的动量输运可以用Brinkman方程来描述:
(2)
式中:ε和κ分别为多孔介质的孔隙率和渗透率;p为压力,Pa;μ为混合气体的动力黏度,N·s·m-2。
1.3.3 物质守恒方程
考虑电极的多孔结构属性,扩散可以使用修正后的菲克定律来表示,各物质的组分守恒方程为
(3)
式中:ωi为物质i的质量分数;
为组分源项;Ji为扩散通量,计算式如下。
(4)
(5)
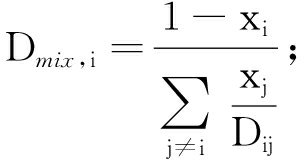
(6)
(7)
(8)
式中:Di,eff为修正后的扩散系数;τ为曲折因子;Dmix,i和Kn,i分别为混合气体的平均扩散系数和努森扩散系数;xi和Mi分别为组分i的摩尔分数和摩尔质量;rpore为多孔介质孔的半径;Dij为二元扩散系数;Vi为物质i的扩散体积。
1.3.4 能量守恒方程
SOFC在运行时会产生并传递大量的热量,其温度也会发生显著变化,因此考虑能量的传输很有必要。能量守恒方程可以表示为
(9)
式中:cp为流体的比热容,J/(kg·K);λeff为电极的有效导热系数,W/(m·K);Qh为热源项,计算式如下:
Qh=Qohm,elec+Qohm,ion+Qact+Qchem。
(10)
式中:Qohm和Qact分别为欧姆极化和活化极化产生的不可逆热;Qchem为电化学熵变引起的可逆热。
1.3.5 电荷守恒方程
电荷转移包括电极中的电子转移和电解质中的离子转移。根据欧姆定律,电荷守恒方程表示为
(11)
(12)
式中:ielec和iion分别为电子电流密度和离子电流密度;
为电极的有效电子电导率;
为电解质的有效离子电导率,其大小取决于电解质的材料和微结构;φelec和φion分别为电子电势和离子电势。
电池存在极化损耗,电压的计算表达式为
Vcell=EOCV-(ηact+ηohm+ηconc)。
(13)
式中:ηact、ηohm和ηconc分别为活化极化、欧姆极化和浓差极化,V;EOCV为开路电压,V。
在电化学反应中,ia和ic为电化学反应时的电流密度,可以由Butler-Volmer方程[10]表示:
(14)
式中:α为电化学反应速率;i0为交换电流密度,可以定义为
(15)
式中:ke为指数前因子;ne为转移电子数;Eact为活化能,J·mol-1。
材料的物性参数如表2所示。
表2 材料的物性参数[11-12]
Table 2 Physical parameters of materials[11-12]
部位孔隙率曲折度渗透率转移系数活化能/(J·mol-1)热导率/(W·m-1·K-1)比热容/(J·kg-1·K-1)阳极0.431.7×10-100.51.0×1056.23650阴极0.431.7×10-100.51.2×1059.60900
注:电解质的热导率为2.70 W·m-1·K-1,比热容为300 J·kg-1·K-1。
1.4 边界条件
对于燃料和空气流道,进气方式设定为顺流进气,燃料和空气的入口流速分别为0.5和3 m·s-1,阳极入口燃料组分(摩尔分数,下同)为90%的氢气和10%的水蒸气,阴极入口组分为21%的氧气和79%的氮气。燃料和空气入口温度均设定为1 073 K,通道出口处的压力设定为环境大气压。电池的顶面和底面为周期性边界条件,而电池左右两侧采用对称边界条件,电池的入口和出口与环境对流换热,进行能量的传递。将电池的顶面和底面分别设为电势和电接地。
2 模型验证
网格无关性结果如图2(a)所示,当网格数为55 200时,与网格数为27 600和110 400时相比,模拟结果中电流密度的最大误差分别为2.54%和1.12%。为了保证计算的准确性并节省计算时间,选取55 200为本研究的网格数量。此外,为了验证模型的有效性,采用与Huang等[9]给出的实验中相同的操作条件及参数进行模拟。设置实验条件:温度为1 073 K,阴极通入空气,阳极通入加湿氢气,入口氢气和水蒸气的浓度分别为9.08和2.27 mol·L-1。从图2(b)可以看出,数值结果与实验结果吻合较好,其误差在4.78%以内,验证了本次模拟结果的准确性。
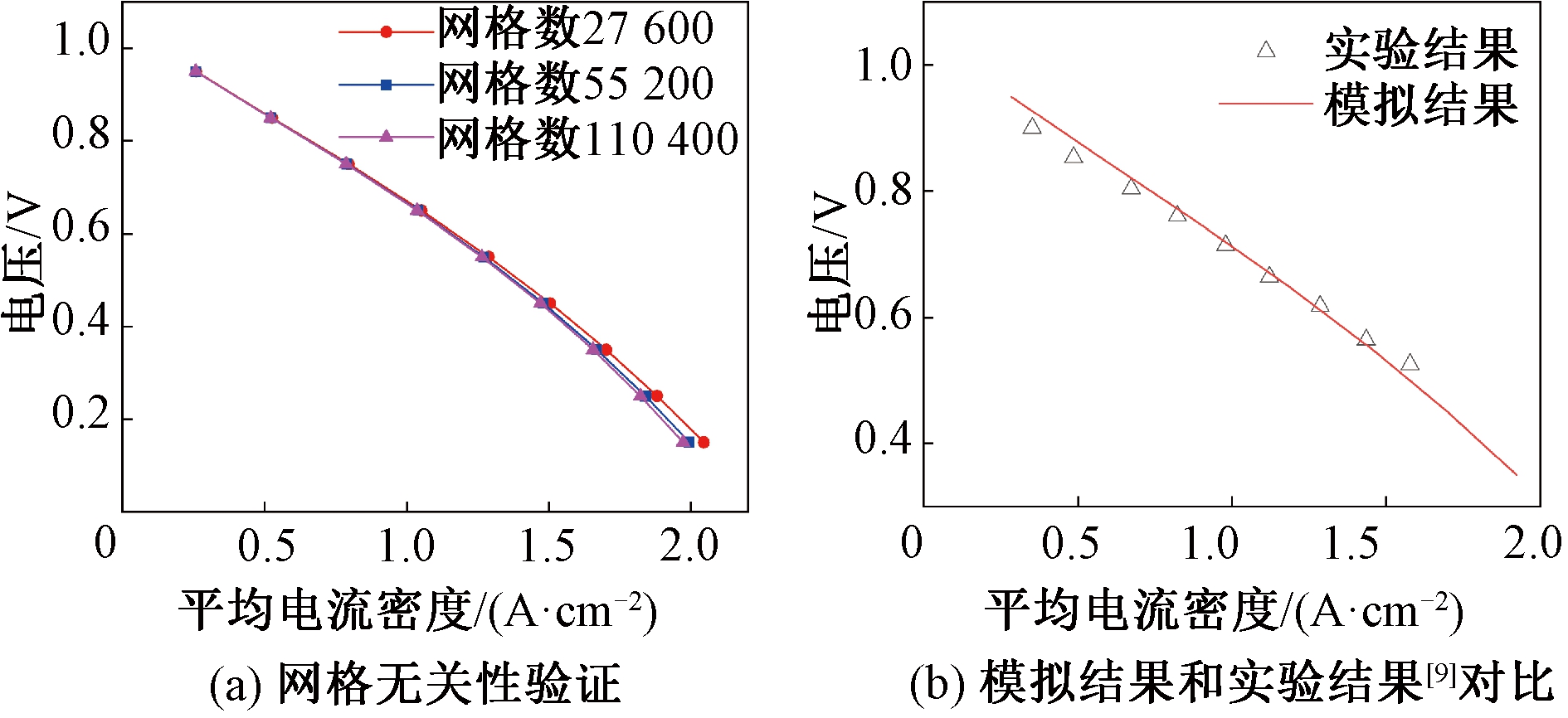
图2 模型验证
Figure 2 Model validation
3 结果与讨论
3.1 肋宽对瓦楞式SOFC性能的影响
图3显示了在0.65 V的工作电压下,不同肋宽下电池Z=0.04 m截面处的氢气摩尔分数分布图。对比Case 1、Case 2、Case 3、Case 4可以发现,Case 1的氢气整体含量最高,且均匀性最为理想,Case 4最差。这表明随着肋宽的增加,电池内氢气的摩尔分数分布梯度逐渐增大,氢气的扩散效果越来越差。这是因为肋下氢气主要沿电极的宽度方向扩散,肋宽的增大导致气体传输路径变长、扩散阻力增加,不利于氢气的质量传输。因此,适当降低肋宽有利于改善电池内氢气分布的均匀性。
图3 不同肋宽下电池Z=0.04 m截面的氢气摩尔分数分布图
Figure 3 Hydrogen molar fraction distribution in the cross section of Z=0.04 m at different rib widths
图4显示了不同肋宽下阳极/电解质交界面浓差极化平均值。可以看出,低电压下的浓差极化要显著高于高电压下的浓差极化。此外,随着肋宽的增加,阳极/电解质交界面的浓差极化逐渐增大。在0.65 V电压下,Case 4与Case 1相比,阳极/电解质交界面浓差极化平均值提高了6.74%,这是因为随着肋宽的增加,氧气的传递受到抑制,低氧区域增加,导致浓差极化逐渐增大。
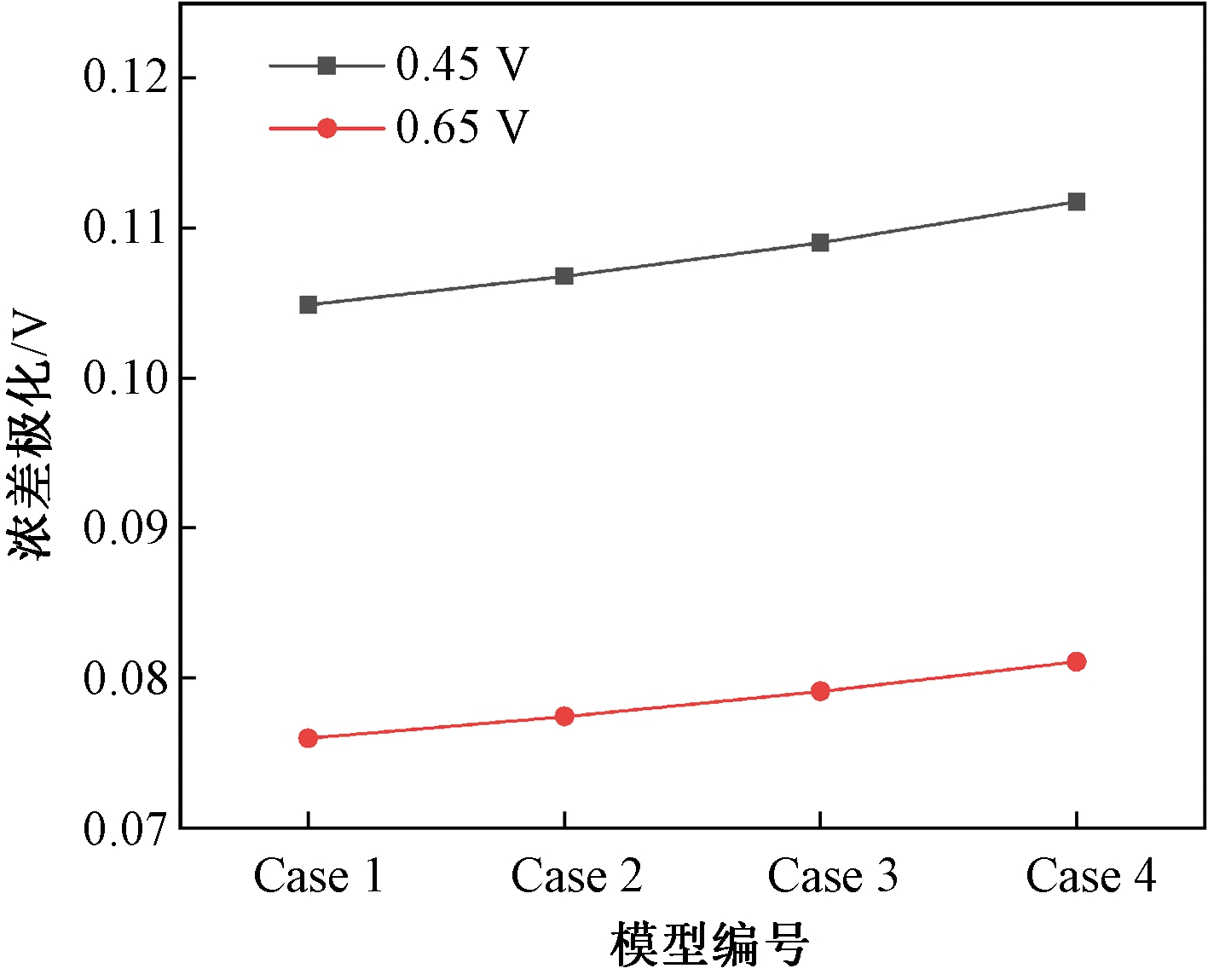
图4 阳极/电解质交界面的浓差极化平均值
Figure 4 Average value of concentration polarization at the anode/electrolyte interface
图5显示了不同肋宽下电池的性能曲线。可以看出,随着电流密度的增大,极化曲线呈逐渐下降的趋势,平均功率密度则随着电流密度的增加先增大后减小。此外,随着SOFC肋宽的减小,电池的电流密度和平均功率密度均逐渐增大。这是因为较小的肋宽会使燃料和空气更容易扩散到肋覆盖下的三相线区域,显著地降低了电池的浓差极化。因此,随着肋宽的减小,电池的总损耗减小,使SOFC的电化学输出性能提高。
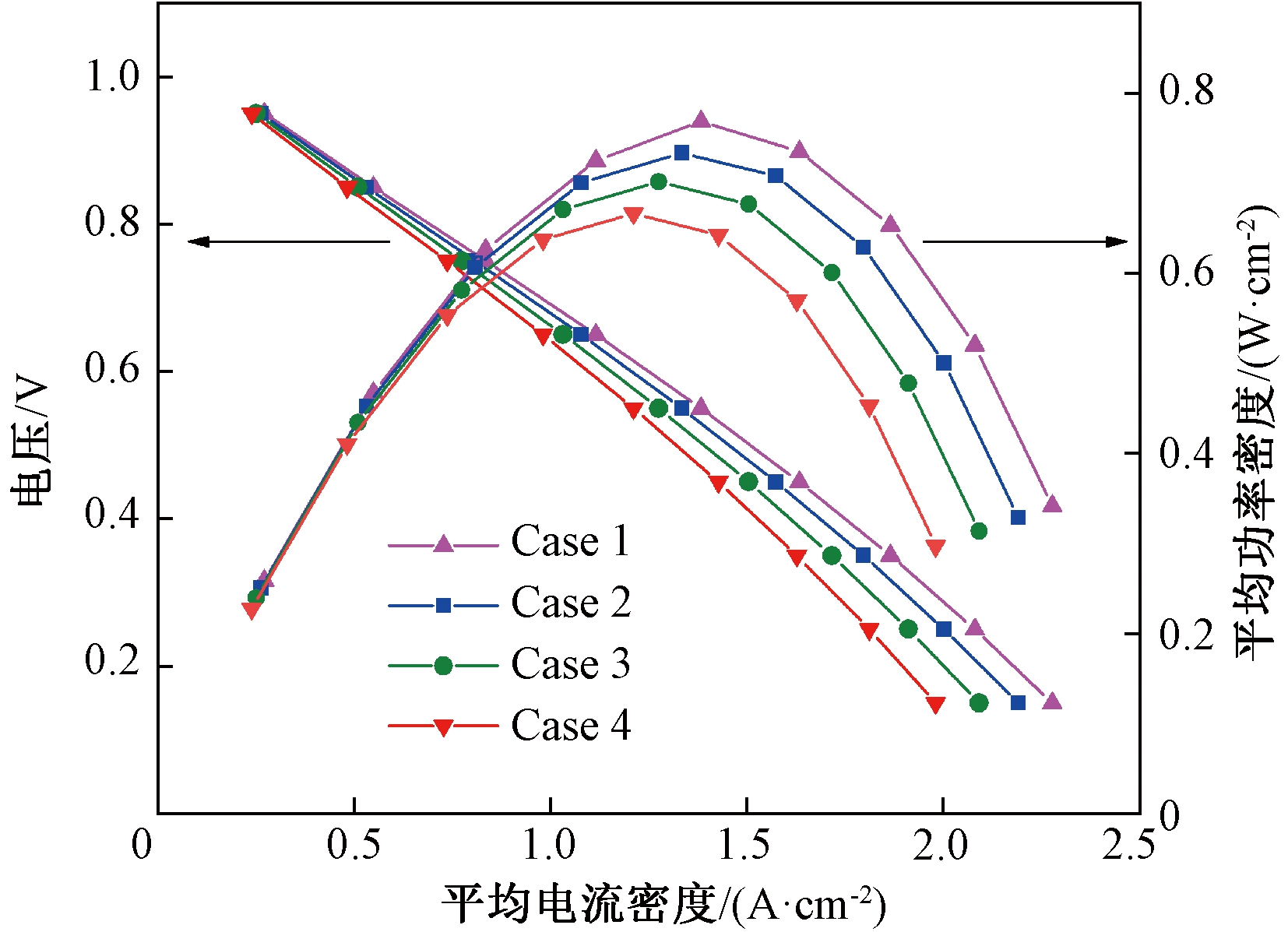
图5 不同肋宽下的性能曲线
Figure 5 Performance curves at different rib widths
3.2 阴极厚度对瓦楞式SOFC性能的影响
图6显示了电池阴极/电解质交界面的氧气的摩尔分数分布,横坐标L为沿阴极与电解质交界面长度。可以看出,氧气摩尔分数分布均匀性较差。阴极肋覆盖下的氧气摩尔分数较低,并沿阴极与电解质交界面逐渐增大;而梯形流道斜边处和阳极肋覆盖下方的氧气摩尔分数相对较高且分布均匀。这是由于梯形流道斜边处和阳极肋下方的多孔电极内氧气沿电极厚度方向传输,扩散面积较大、传输路径较短;而阴极肋下方氧气沿电极宽度方向传输,传输路径较长,不易扩散至肋覆盖下的区域。随着阴极厚度的增加,阴极肋覆盖下的氧气摩尔分数逐渐升高,而梯形流道斜边处和阳极肋下的氧气含量逐渐下降。Case 8的氧气摩尔分数最小值相较Case 5、Case 6、Case 7分别提升74.47%、30.60%、11.39%,表明阴极厚度的增加有利于肋下氧气的扩散。该结果也表明增加阴极厚度可以改善氧气分布的均匀性。
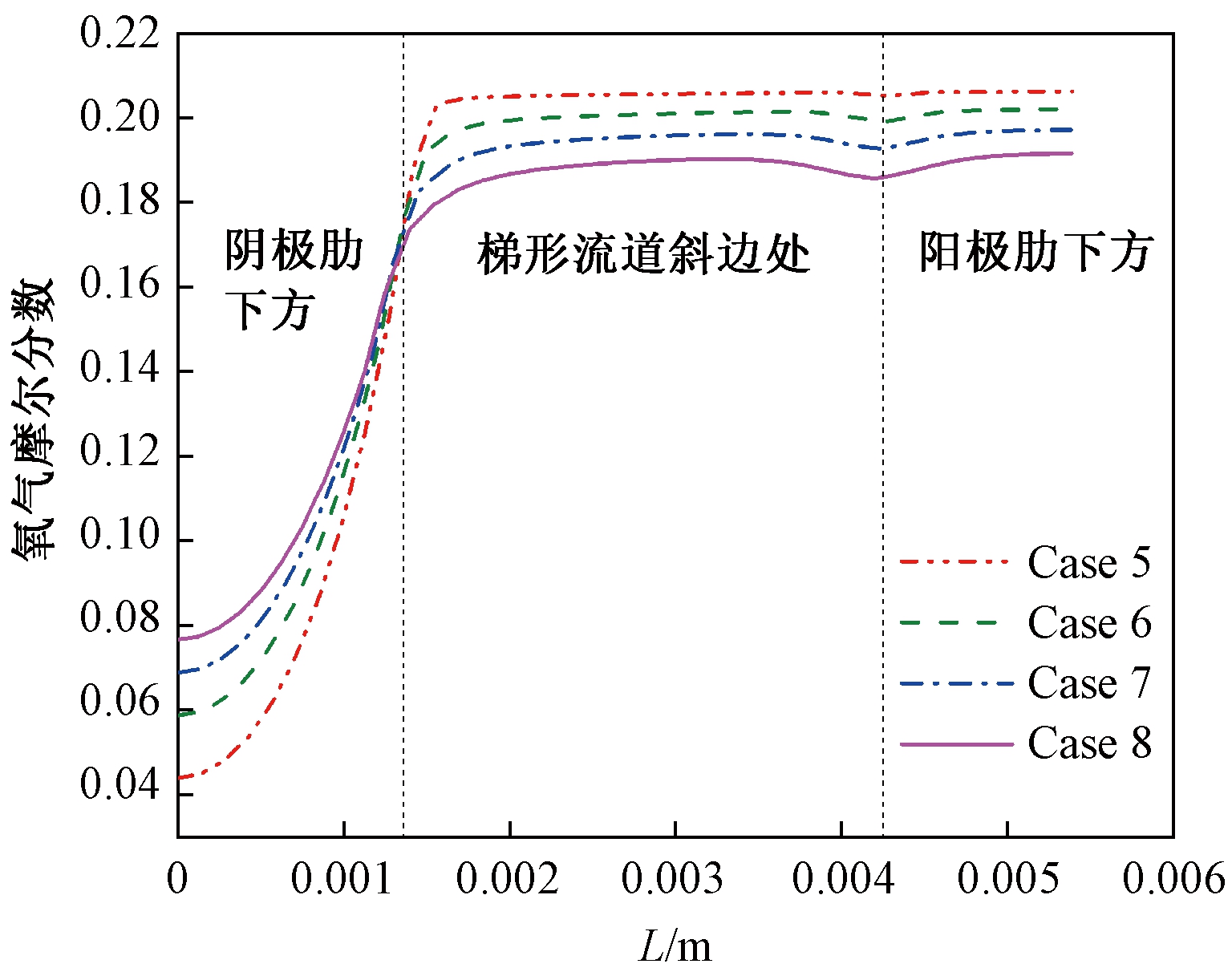
图6 不同阴极厚度下电池阴极/电解质交界面的氧气的摩尔分数分布
Figure 6 Molar fraction distribution of oxygen at different cathode/electrolyte interface thickness
图7显示了4个不同阴极厚度下SOFC的极化曲线和功率曲线。可以看出,随着阴极厚度的增加,电池的平均电流密度和平均功率密度均逐渐增大。其中Case 8的最大平均功率密度为0.856 6 W·cm-2,相较于Case 5的最大平均功率密度提升了53.69%,这是因为随着阴极厚度的增加,肋下方的氧气的质量传输和电子转移得到改善,使电池的输出性能得到明显的提升。此外,随着阴极厚度的增加,增加阴极厚度对电池性能的提升幅度逐渐降低。
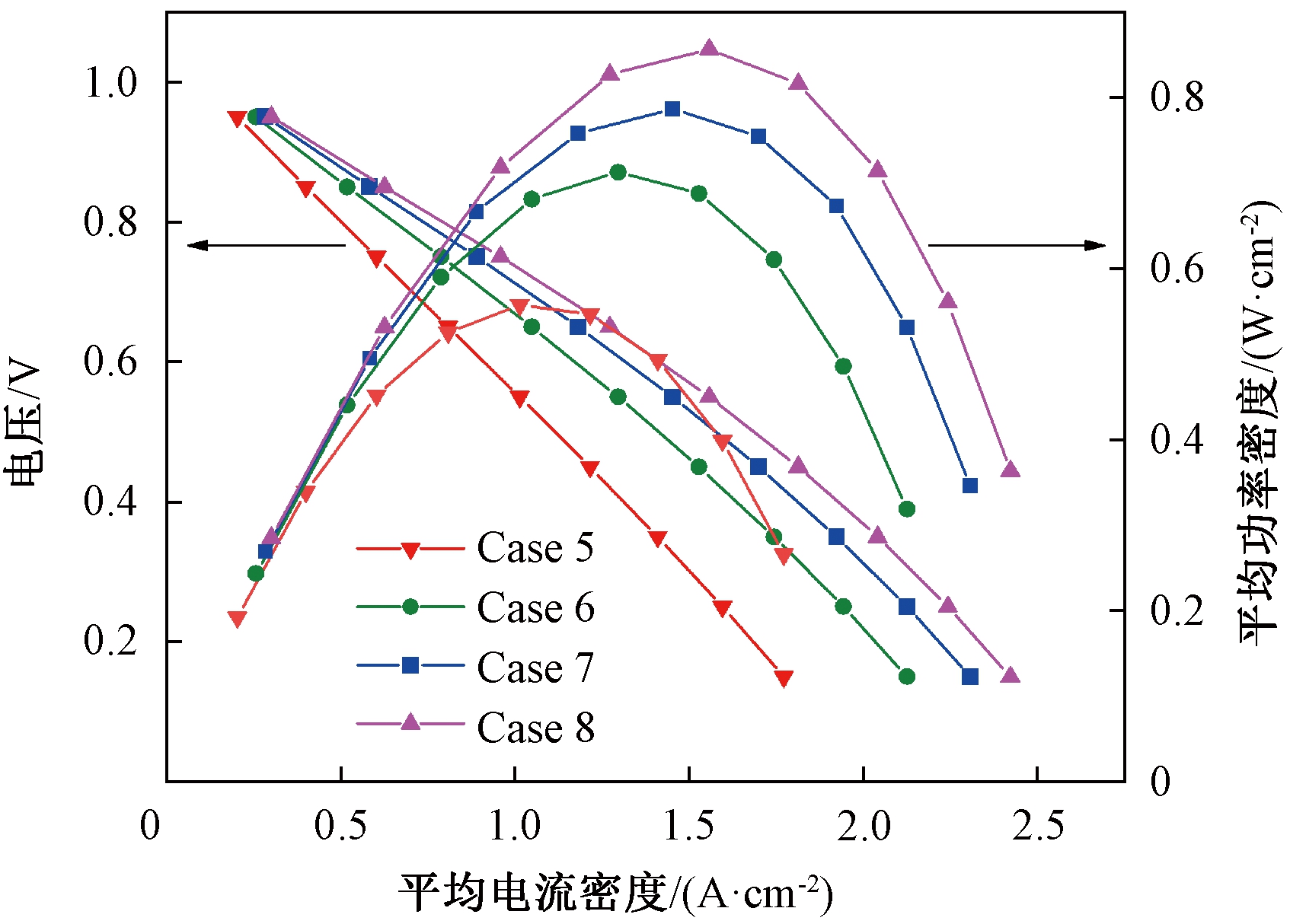
图7 不同阴极厚度下性能曲线
Figure 7 Performance curves at different cathode thicknesses
不同阴极厚度下沿流动方向浓差极化和活化极化分布如图8所示。可以看出,浓差极化沿流动方向逐渐增大,并在出口处达到最大值。此外,随着阴极厚度的增加,电池传质阻力增大,浓差极化也逐渐增大。在电池出口处,Case 8的浓差极化相较于Case 5提高了35.65%。但随着阴极厚度的增加,增加阴极厚度对浓度差极化的影响逐渐减弱。Case 6的浓度差极化比Case 5提高了1.81×10-2 V,而Case 8的浓差极化相较于Case 7提高了3.62×10-3 V。活化极化在电池的极化损失中占主导地位,其变化趋势与浓差极化分布相反,活化极化在入口处达到最大值并沿流动方向逐渐减小。阴极厚度越大,电池的温度越高,反应所需克服的活化能壁垒越低,使活化极化逐渐降低。当阴极厚度从0.15 mm增大到0.45 mm,电池入口处的活化极化降低了28.25%。
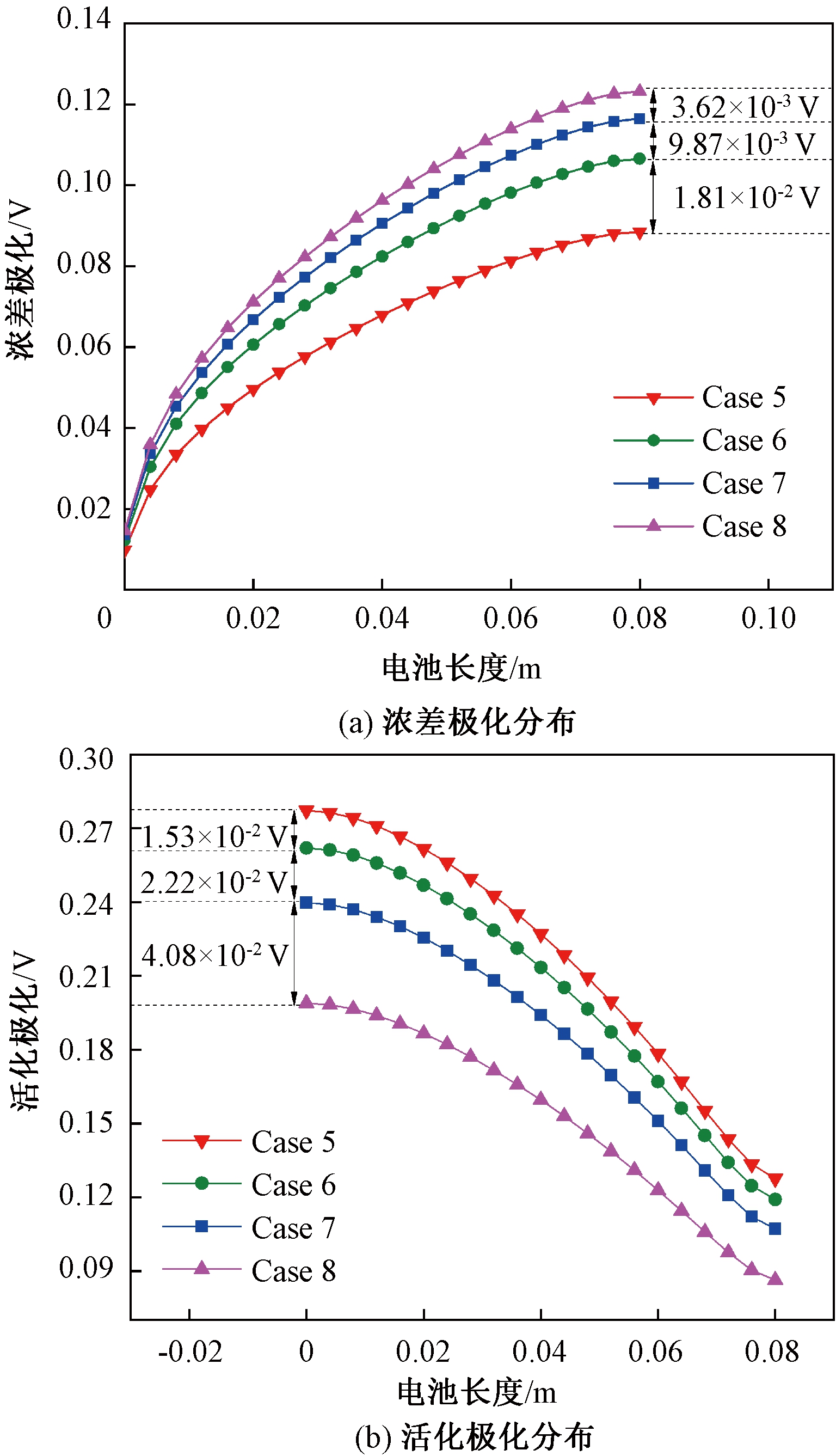
图8 不同阴极厚度下沿流动方向极化损失分布
Figure 8 Distribution of polarization loss along the flow direction at different cathode thicknesses
图9显示了不同阴极厚度下阳极/电解质交界面处沿流动方向的温度分布。可以看出,4个模型下的温度分布均沿流动方向先上升后略微下降,并在电池出口附近处达到温度峰值。这是因为电化学反应的进行导致沿流动方向温度逐渐升高,而在出口处与外界环境进行对流换热导致温度略微下降。此外,随着阴极厚度的增加,电池的温度梯度不断升高。这是由于随着阴极厚度的增加,氧气更容易扩散至阴极肋覆盖下的三相线区域,电化学反应强度得到了提升。
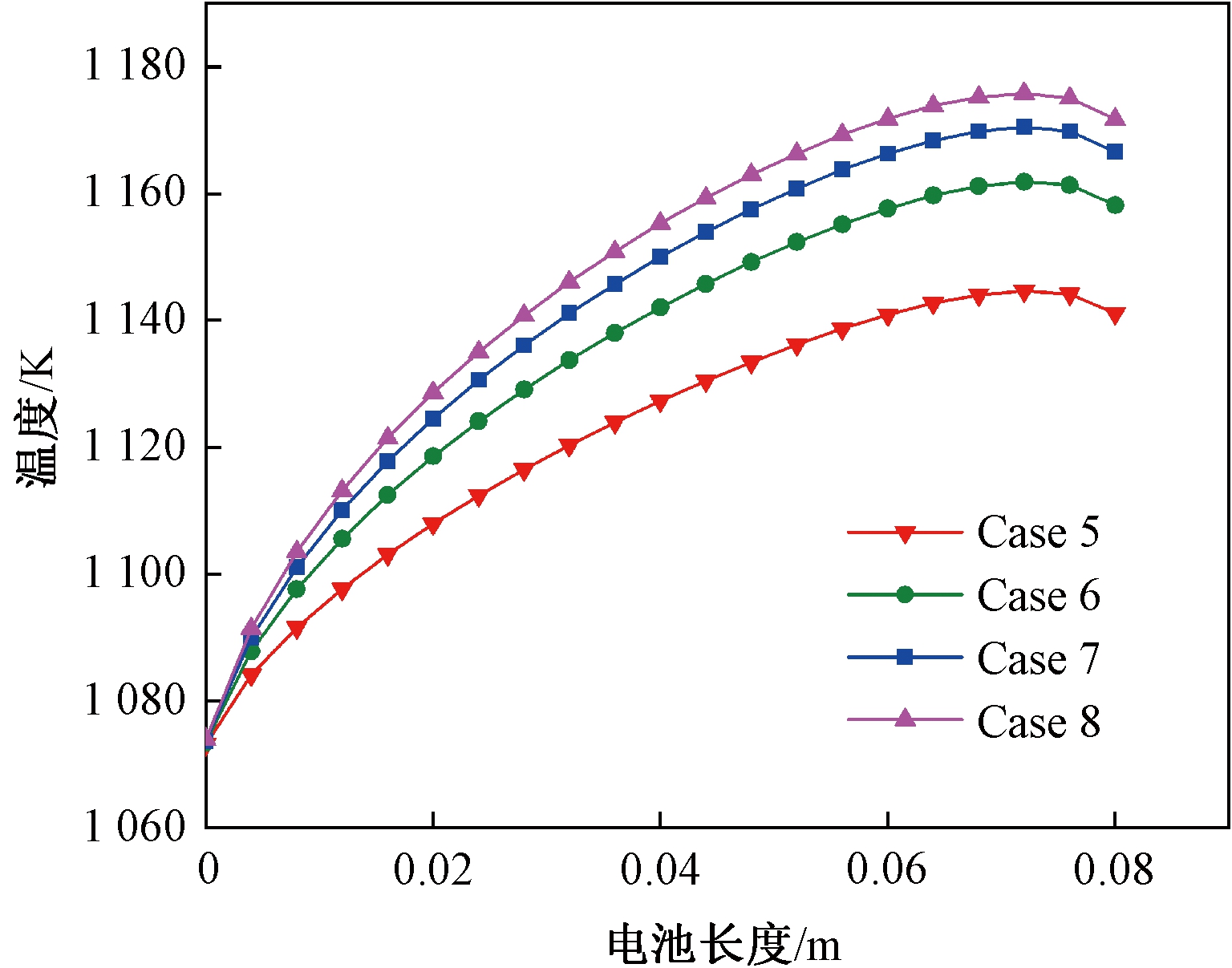
图9 不同阴极厚度下沿流动方向温度分布
Figure 9 Temperature distribution along the flow direction at different cathode thicknesses
为了综合考虑肋宽和阴极厚度对电池性能的影响,定义肋宽与阴极厚度的比值为λ[11],分析了电池最大平均功率密度随λ的变化,如表3所示。结果表明,随着肋宽与阴极厚度比值的减小,电池功率密度逐渐升高。这是由于该比值的减小使肋下方气体传输阻力减小、浓差极化降低、电化学反应速率得到提升,从而使性能提高。λ从10.00减小到3.33时,电池的最大平均功率密度提升了53.68%。
表3 最大平均功率密度随λ的变化
Table 3 Variation of the maximum average power density with λ
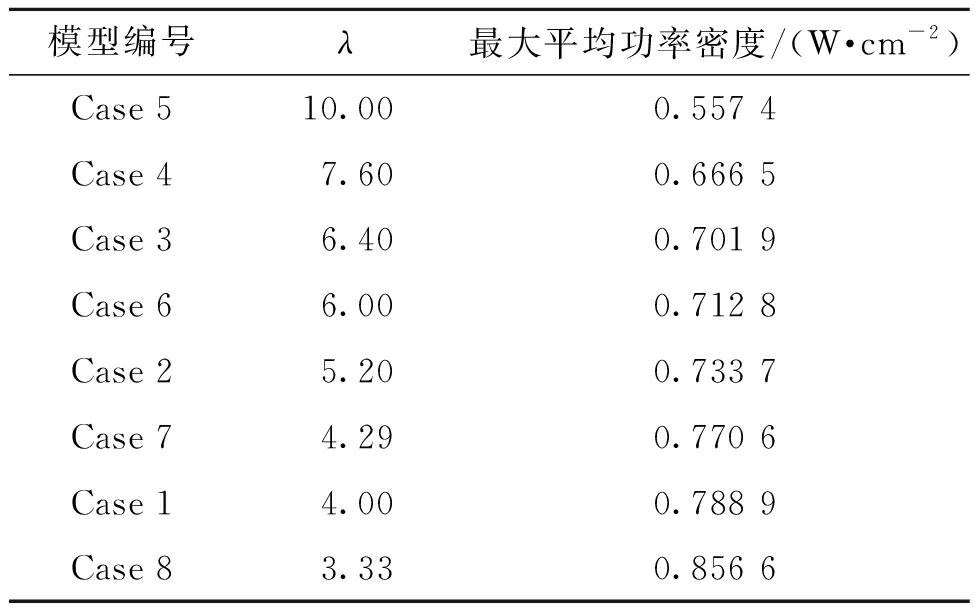
模型编号λ最大平均功率密度/(W·cm-2)Case 510.000.557 4Case 47.600.666 5Case 36.400.701 9Case 66.000.712 8Case 25.200.733 7Case 74.290.770 6Case 14.000.788 9Case 83.330.856 6
4 结论
通过考察气体摩尔分数分布、温度分布以及电化学性能等变化,系统地研究了肋宽和阴极厚度对瓦楞式SOFC性能的影响,所得主要结论如下:肋宽与阴极厚度的比值λ对SOFC多孔电极内气体的质量传输以及电池的输出性能均有着重要影响。采用较小的λ值,可以改善电池内气体摩尔分数分布的均匀性,使电池的总极化损失减小,从而提升电池的输出性能。λ从10.00减小到3.33时,电池的最大平均功率密度提升了53.68%。
[1] 田野, 杨嘉敏, 成少安, 等. 微生物燃料电池处理废水产电及其驱动监控系统的研究[J]. 郑州大学学报(工学版), 2018, 39(1): 90-96.
TIAN Y, YANG J M, CHENG S A, et al. Using microbial fuel cell to dispose waste water to generate electric power and drive the monitoring system[J]. Journal of Zhengzhou University (Engineering Science), 2018, 39(1): 90-96.
[2] CRISALLE O D, 韩闯, 吴莉莉, 等. 质子交换膜燃料电池建模与控制研究进展[J]. 郑州大学学报(工学版), 2015, 36(6): 61-65.
CRISALLE O D, HAN C, WU L L, et al. Review on modeling and control of proton exchange membrane fuel cell[J]. Journal of Zhengzhou University (Engineering Science), 2015, 36(6): 61-65.
[3] HWANG J J, CHEN C K, LAI D Y. Computational analysis of species transport and electrochemical characteristics of a MOLB-type SOFC[J]. Journal of Power Sources, 2005, 140(2): 235-242.
[4] STYGAR M, BRYLEWSKI T, R
KAS M. Effects of changes in MOLB-type SOFC cell geometry on temperature distribution and heat transfer rate in interconnects[J]. International Journal of Heat and Mass Transfer, 2012, 55(15/16): 4421-4426.
[5] YANG Y Z, WANG G L, ZHANG H O, et al. Comparison of heat and mass transfer between planar and MOLB-type SOFCs[J]. Journal of Power Sources, 2008, 177(2): 426-433.
[6] RAM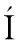
REZ-MINGUELA J J, RODRGUEZ-MU
OZ J L, PÉREZ-GARCA V, et al. Solid oxide fuel cell numerical study: modified MOLB-type and simple planar geometries with internal reforming[J]. Electrochimica Acta, 2015, 159: 149-157.
[7] RAMREZ-MINGUELA J J, URIBE-RAMREZ A R, MENDOZA-MIRANDA J M, et al. Study of the entropy generation in a SOFC for different operating conditions[J]. International Journal of Hydrogen Energy, 2016, 41(21): 8978-8991.
[8] 靳遵龙, 杨友晨, 宫本希, 等. 瓦楞式固体氧化物燃料电池的数值研究[J]. 郑州大学学报(工学版), 2021, 42(6): 42-48.
JIN Z L, YANG Y C, GONG B X, et al. Numerical study of mono-block-layer-built-type solid oxide fuel cell[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(6): 42-48.
[9] HUANG H Y, HAN Z, LU S Y, et al. The analysis of structure parameters of MOLB type solid oxide fuel cell[J]. International Journal of Hydrogen Energy, 2020, 45(39): 20351-20359.
[10] KHAZAEE I, RAVA A. Numerical simulation of the performance of solid oxide fuel cell with different flow channel geometries[J]. Energy, 2017, 119: 235-244.
[11] ANDERSSON M, YUAN J, SUNDÉN B. SOFC cell design optimization using the finite element method based CFD approach[J]. Fuel Cells, 2014, 14(2): 177-188.
[12] RAMREZ-MINGUELA J, MENDOZA-MIRANDA J, RODRGUEZ-MUOZ J, et al. Entropy generation analysis of a solid oxide fuel cell by computational fluid dynamics: influence of electrochemical model and its parameters[J]. Thermal Science, 2018, 22(1): 577-589.