基础数学库函数是计算机系统中最为基础和重要的函数库,生活中各种需要对数据进行处理计算的场景都会用到基础数学函数库。在航天、航空电子等诸多领域中的嵌入式软件通常涉及数学库函数(如sin()、tanh()等)来实现复杂的计算。大到人工智能、智慧城市、智慧医疗,小到日常工作生活,基础数学库函数都提供了重要的数据计算支撑。随着数学库函数计算数据量的增大,提高向量数学函数计算的性能越来越重要,越来越多的向量数学函数得到了广泛的应用。比如英特尔MKL(math kernel library)库中的VM提供了非常丰富的数学向量化函数[1]。Intel Short Vector Math Library[2]是商业界有名的函数库,该库提供了高度优化的子程序,用于评估基本函数,这些子程序可以使用Intel处理器中可用的多种向量扩展,但是这种库是专有的,仅针对Intel处理器进行了优化。AMD提供了一个向量化的libm,称为AMD核心数据库[3]。Anand等[4]实现了32个单精度函数来调整 Cell BE SPU 计算引擎,使用了名为Coconut的环境,该环境支持模式的快速原型设计、汇编语言片段和模式的快速单元测试。Lauter[5]发布了一个用纯C实现的开源Vectorlibm库。VDT数学库[6]是为编译器的自动矢量化功能编写的数学库。实现这些向量化函数库大多采用两种方法:①人为使用汇编指令拼接或者封装一些底层的向量指令;②用编写高级语言程序使用编译器提供的自动向量化来实现[7]。本文主要工作如下。
(1)使用插值方法实现向量数学函数,向量中的每个元素只需要1次乘法运算和1次加法运算即可模拟出函数运算结果,但由于使用分段直线模拟曲线的方式,精度较差。
(2)使用SIMD(single instruction multiple data)加掩码编程方法对向量函数进行优化,解决了数学函数中多分支结构无法向量化的问题,但是使用该方法时大部分复杂数学函数中有临时变量需要申请临时空间,临时空间在向量化函数中变为临时向量空间,所需空间成倍增长,会占用智能处理器宝贵的计算空间。
(3)基于PuDianNao芯片封装出SIMT编程模型,提出了暴露分支范围和分支扁平化的编程方法(方法三),解决了数学函数多分支结构难以向量化的问题,充分发挥国产PuDianNao芯片性能优势。对比实验表明,该方法具有较高的性能和精度,因此本文采用此方法实现向量数学函数库。
(4)基于方法三实现了国产深度学习处理器PuDianNao芯片向量数学库PuDianNao-VecMath。该函数库精度性能较好、功能稳定、运行正确。
1 研究背景
1.1 国产PuDianNao处理器
PuDianNao是一种ML(machine learning)加速器,包含7种代表性的ML技术,包括k-means、k-最近邻、朴素贝叶斯、支持向量机、线性回归、分类树和深度神经网络。PuDianNao通过对不同ML技术的计算原语和局部性属性进行深入分析,可以在3.51 mm2的面积上执行高达1 056 GOP/s的运算(如加法和乘法),仅消耗能量596 mW。与 NVIDIA K20M GPU(28 nm工艺)相比,PuDianNao(65 nm工艺)的速度为其速度的1.20倍,能耗为其能耗的1/128.41。
如图1所示,PuDianNao 由若干个功能单元(FUs)、3个数据缓冲区(HotBuf、ColdBuf 和 OutputBuf)、1个指令缓冲区(InstBuf)、1个控制模块和1个DMA组成。功能单元(FU)是PuDianNao 的基本执行单元,每个FU由两部分组成:1个机器学习功能单元MLU(maching learning unit)和1个算术逻辑单元ALU(arithmetic logic unit)。相比之前针对小范围机器学习技术设计的机器学习加速器,PuDianNao在数据特征变化或应用场景发生变化时更加健壮,因为其为用户提供了一系列候选技术。
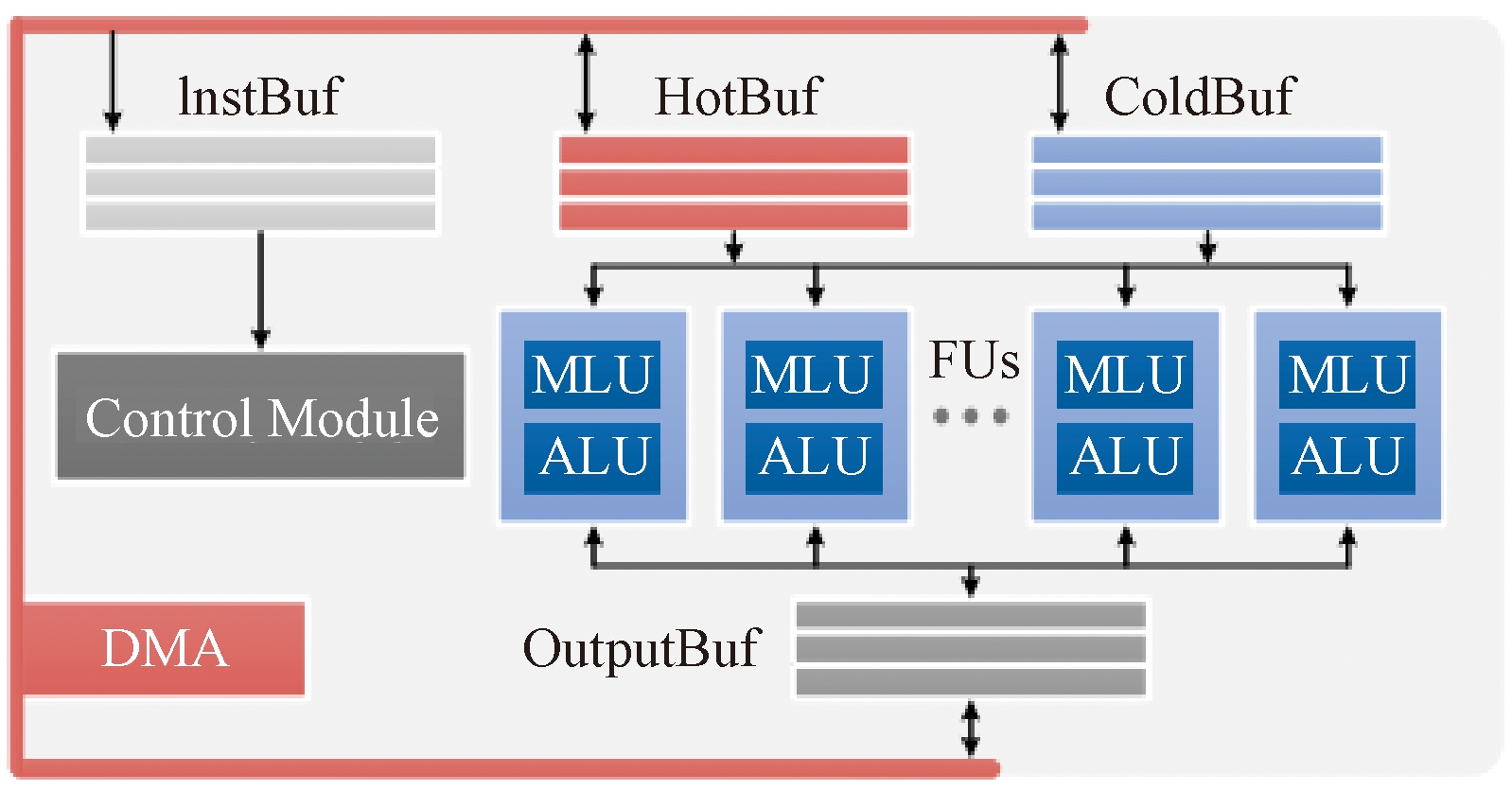
图1 PuDianNao的加速器架构[8]
Figure 1 Accelerator architecture of PuDianNao[8]
1.2 PuDianNao编程模型
1.2.1 VLIW指令集架构
PuDianNao编程模型中的一种指令集使用VLIW(very long instruction word)。VLIW中的每条指令完成多个独立操作,将多个相互没有依赖的指令封装到一条超长的指令字中并且使相应数量的ALU完成指令的一系列操作,使用编译器来控制指令的调度并且解决指令之间的依赖性。
VLIW在一条指令中封装多个并行操作选项,使用VLIW指令操作阵列结构中的处理单元。指令的长度比常见的RISC(reduced instruction set compute)和CISC(complex instruction set computer)指令长度长,因此叫做超长指令集。典型的商用VLIW芯片架构有Intel IA-64,是Itanium系列64位微处理器指令体系结构[9];ATI GPU采用VLIW架构,每个TP是一个5-way的VLIW Processor[10];移动应用领域DSP采用VLIW架构并且取得了成功[11]。
1.2.2 SIMT编程模型
SIMT指的是单指令多线程,有别于SISD(单指令单数据)、SIMD(单指令多数据),SIMT的1条指令可以处理多条线程和多条数据,图2展示了SISD、SIMD和SIMT的区别[12]。由于PuDianNao硬件向量单元本身可以控制每个小核是否执行任务,在此基础上实现了简单的掩码翻译器,给PuDianNao的硬件单元增加了SIMT指令,并且增加SIMT指令的译码器,用VLIW指令集封装出SIMT编程模型。使用SIMT编程模型编程时,只需要描述1个线程的行为,所有线程以锁步的方式并行执行同样的指令。这种方式能批量处理数据,只需要写1份指令,硬件会同时运行1份相同的指令,实现计算的并行化。
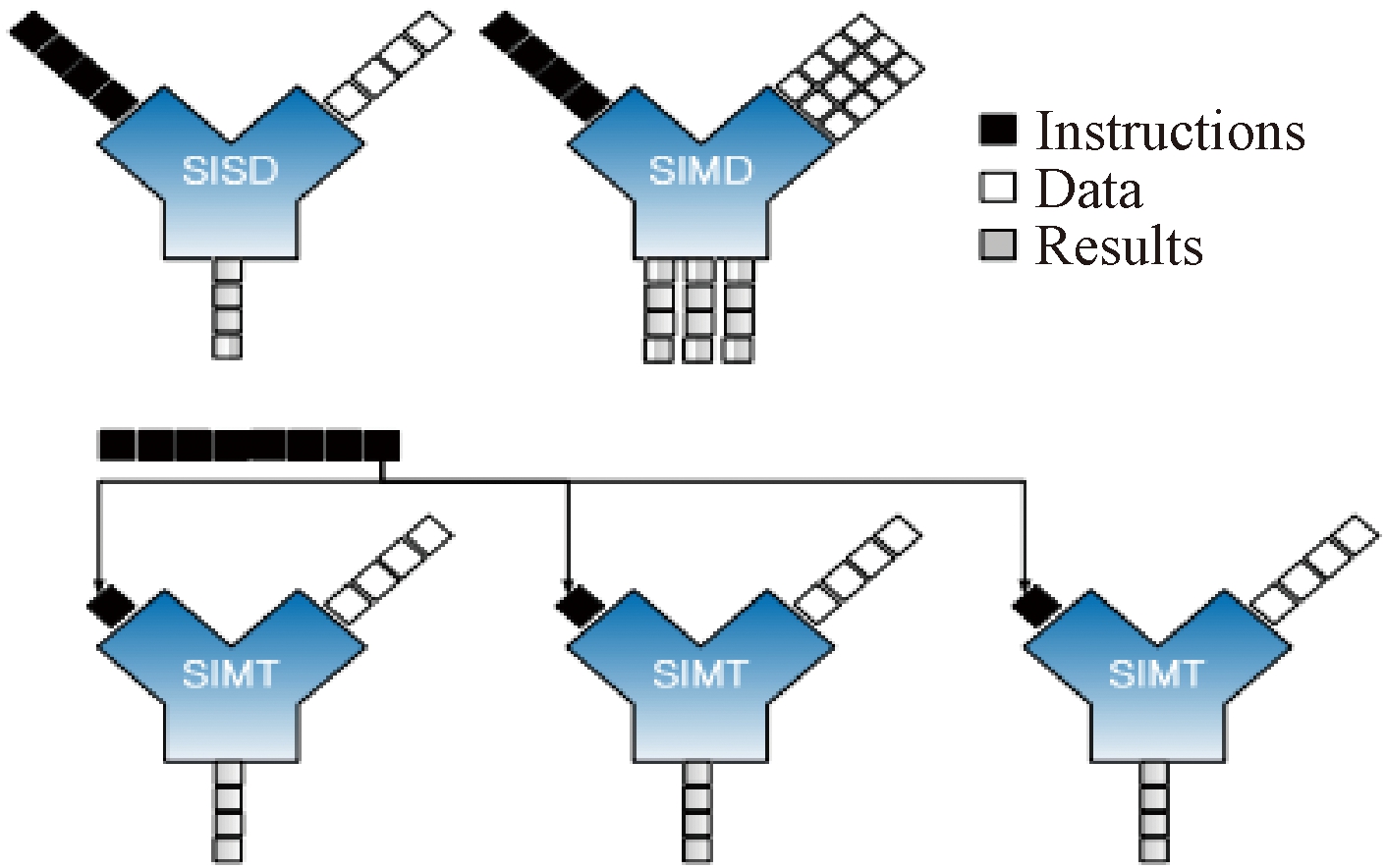
图2 SISD、SIMD、SIMT的区别[12]
Figure 2 Difference among SISD, SIMD, and SIMT[12]
图3为PuDianNao封装出的SIMT编程模型示意图,其结构是一种阵列结构,包括M行N列的处理单元,每个处理单元中包括子运算单元和子存储单元,其中子运算单元可以完成逻辑运算、算术运算等,子存储单元可用于存储数据和谓词信息等。
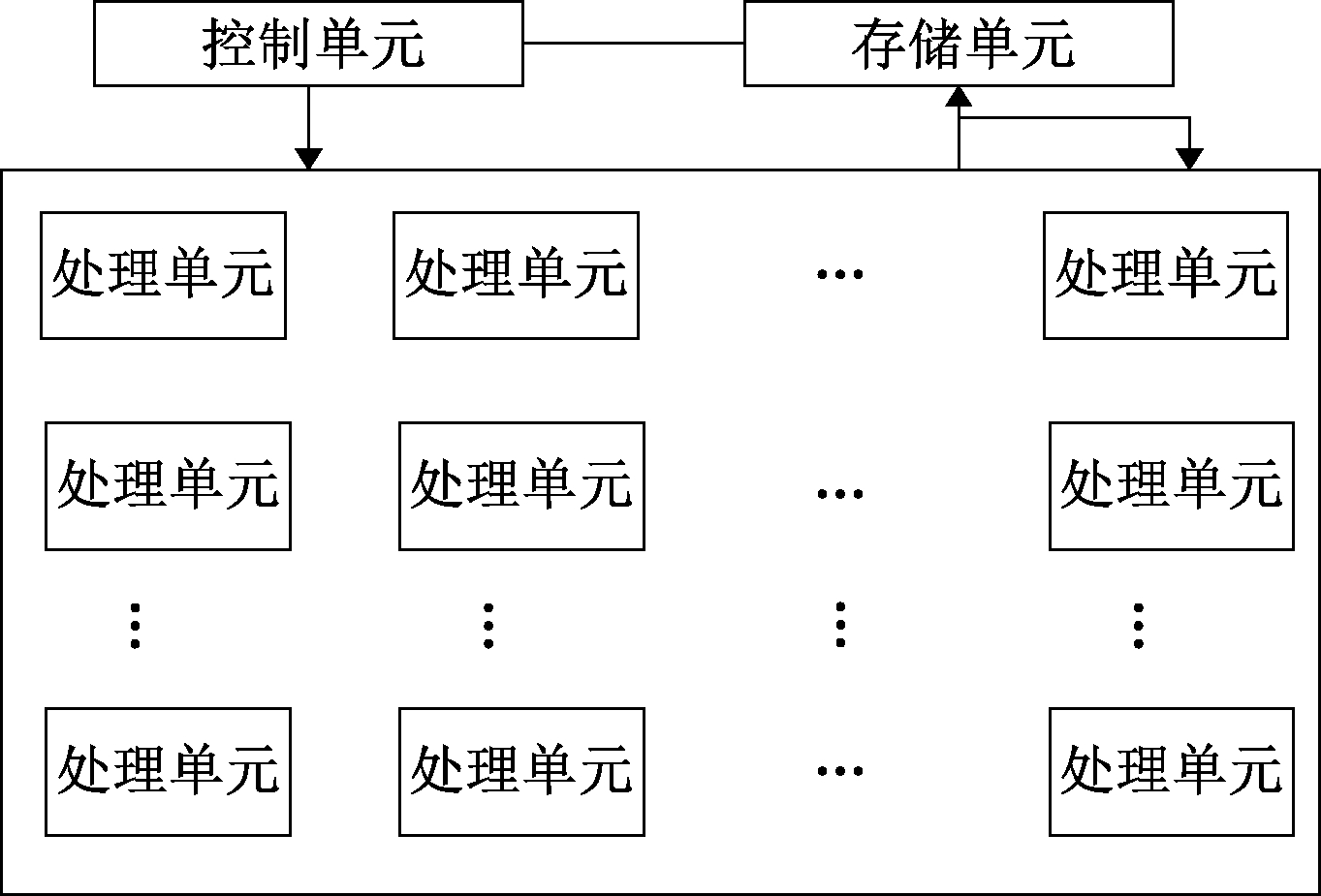
图3 PuDianNao中的SIMT编程模型
Figure 3 SIMT programming model in PuDianNao
每个处理单元可以执行1个线程。处理单元中的子存储单元的多个谓词寄存器决定每个分支是否使能。每个处理单元处理不同的输入数据,所执行的分支可能不同,处理单元的行为也可能不同,以此来实现多线程。阵列结构保证了并行性,阵列结构大小为M×N,每次读取M×N个元素,计算M×N个数据。子存储单元里面的谓词寄存器用于分支限定,子存储单元里面的存储寄存器存储中间运算结果和临时变量;子运算单元进行运算。使用VLIW指令来控制每个处理单元的各种操作,比如输入、输出、数据交互以及计算。
1.2.3 SIMD指令集
PuDianNao处理器支持SIMD指令集。SIMD是单指令多数据流,用1个控制器控制多个处理单元,时间上的并行性是通过对数据中的每个元素进行相同的计算来完成的。在执行SIMD指令时,通过1条指令可以同时对多个元素进行计算。比如1个128 bit的向量寄存器,每次编译的时候可以对4个float类型的数据进行计算。
PuDianNao的SIMD指令集支持非常丰富的指令,不同的指令相互拼接能够完成许多复杂的功能。支持的指令包括配置指令、算术运算指令、比较指令、逻辑和移位指令、谓词指令、扩展精度的算数运算指令、数据移动指令等。
2 实现方法
2.1 插值方法
激活函数(如tanh、relu、sigmoid等)使用分段直线模拟曲线求解。将函数分成多个小段,每段插入多个点使用最小二乘法拟合,每段使用直线模拟曲线,当所分的每一段足够小的时候,误差可以非常小。将斜率和截距存储在激活表中,分段区间存储在常数表中,省去了函数中逻辑判断的部分,通过查表的方式来确定输入区间,对于每个分段使用硬件查表单元选择合适的斜率k和截距b,通过1次乘法和加法运算可以得到函数运算结果,结果较好地拟合原函数。
2.2 SIMD加掩码方法
使用SIMD指令直接对标量函数进行向量化面临以下两个主要的挑战。
(1)条件分支判断。在标量程序中多个条件分支可以使用if、else等语句写出来,然而在向量函数中,每个元素所走的分支可能不同,不能用SIMD的方式让所有元素执行同一个流程。
(2)临时变量。在标量程序中临时变量可以存储在寄存器中。但是在向量程序中,临时变量变为临时向量,占用的空间较大,并且不能存储在寄存器中,必须存储在智能计算器空间中,所需的临时空间成倍增长,占用宝贵的计算资源。
针对条件分支判断问题采用SIMD加掩码的方法解决:使用浮点数0.0和1.0作为掩码,使用SIMD指令将所有的分支都遍历一遍,每个分支所得结果乘以掩码将无效数据清零,最后将各分支有效结果相加拼接出向量输出。
对于临时变量问题,部分简单函数临时向量可以复用输出向量的空间,无须申请临时空间;然而大部分复杂函数无法复用输出向量空间,需要大量的临时空间。
2.3 SIMT编程模型方法
基于PuDianNao芯片上封装出的SIMT编程模型,提出暴露分支范围和分支扁平化来解决数学函数多分支结构难以向量化的难题。注释标注出标量函数中各个复杂嵌套分支的范围,使用谓词寄存器来存储条件分支。SIMT编程模型中的指令会把所有分支都遍历一遍,使用谓词寄存器控制各分支的语句是否执行,若该分支执行,在该分支上使用对应的汇编指令,最终在ALU计算单元对元素进行计算和处理。
异构编程模型通常由通用处理器和多个特定于域的处理器组成[13]:通用处理器叫做主机端(host),用于复杂的控制和调度,主要的任务包括设备获取、数据或者参数准备、执行流创建、任务描述、内核启动和输出获取等;特定于域的处理器作为子设备,用于大规模的并行计算和特定于域的计算任务,二者合作共同完成计算任务。由于device端(智能处理器)不能像host端(通用处理器)那样在特定的分支上返回结果,每个分支的结果都会暂时存储在寄存器里,最终返回寄存器中的值。
数学函数中大部分复杂函数具有多分支、分支嵌套的特性。SIMT编程模型不支持跳转指令,需要把函数的所有分支遍历一遍。这时,SIMT编程变得困难并且容易出现错误。针对这种问题提出了暴露分支范围和分支扁平化的方法。暴露分支范围就是由于标量函数中使用的嵌套的if、else语句块往往难以将每个分支的具体范围分辨清楚,可以人为地将每个分支的具体上限和下限作为注释标注出来。分支扁平化的具体方法是使用存储寄存器存储变量和中间计算结果,使用通过扁平后的分支构造谓词寄存器中的分支条件,或者使用谓词寄存器中已经存在条件的逻辑运算(与或非等)的结合来构造复杂条件分支,并且在相应的条件分支下编写汇编指令执行标量函数中的对应操作。
图4为标量函数中的多分支结构使用暴露分支范围和分支扁平化的方法转化为SIMT编程模型中对应谓词寄存器的映射过程。最左边为高级语言中的多分支条件;中间为暴露分支范围的结果,p代表每个分支条件,p之后为每个分支的具体上下限;右边为分支扁平化过程,将暴露的分支范围用汇编指令表示出来。

图4 暴露分支范围和分支扁平化过程
Figure 4 Expose branch scope and branch flattening process
标量函数中的多分支结构使用暴露分支范围和分支扁平化的方法转化为SIMT编程模型中对应谓词寄存器中的条件,使用SIMT编程模型中阵列结构的每个处理单元操作单个数据,根据处理单元中的多个谓词寄存器决定每个分支是否执行,同时并行处理多个输入数据,每个处理单元相当于运行一个线程,实现计算并行化。
3 优劣分析实验
3.1 实验介绍
本文实验硬件平台基于国产PuDianNao处理器、CPU i7和GPU Tesla T4。向量函数汇编代码采用PuDianNao芯片自研指令集进行编写。编译工具链等软件使用PuDianNao芯片配套软件栈。
(1)精度统计方法。使用输入数据类型所能表示的所有数据和函数定义域的交集作为输入,测试最大ULP(unit in last place)[14]。这种方法的缺点是测试时间较长,比如单精度浮点数据用32位数据表示,全数据区域一共包含232个数据;优点是测试的数据完整,最大ULP比较准确。
(2)求ULP。使用ULP 衡量函数库误差。挑选部分函数在PuDianNao芯片上运行,得到的运行结果和glibc库[15]函数在CPU i7中运行结果进行对比,利用ULP计算公式进行计算。ULP表示浮点数之间的距离,值越大代表误差越大。对于特殊值NAN,INF的处理方式和glibc库函数保持一致。
(3)性能测试。函数定义域全数据区域取不同规模输入数据,测试出计算完所有输入数据所用的时间作为性能数据。使用加速比(原性能时间/新性能时间)来衡量性能加速情况。
3.2 插值方法分析
如图5所示,选取6个复杂函数,分别测试在SIMT编程模型、CUDA MATH API[16]、标量循环、SIMD加掩码方法、插值方法的最大ULP值。结果表明,插值方法最大ULP值为7,最小ULP值为3,使用插值法测试的ULP值最大,精度最差。
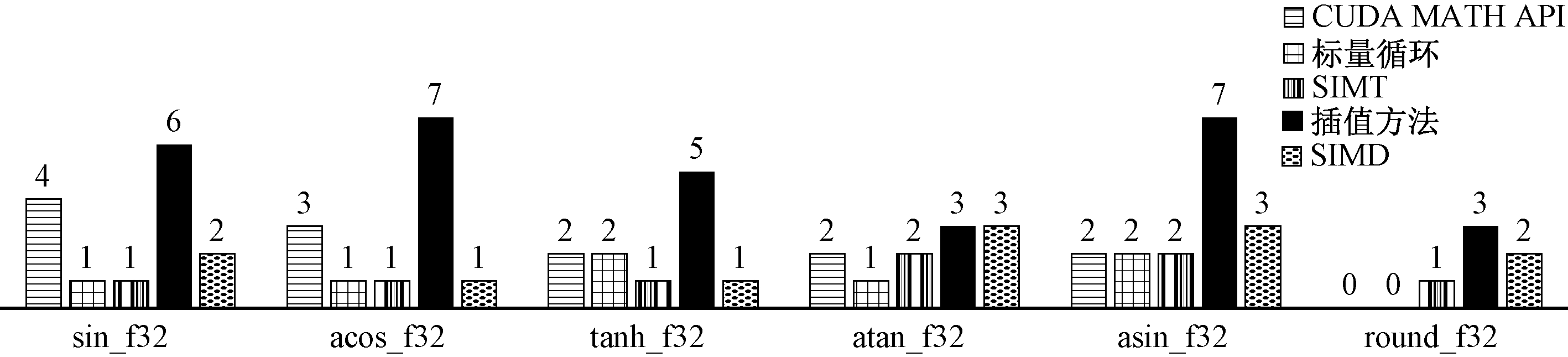
图5 各种方法的ULP值对比
Figure 5 Comparison of ULP values of various methods
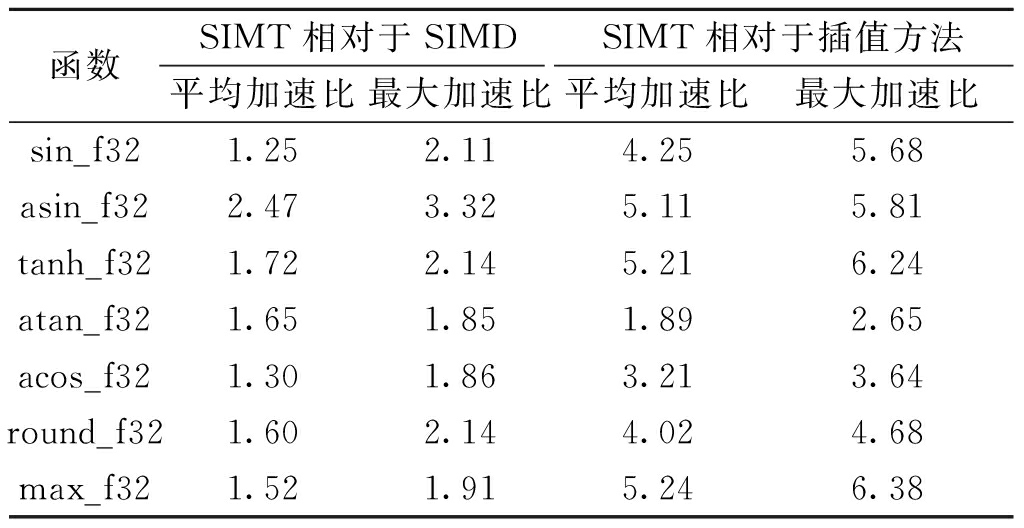
表1为测试出的7个函数中SIMT编程模型相对于插值方法和SIMD方法的平均加速比和最大加速比。测试结果表明,SIMT编程模型相对于插值方法的平均加速比平均值为4.13,最大加速比为6.38,插值方法性能不如SIMT编程模型。
表1 SIMT编程模型相对于SIMD加掩码方法和插值方法的加速比
Table 1 Speedup of SIMT programming model relative to SIMD masking method and interpolation method
函数SIMT相对于SIMDSIMT相对于插值方法平均加速比最大加速比平均加速比最大加速比sin_f321.252.114.255.68asin_f322.473.325.115.81tanh_f321.722.145.216.24atan_f321.651.851.892.65acos_f321.301.863.213.64round_f321.602.144.024.68max_f321.521.915.246.38
插值方法由于使用常数表存储分段区间,激活表存储每个分段的斜率和截距,省去了函数逻辑判断的部分,通过查表的方式来确定输入区间,只需要一次乘法和加法可以得到函数模拟运算结果,但使用直线模拟曲线,始终存在误差,精度较差。
3.3 SIMD 加掩码优化分析
表1结果表明,SIMT方法相对于SIMD方法的平均加速比平均值为1.64,最大加速比为3.32,SIMD加掩码方法性能不如SIMT编程模型。
图5中的结果表明SIMD加掩码方法最大ULP值为3,最小ULP值为1,ULP值在测试函数中均大于等于SIMT编程模型方法,精度不如SIMT编程模型方法。
SIMD加掩码方法需要占用大量的临时空间,以asin函数为例,限定短向量长度为64位,所需要的临时空间为6 784字节,若短向量长度增加,所需要的临时空间会同比例增加。
该方法性能精度不如SIMT编程模型方法,并且大部分函数需要申请临时空间,在向量函数中临时空间成倍增长,并且需要占用智能处理器的空间,浪费大量宝贵的计算资源。
3.4 SIMT编程模型优化分析
精度对比实验使用glibc库[15]函数在CPU i7上运行的结果和PuDianNao-VecMath库中对应函数进行误差计算,得出最大ULP值,并和CUDA MATH API函数库公开的ULP值进行比较。
性能对比实验分为两组:①使用循环调用标量函数性能作为基准,测试PuDianNao-VecMath库中多个函数相对于基准的性能加速比;②使用CUDA MATH API函数库中选定的函数在GPU Tesla T4上的运行性能作为基准,测试出PuDianNao-VecMath库中对应函数在PuDianNao芯片上相对于基准的加速比。
3.4.1 向量函数精度测试
图5结果表明,PuDianNao-VecMath函数库中测试函数的最大ULP值大部分小于等于CUDA MATH API库中的函数,某些函数的ULP值小于标量循环。PuDianNao-VecMath库中单精度浮点数(float)最大ULP为2,具有较好的精度。
由于半精度浮点数(half)所表示数的指数位和小数位相对于单精度浮点数(float)均较短,为了提高计算精度、减小误差,结合PuDianNao芯片的硬件特性,采用单精度计算来实现。实验结果表明,半精度浮点数版本函数最大ULP不超过1。
3.4.2 向量函数性能测试
(1)使用循环调用标量函数作为性能基准,测试PuDianNao-VecMath库中多个函数相对于基准方法的加速比。
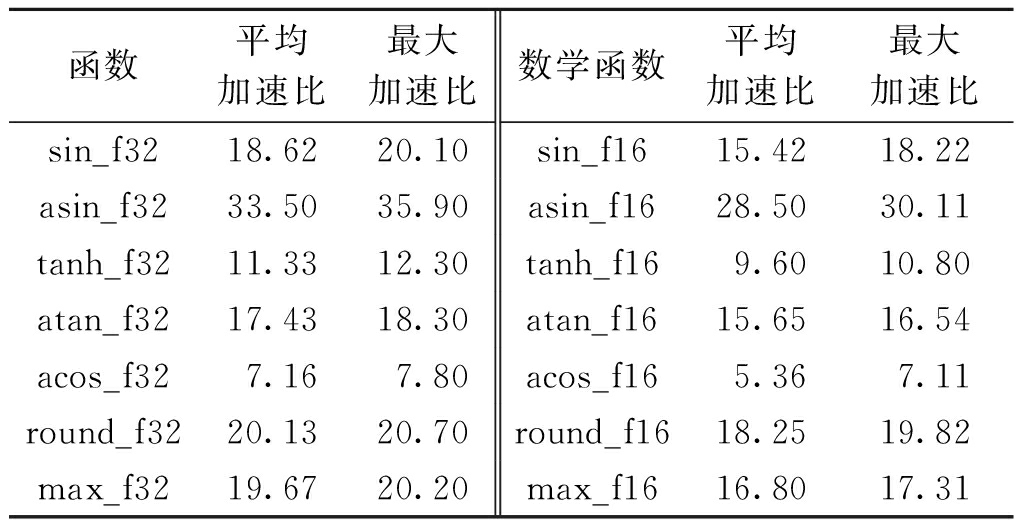
表2表明,PuDianNao-VecMath库中的单精度浮点数函数相对于标量循环方法均有较高的加速比,所测几个函数平均加速比平均值为18.26,最大加速比为35.90;PuDianNao-VecMath库中的半精度浮点数函数相对于标量循环方法均有较高的加速比,所测函数的平均加速比平均值为15.65,最大加速比为30.11。
表2 PuDianNao-VecMath库相对于标量循环的加速比
Table 2 Speedup of PuDianNao-VecMath library relative to scalar loop
函数平均加速比最大加速比数学函数平均加速比最大加速比sin_f3218.6220.10sin_f1615.4218.22asin_f3233.5035.90asin_f1628.5030.11tanh_f3211.3312.30tanh_f169.6010.80atan_f3217.4318.30atan_f1615.6516.54acos_f327.167.80acos_f165.367.11round_f3220.1320.70round_f1618.2519.82max_f3219.6720.20max_f1616.8017.31
(2)使用CUDA MATH API函数库函数在GPU Tesla T4上运行时间作为性能基准,测PuDianNao-VecMath库在PuDianNao处理器上相对于基准方法的加速比。
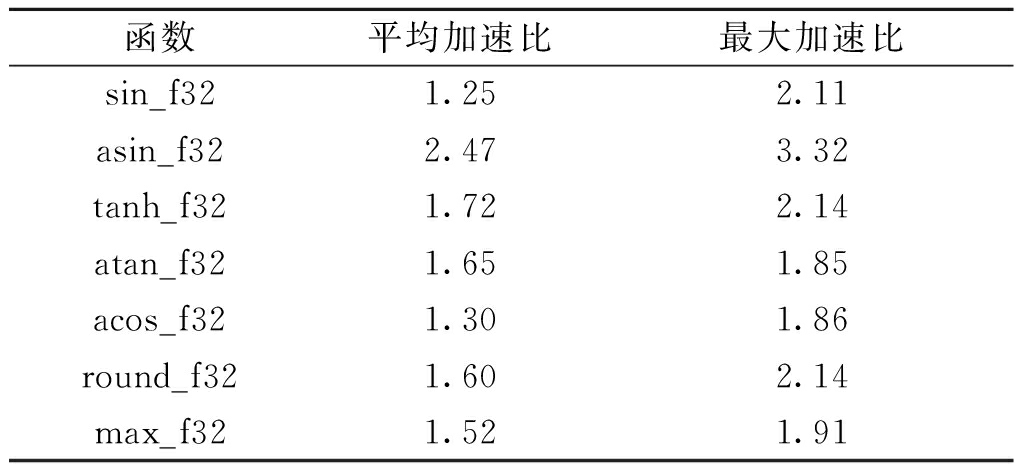
在大数据段,输入浮点数的个数超过1 M时,选取7个复杂函数测试,结果如表3所示。可以看出,PuDianNao-VecMath在PuDianNao硬件上运行,相对于CUDA MATH API中对应测试函数在GPU Tesla T4硬件上的平均加速比平均值为1.64,最大加速比为3.32。
表3 PuDianNao-VecMath库相对于CUDAMATH API的加速比
Table 3 Speedup of PuDianNao-VecMath library relative to CUDA MATH API
函数平均加速比最大加速比sin_f321.252.11asin_f322.473.32tanh_f321.722.14atan_f321.651.85acos_f321.301.86round_f321.602.14max_f321.521.91
SIMT编程模型性能和精度较好,不需要额外的临时空间,使用SIMT编程模型下的专用的存储寄存器和谓词寄存器存储中间变量和条件分支。因此本文的PuDianNao-VecMath函数库使用SIMT编程模型的方法来实现。
综上可得出SIMT编程模型具有最好的性能和精度,且不占用智能处理器空间。可以作为PuDianNao芯片上向量数学函数库PuDianNao-VecMath的实现方法。
4 结论
本文基于国产PuDianNao处理器提出了3种向量化函数优化方法,经过精度和性能测试分析,得出各种优化方法的优劣。
(1)插值方法。所测函数中SIMT方法相对于插值法的平均加速比平均值为4.13,最大加速比为6.38,性能一般;插值方法最大ULP值为7,最小ULP值为3,精度差、实现方法简单。该方法适用于对精度要求不高、实现方法要求简单的场景。
(2)SIMD加掩码方法。SIMT方法相对于SIMD方法的平均加速比平均值为1.64,最大加速比为3.32;SIMD最大ULP值为3,最小ULP值为1。该方法性能和精度均较好,但需要大量的智能处理器临时空间,实现方法较为复杂,适用于精度和性能要求较高、对智能处理器空间限制不高、具有较为全面的SIMD指令支持的场景。
(3)SIMT编程模型方法。性能和精度均最好,但实现较为复杂,且需要有较为全面的汇编指令支持,适用于性能和精度要求高的场景。对PuDianNao-VecMath函数库中选定一些实现较为复杂的函数进行精度和性能测试。单精度版本函数最大ULP不超过2,半精度版本函数最大ULP不超过1。选定该库中某些较为复杂函数和标量循环对比,单精度浮点数平均加速比平均值为18.26,最大加速比为35.90;半精度版本平均加速比平均值为15.65,最大加速比为30.11。单精度版本和GPU Tesla T4对比平均加速比平均值为1.64,最大加速比为3.32。
测试结果表明,使用SIMT编程模型方法构建的PuDianNao-VecMath函数库性能精度较好、功能稳定、运行正确,充分发挥了国产PuDianNao智能处理器的性能优势,为PuDianNao处理器提供了向量数学函数库支持,泛化了人工智能处理器的应用场景。
[1] Intel Corporation. Intel® oneAPI math kernel library [EB/OL].(2019-11-01)[2022-02-10] .https://software.intel.com/en-us/mkl.
[2] Intel Corporation. Intel short vector math library [EB/OL]. (2021-06-20)[2022-02-10]. https://software.intel.com/en-us/node/523613.
[3] Advanced Micro Devices, Inc.. AMD core math library [EB/OL]. (2013-07-24)[2022-02-10]. http://developer.amd.com/tools-and-sdks/archive/acml-product-features/.
[4] ANAND C K, KAHL W. An optimized cell BE special function library generated by coconut[J]. IEEE transactions on computers, 2009, 58(8): 1126-1138.
[5] LAUTER C. A new open-source SIMD vector libm fully implemented with high-level scalar C[C]//2016 50th Asilomar Conference on Signals, Systems and Computers. Piscataway: IEEE, 2016: 407-411.
[6] PIPARO D, INNOCENTE V, HAUTH T. Speeding up HEP experiment software with a library of fast and auto-vectorisable mathematical functions[J]. Journal of physics: conference series, 2014, 513(5): 052027.
[7] 刘聃, 郭绍忠, 郝江伟, 等. 基于SIMD扩展部件的长向量超越函数实现方法[J]. 计算机科学, 2021, 48(6): 26-33.
LIU D, GUO S Z, HAO J W, et al. Implementation of transcendental functions on vectors based on SIMD extensions[J]. Computer science, 2021, 48(6): 26-33.
[8] LIU D F, CHEN T S, LIU S L, et al. PuDianNao[J]. ACM SIGPLAN notices, 2015, 50(4): 369-381.
[9] HUCK J, MORRIS D, ROSS J, et al. Introducing the IA-64 architecture[J]. IEEE micro, 2000, 20(5): 12-23.
[10] ZHANG Y, HU Y, LI B, et al. Performance and power analysis of ATI GPU: a statistical approach[C]//2011 IEEE Sixth International Conference on Networking, Architecture, and Storage. Piscataway: IEEE, 2011: 149-158.
[11] KUMURA T, IKEKAWA M, YOSBIDA M, et al. VLIW DSP for mobile applications[J]. IEEE signal processing magazine, 2002, 19(4): 10-21.
[12] KYUNG G, JUNG C M, LEE K. An implementation of a SIMT architecture-based stream processor[C]//TENCON 2014-2014 IEEE Region 10 Conference. Piscataway: IEEE, 2014: 1-5.
[13] XIONG Y Q. A unified programming model for heterogeneous computing with CPU and accelerator technologies[C]//12th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI). Piscataway: IEEE, 2019: 1-4.
[14] MULLER J K. On the definition of ulp(x)[R/OL].(2005-02-01)[2022-02-10].https://www.researchgate.net/publication/236944278_On_the_definition_of_ulpx.
[15] Free Software Foundation.The GNU C Library (glibc)[EB/OL].(2019-11-01) [2022-02-10].https://www.gnu.org/software/libc/.
[16] NVIDIA. CUDA Math API[EB/OL].(2022-01-12) [2022-02-10].https://docs.nvidia.com/cuda/cuda-math-api/index.html.