由于沸腾换热能在较小的温差下带走大量的潜热,已成为解决高热流密度电子芯片散热问题的重要方法,正确认识和分析沸腾换热微观机理至关重要。由于在气液交界面存在众多复杂变化过程[1],所以采用数值方法分析沸腾换热气液交界面处的微观过程面临巨大挑战。格子玻尔兹曼方法(LBM)具有方程完全线性化、计算效率高和擅长处理界面动力学问题等优点,被广泛应用于多相流模型中,并且得到了不断发展,先后出现了颜色模型、伪势模型、自由能模型和相场模型等4类计算模型,其中伪势模型由于简单易懂、实际使用简便被许多学者逐渐关注。由于原始的伪势模型存在稳定性差的情况,Zhang等[2]把单组分伪势模型引入范德瓦尔斯状态方程,通过引入势函数的方式提高了伪势模型的稳定性。Kupershtokh等[3]提出引入加权的方式将有效密度和势函数结合,通过对不同形式的状态方程合理地调节加权系数获得了更高的稳定性。
LBM在处理沸腾传热的相变过程时常利用温度的扰动及模型本身的性质,在模拟过程中激发自发相变过程,并且根据相变量计算温度方程中的源项以保证能量守恒[4]。该方式采用自发相变的计算方法可在一定程度上更好地反映出相变机理,减少了模拟过程中的假设条件。为避免直接给定相变源项值,Gong等[5]引入一种新的源项形式,避免了密度项对时间的微分,从而降低了计算成本。为保证在计算过程中的能量守恒,Dong等[6]通过使相变量由传入界面热量直接算出,建立了基于LBM的计算模型。胡安杰[7]在考虑到相变量的值不能直接给定和Dong等[6]提出的相变过程很难反映气泡生长过热度等问题后,提出了通过热力学理论推导来获取温度方程中的源项。何航行[8]发现在相界面位置状态方程计算所得的压力和实际情况不符合,同样提出通过引入汽化潜热的方式代替源项中涉及压力的部分,同时进一步对汽化潜热计算进行详解。Wang等[9]在研究非相变的对流换热过程中提出了固液共轭传热模型,对密度分布函数和温度分布函数耦合求解,得出了更加真实的模拟结果。
笔者发现单组分多相伪势模型求解沸腾换热过程时没有考虑固相和液相间存在不同的能量传递速率,导致计算的温度场分布与实际相差较大。目前关于沸腾相变换热的LBM数值研究中,大多采用相同的能量传递速率来处理固相和液相的传热能力,而考虑固相和液相不同能量传递速率的模型少有报道。为更加准确地反映沸腾换热的实际微观机理,本文在Kupershtokh等研究的伪势模型基础上,将固、液相的热物理性质分别引入温度弛豫时间,发展了新的固液共轭沸腾传热格子Boltzmann模型,并验证了模型的准确性、稳定性和合理性,对比分析了原始伪势模型和固液共轭沸腾传热模型对计算区域单气泡热物理场的影响,此外需说明的是本文中的单位无特殊说明外,都是格子单位。
1 固液共轭沸腾传热模型的描述
1.1 多相流LB伪势模型
单组分多相LB模型的密度演化方程可以表示为
fi(x+eiδt,t+δt)-fi(x,t)=
(1)
式中:fi(x,t)为t时刻在x离散方向上的粒子分布函数;τ是弛豫时间;δt为格子离散的时间步长;fieq(x,t)为相对应的平衡态粒子的分布函数,Δfi(x,t)为体积力项。
LBM伪势模型中的两相是由相间的粒子相互作用力驱动产生的。模型中总力F由下式表示:
F=Fint+Fw+Fg。
(2)
式中:Fint为相间的相互作用力项;Fw为壁面的吸附力项;Fg为重力项。
本文采用的相互作用力格式是Kupershtokh等[3]提出的将有效密度形式和势函数形式结合起来的新作用力格式,通过调节加权参数A来提高模型的稳定性,其表达式为
(3)
式(3)中:eα表示离散速度。D2Q9模型中eα的表达形式为
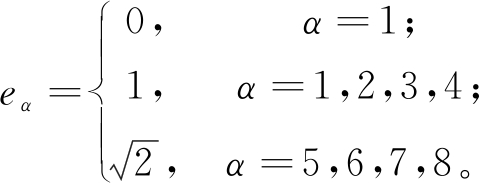
(4)
式(3)中w(|eα|2)表示权系数,与相互作用的2个格点的位置有关,在D2Q9模型中仅考虑相邻格点上粒子的相互作用力时,其值可取为
(5)
式(3)中U(x+eαδt,t)被定义为相邻粒子节点的势函数,具体表达式由非理想气体状态方程得出
(6)
式(3)中Ψ(x,t)由Yuan等[10]逆推有效密度得到
(7)
式中:c0在D2Q9模型中取值为6;压力p由P-R非理想气体状态方程得出,P-R状态方程设置和临界温度Tc、临界密度ρc取值见文献[11]。
流体域壁面的作用力Fw表示为
![]() (8)
(8)
式中:s(x)为壁面作用力函数,当临近壁面是固体时,s(x)=1,为流体时,s(x)=0;Gs为作用力强度系数,本文通过改变Gs值获得不同的壁面接触角。
重力项Fg表示为
Fg=(ρ(x)-ρave)g。
(9)
式中:ρave为流体域中的平均密度;g为重力加速度。
1.2 温度方程
温度演化方程表示如下:
gi(x+eiδt,t+δt)-gi(x,δt)=
(10)
式中:gi(x,t)为t时刻在x离散方向上的粒子温度分布函数;gieq(x,t)为相对应的温度平衡态粒子的分布函数。
在传统的单组分多相LB伪势模型中,固体和液体区域的温度弛豫时间τT常取1,因此固体和液体区域的能量传递速率相等,这导致此模型无法真正反映固液区域不同的传热特性,本文称此伪势模型为“原始伪势模型”。而实际上,固体和液体区域在固液交界面上为耦合共轭传热过程,由于固体和液体区域的λ、cp、ρ等物性参数存在巨大差异,导致固体和液体区域的能量传递速率相差很大,即两个区域的τT相差较大。为了更准确地预测固液共轭传热,本文引入了固液区域不同的热导率λ和比热容cp对τT进行修正[9],发展了一种具有不同能量传递速率的固液共轭沸腾传热LB模型。修正的τT表达式如下:
(11)
为修正状态方程计算所得的压力在界面区域与实际情况不符而导致的相变潜热出现偏差的情况,引入相变源项φ:
(12)
相变过程中的汽化潜热hlg满足hlg=hg-hl,hg和hl分别为饱和气相和饱和液相的焓值,定义函数f(ρ)与hlg存在的关系[8]如下:
(13)
2 模型验证
2.1 准确性验证
在完善了固液共轭沸腾传热模型后,分别采用Maxwell理论解、Young-Laplace定律对模型的准确性和稳定性进行了验证,并对共轭传热模型进行了合理性分析。在热力学中,气、液两相密度大小取决于系统是否处于热力学平衡状态。根据Maxwell定律,系统处于热力学平衡状态时,Gibbs自由能和温度都维持恒定状态。在等温相变两相流模型中,气液两相的自由能相等,Gibbs自由能表达式为
(14)
式中:p0为对应温度下饱和气体和饱和液体对应的压力。
本文选用的非理想气体状态方程为P-R状态方程,在确定非理想气体状态方程的等温两相流模型中,可根据Maxwell定律得到对应温度下密度的理论解曲线。对于伪势模型,通过改变相间作用力下的权系数A得到了不同的数值解,最后通过理论解与数值解的对比判断模型的准确性[12]。图1表示P-R状态方程的Maxwell理论解和文献[3]中提出的作用力格式下不同加权系数A的模型数值解之间的拟合关系。通过伪势模型进行加权系数A=-0.30、-0.16、0.10的模型验证,结果表明,不同加权系数取值得到的数值解和Maxwell理论解都较为接近,当加权系数A=-0.16时,模型数值解和理论解拟合度最好。
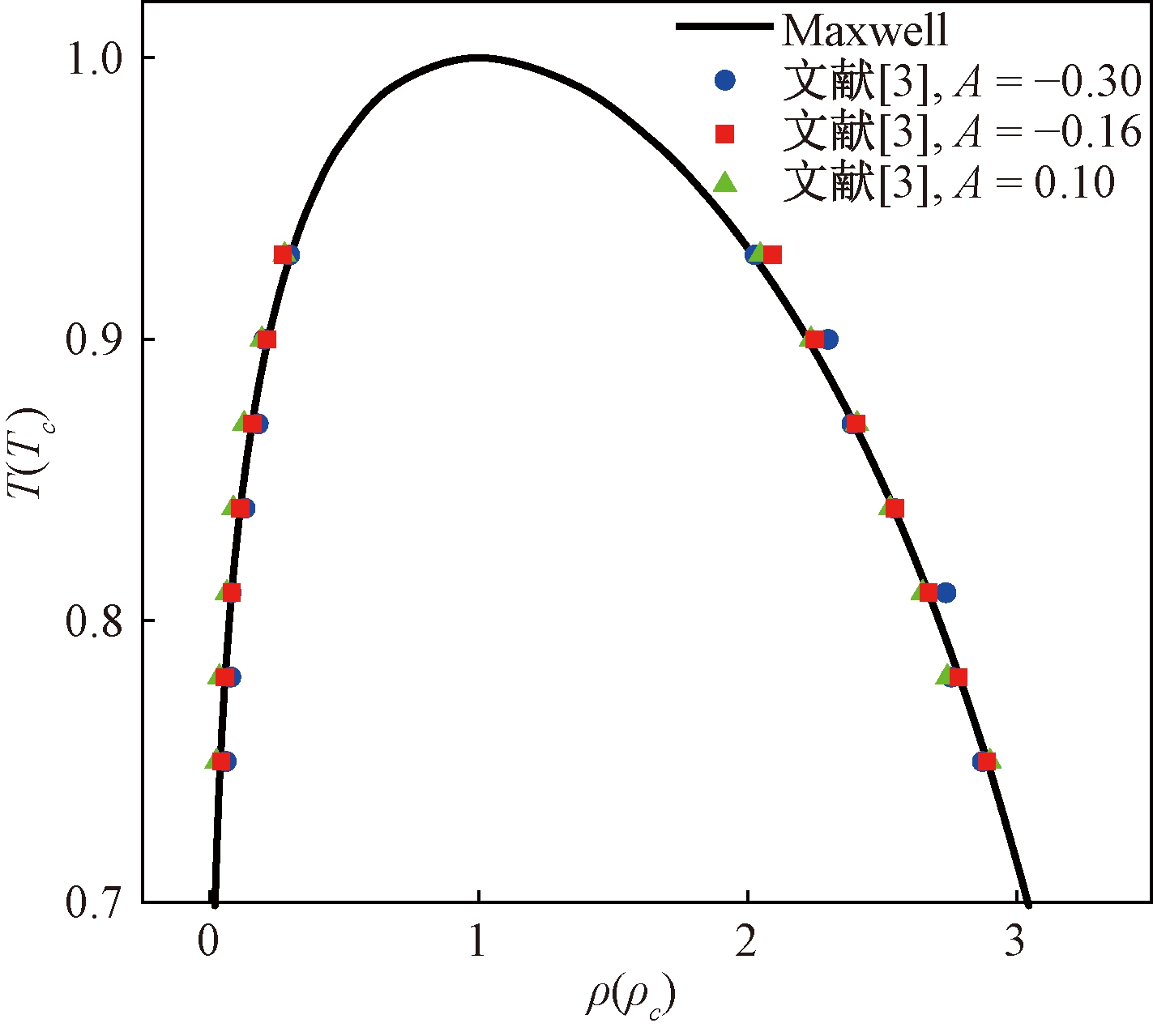
图1 P-R状态方程下Maxwell理论解和不同权系数下模型实际值的对比
Figure 1 Comparison between Maxwell′s result of P-R state equation and model′s value under different weight coefficients
2.2 固液共轭传热模型合理性验证
为了验证共轭传热模型的合理性,设置了100×100的计算域,底部为恒温热源,顶部为恒温冷源,两侧为周期性边界,高度y≤50时为固体区域,y>50时为液体区域,分别采用原始伪势模型和共轭传热模型对计算域固、液间传热进行模拟。图2为在相同的恒温热源和恒温冷源作用下,采用两种模型分析的不同高度y处的温度T变化。由图2可知,在引入影响τT的参数λs、λl、cps、cpl前,原始伪势模型固液区域的传热能力一致,温度场呈现一维传热特征,温度梯度均为ΔT/Δy=5.03×10-4。而固液共轭传热模型引入参数后,温度场呈现出固、液区为不同温度梯度的传热情况,液体区域的温度梯度(ΔT/Δy)l为2.78×10-5,固体区域的温度梯度(ΔT/Δy)s为9.78×10-4,且固液耦合面的温度保持相等Ts=Tl。
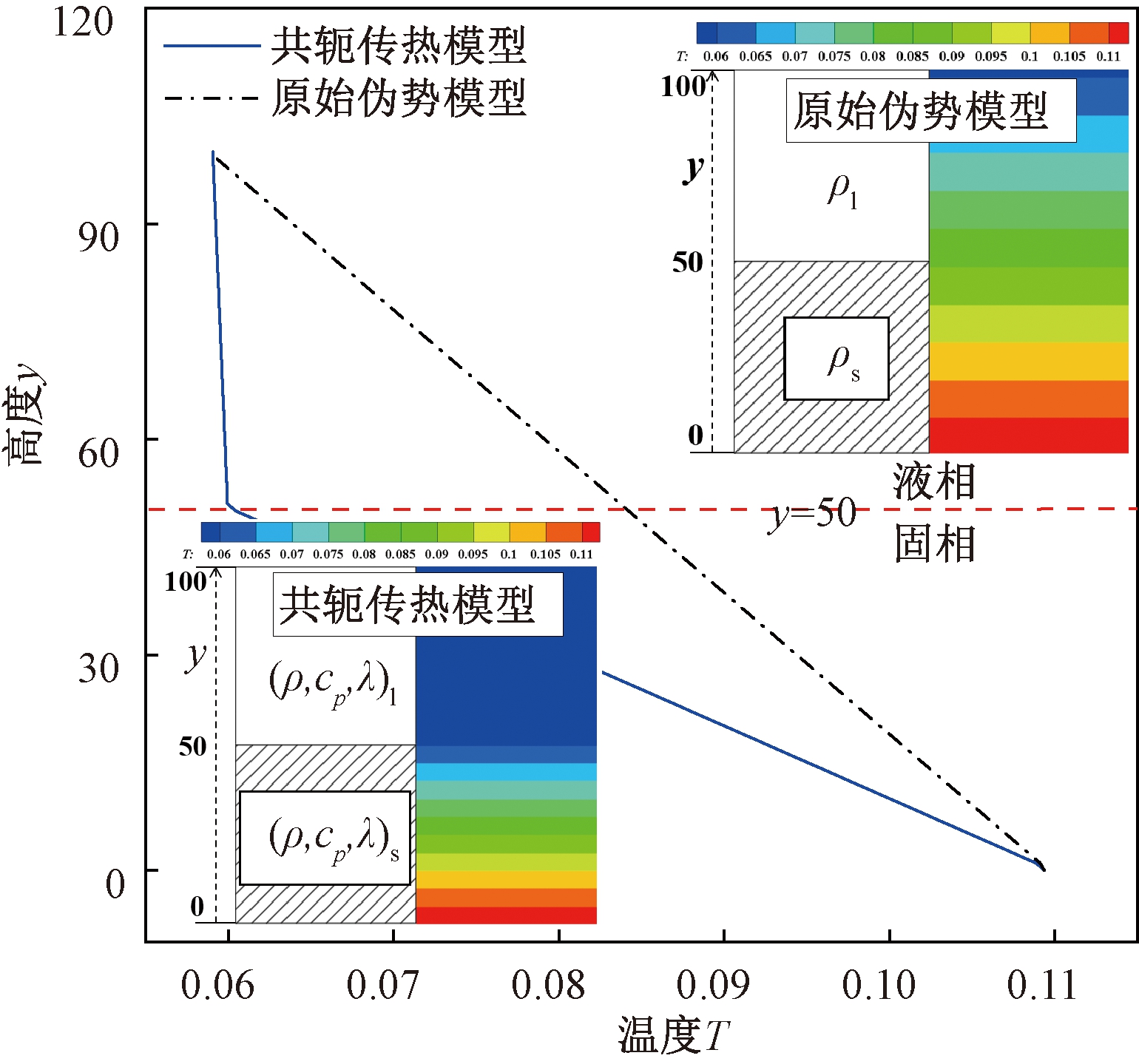
图2 两种模型不同高度上的温度变化
Figure 2 Temperature variation at different heights of two models
通过在固液共轭传热模型中引入固体和液体的物性参数,得到不同的温度弛豫时间τT,从而获得了固液区域不同的能量传递速率,固体区的能量传递速率远高于液体区,这与实际的物理过程情况相符,说明本文提出的共轭沸腾传热模型更为合理。
3 计算域和参数设置
在验证了固液共轭传热模型的稳定性、准确性和合理性后,分别采用原始伪势模型和固液共轭沸腾传热模型对不同润湿性平表面上的沸腾换热过程进行了数值计算,以比较两种模型的差异。为方便地描述无量纲模型中的无量纲长度和无量纲时间,本文引入文献[13]中的特征参数l0、u0、t0的定义,池沸腾的计算域结构如图3所示,沸腾室总体尺寸为8.83l0×5.89l0,高温底面为恒温壁面,左右两侧均为周期性边界,顶部为压力出口边界[14]。在初始时刻,流体区内充满液体,整个计算域温度设置为0.81Tc。因为固体的传热系数大、降温快,为维持换热表面温度高于工质相变温度,固体区域不宜设置太厚,此处Hw=0.294l0。为确保2种模型的沸腾换热强度相同,设定换热表面温度T*=0.091 7,通过核算,采用共轭传热模型和原始伪势模型计算时,高温底面温度需分别设置为1.5Tc和1.18Tc,这样采用2种模型得到的实际换热表面温度Ts几乎相同,为Ts=(100±1)%T*。
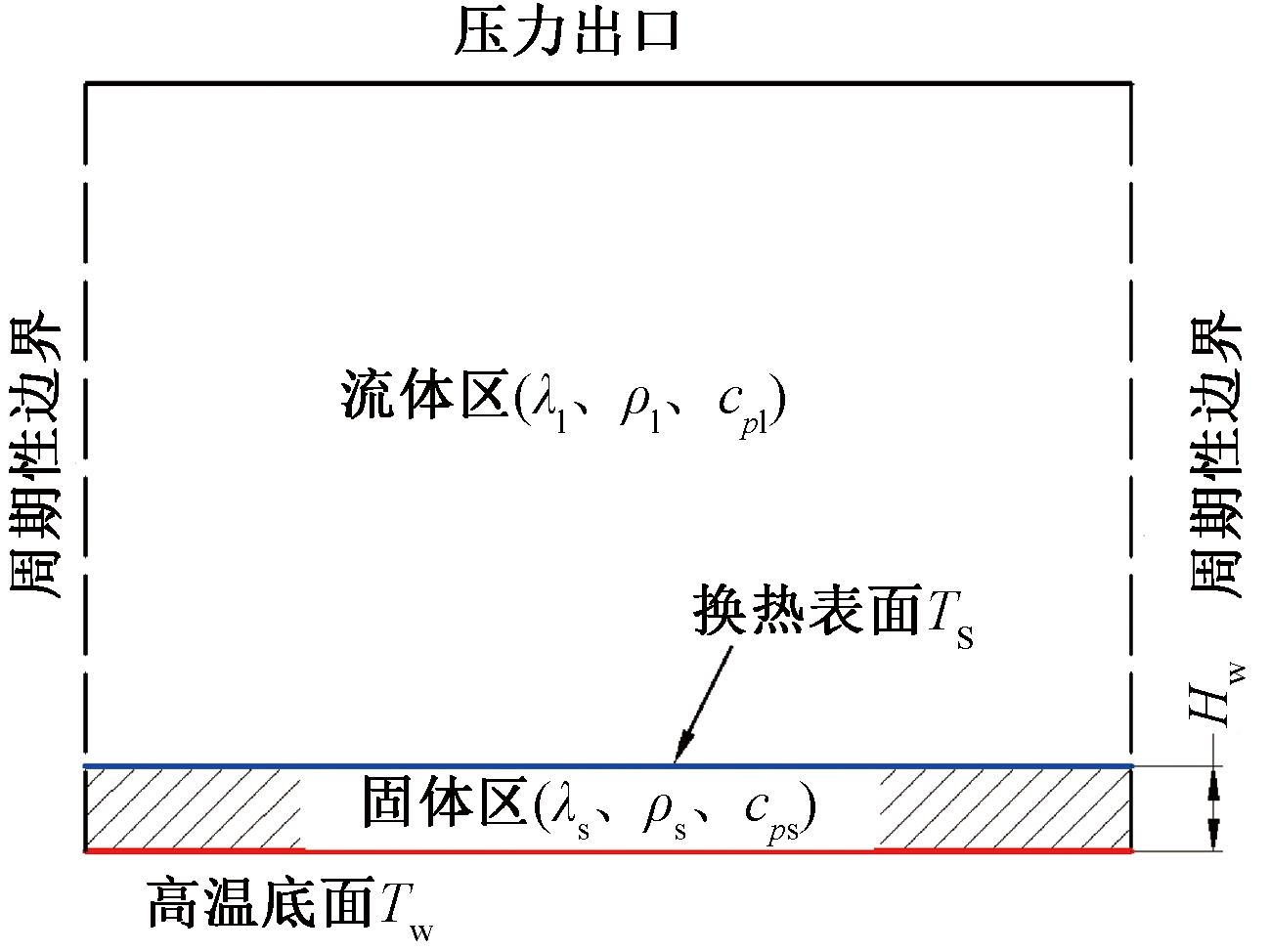
图3 沸腾室原理图
Figure 3 Schematic diagram of boiling domain
为了考察原始伪势模型和固液共轭传热模型在处理相变换热时的差异,本文对换热壁面进行了不同的亲疏水处理,换热表面参数设置如表1所示。
表1 换热表面参数
Table 1 Heat transfer surface parameters

参数数值Ts(100±1)%T*Hw0.294l0θ7.5°、 12.5°、 28.8°、 50.1°、 75.6°、 88.2°、101.7°、 112.7°、 127.7°、 138.5°、 148.9°
4 模型计算结果的对比分析
4.1 对密度场分布的影响
图4为原始伪势模型和共轭传热模型在沸腾过程中生成相同体积气泡时的密度云图。在实际情况下,沸腾区域由于生成气泡带走了大量的汽化潜热,导致气泡根部周围的流体温度降低,不会出现较低密度的相变区。从图4中可以看出,共轭传热模型和原始伪势模型在沸腾过程中都存在低密度相变区,但共轭传热模型中的低密度相变区范围明显小于原始伪势模型,且相变程度更低(ρ共轭=6、ρ原始=5)。对于沸腾计算域,换热表面温度值相等Ts-共轭=Ts-原始,而共轭传热模型的底面温度(1.5Tc)高于原始伪势模型的底面温度(1.18Tc),其温度梯度也大于原始伪势模型的温度梯度,因此底部传输到沸腾区域的热流密度远大于原始伪势模型。以此推理,由于共轭传热模型传输的热流密度大,在固液交界面上方的液体应该更容易过热而出现低密度相变区,但图4中云图显示,相比于原始伪势模型,共轭传热模型计算的气泡根部周围出现低密度相变区的范围更小、程度更低,与实际情况更为贴切,说明固液共轭沸腾传热格子Boltzmann模型更能真实反映沸腾换热过程中气泡周围的微观过程。
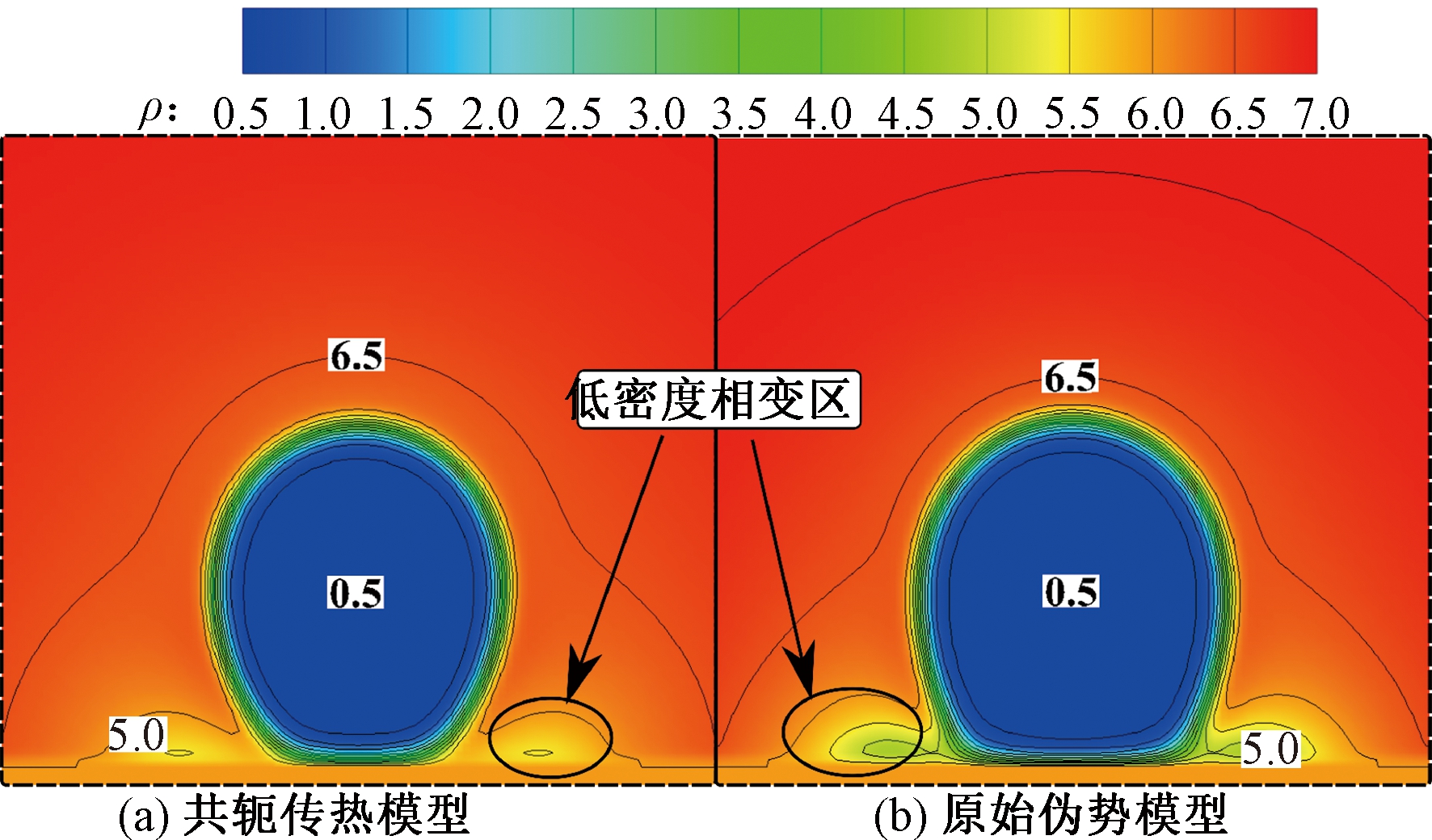
图4 两种模型密度云图
Figure 4 Density contour of the two models
图5为在相同亲水性表面发生液体沸腾时,生成相同体积气泡所受的竖直方向作用力示意图。根据伪势模型的计算公式,竖直方向的作用力Fy由重力Fg、壁面作用力Fw、相间作用力Fint叠加而得。对于原始伪势模型,由于气泡根部周围存在较大范围的低密度相变区,这个低密度相变区会对气泡产生额外的相间作用力Fint-p,导致气泡形状发生改变,使得气泡的实际壁面接触角并不等于预先设定的壁面接触角。而对于共轭传热模型,低密度相变区范围很小,对壁面接触角的影响较小。因此,原始伪势模型的实际壁面接触角与设定壁面接触角的偏差程度远大于共轭传热模型。而壁面接触角的改变对沸腾时气泡的生长、脱离行为有着重要影响,壁面接触角越小,气泡的脱离周期越短,脱离频率越快,越能增强流场的湍流程度[15];另外,壁面接触角越大,气泡可以越早进入核态沸腾,但壁面接触角过大,会导致气泡过早进入膜态沸腾,使得传热恶化。因此,对于沸腾换热格子Boltzmann模型,尽可能减少低密度相变区额外产生的相间作用力Fint-p,获得正确的气泡作用力和壁面接触角,对正确仿真沸腾换热过程非常重要。
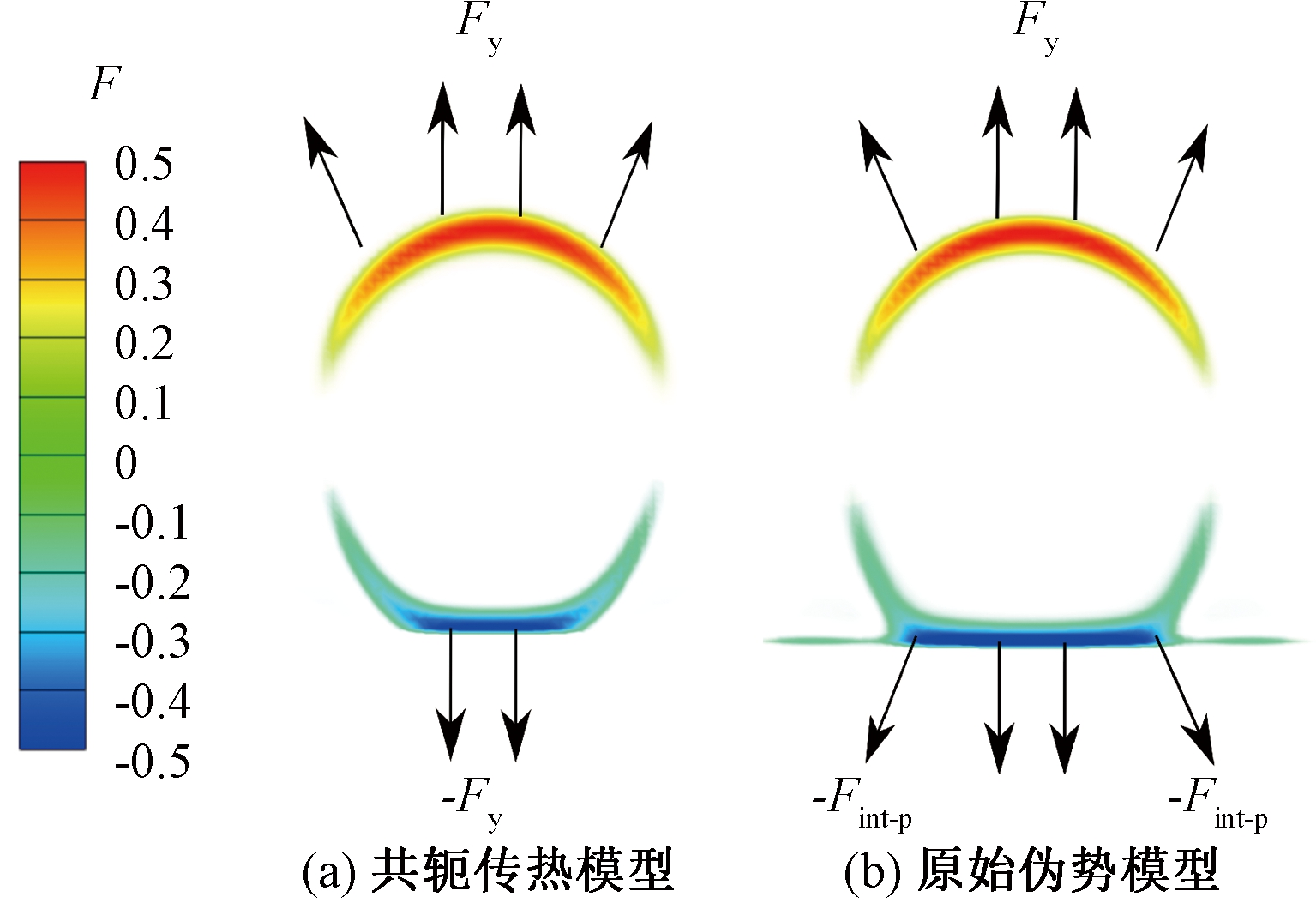
图5 两种模型的竖直方向作用力
Figure 5 Vertical forces of these two models
4.2 对实际壁面接触角的影响
为了进一步证实两种模型获得气泡的实际接触角的差异,设定了不同的初始壁面接触角θ(如表1所示),分别采用两种模型数值仿真了沸腾换热过程,得到了相同气泡体积时的气泡形貌。图6为设定接触角与沸腾时两种模型获得的实际壁接触角之间的变化关系。由图6可见,通过两种模型获得的实际接触角与设定接触角的变化趋势一致,实际接触角都随着设定接触角的增大而增大,但共轭传热模型的实际壁面接触角较原始伪势模型的设定接触角更为接近,切合程度更高,说明共轭传热模型计算的气泡形貌和传热特性更接近于实际。从图6中可以看出,当设定接触角θ<119°,两种模型获得的实际接触角均大于设定值,这是由于两种模型获得的气泡周围均存在低密度相变区,该区的气膜会对气泡产生额外的相间作用力Fint-p,导致气泡受到垂直向下的作用力增强,气膜弱化了壁面处液体的润湿性,所以实际的接触角增大,尤其对于亲水性表面,气膜弱化壁面润湿性的作用更强。随着接触角的减小,共轭传热模型和原始伪势模型同时表现出误差增大的趋势。对于除超亲水表面(θ=7.5°、12.5°)以外的其他润湿性表面,共轭传热模型和原始伪势模型获得的实际接触角的最大相对误差分别为8.6%和18.4%,相较于原始伪势模型,共轭传热模型实际接触角的最大相对误差降低了9.8个百分点。
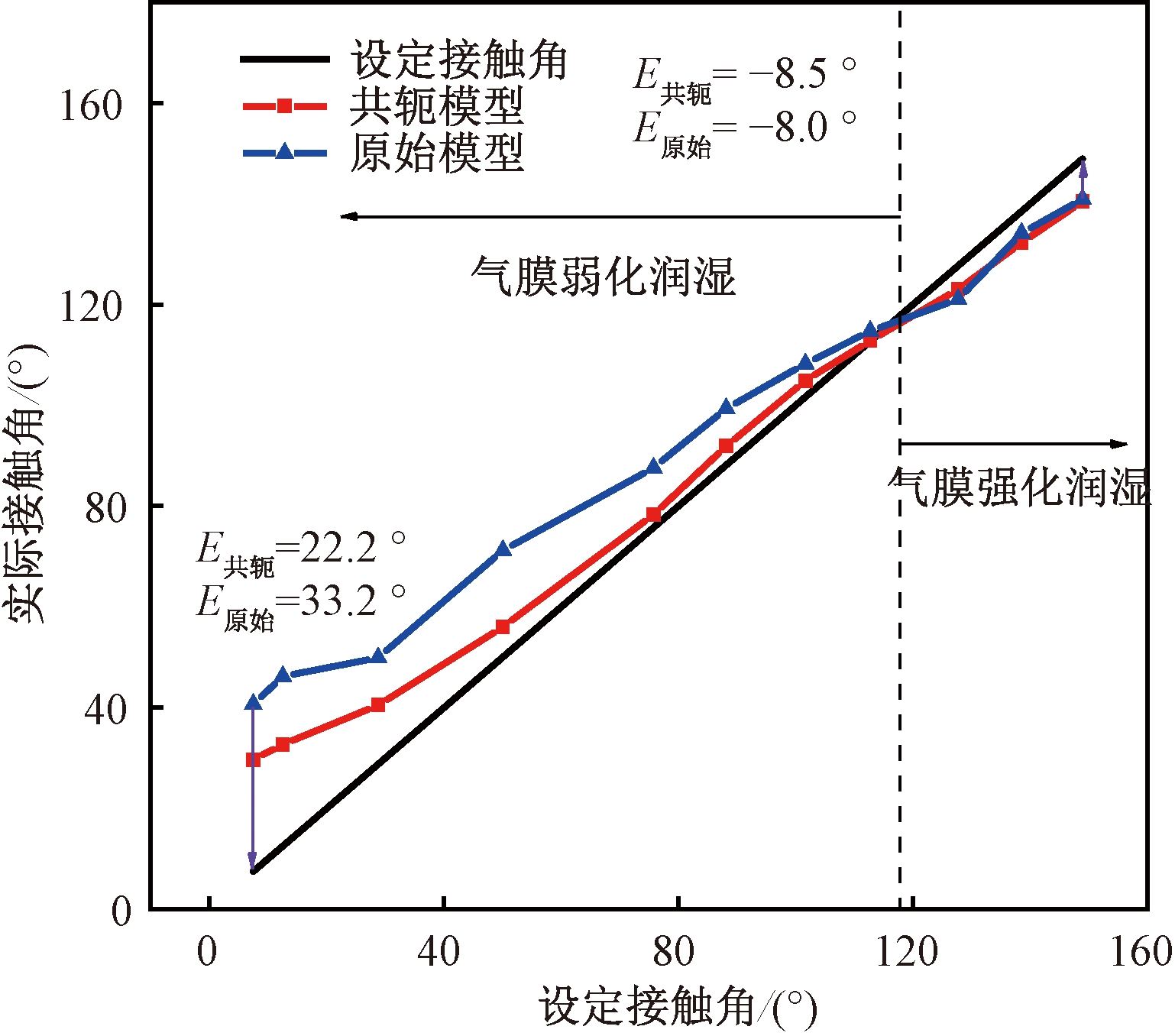
图6 两种模型获得气泡的实际接触角与设定接触角的关系
Figure 6 The actual contact angles and the set contact angles obtained by two LB models
图7为不同润湿性表面上两种模型获得的气泡附着状态。从图7中可看出,对于疏水性表面,由于壁面接触角较大,两种模型获得的气泡平铺于壁面使得气泡和低密度相变区混合,气相密度由原设定值0.51都进一步提高至0.59,壁面作用力Fw进一步减小,表现为气膜强化了壁面的液体润湿性,所以实际的接触角减小。但是对于疏水性表面,气膜强化液体润湿性的影响较小,而且两种模型计算的气泡的实际接触角相差也不大。

图7 不同润湿表面上两种模型获得气泡的附着状态
Figure 7 Adhesion status of bubbles obtained by two LB models at different wettability surfaces
当设定接触角θ>119°时,2种模型获得的实际接触角均小于设定值。当设定接触角θ=148.9°时,共轭传热模型和原始伪势模型的接触角绝对误差分别到达了E共轭=-8.5°,E原始=-8.9°。通过上述分析可知,原始伪势模型在模拟不同接触角相变问题时存在接触角和设定值不符合的现象,而固液共轭传热模型可有效减小模拟结果的误差,使得模拟结果更能反映沸腾换热的真实情况。
5 结论
本文基于原始伪势模型,提出了固液共轭传热沸腾换热格子Boltzmann模型,采用两种模型对不同润湿性表面的沸腾传热过程进行了数值仿真和对比分析,得出以下结论。
(1)原始伪势模型计算获得的气泡根部周围存在范围较大的低密度相变区,其存在导致气泡下部产生了额外的相间作用力,从而改变了气泡的实际接触角,而共轭传热模型获得的低密度相变区范围很小,程度更低,获得的密度场更为真实。
(2)相比于原伪势模型,共轭传热模型获得气泡的实际壁面接触角更接近于设置的气泡接触角,更能准确表征气泡与壁面之间的实际润湿情况。对于除超亲水表面外的其他润湿性表面,共轭传热模型获得的实际接触角的最大相对误差为8.6%,较原始伪势模型降低了9.8%。
(3)通过引入温度弛豫时间函数,实现了对固体和液体区域不同的热物理性质的表征,从而获得了固液共轭沸腾传热LB模型,该模型能够更加准确和真实地反映实际的沸腾换热微观过程。
[1] GONG S, CHENG P. Two-dimensional mesoscale simulations of saturated pool boiling from rough surfaces. Part II: bubble interactions above multi-cavities[J]. International Journal of Heat and Mass Transfer, 2016, 100: 938-948.
[2] ZHANG R Y, CHEN H D. Lattice Boltzmann method for simulations of liquid-vapor thermal flows[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2003, 67(6): 066711.
[3] KUPERSHTOKH A L, MEDVEDEV D A, KARPOV D I. On equations of state in a lattice Boltzmann method[J]. Computers & Mathematics with Applications, 2009, 58(5): 965-974.
[4] 曾建邦, 李隆键, 廖全, 等. 沸腾过程的格子Boltzmann方法模拟[J]. 西安交通大学学报, 2009, 43(7): 25-29.
ZENG J B, LI L J, LIAO Q, et al. Simulation of boiling process with lattice boltzmann method[J]. Journal of Xi′an Jiaotong University, 2009, 43(7): 25-29.
[5] GONG S, CHENG P. A lattice Boltzmann method for simulation of liquid-vapor phase-change heat transfer[J]. International Journal of Heat and Mass Transfer, 2012, 55(17/18): 4923-4927.
[6] DONG Z Q, LI W Z, SONG Y C. Lattice Boltzmann simulation of growth and deformation for a rising vapor bubble through superheated liquid[J]. Numerical Heat Transfer, Part A: Applications, 2009, 55(4): 381-400.
[7] 胡安杰. 多相流动格子Boltzmann方法研究[D]. 重庆: 重庆大学, 2015.
HU A J. Studies on lattice Boltzmann method for multi-phase flow[D]. Chongqing: Chongqing University, 2015.
[8] 何航行. 两相流动及沸腾过程气泡动态特性的多尺度模拟研究[D]. 重庆大学, 2016.
He H X. Multi-scale simulation of two-phase flow and bubble dynamics during boiling period[D]. Chongqing: Chongqing University, 2016.
[9] WANG J K, WANG M R, LI Z X. A lattice Boltzmann algorithm for fluid-solid conjugate heat transfer[J]. International Journal of Thermal Sciences, 2007, 46(3): 228-234.
[10] YUAN P, SCHAEFER L. Equations of state in a lattice Boltzmann model[J]. Physics of Fluids, 2006, 18(4): 042101.
[11] 曾建邦, 李隆键, 廖全, 等. 池沸腾中气泡生长过程的格子Boltzmann方法模拟[J]. 物理学报, 2011, 60(6): 520-529.
ZENG J B, LI L J, LIAO Q, et al. Simulation of bubble growth process in pool boiling using lattice Boltzmann method[J]. Acta Physica Sinica, 2011, 60(6): 520-529.
[12] GONG S, CHENG P. Numerical investigation of droplet motion and coalescence by an improved lattice Boltzmann model for phase transitions and multiphase flows[J]. Computers & Fluids, 2012, 53: 93-104.
[13] SON G, DHIR V K, RAMANUJAPU N. Dynamics and heat transfer associated with a single bubble during nucleate boiling on a horizontal surface[J]. Journal of Heat Transfer, 1999, 121(3): 623-631.
[14] ZOU Q S, HE X Y. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model[J]. Physics of Fluids, 1997, 9(6): 1591-1598.
[15] 王现宝. 多尺度仿生交错润湿性表面沸腾传热性能及机理[D]. 长春: 吉林大学, 2015.
WANG X B. Boiling heat transfer performance and mechanism of biomimetic multi-scale interlaced wettability surface[D]. Changchun: Jilin University, 2015.