0 引言
近年来,随着机器人技术日益广泛应用,对多自由度机器人的需求更加迫切。目前,应用最广泛的是串联机器人,具有工作空间大、结构简单、成本低等特点[1]。但是,串联机器人只有一条控制链,存在误差积累效应,且负载能力较弱[2]。相较而言,并联机器人负载能力强且包含多自由度,已被应用到多个行业[3-6]。
并联机器人结构复杂,包含较多的关节与铰链,在工作过程中存在精度误差。影响机器人精度的参数很多,Roth等[7]将所有参数分为3个级别:关节参数、运动学参数及非运动学参数。为了消除各种参数对精度的影响,需要对参数进行标定,即通过外部手段,对这些影响精度的参数进行辨识,使其更加接近机器人的实际参数。Judd等[8]在研究中发现,运动学参数的标定对机器人精度的提高具有最显著的效果。机器人的运动学标定问题主要分为误差建模、标定位形测量、参数辨识及精度补偿[9]。
运动学参数辨识根据实际运动数据和建立的理论模型来确定模型中涉及的参数值,使辨识出的参数能够更好地符合实际情况,从而减小误差。精准的运动学参数是确保机器人精度的关键,因此,高精度参数辨识的方法尤为重要。目前,多种优化算法被应用到参数辨识领域,且取得了良好的效果[10-12]。Wang等[13]改进基础粒子群(PSO)算法,并将其用于机器人标定中的最佳位姿选择。姜一舟等[14]结合Metropolis接受准则与差分进化(DE)算法提出一种MDE算法,对6自由度串联机器人进行了运动学参数辨识与标定,提高了DE算法优化能力,但收敛速度变慢。寇斌等[15]提出一种LDPSO-BT算法对工业机器人几何参数进行标定,克服了传统PSO算法收敛速度慢的缺点。Luo等[16]使用LM算法和DE算法对机器人运动学参数进行分步辨识标定,提高了机器人定位精度。
基于上述研究,本文以3-RPS并联机器人为实验对象,建立了其逆运动学模型和误差模型,并对引起误差的运动学参数进行了标定。为了确保参数标定的效果,在DE算法的基础上提出了一种基于竞争的多变异策略差分进化(CMDE)算法。利用CMDE算法辨识出的参数对逆运动学理论模型进行修正,并通过Adams验证了修正后逆运动学模型的准确性。
1 运动学分析
1.1 3-RPS并联机器人
3-RPS并联机器人结构如图1所示,主要由静平台、动平台、3条对称支链3部分组成。在工作过程中,静平台固定在下方,通过驱动3条支链控制动平台运动。由图1可以看出,静平台和动平台由3条支链连接,每条支链包含1个转动副、1个移动副、1个球副。其中,移动关节为主动关节,转动关节和球关节为被动关节,动平台在3条支链的约束下可实现旋转和平移功能[17]。
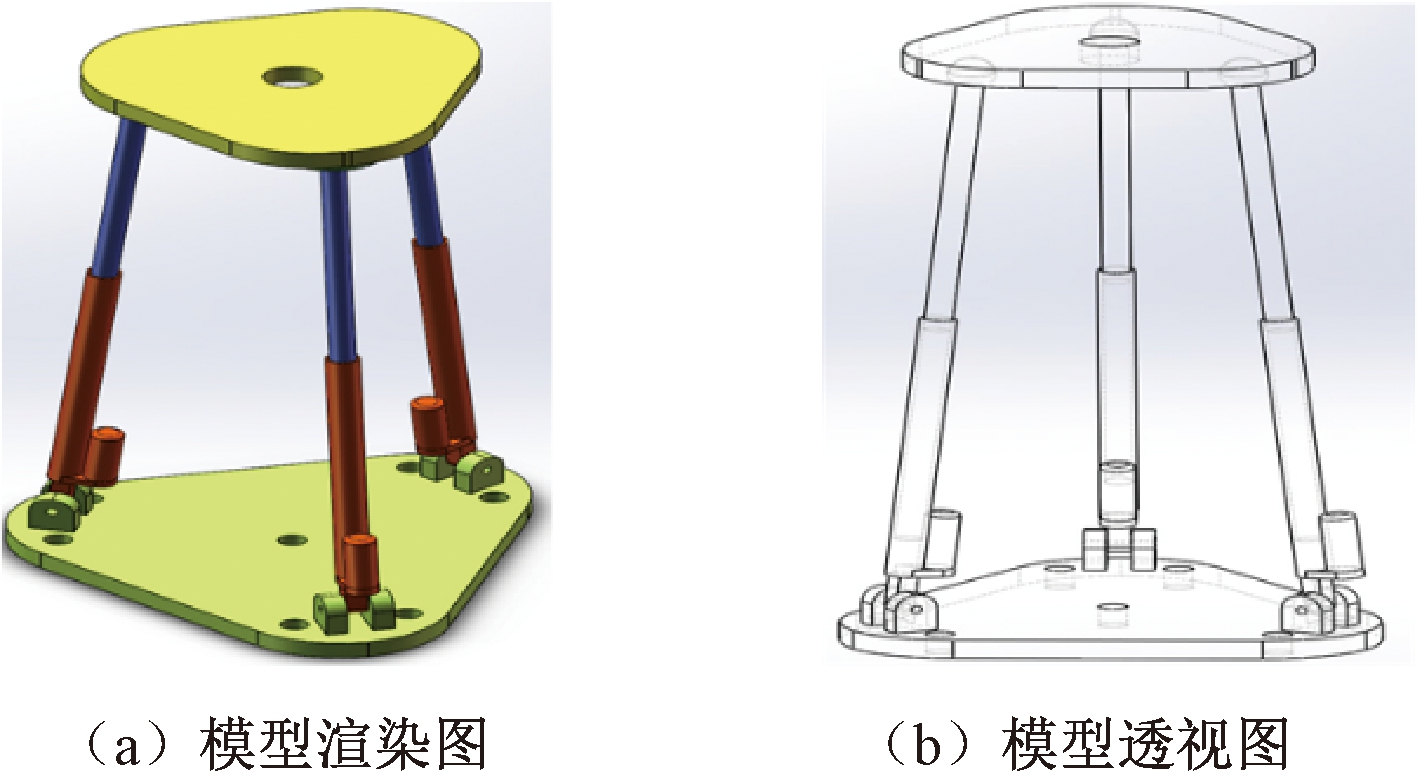
图1 3-RPS并联机器人模型
Figure 1 Model of 3-RPS parallel robot
1.2 逆运动学模型
在初始位姿下,分别在静平台与动平台上建立如图2所示的坐标系。坐标系{a}建立在静平台上,原点位于静平台中心处,3个转动副呈正三角形分布,其外接圆半径为r。坐标系{b}建立在动平台上,原点位于动平台中心,动平台与静平台结构相似,其外接圆半径为R1。
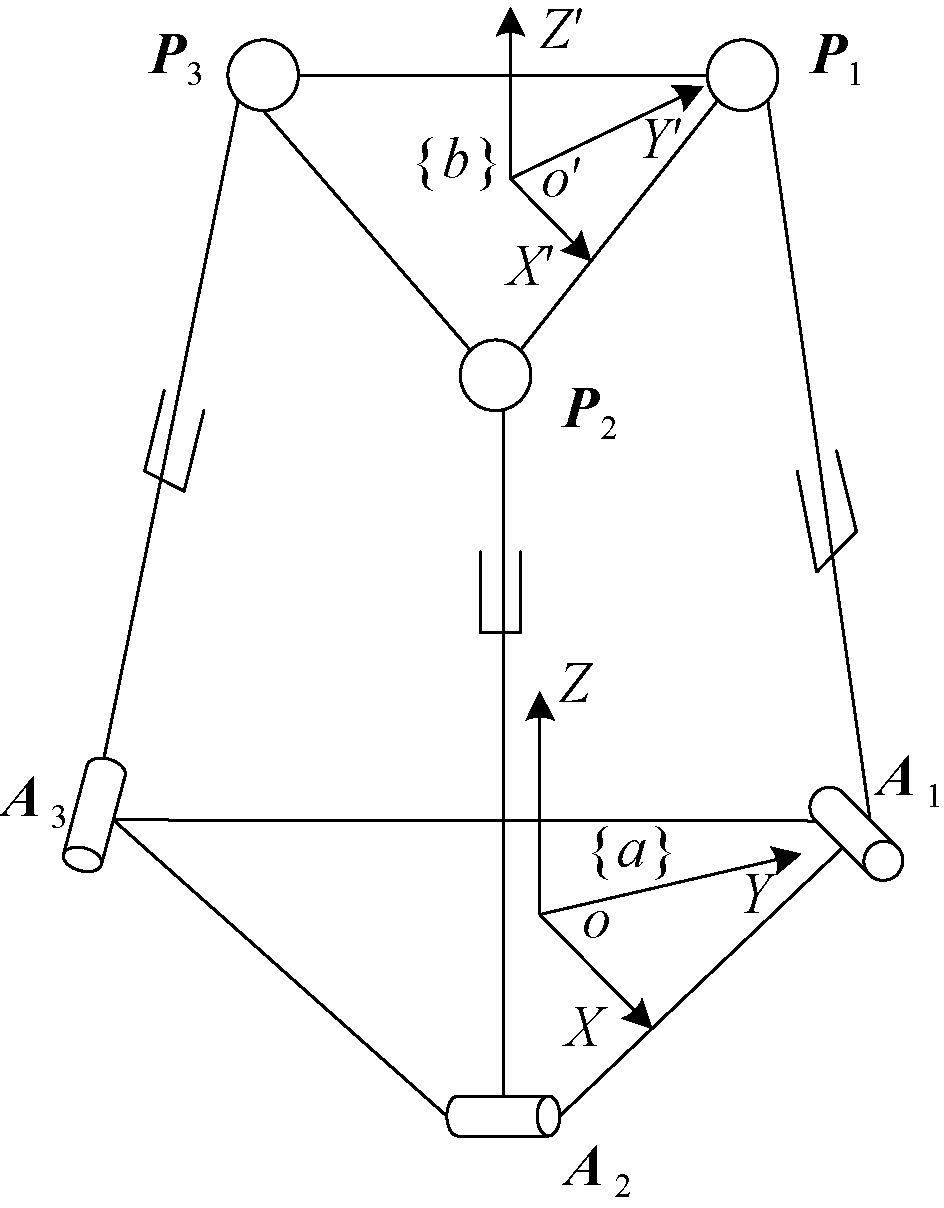
图2 3-RPS坐标系
Figure 2 Coordinate system of 3-RPS
图2中,Ai代表转动副的铰点,Pi代表球副的铰点,其中i=1,2,3。由正三角形特性可知,Ai与Pi在各自坐标系下的空间坐标为
(1)
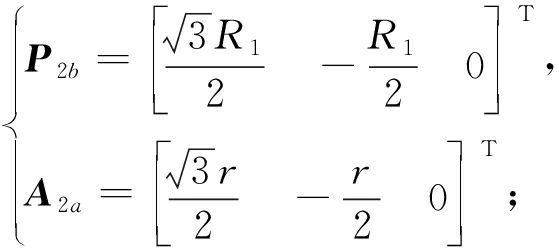
(2)
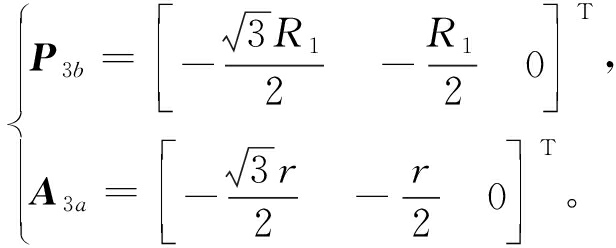
(3)
在并联机器人工作过程中,静平台固定不动,动平台以坐标系{a}为世界坐标系旋转平移后,坐标系{b}相对于坐标系{a}的旋转矩阵和平移矩阵分别为
(4)
旋转平移后,Pi在坐标系{a}中空间坐标为
Pia=RPib+P。
(5)
由于转动副的限制,球副在以下3个平面运动:
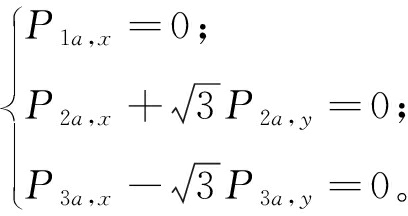
(6)
将Pia的空间坐标分别代入上式,可得出该并联机器人的约束方程式:
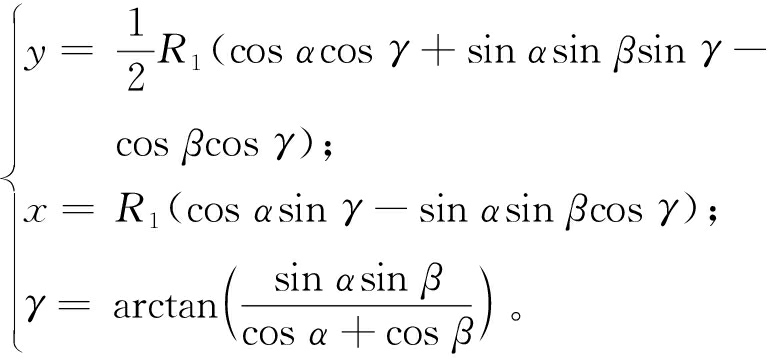
(7)
由式(7)可知,该机构绕Z轴旋转的角度γ受到绕X轴与Y轴旋转角度α、β的约束,沿着X轴和Y轴的平移量受到旋转角度α、β、γ的约束。因此,该并联机器人只有3个独立自由度。在本文中的逆运动学分析时也仅涉及3个独立自由度,以此为输入对运动学参数进行标定。
逆运动学模型,即给定末端执行器的位姿参数,求解在该位姿下驱动关节的数值。对于本文中的3-RPS并联机器人,给定动平台的转角α、β以及沿Z轴的平移量z,求解该位姿下3个驱动杆的位移量。由式(1)~式(3)可算出初始位姿下Pi在坐标系{b}中的空间坐标和Ai在坐标系{a}中的空间坐标。给定动平台的转角α、β以及沿Z轴的平移量z,通过式(4)可求得该位姿下的变换矩阵,从而通过式(5)解出坐标系{a}中Pi的空间坐标。对于3-RPS并联机器人,Pi与Ai之间的距离即为给定位姿下驱动杆的长度,故只需知道初始位姿下驱动杆长度L0i就可求出驱动杆的位移量。因此,该3-RPS并联机器人的逆运动学模型可表示为
mi=‖Pia-Aia‖-L0i, i=1,2,3。
(8)
由式(8)可知每个驱动杆的单位矢量为
(9)
1.3 误差分析及误差模型建立
在并联机器人的构型设计、尺寸设计、加工为成品、投入使用的整套流程中,存在多种因素会引起设计尺寸与实际尺寸的偏差,从而影响精度[18]。不仅如此,在并联机器人工作过程中,往往需要添加传感器来获取运动数据,这又带来测量偏差。因此,按照设计参数建立的逆运动学模型控制并联机器人的运动,其控制效果往往不尽人意。为了避免这种状况的发生,必须对并联机器人进行参数标定,并通过标定后的运动学参数对逆运动学模型进行修正补偿,从而使其达到理想的精度标准[19]。
由式(8)和式(9)可以得出每个连杆的矢量表达式:
Liui=RPib+P-Aia。
(10)
式中:Li为每个连杆的长度;ui为由Ai指向Pi的单位矢量。
对式(10)两端进行微分,可得
(11)
由机器人微分关系,可得
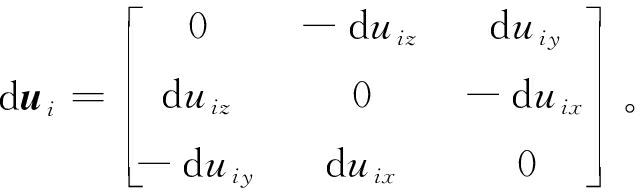
(12)
由旋转矩阵的摄动矩阵得
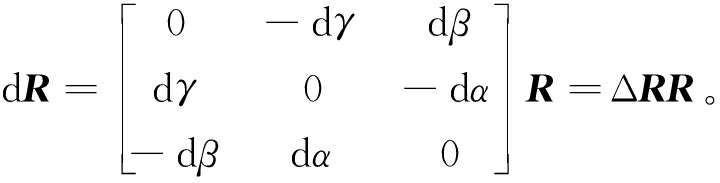
(13)
式中:dα、dβ、dγ为动平台的姿态误差分量,用dω=[dα dβ dγ]T表示旋转矩阵R中的误差分量。对式(11)两端同乘![]() 由于
由于![]() 且
且![]() 故式(11)可化简为
故式(11)可化简为
(14)
式(14)可化为
dLi=J1dM+J2dK。
(15)
对式(15)进行化简,可得其误差模型:
(16)
式中:dM=[dP dω]T,表示动平台位姿误差;dK=[dPib dAia]T,表示球副和转动副引起的误差。
按照图2建立的坐标系与式(16)建立的误差模型对引起位姿误差的参数进行分析。设球副铰点的位置Pi与坐标系{b}中的X′轴的夹角为ai,则Pi在坐标系{b}中的空间坐标为
Pib=[R1cos ai R1sin ai 0]T,i=1,2,3。
(17)
由图1可知,转动副铰点不位于静平台所在平面,因此,按照图2所建立的坐标系,转动副铰点Ai在坐标系{a}中的Z轴分量不为0。设Ai与坐标系{a}中的X轴夹角为bi,则Ai在坐标系{a}中的空间坐标为
Aia=[rcos bi rsin bi Δzi]T,i=1,2,3。
(18)
把Pib和Aia的空间坐标代入式(8)建立的逆运动学模型,可以得出一个多元函数表达式,其数学形式为
Fi(R1,r,ai,bi,Δzi,L0i,mi,α,β,z)=0,i=1,2,3。
(19)
式中:α、β、z为3-RPS并联机器人的3个独立自由度,在逆运动学模型中作为输入变量;mi为在某一位姿下3个驱动杆的位移量,是逆运动学模型中的输出变量;其余6个变量为3-RPS并联机器人的实际参数,如果这6个参数不准确,就会引起动平台的位姿误差。在精密仪器制造领域中,丝毫误差都会造成巨大的经济损失,因此,寻找一种在参数标定领域表现优异的算法是不可或缺的。
2 基于改进差分进化算法的参数标定
差分进化(DE)算法是一种基于种群的全局优化算法,由Storn等[20]提出,该方法涉及的参数较少且具有良好的收敛性。但是,对于一些复杂模型,其参数空间具有较多局部最优解,这对侧重于全局搜索的DE算法是一个严峻挑战。为了避免在3-RPS并联机器人的逆运动学模型和误差模型参数求解过程中陷入局部最优,本文在DE算法的基础上提出CMDE算法。该算法设计2个分别侧重局部开发和全局搜索的种群,每个种群包含3种变异策略,并在种群中的变异策略之间加入竞争环节,有效地弥补了DE算法不擅于局部开发的缺陷。
2.1 差分进化算法
DE算法主要包括4个流程:种群初始化、变异、交叉和选择。其中变异是DE算法的核心操作,通过变异使种群产生变异个体,扩展种群的多样性。下面是常用的6种变异策略[21]。
DE/best/1:
(20)
DE/best/2:
![]()
(21)
DE/rand/1:
(22)
DE/rand/2:
(23)
DE/current-to-rand/1:
![]()
(24)
DE/current-to-best/1:
![]()
(25)
式中:r1,r2,…,r5为在[1,NP]中随机选择的整数且各不相同,NP为种群规模;F为变异因子;g为当前迭代次数;Xbest为当前种群中最优的个体。
变异操作结束后,交叉操作将未变异个体![]() 与变异个体
与变异个体![]() 交叉得到实验个体
交叉得到实验个体![]() 常用的交叉方法为二项式交叉:
常用的交叉方法为二项式交叉:

(26)
式中:CR为交叉因子;D为问题维度;j′为[1,D]区域中随机选的一个整数,用来确保至少存在一个变异个体。
2.2 基于竞争的多变异策略差分进化算法
DE算法的性能对于变异策略的选择以及变异因子、交叉因子的设置较为敏感[22]。连续变化的因子能够根据进程不断调整来适应问题,弥补常值因子的缺陷,但是需要耗费较多的计算时间。为了避免进化过程中过多的计算,3个离散的参数组(F=1.0,CR=0.1)、(F=1.0,CR=0.9)、(F=0.8,CR=0.2)被使用在自适应进化算法中[23]。由于每种变异策略都具有各自的特性,包含多种变异策略的种群侧重点不同[24],为了充分发挥每种策略的独特优势,本文提出CMDE算法。在CMDE算法中,每次迭代都从上述3个离散参数组中随机挑选一组,避免常值因子带来的僵硬性,且减少了不必要的计算。同时根据侧重能力不同设计2个种群,分别侧重全局探索和局部开发,每个种群都包括3种变异策略。
DE/current-to-best/1策略对于解决旋转问题有独特优势,在2个种群中都加入该策略。种群1更加侧重于全局搜索能力,使用DE/rand/1和DE/rand/2两种变异策略,并通过制定一种竞争规则筛选出两种策略中表现较好的变异向量继续进行交叉操作。与之相似,种群2更加侧重于局部开发能力,使用DE/best/1和DE/best/2两种变异策略,同样引入竞争,表现较好的变异向量才能继续进行交叉选择。通过竞争环节的引入,每次迭代都能从两种策略中选出最具竞争力的变异个体,使2个种群的侧重优势更加凸显,制定的竞争规则为
(27)
式中:![]() 与
与![]() 分别表示两种策略变异得到的变异个体;objective_ f(·)表示目标函数;
分别表示两种策略变异得到的变异个体;objective_ f(·)表示目标函数;![]() 为两种策略中竞争力最强的变异个体。
为两种策略中竞争力最强的变异个体。
为了充分利用2个种群的独特优势,设计了权重分配函数。该函数能够在进化过程的前期,为侧重全局探索的种群分配较大的权重;在中后期,为侧重局部开发的种群分配较大的权重。对于2个种群的权重分配,采用如下方式:
w![]()
(28)
(29)
式中:g为当前迭代次数;gmax为最大迭代次数;![]() 表示迭代进程。
表示迭代进程。
上述算法的伪代码如下所示。
输入:种群规模NP,最大迭代次数gmax,问题维度D,参数池,group1,group2。
输出:种群中的最优解。
①g=0,种群初始化![]()
②计算![]()
③while g<gmax;
④ for i=1:NP;
⑤从3组参数池随机选择1组参数;
⑥分别代入group1,group2进行变异操作;
⑦根据式(27)挑选竞争力强的变异个体;
⑧根据式(26)分别计算2个种群中产生的交叉个体;
⑨根据式(29)计算最终的交叉个体;
⑩进行选择操作更新下一代![]()
 end for;
end for;
 g=g+1;
g=g+1;
 end while。
end while。
其中,目标函数objective_ f为式(19)所表示的3-RPS并联机器人逆运动学模型的均方根误差。
3 实验结果与对比
本文分别采用粒子群(PSO)算法、DE算法和CMDE算法对建立的逆运动学模型进行了参数标定,并使用标定后的参数对逆运动学模型进行修正。利用Adams软件对修正后的逆运动学模型进行仿真验证分析,通过对比标定前后理想位姿与实际位姿的误差,验证了CMDE算法相对于其他2种算法的优势以及修正后的逆运动学模型的高精确性。
本实验硬件平台配置:AMD5800 H处理器,16 G内存(3 200 MHz)。实验对象是由Solidworks设计的3-RPS并联机器人模型,仿真平台为Adams2020版本,该并联机器人设计参数见表1。
表1 3-RPS并联机器人模型设计参数
Table 1 Design parameters of 3-RPS parallel robot model

设计参数取值上/下平台外接圆半径/cm26.5/40.03个连杆初始长度/cm143.53个球铰与坐标系{b}中X'轴夹角/(°)90、30、1503个转动副与坐标系{a}中X轴夹角/(°)90、30、150转动副与下平台之间的高度/cm6
3-RPS并联机器人的参数标定具体操作步骤如下:
(1)设定多组目标位姿(α,β,z);
(2)通过逆运动学模型计算杆长位移量mi;
(3)将mi代入Adams仿真得到实际位姿(α*,β*,z*);
(4)以式(19)的均方根误差建立目标函数;
(5)通过优化算法对目标函数进行优化;
(6)用优化得出的参数修正逆运动学模型;
(7)重复步骤(3)和步骤(4),对修正后的模型进行验证。
参数标定流程如图3所示。
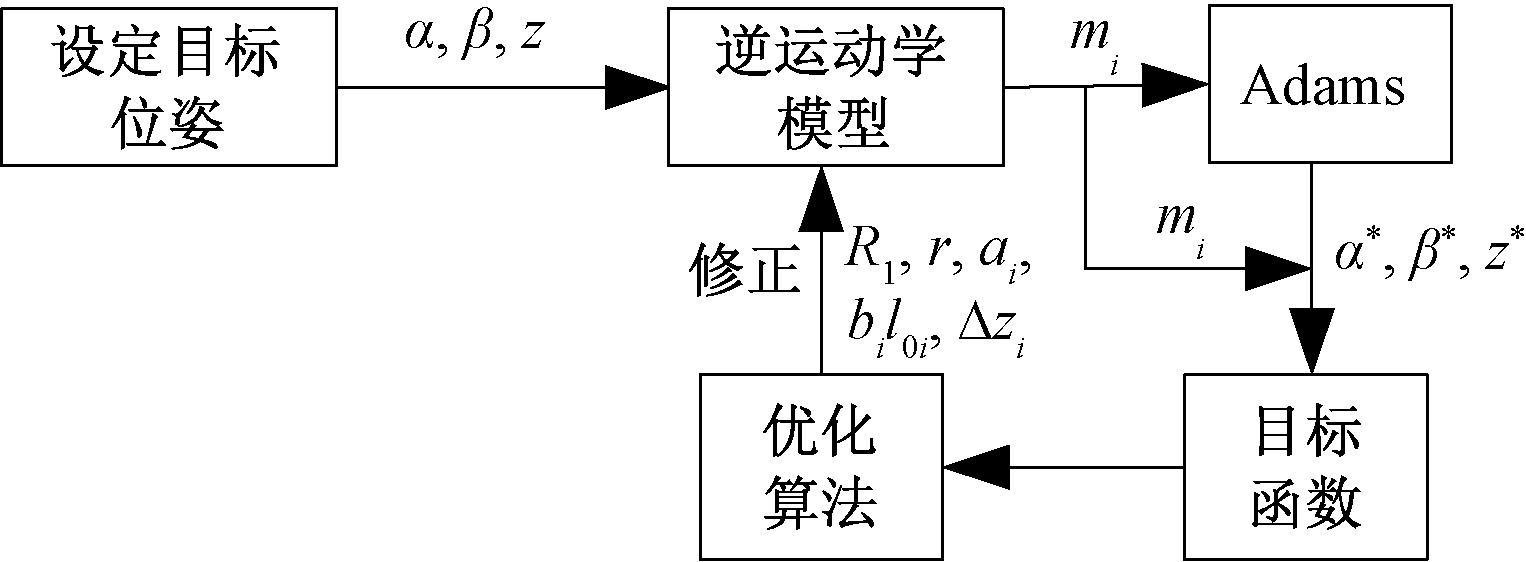
图3 参数标定流程
Figure 3 Parameter calibration process
在本文中,需要标定的参数共6个,因此,必须设定大于6组的位姿才能通过优化算法得出实际参数。在本次实验中,共采用12组不同的位姿以式(19)的均方根误差为目标函数对其优化,优化过程中目标函数适应度变化曲线如图4所示。
由图4可知,CMDE算法大约经过60代达到收敛,而DE算法大约经过120代达到收敛,说明CMDE算法的收敛速度相较于DE算法得到显著提升,提升了50%。不仅如此,对于同一目标函数,CMDE算法优化得到的最小适应度值均小于DE算法,说明在相同解空间,CMDE算法的全局搜索能力更强。为了对比CMDE对3-RPS并联机器人参数标定的效果,采用PSO、DE、CMDE 3种算法进行标定,并对比3种算法标定后的3个独立自由度的误差。表2为数据标定前和3种算法标定后3个自由度的绝对误差均值对比。
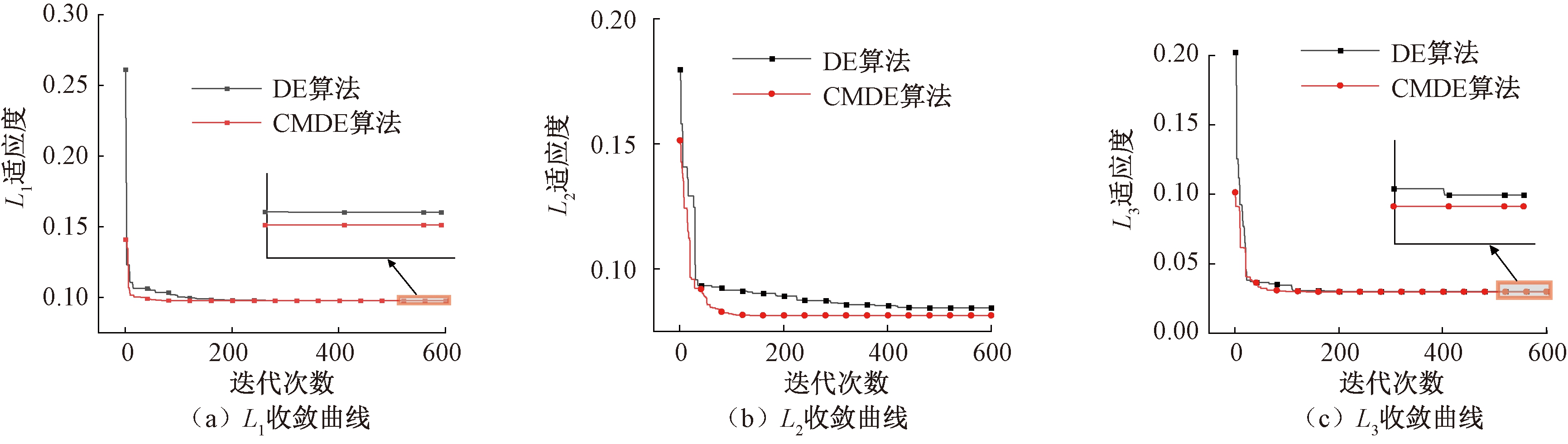
图4 目标函数收敛曲线
Figure 4 Convergence curve of objective functions
表2 标定前后α、β、z误差均值对比
Table 2 Comparison of α,β,z errors mean value before and after calibration
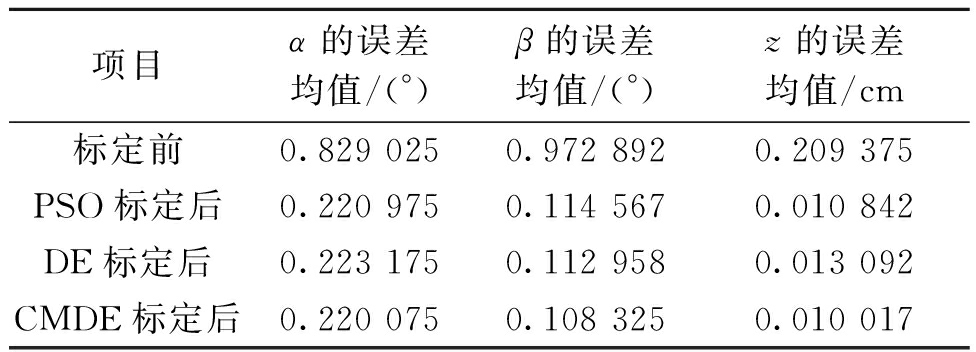
项目α的误差均值/(°)β的误差均值/(°)z的误差均值/cm标定前0.829 0250.972 8920.209 375PSO标定后0.220 9750.114 5670.010 842DE标定后0.223 1750.112 9580.013 092CMDE标定后0.220 0750.108 3250.010 017
通过表2可知,3种算法对该并联机器人的参数标定效果很好,且CMDE标定效果较其余2种更强,3个自由度的精度较标定前分别提升73.5%、88.7%、95.2%。在对目标函数优化过程中3种算法的初始种群都为随机生成,为了削弱随机性对参数标定带来的影响,对每种算法都运行10次,采取优化效果最好的一组参数。在10次优化过程中,3种算法对于不同连杆建立的3个目标函数优化效果如图5所示。
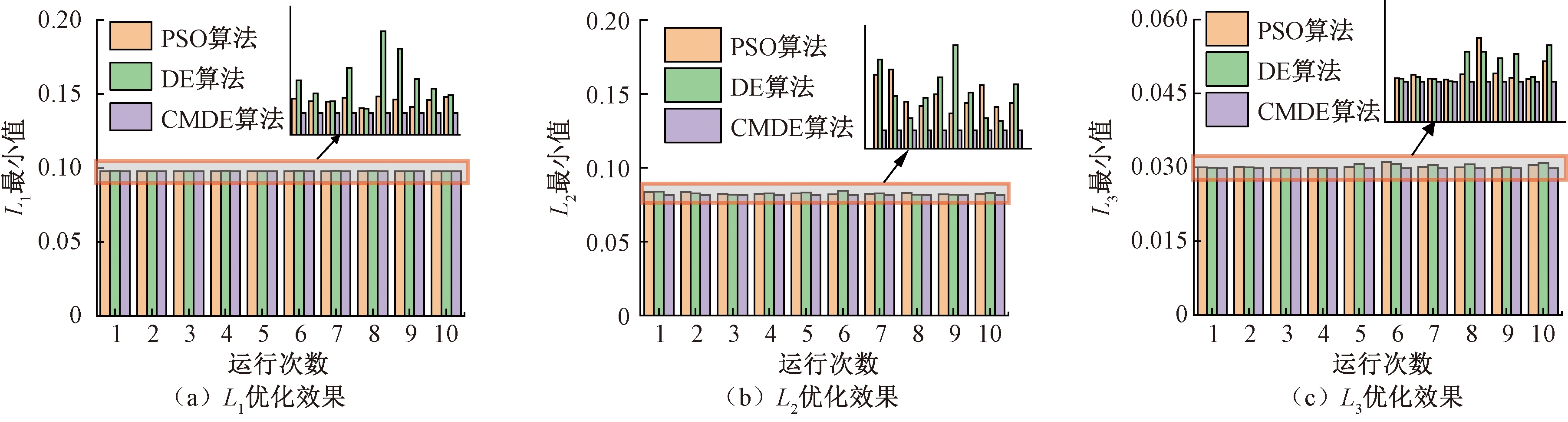
图5 目标函数优化效果
Figure 5 Optimization effect of objective functions
由图5可知,对于同一目标函数,CMDE算法多次运行优化得到的最小值相同,受到种群随机初始化带来的影响较小且优化效果强于其余2种算法。这种现象表明,对于本文建立的目标函数,在相同解空间,CMDE算法对于最优解的搜索相较于PSO算法和DE算法更为彻底,每次都能搜寻出目标函数的全局最优解。
4 结论
本文建立了3-RPS并联机器人的逆运动学模型,通过分析该机构产生误差的原因,建立了该并联机器人的误差模型,并提出了一种基于竞争的多变异策略差分进化(CMDE)算法。以并联机器人的仿真误差最小为目标建立了目标函数,分别采用PSO、DE和CMDE 3种算法对3-RPS并联机器人进行了参数标定。使用标定后的参数对逆运动学模型进行修正,并通过Adams仿真软件对修正后的模型进行了实验验证。结果表明,CMDE算法收敛速度较传统DE算法收敛速度有明显提高,寻优能力更强;优化过程中,CMDE算法对随机性带来的干扰抗衡能力更强,每次都能收敛到同一目标函数最小值;CMDE算法对于参数标定的效果强于PSO、DE 2种算法。修正后的运动学模型相比标定前模型在较大程度上提高了3-RPS并联机器人的精度。
[1] NGUYEN H N, ZHOU J, KANG H J. A calibration method for enhancing robot accuracy through integration of an extended Kalman filter algorithm and an artificial neural network[J]. Neurocomputing, 2015, 151: 996-1005.
[2] 赵磊, 赵新华, 周海波, 等. 并联测量机柔性动力学建模与误差耦合[J]. 光学精密工程, 2016, 24(10): 2471-2479.
ZHAO L, ZHAO X H, ZHOU H B, et al. Flexible dynamic modeling and error coupling of parallel measuring machine[J]. Optics and precision engineering, 2016, 24(10): 2471-2479.
[3] 王海芳, 李新庆, 乔湘洋, 等. 3-SPS/S踝关节并联康复机构控制系统仿真[J]. 东北大学学报(自然科学版), 2019, 40(3): 310-314, 333.
WANG H F, LI X Q, QIAO X Y, et al. Simulation of 3-SPS/S parallel manipulator control system for ankle rehabilitation[J]. Journal of northeastern university (natural science), 2019, 40(3): 310-314, 333.
[4] 胡磊, 胡宁, 王立权, 等. 3SPS-1S并联机构的仿人机械臂系统设计[J]. 哈尔滨工程大学学报, 2015, 36(11): 1515-1521, 1531.
HU L, HU N, WANG L Q, et al. 3SPS-1S parallel mechanism based humanoid manipulator system[J]. Journal of Harbin engineering university, 2015, 36(11): 1515-1521, 1531.
[5] ZHANG D S, XU Y D, YAO J T, et al. Analysis and optimization of a spatial parallel mechanism for a new 5-DOF hybrid serial-parallel manipulator[J]. Chinese journal of mechanical engineering, 2018, 31: 54.
[6] 高建设, 王玉闯, 刘德平, 等. 新型四足步行机器人串并混联腿的轨迹规划与仿真研究[J]. 郑州大学学报(工学版), 2018, 39(2): 23-27, 38.
GAO J S, WANG Y C, LIU D P, et al. Research on trajectory planning and simulation on the serial-parallel leg of a novel quadruped walking robot[J]. Journal of Zhengzhou university (engineering science), 2018, 39(2): 23-27, 38.
[7] ROTH Z, MOORING B, RAVANI B. An overview of robot calibration[J]. IEEE journal on robotics and automation, 1987, 3(5): 377-385.
[8] JUDD R P, KNASINSKI A B. A technique to calibrate industrial robots with experimental verification[J]. IEEE transactions on robotics and automation, 1990,6(1): 20-30.
[9] 刘宇哲, 吴军, 王立平, 等. 5轴混联机床运动学标定的测量轨迹评价及误差补偿[J]. 清华大学学报(自然科学版), 2016, 56(10): 1047-1054.
LIU Y Z, WU J, WANG L P, et al. Measurement trajectory evaluation and error compensation for kinematic calibration of a 5-axis hybrid machine tool[J]. Journal of Tsinghua university (science and technology), 2016, 56(10): 1047-1054.
[10] 高岳林, 武少华. 基于自适应粒子群算法的机器人路径规划[J]. 郑州大学学报(工学版), 2020, 41(4): 46-51.
GAO Y L, WU S H. Robot path planning based on adaptive particle swarm optimization[J]. Journal of Zhengzhou university (engineering science), 2020, 41(4): 46-51.
[11] 张方方, 张文丽, 王婷婷. 基于速度补偿算法的多机器人编队控制研究[J]. 郑州大学学报(工学版), 2022, 43(2): 1-6, 14.
ZHANG F F, ZHANG W L, WANG T T. Research on multi-robot formation control based on speed compensation algorithm[J]. Journal of Zhengzhou university (engineering science), 2022, 43(2): 1-6, 14.[12] 赵磊, 闫照方, 栾倩倩, 等. 大空间运动3-RRRU并联机器人运动学标定与误差分析[J]. 农业机械学报, 2021, 52(11): 411-420.
ZHAO L, YAN Z F, LUAN Q Q, et al. Kinematic calibration and error analysis of 3-RRRU parallel robot in large overall motion[J]. Transactions of the Chinese society for agricultural machinery, 2021, 52(11): 411-420.
[13] WANG W D, SONG H J, YAN Z Y, et al. A universal index and an improved PSO algorithm for optimal pose selection in kinematic calibration of a novel surgical robot[J]. Robotics and computer-integrated manufacturing, 2018, 50: 90-101.
[14] 姜一舟, 于连栋, 常雅琪, 等. 基于改进差分进化算法的机器人运动学参数标定[J]. 光学 精密工程, 2021, 29(7): 1580-1588.
JIANG Y Z, YU L D, CHANG Y Q, et al. Robot calibration based on modified differential evolution algorithm[J]. Optics and precision engineering, 2021, 29(7): 1580-1588.
[15] 寇斌, 郭士杰, 任东城. 改进粒子群算法的工业机器人几何参数标定[J]. 哈尔滨工业大学学报, 2022, 54(1): 9-13.
KOU B, GUO S J, REN D C. Geometric parameter calibration of industrial robot based on improved particle swarm optimization[J]. Journal of Harbin institute of technology, 2022, 54(1): 9-13.
[16] LUO G Y, ZOU L, WANG Z L, et al. A novel kinematic parameters calibration method for industrial robot based on Levenberg-Marquardt and differential evolution hybrid algorithm[J]. Robotics and computer-integrated manufacturing, 2021, 71: 102165.
[17] WANG Y, YU J J, PEI X. Fast forward kinematics algorithm for real-time and high-precision control of the 3-RPS parallel mechanism[J]. Frontiers of mechanical engineering, 2018, 13(3): 368-375.
[18] JOUBAIR A, SLAMANI M, BONEV I A. Kinematic calibration of a 3-DOF planar parallel robot[J]. Industrial robot: an international journal, 2012, 39(4): 392-400.
[19] 张宪民, 曾磊. 考虑减速机背隙的3-RRR并联机构的运动学标定[J]. 华南理工大学学报(自然科学版), 2016, 44(7): 47-54.
ZHANG X M, ZENG L. Kinematic calibration of 3-RRR parallel mechanism considering reducer backlash[J]. Journal of South China university of technology (natural science edition), 2016, 44(7): 47-54.
[20] STORN R, PRICE K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of global optimization, 1997, 11: 341-359.
[21] WANG Y, CAI Z X, ZHANG Q F. Differential evolution with composite trial vector generation strategies and control parameters[J]. IEEE transactions on evolutionary computation, 2011, 15(1): 55-66.
[22] 周雅兰, 徐志. 多变异策略的自适应差分演化算法[J]. 计算机科学, 2015, 42(6): 247-250, 255.
ZHOU Y L, XU Z. Self-adaptive differential evolution with multi-mutation strategies[J]. Computer science, 2015, 42(6): 247-250, 255.
[23] GUI L, XIA X W, YU F, et al. A multi-role based differential evolution[J]. Swarm and evolutionary computation, 2019, 50: 100508.
[24] LIANG J, QIAO K J, YU K J, et al. Parameters estimation of solar photovoltaic models via a self-adaptive ensemble-based differential evolution[J]. Solar energy, 2020, 207: 336-346.