0 引言
列车高速通过隧道或者在隧道内交会时,会形成复杂的压力波,产生列车隧道空气动力学效应。由于列车不能完全密封,车外的压力变化通过车体的缝隙传递到列车内部,导致车内压力发生跟随性的变化。列车的密封性能直接影响车内人员的压力舒适性,列车的气密性分析及评价对车体的密封设计和改善列车的压力舒适度有重要的指导意义。
气密性是反映列车密封性的指标,通常采用静态气密性指数、动态气密性指数和等效泄漏面积等来进行评价。气密性指数是通过分析车外和车内压力的变化进而对列车的气密性进行评价。对车内压力波的分析,相关学者提出了计算方法。张运良等[1]根据时间常数模型,运用车体内部瞬变压力计算公式计算了隧道工况下车内气压波动。梅元贵等[2-3]利用时间常数模型,推导了车内压力计算公式,采用广义黎曼变量特征线求解方法计算了列车在隧道通过工况下的车内外压力变化。有学者[4-7]基于等效泄漏模型,根据质量守恒提出了车外压力引起车内压力变化的计算方法,计算了隧道工况下的车内压力。等效泄漏模型具有明确的物理意义,便于直观理解,被广泛应用于研究列车车内压力。但是无论是时间常数模型还是等效泄漏模型,都是基于一维理论分析方法,忽略了压力波在车体三维空间的流动特性。获得车内外压力变化后,可以根据车内外压力变化关系对列车的气密性进行评价。Nam[8]以试验所得车内外数据为基础,采用动态气密指数评价了列车气密性。王建宇等[9]根据实测所得的车内外气压波动,基于动态气密指数分析了隧道长度对列车密封效果的影响。马瑶等[10]、张芯茹等[11]基于特征线法得出列车通过隧道压力波,在此基础上,采用动态气密指数评价不同隧道长度下列车气密性。万有财等[12]利用等效泄漏面积建立车内外压力关系,结合动态气密指数,给出列车在不同速度下动态等效泄漏面积阈值的建议值。李田等[13]通过建立列车静态泄漏数值模型,采用静态气密指数分析了泄漏孔长细比对列车气密性的影响。Liu等[14]根据实车试验得到车内外压力,研究了不同隧道长度下列车动态气密性。Liu等[15]还基于等效泄漏面积研究了列车在瞬态载荷作用下的气密性。上述研究采用理论或者试验获得车内压力波,在此基础上对列车的气密性进行评价或开展相关影响因素分析,但同时考虑高速列车车体内外流场的动态气密性数值分析方法少有报道。
综上所述,针对隧道工况下列车动态气密性以及车内压力波问题,本文通过建立高速列车车体内外流场准确的数值分析模型,以等效泄漏孔作为车体内外压力传递的接口研究车内压力,进而计算动态气密指数,提出动态气密性指数数值计算方法。
1 气密性评价方法
1.1 静态气密指数
列车静止时,车体气密性一般用泄压时间来表示。目前实测普遍采用的方法是向车内充气至一定压力,然后自然泄压,以泄压前后的时间差来衡量车辆的气密性。静态气密指数τs可以用下式计算:
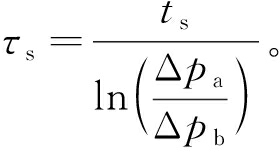
(1)
式中:Δpa为初始压差,Pa;Δpb为经过时间ts后的压差,Pa。
1.2 等效泄漏面积
在研究列车气密性时,也可以采用等效泄漏孔的面积大小来评价列车的气密性能。在实际情况下,车辆的车外压力通过车体、车门、地板等之间的各类不规则复杂缝隙传入车内[16]。为了研究方便,可以将车体内各类型的缝隙等效为统一的泄漏面积表征。一般用等效泄漏孔表示,其对车内压力变化所产生的影响是等效的[17],等效泄漏面积与车内外压力的关系为
(2)
式中:S为等效泄漏面积,m2;V为车厢体积,m3,Δp0为初始压差,Pa;Δpt为截止压差,Pa;td为车内外压力差从Δp0泄漏到Δpt的泄漏时间,s。
1.3 动态气密指数
在列车运行过程中,车厢内部的压力会实时响应外部压力,因此,车辆的实际密封性能与所述的静态密封性能是不同的。在国际铁路联盟(UIC)标准中,动态密封系数τd用来描述列车在实际运行过程中的密封性,τd定义为
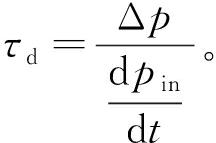
(3)
式中:Δp为在t时刻车内外的压差,Pa,Δp=pex-pin,pex为作用在车体上外部压力,Pa,pin为车内的压力,Pa。由式(3)可以推出列车车内压力计算递推的公式:
(4)
式中:Δt为车内外压力变化的时间步长,s。
2 数值仿真计算
2.1 计算模型的建立
列车通过隧道时可以简化为图1的模型[15],如图1所示,整体仿真模型分为2个域,2个域之间通过等效泄漏孔连接。上部长方体域的长为100 m,宽25 m,高25 m。面EFHG设置为压力入口,面ABCD设置为压力出口,面ABFE、AEGC、BFHD设置为滑移壁面,其余设置为固定壁面。下部域为高速列车头车,其容积为250 m3。
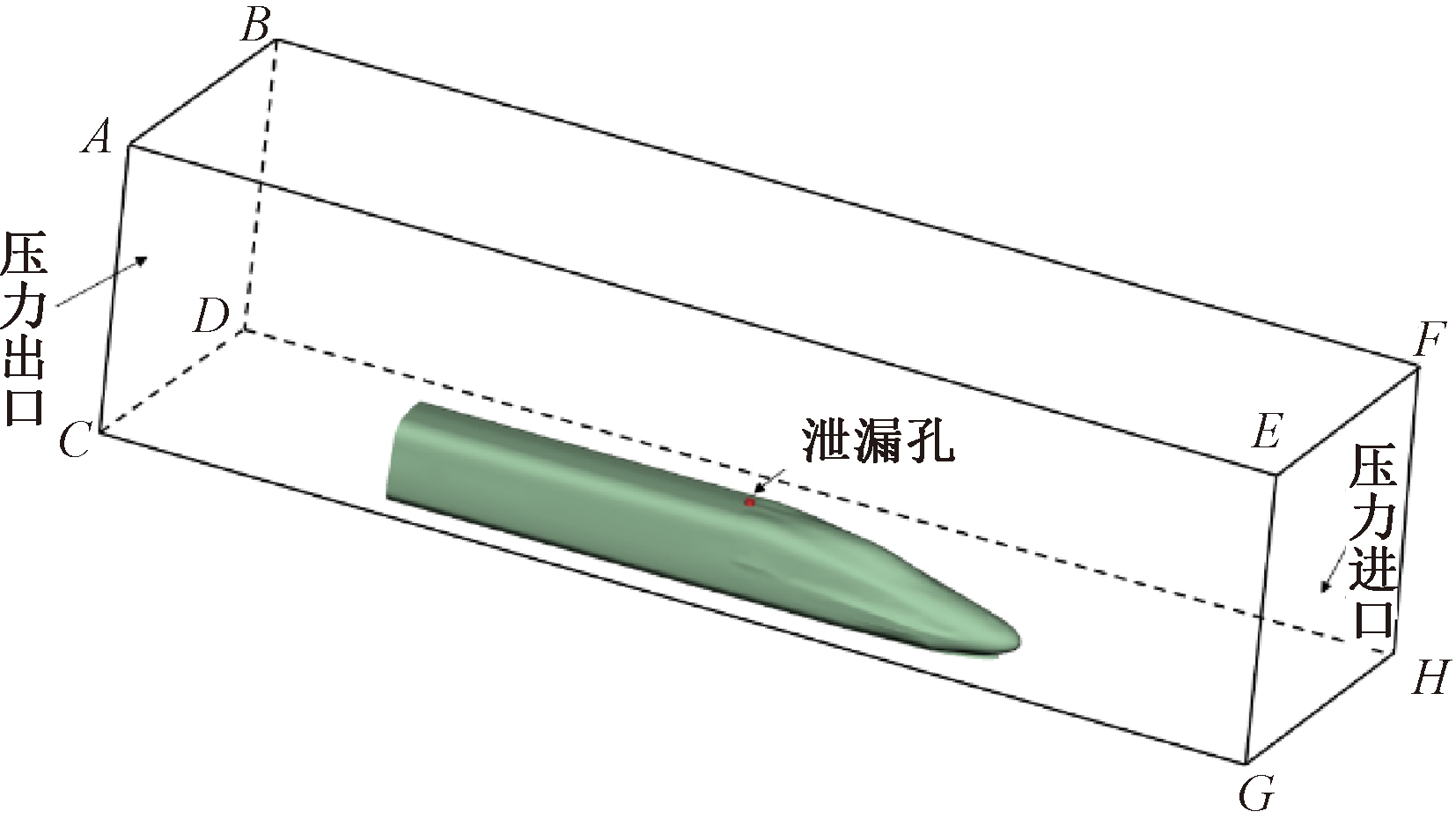
图1 列车通过隧道的计算模型
Figure 1 Calculation model of the train passing throug the tunnel
文献[15]虽然比较详细地介绍了高速列车动态气密性数值模型,但是却没有对泄漏孔的长细比(泄漏孔长度与半径之比)以及泄漏孔的位置进行讨论。为了消除由泄漏孔的长细比以及其位置对车内压力的影响,本文首先讨论泄漏孔长细比以及位置对车内压力的影响。仿真过程都采用ANSYS FLUENT软件进行数值模拟,泄漏孔面积定为15.6 cm2,湍流模型选择 RNGk-ε,收敛条件为残差小于10-3。
2.1.1 泄漏孔长细比影响
为了方便对比计算,在压力入口施加正弦压力波Pex=2 000sin 2πt-1 000。
车内测点如图2所示,测点1与测点3、6、8在列车中轴线上,其中测点3在泄漏孔正下方,且在测点2、4中间。测点2与5、测点4与7处同一水平线上。
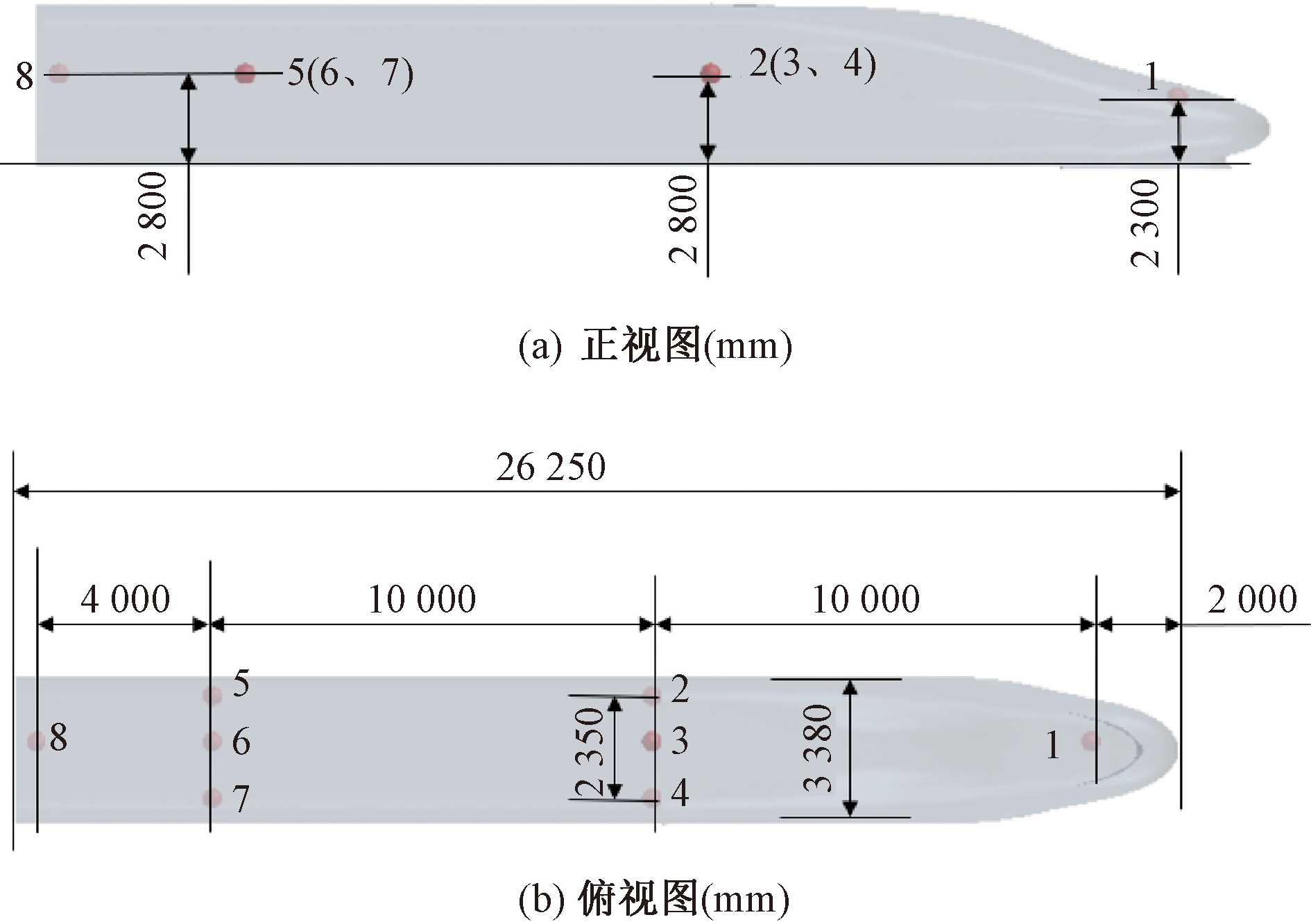
图2 车内测点
Figure 2 Interior measuring points of vehicle
选取长细比为1∶1、1∶4、1∶8进行计算。首先进行网格无关性验证,这里选取1∶1的长细比孔做网格无关性分析。一共划分了3次网格,单元数分别为3 108 113、4 453 008、6 173 543。车内测点压力如图3所示,由图3可以看出,除了泄漏孔正下方的测点3略有不同,车内其余压力测点基本一致,这是由于测点3离泄漏孔最近,受到的影响最大。由于其余测点的压力结果基本一致,后续选择测点6的压力结果进行研究。
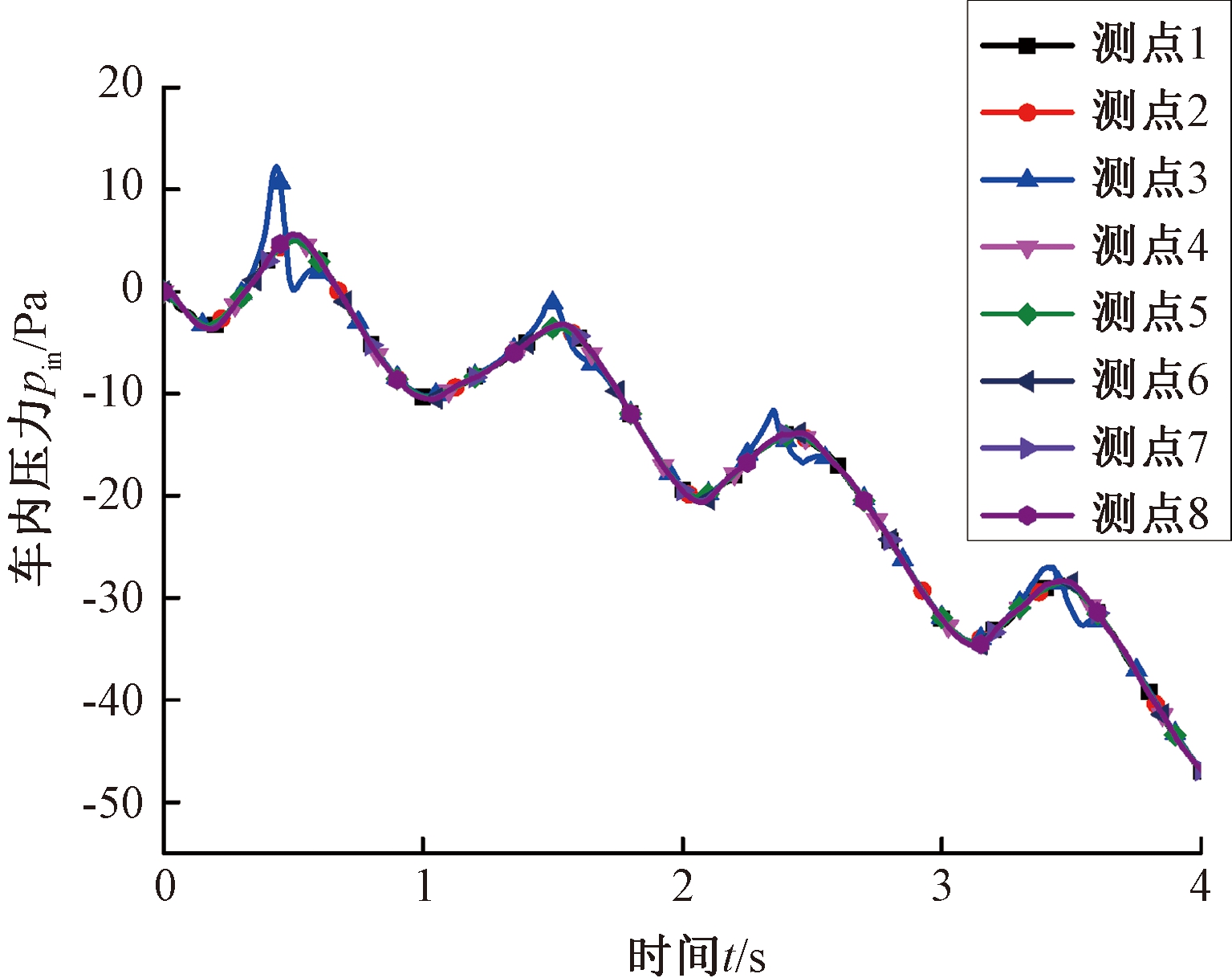
图3 测点压力
Figure 3 Pressure of measuring points
3种不同划分方式计算结果如图4所示,图4中网格1、2、3分别对应的网格单元数为3 108 113、4 453 008、6 173 543。从图4可知,网格1与网格2的计算结果的相对误差较小,网格2与网格3的计算结果基本重合,说明网格2的精度已经达到计算要求,因此,后续将选择网格2的基础尺寸作为网格划分的标准。网格2的划分方式为泄漏孔的面网格尺寸为1~2 mm,头车面网格尺寸为50~100 mm,其他网格尺寸为500~1 000 mm。泄漏孔棱柱层第1层0.1 mm,划分6层,总厚度为1 mm;头车棱柱层第1层0.582 mm,划分10层,总厚度为13.7 mm。
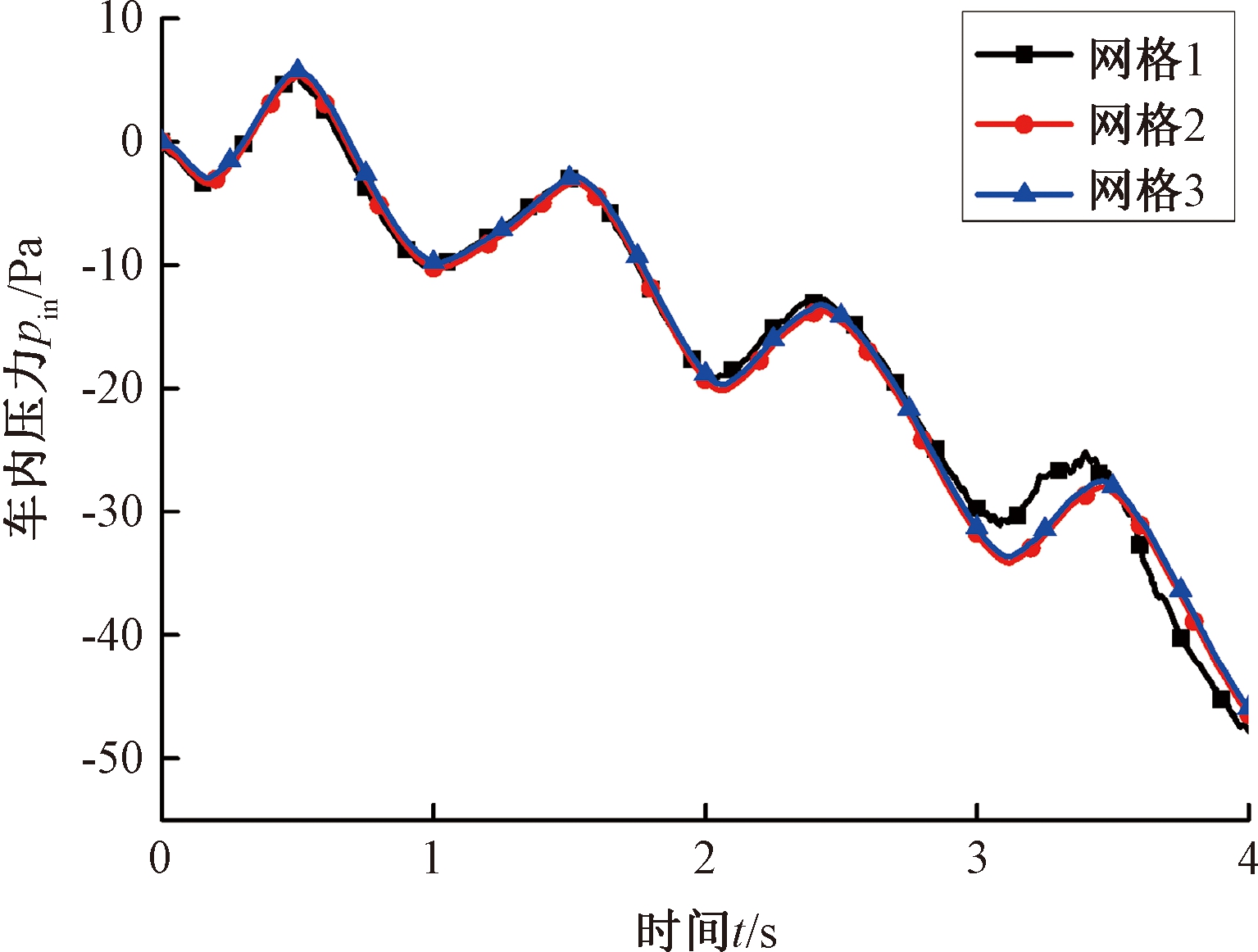
图4 网格无关性验证
Figure 4 Grid independence verification
为了验证时间步长无关性,选取不同的步长,分别为0.005、0.002 5、0.001 s,结果对比如图5所示。时间步0.001 s与0.005 s计算的结果最大的相差为2.99 Pa,相对误差较小;而时间步0.001 s与0.002 5 s的计算结果基本重合,因此,后续选择0.002 5 s时间步长进行计算。
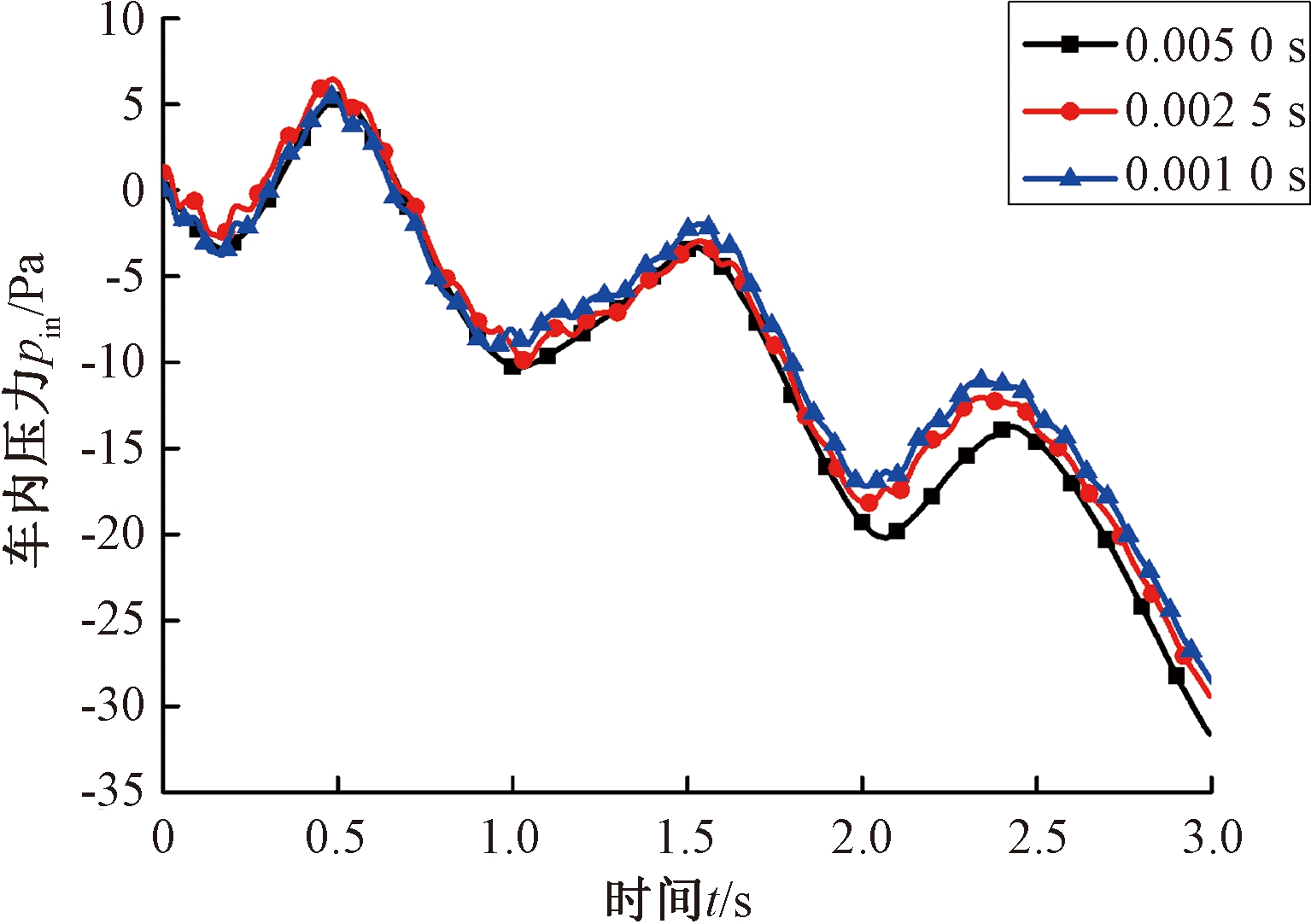
图5 时间步长独立性验证
Figure 5 Time step independence verification
采取网格2的划分方式对不同长细比的等效泄漏孔进行网格划分,计算结果如图6所示,图6中理论计算是将车外压力与动态气密指数代入式(4)所得的结果。从图6可以看出,随着长细比的增大,车内压力趋近于一维理论反推计算,因此数值模型的泄漏孔的长细比不应小于1∶4。后文将采用1∶1的长细比进行计算。
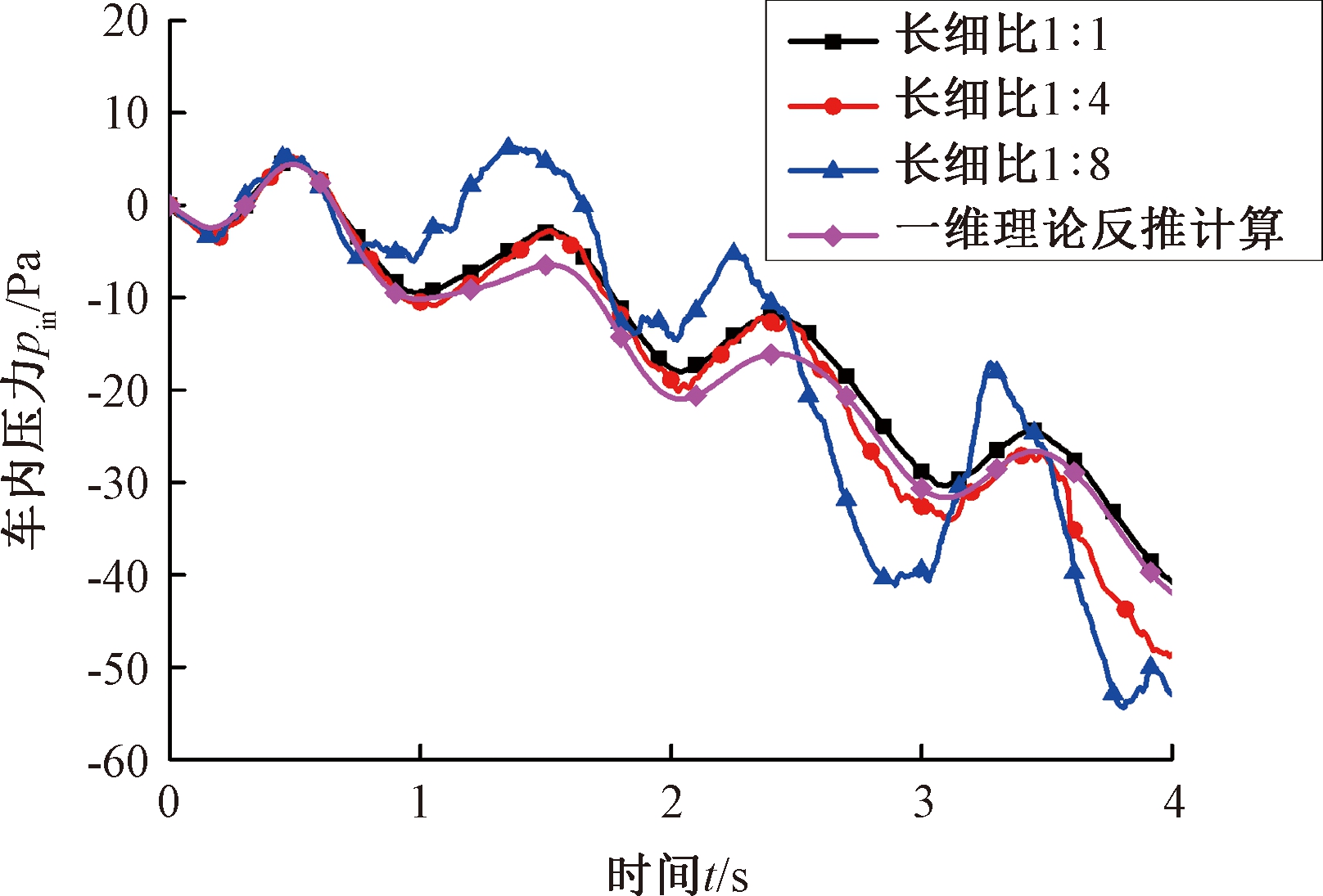
图6 不同长细比泄漏孔计算结果
Figure 6 Calculation results of leakage holes with different slenderness
2.1.2 泄漏孔位置影响
边界条件的设置同上文一样,泄漏孔的位置选取头车的车顶前方、车顶后方、车侧3个位置,计算结果如图7所示。从图7可知,泄漏孔的位置不同,车内压力波动稍有差距,但结果基本一致。这是由于单节车厢的长度较短,压力波在车内传播时,损耗的能量小,表现出压力基本一致的情况。由于压力结果基本一致,因此本文选取车顶前方的位置作为泄漏孔位置。
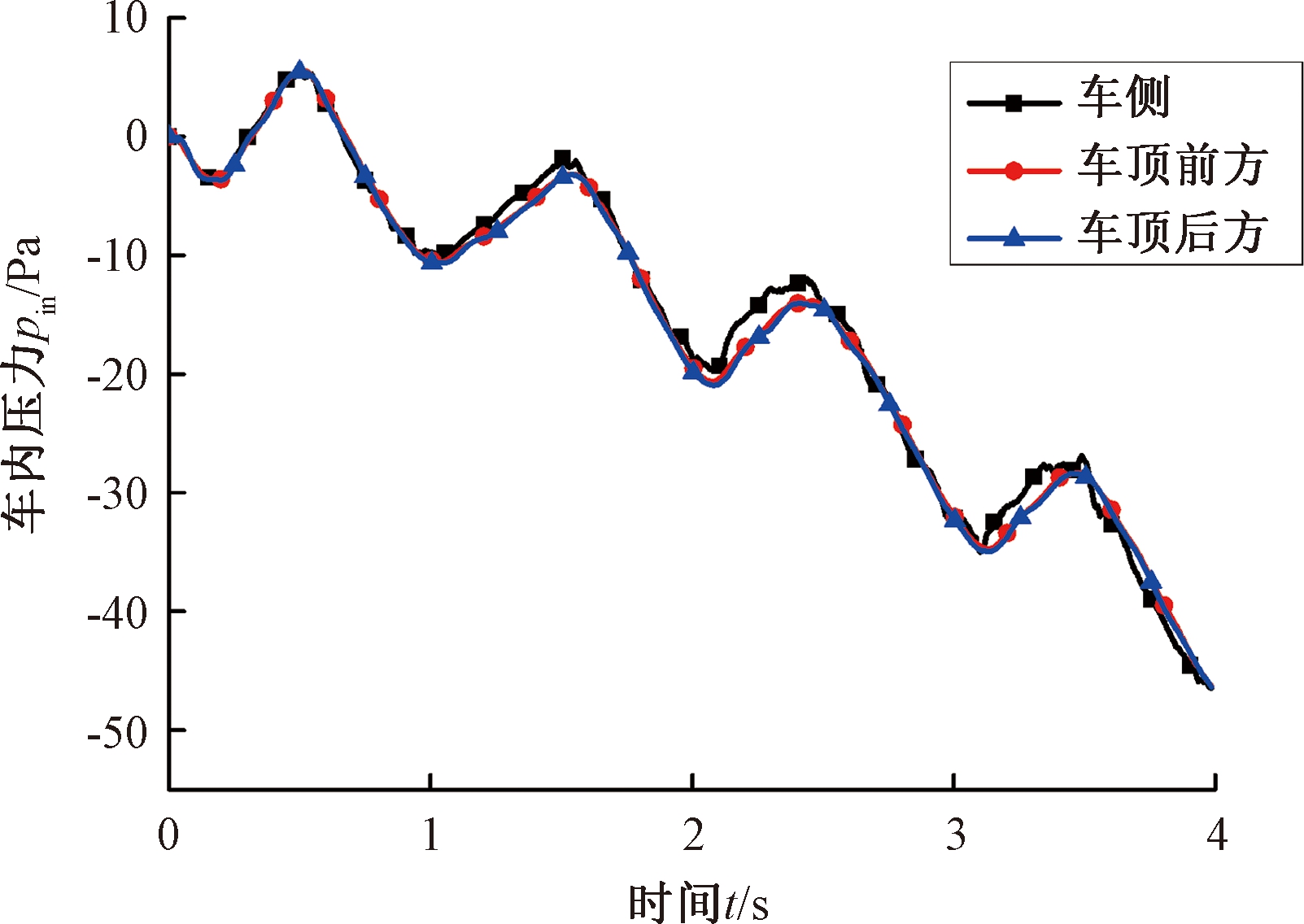
图7 不同位置泄漏孔计算结果
Figure 7 Calculation results of leakage holes at different positions
2.2 仿真计算
2.2.1 隧道交会压力波
为了研究车内外压力传递规律,本文以我国某型高速列车为研究对象,建立其简化的三维几何模型[18],采用三节车编组,包括头车、中间车及尾车,且头车与尾车外形尺寸完全相同。车厢连接处长0.5 m,模型全长78 m,测点位置如图8所示。隧道长为1 000 m,按照铁道行业标准(TB/T 3503.4—2018)要求,计算域的设置为列车距隧道口50 m,距计算域后端62 m,高为32 m,宽为50 m,整个计算域总长为1 380 m,如图9所示。采用滑移网格模拟交会过程,列车速度为350 km/h。测点结果如图10所示。
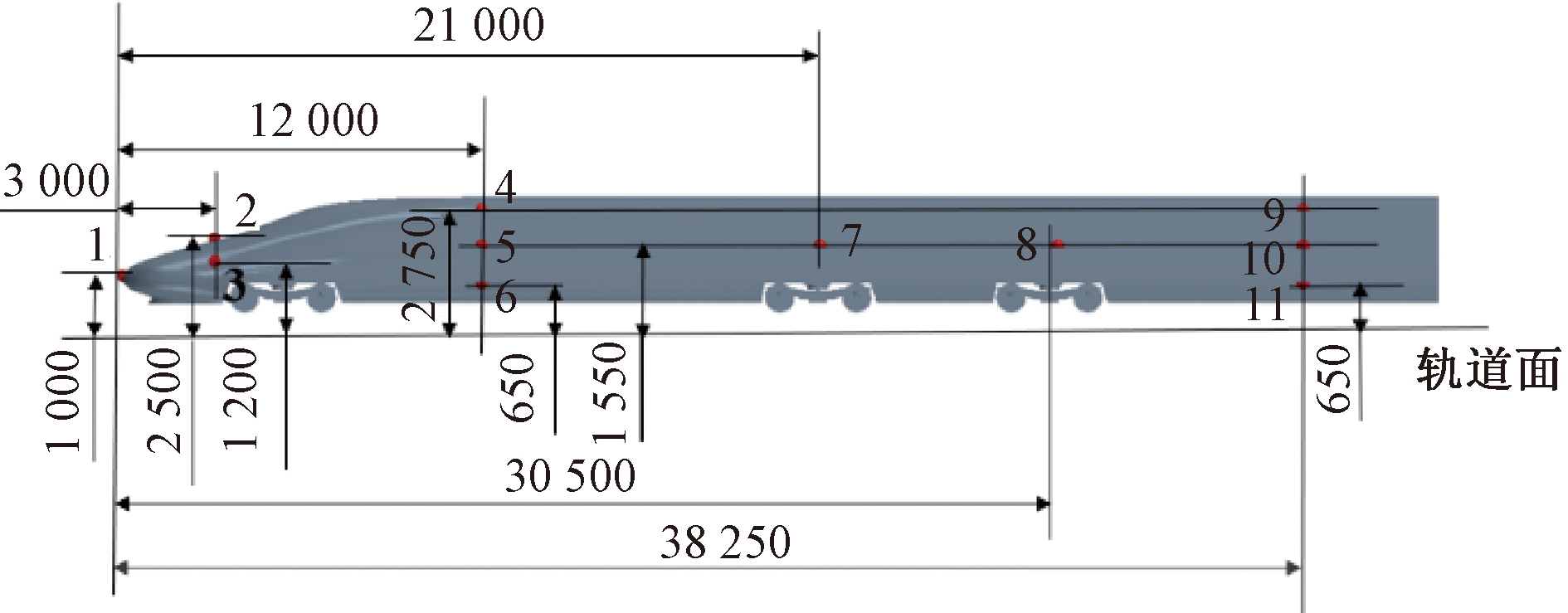
图8 测点位置(mm)
Figure 8 Measuring points location(mm)
图9 整车计算域
Figure 9 Vehicle computing domain
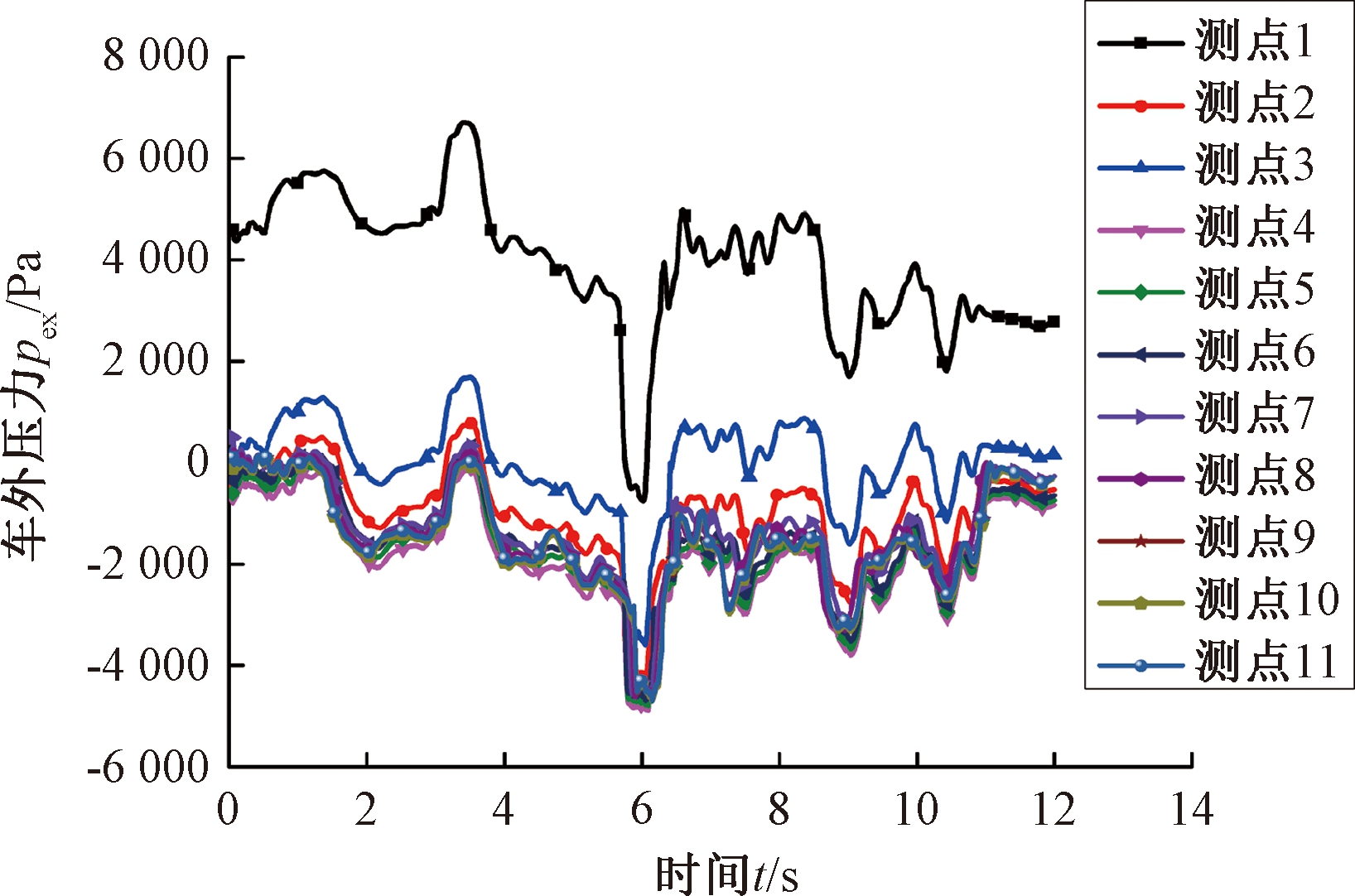
图10 测点压力
Figure 10 Measuring points pressure
2.2.2 动态气密性指数
上文的模型确定了泄漏孔的位置及长细比,仅仅考虑了外形,没有考虑地板、座椅、风挡等影响因素。为了贴近实际情况,建立了考虑地板、座椅、风挡等影响因素的动态气密性模型,座椅数为80个,容积为170 m3,车内测点与图2设置一致。从图10可知,车外测点压力负压情况占多数,选择测点7的压力波添加到上部计算域,取泄漏面积为7.05 cm2进行计算,计算结果如图11所示。
由式(3)可知,根据车内外压差以及车内压力随时间的变化率可求得动态气密性。但仿真结果为一系列散点,为了求得车内压力随时间的变化率,本文利用MATLAB将车内压力数据进行拟合,求得拟合函数后对其求导即是车内压力随时间的变化率。如图11所示,其波动趋势与隧道交会压力波相似。
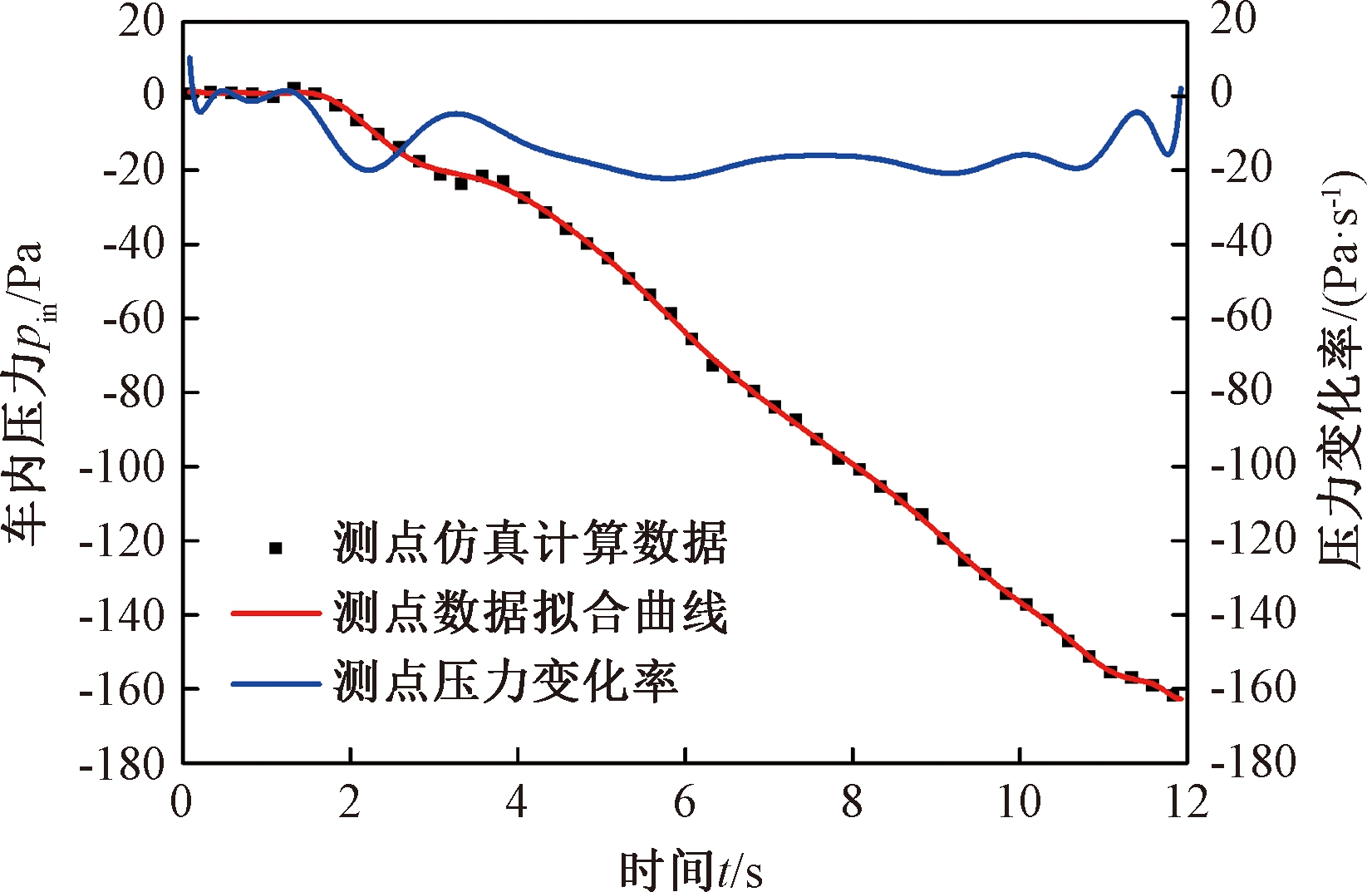
图11 车内压力拟合曲线及压力变化率曲线
Figure 11 Fitting curve and pressure change rate curve of interior pressure
导函数曲线拟合系数R2=0.999,满足拟合要求。将所得的dp/dt以及车内外压差代入式(3),即可求得动态气密指数一系列值,取平均值得τd为66.3。
2.2.3 结果分析
将动态气密指数与车外压力代入式(4),可由公式反推得到车内压力,与本文数值计算的车内压力进行对比分析,如图12所示。对比分析发现,本文提出的数值分析方法计算结果与反推计算结果吻合良好,最大相对误差为8.8%。
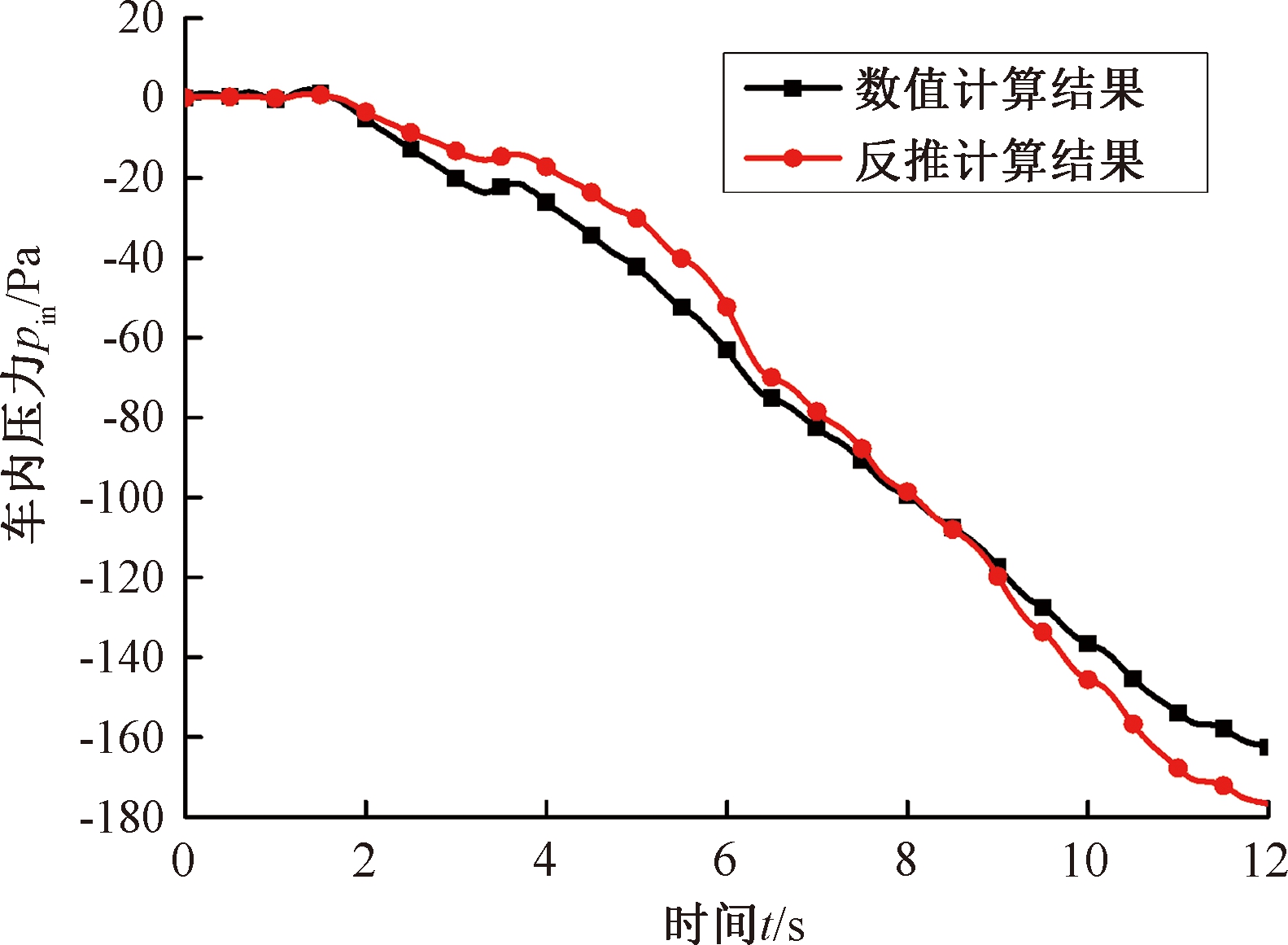
图12 车内压力对比
Figure 12 Comparison of internal pressure
车外测点7的压力均值、压力幅值都为负,车外压力小于车内压力,整个过程中相当于车内向车外排气,车内压力不断减小,呈连续下降趋势。且车内压力的波动幅值远远小于车外压力波动,这是由于密封性对压力波动具有衰减的作用。
文献[16]实测隧道长度为1 067 m,泄漏面积为7.15 cm2,分析的动态气密性指数为36.1~56.0,本文计算结果为66.3,与文献[16]数据接近。产生误差的原因:本文所设定的等效泄漏面积比实车测试工况的小;实测车体的泄漏面积分布在车体的不同位置,导致车内压力的跟随性比仿真计算强,并且实测的车内压力较大;实车测点位置都是布置在车体内墙表面,离泄漏位置比较近,所测压力结果相对仿真计算的车内测点大;车外压力波不一致,本文选取的是头车测点的压力波作为计算域的外部激励,实车测试工况的车外压力波变化存在多点压缩波和膨胀波的叠加,导致车内压力波的响应更复杂。
3 结论
(1)建立了高速列车车体内外流场准确的数值分析模型,以等效泄漏孔作为车内外压力传递接口,对比等效泄漏孔建模中长细比及位置对车内压力的影响,确定了车体内外流场准确的数值模型。
(2)建立了高速列车隧道CFD数值模型,计算了车体外表面压力波,将其作为车体内外流场的激励,计算得到车内压力波响应,分析了车内压力变化率和动态气密指数,并与文献中的实测数据进行了对比验证。
(3)列车气密性数值分析应考虑更多因素的影响,比如多节车、车内设施、多点泄漏、泄漏口的形状等,在未来的研究中将进行更深入的研究。本文提出的列车气密性数值分析方法,对于车体密封性设计和压力舒适度研究具有一定的参考意义。
[1] 张运良, 张志成, 杨伟超, 等. 高速列车隧道等速交会条件下人体舒适度分析[J]. 郑州大学学报(工学版), 2017, 38(2): 26-29.
ZHANG Y L, ZHANG Z C, YANG W C, et al. The human comfort degree analysis of high speed trains intersection at the same speed in the tunnel[J]. Journal of Zhengzhou university (engineering science), 2017, 38(2): 26-29.
[2] 梅元贵, 周朝晖. 高速列车通过隧道时诱发车厢内压力波动的数值分析[J]. 铁道学报, 2005, 27(5): 36-40.
MEI Y G, ZHOU C H. Numerical analysis of transient pressures inside high speed passenger trains through tunnels[J]. Journal of the China railway society, 2005, 27(5): 36-40.
[3] 梅元贵, 张成玉, 周朝晖, 等. 单列高速列车通过特长隧道时耳感不适问题研究[J]. 机械工程学报, 2015, 51(14): 100-107.
MEI Y G, ZHANG C Y, ZHOU C H, et al. Research on the aural discomfort when a single train passes through a super long tunnel[J]. Journal of mechanical engineering, 2015, 51(14): 100-107.
[4] 陈春俊, 聂锡成, 唐猛. 车外空气压力作用下的CRH2型动车组车内空气压力传递函数模型[J]. 中国铁道科学, 2013, 34(4): 84-88.
CHEN C J, NIE X C, TANG M. Transfer function model of the air pressure inside CRH2 EMU under outside air pressure[J]. China railway science, 2013, 34(4): 84-88.
[5] 张相, 梅元贵, 周朝晖. 高速列车车内压力波动值计算方法初探[J]. 铁道机车车辆, 2008, 28(4): 33-35.
ZHANG X, MEI Y G, ZHOU C H. Calculating method of pressure change inside high speed train[J]. Railway locomotive & car, 2008, 28(4): 33-35.
[6] 邵焕霞, 梅元贵, 周朝晖. 高速空调客车通过隧道时车内压力波数值方法初探[J]. 铁道机车车辆, 2006, 26(1): 31-33.
SHAO H X, MEI Y G, ZHOU C H. Study on numerical simulation of pressure changes inside high-speed air-conditioned train passing through tunnels[J]. Railway locomotive & car, 2006, 26(1): 31-33.
[7] 张光鹏, 雷波. 计算高速列车车内压力的热力学模型[J]. 铁道学报, 2006, 28(1): 35-38.
ZHANG G P, LEI B. The thermal dynamics model for calculating the interior pressure of high-speed trains[J]. Journal of the China railway society, 2006, 28(1): 35-38.
[8] NAM S W. A study on estimation of air tightness for train[J]. Journal of the Korean society for railway, 2016, 19(5): 576-584.
[9] 王建宇, 吴剑, 万晓燕. 车辆的密封性及瞬变压力向列车内传递规律[J]. 现代隧道技术, 2009, 46(3): 12-16.
WANG J Y, WU J, WAN X Y. Airtightness of carriages and the law of transient pressure transfering into the train[J]. Modern tunnelling technology, 2009, 46(3): 12-16.
[10] 马瑶, 王雷, 梅元贵. 速度350 km/h高速列车车体时间常数气密阈值特性初探[J]. 铁道机车车辆, 2019, 39(5): 47-52, 69.
MA Y, WANG L, MEI Y G. Study on air-tightness coefficient threshold characteristics of CR400BF EMUs in mountain tunnels at speed of 350 km/h[J]. Railway locomotive & car, 2019, 39(5): 47-52, 69.
[11] 张芯茹, 余以正, 梅元贵. 更高速度下京沪高铁列车整车时间常数动态气密性阈值初探[J]. 铁道机车车辆, 2019, 39(2): 113-118.
ZHANG X R, YU Y Z, MEI Y G. Preliminary study on dynamic air tightness threshold of time constant of Beijing-Shanghai high-speed railway train at higher speed[J]. Railway locomotive & car, 2019, 39(2): 113-118.
[12] 万有财, 李明, 张雷, 等. 京沪高铁隧道背景下列车车体动态气密性当量泄漏面积阈值特征[J]. 振动与冲击, 2021, 40(1): 29-38.
WAN Y C, LI M, ZHANG L, et al. Threshold characteristics of equivalent leakage area of train body dynamic air tightness under background of Beijing-Shanghai high speed railway tunnels[J]. Journal of vibration and shock, 2021, 40(1): 29-38.
[13] 李田, 戴志远, 张继业, 等. 列车气密性静态泄漏理论模型与计算[J]. 交通运输工程学报, 2020, 20(1): 150-158.
LI T, DAI Z Y, ZHANG J Y, et al. Theoretical model and calculation of static leakage for train air tightness[J]. Journal of traffic and transportation engineering, 2020, 20(1): 150-158.
[14] LIU T H, CHEN X D, LI W H, et al. Field study on the interior pressure variations in high-speed trains passing through tunnels of different lengths[J]. Journal of wind engineering and industrial aerodynamics, 2017, 169: 54-66.
[15] LIU T H, GENG S G, CHEN X D, et al. Numerical analysis on the dynamic airtightness of a railway vehicle passing through tunnels[J]. Tunnelling and underground space technology, 2020, 97: 103286.
[16] 李明, 张雷, 刘斌, 等. 动静态气密性分析方法及其在动车组上的应用[J]. 力学学报, 2021, 53(1): 126-135.
LI M, ZHANG L, LIU B, et al. Dynamic and static air tightness analysis method and their application in emu[J]. Chinese journal of theoretical and applied mechanics, 2021, 53(1): 126-135.
[17] 李玉洁, 梅元贵. 动车组车辆气密性指标的初步探讨[J]. 铁道机车车辆, 2009, 29(2): 31-35.
LI Y J, MEI Y G. Primary discussion about pressure tightness of electric mutiple units[J]. Railway locomotive & car, 2009, 29(2): 31-35.
[18] LU Y H, ZHANG D W, ZHENG H Y, et al. Analysis of the aerodynamic pressure effect on the fatigue strength of the carbody of high-speed trains passing by each other in a tunnel[J]. Proceedings of the institution of mechanical engineers, part F: journal of rail and rapid transit, 2019, 233(8): 783-801.