斜拉索是斜拉桥的核心受力构件,是整座桥梁的薄弱受力部位,一旦发生断裂,全桥拉索索力将发生重分配,主梁和索塔的内力将受到较大影响,严重时可能导致斜拉索相继断裂,引发连续倒塌。为了评估斜拉桥在建造和运营期间的安全性,国内外学者对斜拉索断裂引起的桥梁力学性能变化进行了研究。Wolff等[1]考虑拉索横向振动和结构阻尼的影响,对拉索断裂后一座5跨斜拉桥的动力响应进行了分析。Janjic等[2]采用刚度矩阵法,研究了斜拉索的数量、间距对斜拉桥静力、动力特性的影响。张羽等[3]以时程曲线为工具,对斜拉桥结构在多根拉索断裂过程中的动力响应进行了分析。李彦兵[4]选取18个断裂工况,研究了拉索断裂对主梁线形、索力大小、主梁应力及动力性能的影响。黄华等[5]以既有水平索又有斜拉索的双钢拱塔斜拉桥为研究对象,分析了不同工况的斜拉索断裂后拉索索力、主梁应力及索塔偏移的变化规律。柴文浩等[6]以一座下承式拱桥为例,研究了不同吊杆断裂对剩余吊杆内力及主梁线型的影响。陈国胜[7]以一座空间扭转索面斜拉桥为工程背景,研究了单索及双索断裂对加劲梁内力的影响。
由以上研究可看出,目前国内对于常规斜拉桥及中下承式拱桥的断索研究已经较为充分,但有关非常规斜拉桥的研究较少。本文以一座曲线形钢箱梁斜拉桥为工程实例,分析了不同位置、不同数量的斜拉索断裂对剩余拉索索力、主梁挠度、主梁应力及塔顶偏移的影响。
1 工程实例
兰州市西固柴家峡大桥为双塔双索面钢主梁斜拉桥,半漂浮体系,主跨全长598.862 m,跨径布置为(46.800+49.200+364.000+49.200+46.800+42.862)m。平面线形沿长度方向为:半径600 m、长度185.289 m的圆曲线段,100 m缓和曲线段,282.522 m直线段,半径1 020 m、长度为31.051 m的圆曲线段。索塔呈A形,南塔高99.900 m,北塔高115.500 m,主塔材料为C50混凝土。主梁为双箱闭口钢梁截面,材料为Q345qD钢材,主梁顶宽35.5 m,桥面铺装为50 mm厚半刚性高分子沥青混凝土材料。斜拉索采用双索面扇形布置,全桥共计112根斜拉索,钢绞线标准强度为1 860 MPa。桥梁示意图如图1所示。
2 有限元模型
2.1 梁格划分
采用有限元软件MIDAS/Civil建立模型,全桥共2 491个节点,4 363个单元,其中梁单元4 251个,桁架单元112个,材料参数如表1所示。
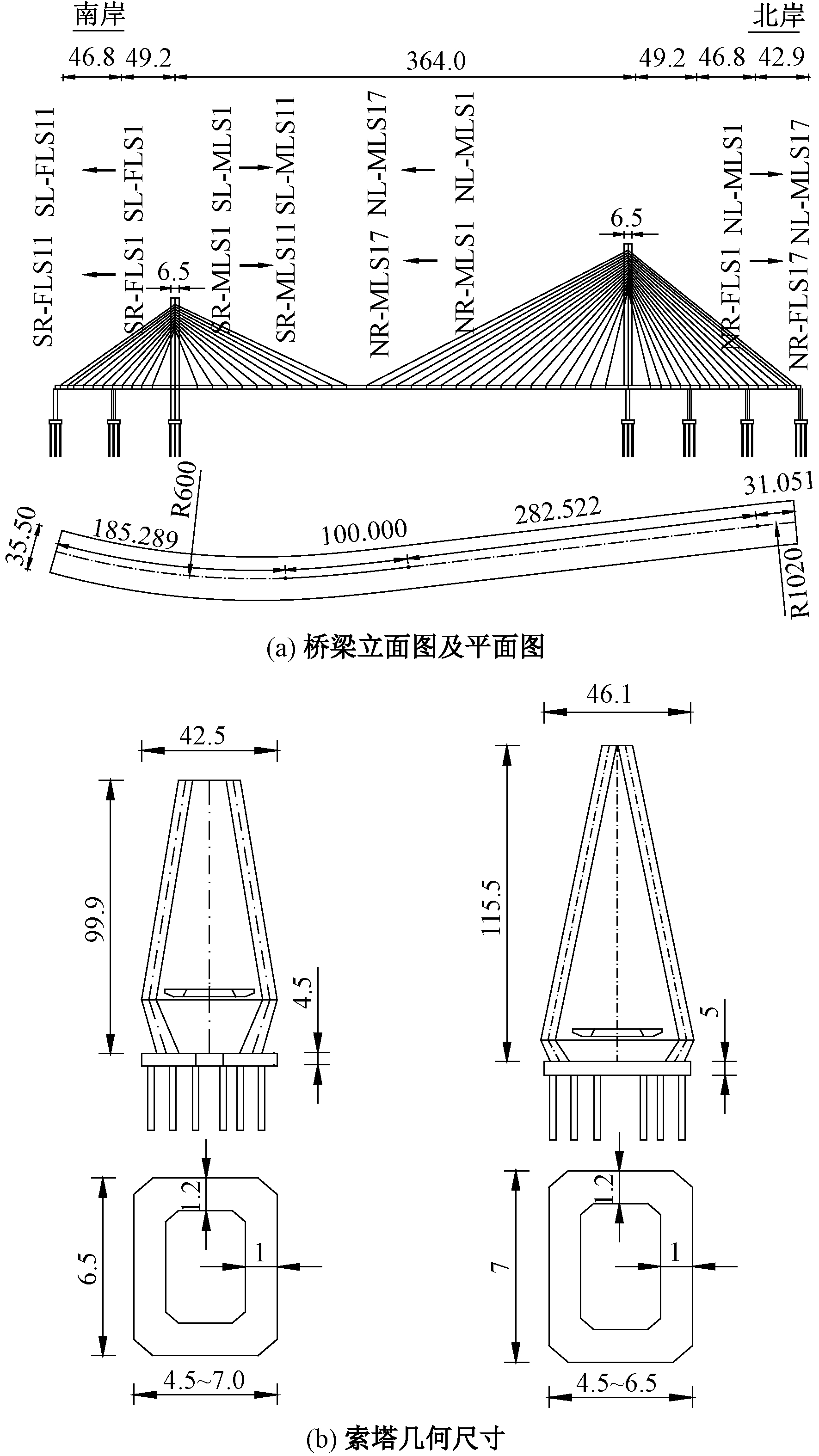
图1 桥梁示意图(m)
Figure 1 Schematic diagram of bridge(m)
表1 材料参数
Table 1 Material parameters

材料等级弹性模量/MPa密度/(kg·m-3)泊松比混凝土C503.45×10425.00.2钢材Q345qD2.06×10578.50.3钢绞线Strand18601.95×10578.50.3
主梁采用梁格法建模,将横截面划分为8段,每一段代表一根纵梁,主梁尺寸及梁格划分如图2所示。纵向梁格构件的抗弯惯性矩用MIDAS/Civil计算,并利用平行移轴定理调整,使各纵向杆件的形心高度与整体截面的形心高度一致。抗扭惯性矩为顶底板整体抗弯惯性矩的2倍(对于边纵梁构件,顶板宽度不包括悬臂翼缘),采用以下公式计算:
Ixx=2(h′2d′b′+h″2d″b″)。
(1)
式中:h′、h″分别为顶、底板中面至中性轴的距离,mm;d′、d″分别为顶、底板厚度,mm;b′、b″分别为顶、底板宽度,mm。
如果只有顶板,计算方法为
(2)
式中:t为顶板厚度,mm;b为顶板宽度,mm。
调整后的各道纵向梁格抗弯惯性矩及抗扭惯性矩如表2所示。该桥横隔板最大间距为3 m,因此横向梁格直接在横隔板处布置,不需加密。其单位宽度抗弯惯性矩和单位宽度抗扭常数计算方法分别为[8]
(3)
(4)
式中:h′、h″分别为顶、底板中面至中性轴的距离,mm;d′、d″分别为顶、底板厚度,mm;d为顶、底板中面间距,mm。
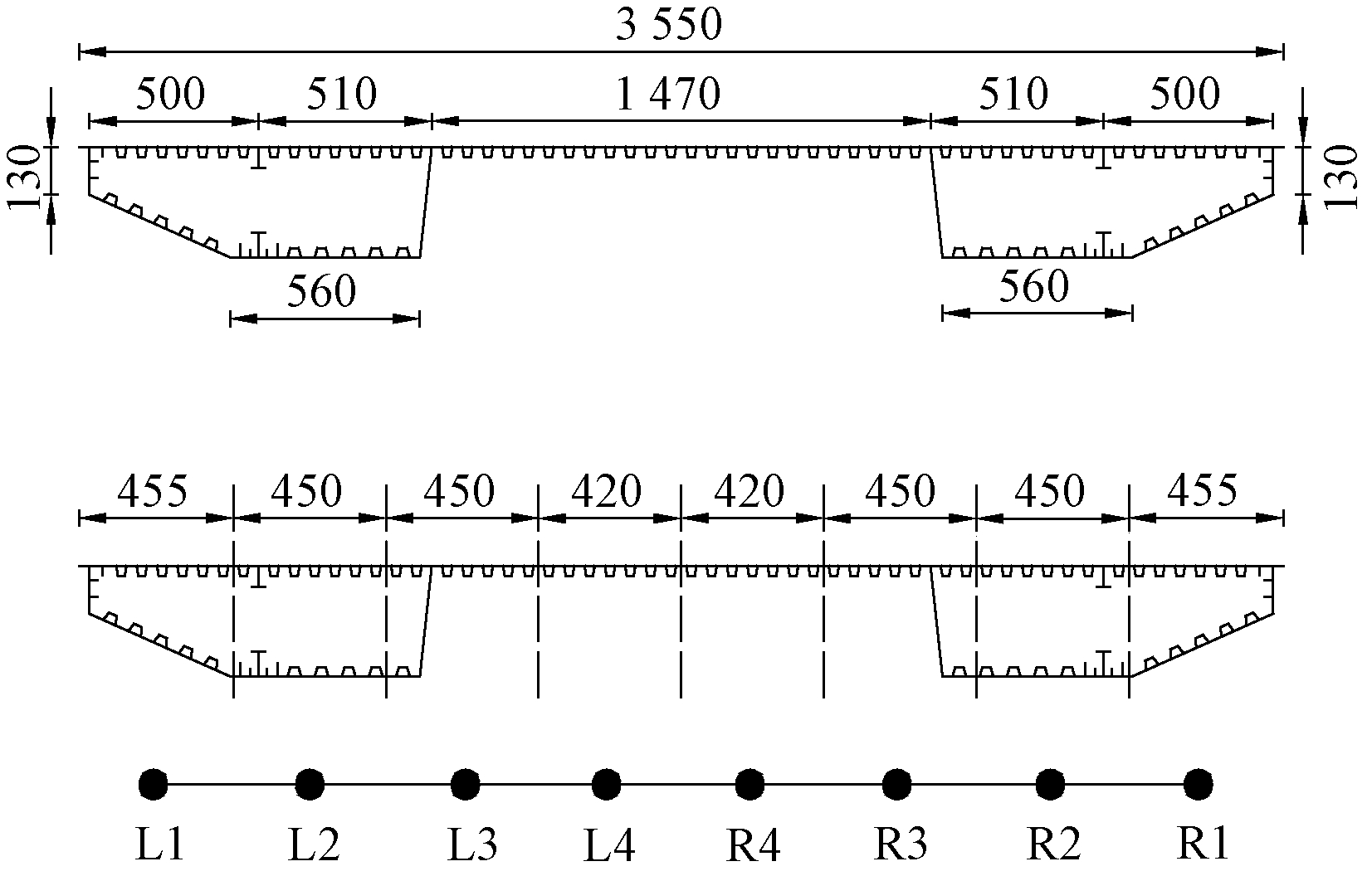
图2 主梁标准横断面图及梁格划分(cm)
Figure 2 Standard cross section of main beam and division of beam grid(cm)
表2 各纵梁抗弯及抗扭惯性矩
Table 2 Bending and torsional moment of inertia of each longitudinal beam
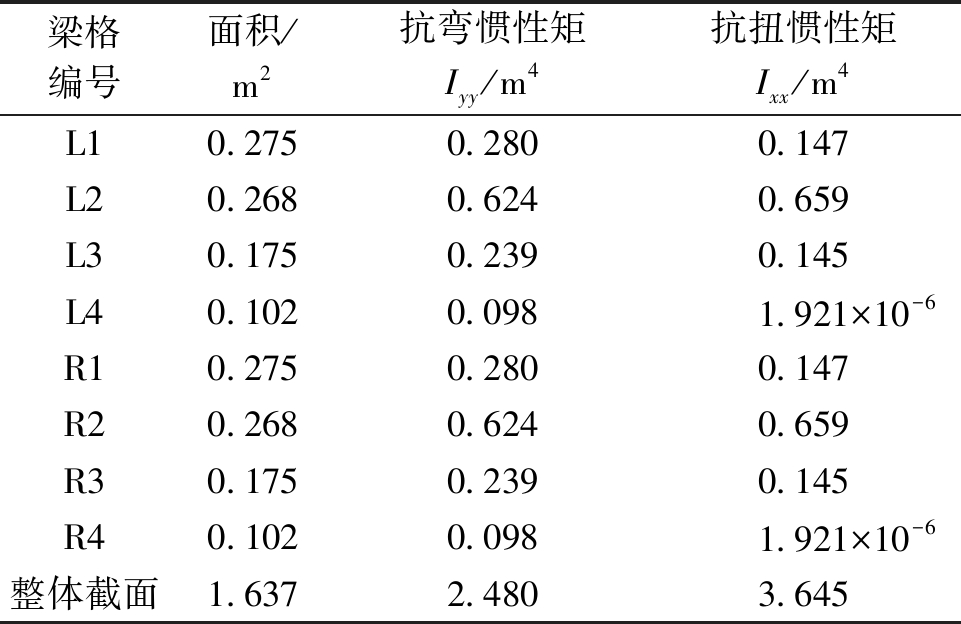
梁格编号面积/m2抗弯惯性矩Iyy/m4抗扭惯性矩Ixx/m4L10.2750.2800.147L20.2680.6240.659L30.1750.2390.145L40.1020.0981.921×10-6R10.2750.2800.147R20.2680.6240.659R30.1750.2390.145R40.1020.0981.921×10-6整体截面1.6372.4803.645
2.2 拉索、索塔及支座的模拟
索塔采用梁单元模拟。本桥斜拉索最长为230.83 m,因此用桁架单元模拟能够满足精度的要求[9]。计算时采用Ernst公式修正弹性模量,以消除拉索垂度对结构非线性的影响。
塔底全部固结,主梁节点与斜拉索之间采用刚性连接,辅助墩支座与主梁节点之间采用弹性连接,竖向刚度为15 294 kN/mm,顺桥向和横桥向刚度为10 000 kN/mm,主塔上的支座采用只受压弹性连接,刚度为19 496 kN/mm。
将自重、二期荷载、压重、索力作用下的计算成桥索力与设计成桥索力进行对比,结果如图3所示。可看出设计成桥索力与计算成桥索力之间的误差均控制在5%以内,其误差值最大为4.96%。计算索力与设计索力基本一致,该模型可以反映该斜拉桥的基本特性。有限元模型如图4所示。
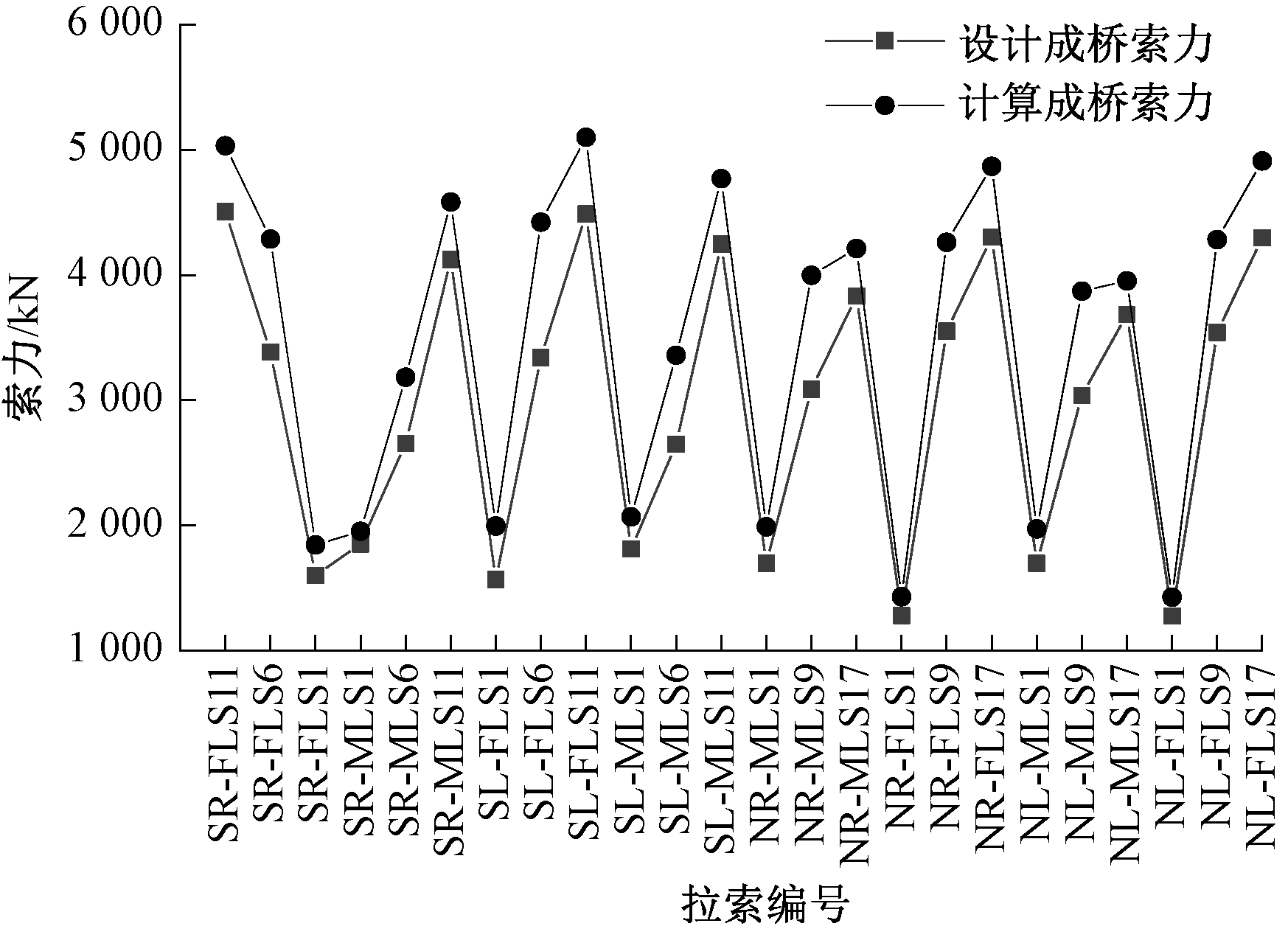
图3 设计索力与计算索力的对比
Figure 3 Comparison between design cable force and calculated cable force

图4 有限元模型图
Figure 4 Finite element model diagram
2.3 断索的模拟
斜拉桥是柔性结构,断索瞬间产生的冲击作用会对结构产生一定的影响[10-11]。本文不考虑断索瞬间产生的冲击效应,仅研究断索前后桥梁的静力特性的变化。斜拉索断裂后的状态通过钝化相应的拉索来模拟,具体做法是将断裂的斜拉索定义为一个单独的结构组,在成桥阶段的基础上新增施工阶段,在相应的施工阶段中将其钝化。
边梁和中梁的支座反力、内力分布不均匀,在研究断索前后的力学性能变化时应选取最不利位置处的数值加以分析。宋嘉宇等[12]以一座弯箱梁桥为例,采用单梁法、梁格法分别建模,对比了在相同荷载作用下支座反力、内力、位移的差别,研究表明,梁格模型与单梁模型的变化趋势基本一致,但梁格模型的计算结果数值偏大,且外弧侧的数值大于内弧侧的数值。因此可以选取外边梁对断索前后的力学性质加以分析。
3 断索对斜拉桥力学特性的影响
3.1 断索工况选择
由于不同位置处的斜拉索断裂产生的响应有所差别,因此在进行单索断裂影响分析时,选择南岸边跨、中跨具有代表性的长、中、短索各一根,共计12个单索断索工况,在进行组合断裂影响分析时,选择纵向断裂、横向断裂、以原点为中心断裂3个组合断索工况,如表3、表4所示。为方便分析,外荷载只施加自重、二期荷载、压重以及索力,不施加温度荷载、移动荷载、风荷载等,不考虑支座沉降。
表3 单索断裂工况
Table 3 Single cable fracture conditions
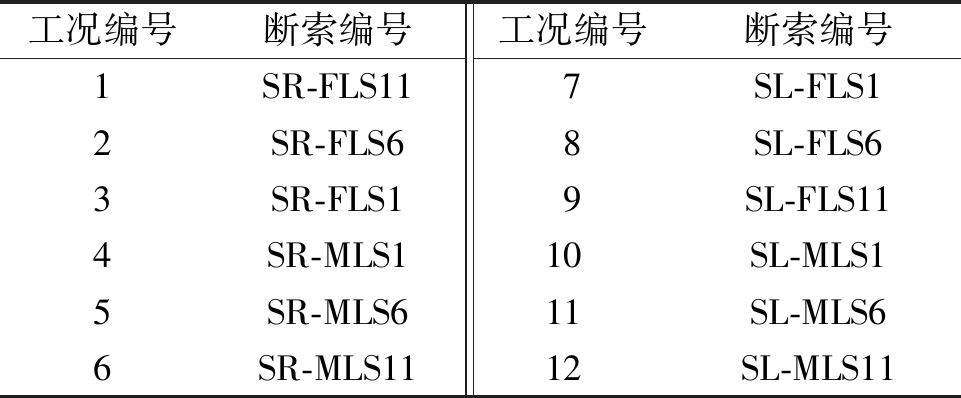
工况编号断索编号工况编号断索编号1SR-FLS117SL-FLS12SR-FLS68SL-FLS63SR-FLS19SL-FLS114SR-MLS110SL-MLS15SR-MLS611SL-MLS66SR-MLS1112SL-MLS11
表4 组合断裂工况
Table 4 Combined fracture conditions

工况编号断索组合断索编号13纵向断裂SR-FLS11+NR-FLS1714横向断裂SR-FLS11+SL-FLS1115以原点为中心断裂SR-FLS11+NL-FLS17
3.2 断索对剩余拉索索力的影响
将各断索工况下的全桥拉索索力值与断索前进行对比,结果如图5、图6所示。
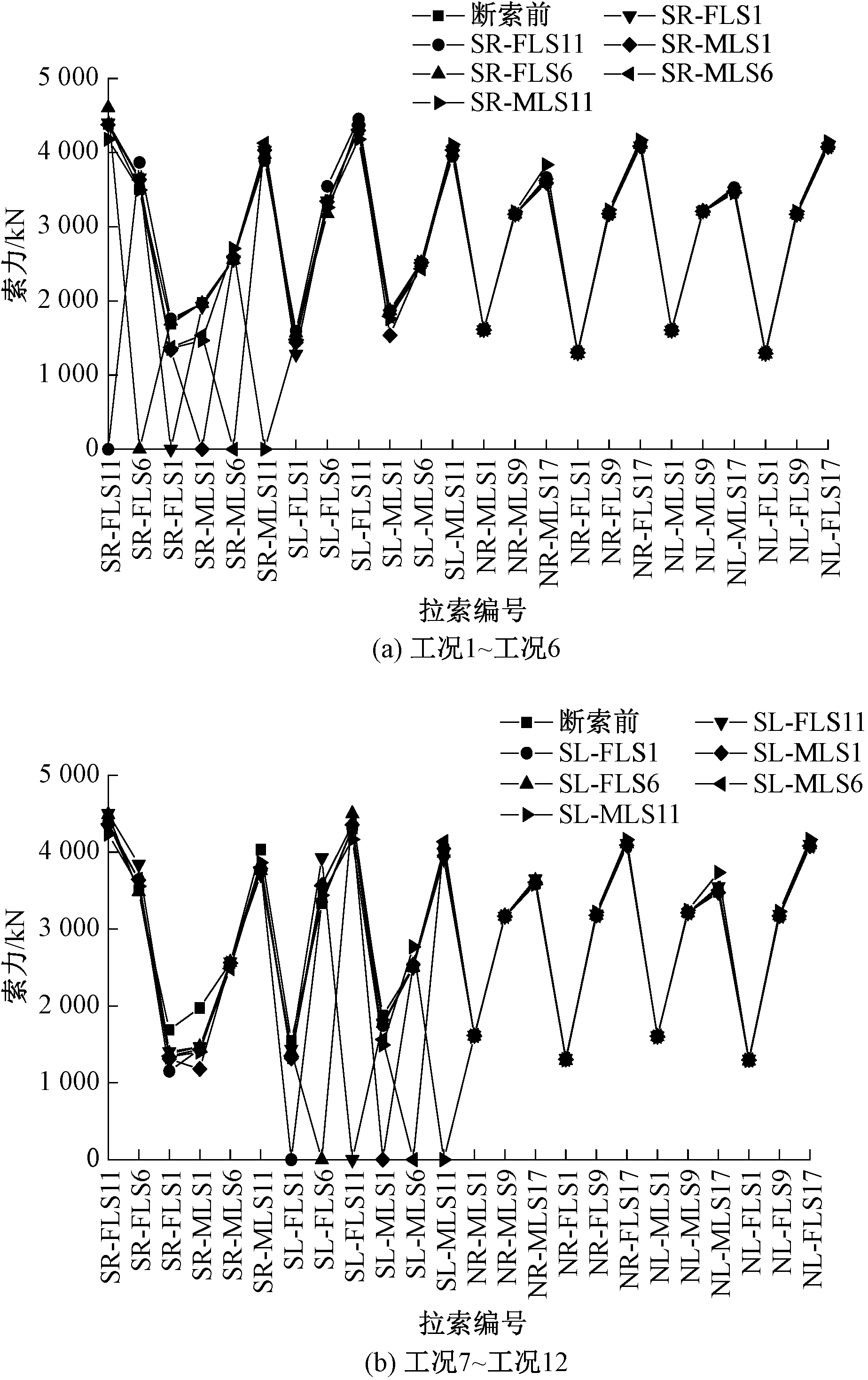
图5 单索断裂工况下的拉索索力
Figure 5 Cable force under single cable fracture condition
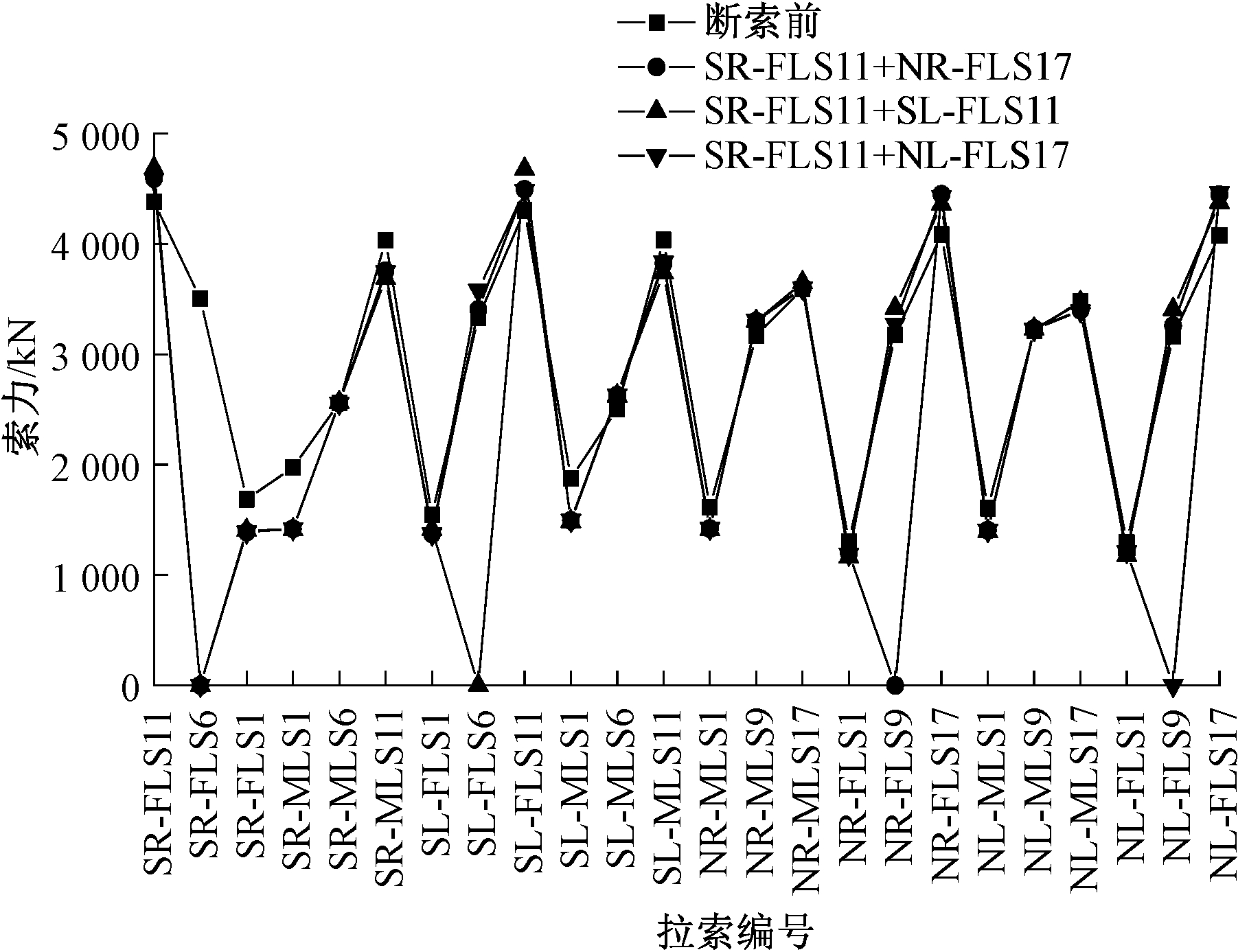
图6 组合断裂工况下的拉索索力
Figure 6 Cable force under combined fracture condition
从图5、图6可以看出,①单索断裂只会产生局部影响,断索附近的拉索索力增大明显,索力变化值随着与断索距离的增加而递减,距离断索较远处的拉索几乎不受影响。如SR-FLS11断裂对SR-FLS10的影响最大,索力增大值为512.54 kN,增幅为13.05%,而距离其较远处的拉索变化幅度很小,大部分在1%以下。②拉索断裂对断索跨拉索的影响比非断索跨大,对断索面拉索的影响比非断索面大。如拉索SL-FLS11断裂后,与断索距离较近且同侧的拉索索力值增大了7%~13%,与之相近且异侧的拉索索力值增大了3%~6%,距离其较远的北侧边跨拉索索力值仅变化了0.5%左右。③长索与中索断裂后索力分配较为分散,而短索断裂后索力由邻近的几根索集中承受。如长索SR-FLS11与中索SR-FLS6断裂对其周围10根拉索的索力影响较大,长索断裂产生的索力增幅峰值为13.05%,中索断裂产生的索力增幅峰值小于长索,为11.37%,而短索SR-FLS1断裂后仅对其相邻的4根拉索索力影响较大,最大增幅达到了17.5%,对其他位置处的拉索影响很小。④中跨斜拉索断裂产生的影响大于边跨。如中跨长索SR-MLS11断裂产生的索力变化峰值为793.25 kN,增幅为18.2%,相比边跨长索SR-FLS11断裂而言,峰值更大,影响范围也更大。⑤组合断裂工况比单索断裂工况产生的影响更大。为验证双索断裂产生的影响与相应两根单索断裂产生的影响之间的关系,以工况14为例,对比SR-FLS11、SL-FLS11单独断裂和两者共同断裂对SR-FLS10索力值的影响,结果如表5所示。
表5 索力值对比
Table 5 Comparison of cable force values

断裂斜拉索研究斜拉索索力变化值/kNSR-FLS11SR-FLS10512.54SL-FLS11SR-FLS1094.07SR-FLS11+SL-FLS11SR-FLS10612.88
从表5可以看出,组合断裂工况与相应的单索断裂工况相比虽有一些放大效应,但近似符合叠加原理。
3.3 断索对主梁挠度的影响
将各断索工况下的主梁挠度值与断索前进行对比,结果如图7、图8所示。
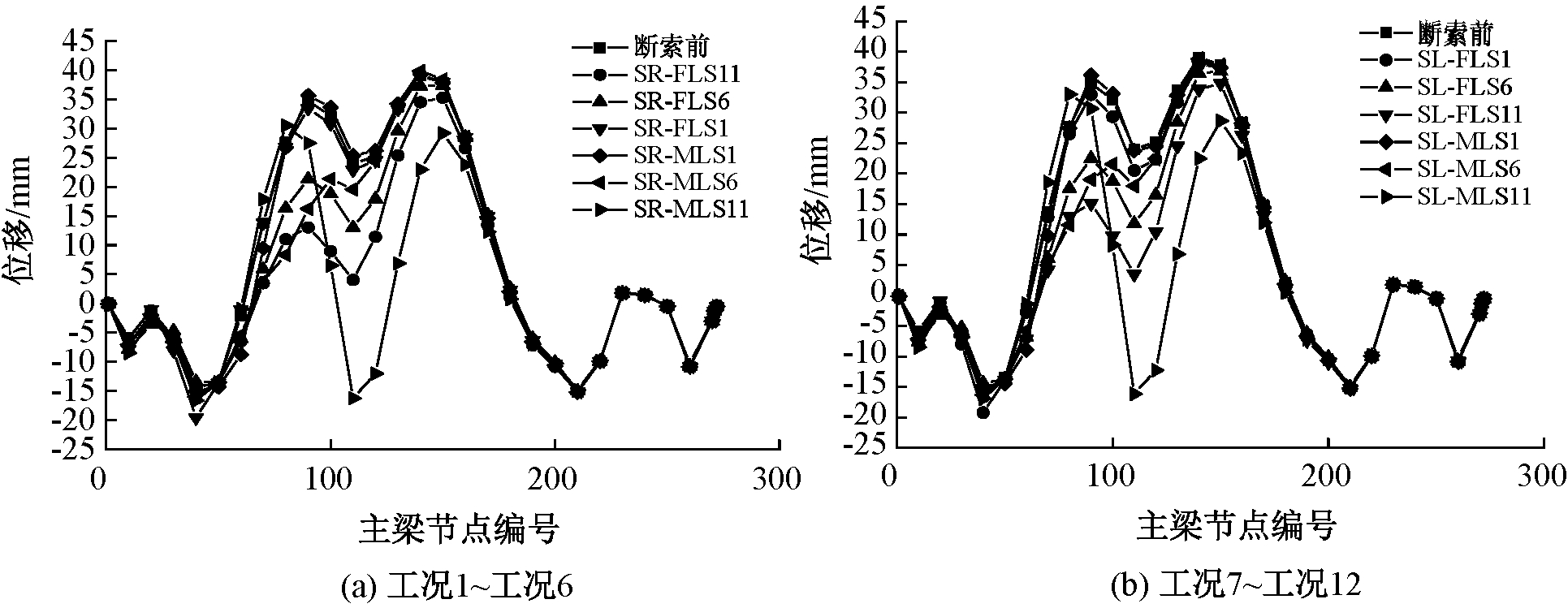
图7 单索断裂工况下的主梁挠度
Figure 7 Deflection of main beam under single cable fracture condition
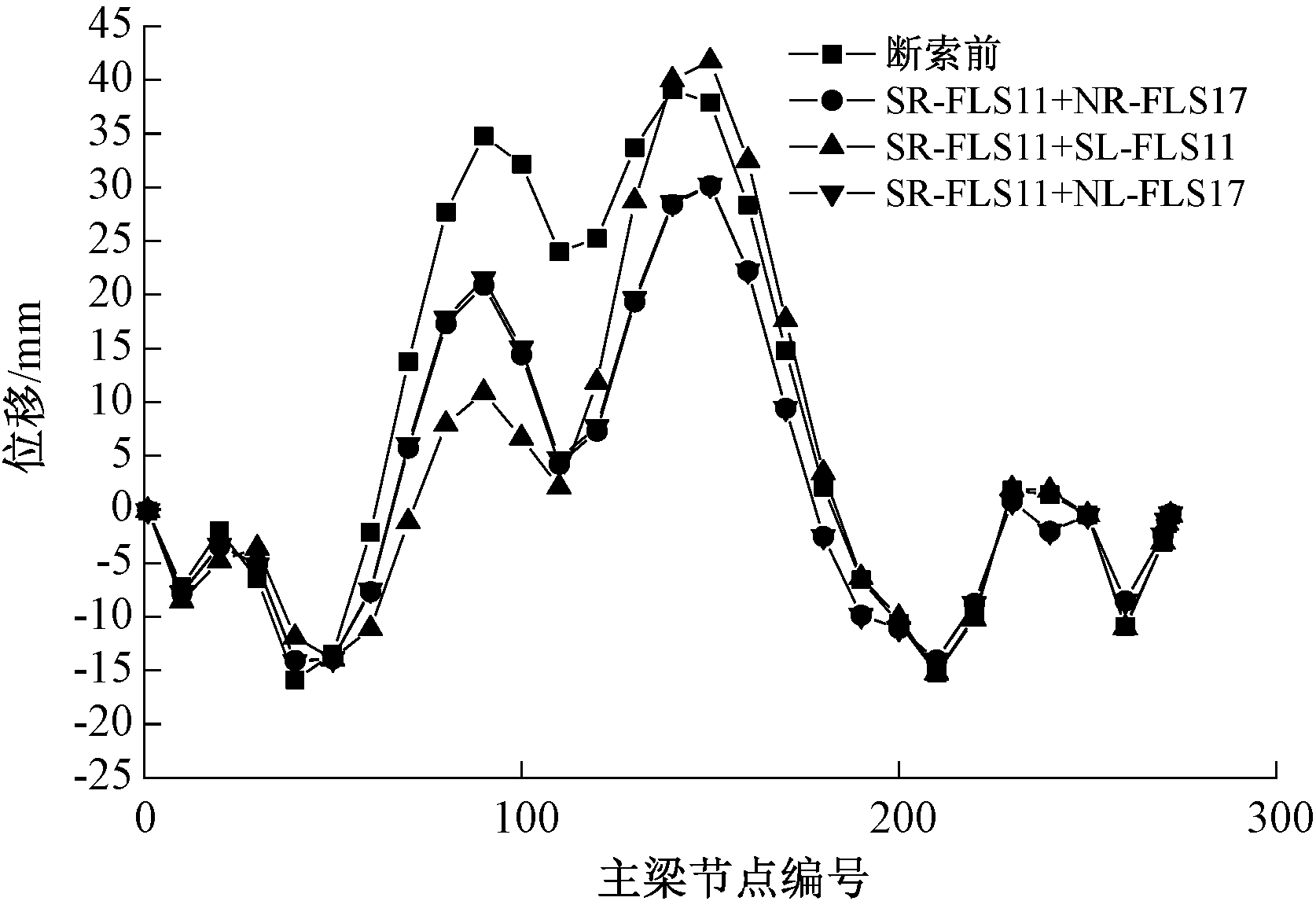
图8 组合断裂工况下的主梁挠度
Figure 8 Deflection of main beam under combined fracture condition
从图7、8可以看出,①长索断裂对主梁线形的影响最大,短索最小,中索介于两者之间。如选取3根不同长度的拉索进行对比,SR-FLS11断裂产生的挠度变化峰值为26.62 mm,SR-FLS6产生的挠度变化峰值为18.43 mm,SR-FLS1断裂后的挠度曲线与断裂前重合程度很高,变化峰值仅为3.52 mm。②边跨长索断裂对主梁挠度的影响峰值在中跨合龙段附近,而其他位置处的拉索断裂对主梁挠度的影响峰值在自身索位处。如SR-FLS11断裂后,峰值在距离跨中24.5 m处,最大偏离值为27.06 mm;SR-MLS6断裂后,挠度变化的峰值在距离断索锚固区1.4 m处,峰值为21.76 mm。③中跨拉索断裂对主梁挠度的影响相比边跨拉索断裂而言,影响范围更大,峰值也更大。如边跨长索SL-FLS11断裂后,中跨合龙段附近的挠度变化为17~24 mm,全桥挠度变化峰值为24.31 mm。而中跨长索SL-MLS11断裂后,断索锚固区附近的主梁挠度变化达到了38~45 mm,峰值也比前者更大,为43.97 mm。④在距离断索较近处,组合断索工况下的主梁挠度变化值比单索断裂工况更大,且近似符合叠加原理。而在距离断索较远处,组合断裂工况产生的挠度变化值与相应单索断裂工况相比相差不大。现以工况14为例,将南塔塔根处(塔根无索区)、SL-MLS11断裂处(有索区)、跨中合龙段中部(跨中无索区)3个典型位置处的挠度值进行对比说明,结果如表6所示。
表6 挠度值对比
Table 6 Comparison of deflection values
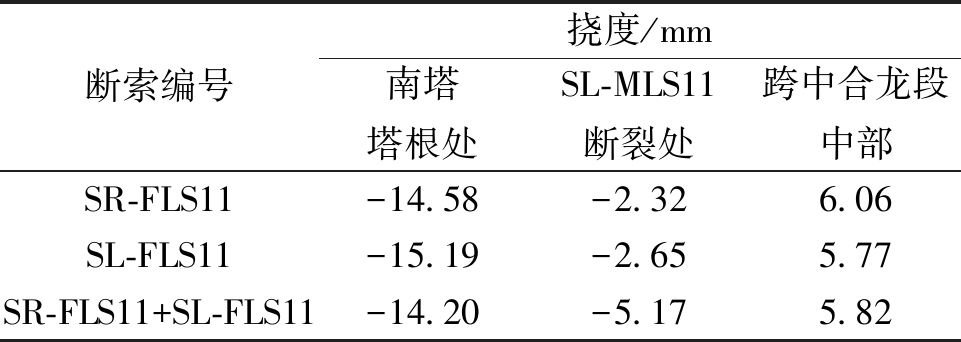
断索编号挠度/mm南塔塔根处SL-MLS11断裂处跨中合龙段中部SR-FLS11-14.58-2.326.06SL-FLS11-15.19-2.655.77SR-FLS11+SL-FLS11-14.20-5.175.82
3.4 断索对主梁应力的影响
斜拉索锚固于主梁之上,拉索断裂不仅会使某些拉索索力突增或突降,使主梁挠度发生改变,还会对主梁应力产生一定的影响。因此,需要对不同断索工况下主梁不同位置处的应力进行分析和总结。对单索断裂工况及组合断裂工况下的主梁应力进行分析,如图9、10所示,并统计其最大应力值见表7。
由图9、10及表7可以看出,断裂拉索的长度和位置对主梁的峰值应力影响不大,仅对断索锚固区的应力有一定的影响。如SR-FLS11断裂后,锚固区附近的应力增大值超过了5 MPa,而距离断索较远处的位置变化值均在0.5 MPa以下;再如SR-FLS11与NR-FLS17断裂后,斜拉索SR-FLS11锚固区附近增大了5.6 MPa,距离其较远处变化值均在1.5 MPa以下。
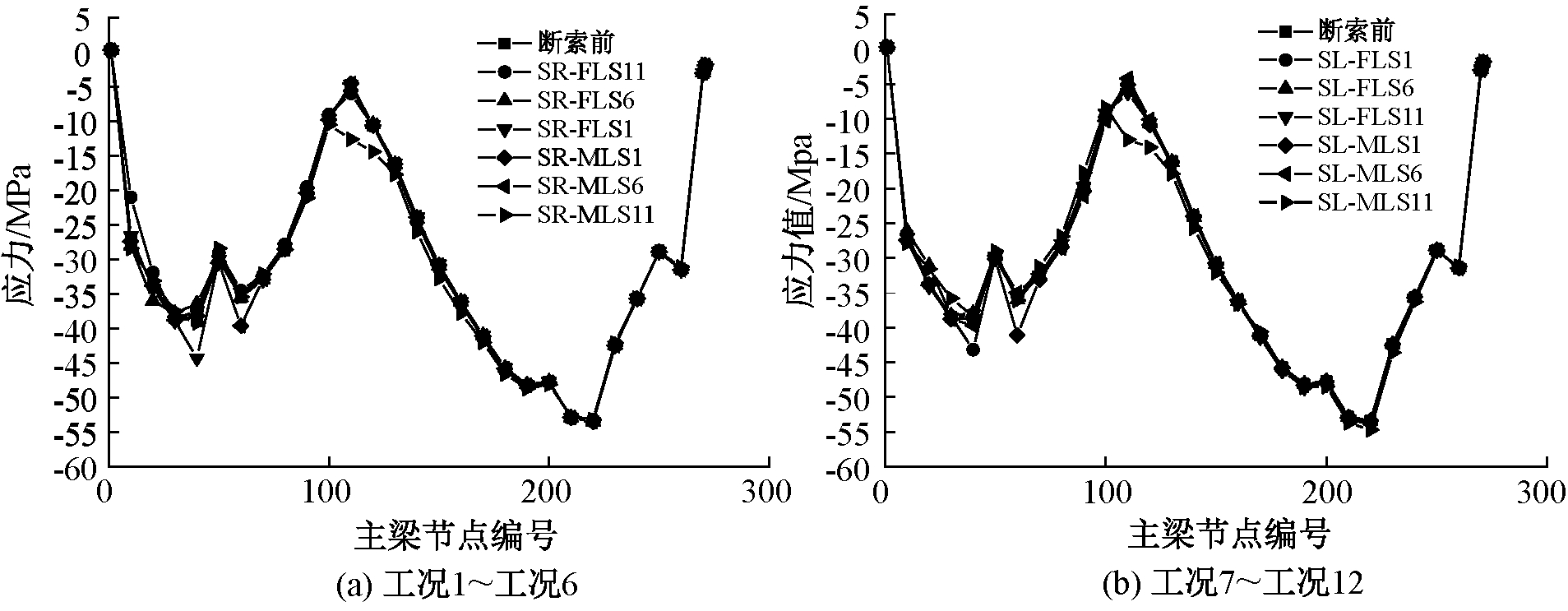
图9 单索断裂工况下的应力值
Figure 9 Stress value under single cable fracture condition
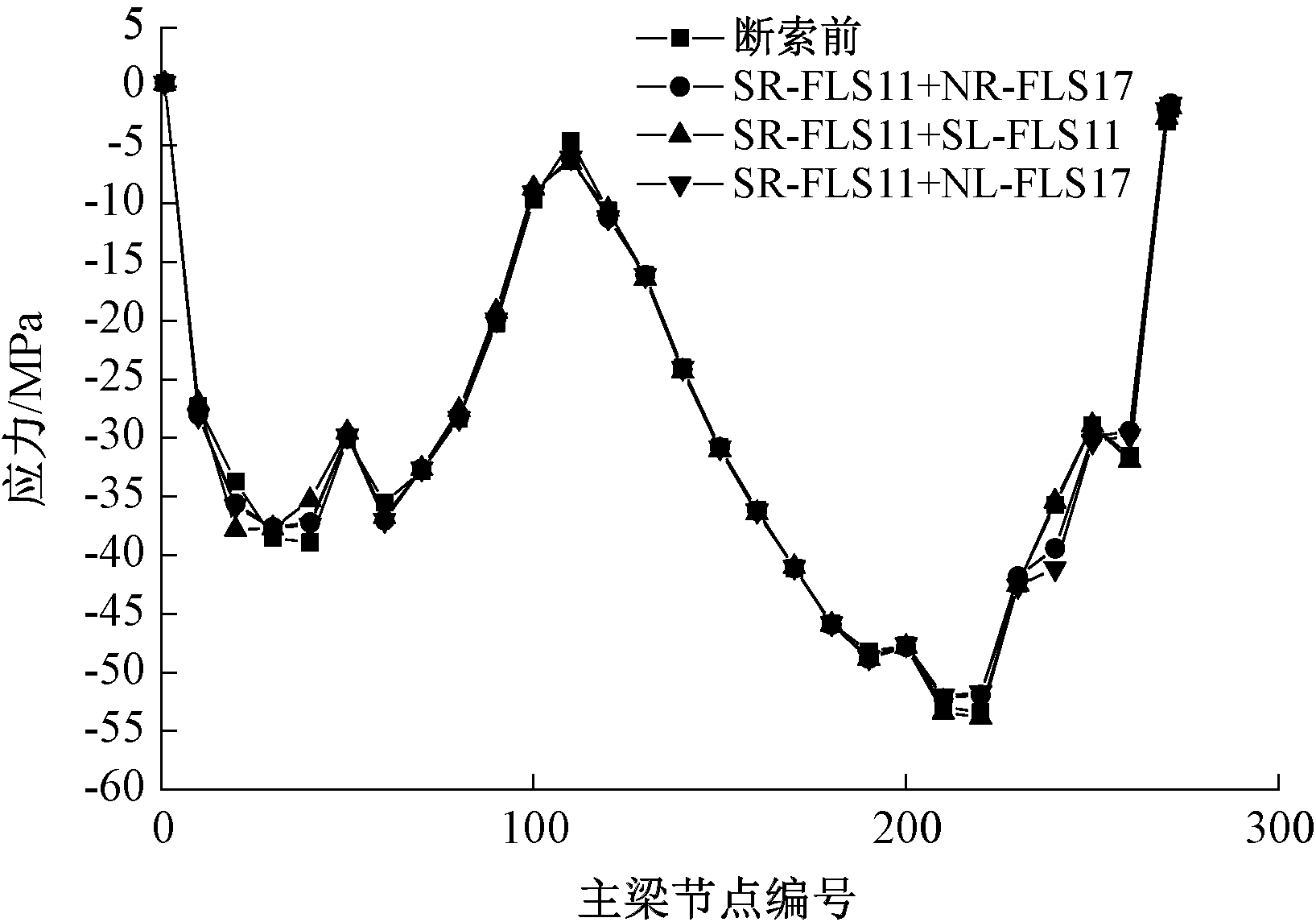
图10 组合断裂工况下的应力值
Figure 10 Stress value under combined fracture condition
表7 不同断索工况下的最大应力值
Table 7 Maximum stress value under different cable breaking conditions
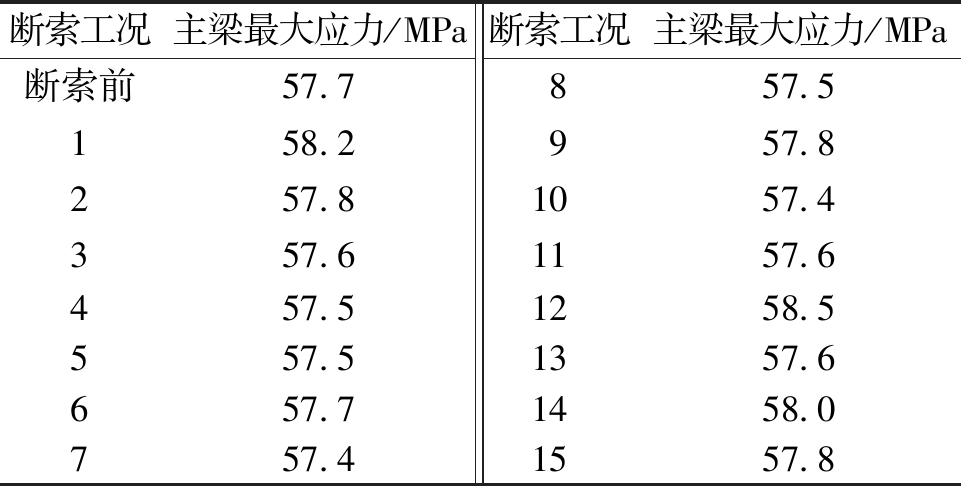
断索工况主梁最大应力/MPa断索工况主梁最大应力/MPa断索前57.7857.5158.2957.8257.81057.4357.61157.6457.51258.5557.51357.6657.71458.0757.41557.8
3.5 断索对塔顶偏移的影响
斜拉索一端锚固于主梁,另一端锚固于桥塔,所以拉索断裂不仅会对主梁的力学性能产生影响,也会改变桥塔的受力,造成塔顶的偏移。规定塔顶沿主跨方向移动时为正值,沿边跨方向移动时为负值。现以南侧拉索SR-FLS11、SR-FLS6、SR-FLS1、SR-MLS1、SR-MLS6、SR-MLS11为例,探究其断裂对两个索塔的塔顶偏移量的影响。由于该桥为弯桥,所以不仅要考虑顺桥向的塔顶偏移,还要综合考虑横桥向、竖向的塔顶偏移。桥塔在3个方向的综合位移如图11所示。
从图11可看出,①长索断裂对塔顶偏移的影响最大,中索次之,短索最小。当SR-FLS11断裂时产生的塔顶偏移量最大,为15.39 mm,而SR-FLS1、SR-MLS1断裂时,塔顶偏移量仅为-0.16、0.53 mm。②拉索断裂仅对与其相连的索塔影响较大,对另一侧的索塔影响很小。如与南塔相连的SR-FLS1断裂后,北塔塔顶位移的偏移量仅为0.50 mm。
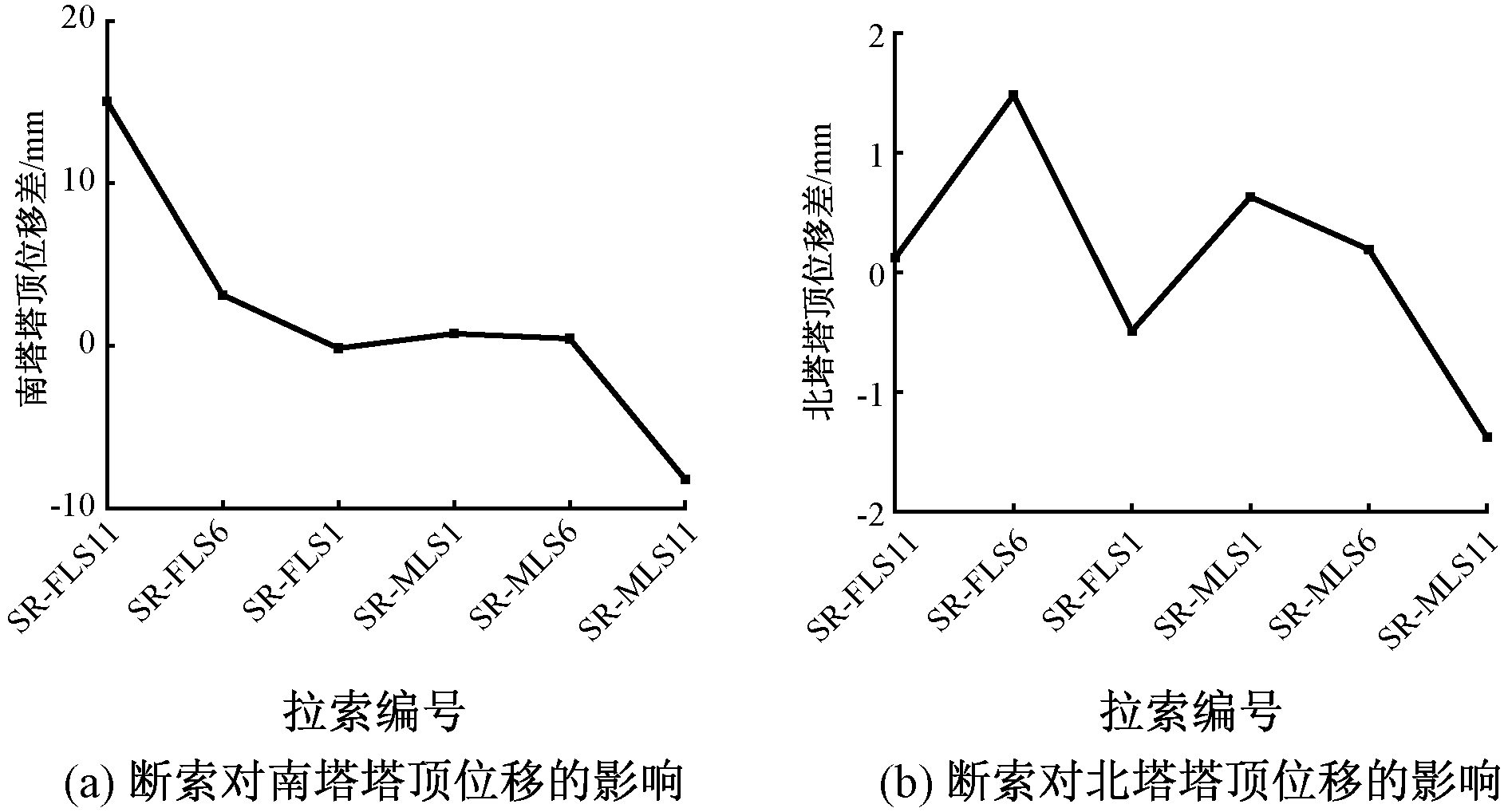
图11 断索对塔顶位移的影响
Figure 11 Influence of broken cable on tower top displacement
4 结论
本文以柴家峡斜拉桥为工程实例,对断索前后桥梁各部分的力学性质进行分析,结论如下。
(1)不同长度、不同位置的拉索断裂产生的影响不同,断索的长度越长、越靠近中跨,产生的影响越大。其余拉索距离其越近,受到的影响越大。
(2)组合断裂工况下的索力变化与相应的单索断裂工况之和相比有一些放大效应,但基本符合叠加原理。
[1] WOLFF M, STAROSSEK U. Cable loss and progressive collapse in cable-stayed bridges[J]. Bridge Structures, 2009, 5(1): 17-28.
[2] JANJIC D, PIRCHER M, PIRCHER H. Optimization of cable tensioning in cable-stayed bridges[J]. Journal of Bridge Engineering, 2003, 8(3): 131-137.
[3] 张羽, 方志, 卢江波, 等. 大跨混凝土斜拉桥施工过程中结构的断索动力响应[J]. 振动与冲击, 2021, 40(5): 237-246.
ZHANG Y, FANG Z, LU J B, et al. Broken cable-induced dynamic response of long-span concrete cable stayed bridge during construction[J]. Journal of Vibration and Shock, 2021, 40(5): 237-246.
[4] 李彦兵. 大跨径斜拉桥断索危害性研究[D]. 重庆:重庆交通大学, 2013.
LI Y B. Research of broken cable hazard for long scale cable-stayed bridge[D]. Chongqing: Chongqing Jiaotong University, 2013.
[5] 黄华, 郭朋, 吴先兵, 等. 断索对双钢拱塔斜拉桥力学性能的影响[J]. 公路交通科技, 2020, 37(4): 62-71, 117.
HUANG H, GUO P, WU X B, et al. Influence of cable breaking on mechanical properties of double-steel-arch-pylon cable-stayed bridge[J]. Journal of Highway and Transportation Research and Development, 2020, 37(4): 62-71, 117.
[6] 柴文浩, 杨雅勋, 张宇航. 吊杆断裂对系杆拱桥力学性能的影响[J]. 公路, 2021, 66(9): 174-179.
CHAI W H, YANG Y X, ZHANG Y H. Influence of suspender fracture on the mechanical properties of tied arch bridges[J]. Highway, 2021, 66(9): 174-179.
[7] 陈国胜. 拉索断裂对空间扭转索面斜拉桥主梁线形的影响研究[J]. 铁道建筑, 2016, 56(3): 17-20.
CHEN G S. Research on influence of cable breaking on line shape of cable-stayed bridge with spatial torsion cable planes[J]. Railway Engineering, 2016, 56(3): 17-20.
[8] HAMBLY E C. Bridge deck behavior[M]. London: Chapman and Hall, 1976: 145-150.
[9] 梁鹏, 徐岳, 刘永健. 斜拉索分析统一理论及其应用[J]. 建筑科学与工程学报, 2006, 23(1): 68-77.
LIANG P, XU Y, LIU Y J. Unified analysis theory of cable stay and its applications[J]. Journal of Architecture and Civil Engineering, 2006, 23(1): 68-77.
[10] 李宇, 李钊, 李琛. 钢-砼混合梁斜拉桥的颤抖振时域分析[J]. 郑州大学学报(工学版), 2016, 37(3): 69-73.
LI Y, LI Z, LI C. Flutter and buffeting analysis for cable-stayed bridge with steel-concrete girder[J]. Journal of Zhengzhou University (Engineering Science), 2016, 37(3): 69-73.
[11] 李胜利, 胡亚楠, 杜道倾, 等. 大跨径悬索桥施工猫道气动力系数数值分析[J]. 郑州大学学报(工学版), 2015, 36(4): 57-61.
LI S L, HU Y N, DU D Q, et al. Numerical analysis of aerodynamic coefficients for catwalk considering Reynolds number effect on long-span suspension bridge during the construction[J]. Journal of Zhengzhou University (Engineering Science), 2015, 36(4): 57-61.
[12] 宋嘉宇, 邬晓光. 基于梁格法对曲线箱梁桥的有限元分析[J]. 公路, 2021, 66(7): 134-138.
SONG J Y, WU X G. Finite element analysis of curved box girder bridge based on grillage method[J]. Highway, 2021, 66(7): 134-138.