0 引言
有机朗肯循环(ORC)因为安全性高、维护要求低、性能良好等优点,在余热发电领域得到了广泛的应用[1-2]。作为ORC系统中重要的热功转换部件,膨胀机的选择和设计对系统的性能有着重要的影响。向心透平由于高压力比、高转速、结构紧凑、制造成本低、效率高等特点,被广泛应用于中小型 ORC系统中[3-4],其设计与分析受到了越来越多的关注。Li等[5] 设计了一个向心透平的一维模型来分析8种工质的动态透平效率。Daabo等[6]以压缩空气作为工质,提出了一种以太阳能为热源的小型向心透平的数值模拟方法。Sauret等[7] 设计了一台以R134a为工质的向心透平,并通过 CFD 数值模拟分析了透平的变工况性能。Xia 等[8] 对以R245fa为工质的向心透平进行了一维设计和CFD数值模拟,结果表明,CFD模拟结果与一维计算结果非常吻合,同时指出在转子通道中添加分流叶片可以有效提高透平的性能。
虽然CFD数值模拟在预测有机工质向心透平的变况性能以及优化设计方面非常方便,但是模拟计算过程所耗费时间较长且模拟结果易受实际气体性质的影响。为了减轻这种影响,本文选用真实气体方程Peng-Robinson方程 [9]来描述工质的性质,通过CFD数值模拟研究了透平在设计和非设计工况下的性能,并将模拟结果与设计参数和实验数据进行了对比。
1 向心透平的一维设计
向心透平主要由蜗壳、定子和转子组成,其结构如图1所示。在图1中,l1和l2分别为转子进出口叶高;r1和r2分别为转子进口半径和出口半径。工质流经蜗壳后在定子入口处均匀分布,接着进入喷嘴后进一步膨胀和加速。定子和转子之间的间隙使得工质可以在定子出口处充分混合。然后工质进入转子,在转子里继续膨胀并将其动能转换为轴的机械能。
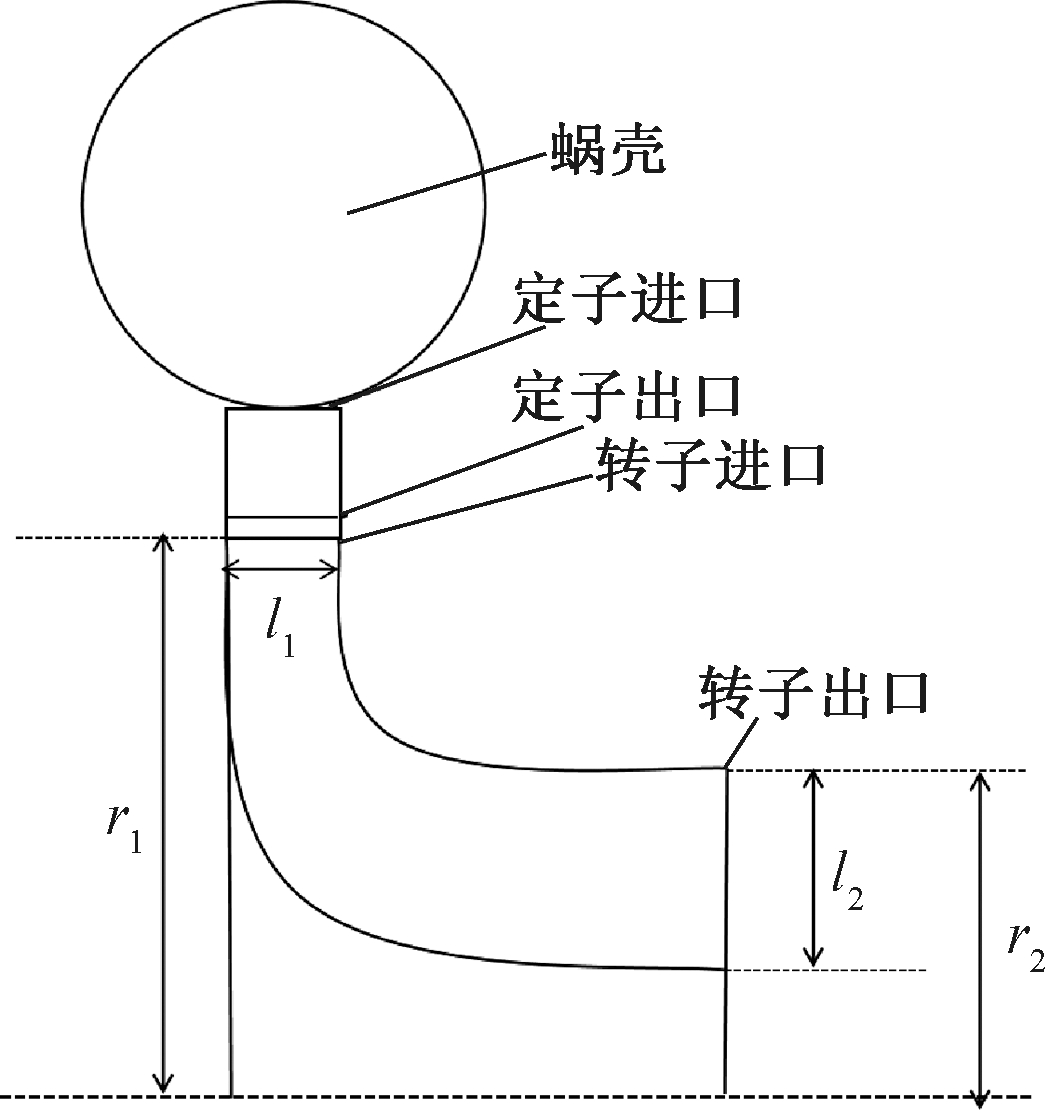
图1 向心透平子午面示意图
Figure 1 Meridional view of radial inflow turbine
向心透平的轮周效率可以由能量方程和速度三角形得出[10],如式(1)所示,然后根据给定的初始参数和一些具体要求,采用筛选法[11] 对向心透平进行设计,因为透平的设计过程涉及公式及计算非常复杂,所以借助计算机编写了Visual Basic热力计算程序,得到与轮周效率相关的7个设计参数和透平主要几何参数,设计流程如图2所示,得到的透平主要设计参数如表1所示。
表1 向心透平主要设计参数
Table 1 Main design parameters of radial inflow turbine
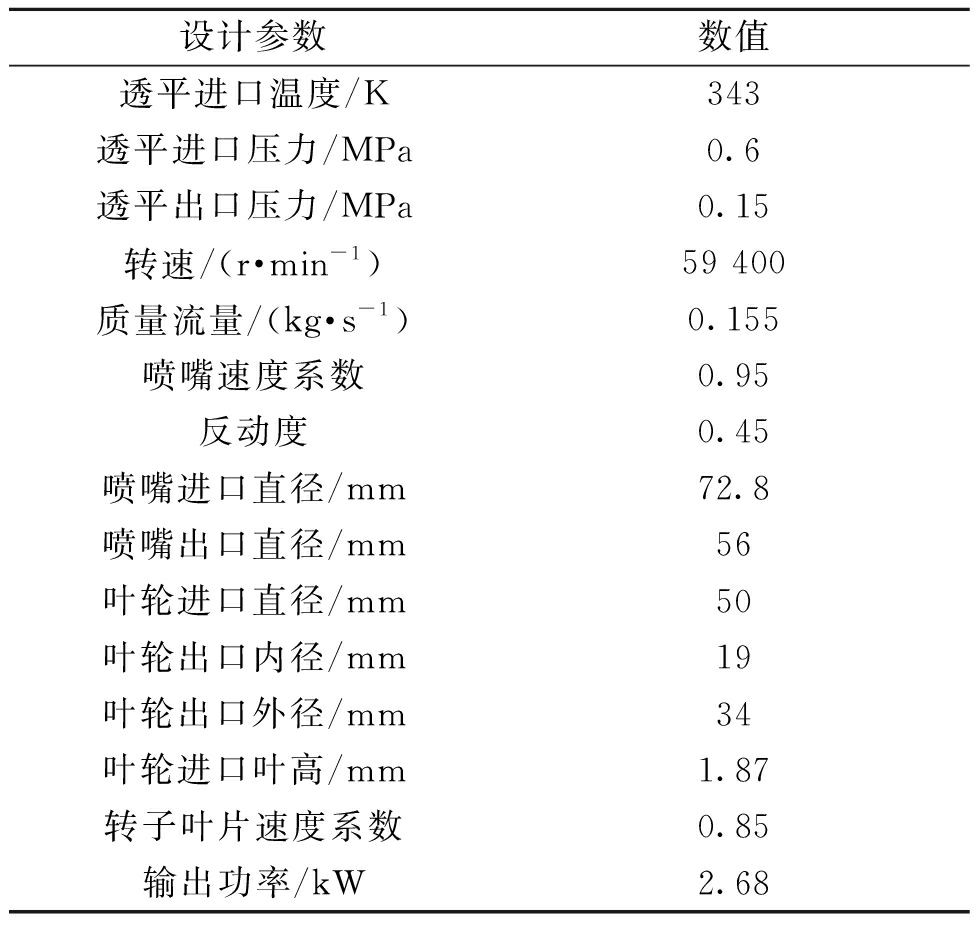
设计参数数值透平进口温度/K343透平进口压力/MPa0.6透平出口压力/MPa0.15转速/(r·min-1)59 400质量流量/(kg·s-1)0.155喷嘴速度系数0.95反动度0.45喷嘴进口直径/mm72.8喷嘴出口直径/mm56叶轮进口直径/mm50叶轮出口内径/mm19叶轮出口外径/mm34叶轮进口叶高/mm1.87转子叶片速度系数0.85输出功率/kW2.68
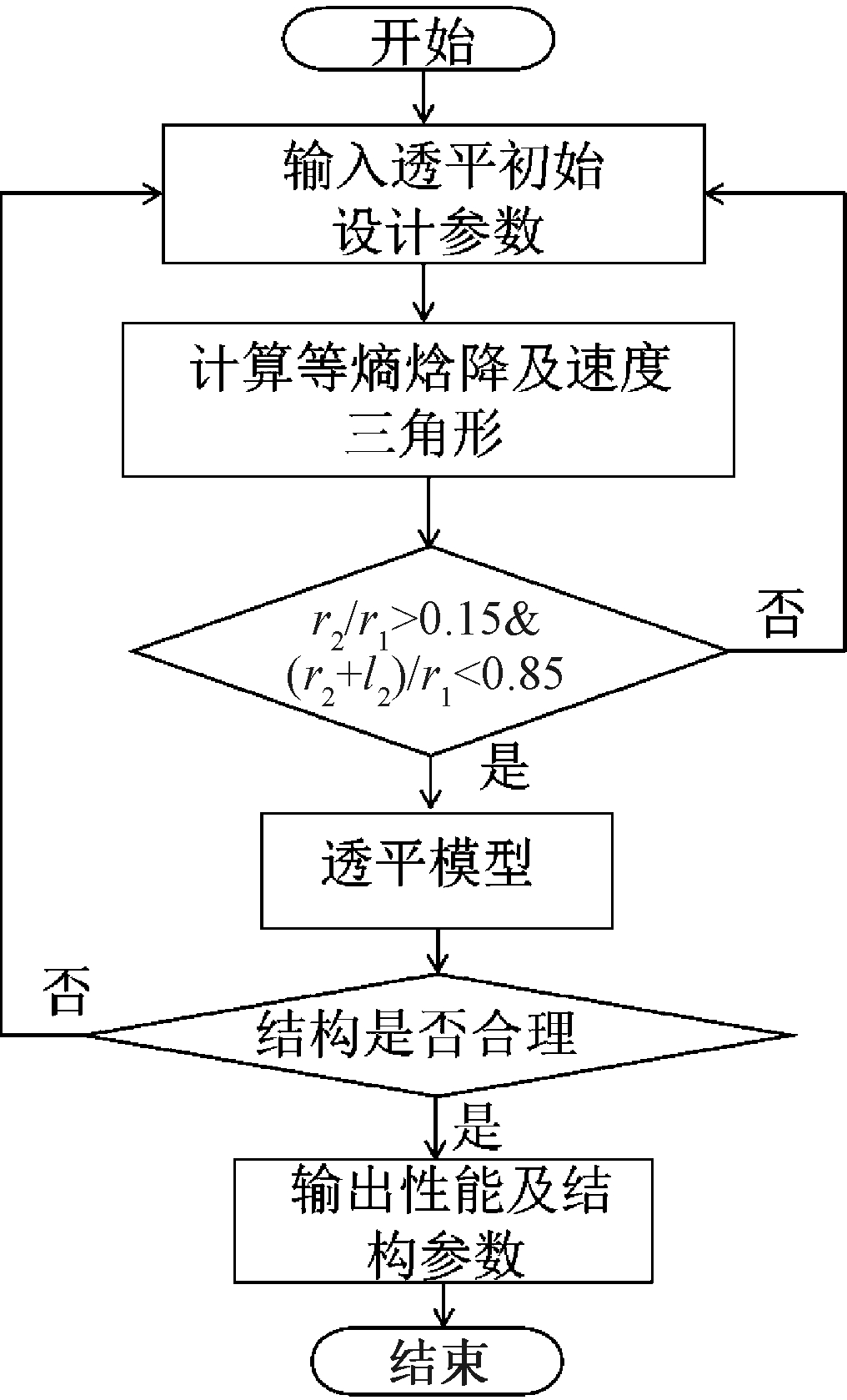
图2 向心透平一维设计流程图
Figure 2 One dimensional design flowchart of radial inflow turbine
(1)
式中:φ为喷嘴速度系数;ψ为转子叶片速度系数;α4为转子进口绝对气流角,(°);β5为转子出口相对气流角,(°);Ω为反动度;xa为速比;μ为轮径比。
2 向心透平的CFD模拟与分析
2.1 设计工况下的性能分析
采用CFX软件对向心透平进行数值模拟,利用ANSYS BladeGen生成定子和转子通道,因为向心透平的叶片呈周期性分布且具有对称性,为了简化模型,只对单个定子通道和转子进行CFD模拟。运用ANSYS-TurboGrid V19.2对定子通道和转子通道进行结构化网格划分,并进行了网格无关性检验,最终确定透平单通道的网格数为500 000。为了保证求解的准确性,将收敛残差设置为10-5。选择具有自动壁面功能的 SST 湍流模型[12],使用第一层网格方法去细化边界层,并将雷诺数设置为1×106,近壁面网格尺寸选用y+来描述,同时将y+控制在1以内,以保证第一层网格节点位于黏性底层。透平入口总温、总压分别定为343 K和0.6 MPa,出口静压定为0.15 MPa。转子域的转速设置为 59 400 r/min。定子和转子域之间的界面采用冻结转子模型,其他壁面采用无滑移边界条件。设计工况下透平一维设计参数与CFD模拟计算结果如表2所示。
表2 CFD计算结果与一维设计参数的比较
Table 2 Comparison between CFD calculation results and one-dimensional design parameters
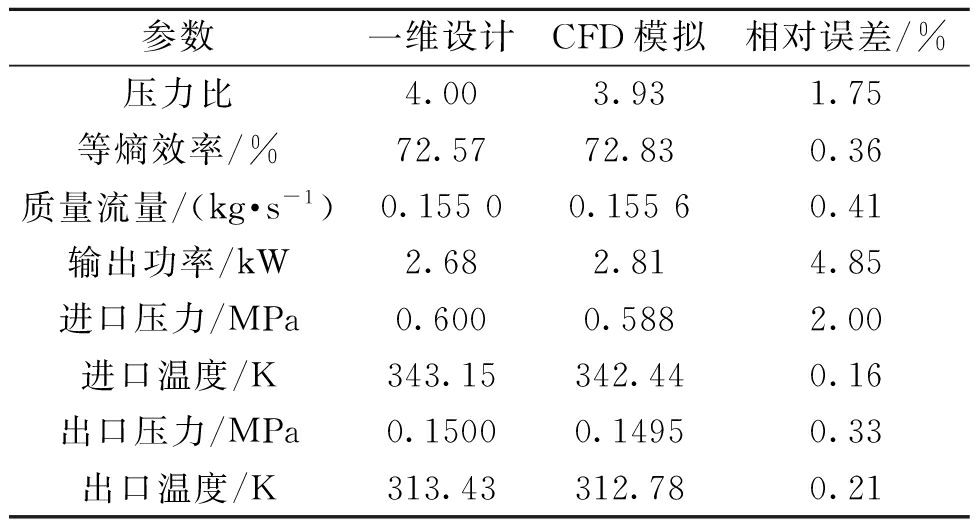
参数一维设计CFD模拟相对误差/%压力比4.003.931.75等熵效率/%72.5772.830.36质量流量/(kg·s-1)0.155 00.155 60.41输出功率/kW2.682.814.85进口压力/MPa0.6000.5882.00进口温度/K343.15342.440.16出口压力/MPa0.15000.14950.33出口温度/K313.43312.780.21
从表2可以发现,一维设计参数与CFD计算值非常接近,两者的等熵效率相差0.36%,输出功率相差4.85%。设计工况下静压和速度流线分布如图3所示,从图3可以看出,定子流道内工质压力梯度明显,透平内部静压分布均匀合理。定子流道内的速度流线比较平滑,没有明显的涡流。同时,工质从定子的入口到出口均匀加速。在转子入口处存在小部分高速区域,这是有机蒸气冲击转子叶片压力侧时产生涡流引起的,将会导致工质的流动摩擦损失增大,后期可通过优化转子叶片的叶型来改善该现象。
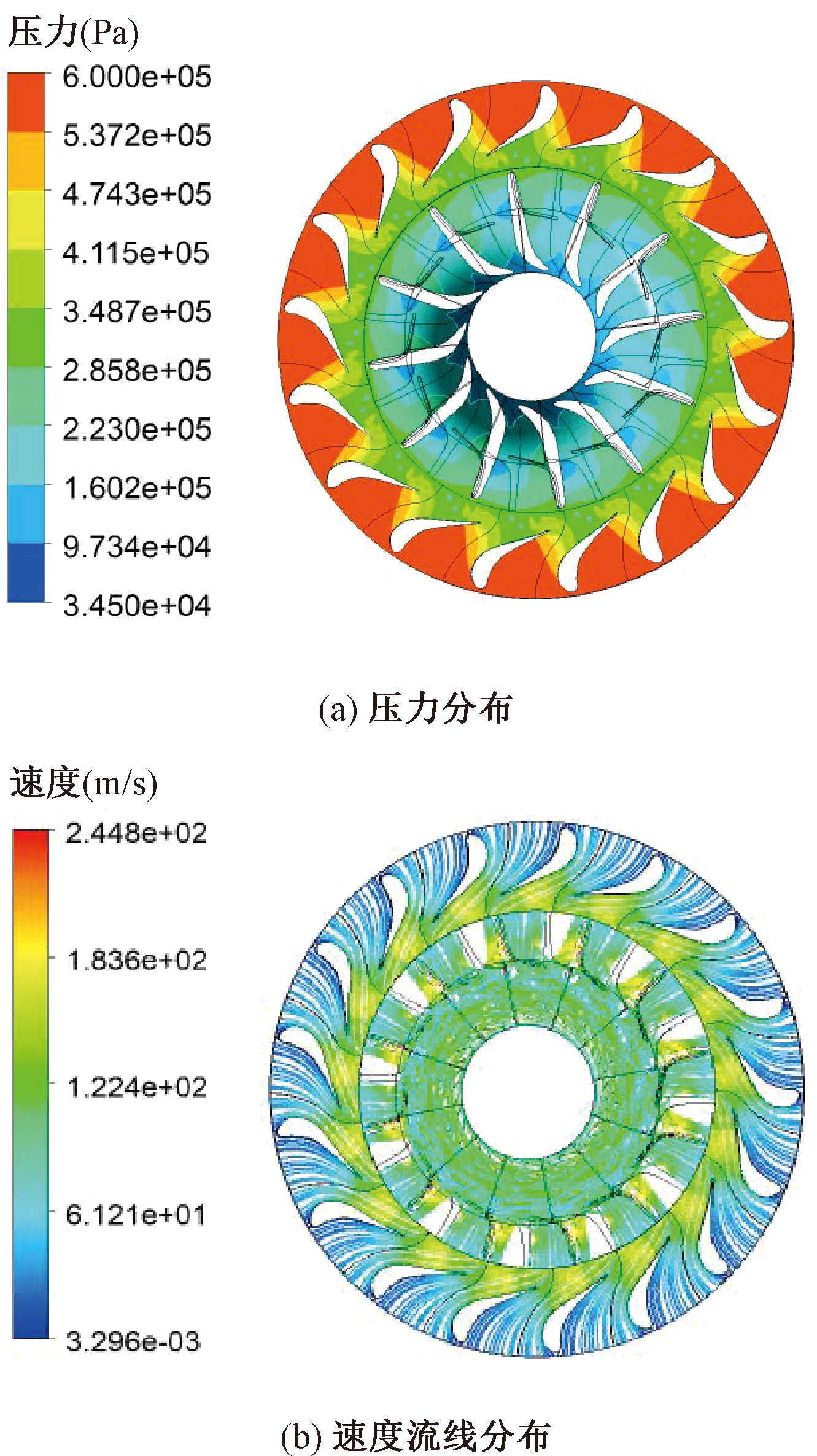
图3 50%叶高处压力和速度流线分布
Figure 3 Pressure and velocity streamline distribution of 50% blade heigh
2.2 非设计工况下的性能分析
为了预测透平模型在偏离设计工况下运行时的性能,对透平模型在非设计工况下进行了CFD模拟。其中,透平进口温度为343~383 K。考虑到设计的透平转速较高,实际转速不应超过设计值的10%,因此,转速比(实际转速与设计转速比值)在0.6~1.1。压力比(实际压力与设计压力比值)在2.5~4.5。
图4显示了向心透平的等熵效率随进口温度和转速的变化。从图4(a)可知,在所有的转速下,透平等熵效率皆是随着进口温度的升高先增大后减小。原因是随着进口温度的升高,透平进口参数和负荷均增加,导致流动损失增加,且转速越高,等熵效率的最大值对应的温度越高,这是因为透平的等熵焓降虽然会随着进口温度的升高而增大,但实际焓降会随着转速的提高而增大,因此等熵效率的最大值在转速较高时对应的温度也较高。随着转速的依次升高,等熵效率的最大值依次在353、358、368、378 K处取得,分别为59.18%、71.08%、77.6%、75.89%。在设计转速下,不同进口温度下的等熵效率最大差异为4.77%,表明透平能够有效处理温度变化。从图4(b)可以看出,当进口温度为343 K和363 K时,透平的等熵效率在设计转速下达到最大值,然后随着转速的提高,效率迅速下降,当进口温度为383 K时,等熵效率的最大值在1.05的转速比下获得。同时,随着进口温度的升高,等熵效率的峰值先增大后减小,并趋向于在较高的转速下获得。从图4可知,当以等熵效率为指标,透平在设计转速工作时,进口温度为368 K时,等熵效率达到最大,为77.6%,且当透平在0.9~1.1的转速比下工作时,等熵效率变化较小,此时进口温度应尽量控制在343~378 K。
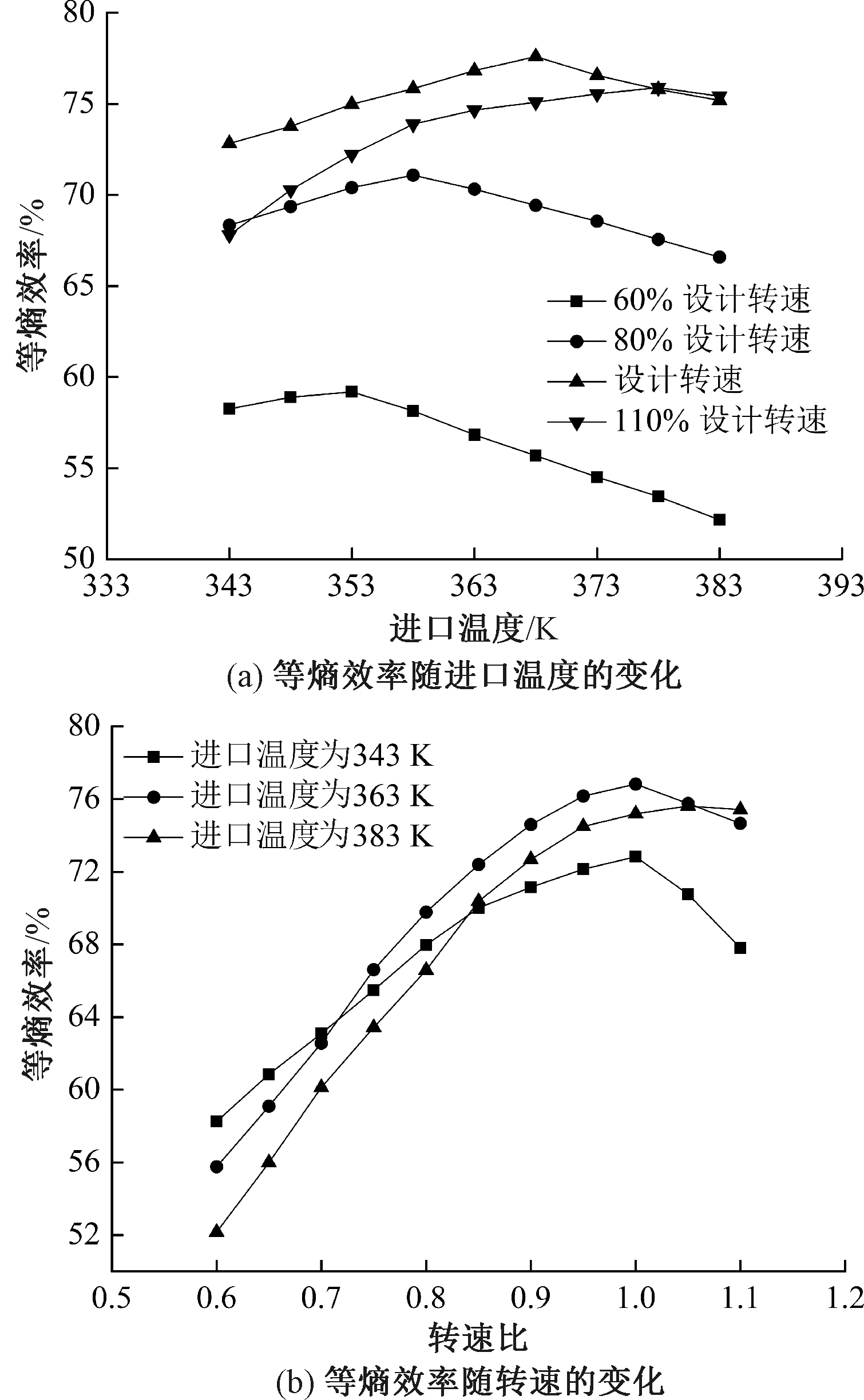
图4 等熵效率随进口温度和转速的变化
Figure 4 Variation of the isentropic efficiency with inlet temperature and rotational speed
图5为向心透平输出功率随进口温度和转速的变化。从图5(a)可知,在80%设计转速、设计转速和110%设计转速的条件下,输出功率随着透平进口温度的升高而增加,并且转速越高,输出功率增加速率越快。这是因为随着进口温度的升高,有机工质通过透平的焓降的增加起了主导作用。在60%设计转速下,进口温度达到353 K之前,输出功率的增加比较明显,然后随着入口温度继续升高,输出功率几乎不变,这是因为在转速较低的条件下,透平所能处理的焓降是有限的,因此当透平转速较低时,进口温度不应过高。图5(b)显示,对于所有的进口温度,透平的输出功率随着转速的升高先增加后减小。此外,随着进口温度的升高,最大输出功率趋向于向更高的转速移动。结合图5可知,当透平在0.9~1.1的转速比下工作时,透平的输出功率较高且随进口温度的变化比较平缓。
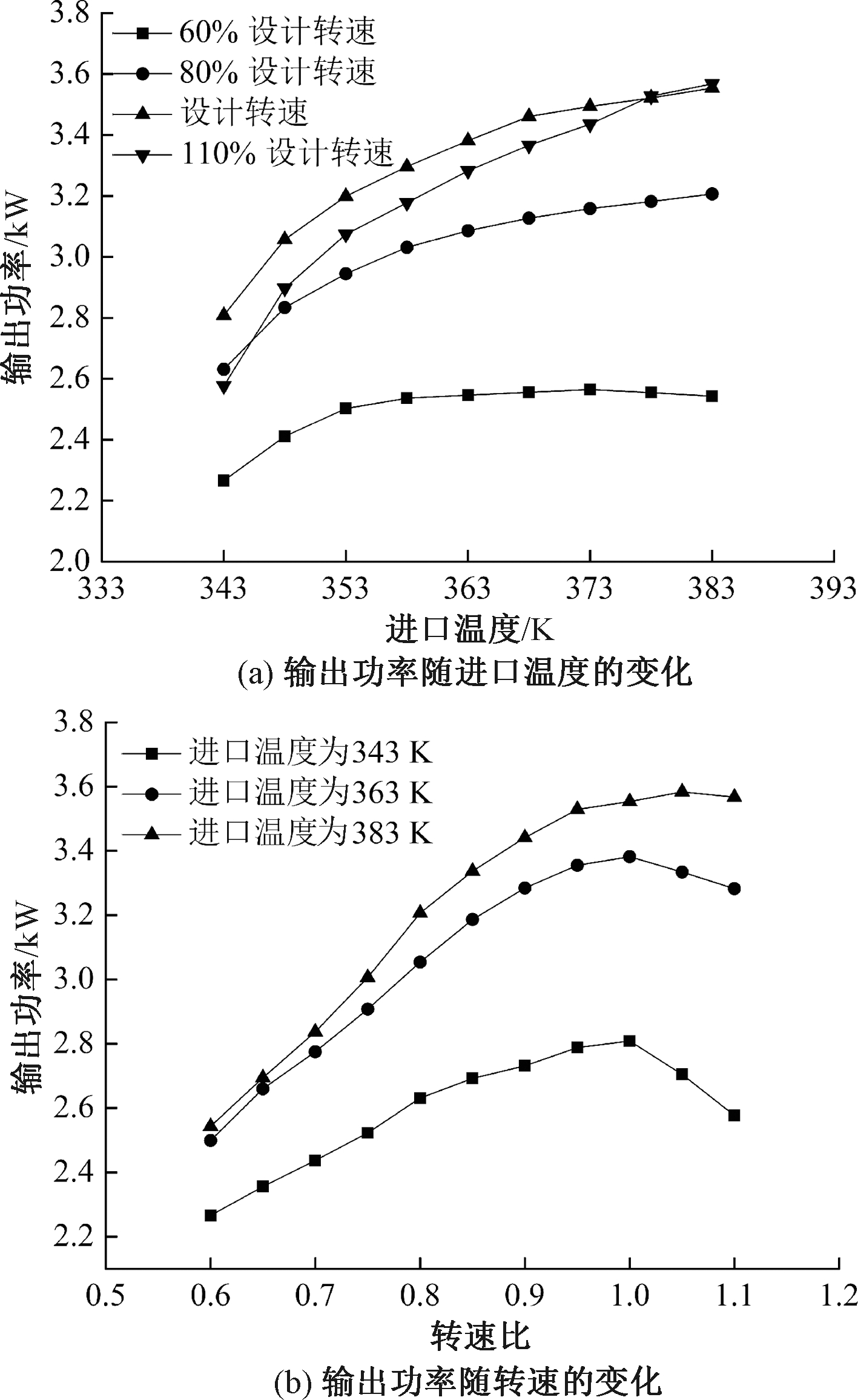
图5 输出功率随进口温度和转速的变化
Figure 5 Variation of the output power with inlet temperature and rotational speed
设计转速下等熵效率随压力比的变化如图6所示。由于R245fa在压力比为4.5时(进口压力为0.675 MPa)蒸发温度为347 K,因此透平进口温度分别取353、368、383 K。在3种进口温度下,等熵效率随压力比的变化规律相同,皆是随着压力比的增大逐渐减小。低压力比下等熵效率较高的原因是透平的摩擦损失较小。随着透平进口温度依次升高,等熵效率相对变化率分别为9.93%、11.65%、14.98%,即进口温度与设计值(343 K)越接近,等熵效率随压力比的变化越小。当进口温度为353 K时,不同转速下等熵效率与压力比的对应关系如图7所示。在所有的转速下,等熵效率随着压力比的增大而减小。同时,随着转速的逐渐升高,各等熵效率随压力比的相对变化率分别为20.76%、17.22%、13.38%、15.75%,即等熵效率的变化幅度随着实际转速与设计转速偏差的增大而增大,因此,透平在设计转速与设计进口温度下工作时能较好地处理压力比的变化。
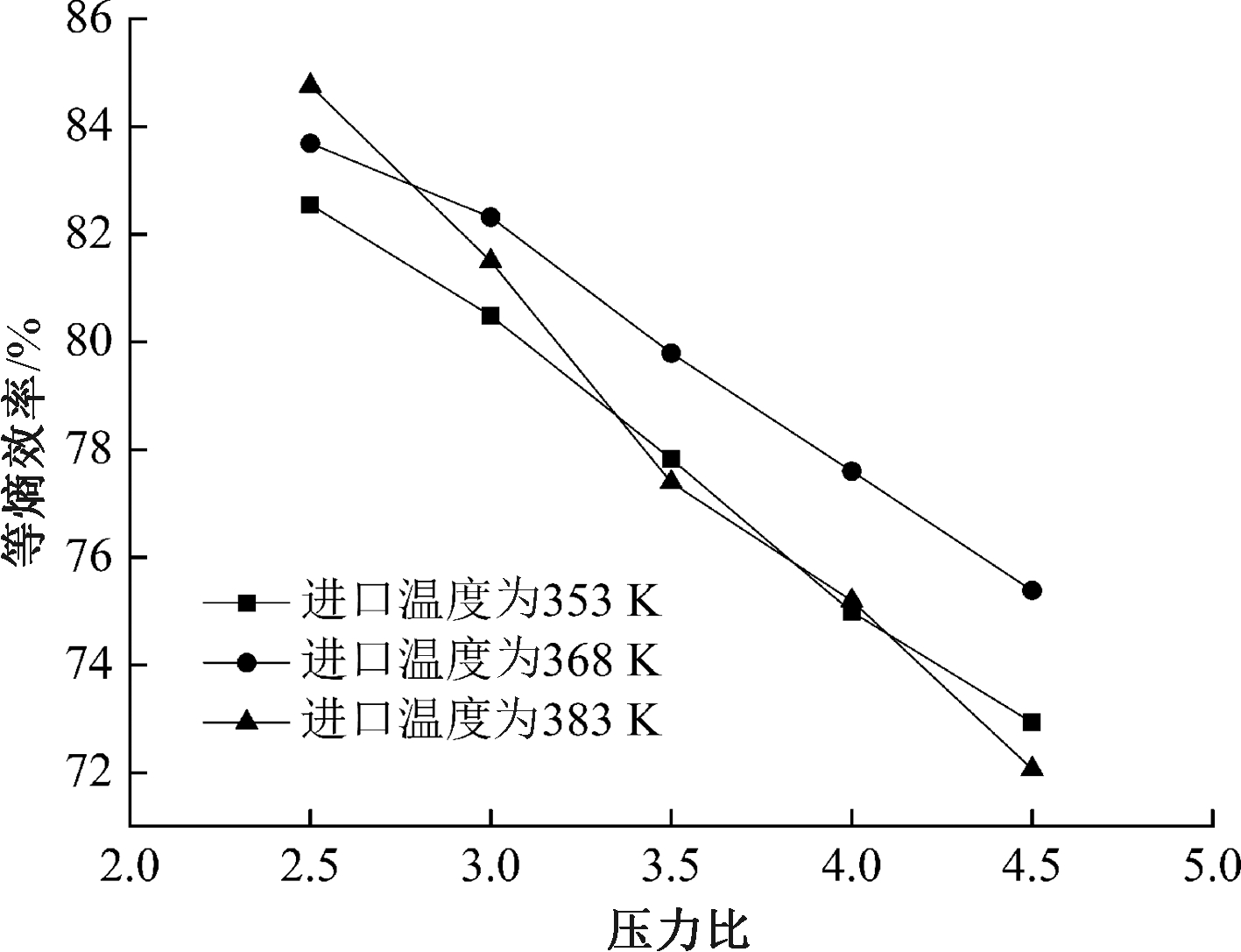
图6 设计转速下等熵效率随压力比的变化
Figure 6 Variation of the isentropic efficiency with pressure ratio for nominal rotational speed
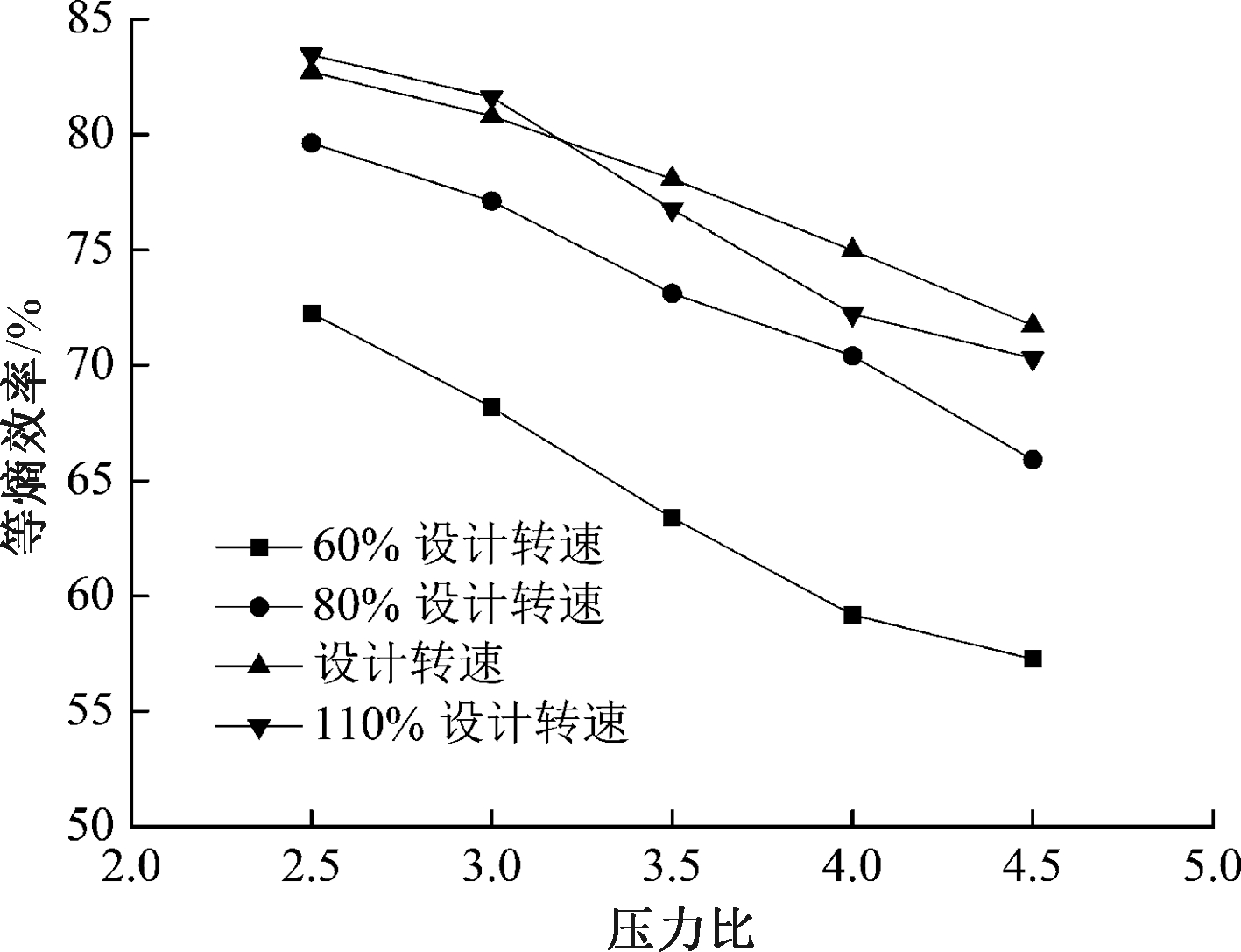
图7 入口温度为353 K时等熵效率随压力比的变化
Figure 7 Variation of the isentropic efficiency with pressure ratio for 353 K inlet temperature
2.3 基于实验数据的透平模型验证
基于向心透平的ORC发电实验台的系统结构图和照片分别如图8和图9所示。ORC实验台设备包括蒸发器、冷凝器、向心透平、发电机、工质泵、储罐、控制系统和数据采集仪器。在实验过程中,首先,通过安装在阀门进出口处的测量装置实时测量温度、压力和质量流量;其次,通过数据采集装置将这些数据采集到计算机中;最后,根据采集到的温度和压力参数,通过NIST发布的REFPROP 9.1获得工质的焓和熵。
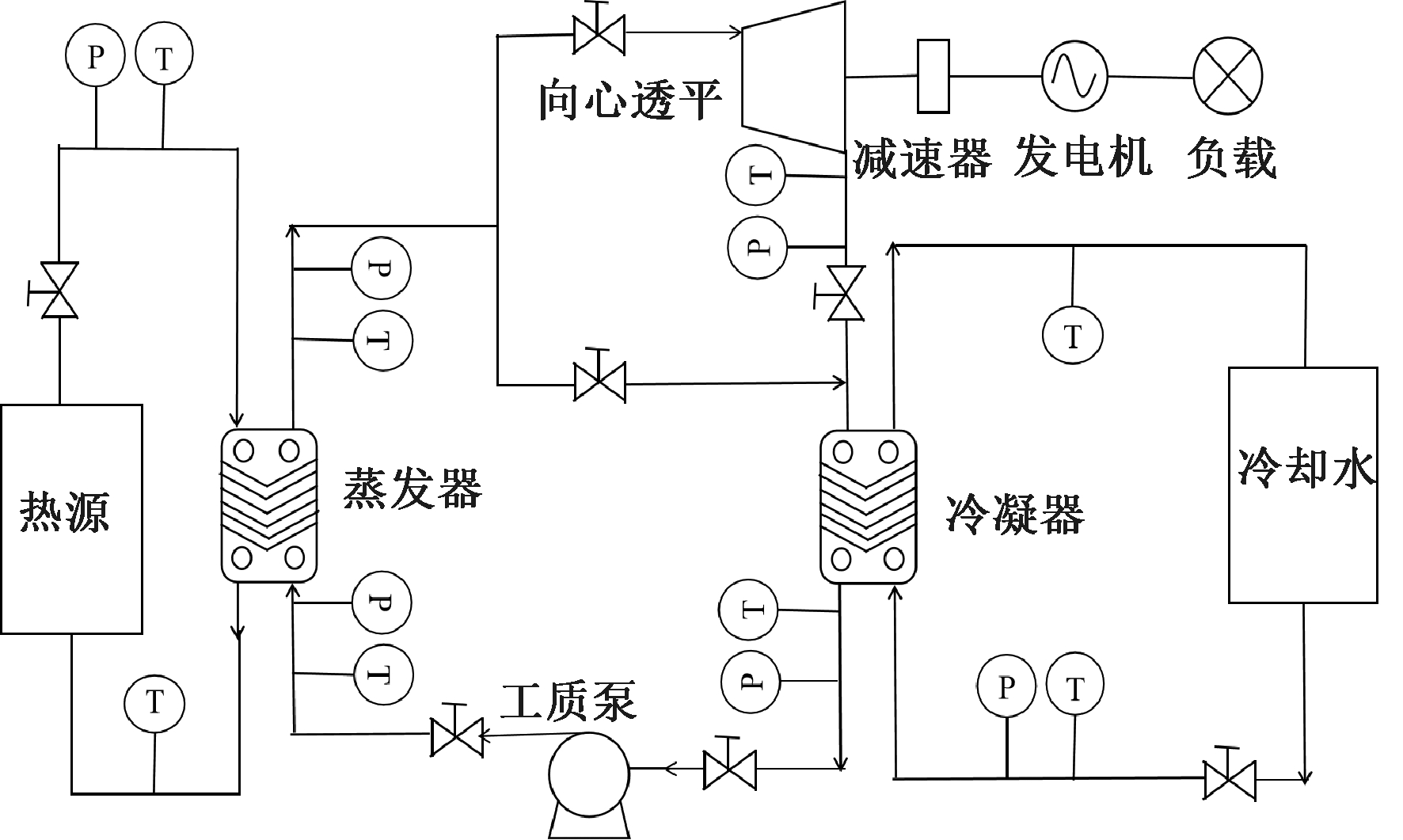
图8 ORC实验台结构示意图
Figure 8 Structural diagram of the ORC testing rig

图9 基于向心透平的ORC实验台照片
Figure 9 Photography of the ORC testing rig based on radial inflow turbine
将ORC发电系统运行过程中向心透平的部分进出口参数作为CFD模拟时的边界条件,以此来验证CFD模拟在预测非设计工况下向心透平性能的可靠性。图10(a)和10(b)分别是实验测量数据和CFD模拟结果中的压力比和等熵效率随工质质量流量的变化关系。从图10(a)可以看出,压力比随着质量流量的增加而增加,但由于实验过程中存在一些不可控因素,导致CFD计算结果与实验数据之间存在一定的误差,最大相对误差为5.58%。由图10(b)可知,在工质质量流量达到0.17 kg/s之前,等熵效率随着流量的增加而增加,之后随着质量流量的增加而降低,当工质质量流量为0.166 kg/s时,两者的等熵效率差异最大,为7.17%。图10(c)为实验和CFD模拟过程中向心透平转速对温降的影响。从图10(c)可以看出,在转速达到设计值的80%之前,温降随着转速的增加而增加,后随着转速的继续增加,温降与转速不再是简单的线性关系,且CFD计算结果与实验数据的变化趋势也有所不同。整体来说,通过CFD计算得到的温降大于实验得到的温降,其原因可能是在数值模拟中,透平的各边界设置为绝热壁面,而在实验过程中透平内部不可能出现绝热的情况。通过CFD计算得到的温降与实验测试数据的最大相对误差为9.42%。
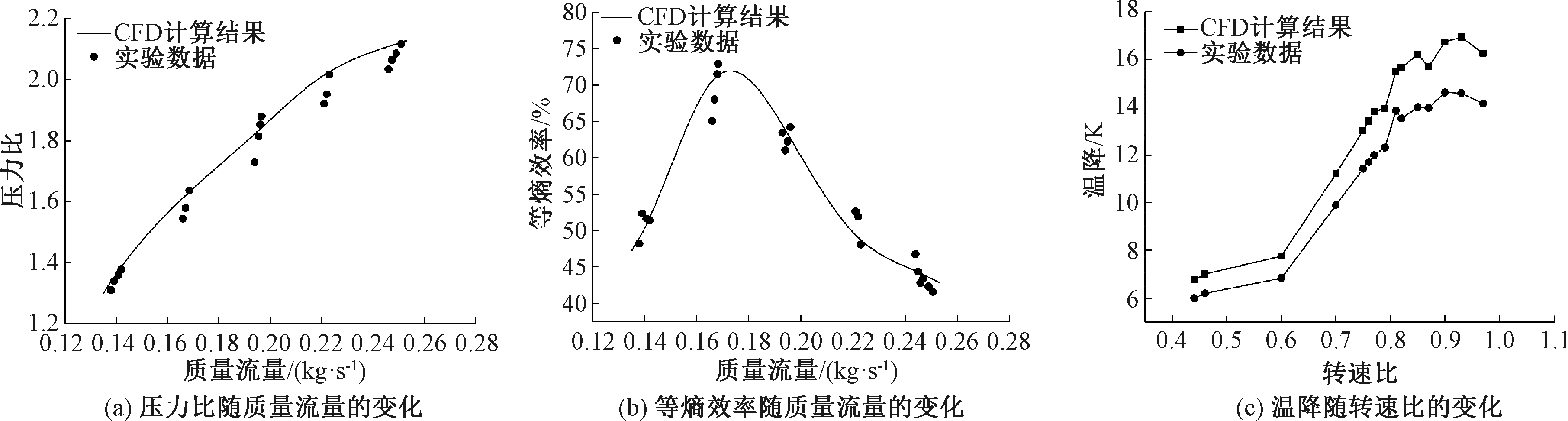
图10 基于实验数据的透平模型验证
Figure 10 Turbine model validation based on experimental data
3 结论
(1)以R245fa为工质,完成了压力比为4的向心透平的一维设计,并通过CFD模拟对其性能进行了预测。结果表明,在设计工况下,透平内部压力分布比较均匀,没有明显的涡流。此外,CFD计算结果与一维设计参数吻合较好,两者的等熵效率和输出功率仅分别相差0.36%和4.85%。
(2)通过CFD模拟发现在转子入口处存在局部高速区域,这将会导致工质的流动摩擦损失增大,后期可以通过优化转子叶片的叶型来改善这种现象,提高透平效率。
(3)研究了进口温度、转速和压力比对透平性能的影响。结果表明,在设计转速下,当进口温度为368 K时透平等熵效率达到最大,为77.6%;透平输出功率随进口温度的升高而增大,当透平在0.9~1.1的转速比下运行时,随着进口温变化,等熵效率的变化很小且具有较高的输出功率;透平在设计转速和设计进口温度下运行时能较好地处理压力比的变化。
(4)以压力比、等熵效率和温降作为评价指标,将实验数据与CFD计算结果进行比较,其最大相对误差分别为5.58%、7.17%、9.42%,证明了CFD模拟对透平性能预测的可靠性。
[1] 魏新利, 李明辉, 马新灵, 等. 有机朗肯循环系统的实验研究和性能分析[J]. 郑州大学学报(工学版), 2016, 37(2): 73-76.
WEI X L, LI M H, MA X L, et al. Experimental investigation and performance analysis of organic Rankine cycle system[J]. Journal of Zhengzhou university (engineering science), 2016, 37(2): 73-76.
[2] EYERER S, DAWO F B, WIELAND C, et al. Advanced ORC architecture for geothermal combined heat and power generation[J]. Energy, 2020, 205: 117967.
[3] 魏新利, 邱志明, 马新灵, 等. 向心透平导向叶栅的结构优 化[J]. 郑州大学学报(工学版), 2014, 35(1): 46-50.
WEI X L, QIU Z M, MA X L, et al. The structural optimization of guide vane of radial-inward-flow turbine[J]. Journal of Zhengzhou university (engineering science), 2014, 35(1): 46-50.
[4] RAHBAR K, MAHMOUD S, AL-DADAH R K, et al. Review of organic Rankine cycle for small-scale applications[J]. Energy conversion and management, 2017, 134: 135-155.
[5] LI P, HAN Z H, JIA X Q, et al. Analysis and comparison on thermodynamic and economic performances of an organic Rankine cycle with constant and one-dimensional dynamic turbine efficiency[J]. Energy conversion and management, 2019, 180: 665-679.
[6] DAABO A M, MAHMOUD S, AL-DADAH R K, et al. Numerical analysis of small scale axial and radial turbines for solar powered Brayton cycle application[J]. Applied thermal engineering, 2017, 120: 672-693.
[7] SAURET E, GU Y T. Three-dimensional off-design numerical analysis of an organic Rankine cycle radial-inflow turbine[J]. Applied energy, 2014, 135: 202-211.
[8] XIA J X, WANG J F, WANG H Y, et al. Three-dimensional performance analysis of a radial-inflow turbine for an organic Rankine cycle driven by low grade heat source[J]. Energy conversion and management, 2018, 169: 22-33.
[9] DAABO A M, AL JUBORI A, MAHMOUD S, et al. Development of three-dimensional optimization of a small-scale radial turbine for solar powered Brayton cycle application[J]. Applied thermal engineering, 2017, 111: 718-733.
[10] SONG J, GU C W, REN X D. Influence of the radial-inflow turbine efficiency prediction on the design and analysis of the organic Rankine cycle (ORC) system[J]. Energy conversion and management, 2016, 123: 308-316.
[11] 李燕生,陆桂林. 向心透平与离心压气机[M]. 北京: 机械工业出版社, 1987.
LI Y S, LU G L. Radial inflow turtbine and centrifugal compressor [M]. Beijing: China Machine Press, 1987.
[12] ROCHA P A C, ROCHA H H B, CARNEIRO F O M, et al. K-ω SST (shear stress transport) turbulence model calibration: a case study on a small scale horizontal axis wind turbine[J]. Energy, 2014, 65: 412-418.